Abstract
A timelike () constant axis ruled surface in (Minkowski 3-space), as determined by its ruling, forms a constant dual angle with its Disteli-axis (striction axis or curvature axis). In this article, we employ the symmetry through point geometry of Lorentzian dual curves and the line geometry of ruled surfaces. This produces the capability to expound a set of curvature functions that specify the local configurations of ruled surfaces. Then, we gain some new constant axis ruled surfaces in Lorentzian line space and their geometrical illustrations. Further, we also earn several organizations among a constant axis ruled surface and its striction curve.
MSC:
53A04; 53A05; 53A17
1. Introduction
In the context of kinematics, the tracks of a directed line linked with a mobile rigid body is normally a ruled surface (). The geometry of has been exceedingly utilized in computer-aided manufacturing (), computer-aided geometric design (), and geometric modeling [1,2,3,4,5]. Nowadays, the assets of ruled surfaces and their applications have been researched in Euclidean and non-Euclidean spaces (see, e.g., [6,7,8,9,10,11,12,13]). One of the popularization comfortable manners to addressing the movement of line space appears to discover an attachment with this space and dual numbers. From the E. Study map in dual number () algebra, the family of all directed lines in Euclidean 3-space is immediately related to the family of points on the dual unit sphere () in the dual 3-space [1,2,3]. Supplementary allocations on the pivotal crucial annotations of the E. Study map and one-parameter dual spherical locomotion were initiated in [4,5,6,7,8].
In Minkowski 3-space, , the addressing of is more distant and engaging than the Euclidean case as the Lorentzian metric function can be non-positive, positive, or zero, whereas the Euclidean metric function can only be positive-definite. Then, if we have as an alternate of , the E. Study map can be given as follows: The family of all timelike () (spacelike )) directed lines in is immediately related to the family of points on the hyperbolic (Lorentzian ) in the Lorentzian dual 3-space . It proceeds that an curve on matches a at . Similarly, an () curve on matches () at . Due to their dealings with engineering and physical sciences in Minkowski space, senior geometers and engineers have researched and acquired extensive ownership of ruled surfaces (see [6,7,8,9,10,11,12,13]).
However, to our knowledge, there is no work on the construction of a constant axis family in Minkowski 3-space . This work intends to pinpoint a set of Lorentzian invariants that elucidate the local shape of a constant axis ruled surface family. As a result, the Hamilton and Mannheim formulae of surfaces theories are accomplished in Lorentzian line-space and their geometrical clarifications are evaluated. Further, we also elucidate the kinematic geometry of a cylindroid created by the Disteli-axis. Subsequently, we explore some situations that command private constant axis ruled surface families, such as the Archimedes helicoid and developable surfaces.
2. Basic Concepts
In this section, we allocate a concise synopsis of the theory, and Lorentzian vectors [11,12,13]. An oriented (non-null) line in may be offered by a point and a normalized vector of , that is, . To earn ingredients for , one makes the moment vector in regard to the origin point in . If is exchanged by a point , on , this leads to being independent of on . The two vectors and are not independent of one another; they fulfill the following mutual relations:
The six components of and are named the normalized Plücker coordinates of the line . Hence, the two non-null vectors and regulate the oriented (non-null)
If and are real numbers, the couple is named a , such that and . This is in actuality very close to the notion of a complex number. Then, the set
associated with the Lorentzian metric
forms the so-named dual Lorentzian 3-space . Thus, a point has dual coordinates . If is a non-null dual vector, the norm of is elucidated by
If is an vector, we possess
If is a vector, we possess
Therefore, is an () dual unit vector () if (). For any two vectors, and of , the vector product is
where , , is the canonical basis of . The hyperbolic and Lorentzian , respectively, are
and
It is evident that
It follows that Equations (1) and (2) are congruous. Due to this we include the following map (E. Study map). The ring-shaped hyperboloid is in bijection with the family of lines, the common asymptotic cone is in bijection with the family of null lines, and the oval-shaped hyperboloid is in bijection with the family of lines (see Figure 1).
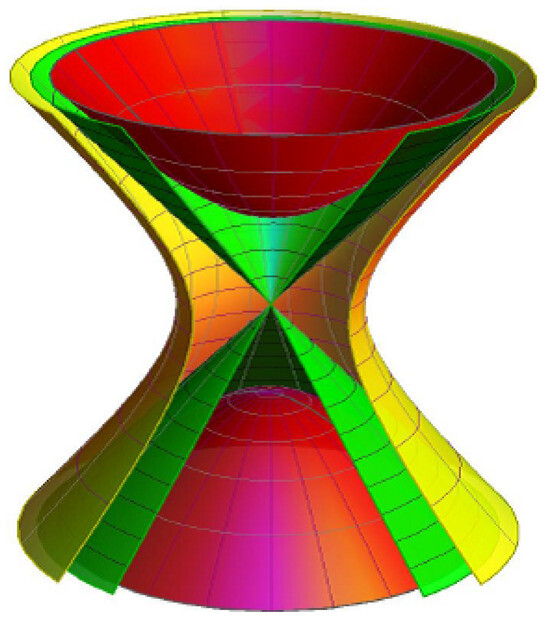
Figure 1.
The hyperbolic and Lorentzian spheres.
In the E. Study map, a differentiable curve defines a in . Comparably, a regular curve defines a or in . is identified with the rulings of the surface.
3. Main Results
In this section, we address the by the E. Study map. Therefore, a differentiable curve
demonstrate a (() for short) in Minkowski 3-space . From spherical kinematics, the Blaschke frame () is
where
The lines of the intersect at the striction curve () , which is the adjacent point through two rulings and . is the central normal to () at the striction point. In the context of spherical kinematics, the locomotion of the is a rotation around the Darboux vector , that is,
where , and
are the Blaschke invariants of . The tangent of the is
The Lorentzian functions of () are
The expositions of , , and are as follows: is the geodesic curvature of the spherical curve ; is the angle through the tangent of the and the ruling of (); and is its distribution parameter at the ruling. Thus, a can be attained as
3.1. Hamilton and Mannheim Formulae
Through the locomotion of the , all kinematic–geometric features can be deduced with the Darboux vector . Therefore, from the presumption that , we designate the Disteli-axis () as
Then, Equation (5) can be formed as
Here, is the angular speed of the movement;
Therefore, the is the instantaneous screw-axis of the .
Proposition 1.
The pitch of the movement around the is
In fact, we find the following:
- (1)
- can be distinguished as .
- (2)
- If is a point on the , then
If the - movement is a pure turnover, that is, , then
whereas if and , then is a line. However, if , that is, the - movement is a pure translational, we let e for a random with . In another form, can have random volition, too.
Let be the radii of the curvature between and (see Figure 2). Then,
where
From the Equations (7), (12), and (16), we attain
Equation (17) is a Lorentzian version of the Hamilton and Mannheim formulae (compared with [1,2,3]).
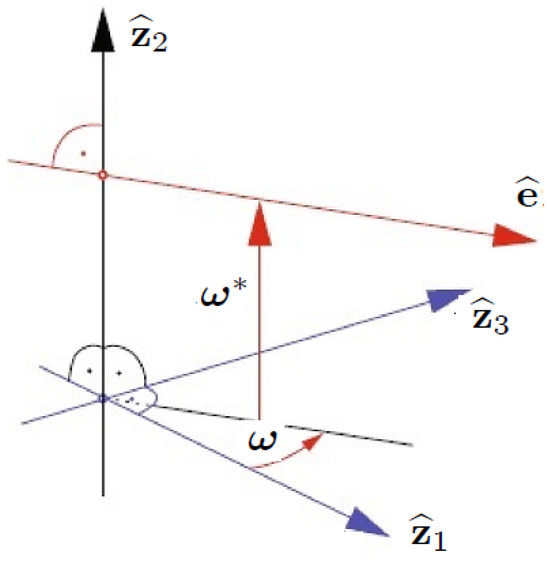
Figure 2.
.
3.2. Timelike Cylindroid
We now clarify and explore the Hamilton and Mannheim formulae. The surface clarified by represents a cylindroid; let be selected along the axis of a fixed Lorentzian frame and the station of be distinguished by angle and distance on the non-negative direction of the axis. The vectors and can be marked with the x- and z-axes, respectively (Figure 2). Therefore, in view of Equations (14), (16), and (18), we locate
For , and , the cylindroid is as shown in Figure 3. For the limits of , the algebraic equation is
Note that it is a third-order polynomial at the coordinates , and z. Also, we have
So, the two limits of are demonstrated by
which represents two isotropic torsal planes, each of them containing one isotropic torsal line .
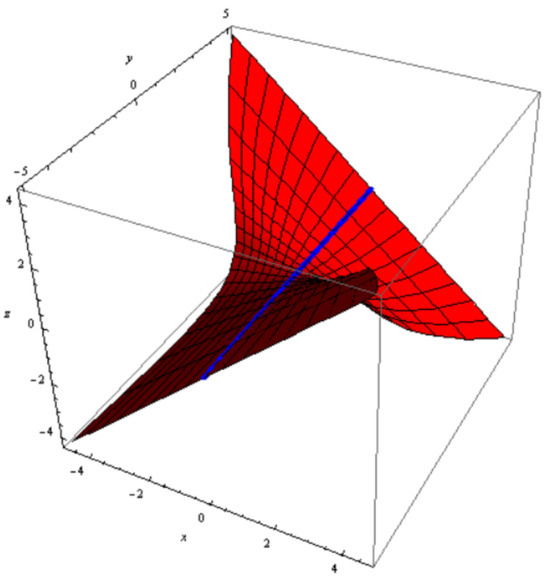
Figure 3.
cylindroid.
In Equation (18), is not-periodic. This means that is not a closed . Further, it mostly has two extreme values: the Lorentzian functions and . This shows that the vectors and are the principal axes of the cylindroid. Moreover, the geometric assets of the cylindroid are as follows:
- A:
- If , that is, the - movement is not a pure turnover, then there are two isotropic rulings crossing through the point .
- B:
- If , that is, the - movement is a pure turnover, then there are two isotropic lines , detected by
3.3. Timelike Constant Axis Ruled Surface Family
From now on, when we say () is a constant axis , we signify that all the rulings of () have a constant with respect to the .
Let be the dual arc length of . Then,
From the Equations (4) and (23), we have
where is the geodesic curvature; , , and are the Lorentzian functions of . The is
Then,
is a in the Minkowski 3-space .
Actually, it is essential to possess the curvature and the torsion . Therefore, the Serret–Frenet frame () of is specified by . Then, the is shown by a turnover of (,) as
where
Comparably, we possess
where
Here, and are the radii of curvature and the radii of torsion of , respectively.
Height Functions
In harmonization with [14], a point will be entitled to a evolute of the , for all , such that but . Here, signals the k-th derivatives of with respect to . For the first evolute of , we have and . So, is at least an evolute of .
We are now heading a dual function , by . We say that is a height function of . We employ for any fixed point . Hence, we offer the following.
Proposition 2.
Under the last suppositions, the below holds:
- i.
- will be invariant in the first evaluation if ,, that is,for some dual numbers and .
- ii.
- will be invariant in the second evaluation if is an evolute of , that is,
- iii.
- will be invariant in the third evaluation if is an evolute of , that is,
- iv.
- will be invariant in the fourth evaluation if is an evolute of , that is,
Proof.
For the first derivation of we obtain
So, we obtain
for some dual numbers and , the outcome is evident.
In view of Proposition 2, we possess the following:
(a) The osculating circle of is attained by
which are identified via the condition that the osculating circle must have osculate of at least the third order at if .
(b) The osculating circle and the curve are at least the fourth order at if and .
In this mode, by considering the evolutes of , we can obtain a concatenation of evolutes , ,..., . The properties and the joint relationships among these evolutes and their involutes are extremely interestings problems. For the model, it is easy to show that when and , is standing at and is immutable relative to . In this issue, the is invariant up to the second order, and the line proceeds over it with immutable pitch. Thus, the () with immutable is formed by line existing at an immutable distance and fixed angle with respect to the , that is,
where .
Theorem 1.
A non-developable is a constant axis if constant and constant.
3.4. Construction of the Constant Axis Family
In this subsection, we make a construction of the constant axis family. In view of Equation (30) and since is constant, we find the ODE, . Via several algebraic manipulations, the general solution of this equation is
Here, , where and ; where and are constants. Then,
and
In view of Equations (31) and (37), we acquire
Then,
From the real and dual parts of Equation (35), respecitvely, we have
and
Let be a point on . From , we acquire the arrangement of linear equations in and :
The matrix of coefficients of unknowns, and , is
It is evident that = 2, where (p is an integer) and . The of the augmented matrix,
is two. Then, this set has infinitely numerous solutions displaced with
Since is assumed at random, then we may let . In this situation, Equation (40) reads as
Then,
By considering Equation (27) with Equations (40) and (42), we achieve
where is located by Equation (39). and can control the shape of . For some values of and , we confer some epitomes for , where we contemplate , , and . Hence, any two of the constant axis family are reciprocal of one another.
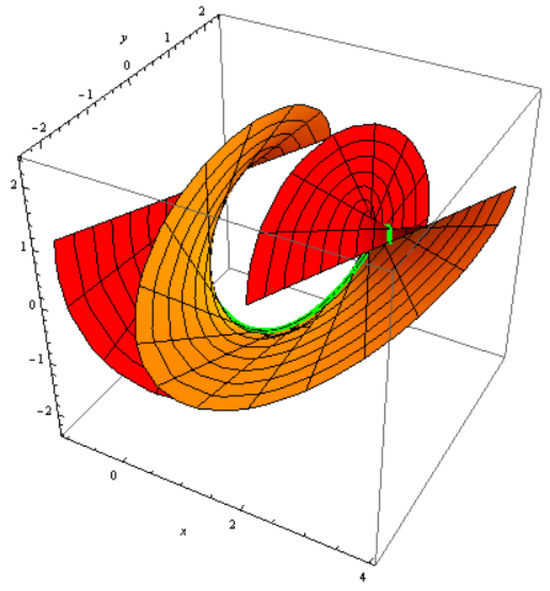
Figure 4.
Archimedes helicoid with and .
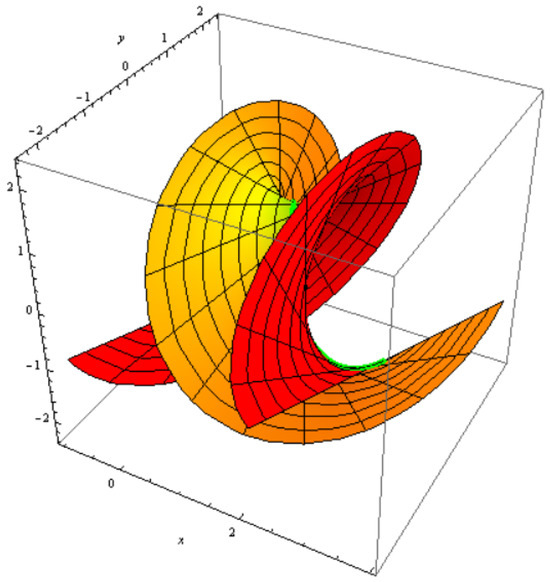
Figure 5.
Archimedes helicoid with and .
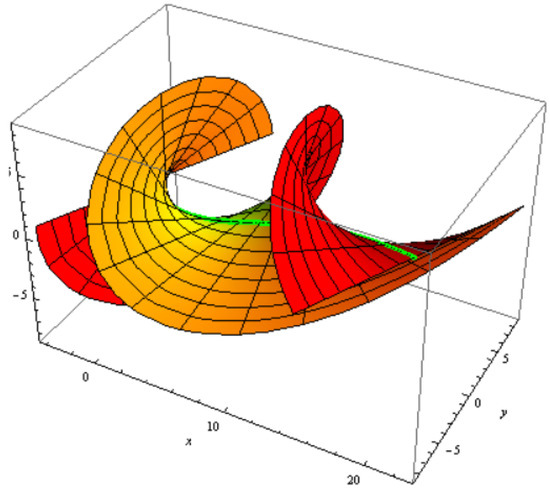
Figure 6.
Archimedes helicoid with and .
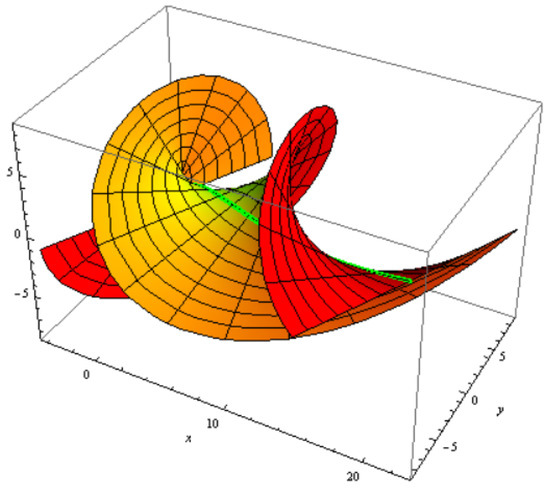
Figure 7.
Archimedes helicoid with and .
3.5. Organizations among a Constant Axis and Its Striction Curve
The major geometrical organizations of a constant axis and its striction curve can be described as follows:
(a) Since , then is a tangential developable. In this situation, from Equations (39) and (43), we attain
and
Since
then the is of type curve of (). The curvature and the torsion , respectively, are
It is clear that is a cylindrical helix with the as the cylindrical axis. Furthermore, we possess
which is a family of two-parameter tangential surfaces; for , , , and (Figure 8 and Figure 9).
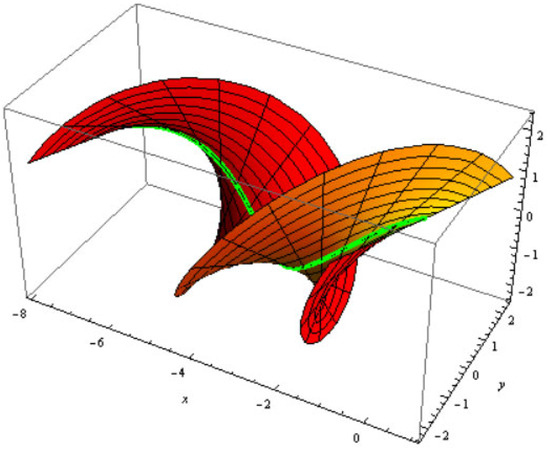
Figure 8.
tangential surface with and
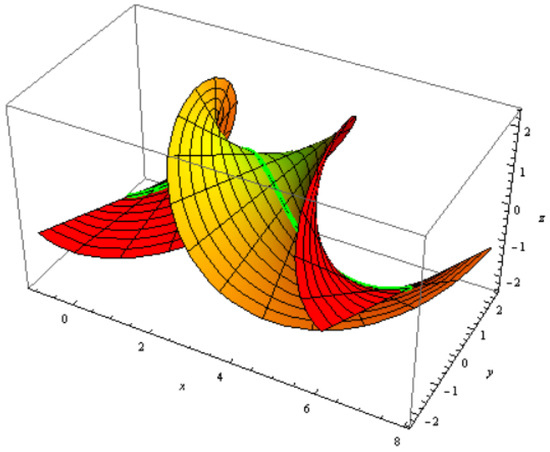
Figure 9.
tangential surface with and
(b) Since , then is a binormal surface. From Equation (39), we attain
and then Equation (42) is
In a similar manner, we find
Thus, the is a type of curve of (). The curvature and the torsion , respectively, are
It is clear that is a cylindrical helix with the as the cylindrical axis. Further, we have
which is a family of two-parameter binormal surfaces; for , , , and (Figure 10 and Figure 11).
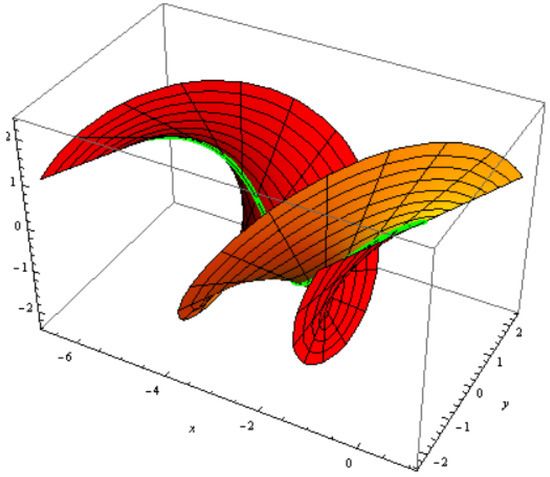
Figure 10.
binormal surface with and
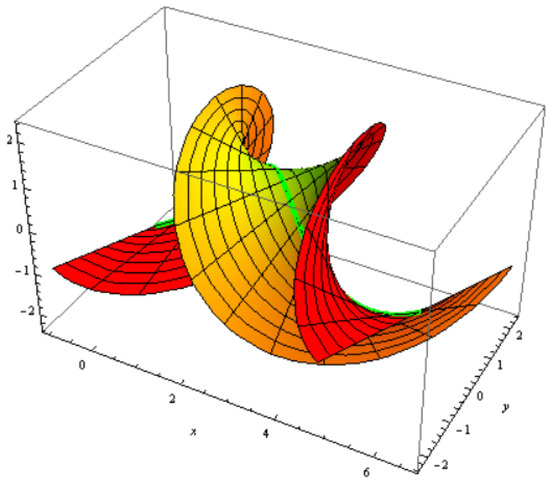
Figure 11.
binormal surface with and
(c) Since is a cone, that is, , and , then
or
This leads to and . Then, the is locally isometric to
which is a one-parameter family of cones for , , and (Figure 12).
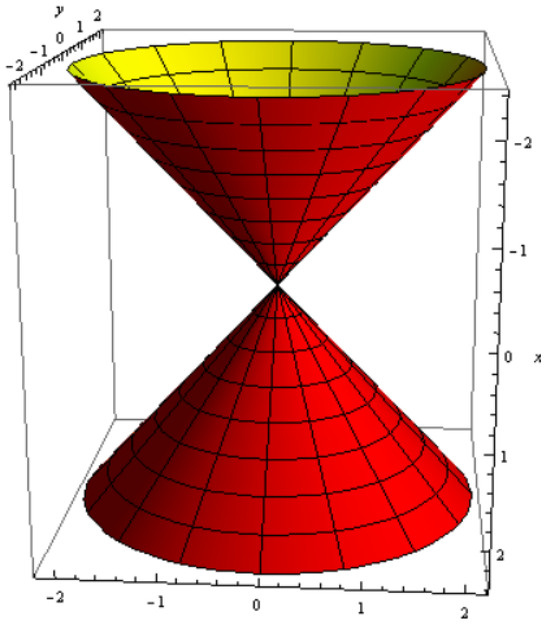
Figure 12.
cone.
(d) A cylindrical surface is produced by the one-parameter locomotion of an oriented line that maintains a fixed direction in space. We found previously from Equation (24) that, in the case of , all rulings are parallel and is a cylindrical surface. In this case, the is not specified since there is no discerned central point. Then, at a cylindrical surface, we performed it in the other direction: we appointed any transverse -curve: on as , that is, the orthogonal section realized by the equation . For a cylindrical surface, any two infinitesimally spaced rulings and are parallel to each other, so (replace with for short) is the arc length of . In this manner and by definition, is continuously orthogonal to and its end point traces out a planar curve, that is, . This means that the of the cylindrical surface is unique for an orthogonal section. Differentiating and noting that is steady vector gives ; ), which designates that the tangent vector of the is orthogonal to the rulings. However, the limit position of the mutual orthogonal to any two infinitesimally spaced rulings and is undefined, that is, the central tangent does not exist in that sense. It is feasible to explain the as follows. The central tangent is explained as
Note that the central tangent is tangent to the . Also, the central normal is specified by
Further, we can find the variation in the following form:
To derive the variation of , we first locate the second derivative of the striction curve. A variation of gives . As we mentioned above, the is planar and constantly columnar to the constant ruling of the cylindrical surface. From the theory of planar curve, the second derivative may be reported by , where is the curvature function of . Therefore, we acquire
So, we acquire
Then,
where . Therefore,
Furthermore, we attain
Hence, the of cylindrical surface is
From Equations (28) and (55), we attain and . Then,
which clarifies a family of two-parameters of cylinders, for , , and (Figure 13).
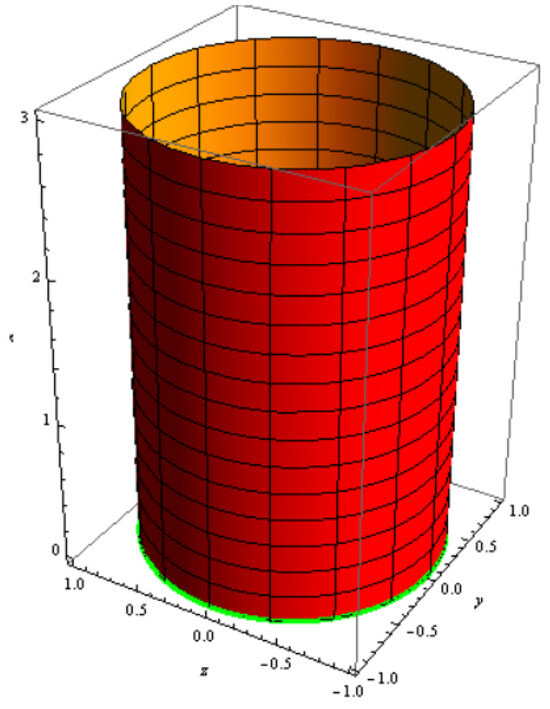
Figure 13.
cylinder with
4. Conclusions
In this paper, based on the constant angle properties of surfaces and using the Blaschke framework, we study and classify ruled surfaces in Minkowski 3-space . Then, we gain some new constant axis ruled surfaces in Lorentzian line space and their geometrical illustrations. We also earn several organizations among a constant axis ruled surface and its striction curve. For future research, we will deal with integrating the study of singularity theory and submanifold theory, as in [15,16,17], with the consequences of this study being to search in a novel manner for further theorems on this topic related to symmetric possessions.
Author Contributions
Conceptualization, R.A.A.-B. and A.A.A.; methodology, R.A.A.-B. and A.A.A.; software, R.A.A.-B. and A.A.A.; validation, R.A.A.-B.; formal analysis, R.A.A.-B. and A.A.A.; investigation, R.A.A.-B. and A.A.A.; resources, R.A.A.-B.; data curation, R.A.A.-B. and A.A.A.; writing—original draft preparation, R.A.A.-B. and A.A.A.; writing—review and editing, A.A.A.; visualization, R.A.A.-B. and A.A.A.; supervision, R.A.A.-B.; project administration, R.A.A.-B.; funding acquisition, A.A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2024R337).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to acknowledge Princess Nourah bint Abdulrahman University Researchers Supporting Project, number (PNURSP2024R337), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, we would like to thank the reviewers for taking the necessary time and effort to review the manuscript. We sincerely appreciate all your valuable comments and suggestions, which helped us improve the quality of the manuscript.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of this paper.
References
- Bottema, O.; Roth, B. Theoretical Kinematics; North-Holland Press: New York, NY, USA, 1979. [Google Scholar]
- Karger, A.; Novak, J. Space Kinematics and Lie Groups; Gordon and Breach Science Publishers: New York, NY, USA, 1985. [Google Scholar]
- Pottman, H.; Wallner, J. Computational Line Geometry; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Köse, Ö.; Sarıoglu, C.C.; Karabey, B.; Karakılıç, I. Kinematic differential geometry of a rigid body in spatial motion using dual vector calculus: Part-II. Appl. Math. 2006, 182, 333–358. [Google Scholar] [CrossRef]
- Jafari, M.; Yayli, Y. The E. Study map of circule on dual elliptical unit sphere. BEU J. Sci. 2015, 4, 12–20. [Google Scholar]
- Turhan, T.; Ayyıldız, N. A study on geometry of spatial kinematics in Lorentzian space. Süleyman Demirel Üniversitesi Fen Bilimleri Enstitüsü Dergisi 2017, 21, 808–811. [Google Scholar] [CrossRef]
- Ali, A.T. A constant angle ruled surfaces. Int. J. Geom. 2018, 7, 69–80. [Google Scholar]
- Alluhaibi, N.; Abdel-Baky, R.A. On the one-parameter Lorentzian spatial motions. Int. Geom. Methods Mod. Phys. 2019, 16, 1950197. [Google Scholar] [CrossRef]
- Gilani, S.M.; Abazari, N.; Yayli, Y. Characterizations of dual curves and dual focal curves in dual Lorentzian space D13. Turk. J. Math. 2020, 44, 1561–1577. [Google Scholar] [CrossRef]
- Aslan, M.C.; Sekerci, G.A. Dual curves associated with the Bonnet ruled surfaces. Int. Geom. Methods Mod. Phys. 2020, 17, 2050204. [Google Scholar] [CrossRef]
- Alluhaibi, N.S.; Abdel-Baky, R.A. Kinematic geometry of timelike ruled surfaces in Minkowski 3-space E13. Symmetry 2022, 14, 749. [Google Scholar] [CrossRef]
- Mofarreh, F. Timelike ruled and developable surfaces in Minkowski 3-space E13. Front. Phys. 2022, 10, 838957. [Google Scholar] [CrossRef]
- Abdel-Baky, R.A.; Unluturk, Y. A new construction of timelike ruled surfaces with stationarfy Disteli-axis. Honam Math. J. 2020, 42, 551–568. [Google Scholar]
- Bruce, J.W.; Giblin, P.J. Curves and Singularities, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Li, Y.L.; Zhu, Y.S.; Sun, Q.Y. Singularities and dualities of pedal curves in pseudo-hyperbolic and de Sitter space. Int. J. Geom. Methods Mod. Phys. 2021, 18, 2150008. [Google Scholar] [CrossRef]
- Li, Y.L.; Nazra, S.; Abdel-Baky, R.A. Singularities Properties of timelike sweeping surface in Minkowski 3-Space. Symmetry 2022, 14, 1996. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, L.; Li, P.; Chang, Y. Singularities of Osculating Developable Surfaces of Timelike Surfaces along Curves. Symmetry 2022, 14, 2251. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).