The Schwarzschild–de Sitter Metric of Nonlocal $\sqrt{\mathit{d}\mathit{S}}$ Gravity

Abstract

It is already known that a simple nonlocal de Sitter gravity model, which we denote as $\sqrt{dS}$ gravity, contains an exact vacuum cosmological solution that mimics dark energy and dark matter and is in very good agreement with the standard model of cosmology. This success of $\sqrt{dS}$ gravity motivated us to investigate how it works at a lower-than-cosmic scale—galactic and the solar system. This paper contains our investigation of the corresponding Schwarzschild–de Sitter metric of the $\sqrt{dS}$ gravity model. To obtain an exact solution, it is necessary to solve the corresponding nonlinear differential equation, which is a very complicated and difficult problem. What we obtained is a solution to a linearized equation, which is related to space metrics far from the massive body, where the gravitational field is weak. The obtained approximate solution is of particular interest for examining the possible role of nonlocal de Sitter gravity $\sqrt{dS}$ in describing the effects in galactic dynamics that are usually attributed to dark matter. This solution was tested on the Milky Way and the spiral galaxy M33 and is in good agreement with observational measurements.

1. Introduction

The general theory of relativity (GR) [1] is considered as one of the most successful and beautiful physical theories. It is worth mentioning the following main predictions and successful confirmations: deflection of light near the Sun, black holes, gravitational light redshift, lensing, and gravitational waves; see, e.g., [2].

In the standard model of cosmology (SMC) [3], also known as the ΛCDM model, GR is adopted as the theory of gravitation at all space–time scales, from the solar system to the galactic and cosmic ones. To describe galactic rotational curves and accelerated expansion of the universe by GR, the existence of dark matter (DM) and dark energy (DE) was supposed, respectively. According to the current SMC, the universe matter/energy budget consists approximately of 68% of dark energy, 27% of dark matter, and only 5% of standard visible matter. However, despite many experimental and theoretical investigations (as a review, see, e.g., [4]), the existence of DM and DE has not been proven, and thus they are still hypothetical constituents of the dark side of the universe.

It should be also mentioned that GR suffers from singularities—the black hole and Big Bang singularity [5]. As we know, if a theory contains a singularity, it means it is inapplicable when approaching the singularity and that a more general appropriate theory should be invented. Also, it should be mentioned that GR can not be consistently quantized [6]. As we know, other physical theories have their own domain of validity, usually limited by the space–time scale and some parameters, or by the complexity of the system. In this sense, GR should not be an exception and serve as a theory of gravity from the Planck scale to the universe as a whole [7].

Based on all the aforementioned shortcomings, it can be concluded that general relativity is not a final theory of gravitation and that there is a sense to look for a more general theory than GR [8]. In principle, there is a huge number of possibilities to extend the Einstein–Hilbert (EH) action, and for now, there is no rule on how to choose the right path [9]. Hence, in practice, there are many phenomenological approaches, and the most elaborated is $f\left(R\right)$ theory [10], where in the EH action, the scalar curvature R is replaced by some function $f\left(R\right)$. Among other interesting approaches is the nonlocal one [11]. In the nonlocal gravity models, besides R in the EH action, there is a nonlocal term with some invariants usually composed of R and □, where □ is the d’Alembert–Beltrami operator.

Depending on how the □ is built into the nonlocal term, there are mainly two typical examples of nonlocal gravity models: (i) the nonpolynomial analytic expansion of □, see, e.g., [12,13,14,15,16,17,18], i.e., $\mathcal{F}(\square )={\sum }_{n=1}^{\infty }{f}_n{\square }^n$ (see various examples [19,20,21,22,23]), and (ii) a polynomial of ${\square }^{-1}$, see, e.g., [11,24,25,26,27]. The motivation for using a local operator of the form (i) is found in string theory—ordinary and p-adic. It is obvious that in case (i), the dynamics depend not only on the first and second space–time derivatives but also on all the higher ones. The nonlocal operator ${\square }^{-1}$ in (ii) has its origin in (one-loop) quantum corrections in some classical field Lagrangians and is used in investigations of the late-time cosmic acceleration without dark energy [11].

In several papers, see [17,27] and references therein, we investigated the following nonlocal de Sitter gravity model ($\sqrt{dS}$ gravity):

$$\begin{array}{c}\hfill S=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left(R-2\Lambda +\sqrt{R-2\Lambda }\mathcal{F}(\square )\sqrt{R-2\Lambda }\right),\end{array}$$

(1)

where $\Lambda$ is the cosmological constant, and the nonlocal operator $\mathcal{F}(\square )$ has the following general form:

$$\begin{array}{c}\hfill \mathcal{F}(\square )=\sum _{n=1}^{+\infty }\left(f_n{\square }^n+f_{-n}{\square }^{-n}\right).\end{array}$$

(2)

This nonlocal model is unique compared to other nonlocal models, and its properties will be described in the next section.

It is worth mentioning that (1) applied to the homogeneous and isotropic universe gives several exact cosmological solutions [17,27]. One of them is $a\left(t\right)=A{t}^{\frac{2}{3}}{e}^{\frac{\Lambda }{14}{t}^2}$, which mimics an interplay of dark matter ($t^{\frac{2}{3}}$) and dark energy ($e^{\frac{\Lambda }{14}{t}^2}$) in very good agreement with the standard model of cosmology. There are also nonsingular bounce solutions in the flat, closed, and open universe as well as singular and cyclic solutions.

The fact that the model works well on a cosmological scale was a motivation to test it on galactic and planetary systems. To this end, it is necessary to obtain the corresponding Schwarzschild–de Sitter metric. In the paper [28], we presented initial research with an approximate solution. In this paper, we provide a much wider and more detailed investigation with some new solutions. It also contains preliminary tests on our galaxy the Milky Way and the spiral galaxy M33 with very satisfactory agreement of the obtained theoretical results and observational measurements.

One important aspect of the validity of any model of nonlocal gravity theory is the absence of ghosts. The existence of ghosts in models of type (7) is discussed in [21]. In the concluding remarks of paper [17], it was stated that there are no ghosts in the excitations over the de Sitter background in model (1). However, for other backgrounds, special research should be conducted.

This paper is organized as follows. In Section 2, nonlocal de Sitter gravity $\sqrt{dS}$ is introduced and the equations of motion for the gravitational field are derived. Various aspects of the Schwarzschild–de Sitter metric are presented in Section 3, which in particular contains the solutions and their comparison with observations of the rotation curves of spiral galaxies. Some discussion and presentation of the main results are contained in the last section.

2. $\sqrt{\mathbf{dS}}$ Nonlocal Gravity

Our nonlocal gravity model is given by its action (1). It can be rewritten in the compact form

$$\begin{array}{c}\hfill S=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\sqrt{R-2\Lambda }F(\square )\sqrt{R-2\Lambda },\end{array}$$

(3)

where $F(\square )$ is

$$\begin{array}{c}\hfill F(\square )=1+\mathcal{F}(\square )=1+\sum _{n=1}^{+\infty }\left(f_n{\square }^n+f_{-n}{\square }^{-n}\right)\end{array}$$

(4)

with the general form of the d’Alembert–Beltrami operator

$$\begin{array}{c}\hfill \square ={\nabla }_{\mu }{\nabla }^{\mu }=\frac{1}{\sqrt{-g}}{\partial }_{\mu }\left(\sqrt{-g}{g}^{\mu \nu }{\partial }_{\nu }\right).\end{array}$$

(5)

If $F(\square )=1$, i.e., $\mathcal{F}(\square )=0$, then (3) becomes local de Sitter gravity with action

$$\begin{array}{c}\hfill S_0=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\sqrt{R-2\Lambda }\sqrt{R-2\Lambda }=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}(R-2\Lambda ).\end{array}$$

(6)

Note that action (3) can be easily obtained from (6) by embedding operator (4) inside the product $\sqrt{R-2\Lambda }\sqrt{R-2\Lambda }.$ It should be noted that the degree of $R-2\Lambda$ remains unchanged when we go from local (6) to nonlocal action (3), as well as that the $F(\square )$ operator is dimensionless. It is also worth noting that the above local and nonlocal action has the same discrete symmetry, i.e., remains unchanged under transformation $\sqrt{R-2\Lambda }\to -\sqrt{R-2\Lambda }.$

In this paper, we will not consider the extension of action (1) with the matter sector, since we are looking for the Schwarzschild–de Sitter metric outside the spherically symmetric massive body.

Equations of Motion

To obtain equations of motion for $\sqrt{dS}$ gravity given by action (1), it is useful to start from the more general nonlocal de Sitter model

$$\begin{array}{c}\hfill S=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}\left(R-2\Lambda +P\left(R\right)\mathcal{F}(\square )Q\left(R\right)\right),\end{array}$$

(7)

where $P\left(R\right)$ and $Q\left(R\right)$ are some differentiable functions of the Ricci scalar $R.$ The variation in (7) with respect to $g^{\mu \nu }$ yields the corresponding equations of motion (EoM) derived in [29], see also [27].

According to [29], the EoM for the nonlocal de Sitter gravity model (7) are as follows:

$$\begin{array}{c}\hfill G_{\mu \nu }+\Lambda g_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }P\left(R\right)\mathcal{F}(\square )Q\left(R\right)+R_{\mu \nu }W-K_{\mu \nu }W+\frac{1}{2}{\Omega }_{\mu \nu }=0,\end{array}$$

(8)

where $G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }$ is the Einstein tensor, $R_{\mu \nu }$ is the Ricci tensor, and

$$\begin{array}{cc}\hfill & W=P^{\prime }\left(R\right)\mathcal{F}(\square )Q\left(R\right)+Q^{\prime }\left(R\right)\mathcal{F}(\square )P\left(R\right),K_{\mu \nu }={\nabla }_{\mu }{\nabla }_{\nu }-g_{\mu \nu }\square ,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & {\Omega }_{\mu \nu }=\sum _{n=1}^{+\infty }{f}_n\sum _{\ell =0}^{n-1}{S}_{\mu \nu }({\square }^{\ell }P,{\square }^{n-1-\ell }Q)-\sum _{n=1}^{+\infty }{f}_{-n}\sum _{\ell =0}^{n-1}{S}_{\mu \nu }({\square }^{-(\ell +1)}P,{\square }^{-(n-\ell )}Q),\hfill \end{array}$$

(10)

where

$$\begin{array}{cc}\hfill & S_{\mu \nu }(A,B)=g_{\mu \nu }\left({\nabla }^{\alpha }A{\nabla }_{\alpha }B+A\square B\right)-2{\nabla }_{\mu }A{\nabla }_{\nu }B.\hfill \end{array}$$

(11)

$P^{\prime }\left(R\right)$ and $Q^{\prime }\left(R\right)$ denote the derivative of $P\left(R\right)$ and $Q\left(R\right)$ with respect to R, respectively.

Comparing the above equations of motion with respect to their local Einstein counterpart $G_{\mu \nu }+\Lambda g_{\mu \nu }=0$, they look very complex, and finding some exact solutions may be a hard problem.

Since we are interested in the EoM of $\sqrt{dS}$, we have to take $Q\left(R\right)=P\left(R\right)=\sqrt{R-2\Lambda }$. To this end, let us first consider the case $Q\left(R\right)=P\left(R\right)$. Consequently, Equations (8)–(11) reduce to

$$\begin{array}{cc}\hfill & G_{\mu \nu }+\Lambda g_{\mu \nu }-\frac{g_{\mu \nu }}{2}P\left(R\right)\mathcal{F}(\square )P\left(R\right)+R_{\mu \nu }W-K_{\mu \nu }W+\frac{1}{2}{\Omega }_{\mu \nu }=0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & W=2P^{\prime }\left(R\right)\mathcal{F}(\square )P\left(R\right),K_{\mu \nu }={\nabla }_{\mu }{\nabla }_{\nu }-g_{\mu \nu }\square ,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\Omega }_{\mu \nu }=\sum _{n=1}^{+\infty }{f}_n\sum _{\ell =0}^{n-1}{S}_{\mu \nu }({\square }^{\ell }P,{\square }^{n-1-\ell }P)-\sum _{n=1}^{+\infty }{f}_{-n}\sum _{\ell =0}^{n-1}{S}_{\mu \nu }({\square }^{-(\ell +1)}P,{\square }^{-(n-\ell )}P).\hfill \end{array}$$

(14)

According to our experience, the above equations of motion (12)–(14) can be significantly simplified and easily solved if there exists a metric tensor $g_{\mu \nu }$ such that for the corresponding d’Alembert–Beltrami operator □, the following equations (eigenvalue problem) are satisfied:

$$\begin{array}{c}\hfill \square P\left(R\right)=qP\left(R\right),{\square }^{-1}P\left(R\right)=q^{-1}P\left(R\right),\mathcal{F}(\square )P\left(R\right)=\mathcal{F}\left(q\right)P\left(R\right),q\ne 0,\end{array}$$

(15)

where q is a parameter of the same dimensionality as □. Applying (15) to Equations (12)–(14), we have

$$\begin{array}{cc}\hfill & W=2\mathcal{F}\left(q\right)P^{\prime }\left(R\right)P\left(R\right),\mathcal{F}\left(q\right)=\sum _{n=1}^{+\infty }\left(f_n{q}^n+f_{-n}{q}^{-n}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\Omega }_{\mu \nu }={\mathcal{F}}^{\prime }\left(q\right)S_{\mu \nu }\left(P,P\right),{\mathcal{F}}^{\prime }\left(q\right)=\sum _{n=1}^{+\infty }n{f}_n{q}^{n-1}-\sum _{n=1}^{+\infty }n{f}_{-n}{q}^{-n-1},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & G_{\mu \nu }+\Lambda g_{\mu \nu }+\mathcal{F}\left(q\right)\left(2(R_{\mu \nu }-K_{\mu \nu })P{P}^{\prime }-\frac{g_{\mu \nu }}{2}{P}^2\left(R\right)\right)+\frac{1}{2}{\mathcal{F}}^{\prime }\left(q\right)S_{\mu \nu }(P,P)=0.\hfill \end{array}$$

(18)

Now, let us take $P\left(R\right)=\sqrt{R-2\Lambda }$. Then, $P^{\prime }\left(R\right)P\left(R\right)=\frac{1}{2}$ and $P^2\left(R\right)=R-2\Lambda .$ Finally, the EoM (18) become

$$\left(G_{\mu \nu }+\Lambda g_{\mu \nu }\right)\left(1+\mathcal{F}\left(q\right)\right)+\frac{1}{2}{\mathcal{F}}^{\prime }\left(q\right)S_{\mu \nu }(\sqrt{R-2\Lambda },\sqrt{R-2\Lambda })=0.$$

(19)

If the nonlocal operator satisfies

$$\begin{array}{c}\hfill \mathcal{F}\left(q\right)=-1,{\mathcal{F}}^{\prime }\left(q\right)=0,\end{array}$$

(20)

then the equations of motion (19) are also satisfied.

According to the above consideration, the main problem is to solve equation $\square \sqrt{R-2\Lambda }=q\sqrt{R-2\Lambda }$ for an appropriate metric tensor $g_{\mu \nu }$. This may be a hard problem, and it is the case with the corresponding Schwarzschild–de Sitter metric in the nonlocal $\sqrt{dS}$ gravity. In the sequel, we will investigate the corresponding Schwarzschild–de Sitter metric around a static spherically symmetric massive body.

3. The Schwarzschild–de Sitter Metric

We are going to explore the Schwarzschild–de Sitter space–time metric in the case of $\sqrt{dS}$ gravity given by its action (1).

3.1. General Consideration

First, we want to consider some general aspects of the corresponding Schwarzschild–de Sitter space–time metric. To this end, we start from the usual expression for the Schwarzschild metric in the pseudo-Rimannian manifold:

$$\mathrm{d}{s}^2=-A\left(r\right)\mathrm{d}{t}^2+B\left(r\right)\mathrm{d}{r}^2+r^2\mathrm{d}{\theta }^2+r^2{sin}^2\theta \mathrm{d}{\phi }^2,(c=1).$$

(21)

Nonzero elements of metric tensor $g_{\mu \nu }\left(r\right)$ are

$$\begin{array}{c}\hfill g_{00}\left(r\right)=-A\left(r\right),g_{11}\left(r\right)=B\left(r\right),g_{22}\left(r\right)=r^2,g_{33}\left(r\right)=r^2{sin}^2\theta .\end{array}$$

(22)

Nonzero components of the corresponding Christoffel symbol ${\Gamma }_{\mu \nu }^{\alpha }=\frac{1}{2}{g}^{\alpha \beta }\left({\partial }_{\mu }{g}_{\nu \beta }+{\partial }_{\nu }{g}_{\nu \beta }-{\partial }_{\beta }{g}_{\mu \nu }\right)$ are

$$\begin{array}{cc}\hfill & {\Gamma }_{10}^0={\Gamma }_{01}^0=\frac{1}{2}\frac{A^{\prime }}{A},{\Gamma }_{00}^1=\frac{1}{2}\frac{A^{\prime }}{B},{\Gamma }_{11}^1=\frac{1}{2}\frac{B^{\prime }}{B},{\Gamma }_{22}^1=-\frac{r}{B},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {\Gamma }_{33}^1=-\frac{r}{B}{sin}^2\theta ,{\Gamma }_{12}^2={\Gamma }_{21}^2=\frac{1}{r},{\Gamma }_{33}^2=-sin\theta cos\theta ,\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill & {\Gamma }_{13}^3={\Gamma }_{31}^3=\frac{1}{r},{\Gamma }_{23}^3={\Gamma }_{32}^3=\frac{cos\theta }{sin\theta },\hfill \end{array}$$

(25)

where $\prime$ denotes derivative with respect to radius $r.$ Nonzero components of the Ricci tensor $R_{\mu \nu }=R_{\mu \alpha \nu }^{\alpha }={\partial }_{\alpha }{\Gamma }_{\mu \nu }^{\alpha }-{\partial }_{\nu }{\Gamma }_{\mu \alpha }^{\alpha }+{\Gamma }_{\alpha \rho }^{\alpha }{\Gamma }_{\mu \nu }^{\rho }-{\Gamma }_{\nu \rho }^{\alpha }{\Gamma }_{\mu \alpha }^{\rho }$ are

$$\begin{array}{cc}\hfill & R_{00}=\frac{A^{\prime \prime }}{2B}-\frac{A^{\prime }{B}^{\prime }}{4B^2}-\frac{A^{\prime 2}}{4AB}+\frac{A^{\prime }}{rB},R_{11}=-\frac{A^{\prime \prime }}{2A}+\frac{A^{\prime }{B}^{\prime }}{4AB}+\frac{A^{\prime 2}}{4A^2}+\frac{B^{\prime }}{rB},\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & R_{22}=-\frac{r{A}^{\prime }}{2AB}+\frac{r{B}^{\prime }}{2B^2}-\frac{1}{B}+1,R_{33}=\left(-\frac{r{A}^{\prime }}{2AB}+\frac{r{B}^{\prime }}{2B^2}-\frac{1}{B}+1\right){sin}^2\theta ,\hfill \end{array}$$

(27)

where, as a result of spherical symmetry, $R_{33}=R_{22}{sin}^2\theta .$

The corresponding Ricci curvature $R=g^{\mu \nu }{R}_{\mu \nu }$ is

$$\begin{array}{c}\hfill R=\frac{2}{r^2}-\frac{1}{B\left(r\right)}\left(\frac{2}{r^2}+\frac{2A^{\prime }\left(r\right)}{rA\left(r\right)}-\frac{A^{\prime }{\left(r\right)}^2}{2A{\left(r\right)}^2}-\frac{2B^{\prime }\left(r\right)}{rB\left(r\right)}-\frac{A^{\prime }\left(r\right)B^{\prime }\left(r\right)}{2A\left(r\right)B\left(r\right)}+\frac{A^{\prime \prime }\left(r\right)}{A\left(r\right)}\right).\end{array}$$

(28)

The equation that should be solved is

$$\begin{array}{c}\hfill \square u\left(r\right)=\frac{1}{B\left(r\right)}\left(▵u\left(r\right)+\frac{1}{2}\left(\frac{A^{\prime }\left(r\right)}{A\left(r\right)}-\frac{B^{\prime }\left(r\right)}{B\left(r\right)}\right)u^{\prime }\left(r\right)\right)=qu\left(r\right),u\left(r\right)=\sqrt{R-2\Lambda },\end{array}$$

(29)

where

$$\begin{array}{c}\hfill ▵=\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^2\frac{\partial }{\partial r}\right]=\frac{{\partial }^2}{\partial r^2}+\frac{2}{r}\frac{\partial }{\partial r}\end{array}$$

(30)

is the Laplace operator in spherical coordinate r.

Note that in the eigenvalue problem (29), the parameter q has the same dimension as operator □, i.e., the dimension is $L^{-2}$. Since the cosmological constant $\Lambda$ also has dimension $L^{-2}$, it is useful to write $q=\zeta \Lambda$, where $\zeta$ is a dimensionless parameter. Note also that the nonlocal operator $\mathcal{F}(\square )$, defined in (2), satisfies conditions $\mathcal{F}\left(q\right)=-1$ and ${\mathcal{F}}^{\prime }\left(q\right)=0$, introduced in (20), if we take it as

$$\begin{array}{c}\hfill \mathcal{F}(\square )=e\left[a\frac{\square }{\zeta \Lambda }{e}^{\left(-\frac{\square }{\zeta \Lambda }\right)}+b\frac{\zeta \Lambda }{\square }{e}^{\left(-\frac{\zeta \Lambda }{\square }\right)}\right],\mathrm{where}a+b=-1.\end{array}$$

(31)

3.2. Solutions

Recall that in the local de Sitter case (6), with a static spherically symmetric body of mass M, the Schwarzschild–de Sitter metric (21) is

$$\begin{array}{c}\hfill A\left(r\right)=A_0\left(r\right)=1-\frac{\mu }{r}-\frac{\Lambda r^2}{3},B\left(r\right)=B_0\left(r\right)=\frac{1}{A_0\left(r\right)}=\frac{1}{1-\frac{\mu }{r}-\frac{\Lambda r^2}{3}},\mu =\frac{2GM}{c^2}.\end{array}$$

(32)

It makes sense to suppose that solution the of Equation (29) is of the form

$$\begin{array}{c}\hfill A\left(r\right)=A_0\left(r\right)-\alpha \left(r\right),B\left(r\right)=\frac{1}{A_0\left(r\right)-\beta \left(r\right)},\end{array}$$

(33)

where $\alpha \left(r\right)$ and $\beta \left(r\right)$ are some dimensionless functions. When $\zeta \to 0$, then the nonlocal operator (31) tends to zero, and consequently, the nonlocal de Sitter $\sqrt{dS}$ gravity model (1) becomes local. Hence, it must be that $A\left(r\right)\to A_0\left(r\right)$ and $B\left(r\right)\to B_0\left(r\right)$ when $\zeta \to 0,$; that is, $\alpha \left(r\right)\to 0$ and $\beta \left(r\right)\to 0$ as $\zeta \to 0$.

Replacing $A=A_0-\alpha \left(r\right)$ and $B=\frac{1}{A_0-\beta \left(r\right)}$ in the scalar curvature R (28) and in the operator □ of Equation (29), we obtain

$$\begin{array}{cc}\hfill R& =\frac{2}{r^2}(1-A_0+\beta )+2\frac{A_0-\beta }{A_0-\alpha }(A_0^{\prime }-{\alpha }^{\prime })\left(\frac{1}{4}\frac{A_0^{\prime }-{\alpha }^{\prime }}{A_0-\alpha }-\frac{1}{r}\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill -2(A_0^{\prime }-{\beta }^{\prime })\left(\frac{1}{4}\frac{A_0^{\prime }-{\alpha }^{\prime }}{A_0-\alpha }+\frac{1}{r}\right)-\frac{A_0-\beta }{A_0-\alpha }(A_0^{\prime \prime }-{\alpha }^{\prime \prime }),\end{array}$$

(34)

$$\begin{array}{cc}\hfill \square u& =(A_0-\beta )▵u+\frac{1}{2}\left[\frac{A_0-\beta }{A_0-\alpha }(A_0^{\prime }-{\alpha }^{\prime })+A_0^{\prime }-{\beta }^{\prime }\right]u^{\prime }=qu,u=\sqrt{R-2\Lambda }\hfill \end{array}$$

(35)

If we substitute Expressions (34) and (35) in Equation (29), then we will obtain a differential equation with two unknown functions: $\alpha \left(r\sqrt{\zeta \Lambda }\right)$ and $\beta \left(r\sqrt{\zeta \Lambda }\right)$. It is obvious that we must have another equation which is a relation between functions $\alpha$ and $\beta$. Recall that in the local case, $B_0\left(r\right)=\frac{1}{A_0\left(r\right)}$ holds. Hence, there is a sense to also take $B\left(r\right)=\frac{1}{A\left(r\right)}$ in the nonlocal case, and it yields

$$\begin{array}{cc}\hfill R\left(r\right)& =\frac{1}{r^2}\left[2-2A\left(r\right)-4r{A}^{\prime }\left(r\right)-r^2{A}^{\prime \prime }\left(r\right)\right]=\frac{1}{r^2}\frac{{\partial }^2}{\partial r^2}\left[r^2\left(1-A\left(r\right)\right)\right],\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill \square u\left(r\right)& =A\left(r\right)u^{″}\left(r\right)+(A^{\prime }\left(r\right)+\frac{2}{r}A\left(r\right))u^{\prime }\left(r\right)=\frac{1}{r^2}\frac{\partial }{\partial r}\left[r^{2}A\left(r\right)\frac{\partial u}{\partial r}\right].\hfill \end{array}$$

(37)

In fact, it means that we take

$$\begin{array}{c}\hfill \beta \left(r\right)=\alpha \left(r\right).\end{array}$$

(38)

Employing (38) in (34) and (35), we obtain

$$\begin{array}{cc}\hfill R& =4\Lambda +\frac{2\alpha }{r^2}+\frac{4{\alpha }^{\prime }}{r}+{\alpha }^{″},\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill \square u& =(A_0-\alpha )▵u+(A_0^{\prime }-{\alpha }^{\prime })u^{\prime }=qu,u=\sqrt{R-2\Lambda }.\hfill \end{array}$$

(40)

We are interested in finding function $\alpha \left(r\right)$, and the next step should be the substitution of

$$\begin{array}{c}\hfill u=\sqrt{R-2\Lambda }=\sqrt{2\Lambda +\frac{2\alpha }{r^2}+\frac{4{\alpha }^{\prime }}{r}+{\alpha }^{\prime \prime }}\end{array}$$

(41)

into Equation (40). In that case, one obtains an ordinary nonlinear differential equation of the fourth order. Because of nonlinearity, it is a very difficult task to find the corresponding exact solution. After many attempts, we did not succeed at finding a reasonable exact solution and concluded that a much more sophisticated approach is required. In the sequel of this paper, we will turn our attention to the corresponding linear differential equation.

It means we will limit ourselves to studying the Schwarzschild–de Sitter metric in weak gravity field approximation. Practically, it is like considering a gravity field far from a massive body (see Figure 1) so that the d’Alembertian □ can be replaced by the Laplacian $▵$ in Equation (40). In such case, we will take $A\left(r\right)\approx 1$ in (40); that is,

$$\begin{array}{c}\hfill A\left(r\right)=A_0\left(r\right)-\alpha \left(r\right)=1-\frac{\mu }{r}-\frac{\Lambda r^2}{3}-\alpha \left(r\right)\approx 1,\end{array}$$

(42)

which makes sense if the following is satisfied:

$$\begin{array}{c}\hfill \frac{\mu }{r}\ll 1,\frac{\Lambda r^2}{3}\ll 1,\left|\alpha \left(r\right)\right|\ll 1.\end{array}$$

(43)

Figure 1. We consider the Schwarzschild–de Sitter metric of nonlocal $\sqrt{dS}$ gravity at the distances far from a spherically symmetric massive body.

Applying approximation (42) in (40), we obtain the following simple linear equation in $u\left(r\right)$:

$$\begin{array}{c}\hfill ▵u=qu,\mathrm{that}\mathrm{is}\frac{{\partial }^{2}u}{\partial r^2}+\frac{2}{r}\frac{\partial u}{\partial r}=qu,u=\sqrt{R-2\Lambda }.\end{array}$$

(44)

Note that the requested function $\alpha \left(r\right)$ is contained in $u\left(r\right)=\sqrt{R-2\Lambda }$, through (39): $R=4\Lambda +\frac{2\alpha }{r^2}+\frac{4{\alpha }^{\prime }}{r}+{\alpha }^{″}$. Hence, the next step is the linearization of $\sqrt{R-2\Lambda }$, and we obtain

$$\begin{array}{c}\hfill \sqrt{R-2\Lambda }=i\sqrt{2\Lambda -R}\approx i\sqrt{2\Lambda }\left(1-\frac{R}{4\Lambda }\right)=-\frac{i}{2\sqrt{2\Lambda }}(R-4\Lambda ),\mathrm{if}\left|\frac{R}{2\Lambda }\right|\ll 1.\end{array}$$

(45)

Since $R-4\Lambda$ is an analytic linear function according to the analytic continuation, it is also valid in the domain $\left|R\right|>2\Lambda$ and can be applied to the galactic system. It is worth noting that approximation (45) was successfully applied in [22,23].

Now, replacing $\sqrt{R-2\Lambda }$ in (44) by $-\frac{i}{2\sqrt{2\Lambda }}(R-4\Lambda )$, we obtain

$$\begin{array}{c}\hfill {(R-4\Lambda )}^{″}+\frac{2}{r}{(R-4\Lambda )}^{\prime }=q(R-4\Lambda ).\end{array}$$

(46)

The next step is to replace the scalar curvature R by $R=4\Lambda +\frac{2\alpha }{r^2}+\frac{4{\alpha }^{\prime }}{r}+{\alpha }^{″}$ (see (39)) in (46), and we obtain

$$\begin{array}{c}\hfill {\alpha }^{\prime \prime \prime \prime }+\frac{6}{r}{\alpha }^{\prime \prime \prime }+\frac{2}{r^2}{\alpha }^{″}-\frac{4}{r^3}{\alpha }^{\prime }+\frac{4}{r^4}\alpha =q({\alpha }^{\prime \prime }+\frac{4}{r}{\alpha }^{\prime }+\frac{2}{r^2}\alpha ),\end{array}$$

(47)

which is a linear differential equation of the fourth order.

Equation (47) has a general solution of the form

$$\begin{array}{c}\hfill \alpha \left(r\right)=\frac{C_1}{r}+\frac{C_2}{r^2}+C_3{e}^{-\sqrt{q}r}\left(\frac{1}{qr}+\frac{2}{q^{\frac{3}{2}}{r}^2}\right)+C_4{e}^{\sqrt{q}r}\left(\frac{1}{qr}-\frac{2}{q^{\frac{3}{2}}{r}^2}\right),q=\zeta \Lambda .\end{array}$$

(48)

There are four constants ($C_1,C_2,C_3,C_4$), and we chose them so that the appropriate particular solution $\alpha \left(r\right)\to 0$ when $\zeta \to 0$ occurs and that it has some physical meaning.

To exclude the term with $e^{\sqrt{q}r}$ in (48), we took $C_4=0$, since this exponential function increases indefinitely for very large values of r. Case $C_1=-\frac{\delta }{\sqrt{q}},C_2=\frac{2\delta }{q},C_3=-\delta \sqrt{q};C_4=0$.

In this case, the solution for $\alpha \left(r\right)$ is

$$\begin{array}{c}\hfill \alpha \left(r\right)=-\frac{\delta }{\sqrt{q}r}\left(1+e^{-\sqrt{q}r}\right)+\frac{2\delta }{q{r}^2}\left(1-e^{-\sqrt{q}r}\right),q=\zeta \Lambda ,\end{array}$$

(49)

where $\delta$ is a dimensionless parameter. Since the integration constants $C_1,C_2,C_3$ are proportional to $\delta$ and $C_4=0$, by this way, we reduced the number of parameters from four to one. Altogether, we have two free parameters ($\delta$ and $\zeta$), which should be determined from measurements.

To see how $\alpha \left(r\right)$ behaves when $\zeta \to 0$, it is useful to expand the exponential function $e^{-\sqrt{q}r}$ into the Taylor series. We have

$$\begin{array}{cc}\hfill \alpha \left(r\right)& =-\frac{\delta }{\sqrt{q}r}\left(1+e^{-\sqrt{q}r}\right)+\frac{2\delta }{q{r}^2}\left(1-e^{-\sqrt{q}r}\right)\hfill \\ \hfill & =\delta \left(-\frac{2}{\sqrt{q}r}+1-\frac{\sqrt{q}r}{2}+\frac{q{r}^2}{6}-\frac{\sqrt{q}q{r}^3}{24}+\cdots \right)\hfill \end{array}$$

(50)

$$\begin{array}{cc}\hfill & +\delta \left(\frac{2}{\sqrt{q}r}-1+\frac{\sqrt{q}r}{3}-\frac{q{r}^2}{12}+\cdots \right)\hfill \end{array}$$

(51)

$$\begin{array}{cc}\hfill & =-\frac{\delta \sqrt{q}r}{6}+\frac{\delta q{r}^2}{12}-\cdots =-\frac{\delta \sqrt{\zeta \Lambda }r}{6}+\frac{\delta \zeta \Lambda r^2}{12}-\cdots \hfill \end{array}$$

(52)

As it follows from (52), we conclude that $\alpha \left(r\right)\to 0$ when $\zeta \to 0$.

According to (49), we obtain

$$\begin{array}{c}\hfill A\left(r\right)=1-\frac{\mu }{r}-\frac{\Lambda r^2}{3}+\frac{\delta }{\sqrt{q}r}\left(1+e^{-\sqrt{q}r}\right)-\frac{2\delta }{q{r}^2}\left(1-e^{-\sqrt{q}r}\right),q=\zeta \Lambda ,\end{array}$$

(53)

where $\mu =\frac{2GM}{c^2}.$ When $\zeta \to 0$, the obtained Expression (53) for $A\left(r\right)$ tends to $A_0\left(r\right)$ as necessary.

3.3. The Rotation Curves of Spiral Galaxies

The rotation curves of spiral galaxies have been the subject of intensive research motivated by the need to determine the amount and distribution of dark matter compared to visible matter, see, e.g., [30,31,32,33,34,35] and the references therein.

It is interesting to examine whether this $\sqrt{dS}$ gravitational model gives the possibility of describing the rotation curves of spiral galaxies. To this end, we should start with $A\left(r\right)$ given by (53) and present the corresponding gravitational potential $\Phi \left(r\right)$, which is

$$\begin{array}{cc}\hfill \Phi \left(r\right)& =\frac{c^2}{2}\left(1-A\left(r\right)\right)=\frac{GM}{r}+\frac{\Lambda c^2{r}^2}{6}+\frac{c^2}{2}\alpha \left(r\right)\hfill \\ \hfill & =\frac{GM}{r}+\frac{\Lambda c^2{r}^2}{6}-\frac{\delta c^2}{2\sqrt{q}r}\left(1+e^{-\sqrt{q}r}\right)+\frac{\delta c^2}{q{r}^2}\left(1-e^{-\sqrt{q}r}\right).\hfill \end{array}$$

(54)

Note that here, $\Phi \left(r\right)$ is the intensity of the gravitational potential.

The corresponding gravitational acceleration for potential (54) is

$$\begin{array}{c}\hfill a_g\left(r\right)=-\frac{\partial \Phi }{\partial r}=\frac{GM}{r^2}-\frac{\Lambda c^{2}r}{3}+\frac{\delta c^2}{\sqrt{q}{r}^2}\left(\frac{2}{\sqrt{q}r}-\frac{1}{2}\right)-\frac{\delta c^2}{r}\left(\frac{1}{2}+\frac{3}{2\sqrt{q}r}+\frac{2}{q{r}^2}\right)e^{-\sqrt{q}r}.\end{array}$$

(55)

The velocity of the rotation curve $\overline{v}\left(r\right)$ follows from equality $\frac{{\overline{v}}^2\left(r\right)}{r}=a_g\left(r\right)$, and it is

$$\begin{array}{c}\hfill \overline{v}\left(r\right)=\sqrt{a_g\left(r\right)r}=c\sqrt{\frac{GM}{c^{2}r}-\frac{\Lambda r^2}{3}+\frac{\delta }{\sqrt{q}r}\left(\frac{2}{\sqrt{q}r}-\frac{1}{2}\right)-\delta \left(\frac{1}{2}+\frac{3}{2\sqrt{q}r}+\frac{2}{q{r}^2}\right)e^{-\sqrt{q}r}}.\end{array}$$

(56)

We checked the validity of the obtained formula for the circular velocity (56) in two cases: the Milky Way galaxy and the spiral galaxy M33. The values of parameters $\delta$ and $\zeta$ in (56) are estimated by best fitting the measured data using the least-squares method. Since, at large distances r, the velocity $\overline{v}$ weakly depends on mass variation, we employed only the mass of the black hole in the center of the galaxy. Namely, the central mass can be taken up to $M\sim {10}^8{M}_{\odot }$, and there will be no significant changes in the calculated circular velocity $\overline{v}\left(r\right)$ at a very large r.

3.3.1. Milky Way Case

The Milky Way rotation curve data were taken from a recent paper [36], where the Keplerian decline in the rotation curve is detected. Measured data for the distance r, velocity v, and velocity error $\Delta v$ are obtained by the Gaia telescope, and they are presented in Table 1, see [36]. In this table, the computed velocity $\overline{v}$ using (56) and relative error $\delta v=\frac{|v-\overline{v}|}{v}$ are also presented. A pictorial comparison of the measured and calculated velocities is presented in Figure 2.

Table 1. Milky Way rotation curve data from [36] and this work.

$\mathit{r}$ [kpc]	$\mathit{v}$ [km/s]	$\Delta \mathit{v}$ [km/s]	$\overline{\mathit{v}}$ [km/s]	Relative Error $\mathit{\delta }\mathit{v}$ [%]
9.5	221.75	3.17	217.36	1.98
10.5	223.32	3.02	220.19	1.40
11.5	220.72	3.47	221.93	0.55
12.5	222.92	3.19	222.72	0.09
13.5	224.16	3.48	222.66	0.67
14.5	221.60	4.20	221.85	0.11
15.5	218.79	4.75	220.37	0.72
16.5	216.38	4.96	218.28	0.88
17.5	213.48	6.13	215.63	1.01
18.5	209.17	4.42	212.47	1.58
19.5	206.25	4.63	208.83	1.25
20.5	202.54	4.40	204.77	1.10
21.5	197.56	4.62	200.29	1.38
22.5	197.00	3.81	195.42	0.80
23.5	191.62	12.95	190.17	0.75
24.5	187.12	8.06	184.57	1.36
25.5	181.44	19.58	178.62	1.55
26.5	175.68	24.68	172.32	1.91

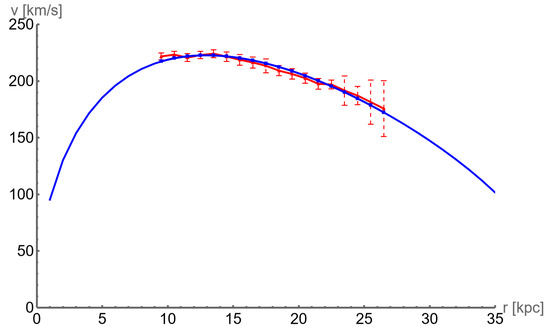
Figure 2. Rotation curve for the Milky Way galaxy. Red points are measured observational values [36] and blue line is computed $\overline{v}\left(r\right)$ by Formula (56), where $\delta =1.9\times {10}^{-5}$, $\zeta =4.4\times {10}^{10}$, $\Lambda ={10}^{-52} {\mathrm{m}}^{-2}$, and $M=4.28\times {10}^6{M}_{\odot }$.

3.3.2. Spiral Galaxy M33 Case

We used data for the galaxy Messier 33 based on observations obtained at the Dominion Radio Astrophysical Observatory and presented in [37]. We compared the measured rotation velocity $v\left(r\right)$ [37] with the computed $\overline{v}\left(r\right)$ using Formula (56). The measured and computed data are presented in Table 2 and illustrated in Figure 3.

Table 2. M33 galaxy data from [37] and this work.

$\mathit{r}$ [kpc]	$\mathit{v}$ [km/s]	$\Delta \mathit{v}$ [km/s]	$\overline{\mathit{v}}$ [km/s]	Relative Error $\mathit{\delta }\mathit{v}$ [%]	$\mathit{r}$ [kpc]	$\mathit{v}$ [km/s]	$\Delta \mathit{v}$ [km/s]	$\overline{\mathit{v}}$ [km/s]	Relative Error $\mathit{\delta }\mathit{v}$ [%]
0.5	42.0	2.4	35.62	15.18	12.2	115.7	9.6	120.69	4.31
1.0	58.8	1.5	49.61	15.63	12.7	115.1	7.7	121.05	5.17
1.5	69.4	0.4	59.83	13.79	13.2	117.1	5.1	121.30	3.58
2.0	79.3	4.0	68.02	14.22	13.7	118.2	3.2	121.45	2.75
2.4	86.7	1.8	73.59	15.12	14.2	118.4	1.4	121.50	2.62
2.9	91.4	3.1	79.64	12.86	14.7	118.2	1.8	121.47	2.76
3.4	94.2	4.8	84.90	9.88	15.1	117.5	2.4	121.38	3.30
3.9	96.5	5.5	89.51	7.25	15.6	119.6	0.8	121.19	1.33
4.4	99.8	3.9	93.58	6.23	16.1	118.6	1.5	120.93	1.96
4.9	102.1	1.7	97.21	4.80	16.6	122.6	0.5	120.59	1.64
5.4	103.6	0.4	100.44	3.05	17.1	124.1	2.9	120.17	3.16
5.9	105.9	0.7	103.32	2.44	17.6	125.0	2.2	119.69	4.24
6.4	105.7	1.7	105.90	0.19	18.1	125.5	2.5	119.15	5.06
6.8	106.8	2.2	107.76	0.90	18.6	125.2	8.1	118.54	5.32
7.3	107.3	3.0	109.86	2.39	19.1	122.0	9.8	117.87	3.38
7.8	108.3	4.0	111.73	3.17	19.5	120.4	8.5	117.29	2.58
8.3	109.7	4.0	113.34	3.37	20.0	114.0	26.6	116.52	2.21
8.8	112.0	4.8	114.86	2.55	20.5	110.0	34.6	115.70	5.18
9.3	116.1	2.2	116.15	0.04	21.0	98.7	27.4	114.82	16.33
9.8	117.2	2.5	117.27	0.06	21.5	100.1	33.4	113.89	13.77
10.3	116.5	6.5	118.24	1.49	22.0	104.3	35.2	112.91	8.25
10.8	115.7	8.1	119.07	2.91	22.5	101.2	27.4	111.88	10.56
11.2	117.4	8.2	119.63	1.90	23.0	123.5	39.1	110.81	10.27
11.7	116.8	8.9	120.22	2.93	23.5	115.3	26.7	109.69	4.86

Figure 3. Rotation curve for spiral galaxy M33. Red points are measured observational values and blue line is computed $\overline{v}\left(r\right)$ by Formula (56), where $\delta =5.7\times {10}^{-6}$, $\zeta =3.62\times {10}^{10}$, $\Lambda ={10}^{-52}$${\mathrm{m}}^{-2}$, and $M=1.5\times {10}^3{M}_{\odot }$.

4. Discussion and Concluding Remarks

This paper presents the results of our research regarding the Schwarzschild–de Sitter metric of the nonlocal $\sqrt{dS}$ gravity model (1). We found the Schwarzschild–de Sitter metric in the form of $A\left(r\right)$ (53), which corresponds to the weak gravity approximation and the linearization of the nonlinear differential Equation (40). The obtained results were tested on the rotation curves of the Milky Way and the spiral galaxy M33. The calculated and measured values of circular velocities are in good agreement.

Some additional explanations should be given to some parts of these investigations. First, we need to clarify why the weak gravitational field approximation works well here. On the one hand, we derived the Schwarzschild–de Sitter metric away from the massive spherically symmetric body. And on the other hand, we applied the obtained formula for the circular motion of the test body to the circular velocities in spiral galaxies far from their centers where the black hole is located. Recall that the rotation curves were observed in the domain 9.5–26.5 kpc for the Milky Way galaxy [36] and 0.5–23.5 kpc for the M33 galaxy [37]. In the Lambda Cold Dark Matter model, it is assumed that dark matter plays an important role in the mentioned domains. However, there is no dark matter in our nonlocal model. The good agreement between observational measurements and theoretical predictions tells us that the role of dark matter can be played by the nonlocality in the presence of the cosmological constant $\Lambda$ in the $\sqrt{dS}$ gravity model.

In the process of obtaining solution (48), we used ansatz (15), constraints (20), and equality $B=\frac{1}{A}$. To consider the consistency of these conditions, we can start from scalar curvature R (39) corresponding to the solution (49), i.e.,

$$\begin{array}{c}\hfill R\left(r\right)=4\Lambda -\phi \left(r\right),\mathrm{where}\phi \left(r\right)=\frac{\delta \sqrt{\zeta \Lambda }{e}^{-r\sqrt{\zeta \Lambda }}}{r}.\end{array}$$

(57)

Ansatz (15) is currently the only known tool for solving equations of motion (12). According to the equations of motion (19) and conditions (20) for the nonlocal operator $\mathcal{F}(\square )$, there exists some scalar function $\eta \left(r\right)$ such that we can write

$$\begin{array}{c}\hfill G_{\mu \nu }+\Lambda g_{\mu \nu }=\eta \left(r\right)g_{\mu \nu }.\end{array}$$

(58)

Taking the trace of (58), we obtain the scalar curvature

$$\begin{array}{c}\hfill R=4\Lambda -4\eta \left(r\right).\end{array}$$

(59)

By choosing $\eta \left(r\right)=\frac{1}{4}\phi \left(r\right)$, we obtain (57), which justifies choice (58), although there may be other possibilities instead of $\eta \left(r\right)$. Combining (58) with (26), we have

$$\begin{array}{c}\hfill B{R}_{00}+A{R}_{11}=\frac{A^{\prime }}{r}+\frac{A{B}^{\prime }}{rB}=(\Lambda -\frac{1}{2}\phi +\eta )(-BA+AB)=0,\end{array}$$

(60)

which gives $A^{\prime }B+A{B}^{\prime }=0$; that is, $AB=C$, where C is a constant that can be given the value $C=1$. According to the above consideration, the applied procedure for finding our solution is consistent. We also expect that there is a unique exact solution to equations of motion (19).

It is worth noting that Equation (47) can be obtained from Equation (44) in the following way. We express R in terms of $\alpha$ as $R=4\Lambda +\frac{2\alpha }{r^2}+\frac{4{\alpha }^{\prime }}{r}+{\alpha }^{″}$ (39) and put it in Equation (44). After differentiation, we have

$$\begin{array}{cc}\hfill & 16\Lambda q{r}^4{\alpha }^{″}\left(r\right)+4q{r}^4{\alpha }^{″}{\left(r\right)}^2+16{\Lambda }^{2}q{r}^4+64\Lambda q{r}^3{\alpha }^{\prime }\left(r\right)+32q{r}^3{\alpha }^{\prime }\left(r\right){\alpha }^{″}\left(r\right)\hfill \\ \hfill & +16q{r}^2\alpha \left(r\right){\alpha }^{″}\left(r\right)+64q{r}^2{\alpha }^{\prime }{\left(r\right)}^2+32\Lambda q{r}^2\alpha \left(r\right)+64qr\alpha \left(r\right){\alpha }^{\prime }\left(r\right)+16q\alpha {\left(r\right)}^2\hfill \\ \hfill & -4\Lambda r^4{\alpha }^{\prime \prime \prime \prime }\left(r\right)+r^4{\alpha }^{\prime \prime \prime }{\left(r\right)}^2-2r^4{\alpha }^{\prime \prime \prime \prime }\left(r\right){\alpha }^{″}\left(r\right)-24\Lambda r^3{\alpha }^{\prime \prime \prime }\left(r\right)-8r^3{\alpha }^{\prime \prime \prime \prime }\left(r\right){\alpha }^{\prime }\left(r\right)\hfill \\ \hfill & -4r^3{\alpha }^{\prime \prime \prime }\left(r\right){\alpha }^{″}\left(r\right)-4r^2\alpha \left(r\right){\alpha }^{\prime \prime \prime \prime }\left(r\right)-8\Lambda r^2{\alpha }^{″}\left(r\right)+12r^2{\alpha }^{″}{\left(r\right)}^2\hfill \\ \hfill & -52r^2{\alpha }^{\prime \prime \prime }\left(r\right){\alpha }^{\prime }\left(r\right)-32r\alpha \left(r\right){\alpha }^{\prime \prime \prime }\left(r\right)-48\alpha \left(r\right){\alpha }^{″}\left(r\right)+16\Lambda r{\alpha }^{\prime }\left(r\right)\hfill \\ \hfill & +36{\alpha }^{\prime }{\left(r\right)}^2-24r{\alpha }^{\prime }\left(r\right){\alpha }^{″}\left(r\right)-16\Lambda \alpha \left(r\right)=0.\hfill \end{array}$$

(61)

In the next step, we perform linearization by removing all quadratic terms in $\alpha$ and its derivatives. We also ignore $\Lambda$ with respect to $\frac{\alpha }{r^2}$. Finally, we obtain Equation (47), with the only difference that factor q is multiplied by four.

Regarding the applicability of the obtained formula for the circular velocity (56) at smaller distances, such as the solar system, the following should be noted. The circular velocity $\overline{v}\left(r\right)$ depends on three terms: (i) $\frac{GM}{c^{2}r}$, (ii) $-\frac{\Lambda r^2}{3}$, and (iii) $\frac{\delta }{\sqrt{q}r}\left(\frac{2}{\sqrt{q}r}-\frac{1}{2}\right)-\delta \left(\frac{1}{2}+\frac{3}{2\sqrt{q}r}+\frac{2}{q{r}^2}\right)e^{-\sqrt{q}r}$. The third term depends linearly on $\delta$, and with a fixed $q(=\zeta \Lambda )$, its value can be controlled by choosing the appropriate value of $\delta$. One can always take a small enough value of $\delta$, e.g., $\delta <|8.2\times {10}^{-14}|$, so that the first term has a dominant role since the second term has an important meaning only at distances of the size of the visible universe. Therefore, the velocity Formula (56) is also valid for the solar system.

The main new results presented in this article can be summarized as follows:

• In the approximation of the weak gravitational field, a fourth-order linear differential equation for the Schwarzschild–de Sitter metric was obtained (47).
• A general solution (48) of Equation (47) was found.
• A particular solution of $\alpha \left(r\right)$ was found (49) such that it satisfies the necessary condition that it tends to zero when the nonlocality vanishes.
• The obtained theoretical formula for circular velocity (56) was tested on the rotation curves of two spiral galaxies: the Milky Way and M33. The agreement between the calculated and measured circular velocities is good, especially for the Milky Way, see Figure 2 and Figure 3 and the corresponding tables. To our knowledge, this is the first good description of “the Keplerian decline in the Milky Way rotation curve” by some modified gravity model.

In summary, it can be said that the presented results in this paper are encouraging and deserve further research, especially taking into account the mass distribution in spiral galaxies using [38]. Bearing in mind also previously obtained results on the evolution of the universe [17,27], where the effects that are usually attributed to dark energy and dark matter can be described by the nonlocality of the gravity model $\sqrt{dS}$, we will continue with the further study of this model of nonlocal de Sitter gravity.