Symmetric Properties of λ-Szász Operators Coupled with Generalized Beta Functions and Approximation Theory

Abstract

This research work focuses on $\lambda$-Szász–Mirakjan operators coupling generalized beta function. The kernel functions used in $\lambda$-Szász operators often possess even or odd symmetry. This symmetry influences the behavior of the operator in terms of approximation and convergence properties. The convergence properties, such as uniform convergence and pointwise convergence, are studied in view of the Korovkin theorem, the modulus of continuity, and Peetre’s K-functional of these sequences of positive linear operators in depth. Further, we extend our research work for the bivariate case of these sequences of operators. Their uniform rate of approximation and order of approximation are investigated in Lebesgue measurable spaces of function. The graphical representation and numerical error analysis in terms of the convergence behavior of these operators are studied.

1. Introduction

Szász [1] presented a generalization of Bernstein polynomials [2] to investigate approximation properties on unbounded intervals, i.e., $[0,\infty )$ as follows:

$$\begin{array}{c}\hfill P_s(\hslash ;y)=\sum _{k=0}^{\infty }\hslash \left({\displaystyle \frac{k}{s}}\right)p_{s,k}\left(y\right),\end{array}$$

(1)

where $y\in [0,\infty ),s\in N$ and $p_{s,k}\left(y\right)=e^{-sy}{\displaystyle \frac{{\left(sy\right)}^k}{k!}}.$

These operators are introduced in the 1950s and have been extensively studied by mathematicians over the years to achieve the flexibility in the approximation properties. The symmetry of the kernel affects how well Szász operators can approximate functions. Symmetric kernels tend to preserve certain functional forms or properties of functions being approximated, leading to specific convergence behaviors. Many mathematicians constructed various sequences of operators based on the classical Szász–Mirakjan operators given by (1). Recently, various scientists are working in the other branches of sciences like medical science, robotics, computer science, and others [3,4,5,6,7] in terms of these types of sequences of linear positive operators. In the recent past, several mathematicians contributed a healthy literature in approximation theory via linear positive operators, viz. Braha et al. [8], Özger et al. [9], Ansari et al. [10], Khan et al. [11], Acar et al. [12], Alotaibi [13], Mohiuddine et al. [14], Nasiruzzaman et al. [15], Çiçek et al. [16], Cai et al. [17], Aslan et al. [18,19], and Izgi [20]. In continuation, Qi et al. [21] presented Szász–Mirakjan operators based on shape parameter $\lambda \in [-1,1]$ as follows:

$$S_{s,\lambda }(\hslash ;y)=\sum _{k=0}^{\infty }{\tilde{t}}_{s,k}(\lambda ;y)\hslash \left({\displaystyle \frac{k}{s}}\right),$$

(2)

where

$$\begin{array}{ccc}\hfill {\tilde{t}}_{s,0}(\lambda ;y)& =& p_{s,0}\left(y\right)-{\displaystyle \frac{\lambda }{s+1}}{t}_{s+1,1}\left(y\right),\hfill \\ \hfill {\tilde{t}}_{s,k}(\lambda ;y)& =& p_{s,k}\left(y\right)+\lambda \left({\displaystyle \frac{s-2k+1}{s^2-1}}{p}_{s+1,k}\left(y\right)-{\displaystyle \frac{s-2k-1}{s^2-1}}{p}_{s+1,k+1}\left(y\right)\right),1\le k\le \infty .\hfill \end{array}$$

(3)

Many generalizations are investigated for the operators is given by (2), viz. Özger et al. [9] constructed a sequence of Kantorovich variants of $\lambda$-Schurer operators to approximate Lebesgue measurable class. For $s\in \mathbb{N}$ and $\nu >0$, the functional (see [22]), $C_{s,k}^{\nu }:C[0,1]\to \mathbb{R}$, is given by

$$\begin{array}{ccc}\hfill C_{s,k}^{\nu }\left(t\right)& =& {\int }_0^1{D}_{s,k}^{\nu }\left(t\right)\hslash \left(t\right)dt(k=1,2,\dots ,s-1),\hfill \\ \hfill C_{s,0}^{\nu }\left(t\right)& =& \hslash \left(0\right),C_{s,s}^{\nu }\left(t\right)=\hslash \left(1\right),\hfill \end{array}$$

(4)

where

$$\begin{array}{c}\hfill D_{s,k}^{\nu }\left(t\right)={\displaystyle \frac{t^{k\nu -1}{(1-t)}^{(s-k)\nu -1}}{B(k\nu ,(s-k\left)\nu \right)}},\end{array}$$

(5)

and

$$B(a,b)={\int }_0^1{t}^{a-1}{(1-t)}^{b-1}dt(a,b>0).$$

Rao et al. [23] introduced a sequence of classical Szász operators, coupling generalized beta function as follows:

$$S_s^{\nu }(\hslash ;y)=\sum _{k=0}^{\infty }{C}_{s,k}^{\nu }\left(t\right)p_{s,k}\left(y\right)\hslash \left(t\right).$$

(6)

Motivated with the above development of the literature, we construct a new sequence of $\lambda -$Szász operators coupling generalized beta function:

$${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)=\sum _{k=0}^{\infty }{C}_{s,k}^{\nu }\left(t\right){\tilde{t}}_{s,k}(\lambda ;y)\hslash \left(t\right),$$

(7)

where ${\tilde{t}}_{s,k}\left(y\right)$ and $C_{s,k}^{\nu }\left(t\right)$ are defined in Equations (3) and (4), respectively. Szász operators, named after the mathematician Gabor Sász, are a class of linear positive operators used in approximation theory and functional analysis. They are typically associated with the properties of symmetry and positivity. Here’s how they relate to symmetry:

Definition and symmetry: Szász operators are constructed using a kernel that exhibits certain symmetrical properties, such as being symmetric or involving symmetric functions. Symmetry in the context of Szász operators can refer to properties such as the following:

Evenness or oddness: The kernel functions used in Szász operators often possess even or odd symmetry. This symmetry influences the behavior of the operator in terms of approximation and convergence properties. Approximation properties: The symmetry of the kernel affects how well Szász operators can approximate functions. Symmetric kernels tend to preserve certain functional forms or properties of functions being approximated, leading to specific convergence behaviors.

Functional analysis perspective: in functional analysis, the symmetry of operators like Szász operators can be studied in terms of their action on function spaces and the preservation of certain structural properties under approximation.

Applications: understanding the symmetry properties of Szász operators is crucial in applications ranging from numerical analysis to signal processing, where approximating functions with known symmetries or preserving symmetrical properties is important.

In summary, Szász operators exhibit symmetry through their construction and the properties of their kernel functions, impacting their approximation capabilities and their role in functional analysis contexts.

Now, to derive the lemmas for the approximation results of sequences of operators given in (7), we consider test functions and the central moments as $e_k\left(t\right)=t^k$ and ${\eta }_k\left(t\right)={(t-y)}^k$, $k\in \{0,1,2\}$. To present this research work, it is divided into some sections. Sections one and two hold for the introductory and preliminary parts of this research work. In sections three and four, approximation theorems and graphical analysis are investigated. In the last two sections, we study the bivariate version of the operators given in (7), and their numerical graphical analysis is discussed.

2. Some Estimates and Approximation Results

Lemma 1

([23]). For the operators $S_s^y(.;.)$ given by (6). Then, we have

$$\begin{array}{ccc}\hfill S_s^{\nu }{e}_0;y)& =& 1,\hfill \\ \hfill S_s^{\nu }(e_1;y)& =& y,\hfill \\ \hfill S_s^{\nu }(e_2;y)& =& \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)y^2+\left({\displaystyle \frac{\nu +1}{s\nu +1}}\right)y,\hfill \\ \hfill S_s^{\nu }(e_3;y)& =& \left({\displaystyle \frac{s^2{\nu }^2}{s^2{\nu }^2+3s\nu +2}}\right)y^3+\left({\displaystyle \frac{3s\nu (\nu +1)}{s^2{\nu }^2+3s\nu +2}}\right)y^2+\left({\displaystyle \frac{{\nu }^2+3\nu +2}{s^2{\nu }^2+3s\nu +2}}\right)y,\hfill \\ \hfill S_s^{\nu }(e_4;y)& =& \left({\displaystyle \frac{s^3{\nu }^3}{s^3{\nu }^3+6s^2{\nu }^2+11s\nu +6}}\right)y^4+\left({\displaystyle \frac{6s^2{\nu }^2(\nu +1)}{s^3{\nu }^3+6s^2{\nu }^2+11s\nu +6}}\right)y^3\hfill \\ & +& \left({\displaystyle \frac{7s{\nu }^3+18s{\nu }^2+11s\nu }{s^3{\nu }^3+6s^2{\nu }^2+11s\nu +6}}\right)y^2+\left({\displaystyle \frac{{\nu }^3+6{\nu }^2+11\nu +6}{s^3{\nu }^3+6s^2{\nu }^2+11s\nu +6}}\right)y.\hfill \end{array}$$

Lemma 2.

Let ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(.;.)$ be given by (7). We have

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }(1;y)& =& 1,\hfill \\ \hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }(t;y)& =& y+\lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s^2-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right]=F_s,\hfill \\ \hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }(t^2;y)& =& \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)y^2+\left({\displaystyle \frac{\nu +1}{s\nu +1}}\right)y\hfill \\ & +& \lambda \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)\left[{\displaystyle \frac{2}{s(s-1)}}y-{\displaystyle \frac{4(s+1)}{s^2(s-1)}}{y}^2+{\displaystyle \frac{e^{-(s+1)y}-1}{s^2(s-1)}}\right]\hfill \\ & +& {\displaystyle \frac{s}{s\nu +1}}\left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right].\hfill \end{array}$$

Proof. 

For $k=0$, then

$$\begin{array}{ccc}\hfill \left(i\right){\mathsf{\Pi }}_{s,\lambda }^{\nu }(1;y)& =& \sum _{k=0}^{\infty }{C}_{s,k}^{\nu }\left(h\right){\tilde{t}}_{s,k}(\lambda ,y)\hfill \\ & =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\tilde{t}}_{s,k}(\lambda ,y)}{B(k\nu ,(s-k\left)\nu \right)}}\times B(k\nu ,(s-k)\nu )\hfill \\ & =& \sum _{k=0}^{\infty }{\tilde{t}}_{s,k}(\lambda ,y)\hfill \\ & =& 1.\hfill \end{array}$$

For $k=1$, then

$$\begin{array}{ccc}\hfill \left(ii\right){\mathsf{\Pi }}_{s,\lambda }^{\nu }(t;y)& =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\tilde{t}}_{s,k}(\lambda ,y)}{B(k\nu ,(s-k\left)\nu \right)}}\times B(k\nu +1,(s-k)\nu )\hfill \\ & =& S_s^{\nu }(t;y)+\lambda [\sum _{k=0}^{\infty }{\displaystyle \frac{k}{s}}\left({\displaystyle \frac{s-2k+1}{s^2-1}}\right)p_{s+1,k}\left(y\right)\hfill \\ & -& \sum _{k=0}^{\infty }{\displaystyle \frac{k}{s}}\left({\displaystyle \frac{s-2k-1}{s^2-1}}\right)p_{s+1,k+1}\left(y\right)]\hfill \\ & =& y+\lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s^2-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right].\hfill \end{array}$$

If $k=2$, then

$$\begin{array}{ccc}\hfill \left(iii\right){\mathsf{\Pi }}_{s,\lambda }^{\nu }(t^2;y)& =& \sum _{k=0}^{\infty }{\displaystyle \frac{{\tilde{t}}_{s,k}(\lambda ,y)}{B(k\nu ,(s-k\left)\nu \right)}}\times B(k\nu +2,(s-k)\nu )\hfill \\ & =& S_s^{\nu }(t^2;y)+\lambda [\left({\displaystyle \frac{s\nu }{s\nu +1}}\right)\sum _{k=0}^{\infty }{\displaystyle \frac{k^2}{s^2}}\left({\displaystyle \frac{s-2k+1}{s^2-1}}\right)p_{s+1,k}\left(y\right)\hfill \\ & -& \sum _{i=0}^{\infty }{\displaystyle \frac{i^2}{s^2}}\left({\displaystyle \frac{s-2i-1}{s^2-1}}\right)p_{s+1,k+1}\left(y\right)]\hfill \\ & +& \lambda [\left({\displaystyle \frac{1}{s\nu +1}}\right)\sum _{k=0}^{\infty }{\displaystyle \frac{k}{s}}\left({\displaystyle \frac{s-2k+1}{s^2-1}}\right)p_{s+1,k}\left(y\right)\hfill \\ & -& \sum _{k=0}^{\infty }{\displaystyle \frac{k}{s}}\left({\displaystyle \frac{s-2k-1}{s^2-1}}\right)p_{s+1,k+1}\left(y\right)]\hfill \\ & =& \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)y^2+\left({\displaystyle \frac{\nu +1}{s\nu +1}}\right)y+\lambda \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)\hfill \\ & \times & \left[{\displaystyle \frac{2}{s(s-1)}}y-{\displaystyle \frac{4(s+1)}{s^2(s-1)}}{y}^2+{\displaystyle \frac{e^{-(s+1)y}-1}{s^2(s-1)}}\right]\hfill \\ & +& {\displaystyle \frac{s}{s\nu +1}}\left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right].\hfill \end{array}$$

□

Lemma 3.

Let ${\xi }_{\nu }^k\left(t\right)={(t-y)}^k,k=0,1,2$. Using Lemma 2, one can easily calculate the central moments of Szász–Mirakjan coupling generalized Beta operators as follows:

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{\nu }^0;y)& =& 1,\hfill \\ \hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{\nu }^1;y)& =& \lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}-2y}{s(s-1)}}\right]=A_s^{\nu },\hfill \\ \hfill {\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{\nu }^2;y)& =& \left({\displaystyle \frac{s\nu }{s\nu +1}}-1\right)y^2+\left({\displaystyle \frac{\nu +1}{s\nu +1}}\right)y\hfill \\ & +& \lambda \left[{\displaystyle \frac{(1+2mu)e^{-(s+1)y}-(1-2s)y-4y^2}{s^2(s-1)}}\right]=B_{s,\lambda }^{\nu }.\hfill \end{array}$$

Definition 1

([24]). Let $\omega (\hslash ;\varphi )$ be the modulus of continuity. Then, for continuous function ℏ defined on closed interval $[0,b],b<\infty ,$ we have

$$\begin{array}{c}\hfill \omega (\hslash ;\varphi )=\underset{|y_1-y_2|\le \varphi }{sup}|\hslash \left(y_1\right)-\hslash \left(y_2\right)|,y_1,y_2\in [0,\infty ).\end{array}$$

For $\hslash \in [0,b]b<\infty$ and $\hslash \in C[0,\infty )$ and $\varphi >0$, we obtain

$$|\hslash \left(y_1\right)-\hslash \left(y_2\right)|\le \left(1+{\displaystyle \frac{|y_1-y_2|}{\varphi }}\right)\omega (\hslash ;\varphi ).$$

(8)

Theorem 1.

For ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(.;.)$ the operators defined by (7) and for every $\hslash \in C[0,\infty )\cap \{\hslash :y\ge 0,{\displaystyle \frac{\hslash \left(y\right)}{1+y^2}}$ is convergent as $y⟶\infty \}$, then ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)\rightrightarrows \hslash$, where ⇉ denotes the uniform convergence.

Proof. 

By Krovkin-type property $\left(iv\right)$ of Theorem $4.1.4$ in [25], it is enough to show that ${\mathsf{\Pi }}_{s,\lambda }^v(e_j;v)⟶e_j,$ for $j\in \{0,1,2\}$. By Lemma 2, it is clear ${\mathsf{\Pi }}_{s,\lambda }^v(e_0;y)⟶e_0\left(y\right)$ as $s⟶\infty$ and for $j=1$

$$\begin{array}{c}\hfill \underset{s}{lim}{\mathsf{\Pi }}_{s,\lambda }^{\nu }(e_1;y)=li{m}_{s⟶\infty }\left(y+\lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s^2-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right]\right)=e_1\left(y\right).\end{array}$$

Similarly, for $j=2$, ${\mathsf{\Pi }}_{s,\lambda }^v(e_2;y)⟶e_2\left(y\right)$. Hence, we arrived at the desired proof of Theorem 1. □

Theorem 2.

For $\hslash \in C_B[0,\infty )$ and ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(.;.)$ given by (7), we have

$$\begin{array}{c}\hfill |{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\le 2\omega (\hslash ;\varphi ),\mathit{where}\varphi =\sqrt{{\mathsf{\Pi }}_{s,\lambda }^{\nu }(B_{s,\lambda }^{\nu };y)}.\end{array}$$

Proof. 

In direction of the relation (8), we obtain

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le \left\{1+{\varphi }^{-1}\sqrt{B_{s,\lambda }^{\nu };y}\right\}\omega (\hslash ;\varphi ).\end{array}$$

Choosing $\varphi =\sqrt{{\mathsf{\Pi }}_{s,\lambda }^{\nu }(B_{s,\lambda }^{\nu };y)}$ completes the proof of Theorem 2. □

3. Graphical and Numerical Analysis

In this section, we examine the convergence behavior of the operator defined by (7).

Example 1.

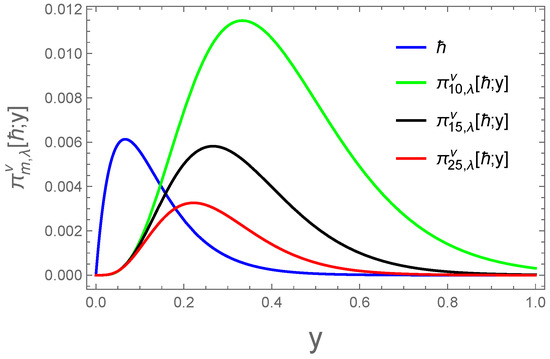
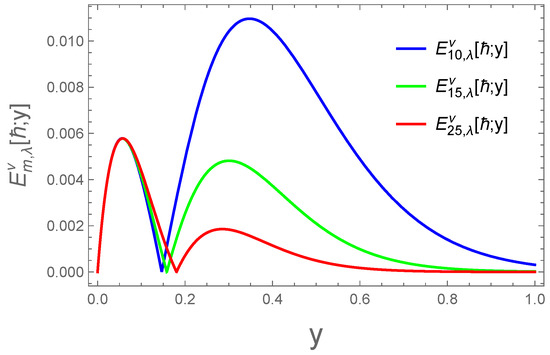
(a) For the function $\hslash \left(y\right)={\displaystyle \frac{1}{4}}{e}^{-15y}y,$ to analyze the numerical behavior of the operator (7), we compute the error using the formula

$E_{s,\lambda }(\hslash ;y)=|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-(\hslash y)|.$ Dor different values of s, specifically 10, 15, and 25, for a fix values of $\nu =0.3,\lambda =0.5$. Then, Table 1 provides the numerical error values for the chosen parameters. Furthermore, Figure 1 and Figure 2 graphically illustrate the convergence behavior and the error approximation of the operator (7) for the same function $\hslash \left(y\right)={\displaystyle \frac{1}{4}}{e}^{-15y}y$ and the parameter values $s=10,15,25.$

Table 1. The error approximation of operators ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)to\hslash \left(y\right)={\displaystyle \frac{1}{4}}{e}^{-15y}y$ for 10, 15, 25.

y	$|{\mathbf{\Pi }}_{10,\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$	$|{\mathbf{\Pi }}_{15,\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$	$|{\mathbf{\Pi }}_{,25\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$
0.1	0.00855716	0.00868693	0.00888307
0.2	0.00331262	0.000933993	0.000881886
0.3	0.010011	0.00441485	0.0014342
0.4	0.0103584	0.00364727	0.00106068
0.5	0.00776931	0.00208241	0.000478021
0.6	0.00488011	0.000981387	0.000172209
0.7	0.00272745	0.00040907	0.000054154
0.8	0.00140172	0.000156346	0.0000155106
0.9	0.000676062	0.0000559933	4.14678 × ${10}^{-6}$

Figure 1. Convergence of operator ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)$$to\hslash \left(y\right)={\displaystyle \frac{1}{4}}{e}^{-15y}y$ for $\lambda =0.5,s=10,15,25$.

Figure 2. Error approximation $E_{s,\lambda }(\hslash ;y)=|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-(\hslash y)|$.

Example 2.

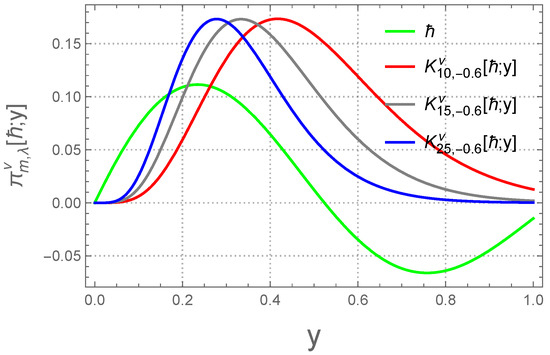
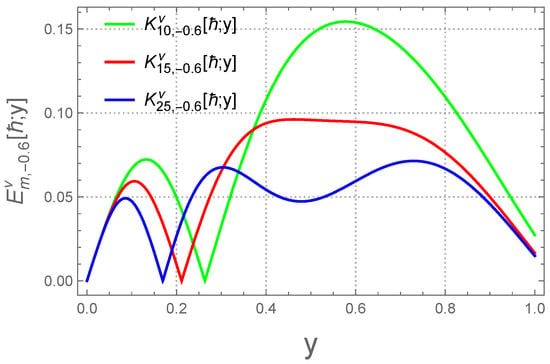
(b) For the function $\hslash \left(y\right)={\displaystyle \frac{1}{7}}{e}^{-y}Sin6y.$ To analyze the numerical behavior of the operator (7), for the different value of $\lambda =-0.6$ and the same value of $s=10,15,25.$ Table 2 illustrates the numerical behavior for the different values of $s=10,15,25$ with the help of $\lambda =-0.6$ and $\nu =0.5$. Figure 3 and Figure 4 show the convergence behavior of the operators (7).

Table 2. The error approximation of operators ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)to\hslash \left(y\right)={\displaystyle \frac{1}{4}}{e}^{-15y}y$ for 10, 15, 25.

y	$|{\mathbf{\Pi }}_{10,\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$	$|{\mathbf{\Pi }}_{15,\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$	$|{\mathbf{\Pi }}_{,25\mathit{\lambda }}^{\mathit{\nu }}(\mathit{\hslash };\mathit{y})-\left(\mathit{\hslash }\mathit{y}\right)|$
0.1	0.0668425	0.05911693	0.0473892
0.2	0.0496822	0.00973307	0.0267445
0.3	0.032826	0.0654061	0.0.0675773
0.4	0.107994	0.0938944	0.0542833
0.5	0.146655	0.0958518	0.0478268
0.6	0.153884	0.0947532	0.000172209
0.7	0.13949	0.0908188	0.0706674
0.8	0.109585	0.0765646	0.0667936
0.9	0.0696738	0.0499619	0.0457327

Figure 3. Convergence of operator ${\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)$$to\hslash \left(y\right)={\displaystyle \frac{1}{7}}{e}^{-y}Sin6y.$ for $\lambda =-0.6,s=10,15,25$.

Figure 4. Error approximation $E_{s,\lambda }(\hslash ;y)=|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-(\hslash y)|$.

4. Local Approximation

In this section, we discuss direct approximation results for $\hslash \in C_B[0,\infty ),$ endowed with the norm. For any $\hslash \in C_B[0,\infty )$ $\left|\right|\hslash \left|\right|=su{p}_{0\le y<\infty }|\hslash \left(y\right)|$. For any $\hslash \in C_B[0,\infty )$ and $\varphi >0,$ Peetre’s K-functional is given as

$$\begin{array}{c}\hfill K_2(\hslash ;\varphi )=inf\left\{\left|\right|\hslash -g\left|\right|+\varphi \left|\right|g^{″}\left|\right|:g\in C_B^2[0,\infty )\right\},\end{array}$$

where $C_B^2[0,\infty )=\left\{g\in C_B[0,\infty ):g^{\prime },g^{″}\in C_B[0,\infty )\right\}$.

By DeVore and Lorentz ([24] p. 177, Theorem $2.4$), there exist $C>0$ such that

$$K_2(\hslash ;\varphi )\le C(\hslash ;\sqrt{\varphi }).$$

(9)

Second-order modulus of continuity ${\omega }_2(\hslash ;\varphi )$ and is given as

$$\begin{array}{c}\hfill {\omega }_2(\hslash ;\sqrt{\varphi })=su{p}_{0<\hslash \le \sqrt{\varphi }}su{p}_{y\in [0,\infty )}|\hslash (y+2t)-2\hslash (y+t)+\hslash \left(y\right)|.\end{array}$$

Now, we consider the auxiliary operator ${\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(.;.)$ as

$${\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)={\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)+\hslash \left(y\right)-\hslash \left(y+\lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s^2-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right]\right).$$

(10)

Lemma 4.

Let $\hslash \in C_B^2[0,\infty )$ and $y\ge 0$. Then, we obtain

$$\begin{array}{c}\hfill |{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\le {\xi }_{s,\lambda }^{\nu }\left(y\right)\left|\right|f^{″}\left|\right|,\end{array}$$

where

$$\begin{array}{ccc}\hfill {\xi }_{s,\lambda }^{\nu }\left(y\right)& =& \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)y^2+\left({\displaystyle \frac{\nu +1}{s\nu +1}}\right)y\hfill \\ & +& \lambda \left({\displaystyle \frac{s\nu }{s\nu +1}}\right)\left[{\displaystyle \frac{2}{s(s-1)}}y-{\displaystyle \frac{4(s+1)}{s^2(s-1)}}{y}^2+{\displaystyle \frac{e^{-(s+1)y}-1}{s^2(s-1)}}\right]\hfill \\ & +& {\displaystyle \frac{s}{s\nu +1}}\left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right].\hfill \end{array}$$

Proof. 

In the light of auxiliary operators defined in (10), we yield

$${\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(1;y)=1,{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(A_s^{\nu };y)=0\mathrm{and}|{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)|\le 3||\hslash ||.$$

(11)

In view of Taylor’s series expansion, for $\hslash \in C_B^2[0,\infty ),$ we obtain

$$g\left(t\right)=\hslash \left(y\right)+(t-y){\hslash }^{\prime }\left(y\right)+{\int }_y^t(t-v){\hslash }^{″}\left(v\right)dv.$$

(12)

Apply the auxiliary operators in the above Equation (10), we yield

$$\begin{array}{c}\hfill {\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)={\hslash }^{\prime }\left(y\right){\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(t-y;y)+{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }\left({\int }_y^1(t-v){\hslash }^{″}\left(v\right)dv;y\right).\end{array}$$

On account of (10) and (11), we obtain

$$\begin{array}{c}\hfill {\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)={\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }\left({\int }_y^1(t-v){(\hslash )}^{″}\left(v\right)dv;y\right)\end{array}$$

$$\begin{array}{c}\hfill ={\mathsf{\Pi }}_{s,\lambda }^{\nu }\left({\int }_y^1(t-y){\hslash }^{″}\left(y\right)dv;y\right)-{\int }_y^{F_s}\left(F_s-v\right)h^{″}\left(v\right)dv,\end{array}$$

(13)

where $F_s=y+\lambda \left[{\displaystyle \frac{1-e^{-(s+1)y}}{s(s^2-1)}}-{\displaystyle \frac{2y}{s(s-1)}}\right].$

Since

$$\left|{\int }_y^1(t-v){\hslash }^{″}\left(v\right)dv\right|\le {(t-y)}^2\left|\right|{\hslash }^{″}\left|\right|.$$

(14)

Therefore, we yield

$$\begin{array}{c}\hfill \left|{\int }_y^{F_s}\left(F_s-v\right){\hslash }^{″}\left(v\right)dv\right|\\ \hfill \le {\left(F_s-y\right)}^2\left|\right|{\hslash }^{″}\left|\right|.\end{array}$$

(15)

Applying (14) and (15) in (13), we obtain

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le \left\{{\mathsf{\Pi }}_{s,\lambda }^{\nu }({(t-y)}^2;y)+\left(F_s\right)\right\}\left|\right|{\hslash }^{″}\left|\right|\\ \hfill ={\xi }_{s,\lambda }^{\nu }\left(y\right){\left|\right|}^{\hslash ″}\left|\right|.\end{array}$$

Hence, we arrived at our desired result. □

Theorem 3.

Let $\hslash \in C_B^2[0,\infty ).$ Then, we have

$$\begin{array}{c}\hfill |{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\le C{\omega }_2(\hslash ;\sqrt{{\xi }_{s,\lambda }^{\nu }\left(y\right)})+\omega (\hslash ;{\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{s,\lambda }^{\nu }\left(y\right);y)),\end{array}$$

where ${\xi }_{s,\lambda }^{\nu }\left(y\right)$ is found in Lemma 4 and $C>0$.

Proof. 

For $g\in C_B^2[0,\infty )$, $\hslash \in C_B[0,\infty )$ and the auxiliary operator ${\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(.;.)$, we have

$$\begin{array}{c}\hfill |{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\le |{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash -g;y)|+|(\hslash -g)\left(y\right)|+|{\widehat{\mathsf{\Pi }}}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\\ \hfill +\left|\hslash \left(F_s\right)-\hslash \left(y\right)\right|.\end{array}$$

From Lemma 4 and Equation (11), we yield

$$\begin{array}{ccc}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|& \le & 4\left|\right|\hslash -g\left|\right|+|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\hfill \\ & +& \left|\hslash \left(F_s\right)-\hslash \left(y\right)\right|\hfill \\ & \le & 4\left|\right|\hslash -g\left|\right|+{\xi }_{s,\lambda }^{\nu }\left(y\right)\left|\right|g^{″}\left|\right|+\omega (\hslash ;{\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{s,\lambda }^{\nu }\left(y\right);y)).\hfill \end{array}$$

Using Peetre’s K-functional, we have

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le C{\omega }_2\left(\hslash ;\sqrt{{\xi }_{s,\lambda }^{\nu }\left(y\right)}\right)+\omega (\hslash ;{\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{s,\lambda }^{\nu }\left(y\right);y)).\end{array}$$

Hence, we completes the proof of Theorem 3. We recall Lipschitz-type space here [26] as

$Li{p}_M^{{\rho }_1{\rho }_2}\left(\gamma \right):=\left\{\hslash \in C_B[0,\infty ):|\hslash \left(t\right)-\hslash \left(y\right)|\le M{\displaystyle \frac{{|t-y|}^{\gamma }}{{(t+{\rho }_{1}y+{\rho }_2{y}^2)}^{\gamma /2}}}:y,t\in (0,\infty )\right\},$ where $M>0$ is a fixed constant and $0<\gamma \le 1$. ${\rho }_1>0$, ${\rho }_2>0$, are two real values. □

Theorem 4.

For $y\in (0,\infty )$, $\hslash \in Li{p}_M^{{\rho }_1,{\rho }_2}\left(\gamma \right)$ and sequence of operators defined by (7), one obtain

$$\left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le M{\left({\displaystyle \frac{{\varphi }_{s,\lambda }^{\nu }\left(y\right)}{{\rho }_{1}y+{\rho }_2{y}^2}}\right)}^{{\displaystyle \frac{\gamma }{2}}},$$

(16)

where $\gamma \in (0,1]$ and ${\varphi }_{s,\lambda }^{\nu }\left(y\right)={\mathsf{\Pi }}_{s,\lambda }^{\nu }({\xi }_{s,\lambda }^2;y).$

Proof. 

First, we consider $y\in (0,\infty )$ and $\gamma =1$ we yield

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le {\mathsf{\Pi }}_{s,\lambda }^{\nu }\left(\right|\hslash \left(t\right)-\hslash \left(y\right);y)\le M{\mathsf{\Pi }}_{s,\lambda }^{\nu }\left({\displaystyle \frac{|t-y|}{{(t+{\rho }_{1}y+{\rho }_2{y}^2)}^{1/2}}};y\right).\end{array}$$

It is obvious that

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{({\rho }_{1}y+{\rho }_2{y}^2)}}>{\displaystyle \frac{1}{t+{\rho }_{1}y+{\rho }_2{y}^2}}.\end{array}$$

Therefore $y\in (0;\infty ),$ one has

$$\begin{array}{ccc}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|& \le & {\displaystyle \frac{M}{{({\rho }_{1}y+{\rho }_2{y}^2)}^{1/2}}}{\left({\mathsf{\Pi }}_{s,\lambda }^{\nu }{(t-y)}^2;y\right)}^{1/2}\hfill \\ & \le & M{\left({\displaystyle \frac{{\varphi }_{\left(s\right)}\left(y\right)}{{\rho }_{1}y+{\rho }_2{y}^2}}\right)}^{1/2}.\hfill \end{array}$$

In the light of H$\ddot{o}$lder’s inequality, Theorem 4, holds good for $\gamma =1$, with ${\rho }_1=2/\gamma$ and ${\rho }_2=2/2-\gamma$, we yield

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le {\left({\mathsf{\Pi }}_{s,\lambda }^{\nu }{\left(\right|\hslash \left(t\right)-\hslash \left(y\right)|}^{\gamma /2};y)\right)}^{\gamma /2}\\ \hfill \le M\left({\mathsf{\Pi }}_{s,\lambda }^{\nu }\right){\left({\displaystyle \frac{{|t-y|}^2}{t+{\rho }_{1}y+{\rho }_2{y}^2}};y\right)}^{\gamma /2}.\end{array}$$

Since ${\displaystyle \frac{1}{t+{\rho }_{1}y+{\rho }_2{y}^2}}<{\displaystyle \frac{1}{{\rho }_{1}y+{\rho }_2{y}^2}}$ we yield

$$\begin{array}{c}\hfill |{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)|\le M{\left({\displaystyle \frac{{\mathsf{\Pi }}_{s,\lambda }^{\nu }{\left(\right|t-y|}^2;y)}{{\rho }_{1}y+{\rho }_2{y}^2}}\right)}^{\gamma /2}\le M{\left({\displaystyle \frac{{\varphi }_{s,\lambda }^{\nu }\left(y\right)}{{\rho }_{1}y+{\rho }_2{y}^2}}\right)}^2.\end{array}$$

Hence, we arrived at our desired result. Now, we recall ${\gamma }^{th}$ term order Lipschitz-type maximal function suggested by Lenze [27] as

$$\tilde{\omega }(\hslash ;y)=su{p}_{t\ne y}{,}_{t\in (0,\infty )}{\displaystyle \frac{|\hslash (t)-\hslash (y\left)\right|}{{|t-y|}^{\gamma }}},y\in [0;\infty ),$$

(17)

and $r\in (0,1]$. □

Theorem 5.

Let $\hslash \in C_B[0,\infty )$ and $r\in (0,1]$. Then, for all $y\in (0,\infty )$, one has

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le {\tilde{\omega }}_{\gamma }(\hslash ;y)({\varphi }_{s,\lambda }^{\nu }{\left(y)\right)}^{\gamma /2}.\end{array}$$

Proof. 

We have

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le {\mathsf{\Pi }}_{s,\lambda }^{\nu }\left(|\hslash (v)-\hslash (y\left)\right|;y\right).\end{array}$$

In the direction of Equation (17), we have

$$\begin{array}{c}\hfill \left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le \widetilde{{\omega }_r}\left({\mathsf{\Pi }}_{s,\lambda }^{\nu }{\left(\right|t-y|}^{\gamma };y)\right).\end{array}$$

Using H$\ddot{o}$lder’s inequality with ${\rho }_1=2/\gamma$ and ${\rho }_2=2/2-\gamma$, we have

$$\left|{\mathsf{\Pi }}_{s,\lambda }^{\nu }(\hslash ;y)-\hslash \left(y\right)\right|\le \widetilde{{\omega }_{\gamma }}(h;y){\left({\mathsf{\Pi }}_{s,\lambda }^{\nu }{|v-y|}^2;y\right)}^{\gamma /2},$$

we arrived at our desired result. □

5. Bivariate Extension of Generalized Beta Type $\mathit{\lambda }$-Szász–Mirakjan Operators

Take $T^2=\{(y,v):0\le y<\infty ,0\le v<\infty \}$ and $C\left(T^2\right)$ represents a class of continuous functions over $T^2$ influenced with norm ${\left|\right|\hslash \left|\right|}_{C\left(T^2\right)}={sup}_{(y,v)\in T^2}|\hslash (y,v)|.$ Then, for all $\hslash \in C\left(T^2\right)$ and $s_1,s_2\in \mathbb{N},$ we introduced a bivariate extension as

$${\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)=\sum _{j=0}^{\infty }\sum _{k=0}^{\infty }{C}_{s_1,s_2,j,k}^{\nu }(t_1,t_2){\tilde{t}}_{s_1,s_2,j,k}(\lambda ;y,v)\hslash (t_1,t_2),$$

(18)

where

$$\begin{array}{c}\hfill C_{S_1,S_2,j,k}^{\nu }(t_1,t_2)=C_{s_1,j}^{\nu }\left(t_1\right)C_{s_2,k}^{\nu }\left(t_2\right),\end{array}$$

and

$$\begin{array}{c}\hfill C_{s_i,j,k}^{\nu }\left(t_i\right)={\int }_0^1{D}_{s_i,j,k}^{\nu }\left(t_i\right)d{t}_i,\end{array}$$

for $i=0,1,2$ and ${\tilde{t}}_{s_1,s_{2}j,k}(y,v)={\tilde{t}}_{s_1,j}(\lambda ;y){\tilde{t}}_{s_2,k}(\lambda ;v).$

Lemma 5.

Suppose $e_{m,n}=y^m{v}^n$ represents the two dimensional test function, then for the operator (18), we obtain

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,0};y,v)& =& 1,\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{1,0};y,v)& =& y+\lambda \left[{\displaystyle \frac{1-e^{-(s_1+1)y}}{s_1(s_1^2-1)}}-{\displaystyle \frac{2y}{s_1(s_1-1)}}\right],\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,1};y,v)& =& v+\lambda \left[{\displaystyle \frac{1-e^{-(s_2+1)v}}{s_1(s_2^2-1)}}-{\displaystyle \frac{2v}{s_1(s_2-1)}}\right],\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{2,0};y,v)& =& \left({\displaystyle \frac{s_1\nu }{s_1\nu +1}}\right)y^2+\left({\displaystyle \frac{\nu +1}{s_1\nu +1}}\right)y\hfill \\ & +& \lambda \left({\displaystyle \frac{s_1\nu }{s_1\nu +1}}\right)[{\displaystyle \frac{2}{s_1(s_1-1)}}y-{\displaystyle \frac{4(s_1+1)}{s_1^2(s_1-1)}}{y}^2\hfill \\ & +& {\displaystyle \frac{e^{-(s_1+1)y}-1}{s_1^2(s_1-1)}}]\hfill \\ & +& {\displaystyle \frac{s_1}{s_1\nu +1}}\left[{\displaystyle \frac{1-e^{-(s_1+1)y}}{s_1(s_2-1)}}-{\displaystyle \frac{2y}{s_1(s_1-1)}}\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,2};y,v)& =& \left({\displaystyle \frac{s_2\nu }{s_2\nu +1}}\right)v^2+\left({\displaystyle \frac{\nu +1}{s_2\nu +1}}\right)v\hfill \\ & +& \lambda \left({\displaystyle \frac{s_2\nu }{s_2\nu +1}}\right)[{\displaystyle \frac{2}{s_2(s_2-1)}}v-{\displaystyle \frac{4(s_2+1)}{s_2^2(s_2-1)}}{v}^2\hfill \\ & +& {\displaystyle \frac{e^{-(s_2+1)v}-1}{s_2^2(s_2-1)}}]\hfill \\ & +& {\displaystyle \frac{s_2}{s_2\nu +1}}\left[{\displaystyle \frac{1-e^{-(s_2+1)v}}{s_2(s_2-1)}}-{\displaystyle \frac{2v}{s(s_2-1)}}\right].\hfill \end{array}$$

Proof. 

In the direction linearity property and (2), we have

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,0};y,v)& =& {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v),\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{1,0};y,v)& =& {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_1;y,v){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v),\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,1};y,v)& =& {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_1;y,v),\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{2,0};y,v)& =& {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_2;y,v){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v),\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{0,2};y,v)& =& {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_0;y,v){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_2;y,v).\hfill \end{array}$$

□

Lemma 6.

For ${\eta }_{m,n}(t_1,t_1)={({\eta }_m\left(t_1\right)-y)}^m{({\eta }_n\left(t_2\right)-v)}^n$ for $m,n=0,1,2,$ then we have following equalities:

$$\begin{array}{ccc}\hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }({\eta }_{0,0};y,v)& =& 1,\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }({\eta }_{1,0};y,v)& =& \lambda \left[{\displaystyle \frac{1-e^{-(s_1+1)y}-2y}{s_1(s_1-1)}}\right],\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }({\eta }_{0,1};y,v)& =& \lambda \left[{\displaystyle \frac{1-e^{-(s_2+1)v}-2v}{s_2(s_2-1)}}\right],\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }({\eta }_{2,0};y,v)& =& \left({\displaystyle \frac{s_1\nu }{s_1\nu +1}}-1\right)y^2+\left({\displaystyle \frac{\nu +1}{s_1\nu +1}}\right)y\hfill \\ & +& \lambda \left[{\displaystyle \frac{(1+2s_{1}y)e^{-(s_1+1)y}-(1-2s_1)y-4y^2}{s_1^2(s_1-1)}}\right],\hfill \\ \hfill {\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }({\eta }_{0,2};y,v)& =& \left({\displaystyle \frac{s_2\nu }{s_2\nu +1}}-1\right)v^2+\left({\displaystyle \frac{\nu +1}{s_2\nu +1}}\right)v\hfill \\ & +& \lambda \left[{\displaystyle \frac{(1+2s_{2}v)e^{-(s_2+1)v}-(1-2s_2)v-4v^2}{s_2^2(s_2-1)}}\right].\hfill \end{array}$$

(19)

Proof. 

In the light of Lemma 5 and linearity property, one can easily prove the required result. □

Now, we prove the rate of convergence and order of approximation.

Definition 2.

Consider $T_1=[0,\infty ),T_2=[0,\infty )\subset \mathbb{R}$ as given intervals and $B(T_1\times T_2)=\{\hslash :T_1\times T_2\to \mathbb{R}:\hslash isdefinedandboundedon{T}_1\times T_2\}.$ Then, for $g\in B(T_1\times T_2)$ present the total modulus of continuity is defined as ${\omega }_{total}(\hslash ;·,\ast ):C\left(T^2\right)\to \mathbb{R}$ provided that $({\varphi }_1,{\varphi }_2)\in T_1\times T_2$ and defined by

$${\omega }_{total}(\hslash ;{\varphi }_1,{\varphi }_2)=\underset{|x_1-x_1^{\prime }|\le {\varphi }_1,|y_1-y_1^{\prime }|\le {\varphi }_2}{sup}\left\{\right|\hslash (x_1,y_1)-\hslash (x_1^{\prime },y_1^{\prime })|:(x_1,y_1),$$

$(x_1^{\prime },y_1^{\prime })\in T_1\times T_2\},$ is termed as the total modulus of continuity corresponding to the function ℏ.

Here, we discuss the convergence rate of the operators given by (9). To discuss convergence rate, we revisit the following result presented by Volkov [28]:

Theorem 6.

Let $L_{s_1,s_2}:C\left(T^2\right)\to C\left(T^2\right),(s_1,s_2)\in \mathbb{N}\times \mathbb{N}$ be linear positive operators. If

$$\begin{array}{ccc}\hfill \underset{s_1,s_2\to \infty }{lim}{L}_{s_1,s_2}\left(e_{mn}\right)& =& e_{y,v},(m,n)\in \{(0,0),(1,0),(0,1)\},\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \underset{s_1,s_2\to \infty }{lim}{L}_{s_1,s_2}(e_{20}+e_{02})& =& e_{20}+e_{02},\hfill \end{array}$$

uniformly on $T^2$, then the sequence $\{L_{s_1,s_2}\hslash \}$ converges to ℏ uniformly on $T^2$ for any $\hslash \in C\left(T^2\right)$.

Theorem 7.

Let $e_{mn}(y,v)=y^m{v}^n(0\le m+n\le 2,m,n\in \mathbb{N})$ be the test functions restricted on $T^2$. If

$$\begin{array}{c}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{mn};y,v)=e_{mn}(y,v),\end{array}$$

and

$$\begin{array}{c}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{20}+e_{02};y,v)=e_{20}(y,v)+e_{02}(y,v),\end{array}$$

uniformly on $T^2$, then

$$\begin{array}{c}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)=\hslash (y,v),\end{array}$$

uniformly for all $\hslash \in C\left(T^2\right)$.

Proof. 

In view of Lemma 5, it is evident for $m=n=0$

$$\begin{array}{c}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{00};y,v)=e_{00}(y,v).\end{array}$$

For $m=1$, $n=0$, we obtain

$$\begin{array}{ccc}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(p_{10};y,v)& =& y,\hfill \\ \hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(p_{10};y,v)& =& p_{10}(y,v).\hfill \end{array}$$

Similarly

$$\begin{array}{ccc}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{01};y,v)& =& v,\hfill \\ \hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{01};y,v)& =& e_{01}(y,v),\hfill \end{array}$$

and in the light Lemma (5), we obtain

$$\begin{array}{ccc}\hfill \underset{s_1,s_2\to \infty }{lim}{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(e_{20}+e_{02};y,v)& =& y^2+v^2,\hfill \\ & =& e_{20}(y,v)+e_{02}(y,v).\hfill \end{array}$$

In the direction Theorem 6, Theorem 7 is easily proved. □

In the last result, we deal approximation order of the sequence of operators ${\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(.;.)$ given by (9) as

Theorem 8

([29]). Let $L:C\left(T^2\right)\to B\left(T^2\right)$ be a linear positive operator. For any $\hslash \in C\left(T^2\right)$, any $(z_1,z_2)\in T^2$ and any ${\varphi }_1,{\varphi }_2>0$, the following inequality

$$\begin{array}{ccc}\hfill |(L\hslash )(z_1,z_2)-\hslash (z_1,z_2)|& \le & |L{e}_{0,0}(z_1,z_2)-1\left|\right|\hslash (z_1,z_2)|+[L{e}_{0,0}(z_1,z_2)\hfill \\ & +& {\varphi }_1^{-1}\sqrt{L{e}_{0,0}(z_1,z_2){\left(L(·-z_1)\right)}^2(z_1,z_2)}\hfill \\ & +& {\varphi }_2^{-1}\sqrt{L{e}_{0,0}(z_1,z_2){\left(L(\ast -z_2)\right)}^2(z_1,z_2)}\hfill \end{array}$$

$$\begin{array}{ccc}& +& {\varphi }_1^{-1}{\varphi }_2^{-1}\sqrt{{\left(L{e}_{0,0}\right)}^2(z_1,z_2){\left(L(·-z_1)\right)}^2(z_1,z_2){\left(L(\ast -z_2)\right)}^2(z_1,z_2)}]\hfill \\ & \times & {\omega }_{total}(\hslash ;{\varphi }_1,{\varphi }_2),\hfill \end{array}$$

(20)

holds.

Theorem 9.

For $\hslash \in C\left(T^2\right)$ and $(y,v)\in T^2$, $(s_1,s_2)\in \mathbb{N}\times \mathbb{N}$ and ${\varphi }_1,{\varphi }_2>0$, one has

$$\begin{array}{c}\hfill |{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)-\hslash (y,v)|\le 4{\omega }_{total}(\hslash ;{\varphi }_1,{\varphi }_2),\end{array}$$

where ${\varphi }_1=\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_1-y)}^2;y,v\right)}$ and ${\varphi }_2=\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_2-v)}^2;y,v)\right)}$.

Proof. 

From Theorem 8, we have

$$\begin{array}{cc}.& |{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)-\hslash (y,v)|\hfill \\ \le & [1++{\varphi }_1^{-1}\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_1-y)}^2;y,v\right)}\hfill \\ +& {\varphi }_2^{-1}\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_2-v)}^2;y,v\right)}\hfill \\ +& {\varphi }_1^{-1}{\varphi }_2^{-1}\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_1-y)}^2;y,v\right){\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_2-v)}^2;y,v\right)}]\hfill \\ \times & {\omega }_{total}(\hslash ;{\varphi }_1,{\varphi }_2).\hfill \end{array}$$

(21)

Selecting ${\varphi }_1=\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_1-y)}^2;y,v\right)}$ and ${\varphi }_2=\sqrt{{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }\left({(t_2-v)}^2;y,v)\right)}$, we arrive at the required result. □

6. Bivariate Graphical Analysis

Example 3.

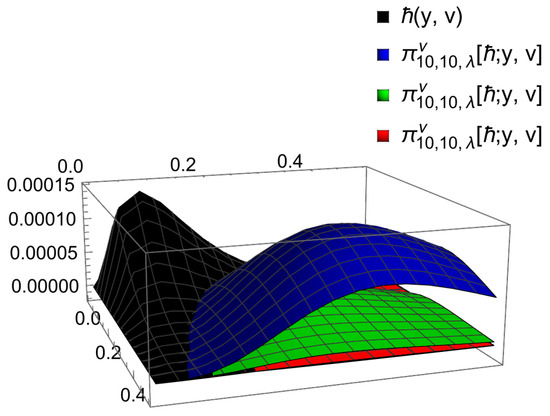
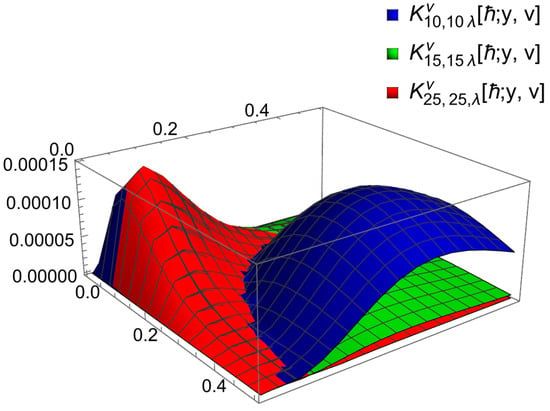
In this section we inspect different values of parameters $\lambda =0.5$ and $\nu =0.3$ through the table and figure presented in the example below. The operators ${\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)$ converge uniformly to the function $\hslash (y,v)={\displaystyle \frac{1}{4}}{e}^{-15(y+v)}$ (Block) for different values of $s_1=s_2=10$ (Blue) $s_1=s_2=15$ (Green), and $s_1=s_2=25$ (Red), which is shown in Figure 5. Moreover, Table 3 shows the approximation error of the proposed operator with the help of a common formula $K_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)=|{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)-\hslash (y,v)|$, and see Figure 6.

Figure 5. ${\mathsf{\Pi }}_{s_1,s_2,\lambda }(\hslash ;y,v)$ converges to $\hslash (y,v)={\displaystyle \frac{1}{4}}{e}^{-15(y+v)}$.

Table 3. Error approximation table of the operators ${\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)$ to $\hslash (y,v)$.

$\mathit{y},\mathit{v}$	$|{\mathbf{\Pi }}_{10,10,\mathit{\lambda }}^{\mathit{\nu }}-\mathit{\hslash }(\mathit{y},\mathit{v})|$	$|{\mathbf{\Pi }}_{15,15,\mathit{\lambda }}^{\mathit{\nu }}-\mathit{\hslash }(\mathit{y},\mathit{v})|$	$|{\mathbf{\Pi }}_{25,25,\mathit{\lambda }}^{\mathit{\nu }}-\mathit{\hslash }(\mathit{y},\mathit{v})|$
0.1 0.1	0.000124468	2.3644 × ${10}^{-6}$	1.46835 × ${10}^{-6}$
0.2 0.2	0.000054595	0.0000251022	0.0000102038
0.3 0.3	0.000126461	0.0000319147	7.12176 × ${10}^{-6}$
0.4 0.4	0.000114291	0.0000158371	1.94043 × ${10}^{-6}$
0.5 0.5	0.0000616724	4.69277 × ${10}^{-6}$	3.15716 × ${10}^{-7}$
0.6 0.6	0.0000240142	1.00341 × ${10}^{-6}$	3.70668 × ${10}^{-8}$
0.7 0.7	7.46513 × ${10}^{-6}$	1.71277 × ${10}^{-7}$	3.47392 × ${10}^{-9}$
0.8 0.8	1.96793 × ${10}^{-6}$	2.47905 × ${10}^{-8}$	2.76057 × ${10}^{-10}$
0.9 0.9	4.574 × ${10}^{-7}$	3.1634 × ${10}^{-9}$	1.9339 × ${10}^{-11}$

Figure 6. Error approximation $K_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)=|{\mathsf{\Pi }}_{s_1,s_2,\lambda }^{\nu }(\hslash ;y,v)-\hslash (y,v)|$.

7. Conclusions

In this study, we explore how well the $\lambda$-Szász generalized Beta operators, based on the generalized beta function, can approximate Lebesgue measurable functions. We focus on several aspects, including how these operators converge to a target function as certain parameters change and how quickly this happens, known as the speed of convergence. To understand their strengths and limitations, we also examine their performance on specific functions, such as polynomials and exponential functions. Furthermore, we assess how effectively the operators work across various functions and values, providing a general idea of their approximation ability. To make the findings more accessible and intuitive, we include graphical representations, showing visual examples of how these operators behave under different conditions. This comprehensive approach clearly shows where these operators excel and where they may face challenges.