PCCDiff: Point Cloud Completion with Conditional Denoising Diffusion Probabilistic Models

Abstract

Point clouds obtained from laser scanners or other devices often exhibit incompleteness, which poses a challenge for subsequent point cloud processing. Therefore, accurately predicting the complete shape from partial observations has paramount significance. In this paper, we introduce PCCDiff, a probabilistic model inspired by Denoising Diffusion Probabilistic Models (DDPMs), designed for point cloud completion tasks. Our model aims to predict missing parts in incomplete 3D shapes by learning the reverse diffusion process, transforming a 3D Gaussian noise distribution into the desired shape distribution without any structural assumption (e.g., geometric symmetry). Firstly, we design a conditional point cloud completion network that integrates Missing-Transformer and TreeGCN, facilitating the prediction of complete point cloud features. Subsequently, at each step of the diffusion process, the obtained point cloud features serve as condition inputs for the symmetric Diffusion ResUNet. By incorporating these condition features and incomplete point clouds into the diffusion process, PCCDiff demonstrates superior generation performance compared to other methods. Finally, extensive experiments are conducted to demonstrate the effectiveness of our proposed generative model for completing point clouds.

1. Introduction

Recent advancements in depth sensing and laser scanning have made point clouds a popular representation for modeling 3D shapes. However, it is true that point cloud data obtained from existing 3D sensors may not always be complete or satisfactory for various reasons, such as self-occlusion, light reflection, limited sensor resolution, etc. Consequently, the task of recovering complete point clouds from partial and sparse raw data has become crucial and of increasing significance [1,2].

Denoising Diffusion Probabilistic Models (DDPMs) [3,4,5] have emerged as a promising approach for generating high-quality and diverse images. Unlike traditional generative models, such as variational auto-encoders (VAEs) [6] and generative adversarial networks (GANs) [7], the DDPM constructs a forward diffusion process by incrementally adding noise to data points and learns the reverse denoising process to generate new samples. One advantage of the DDPM is its ability to handle complex data distributions, making it suitable for modeling point clouds where traditional methods may struggle because of limitations in stability or flexibility. The DDPM has demonstrated impressive results in generating images with diverse and realistic characteristics. Moreover, the DDPM has proven effective in tasks such as super-resolution and deblurring, which require unique ground truth because it captures complex data distributions to accurately reconstruct images [8,9]. In summary, the DDPM offers a powerful alternative to traditional generative models for modeling images. Its forward diffusion process and reverse denoising process enable the synthesis of high-quality and diverse images, making it a valuable tool in various image-related tasks.

Our proposed model, PCCDiff, is a probabilistic generative model inspired by DDPM for point cloud completion. It establishes a connection between the distribution of completion point clouds and the noise distribution through the diffusion process. Specifically, we focus on the reverse diffusion process, which aims to recover the target point distribution from the noise distribution in order to model the point distribution for point cloud generation. To address the challenge of learning the features of complete point clouds during the iterative sampling process, we introduce the condition network. This network captures the point clouds feature throughout the completion process. Furthermore, drawing inspiration from the success of the Transformer architecture in point cloud representation learning, we incorporate the Transformer into our framework. The designed Missing-Transformer network enhances the learning of missing point proxies, resulting in a more comprehensive understanding of the point cloud structure. Then, the obtained point cloud features are utilized as condition inputs in the reverse diffusion process at each step. This improvement enables us to enhance the accuracy of generating completion point clouds by refining the point distribution. Our proposed PCCDiff model utilizes a reverse diffusion process and Missing-Transformer framework to achieve accurate and effective point cloud completion. The primary contributions of our work are as follows:

(1) We introduce PCCDiff, a novel conditional diffusion model specifically designed for point cloud completion.

(2) We develop a Missing-Transformer network to serve as the condition net, effectively learning complete point cloud features.

(3) We demonstrate the effectiveness of PCCDiff through extensive experiments on the ModelNet40 and ShapeNet-34/21 datasets.

2. Related Work

2.1. Point Cloud Completion

Three-dimensional shape completion tasks have traditionally relied on voxel grids or distance fields to describe 3D objects. However, researchers are increasingly turning to unstructured point clouds as a representation of 3D objects because of their compact memory footprint and strong ability to represent fine-grained details. In [10], PointNet was designed as a novel type of neural network that directly consumes point clouds and uses a single symmetric function, max pooling, to aggregate information from all the points. Yuan et al. proposed the first deep learning network, Point Completion Network (PCN) [11], for shape completion without any structural assumption (e.g., symmetry) or annotation (e.g., semantic class) about the underlying shape, building upon PointNet [10] and FoldingNet [12] architectures. Since then, numerous methods have emerged, aiming for higher resolution and improved robustness in point cloud completion. Xie et al. introduced the Gridding Residual Network (GRNet) [13], a novel approach for point cloud completion that incorporates 3D grids as intermediate representations to regularize unordered point clouds. Additionally, Yu et al. proposed innovative architectures, PoinTr [14] and AdaPoinTr [15], which transform the point cloud completion task into a set-to-set translation problem and employ a transformer encoder-decoder architecture for point cloud completion. This approach has demonstrated state-of-the-art performance in various real-world scenarios.

2.2. Diffusion Models for Point Clouds

Denoising Diffusion Probabilistic Models (DDPMs) represent a class of latent variable models renowned for their ability to seamlessly transition from a noise distribution to the target data distribution through the use of Markov chains. This innovative approach has recently found application in the realm of point cloud processing, notably in tasks involving 3D point cloud generation and shape reconstruction. Point·E introduces a system for generating intricate 3D point clouds from diverse prompts, employing a diffusion model to translate images into 3D point clouds [16]. PC² presents a projection-conditioned point cloud diffusion approach for single-image 3D reconstruction [17]. This method progressively refines an initially random point cloud to align with the input image, demonstrating the versatility of DDPM in various applications. Lyu proposed a dual-path Point Diffusion-Refinement (PDR) paradigm supplemented by a ReFinement Network (RFNet) for point cloud completion. This approach combines the coarse completion generated by DDPM with the refined output from RFNet, enhancing the overall quality of point cloud reconstruction [18]. However, existing works primarily utilize diffusion models to generate coarse point clouds, leaving room for improvement in capturing finer details. In this research, we aim to address this limitation by leveraging conditional DDPM to predict fine, complete point clouds. By harnessing the generation power of DDPM, we anticipate achieving more precise and comprehensive representations of 3D point clouds, thus advancing the state-of-the-art in point cloud processing.

3. Methods

The overall framework of PCCDiff is delineated in Figure 1. Below, we provide a comprehensive exposition of our approach. We commence with an introductory overview, followed by a detailed presentation of the diffusion models, which constitute the fundamental pillars of our methodology. Subsequently, we elucidate the conditional point cloud completion network responsible for generating the condition features. Finally, we expound on the training loss utilized within our model.

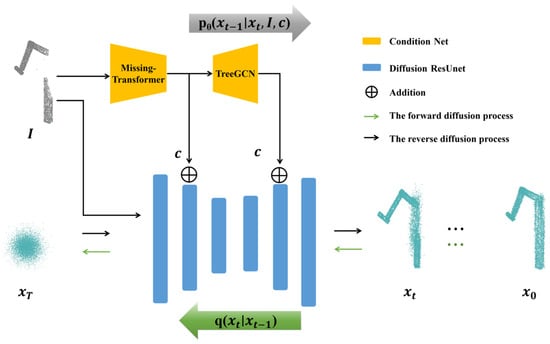
Figure 1. Network architecture of the point cloud completion with conditional denoising diffusion probabilistic model (PCCDiff). It comprises two main components: conditional point cloud completion network and diffusion model.

3.1. Point Cloud Completion Conditional Diffusion Models

Our proposed PCCDiff model builds upon the foundation of DDPMs. When incomplete point clouds $I$ are inputted, the condition network extracts crucial condition features $c$. However, relying solely on incomplete point clouds $I$ for learning the characteristics of complete point clouds can pose challenges. To address this, we introduce a novel approach, wherein we fuse the incomplete point clouds $\mathrm{I}$ and the point clouds features $\mathrm{c}$ to the Diffusion ResUNet for the diffusion step. By leveraging this combined information, our model gains a more comprehensive understanding of the underlying data distribution, facilitating the generation of complete and refined point clouds. This fusion strategy enhances the capability of our PCCDiff model to capture the intricate details and nuances present in complete point clouds. Through this iterative diffusion process, our model effectively bridges the gap between incomplete input data and the desired output, resulting in more accurate and realistic point cloud reconstructions.

3.2. Diffusion Models

The DDPM stands as a versatile generative model inspired by stochastic differential equations and non-equilibrium thermodynamics, encompassing both forward and reverse diffusion processes [19]. In the forward diffusion process, which comprises a series of steps $T$, this process transforms complete point clouds $x_0$ into a Gaussian noise distribution $x_T$. This process is instrumental in capturing the underlying data distribution and facilitating the generation of realistic samples. The forward diffusion process is formally defined as follows:

$$\mathrm{q}\left(x_1,\dots ,x_T|x_0\right)={\prod }_{\mathrm{t}=1}^{\mathrm{T}}\mathrm{q}\left(x_t|x_{t-1}\right),\mathrm{where}\mathrm{q}\left(x_t|x_{t-1}\right)=\mathcal{N}\left(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I\right)$$

(1)

where ${\beta }_1,\dots ,{\beta }_t$ are variance schedule hyper-parameters. We set $T=1000$ and use a linear variance schedule from 0.0001 to 0.02 following the DDPM [19].

Our goal is to generate complete point clouds. We consider the generation process to be the reverse of the forward diffusion process. Unlike the forward diffusion process that adds noise to the points, the purpose of the reverse diffusion process is to reconstruct complete point clouds $x_0$ from the input Gaussian noise $x_T$. Firstly, we sample $x_T~\mathcal{N}\left(0,I_{N\times 3}\right)$, then obtain $x_{t-1}~p_{\theta }\left(x_{t-1}|x_t,I,c\right)$ for $t=T,T-1,\dots ,1$, and finally reconstruct $x_0$. Here, $\mathcal{N}$ represents the Gaussian distribution, and $I_{N\times 3}$ denotes the incomplete point clouds provided as input. To achieve this, the model undergoes training using available data. The reverse diffusion process is mathematically represented as

$${\mathrm{p}}_{\theta }\left(x_0,\dots ,x_{T-1}|x_{\mathrm{T}},\mathrm{I},\mathrm{c}\right)={\prod }_{\mathrm{t}=1}^{\mathrm{T}}{\mathrm{p}}_{\theta }\left(x_{t-1}|x_t,\mathrm{I},\mathrm{c}\right),\mathrm{where}{\mathrm{p}}_{\theta }\left(x_{t-1}|x_t,\mathrm{I},\mathrm{c}\right)=\mathcal{N}\left(x_{t-1};{\mu }_{\theta }(x_t,c,t),{\sigma }_t^{2}I\right)$$

(2)

$${\mu }_{\theta }(x_t,c,t)={\displaystyle \frac{1}{\sqrt{{\alpha }_t}}}(x_t-{\displaystyle \frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}}{\mathsf{ϵ}}_{\theta }(x_t,\mathrm{I},\mathrm{c},t))$$

(3)

The variance ${\sigma }_t^2={\displaystyle \frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}}{\beta }_t$ is a time-step dependent constant. The estimated mean ${\mu }_{\theta }$ is implemented by a neural network ${ϵ}_{\theta }$. Specifically, we utilize a Diffusion ResUNet as the network ${ϵ}_{\theta }$, with $\theta$ representing the parameters of the reverse diffusion process. To enhance the quality of the generated complete point clouds, our network ${ϵ}_{\theta }$ takes multiple inputs. These include the noisy point clouds $x_t$, the diffusion step $t$, the incomplete point clouds $I$, and the condition features $c$. These condition features $c$ serve as latent encodings that capture the target shape of the point clouds, facilitated by the conditional point cloud completion network. By incorporating these inputs into our network architecture, we aim to leverage the synergy between various sources of information to generate more accurate and realistic complete point clouds.

The architecture of our Diffusion ResUNet combines elements from both ResNet and the symmetric UNet, like encoder–decoder architecture, as detailed in Figure 2. This hybrid structure integrates Residual blocks, DownSampling and UpSampling blocks, Self-Attention mechanisms, and Skip Connections. Each Residual block consists of two convolutional blocks, each comprising Group-Norm [20], SiLU activation [21], and convolutional layers, as depicted in Figure 3. Within the Residual block, the time-step embedding undergoes SiLU activation before undergoing linear transformation. Subsequently, it is added to the output of the first convolutional block. Skip Connections connect features with the same resolution in the encoder and the symmetric decoder. The condition features $c$ are seamlessly integrated into both the encoder and decoder stages of the ResUNet network, facilitating the incorporation of latent information about the target point cloud shape (as shown in Figure 1). Finally, a standard convolutional layer is employed to make predictions for the final output. This comprehensive architecture harnesses the strengths of both ResNet and symmetric UNet, enabling our model to effectively capture intricate details and dependencies within the data, thereby enhancing the quality and fidelity of the generated complete point clouds.

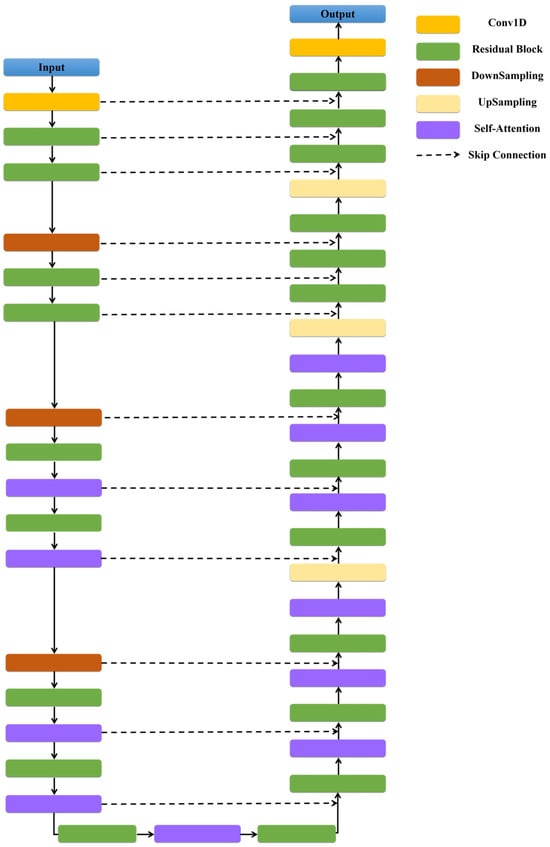
Figure 2. Illustration of symmetric Diffusion ResUNet.

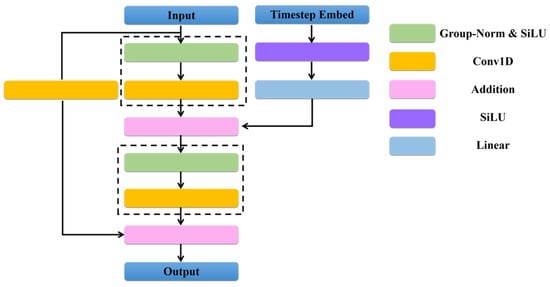
Figure 3. Illustration of Residual block. Convolutional block is framed by dashed line box.

3.3. Conditional Point Cloud Completion Network

In Figure 4a, we present the architecture of the conditional point cloud completion network. The network takes incomplete point clouds $I_{N\times 3}$ as input. Initially, we utilize iterative farthest point sampling (IFPS) [22] to identify the center point clouds and employ an MLP [23] position extractor to obtain positional embeddings for the incomplete point clouds. Additionally, we extract features from the incomplete point clouds using the Dynamic Graph CNN (DGCNN) [24] model as a feature extractor. The combination of positional embeddings and features constitutes the incomplete point proxies. To accurately predict the missing point clouds, we introduce an MLP proxies extractor to learn the missing point proxies. Subsequently, we employ Missing-Transformer to generate predictions for the complete point cloud proxies. The structure of Missing-Transformer is illustrated in Figure 4b, where the network receives incomplete point proxies and missing point proxies as input.

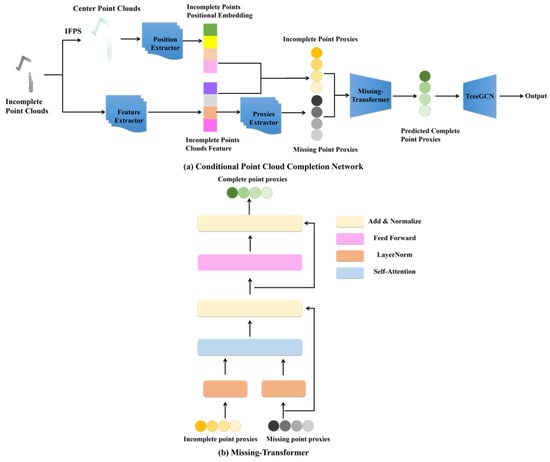
Figure 4. Structures of the proposed conditional point cloud completion network (a) and Missing-Transformer (b).

Then, we utilize TreeGCN [25] to recover complete point clouds. Figure 5a illustrates its structure, comprising 3 layers. TreeGCN is composed of Up Branching Networks and Graph Convolutional Networks (as shown in Figure 5b). The Up Branching Network serves to increase the number of features. Initially, the input features $p^L$ is expanded through linear transformation to increase their quantity by $V^{L+1}$, followed by matrix multiplication (@) to obtain the expanded features. The expansion process is defined as

$$p_0^{L+1}={\left[V^{L+1}·p^L\right]}_{d^L}@p^L$$

(4)

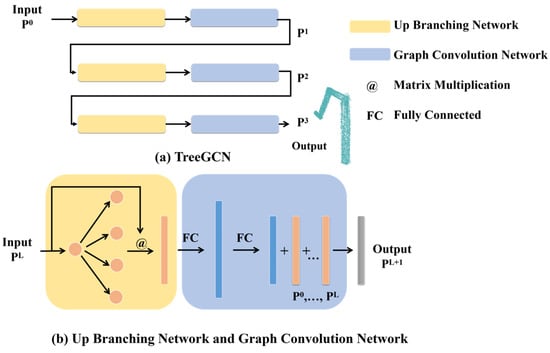
Figure 5. Structures of TreeGCN (a) and its components: Up Branching Network and Graph Convolution Network (b).

Here, $d^L$ represents the expansion factor for the L-th tree layer. Subsequently, using the Graph Convolutional Network, these expanded features $p_0^{L+1}$ are propagated through two fully connected (FC) layers to each point in the 3D space until a complete point cloud is reconstructed. During the reconstruction process, the point cloud features obtained at this layer are fused with the initial features from all tree layers. Through the Graph Convolutional Network, all features are thoroughly integrated, thereby achieving effective prediction of the complete point cloud.

3.4. Training Loss

PCCDiff is trained via variational inference following DDPM [3]. The loss function is represented as

$$L(\theta )=E_{t,x_0,ϵ}\left[{‖ϵ-{ϵ}_{\theta }({\sqrt{{\overline{\alpha }}_t}x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)‖}^2\right]$$

(5)

where $t$ is uniform between 1 and T. The neural network ${ϵ}_{\theta }$ is trained to predict the added noise $ϵ$ in the complete point clouds $x_0$, enabling effective denoising of noisy point clouds $x_t$.

$$x_t\left(x_0,ϵ\right)={\sqrt{{\overline{\alpha }}_t}x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,ϵ\in \mathcal{N}\left(0,I_{N\times 3}\right)$$

(6)

For the conditional point clouds completion network, we use the symmetric version of Chamfer Distance [26] as our completion loss.

$$L_{com}=d_{CD}(F_{pre},F_{gt})$$

(7)

In detail, $d_{CD}$ calculates the squared distance between the predicted point clouds $F_{pre}$ and the ground truth $F_{gt}$. The mean Chamfer Distance can measure the average nearest squared distance between the prediction point cloud $F_{pre}$ and ground truth $F_{gt}$, which is calculated by

$$d_{CD}(F_{pre},F_{gt})={\displaystyle \frac{1}{F_{pre}}}\sum _{x\in F_{pre}}\underset{y\in F_{\mathit{gt}}}{\mathit{min}}{‖x-y‖}_2^2+{\displaystyle \frac{1}{F_{gt}}}\sum _{y\in F_{gt}}\underset{x\in F_{\mathit{pre}}}{\mathit{min}}{‖y-x‖}_2^2$$

(8)

4. Experiments and Results

We evaluate our method on the widely used benchmark of 3D point cloud completion, i.e., ModelNet40 [27] and ShapeNet-34/21 [14]. In these datasets, each complete point clouds consists of 8192 points. During both training and testing, we sample 2048 points as the ground truth $F_{gt}$ of the incomplete point cloud, i.e., missing 25% of original data. The performance of our method is assessed using the mean Chamfer Distance (CD) as the evaluation metric.

We implement all of our models with PyTorch deep learning framework and use AdamW [28] optimizer to update the parameters of the network during training. The learning rate is initially set to 0.0001, and the batch size is set to four.

4.1. Completion Results on ModelNet40

ModelNet40 dataset consists of 12,311 models across 40 categories of man-made objects. It was divided into 9843 models for training and 2468 models for testing.

We compare our point cloud completion method with previous state-of-the-art methods, including FoldingNet [12], TopNet [29], PCN [10], PMP-Net [30], and PMP-Net++ [31], using their open-source code on standard metrics. Table 1 shows that our method achieves a lower average CD (multiplied by 1000) across 40 categories. Although PMP-Net and PMP-Net++ have lower CD loss than ours for categories such as Bathtub and Person, for the majority of categories like Desk, Bench, Radio, Chair, Tent, and Door, our CD is smaller than those of the state-of-the-art methods. These results demonstrate that our network PCCDiff can reconstruct missing point clouds with higher precision in a multi-class dataset.

Table 1. Results of comparison between our method and state-of-the-art methods on ModelNet40 dataset using mean Chamfer Distance (CD) computed and multiplied by 10³. The best results are in bold.

Methods	Desk	Bench	Radio	Chair	Tent	Door	Person	Bathtub	Average
FoldingNet	3.442	1.947	2.165	2.500	2.772	0.965	2.825	2.241	2.474
PCN	3.146	1.916	1.794	1.895	2.806	0.715	3.228	1.947	2.543
TopNet	2.626	1.640	2.141	1.714	2.435	0.825	2.362	1.876	2.112
PMP-Net	0.792	0.514	0.942	0.517	0.903	0.376	0.623	0.808	0.762
PMP-Net++	0.699	0.536	0.684	0.500	0.819	0.373	1.193	0.731	0.726
Ours	0.658	0.494	0.608	0.483	0.799	0.342	0.900	0.811	0.709

Figure 6 illustrates the qualitative results of our method compared to the state-of-the-art methods on ModelNet40. Our method preserves the original input geometry while effectively computing and refining the missing parts for the showcased examples.

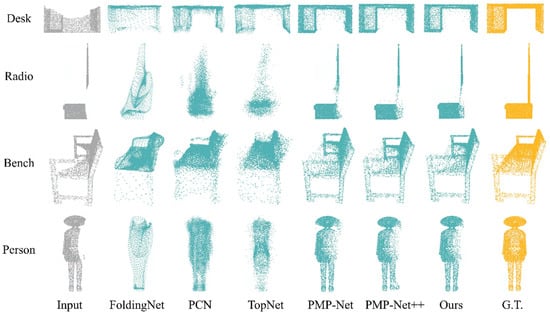
Figure 6. Qualitative results on ModelNet40. We show the input point cloud (Input, gray) and the ground truth (G.T., yellow) as well as the predictions of state-of-the-art methods and our method (blue).

4.2. Completion Results on ShapeNet-34/21

To further investigate the performance of our method with unseen categories in the dataset, we conducted experiments on ShapeNet-34/21. This dataset was derived from the original ShapeNet [27] dataset and was split into two parts: 21 unseen categories (with 2305 models for testing) and 34 seen categories (with 46,765 models for training and 3400 models for testing). For the 21 unseen categories, we employed networks trained on the 34 seen categories to evaluate the performance on novel objects from the remaining 21 categories that were not part of the training phase.

The average CD results for the two classes are presented in Table 2. We selected three categories from each class as examples to demonstrate the results. It can be seen from Table 2 that the average CD result of PCCDiff is improved by 7.6% compared to PMP-Net and 17.3% compared to PMP-Net++ for the 34 seen categories. Our method achieves the best performance on the listed categories and exhibits the lowest CD regardless of whether the object is symmetric or not, demonstrating that the objects completed by PCCDiff are closest to the GT. Among the 21 unseen categories, PCCDiff also achieves the lowest CD, showcasing the generalization performance of PCCDiff. In Table 2, we can also observe that average CD errors for the 21 unseen categories for PMP-Net and PMP-Net++ are higher compared to those for the 34 seen categories. As the difficulty level increases, the performance gap between seen categories and unseen categories significantly widens. However, for our method, there are no significant differences in the average CD errors of the two classes. Our method also achieves the best performance in this more challenging setting. In Figure 7, we present qualitative results of four categories on Shapenet-34/21. As demonstrated by the examples, our method can complete the missing point cloud with higher accuracy and more details for various seen and unseen categories.

Table 2. Results of comparison between our method and state-of-the-art methods on ShapeNet-34/21 dataset using mean Chamfer Distance (CD) computed and multiplied by 10³. The best results are in bold.

Methods	34 Seen Categories				21 Unseen Categories
	Trash Bin	Bed	Cabinet	Average	Printer	Helmet	Washer	Average
FoldingNet	1.527	2.220	1.088	1.259	2.441	3.429	1.664	1.985
PCN	1.561	2.473	1.025	1.217	2.487	4.527	1.625	2.203
TopNet	1.413	1.879	1.020	1.089	2.141	3.317	1.494	1.774
PMP-Net	0.782	0.735	0.553	0.520	0.900	1.361	0.854	0.964
PMP-Net++	0.993	0.811	0.651	0.567	0.945	1.481	0.987	0.877
Ours	0.476	0.560	0.360	0.483	0.527	0.782	0.470	0.522

Figure 7. Qualitative results on ShapeNet-34/21. We show the input point cloud (Input, gray) and the ground truth (G.T., yellow) as well as the predictions of state-of-the-art methods and our method (blue).

Our method consistently demonstrates superior performance in both quantitative comparisons and qualitative analyses across diverse datasets, significantly enhancing the quality of completed point clouds. These results underscore the effectiveness of our approach in tackling the point cloud completion task.

4.3. Ablation Study

To validate the effectiveness and necessity of the proposed conditional point cloud completion network and Missing-Transformer, we tested and compared our method PCCDiff with its variants on ShapeNet-34/21. The results of the ablation study are presented in Table 3. Model A is the variant of the PCCDiff without both the conditional point cloud completion network and Missing-Transformer, which aims to demonstrate the effectiveness of introducing condition features into the network design. The CD increases markedly upon removal, indicating that condition features significantly improve performance. Figure 8 visually demonstrates the intermediate steps of the diffusion reverse process. It can be seen that Model C generates more complete point clouds than Model A. The condition features provide multi-level information during the diffusion process, including local and global features. The reverse diffusion process can effectively utilize condition features to manipulate the noisy input point cloud to form a clean and complete point cloud. When removing Missing-Transformer from the conditional point cloud completion network (Model B), the CD is higher, as expected. It clearly shows that Missing-Transformer can bring performance improvement. Notably, our method, PCCDiff (Model C), achieves the best performance compared to its variants, confirming the effectiveness of its design.

Table 3. Ablation study on different components of our proposed network framework, including conditional point cloud completion network and Missing-Transformer on ShapeNet-34/21 dataset using mean Chamfer Distance (CD) computed and multiplied by 10³. The best results are in bold.

Model		34 Seen Categories			21 Unseen Categories
		Trash Bin	Bed	Average	Helmet	Washer	Average
A	Without condition network (without Missing-Transformer)	0.598	0.819	0.534	0.757	0.549	0.579
B	With condition network (without Missing-Transformer)	0.572	0.607	0.514	0.772	0.525	0.547
C (ours)	With condition network (with Missing-Transformer)	0.476	0.560	0.483	0.782	0.470	0.522

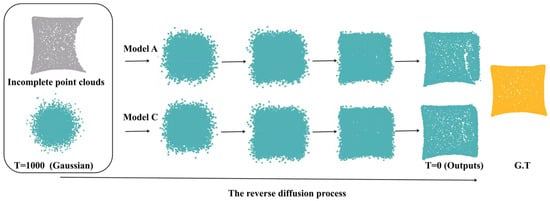
Figure 8. Examples of Model A and Model C (ours) on ShapeNet-34/21 of intermediate steps in the reverse diffusion process. The first and last columns show incomplete point clouds (gray) and ground truth (G.T., yellow), while the subsequent five columns show the evolution of the point cloud from a randomly sampled Gaussian to a final shape over the course of the diffusion process (blue).

4.4. Noise Variance Schedule

Table 4 presents the results of our model with different variance schedule ${\beta }_t$ on ShapeNet-34/21. As can be seen, the CD increases as ${\beta }_t$ enlarges. During the diffusion process, the variance schedule is important for controlling the noise intensity in each step. The smaller ${\beta }_t$ produces higher-quality results.

Table 4. Analysis of the variance schedule ${\beta }_t$ on ShapeNet-34/21 dataset using mean Chamfer Distance (CD) computed and multiplied by 10³. The best results are in bold.

	34 Seen Categories	21 Unseen Categories
${\beta }_t\in \left[\mathrm{0.0001,0.02}\right]$	0.483	0.522
${\beta }_t\in \left[\mathrm{0.0002,0.04}\right]$	0.508	0.557
${\beta }_t\in \left[\mathrm{0.0005,0.10}\right]$	0.554	0.618

5. Conclusions

In this paper, we introduce a novel conditional denoising diffusion probabilistic model (PCCDiff) for point cloud completion. Our method generates complete point clouds through the diffusion process. The conditional point cloud completion network incorporates Missing-Transformer and TreeGCN, which extract detailed object features. The Diffusion ResUNet utilizes these features along with incomplete point clouds to predict the complete point clouds. This approach enables PCCDiff to localize and calibrate completions. Our method can not only efficiently extract multi-level features from partial point clouds to guide the completion process but also precisely predict fine and complete point clouds. Experimental results on ModelNet40 and ShapeNet-34/21 demonstrate the effectiveness and efficiency of our proposed method compared to alternative approaches. The limitation of our model is the need for point cloud ground truth for training with low efficiency. With regard to future work, it would be interesting to accelerate the generation process and generate more dense complete point clouds. Moreover, our method has a broad application prospect, so we are convinced that it can be applied in other point cloud generation tasks, such as point cloud UpSampling.