Approximation Properties of Chlodovsky-Type Two-Dimensional Bernstein Operators Based on (p, q)-Integers

Abstract

In the present study, we introduce the two-dimensional Chlodovsky-type Bernstein operators based on the $(p,q)$-integer. By leveraging the inherent symmetry properties of $(p,q)$-integers, we examine the approximation properties of our new operator with the help of a Korovkin-type theorem. Further, we present the local approximation properties and establish the rates of convergence utilizing the modulus of continuity and the Lipschitz-type maximal function. Additionally, a Voronovskaja-type theorem is provided for these operators. We also investigate the weighted approximation properties and estimate the rate of convergence in the same space. Finally, illustrative graphics generated with Maple demonstrate the convergence rate of these operators to certain functions. The optimization of approximation speeds by these symmetric operators during system control provides significant improvements in stability and performance. Consequently, the control and modeling of dynamic systems become more efficient and effective through these symmetry-oriented innovative methods. These advancements in the fields of modeling fractional differential equations and control theory offer substantial benefits to both modeling and optimization processes, expanding the range of applications within these areas.

1. Introduction

The study provides a comprehensive examination of the theory and applications of mathematical operators, aligning with the content areas of mathematics, engineering, physics, and computer science. The investigation of the convergence properties of Chlodovsky-type Bernstein operators using the Korovkin-type theorem is directly part of mathematical analysis and approximation theory. Such studies yield significant results applicable to fields like mathematical modeling and optimization. Furthermore, the optimization of convergence rates of operators through system control contributes to the more efficient and stable management of systems within control engineering. Lastly, visual illustrations created using Maple demonstrate the convergence rates of operators on specific functions, contributing to modeling and simulation techniques used in computer science. Furthermore, the symmetric properties of $(p,q)$-integers and their integration into our operator framework expand the applicability of these operators, offering new insights into balanced and symmetrical system behaviors. This symmetry-oriented approach supports more precise modeling and control strategies, which are essential for stable and efficient solutions.

Approximation theory is rapidly emerging as an essential tool, extending its influence beyond classical domains to other mathematical areas such as differential equations, orthogonal polynomials, and geometric design. Following the introduction of Korovkin’s renowned theorem in 1950, the topic of approximating functions using linear positive operators has become an increasingly significant focus within approximation theory. A wealth of literature has been produced on this subject [1,2,3,4,5,6,7,8,9,10].

In recent years, particularly over the last twenty years, the role of q-calculus in approximation theory has been thoroughly investigated. The initial work on Bernstein polynomials derived from q-integers was conducted by Lupaş [11]. His findings indicated that q-Bernstein polynomials can provide superior approximations compared with classical methods when an appropriate choice of q is made. This discovery has encouraged numerous researchers to develop q-generalizations of various operators and to explore their approximation properties further. Numerous studies have contributed to this field [12,13,14,15].

Lately, Mursaleen et al. have been concentrating on utilizing $(p,q)$-calculus for approximations through linear positive operators, introducing the $(p,q)$-analogs of Bernstein operators [16]. They analyzed the uniform convergence of these operators and determined their rates of convergence. For additional recent studies related to $(p,q)$-operators, readers can refer to [17,18,19,20,21].

The main motivation behind this study is that, to the authors’ knowledge, there have been no investigations into approximating two-variable operators using $(p,q)$-calculus thus far. In this context, we introduce two-dimensional Chlodovsky-type Bernstein operators based on $(p,q)$-integers. We investigate the approximation properties of our newly defined operators with the aid of the Korovkin-type theorem. Furthermore, we delve into the local approximation characteristics and determine the rates of convergence through the modulus of continuity and a Lipschitz-type maximal function. A Voronovskaja-type theorem relevant to these operators is also presented. Another significant aim of this research is to examine the weighted approximation properties of our operators in the first quadrant of ${\mathbb{R}}_{+}^2$, specifically within the range of $[0,\infty )\times [0,\infty )$. To achieve these results, we intend to apply a weighted Korovkin-type theorem. We begin by revisiting some definitions and notations pertinent to the concept of $(p,q)$-calculus. The $(p,q)$-integer associated with a given number n is defined as

$${\left[n\right]}_{p,q}:={\displaystyle \frac{p^n-q^n}{p-q}},n=1,2,3\dots ,0<q<p\le 1.$$

The $(p,q)$-factorial ${\left[n\right]}_{p,q}!$ and the $(p,q)$-binomial coefficients are defined as:

$${\left[n\right]}_{p,q}!:=\left\{\begin{array}{cc}ll{\left[n\right]}_{p,q}{\left[n-1\right]}_{p,q}\cdots {\left[1\right]}_{p,q},\hfill & n\in \mathbb{N}\\ 1,\hfill & n=0\end{array}\right..$$

and

$${\left[\begin{array}{c}n\\ k\end{array}\right]}_{p,q}={\displaystyle \frac{{\left[n\right]}_{p,q}!}{{\left[k\right]}_{p,q}!{\left[n-k\right]}_{p,q}!}},0\le k\le n.$$

Further, the $(p,q)$-binomial expansions are given as

$${(ax+by)}_{p,q}^n=\sum _{k=0}^n{p}^{\left({\displaystyle \genfrac{}{}{0pt}{}{n-k}{2}}\right)}{q}^{\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)}{a}^{n-k}{b}^k{x}^{n-k}{y}^k.$$

and

$${(x-y)}_{p,q}^n=(x-y)(px-qy)(p^{2}x-q^{2}y)\cdots (p^{n-1}x-q^{n-1}y).$$

Further information related to $(p,q)$-calculus can be found in [22,23].

2. Construction of the Operators

Recently, Ansari and Karaisa [24] have defined and studied $(p,q)$-analog of Chlodovsky operators as follows:

$$C_{n,p,q}\left(f;x\right)={\displaystyle \frac{1}{p^{n(n-1)/2}}}\sum _{k=0}^n{\left[\begin{array}{c}n\\ k\end{array}\right]}_{p,q}{p}^{k(k-1)/2}{\left({\displaystyle \frac{x}{b_n}}\right)}^k{\left(1-{\displaystyle \frac{x}{b_n}}\right)}_{p,q}^{n-k-1}f\left({\displaystyle \frac{{\left[k\right]}_{p,q}}{{\left[n\right]}_{p,q}{p}^{k-n}}}{b}_n\right),$$

(1)

where

$${\left(1-{\displaystyle \frac{x}{b_n}}\right)}_{p,q}^{n-k-1}=\prod _{s=0}^{n-k-1}\left(p^s-q^s{\displaystyle \frac{x}{b_n}}\right).$$

For $0<q_1,q_2<p_1,p_2\le 1$, we define Chlodovsky-type two-dimensional Bernstein operator based on $(p,q)$-integers as follows:

$$C_{n,m}^{(p_1,q_1),(p_1,q_1)}\left(f;x,y\right)=\sum _{k=0}^n\sum _{j=0}^m{\Phi }_{n,k}(p_1,q_1;x){\Phi }_{m,j}(p_2,q_2;y)f\left({\displaystyle \frac{{\left[k\right]}_{p_1,q_1}}{{\left[n\right]}_{p_1,q_1}{p}_1^{k-n}}}{\alpha }_n,{\displaystyle \frac{{\left[j\right]}_{p_2,q_2}}{{\left[m\right]}_{p_2,q_2}{p}_2^{j-m}}}{\beta }_m\right),$$

(2)

for all $n,m\in N$, $f\in C\left(I_{{\alpha }_n{\beta }_m}\right)$ with $I_{{\alpha }_n{\beta }_m}=\{(x,y):0\le {\alpha }_n\le x,0\le {\beta }_m\le y\}$ and $C\left(I_{{\alpha }_n{\beta }_m}\right)=\{f:I_{{\alpha }_n{\beta }_m}⟶R\mathrm{is}\mathrm{continuous}\}$. Here, $\left({\alpha }_n\right)$ and $\left({\beta }_m\right)$ be increasing unbounded sequences of positive real numbers such that

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}& =& 0,\hfill \end{array}$$

(3)

$$\begin{array}{ccc}\hfill \underset{m\to \infty }{lim}{\displaystyle \frac{{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}& =& 0.\hfill \end{array}$$

(4)

Also, the basis elements are

$$\begin{array}{ccc}\hfill {\Phi }_{n,k}(p_1,q_1;x)& =& p_1^{{\displaystyle \frac{k(k-1)-n(n-1)}{2}}}{\left[\begin{array}{c}n\\ k\end{array}\right]}_{p_1,q_1}{\left({\displaystyle \frac{x}{{\alpha }_n}}\right)}^k\prod _{s=0}^{n-k-1}\left(p_1^s-q_1^s{\displaystyle \frac{x}{{\alpha }_n}}\right),\hfill \\ \hfill {\Phi }_{m,j}(p_2,q_2;y)& =& p_2^{{\displaystyle \frac{j(j-1)-m(m-1)}{2}}}{\left[\begin{array}{c}m\\ j\end{array}\right]}_{p_2,q_2}{\left({\displaystyle \frac{y}{{\beta }_m}}\right)}^j\prod _{s=0}^{m-j-1}\left(p_2^s-q_2^s{\displaystyle \frac{y}{{\beta }_m}}\right).\hfill \end{array}$$

We require the following lemmas to establish our main results.

Lemma 1

([24]).

$$\begin{array}{ccc}\hfill C_{n,p,q}\left(1;x\right)& =& 1,\hfill \\ \hfill C_{n,p,q}\left(e_1;x\right)& =& x,\hfill \\ \hfill C_{n,p,q}\left(e_2;x\right)& =& {\displaystyle \frac{p^{n-1}{b}_n}{{\left[n\right]}_{p,q}}}x+{\displaystyle \frac{q{[n-1]}_{p,q}}{{\left[n\right]}_{p,q}}}{x}^2\hfill \\ \hfill C_{n,p,q}\left(e_3;x\right)& =& {\displaystyle \frac{b_n^{2}x}{{\left[n\right]}_{p,q}^2}}{p}^{2n-2}+{\displaystyle \frac{(2p+q)q{[n-1]}_{p,q}{x}^2{b}_n}{{\left[n\right]}_{p,q}^2}}{p}^{n-1}+{\displaystyle \frac{q^3{[n-1]}_{p,q}{[n-2]}_{p,q}{x}^3}{{\left[n\right]}_{p,q}^2}},\hfill \\ \hfill C_{n,p,q}\left(e_4;x\right)& =& {\displaystyle \frac{b_n^{3}x}{{\left[n\right]}_{p,q}^3}}{p}^{3n-3}+{\displaystyle \frac{q(3p^2+3qp+q^3){[n-1]}_{p,q}{b}_n^2{x}^2}{{\left[n\right]}_{p,q}^3}}{p}^{2n-4}\hfill \\ & & +{\displaystyle \frac{q^3(3p^2+2pq+q^2){[n-1]}_{p,q}{[n-2]}_{p,q}{b}_n{x}^3}{{\left[n\right]}_{p,q}^3}}{p}^{n-3}+{\displaystyle \frac{q^6{[n-1]}_{p,q}{[n-2]}_{p,q}{[n-3]}_{p,q}{x}^4}{{\left[n\right]}_{p,q}^3}}.\hfill \end{array}$$

From Lemma 1, we have the following:

Lemma 2.

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(1;x,y\right)& =& 1,\hfill \\ \hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(s;x,y\right)& =& x,\hfill \\ \hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(t;x,y\right)& =& y,\hfill \\ \hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(st;x,y\right)& =& xy,\hfill \\ \hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(s^2;x,y\right)& =& {\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}x+{\displaystyle \frac{q_1{[n-1]}_{p_1,q_1}}{{\left[n\right]}_{p_1,q_1}}}{x}^2,\hfill \\ \hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(t^2;x,y\right)& =& {\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}y+{\displaystyle \frac{q_2{[m-1]}_{p_2,q_2}}{{\left[m\right]}_{p_2,q_2}}}{y}^2.\hfill \end{array}$$

Using Lemma 2, and by the linearity of $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$, we have

Remark 1.

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(t-x)}^2;x,y\right)& =& {\displaystyle \frac{-p_1^{n-1}{x}^2}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{x{p}_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}},\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s-y)}^2;x,y\right)& =& {\displaystyle \frac{-p_2^{m-1}{y}^2}{{\left[m\right]}_{p_2,q_2}}}+{\displaystyle \frac{y{p}_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}.\hfill \end{array}$$

(6)

Theorem 1.

Let $q_1:=\left(q_{1,n}\right)$, $p_1:=\left(p_{1,n}\right)$, $q_2:=\left(q_{2,m}\right)$, $p_2:=\left(p_{2,m}\right)$

such that $0<q_{1,n},q_{2,m}<p_{1,n},p_{2,m}\le 1$. If

$$\begin{array}{c}\hfill \underset{n}{lim}{p}_{1,n}=1,\underset{n}{lim}{q}_{1,n}=1,\underset{m}{lim}{p}_{2,m}=1,\underset{m}{lim}{q}_{2,m}=1,\underset{n}{lim}{p}_{1,n}^n=a_1\mathrm{and}\underset{m}{lim}{p}_{1,m}^m=a_2,\end{array}$$

(7)

the sequence $C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(f;x,y\right)$ convergence uniformly to $f(x,y)$, on $[0,a]\times [0,b]=I_{ab}$ for each $f\in C\left(I_{ab}\right)$, where $a,b$ be real numbers such that $a\le {\alpha }_n$, $b\le {\beta }_m$ and $C\left(I_{ab}\right)$ be the space of all real-valued continuous functions on $I_{ab}$ with the norm

$$\begin{array}{c}\hfill {\Vert f\Vert }_{C\left(I_{ab}\right)}=\underset{(x,y)\in I_{ab}}{sup}\left|f(x,y)\right|.\end{array}$$

Proof. 

Assume that the equities (7), (3), and (4) hold. Then, we have

$$\begin{array}{c}\hfill {\displaystyle \frac{p_{1,n}^{n-1}{\alpha }_n}{{\left[n\right]}_{p_{1,n},q_{1,n}}}}\to 0,{\displaystyle \frac{p_{2,m}^{m-1}{\beta }_m}{{\left[m\right]}_{p_{2,m},q_{2,m}}}}\to 0,{\displaystyle \frac{q_{1,n}{\left[n\right]}_{p_{1,n},q_{1,n}}}{{\left[n\right]}_{p_{1,n},q_{1,n}}}}\to 1\mathrm{and}{\displaystyle \frac{q_{2,m}{\left[m-1\right]}_{p_{2,m},q_{2,m}}}{{\left[m\right]}_{p_{2,m},q_{2,m}}}}\to 1.\end{array}$$

as $n,m⟶\infty$. From Lemma 2, we obtain ${lim}_{n,m\to \infty }{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(e_{ij};x,y\right)=e_{ij}(x,y)$ uniformly on $I_{ab}$, where $e_{ij}(x,y)=x^i{y}^j,0\le i+j\le 2$ are the test functions. From Korovkin’s theorem for functions of two variables presented by Volkov [25], it follows that ${lim}_{n,m\to \infty }{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(f;x,y\right)=f(x,y)$, uniformly on $I_{ab}$, for each $f\in C\left(I_{ab}\right)$. □

3. Rate of Convergence

In this section, we analyze the convergence rates of the operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ to the function $f(x,y)$ using the modulus of continuity. Furthermore, we present a summary of the relevant notations and definitions concerning the modulus of continuity and Peetre’s K-functional for bivariate real-valued functions.

For a function $f\in C\left(I_{ab}\right)$, the complete modulus of continuity in the bivariate context is defined as follows:

$$\omega (f,\delta )=sup\left\{|f(t,s)-f(x,y)|:\sqrt{{(t-x)}^2+{(s-y)}^2}\le \delta \right\}.$$

for every $(t,s),(x,y)\in I_{ab}$. Additionally, the partial moduli of continuity concerning x and y are defined as follows:

$$\begin{array}{ccc}\hfill {\omega }^1(f,\delta )& =& sup\left\{|f(x_1,y)-f(x_2,y)|:y\in [0,b]\mathrm{and}|x_1-x_2|\le \delta \right\}\hfill \\ \hfill {\omega }^2(f,\delta )& =& sup\left\{|f(x,y_1)-f(x,y_2)|:x\in [0,a]\mathrm{and}|y_1-y_2|\le \delta \right\},\hfill \end{array}$$

It is evident that they fulfill the properties of the standard modulus of continuity [26].

For $\delta >0$, the Peetre K-functional [27] is defined as follows:

$$\begin{array}{c}\hfill K(f,\delta )=\underset{g\in C^2\left(I_{ab}\right)}{inf}\left\{{\parallel f-g\parallel }_{C\left(I_{ab}\right)}+\delta {\parallel g\parallel }_{C^2\left(I_{ab}\right)}\right\},\end{array}$$

where $C^2\left(I_{ab}\right)$ is the space of functions of f such that f, ${\displaystyle \frac{{\partial }^{j}f}{\partial x^j}}$ and ${\displaystyle \frac{{\partial }^{j}f}{\partial y^j}}$$(j=1,2)$ in $C\left(I_{ab}\right)$. The norm $\parallel .\parallel$ on the space $C^2\left(I_{ab}\right)$ is defined by

$$\begin{array}{c}\hfill {\parallel f\parallel }_{C^2{I}_{ab}}={\parallel f\parallel }_{C\left(I_{ab}\right)}+\sum _{j=1}^2\left({∥{\displaystyle \frac{{\partial }^{j}f}{\partial y^j}}∥}_{C\left(I_{ab}\right)}+{∥{\displaystyle \frac{{\partial }^{j}f}{\partial y^j}}∥}_{C\left(I_{ab}\right)}\right).\end{array}$$

We now provide an estimate for the rate of convergence of the operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$.

Theorem 2.

Let $f\in C\left(I_{ab}\right)$. For all $x\in I_{ab}$, we have

$$|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|\le 2\omega \left(f;{\delta }_{n,m}\right),$$

where

$$\begin{array}{ccc}\hfill {\delta }_{n,m}^2& =& {\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}.\hfill \end{array}$$

Proof. 

By definition, the complete modulus of continuity of $f(x,y)$, along with the linearity and positivity of our operator, allows us to express:

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|& \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|f\right(t,s)-f(x,y\left)\right|\right)\hfill \\ & \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\omega \left(f;\sqrt{{(t-x)}^2+{(s-y)}^2}\right)\right)\hfill \\ & \le & \omega (f,{\delta }_{n,m})\left[{\displaystyle \frac{1}{{\delta }_{n,m}}}{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\sqrt{{(t-x)}^2+{(s-y)}^2}\right)\right].\hfill \end{array}$$

Using Cauchy–Schwarz inequality, from (5) and (6), one can write the following:

$$\begin{array}{ccc}& & |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|\hfill \\ & \le & \omega (f,{\delta }_{n,m})\left[1+{\displaystyle \frac{1}{{\delta }_{n,m}}}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(t-x)}^2+{(s-y)}^2\right)\right\}}^{1/2}\right]\hfill \\ & =& \omega (f,{\delta }_{n,m})\left[1+{\displaystyle \frac{1}{{\delta }_{n,m}}}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(t-x)}^2\right)+C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s-y)}^2\right)\right\}}^{1/2}\right]\hfill \\ & \le & \omega (f,{\delta }_{n,m})\left[1+{\displaystyle \frac{1}{{\delta }_{n,m}}}{\left({\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\right)}^{1/2}\right].\hfill \end{array}$$

Choosing ${\delta }_{n,m}={\left({\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\right)}^{1/2}$, for all $(x,y)\in I_{ab}$, we obtain the desired result. □

Theorem 3.

Let $f\in C\left(I_{ab}\right)$; then, the following inequalities satisfy

$$|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|\le {\omega }^1\left(f;{\delta }_n\right)+{\omega }^2\left(f;{\delta }_m\right),$$

where

$$\begin{array}{ccc}\hfill {\delta }_n^2& =& {\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}},\hfill \end{array}$$

(8)

$$\begin{array}{ccc}\hfill {\delta }_m^2& =& {\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}.\hfill \end{array}$$

(9)

Proof. 

By definition, the partial moduli of continuity of $f(x,y)$ and the application of the Cauchy–Schwarz inequality imply that

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|& \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|f\right(t,s)-f(x,s)+f(x,s)-f(x,y\left)\right|\right)\hfill \\ & \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|f\right(t,s)-f(x,s\left)\right|\right)+C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|f\right(x,s)-f(x,y\left)\right|\right)\hfill \\ & \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|{\omega }^1(f;|t-x\left|\right)|\right)+C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|{\omega }^2(f;|s-y\left|\right)|\right)\hfill \\ & \le & {\omega }^1(f,{\delta }_n)\left[1+{\displaystyle \frac{1}{{\delta }_n}}{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|t-x|\right)\right]\hfill \\ & & +{\omega }^2(f,{\delta }_m)\left[1+{\displaystyle \frac{1}{{\delta }_m}}{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|s-y|\right)\right]\hfill \\ & \le & {\omega }^1(f,{\delta }_n)\left[1+{\displaystyle \frac{1}{{\delta }_n}}{\left(C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(t-x)}^2\right)\right)}^{1/2}\right]\hfill \\ & & +{\omega }^2(f,{\delta }_m)\left[1+{\displaystyle \frac{1}{{\delta }_m}}{\left(C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s-y)}^2\right)\right)}^{1/2}\right].\hfill \end{array}$$

Consider

$$\begin{array}{ccc}\hfill {\delta }_n^2& =& {\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}},\hfill \\ \hfill {\delta }_m^2& =& {\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\hfill \end{array}$$

we reach the result. □

For ${\widehat{\alpha }}_1,{\widehat{\alpha }}_2\in (0,1]$ and $(s,t),(x,y)\in I_{ab}$, we define the Lipschitz class $LipM({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$ for the bivariate case as follows:

$$\begin{array}{c}\hfill \left|f(t,s)-f(x,y)\right|\le M{\left|t-x\right|}^{{\widehat{\alpha }}_1}{\left|s-y\right|}^{{\widehat{\alpha }}_2}.\end{array}$$

Theorem 4.

Let $f\in Li{p}_M({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$. Then, for all $(x,y)\in I_{ab}$, we have

$$|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|\le M{\delta }_n^{{\widehat{\alpha }}_1/2}{\delta }_m^{{\widehat{\alpha }}_2/2},$$

where ${\delta }_n$ and ${\delta }_m$ defined in (8) and (9), respectively.

Proof. 

As $f\in Li{p}_M({\widehat{\alpha }}_1,{\widehat{\alpha }}_2)$, it follows that

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|& \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\right|f(t,s)-f(x,y)|;x,y)\hfill \\ & \le & M{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}{\left(\right|t-x|}^{{\widehat{\alpha }}_1}{|s-y|}^{{\widehat{\alpha }}_2};x,y)\hfill \\ & =& M{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}{\left(\right|t-x|}^{{\widehat{\alpha }}_1}|;x)C_{n,m}^{(p_1,q_1),(p_2,q_2)}{\left(\right|s-y|}^{{\widehat{\alpha }}_2};y).\hfill \end{array}$$

For

$\widehat{p}={\displaystyle \frac{1}{{\widehat{\alpha }}_1}},\widehat{q}={\displaystyle \frac{{\widehat{\alpha }}_1}{2-{\widehat{\alpha }}_1}}$ and $\widehat{p}={\displaystyle \frac{1}{{\widehat{\alpha }}_2}},\widehat{q}={\displaystyle \frac{{\widehat{\alpha }}_2}{2-{\widehat{\alpha }}_2}}$ applying the Hölder’s inequality, we obtain

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)|& \le & M\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}{\left(\right|t-x|}^2;x{\left)\right\}}^{{\widehat{\alpha }}_1/2}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}(1;x)\right\}}^{{\widehat{\alpha }}_1/2}\hfill \\ & & \times \{C_{n,m}^{(p_1,q_1),(p_2,q_2)}{\left(\right|s-y|}^2;y{\left)\right\}}^{{\widehat{\alpha }}_{12}/2}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}(1;y)\right\}}^{{\widehat{\alpha }}_2/2}\hfill \\ & =& M{\delta }_n^{{\widehat{\alpha }}_1/2}{\delta }_m^{{\widehat{\alpha }}_2/2}.\hfill \end{array}$$

Hence, we obtain the desired result. □

Theorem 5.

Let $f\in C^1\left(I_{ab}\right)$ and $0<q_{1,n},q_{2,m}<p_{1,n},p_{2,m}\le 1$. Then, we have

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f\left(t\right)-f\left(s\right)|& \le & \Vert f_x^{\prime }{\Vert }_{C\left(I_{ab}\right)}{\delta }_n+{\Vert f_y^{\prime }\Vert }_{C\left(I_{ab}\right)}{\delta }_m.\hfill \end{array}$$

Proof. 

For $(t,s)\in I_{ab}$, we obtain

$$\begin{array}{c}\hfill f\left(t\right)-f\left(s\right)={\int }_x^t{f}_u^{\prime }(u,s)du+{\int }_y^s{f}_v^{\prime }(x,v)dv\end{array}$$

By applying our operator to both sides of the above equation, we deduce

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f\left(t\right)-f\left(s\right)|& \le & C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|{\int }_x^t{f}_u^{\prime }(u,s)du\right|;x,y\right)\hfill \\ & & +C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(\left|{\int }_y^s{f}_v^{\prime }(x,v)dv\right|;x,y\right).\hfill \end{array}$$

As

$$\begin{array}{c}\hfill \left|{\int }_x^t{f}_u^{\prime }(u,s)du\right|\le \Vert f_x^{\prime }{\Vert }_{C\left(I_{ab}\right)}|t-x|\mathrm{and}\left|{\int }_y^s{f}_v^{\prime }(x,v)dv\right|\le \Vert f_y^{\prime }{\Vert }_{C\left(I_{ab}\right)}|s-y|,\end{array}$$

we have

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f\left(t\right)-f\left(s\right)|& \le & \Vert f_x^{\prime }{\Vert }_{C\left(I_{ab}\right)}{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|t-x|;x,y\right)\hfill \\ & & +\Vert f_y^{\prime }{\Vert }_{C\left(I_{ab}\right)}{C}_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(|s-y|;x,y\right).\hfill \end{array}$$

Using the Cauchy–Schwarz inequality, we can write the following:

$$\begin{array}{ccc}\hfill |C_{n,m}^{(p_1,q_1),(p_2,q_2)}f\left(t\right)-f\left(s\right)|& \le & \Vert f_x^{\prime }{\Vert }_{C\left(I_{ab}\right)}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(t-x)}^2;x,y\right)\right\}}^{1/2}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(1;x,y\right)\right\}}^{1/2}\hfill \\ & & +\Vert f_y^{\prime }{\Vert }_{C\left(I_{ab}\right)}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s-y)}^2;x,y\right)\right\}}^{1/2}{\left\{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(1;x,y\right)\right\}}^{1/2}.\hfill \end{array}$$

Form (5) and (6), we obtain the desired result. □

Below, we obtained three-dimensional graphs illustrating the convergence rates of operators to specific functions using the Maple [28] software.

Example 1.

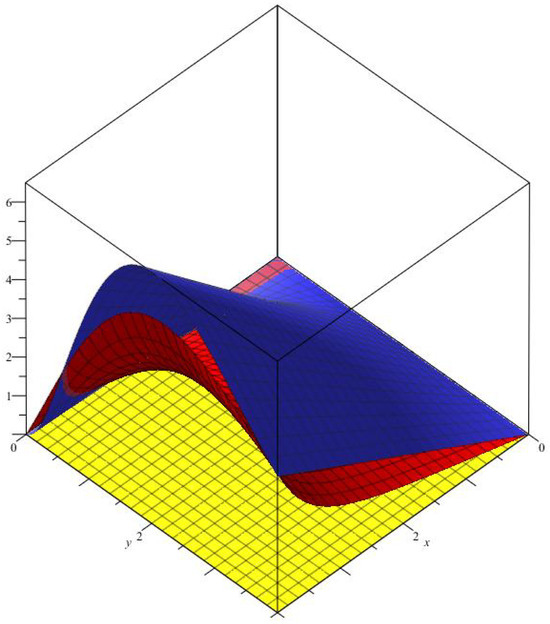
Figure 1 shows the optimal approximation of operators

Figure 1. Convergence of two−dimensional $(p,q)$-Bernstein–Chlodowsky polynomials.

$C_{20,20}^{(0.999,0.9),(0.999,0.9)}(f;x,y)$(red), $C_{20,20}^{(0.90,0.86),(0.996,0.89)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=\sqrt{m}$ to function $f(x,y)=3x{y}^2{e}^{-y}$(blue).

Example 2.

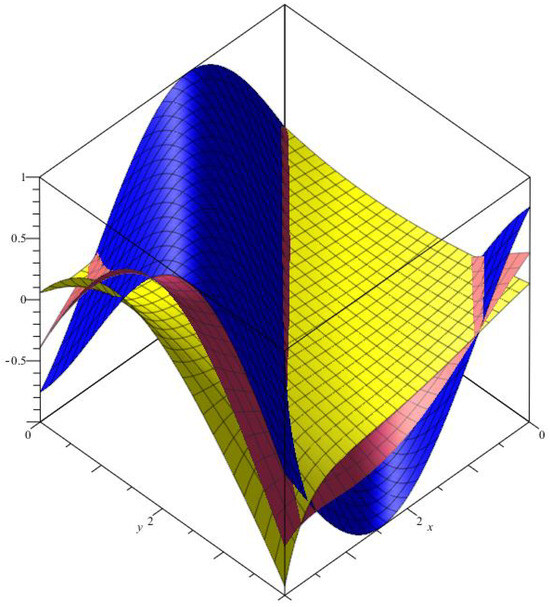
Figure 2 shows the optimal approximation of operators

Figure 2. Convergence of two−dimensional $(p,q)$-Bernstein–Chlodowsky polynomials.

$C_{20,20}^{(0.999,0.9),(0.99,0.9)}(f;x,y)$(red), $C_{20,20}^{(0.990,0.86),(0.996,0.89)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=\sqrt{m}$ to function $f(x,y)=sin(x-y)$(blue).

Example 3.

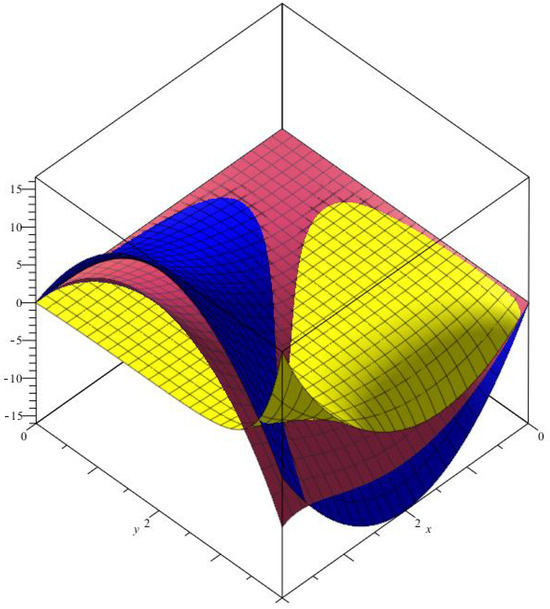
Figure 3 shows the optimal approximation of operators

Figure 3. Convergence of two−dimensional $(p,q)$-Bernstein–Chlodowsky polynomials.

$C_{20,20}^{(0.99,0.9),(0.999,0.96)}(f;x,y)$(red), $C_{20,20}^{(0.99,0.9),(0.990,0.90)}(f;x,y)$(yellow)

with ${\alpha }_n=ln\left(n\right)$, ${\beta }_m=ln\left(m\right)$ to function $f(x,y)=x^{2}y-x{y}^2)$(blue).

Theorem 6.

Let $f\in C\left(I_{ab}\right)$, then we have

$$\begin{array}{c}\hfill {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(f;x,y\right)-f(x,y)∥}_{C\left(I_{ab}\right)}\le 2M\left(f;{\delta }_{n,m}(x,y)/2\right),\end{array}$$

where

$$\begin{array}{c}\hfill {\delta }_{n,m}(x,y)={\displaystyle \frac{1}{2}}max\left({\displaystyle \frac{a{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}},{\displaystyle \frac{b{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\right).\end{array}$$

Proof. 

Let $g\in C^2\left(I_{ab}\right)$. Utilizing Taylor’s formula, we derive

$$\begin{array}{ccc}\hfill g(s_1,s_2)-g(x,y)& =& g(s_1,y)-g(x,y)+g(s_1,s_2)-g(s_1,y)\hfill \\ & =& {\displaystyle \frac{\partial g(x,y)}{\partial x}}(s_1-x)+{\int }_x^{s_1}(s_1-u){\displaystyle \frac{{\partial }^{2}g(u,y)}{\partial u^2}}du\hfill \\ & & +{\displaystyle \frac{\partial g(x,y)}{\partial x}}(s_2-y)+{\int }_y^{s_2}(s_2-v){\displaystyle \frac{{\partial }^{2}g(x,v)}{\partial v^2}}dv\hfill \\ & =& {\displaystyle \frac{\partial g(x,y)}{\partial x}}(s_1-x)+{\int }_0^{s_1-x}(s_1-x-u){\displaystyle \frac{{\partial }^{2}g(u,y)}{\partial u^2}}du\hfill \\ & & +{\displaystyle \frac{\partial g(x,y)}{\partial x}}(s_2-y)+{\int }_0^{s_2-y}(s_2-y-v){\displaystyle \frac{{\partial }^{2}g(x,v)}{\partial v^2}}dv\hfill \end{array}$$

By applying $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ to both sides of the above equation, we obtain

$$\begin{array}{ccc}\hfill \left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}g(s_1,s_2)-g(x,y)\right|& \le & \left|{\displaystyle \frac{\partial g(x,y)}{\partial x}}\right|\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left((s_1-x);x,y\right)\right|\hfill \\ & & +\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\int }_0^{s_1-x}(s_1-x-u){\displaystyle \frac{{\partial }^{2}g(u,y)}{\partial u^2}}du;x,y\right)\right|\hfill \\ & & +\left|{\displaystyle \frac{\partial g(x,y)}{\partial y}}\right|\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left((s_2-y);x,y\right)\right|\hfill \\ & & +\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\int }_0^{s_2-y}(s_2-y-v){\displaystyle \frac{{\partial }^{2}g(v,x)}{\partial v^2}}dv;x,y\right)\right|\hfill \end{array}$$

As $C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left((s_1-x);x,y\right)=0$ and $C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left((s_2-y);x,y\right)=0$, one can write the following:

$$\begin{array}{ccc}\hfill {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}g(s_1,s_2)-g(x,y)∥}_{C\left(I_{ab}\right)}& \le & {\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{\partial g(x,y)}{\partial x}}∥}_{C\left(I_{ab}\right)}\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s_1-x)}^2;x,y\right)\right|\hfill \\ & & +{\displaystyle \frac{1}{2}}{∥{\displaystyle \frac{\partial g(x,y)}{\partial y}}∥}_{C\left(I_{ab}\right)}\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({(s_2-y)}^2;x,y\right)\right|.\hfill \end{array}$$

By (5), (6), we deduce

$$\begin{array}{ccc}\hfill {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}g(s_1,s_2)-g(x,y)∥}_{C\left(I_{ab}\right)}& \le & {\displaystyle \frac{1}{2}}max\left({\displaystyle \frac{-p_1^{n-1}{x}^2}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{x{p}_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}},{\displaystyle \frac{-p_2^{m-1}{y}^2}{{\left[m\right]}_{p_2,q_2}}}+{\displaystyle \frac{y{p}_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\right)\hfill \\ & & \times \left[{∥{\displaystyle \frac{\partial g(x,y)}{\partial x}}∥}_{C\left(I_{ab}\right)}+{∥{\displaystyle \frac{\partial g(x,y)}{\partial x}}∥}_{C\left(I_{ab}\right)}\right]\hfill \\ & \le & {\Vert g\Vert }_{C\left(I_{ab}\right)}{\delta }_{n,m}.\hfill \end{array}$$

(10)

By the linearity $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$, we obtain

$$\begin{array}{ccc}\hfill {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(f;x,y\right)-f(x,y)∥}_{C\left(I_{ab}\right)}& \le & {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}f-C_{n,m}^{(p_1,q_1),(p_2,q_2)}g∥}_{C\left(I_{ab}\right)}\hfill \\ & & +{∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}g-g∥}_{C\left(I_{ab}\right)}+{∥f-g∥}_{C\left(I_{ab}\right)}.\hfill \end{array}$$

(11)

By (10) and (11), one can see that

$$\begin{array}{c}\hfill {∥C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(f;x,y\right)-f(x,y)∥}_{C\left(I_{ab}\right)}\le 2M\left(f;{\delta }_{n,m}(x,y)/2\right).\end{array}$$

This step completes the proof. □

Initially, we need to establish the auxiliary result found in the subsequent lemma.

Lemma 3.

Let $0<q_n<p_n\le 1$ be sequences such that $p_n,q_n⟶1$ and $p_n^n⟶a_1$ as $n⟶\infty$. Then, we have the following limits:

(i) 

${lim}_{n\to \infty }{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}}{{\alpha }_n}}{C}_{n,n}^{(p_n,q_n)}({(t-x)}^2;x)=a_{1}x$

(ii) 

${lim}_{n\to \infty }{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}^2}{{\alpha }_n^2}}{C}_{n,n}^{(p_n,q_n)}({(t-x)}^4;x)=3a_1{x}^2$.

Proof. 

(i) Using Lemma 1, we have

$$\begin{array}{c}\hfill C_{n,n}^{(p_n,q_n)}({(t-x)}^2;x)={\displaystyle \frac{-p_n^{n-1}{x}^2}{{\left[n\right]}_{p_n,q_n}}}+{\displaystyle \frac{x{p}_n^{n-1}{\alpha }_n}{{\left[n\right]}_{p_n,q_n}}}\end{array}$$

(12)

Then, we obtain

$$\begin{array}{c}\hfill {\displaystyle \frac{{\left[n\right]}_{p_n,q_n}}{{\alpha }_n}}{C}_{n,n}^{(p_n,q_n)}({(t-x)}^2;x)={\displaystyle \frac{-p_n^{n-1}{x}^2}{{\alpha }_n}}+x{p}_n^{n-1}.\end{array}$$

Takingthe limit of both sides of the above equality as $n\to \infty$, we can write:

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}}{{\alpha }_n}}\left\{C_{n,n}^{(p_n,q_n)}({(t-x)}^2,x)\right\}& =& \underset{n\to \infty }{lim}\left\{{\displaystyle \frac{-p_n^{n-1}{x}^2}{{\alpha }_n}}+x{p}_n^{n-1}\right\}\hfill \\ & =& a_{1}x.\hfill \end{array}$$

(ii) Utilizing Lemma 1 along with the linearity of the operators $C_{n,n}^{(p_n,q_n)}$, we arrive at

$$\begin{array}{c}\hfill C_{n,n}^{(p_n,q_n)}({(t-x)}^4;x)=A_{1,n}{x}^4+A_{2,n}{x}^3+A_{3,n}{x}^2+A_{4,n}x\end{array}$$

(13)

where

$$\begin{array}{ccc}\hfill A_{1,n}& =& {\displaystyle \frac{p_n^{n-3}{\left[n\right]}_{p_n,q_n}^2(-p_n^2+2p_n{q}_n-q_n^2)+p_n^{n-5}{\left[n\right]}_{p_n,q_n}(-p_n^3+3p_n{q}_n^2+q_n^3)-p_n^{3n-6}(p_n^2+p_n^3+2p_n{q}_n^2+q_n^3)}{{\left[n\right]}_{p_n,q_n}^3}}\hfill \\ \hfill A_{2,n}& =& {\displaystyle \frac{p_n^{n-3}{\left[n\right]}_{p_n,q_n}^2(p_n^2-2p_n{q}_n+q_n^2)}{{\left[n\right]}_{p_n,q_n}^3}}{\alpha }_n\hfill \\ & & +{\displaystyle \frac{p^{2n-5}{\left[n\right]}_{p_n,q_n}(-q_n^3-4p_n{q}_n^2-3p_n^2{q}_n+2p_n^3)-p_n^{3n-6}(3p_n^3+3p_n{q}_n^2+5p_n^2{q}_n+q_n^3)}{{\left[n\right]}_{p_n,q_n}^3}}{\alpha }_n\hfill \\ \hfill A_{3,n}& =& {\displaystyle \frac{p_n^{2n-4}{\left[n\right]}_{p_n,q_n}(-p_n^2+3p_n{q}_n+q_n^2)-p_n^{3n-5}(3p_n^2+q_n^2+3p_n{q}_n)}{{\left[n\right]}_{p_n,q_n}^3}}{\alpha }_n^2\hfill \\ \hfill A_{4,n}& =& {\displaystyle \frac{p^{3n-3}{\alpha }_n^3}{{\left[n\right]}_{p_n,q_n}^3}},\hfill \end{array}$$

It is clear that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}^2}{{\alpha }_n^2}}\left\{A_{4,n}x\right\}=0.\end{array}$$

(14)

Taking the limit of both sides of $A_{1,n}$, we arrive at

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}^2}{{\alpha }_n^2}}\left\{A_{1,n}\right\}& =& \underset{n\to \infty }{lim}\left\{{\displaystyle \frac{-p_n^{n-3}{\left[n\right]}_{p_n,q_n}{(p_n-q_n)}^2}{{\alpha }_n^2}}+{\displaystyle \frac{p_n^{n-5}(-p_n^3+3p_n{q}_n^2+q_n^3)}{{\alpha }_n^2}}-{\displaystyle \frac{p_n^{3n-6}(p_n^2+p_n^3+2p_n{q}_n^2+q_n^3)}{{\left[n\right]}_{p_n,q_n}{\alpha }_n^2}}\right\}\hfill \\ & =& \underset{n\to \infty }{lim}\left\{{\displaystyle \frac{-p_n^{n-3}(p_n^n-q_n^n)(p_n-q_n)}{{\alpha }_n^2}}+{\displaystyle \frac{p^{n-5}(-p_n^3+3p_n{q}_n^2+q_n^3)}{{\alpha }_n^2}}-{\displaystyle \frac{p_n^{3n-6}(p_n^2+p_n^3+2p_n{q}_n^2+q_n^3)}{{\left[n\right]}_{p_n,q_n}{\alpha }_n^2}}\right\}\hfill \\ & =& 0.\hfill \end{array}$$

(15)

Similarly, we can show that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}^2}{{\alpha }_n^2}}\left\{A_{2,n}\right\}=0\mathrm{and}\underset{n\to \infty }{lim}{\displaystyle \frac{{\left[n\right]}_{p_n,q_n}^2}{{\alpha }_n^2}}\left\{A_{3,n}\right\}=3a_1{x}^2\end{array}$$

(16)

By combining (14)–(16), we reach the desired result. □

Now, we are ready to present a Voronovskaja-type theorem for $C_{n,n}^{(p_n,q_n)}(f;x,y)$.

Theorem 7.

Let $f\in C^2\left(I_{ab}\right)$. Then, we have

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}{C}_{n,n}^{(p_n,q_n)}(f;x,y)-f\left(x_{,}y\right))& =& {\displaystyle \frac{a_{1}x{f}_{x^2}^{\prime \prime }(x,y)}{2}}+{\displaystyle \frac{a_{1}y{f}_{y^2}^{\prime \prime }(x,y)}{2}}.\hfill \end{array}$$

Proof. 

Let $(x,y)\in I_{ab}$. Then, we write Taylor’s formula of f as follows:

$$\begin{array}{ccc}\hfill f(s,t)& =& f(x,y)+f_x^{\prime }(s-x)+f_y^{\prime }(t-y)\hfill \\ & & +{\displaystyle \frac{1}{2}}\left\{f_{x^2}^{\prime \prime }{(t-x)}^2+2f_{xy}^{\prime }(s-x)(t-y)+f_{y^2}^{\prime \prime }{(t-y)}^2\right\}+\epsilon (s,t)\left({(s-x)}^2+{(t-y)}^2\right)\hfill \end{array}$$

(17)

where $(s,t)\in I_{ab}$ and $\epsilon (s,t)⟶0$ as $(s,t)⟶(x,y)$.

If we apply the operator $C_{n,n}^{(p_n,q_n)}(f;s,t)$ on (17), we obtain

$$\begin{array}{ccc}\hfill C_{n,n}^{(p_n,q_n)}(f;s,t)-f\left(x_{,}y\right)& =& f_x^{\prime }(x,y)C_{n,n}^{(p_n,q_n)}((s-x);x,y)+f_y^{\prime }(x,y)C_{n,n}^{(p_n,q_n)}((t-y);x,y)\hfill \\ & & +{\displaystyle \frac{1}{2}}\{f_{x^2}^{\prime \prime }{C}_{n,n}^{(p_n,q_n)}({(t-x)}^2;x,y)+2f_{xy}^{\prime }{C}_{n,n}^{(p_n,q_n)}((s-x)(t-y);x,y)\hfill \\ & & +f_{y^2}^{\prime \prime }{C}_{n,n}^{(p_n,q_n)}({(t-y)}^2;x,y)\}+C_{n,n}^{(p_n,q_n)}\left(\epsilon (s,t)\left({(s-x)}^2+{(t-y)}^2\right);x,y\right).\hfill \end{array}$$

Applying the limit of both sides of the above equality, we obtain $n⟶\infty$, □

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}{C}_{n,n}^{(p_n,q_n)}(f;s,t)-f(x,y))& =& \underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}{\displaystyle \frac{1}{2}}\{f_{x^2}^{\prime \prime }{C}_{n,n}^{(p_n,q_n)}({(t-x)}^2;x,y)\hfill \\ & & +2f_{xy}^{\prime }{C}_{n,n}^{(p_n,q_n)}((s-x)(t-y);x,y)+f_{y^2}^{\prime \prime }{C}_{n,n}^{(p_n,q_n)}({(t-y)}^2;x,y)\}\hfill \\ & & +\underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}{C}_{n,n}^{(p_n,q_n)}\left(\epsilon (s,t)\left({(s-x)}^2+{(t-y)}^2\right);x,y\right).\hfill \end{array}$$

By Cauchy–Schwarz inequality, we can write the following

$$\begin{array}{ccc}\hfill C_{n,n}^{(p_n,q_n)}\left(\epsilon (s,t)\left({(s-x)}^2+{(t-y)}^2\right);x,y\right)& \le & \sqrt{{lim}_{n\to \infty }{C}_{n,n}^{(p_n,q_n)}\left({\epsilon }^2(s,t);x,y\right)}\hfill \\ & \times & \sqrt{2{lim}_{n\to \infty }{\left[n\right]}_{p_n,q_n}^2{C}_{n,n}^{(p_n,q_n)}\left(\epsilon (s,t)\left({(s-x)}^4+{(t-y)}^4\right);x,y\right)}.\hfill \end{array}$$

As ${lim}_{n\to \infty }{C}_{n,n}^{(p_n,q_n)}\left({\epsilon }^2(s,t);x,y\right)={\epsilon }^2(x,y)=0$ and from Lemma 3(ii)

${lim}_{n\to \infty }{\left[n\right]}_{p_n,q_n}^2{C}_{n,n}^{(p_n,q_n)}\left({(s-x)}^4+{(t-y)}^4);x,y\right)$ is finite, then we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}^2{C}_{n,n}^{(p_n,q_n)}\left(\epsilon (s,t)\left({(s-x)}^4+{(t-y)}^4\right);x,y\right)=0.\end{array}$$

Hence, we deduce

$$\begin{array}{ccc}\hfill \underset{n\to \infty }{lim}{\left[n\right]}_{p_n,q_n}{C}_{n,n}^{(p_n,q_n)}(f;x,y)-f\left(x_{,}y\right))& =& {\displaystyle \frac{a_{1}x{f}_{x^2}^{\prime \prime }(x,y)}{2}}+{\displaystyle \frac{a_{1}y{f}_{y^2}^{\prime \prime }(x,y)}{2}}.\hfill \end{array}$$

Thisstep completes the proof.

4. Weighted Approximation Properties of Two-Variable Function

In this section, we investigate the convergence of the sequence of linear positive operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ to a function of two variables defined within a weighted space. We also compute the rate of convergence using the weighted modulus of continuity.

Let $\rho (x,y)=x^2+y^2+1$, and define $B_{\rho }$ as the space of all functions f defined on the real axis that satisfy $\left|f(x,y)\right|\le M_f\rho (x,y)$, where $M_f$ is a positive constant dependent solely on f. The subspace $C_{\rho }$ of $B_{\rho }$ consists of all continuous functions and is equipped with the norm

$${\parallel f\parallel }_{\rho }=\underset{(x,y)\in {\mathbb{R}}_{+}^2}{sup}{\displaystyle \frac{\left|f\right(x,y\left)\right|}{\rho (x,y)}}.$$

Let $C_{\rho }^0$ represent the subspace of all functions $f\in C_{\rho }$ for which ${lim}_{x\to \infty }{\displaystyle \frac{f(x,y)}{\rho (x,y)}}$ exists and is finite. For every $f\in C_{\rho }^0$, the weighted modulus of continuity is defined as

$${\Omega }_f(f;{\delta }_1,{\delta }_2)=\underset{(x,y)\in {\mathbb{R}}_{+}^2}{sup}\underset{\left|h_1\right|\le {\delta }_1,\left|h_2\right|\le {\delta }_2}{sup}{\displaystyle \frac{\left|f(x+h_1,y+h_2)-f(x,y)\right|}{\rho (x,y)\rho (h_1,h_2)}}.$$

(18)

Lemma 4.

The operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ defined (2) act from $C_{\rho }\left({\mathbb{R}}_{+}^2\right)$ to $B_{\rho }\left({\mathbb{R}}_{+}^2\right)$ if and only if the inequality

$$\begin{array}{c}\hfill \Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}{(\rho ;x,y)\Vert }_{x^2}\le c.\end{array}$$

holds for some positive constant c.

Theorem 8.

Consider the sequence of linear positive operators $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ defined in (2). For any function $f\in C_{\rho }^0$ and for all points $(x,y)\in I_{{\alpha }_n{\beta }_m}$, it follows that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}{\parallel C_{n,m}^{(p_1,q_1),(p_2,q_2)}(f;x,y)-f(x,y)\parallel }_{\rho }=0.\end{array}$$

Proof. 

From Lemma 2, we obtain

$$\begin{array}{ccc}\hfill \Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(1;x,y\right){-1\Vert }_{\rho }& =& 0,\hfill \\ \hfill \Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(s;x,y\right){-x\Vert }_{\rho }& =& 0\hfill \\ \hfill \Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left(t;x,y\right){-y\Vert }_{\rho }& =& 0.\hfill \end{array}$$

Again by Lemma 2, we can write the following

$$\begin{array}{ccc}& & \Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}(s^2+t^2;x,y)-(x^2+y^2){\Vert }_{\rho }\hfill \\ & =& \underset{(x,y)\in {\mathbb{R}}_{+}^2}{sup}\left\{{\displaystyle \frac{p_1^{n-1}{\alpha }_{n}x}{{\left[n\right]}_{p_1,q_1}(x^2+y^2+1)}}+{\displaystyle \frac{p_1^{n-1}{x}^2}{{\left[n\right]}_{p_1,q_1}(x^2+y^2+1)}}+{\displaystyle \frac{p_2^{m-1}{\beta }_{m}y}{{\left[m\right]}_{p_2,q_2}(x^2+y^2+1)}}+{\displaystyle \frac{p_2^{m-1}{y}^2}{{\left[m\right]}_{p_2,q_2}(x^2+y^2+1)}}\right\}\hfill \\ & \le & {\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{p_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}+{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}+{\displaystyle \frac{p_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\hfill \end{array}$$

Considering the limit of both sides of the preceding inequality as $n,m\to \infty$ and applying (3) and (4), we derive

$$\begin{array}{c}\hfill \underset{m,n\to \infty }{lim}{\Vert C_{n,m}^{(p_1,q_1),(p_2,q_2)}(s^2+t^2;x,y)-(x^2+y^2)\Vert }_{\rho }=0.\end{array}$$

By applying the weighted Korovkin theorem for functions of two variables as established by Gadzhiev in references [29,30], we derive the intended results. □

To estimate the rate of convergence, we need the following lemma:

Lemma 5.

For all $(x;y)\in I_{{\alpha }_n{\beta }_m}$, by (5), (6) and (13), one can write the following:

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^2;x,y\right)& =& O\left({\displaystyle \frac{{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}\right)\left(x^2+x\right),\hfill \end{array}$$

(19)

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^4;x,y\right)& =& O\left({\displaystyle \frac{{\alpha }_n{p}_1^{n-1}}{{\left[n\right]}_{p_1,q_1}}}\right)\left(x^4+x^3+x^2+x\right)\hfill \end{array}$$

(20)

and

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^2;x,y\right)& =& O\left({\displaystyle \frac{{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\right)\left(y^2+y+1\right),\hfill \end{array}$$

(21)

$$\begin{array}{ccc}\hfill C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^4;x,y\right)& =& O\left({\displaystyle \frac{{\beta }_m{p}_2^{m-1}}{{\left[m\right]}_{p_2,q_2}}}\right)\left(y^4+y^3+y^2+y+1\right).\hfill \end{array}$$

(22)

Now, compute the rate of convergence of the operator $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ in weighted spaces.

Theorem 9.

If $f\in C_{\rho }^0,$ then we have

$$\underset{\left(x,y\right)\in {\mathbb{R}}_{+}^2}{sup}{\displaystyle \frac{\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}(f;x,y)-f(x,y)\right|}{\rho {\left(x,y\right)}^3}}\le {\mathcal{C}}_2{\omega }_{\rho }(f;{\delta }_n,{\delta }_m),$$

where ${\mathcal{C}}_2$ is a constant independent of $n,m$ and ${\delta }_n={\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}$, ${\delta }_n={\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}$.

Proof. 

Taking into account the following inequality given in [31], we deduce

$$\left|f\left(t,s\right)-f\left(x,y\right)\right|\le 8\left(1+x^2+y^2\right){\omega }_{\rho }(f;{\delta }_n,{\delta }_m)$$

$$\times \left(1+{\displaystyle \frac{\left|t-x\right|}{{\delta }_n}}\right)\left(1+{\displaystyle \frac{\left|s-y\right|}{{\delta }_m}}\right)\left(1+{\left(t-x\right)}^2\right)\left(1+{\left(s-y\right)}^2\right).$$

Applying $C_{n,m}^{(p_1,q_1),(p_2,q_2)}$ to both sides above inequality and using Cauchy–Schwarz inequality, one can write following:

$$\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)\right|\le 8\left(1+x^2+y^2\right){\omega }_{\rho }(f;{\delta }_n,{\delta }_m)$$

$$\times \left[1+C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^2;x,y\right)+{\displaystyle \frac{1}{{\delta }_n}}\sqrt{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^2;x,y\right)}\right.$$

$$\left.{\displaystyle \frac{1}{{\delta }_n}}\sqrt{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^2;x,y\right)C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(t-x\right)}^4;x,y\right)}\right]$$

$$\times \left[1+C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^2;x,y,a\right)+{\displaystyle \frac{1}{{\delta }_m}}\sqrt{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^2;x,y\right)}\right.$$

$$\times \left.{\displaystyle \frac{1}{{\delta }_m}}\sqrt{C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^2;x,y\right)C_{n,m}^{(p_1,q_1),(p_2,q_2)}\left({\left(s-y\right)}^4;x,y\right)}\right].$$

By (19)–(22), we obtain

$$\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)\right|\le 8\left(1+x^2+y^2\right){\omega }_{\rho }(f;{\delta }_n,{\delta }_m)$$

$$\times \left[1+O\left({\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}\right)\left(x^2+x\right)+{\displaystyle \frac{1}{{\delta }_n}}\sqrt{O\left({\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}\right)\left(x^2+x\right)}\right.$$

$$\left.+{\displaystyle \frac{1}{{\delta }_n}}\sqrt{O\left({\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}\right)\left(x^2+x\right)\left(x^4+x^3+x^2+x\right)}\right]$$

$$\times \left[1+{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\left(y^2+y\right)+{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\sqrt{{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}}\right.$$

$$\left.+{\displaystyle \frac{1}{{\delta }_m}}\sqrt{{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\left(y^2+y\right){\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\left(y^4+y^3+y^2+y\right)}\right].$$

Taking ${\delta }_n={\left({\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}\right)}^{1/2},{\delta }_m={\left({\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}\right)}^{1/2}$, one can write the following:

$$\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}f(t,s)-f(x,y)\right|\le {\mathcal{C}}_2\left(1+x^2+y^2\right){\omega }_{\rho }(f;{\delta }_n,{\delta }_m)$$

$$\times \left[1+{\delta }_n^2\left(x^2+x\right)+\sqrt{x^2+x}+\sqrt{\left(x^2+x\right)\left(x^4+x^3+x^2+x\right)}\right]$$

$$\times \left[1+{\delta }_m^2\left(y^2+y\right)+\sqrt{\left(y^2+y\right)}+\sqrt{\left(y^2+y\right)\left(y^4+y^3+y^2+y\right)}\right],$$

where ${\mathcal{C}}_2$ is a constant independent of $n,m.$ Since ${\delta }_n^2<1,{\delta }_m^2<1,$ for sufficiently large $n,m,$ we obtain

$$\underset{\left(x,y\right)\in {\mathbb{R}}_{+}^2}{sup}{\displaystyle \frac{\left|C_{n,m}^{(p_1,q_1),(p_2,q_2)}(f;x,y)-f(x,y)\right|}{{\left(1+x^2+y^2\right)}^3}}\le {\mathcal{C}}_2{\omega }_{\rho }\left(f;\sqrt{{\displaystyle \frac{p_1^{n-1}{\alpha }_n}{{\left[n\right]}_{p_1,q_1}}}},\sqrt{{\displaystyle \frac{p_2^{m-1}{\beta }_m}{{\left[m\right]}_{p_2,q_2}}}}\right).$$

This step completes the proof. □