Exploring Symmetry in Industrial Decision-Making: A New Framework Based on Cubic Type-2 Fuzzy Soft Sets

Abstract

Industry 4.0 supply chains, characterized by dynamic environments, uncertainty, and intricate interdependencies, necessitate robust decision-making tools. While existing models have made strides in addressing these complexities, they often struggle to effectively handle the high degree of uncertainty inherent in such systems. To bridge this gap, this research introduces a novel framework grounded in the axioms of Cubic Type-2 Fuzzy Soft Sets (CT2FSSs). By leveraging the enhanced flexibility and uncertainty-handling capabilities of CT2FSSs, our proposed framework empowers decision-makers to navigate complexities, optimize supply chain processes, and mitigate risks while maintaining symmetry in decision-making. Through rigorous theoretical analysis and practical applications, this study not only advances fuzzy set theory but also demonstrates its efficacy in the context of Industry 4.0. The unique contribution of this research lies in the development of a CT2FSS-based framework that offers superior adaptability to uncertain and complex environments, thereby enhancing the resilience and performance of supply chains in symmetrical scenarios.

1. Introduction

Industry 4.0, characterized by the convergence of advanced technologies such as the Internet of Things (IoT), artificial intelligence (AI), and big data analytics, has revolutionized manufacturing and supply chain operations. However, the dynamic and complex nature of Industry 4.0 supply chains presents significant challenges in decision-making, including uncertainty, ambiguity, and information overload. Traditional decision-making approaches often fall short in effectively addressing these complexities, particularly in scenarios demanding symmetrical and equitable outcomes.

To bridge this gap, this research introduces a novel framework grounded in the axioms of Cubic Type-2 Fuzzy Soft Sets (CT2FSSs). By leveraging the enhanced flexibility and uncertainty-handling capabilities of CT2FSSs, our proposed framework empowers decision-makers to navigate complexities, optimize supply chain processes, and mitigate risks while maintaining symmetry in decision-making. This framework is particularly well-suited for Industry 4.0 environments, where symmetrical and equitable outcomes are essential for ensuring fair and efficient operations [1].

To address these challenges, researchers have explored various methodologies, including fuzzy set theory and soft set theory. Fuzzy set theory, introduced by Zadeh [2], provides a framework for representing and manipulating imprecise and uncertain information. Soft set theory, proposed by Molodtsov [3], offers a mathematical tool for dealing with uncertainty by associating a set of parameters with a set of objects. However, both fuzzy set theory and soft set theory have limitations in handling complex decision-making scenarios that involve both uncertainty and ambiguity.

In recent years, Cubic Type-2 Fuzzy Soft Sets (CT2FSSs) have emerged as a promising approach to addressing these limitations [4]. CT2FSSs combine the advantages of type-2 fuzzy sets and soft sets, providing a more flexible and expressive framework for representing and reasoning with uncertain and ambiguous information. By incorporating membership grades and hesitancy degrees, CT2FSSs can capture the inherent complexities of real-world decision-making problems.

Zadeh proposed fuzzy set theory in 1965, which significantly transformed the management of uncertainty in intricate systems and has since emerged as a fundamental method in many fields. Recognizing the inherent uncertainty in real-world systems, researchers extended traditional fuzzy logic to create type-2 fuzzy sets, offering a more robust framework for handling imprecise information [2,5].

The introduction of T2F logic systems has significantly advanced the management of uncertainty and the provision of resilient solutions. Liang and Mendel provided evidence for the effectiveness of T2F adaptive filters in compensating for nonlinear time-varying channels [3,6]. Mendel’s research on uncertainty and fuzzy logic in signal processing demonstrated the efficacy of T2F logic in this field [4,7].

Karnik and Mendel presented T2F logic systems [8] and investigated their utilization in predicting time-series data [9]. The authors established the groundwork for future investigations on interval T2F logic systems [10]. The theory and design of Liang and Mendel’s interval T2F logic systems provided valuable insights in this area [10].

The adaptive T2F system developed by John and Czarnecki in 1999 demonstrated the capacity to enhance the interpretability and flexibility of fuzzy systems in the context of learning linguistic membership grades [11]. John, Innocent, and Barnes made significant contributions to the utilization of T2F sets in the fields of image processing and medical imaging applications [12,13].

The goal of further developing fuzzy set theory led to the investigation of cubic T2F sets, which combine cubic sets’ strengths and T2F logic [14]. By providing a new dimension to uncertainty management, these sets offer a nuanced framework for complicated decision-making situations, particularly in data-driven environments [15,16].

T2F soft sets are adopted primarily due to their capacity to effectively handle significant levels of uncertainty and imprecision in decision-making procedures. This technique offers a robust tool for decision-making in situations with uncertainty by combining soft sets with T2F sets [17]. This innovation has demonstrated potential in bolstering decision-making across various fields, including supplier selection and group decision-making [18,19].

Due to their versatility and flexibility, T2F soft sets are also particularly useful when there is a lack of information or subjective assessment. Resolving complex optimization problems necessitates the ability to handle uncertainty at a higher level [17]. Additionally, they make it possible to include expert knowledge and preferences. This framework facilitates robust and informed decision-making by providing a structured approach to handling complex and uncertain information.

By investigating cubic T2F soft sets and their decision-making applications, this research seeks to improve decision accuracy and reliability across multiple industries. This study examines the fundamental principles and operational capacities of cubic T2F sets, as well as their practical applications in decision-making scenarios. While previous research has explored the potential of T2F sets and cubic sets independently, this study focuses on the synergistic combination of these concepts, leading to the development of cubic T2F soft sets. By integrating the advantages of both frameworks, this research aims to enhance decision-making efficacy by offering a more comprehensive and robust framework capable of handling complex uncertainties.

An important deficiency in the current body of research is the limited investigation into the practical use of cubic T2F soft sets in real-life situations. To address this gap, this study investigates the potential of Cubic Type-2 Fuzzy Soft Sets in tackling complex decision-making problems, thereby advancing fuzzy set theory.

This research delves into the application of CT2FS within the framework of soft sets, creating a novel approach to address complex decision-making problems in Industry 4.0 supply chains. By combining the strengths of both CT2FS and soft set theory, this study aims to develop a robust and flexible decision-making tool capable of handling the inherent uncertainties and complexities of supply chain management.

While existing decision-making models have shown promise in addressing the challenges of Industry 4.0, they often struggle to effectively handle the high degree of uncertainty and complexity inherent in these environments. This research aims to fill this gap by developing a novel framework based on Cubic Type-2 Fuzzy Soft Sets, which offers a more flexible and robust approach to decision-making under uncertainty, thereby improving the quality of decisions in complex industrial settings.

This paper is structured as follows: Section 2 introduces Cubic Type-2 Fuzzy (T2F) sets, delineating their definitions, operations, and fundamental properties. Building upon this foundation, Section 3 extends the concept to Cubic Type-2 Fuzzy Soft Sets, providing a comprehensive overview of their operations and characteristics. The practical implications of these sets are explored in Section 4, where their application to decision-making problems across diverse domains is demonstrated, highlighting the potential benefits and advancements offered by this novel approach. Section 5 delves into the specific applications of Cubic Type-2 Fuzzy Soft Sets in Industry 4.0 supply chains, showcasing their potential to address complex challenges and improve decision-making processes. Finally, Section 6 concludes the paper by summarizing the key findings, highlighting the contributions of this research, and outlining potential future directions for further exploration.

2. Related Work

The application of fuzzy set theory and its extensions to decision-making problems in supply chains has been extensively explored in recent years. However, the use of Cubic Type-2 Fuzzy Soft Sets (CT2FSSs) in this context remains relatively limited. This research aims to contribute to this emerging area by proposing a novel framework based on CT2FSSs for decision-making in Industry 4.0 supply chains.

Several studies have explored the application of CT2FSSs in various domains, including medical diagnosis [20], pattern recognition [21], and decision-making [22]. However, the application of CT2FSSs in the context of Industry 4.0 supply chains remains relatively unexplored. This paper aims to fill this gap by proposing a novel framework based on CT2FSSs for decision-making in Industry 4.0 supply chains.

To tackle the challenges posed by vagueness, inconsistency, and uncertainty in data, the authors of ref. [23] proposed Cubic Intuitionistic Fuzzy Soft Sets (CIFS-sets). This framework offers a refined representation of imprecise information compared to traditional approaches. The authors further contributed by defining distance metrics and aggregation operations for CIFS-sets. Their research indicates the potential of CIFS-sets in decision-making scenarios and suggests avenues for future exploration, including multi-criteria decision-making and hybrid models.

Building upon the foundations of fuzzy logic, the development of intelligent systems has witnessed the integration of sophisticated techniques such as Complex Fuzzy Soft Relations (CFSRs) [24]. These relations, derived from the Cartesian product of complex fuzzy soft sets, present a groundbreaking approach to model intricate system behaviors. CFSR aims to effectively manage the complexities and unreliability of information encountered in real-world problems. It surpassed existing methods by combining the strengths of fuzzy set (FS) and soft set (SS) theories, resulting in a more robust and versatile framework. The study demonstrated the potential application of CFSR in practical decision-making processes, such as choosing a suitable network. This highlights the practical value of CFSR in various decision-making scenarios.

While traditional fuzzy soft sets assign equal importance to membership and non-membership degrees, the authors of ref. [25] proposed (a, b)-FSSs, which provide a more nuanced approach by enabling differential weighting of these evaluations. This flexibility proves valuable in addressing complex decision-making scenarios across various domains, including risk assessment, pattern recognition, and data mining.

Researchers are continuously devising novel methods to manage uncertainties in data. In a recent study, the authors of ref. [26] introduced an expansion of an established idea by integrating the strengths of interval-valued Pythagorean fuzzy sets and Pythagorean fuzzy sets. Cubic Pythagorean Fuzzy Soft Sets (CPFSs) offer a more comprehensive framework for handling complex uncertainties, resulting in a more accurate and focused approach to handling uncertainty. This hybrid framework combines the benefits of fuzzy sets with soft sets, enabling a more intricate examination of qualities in decision-making situations, which is especially pertinent in illness detection. The work delineated the fundamental constituents of CPFSs, examined several procedures, and established a distance-based algorithm for illness detection, showcasing its pragmatic implementation. Table 1 illustrates a summary of the related work mentioned above.

Table 1. Summary of related work.

Year	Paper Ref	Methodology	Contribution	Objectives	Potential Drawbacks
2023	[1]	1. Recognizing the limitations of existing models in handling vagueness, inconsistency, and uncertainty, Cubic Intuitionistic Fuzzy Soft Sets (CIFS-sets) were proposed as an enhanced framework building upon cubic intuitionistic fuzzy sets. 2. Proposed distance measures (Hamming distance, Euclidean distance, and separation measures) to compare CIFS-sets. 3. Developed aggregate operators (P-union and R-intersection) for combining CIFS-sets.	1. Introduced CIFS-sets as a new approach to representing and handling imprecise information. 2. Proposed distance measures and aggregate operators for CIFS-sets. 3. Claimed that CIFS-sets offer improved reliability, efficiency, and accuracy compared to traditional methods.	1. Address challenges related to vagueness, inconsistency, and uncertainties in data representation. 2. Develop a more nuanced and effective approach for handling imprecise information. 3. Lay the foundation for potential applications of CIFS-sets in MCDM and MCGDM techniques.	1. The complexity of CIFS-sets may require more computational resources compared to simpler approaches. 2. The study primarily focuses on the theoretical aspects and may require further research to demonstrate the practical effectiveness of CIFS-sets in real-world applications. 3. The potential limitations of CIFS-sets in handling extreme levels of uncertainty or conflicting information need to be further investigated.
2012	[4]	1.Introduced Complex Fuzzy Soft Relations (CFSRs) as a novel construct derived from the Cartesian product of complex fuzzy soft sets. 2. Developed a theoretical framework and associated operations for CFSRs. 3. Demonstrated the application of CFSRs in a decision-making scenario involving network selection.	1. Proposed a novel approach, CFSR, for managing 2. complex and unreliable information in real-world problems. 3. Integrated the advantages of fuzzy set and soft set theories to develop a versatile and comprehensive approach. 4. Illustrated the practical effectiveness of CFSRs in tackling real-world decision problems.	1. Develop a new and effective method for handling uncertainties and complexities in real-world data. 2. Provide a robust framework for managing unreliable information in decision-making scenarios. 3. Explore potential applications of CFSRs in various domains.	1. The complexity of CFSRs may require more computational resources compared to simpler approaches. 2. The study primarily focuses on the theoretical aspects and may require further research to demonstrate the practical effectiveness of CFSRs in a wider range of applications. 3. The potential limitations of CFSRs in handling extreme levels of uncertainty or conflicting information need to be further investigated.
2019	[14]	1. To address the limitations of traditional fuzzy soft sets, which impose equal importance on membership and non-membership degrees, (a, b)-fuzzy soft sets were introduced. 2. Established fundamental arithmetic operations and explored the characteristics of (a, b)-FSSs. 3.Constructed aggregation operators for (a, b)-FSSs and analyzed their properties and relationships. 4. Contributed to the field of multi-criteria decision-making by proposing a new method based on (a, b)-FSSs and their associated scoring functions. 5. Validated the applicability of (a, b)-FSSs through a real-world decision-making problem.	1. Developed a novel framework, (a, b)-FSSs, for managing uncertainties with varying degrees of importance. 2.Enhanced the flexibility and robustness of fuzzy soft set theory for tackling diverse decision-making challenges. 3. Provided a practical approach to handling situations where membership and non-membership evaluations have different weights.	1. Address the limitations of existing fuzzy soft set models that restrict the importance of membership and non-membership evaluations to be equal. 2. Develop a more versatile and adaptable tool for managing uncertainties with varying degrees of importance. 3. Extend the domain of application for fuzzy soft set theory to encompass a broader array of decision-making challenges.	1. The introduction of additional parameters (a and b) may increase the complexity of the model compared to simpler fuzzy soft set approaches. 2. The study primarily focuses on the theoretical aspects and may require further research to demonstrate the practical effectiveness of (a, b)-FSSs in a broader range of applications. 3. The potential limitations of (a, b)-FSSs in handling extreme levels of uncertainty or conflicting information need to be further investigated.
2022	[17]	1. To address the limitations of existing fuzzy set models, Cubic Pythagorean Fuzzy Soft Sets (CPFSs) were introduced as a novel framework. 2. Defined the internal and external components of CPFSs.Established set operators and aggregation operators for CPFSs. 3. Developed a distance-based algorithm for disease diagnosis using CPFSs. 4. Applied the proposed approach to a real-world disease diagnostic decision-making problem.	1. Proposed a novel hybrid framework, CPFSs, for handling uncertainties in data analysis. 2.By merging the strengths of interval-valued Pythagorean fuzzy sets and Pythagorean fuzzy sets, Cubic Pythagorean Fuzzy Soft Sets (CPFSs) offer a refined framework for capturing uncertainty and imprecision. 3. Developed an algorithm for disease diagnosis using CPFSs, demonstrating its practical application.	1. Develop a more precise and targeted approach to dealing with uncertainties in data analysis, particularly in decision-making scenarios. 2. Address the limitations of existing fuzzy set methods by incorporating their strengths into a unified framework. 3. Provide a novel tool for disease diagnosis and other applications involving uncertain data.	1. The inclusion of membership, non-membership, and indeterminacy values may increase the complexity of the model compared to simpler fuzzy set approaches. 2. The study primarily focuses on the theoretical aspects and may require further research to demonstrate the practical effectiveness of CPFSs in a broader range of applications. 3. The potential limitations of CPFSs in handling extreme levels of uncertainty or conflicting information need to be further investigated.
2020	[18]	1. Decision Matrix Formulation: Construct an Agri4SC decision matrix intersecting alternatives and evaluation criteria. 2. Novel FPHFSs: Introduce FPHFSs with operational laws, score function, accuracy function, and aggregation operators. 3. Weight Assignment: Assign weights to evaluation criteria using Fermatean probabilistic hesitant fuzzy weighted zero inconsistency. 4. FPH-FDOSM: Use FPH-FDOSM to score alternatives evaluated subjectively based on SCV criteria. 5. MAIRCA Scoring (Equal Probabilities): Apply MAIRCA scoring method to score alternatives evaluated subjectively based on weighted economic, environmental, and social factors. 6. MAIRCA Ranking (Unequal Probabilities): Use MAIRCA ranking method to benchmark Agri4SC alternatives evaluated objectively based on weighted subcriteria of SP and trade-offs among criteria.	1. Developed a comprehensive Agri4SC benchmarking framework based on FPHFSs and MCDM methods. 2. Addressed challenges of multiple criteria evaluation and uncertainty in expert judgments. 3. Provided a robust and reliable tool for evaluating and comparing Agri4SC initiatives.	1. Develop a benchmarking framework for Agri4SC addressing multiple criteria evaluation and uncertainty. 2. Propose novel FPHFSs and MCDM methods for Agri4SC evaluation. 3. Evaluate and rank Agri4SC alternatives based on SCV, SCRI, and SP criteria. 4. Provide a robust and reliable tool for benchmarking Agri4SC initiatives.	1. Complexity of the FPHFS-based approach. 2. Subjectivity in expert judgments. 3. Data availability challenges.
2022	[23]	1. Develop LDFSTAOs based on operational laws of LDFNs and STFs. 2. Construct MCDM framework using LDFSTAOs for HSC performance evaluation. 3. Select relevant criteria and assign weights. Evaluate HSC suppliers using LDFSTAOs. 4. Rank suppliers and select the most suitable one.	1. Introduced novel LDFSTAOs. 2. Developed MCDM framework for Industry 4.0 healthcare supplier selection. 3. Provided a flexible and an expressive approach to handling uncertainty and vagueness. 4. Demonstrated effectiveness through credibility testing, sensitivity analysis, and comparative analysis.	1. Develop MCDM framework for supplier selection in Industry 4.0 healthcare. 2. Utilize LDFSTAOs for information aggregation and decision-making. 3. Evaluate HSC supplier performance based on multiple criteria. 4. Identify the most suitable supplier for Industry 4.0 healthcare.	1. Computational complexity of LDFSTAOs. 2. Subjectivity in weight assignment and supplier evaluation. 3. Data availability challenges. 4. Sensitivity to parameter values.
2022	[24]	1. Define Hamacher operational laws for PCFNs. 2. Develop PCFHWA, PCFHOWA, PCFHHA, PCFHWG, PCFHOWG, and PCFHHA operators. 3. Construct decision-making algorithm using aggregation operators and score function. 4. Apply method to green supplier selection. 5. Compare with other group decision techniques.	1. Introduced Hamacher operational laws for PCFNs and developed aggregation operators. 2. Provided novel decision-making framework for green chain supplier selection. 3. Enhanced flexibility and effectiveness of group decision-making. 4. Demonstrated superiority through comparative analysis and sensitivity analysis.	1. Develop decision-making mechanism for green chain supplier selection. 2. Introduce Hamacher operational laws for PCFNs and develop aggregation operators. 3. Provide flexible and effective group decision-making framework. 4. Identify the best green supplier for green supply chain management.	1. Computational complexity. 2. Subjectivity in weight assignment and evaluation. 3. Data availability challenges. 4. Sensitivity to parameters.
2023	[25]	1. Two-Phase Group Decision-Making Approach: Combine PF-AHP and MARCOS-G models for supplier selection in CSCM. 2. PF-AHP: Use PF-AHP to determine weights of criteria based on individual DMs’ opinions. 3. MARCOS-G: Employ MARCOS-G to rank suppliers and select the most appropriate one. 4. Sensitivity Analysis: Conduct a comprehensive sensitivity analysis with 50 scenarios to validate the results. 5. Comparative Analysis: Compare the proposed method with other gray COPRAS, TOPSIS, ARAS, and WASPAS methods.	1. Proposed a novel two-phase group decision-making approach to supplier selection in CSCM. 2. Leveraged PF-AHP and MARCOS-G for effective decision-making. 3. Provided a more robust and reliable supplier selection process. 4. Conducted a comprehensive sensitivity analysis and comparative analysis to validate the proposed method.	1. Develop a novel group decision-making approach to supplier selection in CSCM. 2. Combine PF-AHP and MARCOS-G for effective decision-making. 3. Evaluate and rank railway material suppliers within a circular economy perspective. 4. Provide a robust and reliable supplier selection process.	1. Computational Complexity: The PF-AHP and MARCOS-G methods may be computationally intensive for large-scale decision problems. 2. Subjectivity: The assignment of weights and the evaluation of criteria may involve subjective judgments. 3. Data Availability: The availability of accurate and comprehensive data on railway material suppliers and their performance may be a challenge. 4. Sensitivity to Parameters: The results of the method may be sensitive to the choice of parameters used in the PF-AHP and MARCOS-G models.
	Our study	1. Dedicated to the investigation of Cubic Type-2 Fuzzy Sets (CT2FS) and their extension to Cubic Type-2 Fuzzy Soft Sets (CT2FSSs). 2. Introduced the fundamental concepts, definitions, and operations related to CT2FS. 3. Examined the operations and characteristics of CT2FSSs.	Provided a comprehensive exploration of CT2FS and CT2FSSs, including their theoretical underpinnings.	Enhanced understanding of CT2FS and CT2FSSs, both theoretically and practically.Established CT2FSSs as a potential solution for complex decision problems involving uncertainty, recognizing the associated.	Increase in computational complexity compared to traditional fuzzy set approaches.

The proposed framework leverages the flexibility and uncertainty-handling capabilities of CT2FSSs to address the complex decision-making challenges prevalent in Industry 4.0 supply chains. By representing uncertain and ambiguous information in a structured manner, the framework enables decision-makers to make informed choices and mitigate risks. Through a rigorous theoretical analysis and practical implementation, this research contributes to the advancement of fuzzy set theory and its application in the context of Industry 4.0.

The proposed framework offers unique advantages compared to other approaches owing to its ability to enhance flexibility, improve decision-making processes, and bridge the gap between theory and practice. This approach is particularly beneficial for Industry 4.0 supply chains, which face significant challenges in dealing with complexities and uncertainties.

3. Preliminaries

This research delves into the theoretical underpinnings of Cubic Type-2 Fuzzy Soft Sets (CT2FSSs) as a robust foundation for developing a decision-making framework tailored to the complexities of Industry 4.0 supply chains. CT2FSSs, a novel extension of both type-2 fuzzy sets and cubic sets, offer a powerful mechanism for capturing the uncertainty and imprecision inherent in real-world systems.

Type-2 fuzzy sets (T2FS), introduced by Zadeh [2], extend the concept of fuzzy sets by allowing membership grades themselves to be fuzzy. This enables a more nuanced representation of uncertainty, particularly in complex systems. Cubic sets, a generalization of interval-valued fuzzy sets, provide a richer framework for representing uncertainty by combining interval-valued membership grades with type-2 fuzzy membership grades.

CT2FSSs, by integrating the concepts of T2FS and cubic sets, offer a hybrid model capable of handling a wider range of uncertainties and complexities. This unique combination makes CT2FSSs particularly well-suited for addressing decision-making problems in dynamic and uncertain environments like Industry 4.0 supply chains.

Industry 4.0, characterized by the integration of cyber-physical systems, the Internet of Things, and big data analytics, has significantly increased the complexity and volatility of supply chains. The need for real-time decision-making in such environments necessitates decision-making tools that can effectively handle uncertainty and navigate complex interdependencies.

In the context of Industry 4.0 supply chains, CT2FSSs can be particularly useful for the following:

• Modeling complex relationships: CT2FSSs can capture the intricate relationships between various factors that influence supply chain performance, such as demand, supply, and logistics.
• Handling uncertainty and imprecision: CT2FSSs can effectively handle the uncertainty and imprecision inherent in Industry 4.0 data, such as sensor readings, forecasts, and market trends.
• Supporting decision-making under uncertainty: CT2FSSs can provide a framework for making informed decisions in the face of uncertainty, such as selecting suppliers, allocating resources, and managing risks.

Definition 1 

([18]). (Cubic Fuzzy Set) Let Ω be a non-empty set. A cubic set over Ω is defined as

$$B=\left\{\right(w,A\left(w\right),\lambda \left(w\right))\mid w\in \mathrm{\Omega }\}$$

where A is an interval-valued fuzzy set in Ω and λ is a fuzzy set in Ω.

Definition 2 

([12]). A type-2 fuzzy set (T2FS) is a fuzzy set that accounts for uncertainty in its membership function, where the membership degree itself becomes a type-1 fuzzy set. The T2FS introduces a third dimension by using a secondary membership function. Mathematically, a T2FS $\tilde{A}$ is represented as follows:

$$\tilde{A}=\left\{\left((w,z),{\mu }_{\tilde{A}}(w,z)\right)|w\in \mathrm{\Omega },J_w\subseteq [0,1]\right\},$$

where:

1.

${\mu }_{\tilde{A}}(w,z)$ is the secondary membership function, which satisfies $0\le {\mu }_{\tilde{A}}(w,z)\le 1$.

2.

$J_w$ is the primary membership function domain for each $w\in \mathrm{\Omega }$, representing the range of the secondary membership function.

The T2FS $\tilde{A}$ can also be expressed as follows:

$$\tilde{A}={\int }_{w\in \mathrm{\Omega }}\left({\int }_{z\in J_w}{\mu }_{\tilde{A}}(w,z)z\right)w,$$

where the integral denotes the union of all permissible values of w and z. In a discrete universe of discourse, the integral is replaced by a sum. The secondary membership function ${\mu }_{\tilde{A}}(w,z)$ is defined for each $w\in \mathrm{\Omega }$ as

$${\mu }_{\tilde{A}}(w,z)={\int }_{z\in J_w}{\mu }_{\tilde{A}}(w,z)/z.$$

For a specific $z=z^{\prime }\in J_w$, the secondary membership grade of $(w,z)$ is referred to as ${\mu }_{\tilde{A}}(w,z)$.

Definition 3 

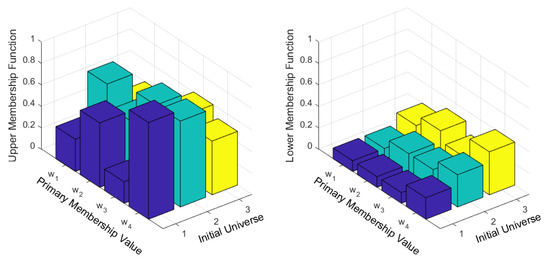
([27]). A Cubic Type-2 Fuzzy Set (CT2FS) over the initial universe as shown Figure 1 Ω is characterized by an interval-valued type-2 fuzzy set $({\mu }_A^{+}(w,z),{\mu }_A^{-}(w,y))$, where

Figure 1. Cubic Type-2 Fuzzy Set.

1.

${\mu }_A^{+}:\mathrm{\Omega }\times [0,1]\to [0,1]$ is the upper membership function,

2.

${\mu }_A^{-}:\mathrm{\Omega }\times [0,1]\to [0,1]$ is the lower membership function,

3.

$V_A(w,z)$ is a type-2 fuzzy set in w.

The CT2FS A is represented as

$$A=\left\{(w,z),{\mu }_A^{+}(w,z),{\mu }_A^{-}(w,z),V_A(w,z)|w\in \mathrm{\Omega },z\in J_w\subseteq [0,1]\right\}.$$

The set A is defined by

$$A={\int }_{w\in \mathrm{\Omega }}\left(\sum _{z\in J_w\subseteq [0,1]}\left({\mu }_A^{+}(w,z),{\mu }_A^{-}(w,z),V_A(w,z)\right)/z\right)/w.$$

This represents the set of all CT2FS in w.

Example 1. 

Let $w=\{w_1,w_2,w_3,w_4\}$ be the initial universal set, and let $z=\{0.1,0.3,0.5,0.7,0.9\}$. Let ${\phi }_b$ be a Cubic Type-2 Fuzzy Set (CT2FS) defined as

$$\begin{array}{cc}\hfill {\phi }_b& ={\displaystyle \frac{\frac{(0.3,0.1,0.2)}{0.3}}{w_1}}\hfill \\ & +{\displaystyle \frac{\frac{(0.7,0.1,0.4)}{0.5}+\frac{(0.4,0.12,0.3)}{0.7}}{w_2}}\hfill \\ & +{\displaystyle \frac{\frac{(0.2,0.1,0.1)}{0.1}+\frac{(0.6,0.9,0.2)}{0.3}+\frac{(0.4,0.2,0.3)}{0.9}}{w_3}}\hfill \\ & +{\displaystyle \frac{\frac{(0.9,0.2,0.6)}{0.3}+\frac{(0.8,0.5,0.6)}{0.7}}{w_4}}.\hfill \end{array}$$

In this example, we consider a relatively balanced distribution of membership grades, with both high and low values for both primary and secondary membership degrees. This suggests a situation where uncertainty is present, but there is still some degree of confidence in the membership of elements.

Example 2. 

Consider the initial universal set $y=\{y_1,y_2,y_3,y_4\}$ and a Cubic Type-2 Fuzzy Set ${\psi }_a$ defined as follows. Let $w=\{0.2,0.4,0.6,0.8,1.0\}$:

$$\begin{array}{cc}& {\psi }_a={\displaystyle \frac{\frac{(0.4,0.2,0.5)}{0.2}}{y_1}}\hfill \\ & +{\displaystyle \frac{\frac{(0.6,0.1,0.7)}{0.6}+\frac{(0.5,0.3,0.8)}{0.8}}{y_2}}\hfill \\ & +{\displaystyle \frac{\frac{(0.7,0.4,0.9)}{0.5}+\frac{(0.3,0.2,0.6)}{1.0}}{y_3}}\hfill \\ & +{\displaystyle \frac{\frac{(0.1,0.8,0.2)}{0.2}+\frac{(0.9,0.7,0.5)}{0.6}}{y_4}}.\hfill \end{array}$$

For this example, a more polarized distribution of membership grades is considered. Some elements have high primary membership degrees with narrow fuzzy sets, indicating a high degree of certainty. Others have lower primary membership degrees with wider fuzzy sets, indicating more uncertainty.

Example 3. 

Consider the initial universal set $u=\{u_1,u_2,u_3,u_4\}$ and a Cubic Type-2 Fuzzy Set ${\theta }_c$ defined as follows. Let $v=\{0.15,0.35,0.55,0.75,0.95\}$:

$$\begin{array}{cc}& {\theta }_c={\displaystyle \frac{\frac{(0.3,0.1,0.4)}{0.15}}{u_1}}\hfill \\ & +{\displaystyle \frac{\frac{(0.5,0.2,0.7)}{0.5}+\frac{(0.4,0.6,0.9)}{0.75}}{u_2}}\hfill \\ & +{\displaystyle \frac{\frac{(0.9,0.3,0.2)}{0.55}+\frac{(0.2,0.7,0.8)}{0.95}}{u_3}}\hfill \\ & +{\displaystyle \frac{\frac{(0.6,0.5,0.3)}{0.35}+\frac{(0.7,0.8,0.4)}{0.95}}{u_4}}.\hfill \end{array}$$

In this example, a mix of high and low primary membership degrees is considered but with a noticeable skew towards higher secondary membership degrees. This suggests a situation where there’s a relatively high level of confidence in the overall membership of elements, even if there is uncertainty about the exact membership grade.

The provided examples showcase the ability of CT2FS to model different levels of ambiguity and certitude associated with element inclusion. By carefully selecting the universal set and the values of the primary and secondary membership degrees, it is possible to tailor a CT2FS to a specific application.

Remark 1 

([17]). The notion ∫ denotes the union over all admissible Ω and z, and the plus sign (+) also denotes union.

Suppose ${\phi }_t$ and $f_t$ are two Cubic Type-2 Fuzzy Sets (CT2FS) defined over $\mathrm{\Omega }$, then

$${\phi }_t={\int }_{w\in \mathrm{\Omega }}\left({\displaystyle \frac{{\displaystyle \sum _{z\in J_w\subseteq [0,1]}\left({\mu }_{{\phi }_t}^{+}(w,z),{\mu }_{{\phi }_t}^{-}(w,z),V_{{\phi }_t}(w,z)\right)}}{z}}\right)/w,$$

and

$$f_t={\int }_{w\in \mathrm{\Omega }}\left({\displaystyle \frac{{\displaystyle \sum _{n\in J_w\subseteq [0,1]}\left({\mu }_{f_t}^{+}(w,n),{\mu }_{f_t}^{-}(w,n),V_{f_t}(w,n)\right)}}{n}}\right)/w.$$

For two CT2FSs ${\phi }_t$ and $f_t$ over $\mathrm{\Omega }$, we say that $f_t$ is a Cubic Type-2 Fuzzy (CT2F) subset of ${\phi }_t$ if and only if

(i)

$n⩽z$;

(ii)

${\mu }_{{\phi }_t}^{+}(w,z)⩽{\mu }_{f_t}^{+}(w,n)$ for the upper bound of the membership interval;

(iii)

${\mu }_{{\phi }_t}^{-}(w,z)⩽{\mu }_{f_t}^{-}(w,n)$ for the lower bound of the membership interval;

(v)

$V_{{\phi }_t}(w,z)⩽V_{f_t}(w,n)$ for a type-2 fuzzy set.

Here, z is the primary membership value of ${\phi }_t$, and n is the primary membership value of $f_t$.

3.1. Operations of Cubic Type-2 Fuzzy Sets

This paper delves into the essential arithmetic operations of complement, union, and intersection within the framework of CT2FS.

1.

Let ${\mathrm{\Omega }}_t$ and $f_t$ be Cubic Type-2 Fuzzy Sets (CT2FSs) defined over $\mathrm{\Omega }$. The union of ${\mathrm{\Omega }}_t$ and $f_t$ in $F_t$ is represented as

$$F_t={\mathrm{\Omega }}_t\cup f_t={\int }_{w\in \mathrm{\Omega }}\left({\displaystyle \frac{{\displaystyle \sum _{n\in J_w\subseteq [0,1]}\left(\left({\mu }_{F_t}^{+}(w,n),{\mu }_{F_t}^{-}(w,n),{\lambda }_{F_t}(w,n)\right)\right)}}{n}}\right)/w,$$

where $n=z\cup v$. The functions ${\mu }_{F_t}^{+}(w,n)$ and ${\mu }_{F_t}^{-}(w,n)$ can be defined as follows:

$${\mu }_{F_t}^{+}(w,n)={\mu }_{X_t}^{+}(w,z)\cup {\mu }_{f_t}^{+}(w,v),$$

$${\mu }_{F_t}^{-}(w,n)={\mu }_{X_t}^{-}(w,z)\cup {\mu }_{f_t}^{-}(w,v).$$

2.

Let $X_t$ and $f_t$ be CT2FSs defined over $\mathrm{\Omega }$. The intersection of $X_t$ and $f_t$ in $F_t$ is represented as

$$F_t=X_t\cap f_t={\int }_{w\in \mathrm{\Omega }}\left({\displaystyle \frac{{\displaystyle \sum _{n\in J_w\subseteq [0,1]}\left(\left({\mu }_{F_t}^{+}(w,n),{\mu }_{F_t}^{-}(w,n),{\lambda }_{F_t}(w,n)\right)\right)}}{n}}\right)/w,$$

where $n=z\cap v$. The functions ${\mu }_{F_t}^{+}(w,n)$ and ${\mu }_{F_t}^{-}(w,n)$ can be defined as follows:

$${\mu }_{F_t}^{+}(w,n)={\mu }_{X_t}^{+}(w,z)\cap {\mu }_{f_t}^{+}(w,v),$$

$${\mu }_{F_t}^{-}(w,n)={\mu }_{X_t}^{-}(w,z)\cap {\mu }_{f_t}^{-}(w,v).$$

3.

The complement of $f_t$, denoted as $F_t^c$, is a CT2FS defined as

$$F_t^c={\int }_{w\in \mathrm{\Omega }}\left({\displaystyle \frac{{\displaystyle \sum _{n\in J_w\subseteq [0,1]}\left(\left({\mu }_{F_t^c}^{+}(w,n),{\mu }_{F_t^c}^{-}(w,n),{\lambda }_{F_t^c}(w,n)\right)\right)}}{n}}\right)/w.$$

3.2. Properties of Cubic Type-2 Multifuzzy Sets

We discuss some fundamental properties of CT2MFS.

Theorem 1. 

1.

$f_t\cup f_t=f_t$

2.

$f_t\cap f_t=f_t$

3.

${(f_t\cup T_s)}^c=f_t^c\cap T_s^c$

4.

${(f_t\cap T_s)}^c=f_t^c\cup T_s^c$

5.

$f_t\cup T_s=T_s\cup f_t$

6.

$f_t\cap T_s=T_s\cap f_t$

7.

$f_t\cup (T_s\cup {\mathrm{\Omega }}_b)=(f_t\cup T_s)\cup {\mathrm{\Omega }}_b$

8.

$f_t\cap (T_s\cap X_b)=(f_t\cap T_s)\cap {\mathrm{\Omega }}_b$

9.

$(f_t\cup T_s)\cap {\mathrm{\Omega }}_b=(f_t\cap {\mathrm{\Omega }}_b)\cup (T_s\cap {\mathrm{\Omega }}_b)$

10.

$(f_t\cap T_s)\cup {\mathrm{\Omega }}_b=(f_t\cup {\mathrm{\Omega }}_b)\cap (T_s\cup {\mathrm{\Omega }}_b)$

Proof. 

The proofs for statements (1) through (6) are clear. Now, we will prove statements (7) and (10).

Proof of (7):

$$\begin{array}{cc}\hfill f_t\cup (T_s\cup {\mathrm{\Omega }}_b)& ={\int }_{w\in \mathrm{\Omega }}{\int }_{z\in J_{\mathrm{\Omega }}\subseteq [0,1]}({\mu }_{f_t}^{+}(w,z),{\mu }_{f_t}^{-}(w,z),{\lambda }_{f_t}(w,z))/z/w\hfill \\ & \cup \left({\int }_{w\in \mathrm{\Omega }}{\int }_{n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}({\mu }_{T_s}^{+}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{+}(w,v),\right.\hfill \\ & \left.{\mu }_{T_s}^{-}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),{\lambda }_{T_s}(w,n)\cup {\lambda }_{{\mathrm{\Omega }}_b}(w,v))/(n\cup v)/w\right)\hfill \\ & ={\int }_{w\in \mathrm{\Omega }}{\int }_{z,n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{f_t}^{+}(w,z)\cup {\mu }_{T_s}^{+}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{+}(w,v),\hfill \\ & {\mu }_{f_t}^{-}(w,z)\cup {\mu }_{T_s}^{-}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),\hfill \\ & {\lambda }_{f_t}(w,z)\cup {\lambda }_{T_s}(w,n)\cup {\lambda }_{{\mathrm{\Omega }}_b}(w,v))/(z\cup n\cup v)/w\hfill \\ & ={\int }_{w\in \mathrm{\Omega }}{\int }_{z,n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{f_t}^{+}(w,z)\cup {\mu }_{T_s}^{+}(w,n),{\mu }_{f_t}^{-}(w,z)\cup {\mu }_{T_s}^{-}(w,n),\hfill \\ & {\lambda }_{f_t}(w,z)\cup {\lambda }_{T_s}(w,n))/(z\cup n)/w\hfill \\ & \cup {\int }_{w\in \mathrm{\Omega }}{\int }_{z,n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{{\mathrm{\Omega }}_b}^{+}(w,z),{\mu }_{f_t}^{-}(w,z),\hfill \\ & {\lambda }_{{\mathrm{\Omega }}_b}(w,n)\cup {\lambda }_{X_b}(w,n))/v/w\hfill \\ & =(f_t\cup T_s)\cup {\mathrm{\Omega }}_b.\hfill \end{array}$$

Similarly, we can prove statement (8).

Proof of (9):

$$\begin{array}{cc}\hfill (f_t\cup T_s)\cap {\mathrm{\Omega }}_b& ={\int }_{w\in \mathrm{\Omega }}{\int }_{z,n\in J_{\mathrm{\Omega }}\subseteq [0,1]}({\mu }_{f_t}^{+}(w,z)\cup {\mu }_{T_s}^{+}(w,n),{\mu }_{f_t}^{-}(w,z)\cup {\mu }_{T_s}^{-}(w,n),\hfill \\ & {\lambda }_{f_t}(w,z)\cup {\lambda }_{T_s}(w,n))/(z\cup n)/w\hfill \\ & \cap \left({\int }_{w\in \mathrm{\Omega }}{\int }_{n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}({\mu }_{{\mathrm{\Omega }}_b}^{+}(w,v),{\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),{\lambda }_{{\mathrm{\Omega }}_b}(w,v))/v/w\right)\hfill \\ & ={\int }_{w\in \mathrm{\Omega }}{\int }_{z,n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{f_t}^{+}(w,z)\cup {\mu }_{T_s}^{+}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{+}(w,v),\hfill \\ & {\mu }_{f_t}^{-}(w,z)\cup {\mu }_{T_s}^{-}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),\hfill \\ & {\lambda }_{f_t}(w,z)\cup {\lambda }_{T_s}(w,n)\cup {\lambda }_{{\mathrm{\Omega }}_b}(w,v))/(z\cup n)\cap v/w\hfill \\ & ={\int }_{w\in \mathrm{\Omega }}{\int }_{z,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{f_t}^{+}(w,z)\cup {\mu }_{X_b}^{+}(w,v),{\mu }_{f_t}^{-}(w,z)\cup {\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),\hfill \\ & {\lambda }_{f_t}(w,z)\cup {\lambda }_{{\mathrm{\Omega }}_b}(w,v))/(z\cap v)/w\hfill \\ & \cup {\int }_{w\in \mathrm{\Omega }}{\int }_{n,v\in J_{\mathrm{\Omega }}\subseteq [0,1]}\hfill \\ & ({\mu }_{T_s}^{+}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{+}(w,v),{\mu }_{T_s}^{-}(w,n)\cup {\mu }_{{\mathrm{\Omega }}_b}^{-}(w,v),\hfill \\ & {\lambda }_{T_s}(w,n)\cup {\lambda }_{{\mathrm{\Omega }}_b}(w,v))/(n\cap v)/w\hfill \\ & =(f_t\cap {\mathrm{\Omega }}_b)\cup (T_s\cap {\mathrm{\Omega }}_b).\hfill \end{array}$$

Similarly, we can prove statement (10).    □

Theorem 2. 

Let $B=(B,\lambda )$ be a CT2FS such that $A=(B,\lambda )$ and $F=(F,\lambda )$; then, B is equal to F.

Definition 4 

([15]). Let Ω be a non-empty set. A Cubic Type-2 Set $B=\left(B\right(w,z),\lambda (w,z\left)\right)$ in Ω is said to be an internal Cubic Type-2 Set if $B^{-}(w,z)\le \lambda (w,z)\le B^{+}(w,z)$ for all $w\in \mathrm{\Omega }$.

Definition 5 

([15]). Let Ω be a non-empty set. A Cubic Type-2 Set $B=\left(B\right(w;z),\lambda (w,z\left)\right)$ in Ω is said to be an external Cubic Type-2 Set (ECT2S) if $\lambda (w,z)\notin \left(B^{-}(w,z),B^{-}(w,z)\right)$ for all $w\in \mathrm{\Omega }$.

Theorem 3. 

Let $B=\left(B\right(w,z),\lambda (w,z\left)\right)$ be a CT2FS in w that is not an ECT2S. Then, there exist $w\in \mathrm{\Omega }$ and $z\in J_w\subseteq [0,1]$ such that

$$\lambda (w,z)\in \left(B^{-}(w,z),B^{+}(w,z)\right).$$

Proof. 

Straightforward.    □

Theorem 4. 

Let $B=\left(B\right(w,z),\lambda (w,z\left)\right)$ be a CT2FS in w. If B is both an ICT2FS and an ECT2FS, we have

$$\left(\forall w\in \mathrm{\Omega },z\in J_w\in [0,1]\right)(\lambda (w,z)\in U\left(B\right)\cup L\left(B\right)),$$

where $U\left(B\right)=\left\{B^{+}(w,z)\mid w\in \mathrm{\Omega },z\in J_w\le [0,1)\right\}$ and $L\left(B\right)=\left\{B^{-}(w,z)\mid w\in \mathrm{\Omega }\right.\mathrm{and}\left.z\in J_w\le [0,1)\right\}$.

Theorem 5. 

Let $B=(B,\lambda )$ be a CT2FS in Ω. If B is an ICT2FS (resp. ECT2FS), then $B^c$ is an ICT2FS (resp. ECT2FS).

Proof. 

Let $B=(B,\lambda )$ be a Cubic Type-2 Set in $\mathrm{\Omega }$. Suppose $B=(B,\lambda )$ is an ICT2FS (resp. ECT2FS) in $\mathrm{\Omega }$. Then, we have $B^{-}(w,z)\le \lambda (w,z)\le B^{+}(w,z)$ (resp. $\lambda (w,z)\notin (B^{-}(w,z),B^{+}(w,z))$) for all $w\in \mathrm{\Omega }$ and $z\in J_{\mathrm{\Omega }}\subseteq [0,1]$.

This implies the following:

$$1-B^{+}(w,z)\le 1-\lambda (w,z)\le 1-B^{-}(w,z)$$

(resp. $1-\lambda (w,z)\notin \left(1-B^{+}(w,z),1-B^{-}(w,z)\right)$).

Hence,

$$\begin{array}{cc}\hfill B^c& =\left\{\left(w,z,1-B^{+}(w,z),1-B^{-}(w,z)\right)\mid w\in \mathrm{\Omega },z\in J_w\subseteq [0,1]\right\}.\hfill \end{array}$$

Therefore, $B^c$ is an ICT2FS (resp. ECT2FS) in $\mathrm{\Omega }$.    □

4. Cubic Type-2 Fuzzy Soft Set

To address the intricate and dynamic nature of Industry 4.0 supply chains, characterized by multiple, often uncertain parameters, this research introduces Cubic Type-2 Fuzzy Soft Sets (CT2FSSs). This novel framework integrates the concepts of cubic fuzzy sets, type-2 fuzzy sets, and soft sets to provide a robust and flexible modeling approach. CT2FSSs offer a comprehensive representation of uncertainty and imprecision, enabling the capture of complex interdependencies between supply chain elements.

Core operations on CT2FSSs include union, intersection, complement, and difference, which are adapted to handle the unique characteristics of this hybrid structure. These operations allow for the manipulation and analysis of uncertain information within the context of supply chain decision-making.

By combining the strengths of fuzzy sets, type-2 fuzzy sets, and soft sets, CT2FSSs provide a powerful tool for modeling and reasoning under uncertainty, making them suitable for addressing a wide range of challenges in supply chain management.

Definition 6 

([28]). Let $H\subseteq E$ be a set of parameters, and m be a mapping defined by

$$m:H⟶CT2FS\left(w\right).$$

Then, the pair $(m,H)$ is referred to as a Cubic Type-2 Fuzzy Soft Set (CT2FSS) over Ω, where CT2FS $\left(w\right)$ includes all CT2FSSs over Ω. The CT2FSS is a parameterized family of CT2F subsets of X. For any $\phi \in H$, $m\left(\phi \right)$ refers to the set of φ approximate elements of the CT2FSS $(m,H)$. It is actually a CT2FSS on Ω and can be written as

$$\begin{array}{cc}\hfill m\left(\phi \right)& ={\int }_{w\in \mathrm{\Omega }}\left({\int }_{z\in J_w\subseteq [0,1]}\left({\mu }_m^{+}\left(\phi \right)(w,z),{\mu }_m^{-}\left(\phi \right)(w,z),{\lambda }_{w,\phi }(w,z)\right)/z\right)/w.\hfill \end{array}$$

Here, Z is the interval-valued fuzzy set, ${\mu }_m^{+}(w,z)$ is the upper interval-valued membership function, ${\mu }_m^{-}\left(\phi \right)(w,z)$ is the lower interval-valued membership function, and $\lambda (w,z)$ is the type-2 fuzzy set.

Example 4. 

Consider $(m,\phi )\in$ CT2FS(w) over Ω, where Ω is a collection of five cars under consideration by a decision-maker for purchase. W is a set of parameters. The set $W=\{f_1,f_2,f_3,f_4\}$ and $\mathrm{\Omega }=\{w_1,w_2,w_3,w_4\}$ include the attributes {expensive, beautiful, convenient, mountainous surroundings}. The CT2FS function space $(m,\phi )$ describes the “attractiveness of the car” to this decision-maker.

Assume the following:

$$\begin{array}{cc}\hfill m\left(f_1\right)& =\left({\displaystyle \frac{(0.5,0.3,0.1)}{0.1}}+{\displaystyle \frac{(0.6,0.4,0.5)}{0.2}}\right)/w_1\hfill \\ & +\left({\displaystyle \frac{(0.7,0.3,0.6)}{0.4}}\right)/w_2\hfill \\ & +\left({\displaystyle \frac{(0.5,0.2,0.3)}{0.7}}\right)/w_3\hfill \\ & +\left({\displaystyle \frac{(0.6,0.2,0.3)}{0.8}}+{\displaystyle \frac{(0.5,0.1,0.2)}{0.3}}\right)/w_4.\hfill \end{array}$$

$$\begin{array}{c}m\left(f_2\right)=\left({\displaystyle \frac{(0.3,0.1,0.4)}{0.6}}\right)/w_1+\left({\displaystyle \frac{(0.8,0.0,0.4)}{0.9}}\right)/w_2\hfill \\ \hfill +\left({\displaystyle \frac{(0.5,0.11,0.0)}{0.3}}\right)/w_3+\left({\displaystyle \frac{(0.8,0.0,0.5)}{0.2}}+{\displaystyle \frac{(0.7,0.0,0.6)}{0.6}}\right)/w_4.\end{array}$$

$$\begin{array}{c}m\left(f_3\right)=\left({\displaystyle \frac{(0.4,0.2,0.2)}{0.6}}+\left({\displaystyle \frac{(0.8,0.5,0.6)}{0.4}}+{\displaystyle \frac{(0.3,0.0,0.2)}{0.6}}\right)\right)/w_1\hfill \\ +\left({\displaystyle \frac{(0.9,0.6,0.81)}{0.4}}\right)/w_2+\left({\displaystyle \frac{(0.3,0.0,0.2)}{0.8}}+{\displaystyle \frac{(0.7,0.7,0.0)}{0.4}}\right)/w_3\\ \hfill +\left({\displaystyle \frac{(0.3,0.0,0.2)}{0.8}}+{\displaystyle \frac{(0.2,0.0,0.1)}{0.9}}\right)/w_4.\end{array}$$

$$\begin{array}{cc}\hfill m\left(f_4\right)& =\left({\displaystyle \frac{(0.3,0.1,0.2)}{0.4}}+{\displaystyle \frac{(0.5,0.0,0.2)}{0.9}}\right)/w_1\hfill \\ & +\left({\displaystyle \frac{(0.7,0.3,0.5)}{0.5}}+{\displaystyle \frac{(0.6,0.2,0.4)}{0.8}}\right)/w_2\hfill \\ & +\left({\displaystyle \frac{(0.9,0.1,0.5)}{0.2}}\right)/w_3\hfill \\ & +\left({\displaystyle \frac{(0.6,0.2,0.8)}{0.3}}\right)/w_4.\hfill \end{array}$$

The CT2FS $(p,\eta )$ provides insight into how the decision-maker evaluates each vacation package based on the given attributes. This assessment aids the decision-maker in selecting the most preferred vacation package from the available options.

Refer to Table 2 for a tabular representation of the membership functions for each attribute.

Table 2. Tabular representation of the Cubic Type-2 Fuzzy Set functions for car attributes.

Attribute	${\mathit{w}}_1$	${\mathit{w}}_2$	${\mathit{w}}_3$	${\mathit{w}}_4$
$f_1$	${\displaystyle \frac{(0.5,0.3,0.1)}{0.1}}+{\displaystyle \frac{(0.6,0.4,0.5)}{0.2}}$	${\displaystyle \frac{(0.7,0.3,0.6)}{0.4}}$	${\displaystyle \frac{(0.5,0.2,0.3)}{0.7}}$	${\displaystyle \frac{(0.6,0.2,0.3)}{0.8}}+{\displaystyle \frac{(0.5,0.1,0.2)}{0.3}}$
$f_2$	${\displaystyle \frac{(0.3,0.1,0.4)}{0.6}}$	${\displaystyle \frac{(0.8,0.0,0.4)}{0.9}}$	${\displaystyle \frac{(0.5,0.11,0.0)}{0.3}}$	${\displaystyle \frac{(0.8,0.0,0.5)}{0.2}}+{\displaystyle \frac{(0.7,0.0,0.6)}{0.6}}$
$f_3$	${\displaystyle \frac{(0.4,0.2,0.2)}{0.6}}+{\displaystyle \frac{(0.8,0.5,0.6)}{0.4}}+{\displaystyle \frac{(0.3,0.0,0.2)}{0.6}}$	${\displaystyle \frac{(0.9,0.6,0.81)}{0.4}}$	${\displaystyle \frac{(0.3,0.0,0.2)}{0.8}}+{\displaystyle \frac{(0.7,0.7,0.0)}{0.4}}$	${\displaystyle \frac{(0.3,0.0,0.2)}{0.8}}+{\displaystyle \frac{(0.2,0.0,0.1)}{0.9}}$
$f_4$	${\displaystyle \frac{(0.3,0.1,0.2)}{0.4}}+{\displaystyle \frac{(0.5,0.0,0.2)}{0.9}}$	${\displaystyle \frac{(0.7,0.3,0.5)}{0.5}}+{\displaystyle \frac{(0.6,0.2,0.4)}{0.8}}$	${\displaystyle \frac{(0.9,0.1,0.5)}{0.2}}$	${\displaystyle \frac{(0.6,0.2,0.8)}{0.3}}$

Example 5. 

Consider the initial universal set $S=\{s_1,s_2,s_3,s_4\}$ representing four smartphones under consideration by a decision-maker for purchase. Let $F=\{f_1,f_2,f_3,f_4\}$ represent the attributes of the smartphones, such as performance, design, battery life, and camera quality.

The CT2FS $(n,\theta )\in CT2FS\left(S\right)$ over S represents the decision-maker’s assessment of each smartphone based on these attributes. The CT2FS $(n,\theta )$ describes the “satisfaction level of the decision-maker” with each smartphone.

Given the decision-maker’s evaluations, the membership functions $n\left(f_i\right)$ for each attribute $f_i$ are detailed in Table 3.

$$\begin{array}{cc}\hfill n\left(f_1\right)& ={\displaystyle \frac{\frac{(0.7,0.5,0.3)}{0.2}+\frac{(0.4,0.2,0.6)}{0.7}}{s_1}}+{\displaystyle \frac{\frac{(0.3,0.1,0.4)}{0.5}}{s_2}}+{\displaystyle \frac{\frac{(0.8,0.3,0.2)}{0.6}}{s_3}}+{\displaystyle \frac{\frac{(0.2,0.5,0.7)}{0.4}}{s_4}},\hfill \\ \hfill n\left(f_2\right)& ={\displaystyle \frac{\frac{(0.5,0.2,0.3)}{0.3}}{s_1}}+{\displaystyle \frac{\frac{(0.6,0.4,0.8)}{0.7}}{s_2}}+{\displaystyle \frac{\frac{(0.3,0.2,0.7)}{0.5}}{s_3}}+{\displaystyle \frac{\frac{(0.9,0.6,0.4)}{0.2}}{s_4}},\hfill \\ \hfill n\left(f_3\right)& ={\displaystyle \frac{\frac{(0.3,0.2,0.4)}{0.3}}{s_1}}+{\displaystyle \frac{\frac{(0.8,0.5,0.2)}{0.6}}{s_2}}+{\displaystyle \frac{\frac{(0.4,0.7,0.3)}{0.4}}{s_3}}+{\displaystyle \frac{\frac{(0.6,0.1,0.5)}{0.7}}{s_4}},\hfill \\ \hfill n\left(f_4\right)& ={\displaystyle \frac{\frac{(0.7,0.4,0.2)}{0.5}}{s_1}}+{\displaystyle \frac{\frac{(0.3,0.2,0.6)}{0.8}}{s_2}}+{\displaystyle \frac{\frac{(0.6,0.5,0.3)}{0.4}}{s_3}}+{\displaystyle \frac{\frac{(0.8,0.7,0.5)}{0.9}}{s_4}}.\hfill \end{array}$$

Table 3. Tabular representation of the CT2FS for smartphone attributes.

Attribute	${\mathit{s}}_1$	${\mathit{s}}_2$	${\mathit{s}}_3$	${\mathit{s}}_4$
$f_1$	${\displaystyle \frac{(0.7,0.5,0.3)}{0.2}}+{\displaystyle \frac{(0.4,0.2,0.6)}{0.7}}$	${\displaystyle \frac{(0.3,0.1,0.4)}{0.5}}$	${\displaystyle \frac{(0.8,0.3,0.2)}{0.6}}$	${\displaystyle \frac{(0.2,0.5,0.7)}{0.4}}$
$f_2$	${\displaystyle \frac{(0.5,0.2,0.3)}{0.3}}$	${\displaystyle \frac{(0.6,0.4,0.8)}{0.7}}$	${\displaystyle \frac{(0.3,0.2,0.7)}{0.5}}$	${\displaystyle \frac{(0.9,0.6,0.4)}{0.2}}$
$f_3$	${\displaystyle \frac{(0.3,0.2,0.4)}{0.3}}$	${\displaystyle \frac{(0.8,0.5,0.2)}{0.6}}$	${\displaystyle \frac{(0.4,0.7,0.3)}{0.4}}$	${\displaystyle \frac{(0.6,0.1,0.5)}{0.7}}$
$f_4$	${\displaystyle \frac{(0.7,0.4,0.2)}{0.5}}$	${\displaystyle \frac{(0.3,0.2,0.6)}{0.8}}$	${\displaystyle \frac{(0.6,0.5,0.3)}{0.4}}$	${\displaystyle \frac{(0.8,0.7,0.5)}{0.9}}$

The CT2FS $(n,\theta )$ provides an understanding of how the decision-maker evaluates each smartphone based on the given attributes. This assessment guides the decision-maker in making a choice from the available options.

Example 6. 

Consider the initial universal set $V=\{v_1,v_2,v_3,v_4\}$ representing four vacation packages under consideration by a decision-maker. Let $A=\{a_1,a_2,a_3,a_4\}$ represent the attributes of the vacation packages, such as cost, location, amenities, and activities.

The Cubic Type-2 Fuzzy Set (CT2FS) $(p,\eta )\in CT2FS\left(V\right)$ over V represents the decision-maker’s evaluation of each vacation package based on these attributes. The CT2FS $(p,\eta )$ describes the “preference level of the decision-maker” with each vacation package.

Given the decision-maker’s evaluations, the membership functions $p\left(a_i\right)$ for each attribute $a_i$ are detailed in Table 4.

$$\begin{array}{cc}\hfill p\left(a_1\right)& ={\displaystyle \frac{\frac{(0.5,0.3,0.7)}{0.3}+\frac{(0.6,0.4,0.8)}{0.4}}{v_1}}+{\displaystyle \frac{\frac{(0.4,0.1,0.6)}{0.5}}{v_2}}+{\displaystyle \frac{\frac{(0.7,0.2,0.4)}{0.6}}{v_3}}+{\displaystyle \frac{\frac{(0.3,0.4,0.5)}{0.3}}{v_4}},\hfill \\ \hfill p\left(a_2\right)& ={\displaystyle \frac{\frac{(0.3,0.1,0.6)}{0.4}}{v_1}}+{\displaystyle \frac{\frac{(0.7,0.3,0.5)}{0.5}}{v_2}}+{\displaystyle \frac{\frac{(0.5,0.4,0.7)}{0.3}}{v_3}}+{\displaystyle \frac{\frac{(0.6,0.1,0.8)}{0.4}}{v_4}},\hfill \\ \hfill p\left(a_3\right)& ={\displaystyle \frac{\frac{(0.8,0.4,0.2)}{0.5}}{v_1}}+{\displaystyle \frac{\frac{(0.6,0.5,0.4)}{0.4}}{v_2}}+{\displaystyle \frac{\frac{(0.3,0.1,0.6)}{0.3}}{v_3}}+{\displaystyle \frac{\frac{(0.5,0.3,0.7)}{0.6}}{v_4}},\hfill \\ \hfill p\left(a_4\right)& ={\displaystyle \frac{\frac{(0.2,0.6,0.8)}{0.3}}{v_1}}+{\displaystyle \frac{\frac{(0.7,0.4,0.5)}{0.2}}{v_2}}+{\displaystyle \frac{\frac{(0.4,0.1,0.7)}{0.6}}{v_3}}+{\displaystyle \frac{\frac{(0.5,0.3,0.8)}{0.4}}{v_4}}.\hfill \end{array}$$

Table 4. Tabular representation of the CT2FS for vacation packages.

Attribute	${\mathit{v}}_1$	${\mathit{v}}_2$	${\mathit{v}}_3$	${\mathit{v}}_4$
$a_1$	${\displaystyle \frac{(0.5,0.3,0.7)}{0.3}}+{\displaystyle \frac{(0.6,0.4,0.8)}{0.4}}$	${\displaystyle \frac{(0.4,0.1,0.6)}{0.5}}$	${\displaystyle \frac{(0.7,0.2,0.4)}{0.6}}$	${\displaystyle \frac{(0.3,0.4,0.5)}{0.3}}$
$a_2$	${\displaystyle \frac{(0.3,0.1,0.6)}{0.4}}$	${\displaystyle \frac{(0.7,0.3,0.5)}{0.5}}$	${\displaystyle \frac{(0.5,0.4,0.7)}{0.3}}$	${\displaystyle \frac{(0.6,0.1,0.8)}{0.4}}$
$a_3$	${\displaystyle \frac{(0.8,0.4,0.2)}{0.5}}$	${\displaystyle \frac{(0.6,0.5,0.4)}{0.4}}$	${\displaystyle \frac{(0.3,0.1,0.6)}{0.3}}$	${\displaystyle \frac{(0.5,0.3,0.7)}{0.6}}$
$a_4$	${\displaystyle \frac{(0.2,0.6,0.8)}{0.3}}$	${\displaystyle \frac{(0.7,0.4,0.5)}{0.2}}$	${\displaystyle \frac{(0.4,0.1,0.7)}{0.6}}$	${\displaystyle \frac{(0.5,0.3,0.8)}{0.4}}$

The CT2FS $(p,\eta )$ provides insight into how the decision-maker evaluates each vacation package based on the given attributes. This assessment aids the decision-maker in selecting the most preferred vacation package from the available options.

4.1. Operations of Cubic Type-2 Fuzzy Soft Set

• Union Let $(f,\phi ),(\psi ,m)\in CT2FS\left(w\right)$. The union of $(f,\phi )$ and $(\psi ,m)$ is $(\epsilon ,w)\in CT2FS\left(w\right)$, defined for all

  $$\begin{array}{cc}& z\in w=\phi \cup m\hfill \\ & \epsilon \left(z\right)=\left\{\begin{array}{c}f\left(z\right)\mathrm{if}z\in \phi -m\hfill \\ \psi \left(z\right)\mathrm{if}z\in m-\phi \hfill \\ f\left(z\right)\cup \psi \left(z\right)\mathrm{if}z\in \phi \cap m\hfill \end{array}\right.\hfill \end{array}$$
• Complement
  The complement of a CT2FSS is defined as

  $${(f,\phi )}^c=\left(f^c,\daleth \phi \right)$$

  $$f^c\left(z\right)=\daleth \left(f(\daleth z)\right),\mathrm{for}\mathrm{all}z\in \daleth \phi .$$
• Intersection
  Let $(f,\phi ),(\psi ,m)\in CT2FS\left(w\right)$. The intersection of $(f,\phi )$ and $(\psi ,m)$ is $(\epsilon ,\omega )\in CT2FS\left(w\right)$, defined for all $z\in W=\phi \cap m$ as

  $$\epsilon \left(z\right)=\left\{\begin{array}{cc}f\left(z\right),\hfill & \mathrm{if}z\in \phi \setminus m,\hfill \\ \psi \left(z\right),\hfill & \mathrm{if}z\in m\setminus \phi ,\hfill \\ f\left(z\right)\cap \psi \left(z\right),\hfill & \mathrm{if}z\in \phi \cap m.\hfill \end{array}\right.$$

Definition 7 

([12]). A null CT2FSS, denoted ${\mathrm{\Omega }}_{\phi }$, is a CT2FSS $(n,\phi )$ on Ω if for all $m\in \phi$ for all $w\in \mathrm{\Omega }$:

$$\begin{array}{cc}& {\mu }_w^{+}(w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \\ & {\mu }_w^{-}(w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \\ & \lambda (w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \end{array}$$

Definition 8 

([12]). An absolute CT2FSS, denoted ${\mathrm{\Omega }}_{\phi }$, is a CT2FSS $(n,\phi )$ on X if for all $m\in \phi$ for all $w\in \mathrm{\Omega }$:

$$\begin{array}{cc}& {\mu }_w^{+}(w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \\ & {\mu }_w^{-}(w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \\ & \lambda (w,z)=\left\{\begin{array}{cc}1\hfill & ifz=0\hfill \\ 0\hfill & ifz\ne 0\hfill \end{array}\right.\hfill \end{array}$$

Theorem 6. 

(De Morgan’s Laws for CT2FSSs) Let $(w,A)$ and $(y,B)$ be two CT2FSSs. Then,

1.

${((w,A)\wedge (y,B))}^c={(w,A)}^c\vee {(y,B)}^c$

2.

${((w,A)\vee (y,B))}^c={(w,A)}^c\wedge {(y,B)}^c$

Proof. 

$$\begin{array}{cc}& {(w,A)}^c\vee {(y,B)}^c=\left(w^c,\neg A\right)\vee \left(y^c,\neg B\right)=\left(z^c,\neg A\times \neg B\right)\hfill \\ & \mathrm{where}{z}^c=(v,\neg v)=A^c(\neg z)\vee y^c(\neg B)=\left(z^c,\neg (A\times B)\right)\hfill \\ & \Rightarrow \mathrm{Let}\mathrm{us}\mathrm{say}\mathrm{that}(w,A)\wedge (y,B)=(f,A\times B)\hfill \\ & \Rightarrow {((w,A)\wedge (y,B))}^c={(f,A\times B)}^c=(f,\neg (A\times B))\hfill \\ & \forall (z,v)\in A\times B,\mathrm{we}\mathrm{obtain}\hfill \\ & f^c(\neg z,\neg v)={\left(f^c(z,z)\right)}^c\hfill \\ & ={(w\left(z\right)\wedge y\left(v\right))}^c\hfill \\ & ={\left(w\left(z\right)\right)}^c\vee {\left(y\left(v\right)\right)}^c\hfill \\ & =w^c(\left(z\right)\vee y^c(\neg v))\hfill \\ & \Rightarrow {((w,A)\wedge (y,B))}^c={(w,A)}^c\vee (y,B).\hfill \end{array}$$

Similarly, we prove:

$${((w,A)\vee (y,B))}^c={(w,A)}^c\wedge {(y,B)}^c.$$

   □

4.2. Comparison of CT2FSSs with Existing Tools for Industrial Decision Making

We compare CT2FSSs with the following widely used tools for decision-making:

• Fuzzy Multi-Criteria Decision Making (FMCDM): A popular approach that uses fuzzy logic to handle uncertainty in decision-making problems.
• Rough Set Theory (RST): A mathematical tool for dealing with uncertainty and imprecision in data.
• Analytic Hierarchy Process (AHP): A structured technique for making complex decisions by breaking them down into smaller, more manageable parts.

Key Performance Metrics: To evaluate the performance of these tools, we focus on the following metrics:

• Accuracy: The ability of the tool to make correct decisions.
• Efficiency: The computational time required to solve decision-making problems.
• Interpretability: The ease with which the decision-making process can be understood and explained.
• Flexibility: The ability of the tool to handle different types of data and decision-making scenarios.

4.3. Comparison of the Proposed Framework with Existing Methods

The proposed framework, rooted in Cubic Type-2 Fuzzy Soft Sets (CT2FSSs), offers several distinct advantages over existing decision-making models in the context of Industry 4.0 supply chains.

• Enhanced Uncertainty Handling:
  • Traditional fuzzy set theory: While fuzzy set theory has been widely used in decision-making, it often struggles to capture the complex uncertainties inherent in Industry 4.0 supply chains.
  • CT2FSS: By incorporating type-2 fuzzy sets and cubic sets, CT2FSSs provide a more flexible and expressive framework for representing uncertainty. This allows for the proposed framework to better handle the dynamic and unpredictable nature of Industry 4.0 environments.
• Improved Flexibility:
  • Existing models: Many existing models may be limited in their ability to adapt to changing conditions and unforeseen events.
  • CT2FSS: The flexibility of CT2FSSs enables the proposed framework to accommodate a wider range of scenarios and uncertainties, making it more adaptable to the dynamic nature of Industry 4.0 supply chains.
• Enhanced Decision-Making Capabilities:
  • Traditional models: Some traditional models may struggle to provide accurate and timely decision-making support in complex and uncertain environments.
  • Proposed framework: By leveraging the capabilities of CT2FSSs, the proposed framework offers a more robust and reliable approach to decision-making, enabling decision-makers to navigate complexities and optimize supply chain processes.
• Integration of Theory and Practice:
  • Existing models: While some models may focus primarily on theoretical aspects, the proposed framework integrates rigorous theoretical analysis with practical applications, demonstrating its real-world applicability.
  • Proposed framework: This integration ensures that the framework is not only theoretically sound but also effective in addressing the challenges faced by Industry 4.0 supply chains. Table 5 summarizes a comparison of the proposed framework with existing methods.
    Table 5. Comparison of the proposed framework with existing methods.

    Feature	Proposed Framework (CT2FSS-Based)	Existing Models
    Uncertainty Handling	Superior ability to handle complex uncertainties	Limited ability to handle complex uncertainties
    Flexibility	Highly adaptable to changing conditions	Less adaptable to changing conditions
    Decision-Making Capabilities	Robust and reliable decision-making	May struggle to provide accurate and timely decisions
    Theory and Practice	Integrates rigorous theory with practical applications	May focus primarily on theoretical aspects

The proposed framework, based on CT2FSSs, offers several distinct advantages over existing decision-making models in the context of Industry 4.0 supply chains. By enhancing uncertainty handling, flexibility, decision-making capabilities, and integrating theory and practice, this framework provides a valuable tool for navigating the complexities and uncertainties of Industry 4.0 environments.

5. Applications of Cubic Type-2 Fuzzy Soft Set in Industry 4.0 Supply Chains

The versatility of Cubic Type-2 Fuzzy Soft Sets (CT2FSSs) renders them particularly suitable for addressing the intricate and dynamic challenges inherent in Industry 4.0 supply chains. By capturing uncertainty on multiple levels, CT2FSSs can effectively model complex relationships among various supply chain components.

Supplier Selection: CT2FSSs can be employed to evaluate and rank potential suppliers based on multiple criteria, including price, quality, delivery performance, and risk. By considering the inherent uncertainty in supplier assessment, CT2FSSs can provide a more robust decision-making framework [29].

Demand Forecasting: The ability of CT2FSSs to handle imprecise and uncertain information makes them applicable to demand forecasting in volatile markets. By incorporating various factors such as economic indicators, competitor actions, and customer behavior, CT2FSSs can improve the accuracy of demand predictions [30].

Risk Assessment: CT2FSSs can be used to assess and prioritize supply chain risks, such as disruptions, natural disasters, and geopolitical uncertainties. By modeling complex interdependencies between risk factors, CT2FSSs can support proactive risk management strategies.

Inventory Management: CT2FSSs can optimize inventory levels by considering factors such as demand variability, lead times, and holding costs. By handling uncertainty in demand and supply, CT2FSSs can help reduce inventory carrying costs and stockouts.

Through these applications, the CT2FSS demonstrates its potential to enhance decision-making capabilities in Industry 4.0 supply chains by providing a robust and flexible approach to handling complex and uncertain information.

To further illustrate the applicability of CT2FSSs in Industry 4.0 supply chains, we replace the personal selection problem with a more relevant example: predictive maintenance of industrial equipment.

Predictive maintenance involves using data analytics to predict equipment failures and schedule maintenance proactively, reducing downtime and improving overall efficiency. CT2FSSs can be used to model the uncertainty associated with equipment degradation and failure, enabling more accurate predictions and optimized maintenance schedules. By incorporating various factors such as sensor data, historical maintenance records, and external conditions, CT2FSSs can provide a more reliable and effective approach to predictive maintenance in Industry 4.0 supply chains.

Definition 9 

([12]). Let $Z\subset E$. Let $(v,Z)$ be a CT2FSS over the initial universe Ω. For $w\in [0,1]$ and $\lambda \in [0,1]$, the $(w,\lambda )$ level fuzzy soft set of $(v,Z)$ is a crisp soft set $T\left(\right(v,Z),w,\lambda )=\left(v\right(w,\lambda ),Z)$ for all $\epsilon \in Z$, defined by

$$v(w,\lambda )\left(\epsilon \right)=v{\left(\epsilon \right)}_{\lambda }^w=\left\{w\in \mathrm{\Omega }\mid f\left(w\right)⩾\lambda :\forall f\left(w\right)\in J_{\lambda }^w\right\}$$

where

$$J_w^w=\{f\mid \left({\mu }_{v\left(\epsilon \right)}^{+}(x,f),{\mu }_{v\left(\epsilon \right)}^{-}(w,f),A(w,f)\right)\ge w:f\in J_w\}$$

Definition 10 

([12]). Let $z\subset E$. Let $(v,z)$ be a CT2FSS over Ω. Let $w:z\to [0,1]$ and $d:w\to [0,1]$ be two fuzzy sets in z, which are two threshold fuzzy sets. Then, the level set fuzzy soft set of $(v,z)$ with respect to w and d is a crisp soft set $T\left(\right(v,z),w,d)$, defined by

$$\begin{array}{cc}\hfill T\left(\right(v,z),w,d)& =\left(v\right(w,\lambda ),z)\mathit{for}\mathit{all}\epsilon \in z,\mathit{defined}\mathit{by}\hfill \\ \hfill v(w,d)\left(\epsilon \right)& =v{\left(\epsilon \right)}^{\omega }=\sum w\in \mathrm{\Omega }\mid f\left(w\right)⩾\lambda {\left(\epsilon \right)}_{:}\forall f\left(w\right)\in J_w^w\hfill \end{array}$$

where $J_w^{\omega }=\left\{f\mid \left({\mu }_v^t\left(\epsilon \right)(w,f),{\mu }_{\overline{v}}\left(\epsilon \right)(w,f)\right)⩾w\left(\epsilon \right):f\in {\mathcal{J}}_w\right\}$.

Definition 11 

([12]). Let $Z\subset E$ be a central interval set. Let $(v,z)$ be a CT2FSS over Ω. Let $\phi :z⟶[0,1]$ be the weight function specifying the weight ${\phi }_i=\phi \left({\epsilon }_i\right)$ for all ${\epsilon }_i\in Z$. Then, the triple $(v,z,\phi )$ is a weighted CT2FSS. See the Algorithm 1:

Algorithm 1: Example Algorithm.

Algorithm Description: Consider the following: Step 1: Provide a weighted Cubic Type-2 Fuzzy Soft Set (CT2FSS) as an input parameter: $$\mathrm{\Gamma }=(v,\tau ,\epsilon ).$$ Step 2: Provide two fuzzy sets with thresholds: $$w:z\to [0,1],\mathrm{and}\lambda :z\to [0,1].$$ These sets are used for decision-making. Step 3: Determine the alpha-cut of the cubic fuzzy soft set $T\left((v,z),w_0\right)$ of $\Gamma$ with respect to the two threshold fuzzy sets w and $\lambda$. Step 4: Present the level set $T\left(\right(v,z),w,d)$ in tabular form. For each $w_i\in \mathrm{\Omega }$, compute the weighted choice value $C_i$ using $$C_i=\sum _{\epsilon \in w}\vee \left(\epsilon \right)\left(w_i\right)·\Gamma \left(\epsilon \right).$$ Step 5: Select the alternative corresponding to the maximum computed value. Choose $w_i$ if it maximizes $C_i$: $$C_B=\underset{w_i\in \mathrm{\Omega }}{max}\left\{C_i\right\}.$$ Step 6: If B multiple optimal solutions exist, any can be selected as the final decision.

A detailed explanation of the algorithm with an illustrative example.

Algorithm: Decision-Making using Weighted Cubic Type-2 Fuzzy Soft Sets (CT2FSSs).

Input:

• $\mathrm{\Gamma }=(v,\tau ,ϵ)$: A weighted Cubic Type-2 Fuzzy Soft Set.
• $w:z\to [0,1]$: A threshold fuzzy set used for decision-making.
• $\lambda :z\to [0,1]$: Another threshold fuzzy set used for decision-making.

Output:

• CB: The optimal decision based on the CT2FSS and thresholds.

Steps:

• We start with a CT2FSS named $\mathrm{\Gamma }$, represented by $(v,\tau ,ϵ)$. Here, v is the universe of discourse, $\tau$ defines fuzzy membership functions, and $ϵ$ represents weight information.
• We also provide two threshold fuzzy sets, w and $\lambda$. These sets define what level of membership is considered acceptable for decision-making.
• Compute Level Set Fuzzy Soft Set:
  • This step involves calculating a new fuzzy soft set based on the original CT2FSS and the thresholds. We denote this new set as $T((v,z),w_0)$.
  • Essentially, we are identifying elements in the CT2FSS that meet the membership criteria defined by w and $\lambda$.
• Present Level Set in Tabular Form:
  • Organize the computed level set $T\left(\right(v,z),w,d)$ in a table for better understanding.
  • Each row in the table will represent a possible element $\left(w_i\right)$ from the universe of discourse.
• Calculate Weighted Choice Value:
  • For each element $\left(w_i\right)$ in the table, we calculate a weighted choice value $\left(C_i\right)$. This value signifies the suitability of choosing that element based on the CT2FSS and thresholds.
  • The formula for $C_i$ is

    $$C_i=\sum _{ϵ\in w}\vee \left(ϵ\right)\left(w_i\right)·\mathrm{\Gamma }\left(ϵ\right)$$

    (1)
  • Here, $\vee \left(ϵ\right)\left(w_i\right)$ represents the membership degree of $w_i$ in the threshold set w for a specific weight $ϵ$. $\mathrm{\Gamma }\left(ϵ\right)$ represents the weight of $ϵ$ in the CT2FSS.
  • In simpler terms, we are considering both the membership level in the thresholds and the weight associated with each element in the CT2FSS to compute a score.
• Determine Optimal Decision:
  • Analyze the calculated $C_i$ values for all elements $\left(w_i\right)$.
  • The element with the highest $C_i$ value is considered the optimal decision $\left(C_B\right)$. This means it has the strongest membership according to the CT2FSS and satisfies the thresholds.
• Handle Multiple Optimal Decisions (Optional):
  • In some cases, there might be multiple elements with the same maximum $C_i$ value. This indicates that several options are equally suitable based on the CT2FSS and thresholds.
  • If this occurs, B represents the set of elements with the maximum $C_i$. Any element from set B can be chosen as the final decision. The choice can be based on additional criteria or user preference.
• Illustrative Example:

  (a)

  • Imagine you are selecting a candidate for a job position. The CT2FSS $\left(\mathrm{\Gamma }\right)$ represents the evaluation of each candidate with factors like experience and skills weighted according to their importance.
  • The thresholds $(w$ and $\lambda )$ define the minimum acceptable level of qualification for each factor.
  • By following this algorithm, you can systematically evaluate candidates, identify those who meet the criteria, and choose the one with the strongest overall suitability $\left(C_B\right)$. The flowchart for the given algorithm is shown in Figure 2.
    

    Figure 2. Flowchart for the given algorithm.

  (b)

  Imagine you are managing a manufacturing facility and want to implement a predictive maintenance strategy to minimize downtime and optimize equipment performance. You can use the CT2FSS algorithm to evaluate the condition of different machines and prioritize maintenance tasks.

  CT2FSS Parameters:

  • Evaluation Factors (F): Vibration levels, temperature, energy consumption, and other relevant machine parameters.
  • Weights (c): Assign weights to each factor based on its importance in predicting equipment failure.
  • Thresholds (w and $\lambda$): Define acceptable thresholds for each factor to determine when maintenance is necessary.

  Algorithm Steps:

  • Collect data: Gather data on the machine’s parameters over time. Construct CT2FSS: Create a CT2FSS to represent the machine’s condition,
  • considering uncertainty and imprecision in the data. Apply algorithm: Use the CT2FSS algorithm to evaluate the machine’s condition based on the weights and thresholds.
  • Prioritize maintenance: Identify machines with the highest risk of failure and prioritize maintenance tasks accordingly.

  Benefits:

  • Early detection of anomalies: CT2FSS can help identify potential equipment failures before they occur, preventing costly downtime.
  • Optimized maintenance scheduling: By prioritizing tasks based on risk, you can allocate resources effectively and minimize disruptions to production.
  • Improved equipment reliability: Predictive maintenance can extend the lifespan of your equipment and improve overall reliability.

The proposed CT2FSS algorithm introduces a novel paradigm for addressing complex decision problems characterized by uncertainty and imprecision. By harnessing the capabilities of Cubic Type-2 Fuzzy Soft Sets, the algorithm offers several key benefits:

• CT2FSSs offer a refined representation of uncertainty, surpassing traditional fuzzy sets in decision-making accuracy.
• Flexibility in choosing a threshold: Using threshold fuzzy sets lets you change the way decisions are made to fit people with different levels of risk tolerance.
• Engineering, business, and medical diagnostics are just a few of the many fields that can benefit from the algorithm’s adaptability.

While the proposed algorithm offers several advantages, it also has some limitations:

• Sensitivity to threshold values: The choice of threshold values significantly impacts the algorithm’s output. Sensitivity analysis is necessary to determine the robustness of the results.
• The algorithm operates under the assumption of attribute independence, which might not always hold true in real-world scenarios, potentially compromising result accuracy.
• The algorithm’s computational complexity increases significantly with problem size, potentially limiting its applicability to large-scale datasets.
• The complexity of the underlying mathematical framework can hinder the interpretability of results derived from CT2FSS-based decision-making processes.

Example 7. 

A company seeks to fill a vacant position by evaluating a pool of candidates. This is a classic decision-making problem that can be structured using various methods $Z=\{z_1,z_2\}$. The hiring committee evaluates the candidates based on a set of parameters $F=\{f_1,f_2,f_3\}\equiv$ { years of experience, computer skills, educational qualifications }.

The weights for the parameters in F are as follows:

$$\begin{array}{cc}& c_1=c\left(f_1\right)=0.3,\hfill \\ & c_2=c\left(f_2\right)=0.5,\hfill \\ & c_3=c\left(f_3\right)=0.7.\hfill \end{array}$$

The hiring committee uses two threshold fuzzy sets:

$$\begin{array}{cc}& w:F⟶[0,1]\mathrm{and}\lambda :F⟶[0,1],\hfill \\ & w={\displaystyle \frac{0.7}{f_1}}+{\displaystyle \frac{0.4}{f_2}}+{\displaystyle \frac{0.25}{f_3}},\hfill \\ & \lambda ={\displaystyle \frac{0.35}{f_1}}+{\displaystyle \frac{0.5}{f_2}}+{\displaystyle \frac{0.85}{f_3}}.\hfill \end{array}$$

The hiring committee considers a Cubic Type-2 Fuzzy Soft Set $(v,F)$ as follows:

$$(v,F)=\left\{\begin{array}{c}\left(f_1,\left({\displaystyle \frac{(0.4,0.15,0.35)}{0.4}}+\left({\displaystyle \frac{(0.5,0.2,0.45)}{z_1}}\right)\right)+\left(\left({\displaystyle \frac{(0.85,0.5,0.6)}{0.55}}\right)+\left({\displaystyle \frac{(0.55,0.1,0.3)}{z_2}}\right)\right)\right),\hfill \\ \left(f_2,\left(\left({\displaystyle \frac{(0.4,0.1,0.2)}{0.3}}\right)z_1\right)+\left(\left({\displaystyle \frac{(0.9,0.5,0.7)}{0.35}}\right)z_2\right)\right),\hfill \\ \left(f_3,\left(\left({\displaystyle \frac{(0.75,0.35,0.5)}{0.6}}\right)+\left({\displaystyle \frac{(0.80,0.25,0.75)}{0.2}}\right)z_1\right)+\left(\left({\displaystyle \frac{(0.5,0.1,0.35)}{0.4}}\right)z_2\right)\right).\hfill \end{array}\right\}$$

The weighted optimal choice value is deduced as

$$x_1\le i\le 2\left\{c_i\right\}=c_2$$

Hence, the required optimal choice is candidate $U_2$.

Example 8. 

Suppose a university admissions committee wants to evaluate candidates for a scholarship program, and there are candidates $A=\{a_1,a_2\}$. The admissions committee looks at a set of parameters $F=\{f_1,f_2,f_3\}\equiv \{academicperformance,extracurricularactivities,personalstatement\}$.

Assume the weights for the parameters in F are as follows:

$$\begin{array}{cc}& c_1=c\left(f_1\right)=0.4,\hfill \\ & c_2=c\left(f_2\right)=0.3,\hfill \\ & c_3=c\left(f_3\right)=0.3.\hfill \end{array}$$

The admissions committee uses two threshold fuzzy sets $w:F⟶[0,1]$ and $\lambda :F⟶[0,1]$ to evaluate the candidates:

$$\begin{array}{cc}& w={\displaystyle \frac{0.6}{f_1}}+{\displaystyle \frac{0.4}{f_2}}+{\displaystyle \frac{0.3}{f_3}},\hfill \\ & \lambda ={\displaystyle \frac{0.5}{f_1}}+{\displaystyle \frac{0.6}{f_2}}+{\displaystyle \frac{0.7}{f_3}}.\hfill \end{array}$$

The Cubic Type-2 Fuzzy Soft Set $(v,F)$ is defined as follows:

$$(v,F)=\left\{\begin{array}{c}\left(f_1,\left({\displaystyle \frac{\left((0.7,0.4,0.3)/0.4\right)}{a_1}}\right)+\left({\displaystyle \frac{\left((0.8,0.5,0.6)/0.5\right)}{a_2}}\right)\right),\hfill \\ \left(f_2,\left({\displaystyle \frac{\left((0.6,0.3,0.2)/0.3\right)}{a_1}}\right)+\left({\displaystyle \frac{\left((0.9,0.7,0.5)/0.4\right)}{a_2}}\right)\right),\hfill \\ \left(f_3,\left({\displaystyle \frac{\left((0.5,0.4,0.2)/0.5\right)}{a_1}}\right)+\left({\displaystyle \frac{\left((0.7,0.5,0.3)/0.4\right)}{a_2}}\right)\right).\hfill \end{array}\right\}$$

Based on the evaluation, the admissions committee deduces the weighted optimal choice value as $a_1$ or $a_2$ depending on which candidate aligns best with the weighted criteria. The final decision can be made by considering the threshold fuzzy sets and the weights of each attribute.

6. Conclusions

This research introduces a novel framework rooted in Cubic Type-2 Fuzzy Soft Sets (CT2FSSs) to effectively address the intricate and dynamic challenges prevalent in contemporary Industry 4.0 supply chains, particularly in scenarios demanding symmetrical and equitable outcomes. By capturing uncertainty, imprecision, and interdependencies, a CT2FSS offers a robust and adaptable decision-making tool. Through its ability to model complex relationships and handle multiple levels of uncertainty, this framework proves invaluable in enhancing supply chain resilience, adaptability, and overall performance, while maintaining symmetry in decision-making.

Real-world applications, including supplier selection, demand forecasting, and risk assessment, demonstrate the practical utility of CT2FSSs in addressing critical supply chain challenges. By providing a structured approach to decision-making under uncertainty, the framework contributes to improved operational efficiency, cost reduction, and customer satisfaction.

This research represents a significant advancement in the application of CT2FSSs to supply chain management, offering a novel and effective tool for decision-makers. Future research avenues include integrating CT2FSSs with advanced optimization techniques, such as genetic algorithms and simulated annealing, exploring real-time data integration using machine learning algorithms, and conducting larger-scale empirical studies across various industry sectors to further validate and refine the proposed framework.

In conclusion, this research establishes CT2FSSs as a powerful tool for navigating the complexities of Industry 4.0 supply chains, particularly in scenarios requiring symmetrical and equitable outcomes. By offering a robust and flexible decision-making framework, this study not only advances supply chain management practices but also paves the way for future innovations in this field.