Results on Third-Order Differential Subordination for Analytic Functions Related to a New Integral Operator

Abstract

In this paper, we aim to give some results for third-order differential subordination for analytic functions in the open unit disk $\mathcal{U}=\left\{z:z\in \mathbb{C} \mathrm{a}\mathrm{n}\mathrm{d} \left|z\right|<1\right\}$ involving the new integral operator ${\mu }_{\alpha ,n}^m(f\ast g)$. The results are obtained by examining pertinent classes of acceptable functions. New findings on differential subordination have been obtained. Additionally, some specific cases are documented. This work investigates appropriate classes of admissible functions, presents a novel of new integral operator, and discusses the properties of third-order differential subordination. The properties and results of the differential subordination are symmetrical to the properties of the differential superordination to form the sandwich theorems.

1. Introduction

Several authors, such as Antonino and Miller [1], have expanded the scope of second-order differential subordinations, which were initially formulated by Mocanu and Miller [2], to encompass third-order differential subordinations. Approaches suggested by Miller and Antonino offer a possibility of acquiring intriguing novel findings. Furthermore, some authors have commenced their work in this specific line of investigation [3,4]. The concept of expanding the pair theory of differential superordination [5] to third-order differential superordination was introduced in 2014 [6], with novel and intriguing outcomes soon following [7,8]. The next symbols and concepts serve as the fundamental framework in this study.

Many scholars have discussed and dealt with second-order differential subordination and superordination, see [9,10,11,12,13,14,15,16,17,18,19,20,21]. Several authors have recently written about superordination and the principle of third-order differential subordination. For examples of asymmetrical subordination and superordination on a third-order case, see [1,3,4,6,7,8,22,23,24,25,26,27,28,29]. Antonino and Miller [1] presented basic concepts and expanded Miller and Mocanu’s [30] principle of second-order differential subordination in the open unit disk to the third-order case.

The family of analytic functions is denoted as $H\left(\mathcal{U}\right)$, when the open unit disk $\mathcal{U}=\left\{z:z\in \mathbb{C} \mathrm{a}\mathrm{n}\mathrm{d} \left|z\right|<1\right\}$, and $\overline{\mathcal{U}}=\left\{z\in \mathbb{C}:\left|z\right|\le 1\right\},$ also $\partial \mathcal{U}=\left\{z\in \mathbb{C}:\left|z\right|=1\right\}.$ Let $n$ will be a positive integer as well, $a$ will be a complex number, and the next major subfamilies of $H\left(\mathcal{U}\right)$ are defined as follows:

$$H\left[a,n\right]=\left\{f\in H\left(\mathcal{U}\right):f\left(z\right)=a+a_n z^n+a_{n+1} z^{n+1}+\cdots , z\in \mathcal{U}\right\},$$

such that $H_0=H\left[\mathrm{0,1}\right]$ and $H_1=H\left[\mathrm{1,1}\right].$

Let $K$ be a subclass of $H\left(\mathcal{U}\right)$ consisting of functions that are analytic in $\mathcal{U}$ and possess the normalized Taylor–Maclaurin series:

$$f\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{z}^n \left(z\in \mathcal{U}\right).$$

(1)

Assume the functions $f$ and$g$ $\in H\left(\mathcal{U}\right)$. If $f$ is subordinate to $g$, or $g$ is superordinate to $f$, it is defined as

$$f\prec g in \mathcal{U} or f\left(z\right)\prec g\left(z\right) , \left(z\in \mathcal{U}\right)$$

if there exists a Schwarz function $\omega \in H\left(\mathcal{U}\right),$ which is analytic in $\mathcal{U}$ with $\omega \left(0\right)=0$ and $\left|\omega \left(z\right)\right|<1 (z\in \mathcal{U})$, such that $f\left(z\right)=g\left(\omega \left(z\right)\right), (z\in \mathcal{U})$.

Furthermore, if $g$ is a univalent function in $\mathcal{U}$, it satisfies the following equivalence relationship [27]:

$$g\left(z\right)\prec f\left(z\right) \iff g\left(0\right)=f\left(0\right) and g\left(\mathcal{U}\right)\subset f\left(\mathcal{U}\right), \left(z\in \mathcal{U}\right).$$

Example 1. 

Consider $f\left(z\right)=z+z^2$ and $g\left(z\right)={\displaystyle \frac{z}{1-z}}$. Choose $\omega \left(z\right)={\displaystyle \frac{z+z^2}{1+z+z^2}}$. We note that $\omega \left(0\right)=0$ and $\left|\omega \left(z\right)\right|=\left|{\displaystyle \frac{z+z^2}{1+z+z^2}}\right|<1$, hence $\omega \left(z\right)$ is a Schwarz function. Using the function $\omega :\mathbb{U}⟶\mathbb{U}$, we observe that

$$g\left(\omega \left(z\right)\right)={\displaystyle \frac{\omega \left(z\right)}{1-\omega \left(z\right)}}={\displaystyle \frac{\frac{z+z^2}{1+z+z^2}}{1-\frac{z+z^2}{1+z+z^2}}}=z+z^2=f\left(z\right).$$

Therefore, $f\left(z\right)\prec g\left(z\right)$.

Example 2. 

It is well known that the properties of the sine function qualify it to satisfy the conditions of a Schwarz function, i.e., $\sin \left(0\right)=0$ and $\left|\sin z\right|<1 (z\in \mathbb{U})$. Therefore, $\sin z\prec z$ with $\omega \left(z\right)=\sin z$.

Example 3. 

Here, we will take two functions that cannot subordinate one another. Assume that $f\left(z\right)=z^2$ and $g\left(z\right)=e^z$. We will prove $f\left(z\right)\nprec g\left(z\right)(z\in \mathbb{U})$ by contradiction. Suppose that $f\left(z\right)\prec g\left(z\right)⟺z^2=e^{\omega \left(z\right)}$ for some Schwarz function $\omega \left(z\right)$, yields $0=e^{\omega \left(0\right)}=1$, and this a contradiction.

If $f\in K$ is given by (1), and $g\in K$ defined by

$$g\left(z\right)=z+\sum _{n=2}^{\infty }{b}_n{z}^n ,$$

the Hadamard product (or convolution) of $f$ and $g$ is given by

$$\left(f\ast g\right)\left(z\right)=z+\sum _{n=2}^{\infty }{a}_n{b}_n{z}^n=\left(g\ast f\right)\left(z\right),\left(z \in \mathcal{U}\right).$$

Differential subordination is an extension of multiple inequalities related to complex variables. Additional concepts and terminologies from the theory of differential subordinations are presented through the introduction of novel operators.

In this paper, we define a new integral operator ${\mu }_{\alpha ,n}^m(f\ast g)$, ${\mu }_{\alpha ,n}^m:K\to K,where \alpha \ge 0, m\in \mathbb{N}\cup \left\{0\right\},$ which is defined as follows:

$$\begin{array}{c}{\mu }_{\alpha ,n}^1(f\ast g)=2\left({\mu }_{\alpha ,n}^0(f\ast g)\right)-\left(\alpha +2\right)z^{-1-\alpha }{\int }_0^z{t}^{\alpha }\left({\mu }_{\alpha ,n}^0\right(f\ast g\left(t\right)\left)\right)dt\\ =z+{\displaystyle \sum _{n=2}^{\infty }}{\left({\displaystyle \frac{\alpha +2n}{\alpha +n+1}}\right)}^1{a}_n{b}_n{z}^n,\end{array}$$

where

$${\mu }_{\alpha ,n}^0\left(f\ast g\right)\left(z\right)=\left(f\ast g\right)\left(z\right).$$

In general,

$$\begin{array}{c}{\mu }_{\alpha ,n}^m(f\ast g)=2\left({\mu }_{\alpha ,n}^{m-1}(f\ast g)\right)-\left(\alpha +2\right)z^{-1-\alpha }{\int }_0^z{t}^{\alpha }\left({\mu }_{\alpha ,n}^{m-1}\right(f\ast g\left(t\right)\left)\right)dt\\ =z+{\displaystyle \sum _{n=2}^{\infty }}{\left({\displaystyle \frac{\alpha +2n}{\alpha +n+1}}\right)}^m{a}_n{b}_n{z}^n .\end{array}$$

Figure 1 below describe the geometric changes on $f\left(z\right)=z+z^2+z^3\in K$ under ${\mu }_{\alpha ,n}^m$ whenever $\left(z\right)=z/1+z$, $\alpha =1/2$, and $(m=\mathrm{0,1},\mathrm{5,10}, \mathrm{r}\mathrm{e}\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{l}\mathrm{y})$

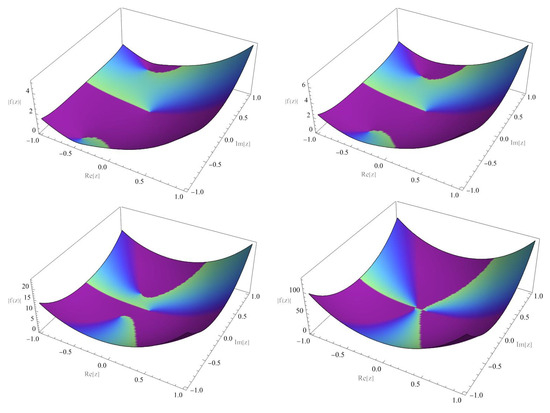
Figure 1. ${\mu }_{0.5,n}^0$, ${\mu }_{0.5,n}^1$,${\mu }_{0.5,n}^5$, and ${\mu }_{0.5,n}^{10}$ of $f\left(z\right)=z+z^2+z^3$.

Colors play an important role in visualizing complex functions. In a $3D$ plot of a complex function $f\left(z\right)$, colors are used to represent the angle (or phase) of the function’s values. The angle $Arg\left(f\right(z\left)\right)$ is determined by the following formula:

$$Arg \left(f\left(z\right)\right)={\tan }^{-1}{\displaystyle \frac{Im\left(f\left(z\right)\right)}{Re\left(f\left(z\right)\right)}}.$$

This angle helps us to understand the direction of points in the complex plane. To represent the angle with colors, we use a color gradient like the rainbow, which maps different angles to specific colors. The angle is normalized to a range between 0 and 2π. The resulting plot shows how colors change with the angle. Areas with similar angles will have similar colors, while different angles will display contrasting colors. This visual representation helps researchers analyze the behavior of complex functions more effectively. However, the simple calculations give

$$z{\left({\mu }_{\alpha ,n}^m\left(f\ast g\right)\left(z\right)\right)}^{\prime }=\left(\sigma +n+1\right)\left({\mu }_{\alpha ,n}^{m+1}\left(f\ast g\right)\left(z\right)\right)-(\sigma +n)\left({\mu }_{\alpha ,n}^m\left(f\ast g\right)\left(z\right)\right).$$

(2)

The idea of third-order differential subordination is discussed in the study conducted by Ponnusamy and Juneja [29] and recent works by some authors (for instance, [4,8]). The second- and third-order differential subordination has garnered significant attention from authors in this field. (for instance, [1,9,10,11,12,13,14,15,16,17,18,22,30,31,32,33]). In this study, we examine a specific family of admissible functions involved in the new integral operator ${\mu }_{\alpha ,n}^m$and establish adequate criteria for the normalized analytic function known as the differential subordination condition. There are advantages of creating a new operator for the purpose of obtaining new applications about the differential subordination and superordination of the third order, which are important in medical physics applications such as, brain diseases.

2. Preliminary Results

The acquisition of the next definitions and lemmas is an important to fulfil our outcomes.

Definition 1. 

[1]: Let $\chi :{\mathbb{C}}^4\times \mathcal{U}⟶\mathbb{C}$ and suppose that the function $h\left(z\right)$ is univalent in $\mathcal{U}$. If the function $p\left(z\right)$ is analytic in $\mathcal{U}$ and it satisfies the following third-order differential subordination

$$\chi \left(p\left(z\right),z{p}^{\prime }\left(z\right), z^2{p}^{″}\left(z\right),z^3{p}^{‴}\left(z\right);z\right)\prec h\left(z\right),$$

(3)

then  $p\left(z\right)$  is called a solution of the differential subordination n (3). Furthermore, a given univalent function $q\left(z\right)$  is called a dominant of the solutions of (3) or, more simply, a dominant if $p\left(z\right)\prec q\left(z\right)$  for all  $p\left(z\right)$  satisfying (3). A dominant $q̌\left(z\right)$  that satisfies  $q̌\left(z\right)\prec q\left(z\right)$ for all dominants  $q\left(z\right)$  of (3) is said to be the best dominant.

Definition 2. 

[1]: Suppose that $\mathfrak{Q}$, the set of all functions $q$, which is analytic and injective on $\overline{\mathcal{U}}\backslash E\left(q\right)$, when$\overline{\mathcal{U}}=\mathcal{U}\cup \left\{z\in \partial \mathcal{U}\right\}$,$E\left(q\right)=\left\{\zeta \in \partial \mathcal{U}:\underset{z\to \zeta }{lim}q\left(z\right)=\infty \right\},$ where $q^{\prime }\left(\zeta \right)\ne 0$ for $\zeta \in \partial \mathcal{U}\backslash E\left(q\right)$. Additionally, let the subclass of $\mathfrak{Q}$ for which $q\left(0\right)=a$ be denoted as$\mathfrak{Q}\left(a\right)$, and$\mathfrak{Q}\left(0\right)={\mathfrak{Q}}_0$, $\mathfrak{Q}\left(1\right)=$ ${\mathfrak{Q}}_1=\left\{q\in \mathfrak{Q}:q\left(0\right)=1\right\}.$

Applications of the subordination methodology are applied to suitable classes of admissible functions. According to Antonino and Miller [1], the following class of admissible functions is defined.

Definition 3. 

[1]: Let $\Omega$ be a set in $\mathbb{C}$, $q\in \mathfrak{Q}$ and $n\in \mathbb{N}\backslash${1} be the set of positive integers. The class ${\psi }_n\left[\Omega ,q\right]$ of admissible functions consists of those functions $\chi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C}$, which satisfy the following admissibility conditions:

$$\chi \left(r,s,t,u:z\right)\notin \Omega ,$$

where

$$r=q\left(\xi \right), s=k\xi q\prime \left(\xi \right), R\left({\displaystyle \frac{t}{s}}+1\right)\geqq kR\left({\displaystyle \frac{\xi q″\left(\xi \right)}{q\prime \left(\xi \right)}}+1\right),$$

and

$$R\left({\displaystyle \frac{u}{s}}\right)\geqq k^{2}R\left({\displaystyle \frac{{\xi }^2{q}^{‴}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right),$$

$$z\in \mathcal{U},\xi \in \partial \mathcal{U}\backslash E\left(q\right) \mathrm{and} k\geqq n.$$

The following lemma is a foundation result in the theory of third-order differential subordination.

Lemma 1. 

[1]: Let $p\in H\left[a,n\right] with n\geqq 2$and$q\in \mathfrak{Q}\left(a\right)$ are satisfying the following conditions:

$$R\left({\displaystyle \frac{\xi q″\left(\xi \right)}{q\prime \left(\xi \right)}}\right)\geqq 0 \mathrm{a}\mathrm{n}\mathrm{d} \left|{\displaystyle \frac{z{p}^{\prime }\left(z\right)}{q^{\prime }\left(\xi \right)}}\right|\leqq k,$$

where $z\in \mathcal{U},\xi \in \partial \mathcal{U}\backslash E\left(q\right)$and$k\geqq n,$ then $p\left(z\right)\prec q\left(z\right), \left(z\in \mathcal{U}\right)$ if $\Omega$ $\subset$, $\chi \in {\psi }_n\left[\Omega ,q\right]$ and $\chi \left(p\left(z\right),z{q}^{\prime }\left(z\right),z^2{q}^{″}\left(z\right),z^3{p}^{‴}\left(z\right);z\right)\in \Omega .$

Novelty of the Study for Third-Order Differential Subordination and Superordination

An essential method within the research of third-order differential subordination involves utilizing a fundamental notion of an admissible function, as presented within [15]. Utilizing that approach, notable outcomes were attained by several authors investigating suitable classes of admissible functions including generalized Bessel functions [8], some operators [7,31], the Srivastava–Attiya operator [27,28], linear operators [25,26], meromorphic functions [14], or Mittag–Leffler functions [26]. The two pairs of hypotheses of third-order differential subordination with superordination are developing well. Very recent outcomes acquired utilizing this approach can be found in papers such as [19,23,24,25,34]. A novel approach for third-order differential subordination has been obtained within modern study taking another essential notion within the theory of differential subordination, which is the best dominant of the differential subordination. From [27,28], approaches to determine the dominant of a third-order differential subordination’s best dominant are also provided. Creating a new operator for the purpose of obtaining new applications about the differential subordination and superordination of the third order is important in medical physics applications such as, brain diseases.

3. Results Related to the Third-Order Differential Subordination

In this context, we present a set of differential subordination outcomes utilizing the new integral operator.

Definition 4. 

Let $\Omega$ be a set in $\mathbb{C}$ and $q\in {\mathfrak{Q}}_0\bigcap H_0.$ The class ${\mathcal{J}}_j\left[\Omega ,q\right]$ of admissible functions consists of those functions $\psi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C},$ which satisfy the following admissibility conditions:

$$\psi \left(\alpha ,\beta ,\gamma ,\nu ; z\right)\notin \Omega ,$$

whenever

$$\alpha =q\left(\xi \right), \beta ={\displaystyle \frac{k+\left(\sigma +n\right)q\left(\xi \right) }{\left(\sigma +n+1\right)}},$$

$$R\left({\displaystyle \frac{{\alpha {\left(\sigma +n\right)}^2+\gamma \alpha {\left(\sigma +n\right)}^2\left(\sigma +n+1\right)}^2-\beta \left(\sigma +n+1\right)\left(2\sigma +2n\right)}{\beta \left(\sigma +n+1\right)-\alpha {\left(\sigma +n\right)}^2}}\right)\geqq kR\left({\displaystyle \frac{\xi q^{″}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}+1\right),$$

and

$$\begin{array}{c}R\left({\displaystyle \frac{\begin{array}{c}{\left(\sigma +n+1\right)}^3\left(\nu -3\gamma \right)-\beta \left(4\left(2\sigma +2n+1\right){\left(\sigma +n+1\right)}^2+\left(\sigma +n+1\right){\left(\sigma +n\right)}^2\right)\\ -\alpha \left(\left(\sigma +n+1\right)\left(\sigma +n+2\right)\left(\sigma +n\right)\right)\end{array} }{\beta \left(\sigma +n+1\right)-\alpha {\left(\sigma +n\right)}^2}}\right)\\ \geqq k^{2}R\left({\displaystyle \frac{{\xi }^2{q}^{‴}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right),\end{array}$$

where $z\in \mathcal{U},\xi \in \partial \mathcal{U}\backslash E\left(q\right) and k\geqq 2.$

Theorem  1. 

Let $\psi \in {\mathcal{J}}_j\left[\Omega ,q\right]$. If the functions $f,g\in K$and$q\in {\mathfrak{Q}}_0$, are satisfying the following conditions:

$$R\left({\displaystyle \frac{\xi q^{″}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right)\geqq 0 , \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{q^{\prime }\left(\xi \right)}}\right|\leqq k$$

(4)

and

$$\left\{\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right):z\in \mathcal{U}\right\}\subset \Omega ,$$

(5)

then

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q\left(z\right), \left(z\in \mathcal{U}\right).$$

Proof  1. 

Define the analytic function $p\left(z\right)$in $\mathcal{U}$ by

$$p\left(z\right)={\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right).$$

(6)

Form Equations (2) and (4), we have

$${\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)={\displaystyle \frac{z{p}^{\prime }\left(z\right)+\left(\sigma +n\right)p\left(z\right) }{\left(\sigma +n+1\right)}}.$$

(7)

By a similar argument, yields

$${\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)={\displaystyle \frac{z^2{p}^{″}\left(z\right)+\left(2\sigma +2n+1\right)z{p}^{\prime }\left(z\right)+({\sigma +n)}^{2}p\left(z\right) }{{\left(\sigma +n+1\right)}^2}},$$

(8)

and

$$\begin{array}{c}{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)={\displaystyle \frac{z^3{p}^{‴}\left(z\right)+3\left(\sigma +n+1\right)z^2{p}^{″}\left(z\right) }{{\left(\sigma +\delta +\lambda \right)}^3}}\\ +{\displaystyle \frac{\left[\left(2\sigma +2n+1\right)\left(\sigma +n+1\right)+({\sigma +n)}^2\right]zp\prime \left(z\right)+({\sigma +n)}^{3}p\left(z\right)}{{\left(\sigma +\delta +\lambda \right)}^3}}. \end{array}$$

(9)

Define the transformation from ${\mathbb{C}}^4 to\mathbb{C}$ by 

$$\alpha \left(r,s,t,u\right)=r, \beta \left(r,s,t,u\right)={\displaystyle \frac{s+\left(\sigma +n\right)r }{\left(\sigma +n+1\right)}},$$

$$\gamma \left(r,s,t,u\right)={\displaystyle \frac{t+\left(2\sigma +2n+1\right)s+({\sigma +n)}^{2}r }{{\left(\sigma +n+1\right)}^2}},$$

and

$$\nu \left(r,s,t,u\right)={\displaystyle \frac{u+3\left(\sigma +n+1\right)t }{{\left(\sigma +\delta +\lambda \right)}^3}}+{\displaystyle \frac{\left[\left(2\sigma +2n+1\right)\left(\sigma +n+1\right)+({\sigma +n)}^2\right]s+({\sigma +n)}^{3}r}{{\left(\sigma +\delta +\lambda \right)}^3}}.$$

Let

$$\begin{array}{l}\Pi \left(r,s,t,u\right)=\psi \left(\alpha ,\beta ,\gamma ,\nu ; z\right)\\ =\psi \left(r,{\displaystyle \frac{s+\left(\sigma +n\right)r }{\left(\sigma +n+1\right)}},{\displaystyle \frac{t+\left(2\sigma +2n+1\right)s+({\sigma +n)}^{2}r }{{\left(\sigma +n+1\right)}^2}} ,{\displaystyle \frac{u+3\left(\sigma +n+1\right)t }{{\left(\sigma +\delta +\lambda \right)}^3}}+{\displaystyle \frac{\left[\left(2\sigma +2n+1\right)\left(\sigma +n+1\right)+({\sigma +n)}^2\right]s+({\sigma +n)}^{3}r}{{\left(\sigma +\delta +\lambda \right)}^3}}\right). \end{array}$$

(10)

The proof will utilize the Lemma 1. Applying (6)–(9) and by (10), we acquire

$$\Pi \left(p\left(z\right),z{q}^{\prime }\left(z\right),z^2{q}^{″}\left(z\right),z^3{q}^{‴}\left(z\right);z\right)=\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3} \left(f\ast g\right)\left(z\right);z\right).$$

Hence,  $\left(5\right)$  leads to

$$\Pi \left(p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right),z^3{p}^{‴}\left(z\right);z\right)\in \Omega .$$

We observed that

$${\displaystyle \frac{t}{s}}+1={\displaystyle \frac{{\gamma \left(\sigma +n+1\right)}^2-\beta \left(\sigma +n+1\right)\left(2\sigma +2n\right)+\alpha {\left(\sigma +n\right)}^2}{\beta \left(\sigma +n+1\right)-\alpha {\left(\sigma +n\right)}^2}},$$

and

$${\displaystyle \frac{u}{s}}={\displaystyle \frac{ \begin{array}{c}{\left(\sigma +n+1\right)}^3\left(\nu -3\gamma \right)-\beta \left(4\left(2\sigma +2n+1\right){\left(\sigma +n+1\right)}^2+\left(\sigma +n+1\right){\left(\sigma +n\right)}^2\right)\\ -\alpha (\left(\sigma +n+1\right)\left(\sigma +n+2\right)\left(\sigma +n\right)\end{array} }{\beta \left(\sigma +n+1\right)-\alpha {\left(\sigma +n\right)}^2}}.$$

Thus, the admissibility conditions for $\psi \in {\mathcal{J}}_j\left[\Omega ,q\right]$ in Definition 4 is equivalent to admissibility condition $\Pi \in {\psi }_2\left[\Omega ,q\right]$ as given in Definition 3 with $n=2.$

Therefore, using (4) and Lemma 1, we have

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q\left(z\right).$$

This completes the proof. □

The subsequent outcome is a continuation of Theorem 1, for the situation when the conduct of $q\left(z\right)$ on $\partial \mathcal{U}$ is unknown.

Corollary  1. 

Let $\Omega \subset \mathbb{C}$ and $q\in$ $\mathcal{U} with q\left(0\right)=1.$ Let $\psi \in {\mathcal{J}}_j\left[\Omega ,q_{\rho }\right] for some \rho \in \left(\mathrm{0,1}\right),$ where $q_{\rho }\left(z\right)=q\left(\rho z\right).$ If the functions $f,g\in K$ with $q_{\rho }$ satisfy the following conditions:

$$R\left({\displaystyle \frac{\xi q_{\rho }^{″\left(\xi \right)}}{q_{\rho }\prime \left(\xi \right)}}\right)\geqq 0 , \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{{q_{\rho }}^{\prime }\left(\xi \right)}}\right|\leqq k,\left(z\in \mathcal{U};k\geqq 2;\xi \in \partial \mathcal{U}\backslash E\left(q_{\rho }\right)\right),$$

 and

$$\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right)\in \Omega ,$$

then

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q\left(z\right), \left(z\in \mathcal{U}\right).$$

Proof  2. 

Applying Theorem 1, to get

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q_{\rho }\left(z\right), \left(z\in \mathcal{U}\right).$$

The result asserted by Corollary 1 is now deduced from the following subordination property

$$q_{\rho }\left(z\right)\prec q\left(z\right) \left(z\in \mathcal{U}\right).$$

This completes the proof □

If $\Omega \ne \mathbb{C},$ is a simply connected domain, the $\Omega =h\left(\mathcal{U}\right)$for some conformal mapping $h\left(z\right) of \mathcal{U}$ on to $\Omega .$ In this case the class ${\mathcal{J}}_j\left[h\left(\mathcal{U}\right) ,q\right]$is written as ${\mathcal{J}}_j\left[h ,q\right]$. This leads to the following immediate consequence of Theorem 1.

Theorem  2. 

Let $\psi \in {\mathcal{J}}_j\left[h,q\right].$  If the functions   $f,g\in K and q\in {\mathfrak{Q}}_0,$ satisfying the following conditions:

$$R\left({\displaystyle \frac{\xi q^{\prime \prime \left(\xi \right)}}{q^{\prime \left(\xi \right)}}}\right)\geqq 0 , \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{q^{\prime }\left(\xi \right)}}\right|\leqq k$$

(11)

and

$$\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right)\prec h\left(z\right),$$

(12)

then

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q\left(z\right), \left(z\in \mathcal{U}\right).$$

The subsequent result is a direct consequence of Corollary 2.

Corollary  2. 

Let $\Omega \subset \mathbb{C}$ and let the function $q$ be univalent within $\mathcal{U} with q\left(0\right)=1.$Assume $\psi \in {\mathcal{J}}_j\left[\Omega ,q_{\rho }\right]$for some$\rho \in \left(\mathrm{0,1}\right),$ where $q_{\rho }\left(z\right)=q\left(\rho z\right).$ If the functions $f,g\in K$ and $q_{\rho }$ satisfiing the following conditions:

$$R\left({\displaystyle \frac{\xi q_{\rho }^{″\left(\xi \right)}}{q_{\rho }\prime \left(\xi \right)}}\right)\geqq 0 , \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{{q_{\rho }}^{\prime }\left(\xi \right)}}\right|\leqq k,\left(z\in \mathcal{U};k\geqq 2;\xi \in \partial \mathcal{U}\backslash E\left(q_{\rho }\right)\right)$$

and

$$\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right)\prec h\left(z\right),$$

then

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec \left(f\ast g\right)\left(z\right), \left(z\in \mathcal{U}\right).$$

The following result yields the best dominant of differential subordination (12).

Theorem  3. 

Suppose that $h$ be univalent function within $\mathcal{U}.$ Also, assume that$\psi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C}$ such that $\Pi$ is given in (10). Consider that subsequent differential equation

$$\Pi \left(q\left(z\right),z{q}^{\prime }\left(z\right),z^2{q}^{″}\left(z\right),z^3{q}^{‴}\left(z\right);z\right)=h\left(z\right),$$

Possesses a solution  $q\left(z\right)$  such that  $q\left(0\right)=1$, which fulfils condition (4). When $f\in K$ meets the criterion (12), and $\psi \left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right)$, is analytic within $\mathcal{U}$, thus

$${\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\prec q\left(z\right), \left(z\in \mathcal{U}\right)$$

with$q\left(z\right)$is the best dominant.

Proof  3. 

According to Theorem 1, it is evident that $q$ is a dominant of (12). Given that $q$ satisfies (11), it consequently serves as a solution to (12). Consequently, $q$ will be overshadowed by all dominant entities. Therefore, $q$ is the optimal dominant. This concludes the proof. □

In view of Definition 4, a special case when $q\left(z\right)=Mz \left(M>0\right),$ the class ${\mathcal{J}}_j\left[\Omega ,q\right],$ of admissible functions, denoted by ${\mathcal{J}}_j\left[\Omega ,M\right]$ is expressed as follows.

Definition  5. 

Let $\Omega$ $\subset$ $\mathbb{C}$ and $M>0.$ The class ${\mathcal{J}}_j\left[\Omega ,M\right]$ of admissible functions consists of those functions $\psi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C},$ such that 

$$\begin{array}{l}\psi (M{e}^{i\theta },\left[{\displaystyle \frac{k+\left(\sigma +n\right)r }{\left(\sigma +n+1\right)}}\right]M{e}^{i\theta }, {\displaystyle \frac{L+\left(2\sigma +2n+1\right)k+({\sigma +n)}^{2}M{e}^{i\theta } }{{\left(\sigma +n+1\right)}^2}}, {\displaystyle \frac{N+3\left(\sigma +n+1\right)L }{{\left(\sigma +\delta +\lambda \right)}^3}}\\ +{\displaystyle \frac{\left[\left(2\sigma +2n+1\right)\left(\sigma +n+1\right)+({\sigma +n)}^2\right]k+({\sigma +n)}^{3}M{e}^{i\theta }}{{\left(\sigma +\delta +\lambda \right)}^3}} )\notin \Omega ,\end{array}$$

 where  $z\in \mathcal{U},$

$$R\left(L{e}^{-i\theta }\right)\geqq \left(k-1\right)kM,$$

and

$$R\left(N{e}^{-i\theta }\right)\geqq 0, \forall \theta \in \mathbb{R};k\geqq 2.$$

Corollary  3. 

Assume $\psi$ belongs to ${\mathcal{J}}_j\left[\Omega ,M\right]$ . If the functions $f$ and $g$ belong to $K$ and satisfy the following requirements:

$$\left|{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)\right|\leqq kM, \left(z\in \mathcal{U};k\geqq 2; M>0\right)$$

and

$$\left({\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right)\in \Omega ,$$

then

$$\left|{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\right|<M.$$

When  $\Omega =q\left(\mathcal{U}\right)=\left\{\omega :\left|\omega \right|<M\right\},$  the class  ${\mathcal{J}}_j\left[\Omega ,M\right]$  is simple denoted by  ${\mathcal{J}}_j\left[M\right].$  Corollary 3 can now be rewritten as follows.

Corollary  4. 

Let $\psi \in {\mathcal{J}}_j\left[M\right].$ If the functions $f,g\in K$ satisfies the following conditions:

$$\left|{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)\right|\leqq kM, \left(z\in \mathcal{U};k\geqq 2; M>0\right)$$

and

$$\left|{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right), {\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right);z\right|<M,$$

then

$$\left|{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\right|<M.$$

Definition  6. 

Let $\Omega$ $\subset \mathbb{C} and q\in {\mathfrak{Q}}_1\bigcap H_1.$ The class ${\mathcal{J}}_{j,1}\left[\Omega ,q\right]$ of admissible functions consists of those functions $\psi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C},that$satisfying the following admissibility conditions:

$$\psi \left(\alpha ,\beta ,\gamma ,\nu ;z\right)\notin \Omega ,$$

whenever

$$\alpha =q\left(\xi \right), \beta ={\displaystyle \frac{k+\left(\sigma +n+1\right)q\left(\xi \right)}{\left(\sigma +n+1\right)}},$$

$$R\left({\displaystyle \frac{{\left(\sigma +n+1\right)}^2\left(\gamma -\alpha \right)-2\left(\sigma +n+1\right)\beta +2\alpha \left(\sigma +n+1\right)}{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}}\right)\geqq kR\left({\displaystyle \frac{\xi q^{″}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}+1\right),$$

and

$$\begin{array}{l}R({\displaystyle \frac{{\left(\sigma +n+1\right)}^3\nu -\left(3\sigma +3n+6\right){\left(\sigma +n+1\right)}^2\left(\gamma -\alpha \right)-{\left(\sigma +n+1\right)}^3\alpha }{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}}\\ -{\displaystyle \frac{\left(3\sigma +3n+2\right)\left(3\sigma +3n+6\right)\left(\sigma +n+1\right)+2{\left(\sigma +n+1\right)}^2+\left(\sigma +n+1\right)(\sigma +n)\left(\beta -\alpha \right)}{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}})\\ \geqq k^{2}R\left({\displaystyle \frac{{\xi }^2{q}^{‴}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right),\end{array}$$

where $z\in \mathcal{U},\xi \in \partial \mathcal{U}\backslash E\left(q\right) and k\geqq n.$

Theorem  4. 

Let$\psi \in {\mathcal{J}}_{j,1}\left[\Omega ,q\right].$ If the functions $f,g\in K and q\in {\mathfrak{Q}}_1,$ are satisfying the following conditions:

$$R\left({\displaystyle \frac{\xi q^{″}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right)\geqq 0, \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z{q}^{\prime }\left(\xi \right)}}\right|\leqq k$$

(13)

and

$$\left\{\psi \left({\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}};z\right); z\in \mathcal{U}\right\}\subset \Omega ,$$

(14)

then

$${\displaystyle \frac{{ \mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}\prec q\left(z\right) \left(z\in \mathcal{U}\right).$$

Proof  4. 

Define the analytic function $p\left(z\right) in \mathcal{U},$ by

$$p\left(z\right)={\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}.$$

(15)

From Equations (2) and (15), we have

$${\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}={\displaystyle \frac{z{p}^{\prime \left(z\right)}+\left(\sigma +n+1\right)p\left(z\right)}{\left(\sigma +n+1\right)}}.$$

(16)

By similar argument, we get

$${\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}={\displaystyle \frac{z^2{p}^{″\left(z\right)}}{{\left(\sigma +n+1\right)}^2}}+{\displaystyle \frac{\left(2\sigma +2n+1\right)z{p}^{\prime \left(z\right)}+{\left(\sigma +n+1\right)}^{2}p\left(z\right)}{{\left(\sigma +n+1\right)}^2}},$$

(17)

and

$${\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}}={\displaystyle \frac{z^3{p}^{‴}\left(z\right)+\left[3\sigma +3n+6\right]z^2{p}^{″}\left(z\right)}{{\left(\sigma +n+1\right)}^3}}+{\displaystyle \frac{\left[\left(2\sigma +2n+3\right){(2\left(\sigma +n+1\right)}^2+(\sigma +n))\right]z{p}^{\prime }\left(z\right)}{{\left(\sigma +n+1\right)}^3}}+{\displaystyle \frac{{\left(\sigma +n+1\right)}^{3}p\left(z\right)}{{\left(\sigma +n+1\right)}^3}}.$$

(18)

Define the transformation from ${\mathbb{C}}^4 to \mathbb{C}$  by

$$\alpha \left(r,s,t,u\right)=r, \beta \left(r,s,t,u\right)={\displaystyle \frac{s+\left(\sigma +n+1\right)r}{\left(\sigma +n+1\right)}},$$

$$\gamma \left(r,s,t,u\right)={\displaystyle \frac{t+\left(2\sigma ++2n+3\right)s+{\left(\sigma +n+1\right)}^{2}r}{{\left(\sigma +n+1\right)}^2}}$$

and

$$\nu \left(r,s,t,u\right)={\displaystyle \frac{u+\left[3\sigma +3n+6\right]t}{{\left(\sigma +n+1\right)}^3}}+{\displaystyle \frac{\left[\left(2\sigma +2n+3\right){(2\left(\sigma +n+1\right)}^2+(\sigma +n))\right]s}{{\left(\sigma +n+1\right)}^3}}+r.$$

(19)

Let

$$\begin{array}{c}\Pi \left(r,s,t,u\right)=\psi \left(\alpha ,\beta ,\gamma ,\nu ;z\right)\\ =\psi (r,{\displaystyle \frac{s+\left(\sigma +n+1\right)r}{\left(\sigma +n+1\right)}}, {\displaystyle \frac{t+\left(2\sigma ++2n+3\right)s+{\left(\sigma +n+1\right)}^{2}r}{{\left(\sigma +n+1\right)}^2}}, {\displaystyle \frac{u+\left[3\sigma +3n+6\right]t}{{\left(\sigma +n+1\right)}^3}}\\ +{\displaystyle \frac{\left[\left(2\sigma +2n+3\right){(2\left(\sigma +n+1\right)}^2+(\sigma +n))\right]s}{{\left(\sigma +n+1\right)}^3}}+r ).\end{array}$$

(20)

Using Lemma 1 with the Equations (15)–(18) and (20), we have

$$\begin{array}{l}\Pi \left(p\left(z\right),z{p}^{\prime }\left(z\right),z^2{p}^{″}\left(z\right),z^3{p}^{‴}\left(z\right);z\right)\\ =\psi \left({\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}};z \right).\end{array}$$

Hence, clearly (14) becomes

$$\Pi \left(p\left(z\right),z{p}^{\prime \left(z\right)},z^2{p}^{″\left(z\right)},z^3{p}^{‴}\left(z\right);z\right)\in \Omega .$$

We observed that

$${\displaystyle \frac{t}{s}}+1={\displaystyle \frac{{\left(\sigma +n+1\right)}^2\left(\gamma -\alpha \right)-2\left(\sigma +n+1\right)\left(\beta -\alpha \right)}{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}},$$

and

$$\begin{array}{c}{\displaystyle \frac{u}{s}}={\displaystyle \frac{{\left(\sigma +n+1\right)}^3\left(\nu -\alpha \right)-\left(3\sigma +3n+6\right){\left(\sigma +n+1\right)}^2\left(\gamma -\alpha \right)}{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}}-\\ {\displaystyle \frac{\left(3\sigma +3n+2\right)(\left(3\sigma +3n+6\right)\left(\sigma +n+1\right)+2{\left(\sigma +n+1\right)}^2+\left(\sigma +n+1\right)(\sigma +n)\left(\beta -\alpha \right)}{\left(\sigma +n+1\right)\left(\beta -\alpha \right)}}.\end{array}$$

Therefore, the admissibility criterion for $\varphi \in {\mathcal{J}}_{j,1}\left[\Omega ,q\right]$ in Definition 6 is similar to the admissibility criterion for $\Pi \in {\psi }_2\left[\Omega ,q\right]$, as specified in Definition 3 with  $n=2$.

Consequently, employing (13) and Lemma 1, we obtain

$${\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}\prec q\left(z\right).\square$$

If $\mathsf{\Omega }\ne \mathbb{C},$ is a simply connected domain, the $\mathsf{\Omega }=\mathrm{h}\left(\mathcal{U}\right)$ for some conformal mapping $\mathrm{h}\left(\mathrm{z}\right) \mathrm{o}\mathrm{f} \mathcal{U}$ onto $\mathsf{\Omega }.$ In this case, the class ${\mathcal{J}}_{\mathrm{j},1}\left[\mathrm{h}\left(\mathcal{U}\right),\mathrm{q}\right]$ is written as ${\mathcal{J}}_{\mathrm{j},1}\left[\mathrm{h},\mathrm{q}\right],$ which leads to the following immediate consequence of Theorem 4.

Theorem  5. 

Let $\psi \in {\mathcal{J}}_{j,1}\left[\Omega ,q\right].$If $f,g\in K$and$q\in {\mathfrak{Q}}_1,$ satisfy the following conditions:

$$R\left({\displaystyle \frac{\xi q^{″}\left(\xi \right)}{q^{\prime }\left(\xi \right)}}\right)\geqq 0, \left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z{q}^{\prime }\left(\xi \right)}}\right|\leqq k$$

 and

$$\psi \left({\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}};z\right)\prec h\left(z\right),$$

then

$${\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}\prec q\left(z\right) \left(z\in \mathcal{U}\right).$$

In view of Definition 6, and in special case when  $q\left(z\right)=Mz, \left(M>0\right),$  the class  ${\mathcal{J}}_{j,1}\left[\Omega ,q\right],$  of admissible functions, denoted by  ${\mathcal{J}}_{j,1}\left[\Omega ,M\right]$  is expressed follows.

Definition  7. 

Let $\Omega$ be set in $\mathbb{C}$ and$M>0.$ The class ${\mathcal{J}}_{j,1}\left[\Omega ,M\right]$ of admissible functions consists of those functions  $\psi :{\mathbb{C}}^4\times \mathcal{U}\to \mathbb{C},$ such that

$$\begin{array}{c}\psi (M{e}^{i\theta },{\displaystyle \frac{K+\left(\sigma +n+1\right)M{e}^{i\theta }}{\left(\sigma +n+1\right)}}, {\displaystyle \frac{L+\left(2\sigma ++2n+3\right)K+{\left(\sigma +n+1\right)}^{2}M{e}^{i\theta }}{{\left(\sigma +n+1\right)}^2}}, {\displaystyle \frac{N+\left[3\sigma +3n+6\right]L}{{\left(\sigma +n+1\right)}^3}}\\ +{\displaystyle \frac{\left[\left(2\sigma +2n+3\right){(2\left(\sigma +n+1\right)}^2+(\sigma +n))\right]K+{\left(\sigma +n+1\right)}^{3}M{e}^{i\theta }}{{\left(\sigma +n+1\right)}^3}} ;z )\notin \Omega ,\end{array}$$

whenever, $z\in \mathcal{U},$ $R\left(L{e}^{-i\theta }\right)\geqq \left(K-1\right)KM$ and $R\left(N{e}^{-i\theta }\right)\geqq 0, \forall \theta \in \mathbb{R};k\geqq 0.$

Corollary  5. 

Let $\psi \in {\mathcal{J}}_{j,1}\left[\Omega ,M\right].$ If the functions $f,g\in K$ are satisfied the following conditions 

$$\left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}\right|\leqq kM, \left(z\in \mathcal{U};k\geqq 2; M>0\right)$$

 and

$$\psi \left({\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}};z\right)\in \Omega ,$$

then

$$\left|{\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}\right|<M.$$

When  $\Omega =q\left(\mathcal{U}\right)=\left\{\omega :\left|\omega \right|<M\right\},$  the class  ${\mathcal{J}}_{j,1}\left[\Omega ,M\right]$  is simple and denoted by  ${\mathcal{J}}_{j,1}\left[M\right].$  Corollary 6 can now be rewritten in the following from.

Corollary  6. 

Let $\psi \in {\mathcal{J}}_{j,1}\left[\Omega ,M\right].$ If the functions $f,g\in K$ are satisfied the following conditions

$$\left|{\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}\right|\leqq kM, \left(z\in \mathcal{U};k\geqq 2; M>0\right)$$

and

$$\left|\psi \left({\displaystyle \frac{{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+1}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+2}\left(f\ast g\right)\left(z\right)}{z}}, {\displaystyle \frac{{\mu }_{\sigma ,n}^{m+3}\left(f\ast g\right)\left(z\right)}{z}};z\right)\right|<M$$

then

$$\left|{\mu }_{\sigma ,n}^m\left(f\ast g\right)\left(z\right)\right|<M.$$

4. Conclusions

In this paper, we have established new results on third-order differential subordination for analytic functions within the open unit disk, utilizing the newly introduced integral operator ${\mathsf{\mu }}_{\mathsf{\alpha },\mathrm{n}}^{\mathrm{m}}(\mathrm{f}\ast \mathrm{g})$. Through the examination of admissible function classes, we derived significant findings that enhance the understanding of differential subordination. Additionally, specific cases were highlighted to demonstrate the applicability of the results. The introduced operator and its associated properties open up further avenues for research in the field of differential subordination, providing valuable insights for future studies. In the future, fractional operators or those with probabilistic parameters (see [20,21,35]) can be used to expand the scope of these results and explore new applications.

5. Discussion

Our research enhances the comprehensive understanding of univalent functions, their subclasses, and their prospective applications across several mathematical domains, such as concepts the differential subordination and superordination using new operators. The data acquired may provide a basis for subsequent research into the characteristics and uses of univalent functions and their subclasses. Future research endeavors may investigate more improvements of the boundaries and analyze other subclasses of univalent functions to reveal new insights into their properties and potential applications defined by fractional operators, or those with probabilistic parameters can be used to expand the scope of these results and explore new applications. This study facilitates a more profound investigation of the intriguing domain of bi-univalent functions and their significance in mathematics.