Plane Partitions and Divisors

Abstract

In this paper, we consider the sum of divisors d of n such that $n/d$ is a power of 2 and derive a new decomposition for the number of plane partitions of n in terms of binomial coefficients as a sum over partitions of n. In this context, we introduce a new combinatorial interpretation of the number of plane partitions of n.

1. Introduction

Recall that a plane partition $\pi$ of the positive integer n is a two-dimensional array $\pi ={\left({\pi }_{i,j}\right)}_{i,j⩾1}$ of non-negative integers ${\pi }_{i,j}$ such that

$$n=\sum _{i,j⩾1}{\pi }_{i,j},$$

which is weakly decreasing in rows and columns:

$${\pi }_{i,j}⩾{\pi }_{i+1,j},{\pi }_{i,j}⩾{\pi }_{i,j+1},\mathrm{for}\mathrm{all}i,j⩾1.$$

If we ignore the entries equal to zero in a plane partition, it can be considered as the filling of a Young diagram with positive integers with entries weakly decreasing in rows and columns and such that the sum of all entries is equal to n. On the other hand, there is a desirable way to represent a plane partition as a three-dimensional object: this is achieved by replacing each part of size k of the plane partition by a stack of k unit cubes (Figure 1). This is a natural generalization of the concept of classical partitions [1]. Different configurations are counted as different plane partitions. As usual, we denote by $PL\left(n\right)$ the number of plane partitions of n. For convenience, we define $PL\left(0\right)=1$.

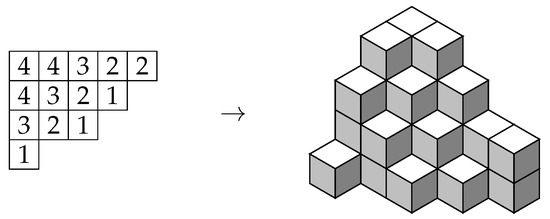
Figure 1. Representation of a plane partition of 32.

Plane partitions were introduced by MacMahon [2] who proved the following highly non-trivial result:

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }PL\left(n\right)q^n=\prod _{n=1}^{\infty }\frac{1}{{(1-q^n)}^n},\left|q\right|<1.\end{array}$$

(1)

The expansion starts as

$$\begin{array}{c}\hfill \prod _{n=1}^{\infty }\frac{1}{{(1-q^n)}^n}=1+q+3q^2+6q^3+13q^4+24q^5+48q^6+86q^7+\cdots .\end{array}$$

(2)

An n-color partition of a positive integer m is a partition in which a part of size n can come in n different colors denoted by subscripts: $n_1,n_2,\dots ,n_n$. The parts satisfy the following order:

$$\begin{array}{c}\hfill 1_1<2_1<2_2<3_1<3_2<3_3<4_1<4_2<4_3<4_4<\dots \end{array}$$

They were introduced by A. K. Agarwal and G. E. Andrews [3] nearly a century after MacMahon introduced pane partitions. For example, there are thirteen n-color partitions of 4:

$$\begin{array}{cc}\hfill & \left(4_4\right),\left(4_3\right),\left(4_2\right),\left(4_1\right),(3_3,1_1),(3_2,1_1),(3_1,1_1),(2_2,2_2)\hfill \\ \hfill & (2_2,2_1),(2_1,2_1),(2_2,1_1,1_1),(2_1,1_1,1_1),(1_1,1_1,1_1,1_1).\hfill \end{array}$$

It was pointed out in [3] that the right-hand side of (1) is also a generating function for the number of n-color partitions. Thus, the following statement holds.

Theorem 1.

The number of plane partitions of m equals the number of n-color partitions of m.

We also note that the set of plane partitions with strict decrease along columns (of the Young diagram) is in one-to-one correspondence with the set of symmetric matrices with non-negative integer entries ([1], Corollary 11.6). Moreover, by the Knuth–Schensted correspondence ([1], Theorem 11.4), in the set of pairs of plane partitions $(\pi ,{\pi }^{\prime })$ in which there is strict decrease along columns, each entry is at most k, and the corresponding rows of $\pi$ and ${\pi }^{\prime }s$ are of the same length are in bijection with the set of $k\times k$ matrices with non-negative integer entries.

There is a well-known connection between plane partitions and divisors. In [4], it is shown that

$$\begin{array}{c}\hfill nPL\left(n\right)=\sum _{k=1}^{n}PL(n-k){\sigma }_2\left(k\right),\end{array}$$

where ${\sigma }_2\left(n\right)$ is the sum of squares of divisors of n, i.e.,

$${\sigma }_2\left(n\right)=\sum _{d|n}{d}^2.$$

In this article, we consider a restricted sum of divisors function and find connections with the sequence $PL\left(n\right)$.

For a positive integer n, we denote by $s_n$ the sum of divisors d of n such that $n/d$ is a power of 2. For example, the divisors of 12 are

$$1,2,3,4,6,12.$$

Since

$$12/3=2^2,12/6=2^1\mathrm{and}12/12=2^0,$$

we have

$$s_{12}=3+6+12=21.$$

We remark that the sequence

$${\left(s_n\right)}_{n⩾1}=(1,3,3,7,5,9,7,15,9,15,11,21,13,21,15,31,17,27,\dots )$$

is known and can be found in the On-Line Encyclopedia of Integer Sequence ([5], A129527). The generating function for $s_n$ is given on the page for A129527. It can be derived as follows:

$$\begin{array}{cc}\hfill \sum _{n=1}^{\infty }{s}_n{q}^n& =\sum _{n=1}^{\infty }{q}^n\sum _{\begin{array}{c}d|n\\ {log}_2(n/d)\in {\mathbb{N}}_0\end{array}}d=\sum _{d=1}^{\infty }d\sum _{n=0}^{\infty }{q}^{2^{n}d}\hfill \\ & =\sum _{n=0}^{\infty }\sum _{d=1}^{\infty }d{q}^{2^{n}d}=\sum _{n=0}^{\infty }\frac{q^{2^n}}{{(1-q^{2^n})}^2},\hfill \end{array}$$

where we have used the identity

$$\sum _{d=1}^{\infty }d{q}^d=\frac{q}{{(1-q)}^2},\left|q\right|<1.$$

with q replaced by $q^{2^n}$. On the other hand, it is not difficult to prove that

$$s_n=\left\{\begin{array}{cc}n,\hfill & \mathrm{for}n\mathrm{odd},\hfill \\ n+s_{n/2},\hfill & \mathrm{for}n\mathrm{even}.\hfill \end{array}\right.$$

(3)

Logarithmic differentiation of the generating Function (1) gives the following identity:

$$\begin{array}{cc}\hfill \frac{\partial }{\partial q}ln\left(\sum _{n=0}^{\infty }PL\left(n\right)q^n\right)& =\frac{\partial }{\partial q}ln\prod _{n=1}^{\infty }\frac{1}{{(1-q^n)}^n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{\partial }{\partial q}ln\frac{1}{{(1-q^n)}^n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{n^2{q}^{n-1}}{1-q^n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }{\sigma }_2\left(n\right)q^{n-1},\left|q\right|<1.\hfill \end{array}$$

(4)

In Section 3, we show that

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }PL\left(n\right)q^n=\prod _{n=1}^{\infty }{(1+q^n)}^{s_n},\left|q\right|<1.\end{array}$$

(5)

Then, logarithmic differentiation of the generating function (5) gives

$$\begin{array}{cc}\hfill \frac{\partial }{\partial q}ln\left(\sum _{n=0}^{\infty }PL\left(n\right)q^n\right)& =\frac{\partial }{\partial q}ln\prod _{n=1}^{\infty }{(1+q^n)}^{s_n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{\partial }{\partial q}ln{(1+q^n)}^{s_n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{n{s}_n{q}^{n-1}}{1+q^n}\hfill \\ \hfill & =\sum _{n=1}^{\infty }\left(\sum _{d|n}{(-1)}^{1+n/d}d{s}_d\right)q^{n-1},\left|q\right|<1.\hfill \end{array}$$

(6)

Equating the coefficients of $q^{n-1}$ in the Equations (4) and (6), we obtain the following identity:

Theorem 2.

For $n⩾1$,

$${\sigma }_2\left(n\right)=\sum _{d|n}{(-1)}^{1+n/d}d{s}_d.$$

On the other hand, by (4) and (6), we see that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }\frac{n^2{q}^n}{1-q^n}=\sum _{n=1}^{\infty }\frac{n{s}_n{q}^n}{1+q^n}=\sum _{n=1}^{\infty }\frac{n{s}_n{q}^n}{1-q^n}-2\sum _{n=1}^{\infty }\frac{n{s}_n{q}^{2n}}{1-q^{2n}},\left|q\right|<1.\end{array}$$

Therefore, we deduce the relation

$$n=\left\{\begin{array}{cc}{s}_n,\hfill & \mathrm{for}n\mathrm{odd},\hfill \\ s_n-s_{n/2},\hfill & \mathrm{for}n\mathrm{even},\hfill \end{array}\right.$$

which implies identity (3).

From (3), we see that Theorem 2 is trivial when n is odd. However, for n even, this theorem provides an interesting decomposition of ${\sigma }_2\left(n\right)$. For example,

$${\sigma }_2\left(6\right)=1^2+2^2+3^2+6^2=50.$$

The case $n=6$ of Theorem 2 reads as follows:

$${\sigma }_2\left(6\right)=-1\times 1+2\times 3-3\times 3+6\times 9=50.$$

For any positive integer m, we denote by $P{L}^{\left(m\right)}\left(n\right)$ the number of m-tuples of plane partitions of non-negative integers $n_1,n_2,\dots ,n_m$ where $n_1+n_2+\cdots +n_m=n$. Clearly, $PL\left(n\right)=P{L}^{\left(1\right)}\left(n\right)$ and

$$P{L}^{\left(m\right)}\left(n\right)=\sum _{n_1+n_2+\cdots +n_m=n}PL\left(n_1\right)PL\left(n_2\right)\cdots PL\left(n_m\right).$$

For $r\in \{-1,0,1\}$, we define the numbers $P{L}^{(m,r)}\left(n\right)$ as follows:

$$\begin{array}{c}\hfill P{L}^{(m,r)}\left(n\right)=\left\{\begin{array}{cc}P{L}^{\left(m\right)}\left(n\right),\hfill & \mathrm{for}r=0,\hfill \\ P{L}^{\left(m\right)}\left(n\right)-P{L}^{\left(m\right)}(n-1),\hfill & \mathrm{for}r=-1,\hfill \\ \sum _{k=0}^{n}P{L}^{\left(m\right)}\left(k\right),\hfill & \mathrm{for}r=1.\hfill \end{array}\right.\end{array}$$

(7)

Recently, Merca and Radu [6] considered specializations of complete homogeneous symmetric functions and provided the following formula for $P{L}^{(m,r)}\left(n\right)$.

Theorem 3.

For $m⩾1$, $r\in \{-1,0,1\}$ and $n⩾0$,

$$\begin{array}{c}\hfill P{L}^{(m,r)}\left(n\right)=\sum _{t_1+2t_2+\cdots +n{t}_n=n}\left(\genfrac{}{}{0pt}{}{m-1+r+t_1}{t_1}\right)\prod _{j=2}^n\left(\genfrac{}{}{0pt}{}{jm-1+t_j}{t_j}\right).\end{array}$$

This formula provides a decomposition of $P{L}^{(m,r)}\left(n\right)$ as a sum over all the partitions of n in terms of binomial coefficients involving the multiplicities of the parts.

In this paper, we provide a new decomposition of $P{L}^{(m,r)}\left(n\right)$ as a sum over partitions of n in terms of binomial coefficients. This time, in addition to the multiplicities of part sizes, we also need the sequence $s_n$.

Theorem 4.

For $m⩾1$, $r\in \{-1,0,1\}$ and $n⩾0$,

$$\begin{array}{c}\hfill P{L}^{(m,r)}\left(n\right)=\sum _{t_1+2t_2+\cdots +n{t}_n=n}\prod _{j=1}^n\left(\genfrac{}{}{0pt}{}{S_j^{(m,r)}}{t_j}\right),\end{array}$$

where

$$S_n^{(m,r)}=\left\{\begin{array}{cc}m·s_n+r,\hfill & \mathrm{if}n=2^k,k\in {\mathbb{N}}_0,\hfill \\ m·s_n,\hfill & \mathit{otherwise}.\hfill \end{array}\right.$$

The case $m=1$ and $r=0$ of Theorem 4 reads as follows.

Corollary 1.

For $n⩾0$,

$$\begin{array}{c}\hfill PL\left(n\right)=\sum _{t_1+2t_2+\cdots +n{t}_n=n}\left(\genfrac{}{}{0pt}{}{s_1}{t_1}\right)\left(\genfrac{}{}{0pt}{}{s_2}{t_2}\right)\cdots \left(\genfrac{}{}{0pt}{}{s_n}{t_n}\right).\end{array}$$

While the sum above is over all partitions of n, not all terms are non-zero. Due to the fact that $\left(\genfrac{}{}{0pt}{}{s_j}{t_j}\right)=0$ when $t_j>s_j$, in this sum it suffices to consider the partitions of n in which, for each $j\in \{1,2,\dots ,n\}$, part j occurs at most $s_j$ times. For example, the partitions of four with this restriction can be rewritten as

$$\begin{array}{cc}\hfill & 1\times 0+2\times 0+3\times 0+4\times 1,\hfill \\ \hfill & 1\times 1+2\times 0+3\times 1+4\times 0,\hfill \\ \hfill & 1\times 0+2\times 2+3\times 0+4\times 0.\hfill \end{array}$$

(8)

Therefore, the case $n=4$ of Corollary 1 reads as follows:

$$\begin{array}{cc}\hfill PL\left(4\right)& =\left(\genfrac{}{}{0pt}{}{1}{0}\right)\left(\genfrac{}{}{0pt}{}{3}{0}\right)\left(\genfrac{}{}{0pt}{}{3}{0}\right)\left(\genfrac{}{}{0pt}{}{7}{1}\right)+\left(\genfrac{}{}{0pt}{}{1}{1}\right)\left(\genfrac{}{}{0pt}{}{3}{0}\right)\left(\genfrac{}{}{0pt}{}{3}{1}\right)\left(\genfrac{}{}{0pt}{}{7}{0}\right)+\left(\genfrac{}{}{0pt}{}{1}{0}\right)\left(\genfrac{}{}{0pt}{}{3}{2}\right)\left(\genfrac{}{}{0pt}{}{3}{0}\right)\left(\genfrac{}{}{0pt}{}{7}{0}\right)\hfill \\ \hfill & =7+3+3=13.\hfill \end{array}$$

The case $m=2$ and $r=0$ of Theorem 4 gives the following identity:

Corollary 2.

For $n⩾0$,

$$\begin{array}{c}\hfill \sum _{k=0}^{n}PL\left(k\right)PL(n-k)=\sum _{t_1+2t_2+\cdots +n{t}_n=n}\left(\genfrac{}{}{0pt}{}{2s_1}{t_1}\right)\left(\genfrac{}{}{0pt}{}{2s_2}{t_2}\right)\cdots \left(\genfrac{}{}{0pt}{}{2s_n}{t_n}\right).\end{array}$$

Considering the partitions of four with $t_1⩽2$, the case $n=4$ of Corollary 1 reads as follows:

$$\begin{array}{cc}\hfill \sum _{k=0}^{4}PL\left(k\right)PL(4-k)& =\left(\genfrac{}{}{0pt}{}{2}{0}\right)\left(\genfrac{}{}{0pt}{}{6}{0}\right)\left(\genfrac{}{}{0pt}{}{6}{0}\right)\left(\genfrac{}{}{0pt}{}{14}{1}\right)+\left(\genfrac{}{}{0pt}{}{2}{1}\right)\left(\genfrac{}{}{0pt}{}{6}{0}\right)\left(\genfrac{}{}{0pt}{}{6}{1}\right)\left(\genfrac{}{}{0pt}{}{14}{0}\right)\hfill \\ \hfill & +\left(\genfrac{}{}{0pt}{}{2}{0}\right)\left(\genfrac{}{}{0pt}{}{6}{2}\right)\left(\genfrac{}{}{0pt}{}{6}{0}\right)\left(\genfrac{}{}{0pt}{}{14}{0}\right)+\left(\genfrac{}{}{0pt}{}{2}{2}\right)\left(\genfrac{}{}{0pt}{}{6}{1}\right)\left(\genfrac{}{}{0pt}{}{6}{0}\right)\left(\genfrac{}{}{0pt}{}{14}{0}\right)\hfill \\ \hfill & =14+12+15+6=47.\hfill \end{array}$$

On the other hand, according to (2) we can write

$$\begin{array}{cc}\hfill \sum _{k=0}^{4}PL\left(k\right)PL(4-k)& =1\times 13+1\times 6+3\times 3+6\times 1+13\times 1\hfill \\ \hfill & =13+6+9+6+13=47.\hfill \end{array}$$

By Corollary 2, we easily deduce the following congruence identity.

Corollary 3.

For $n⩾0$,

$$\begin{array}{c}\hfill \sum _{t_1+2t_2+\cdots +n{t}_n=n}\left(\genfrac{}{}{0pt}{}{2s_1}{t_1}\right)\left(\genfrac{}{}{0pt}{}{2s_2}{t_2}\right)\cdots \left(\genfrac{}{}{0pt}{}{2s_n}{t_n}\right)\equiv PL\left(\frac{n}{2}\right)(mod2),\end{array}$$

where $PL\left(x\right)=0$ if x is not a non-negative integer.

As a consequence of Theorems 3 and 4, we remark the following identity.

Corollary 4.

For $m⩾1$, $r\in \{-1,0,1\}$ and $n⩾0$,

$$\begin{array}{cc}\hfill \sum _{t_1+2t_2+\cdots +n{t}_n=n}\left(\genfrac{}{}{0pt}{}{m-1+r+t_1}{t_1}\right)& \prod _{j=2}^n\left(\genfrac{}{}{0pt}{}{jm-1+t_j}{t_j}\right)\hfill \\ & =\sum _{t_1+2t_2+\cdots +n{t}_n=n}\prod _{j=1}^n\left(\genfrac{}{}{0pt}{}{S_j^{(m,r)}}{t_j}\right).\hfill \end{array}$$

The remainder of this paper is organized as follows. In Section 2, we provide an analytic proof of Theorem 4. In Section 3, we introduce a new combinatorial interpretation for $PL\left(n\right)$. In Section 4, we make a connection to the Josephus problem. In Section 5, we give some concluding remarks.

2. Proof of Theorem 4

Elementary techniques in the theory of partitions [1] give the following generating function:

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }P{L}^{(m,r)}\left(n\right)q^n=\frac{1}{{(1-q)}^r}\prod _{n=1}^{\infty }\frac{1}{{(1-q^n)}^{mn}},\left|q\right|<1.\end{array}$$

(9)

In order to prove our theorem, we consider the identity

$$1=(1-q)\prod _{k=0}^{\infty }(1+q^{2^k}),\left|q\right|<1,$$

which can be rewritten as

$$\begin{array}{c}\hfill \frac{1}{1-q}=\prod _{k=0}^{\infty }(1+q^{2^k}),\left|q\right|<1.\end{array}$$

(10)

Then, by (10), with q replaced by $q^n$, we obtain

$$\begin{array}{c}\hfill \frac{1}{1-q^n}=\prod _{k=0}^{\infty }(1+q^{2^k·n}),\left|q\right|<1.\end{array}$$

(11)

For $\left|q\right|<1$, considering (10) and (11), the generating function of $P{L}^{(m,r)}\left(n\right)$ can be rewritten as follows:

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }P{L}^{(m,r)}\left(n\right)q^n& =\frac{1}{{(1-q)}^r}\prod _{n=1}^{\infty }\frac{1}{{(1-q^n)}^{m·n}}\hfill \\ \hfill & =\prod _{k=0}^{\infty }{(1+q^{2^k})}^r·\prod _{n=1}^{\infty }\prod _{k=0}^{\infty }{(1+q^{2^k·n})}^{m·n}\hfill \\ \hfill & =\prod _{n=1}^{\infty }{(1+q^n)}^{S_n^{(m,r)}}\hfill \\ \hfill & =\prod _{n=1}^{\infty }\left(\sum _{j=0}^{S_n^{(m,r)}}\left(\genfrac{}{}{0pt}{}{S_n^{(m,r)}}{j}\right)q^{j·n}\right)\hfill \\ \hfill & =\sum _{n=0}^{\infty }{q}^n\sum _{t_1+2t_2+\cdots +n{t}_n=n}\prod _{j=1}^n\left(\genfrac{}{}{0pt}{}{S_j^{(m,r)}}{t_j}\right),\hfill \end{array}$$

(12)

where we have used Cauchy multiplication of power series.

3. A New Combinatorial Interpretation

In this section, we introduce a notion related to n-color partitions and use it to give a new combinatorial interpretation for plane partitions.

Definition 1.

An $s_n$-color partition of a positive integer m is a partition in which a part of size n can come in $s_n$ different colors denoted by subscripts: $n_1,n_2,\dots ,n_{s_n}$. The parts satisfy the following order:

$$\begin{array}{c}\hfill 1_1<2_1<2_2<2_3<3_1<3_2<3_3<4_1<4_2<4_3<4_4<4_5<4_6<4_7<\dots \end{array}$$

We denote by $Q_{s_n}\left(m\right)$ the number of $s_n$-color partitions of m into distinct parts. We set $Q_{s_n}\left(0\right):=1$. For example, there are thirteen $s_n$-color partitions into distinct parts of 4:

$$\begin{array}{cc}\hfill & \left(4_7\right),\left(4_6\right),\left(4_5\right),\left(4_4\right),\left(4_3\right),\left(4_2\right),\left(4_1\right),(3_3,1_1),\hfill \\ \hfill & (3_2,1_1),(3_1,1_1),(2_3,2_2),(2_3,2_1),(2_2,2_1).\hfill \end{array}$$

(13)

Using elementary techniques [1], we obtain the following generating function for $Q_{s_n}\left(m\right)$:

$$\sum _{m=0}^{\infty }{Q}_{s_n}\left(m\right)q^m=\prod _{n=1}^{\infty }{(1+q^n)}^{s_n},\left|q\right|<1.$$

On the other hand, by (12) with $m=1$ and $r=0$, we obtain a new expression of the generating function of $PL\left(n\right)$:

$$\begin{array}{c}\hfill \sum _{n=0}^{\infty }PL\left(n\right)q^n=\prod _{n=1}^{\infty }{(1+q^n)}^{s_n},\left|q\right|<1.\end{array}$$

(14)

Thus, we deduce the following result for which we give a combinatorial proof.

Theorem 5.

The number of n-color partitions of m equals the number of $s_n$-color partitions of m into distinct parts.

Proof. 

Given an integer n, we denote by $n_o$ the largest odd divisor of n. Then, $n=2^k{n}_o$ for some non-negative integer k and

$$s_n=n_o(1+2+2^2+\cdots +2^k)=n_o(2^{k+1}-1)=2n-n_o.$$

Since $1⩽n_o⩽n$, it follows that $n⩽s_n⩽2n-1$. Note that, for odd n, we have $s_n=n$.

Denote by ${\mathcal{P}}_n\left(m\right)$ the set of n-color partitions of m. We define a bijection $\phi :{\mathcal{P}}_n\left(m\right)\to {\mathcal{Q}}_{s_n}\left(m\right)$.

Start with $\lambda \in {\mathcal{P}}_n\left(m\right)$. For each part $k_j$ (size k, color j with $1⩽j⩽k$) that occurs more than once, we replace two parts equal to $k_j$ by a single part ${\left(2k\right)}_{2k+j}$ (part of size $2k$, color $2k+j$). Since $1⩽j⩽k$, we have $2k+1⩽2k+j⩽3k$. Since $s_{2k}=4k-k_o$ and $k_o⩽k$, the obtained partition is an $s_n$-partition. We repeat the process until parts are distinct and obtain a partition $\mu \in {\mathcal{Q}}_{s_n}\left(m\right)$. We define $\phi \left(\lambda \right)=\mu$.

To determine the inverse ${\phi }^{-1}$, start with $\mu \in {\mathcal{Q}}_{s_n}\left(m\right)$. Note that if $k_j$ is a part of $\mu$, and k is odd then $1⩽j⩽k$. For each part $k_j$ with $j>k$, it follows that k is even and we replace $k_j$ by two parts ${(k/2)}_{j-k}$. Note that if $k/2$ is odd, then $k_o=k/2$ and $s_k=2k-k/2$. Then, $1⩽j⩽2k-k/2$ and $1⩽j-k⩽k/2$. We continue the process until there are no parts $k_j$ with $j>k$ to obtain a partition $\lambda \in {\mathcal{P}}_n\left(m\right)$. Then, ${\phi }^{-1}\left(\mu \right)=\lambda$. □

Example 1.

Consider

$$\lambda =(5_5^5,5_4^2,3_2^4,3_1^3,1_1^7)\in {\mathcal{P}}_n\left(73\right).$$

Here, we used the frequency notation: $3_2^4$ means that there are four parts of size 3 in color 2.

We replace two parts $5_5$ by a part ${10}_{10+5}={10}_{15}$, etc. After replacing pairs of equal parts (with equal colors), we obtain

$$({10}_{15},{10}_{15},{10}_{14},6_8,6_8,6_7,5_5,3_1,2_3,2_3,2_3,1_1).$$

Since the parts are not distinct, we continue to replace pairs. We obtain

$$\phi \left(\lambda \right)=({20}_{35},{10}_{14},{12}_{20},6_7,5_5,4_7,3_1,2_3,1_1)\in {\mathcal{Q}}_{s_n}\left(73\right).$$

To see that $\phi \left(\lambda \right)\in {\mathcal{Q}}_{s_n}\left(73\right)$, notice that

$$\begin{array}{cc}\hfill & s_{20}=40-5=35,s_{10}=20-5=15,s_6=12-3=9,\hfill \\ \hfill & s_5=5,s_4=8-1=7,s_3=3,s_2=4-1=3,s_1=1.\hfill \end{array}$$

Conversely, starting with

$$\mu =({20}_{35},{10}_{14},{12}_{20},6_7,5_5,4_7,3_1,2_3,1_1)\in {\mathcal{Q}}_{s_n}\left(73\right),$$

we replace parts $k_j$ with $j>k$ with two parts ${(k/2)}_{j-k}$. For example, ${20}_{35}$ is replaced by ${10}_{15},{10}_{15}$. After replacing each such part with a pair, we obtain

$$({10}_{15},{10}_{15},6_8,6_8,5_5,5_4,5_4,3_1,3_1,3_1,2_3,2_3,2_3,1_1).$$

Since there are still parts $k_j$ with $j>k$, we continue the process to obtain

$${\phi }^{-1}\left(\mu \right)=(5_5,5_5,5_5,5_5,5_5,5_4,5_4,3_2,3_2,3_2,3_2,3_1,3_1,3_1,1_1,1_1,1_1,1_1,1_1,1_1,1_1).$$

We remark the following consequence of Theorems 1 and 5.

Corollary 5.

The number of plane partitions of m equals the number of $s_n$-color partitions of m into distinct parts.

4. A Connection with Josephus Problem

The Josephus problem is a math puzzle with a grim description for which we refer the reader to [7]. Here, we give a friendlier adaptation of the problem: n rocks, labeled 1 to n, are placed in a circle. An person walks along the circle and, starting from the rock labeled 1, removes every k-th rock. As the process goes on, the circle becomes smaller and smaller, until only one rock remains.

We are interested in the case $k=2$ of the Josephus problem. For $k=2$, we denote by $J_n$ the order in which the first rock is removed. For example, if there are $n=7$ rocks to begin with, they are removed in the following order:

$$2,4,6,1,5,3,7.$$

Therefore, the rock labeled 1 is eliminated at the fourth removal. Therefore, $J_7=4$.

The sequence

$${\left(J_n\right)}_{n⩾1}=(1,2,2,4,3,5,4,8,5,8,6,11,7,11,8,16,9,14,10,\dots )$$

is known and can be seen in the On-Line Encyclopedia of Integer Sequence ([5], A225381). The sequence ${\left(J_n\right)}_{n⩾1}$ can be defined as follows:

$$J_n=\left\{\begin{array}{cc}(n+1)/2,\hfill & \mathrm{for}n\mathrm{odd},\hfill \\ n/2+J_{n/2},\hfill & \mathrm{for}n\mathrm{even}.\hfill \end{array}\right.$$

(15)

By (3) and (15), we easily deduce that

$$\begin{array}{c}\hfill J_n=\frac{1+s_n}{2},\end{array}$$

for any positive integer n.

It is clear that our results can be expressed in terms of $J_n$. For example, we remark the following version of Corollary 1:

Corollary 6.

For $n⩾0$,

$$\begin{array}{c}\hfill PL\left(n\right)=\sum _{\begin{array}{c}{t}_1+2t_2+\cdots +n{t}_n=n\\ t_k⩽2J_k-1\end{array}}\left(\genfrac{}{}{0pt}{}{2J_1-1}{t_1}\right)\left(\genfrac{}{}{0pt}{}{2J_2-1}{t_2}\right)\cdots \left(\genfrac{}{}{0pt}{}{2J_n-1}{t_n}\right).\end{array}$$

In this context, we denote by ${\mathcal{P}}_s\left(n\right)$ the set of partitions of n with $t_j⩽2J_j-1$, for each $j\in \{1,2,\dots ,n\}$, and define $p_s\left(n\right):=\left|{\mathcal{P}}_s\left(n\right)\right|$. We set

$${\mathcal{P}}_s:=\bigcup _{n⩾0}{\mathcal{P}}_s\left(n\right).$$

We also consider the set $\mathcal{J}$ defined as

$$\mathcal{J}=\left\{n{J}_n\right|n\in \mathbb{N}\}.$$

Conjecture 1.

Let m, n be positive integers. If $m\ne n$, then $m{J}_m\ne n{J}_n$.

Note that, if n is odd, then $n{J}_n=\frac{n(n+1)}{2}$, a triangular number. Thus, if $m,n$ are both odd and $m\ne n$, then $m{J}_m\ne n{J}_n$.

For $n⩾0$, we define:

• $Q{J}_e\left(n\right)$ to be the number of partitions of n into an even number of distinct parts from $\mathcal{J}$;
• $Q{J}_o\left(n\right)$ to be the number of partitions of n into an odd number of distinct parts from $\mathcal{J}$;
• $Q{J}_{eo}\left(n\right)=Q{J}_e\left(n\right)-Q{J}_o\left(n\right).$

In certain conditions, $p_s\left(n\right)$ satisfies Euler’s pentagonal number recurrence.

Theorem 6.

Assuming Conjecture 1, for $n⩾0$,

$$\sum _{k=-\infty }^{\infty }{(-1)}^k{p}_s\left(n-k(3k-1)/2\right)=\left\{\begin{array}{cc}0,\hfill & \mathrm{for}n\mathrm{odd},\hfill \\ Q{J}_{eo}(n/2),\hfill & \mathrm{for}n\mathrm{even}.\hfill \end{array}\right.$$

(16)

Analytic Proof.

The generating function for $p_s\left(n\right)$ is given by:

$$\begin{array}{cc}\hfill \sum _{n=0}^{\infty }{p}_s\left(n\right)q^n& =\prod _{n=1}^{\infty }(1+q^n+q^{2n}+\cdots +q^{(2J_n-1)n})=\prod _{n=1}^{\infty }\frac{1-q^{2n{J}_n}}{1-q^n}.\hfill \end{array}$$

Assuming Conjecture 1, elementary techniques in the theory of partitions [1] give the following generating function:

$$\sum _{n=0}^{\infty }Q{J}_{eo}\left(n\right)q^n=\prod _{n=1}^{\infty }(1-q^{n{J}_n}).$$

Thus, we can write

$$\begin{array}{cc}\hfill & \sum _{n=0}^{\infty }{q}^n\sum _{k=0}^{\infty }{(-1)}^k{p}_s\left(n-k(3k-1)/2\right)\hfill \\ \hfill & =\left(\sum _{n=-\infty }^{\infty }{(-1)}^n{q}^{n(3n-1)/2}\right)\left(\sum _{n=0}^{\infty }{p}_s\left(n\right)q^n\right)\hfill \\ \hfill & =\prod _{n=1}^{\infty }(1-q^{2n{J}_n})\hfill \\ \hfill & =\sum _{n=0}^{\infty }Q{J}_{eo}\left(n\right)q^{2n}.\hfill \end{array}$$

This concludes the analytic proof. □

We also provide a combinatorial proof of Theorem 6. First, we introduce some notation. We denote by $\mathcal{P}\left(n\right)$ the set of all partitions of n and set $\mathcal{P}:={\cup }_{n⩾0}\mathcal{P}\left(n\right)$. Given $\lambda \in \mathcal{P}$, we denote by $\ell \left(\lambda \right)$ the number of parts in $\lambda$ and by $\left|\lambda \right|$ the sum of parts of $\lambda$ (also referred to as the size of $\lambda )$. For a pair of partitions $(\lambda ,\mu )$, we write $(\lambda ,\mu )⊢n$ to mean $\left|\lambda \right|+\left|\mu \right|=n$ (and similarly for a triple of partitions). In general, given a set $\mathcal{A}\left(n\right)$ of partitions of n (or pairs of partitions with sizes adding up to n), we set $\mathcal{A}:={\cup }_{n⩾0}\mathcal{A}\left(n\right)$. We also write ${\mathcal{A}}_e\left(n\right)$ (respectively, ${\mathcal{A}}_e\left(n\right)$) for the subset of $\lambda \in \mathcal{A}\left(n\right)$ with $\ell \left(\lambda \right)$ even (respectively, odd).

Combinatorial Proof of Theorem 6.

Let $\mathcal{Q}\left(n\right)$ be the set of distinct partitions of n. As explained for example in [1], Franklin defined a sign-reversing involution ${\phi }_F$ on a subset of the set of distinct partitions of n to prove combinatorially that the generating function for $|{\mathcal{Q}}_e\left(n\right)|-|{\mathcal{Q}}_o\left(n\right)|$ equals

$$\sum _{k=-\infty }^{\infty }{(-1)}^k{q}^{k(3k-1)/2}.$$

We define

$$\mathcal{B}\left(n\right):=\{(\lambda ,\mu )⊢n\mid \lambda \in \mathcal{Q},\mu \in {\mathcal{P}}_s\}.$$

Hence, the left-hand side of (16) is the generating function for

$$\begin{array}{c}\hfill \left|\right\{(\lambda ,\mu )\in \mathcal{B}\left(n\right)\mid \ell \left(\lambda \right)\mathrm{even}\left\}\right|-\left|\right\{(\lambda ,\mu \in \mathcal{B}(n)\mid \ell (\lambda \left)\mathrm{odd}\right\}|.\end{array}$$

(17)

We set $2\mathcal{J}:=\{2n{J}_n\mid n\in \mathbb{N}\}$ and define

$$\mathcal{C}\left(n\right)=\left\{\right(\alpha ,\beta )⊢n\mid \alpha \in \mathcal{P},\beta \mathrm{has}\mathrm{parts}\mathrm{in}2J\}$$

and prove combinatorially that

$$p_s\left(n\right)=|(\alpha ,\beta )\in \mathcal{C}\left(n\right)\mid \ell \left(\beta \right)\mathrm{even}\left\}\right|-|(\alpha ,\beta )\in \mathcal{C}\left(n\right)\mid \ell \left(\beta \right)\mathrm{odd}\}|.$$

To do this, we define an involution $\psi$ on the subset ${\mathcal{C}}^{*}\left(n\right)$ of pairs $(\alpha ,\beta )\in \mathcal{C}\left(n\right)$ such that $\alpha$ has at least one part in $2\mathcal{J}$ or $\beta \ne \varnothing$. Let a be the largest part from $2\mathcal{J}$ in $\alpha$ and ${\beta }_1$ the largest part in $\beta$. If $a>{\beta }_1$, remove part a from $\alpha$ and insert a part of size a into $\beta$. If $a⩽{\beta }_1$, remove part ${\beta }_1$ from $\beta$ and insert a part of size ${\beta }_1$ into $\alpha$. The obtained partition $(\gamma ,\eta ):=\psi (\alpha ,\beta )$ has $\ell \left(\eta \right)\neg \equiv \ell \left(\beta \right)mod2$. Hence, $p_s\left(n\right)=|\mathcal{C}\left(n\right)\setminus {\mathcal{C}}^{*}\left(n\right)|$. Moreover, $\mathcal{C}\left(n\right)\setminus {\mathcal{C}}^{*}\left(n\right)$ consists of pairs $(\alpha ,\varnothing )\in \mathcal{C}\left(n\right)$ such that $\alpha$ has no parts from $2\mathcal{J}$.

Next, we define a Glaisher-type bijection ${\phi }_G$ between $\mathcal{C}\left(n\right)\setminus {\mathcal{C}}^{*}\left(n\right)$ and ${\mathcal{P}}_s\left(n\right)$. Let $(\alpha ,\varnothing )\in \mathcal{C}\left(n\right)\setminus {\mathcal{C}}^{*}\left(n\right)$. For each part j is $\alpha$ with $t_j⩾2J_j$, replace $2J_j$ parts of size j by a part of size $2j{J}_j$. We repeat the process until we obtain a partition $\xi \in {\mathcal{P}}_s\left(n\right)$, i.e., each part j of $\xi$ satisfies $t_j⩽2J_j-1$. Set ${\phi }_G(\alpha ,\varnothing ):=\xi$.

If the mapping $j\mapsto j{J}_j$ is injective (i.e., if Conjecture 1 holds), the transformation ${\phi }_G$ is invertible. Starting with a partition $\xi \in {\mathcal{P}}_s\left(n\right)$ if $\xi$ has a part equal to $2j{J}_j$ for some j, we replace part $2j{J}_j$ into $2J_j$ parts equal to j. We repeat the process until we obtain a partition $\alpha$ with no parts in $2\mathcal{J}$.

Therefore, (17) equals

$$\begin{array}{cc}\hfill \left|\right\{(\lambda ,\alpha ,\beta )⊢n& \mid \lambda \in \mathcal{Q},(\alpha ,\beta )\in \mathcal{C}\},\ell (\lambda )\mathrm{even},\ell (\beta \left)\mathrm{even}\right\}|\hfill \\ & -\left|\right\{(\lambda ,\alpha ,\beta )⊢n\mid \lambda \in \mathcal{Q},(\alpha ,\beta )\in \mathcal{C}\},\ell (\lambda )\mathrm{even},\ell (\beta \left)\mathrm{odd}\right\}|\hfill \\ \hfill -\left|\right\{(\lambda ,\alpha ,\beta )⊢n& \mid \lambda \in \mathcal{Q},(\alpha ,\beta )\in \mathcal{C}\},\ell (\lambda )\mathrm{odd},\ell (\beta \left)\mathrm{even}\right\}|\hfill \\ & +\left|\right\{(\lambda ,\alpha ,\beta )⊢n\mid \lambda \in \mathcal{Q},(\alpha ,\beta )\in \mathcal{C}\},\ell (\lambda )\mathrm{odd},\ell (\beta \left)\mathrm{odd}\right\}|.\hfill \end{array}$$

Finally, in a manner similar to $\psi$, we define an involution $\zeta$ on the set

$$\left\{\right(\lambda ,\alpha )⊢n\mid \lambda \in \mathcal{Q},\alpha \in \mathcal{P}\}\setminus \left\{\right(\varnothing ,\varnothing \left)\right\}.$$

If ${\lambda }_1>{\alpha }_1$, move part ${\lambda }_1$ from $\lambda$ to $\alpha$. Otherwise, move part ${\alpha }_1$ form $\alpha$ to $\lambda$. Clearly, $\zeta$ changes the parity of $\ell \left(\lambda \right)$.

The transformation that maps $(\lambda ,\alpha ,\beta )$ satisfying $\lambda \in \mathcal{Q}$, $\alpha \in \mathcal{P}$ and $\beta$ has parts in $2\mathcal{J}$ to $\left(\zeta \right(\lambda ,\alpha ),\beta )$ shows that that (17) equals

$$\begin{array}{cc}\hfill \left|\right(\varnothing ,\varnothing ,\beta )⊢n& \mid \beta \mathrm{has}\mathrm{parts}\mathrm{in}2\mathcal{J},\ell \left(\beta \right)\mathrm{even}\left\}\right|\hfill \\ & -\left|\right(\varnothing ,\varnothing ,\beta )⊢n\mid \beta \mathrm{has}\mathrm{parts}\mathrm{in}2\mathcal{J},\ell (\beta \left)\mathrm{odd}\right\}|.\hfill \end{array}$$

Halving the parts of $\beta$ completes the proof. □

5. Concluding Remarks and Open Problems

In this section, we introduce some conjectures on the non-negativity of certain truncated theta series involving sequences studied in this article.

In [8], Andrews and Merca considered the truncation of the theta series arising from Euler’s pentagonal number theorem. They considered the number $M_k\left(n\right)$ of partitions of n in which k is the smallest integer that does not occur as a part and there are more parts $>k$ than there are $<k$. For example, we have $M_3\left(18\right)=3$ because the three partitions in question are

$$(5,5,5,2,1),(6,5,4,2,1),(7,4,4,2,1).$$

As shown in [8], for every $k⩾1$, $M_k\left(n\right)$ is the coefficient of $q^n$ in the series

$$\begin{array}{c}\hfill {(-1)}^k\left(1-\frac{1}{{(q;q)}_{\infty }}\sum _{n=1-k}^k{(-1)}^n{q}^{n(3n-1)/2}\right).\end{array}$$

There is a substantial amount of numerical evidence to state the following conjecture.

Conjecture 2.

For $k⩾1$, all the coefficients of the series

$$\begin{array}{c}\hfill {(-1)}^k\left(1-\frac{1}{{(q;q)}_{\infty }}\sum _{n=1-k}^k{(-1)}^n{q}^{n(3n-1)/2}\right)\prod _{n=1}^{\infty }(1-q^{2n{J}_n})\end{array}$$

are non-negative. The coefficient of $q^n$ is positive if and only if $n⩾k(3k+1)/2$.

Considering the generating functions of $p_s\left(n\right)$ and $Q{J}_{eo}\left(n\right)$, Conjecture 2 can be reformulated in its combinatorial form:

Conjecture 3.

For $k⩾1$,

1.

For n odd, we have

$${(-1)}^{k-1}\sum _{j=1-k}^k{(-1)}^j{p}_s\left(n-j(3j-1)/2\right)⩾0,$$

with strict inequality if and only if $n⩾k(3k+1)/2$.

2.

For n even, we have

$${(-1)}^k\left(Q{J}_{eo}(n/2)-\sum _{j=1-k}^k{(-1)}^j{p}_s\left(n-j(3j-1)/2\right)\right)⩾0,$$

with strict inequality if and only if $n⩾k(3k+1)/2$.

The work of Andrews and Merca was the impetus of much work on truncations of different theta series. See, for example, [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24]. Recently, Xia and Zhao [25] introduced a new truncated version of Euler’s pentagonal number theorem. They considered the number, ${\tilde{P}}_k\left(n\right)$, of partitions of n in which every positive integer $⩽k$ occurs as a part at least once and the first part larger that k occurs at least $k+1$ times. For example, ${\tilde{P}}_2\left(17\right)=9$, and the partitions in question are as follows:

$$\begin{array}{cc}\hfill & (5,3,3,3,2,1),(4,4,4,2,2,1),(4,4,4,2,1,1,1),(4,3,3,3,2,1,1),\hfill \\ \hfill & (3,3,3,3,2,2,1),(3,3,3,3,2,1,1,1),(3,3,3,2,2,2,1,1),\hfill \\ \hfill & (3,3,3,2,2,1,1,1,1),(3,3,3,2,1,1,1,1,1,1).\hfill \end{array}$$

As shown in [25], for every $k⩾1$, ${\tilde{P}}_k\left(n\right)$ is the coefficient of $q^n$ in the series

$$\begin{array}{c}\hfill {(-1)}^{k-1}\left(1-\frac{1}{{(q;q)}_{\infty }}\sum _{n=-k}^k{(-1)}^k{q}^{n(3n-1)/2}\right).\end{array}$$

Based on numerical evidence, we make the following conjecture which is analogous to Conjecture 2.

Conjecture 4.

For $k⩾1$, all the coefficients of the series

$$\begin{array}{c}\hfill {(-1)}^{k-1}\left(1-\frac{1}{{(q;q)}_{\infty }}\sum _{n=-k}^k{(-1)}^k{q}^{n(3n-1)/2}\right)\prod _{n=1}^{\infty }(1-q^{2n{J}_n})\end{array}$$

are non-negative. The coefficient of $q^n$ is positive if and only if $n⩾(k+1)(3k+2)/2$.

The combinatorial interpretation of this conjecture reads as follows.

Conjecture 5.

For $k⩾1$,

1.

For n odd, we have

$${(-1)}^k\sum _{j=-k}^k{(-1)}^j{p}_s\left(n-j(3j-1)/2\right)⩾0,$$

with strict inequality if and only if $n⩾(k+1)(3k+2)/2$.

2.

For n even, we have

$${(-1)}^{k-1}\left(Q{J}_{eo}(n/2)-\sum _{j=-k}^k{(-1)}^j{p}_s\left(n-j(3j-1)/2\right)\right)⩾0,$$

with strict inequality if and only if $n⩾(k+1)(3k+2)/2$.