Abstract
We demonstrate the emergence of an effective “time” axis in the ground state of a gauged rotational symmetry theory in four-dimensional Euclidean space. In so doing, we remove the necessity of Wick rotation to Lorentz spacetime, an arbitrary and sometimes ill-defined procedure, especially for gravity-related theories. We begin by adapting the Cho-Duan-Ge decomposition to the gauge theory of the four-dimensional rotational symmetry group , where it identifies the maximal Abelian subgroup in a gauge covariant manner. We then find the one-loop effective theory to have a stable condensate of monopoles corresponding to the reduction of symmetry to . The construction of the condensate ensures that the four-dimensional spatial direction of its field strength must coincide with that of this embedding, and that a magnetic potential must be worked against to divert a trajectory away from this direction. Indeed, movement along this direction represents minimal potential energy. We take it to be the time direction. The gauge-dependent nature of the condensate is such that different gauge choices may lead to different time axes and we show on very general grounds that these different coordinate systems must be relatable by transformations of Lorentz form.
1. Introduction
With the discovery of Einsteinian relativity [1] came the realisation that space and time are both parts of a unified “spacetime” in which time is treated as a dimension in the same way as the spatial dimensions. However, even in this picture and despite its axis also rotating between observers, the time dimension is still distinguishable from the three space dimensions. Momentum, for example, is limited to fall within a certain angle, the light cone, of any observer’s time axis. Even the metric of spacetime distinguishes the time axis from the spatial ones with a sign change. The conventional model of one time plus three space dimensions may fit our intuition well but the existence of a distinguishable time dimension is still ad hoc. Why is there a distinguishable direction, and if there must be, then why only one? The metric of spacetime, in the absence of gravity, could just as well have been diag(−1, −1, 1, 1).
The problematic nature of relativistic time goes beyond aesthetics. Attempts to formulate quantum gravity are typically brought low by ill-defined path integrals and indefinite actions [2]. The problem is often avoided by working in Euclidean space where the negative norm does not occur because the Lorentz group becomes the compact rotation group but the negative norm arises upon transition to Minkowski space. Indeed, the reason for Wick rotation between Minkowski and Euclidean space in the first place is because the path integral, on which quantum field theory is based, is ill-defined in Minkowski space due to the oscillatory nature of its integrand [3]. Some authors even argue that quantum field theory should always be formulated in Euclidean space [4], especially asymptotically free theories [5].
The fundamental problem with avoiding such problems this way is that the Wick rotation is not well-defined for arbitrary metrics [6] and this is a curse on most approaches to quantising gravity [7]. We note in passing that dynamic triangulation [8] is an exception to this, as it features a well-defined Wick rotation [9,10] and the unboundedness of its action is cured nonperturbatively [11,12].
Unfortunately, gauged Poincaré symmetry theory is not so fortunate and is plagued by the negative norm states originating in the non-compactness of the Lorentz group. Our approach is to accept that spacetime is fundamentally locally Euclidean so that all field theories must be formulated in Euclidean space for physical accuracy and not just for mathematical consistency. We shall argue that a time axis consistent with special relativity emerges from the vacuum condensate of rotational gauge theory. We shall refer to four-dimensional Euclidean space as “four-space” in this context, and sometimes describe the properties of four-space as being “four-spatial”. Since this work is exclusively in Euclidean space, we use latin letters as four-spatial indices.
In our model the relativistic time axis emerges from a non-trivial vacuum state, itself derived from the emergence of a favoured direction and dominant generator in a gauge symmetry theory. The spontaneous dominance of a theory by its Abelian generators is long-known from confinement studies in quantum chromodynamics (QCD) [13,14,15,16] in which the QCD ground state was considered to be a condensate of (chromo)magnetic monopoles dual to the superconducting ground state of Cooper pairs. Confinement is then attributed to a dual-Meissner effect, with the (chromo)electric flux restricted to flux tubes between colour charges. Early studies of this model in the colour theory simply assumed the dominance of one generator, typically , in what is known as the Maximal Abelian Gauge (MAG) because a single generator yields an Abelian subgroup, and posited the associated magnetic flux to lie in a particular spatial direction, usually [13,14,15,16]. While insights into the stability of the magnetic vacuum were available this way, the arbitrary selection of a particular generator and spatial direction is a blatant violation of isotropy and gauge covariance and furthermore gives no indication that the magnetic ground state is due to magnetic monopoles. These weaknesses were addressed by Cho [17] and by Duan and Ge [18], and later by Faddeev and Niemi [19], and Shabanov [20] by allowing the MAG to vary arbitrarily throughout spacetime and defining a connection, called the “Cho” connection, in such a way that its covariant derivative of the internal direction is zero. The gauge field is then decomposed into its Abelian component, its monopole component, and its off-diagonal components. Correctly accounting for the degrees of freedom (DOFs) and other mathematical subtleties took significant effort from various independent groups [20,21,22,23,24,25,26], with some initial confusion regarding its dynamical DOFs and gauge-fixing. This so-called “Cho-Duan-Ge” (CDG) decomposition has since been applied to the complete colour theory [27,28,29] and Kondo et al. have used it to study the confinement under subgroups greater than the MAG via the non-Abelian Stoke’s theorem [30,31,32,33,34].
Another source of difficulty was the apparent existence of an imaginary part to the one-loop effective action, attributable to interaction between any magnetic condensate and gluon spin. Cho et al. argued this to be an artifact of subtleties concerning regularisation [23,35,36], but other authors [25] also demonstrated the emergence of an effective gluon mass sufficiently large to overcome this spin interaction.
The CDG decomposition has also been applied to studies of gravity, both to the Einstein-Hilbert Lagrangian and to Lorentz gauge theory [37,38]. These studies Wick rotated to , and then exploited the local isometry between that and , where the groups are generated by the complex linear combinations of rotation and boost generators , where and represent, respectively, rotations around and boosts along the k-axis. Cho et al. [37,38] applied this decomposition to the Einstein-Hilbert Lagrangian with particular emphasis on representation theory, while the author, together with a collaborator, applied the CDG decomposition to a gauge theory in Euclidean space and found evidence for a nontrivial spacetime vacuum due to quantum corrections [39]. The task of Wick rotating this work to Minkowski space as a Lorentz gauge theory was deferred as the canonical approach leads to negative kinetic energy terms and, at first appearance, a non-positive definite Hamiltonian. We say “at first appearance” because Kim and Pak made a similar decision in their initial study of torsion confinement [40], where a low-energy topological background, analogous to the QCD monopole background discussed above, yields a Rieman-Cartan geometry while confining torsion. Their subsequent paper [41] demonstrated the existence of positive energy propagators in the presence of the topological background and a positive semi-definite Hamiltonian, neither of which were obvious initially.
In this paper we adapt the CDG decomposition from QCD gauge symmetry to the rotational symmetries of Eucliden spacetime, though in a different manner to the author’s earlier collaboration [39], and find that the lowest energy state of spacetime is a rotational monopole condensate, henceforth called the “Minkowski condensate”, which selects a local direction and interacts with momentum to produce the effects of Einsteinian relativity. We establish our notation in Section 2, where we outline the application of the CDG decomposition to QCD, and in Section 3 we describe the gauge theory used in this paper, and we demonstrate that the lowest energy state of the theory has a finite, non-zero field strength in Section 4. The main result of this paper is presented in Section 5 in which we argue for an emergent time direction corresponding to the field strength of the rotation group’s MAG, and that any momentum vector in Euclidean four-space is dressed by this background in such a way as to reproduce the effects of a Lorentz transformation. The specific mathematical form of the Lorentz transforms is shown to follow from very general and already known considerations [42] so that a detailed calculation is not needed. We finish with a discussion of some the implications of this work, such as tachyon bound states and the need for inflation in the early universe in Section 6.
2. The CDG Decomposition—A Review
The Cho Connection
To simplify the presentation, we first describe the CDG decomposition of and . It was first developed for QCD in the context of confinement but local isomorphism between these groups means that the notation remains identical and that most results transfer across. The confinement model is a magnetic monopole background confining (chromo)electric flux by means of a dual-Meissner effect [23]. To respect gauge covariance and to ensure that the corresponding magnetic field is of monopole origin, the MAG is specified at each point in spacetime by the internal unit vector , where is a spacetime-varying unitary operation and , where , represent the group generators. Defining the Cho connection by
where g is the coupling constant, yields the covariant derivative
where
with representing the gluon DOFs along the Abelian direction, so that
The gluon field now decomposes into
where contains the DOFs orthogonal to not contained in the Cho connection. The contribution of the Cho connection to the field strength, i.e., the monopole field strength, is given by
where the last equality can be derived by substituting Equation (1). It follows from Equation (6) that the monopole field strength is parallel to , implicitly defining by
The full field strength decomposes as an Abelian part with the derivative terms of the valence gluons .
where
We can now give the Lagrangian in terms of the decomposed gauge field, namely
If we restrict the theory to the Abelian field strength and exclude the valence gluons then this so-called “restricted” theory still posseses the original symmetry of the complete theory [17,23].
The CDG decomposition naively appears to add two extra DOFs to the theory. Shabanov [22] sought to remove them by imposing the condition
However, Bae et al. [26] pointed out that the Cho connection carries only topological DOFs and not dynamic ones, and that the condition (11) is simply a consistency condition of which must be imposed as a gauge-fixing term:
The corresponding ghost term is given by
We neglect the ghost fields for the Abelian component because they disengage from the dynamics and do not contribute to the final outcome [26].
3. Rotational Gauge Symmetry in Euclidean Space
3.1. The CDG Decomposition of Gauge Theory
A Euclidean four-space has six independent rotation generators where the axis labels have four possible values but are never equal. There is no unique way of writing them so we use the skew-symmetric matrices whose entries are all zero except at the row in the column, equal to when , and vice versa. As with the generators of three-dimensional space, these generators specify a plane of rotation, but unlike a three-dimensional space the orthogonal complement to this plane is another plane. For example, if the four-space is spanned by the orthonormal axes then the generator acts within a plane-of-rotation containing the axes, the orthogonal complement of which is the plane described by the axes, orthogonal planes intersecting at a point in four-space. We advise that, unlike the approach taken in references [37,39,43], this paper does not use the local isomorphism to generate the condensate.
Specific embeddings of this subgroup are given by any where are all different. We employ the CDG decomposition to specify the DOFs associated with this subgroup in a gauge-covariant way. To apply the CDG decomposition to this rotation group we must first identify the possible Abelian subgroups. We define the gauge covariant generators of the MAG
For every available embedding of the MAG in , there is a two-dimensional space of embeddings of , spanned by the pairs
The embedding is then a linear combination of these pairs combined with . It is useful to define
to represent the remaining two generators of the covariantly embedded . With the observation
we can then define the unit vectors
and the general notation
where and dependence on the spacetime coordinate w is suppressed for clarity of expression until the end of this subsection so that we may focus on the algebra.
To complete this notation we state the following identities which are easily verified. (Please note that is used in Equation (16) and not ).
where are taken to mean , respectively.
The vectors in ceiling brackets identify the embedding in a gauge covariant manner which may vary throughout spacetime and change under local gauge transformations, so
for arbitrary . Combinations of operators not in this subgroup are indicated by the floor brackets ,
while a mixed product yields a floor bracket,
It is also useful to represent the sum,
where any quantity , including the Cho connection defined in Equation (29), is understood to have a ceiling component and a floor component. We may therefore take
We shall find it helpful in Section 4.2 to refer to specific indices, shown in upper case latin characters. Indices refer to the internal directions of the unit vectors , as appropriate, while refers to those of , as appropriate. We also define
Finally, we need to adapt the scalar product to this notation:
3.2. Monopole Field Strength
We may now construct the Cho connection
with the defining property
Note that the Cho connection requires a complete square bracket because the derivative of a pure ceiling bracket may contain a floor bracket component and vice versa. This is different from the square bracket notation defined in references [37,38,39] whose Cho connection was equivalent to a ceiling bracket. This is because those works had preselected the timelike directions, whereas this work does not. Note too that the derivatives of the mutually Abelian generators are sufficient to determine each other by the group algebra. The parallel with is now straightforward, where we identify the DOFs of the MAG and identify the Abelian dynamics
The covariant derivative is then
which has the properties
The monopole field strength is given by
Denoting the complete gauge field by we complete the CDG decomposition with
where are the remaining dynamic, also called valence, DOFs. They are orthogonal to the Abelian directions .
The decomposed full field strength is now,
where
We can now give the Lagrangian in terms of the decomposed gauge field, namely
where we have left out w dependence for the sake of clarity.
If we restrict the theory to the Abelian field strength and exclude the valence gluons then this so-called “restricted” theory still posseses the original symmetry of the complete theory [17,23]. The parallel result for our gauged theory is discussed in Section 6.
3.3. Invariant Transformations of CDG Decomposition of Gauged Rotational Theory
Introducing the CDG decomposition to this theory leaves us with two gauge invariant gauge transformations. The first is the “active” or “background” transformation, given by
We see off-diagonal fields, sometimes called “valence” fields because they transform as valence DOFs under the active transformation. They are not true valence fields, however, because giving them an explicit mass term would spoil the renormalisability of the theory. The second, passive, transformation is given by
These symmetries, of course, have their counterparts in QCD. We do not present them in the main part of the text in order to minimise repetition but have presented them in Appendix A. The rotational monopole DOFs are thought to provide a slow-moving passive background to the fast-moving quantum DOFs provided by the fields . The reader will have observed that our notation has become quite involved so, for the sake of clearer presentation, we shall no longer explicitly indicate dependence on the spacetime coordinate w, trusting that the text leading up to this point has indicated where it is appropriate with sufficient clarity.
We point out that the transform of rotates between and when contains a component, corresponding to the change in embedding alluded to earlier. The gauge fixing and ghost terms follow easily, with
as the gauge fixing conditions and their corresponding ghost terms
where the ghost fields corresponding to the Abelian components do not contribute to the final outcome [26] and are left out for the sake of clarity.
4. Vacuum State at One Loop
4.1. Magnitude of Monopole Condensate
The non-zero monopole condensate was demonstrated for QCD at one loop via the background field method using dimensional regularisation. In this calculation the Cho connection provided the background rendered energetically favourable by the gluon and ghost loops described by the Feynman diagrams in Figure 1. The corresponding one-loop correction to the effective action, originally stated in references [35] (Equation (19)) and [36] (Equation (6.2)) is
given in momentum space after dimensional regularisation. They went on to analyse the imaginary part arising from the term but since their argument rests on whether the momenta are spacelike or timelike we cannot use it here since we are trying to construct a time direction from first principles. We therefore defer the issue of stability to the following Section 4.2.
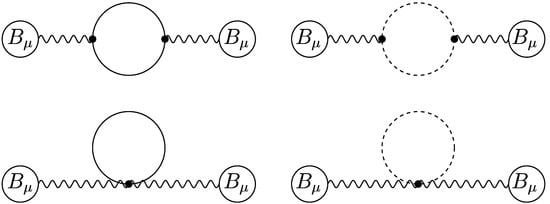
Figure 1.
Feynman diagrams of one-loop contributions to the effective action of QCD. The loops on the left of the figure are due to gluons, while those on right are due to ghosts. Note that the contributions of the tadpole diagrams in the bottom row are removed by dimensional renormalisation.
The other calculation in those papers, based on Schwinger’s seminal paper [44], calculates the functional determinants in the effective action by means of the identity
Unfortunately, this calculation of the condensate’s magnitude relies on causality considerations during infrared regularisation as well a Wick rotation, which makes it unsuitable for the purposes of this paper. The interested reader is referred to references [35,36] for its complete details.
The corresponding calculation for perturbative gauge theory is easily inferred from that of gauge theory, which can be lifted from perturbative QCD at one loop. The ceiling bracket portion of the rotational monopole field strength has twice the contribution of the above QCD field monopole field strength, one gauge field loop containing , another , plus their corresponding ghost loop contributions. Similarly, receives contributions from one loop containing and one containing , in addition to corresponding ghost loop contributions. The corresponding one-loop correction to the effective action is therefore
Defining
in the context of the gauge theory, gives the real part of the effective potential as
After defining the running coupling by [13,36,45]
The renormalised potential is now given by
for which the local minimum is
Hence, the lowest energy state of gauge theory has a non-zero monopole condensate which we call the Minkowski condensate.
4.2. Stability of the Minkowski Condensate
Concerns about monopole condensate stability were raised early in the study of the dual Meissner effect as a confinement mechanism [13,14,15], specifically that the interaction between the condensate and the negative spin mode of the gluon might, at low energy, render the gluon energy imaginary. The interaction term in question, from Equation (37), generates an energy contribution such that a valence field whose energy would otherwise be k instead has an energy mode of [13,14,15]
where was defined in Equation (44). A negative sign clearly leads to an imaginary part at low .
Following references [25,27,46], we observe at the classical level that the monopole condensate gives the off-diagonal gluons an effective mass via
The latter term gives
which provides the effective gauge field mass matrix
So, the tachyon mode becomes
where the off-diagonal modes have mass eigenvalues
which is a stronger result than its QCD counterpart, especially for larger numbers of colours [27]. Dudal et al. have studied the implications of the tachyon mode with a focus on gluon [47] and even ghost [48] related condensates, but we do not consider those in this paper.
The arguments for monopole condensate stability in QCD primarily pursued by Cho and collaborators [23,35,35] argue the tachyonic modes to be an artefact of poorly chosen renormalisation and take special care in handling singularities. These methods then find that it is the electric background and not the magnetic one which generates an imaginary part. Unfortunately for this work, these derivations are either based on causality or include considerations of whether the momentum is spacelike or timelike, which makes them unsuitable for work seeking to construct a relativistic time axis from base principles.
5. The Emergence of Effective Minkowski Space
5.1. Identifying the Local Time Axis
The monopole field strength, where from now on we intend monopoles from the MAG embedded in rather than , points along the internal Abelian directions described in Equation (27) by the construction in Section 3.2. Since the field strength components are built from the derivatives of with respect to orthogonal axes, it follows that must be constant in the four-spatial direction of the monopole field strength. We take that four-spatial direction to be a time axis, which renders the background purely magnetic, as expected from a monopole condensate, since an electric component to the field strength requires to have a non-zero time derivative.
From the form of the Cho connection, given in Equation (29), any field strength component is proportional to the derivative of (equivalently ) in the corresponding direction, so in the coordinate system constructed here the time component must vanish. Since the Cho connection in this theory provides the connection coefficient, we see that any object being transported in the time direction is unaffected by it. However, a trajectory deviating from this direction is undergoing geodesic acceleration which, consistently, leads to greater interaction with the condensate, elevating the potential by , where p is the Euclidean four-momentum in four-space.
The corresponding monopole field strength tensor constructed in this frame has, by the construction in Equation (33), all zero entries at every component with a time index. This indicates vanishing “electric” components and non-zero “magnetic” components, consistent with the background being generated by a monopole condensate. Observers differing by an active gauge choice, corresponding to different inertial frames, will have different time and space coordinates. We shall show soon that they are related by a Lorentz transformation, but first we must establish an invariant speed of light.
5.2. The Constant Speed of Light
A feature unique to and universal among massless field particles such as the photon is that the phase change with time is proportional to the phase change with distance travelled, whereas a massive field particle can be stationary or slow-moving but still demonstrate a rapid phase change with respect to time. Currently, all known massless particles are spin one gauge fields with circularly polarised states, with the rotation of polarisation locked to the phase and therefore to motion along both time and space axes. Since the time direction in this model coincides with the generators of both and , a massless spin one field, which we shall call the “gauge field” or “gauge boson”, might couple to the components of the condensate’s field strength through its linear momentum and to the component via the angular momentum of its spin, remembering that the two MAG generators correspond to orthogonal planes. If it is travelling though the Minkowski condensate at a suitable angle between the and directions, then the coupling described in Section 5.1 with the component may equal in magnitude but exactly cancel the coupling between the component with the angular momentum arising from its spin, so that the additional magnetic dressing of a massive particle described above does not occur for this massless one. This is not mere wishful thinking as this angular momentum is proportional to the frequency of the gauge particle, as is the component of the momentum. This lockstepping of angular momentum with the rate of phase change with , and equivalently , strongly suggests that this outcome is common to all observers. Hence, observers in relative motion in four-space, implying different and possibly axes, should still observe the massless particle to have no net coupling effects with the monopole condensate. Exact proof eludes us but this seems simpler if the angle of the gauge particle’s motion through four-space has the same angle between the and axes for all observers.
5.3. Emergence of Lorentz Transformations
We now have that the and axes differ between observers after a suitable active gauge transform of the MAG generators, but do they obey the Lorentz transform? In fact, there is very little flexibility in the form of coordinate transformations once certain, quite general, criteria are met. These criteria have been reduced and summarized in chapter 6.4 (page 224) of reference [42], which uses them to derive the form of the Lorentz transformations without requiring that the transformation necessarily be between observers in relative motion. Einstein’s original paper [1] needed only (i) linearity, (ii) invariance of the speed of light in vacuum, (iii) the existence of a composition law, (iv) the existence of a neutral element, and (v) reflection invariance. This was reduced to four conditions by Levy-Leblond [49] and since reduced further by Nottale [42] (chapter 6 section 4) to
- 1.
- Linearity;
- 2.
- An internal composition law;
- 3.
- Reflection invariance.
An outline of the proof is given in Appendix B, although the reader is referred to reference [42] for the full details. Here we merely note that these conditions are met so that the coordinate axes of observers in relative motion vary according to Lorentz transformations while they all observe the same speed of light, so that special relativity holds in the low energy effective theory.
We have avoided equating the active gauge transform with the Lorentz transform because they are not the same thing. The active gauge transform rotates the internal direction of the MAG but not, directly, the axis. However, the axis is determined by the four-spatial derivative and is therefore affected by the active transformation because it acts locally and may vary throughout spacetime. The exact relationship between them has not yet been determined but we can provide some insights. Given the time direction as described in Section 5, we have . Performing an active gauge transformation, this becomes
indicating that the emergent time axis may change after an active gauge transformation whose parameter has a non-zero time derivative. The transformed time axis is the one whose derivative makes this equation vanish, so
We might then hope to find some restrictions using
The details of this relationship will be the subject of further investigation in the near future.
6. Discussion
We have shown that locally Minkowski spacetime need not be taken as fundamental but can be seen as a low energy model arising from perturbative quantum effects. The advantage of such a model is that it naturally avoids the mathematical inconsistencies inherent to Minkowski spacetime. The most fundamental would be that the path integral is ill-defined because of oscillating integrands. It is now textbook procedure to work around the issue in Euclidean space via the Wick rotation. This works well with non-gravitational theories, even if the issue still remains in principle [4,5], but not for most quantum theories of gravity [2,6,7]. This includes gauge theories of the Lorentz group where its non-compact nature leads to non-positive definite Hamiltonians. This can be temporarily worked around in Euclidean space using , but we must then return to Lorentz symmetry in physical Minkowski space and no Wick rotation is known in continuum gravity for general metrics (See reference [6] and also page 34 of reference [7] which is a summary of issues relevant to quantum gravity). In our model, gauged rotational symmetry leads to a non-trivial vacuum whose interaction with matter and four momentum mimics the effects of special relativity. The fundamental theory is still in Euclidean space, however, so it is not necessary to Wick rotate to Minkowski space and incur these issues.
Our construction is challenging, however, in its own ways. The effective spacetime axes experienced by observers are unlikely to be linear in the underlying Euclidean axes , probably requiring a complicated mapping when considering fundamental theories. We would also like to address the complications of relating an active gauge transformation to its emergent Lorentz transform discussed earlier. Also, our construction of an invariant lightspeed is dependent on all known massless fields having a spin of one. If a more general construction is not found then this would predict that masslessness, or perceived masslessness with the effective spacetime axes, requires this property so that the model fails if an exception is found.
The Minkowski condensate, being a vacuum state, is not present above some critical temperature, probably the Planck temperature since this is a fundamental theory of spacetime symmetry. Such temperatures are thought to have occurred in the early stages of the universe, and we predict the lack of a time axis in its absence. It would follow that particle content at such temperatures is not confined to move within light cones but move in four, independent space dimensions. Note that without a Minkowski condensate there is no relativistic speed limit so there is no need for inflationary physics to explain the observed uniformity of the early universe. The dynamics in this regime would seem to indicate Newtonian concepts of space and time with dynamics playing out in a spatial arena, though with four dimensions rather than three, while some universal time linearly passes. However, as matter and energy spread, the temperature falls until the Minkowski condensate forms and motion along the emergent local time axis correlates with this Newtonian time.
Tachyons are not forbidden by the equations of special relativity, though they are assumed not to exist because they generate issues with causality and are associated with instability in quantum field theories. They are not required by our model but perhaps a condensate coupling to momentum offers a causally acceptable way to accommodate them? We expect from the construction in Section 5.1 that the coupling between superluminal momenta and the Minkowski condensate is stronger than for subluminal momenta. Guidance is provided by the Yang-Mills theories for which the CDG decomposition was originally constructed, with weak colour coupling at low momentum but confinement from some critical coupling at smaller length scales. By analogy, tachyons with superluminal momenta may exist but are confined and never directly observed, just as quarks with colour are confined and never directly observed. This suggests Planck-scale massive composite particles composed of tachyons whose net momentum is subluminal, just as quarks make up baryons with no net colour charge.
Movement, expansion and changing temperature all suggest the passing of something akin to what we consider time. This paper has focussed on the low-energy steady state, but meaningful discussion of dynamics without a relativistic time axis will require some broadening of how we understand time. The elucidation of such a variable is beyond the scope of this paper but should be the subject of future consideration.
Since the gauged symmetry is ultimately one of spacetime symmetry, we hope that coupling the Minkowski condensate to the stress-energy tensor in a suitable fashion might reproduce general relativity as a low energy, topological model. It is encouraging that the restricted theory without valence fields enjoys the original gauge symmetry of the full theory, as noted in Section 2.
Other authors have supported the notion that general relativity is a topological theory with quantum dynamics playing out at higher energies. Pursuit of this program to include a complete description of gravity would include the derivation of an effective metric and the introduction of tetrads for the inclusion of spinors [38]. The occurence of a positive semidefinite Hamiltonian, at least as perceived by observers within the Minkowski condensate, will also need to be demonstrated. All this may well prove to be very difficult as the effective axes are likely to be curvilinear with respect to the underlying Euclidean .
A complete understanding of gravity in the context of quantum field theory requires that we be able to transfer other field theories on to the Minkowski condensate in a mathematically consistent manner. Finally, of course, any quantum gravity program must include translation as a fundamental symmetry.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| QCD | Quantum ChromoDynamics |
| MAG | Maximal Abelian Gauge |
| DOFs | Degrees of Freedom |
| CDG | Cho-Duan-Ge |
Appendix A. Gauge Degrees of Freedom in SU(2)
Under the CDG decomposition QCD is invariant under two gauge transformations [23]. The first, described by Cho et al. [23] as the “active” or “background” transformation, is given by
We see here why the off-diagonal gluons are sometimes called “valence” gluons, because they transform as valence DOFs under the active transformation. However, they are not true valence fields because giving them an explicit mass term would spoil renormalisability. The second transformation, sometimes called the “passive” transformation, is given by
where is the QCD covariant derivative
The active transform is also known as the background transform because it contains the gauge freedom of the MAG and therefore monopole field, expected to provide a slow-moving background to the fast-moving quantum DOFs provided by the fields . It is on this basis that the passive gauge symmetry is fixed against the monopole background.
Appendix B. General Derivation of Lorentz Transformation
In Section 5.3 we skipped the details of why the Lorentz transformation specifically relates the observed four momenta between different active gauge choices, equivalent to reference frames. Our claim is based on a very general argument with application outside of changes in velocity [42]. Here we sketch an outline of this argument, though the reader is still referred to pages 224–229 of reference [42] for complete details.
The required conditions are:
- 1.
- Linearity;
- 2.
- An internal composition law;
- 3.
- Reflection invariance.
We begin with the linearity of the transformation:
where z and t refer to position and time, respectively in our work, but may be interpreted more broadly. We may define to gain the general form
where are new functions. Performing a successive transformation of the same form yields,
leading to the transformation
The combined transform is required to be of the same form as the initial one in Equation (A5) by the principle of relativity, or gauge covariance for our purposes, yielding the four conditions:
We now invoke the postulate of reflection invariance, that changes in spatial orientation should not affect the form of the transformations, to find parity relations on :
Combining Equations (A13) and (A12) and considering the special cases and eventually restricts to yield to the Einstein-Lorentz form [42]:
Similarly, considering the special case restricts to the form
where is easily redefined to the inverse of the square of the speed of light for the purposes of Section 5.3 but can also be taken to zero for a Galilean transformation.
References
- Einstein, A. On the electrodynamics of moving bodies. Ann. Der Phys. 1905, 17, 891–921. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path integrals and the indefiniteness of the gravitational action. Nucl. Phys. B 1978, 138, 141–150. [Google Scholar] [CrossRef]
- Frampton, P.H. Quantum Field Theories; Benjamin-Cummings: San Francisco, CA, USA, 1987. [Google Scholar]
- Ding, M.; Roberts, C.D.; Schmidt, S.M. Emergence of hadron mass and structure. Particles 2023, 6, 57–120. [Google Scholar] [CrossRef]
- Roberts, C.D. Strong QCD and Dyson-Schwinger Equations. arXiv 2012, arXiv:1203.5341. [Google Scholar]
- Visser, M. How to Wick rotate generic curved spacetime. arXiv 2017, arXiv:1702.05572. [Google Scholar]
- Loll, R.; Fabiano, G.; Frattulillo, D.; Wagner, F. Quantum Gravity in 30 Questions. arXiv 2022, arXiv:2206.06762. [Google Scholar]
- Ambjørn, J. Quantum gravity represented as dynamical triangulations. Class. Quantum Gravity 1995, 12, 2079. [Google Scholar] [CrossRef]
- Ambjørn, J.; Görlich, A.; Jurkiewicz, J.; Loll, R. Quantum Gravity via Causal Dynamical Triangulations. In Springer Handbook of Spacetime; Springer: Berlin/Heidelberg, Germany, 2014; pp. 723–741. [Google Scholar] [CrossRef]
- Loll, R. Quantum gravity from causal dynamical triangulations: A review. Class. Quantum Gravity 2019, 37, 013002. [Google Scholar] [CrossRef]
- Ambjørn, J.; Dasgupta, A.; Jurkiewicz, J.; Loll, R. A Lorentzian cure for Euclidean troubles. Nucl. Phys. Proc. Suppl. 2002, 106–107, 977–979. [Google Scholar] [CrossRef]
- Dasgupta, A.; Loll, R. A proper-time cure for the conformal sickness in quantum gravity. Nucl. Phys. B 2001, 606, 357–379. [Google Scholar] [CrossRef]
- Savvidy, G.K. Infrared instability of the vacuum state of gauge theories and asymptotic freedom. Phys. Lett. 1977, B71, 133. [Google Scholar] [CrossRef]
- Nielsen, N.K.; Olesen, P. An unstable yang-mills field mode. Nucl. Phys. 1978, B144, 376. [Google Scholar] [CrossRef]
- Flyvbjerg, H. Improved qcd vacuum for gauge groups su(3) and su(4). Nucl. Phys. 1980, B176, 379. [Google Scholar] [CrossRef]
- ’t Hooft, G. Topology of the gauge condition and new confinement phases in nonabelian gauge theories. Nucl. Phys. 1981, B190, 455. [Google Scholar] [CrossRef]
- Cho, Y.M. A restricted gauge theory. Phys. Rev. 1980, D21, 1080. [Google Scholar] [CrossRef]
- Duan, Y.S.; Ge, M.L. S. Sinica 11, 1072.
- Faddeev, L.D.; Niemi, A.J. Partial duality in su(n) yang-mills theory. Phys. Lett. 1999, B449, 214–218. [Google Scholar] [CrossRef]
- Shabanov, S.V. An effective action for monopoles and knot solitons in yang-mills theory. Phys. Lett. 1999, B458, 322–330. [Google Scholar] [CrossRef]
- Faddeev, L.D.; Niemi, A.J. Decomposing the yang-mills field. Phys. Lett. 1999, B464, 90–93. [Google Scholar] [CrossRef]
- Shabanov, S.V. Yang-Mills theory as an Abelian theory without gauge fixing. Phys. Lett. 1999, B463, 263–272. [Google Scholar] [CrossRef]
- Cho, Y.M.; Pak, D.G. Monopole condensation in su(2) qcd. Phys. Rev. 2002, D65, 074027. [Google Scholar]
- Kondo, K.I.; Murakami, T.; Shinohara, T. Brst symmetry of su(2) yang-mills theory in cho-faddeev-niemi decomposition. Eur. Phys. J. 2005, C42, 475–481. [Google Scholar] [CrossRef]
- Kondo, K.I. Gauge-invariant gluon mass, infrared Abelian dominance and stability of magnetic vacuum. Phys. Rev. 2006, D74, 125003. [Google Scholar] [CrossRef]
- Bae, W.S.; Cho, Y.M.; Kimm, S.W. Qcd versus skyrme-faddeev theory. Phys. Rev. 2002, D65, 025005. [Google Scholar]
- Walker, M.L. Stability of the magnetic monopole condensate in three- and four-colour qcd. JHEP 2007, 01, 056. [Google Scholar] [CrossRef]
- Walker, M.L. Higgs-free confinement hierarchy in five colour QCD. Prog. Theor. Phys. 2007, 119, 139–148. [Google Scholar] [CrossRef]
- Walker, M.L. Extending SU(2) to SU(N) QCD. Phys. Lett. B 2008, 662, 383–387. [Google Scholar] [CrossRef]
- Kondo, K.I.; Taira, Y. Non-abelian stokes theorem and quark confinement in su(3) yang-mills gauge theory. Mod. Phys. Lett. 2000, A15, 367–377. [Google Scholar] [CrossRef]
- Kondo, K.I.; Taira, Y. Non-abelian stokes theorem and quark confinement in su(n) yang-mills gauge theory. Prog. Theor. Phys. 2000, 104, 1189–1265. [Google Scholar] [CrossRef]
- Kondo, K.I. Wilson loop and magnetic monopole through a non-Abelian Stokes theorem. Phys. Rev. 2008, D77, 085029. [Google Scholar] [CrossRef]
- Matsudo, R.; Kondo, K.I. Non-Abelian Stokes theorem for the Wilson loop operator in an arbitrary representation and its implication to quark confinement. Phys. Rev. D 2015, 92, 125038. [Google Scholar] [CrossRef]
- Kondo, K.I.; Kato, S.; Shibata, A.; Shinohara, T. Quark confinement: Dual superconductor picture based on a non-Abelian Stokes theorem and reformulations of Yang–Mills theory. Phys. Rep. 2015, 579, 1–226. [Google Scholar] [CrossRef]
- Cho, Y.M.; Walker, M.L. Stability of monopole condensation in su(2) qcd. Mod. Phys. Lett. 2004, A19, 2707–2716. [Google Scholar] [CrossRef]
- Cho, Y.M.; Walker, M.L.; Pak, D.G. Monopole condensation and confinement of color in su(2) qcd. JHEP 2004, 05, 073. [Google Scholar] [CrossRef]
- Cho, Y.M.; Oh, S.H.; Kim, S. Abelian dominance in Einstein’s theory. Class. Quantum Gravity 2012, 29, 205007. [Google Scholar] [CrossRef]
- Cho, Y.M.; Oh, S.H.; Park, B.S. Abelian decomposition of Einstein’s theory: Restricted gravity. Grav. Cosm. 2015, 21, 257–269. [Google Scholar] [CrossRef]
- Walker, M.L.; Duplij, S. Gauge gravity vacuum in constraintless Clairaut-type formalism. Universe 2022, 8, 176. [Google Scholar] [CrossRef]
- Kim, S.W.; Pak, D.G. Lorentz Gauge Gravity and Induced Effective Theories. arXiv 2005, arXiv:gr-qc/0512151. [Google Scholar]
- Pak, D.G.; Kim, Y.; Tsukioka, T. Lorentz gauge theory as a model of emergent gravity. Phys. Rev. D 2012, 85, 084006. [Google Scholar] [CrossRef]
- Nottale, L. Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity; World Scientific: Singapore, 1993; pp. 224–229. [Google Scholar]
- Cho, Y.M.; Pak, D.G.; Park, B.S. A Minimal model of Lorentz gauge gravity with dynamical torsion. Int. J. Mod. Phys. A 2010, 25, 2867–2882. [Google Scholar] [CrossRef]
- Schwinger, J. On gauge invariance and vacuum polarization. Phys. Rev. 1951, 82, 664. [Google Scholar] [CrossRef]
- Cho, Y.M.; Lee, H.W.; Pak, D.G. Faddeev–Niemi conjecture and effective action of QCD. Phys. Lett. B 2002, 525, 347–354. [Google Scholar] [CrossRef]
- Shibata, A.; Ito, S.; Kato, S.; Kondo, K.-I.; Murakami, T.; Shinohara, T. Gluon mass generation and infrared Abelian dominance in Yang-Mills theory. PoS 2006, LAT2006, 074. [Google Scholar]
- Dudal, D.; Verschelde, H.; Browne, R.E.; Gracey, J.A. The 2PPI expansion: Dynamical mass generation and vacuum energy. In Proceedings of the Color Confinement and Hadrons in Quantum Chromodynamics; World Scientific: Singapore, 2004. [Google Scholar] [CrossRef]
- Dudal, D.; Gracey, J.A.; Lemes, V.E.R.; Sarandy, M.S.; Sobreiro, R.F.; Sorella, S.P.; Verschelde, H. Analytic study of the off-diagonal mass generation for Yang-Mills theories in the maximal Abelian gauge. Phys. Rev. D 2004, 70, 114038. [Google Scholar] [CrossRef]
- Lévy-Leblond, J.M. One more derivation of the Lorentz transformation. Am. J. Phys. 1976, 44, 271–277. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).