Abstract
We present a new exact solution of the thermal diffusion equations for steady-state shear flows of a binary fluid. Shear fluid flows are used in modeling and simulating large-scale currents of the world ocean, motions in thin layers of fluid, fluid flows in processes, and apparatuses of chemical technology. To describe the steady shear flows of an incompressible fluid, the system of Navier–Stokes equations in the Boussinesq approximation is redefined, so the construction of exact and numerical solutions to the equations of hydrodynamics is a very difficult and urgent task. A non-trivial exact solution is constructed in the Lin-Sidorov-Aristov class. For this class of exact solutions, the hydrodynamic fields (velocity field, pressure field, temperature field, and solute concentration field) were considered as linear forms in the x and y coordinates. The coefficients of linear forms depend on the third coordinate z. Thus, when considering a shear flow, the two-dimensional velocity field depends on three coordinates. It is worth noting that the solvability condition given in the article imposes a condition (relation) only between the velocity gradients. A theorem on the uniqueness of the exact solution in the Lin–Sidorov–Aristov class is formulated. The remaining coefficients of linear forms for hydrodynamic fields have functional arbitrariness. To illustrate the exact solution of the overdetermined system of Oberbeck–Boussinesq equations, a boundary value problem was solved to describe the complex convection of a vertical swirling fluid without its preliminary rotation. It was shown that the velocity field is highly stratified. Complex countercurrents are recorded in the fluid.
1. Introduction
World science knows the difficulty of integrating the Navier–Stokes equations for incompressible fluids (with constant density) [1,2,3,4]. The complexity of the analytical and numerical integration of the equations of motion of dissipative continuous media is a generally recognized Sixth Millennium Problem [5]. There is no doubt about the relevance of finding new classes of exact solutions of the three-dimensional Navier–Stokes equations for approaching the formulation of the existence and uniqueness theorem. It is clear that when describing real fluids and flows in technological, technical, natural, and biological processes, one must take into account that density is a thermodynamic medium (it depends on one or more physical parameters).
The functional dependence of density on temperature determines the basis for describing the convective motion of a fluid [6,7,8]. The first equations to describe the convective motion of a viscous fluid were obtained experimentally and theoretically from the Oberbeck–Boussinesq equations. In their derivation, a linear dependence of density on temperature was used [7,8,9,10,11,12,13,14]. It was further established that an impurity (solute) in a fluid similarly causes convection [15,16,17]. It should be noted that the thermal and concentration mechanisms of convection generation are fundamentally different physically. Mathematically speaking, the Oberbeck–Boussinesq equations for thermal convection and concentration convection differ only in dissipative coefficients in the heat conduction equation and in the diffusion equation, respectively [14,18,19,20,21,22,23,24]. These coefficients differ from each other by several orders of magnitude; therefore, one should expect differences in the structure and evolution of thermal and thermal solution flows.
Binary fluids (mixtures) are characterized by the appearance of a new source for the Archimedes force (heterogeneity of the concentration of a dissolved substance) and the competition of dissipative effects, due to which, unlike a pure medium, even the state of mechanical equilibrium in a mixture can be unstable. The interaction between convection, thermal conductivity, and diffusion is complicated by the presence of reverse effects: the appearance of a concentration gradient due to a change in temperature (thermal diffusion or the Soret effect) and the appearance of a temperature gradient due to a change in the concentration field (diffusion thermal conductivity or the Dufour effect) [15,16,17]. This physical mechanism further complicates the study of the Oberbeck–Boussinesq equations for thermal diffusion and the construction of exact solutions. A typical example illustrating the reasoning given above is seawater.
To solve problems, one can often use the reduction in the dimension of the velocity vector for three-dimensional fields of pressure, temperature, and concentration. In this case, mathematical models based on unidirectional and shear flows are used [18,19,20,21,25,26,27,28,29,30,31]. Exact solutions for unidirectional thermal diffusion flows are built on the basis of the Ostroumov–Birich class of exact solutions for a horizontal fluid layer or the Gershuni–Bachelor family of exact solutions for a vertical fluid layer [7,32,33,34,35,36,37,38]. Reviews on exact solutions for problems of convective, concentration, and thermal diffusion flows are contained in bibliographic sources [39,40,41,42,43,44,45].
In the transition to the study of shear flows, the researcher encounters an overdetermined Oberbeck–Boussinesq system [14,20,26,46,47]. The overdetermination of the system of equations arises due to the existence of a zero component of the velocity vector. For isothermal flows, first, in the Lin–Sidorov–Aristov class, the first non-trivial exact solution for isobaric flows was constructed [48,49,50]. Next, exact solutions were constructed for gradient and convective flows. In articles [20,21], the exact solutions for the thermal diffusion equations were obtained taking into account one of the Soret and Dufour effects. It was shown that these solutions differ due to different dissipative coefficients.
In this article, a new exact solution is constructed for steady-state shear thermal diffusion flows of viscous fluids, taking into account both cross effects (the Soret–Dufour effect). The corresponding theorem on the existence of a solution as a solution of the obtained overdetermined system in the class of functions linearly dependent on a part of spatial coordinates is formulated and proved. It is shown that the results obtained generalize the conclusions made by the authors earlier when analyzing more particular cases (taking into account only one of the thermal diffusion effects or completely ignoring them). The relevance of finding a new exact solution for describing shear flows of a viscous incompressible fluid is due to the fact that pioneering exact solutions for describing unidirectional Ostroumov–Birich and Gershuni–Butchelor flows are used as a basic flow for studying the hydrodynamic stability of convective and thermal diffusion flows [7,32,33,34,35,36,37,38]. It is clear that it is important to have an exact solution for a two-dimensional velocity field with a dependence on three coordinates in order to describe new non-trivial physical effects for steady flows, followed by a study of the hydrodynamic stability of new exact solutions for classical and non-classical perturbations.
2. Problem Statement
We consider the steady-state thermal diffusion flow of a Newtonian incompressible fluid, taking into account the cross-dissipative Soret and Dufour effects. The motion of a binary fluid is described by a system of thermal diffusion equations [7]:
To study the binary fluid flows, a three-dimensional rectangular Cartesian coordinate system was chosen. In the system of Equations (1)–(4), the following notations are introduced: is fluid velocity; is the deviation of pressure from hydrostatic, normalized to the average constant density of the fluid ; is the temperature deviation from the equilibrium state; is the deviation of the concentration of the light phase (impurity) of the binary fluid mixture from the equilibrium value; is the gravitational acceleration, and are the coefficients of thermal and concentration expansion, respectively; k is the unit vector of the Oz axis (applicate); is kinematic (molecular) viscosity; is the thermal diffusivity, is the diffusion coefficient; is the thermal diffusion coefficient (the Soret parameter); is the Dufour parameter; is the Hamilton operator; is the convective derivative; and is the Laplace operator.
We note that in the Navier–Stokes Equation (1), the last term describes the influence of the Archimedes force on the Boussinesq [9] approximation. System (1)–(4) is closed, since the number of equations in it coincides with the number of unknown functions for describing the distribution of hydrodynamic fields.
Next, we consider the shear flow of a fluid. In this case, the velocity vector contains one zero coordinate: . The use of shear flows is justified in describing large-scale fluid flows, taking into account the geometric anisotropy of the fluid layer (thin fluid layer). For large-scale fluid flows (in the world ocean), free-fall acceleration is a weakly changing parameter (up to 1% of the average value). Despite the fact that the real movement of the fluid is three-dimensional, for small values of one of the velocity components, it can be set equal to zero in the initial studies. The study of fluid motions for boundary conditions such as a “solid” cover can be carried out exhaustively using the model of shear flows [18,19,20,21,25,26,27,28,29,30,31].
We now write the reduced Equations (1)–(4) in coordinate form, taking into account the equality [21,51]:
The nonlinear overdetermined system (5) describes the flows of a binary fluid with a two-dimensional velocity field. Note that all hydrodynamic fields are three-dimensional. System (5) does not contain an isolated equation for the hydrodynamic field that could be used to find the compatibility condition (resolvability condition). Next, we pose the problem of obtaining an exact solution to the nonlinear overdetermined system (5) that differs from the trivial (zero) solution.
We find a nontrivial solution to the system (5) in the Lin–Sidorov–Aristov class [48,49,50]. Let hydrodynamic fields be represented by linear forms in terms of the coordinates:
The linear forms that define class (6) describe the nonlinear properties of a moving fluid due to the complex dependence of the coefficients of the exact solution (6) on the vertical coordinate z.
The structure of the family of exact solutions (6) using the method of indefinite coefficients makes it possible to make an equivalent transition from system (5) to a system of ordinary differential equations. To perform this, it suffices to substitute expressions (6) into each of the equations of system (5) and equate the coefficients in the resulting relations for the same degrees of horizontal coordinates x and y. As a result, we obtain a system of ordinary differential equations written in a way convenient for integrating the overdetermined system:
The prime in system (7)–(13) denotes taking the total derivative with respect to the variable z. System (7)–(13) inherits from system (5) the properties of nonlinearity and overdetermination. Note that the balance between the number of unknowns and the number of equations is violated only in system (7). In other words, if it is possible to find a non-trivial joint solution of the overdetermined subsystem (7), then a solution to any of the systems (8)–(13) can be found by successive integration.
In [14], a theorem was formulated and proved that determines the conditions for the existence of a necessary joint solution to subsystem (7). According to this theorem, the overdetermined system (7)–(13) has a non-trivial exact solution in class (6), which is an exact solution of system (5) if and only if the spatial accelerations , , , and satisfy the relations:
where is a function that satisfies the simplest second-order differential equation ; and is a real number.
A similar problem of finding a non-trivial joint solution of an overdetermined nonlinear system of constitutive relations arises not only when solving problems of thermal diffusion [20,51], but also when considering both convective flows [14] and isothermal flows [46] of a viscous incompressible fluid.
3. Construction of the Exact Solution
Furthermore, it will be established that the exact solution describing the steady flow of a binary fluid in class (6) is described by a polynomial in three variables. To perform this, we prove the following theorem.
Theorem 1.
For any values of the parameters
, , , defining the set of functions (14), for
the overdetermined system of differential Equations (8)–(13) has a unique solution.
For the case considered in [20], and in the case considered in [51], the condition is automatically satisfied. In other words, the problem posed in this article can be considered a generalization of the results obtained in [20,51]. Note that both dissipative coefficients (the Soret coefficient and the Dufour coefficient) are small in magnitude; therefore, the assumption of the theorem on the fulfillment of the condition is physically justified and interesting [52].
System (1)–(4) is used both for describing incompressible fluids and for modeling the flows of incompressible gases, which, in a certain range of physical conditions, is applicable to real (i.e., compressible) gases. It is for this reason that none of the coefficients are neglected in this case, and both dissipative coefficients are used in writing the basic equations of the model to create the most symmetrical form of writing, suitable for both fluid and gas flows.
We will prove the formulated theorem in a constructive way, i.e., we indicate an algorithm for integrating the equations of system (7)–(13). After the joint solution (14) of the overdetermined system (7) is obtained, the difficulty in obtaining a solution to system (8)–(13) lies only in constructing the order of integration of the remaining equations. For this reason, further proof of the formulated theorem with an indication of the order of integration of the equations and comments are given regarding the properties of the resulting solution.
Proof.
Equations (8) and (9) will be considered jointly since they constitute an isolated subsystem, taking into account expressions (14):
We transform Equation (15) as follows: we multiply the first equation of the system by and subtract from it the multiplied by the second equation of this system. After that, we integrate the resulting equation:
From the third and fourth equations of system (15), by analogous transformations, we obtain the following expression:
Let us solve relations (16), (17) with respect to horizontal gradients and :
The main determinant of the resulting matrix Equation (18) is as follows:
The last factor is assumed to be different from zero due to the conditions of the theorem being proved. Thus, the solvability of Equation (18) (and hence other equations of the system (10)–(13)) depends on the value of the parameter .
When , system (15) is greatly simplified and contains an isolated subsystem with respect to gradients and :
The first two equations of system (19) are a system of homogeneous linear equations with respect to derivatives and , with a non-degenerate (due to the conditions of the theorem) matrix. Hence, linear functions are its solution:
The last two equations of system (19) are (taking into account expressions (20)) a system of already inhomogeneous linear equations with respect to derivatives and , which is uniquely integrated:
The solution of the Equations (21) and (22) is a set of fourth-order polynomial functions. Thus, the solution of Equations (8) and (9) is constructed. The exact solution of Equation (10) for horizontal pressure gradients is easily obtained after a single solving of Equations (8) and (9). They are described by a polynomial of the fifth degree.
Equation (11) for the case are written more compactly:
First, the isolated equation of system (23) for the velocity V is integrated. A seventh-order polynomial is obtained, further substitution of which into the first equation of system (24) (presented below) makes it possible to determine the form of the velocity U as a tenth-order polynomial.
After this, we represent Equation (12) as a non-homogeneous matrix algebraic equation with respect to the second derivatives of the background components and of linear forms (6) with known polynomial homogeneity and a nonsingular matrix:
Having inverted the matrix of the system, we construct a solution after double integration and obtain a solution for the homogeneous components of the concentration and pressure fields. Then, based on them, we integrate Equation (13) and obtain a unique solution for the background pressure. The above-mentioned exact solutions for the components of class (6) are not given because of their cumbersomeness and elementary nature of calculations.
Let us return to the general case of Equation (19), setting . The matrix of the system will be non-degenerate, which means that the equation is solvable in a unique way:
Substituting expressions (24) into the first and third equations of system (15), we reach the following relations:
Resolving system (33) (its matrix is again non-singular) with respect to the second derivatives of the gradients and , we obtain:
The right-hand sides of system (26) contain polynomials of the second degree, so it can be easily integrated. After the exact solutions for the gradients and are found, according to (26), expressions for the gradients and are easily written out. Thus, system (8) and (9) are completely solved.
Further proof of the theorem is reduced to sequential integration of systems (10)–(13), the algorithm of which (and the justification for the uniqueness of the resulting solution) is given above when considering the case. Thus, the formulated theorem is completely proved. □
4. Boundary Value Problem
As an interpretation of the structure of the exact solution obtained by proving the theorem formulated above, we formulate a boundary value problem. We will consider a steady thermal diffusion shear flow of a viscous incompressible fluid in a horizontal infinitely extended layer with both non-deformable boundaries (Figure 1).
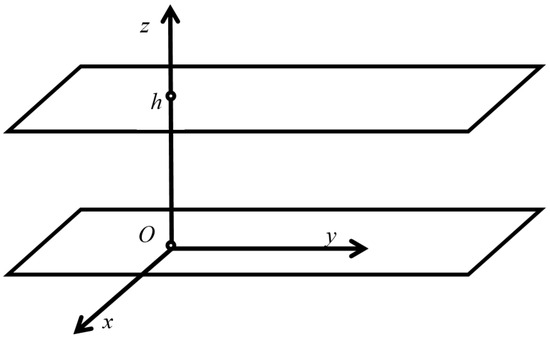
Figure 1.
The flow scheme.
The solution of system (7)–(13) we will look for the exact solution of the Oberbeck–Boussinesq system (5) in the following form:
Class (27) is a special case of class (6), when the spatial gradients , , and are assumed to be equal to zero. In this case, the overdetermined system (7) is reduced to one isolated equation for determining the only non-zero spatial acceleration:
This solution satisfies relations (14) for . Previously, the exact solution (27) was proposed to study a vertically swirling fluid in the absence of rotation for isothermal, gradient, and convective flows [14,18,25,26,51]. In articles [19,20,21,46,47,51], it was shown that the velocity field (27) can be used to model and simulate equatorial countercurrents. The formulas given below will take into account not only the effect of heat on the structure of the ocean, but also the distribution of salt in water.
To determine the constants of integration arising in the process of constructing a solution to system (27), we formulate the boundary conditions. We will assume that the no-slip condition is satisfied at the lower boundary (bottom):
In addition, the lower boundary will be considered impenetrable and thermally insulated:
On the upper boundary, we consider that the inhomogeneous distribution of the given velocities corresponds to the movement of the upper boundary as a solid surface:
Here, is the value of the velocity at the upper boundary and is the angle that the velocity vector forms with the abscissa axis Ox.
We represent the boundary condition for pressure in the following form:
where corresponds to the atmospheric pressure.
In addition, we assume that the temperature and concentration are distributed nonuniformly at the upper boundary of the layer:
According to the representation (27) for hydrodynamic fields, the formulated boundary conditions are reduced to the following conditions:
on the lower border;
at the upper boundary of the considered layer.
The solution of the boundary value problem (27)–(29) is a set of polynomial functions:
In the representation of solution (30), a dimensionless vertical coordinate Z = z/h is introduced, the values of which vary within the considered layer in the range [0, 1]. This makes it possible to analyze the behavior of flows in layers of different thicknesses from a unified standpoint. Note that the solution to the boundary value problem is given incompletely due to two circumstances:
(1) the expressions for the fields of temperature, concentration, and pressure turn out to be too cumbersome;
(2) the main interest is the structure (profile) of the velocity field and its mapping onto the phase space.
The homogeneous components of the velocity field (27) are described by high-order polynomials, which indicates the possibility of the existence of several stagnant points of the field. Passing through the latter, the fluid flow is able to change the direction of the flow. In other words, multiple stratification of the velocity field is possible due to the mutual influence of thermal and diffusion factors.
The velocity U is described by a polynomial of the ninth degree; however, the number of zero points of this speed does not exceed seven, and one of these zero points is located on the lower boundary of the layer. Similar conclusions are given for the velocity V: this polynomial of the sixth degree vanishes within the considered layer no more than three times. The corresponding profiles are shown in Figure 2 and Figure 3, respectively.
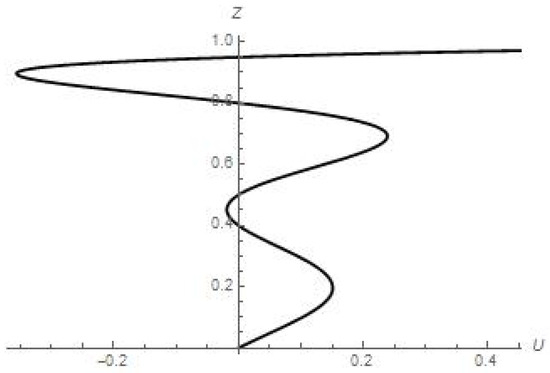
Figure 2.
The velocity U profile.
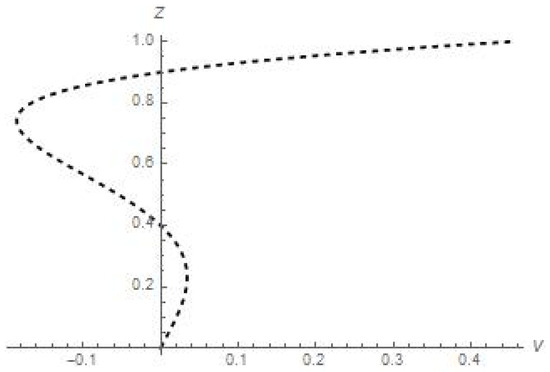
Figure 3.
The velocity V profile.
The existence of a large number of zero points (stratification points) for these velocity field components leads to the fact that the shape of the velocity field hodograph turns out to be extremely complex (Figure 4).
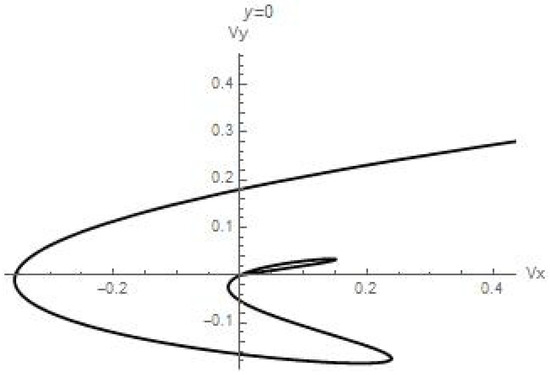
Note that the view of the hodograph , shown in Figure 4 is valid only for the cross-section y = 0, since, strictly speaking, due to expressions (27), it is also necessary to take into account the inhomogeneous terms in the expression for the velocity Vx. The corresponding term u2y, according to solution (30), is a linear dependence on the vertical coordinate Z, which leads to a “straightening” of the velocity profile U with distance from the control section y = 0 (Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10).
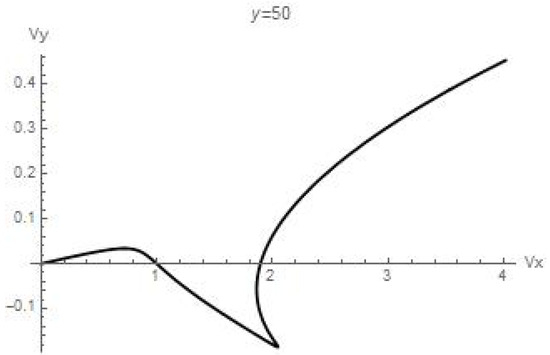
Figure 5.
The hodograph of the velocity field.
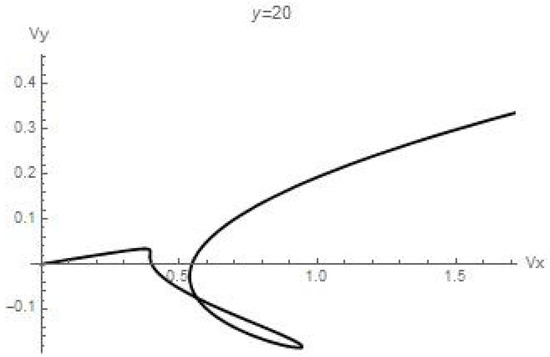
Figure 6.
The hodograph of the velocity field.
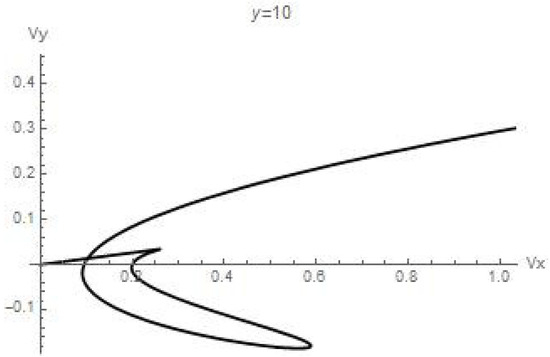
Figure 7.
The hodograph of the velocity field.
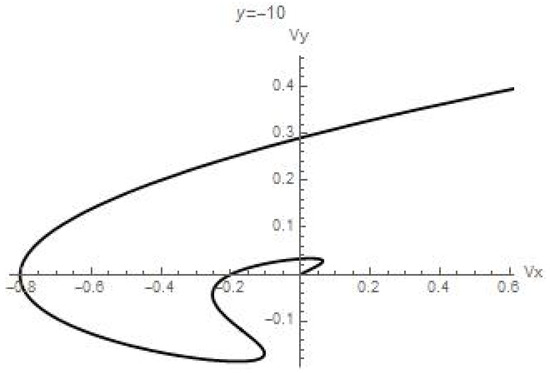
Figure 8.
The hodograph of the velocity field.
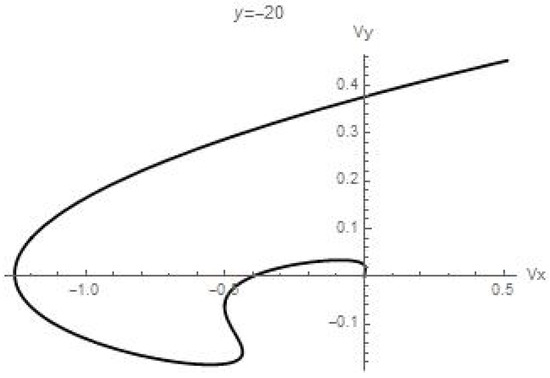
Figure 9.
The hodograph of the velocity field.
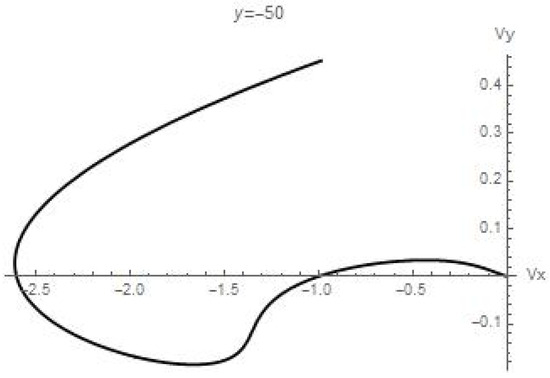
Figure 10.
The hodograph of the velocity field.
An interesting effect of localization of vortex structures can be observed on the graph of the stream function corresponding to the constructed solution (Figure 11). It illustrates the complex flow structure. Counterflows with several zones of return flows are registered in the fluid. Such a complex flow structure is due to the inhomogeneous velocity distribution, thermal convection, concentration convection, and thermal diffusion.
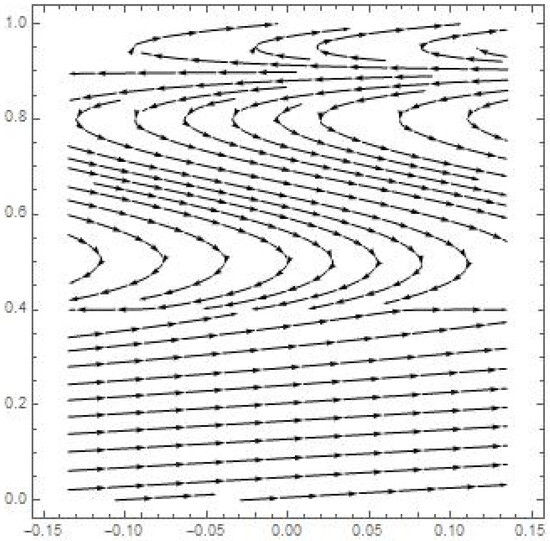
Figure 11.
The stream function.
The stream function characterizes the value of the volumetric flow rate of the fluid through the cross-section of the channel built on streamlines. The curves in Figure 11 illustrate the non-uniformity of this flow rate. Consideration of both dissipative Soret and Dufour effects when describing thermal diffusion flows leads to the appearance of an additional stagnation point for the velocity field (29) and (30) if we consider the exact solutions only with the Soret effect [21] or only with the Dufour effect [51] taken into account. Thus, the competing interaction of the Soret and Dufour effects leads not only to quantitative changes for hydrodynamic fields, but also to a qualitative (topological) change in the stratification of the velocity field, pressure field, temperature field, and solute concentration field.
5. Conclusions
This article considers the problem of describing thermal diffusion flows, taking into account both cross effects (the Soret–Dufour effect) for shear flows. It is shown that consideration of shear flows simplifies the structure of the velocity field; however, it leads to overdetermination of the system of model equations. The solution of the overdetermined system is sought in the class of functions that can be represented as complete linear forms in two spatial coordinates. This class is capable of describing the nonlinear effects observed in a fluid in view of the nonlinear dependence of the coefficients of the mentioned linear forms on the third coordinate, despite the external simplicity of its structure. A theorem on the solvability of the resulting overdetermined nonlinear system is formulated and proved under the compatibility conditions presented in the earlier studies of the authors [14,20,26,51] and the fulfillment of an additional condition on thermal diffusion coefficients. The study (the formulated solvability theorem and its proof) generalizes the results obtained by the authors earlier [20,51] for thermal diffusion shear flows. In addition, while proving the central theorem of the article, we identified the conditions under which branching into the structures of the constructed exact solution of the overdetermined system appears. To illustrate the exact solution found, we consider a boundary value problem for describing an inhomogeneous shear flow of a vertically swirling fluid. The field of velocities described by polynomials for the ninth degree is investigated. It is shown that the velocity field is stratified depending on the boundary conditions and dissipative coefficients in different ways. In this case, counterflows are recorded in the liquid, and the flow itself is spiral. In addition, an example of velocity profiles that differ from studies [21,51] is given. Accounting for both the Soret and Dufour effects leads to the appearance of new effects even for steady flows with subsequent ones. Thus, it will be important to use the exact solution obtained in the article as a basic flow for studying hydrodynamic instability. Let us also mention works among [53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75,76,77,78,79,80,81,82,83,84,85], where these refs. are within the framework of the analytical approach to the study of mathematical hydrodynamical models.
Author Contributions
Conceptualization, N.B., S.E. and E.Y.P.; methodology, N.B., S.E., E.Y.P. and D.D.L.; writing—original draft preparation, N.B., S.E. and E.Y.P.; writing—review and editing, N.B., S.E., E.Y.P. and D.D.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data for this paper are available by contacting the corresponding author.
Conflicts of Interest
The authors declare that there are no conflicts of interest regarding the publication of article.
References
- Ladyzhenskaya, O.A.; Seregin, G.A. Mathematical Problems of Hydrodynamics and Magnetohydrodynamics of a Viscous Incompressible Fluid. Proc. V.A. Steklov Math. Inst. 1960, 59, 115–173. [Google Scholar]
- Serrin, J. Mathematical Principles of Classical Fluid Mechanics. In Fluid Dynamics I/Strömungsmechanik I; Springer: Berlin/Heidelberg, Germany, 1959; p. 139. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; VI: Fluid Mechanics; Pergamon Press: Oxford, UK, 1959; Volume 10, p. 229. [Google Scholar]
- Andreev, V.K.; Kaptsov, O.V.; Pukhnachev, V.V.; Rodionov, A.A. Applications of Group-Theoretical Methods in Hydrodynamics; Springer Science + Business Media B.V.: Berlin, Germany; Springer: Dordrecht, The Netherlands, 1998. [Google Scholar]
- Carlson, J.A.; Jaffe, A.; Wiles, A. The Millennium Prize Problems. Clay Mathematics Institute; American Mathematical Society: Cambridge, MA, USA, 2006; ISBN 978-0-8218-3679-8. [Google Scholar]
- De Groot, S.R. Thermodynamik Irreversibler Prozesse; North-Holland Publishing Comp.: Amsterdam, The Netherlands, 1951. [Google Scholar]
- Gershuni, G.Z.; Zhukhovitskii, E.M. Convective Stability of Incompressible Fluids; Keter Publishing House: Jerusalem, Israel, 1976; p. 299. [Google Scholar]
- Kochin, N.E.; Kibel, I.A.; Radok, J.R.M.; Roze, N.V. Theoretical Hydromechanics; Interscience Publishers: New York, NY, USA, 1964; p. 569. [Google Scholar]
- Boussinesq, J. Théorie Analytique de la Chaleur; Gauthier-Villars: Paris, France, 1903; Volume 2. [Google Scholar]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Marshall, W., Wilkinson, D.H., Eds.; International Series of Monographs on Physics Clarendon Press; Oxford University Press: Oxford, UK, 1961. [Google Scholar]
- Barletta, A.; Celli, M.; Rees, D.A.S. On the Use and Misuse of the Oberbeck–Boussinesq Approximation. Physics 2023, 5, 298–309. [Google Scholar] [CrossRef]
- Mizerski, K.A. The Oberbeck-Boussinesq Convection. In Foundations of Convection with Density Stratification; GeoPlanet: Earth and Planetary Sciences; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Mayeli, P.; Sheard, G.J. Buoyancy-driven flows beyond the Boussinesq approximation: A brief review. Int. Commun. Heat Mass Transf. 2021, 125, 105316. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Prosviryakov, E.Y. Exact Solutions for Steady Convective Layered Flows with a Spatial Acceleration. Russ. Math. 2021, 65, 8–16. [Google Scholar] [CrossRef]
- Ludwig, C. Diffusion Zwischen Ungleich Erwärmten Orten Gleich Zusammengesetzter. Lösungen. In Enthalten in Sitzungsberichte der Mathematisch-Naturwissenschaftlichen Classe der Kaiserlichen Akademie der Wissenschaften; Sitzungsbericht; Aus Der K.K. Hof-Und Staatsdruckerei: Wien, Austria, 1856; 540p. [Google Scholar]
- Soret, C. Sur L’état d’équilibre que prend, du point de vue de sa concentration, une dissolution saline primitivement homogène, dont deux parties sont portées à des températures différentes. Arch. Sci. Phys. Natur. 1879, 2, 48–61. [Google Scholar]
- Dufour, L. Ueber die diffusion der gase durch poröse wände und die sie begleitenden temperaturveränderungen. Arc. Phys. Nat. Sci. 1872, 45, 490–492. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Prosviryakov, E.Y. Exact solution for Couette-type steady convective concentration flows. J. Appl. Mech. Tech. Phys. 2021, 62, 1199–1210. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Privalova, V.V.; Prosviryakov, E.Y. Layered Marangoni convection with the Navier slip condition. Sādhanā 2021, 46, 55. [Google Scholar] [CrossRef]
- Burmasheva, N.; Prosviryakov, E. Influence of the Dufour Effect on Shear Thermal Diffusion Flows. Dynamics 2022, 2, 367–379. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Prosviryakov, E.Y. On Marangoni shear convective flows of inhomogeneous viscous incompressible fluids in view of the Soret effect. J. King Saud Univ.–Sci. 2020, 32, 3364–3371. [Google Scholar] [CrossRef]
- Semin, M.; Levin, L. Study of the Influence of Thermal Convection on Temperature Measurement in Thermal Control Boreholes during Artificial Ground Freezing. Fluids 2022, 7, 298. [Google Scholar] [CrossRef]
- Rajesh, V.; Sheremet, M. Natural Convection of Ternary Hybrid Nanofluid in a Differential-Heated Enclosure with Non-Uniform Heating Wall. Micromachines 2023, 14, 1049. [Google Scholar] [CrossRef] [PubMed]
- Astanina, M.S.; Sheremet, M.A. Unsteady Free Convection of Fluid with Variable Viscosity in a Partially Porous Cube Under an Influence of Energy Source. In Recent Advances in Fluid Dynamics; Banerjee, J., Shah, R.D., Agarwal, R.K., Mitra, S., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2023. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Prosviryakov, E.Y. Convective layered flows of a vertically whirling viscous incompressible fluid. Velocity field investigation. J. Samara State Tech. Univ., Ser. Phys. Math. Sci. 2019, 23, 341–360. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Burmasheva, N.V.; Prosviryakov, E.Y. Exact Solutions to the Navier–Stokes Equations with Couple Stresses. Symmetry 2021, 13, 1355. [Google Scholar] [CrossRef]
- Yariv, E. Effective slip length for longitudinal shear flow over partially invaded grooves: Small solid-fraction approximations. Phys. Rev. Fluids 2023, 8, L012101. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rajagopal, K.R.; Vergori, L. Channel flows of shear-thinning fluids that mimic the mechanical response of a Bingham fluid. Int. J. Non-Linear Mech. 2022, 138, 103847. [Google Scholar] [CrossRef]
- Fu, X.; Fu, S.; Ren, H.; Xie, W.; Xu, Y.; Zhang, M.; Liu, Z.; Meng, S. Experimental investigation of vortex-induced vibration of a flexible pipe in bidirectionally sheared flow. J. Fluids Struct. 2022, 114, 103722. [Google Scholar] [CrossRef]
- Rezghi, A.; Zhang, J. Tank-treading dynamics of red blood cells in shear flow: On the membrane viscosity rheology. Biophys. J. 2022, 121, 3393–3410. [Google Scholar] [CrossRef]
- Raghav, M.S.; Jose, S.; Apte, A.; Govindarajan, R. Effects of equatorially-confined shear flow on MRG and Rossby waves. Dyn. Atmos. Ocean. 2022, 100, 101331. [Google Scholar] [CrossRef]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Ostroumov, G.A. Svobodnaya Konvektsiya v Usloviyakh Vnutrennei Zadachi (Free Convection in Inner Problem Conditions); Gostekhizdat: Moscow, Russia, 1952. [Google Scholar]
- Birikh, R.V. Thermocapillary convection in a horizontal layer of fluid. J. Appl. Mech. Tech. Phys. 1966, 7, 43–44. [Google Scholar] [CrossRef]
- Andreev, V.K.; Bekezhanova, V.B. Stability of Non-Isothermal Fluids. J. Appl. Mech. Tech. Phys. 2013, 54, 171–184. [Google Scholar] [CrossRef]
- Schwarz, K.G. Plane-Parallel Advective Flow in a Horizontal Incompressible Fluid Layer with Rigid Boundaries. Fluid Dyn. 2014, 49, 438–442. [Google Scholar] [CrossRef]
- Goncharova, O.; Kabov, O. Gas Flow and Thermocapillary Effects of Fluid Flow Dynamics in a Horizontal Layer. Micrograv. Sci. Technol. 2009, 21 (Suppl. 1), 129–137. [Google Scholar] [CrossRef]
- Andreev, V.K.; Ryzhkov, I.I. On thermocapillary instability of a fluid column with a co-axial gas flow. J. Sib. Fed. Univ. Math. Phys. 2013, 6, 3–17. [Google Scholar]
- Bazant, M.Z. Exact solutions and physical analogies for unidirectional flows. Phys. Rev. Fluids 2016, 1, 024001. [Google Scholar] [CrossRef]
- Subin, P.J. Different families of new exact solutions for planar and nonplanar second grade fluid flows. Chin. J. Phys. 2022, 77, 1225–1235. [Google Scholar] [CrossRef]
- El Moutaouakil, L.; Boukendil, M.; Hidki, R.; Charqui, Z.; Zrikem, Z.; Abdelbaki, A. Analytical solution for natural convection of a heat-generating fluid in a vertical rectangular cavity with two pairs of heat source/sink. Therm. Sci. Eng. Prog. 2023, 40, 101738. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Jan, S.A.A. Samiulhaq. Exact solutions for free convection flow of generalized Jeffrey fluid: A Caputo-Fabrizio fractional model. Alex. Eng. J. 2018, 57, 1849–1858. [Google Scholar] [CrossRef]
- Song, J.-J.; Li, P.-X.; Chen, L.; Li, C.-H.; Li, B.-W.; Huang, L.-Y. A review on Rayleigh-Bénard convection influenced by the complicating factors. Int. Commun. Heat Mass Transf. 2023, 144, 106784. [Google Scholar] [CrossRef]
- Bekezhanova, V.B.; Stepanova, I.V. Evaporation convection in two-layers binary mixtures: Equations, structure of solution, study of gravity and thermal diffusion effects on the motion. Appl. Math. Comput. 2022, 414, 126424. [Google Scholar] [CrossRef]
- Molati, M.; Murakawa, H. Exact solutions of nonlinear diffusion-convection-reaction equation: A Lie symmetry analysis approach. Commun. Nonlinear Sci. Numer. Simul. 2019, 67, 253–263. [Google Scholar] [CrossRef]
- Burmasheva, N.V.; Prosviryakov, E.Y. Exact solution of Navier–Stokes equations describing spatially inhomogeneous flows of a rotating fluid. Tr. Instituta Mat. Mekhaniki URO RAN 2020, 26, 79–87. [Google Scholar]
- Burmasheva, N.V.; Prosviryakov, E.Y. Exact solutions to the Navier–Stokes equations describing stratified fluid flows. J. Samara State Tech. Univ. Ser. Phys. Math. Sci. 2021, 25, 491–507. [Google Scholar] [CrossRef]
- Lin, C.C. Note on a class of exact solutions in magneto-hydrodynamics. Arch. Ration. Mech. Anal. 1957, 1, 391–395. [Google Scholar] [CrossRef]
- Sidorov, A.F. Two classes of solutions of the fluid and gas mechanics equations and their connection to traveling wave theory. J. Appl. Mech. Tech. Phys. 1989, 30, 197–203. [Google Scholar] [CrossRef]
- Aristov, S.N. Eddy Currents in Thin Fluid Layers. Ph.D. Thesis, Institute of Automation and Control Processes, Vladivostok, Russia, 1990. (In Russian). [Google Scholar]
- Burmasheva, N.V.; Prosviryakov, E.Y. Exact solutions to the Oberbeck–Boussinesq equations for shear flows of a viscous binary fluid with allowance made for the Soret effect. The Bulletin of Irkutsk State University. Ser. Math. 2021, 37, 17–30. [Google Scholar]
- Karlin, L.N.; Klyukov, E.Y.; Kutko, V.P. Small–Scale Structure of Hydrophysical Fields of the Upper Ocean Layer; M.: Hydrometeoizdat, Moscow, 1988; 162p. [Google Scholar]
- Ershkov, S.V. Non-stationary helical flows for incompressible 3D Navier-Stokes equations. Appl. Math. Comput. 2016, 274, 611–614. [Google Scholar] [CrossRef]
- Thambynayagam, R.K.M. A class of exact solutions of the Navier–Stokes equations in three and four dimensions. Eur. J. Mech. B/Fluids 2023, 100, 12–20. [Google Scholar] [CrossRef]
- Nadeem, S.; Akhtar, S.; Alharbi, F.M.; Saleem, S.; Issakhov, A. Analysis of heat and mass transfer on the peristaltic flow in a duct with sinusoidal walls: Exact solutions of coupled PDEs. Alex. Eng. J. 2022, 61, 4107–4117. [Google Scholar] [CrossRef]
- Pukhnachev, V.V. Symmetries in the Navier–Stokes equations. Uspekhi Mekhaniki 2006, 1, 6–76. [Google Scholar]
- Ershkov, S.; Prosviryakov, E.; Leshchenko, D. Exact solutions for isobaric inhomogeneous Couette flows of a vertically swirling fluid. J. Appl. Computat. Mech. 2023, 9, 521–528. [Google Scholar]
- Korobkov, M.V.; Pileckas, K.; Pukhnachov, V.V.; Russo, R. The flux problem for the Navier–Stokes equations. Russ. Math. Surv. 2014, 69, 1065–1122. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Nonlinear Partial Differential Equations; Chapman & Hall: Boca Raton, FL, USA; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Ershkov, S.V.; Christianto, V.; Shamin, R.V.; Giniyatullin, A.R. About analytical ansatz to the solving procedure for Kelvin–Kirchhoff equations. Eur. J. Mech. B/Fluids 2020, 79C, 87–91. [Google Scholar] [CrossRef]
- Ershkov, S.V. Non-stationary creeping flows for incompressible 3D Navier–Stokes equations. Eur. J. Mech. B/Fluids 2017, 61, 154–159. [Google Scholar] [CrossRef]
- Ershkov, S.V. On Existence of General Solution of the Navier-Stokes Equations for 3D Non-Stationary Incompressible Flow. Int. J. Fluid Mech. Res. 2015, 42, 206–213. [Google Scholar] [CrossRef]
- Joseph, S.P. New classes of periodic and non-periodic exact solutions for Newtonian and non-Newtonian fluid flows. Int. J. Eng. Sci. 2022, 180, 103740. [Google Scholar] [CrossRef]
- Fushchich, V.I.; Popovich, R.O. Symmetry reduction and exact solutions of the Navier–Stokes equations. I. J. Nonlinear Math. Phys. 1994, 1, 75–113. [Google Scholar] [CrossRef]
- Fushchich, V.I.; Popovich, R.O. Symmetry reduction and exact solutions of the Navier–Stokes equations. II. J. Nonlinear Math. Phys. 1994, 1, 156–188. [Google Scholar] [CrossRef]
- Ludlow, D.K.; Clarkson, P.A.; Bassom, A.P. Nonclassical symmetry reductions of the three-dimensional incompressible Navier–Stokes equations. J. Phys. A 1998, 31, 7965–7980. [Google Scholar] [CrossRef]
- Meleshko, S.V. A particular class of partially invariant solutions of the Navier–Stokes equations. Nonlinear Dyn. 2004, 36, 47–68. [Google Scholar] [CrossRef]
- Shapeev, V.P.; Sidorov, A.F.; Yanenko, N.N. Methods of Differential Constrains and Its Applications in Gas Dynamics; Nauka: Novosibirsk, Russia, 1984; p. 272. (In Russian) [Google Scholar]
- Baranovskii, E.S. Optimal boundary control of nonlinear-viscous fluid flows. Sb. Math. 2020, 211, 505–520. [Google Scholar] [CrossRef]
- Baranovskii, E.S.; Artemov, M.A. Existence of optimal control for a nonlinear-viscous fluid model. Int. J. Differ. Equ. 2016, 2016, 9428128. [Google Scholar] [CrossRef]
- Burmasheva, N.; Ershkov, S.; Prosviryakov, E.; Leshchenko, D. Exact Solutions of Navier–Stokes Equations for Quasi-Two-Dimensional Flows with Rayleigh Friction. Fluids 2023, 8, 123. [Google Scholar] [CrossRef]
- Meleshko, S.V.; Pukhnachev, V.V. On a class of partially invariant solutions of the Navier-Stokes equations. J. Appl. Mech. Tech. Phys. 1999, 40, 208–216. [Google Scholar] [CrossRef]
- Christianto, V.; Smarandache, F. An Exact Mapping from Navier-Stokes Equation to Schroedinger Equation. Prog. Phys. 2008, 1, 38–39. [Google Scholar]
- Pukhnachev, V.V. Group properties of the Navier-Stokes equations in a plane case Prikl. Mekh. Tekh. Fiz. 1960, 1, 83–90. [Google Scholar]
- Aristov, S.N.; Schwarz, K.G. Vortex Flows of Advective Nature in a Rotating Fluid Layer; Perm State University: Perm, Russia, 2006; p. 154. (In Russian) [Google Scholar]
- Aristov, S.N.; Schwarz, K.G. Vortex Currents in Thin Fluid Layers; Perm State University: Perm, Russia, 2011; p. 207. (In Russian) [Google Scholar]
- Alekseev, G.; Tereshko, D. Stability of optimal controls for the stationary Boussinesq equations. Int. J. Differ. Equat. 2011, 2011, 535736. [Google Scholar] [CrossRef]
- Pukhnachev, V.V. Non-stationary Analogues of the Birikh Solution. Izv. Altai State Univ. 2011, 69, 62–69. (In Russian) [Google Scholar]
- Birikh, R.V.; Pukhnachev, V.V. An axial convective flow in a rotating tube with a longitudinal temperature gradient. Dokl. Phys. 2011, 56, 47–52. [Google Scholar] [CrossRef]
- Polyanin, A.D. Exact solutions to the Navier-Stokes equations with generalized separation of variables. Dokl. Phys. 2001, 46, 726–731. [Google Scholar] [CrossRef]
- Baranovskii, E.S. Steady flows of an Oldroyd fluid with threshold slip. Commun. Pure Appl. Anal. 2019, 18, 735–750. [Google Scholar] [CrossRef]
- Baranovskii, E.S. On flows of Bingham-type fluids with threshold slippage. Adv. Math. Phys. 2017, 2017, 7548328. [Google Scholar] [CrossRef]
- Korobkov, M.; Pileckas, K.; Russo, R. On the Flux Problem in the Theory of Steady Navier–Stokes Equations with Nonhomogeneous Boundary Condition. Arch. Ration. Mech. Anal. 2013, 207, 185–213. [Google Scholar] [CrossRef][Green Version]
- Polyanin, A.D.; Zhurov, A.I. Methods of Separation of Variables and Exact Solutions of Nonlinear Equations of Mathematical Physics; Institute for Problems of Mechanics of RAS: Moscow, Russia, 2020; p. 384. [Google Scholar]
- Koptev, A.V. Nonlinear Effects in Poiseuille Problem. J. Sib. Fed. Univ.-Math. Phys. 2013, 6, 308–314. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).