Accelerated Subgradient Extragradient Algorithm for Solving Bilevel System of Equilibrium Problems

Abstract

In this research paper, we propose a novel approach termed the inertial subgradient extragradient algorithm to solve bilevel system equilibrium problems within the realm of real Hilbert spaces. Our algorithm is capable of circumventing the necessity for prior knowledge about the Lipschitz constant of the involving bifunction and only computes the minimization of strong bifunctions onto the feasible set that is required. Under appropriate conditions, we establish strong convergence theorems for our proposed algorithms. To validate our algorithms, we illustrate a series of numerical examples. Through these examples, we demonstrate the performance of the algorithms we have put forth in this paper.

1. Introduction

Throughout this article, let H be a real Hilbert space and C be a nonempty closed convex subset of H. $I=1,2,\dots ,N$ is set a finite index. This work studies the bilevel system of equilibrium problems (shortly, $BSEP(g_i,f,C)$) as follows:

$$\mathrm{Find}{x}^{*}\in \mathsf{\Omega }=\bigcap _{i=1}^{N}SEP(g_i,C)\mathrm{such}\mathrm{that}f(x^{*},y)\ge 0\mathrm{for}\mathrm{every}y\in \mathsf{\Omega }.$$

(1)

where f and ${\left\{g_i\right\}}_{i\in I}$ are finite family of bifunctions from $H\times H$ to $\mathbb{R}$, such that $f(x,x)=0$ and $g_i(x,x)=0$ for every $x\in H$; $SEP(g_i,C)$ is the nonempty solution set of the equilibrium problem defined as follows:

$$g_i(x^{*},y)\ge 0\mathrm{for}\mathrm{all}y\in C.$$

The solution set of (1) is denoted as ${\mathsf{\Omega }}^{*}$.

In the case of $N=1$, we see that the $BSEP(g_i,f,C)$ can be considered on bilevel equilibrium problems, introduced in 2000 by Chadli et al. [1] and developed by Moudafi [2] (see also [3,4,5,6,7,8,9]), such that the bilevel equilibrium problem is defined by the following:

$$\mathrm{Find}{x}^{*}\in SEP(g,C)\mathrm{such}\mathrm{that}f(x^{*},y)\ge 0\mathrm{for}\mathrm{every}y\in SEP(g,C).$$

(2)

where f and g are bifunctions from $H\times H$ to $\mathbb{R}$. $SEP(g,C)$ is the nonempty solution set of the equilibrium problem defined as follows:

$$g(x^{*},y)\ge 0\mathrm{for}\mathrm{every}y\in C.$$

(3)

The authors of [10] show that the function f is strong monotonicity and of Lipschitz-type continuity. Then, the Equation (2) has a unique solution. Equation (3), referred to as the Ky Fan inequality, is an homage to the contributions of this field [11], and Equation (3) can be transformed into many special cases, for instance, fixed point problems, variational inequality problems, optimization problems, saddle point problems, and the Nash equilibrium problem in noncooperative game; see details in [12,13,14,15,16].

The proximal-like method was presented as the first methods to solve the Equation (3). This methodology, rooted in the auxiliary problem principle, was presented in [17]. Under different assumptions, the bifunction is pseudomonotone and Lipschitz-type continuous; it obtains the convergence result see more in [18]. More precisely, the method in [18] is generated by sequence $\left\{x_n\right\}$ and $\left\{y_n\right\}$ as follows:

$$\left\{\begin{array}{cc}{x}_0\in C\hfill & \\ y_n=\mathrm{argmin}\{\lambda f(x_n,y)+\frac{1}{2}\parallel y-x_n{\parallel }^2:y\in C\}\hfill & \\ x_{n+1}=\mathrm{argmin}\{\lambda f(y_n,z)+\frac{1}{2}\parallel z-x_n{\parallel }^2:z\in C\},\hfill & \end{array}\right.$$

where $\lambda >0$ is a suitable parameter. In recent years, many authors paid attention to the integration of inertial techniques into traditional algorithms that aimed to modify algorithms to solve Equation (3) (see [19,20]). It is underscored that most algorithms must use the knowledge of Lipschitz-type constants of the bifunction in order to choose suitable stepsize $\lambda$. These constants are often limitations or not practical for actual use in practice. Nevertheless, two optimization sub-problems on the feasible set C need to be solved during each iteration, which is high overhead and affects the performance of the algorithm. To circumvent this problem, many authors introduced a self-adaptive stepsize procedure so that the knowledge of Lipschitz-type constants of the bifunction is not necessary (see [21,22]).

For the bilevel equilibrium Equation (2), there are many methods to solve Equation (2). The authors of [2] introduced a simple proximal method and obtained a weak convergence to solve Equation (2). By using the proximal method and Halpern method to solve the bilevel monotone equilibrium and fixed point problem [6]. For more bilevel equilibrium problem details and recent works on the methods to solve equilibrium problems, we refer the reader to [3,4,5,23,24].

Recently, Anh et al. [25] proposed a new explicit extragradient algorithm for solving a class of bilevel equilibriums, which is generated by

$$\left\{\begin{array}{cc}{x}_0\in C\hfill & \\ y_n=\mathrm{argmin}\{{\lambda }_n(g(x_n,y)+\Phi \left(y\right))+\frac{1}{2}\parallel y-x_n{\parallel }^2:y\in C\}\hfill & \\ z_n=\mathrm{argmin}\{{\lambda }_n(g(y_n,z)+\Phi \left(z\right))+\frac{1}{2}\parallel z-x_n{\parallel }^2:z\in C\}\hfill & \\ x_{n+1}=\mathrm{argmin}\{{\beta }_{n}f(z_n,t)+\frac{1}{2}\parallel y-z_n{\parallel }^2:t\in C\}\hfill & \end{array}\right.$$

under the bifunctions f and g, which are Lipschitz continuous and monotone on C. The convergence of $\left\{x_n\right\}$ is obtained. Moreover, the strong convergence is obtained under the main assumptions that the Lipschitz-type constant of the bifunction is known.

Motivated and inspired by all of the above contributions, in this work, we will propose iterative algorithms for finding the solution of the bilevel system of equilibrium problems. The strong convergence of the sequence generated by the proposed method is obtained under the main assumptions that the Lipschitz-type constant of the bifunction is unknow. Finally, we present a numerical result of our algorithm, which show that our algorithm has efficiency.

2. Preliminaries

In this part, we present some definitions and lemmas in the following for proving convergent theorem. For each $x,y\in H,$ we have

$${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2⟨y,x+y⟩.$$

(4)

Let $f:H\times H\to \mathbb{R}$.

(i)

f is $\beta$-strongly monotone on C if

$$f(x,y)+f(y,x)\le {-\beta \parallel x-y\parallel }^2\forall x,y\in C;$$

(ii)

f is monotone on C if

$$f(x,y)+f(y,x)\le 0\forall x,y\in C;$$

(iii)

f is pseudomonotone on C if

$$f(x,y)\ge 0\Rightarrow f(y,x)\le 0,\forall x,y\in C.$$

For each $x\in H,$ let $f(x,·)$ be convex, and the subdifferential of $f(x,.)$ at x, denoted by ${\partial }_{2}f(x,x)$, is defined by

$$\begin{array}{ccc}\hfill {\partial }_{2}f(x,x)& =& \{w\in H:f(x,y)-f(x,x)\ge ⟨w,y-x⟩\forall y\in H\}\hfill \\ & =& \{w\in H:f(x,y)\ge ⟨w,y-x⟩\forall y\in H\},\hfill \end{array}$$

(5)

studied in [26].

Lemma 1

([15]). Let H be a real Hilbert space and C be a nonempty closed convex subset in $H.$ Let $g:C\to \mathbb{R}$ be a convex, lower semicontinuous, and subdifferentialble function on $C.$ Then, we have $x^{*}$ is a solution to the convex optimization problem

$$min\left\{g\right(x):x\in C\}$$

if and only if $0\in \partial g\left(x^{*}\right)+N_C\left(x^{*}\right),$ where $\partial g(·)$ denote the subdifferential of g and $N_C\left(x^{*}\right)$ is the normal cone of C at $x^{*}.$

Lemma 2

([27]). Let $\left\{x_n\right\}$ be a sequence of non-negative real numbers, $\left\{{\alpha }_n\right\}$ be a sequence of real numbers in $(0,1)$ with ${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty$, and $\left\{y_n\right\}$ be a sequence of real numbers. Assume that

$$x_{n+1}\le (1-{\alpha }_n)x_n+{\alpha }_n{y}_n$$

for all $n\in \mathbb{N}.$ If ${lim\; sup}_{k\to \infty }{y}_{n_k}\le 0$ for every subsequence $\left\{x_{n_k}\right\}$ of $\left\{x_n\right\}$ satisfying ${lim\; inf}_{k\to \infty }(x_{n_k+1}-x_{n_k})\ge 0,$ then ${lim}_{n\to \infty }{x}_n=0.$

Lemma 3

([23]). Let $f:H\times H\to \mathbb{R}$ be β-strongly monotone, and $x\mapsto {\partial }_{2}f(x,x)$ is L-Lipschitz continuous on every bounded subset of C. Let $0<\alpha <1,0\le \eta \le 1-\alpha$ and $0<\mu <\frac{2\beta }{L^2}$. For each $x,y\in C,w\in {\partial }_{2}f(x,x)$ and $v\in {\partial }_{2}f(y,y)$, we have

$$\parallel (1-\eta )x-\alpha \mu w-\left[\right(1-\eta )y-\alpha \mu v]\parallel \le (1-\eta -\alpha \tau )\parallel x-y\parallel$$

where $\tau =1-\sqrt{1-\mu (2\beta -\mu L^2)}\in (0,1].$

In order to solve a solution of $BSEP(g_i,f,C)$, we must use the following assumptions:

Conditions I

(1)

$f(x,·)$ is convex, weakly lower semicontinuous, and subdifferentiable on H for every fixed $x\in C$;

(2)

$f(·,y)$ is weakly upper semicontinuous on H for every fixed $y\in C;$

(3)

$f:H\times H\to \mathbb{R}$ is $\beta$-strongly monotone on $H.$

(4)

The mapping $x\to {\partial }_{2}f(x,x)$ is bounded and L-Lipschitz continuous on every bounded subset of C.

Conditions II

(1)

$g(x,.)$ is convex, weakly lower semicontinuous, and subdifferentiable on H, for every fixed $x\in C$.

(2)

$g(·,y)$ is weakly upper semicontinuous on H for every fixed $y\in C;$

(3)

g is pseudomonotone on C with respect to $SEP(g,C)$, i.e.,

$$g(x,x^{*})\le 0,\forall x\in C,x^{*}\in SEP(g,C);$$

(4)

g is Lipschitz-type continuous, i.e, there is two positive constants $L_1,L_2$ such that

$$g(x,y)+g(y,z)\ge g(x,z)-L_1{\parallel x-y\parallel }^2-L_2{\parallel y-z\parallel }^2,\forall x,y,z\in H;$$

(5)

g is jointly weakly continuous on $H\times H$ in the sense that, if $x,y\in C$ and $\left\{x_n\right\},\left\{y_n\right\}\in C$ converge weakly to x and y, respectively, then $g(x_n,y_n)\to g(x,y)$ as $n\to +\infty ;$

(6)

Let $\left\{{\epsilon }_n\right\}$ be a positive sequence such that ${lim}_{n\to \infty }\frac{{\epsilon }_n}{{\alpha }_n}=0$, where $\left\{{\alpha }_n\right\}\subset (0,1)$ satisfies the following conditions: ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$ and ${lim}_{n\to \infty }{\alpha }_n=0.$ Moreover, the sequence $\left\{{\eta }_n^i\right\}\subseteq [\eta ,\overline{\eta })\subseteq (0,1]$ such that $\sum _{i=1}^N{\eta }_n^i=1.$

3. Main Results

In this part, we introduce a inertial subgradient extragradient algorithm to solve the bilevel system of equilibrium problems. The strong convergence is obtained under the Lipschitz-type constant of the bifunction, which is unknown.

The modified inertial subgradient extragradient algorithm (shortly, MISE Algorithm)

• $(Initialization:)$ Set $\theta >0,{\lambda }_1^i>0,\mu \in (0,1),0<\gamma <\frac{2\beta }{L^2},0<\overline{\alpha }\le \underline{\alpha }\le 1,{\displaystyle \sum _{i=1}^N}{\eta }_n^i=1$ and choose $x_0,x_1\in H$

Step 1:

Given the iterates $x_{n-1}$ and $x_n(n\ge 1)$, set

$$w_n=x_n+{\theta }_n(x_n-x_{n-1})$$

where

$${\theta }_n=\left\{\begin{array}{cc}min\{{\displaystyle \frac{{\epsilon }_n}{\parallel x_n-x_{n-1}\parallel }},\theta \},\hfill & \mathrm{if}{x}_n\ne x_{n-1}\hfill \\ \theta ,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

Step 2:

Compute

$$y_n^i=\arg \underset{y\in C}{min}\{g_i(w_n,y)+{\displaystyle \frac{1}{2{\lambda }_n^i}}\parallel y-w_n\parallel \}$$

Step 3:

Select $u_n^i\in {\partial }_2{g}_i(w_n,y_n^i)$ and compute

$$z_n^i=\arg \underset{y\in H_n^i}{min}\{g_i(y_n^i,y)+\frac{1}{2{\lambda }_n^i}\parallel y-w_n\parallel \}$$

where $H_n^i=\{x\in H:⟨w_n-{\lambda }_n^i{u}_n^i-y_n^i,x-y_n^i⟩\le 0\}$

Step 4:

Compute $z_n={\displaystyle \sum _{i=1}^N}{\eta }_n^i{z}_n^i$. Select $v_n\in {\partial }_{2}f(z_n,z_n)$ and compute

$$x_{n+1}=z_n-{\alpha }_n\gamma v_n.$$

Step 5:

Set ${\lambda }^i=g_i(w_n,z_n^i)-g_i(y_n^i,z_n^i)-g_i(w_n,y_n^i)$

$${\lambda }_{n+1}^i=\left\{\begin{array}{cc}\min \{\frac{\mu }{2{\lambda }^i}(\parallel w_n-y_n^i{\parallel }^2+\parallel z_n^i-y_n^i{\parallel }^2),{\lambda }_n^i\},\hfill & \mathrm{if}{\lambda }^i>0\hfill \\ {\lambda }_n^i,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(7)

Remark 1.

We obtain that

$$\underset{n\to \infty }{lim}\frac{{\theta }_n}{{\alpha }_n}\parallel x_n-x_{n-1}\parallel =0.$$

Indeed, let $x_n\ne x_{n-1}$, we obtain

$$0\le {\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel \le {\displaystyle \frac{{\epsilon }_n}{{\alpha }_n}}{\displaystyle \frac{\parallel x_n-x_{n-1}\parallel }{\parallel x_n-x_{n-1}\parallel }}.$$

(8)

Taking $n\to \infty$ in (8), we obtain

$$\underset{n\to \infty }{lim}{\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel =0.$$

Lemma 4.

Let the bifunctions $g_i$ satify Condition II. It follows that the sequence $\left\{{\lambda }_n^i\right\}$ generated by (7) is a nonincreasing sequence and

$$\underset{n\to \infty }{lim}{\lambda }_n^i=\phi =min\{\frac{\mu }{2max\{L_1^i,L_2^i\}},{\lambda }_0^i\}\mathit{for}\mathit{all}i=1,2,\cdots ,N.$$

Proof. 

Let $i=1,2,\cdots ,N$. It obvious that

$${\lambda }_{n+1}^i\le {\lambda }_n^i$$

for all $n\in \mathbb{N}.$ Therefore, $\left\{{\lambda }_n^i\right\}$ is a non-increasing sequence. Since $g_i$ is Lipschitz-type continuous on C, there is $L_1^i,L_2^i>0$ such that

$$g_i(w_n,y_n^i)+g_i(y_n^i,z_n^i)\ge g_i(w_n,z_n^i)-L_1^i\parallel w_n-y_n^i{\parallel }^2-L_2^i{\parallel y_n^i-z_n^i\parallel }^2.$$

So, we have

$$\begin{array}{ccc}\hfill {\lambda }^i=g_i(w_n,z_n^i)-g_i(w_n,y_n^i)-g_i(y_n^i,z_n^i)& \le & L_1^i\parallel w_n-y_n^i{\parallel }^2+L_2^i{\parallel y_n^i-z_n^i\parallel }^2\hfill \\ \hfill & \le & max\{L_1^i,L_2^i\}(\parallel w_n-y_n^i{\parallel }^2+\parallel y_n^i-z_n^i{\parallel }^2).\hfill \end{array}$$

This implies that

$${\lambda }^i\le max\{L_1^i,L_2^i\}(\parallel w_n-y_n^i{\parallel }^2+\parallel y_n^i-z_n^i{\parallel }^2).$$

So, for each ${\lambda }^i>0$, we have

$$\begin{array}{ccc}\hfill \frac{\mu }{2{\lambda }^i}(\parallel w_n-y_n^i{\parallel }^2+\parallel z_n^i-y_n^i{\parallel }^2)& \ge & {\displaystyle \frac{\mu (\parallel w_n-y_n^i{\parallel }^2+\parallel z_n^i-y_n^i{\parallel }^2)}{2max\{L_1^i,L_2^i\}(\parallel w_n-y_n^i{\parallel }^2+\parallel y_n^i-z_n^i{\parallel }^2)}}\hfill \\ \hfill & =& \frac{\mu }{2max\{L_1^i,L_2^i\}}.\hfill \end{array}$$

It follows that

$${\lambda }_n^i\ge min\{\frac{\mu }{2max\{L_1^i,L_2^i\}},{\lambda }_0^i\},$$

for all $n\in \mathbb{N}$. Thus, we conclude that ${lim}_{n\to \infty }{\lambda }_n^i$ exists such that

$$\underset{n\to \infty }{lim}{\lambda }_n^i=\phi \ge min\{{\displaystyle \frac{\mu }{2max\{L_1^i,L_2^i\}}},{\lambda }_0^i\}.$$

□

Lemma 5.

Let the bifunctions $g_i$ satify Condition II, and $\left\{z_n^i\right\}$ be sequences generated by (7). Then, for all $p\in \mathsf{\Omega }={\displaystyle \bigcap _{i=1}^N}SEP(g_i,C),$ we have

$$\parallel z_n^i{-p\parallel }^2\le \parallel w_n{-p\parallel }^2-(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2-(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2,$$

for all $i=1,2,\cdots ,N.$

Proof. 

Let $i=1,2,\cdots ,N$ via the definition of the equation:

$$z_n^i=\arg \underset{y\in H_n^i}{min}\{g_i(y_n^i,y)+{\displaystyle \frac{1}{2{\lambda }_n^i}}\parallel y-w_n\parallel \}.$$

Thus,

$${\lambda }_n^i(g_i(y_n^i,y)-g_i(y_n^i,z_n^i))\ge ⟨w_n-z_n^i,y-z_n^i⟩,\mathrm{for}\mathrm{all}y\in H_n^i.$$

□

Since $p\in SEP(g_i,C)\subseteq H_n^i$ for all $i=1,2,\cdots ,N$, we have

$${\lambda }_n^i(g_i(y_n^i,p)-g_i(y_n^i,z_n^i))\ge ⟨w_n-z_n^i,p-z_n^i⟩.$$

(9)

Since $p\in SEP(g_i,C)$ and $y_n^i\in C$, we have $g_i(p,y_n^i)\ge 0$. Using the pseudo monotoxicity of $g_i$, we have $g_i(y_n^i,p)\le 0$, which we obtain from (9) that

$$\begin{array}{ccc}\hfill -{\lambda }_n^i{g}_i(y_n^i,z_n^i)& \ge & ⟨w_n-z_n^i,p-z_n^i⟩-{\lambda }_n^i{g}_i(y_n^i,p)\hfill \\ & \ge & ⟨w_n-z_n^i,p-z_n^i⟩.\hfill \end{array}$$

(10)

Since $u_n^i\in {\partial }_2{g}_i(w_n,y_n^i)$, we have

$$g_i(w_n,y)-g_i(w_n,y_n^i)\ge ⟨u_n^i,y-y_n^i⟩,\mathrm{for}\mathrm{all}y\in H.$$

Therefore,

$$g_i(w_n,z_n^i)-g(w_n,y_n^i)\ge ⟨u_n^i,z_n^i-y_n^i⟩.$$

So,

$$2{\lambda }_n^i(g(w_n,z_n^i)-g_i(w_n,y_n^i))\ge 2{\lambda }_n^i⟨u_n^i,z_n^i-y_n^i⟩.$$

(11)

Since $z_n^i\in H_n^i$, we have

$$⟨w_n-{\lambda }_n^i{u}_n^i-y_n^i,z_n^i-y_n^i⟩\le 0.$$

Thus,

$$2{\lambda }_n^i⟨u_n^i,z_n^i-y_n^i⟩\ge 2⟨w_n-y_n^i,z_n^i-y_n^i⟩.$$

(12)

From (10)–(12), we obtain

$$\begin{array}{c}2{\lambda }_n^i(g_i(w_n,z_n^i)-g_i(w_n,y_n^i)-g_i(y_n^i,z_n^i))\hfill \\ \ge 2(⟨w_n-z_n^i,p-z_n^i⟩+⟨w_n-y_n^i,z_n^i-y_n^i⟩)\hfill \\ =\parallel z_n^i{-p\parallel }^2-\parallel w_n{-p\parallel }^2+\parallel w_n-y_n^i{\parallel }^2+{\parallel y_n^i-z_n^i\parallel }^2\hfill \end{array}$$

(13)

Therefore,

$$\parallel z_n^i{-p\parallel }^2\le \parallel w_n{-p\parallel }^2-\parallel w_n-y_n^i{\parallel }^2-{\parallel z_n^i-y_n^i\parallel }^2+2{\lambda }_n^i(g(w_n^i,z_n^i)-g_i(w_n,y_n^i)-g_i(y_n^i,z_n^i)).$$

Using the definition of ${\lambda }_n^i$, we have

$$\begin{array}{ccc}\hfill \parallel z_n^i{-p\parallel }^2& \le & \parallel w_n{-p\parallel }^2-\parallel w_n-y_n^i{\parallel }^2-{\parallel z_n^i-y_n^i\parallel }^2\hfill \\ \hfill & & +2{\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}{\lambda }_{n+1}^i\left(g_i(w_n,z_n^i)\right)-g_i(y_n^i,z_n^i)-g_i(w_n,y_n^i)\hfill \\ \hfill & \le & \parallel w_n{-p\parallel }^2-\parallel w_n-y_n^i{\parallel }^2-{\parallel z_n^i-y_n^i\parallel }^2\hfill \\ \hfill & & {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}\mu (\parallel w_n-y_n^i{\parallel }^2-\parallel z_n^i-y_n^i{\parallel }^2)\hfill \\ & =& \parallel w_n{-p\parallel }^2-(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel w_n-y_n^i{\parallel }^2-(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2.\hfill \end{array}$$

Theorem 1.

Let bifunctions f satisfy Condition I, and $g_i$ satisfy Condition II. Suppose that $\mathsf{\Omega }={\displaystyle \bigcap _{i=1}^N}SEP(g_i,C)$ is a nonempty set. Then, we have the sequence $\left\{x_n\right\}$ generated by the MISE Algorithm, which converges to the unique solution of (BSEP).

Proof. 

Under the assumptions of the bifunctions $g_i$ and $f,$ we obtain the unique solution of the bilevel system equilibrium Equation (1), denoted as $p.$ It implies that $f(p,y)\ge 0$ for all $y\in \mathsf{\Omega }.$ Thus, p is a minimum of the convex function $f(p,·)$ over $\mathsf{\Omega }$. Using the optimality condition, we obtain

$$0\in {\partial }_{2}f(p,p)+N_{\mathsf{\Omega }}\left(p\right).$$

Then, there exists $v^{*}\in {\partial }_{2}f(p,p)$ such that

$$⟨v^{*},z-p⟩\ge 0\mathrm{for}\mathrm{all}z\in \mathsf{\Omega }.$$

(14)

□

Next, we prove that $\left\{x_n\right\}$ generated by the MISE Algorithm converges to $p.$ We divide the proof into four steps.

Step 1: We show that the sequence $\left\{x_n\right\}$ is bounded since

$$\underset{n\to \infty }{lim}(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})=1-\mu >0.$$

For each $i=1,2,\cdots ,N$, there is $n_0^i\in N$ such that

$$1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}>0,\forall n\ge n_0^i.$$

Choose $n_0=max\{n_0^i:i=1,2,\cdots ,N\}$. For each $n\ge n_0$, we have

$$1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}>0,\forall i=1,2,\cdots ,N.$$

(15)

Therefore,

$$\begin{array}{ccc}\hfill \parallel z_n{-p\parallel }^2& =& \parallel \sum _{i=1}^N{\eta }_n^i{z}_n^i{-p\parallel }^2\hfill \\ & \le & \parallel \sum _{i=1}^N{\eta }_n^i(z_n^i-p){\parallel }^2\hfill \\ & =& \sum _{i=1}^N{\eta }_n^i\parallel z_n^i{-p\parallel }^2-\frac{1}{2}\sum _{i=1}^N\sum _{t=1}^N{\eta }_n^i{\eta }_n^t{\parallel z_n^i-z_n^t\parallel }^2\hfill \end{array}$$

(16)

Combining Lemma 5 and (16), we have

$$\parallel z_n{-p\parallel }^2\le \parallel w_n{-p\parallel }^2-\sum _{i=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2-\sum _{i=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2.$$

(17)

It implies from (15) that

$$\parallel z_n-p\parallel \le \parallel w_n-p\parallel ,\forall n\ge n_0.$$

(18)

Therefore,

$$\begin{array}{ccc}\hfill \parallel w_n-p\parallel & \le & \parallel x_n+{\theta }_n(x_n-x_{n-1})-p\parallel \hfill \\ & \le & \parallel {\theta }_n(x_n-x_{n-1})\parallel +\parallel x_n-p\parallel \hfill \\ & =& {\alpha }_n{\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel +\parallel x_n-p\parallel .\hfill \end{array}$$

(19)

According to Remark 1, we have ${\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\left|\right|\to 0$. There exists a constant $M_1>0$ such that

$${\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel \le M_1,\forall n\ge 1.$$

(20)

Combining (18)–(20), we obtain

$$\begin{array}{ccc}\hfill \parallel z_n-p\parallel \le \parallel w_n-p\parallel & \le & {\alpha }_n{\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel +\parallel x_n-p\parallel \hfill \\ \hfill & \le & {\alpha }_n{M}_1+\parallel x_n-p\parallel ,\forall n\ge n_0.\hfill \end{array}$$

(21)

Using Lemma 3 and (7), it follows that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-p\parallel & =& \parallel z_n-{\alpha }_n\gamma v_n-p+{\alpha }_n\gamma v^{*}-{\alpha }_n\gamma v^{*}\parallel \hfill \\ \hfill & =& \parallel (z_n-{\alpha }_n\gamma v_n)-(p-{\alpha }_n\gamma v^{*})-{\alpha }_n\gamma v^{*}\parallel \hfill \\ \hfill & \le & (1-{\alpha }_n\tau )\parallel z_n-p\parallel +{\alpha }_n\gamma \parallel v^{*}\parallel \hfill \\ \hfill & \le & (1-{\alpha }_n\tau )({\alpha }_n{M}_1+\parallel x_n-p\parallel )+{\alpha }_n\gamma \parallel v^{*}\parallel \hfill \\ \hfill & =& {\alpha }_n{M}_1-{\alpha }_n^2\tau M_1+(1-{\alpha }_n\tau )\parallel x_n-p\parallel +{\alpha }_n\gamma \parallel v^{*}\parallel \hfill \\ \hfill & \le & (1-{\alpha }_n\tau )\parallel x_n-p\parallel +{\alpha }_n\tau {\displaystyle \frac{M_1}{\tau }}+{\alpha }_n\tau {\displaystyle \frac{\gamma }{\tau }}\parallel v^{*}\parallel \hfill \\ \hfill & =& (1-{\alpha }_n\tau )\parallel x_n-p\parallel +{\alpha }_n\tau ({\displaystyle \frac{M_1}{\tau }}+{\displaystyle \frac{\gamma }{\tau }}\parallel v^{*}\parallel )\hfill \\ \hfill & \le & max\{{\displaystyle \frac{M_1+\gamma \parallel v^{*}\parallel }{\tau }},\parallel x_n-p\parallel \}\hfill \end{array}$$

for all $n\ge n_0$, where $\tau =1-\sqrt{1-\gamma (2\beta -\gamma L^2)}.$ Through induction, we obtain

$$\parallel x_n-p\parallel \le max\{{\displaystyle \frac{M_1+\gamma \parallel v^{*}\parallel }{\tau }},\parallel x_{n_0}-x^{*}\parallel \}.$$

Hence, the sequence $\left\{x_n\right\}$ is bounded.

Step 2: Show that there is $M_4\ge 0$ such that

$$\begin{array}{c}{\displaystyle \sum _{t=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2+{\displaystyle \sum _{t=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2\hfill \\ \le \parallel x_n{-p\parallel }^2-{\parallel x_n-p\parallel }^2+{\alpha }_n{M}_4,\hfill \end{array}$$

for all $n\ge n_0.$ One has

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & \parallel z_n-{\alpha }_n\gamma v_n+{\alpha }_n\gamma v^{*}-{\alpha }_n\gamma v^{*}{-p\parallel }^2\hfill \\ \hfill & \le & \parallel (z_n-{\alpha }_n\gamma v_n)-[p-{\alpha }_n\gamma v^{*}]-{\alpha }_n\gamma v^{*}{\parallel }^2\hfill \\ \hfill & \le & \parallel (z_n-{\alpha }_n\gamma v_n)-[p-{\alpha }_n\gamma v^{*}]{\parallel }^2\hfill \\ & & -2⟨{\alpha }_n\gamma v^{*},z_n-{\alpha }_n\gamma v_n-p+{\alpha }_n\gamma v^{*}-{\alpha }_n\gamma v^{*}⟩\hfill \\ \hfill & =& \parallel (z_n-{\alpha }_n\gamma v_n)-(p-{\alpha }_n\gamma v^{*}){\parallel }^2-2{\alpha }_n\gamma ⟨v^{*},p-x_{n+1}⟩\hfill \\ \hfill & \le & {(1-{\alpha }_n\tau )}^2{\parallel z_n-p\parallel }^2+{\alpha }_n{M}_2\hfill \\ & \le & \parallel z_n{-p\parallel }^2+{\alpha }_n{M}_2\hfill \end{array}$$

(22)

for some $M_2>0.$ Using (17), we obtain

$$\parallel x_{n+1}{-p\parallel }^2\le \parallel w_n{-p\parallel }^2-\sum _{t=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2-\sum _{t=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2+{\alpha }_n{M}_2.$$

(23)

It follows from (21) that

$$\begin{array}{ccc}\hfill \parallel w_n{-p\parallel }^2& \le & (\parallel w_n-p{\parallel {\alpha }_n{M}_1)}^2\hfill \\ & \le & \parallel x_n{-p\parallel }^2+2{\alpha }_n{M}_1\parallel x_n-p\parallel +{\alpha }_n^2{M}_1^2\hfill \\ & \le & \parallel x_n{-p\parallel }^2+{\alpha }_n{M}_3\hfill \end{array}$$

(24)

for some $M_3>0.$ Combining (23) and (24), we obtain

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & \parallel x_n{-p\parallel }^2+{\alpha }_n{M}_3-\sum _{i=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel y_n^i-w_n\parallel }^2\hfill \\ \hfill & & -\sum _{i=1}^N{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2+{\alpha }_n{M}_2.\hfill \end{array}$$

Hence,

$$\begin{array}{c}{\displaystyle \sum _{i=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2+{\displaystyle \sum _{i=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}}){\parallel z_n^i-y_n^i\parallel }^2\hfill \\ \le \parallel x_n{-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2+{\alpha }_n(M_3+M_2)\hfill \\ =\parallel x_n{-p\parallel }^2-{\parallel x_{n+1}-p\parallel }^2+\alpha M_4\hfill \end{array}$$

where $M_4=M_2+M_3.$

Step 3: Show that

$$\parallel x_{n+1}{-p\parallel }^2\le (1-{\alpha }_n\tau )\parallel x_n{-p\parallel }^2+{\alpha }_n\tau [{\displaystyle \frac{2\gamma }{\tau }}⟨v^{*},p-x_{n+1}⟩+3{\displaystyle \frac{M{\theta }_n}{{\alpha }_n\tau }}\parallel x_n-x_{n+1}\parallel ]$$

for all $n\ge n_0.$ Indeed, we have

$$\begin{array}{ccc}\hfill \parallel w_n{-p\parallel }^2& =& \parallel x_n+{\theta }_n(x_n-x_{n+1}){-p\parallel }^2\hfill \\ \hfill & =& \parallel (x_n-p)+{\theta }_n(x_n-x_{n+1}){\parallel }^2\hfill \\ & =& \parallel x_n{-p\parallel }^2+2{\theta }_n⟨x_n-p,x_n-x_{n+1}⟩+{\theta }_n^2{\parallel x_n-x_{n+1}\parallel }^2\hfill \\ & \le & \parallel x_n{-p\parallel }^2+2{\theta }_n\parallel x_n-p\parallel \parallel x_n-x_{n+1}\parallel +{\theta }_n^2{\parallel x_n-x_{n+1}\parallel }^2.\hfill \end{array}$$

(25)

Combining (18) and (22), we obtain

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & (1-{\alpha }_n\tau ){\parallel z_n-p\parallel }^2+2{\alpha }_n\gamma ⟨v^{*},p-x_{n+1}⟩\hfill \\ & \le & (1-{\alpha }_n\tau ){\parallel w_n-p\parallel }^2+2{\alpha }_n\gamma ⟨v^{*},p-x_{n+1}⟩.\hfill \end{array}$$

(26)

for all $n\ge n_0.$ Substituting (25) into (26), we obtain

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & (1-{\alpha }_n\tau ){\parallel x_n-p\parallel }^2+2{\alpha }_n\gamma ⟨v^{*},p-x_{n+1}⟩\hfill \\ \hfill & & +{\theta }_n\parallel x_n-x_{n+1}\parallel (2\parallel x_n-p\parallel +\theta \parallel x_n-x_{n+1}\parallel )\hfill \\ \hfill & \le & (1-{\alpha }_n\tau )\parallel x_n{-p\parallel }^2+{\alpha }_n\tau ({\displaystyle \frac{2\gamma }{\tau }}⟨v^{*},p-x_{n+1}⟩+3{\displaystyle \frac{M{\theta }_n}{{\alpha }_n\tau }}\parallel x_n-x_{n-1}\parallel )\hfill \end{array}$$

for all $n\ge n_0$ where $M=sup\{\parallel x_n-p\parallel ,\theta \parallel x_n-x_{n-1}\parallel \}>0.$

Step 4: $\{\parallel x_n-p{\parallel \}}^2$ converges to zero. Indeed, using Lemma 2, it suffices to show that

$$\underset{k\to \infty }{lim\; sup}⟨v^{*},p-x_{n_k+1}⟩\le 0,$$

for every subsequence $\{\parallel x_{n_k}-p\parallel \}$ of $\{\parallel x_n-p\parallel \}$ satisfying ${lim\; inf}_{k\to \infty }(\parallel x_{n_k+1}-p\parallel -\parallel x_{n_k}-p\parallel )\ge 0.$ Assume that $\{\parallel x_{n_k}-p\parallel$ is a subsequence of $\{\parallel x_n-p\parallel \}$ such that

$$\underset{k\to \infty }{lim\; inf}(\parallel x_{n_k}{-p\parallel }^2-\parallel x_{n_k+1}-p{\parallel }^2)\ge 0.$$

In Step 2, one has

$$\begin{array}{c}{lim\; sup}_{k\to \infty }[{\displaystyle \sum _{i=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel y_n^i-w_n{\parallel }^2+{\displaystyle \sum _{i=1}^N}{\eta }_n^i(1-\mu {\displaystyle \frac{{\lambda }_n^i}{{\lambda }_{n+1}^i}})\parallel z_n^i-y_n^i{\parallel }^2]\hfill \\ \le \underset{k\to \infty }{lim\; sup}[{\alpha }_{n_k}{M}_4+\parallel x_{n_k}{-p\parallel }^2-\parallel x_{n_k+1}-p{\parallel }^2]\hfill \\ \le \underset{k\to \infty }{lim\; sup}{\alpha }_{n_k}{M}_4+\underset{k\to \infty }{lim\; sup}[\parallel x_{n_k}{-p\parallel }^2-\parallel x_{n_k+1}-p{\parallel }^2]\hfill \\ =-\underset{k\to \infty }{lim\; inf}[\parallel x_{n_k+1}{-p\parallel }^2-\parallel x_{n_k}-p{\parallel }^2]\hfill \\ \le 0,\hfill \end{array}$$

for all $i=1,2,\cdots ,N.$ This implies that

$$\underset{k\to \infty }{lim}\parallel y_{n_k}^i-w_{n_k}\parallel =0\mathrm{and}\underset{k\to \infty }{lim}\parallel z_{n_k}^i-y_{n_k}^i\parallel =0,$$

(27)

for all $i=1,2,\cdots ,N.$ Therefore

$$\underset{k\to \infty }{lim}\parallel z_{n_k}^i-w_{n_k}\parallel =0.$$

(28)

for all $i=1,2,\cdots ,N.$ We know that

$$\begin{array}{ccc}\hfill \parallel z_{n_k}-w_{n_k}{\parallel }^2& =& \parallel \sum _{i=1}^N{\eta }_{n_k}^i{z}_{n_k}^i-w_{n_k}{\parallel }^2\hfill \\ \hfill & =& \parallel \sum _{i=1}^N{\eta }_{n_k}^i(z_{n_k}^i-w_{n_k}){\parallel }^2\hfill \\ \hfill & =& \sum _{i=1}^N{\eta }_{n_k}^i\parallel z_{n_k}^i-w_{n_k}{\parallel }^2-\frac{1}{2}\sum _{i=1}^N\sum _{t=1}^N{\eta }_{n_k}^i{\eta }_{n_k}^t{\parallel z_{n_k}^i-z_{n_k}^t\parallel }^2.\hfill \end{array}$$

Taking $k\to \infty$ in the above inequality, we obtain

$$\underset{k\to \infty }{lim}\parallel z_{n_k}-w_{n_k}\parallel =0.$$

(29)

Moreover, we can show that

$$\underset{k\to \infty }{lim}\parallel x_{n_k+1}-z_{n_k}\parallel =\underset{k\to \infty }{lim}{\alpha }_{n_k}\gamma \parallel v_{n_k}\parallel =0$$

(30)

and

$$\underset{k\to \infty }{lim}\parallel x_{n_k}-w_{n_k}\parallel =\underset{k\to \infty }{lim}{\theta }_{n_k}\parallel x_{n_k}-x_{n_k-1}\parallel =\underset{k\to \infty }{lim}{\alpha }_{n_k}{\displaystyle \frac{{\theta }_{n_k}}{{\alpha }_{n_k}}}\parallel x_{n_k}-x_{n_k-1}\parallel =0.$$

(31)

We know that

$$\parallel x_{n_{k+1}}-x_{n_k}\parallel \le \parallel x_{n_k+1}-z_{n_k}\parallel + \parallel z_{n_k}-w_{n_k}\parallel + \parallel w_{n_k}-x_{n_k}\parallel .$$

(32)

Taking $k\to \infty$ in (32) and using (29)–(31), we obtain

$$\underset{k\to \infty }{lim}\parallel x_{n_k+1}-x_{n_k}\parallel =0.$$

(33)

Since the sequence $\left\{x_{n_k}\right\}$ is bounded, there exists a subsequence $\left\{x_{n_{k_j}}\right\}$ of $\left\{x_{n_k}\right\}$, which converges weakly to some $z\in H$ such that

$$\underset{k\to \infty }{lim\; sup}⟨v^{*},p-x_{n_k}⟩=\underset{j\to \infty }{lim}⟨v^{*},p-x_{n_j}⟩=⟨v^{*},p-z⟩.$$

(34)

It follows from (31) and (27) that $\left\{w_{n_k}\right\}$ and $\left\{y_{n_k}^i\right\}$ converge weakly to some $z\in H$. Since C is closed and convex, it is also weakly closed, and thus, $z\in C.$ Next, we show that $z\in \mathsf{\Omega }={\displaystyle \bigcap _{i=1}^N}SEP(g_i,C).$ It follows from Lemma 1 and the definition of $\left\{y_n^i\right\}$ that

$$0\in {\partial }_2\{g_i(w_n,y)+\frac{1}{2{\lambda }_n^i}\parallel y-w_n{\parallel }^2\}\left(y_n^i\right)+N_C\left(y_n^i\right).$$

Therefore,

$${\lambda }_n\{g_i(w_n,y)-g_i(w_n,y_n^i)\}\ge ⟨w_n-y_n^i,y-y_n^i⟩\mathrm{for}\mathrm{all}y\in C.$$

(35)

Let $n=n_k$ in (35) and taking $k\to \infty$, using the assumption of the sequence $\left\{{\lambda }_n\right\}$ and Condition II (5), we obtain $g_i(\overline{x},y)\ge 0$ for all $y\in C$ and for all $i=1,2,\cdots ,N.$ This implies that $z\in \mathsf{\Omega }.$ By using (14), we obtain $⟨v^{*},p-z⟩\le 0.$ It follows from (34) and the above inequality that

$$\underset{k\to \infty }{lim\; sup}⟨v^{*},p-x_{n_k+1}⟩\le 0.$$

(36)

Since ${lim}_{n\to \infty }{\displaystyle \frac{{\theta }_n}{{\alpha }_n}}\parallel x_n-x_{n-1}\parallel =0$ and (36), we obtain

$$\underset{k\to \infty }{lim\; sup}[{\displaystyle \frac{2\gamma }{\tau }}⟨v^{*},p-x_{n_k+1}⟩+{\displaystyle \frac{3M{\theta }_{n_k}}{{\alpha }_{n_k}}}\parallel x_{n_k}-x_{n_k+1}\parallel ]\le 0.$$

(37)

Combining Step 3 and (37) with Lemma 2, we can conclude that $\left\{x_n\right\}$ converges strongly to $p.$ This completes the proof.

4. Numerical Example

In this section, we present a numerical example for testing the modified inertial subgradient extragradient algorithm (shortly, MISE Algorithm) to solve the bilevel system of equilibrium problems. We consider the following problem. Let $H={\mathbb{R}}^n$ and $C=\{x\in {\mathbb{R}}^n:-20\le x_j\le 20,\forall j\in \{1,2,\cdots ,n\}\}$. Let the bifunction $f:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ and $g_i:{\mathbb{R}}^n\times {\mathbb{R}}^n\to \mathbb{R}$ for all $i=1,2,\cdots ,N$ be defined via

$$\begin{array}{ccc}\hfill f(x,y)& =& ⟨Px+Qy,y-x⟩,\hspace{1em}\forall x,y\in {\mathbb{R}}^n,\hfill \\ \hfill g_i(x,y)& =& ⟨A^{i}x,y-x⟩\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\forall x,y\in {\mathbb{R}}^n,\forall i=1,\cdots ,N,\hfill \end{array}$$

(38)

where P and Q are randomly symmetric positive definite matrices defined via

$$Q=W^{\top }W+n{I}_n,P=Q+V^{\top }V+n{I}_n$$

where W and V are random $n\times n$ matrices, and $I_n$ is the identity $n\times n$ matrix. $A^i:{\mathbb{R}}^n\to {\mathbb{R}}^n$ are linear operators given via $A^i={\left(a_{ls}^i\right)}_{n\times n}\in {\mathbb{R}}^{n\times n}$, which are randomly symmetric positive definite matrices for all $i=1,2,\cdots ,N.$

Note that the bifunction $f(x,y)$ is n-strongly monotone on ${\mathbb{R}}^n$, and for fixed $x\in H$, we have $f(x,·)$, which is convex on ${\mathbb{R}}^n$. Moreover, we obtain that the subdifferential ${\partial }_{2}f(x,x)=\left\{(P+Q)x\right\}$. We also obtain that the function $x\mapsto {\partial }_{2}f(x,x)$ is bounded, and $g_i$ are pseudomonotone on ${\mathbb{R}}^n$ and Lipschitz-type continuous with $L_1^i=L_2^i=\frac{1}{2}\parallel A^i\parallel$ for all $i=1,2,\cdots ,N.$

We have tested our algorithm for this example in which the dimension is expressed as follows:

$$n=10,50,100,500,1000;$$

the number of system $N=10,50,100,500.$ The matrices P and Q are matrices of W and V, respectively, being randomly generated in the interval $[-5,5].$ The linear operators $A^i:C\to {\mathbb{R}}^n$ are defined via $A^i={\left(a_{ls}^i\right)}_{n\times n},$ where $a_{ls}^i$ are randomly generated in C for all $i=1,2,\cdots ,N.$ We choose the starting point of the MISE Algorithm $x_0$ and $x_1$ to be vectors with coordinates that are one and parameters that are as follows: $\overline{L}=\frac{1}{2}\parallel P+Q\parallel$; $L_1^i=L_2^i=\frac{1}{2}\parallel A^i\parallel ,\forall i=1,\cdots ,N$; $L=max\{\overline{L},L_1^i,L_2^i:i=1,\cdots ,N\}$; $\theta =\frac{1}{4L}$; ${\lambda }_1^i=\frac{1}{4L},\forall i=1,\cdots ,N$; $\mu =\frac{1}{4L}$; $\gamma =\frac{2}{{\parallel P+Q\parallel }^2}$; ${\eta }_n^i=\frac{1}{N}$; ${\alpha }_n=\frac{1}{n+1}$ and ${ϵ}_n=\frac{1}{{(n+1)}^2}.$

Note that at each iteration in the MISE Algorithm, we obtain $y_n^i$ and $z_n^i$ via

$$\begin{array}{c}\hfill y_n^i=P_C(w_n-{\lambda }_n^i{A}^i{w}_n)\end{array}$$

(39)

and

$$\begin{array}{c}\hfill z_n^i=P_{H_n^i}(y_n^i-{\lambda }_n^i{A}^i{y}_n^i).\end{array}$$

(40)

Since $C=\{x\in {\mathbb{R}}^n:-20\le x_j\le 20,\forall j\in \{1,2,\cdots ,n\}\}$ is box and $H_n^i=\{x\in {\mathbb{R}}^n:⟨w_n-{\lambda }_n^i{u}_n^i-y_n^i,x-y_n^i⟩\}$ is a half space, $y_n^i$ and $z_n^i$ can be computed explicitly. For more details, see [21].

The experiment is performed under MATLAB R2018a running on a laptop with 2.59 GHz Intel Core i7 and 4 GB RAM. We terminate Algorithm via the stopping criterions

$$\frac{\parallel x_{n+1}-x_n\parallel }{\parallel x_n\parallel +1}\le \epsilon ,$$

where $\epsilon ={10}^{-6}$ to obtain the number of iteration and CPU times, and the CPU times are considered in the second unit. The results are presented in Table 1, where the following are noted:

Table 1. The result of the modified inertial subgradient extragradient algorithm.

n	N	N.P	Average Iteration	Average Times
10	10	10	300	0.0703
	50	10	254	0.1813
	100	10	238	0.4266
	500	10	253	1.9734
50	10	10	204	0.1797
	50	10	207	0.2828
	100	10	196	0.6547
	500	10	197	2.7172
100	10	10	90	0.2469
	50	10	89	1.2828
	100	10	90	2.2328
	500	10	91	12.1719
500	10	10	17	1.7171
	50	10	18	8.8781
	100	10	19	15.7156
	500	10	17	80.5547
1000	10	10	9	7.9687
	50	10	8	33.2968
	100	10	8	73.9375
	500	10	9	362.4844

• The number of the tested problems denoted as N.P;
• The average number of iterations denoted as Average iteration;
• The average CPU computation times denoted as Average times.

We see the computed results reported in Table 1. The sequence generated by our proposed MISE Algorithm is convergent and effective for finding the solution of bilevel system of equilibrium problems.

Next, we present the comparison of the proposed MISE Algorithm and the extragradient subgradient Halpern method (shortly, ESH Algorithm) [23]. We consider Problem (38) in the case of the number of systems, $N=1.$ We tested the example with the dimension $n=50,100$, and the matrices P and Q are the matrices of W and V, respectively, being randomly generated in the interval $[-5,5].$ The matrix $A=\left(a_{ls}\right)$, where $a_{ls}$ are randomly generated in C. The parameters are defined as follows:

• MISE Algorithm: the starting point of $x_0=x_1={(1,\cdots ,1)}^{\top }$; $\overline{L}=\frac{1}{2}\parallel P+Q\parallel$; $L_1^i=L_2^i=\frac{1}{2}\parallel A^i\parallel ,\forall i=1,\cdots ,N$; $L=max\{\overline{L},L_1^i,L_2^i:i=1,\cdots ,N\}$; $\theta =\mu ={\lambda }_1^i=\frac{1}{4L}\forall i=1,\cdots ,N$; $\gamma =\frac{2}{{\parallel P+Q\parallel }^2}$; ${\eta }_n^i=\frac{1}{N}$; ${\alpha }_n=\frac{1}{n+1}$ and ${ϵ}_n=\frac{1}{{(n+1)}^2}.$
• ESH Algorithm: $x_0={(1,\cdots ,1)}^{\top }$; ${\lambda }_n=\frac{1}{4\parallel A\parallel }$; $\mu =\frac{2}{{\parallel P+Q\parallel }^2}$; ${\alpha }_n=\frac{1}{n+1}$ and ${\eta }_n=\frac{n+1}{2(n+1)}.$

We terminate the algorithms by stopping the criterion $\frac{\parallel x_{n+1}-x_n\parallel }{\parallel x_n\parallel +1}\le {10}^{-6}.$ The results are presented in Figure 1 and Figure 2.

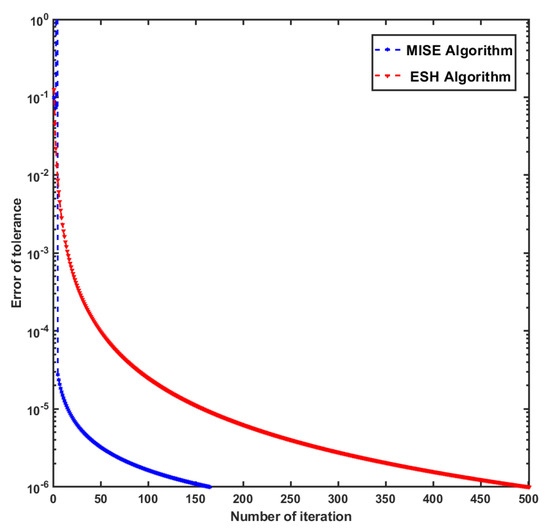
Figure 1. The number of iterations of MISE Algorithm and ESH Algorithm, where dimension is $n=50$.

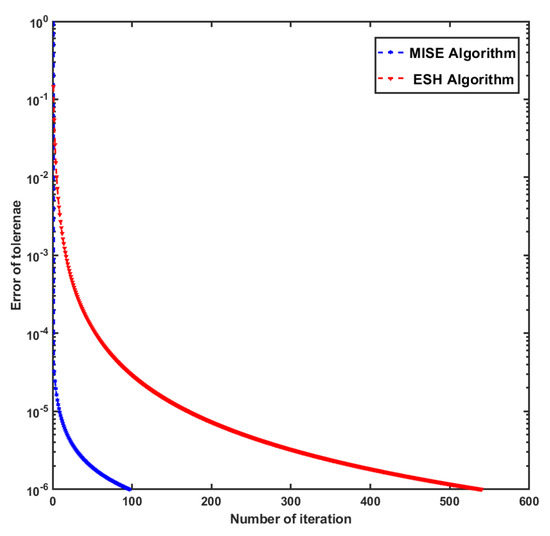
Figure 2. The number of iterations of MISE Algorithm and ESH Algorithm, where dimension is $n=100$.

From the result reported in Figure 1 and Figure 2, we obtain that the sequence generated by the MISE Algorithm is significantly better than the ESH Algorithm.

5. Conclusions

We have proposed the inertial subgradient extragradient algorithms to solve the bilevel system equilibrium problems in real Hilbert spaces. Our algorithm obtained without the prior knowledge of the Lipschitz constant of the involving bifunction. Under oppropriate conditions, we obtain strong convergence theorems of our algorithms. Finally, we have presented some numerical examples and shown that our algorithms are efficient.