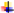A New Method for Solving the Flow Shop Scheduling Problem on Symmetric Networks Using a Hybrid Nature-Inspired Algorithm

Abstract

Recently, symmetric networks have received much attention in various applications. They are a single route for incoming and outgoing network traffic. In symmetric networks, one of the fundamental categories of wide-ranging scheduling problems with several practical applications is the FSSP. Strictly speaking, a scheduling issue is found when assigning resources to the activities to maximize goals. The difficulty of finding solutions in polynomial time makes the flow shop scheduling problem (FSSP) NP-hard. Hence, the utilization of a hybrid optimization technique, a new approach to the flow shop scheduling issue, on symmetric networks is given in the current research. In order to address this issue, each party’s strengths are maximized and their weaknesses reduced, and this study integrates the Ant Colony Algorithm with Particle Swarm Optimization (ACO-PSO). Even though these methods have been employed before, their hybrid approach improves their resilience in a variety of sectors. The ACO-PSO is put to the test by contrasting it with innovative algorithms in the literature. The search space is first filled with a variety of solutions by the algorithm. Using pheromones in the mutual region, the ACO algorithm locally controls mobility. Moreover, the PSO-based random interaction among the solutions yields the global maximum. The PSO’s random interaction among the solutions typically results in the global maximum. The computational research demonstrates that the recommended ACO-PSO method outperforms the existing ones by a large margin. The Friedman test also shows that the average algorithm ranks for ACO and PSO are 1.79 and 2.08, respectively. The proposed method has an average rank of 2.13 as well. It indicates that the suggested algorithm’s effectiveness increased.

1. Introduction

Symmetry, a fundamental idea in numerous branches of physics, can be expressed explicitly using mathematical methods, namely, invariance under a particular group action. Symmetric networks are expressive enough to represent the behavior of any nonoscillating recurrent network that is based on binary threshold units. Recent scientific emphasis has been drawn to symmetry in complex network systems [1]. One of the fascinating problems in this network is the flow shop scheduling problem (FSSP). The FSSP was first presented in the 1970s [2]. In the past two decades, the FSSP has attracted a lot of attention as one of the most challenging decision-making challenges for selecting the machine for each type of work and the sequence in which each machine should process all jobs [3,4]. The FSSP is an active field of study and has been extensively studied since Johnson [5] suggested it. The FSSP has recently been a hot topic in academic research for suggesting better service providers [6,7]. In the standard FSSP, a collection of n jobs should be processed in phases along the same output path, and in each stage, there is a single machine [8,9]. The standard flow shop architecture is applied to a hybrid flow shop, where parallel machines operate on some levels to improve the shop floor’s performance [10,11]. This architecture is often referred to in the literature as an FSSP and a multi-processor flow shop [12,13]. Each phase has at least one device in parallel in the hybrid flow shop layout, and there is exclusively more than one machine at least in one of the phases [14]. Since it takes into account both the allocation and scheduling of work at each point, the hybrid FSSP is trickier to answer than the regular FSSP [15]. The FSSP is a challenging optimization decision problem that is often NP-hard [16]. We limit ourselves to symmetric networks. One route serves both incoming and outgoing network traffic in a symmetric network. Thus, traffic entering the network follows the same path. If the input and output impedances of a network are equal, the network is symmetrical.

Symmetrical networks are typically, but not always, symmetrical in terms of their physical structure. Additionally, antimetrical networks are occasionally of interest [17,18]. These networks have input and output impedances that are opposites. Symmetric networks are the problem of this research, and the proposed method works on these networks. This research aims to use a combination of the Ant Colony Algorithm and Particle Swarm Optimization (ACO-PSO) to optimize the two scheduling interaction targets’ priority, reduce delays, and reduce makespan, or the highest completion time of all tasks. The main goal of integrating ACO and PSO is to minimize each other’s flaws and emphasize each other’s advantages. Heuristic algorithms have taken the role of enumeration due to their rapid search capabilities [19,20], and they are frequently employed to resolve complex or large-scale problems such as flow shop with multi-processor scheduling [21]. Chaotic sequences can boost the effectiveness of PSO random components because of their unpredictability and ergodicity. By drastically lowering the number of ACO iterations that are triggered by each PSO particle, this hybrid algorithm will also significantly shorten the method’s makespan and delay time. In order to solve the FSSP, a hybrid optimization approach inspired by nature is presented in this study. As far as we know, the proposed method in this paper has not been used for FSSPs on symmetric networks. The main focuses of the current article are:

• Minimizing the delay time of FSSPs on symmetric networks using a hybrid algorithm;
• Minimizing the makespan of FSSPs on symmetric networks using a hybrid algorithm.

Section 2 contains a list of related works. The problem statement, the method for the FSSP, and the fitness function are explained in Section 3. The recommended optimization algorithm is described in Section 4. Experimental results are addressed and explained in Section 5. The concluding section brings the article to a close.

2. Related Work

When uncertainties exist, procedures for tackling an FSSP can be categorized into two groups. The first group develops a stable mathematical model and transforms uncertainties into a deterministic problem [22,23]. Substitute steps often set defined, unique terminal intervals utilizing discrete or constant scenarios and then solve them using available algorithms [24,25]. In addition to the difficulties, the second group modifies a current timetable technique: rescheduling strategies [26]. The production time of a job can be exceedingly unpredictable in the real world [27,28]. Up to now, there have been three kinds of approaches to the FSSP to fix the ambiguity of processing time. The initial one is to model the unknown processing period utilizing a gamma distribution, with the predicted processing time being gamma [29]. The next is to classify the unknown processing period by employing an interval number, with any range of the interval being the real processing time [30]. The third approach provides a fuzzy number to grasp the ambiguity in processing time. Therefore, the targets of makespan and (or) the whole weighted completion time are (is) also considered fuzzy number(s) [31]. Below is a list of optimization algorithms employed in the FSSP domain.

Goli, Ala [32] investigated the optimization of a non-permutation FSSP and lot-sizing simultaneously. They first studied the energy awareness of the non-permutation FSSP and lot-sizing using modified metaheuristic algorithms. First, a mixed-integer linear mathematical model was proposed in this regard. This model intended to determine the size of each subcategory and the speed of each machine within each subcategory to decrease makespan concurrently and the used energy. The Multi-Objective Ant Lion Optimizer (MOALO), Multi-Objective Keshtel Algorithm (MOKA), and Multi-Objective Keshtel and Social Engineering Optimizer (MOKSEA) were presented to optimize this technique. First, the mathematical model’s validity was assessed by applying it to a real-world food business scenario using the GAMS software. Next, the Taguchi experimental design was used. Afterward, the effectiveness of these metaheuristic algorithms was determined by comparing them with the Epsilon-Constraint (EPC) method, Non-dominated Sorting Genetic Algorithm II (NSGA-II), and Multi-Objective Particle Swarm Optimization (MOPSO) on a variety of test situations. The results revealed that the MOALO, MOKA, and MOKSEO algorithms could locate optimal solutions that may be considered as a set of Pareto solutions, indicating that the employed method had the required validity. In addition, the suggested hybrid algorithm generated Pareto solutions in less time than EPC and with higher quality than NSGA-II and MOPSO. In conclusion, the outcomes demonstrated a linear relationship between processing time and the first and second objective functions.

Alburaikan, Garg [6] looked into scheduling a three-stage flow shop with an uncertain processing time. A ranking function and the near interval approximation of the pentagonal fuzzy number were two separate methodologies that were developed in this research. The close interval approximation of the pentagonal fuzzy number was deemed the best acceptable approximation interval for those who needed to be more particular in their demands. The findings indicated that the suggested strategy might lower rental costs and perform better than the alternatives.

Lei, Guo [33] presented an end-to-end deep reinforcement framework to automatically learn a policy for solving a flexible FSSP employing a graph neural network. In addition, to solve the multiple Markov decision process (MMDP), they proposed a multi-pointer graph networks (MPGN) architecture and a training algorithm named multi-Proximal Policy Optimization (multi-PPO), to learn two sub-policies, namely, a job operation action policy and a machine action policy, to allocate a job operation to a machine. They created a disjunctive graph model of FJSP and employed a graph neural network to include the scheduling-related local state. The results demonstrated that the agent could learn a high-quality dispatching policy and outperform both handmade heuristic dispatching rules and a metaheuristic algorithm regarding solution quality and execution time.

Liu and Shi [34] proposed a hyper-heuristic methodology in order to automate the laborious trial-and-error design process of heuristics. In order to reduce the overall completion time, this research sought to develop effective dispatching rules for detecting full schedules. Genetic programming with a cooperative coevolution technique was presented to develop the timetable policy automatically. The findings demonstrated that the suggested method quickly produced high-quality schedules and outperformed constructive and metaheuristic algorithms.

Gu, Li [35] suggested a Hybrid Cuckoo Search Algorithm (HCSA) to resolve the Multi-Objective Permutation (MOP) flow shop scheduling issue. The method balances the global and local searches using the adaptive step size control factor and multi-neighborhood local search. The algorithm’s performance and rate of convergence were enhanced by this procedure. The outcomes demonstrated that the HCS algorithm could handle the issue fast, and it outperformed the CS and INSGA-II algorithms in terms of performance.

Motair [36] considered a two-machine permutation FSSP with the bi-objective of minimizing the makespan (C_max) and maximum tardiness (T_max). They introduced a branch and bound-based algorithm along with two dominance conditions to find the optimal solution to the problem. They utilized simulated annealing to enhance a metaheuristic method for moderate and large-sized issues. The outcomes demonstrated the effectiveness of both the suggested modification to the original metaheuristic algorithm and the dominance conditions.

Zuo, Fan [8] investigated the energy-efficient hybrid FSSP (EHFSP) with a variable speed constraint, considering green scheduling and sustainable manufacturing. In addition, they developed a Multi-Population Artificial Bee Colony (MPABC) algorithm to minimize the makespan, delay, and energy consumption. The population was divided into many subpopulations at random, and then a number of groups were created based on the quality of the subpopulations. For each group, a different search strategy was used in order to maintain population diversity. The data from the past were also utilized to improve the solutions’ quality. The results showed that the MPABC could achieve outstanding performance on three metrics.

Huang, Pan [37] introduced the distributed permutation FSSP by considering the Sequence-Dependent Setup Time (SDST). They also introduced a mathematical model with a restart scheme and an iterated greedy algorithm. A restart scheme was suggested with six diverse operators to guarantee the variety of the approaches and assist the algorithm in surviving local optimizations. Moreover, they suggested two search approaches that rely on a job block developed in the evolution process to enhance the algorithm’s performance further. The findings found that, in contrast, their suggested algorithm was the best-performing of all of the algorithms.

Rashid and Osman [38] suggested an optimization layout for the energy-efficient hybrid FSSP (EE-HFSP). The EE-HFSP optimization was performed using the Firefly Algorithm (FA) on HFSP issues. The outcomes showed that the FA performed better in most issues than the ACO, PSO, and Artificial Bee Colony (ABC) algorithms. Additionally, in 82 percent of the individual optimization targets, FA performed better and obtained the highest convergence according to comparable algorithms.

Lu, Gao [39] investigated a multi-objective HFSP considering production efficiency, noise pollution, and energy utilization. Initially, they proposed a mixed-integer programming model for this multi-objective FSSP. An energy conservation/noise prevention solution was incorporated into the model to conduct green scheduling. Afterward, a Multi-Objective Cellular Grey Wolf Optimizer (MOCGWO) was suggested to fix this issue. The MOCGWO combined the merits of Diversification Cellular Automata (DCA) and Intensification Variable Neighborhood Search (IVNS), which balanced discovery and development. The findings showed that the suggested MOCGWO on this subject was considerably better than its rivals.

Fu, Ding [40] investigated an FSSP considering several targets, such as time-aware processing time and uncertainty. For this issue, a mixed-integer programming model was presented. A fireworks algorithm was built where certain unique methods were planned, e.g., explosion sparks and the choice solution process. The findings revealed that the model and the suggested algorithm could produce adequate outcomes.

Additionally, Li, Sang [41] suggested an Energy-Aware Multi-Objective Optimization Algorithm (EA-MOA) to tackle the hybrid FSSP, considering the setup energy utilization. There was a suggested method for encoding and decoding. Eight categories of neighborhood architectures and an adaptive neighborhood structure choice framework were also built in this article to develop both the capacities of exploration and exploitation. Moreover, a right-shifting approach was planned to boost the energy utilization goal of the strategy. Lastly, a hybrid deep exploitation/exploration approach was suggested to balance the local and global quest skills. Empirical findings showed that the suggested EA-MOA algorithm is robust and efficient.

Santosa and Siswanto [42] suggested a discrete PSO tackling the hybrid FSSP. To accommodate the FSSP, they adjusted the PSO. The adjustment was achieved utilizing the mechanism of the probability transition matrix. However, they used Pareto Optimal (MPSO) to cope with different targets. The findings revealed that MPSO is better than PSO because there was an increase in the chance of finding the best solution from the MPSO solution package. In comparison, the MPSO solution bundle was similar to the optimum solution.

Table 1 compares the available methods for FSSP and shows the main features.

Table 1. Comparing the discussed works side by side.

Article	Goals	Main Features
Goli, Ala [32]	Optimization of non-permutation FSSP and lot-sizing simultaneously	Improving total energy consumption Minimizing time for providing Pareto solutions
Alburaikan, Garg [6]	Minimizing processing times of three-stage FSSPs under fuzziness	Reducing the rental cost
Lei, Guo [33]	Proposing a multi-action deep reinforcement learning framework for flexible job shop scheduling problem	Minimizing the total completion time Increasing efficiency
Liu and Shi [34]	Generating efficient dispatching rules for identifying complete schedules	Minimizing the total completion time Producing high-quality schedules
Gu, Li [35]	Providing an improved HCSA to solve the MOPFSP	Improving the performance and convergence speed of the algorithm
Motair [36]	Finding the optimal solution for solving the problem for a job sequence with up to 14 jobs	Increasing efficiency Reducing delay time
Zuo, Fan [8]	Proposing a MPABC for EHFSP	Minimizing makespan Minimizing total tardiness Improving total energy consumption
Huang, Pan [37]	Providing a mathematical model and an iterated greedy algorithm	Minimizing the makespan Not considering release date, no-wait, or blocking
Rashid and Osman [38]	Optimizing the production scheduling with the FA algorithm.	Minimizing makespan Improving energy utilization
Lu, Gao [39]	Providing one energy conservation strategy and a cellular grey optimizer Developing a variable neighborhood search relying on the issue properly	Improving production efficiency Improving energy consumption Decreasing noise pollution
Fu, Ding [40]	Designing a MO-DFWA to cope with the studied FSSP	Reducing the total tardiness Helping decision makers make a rational decision Does not consider cooperation and collaboration scheduling model in productive systems
Li, Sang [41]	Tackling the HFSP with the EA-MOA algorithm	Minimizing the energy consumption Being weak in search capabilities
Santosa and Siswanto [42]	Tackling the multi-objective discrete problem (FSSP) with the MPSO algorithm	Improving the quality of solution sets Improving the distance of solution sets Increasing computing time
Proposed Method	Solving the FSSP on symmetric networks using a hybrid nature-inspired algorithm	Minimizing the delay time of FSSPs on symmetric networks Minimizing the makespan of FSSP on symmetric networks

According to Table 1, several methods have been used for the FSSP, each of which has its own features. Since the FSSP is one of the main challenges of the symmetric networks, this paper proposed a method for the FSSP using ACO-PSO to decrease delay time and makespan, which is presented in the next section.

3. Proposed Method

The wide range of problems, such as permutation flow shop, job shop, and open shop scheduling problems, have been extensively investigated using exact or heuristic methods [43,44]. However, the methods introduced for scheduling tasks contain some drawbacks: long scheduling process, not considering delay, makespan, and in some cases, not considering efficient and effective use of resources. This section introduces a new method for task scheduling to address these issues. First, a problem statement is defined, and then a proposed method is designed and described based on it.

3.1. Symmetric Networks

All nodes in a network have the same degree. By symmetry, the medial centrality of all nodes is constant. If $C_B\left(w\right)=c$ then [45]:

$$C=\frac{1}{S}\sum _{W\in V}{C}_B\left(W\right)=\frac{1}{S}\sum _{s.d}{\mathcal{l}}_{s.d}-1$$

(1)

Definition 1.

A topology $T=⟨V.\left|P_T\right|.R_{T. }W⟩$ is symmetric, if and only if for any distinct $i. j \in \{0 \dots |P_T|-1\}$, there exists [46]

–

a bijection f: ${\mathit{R}}_{\mathit{T}}$ (i) → ${\mathit{R}}_{\mathit{T}}$ (j), such that ∀v ∈ ${\mathit{R}}_{\mathit{T}}$ (i): ${\mathit{D}}_{\mathit{V}}$ = ${\mathit{D}}_{\mathit{f}\left(\mathit{V}\right)}$, and

–

a bijection g: $W_T$ (i) → $W_T$ (j), such that ∀v ∈ WT (i): $D_V$ = $D_{g\left(V\right)}$.

For example, we call a symmetric topology a bi-directional ring (of sizek = |$P_T$|) if for every$i \in \left\{0\right|P_T |-1\}$ we have:

$$R_T\left(i\right)=W_T(i-1 modk)\cup W_T\left(i\right)\cup W_T\left(i+1 modk\right)$$

(2)

3.2. Problem Statement

The issue is best described as follows: At one of the f flow shop businesses with m machines, n jobs must be arranged. Any jobs can be processed by these machines. A task cannot be moved to another firm after it has been allocated to one; it must be completed by that firm. Each job j on each machine i has a processing time indicated by the symbol p_ij. The issue establishes the sequence π^f, made up of n_f jobs, that must be scheduled in each f. Hence, the sequence $(\pi =\left[{\pi }^1.\dots .{\pi }^f.\dots .{\pi }^F\right])$ results in a solution π. Imagine $C_{i.j}^f$ is the completion time related to j in i (allocated to f), and $C_{max}^f=C_{max}\left({\pi }^f\right)$ makes up the makespan of f. In addition, $C_{max}=C_{max}\left(\pi \right)$ means the global makespan. Moreover, ${\pi }^f\left[\mathcal{i}\right]$ is utilized to indicate the element of f in position i. By using $f_{max}$, the global makespan can also be written as $C_{max}^{fmax}$ [47].

3.3. Designing a Method

FSSP concerns mapping a set of tasks to resources to use resources effectively and efficiently to process and produce results [48]. FSSP is an NP-hard issue, where m machines do n tasks. Each of these machines must process each task in this set to have less implementation time. From an economic perspective, proper use of tasks and task scheduling solutions among machines reduces processing costs and increases the efficient use of resources.

3.3.1. Ant Colony Optimization (ACO)

ACO utilizes swarm-inspired methods to solve complex issues [49]. The main idea of ACO is to employ ant search behavior in finding food [50]. When an ant is trying to find food, it uses a particular chemical called a pheromone to communicate with other ants [51]. At the beginning of the search, the ant starts the search randomly, and when it finds a food path, it leaves the pheromone in that path. Other ants can access the food source using the leftover pheromone [52,53]. When this process is repeated several times, the ants are gradually attracted to shorter paths and paths with a large amount of pheromones [54]. This algorithm and its advantages can also search and obtain an optimal response in task scheduling. When a new request enters the scheduling cycle, the probability of ants choosing paths from existing hosts is calculated using Equation (3). In other words, this relation indicates the possibility of sending request j to host i. τ_i,j represents the concentration of pheromones, and the heuristic function η_i,j is calculated by Equations (4)–(6) in each iteration. ϰ and β are the factors affecting the pheromone and the heuristic function, respectively, both of which take a value of one in the proposed method. us is a set of remaining requests that are not currently scheduled, and r is a request. Equations (5)–(7) indicate the fitness of host i for the three sources used in the proposed method. ηΜ_i indicates the quality of the amount of memory remaining in host i, and similarly, ηC_i, and ηD_i indicate the quality of the amount of processor and storage remaining in host i, respectively. ω₁, ω₂, and ω₃ are the weight of memory, processor, and storage as three utilized sources. They have been used with constant and determined amounts. Max_m, Max_c, and Max_d represent the maximum amount of memory, the maximum amount of processor consumption, and the maximum storage capacity each host can have. MR_i represents the amount of memory remaining in host i, and UC_i and UD_i represent the amount of processor consumption and storage of host i, respectively [55].

$$p_{i.j }=\frac{{\tau }_{i.j}^{\varkappa }\times {\eta }_{i.j}^{\beta }}{{\sum }_{rϵ us}⟨{\tau }_{i.j}^{\varkappa }\times {\eta }_{i.j}^{\beta }⟩}$$

(3)

$${\eta }_{i.j}={\omega }_1\times \eta M_i+{\omega }_2\times \eta C_i+{\omega }_3\times \eta D_i$$

(4)

$$\eta M_i=\frac{{MR}_i}{{Max}_m}$$

(5)

$$\eta C_i=\frac{{{Max}_c-UC}_i}{{Max}_c}$$

(6)

$$D_i=\frac{{{Max}_d-UD}_i}{{Max}_d}$$

(7)

In the ACO algorithm, the heuristic function belongs to local points [56]. Each ant has a personal opinion about choosing the next path [57]. As a result, according to the relations above, each ant chooses the next path based on the remaining resources of each path. Therefore, from a memory perspective, the longer the path memory, the better. However, from a processor and storage perspective, less use means more residual resources. Thus, the average of the remaining resources from these three resources is calculated using Equation (4) and based on the weight.

The general protocol of the ACO algorithm handles the four-stage scheduling [58]:

Step 1: Initialization. The parameters of the ACO and the ants’ initial locations are initialized.

Step 2: Solution construction. According to a probabilistic state transformation principle, each ant builds a full solution to the issue. The principle of state transformation relies largely on the pheromone state and the visibility of ants.

Step 3: Pheromone updating rule. The pheromone trails’ strength on each edge is modified by the pheromone-updating principle when each ant has built a solution.

Step 4: Terminating criterion. Steps 2–3 are iterated before the condition for termination is set.

3.3.2. Particle Swarm Optimization (PSO)

PSO is a powerful optimization method. As with fish and bird flocks, the cooperative conduct of insect colonies is inspired by this technique [59]. After all, it is interesting how these animals pass in one direction, often breaking into 2 groups to escape a predator and reforming the initial group [52]. Each one utilizes local information it can obtain to determine its relocation of its nearest neighbors. Simple rules such as ‘keep reasonably close to other individuals’, ‘walk in the same direction’, and ‘go at the same pace’ are adequate to preserve community cohesion and allow dynamic and adapted collective attitude. The PSO is planned to optimize nonlinear continuous functions [60]. Each individual is a particle reflecting a possible solution to optimize the issue. Let f the fitness function be reduced. Each particle k can be illustrated at iteration t by the characteristics below [61]:

1. Each particle k is demonstrated in n-dimension search space by its position vector $X_k^t=\left(X_{k1}^t. X_{k2}^t. \dots . X_{kn}^t\right)$ and its velocity vector $V_k^t=\left(V_{k1}^t. V_{k2}^t. \dots . V_{kn}^t\right)$ at iteration t, where $X_{kd}^t$: the position of the k at the dimension $d=1. n$ and $V_{kd}^t$: the velocity of the k at the dimension $d=1. n$.

2. Each particle k remembers its best location attained until iteration t is denoted by Equation (8).

$$P_k^t=\left(P_{k1}^t. P_{k2}^t. \dots . P_{kn}^t\right)$$

(8)

3. $P_g^t$ is the best position in the swarm until iteration t and defined by Equation (9).

$$P_g^t=\left(P_{g1}^t.P_{g2}^t. \dots . P_{gn}^t\right)$$

(9)

4. The current velocity of the dth is updated based on Equation (10).

$$V_{kd}^t=\omega V_{kd}^{t-1}+c_1{r}_1\left(P_{kd}^{t-1}-X_{kd}^{t-1}\right)+c_2{r}_2\left(P_{gd}^{t-1}-X_{gd}^{t-1}\right)$$

(10)

$\omega$ controls the impact of the previous velocity on the current one, $c_1. c_2$ are two positive constants employed to decide whether the particles prefer moving toward to $P_k^t$ or $P_g^t$ position, and $r_1.r_2$ are random distributed real numbers in [0, 1].

5. The position vector of the particle k at iteration t is given by Equation (11) [62].

$$X_{kd}^t=X_{kd}^{t-1}+V_{kd}^t$$

(11)

6. The best position of each particle is obtained using Equation (12).

$$P_k^t=\left\{\begin{array}{c}{P}_k^{t-1} if f\left(X_k^t\right)\ge f\left(P_k^{t-1}\right)\\ X_k^{t } if f\left(X_k^t\right)<f\left(P_k^{t-1}\right)\end{array}\right.$$

(12)

7. The global best position found so far is obtained using Equation (13).

$$P_g^t=\left\{\begin{array}{c}{argmin f(P}_k^t) \mathrm{if} f\left(P_k^t\right)<f\left(P_g^{t-1}\right)\\ P_g^{t-1 } \mathrm{otherwise}\end{array}\right.$$

(13)

Here, the objective f is to reduce the makespan C_max. According to their series in the vector location, the method must first schedule the workers on the towing machines utilizing a list algorithm to determine this value. Afterward, in the second unit, it calculates the average completion time. The pseudo-code of the PSO algorithm can be summarized [63]:

Step 1: Initialization. Initialize an array of particles based on random locations.

Step 2: Local best updating. Assess the fitness function of the particles and update the ${\mathrm{P}}_{\mathrm{i}}^{\mathrm{k}}$ using the best current value.

Step 3: Global best updating. Calculate the current best global value among the existing positions and update ${\mathrm{P}}_{\mathrm{g}}^{\mathrm{k}}$.

Step 4: Solution construction. Each particle is moved to a new spot by altering the velocities.

Step 5: Terminating criterion. Repeat Steps 2–4 until a terminating condition is satisfied [64].

3.3.3. Particle Representation

Representing a particle phase tries to translate a solution to the FSSP into a particle (or ant). In this problem, a position in a particle represents a job number, and the number of positions (i.e., particle size) corresponds to the number of jobs, as shown in Figure 1. For example, consider particle 2 (J₄ → J₁ → J₂ → J₃). The J₄ is scheduled on the corresponding stage and assigned to a machine that can complete J₄ at the earliest completion time. Then the J₁ is scheduled, and so on.

Figure 1. Example of two particles.

3.3.4. Proposed Method for Flow Shop Scheduling

Most current feature selection algorithms struggle with the issue of local optima stagnation [65,66,67]. ACO, GA, and PSO randomize the search space and use historical data to get around this problem. However, evolution operators such as crossover and mutation are absent from ACO and PSO. However, both have memory, which is necessary for creating useful algorithms. In contrast to GA, where individuals compete with one another, PSO and ACO are more effective since agents cooperate (particles or ants) [68]. Moreover, some other methods that are proposed for scheduling problems, such as the Pareto approach, have some other disadvantages. One disadvantage is that the Pareto technique is not very suitable for combining with local search since several local movements might not affect how well a solution ranks [69]. Thus, in this research, a hybrid method is employed to solve the flow shop scheduling issue, which has a higher speed. The proposed method uses two heuristic and fitness functions to achieve makespan and optimal delay. In the following, its integration with the PSO algorithm in achieving convergence solves the problem of scheduling tasks with optimal makespan and minimum delay of tasks. In the proposed method, tasks are sent to processing hosts as a set of requests, including the number of requested resources and the amount of time required to use these resources. Resources in this method include all three processors, memory, and storage. The proposed method uses two heuristic and fitness functions to achieve makespan and optimal delay.

3.4. The Proposed Method

This algorithm improves the search results after the ACO’s search step is designed to optimize the particle swarm. The reason for this fact is the high convergence speed of this algorithm, which makes the proposed method complete the scheduling operation as soon as convergence is achieved. The main use of PSO is to obtain the best individual and overall solution in each iteration to solve the scheduling problem for new requests [70]. Equation (10) is used to obtain the velocity vector in the proposed method. S_pby represents the best individual solution of ant y to iteration t. S_gb is the best overall answer. Values C₁ and C₂ are two random weighting factors to choose either individual or general solutions. The difference is that the best individual solution signifies the best answer of the ant y in the iteration of t. In the main PSO algorithm, the addition operator and weighting factors are used to move the particle to the best individual solution and a certain amount toward the best general solution. However, the addition operator has attained another meaning for simplification and scheduling in the proposed method. In this paper, the A+B relation means selecting the A and B solutions in the population swarm optimization algorithm. The process is such that to generate the velocity vector after the random production of weighting factors, according to these weighting factors, the solutions are selected from one of the sets of best individual answers or best overall answers using the Roulette Wheel selection method. If the scheduling is selected from a solution already in the list, that scheduling will be rejected, and another path will be selected again from another solution. The same process is repeated to obtain a new position, and the roulette wheel selection method is employed. The only difference is that the selection coefficient for selecting the velocity vector or the previous position is the same. Ultimately, the probability of selection between both of them is considered equal.

After each ant has produced its solution, Equation (14) evaluates each ant’s score from the existing scheduling. The best solution for the current iteration is searched using this equation, and the best overall answer value is updated. Equation (15) uses the fuzzy set theory to sum the answers related to the makespan and the delay. In this equation, σ₁ and σ₂ are weighting factors. In Equations (16)–(18), the values Υ₁, Υ₂, Υ₃, b₁, and b₂ are weighting factors. A value of V is a characteristic of resource utilization distribution, and a value of D is known as the property of maximum use difference. Equation (15) represents makespan in hosts. The lower the value of this equation, the better the makespan. In Equation (16), the values CV_mr, CV_c, and CV_d, respectively, determine the residual coefficient of variation for memory, processor, and storage among all hosts. Since this method uses three different resources, their values need to be normalized. Using the coefficient of variation can solve this issue. For example, if the value of CV_mr is small, it means that the difference between the remaining values of memory is small among all hosts, and as a result, one minus this value results in a larger number. The values MR_max and MR_min express the maximum and minimum amount of remaining memory, respectively. The values UC_max and UC_min indicate the maximum and minimum CPU consumption, respectively. The values UD_max and UD_min are the maximum and minimum values of storage utilization, respectively.

$$Evaluation={\sigma }_1{f}_1+{\sigma }_2{f}_2$$

(14)

$$f_1:DB=b_1\times V+b_2\times \left(1-D\right)$$

(15)

$$V={{\rm Y}}_1\times \left(1-{CV}_{mr}\right)+{{\rm Y}}_1\times \left(1-{CV}_c\right)+{{\rm Y}}_1\times \left(1-{CV}_d\right)$$

(16)

$$\begin{gathered} D={{\rm Y}}_1\times \frac{{MR}_{max}-{MR}_{min}}{{Max}_m}+{{\rm Y}}_2\times \frac{{UC}_{max}-{UC}_{min}}{{Max}_{uc}}+ \\ {{\rm Y}}_3\times \frac{{UD}_{max}-{UD}_{min}}{{Max}_{ud}} \end{gathered}$$

(17)

$$f_2:makespan=\max ⟨\sum _{jϵJ_{m_i}}{ETC}_{ij}⟩$$

(18)

In the proposed method, only the total pheromone values are updated. In other words, increasing the pheromone is possible if the selected path in the current iteration belongs to the best solution. Otherwise, in Equation (19), the value of f_cb equals zero, resulting in increased evaporation of the pheromone evaporation process.

$${\tau }_{t+1}=\left(1-p\right)\times {\tau }_t+p\times f_{cb}$$

(19)

where p is the evaporation rate, and f_cb is the best solution value for the current iteration. In the proposed method, two conditions are considered for completing the iterations of the hybrid algorithm and obtaining the scheduling. The first situation is when the algorithm has reached the maximum value possible for repetition. The second situation is one in which the function of the solution’s solutions does not change for some time. The pseudo-code of the proposed hybrid method is outlined in Algorithm 1.

Algorithm 1. Pseudo-code for hybrid ACO/PSO algorithm

Algorithm HACOPSO

Begin Input: Number of ants, Number of particles (solutions), Maximum number of generations Output: The best solution for the flow shop scheduling  Generate n particle agents randomly and distribute them uniformly over the search space   while (itr < Countmax)      For i = 1 to n          Update the pheromone of the particle i,                   For j = 1 to m                          Update the pheromone of all attributes trail by increasing the pheromone in the paths followed by i.                End for    End for   For i = 1 to n       Update the pheromone              If the fitness of the current position < their best neighbors’ fitness value,              Then move to the neighbor’s pattern              If the fitness value of the last position is higher than the new position,              Then replace that lower fitness value with the higher-fitness-value              If the newly generated particle has more fitness than the earlier fitness,              Then update the pheromone  End for End.

❖

Steps in Hybrid ACO-PSO Optimization Algorithm

The steps of the proposed method are described in the following [71]:

Step 1: Receiving the inputs.

■

Set the servers with their resource capacity.

■

Set the VMs with their resource requirements.

Step 2: Initialization.

▪

Initialize population size, number of ants, and maximum number of iterations.

Step 3: Generate the initial population by VM placement solutions based on each server’s power consumption and resource wastage.

Step 4: Update the particle-pheromone table with solutions obtained from ACO.

Step 5: Generate new particles.

Step 6: Calculate the fitness of all particles and find their local best position.

Step 7: Update the particle’s velocity.

Step 8: Update the particle’s position.

Step 9: Update the particle-pheromone table with solutions obtained from PSO.

Step 10: Discover the global-best solution.

Step 11: Go to step 3 if the iteration value is less than maximum number of iterations, or go to step 12.

Step 12: Output the global-best solution for VM placement.

Figure 2 depicts the flowchart of the proposed method.

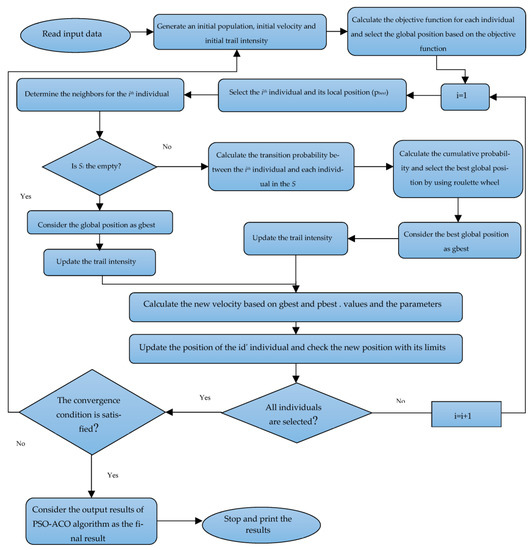
Figure 2. Flowchart of ACO-PSO optimization algorithm.

3.5. Fitness Function

A fitness function determines the appropriateness of the solution. To calculate fitness values, the relative error is employed. By using synchronous master–slave parallelization, the fitness is achieved from Equations (20)–(22) by normalizing the values of makespan and delay into [0, 1].

$$F=W_1\times Makespan+W_2\times Delay$$

(20)

$$Makespan=\frac{{Makespan}_{max}-Makespan}{{Makespan}_{max}-{Makespan}_{min}}$$

(21)

$$Delay=\frac{{Delay }_{max}-Delay }{{Delay }_{max}-{Delay }_{min}}$$

(22)

4. Experimental Results

These two goals (makespan and delay) are the most important, so they are considered in this paper. If the other goals, such as the flow time, tardy jobs, tardiness, earliness, etc., are added, it is likely to affect the results of these two goals. In this section, the simulation process is explained first. The algorithm is then examined with two other algorithms in three different scenarios, and the results are presented. At the end of this section, the statistical test results are presented.

4.1. Simulation Process

The simulations were performed on a PC with an Intel 6600 processor with 4 GB of memory and a Windows 8 operational system. To evaluate the algorithm’s efficiency, MATLAB version 2019 was employed, and the system environment with several different scenarios was considered. The method’s performance was compared to other approaches. The analysis of the results was reviewed and evaluated based on various criteria. Three different scenarios (with different sources) were considered to analyze the simulation results, and simulations were performed at different system scales.

4.2. Results

The issue of the FSSP is one of the main issues when trying to determine optimal scheduling for executing tasks and allocating optimal resources. The main focus of this article is minimizing delay and reducing makespan in symmetric networks. To compare the efficiency of the proposed method, the Ant Lion Optimizer (ALO) algorithm, Grey Wolf Optimization (GWO), ACO [72], PSO [42], and Motair [36] were taken into account. The values used as simulation parameters in MATLAB were considered according to Table 2. The method was implemented with tasks ranging from 2000 to 8000 in three different scenarios. The distribution was considered uniform. The efficiency of the approach was compared to the ACO-PSO algorithm in terms of delay time and makespan parameters. A comparison of evaluation parameters is discussed below.

Table 2. Simulation parameters.

Parameter	Value
Number of resources	70, 120, 200
Number of tasks	2000, 4000, 6000, 8000
Execution start time	0
Processing speed	Variable between 3000 and 19,000 MIPS
Bandwidth	Variable between 1100 and 7200 Mbps
The amount of data	Variable between 1700 and 3000 Mb
Instruction rate	Variable between 500 and 1600 MI
θ1 and θ2	0.5
Proposed method
Number of solutions	100–300
Pheromone evaporation rate	0.5
α	1
β	3
Maximum number of generations	100
C1	Rand * 2
C2 (C1 + C2 <= 4)	Rand * 1.5
Inertial weight	First 0.9, then decrease to 0.4
Maximum speed	Rand * Number of tasks
Maximum number of generations	100
GWO algorithm
Maximum number of iterations	100
Dimension	5
Best source	Alpha source
Best_pos	Destination position
PSO algorithm
Number of particles (solutions)	100–300
Inertial weight	First 0.9, then decrease to 0.4
C1	Rand * 2
C2 (C1 + C2 <= 4)	Rand * 1.5
Maximum speed	Rand * Number of tasks
Maximum number of generations	100
Ant Lion Optimizer (ALO) algorithm
Max no. of iterations	100
Number of dim	5
Lower bound	1
Upper bound	8–13
Best score	Elite ant lion fitness
Best position	Elite ant lion position
ACO algorithm
Number of ants (solutions)	100–300
Pheromone evaporation rate	0.5
α	1
β	3
Maximum number of generations	100

Comparing the relative performance for different iteration counts is possible by computing the objective function, as shown in Figure 3. The fitness amount ranges from 0 to 1, as shown in Figure 3. The fitness value declines as the number of generations rises. As illustrated, the fitness value between the 140th and 240th generations fells to its lowest point of 0.26. The stability findings for the integers between 0.20 and 0.25 were achieved for 60 iterations, as shown in Figure 4. Therefore, the best and most frequent answer was 0.24.

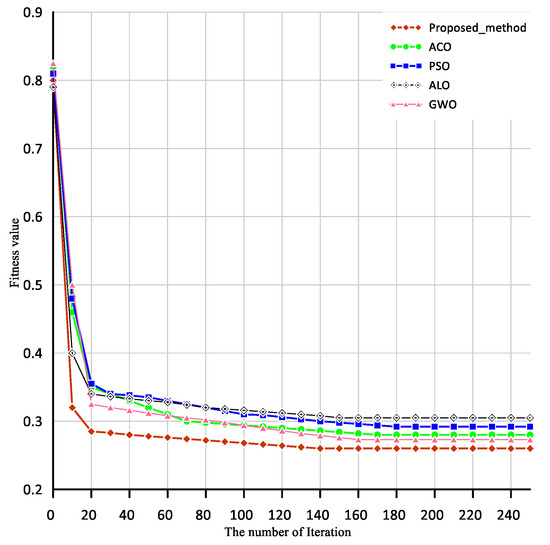
Figure 3. The result of convergence in 240 generations.

Figure 4. Stability of the proposed method.

• ❖ Delay Time

In this part, we compare the performance of the suggested method to the ACO-PSO strategy in three scenarios regarding latency.

• Scenario 1: The number of resources is 70

Figure 5 shows the amount of delay presented over 70 scheduled resources. According to Figure 5, when the number of tasks is 2000, the delay is 5865 s in the Motaier, 6014 s in the proposed method, 6201 s in the ALO, 6225 s in the GWO, 6350 s in the ACO algorithm, and 6380 s in the PSO algorithm. Similarly, when the number of tasks is 8000, the delay is 14,059 s in the Motaier (2021), 15,550 s in the proposed method, 16,123 s in the GWO, 16,325 s in the ALO, 16,470 s in the ACO algorithm, and 16,850 s in the PSO algorithm. According to Figure 5, the delay increases with an increase in the number of tasks, which is less in the proposed method than in the compared methods except for Motaier (2021). It is a little better than the proposed method.

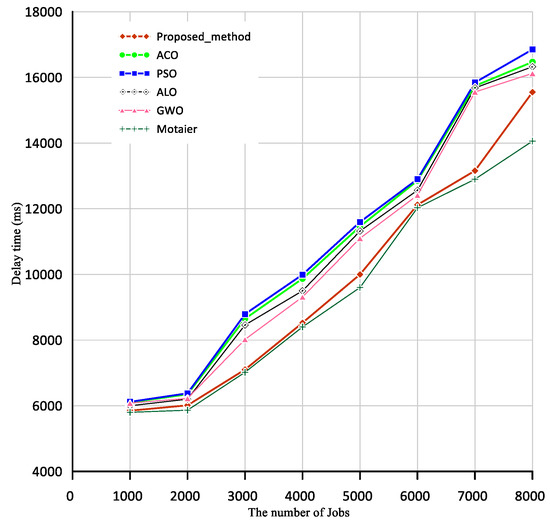
Figure 5. Comparison of delay time in the proposed method and other algorithms; Scenario 1.

• Scenario 2: The number of resources is 120

Figure 6 shows the delay time of 120 scheduled resources. According to Figure 6, when the number of tasks is 2000, the delay is 2010 s in the Motaier, 2050 s in the proposed method, 2180 s in the GWO, 2410 s in the ALO, 2459 s in the ACO algorithm, and 2342 s in the PSO algorithm. Similarly, when the number of tasks is 8000, the delay time is 8106 s in the Motaier (2021), 8300 s in the proposed method, 8456 s in the GWO, 8850 s in the ALO, 9613 s in the ACO algorithm, and 8580 s in the PSO algorithm. The delay increases with an increase in the number of tasks, which is less in the proposed method than in the compared methods except for Motaier (2021). It is a little better than the proposed method.

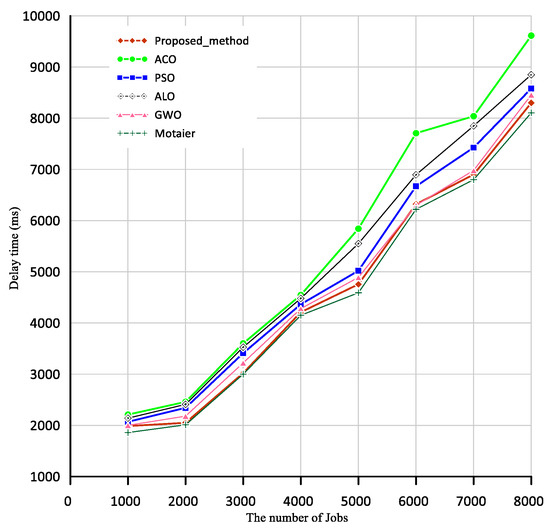
Figure 6. Comparison of delay time in the proposed method and other algorithms; Scenario 2.

• Scenario 3: The number of resources is 200

Figure 7 shows the total delay of over 200 scheduling resources. According to Figure 7, when the number of jobs is 2000, the delay is about 1225 s in the Motaier, 1250 s in the proposed method, 1302 s in the GWO, 1425 s in the ALO, 1597 s in the ACO algorithm, and 1323 s in the PSO algorithm. Similarly, when the number of tasks is 8000, the delay is about 4836 s in the Motaier, 5000 s in the proposed method, 5125 in the GWO, 5896 in the ALO, 6093 s in the ACO algorithm, and 5539 s in the PSO algorithm. According to Figure 7, the delay increases with an increase in the number of tasks, which is less in the proposed method than in the compared methods except for Motaier (2021). It is a little better than the proposed method.

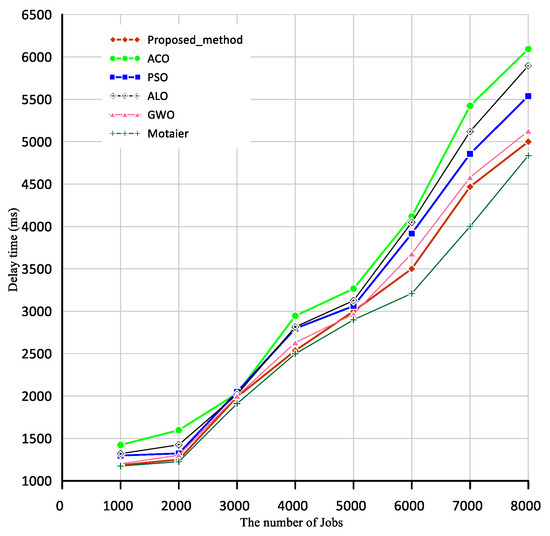
Figure 7. Comparison of delay in the proposed method and other algorithms; Scenario 3.

• ❖ Makespan

This section examines the proposed method’s performance in terms of makespan, with the ACO-PSO approach in three different scenarios.

• Scenario 1: The number of resources is 70

Figure 8 shows the amount of makespan that is scheduled for 70 resources. According to Figure 8, when the number of jobs is 1000, the makespan is about 500 in the proposed method, 520 in the GWO, 535 in the ALO, 595 in the Motaier, 555 in the PSO algorithm, and 575 in the ACO algorithm. Similarly, when the number of tasks is 8000, the makespan is about 1411 in the proposed method, 1490 in the GWO, 1509 in the ALO, 1600 in the Motaier, 1520 in the PSO algorithm, and 1550 in the ACO algorithm.

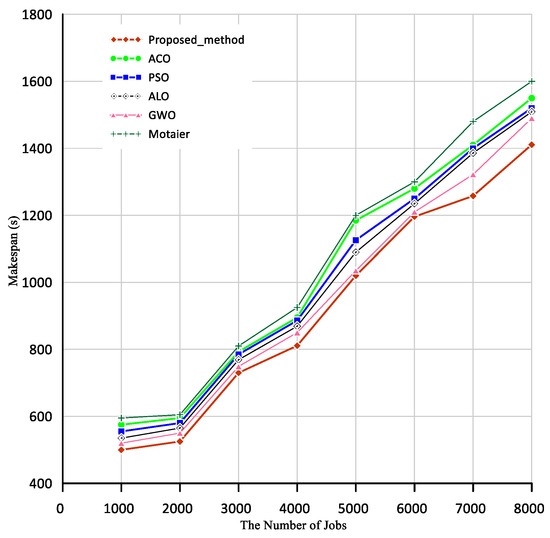
Figure 8. Comparison of makespan in the proposed method and other algorithms; Scenario 1.

• Scenario 2: The number of resources is 200

Figure 9 shows the amount of makespan presented on 120 scheduled resources. According to Figure 9, when the number of tasks is 2000, the makespan is about 200 in the proposed method, 208 in the Motaier, 210 in the GWO algorithm, 240 in the ALO, 245 in the PSO, and 235 in the ACO algorithm. Similarly, when the number of jobs is 8000, the makespan is about 819 in the proposed method, 823 in the Motaier, 835 in the GWO, 850 in the ALO, 876 in the PSO algorithm, and 840 in the ACO algorithm. According to Figure 9, as the number of jobs rises, the increase in the makespan in the proposed method is less than in other algorithms.

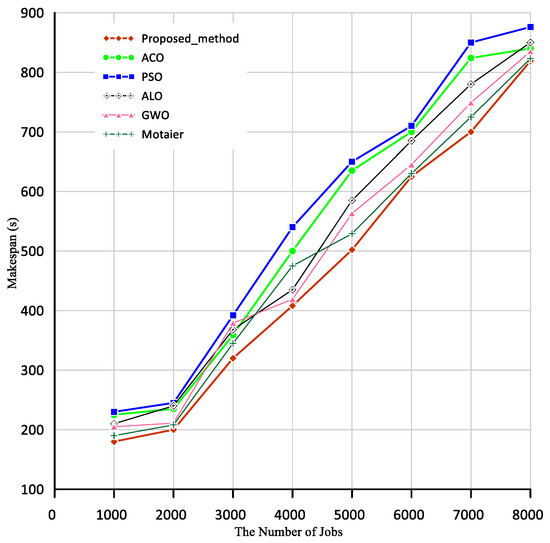
Figure 9. Comparison of makespan in the proposed method and other algorithms; Scenario 2.

• Scenario 3: The number of resources is 200

Figure 10 shows the amount of makespan presented over 200 scheduled resources. When the number of jobs is 2000, the makespan is about 110 in the proposed method, 136 in the Motaier, 159 in the GWO algorithm, 165 in the ALO, 193 in the PSO, and 185 in the ACO algorithm. Similarly, when the number of tasks is 8000, the makespan is about 528 in the proposed method, 543 in the Motaier, 560 in the GWO, 574 in the ALO, 588 in the ACO algorithm, and 598 in the PSO algorithm.

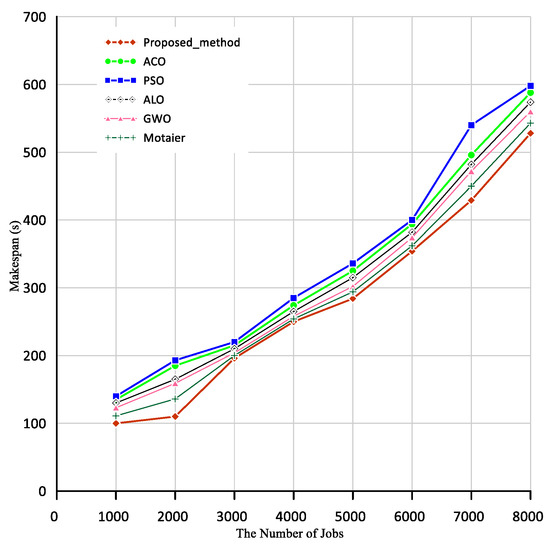
Figure 10. Comparison of makespan in the proposed method and other algorithms; Scenario 3.

4.3. Statistical Analysis

The proposed method was examined analytically and compared to the ACO and PSO algorithms. Friedman has been used for many comparative studies. To provide a statistical study of the algorithms built to measure the experiment categories, we obtained the required post hoc procedures, and estimated the controlled p-values. Algorithms were statistically evaluated for the generalized implementation graphs generated at random.

H1. 

The proposed method’s efficiency seems to be different from that of the other methods.

H0. 

The proposed method’s efficiency does not seem to differ from that of the other methods.

Table 3 and Table 4 show Friedman’s results for the average rankings attained by the algorithms. To evaluate the Friedman test results and determine if the difference in the average success methods is significant, the results of Table 3 (Test Statistics) must be used.

Table 3. Test Statistics ^a.

Parameters	Value
N	195
Chi-Square	37.280
df	2
Asymp. Sig.	0.000

Note: ^a Friedman Test.

Table 4. Friedman Test (Ranks).

	Mean Rank
ACO	1.99
ALO	2.06
GWO	2.19
PSO	1.86
Proposed Method	2.25

Table 4 determines which proposed method has the least performance and which has the most. The table shows that the mean ranks of the GWO, ALO, ACO, and PSO algorithms were 2.19, 2.06, 1.99, and 1.86, respectively. However, the average of the proposed method was 2.25, indicating that the proposed method was now more efficient.

5. Conclusions and Future Work

In symmetric networks, scheduling deals with allocating resources over a given time frame to minimize one or more targets. Scheduling plays an essential part as a decision-making method for manufacturing and processing systems, transport, distribution structures, and even certain kinds of service. Investigators in this field have made a major contribution, from the classical issues of the literature to experimental applications. Because of its varied economic and industrial uses, several scholars have investigated the FSSP widely. The standard FSSP includes workers on a collection of machines with the same output flow. The aim is to find the job sequence that satisfies one or a set of criteria. An ACO-PSO algorithm is proposed to lessen the makespan and delay time in symmetric networks. To forecast the workload of novel input demands, ACO-PSO utilizes historical information. The proposed method selects the best host from the available hosts based on heuristic and fitness functions considering the two factors, makespan and delay, by searching all hosts over several iterations and assigning it to the host based on the requested resources. Combining the ACO and PSO algorithms can significantly reduce the delay and makespan. The proposed technique has higher effectiveness than the previous approaches. The results prove that the delay time was improved compared with the PSO and ACO algorithms; therefore, the proposed method is suitable for real-time applications. Moreover, the makespan of the suggested approach was enhanced when compared to PSO and ACO. In future work, the ACO-PSO algorithm can be extended to the FSSP considering other metrics, such as energy consumption, to realize green systems. In addition, utilizing the provided method in other distributed environments, such as the NSGA-III algorithm [73], distributionally robust optimization (DRO) [74], and Deep Belief Networks [75], is a very interesting line for future research. Furthermore, employing learning analytics and epistemic network analysis [76], grey wolf optimization [77], and Kalman filtering [78,79] for solving the FSSP can be investigated in the future. Finally, considering the dynamics approach [80,81] and human resources [82] in the symmetric networks can be investigated in future research.