Abstract
As a top-down holographic approach, the D4/D8 model is expected to be a holographic version of QCD, since it almost includes all the elementary features of QCD based on string theory. In this manuscript, we review the fundamental properties of the D4/D8 model with respect to the D4-brane background and the embedding of the flavor branes, holographic quark, gluon, meson, baryon and glueball with various symmetries; then, we take a look at some interesting applications and developments based on this model.
1. Introduction
Although it has been about 25 years since the proposal of AdS/CFT and gauge–gravity duality with holography [,,], it continues to attract great interest today. The most significant part of AdS/CFT and gauge–gravity duality is that people can evaluate strongly coupled quantum field theory (QFT) by quantitatively analyzing its associated gravity theory in the weak coupling region. Thus, it provides a holographic way to study strongly coupled QFT, in which traditional QFT based on the perturbation method is out of reach. Accordingly, a large number of publications on strongly coupled QFT through AdS/CFT and gauge–gravity duality have appeared, for example, on the Wilson loop and quark potential [,,], the transport coefficient [,,], the fermionic correlation function [,], the Schwinger effect [], quantum entanglement entropy [,] and quantum information on black holes [], which have become most remarkable works in this field.
On the other hand, QCD (quantum chromodynamics), as the fundamental theory describing the property of strong interaction, is extremely complex in the strong coupling region, especially at a finite temperature with dense matter, due to its asymptotic freedom [,]; hence, the holographic version of QCD is naturally becoming an interesting topic. While there are several models and theories attempting to give a holographic version of QCD (e.g., bottom-up approaches [,,], the D3/D7 approach [], the D4/D6 approach []), one of the most successful achievements in holography is the D4/D8 model (also called the Witten–Sakai–Sugimoto model) [,,], which includes almost all the elementary features of QCD in a very simple way, e.g., mesons, baryons [,,], glueballs [,,,], deconfinement transition [,,], a chiral phase [,], a heavy flavor [,,], a term and QCD axion [,,,,], and a nucleon interaction [,,,,,,]. The D4/D8 model is based on the holographic duality between the 11-dimensional (11d) M-theory on and the super conformal field theory (SCFT) on M5-branes []. By using the dimensional reduction in [,], it reduces to the correspondence of the pure Yang–Mills theory on D4-branes compactified on a circle and 10d IIA supergravity (SUGRA). Flavors as pairs of D8- and anti-D8-branes () can be further introduced into the geometric background produced by the D4-branes, so the dual theory includes flavored fundamental quarks, which would be more close to the realistic QCD. Moreover, as the D4/D8 model is a T-dualized version of the D3/D9 system [], the fundamental quark and meson in the D4/D8 model can therefore be identified to the 4–8 (The 4–8 string refers to the open string connecting the D4-brane and D8-branes; it is similar for, e.g., the 8–8 or 4– string.) and 8–8 strings, respectively, by following the same discussion in the D3/D9 system []. Moreover, the baryon vertex is identified as a D4-brane wrapped on [], and the glueball is recognized to be the bulk gravitational polarization [,]. The chiral phase is determined by the embedding configuration of the -branes due to the gauge symmetry on their worldvolume [], while the deconfinement transition is suggested to be the Hawking–Page transition in this model [,,,]. Altogether, this model includes all the fundamental elements of QCD; thus, it can be treated as a holographic version of QCD.
In this review, we revisit the above properties of the D4/D8 model, then take a brief look at some recently relevant developments and holographic approaches with this model. The outline of this review is as follows. In Section 2, we review the relation of 11d M-theory and IIA SUGRA with respect to the case of the M5-brane and D4-brane. Afterwards, we review the embedding configuration of the -branes to the D4-brane background and the holographic quark, gluon, meson, baryon and glueball with various symmetries, which are all the relevant objects in hadron physics. In Section 3, we review several topics about the developments and holographic approaches of this model, which include deconfinement transition, chiral transition, the Higgs mechanism and heavy–light mesons or baryons, interactions involving glueballs and the QCD term in holography. In the Appendix A, Appendix B and Appendix C, we give the general form of the black brane solution in type II SUGRA, the relevant dimensional reduction for spinors and discussion about supersymmetric mesons, which are useful to the main content of this paper.
2. The D4/D8 Model
In this section, we revisit the D4-brane background and the embedding of the probe -branes. Then, we review how to identify quarks, gluons, mesons, baryons and glueballs with various symmetries in this model.
2.1. Eleven-Dimensional Supergravity and D4-Brane Background
The D4-brane background of the D4/D8 model is based on the holographic duality between the type super conformal field theory (SCFT) on coincident M5-branes and 11-dimensional (11d) M-theory on []. In order to obtain a geometric solution, the effective action of the M-theory is necessary, which is known as the 11d supergravity action. In the large- limit, the geometric background can be obtained by solving its bosonic part, which consists of a metric (elfbein) and a three-form : [],
where . The convention in (1) is as follows. refers to the 11d scalar curvature; is the 11d gravity coupling constant, given by
where is 11d Newton’s constant and is the Planck length. The quantity can be obtained by a general notation of an n-form :
where refers to the metric on the manifold. We note that in (1), the last term is a Chern–Simons structure. which is independent on the metric or elfbein, while the first term depends on the metric or elfbein through the metric combination
The solution for extremal coincident M5-branes is obtained:
where r denotes the radial coordinate to the M5-branes and run over the M5-branes. Using the BPS condition for M5-brane,
which leads to
where refers to the tension of the M5-brane. Taking the near-horizon limit and replacing the variables
the metric presented in (5) reduces to
describing the standard form of , where the radius of is . In addition, the action (1) also allows for the near-extremal M5-brane solution, which, after taking near-horizon limit and replacement (8), is
The constant refers to the location of the horizon, which can be determined by omitting the conical singularity,
where is the size of the compactified direction .
In order to obtain a QCD-like low-energy theory in holography, Witten proposed a scheme in [] based on the above M5-brane solution. Specifically, the first step is to compactify one spacial direction (denoted by ) of M5-branes on a circle with periodic condition for fermions, which means the supersymmetry remains. Accordingly, the resultant theory is a supersymmetric gauge theory above the size of the circle. Then, recalling the relation between M-theory and IIA string theory, the 11d metric presented in (9) or (10) reduces to a 10d metric,
with the nontrivial dilaton . For later use, let us introduce another radial coordinate, , as follows:
So, in the large limit, the 11th direction presented in (12) vanishes due to (7) and (8), which means the coincident M5-branes correspond to coincident D4-branes for . In addition, the remaining 10d metric in (12) becomes the near-extremal black D4-brane solution (the extremal D4-brane solution can be obtained by setting ):
where refers to the volume form of a unit . Once the formula (12) is imposed to action (1), the 11d SUGRA action reduces to the 10d type IIA SUGRA action exactly, which is given as follows (there could be a Chern–Simons term to the IIA SUGRA action (15), such as with . For the purely black brane solution, the field can be gauged away by setting , which implies that this CS term could be absent in 10d action [,]):
where is the 10d gravity coupling constant. It would be straightforward to verify that the solution (14) satisfies the equation of motion obtained by varying action (15).
The next step is to perform the double Wick rotation on the metric (14), leading to a bubble D4-brane solution,
which is defined only for . We renamed as in (16), since there is not a horizon in the bubble solution, as illustrated in Figure 1.
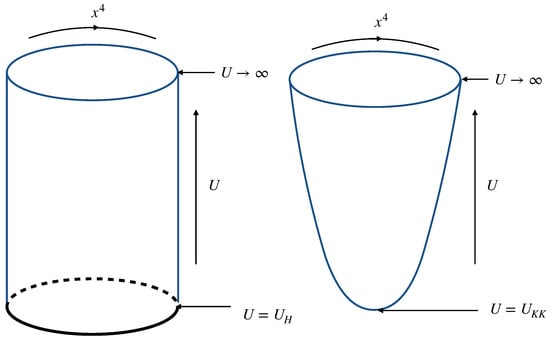
Figure 1.
The compactified D4-brane geometry on plane. (Left) The black D4-brane background geometry. (Right) The D4 bubble geometry.
Now, the direction of is periodic:
because it is identified as the time direction in the black brane solution (14). refers to the Klein–Kaluza (KK) energy scale, and the supersymmetry on the D4-branes breaks down below by imposing the antiperiodic condition to the supersymmetric fermions along . Accordingly, the low-energy zero modes on the D4-branes are the massless gauge field on the D4-branes and the scalar fields as the transverse modes of the D4-branes. While the scalar fields acquire mass via one-loop corrections, the trace part of the scalars and gauge field along direction remain massless. As they give irrelevant coupling terms in the low-energy effective theory on the D4-branes, it means that the dual theory below only contains 4d pure Yang–Mills gauge field, as expected. Note that the three-form in 11d SUGRA (1) corresponds to the Ramond–Ramond (R-R) three-form in type IIA string theory.
Moreover, as the wrap factor in (16) never goes to zero, the dual theory will be able to exhibit confinement according to the behavior of the Wilson loop in this geometry. Since the solution (16) allows for an arbitrarily large period for , it implies that the dual theory on the D4-brane could be defined at a temperature of zero (or very low). Furthermore, in order to obtain a deconfined version of holographic QCD based on (16) at finite temperature, it is also possible to compactify one spacial direction (denoted by ) of the D4-branes in the background (14) with the antiperiodic condition for the supersymmetric fermions (there might be an issue if we identify the black brane background (14) to the deconfinement phase exactly since Wilson loop on this background may not match to the deconfinement QCD [,]. Nevertheless, we can identify the black brane background (14) to QCD phase at high temperature in which the deconfinement will occur), as is displayed in (17) and Figure 1. In this case, the Hawking temperature T in compactified background (14) is given by (11) as
which can, therefore, be identified as the temperature in the dual theory. The variables in terms of the dual theory are summarized as
where is the Yang–Mills (YM) coupling constant.
2.2. Embedding the Probe D8/-Branes
In the D4/D8 model, there is a stack of coincident pairs of D8- and (anti-D8) -branes as probes embedded into the bulk geometry illustrated in Figure 1. The relevant D-brane configuration is given in Table 1.

Table 1.
The D-brane configuration in the D4/D8 model. “-” denotes that the D-brane extends along this direction.
The embedding configuration of -branes is determined by solving the bosonic action for -branes, which consists of Dirac–Born–Infeld (DBI) and Wess–Zumino (WZ) terms. The action reads as follows []:
with the D-brane tension and ,
Here and refer, respectively, to the metric, the antisymmetric tensor and the dilaton field in the background spacetime. refers to the transverse mode of the -brane under the T-duality. By choosing , the action (20) leads to the action for D8-brane on the D4-brane background as follows (in the D4/D8 approach, the antisymmetric tensor has been gauged away):
Using the induced metric on -branes with respect to the bubble D4 background (16),
and the black D4-brane background (14),
the DBI action for D8-branes becomes, respectively,
and
Here, we use to refer to the volume of a unit . Note that the WZ action is independent on the metric or elfbein. Varying actions (25) and (26) with respect to , the associated equations of motion are, respectively, obtained as
and
As the D8- and -branes are the only probe branes, they could be connected smoothly at the location , which means . With this boundary condition, (27) and (28) reduce, respectively, to the following solutions:
and
In particular, in the bubble D4-brane background, solution (29) implies and . Thus, is a solution to (29) representing D8- and -branes located at the antipodal points of , while they are connected at , because the size of shrinks to zero at . On the other hand, in the black D4-brane background, if , (30) also implies a constant solution for , while the separation of the D8- and -branes could be arbitrary, but no more than . For , solutions (28) and (29) represent D8- and -branes joined into a single brane at . The configuration of the D8- and -branes in bubble and black D4-brane backgrounds is illustrated in Figure 2 and Figure 3.
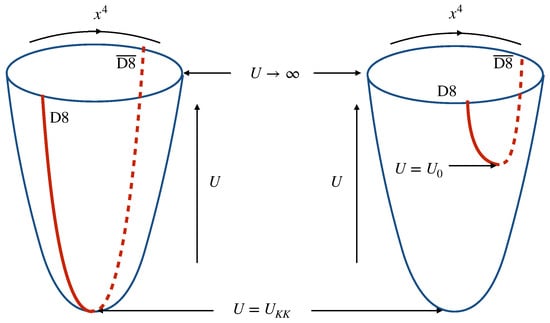
Figure 2.
The D8-brane configuration in the bubble D4-brane background. (Left) D8- and -branes are located at the antipodal points of . (Right) D8- and -branes are located at the nonantipodal points of .
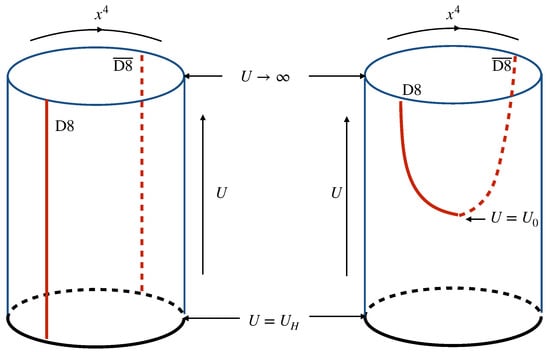
Figure 3.
The D8-brane configuration in the black D4-brane background. (Left) D8- and -branes are parallelly located. (Right) D8- and -branes are connected at .
2.3. Gluon, Quark and Symmetries
As the dual theory in the D4/D8 model is expected to be QCD in the large limit, it is natural to identify the effective theory on D4-branes below to the color sector in QCD, which implies that the gauge field on the D4-branes can be interpreted as gluon in holography. The reason is that the low-energy theory on D4-branes is pure Yang–Mills theory, and it has a SUGRA duality in the strong coupling region in the large limit, as discussed in Section 2.1. We note that the Lorentz symmetry of the 10d spacetime breaks down to when a stack of D4-branes is introduced. However, the worldvolume symmetry of the D4-branes becomes , since the D4-branes are compactified on a circle in the D4/D8 model. Furthermore, when the flavors, as D8- and -branes, are introduced, it is possible to create chiral fermions in the low-energy theory, which can be obtained by analyzing the spectrum of 4–8 or 4– strings in R-sector (Ramond-sector). Both the spectra of 4–8 and 4– strings in R-sector contain spinors with positive and negative chirality as the representations of the Lorentz group . Since the GSO (Gliozzi–Scherk–Olive) projection removes the spinor with one of the chiralities in string theory, we can choose the spinor with positive and negative chirality as the massless fermionic modes (denoted by ) of 4–8 and 4– strings, respectively, which accordingly can be identified as the fundamental chiral quarks in the dual theory. We note that these chirally fermionic fields are complex spinors since the 4–8 and 4– strings have two orientations. They are also the fundamental representation of and . The massless modes and symmetries in the D4/D8 system are collected in Table 2.

Table 2.
The fields in the D4/D8 model. Here 2+,2− denote the positive and negative chirality spinor representations of . and are the trace parts of the gauge field along direction on the D4-branes and the transverse modes of the D4-branes, which are decoupled to the gluon and fundamental quarks in the low-energy theory.
Due to the above holographic correspondence, the chirally symmetric and broken phase in the dual theory can be identified, respectively, to the disconnected and connected configuration of the -branes. This would be clear if we employed the configuration presented in Figure 2, for example. The effective action for the gauge fields and fundamental fermions on the D4-branes with -branes can be evaluated by expanding the DBI action, which leads to
where denotes the intersection of the D4- and D8-branes as well as the D4- and -branes, and we omit the notation “D4” in . As all the fields depend on , is identified to be if , which leads to an action with single flavor symmetry . For the connected configurations, we can therefore see that the D8- and -branes are separated at high energy (, ) according to the solutions (29) and (30), which leads to an approximated chiral symmetry. However, at low energy , D8- and -branes are joined into a single pair of D8-branes at () which implies that the symmetry breaks down to a single . This configuration of -branes provides a geometric interpretation of chiral symmetry in this model [].
2.4. Mesons on the Flavor Brane
As meson is the bound state in the adjoint representation of the chiral symmetry group, it is identified as the gauge field on the flavor branes, which is the massless mode excited by 8–8 string (massless mode excited by – string is therefore identified as antimeson). The reason is that the gauge field is excited by 8–8 (and –) is the generator of (and ). Hence, we consider the gauge field on the flavor branes with nonzero components as in the bubble D4-brane background (16). We note that while the supersymmetry on D4-branes breaks down by compactifying on a circle, there is no mechanism to break down the supersymmetry on -branes, since -branes are vertical to . Therefore, the 8–8 string is supersymmetric, leading to a super partner fermion of the gauge field in the low-energy theory. As we see in Appendix C, this supersymmetric fermion is Majorana spinor, which leads to the fermionic meson (mesino), while they are absent in the realistic QCD.
Nonetheless, let us assume that the supersymmetry on the flavor branes somehow breaks down and the supersymmetric meson can be turned off in order to continue the discussion about the QCD sector of this model. Since the D8-branes are probes, the worldvolume gauge field is fluctuation. Thus, the effective action for can be obtained by expanding (22), which for Abelian case is
leading to the Yang–Mills (YM) action
where we use the Cartesian coordinates z and dimensionless Z, defined as
and
with the induced metric on the D8-branes,
We employ the configuration that -branes are located at the antipodal points of . Then, in order to obtain a 4d mesonic action, let us assume that can be expanded in terms of complete sets :
where refers to the 4d meson field. To obtain a finite action, the normalization condition for is chosen as
with the eigen equation (),
where is the associated eigenvalue. In this sense, the basic function can be chosen as ():
Keeping these in hand, imposing (38)–(40) into (33), then defining the vector field by a gauge transformation,
the Yang–Mills action (33) reduces to a 4d effective action for mesons:
where . Accordingly, can be interpreted as pion meson, which is the Nambu–Goldstone boson associated with the chiral symmetry breaking. By analyzing the parity, it turns out that is a pseudoscalar field, as expected.
The above discussion implicitly assumes that the gauge field and its field strength should vanish at in order to obtain a finite 4d mesonic action. However, there is an alternative gauge choice , which is recognized as a gauge transformation:
to (37). Here, is solved:
where
Thus, the components of under gauge condition become
In the region , the gauge potential , which implies that the gauge field strength remains vanished and the effective 4d action remains finite.
The above setup for mesons can be generalized into multiflavor case by taking into account the non-Abelian version of (33),
where , is the gauge field strength of . As has been discussed, in order to obtain a finite 4d action, the gauge field strength must vanish in the limit . Under the gauge condition , must asymptotically take a pure gauge configuration for :
To obtain the chiral Lagrangian for mesons from the Yang–Mills action (47), we identify the lowest vector meson field as the meson and choose the following gauge conditions:
or
Inserting (49) into action (47) with the gauge condition (51), the 4d Yang–Mills action (47) includes a part of Skyrme model [],
where the coupling constants are given as
Moreover, the interaction terms of mesons would be determined by the Yang–Mills action (47) with the gauge condition (52), as
where is the gauge field strength of , and the associated coupling constants are given as
Therefore, we can reach the meson tower or chiral Lagrangian starting with the D8-brane action, which provides a description of the meson in holography.
To close this section, let us finally take a look at the WZ term presented in action (22), which can be integrated as
Here, is the Ramond–Ramond field given in (14), and is the Chern–Simons (CS) 5-form, given as
where is the gauge field strength. Under the gauge transformation on the D8-brane,
we can compute
Hence, by defining the boundary value of the gauge potential as
the WZ term is reduced to the chiral anomaly of in QCD,
Moreover, the formula for the chiral anomaly can also be expressed in the gauge condition , which is used to perform the gauge transformation
Then, the CS 5-form is reduced to
where
Recalling Formulas (49) in the gauge and choosing gauge condition (51), the WZ term (57) can be rewritten, after somewhat lengthy but straightforward calculations, as
where is the Wess–Zumino–Witten (WZW) term in [,], given as
Note that “” refers to the terms by exchanging . One can further work out the couplings to the vector mesons by using (49) with .
2.5. The Wrapped D4-Brane and Baryon Vertex
In the gauge theory, a baryon vertex connects to external fundamental quarks with the color wave function combined together by an -th antisymmetric tensor of group. Accordingly, the baryon vertex in gauge–gravity duality is recognized as a D-brane wrapped on the internal sphere [,]. To clarify this briefly, let us first recall the baryon vertex in the holographic duality between super Yang–Mills theory and IIB string theory on . As the fundamental quark in the super Yang–Mills theory is created by the elementary superstrings in , it is represented by the endpoints of elementary superstrings at the boundary of . Hence, we need elementary superstrings with the same orientation to somehow terminate in the .
On the other hand, since the baryon current must be conserved, one needs to find a source to cancel the charges (baryon charge) contributed by the elementary superstrings. To figure out these problems and work out a baryon vertex, a probe D5-brane wrapped on provides us with a good answer. The elementary superstrings ending on the D5-brane contribute to the D5-brane; however, the WZ action for such a wrapped D5-brane,
where is the Ramond–Ramond field strength, nicely provides charges to cancel the charges given by elementary superstrings (the sign of the charge depends on the orientation of the elementary superstrings and D5-branes.). Therefore, the A current would be conserved, which implies that the D5-brane is a baryon vertex.
The construction of the baryon vertex can also been employed in the D4/D8 model, which is identified as a D4-brane (to distinguish the D4-branes as the baryon vertex from the D4-branes, we denote the baryon vertex as -brane in the rest of this paper) wrapped on with elementary superstrings ending on it. A remarkable point here is that the -branes can be described equivalently by the instanton configuration of the gauge field on the D8-branes [,]. To see this clearly, let us consider a -brane with its worldvolume gauge field strength F. According to (20), The WZ action for such a -brane includes a term as a source,
For the single instanton configuration, the gauge field strength can be integrated as follows:
Hence, (69) can be written as
giving rise to a same source included by a -brane. Accordingly, we obtain a simple and interesting conclusion here, that is, the instanton in the -brane is the same object as a -brane inside it.
Let us return to the D4/D8 model; it implies that the -branes as the baryon vertex are equivalent to the instanton in the -branes. For multiple instantons, (70) is replaced by
where n refers to the instanton number. Inserting the instanton configuration of the gauge field denoted as with a fluctuation into the WZ action (57) of D8-brane, it reduces to
which implies that the instantons take charge . Since the baryon number is defined as times the charge of the diagonal subgroup of the symmetry, it is obvious that the instanton number is equivalent to the baryon number in this holographic system.
Moreover, when (71) is integrated out to be a Chern–Simons 3-form , as
the baryon number can be obtained:
where we impose a similar boundary condition as is given in (51):
Equation (74) gives the winding number of U, which means the homotopy is . This agrees with the baryon number charge in the Skyrme model [,].
The baryon mass can be roughly obtained by evaluating the energy carried by the -branes, which can be read from its DBI action as
where the bubble D4-brane background has been chosen for the confined property of baryon, and refers to the metric on presented in (16). This formula illustrates a stable position of the baryonic -brane by minimizing its energy, which is , since the bubble geometry shrinks at . In the black D4-brane, one can follow the same Formula (76) to evaluate the baryon mass. However, if the baryonic -brane is the only probe brane, it can not stay at stably in the black D4-brane background, since gravity will pull it into the horizon. In this sense, the baryon vertex exists in the bubble D4-brane background only, and it is consistent with its property of confinement. When the probe -branes are embedded into the bulk geometry, due to the balance condition, the baryonic -brane can be restricted inside the D8-branes if -branes are connected, as is displayed in Figure 4 (the authors of [] claim thataccording to the numerical calculation, there is not a wrapped configuration for the baryonic -brane in the black D4-brane background; thus, this background may correspond to the deconfinement phase of QCD. We note that this issue is not figured out, even if the baryon vertex is introduced into the black D4-brane background).
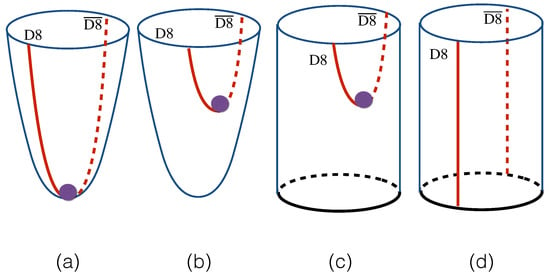
Figure 4.
Various D-brane configurations in the D4/D8 model. Purple refers to the baryon vertex (-brane) located at the stable position. When the -branes are connected as in (a–c), the baryon vertex can be located stably at the connected position inside the -branes. There is no stable position for baryon vertex if -branes are parallel, as in (d).
Therefore, it can be described equivalently by the instanton configuration on the D8-branes.
To obtain the baryon mass or baryon spectrum in this model, it is worth searching for an exact instanton solution for the gauge field on the D8-branes. As baryon lives in the low-energy region of QCD, we may find an approximated solution for the instanton configuration in the strong coupling limit, i.e., . To achieve this goal, let us take a look at the gauge field on the D8-branes, whose dynamic is described by the Yang–Mills action (33) and the Chern–Simons action presented in (57) (as the size of instanton takes order of , it may lead to a puzzle if the Yang–Mills action is taken into account, only because the high-order derivatives in the DBI action contribute more importantly. However, according to the holographic duality, taking the near-horizon limit requires , which implies that the Yang–Mills action dominates the dynamics in the DBI action. This puzzle is not figured out completely in [,], and we may additionally set when Yang–Mills action is taken into account only in this setup.). Since the size of instanton is of order , it would be convenient to rescale the coordinate and the gauge potential A as
where . In the large limit, the Yang–Mills action (33) can be expanded as follows:
while the Chern–Simons action (57) remains under the rescaling (77). We employed the D-brane configuration presented in Figure 4a. The group is decomposed as , and correspondingly, its generator is decomposed as follows:
where refers to the generators of , , respectively, and () are the normalized bases, satisfying
So, the Chern–Simons action (57) can be derived as follows:
Furthermore, the equation of motion for can be derived by varying actions (78) and (81), which allows for an instanton solution as follows:
where
Here, is an identity matrix and ’s are the Pauli matrices. The position and the size of the instanton are denoted by the constants and , respectively which have been rescaled as (77). The configuration (82) and (83) is the Belavin–Polyakov–Schwartz–Tyupkin (BPST) solution embedding into , which represents the Euclidean instanton, and one may verify that this solution satisfies (70). Then, the part of the gauge field is solved as follows:
which leads to a nonzero ,
where is an matrix .
Keeping these in hand, it is possible to evaluate the classical baryon mass through the soliton mass M with respect to the D8-brane action as , which is obtained as follows:
by inserting (82)–(85) into action (78) plus (81). On the other hand, since the low-energy effective theory on the D8-branes can reduce to Skyrme model, we can further employ the idea in the Skyrme model of baryon, which is identified as the excitation of the collective modes, in order to search for the baryon spectrum. The classically effective Lagrangian for baryon describes the dynamics of the collective coordinates in the moduli space by the one instanton solution, which refers to the world line element with a baryonic potential in the moduli space:
where “·” refers to the derivative respected to time; the collective coordinates denote ; and is the orientation of the instanton. The potential is the classical soliton mass given by . The basic idea to quantize the classical Lagrangian (87) is to slowly move the classical soliton so that the collective coordinates are promoted to be time-dependent []. Approximately, the gauge field potential becomes time-dependent by a gauge transformation,
and the associated field strength becomes
where
must be determined by its equation of motion:
While for generic , the exact solution for may be out of reach, the solution with is collected, respectively, in [,]. Accordingly, the Lagrangian of the collective modes is given by
which leads to
where
and
Here, we note that the formulas in the unit of , ’s are constants dependent on the instanton, solution and the metric of the moduli space can be further obtained by comparing (93) with (87). For example, we have for , and for . Afterwards, the baryon states can be obtained by quantizing the Lagrangian (93), that is, to replace the derivative term by straightforwardly. Hence, the quantized Hamiltonian associated with (93) is collected as follows (we note that for generic , the baryonic Hamiltonian must be supported by additional constraint, according to [] although it may not change the baryon spectrum):
where and ’s are the operators of the angular momentum of . The baryon spectrum can be finally obtained by evaluating the eigenvalues of the Hamiltonian (96), which fortunately takes an analytical formula [,].
2.6. Gravitational Wave as Glueball
According to AdS/CFT and gauge–gravity duality [,,,], the glueball operator can be identified as the source of gravitational fluctuation in bulk, since it is included in energy–momentum tensor of Yang–Mills theory in the dual theory as coupling to metric. Thus, due to the confined property of glueball, we can choose the bubble D4-brane background (16) compactified on a circle with gravitational fluctuation in order to investigate glueball in holography.
The dual field to the glueball operator is the gravitational fluctuation coupling the energy–momentum, which therefore refers to the gravitational polarization. By employing the relation of 11d M-theory and 10d type IIA string theory in Section 2.1, it would be convenient to find the gravitational polarization in 11d theory. For example, the lowest exotic scalar glueball with quantum number corresponds to the exotic polarizations of the bulk gravitational polarization, and its 11d components are given as ():
where must be determined by its eigen equation, given as
and refers to the 4d glueball field. By imposing the metric with gravitational fluctuation (97) as and solution of into 11d SUGRA action (1), we can obtain
representing the standard kinetic action for scalar glueball field , where , refer, respectively, to the size of and the bubble version of (10). is a numerical constant, given as
Hence, the eigenvalue of (98) determines the mass spectrum of exotic scalar glueball. The mass spectrum for various glueballs can be obtained by taking into account different gravitational polarizations, e.g., dilatonic scalar glueball with ,
and tensor glueball with ,
The eigen equations for and are given as
which determines the mass spectrum of dilatonic scalar and tensor glueball. The mass spectrum of various glueballs are collected in Table 3 for the reader’s convenience. The labels refer to the solutions for six independent wave equations for various scalar, vector and tensor modes of glueballs.

Table 3.
Glueball mass spectrum of in the units of in [].
This model predicts the properties of glueballs in a very simple and powerful way.
3. Developments and Holographic Approaches to QCD
In this section, we will review some holographic approaches to QCD by using the D4/D8 model and some developments of this model in recent years, which includes the topics of phase transition, heavy flavor, hadron interaction and the theta angle in QCD.
3.1. QCD Deconfinement Transition
While the confinement phase of QCD corresponds to the bubble D4-brane geometry given in (16), it is less clear whether the black D4-brane background (14) corresponds exactly to the deconfinement phase in holography [,]. This issue is recognized by investigating the associated Wilson loop in the bubble (16) and black brane backgrounds, (14) respectively. Nonetheless, it would be interesting to compare the deconfinement transition in QCD with the Hawking–Page transition in the D4-brane system through the gauge–gravity duality to find an exact holographic description of the deconfinement transition. To achieve this goal, let us first recall the holographic relation between the partition functions Z of the bulk gravity and its dual field theory,
which implies that the classical (onshell) renormalized SUGRA action is equivalent to the free energy F of the dual theory (in the Euclidean version). The classical SUGRA action can be collected by
where refers to the Euclidean version of the IIA SUGRA action given in (15), and refers to the standard Gibbons–Hawking term given as []
where refers to the metric on the holographic boundary with , and
is the trace of the extrinsic curvature. refers to the counterterm of the bulk fields presented in action (15), given as []
Using (105)–(108), by picking up the bubble (16) and black brane background (14) solutions, respectively, we can obtain the free energy of the dual theory by a simple formula:
where refers to the volume of ; T is the Hawking temperature in the black D4-brane solution (16). Comparing the free energies given in (109), we obtain the critical temperature with for the Hawking–Page transition as follows:
which is expected to be the deconfinement transition in QCD in the large limit. While this may be a trivial result for QCD, it is theoretically expected in the gravity side since, the bubble solution (14) is obtained by a double Wick rotation to the black brane solution (16), i.e., (110) means exactly . However, this does not mean that the Hawking–Page transition has nothing to do with the QCD deconfinement transition, because the fundamental flavored matter has not been taken into account.
In order to obtain a critical temperature close to the realistic QCD with the D4/D8 model, the flavored matter on the D8-branes must somehow contribute to the free energy. This means that in the gravity side, flavor branes have to back-react to the bulk geometry; thus, they would not be probes. For such a holographic setup, we require to be fixed in the large limit in order to go beyond the probe approximation for the flavor branes. Moreover, we further need , otherwise the dynamics of the dual theory is determined by flavors instead of colors, and in the gravity side, is also necessary, since D4-branes must dominate the bulk geometry, otherwise the holographic duality given in the previous sections would not be valid (see similar setups in [,,] for the D3/D7 system).
Then, the next step is to confirm the embedding configuration of the -branes. Since the configuration of the -branes relates to the chiral symmetry discussed in Section 2.2 and Section 2.3, we can identify, respectively, the bubble D4-brane background, where -branes are located at the antipodal points of (the left one in Figure 2) to the confined phase with broken chiral symmetry; and the black D4-brane background, where -branes are parallel (the left one in Figure 3) to the deconfined phase with the restored chiral symmetry. does not exactly distinguish the chiral transition from the deconfinement transition and is not unique, it is the most simple setup to include the elementary features in the QCD deconfinement transition. However, keeping the above requirements in hand, it is not enough to give a holographic setup quantitatively, because when the flavored backreaction is considered, it would be extremely challenging to search for a SUGRA solution technologically with respect to the D-brane configuration in the D4/D8 model as in Table 1. To simplify the calculation and keep the fundamental features of QCD, the authors of [,] suggest to consider the case that the -branes are smeared on the direction homogeneously so that the harmonic function for the D8-branes is identified uniquely; thus, it is possible to search for a geometric solution in this setup.
Altogether, let us write down the IIA SUGRA action plus the dynamics of D8-branes smeared on as the total action S,
To search for an approximate solution under the condition , the solution with is therefore the zero-th order solution to the equations of motion from (111), which is nothing but the bubble and black D4-brane solution given in (14) and (16). Then, let us attempt to find a solution of to the bubble D4-brane (16) first. For a homogeneous solution, the ansatz of the metric to solve the action (111) can be chosen as [,,]
where refers to the dilaton field; are unknown functions depending on the holographic coordinate only. is the logarithmic coordinate, defined as
Impose the ansatz (112) into (111); it reduces to a 1d effective action,
which has to be supported by the zero-energy constraint (dot refers to the derivative with respect to )
with
Here, is the size of , representing the temperature in the dual theory , and the only nonzero component of the gauge field potential on the D8-branes is a constant , representing the chemical potential in the dual theory. Next, we expand all the relevant functions up to , as follows:
where
So, the zero-th order solution of reads by comparing the metric ansatz (112) with the bubble D4-brane solution (16) as follows:
Putting (117)–(119) back into the equation of motion varied from action (114), we can obtain a series of equations for :
which can be solved analytically by
with hypergeometrical functions
where are integration constants. The integration constants can be determined by analyzing the asymptotics and using the zero-energy constraint (115), which leads to
while the other constants must be confirmed by imposing additional physical conditions. Nevertheless, one may find that the phase transition depends only on the integration constants given in (123).
Following the same step, it is also possible to obtain a solution of order to the black D4-brane solution by using the metric ansatz:
with a nonzero dynamical chemical potential:
We note that is replaced by in the black brane case. Putting (124) and (125) into action (111), it leads to a 1d action:
Taking into account the near-horizon geometry, the DBI action presented in (126) can be expanded with respect to small gauge field potential. Then, keeping the quadratic action for , we can obtain an analytical leading-order solution by the equations of motion derived from (126):
with
where are integration constants and n refers to the charge density. The zero-energy constraint is given by
with
Now. it is possible to obtain the free energy of the dual theory involving the flavored matters by imposing the above leading-order solutions into the action given in (111) after holographic renormalization. Before this, we need to add an additional holographic counterterm to (105) in order to cancel the divergence in the DBI action presented in (111), which turned out to be [,,,]
Here, refers to the normal vector of , and are renormalized constants. For example, with the back reaction from D8-branes to the bubble background, it leads to
For the black brane background, it leads to
Hence, we finally obtained the renormalized SUGRA action,
with suitable choice of . Respectively, the confined and deconfined free energy with flavors can be computed straightforwardly by plugging the solutions of order into (134)
where
and we use the choice of the relevant constants given in (123). Therefore, comparing the free energy given in (135), we can obtain the critical temperature with flavors as follows:
where is the chemical potential in the dual theory given by . The behavior of the Hawking–Page transition given in (137) agrees qualitatively with the QCD deconfinement transition [,,,].
Moreover, when the backreaction to the bulk geometry of the flavor branes is picked up, it is also possible to evaluate QCD deconfinement transition under an external magnetic field, because extremely strong magnetic field may also give rise to deconfinement transition in QCD [,,,]. The setup mostly follows the same discussion given above, while we need to turn on a constant magnetic field in the DBI action is presented in (111), as the only nonzero component of the gauge field strength. Then, we can derive the effective 1d action by using the metric ansatz (112) and (124) with respect to the bubble and black D4-brane background. Fortunately, it is possible to find an analytical solution, which leads to critical temperature as
by comparing free energy in the same way. Here, B refers to the external magnetic field, and are numerical numbers. For the probe approximation limit of the D8-brane, are calculated as
By considering the backreaction of the D8-branes, are calculated as
The behavior of the critical temperature illustrated in (138) also coincides qualitatively with the QCD deconfinement transition under external magnetic field predicted by lattice QCD []. We plot out the behavior of the critical temperature given in (137) and (138) in Figure 5. In this sense, we could conclude, at least, that investigating the Hawking–Page transition in the D4/D8 model is very suggestive to study the QCD deconfinement transition in holography, which also partly covers the discussion in some bottom-up approaches [,].
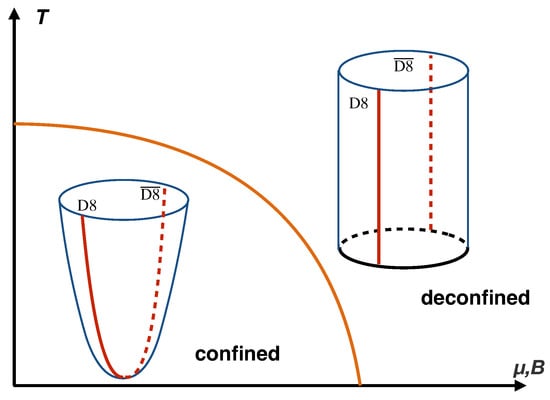
Figure 5.
The critical temperature of Hawking–Page transition as the temperature of QCD deconfinement transition in the D4/D8 model with chemical potential or magnetic field B.
3.2. Phase Diagram with Chiral Transition
As we have reviewed the deconfinement transition in the D4/D8 model, which can not be distinguished from the chiral transition, let us focus on the chiral transition in the D4/D8 model, since QCD has various phases with chiral symmetry.
Recalling the relation of -brane configuration and chiral symmetry, the chiral transition is identified as the transition from connected to disconnected configuration of the -branes. Hence, we need to choose the black D4-brane background in order to include both the connected and disconnected -brane configurations. The main idea for evaluating the phase transition follows Section 3.1, which is to compute the free energy in holography. As we will work with respect to the black D4-brane background only, the contribution from the bulk geometry would be irrelevant, because the difference of the free energy determines the phase transition. Keeping this in mind, we can quickly write down the D8-brane action for mesonic (broken chiral symmetry) and quark matter phases (restored chiral symmetry) with a chemical potential , which corresponds to the connected and disconnected D8-brane configuration, respectively, in Figure 3 as follows (we note that in this setup, the Chern–Simons action vanishes):
where the variables in (141) are dimensionless, as follows:
The equation of motion can be obtained by varying (141) with respect to and , which are
where “′” refers to the derivative with respect to u. The constant corresponds to the charge density, which is therefore the baryon number in this setup. In the mesonic phase, the baryon number is zero, i.e., , and the equations of motion in (143) can be solved by the following boundary condition, according to the connected configuration in Figure 3:
where constant refers to the chemical potential in the dual theory; constant l refers to the separation of the -branes at boundary . Thus, the solution is
For the quark matter phase, the boundary condition reads from the disconnected configuration in Figure 3 as
which leads to a solution with the hypergeometrical functions
Therefore, the free energy is computed as follows:
We note that the condition implies that is a function of :
Then, the phase diagram can be obtained by comparing the free energies given in (146) and (150) with constraint (149). Notice that while the free energies given in (146) and (150) are divergent, their difference, which determines the phase diagram, remains finite. Thus, it is not necessary to perform holographic renormalization in this case.
For a more ambitious approach, let us include the baryonic phase in the black D4-brane background, that is, to take into account the configuration (c) in Figure 4, which has broken chiral symmetry with baryon vertex. Since baryon vertex is identified as -brane, described equivalently by instantons on the D8-branes, we employ the BPST instanton solution given in (83) to represent baryon on the flavor brane. For multiple baryons, we can summarize the instanton field strength as what we have discussed in Section 2.5; in this sense, baryons are treated as instanton gas on the flavor brane. On the other hand, as the instanton size takes order of and the DBI action (20) does not define how to treat it with non-Abelian gauge field (the symmetrized trace in DBI action is usually used for all terms of and higher; however, it is known to be incomplete, starting from []), we may generalize the DBI action by taking all orders of gauge field strength into non-Abelian case through the identity of Abelian gauge field strength as
For non-Abelian generalization, we follow [] to replace the quadratic terms of by its non-Abelian version F, then take trace of each term separately, as follows:
Afterwards, we impose the BPST instanton solution (83) with multiple numbers to F in order to represent baryons (Refs. [,] illustrate that in the case of , the non-Abelian part of presented in (85) vanishes. We do not attempt to consider baryons with in this section). Altogether, we reach a generalized version of action for baryonic phase,
where
We note that the last term in (153) is the Chern–Simons action and is the average instanton field strength defined by the summary of the BPST instanton (83), as []
with the normalization condition
refers to the center of the n-th instanton. Z is the Cartesian coordinate, in the case in Figure 4c, it is defined as
where we use to denote the connected position of -branes with instantons to distinguish it from , in which instantons are absent. is the instanton number, which relates to its number density , as . With the boundary condition
the equations of motion obtained by varying (153) are
where k is an integration constant to be determined, and
can be solved as
Plugging solution (161) back into (153), we can obtain the free energy of the baryonic phase. In order to obtain the phase transition, we need to further minimize the free energy given in (153) with respect to as the parameters, which leads to three constraints:
where
With all of the above in hand, we can numerically obtain a holographic diagram including mesonic, baryonic and quark matter phases of QCD by comparing the associated free energies given in (146), (149) and (153). The resultant phase diagram is given in Figure 6.
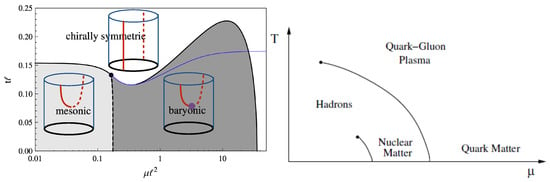
Figure 6.
Holographic QCD phase diagram vs. realistic QCD phase diagram in the plane.
We can see that the holographic diagram includes all the elementary phases in realistic QCD, although the confined geometry is not included in the current discussion.
We note that it is very difficult to work out a reasonable model describing QCD matter over a very wide density regime with traditional models or theories of QCD. For example, the quark–meson model (e.g., [,]) and the Nambu–Jona–Lasinio (NJL) model [,,,,] are very useful to obtain some insight into the chiral and deconfinement phase transitions and quark matter phases; however, nuclear matter is usually not included in these models. In addition, nucleon–meson models, e.g., [,,,] are based on the properties of nuclear matter, and may be able to describe moderately dense nuclear matter realistically, but they give a poor description of quark matter with restored chiral symmetry. In this sense, this holographic model provides a very powerful way to study QCD phase diagrams in a very wide density regime based on string theory.
3.3. Higgs Mechanism and Heavy–Light Meson Field
One of the interesting developments of the D4/D8 model is including heavy flavor by using the Higgs mechanism in D-brane system. Recall that the fundamental quarks in the D4/D8 model are identified to be the 4–8 and 4– strings; since D4-branes and D8-branes are coincident, we find that the 4–8 and 4– strings have a vanishing vacuum expectation value (VEV). Therefore, the fundamental quarks created by 4–8 and 4– strings are massless, which implies that this model can describe the mesons with light flavors only. Hence, it is naturally motivated to include the massive heavy flavor in this model. To achieve this goal, in this section, we review the Higgs mechanism in D-brane system and see how to use it to introduce heavy flavor.
First, we take a look at the Higgs mechanism in D-brane system by considering the configuration of an open string connecting two stacks of the separated D-branes, as illustrated in Figure 7a.
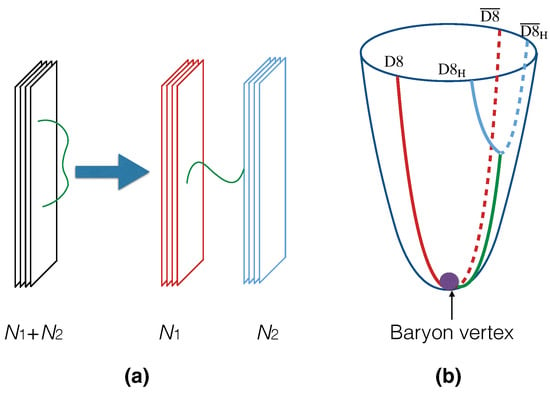
Figure 7.
The Higgs mechanism in string theory (a) and the configuration of heavy flavor in D4/D8 model (b). (a) Higgs mechanism in string theory: The gauge symmetry on a stack of coincident D-branes could be , while it breaks down to if the D-branes somehow move apart to become two stacks of coincident and D-branes. The open string connecting the two stacks of the D-branes has a nonzero VEV; hence, its ground states acquire nonzero mass, which corresponds to the separation of the D-branes. (b) Configuration of heavy flavor in D4/D8 model: Red line refers to the stack of -branes in the original model, which now is identified as light flavor. Blue line refers to another pair of -branes separated from -branes, which is identified as heavy flavor. The green line refers to the open string connecting the light and heavy brane, which is the heavy–light string, and it acquires nonzero VEV to create massive ground states.
In this D-brane configuration, the worldvolume symmetry breaks down to when the D-branes move separately, where we use to refer to the D-branes number in each stack. Accordingly, the transverse modes of the D-brane acquire a nonzero VEV due to the separation of the D-branes. Hence, the multiplets created by the open string connecting the separated D-branes become massive, just like the Higgs mechanism in the standard model of particle physics [,]. Let us investigate this mechanism quantitatively by recalling the D-brane action in (20). In the holographic approach, we need the near-horizon limit, i.e., ; thus, the D-brane action can be expanded to be a Yang–Mills plus Wess–Zumino action, as it is in Section 2.4. Now, we pick up the transverse modes in the DBI action; it reduces to an additional quadratic action for the transverse modes with :
where the covariant derivative is
and is the gauge field potential on the D-brane. Consider a stack of coincident D-branes; could be the generator as an matrix. However, if the coincident D-branes move apart to become two stacks of and D-branes, the gauge potential becomes
where is the gauge potential as an matrix. is the multiplet created by the open string connecting to the two stacks of the D-brane, which is an matrix-valued field, and the last element can be gauged away by residual symmetry. On the other hand, when the D-branes are separated, the transverse mode will have a nonzero VEV, since the open string connecting the separated D-branes cannot shrink to zero. Therefore, we can write with a VEV as
where
to represent . Thus, plugging (165)–(168) into (164), one obtains a mass term in the action as follows:
and can be interpreted as the heavy–light field acquiring a mass through the VEV of the transverse mode .
With this Higgs mechanism in string theory, let us employ it in the D4/D8 model by considering Figure 7b. In this configuration, there is one pair of -branes separated from -branes, which are identified as heavy flavor branes with an open string (the heavy–light string) connecting them. We note that the configuration in Figure 7b is a generalized version of Figure 7a in the curved spacetime. Then, we can write down the D8-brane action with heavy flavor by imposing the following replacement:
to (33), where are matrix-valued fields, as we have specified in Section 2. is an matrix-valued multiplet created by the heavy–light string, which is interpreted as the heavy–light meson field, and the index in the square brackets is ranked as , and we choose the gauge field as Hermitian field :
we obtain the action (164) for as follows:
where z is the Cartesian coordinates given in (34), and the VEV of T-dualized is chosen as []
with
Note that is the only transverse mode of D8-brane. The heavy–light meson tower can be obtained by expanding , as specified in Section 2.4. For example, the transverse modes of heavy–light meson field are suggested, given as [,]
which leads to
with the normalization
and eigenvalue equation
For the transverse modes and longitudinal modes, the expansion is suggested as
leading to
with the normalization
We note that with the replacement (170), the Chern–Simons action (57) for the D8-branes reduces to additional terms as follows:
Using the expansions (175), (179) and (46), the DBI and CS term includes the interaction between light and heavy–light mesons.
It is also possible to obtain the baryon spectrum with heavy flavor by considering the baryon vertex as the instantons on the flavor brane [,,]. Following the steps in Section 2.5, the equations of motion for the heavy–light meson field are derived as follows:
where , and
where is computed by the BPST instanton solution given in (82)–(85). Thus, can be solved as with
where is the embedded Pauli matrices, as , and is the spinor independent on . The soliton mass as the baryonic potential can be evaluated by inserting (185) and the BPST solution (82)–(85) to the full action for the D8-branes. Afterwards, one reaches to an effective Hamiltonian for baryon state by following Section 2.5, as given in [,]. We note that [] also gives another generalization with heavy flavor into black D4-brane background.
3.4. Interactions of Hadrons and Glueballs
The interaction of hadrons relates to many significant topics in QCD and nuclear physics, and its holographic description by the D4/D8 model was reviewed briefly in Section 2 and [,]. In this section, we will take a look at the interactions in hadron physics involving glueballs, since the D4/D8 model provides explicit definitions of mesons, baryons and glueballs.
The main idea to include the interactions of mesons and glueballs is to consider the D8-brane action with a gravitational fluctuation. Recalling the discussion in Section 2.4 and Section 2.6, since meson is identified as the gauge field on the D8-branes (created by 8–8 string) and glueball is identified as the gravitational polarization (closed string), the interaction of meson and glueball is nothing but the interaction of open and closed strings, which can therefore be included into the D8-brane action when the metric fluctuation is picked up. For example, when we put the gravitational polarization (97) into the D8-brane action (32) with the meson tower given in (37), by integrating out the z dependence (the holographic coordinate), it reduces to an interaction action involving meson and exotic glueball , after some straightforward but messy calculations, as follows:
where the and coefficients are coupling constants and are numerically computed as (in the unit of )
Then, the associated amplitude of glueball decay can be further evaluated by using the effective action with the coupling constants. One can also compute the effective action of meson involving other types of glueball by changing the formulas of the bulk gravitational polarization, as discussed in [,,,].
The current setup to obtain an effective action of meson and glueball interaction can also be generalized by including heavy flavor [], which is to take into account the configuration in Figure 7b and the heavy–light meson field. The main idea is to pick up the gravitational polarization in bulk metric when we write down the D8-brane action with heavy flavor brane (i.e., with the replacement given in (170)). For example, by considering the gravitational polarization for the exotic glueball in (97), the effective action of heavy–light meson and glueball provides such terms as
which are the same types as the interaction given in (186). Here, we use to denote the vector and scalar heavy–light meson field, and the lowest heavy–light meson is identified to be D-meson with a charm quark. Accordingly, the effective action with heavy flavor and glueball may be useful to study the oscillation of D-meson pairs () or B-meson pairs () [,]. Note that since the heavy–light multiplet is created by the heavy–light string, even if the heavy flavor is taken into account, the interaction of heavy–light meson and glueball remains an open/closed string interaction through holography. Moreover, in the presence of the heavy–light meson and glueball, the effective action also mixes the interaction terms of glueball, light and heavy–light meson, which may describe the various interactions in hadron physics.
It is also possible to include the interaction of baryon (or baryonic meson) and glueball in a parallel way, that is, to consider the interaction of baryonic -branes and bulk closed string []. Specifically, one can derive the Yang–Mills action presented in (32) with the gravitational polarization (97), then insert the BPST instanton configuration (82)–(85) as baryon under the large rescaling (77). Afterwards, by following the discussion in Section 2.5, we can obtain additional terms to the collective Hamiltonian (96) as follows:
Using the standard technique in quantum mechanics for the time-dependent perturbed Hamiltonian, it is possible to work out the decay rate of baryon involving glueball and its associated select rule. We note that when the heavy flavor is included, as in Section 2.3, the decay rate of heavy–light baryon or baryonic meson involving glueball can be achieved. For example, considering the exotic gravitational polarization (97), we can reach the time-dependent perturbed Hamiltonian, given as []:
where we take the limit followed to simplify the formula, and refers to the number of heavy flavor quarks in the heavy–light meson. Then, the decay of heavy–light baryonic matter involving glueball can be evaluated using (190) to the quantum mechanical system (96) with heavy flavors. To close this section, we summarize the strings as various hadrons in the D4/D8 model in Figure 8, and we can see the various interactions of hadrons are interactions of strings through gauge–gravity duality in this model.
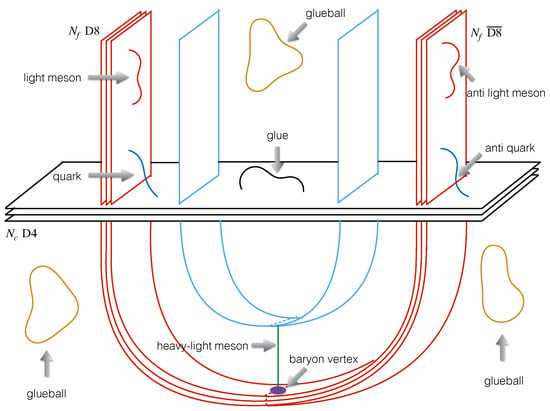
Figure 8.
Strings as various hadrons in the D4/D8 model.
3.5. Theta Dependence in QCD
In Yang–Mills theory, there could be an topological term proportional to the angle []. In the large limit, the full Lagrangian takes the following form:
While the value of angle may be experimentally small, it leads to many interesting effects, e.g., glueball spectrum [], deconfinement transition [,], chiral magnetic effect [,], especially its large limit []. Since the D4/D8 model is a holographic version of QCD, it is possible to introduce the term to the dual theory through the gauge–gravity duality.
The main goal of including a Yang–Mills term in holography is to introduce coincident D0-branes acting to the D4-brane background (14). In this sense, we have to require to be fixed when . For the SUGRA approach, the dynamics of the Ramond–Ramond 1-form must be picked up into the IIA SUGRA action (15) in order to include the charge in the D0-branes:
where . To obtain an analytical solution, we assume that the D0-branes are smeared homogeneously along ; hence, the associated equations of motion to (192) can be solved as follows:
where is a constant parameter. Taking the near-horizon limit so that and imposing the double Wick rotation, as discussed in Section 2.1, we can obtain a D0–D4 bubble background associated to (16), as follows:
Due to the presence of the D0-branes, we can see that the dual theory of (194) is pure Yang–Mills theory, with a term if a probe D4-brane located at the holographic boundary is taken into account:
which further implies that the bare angle relates to the parameter in the solution (194) by
as a fixed constant in the large limit.
With the geometry background (194), it is possible to evaluate several properties of Yang–Mills theory with a term by following the discussions in previous sections; let us take a brief look at them for examples. First, we focus on the the ground state energy, which can be evaluated by using (104)–(108) as follows:
In the expansion with respect to small , (197) reduces to the minimized free energy difference,
as the energy of the vacuum, and the topological susceptibility reads as
with
Moreover, one can consider a constant in the black D4-brane background (14), so that . Hence, the ground state energy of deconfined Yang–Mills theory with a constant term can be identified as , presented in (109).
Then, the QCD deconfinement phase transition can be obtained by comparing the free energy (197) with in (109) which leads to the critical temperature
Second, the QCD string tension also takes a correction due to the presence of term. Consider an open string stretched in the background (194) ending on a probe D4-brane at boundary. Using the AdS/CFT dictionary, the Wilson loop in the dual theory relates to the classical Nambu–Goto (NG) action of the open string corresponding to the tension T with quark potential V, as follows:
In the static gauge, the relevant string embedding can be chosen as follows:
then the NG action is given as
To quickly evaluate the QCD tension, let us consider the limit . In this limit, the open string must minimize its energy as much as possible; it forces the factor to become minimal to take the value at , since the size of shrinks at . Therefore, the QCD tension is obtained from
as
Next, let us investigate the glueball mass with the background (194). As the glueball corresponds to the gravitational fluctuation, by adding a perturbation to the metric presented in (194) as , it reduces to an equation of motion for , given as
Here, since IIA SUGRA can be obtained by the dimension reduction from 11d M-theory, refers to the fluctuation on , which means runs over 0–6. Setting with the ansatz
it gives the eigen equation for as
which implies that the mass spectrum M with a correction due to is
The presence of also decreases the baryon mass ,
by imposing the metric presented in (194) into (76), which implies the evidence of metastable particles in QCD. By further analyzing the entanglement entropy on (194), it agrees consistently with the property of the possible metastable states in this model. Moreover, when we follow the discussion in Section 2.2, it is possible to introduce flavored meson in the D0–D4 background. The meson mass also acquires the correction by the angle, as in [,]. Further, following the instantonic description for baryon in Section 2.5, one can see the metastable baryonic spectrum in this model, as in []. In this sense, the Witten–Sakai–Sugimoto model in the D0-D4 brane background is recognized as a holographic version of QCD with a term.
4. Summary and Outlook
In this review, we look back to the fundamental properties of the D4/D8 model, which include the D4-brane background, the embedding of the -branes, and how to identify mesons, baryons and glueballs in this model. Moreover, we revisit some interesting topics about QCD by using this model, which relate to the deconfinement transition, chiral phase, heavy flavor, various interactions of hadrons and the term in QCD. This review illustrates that string theory can provide a powerful method for studying the strongly coupled regime of QCD, which is out of the reach of the traditional methods of perturbative QFT. We particularly note here that there are additional interesting approaches based on this model that are absent in the main text of this review; they relate to the holographic Schwinger effect [,,,], the fluid/gravity correspondence [,,,,], corrections to the instanton as baryon [,], the approaches to the D3/D7 model [,] and applications in studying neutron stars [,]. With all of these achievements, it may be possible to work out an exact holographic version of QCD based on the D4/D8 model in future work, to reinterpret the fundamental element of strong interactions according to gauge–gravity duality.
Author Contributions
Conceptualization, S.-W.L.; methodology, S.-W.L.; software, X.-T.Z.; validation, X.-T.Z.; formal analysis, X.-T.Z.; investigation, S.-W.L.; writing—original draft preparation, S.-W.L.; writing—review and editing, S.-W.L. and X.-T.Z.; supervision, S.-W.L. and X.-T.Z.; project administration, S.-W.L.; funding acquisition, S.-W.L. and X.-T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (NSFC) under Grant No. 12005033 and the Fundamental Research Funds for the Central Universities under Grant No. 3132023198.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Type II Supergravity Solution
In this appendix, let us collect the -brane solution in the type II SUGRA. We note that all the discussion in this appendix is valid to the gravity solution presented in the main text if we set . In the string frame, the action for type II SUGRA sourced by a stack of coincident -branes can be written as
where is the 10d gravity coupling constant, are, respectively the 10d curvature, dilaton and Ramond–Ramond -form field with . Note that in string theory, the dilaton field may also be defined as by
Since a -brane for is magnetically dual to the -brane for and the D3-brane is self-dual, we only consider the case for in (A1). Varying action (A1) with respect to , the associated equations of motion are collected as follows:
The solution for (A3) can be obtained by using the simply homogeneous ansatz,
where the harmonic function is solved through (A3) as follows:
Here, r refers to the radial coordinate vertical to the -brane; is the associated angle coordinate in the transverse space. The constant relates to the charge of the -brane, computed as follows:
Solution (A4), representing extremal black -branes, reduces to the BPS condition as follows:
due to the action for the Ramond–Ramond (R-R) field with a source of coincident -branes,
The equations of motion (A3) also allow for the near-extremal solution, as follows:
where run over the spacial index of the -branes. The functions are solved, respectively, as follows:
where refers to the horizon of the -branes. Notice that the equation of motion (A3) reduces to a constraint,
which implies that
So, we have if ; thus, the near-extremal solution will return to the extremal solution in this limit.
Appendix B. Dimensional Reduction for Spinors
In this section, we collect the dimensional reduction for spinors, and one can see that various boundary conditions determine the associated mass of fermion in the lower dimension. Consider a complex massless spinor in satisfying the Dirac equation
where M runs over . When one of the spatial directions is compactified on a circle , becomes . Let us denote the coordinates on as , respectively. Then Fourier series of can be written as the summary of its modes on as
where L refers to the radius of and k is integer or half-integer. Thus, the boundary of the spinor can be periodic or antiperiodic:
where k is integer and half-integer, respectively. Mostly, the antiperiodic boundary condition for fermion is permitted, since observables are usually the combination of an even power of spinors. Inserting (A14) into (A13), it leads to
where . So, we can see that is massive spinor in with an effective mass , unless . This implies that under the dimension reduction, the spinor in the lower dimension is always massive if the antiperiodic boundary condition is imposed. Note that in the low-energy theory, only the mode with minimal k is of concern; thus, it means that the fermion is massless/massive with periodic and antiperiodic boundary conditions, respectively, in the low-energy theory.
Appendix C. Supersymmetric Meson on the Flavor Brane
While the D4/D8 model achieves great success, it contains issues. The most important issue is that due to the remaining supersymmetry on the D8-branes, the D4/D8 model contains supersymmetrically fermionic mesons (mesino) on the flavor -branes, which should not be presented in QCD []. As we specified in Section 2.1, the supersymmetry on D4-branes breaks down due to its compactified direction ; however, there is no mechanism to break down the supersymmetry on the flavor branes, since the -branes are perpendicular to the compactified direction . Therefore, in principle, there is no reason to neglect the supersymmetric fermions in this model. So, let us pick up the fermionic action for the D8-branes in addition to their bosonic action (22). Up to the quadratic order, the fermionic action for the D8-brane reads as follows [,,]:
where refers to 32-component Majorana spinor in 10d spacetime, and
Action (A17) is the fermionic action for D8-brane obtained under T-duality. The notation in (A17) and (A18) is given as follows. The index labeled by capital letters runs over 10d spacetime, and that labeled by lowercase letters runs over D8-brane. The index with underline corresponds to index in the flat tangent space used by elfbein, e.g., ; so, we have, e.g., . refers to the Dirac matrix, satisfying , and refers to the spin connection. refers to the components of the Ramond–Ramond and is the dilaton field, which are all given in Section 2. The gamma matrix is given by . Here, , where is the gauge field strength on the flavor brane and is the antisymmetric tensor induced on the flavor brane, which can be set to zero.
Imposing the bubble solution given in (16) and supergravity solutions for the dilaton and Ramond–Ramond to (A17), after some calculations, it becomes
where is the Dirac operator on , i.e., the index m runs over , and
Since we are interested in the fermionic part, the gauge field included by is turned off, i.e., . Afterwards, in order to obtain a 5d effective action, such as the mesonic action given in (33), we can decompose the spinor into a 3+1-dimensional part as mesino, an part and a remaining 2d part , as follows:
The associated gamma matrices can be chosen as
where refer to the Pauli matrices. In this decomposition, the 10d chirality matrix takes a very simple form as . If we chose the representation, can be decomposed by the eigenstates of with
where refers to the two eigenstates of . Since the kappa symmetry fixes the condition , we have to chose . Moreover, as must satisfy the Dirac equation on , it can be decomposed by the spherical harmonic function. So, the eigenstates of can be chosen as [],
where are angular quantum numbers carried by spherical harmonic function.
Putting (A21) into (A19) with the decomposition (A22)–(A24) for and , we finally reach a 5d effective action for then mesino field:
The 5d mesino can be further decomposed by working with
where are real eigenfunctions of the coupled equations
with the normalizations
Defining the Dirac spinor written in the Wely basis as
action (A29) can be rewritten as ()
leading to a standard action for fermion. As we can see, the fermionic action illustrates that the mesino mass takes the same order of meson mass; hence, it should be not neglected in principle, and the authors of [] also confirm this conclusion, which is consistent with the remaining supersymmetry on D8-branes.
Moreover, when the bosonic gauge field is turned on, action (A17) reduces to interaction terms of meson and mesino up to , as follows:
Using decomposition (46) for and (A22)–(A24) for , action (A32) includes interaction of meson and mesino as follows:
where the coupling constant is evaluated numerically as
One can further work out the interaction terms of meson and mesino similarly. Since there is no mechanism to suppress the interaction of meson and mesino or break down the supersymmetry on the D8-brane, we have to take into account these interactions in this model in principle while they are absent in realistic QCD.
Although we do not attempt to figure out this issue completely in this review, we give some comments that may be suggestive. The way to break down the supersymmetry on D8-branes may follow the discussion in [], that is, to compactify one of the directions of the D8-brane (which is vertical to the D4-branes) on another circle, then impose the periodic and antiperiodic boundary condition to the meson and mesino, respectively. Afterwards, the supersymmetry on the D8-branes breaks down, then the spectrum of meson and mesino is separated by a energy scale , where refers to the size of the compactified direction of the D8-brane. Another alternative scheme is to consider that the bubble solution (16) has a period with ; hence, the dual theory is nonsupersymmetric above the size if we perform the same dimension reduction as []. Therefore, it means that the supersymmetry gets to rise only at a temperature of exactly zero due to , which is the ideal case, out of reach physically. So, the dual theory on the D8-brane would be nonsupersymmetrical at any finite temperature.
References
- Witten, E. Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 1998, 2, 253–291. [Google Scholar] [CrossRef]
- Maldacena, J.M. The Large N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Aharony, O.; Gubser, S.S.; Maldacena, J.M.; Ooguri, H. Large N field theories, string theory and gravity. Phys. Rept. 2000, 323, 183. [Google Scholar] [CrossRef]
- Maldacena, J. Wilson loops in large N field theories. Phys. Rev. Lett. 1998, 80, 4859–4862. [Google Scholar] [CrossRef]
- Rey, S.; Theisen, S.; Yee, J. Wilson-Polyakov loop at finite temperature in large N gauge theory and anti-de Sitter supergravity. Nucl. Phys. B 1998, 527, 171–186. [Google Scholar] [CrossRef]
- Brandhuber, A.; Itzhaki, N.; Sonnenschein, J.; Yankielowicz, S. Wilson loops in the large N limit at finite temperature. Phys. Lett. B 1998, 434, 36–40. [Google Scholar] [CrossRef]
- Policastro, G.; Son, D.T.; Starinets, A.O. From AdS/CFT correspondence to hydrodynamics. J. High Energy Phys. 2002, 9, 43. [Google Scholar] [CrossRef]
- Son, D.T.; Starinets, A.O. Minkowski space correlators in AdS/CFT correspondence: Recipe and applications. J. High Energy Phys. 2002, 9, 42. [Google Scholar] [CrossRef]
- Kovtun, P.; Son, D.T.; Starinets, A.O. Viscosity in strongly interacting quantum field theories from black hole physics. Phys. Rev. Lett. 2005, 94, 111601. [Google Scholar] [CrossRef]
- Iqbal, N.; Liu, H. Real-time response in AdS/CFT with application to spinors. Fortsch. Phys. 2009, 57, 367–384. [Google Scholar] [CrossRef]
- Liu, H.; McGreevy, J.; Vegh, D. Non-Fermi liquids from holography. Phys. Rev. D 2011, 83, 065029. [Google Scholar] [CrossRef]
- Semenoff, G.W.; Zarembo, K. Holographic Schwinger Effect. Phys. Rev. Lett. 2011, 107, 171601. [Google Scholar] [CrossRef] [PubMed]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from AdS/CFT. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Klebanov, I.R.; Kutasov, D.; Murugan, A. Entanglement as a probe of confinement. Nucl. Phys. B 2008, 796, 274–293. [Google Scholar] [CrossRef]
- Harlow, D. Jerusalem Lectures on Black Holes and Quantum Information. Rev. Mod. Phys. 2016, 88, 015002. [Google Scholar] [CrossRef]
- Gross, D.J.; Wilczek, F. Ultraviolet Behavior of Nonabelian Gauge Theories. Phys. Rev. Lett. 1973, 30, 1343–1346. [Google Scholar] [CrossRef]
- Politzer, H.D. Reliable Perturbative Results for Strong Interactions? Phys. Rev. Lett. 1973, 30, 1346–1349. [Google Scholar] [CrossRef]
- Erlich, J.; Katz, E.; Son, D.T.; Stephanov, M.A. QCD and a holographic model of hadrons. Phys. Rev. Lett. 2005, 95, 261602. [Google Scholar] [CrossRef]
- Karch, A.; Katz, E.; Son, D.T.; Stephanov, M.A. Linear Confinement and AdS/QCD. arXiv 2006, arXiv:hep-ph/0602229. [Google Scholar] [CrossRef]
- Rold, L.; Pomarol, A. Chiral symmetry breaking from five dimensional spaces. Nucl. Phys. B 2005, 721, 79–97. [Google Scholar] [CrossRef]
- Casalderrey-Solana, J.; Liu, H.; Mateos, D.; Rajagopal, K.; Wiedemann, U.A. Gauge/Gravity Duality, Hot QCD and Heavy Ion Collisions; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Kruczenski, M.; Mateos, D.; Myers, R.C.; Winters, D.J. Towards a holographic dual of large N(c) QCD. J. High Energy Phys. 2004, 5, 41. [Google Scholar] [CrossRef]
- Witten, E. Anti-de Sitter space, thermal phase transition, and confinement in gauge theories. Adv. Theor. Math. Phys. 1998, 2, 505–532. [Google Scholar] [CrossRef]
- Sakai, T.; Sugimoto, S. Low energy hadron physics in holographic QCD. Prog. Theor. Phys. 2005, 113, 843–882. [Google Scholar] [CrossRef]
- Sakai, T.; Sugimoto, S. More on a holographic dual of QCD. Prog. Theor. Phys. 2005, 114, 1083–1118. [Google Scholar] [CrossRef]
- Witten, E. Baryons and branes in anti-de Sitter space. J. High Energy Phys. 1998, 7, 6. [Google Scholar] [CrossRef]
- Hata, H.; Sakai, T.; Sugimoto, S.; Yamato, S. Baryons from instantons in holographic QCD. Prog. Theor. Phys. 2007, 117, 1157. [Google Scholar] [CrossRef]
- Hata, H.; Murata, M. Baryons and the Chern-Simons term in holographic QCD with three flavors. Prog. Theor. Phys. 2008, 119, 461–490. [Google Scholar] [CrossRef]
- Constable, N.R.; Myers, R.C. Spin-two glueballs, positive energy theorems and the AdS/CFT correspondence. J. High Energy Phys. 1999, 9910, 37. [Google Scholar] [CrossRef]
- Brower, R.C.; Mathur, S.D.; Tan, C.-I. Glueball spectrum for QCD from AdS supergravity duality. Nucl. Phys. B 2000, 587, 249–276. [Google Scholar] [CrossRef]
- Hashimoto, K.; Tan, C.-I.; Terashima, S. Glueball Decay in Holographic QCD. Phys. Rev. 2008, D77, 086001. [Google Scholar] [CrossRef]
- Brünner, F.; Parganlija, D. Rebhan Glueball Decay Rates in the Witten-Sakai-Sugimoto Model. Phys. Rev. 2015, D91, 106002, Erratum in Phys. Rev. 2016, D93, 109903. [Google Scholar]
- Aharony, O.; Sonnenschein, J.; Yankielowicz, S. A Holographic model of deconfinement and chiral symmetry restoration. Ann. Phys. 2007, 322, 1420–1443. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L. Holographic QCD with Dynamical Flavors. J. High Energy Phys. 2015, 1501, 104. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Dynamically flavored description of holographic QCD in the presence of a magnetic field. Phys. Rev. D 2017, 96, 066032. [Google Scholar] [CrossRef]
- Bergman, O.; Lifschytz, G.; Lippert, M. Holographic Nuclear Physics. J. High Energy Phys. 2007, 11, 56. [Google Scholar] [CrossRef]
- Li, S.; Schmitt, A.; Wang, Q. From holography towards real-world nuclear matter. Phys. Rev. D 2015, 92, 026006. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy-light mesons in chiral AdS/QCD. Phys. Lett. B 2017, 769, 314–321. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Holographic Heavy-Light Chiral Effective Action. Phys. Rev. D 2017, 95, 056022. [Google Scholar] [CrossRef]
- Kovensky, N.; Schmitt, A. Heavy Holographic QCD. J. High Energy Phys. 2020, 2, 96. [Google Scholar] [CrossRef]
- Wu, C.; Xiao, Z.; Zhou, D. Sakai-Sugimoto model in D0–D4 background. Phys. Rev. D 2013, 88, 026016. [Google Scholar] [CrossRef]
- Seki, S.; Sin, S. A New Model of Holographic QCD and Chiral Condensate in Dense Matter. J. High Energy Phys. 2013, 10, 223. [Google Scholar] [CrossRef]
- Bartolini, L.; Bigazzi, F.; Bolognesi, S.; Cotrone, A.L.; Manenti, A. Theta dependence in Holographic QCD. J. High Energy Phys. 2017, 2, 29. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Sisca, R. Notes on Theta Dependence in Holographic Yang-Mills. J. High Energy Phys. 2015, 8, 90. [Google Scholar] [CrossRef]
- Bigazzi, F.; Caddeo, A.; Cotrone, A.L.; Vecchia, P.D.; Marzolla, A. The Holographic QCD Axion. J. High Energy Phys. 2019, 12, 56. [Google Scholar] [CrossRef]
- Hashimoto, K.; Sakai, T.; Sugimoto, S. Nuclear Force from String Theory. Prog. Theor. Phys. 2009, 122, 427–476. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N.; Yi, P. A Matrix Model for Baryons and Nuclear Forces. J. High Energy Phys. 2010, 10, 3. [Google Scholar] [CrossRef]
- Hashimoto, K.; Iizuka, N. Three-Body Nuclear Forces from a Matrix Model. J. High Energy Phys. 2010, 11, 58. [Google Scholar] [CrossRef]
- Hashimoto, K.; Matsuo, Y. Nuclear binding energy in holographic QCD. Phys. Rev. D 2021, 104, 026006. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Matrix model and Holographic Baryons in the D0–D4 background. Phys. Rev. D 2015, 92, 046007. [Google Scholar] [CrossRef]
- Li, S.; Jia, T. Three-body force for baryons from the D0–D4/D8 brane matrix model. Phys. Rev. D 2016, 93, 065051. [Google Scholar] [CrossRef]
- Kaplunovsky, V.; Sonnenschein, J. Searching for an Attractive Force in Holographic Nuclear Physics. J. High Energy Phys. 2011, 5, 58. [Google Scholar] [CrossRef]
- Becker, K.; Becker, M.; Schwarz, J.H. String Theory and M-Theory, A Modern Introduction; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Witten, E. String Theory Dynamics in Various Dimensions. Nucl. Phys. B 1995, 443, 197. [Google Scholar] [CrossRef]
- Sugimoto, S.; Takahashi, K. QED and string theory. J. High Energy Phys. 2004, 4, 51. [Google Scholar] [CrossRef]
- Antonyan, E.; Harvey, J.A.; Jensen, S.; Kutasov, D. NJL and QCD from String Theory. arXiv 2006, arXiv:hep-th/0604017. [Google Scholar]
- Freedman, D.Z.; Proeyen, A.V. Supergravity; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Mandal, G.; Morita, T. Gregory-Laflamme as the confinement/deconfinement transition in holographic QCD. J. High Energy Phys. 2011, 9, 73. [Google Scholar] [CrossRef]
- Mandal, G.; Morita, T. What is the gravity dual of the confinement/deconfinement transition in holographic QCD? J. Phys. Conf. Ser. 2012, 343, 012079. [Google Scholar]
- Johnson, C.V. D-Branes; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Zahed, I.; Brown, G.E. The Skyrme Model. Phys. Rept. 1986, 142, 1–102. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. B 1983, 223, 422. [Google Scholar] [CrossRef]
- Kaymakcalan, O.; Rajeev, S.; Schechter, J. Nonabelian Anomaly and Vector Meson Decays. Phys. Rev. D 1984, 30, 594. [Google Scholar] [CrossRef]
- Rey, S.-J.; Yee, J.-T. Macroscopic strings as heavy quarks in large N gauge theory and anti-de Sitter supergravity. Eur. Phys. J. C 2001, 22, 379–394. [Google Scholar] [CrossRef]
- Gross, D.J.; Ooguri, H. Aspects of large N gauge theory dynamics as seen by string theory. Phys. Rev. D 1998, 58, 106002. [Google Scholar] [CrossRef]
- Tong, D. TASI lectures on solitons: Instantons, monopoles, vortices and kinks. arXiv 2005, arXiv:hep-th/0509216. [Google Scholar]
- Witten, E. Current Algebra, Baryons, and Quark Confinement. Nucl. Phys. B 1983, 223, 433–444. [Google Scholar] [CrossRef]
- Seo, Y.; Sin, S.-J. Baryon Mass in medium with Holographic QCD. J. High Energy Phys. 2008, 4, 10. [Google Scholar] [CrossRef]
- Adkins, G.; Nappi, C.; Witten, E. Static Properties of Nucleons in the Skyrme Model. Nucl. Phys. B 1983, 228, 552. [Google Scholar] [CrossRef]
- Lau, P.; Sugimoto, S. Chern-Simons 5-form and Holographic Baryons. Phys. Rev. D 2017, 95, 126007. [Google Scholar] [CrossRef]
- Mateos, D.; Myers, R.C.; Thomson, R.M. Thermodynamics of the brane. J. High Energy Phys. 2007, 705, 67. [Google Scholar] [CrossRef]
- Bayona, A.B. Holographic deconfinement transition in the presence of a magnetic field. J. High Energy Phys. 2013, 1311, 168. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Mas, J.; Mayerson, D.; Tarrio, J. D3–D7 Quark-Gluon Plasmas at Finite Baryon Density. J. High Energy Phys. 2011, 1104, 60. [Google Scholar] [CrossRef]
- Cotrone, A.L.; Tarrio, J. Consistent reduction of charged D3–D7 systems. J. High Energy Phys. 2012, 164, 1210. [Google Scholar] [CrossRef]
- Bigazzi, F.; Cotrone, A.L.; Tarrio, J. Charged D3–D7 plasmas: Novel solutions, extremality and stability issues. J. High Energy Phys. 2013, 1307, 74. [Google Scholar] [CrossRef]
- Benincasa, P. A note on Holographic Renormalization of Probe D-Branes. arXiv 2009, arXiv:0903.4356. [Google Scholar]
- Papadimitriou, I. Holographic renormalization as a canonical transformation. J. High Energy Phys. 2010, 1011, 14. [Google Scholar] [CrossRef]
- Papadimitriou, I. Holographic Renormalization of general dilaton-axion gravity. J. High Energy Phys. 2011, 1108, 119. [Google Scholar] [CrossRef]
- Giataganas, D.; Irges, N. Flavor Corrections in the Static Potential in Holographic QCD. Phys. Rev. D 2012, 85, 046001. [Google Scholar] [CrossRef]
- Deuzeman, A.; Lombardo, M.P.; Miura, K.; da Silva, T.N.; Pallante, E. Phases of many flavors QCD: Lattice results. arXiv 2012, arXiv:1304.3245. [Google Scholar]
- Braun, J.; Gies, H. Scaling laws near the conformal window of many-flavor QCD. J. High Energy Phys. 2010, 1005, 60. [Google Scholar] [CrossRef]
- Liao, J.; Shuryak, E. Effect of Light Fermions on the Confinement Transition in QCD-like Theories. Phys. Rev. Lett. 2012, 109, 152001. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrodi, G.; Fodor, Z.; Katz, S.D.; Krieg, S.; Schafer, A.; Szabo, K.K. The QCD phase diagram for external magnetic fields. J. High Energy Phys. 2012, 2, 44. [Google Scholar] [CrossRef]
- Bali, G.S.; Bruckmann, F.; Endrődi, G.; Katz, S.D.; Schäfer, A. The QCD equation of state in background magnetic fields. J. High Energy Phys. 2014, 8, 177. [Google Scholar] [CrossRef]
- Fukushima, K.; Hidaka, Y. Magnetic Catalysis Versus Magnetic Inhibition. Phys. Rev. Lett. 2013, 110, 031601. [Google Scholar] [CrossRef] [PubMed]
- Fraga, E.S.; Palhares, L.F. Deconfinement in the presence of a strong magnetic background: An exercise within the MIT bag model. Phys. Rev. D 2012, 86, 016008. [Google Scholar] [CrossRef]
- Sachan, S.; Siwach, S. Thermodynamics of soft wall AdS/QCD at finite chemical potential. Mod. Phys. Lett. A 2012, 27, 1250163. [Google Scholar] [CrossRef]
- Sachan, S. Study of confinement/deconfinement transition in AdS/QCD with generalized warp factors. Adv. High Energy Phys. 2014, 2014, 543526. [Google Scholar] [CrossRef]
- Sevrin, A.; Troost, J.; Troost, W. The non-Abelian Born-Infeld action at order F6. Nucl. Phys. B 2001, 603, 389–412. [Google Scholar] [CrossRef]
- Rozali, M.; Shieh, H.-H.; Raamsdonk, M.V.; Wu, J. Cold Nuclear Matter in Holographic QCD. J. High Energy Phys. 2008, 1, 53. [Google Scholar] [CrossRef]
- Ghoroku, K.; Kubo, K.; Tachibana, M.; Taminato, T.; Toyoda, F. Holographic cold nuclear matter as dilute instanton gas. Phys. Rev. D 2013, 87, 066006. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Pawlowski, J.M.; Wambach, J. The Phase Structure of the Polyakov–Quark–Meson Model. Phys. Rev. D 2007, 76, 074023. [Google Scholar] [CrossRef]
- Schaefer, B.-J.; Wagner, M.; Wambach, J. Thermodynamics of (2 + 1)-flavor QCD: Confronting Models with Lattice Studies. Phys. Rev. D 2010, 81, 074013. [Google Scholar] [CrossRef]
- Nambu, Y.; Lasinio, G.J. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I. Phys. Rev. 1961, 122, 345–358. [Google Scholar] [CrossRef]
- Nambu, Y.; Lasinio, G.J. Dynamical model of elementary particles based on an analogy with superconductivity. II. Phys. Rev. 1961, 124, 246–254. [Google Scholar] [CrossRef]
- Fukushima, K. Chiral effective model with the Polyakov loop. Phys. Lett. B 2004, 591, 277–284. [Google Scholar] [CrossRef]
- Buballa, M. NJL model analysis of quark matter at large density. Phys. Rept. 2005, 407, 205–376. [Google Scholar] [CrossRef]
- Ruester, S.B.; Werth, V.; Buballa, M.; Shovkovy, I.A.; Rischke, D.H. The Phase diagram of neutral quark matter: Self-consistent treatment of quark masses. Phys. Rev. D 2005, 72, 034004. [Google Scholar] [CrossRef]
- Walecka, J.D. A Theory of highly condensed matter. Ann. Phys. 1974, 83, 491–529. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic Calculation of Nuclear Matter and the Nuclear Surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Gallas, S.; Giacosa, F.; Pagliara, G. Nuclear matter within a dilatation-invariant parity doublet model: The role of the tetraquark at nonzero density. Nucl. Phys. A 2011, 872, 13–24. [Google Scholar] [CrossRef]
- Floerchinger, S.; Wetterich, C. Chemical freeze-out in heavy ion collisions at large baryon densities. Nucl. Phys. A 2012, 891, 11–24. [Google Scholar] [CrossRef]
- Myers, R.C. Dielectric-Branes. J. High Energy Phys. 1999, 22, 9912. [Google Scholar] [CrossRef]
- Liu, Y.; Nowak, M.A. Hyperons and θ s + in holographic QCD. Phys. Rev. D 2022, 105, 114021. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy Baryons and their Exotics from Instantons in Holographic QCD. Phys. Rev. D 2017, 95, 116012. [Google Scholar] [CrossRef]
- Liu, Y.; Zahed, I. Heavy and Strange Holographic Baryons. Phys. Rev. D 2017, 96, 056027. [Google Scholar] [CrossRef]
- Li, S. The interaction of glueball and heavy-light flavoured meson in holographic QCD. Eur. Phys. J. C 2020, 80, 881. [Google Scholar] [CrossRef]
- BESIII Collaboration. Measurement of yCP in D0−D0 oscillation using quantum correlations in e−e+→D0D0 at √s = 3.773 GeV. Phys. Lett. B 2015, 774, 339–346. [Google Scholar]
- CDF Collaboration. Observation of Bs-Bsbar Oscillations. Phys. Rev. Lett. 2006, 97, 242003. [Google Scholar] [CrossRef] [PubMed]
- Li, S.-W. Glueball–baryon interactions in holographic QCD. Phys. Lett. B 2017, 773, 142–149. [Google Scholar] [CrossRef]
- Li, S.-W. Holographic description of heavy-flavored baryonic matter decay involving glueball. Phys. Rev. D 2019, 99, 046013. [Google Scholar] [CrossRef]
- Vicari, E.; Panagopoulos, H. Theta dependence of SU(N) gauge theories in the presence of a topological term. Phys. Rept. 2009, 470, 93–150. [Google Scholar] [CrossRef]
- Debbio, L.D.; Manca, G.M.; Panagopoulos, H.; Skouroupathis, A.; Vicari, E. Theta-dependence of the spectrum of SU(N) gauge theories. J. High Energy Phys. 2006, 6, 5. [Google Scholar] [CrossRef]
- D’Elia, M.; Negro, F. Phase diagram of Yang-Mills theories in the presence of a θ term. Phys. Rev. D 2013, 88, 034503. [Google Scholar] [CrossRef]
- D’Elia, M.; Negro, F. θ dependence of the deconfinement temperature in Yang-Mills theories. Phys. Rev. Lett. 2012, 109, 072001. [Google Scholar] [CrossRef] [PubMed]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. D 2008, 78, 074033. [Google Scholar] [CrossRef]
- Kharzeev, D.E. The Chiral Magnetic Effect and Anomaly-Induced Transport. Prog. Part. Nucl. Phys. 2014, 75, 133–151. [Google Scholar] [CrossRef]
- Witten, E. Theta dependence in the large N limit of four-dimensional gauge theories. Phys. Rev. Lett. 1998, 81, 2862–2865. [Google Scholar] [CrossRef]
- Cai, W.; Wu, C.; Xiao, Z. Baryons in the Sakai-Sugimoto model in the D0–D4 background. Phys. Rev. D 2014, 90, 106001. [Google Scholar] [CrossRef]
- Cai, W.; Li, K.; Li, S. Electromagnetic instability and Schwinger effect in the Witten–Sakai–Sugimoto model with D0–D4 background. Eur. Phys. J. C 2019, 79, 904. [Google Scholar] [CrossRef]
- Hashimoto, K.; Oka, T.; Sonoda, A. Electromagnetic instability in holographic QCD. J. High Energy Phys. 2015, 6, 1. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Li, H. Holographic Schwinger effect and electric instability with anisotropy. J. High Energy Phys. 2022, 8, 206. [Google Scholar] [CrossRef]
- Li, S. Holographic Schwinger effect in the confining background with D-instanton. Eur. Phys. J. C 2021, 81, 797. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Fluid/gravity correspondence: A nonconformal realization in compactified D4 branes. Phys. Rev. D 2016, 93, 066005. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Fluid/gravity correspondence: Second order transport coefficients in compactified D4-branes. J. High Energy Phys. 2017, 1, 118. [Google Scholar] [CrossRef]
- Wu, C.; Chen, Y.; Huang, M. Chiral vortical effect from the compactified D4-branes with smeared D0-brane charge. J. High Energy Phys. 2017, 3, 82. [Google Scholar] [CrossRef]
- Cai, W.; Li, S. Sound waves in the compactified D0–D4 brane system. Phys. Rev. D 2016, 94, 066012. [Google Scholar] [CrossRef]
- Benincasa, P.; Buchel, A. Hydrodynamics of Sakai-Sugimoto model in the quenched approximation. Phys. Lett. B 2006, 640, 108–115. [Google Scholar] [CrossRef]
- Imaanpur, A. Correction to baryon spectrum in holographic QCD. Phys. Lett. B 2022, 832, 137233. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Luo, S. Corrections to the instanton configuration as baryon in holographic QCD. Phys. Rev. D 2022, 106, 126027. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Hu, Y. Holographic QCD3 and Chern-Simons theory from anisotropic supergravity. J. High Energy Phys. 2022, 6, 40. [Google Scholar] [CrossRef]
- Li, S.; Luo, S.; Tan, M. Three-dimensional Yang-Mills-Chern-Simons theory from a D3-brane background with D-instantons. Phys. Rev. D 2021, 104, 066008. [Google Scholar] [CrossRef]
- Schmitt, A.; Shternin, P. Reaction rates and transport in neutron stars. Astrophys. Space Sci. Libr. 2018, 457, 455–574. [Google Scholar]
- Kovensky, N.; Poole, A.; Schmitt, A. Building a realistic neutron star from holography. Phys. Rev. D 2022, 105, 034022. [Google Scholar] [CrossRef]
- Heise, R.; Svendsen, H. A Note on fermions in holographic QCD. J. High Energy Phys. 2007, 8, 65. [Google Scholar] [CrossRef]
- Marolf, D.; Martucci, L.; Silva, P.J. Fermions, T-duality and effective actions for D-branes in bosonic backgrounds. J. High Energy Phys. 2003, 4, 51. [Google Scholar] [CrossRef]
- Marolf, D.; Martucci, L.; Silva, P.J. Actions and fermionic symmetries for D-branes in bosonic backgrounds. J. High Energy Phys. 2003, 7, 19. [Google Scholar] [CrossRef]
- Martucci, L.; Rosseel, J.; Van den Bleeken, D.; Van Proeyen, A. Dirac actions for D-branes on backgrounds with fluxes. Class. Quant. Grav. 2005, 22, 2745–2764. [Google Scholar] [CrossRef]
- Camporesi, R.; Higuchi, A. On the eigenfunctions of the Dirac operator on spheres and real hyperbolic spaces. J. Geom. Phys. 1996, 20, 1–18. [Google Scholar] [CrossRef]
- Nakas, T.; Rigatos, K.S. Fermions and baryons as open-string states from brane junctions. J. High Energy Phys. 2020, 12, 157. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).