Abstract
Unsupervised domain adaptation (UDA) is a popular approach to reducing distributional discrepancies between labeled source and the unlabeled target domain (TD) in machine learning. However, current UDA approaches often align feature distributions between two domains explicitly without considering the target distribution and intra-domain category information, potentially leading to reduced classifier efficiency when the distribution between training and test sets differs. To address this limitation, we propose a novel approach called Cluster Matching-based Improved Kernel Fisher criterion (CM-IKFC) for object classification in image analysis using machine learning techniques. CM-IKFC generates accurate pseudo-labels for each target sample by considering both domain distributions. Our approach employs K-means clustering to cluster samples in the latent subspace in both domains and then conducts cluster matching in the TD. During the model component training stage, the Improved Kernel Fisher Criterion (IKFC) is presented to extend cluster matching and preserve the semantic structure and class transitions. To further enhance the performance of the Kernel Fisher criterion, we use a normalized parameter, due to the difficulty in solving the characteristic equation that draws inspiration from symmetry theory. The proposed CM-IKFC method minimizes intra-class variability while boosting inter-class variants in all domains. We evaluated our approach on benchmark datasets for UDA tasks and our experimental findings show that CM-IKFC is superior to current state-of-the-art methods.
1. Introduction
In machine learning (ML) applications, such as object detection and image classification, a vast amount of labeled data is necessary to build a model for there to be a good achievement on test data that has the same distribution as the model training data. Several practical applications, such as the diagnosis of medical images [1], require an enormous quantity of labeled data to be collected, and such efforts are time- and money-consuming.
To handle this issue, the ML paradigm known as “Domain Adaptation” (DA) [2,3] transfers information from a source domain (SD) that has already been labeled to a target domain (TD) that has only recently been labeled by assuming that both domains have the same classification task (see Figure 1). We focus on the UDA scenario in this study, where all target samples are taken to be unlabeled [4]. UDA is used for predicting unlabeled data in a particular TD in a similar label space in which various divergences exist among two domains [5,6]. Typically, because of the distribution shifts, various models from the SD to the TD are unsuccessful. These issues are figured out by employing numerous methods that seek to match the specified source and target distribution and are used to perform several tasks in computer vision (CV). UDA is becoming more popular due to its applications in numerous CV fields, and different methods are being used to solve the issue [7,8,9,10]. During the time of the training process, there are various distributions for two domains, and UDA is concerned with situations in which both an unlabeled TD and a labeled SD are accessible [11]. Several methods, including [12,13], suggest matching the two different distributions in a latent subspace to categorize the unlabeled target data. Reference [12] suggested that, in order to minimize the distribution shift, samples from both domains should be projected onto a new subspace, while also including marginal and conditional distributions. Adaptively weighting the marginal and conditional distributions was suggested by J. Wang et al. [14], based on [12], to further reduce the distribution shift.
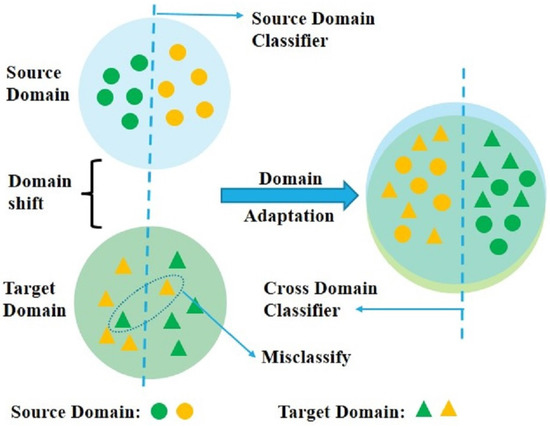
Figure 1.
An illustration of how DA techniques can solve the “domain shift” issue between the SD and TD. The feature distributions of the SD and TD are compared, with the original feature distributions on the left and the new feature distributions on the right, after DA.
The current approaches are classified into four categories [13]: (a) instance-based adaptation, which decreases domain discrepancy by adjusting sample weights in either the SD or both domains [15], (b) feature representation-based adaptation, which creates feature representations to reduce either learning task inaccuracy, domain shift, or both [13], (c) classifier-based adaptation [16], which uses training data from both domains and develops a new model that lowers the generalization error within the TD and (d) hybrid knowledge-based adaptation, which offers several knowledge types, such as joint instance and feature representation-based adaption [12], joint instance and classifier-based adaptation, or joint feature representation and classifier-based adaptation. Regardless of the classifier’s apparent high performance, the majority of the techniques covered above, including the support vector machine and the nearest neighbor classifier, instruct a straightforward classifier on the projected source data, provide each target sample with a pseudo-label, after that, utilise the capabilities of the classifier. The classification procedure, independent of the target data, may lead to a considerable distribution shift.
This study introduces a novel technique, known as the cluster matching-based improved kernel Fisher criterion (CM-IKFC). To reduce the distribution shift, CM-IKFC suggests aligning the conditional and marginal distributions of the SD and TD using cluster matching and the Fisher criteria. Particularly, K-means clustering is utilised to cluster the samples in the latent subspace in both domains [17]. After that, we provide pseudo-labels to the target cluster by comparing the TD cluster centroid with the centroid of the SD class. This way, when giving pseudo-labels, the distributions of both domains are considered. Additionally, we used the Improved Kernel Fisher Criterion (IKFC) to reduce intra-class discrepancy, while increasing inter-class discrepancy, in both domains. This promotes cluster matching and the minimization of distribution shifts. In the training phase, the IKFC is introduced to extend the technique, so that the adapted image class transitions and the semantic structures are preserved. The highlights of our paper’s contributions are listed below:
- The proposed method, CM-IKFC, clusters the data from both domains using the K-Means technique in a learnt subspace.
- The cluster centroid of both the SD and TD should be matched with one another in order to more accurately assign the target sample pseudo-labels. In this manner, while assigning pseudo-labels, the SD and TD distributions are considered.
- In the training phase of cluster matching, the IKFC increases inter-class discrepancy in both domains while decreasing intra-class discrepancy. The KFC is improved by utilizing normalized parameters.
- Based on experimental results on three benchmark datasets, CM-IKFC shows superior performance over state-of-the-art UDA approaches.
The remaining sections of the paper are arranged as follows: In Section 2, a literature review is described; In Section 3, the proposed method is demonstrated; In Section 4, the experimental results, which demonstrate that the proposed technique is both successful and efficient, are discussed; In Section 5, the paper’s conclusion is presented.
2. Related Work
Domain adaptation (DA) employs labelled source data with a distribution different from the TD in an effort to improve target learning. Due to recent developments in CV, several techniques for UDA have been developed that employ deep learning (DL). Li et al. [18] provided a brand-new UDA technique that attempts to produce target image–label pairings on the spot, and, moreover, creates semantic loss conditional on randomly selected labels. In addition, it uses an adversarial training approach in GAN for similar target styles. The labels on the output images must, specifically, match those on the input images. Due to the reliable target-style preparation data used during training, the model performs well in the TD. Our model performs better when dealing with problems having high domain disagreement because it prevents lead distribution alignment between two domains.
Das et al. [19] suggested a form of UDA that takes into account the presence of the TD unlabeled statistics. The method focuses on connections between samples from SD and TD. To find the correlations, the source and target samples are both considered as graphs and paired using a convex criterion. The measures are class-based regularization and first- and second-order similarity among the graphs. Additionally, they created a convex optimization process that was computationally effective, making the suggested strategy generally applicable. Furthermore, it is indeed necessary to test conventional DA datasets for structured data.
Guan et al. [20] proposed “Cross-Domain Minimization with Deep Autoencoder” (CDMDA) for UDA. CDMDA implements a strategy for multitask learning in which, in a single architecture, CORAL-aligned sharable feature representations are utilized to simultaneously train the SD’s label prediction and input reconstruction on the TD. Additionally, the cluster assumption can be supported by attaching a label discriminator to the adversarial training procedure, which causes the projected target label distribution and the category distribution to appear to have different distributions. Several domain adaptations on visual, as well as on non-visual, datasets demonstrated that the developed method consistently outperformed competing UDA methods. These proposed methods have to be applied to several other domain-adaptable tasks, such as semantic segmentation and classification.
Tian et al. [21] suggested a brand-new DA strategy that extensively investigates the TD data distribution structure and, particularly, treats samples that are part of a similar cluster as a whole, rather than as individuals in the TD. The strategy gives the target cluster pseudo-labels through class matching of the centroid. A self-learning technique for local manifolds was also included in the presentation to fully leverage the target data’s different structural information and to adaptively capture the local connectedness the target samples naturally possessed. The objective function was to be solved with a theoretical convergence guarantee by a powerful iterative optimization technique. A more comprehensive design of semi-supervised algorithms needs further investigation.
Some recent UDA techniques employ the pseudo-labeling approach to take advantage of the semantic information of the target samples. Pseudo labels were used by Xie et al. [22] to estimate class centroids for the TD and to compare them to those in the SD. A self-training system, that alternatively executes model training and pseudo label refinement, was proposed by Zou et al. [23]. Recent studies [24,25] have demonstrated the superiority of clustering-based pseudo-labeling approaches and have demonstrated how these approaches may be successfully applied to DA.
The Kernel Fisher discrimination analysis (KFDA) is a nonlinear technique for two-class and multi-class problems with origins in FDA [26]. KFDA works by transforming the low-dimensional sample space into a high-dimensional feature space, where the FDA is then carried out. To make the computation simpler, the kernel matrix was replaced by its submatrix by [27]. Liu et al. suggested a new KFDA criterion to maximize the uniformity of class–pair separabilities, which was assessed by the entropy of the normalized class–pair separabilities [28]. One of the theoretical study fields that has received a lot of interest recently is optimal kernel selection. Based on FDA’s quadratic programming formulation, Fung et al. devised an iterative technique [29]. By using second-order cone programming, Khemchandani et al. looked at the issue of locating the data-dependent “optimal” kernel function [30]. In order to solve identification or classification issues, KFDA is increasingly being used in conjunction with strong nonlinear feature extraction abilities, and, as a result, is used extensively and successfully in numerous fields.
In this context, Deng et al. [31] proposed a deep clustering method using a Fisher-like criteria-based loss to align the feature distributions of the SD and TD. However, they only used target clustering as an incremental strategy to increase explicit feature alignment, while our proposed method uses cluster matching to take into account both domains’ distributions and intra-domain category information. Chang et al. [32] proposed a discriminative feature learning method to estimate the inter-class separability in UDA. They calculated inter-class separability using the distances between pairs of class centers, whereas our proposed method utilizes preserved semantic structure and class transitions. Meng et al. [33] proposed a method that utilizes pseudo-labels and iterative clustering to incorporate label structure information in UDA. Their approach aims to improve the accuracy of the pseudo-labels generated for the TD, while our proposed method focuses on generating an accurate pseudo-label in a latent discriminative subspace for each target sample. The majority of modern approaches use a method that explicitly aligns feature distributions between the two domains, while ignoring the target distribution and intra-domain category information. The findings of published works first create a classifier on the labeled domain to generate pseudo-labels for unlabeled samples and then compute the unlabeled class distribution using the pseudo-labels, before aligning the distributions. Unfortunately, if the classifier ignores the unlabeled distribution, it may fail to learn the TD. In the prediction of the unlabeled domain distribution, mislabeled data results in large errors. In order to solve the issue, this research suggests a novel CM-IKFC to produce a precise pseudo-label in a latent discriminative subspace for each target sample, while taking into account both domain distributions.
3. Proposed Method
We start with the basic definitions of the UDA problem before providing an overview and delving into the details of the proposed method.
3.1. Problem Statement
We start with the formal concept of DA [6]. The terminology definitions and the notations used are listed in Table 1 for clarification.

Table 1.
Notations used for this paper.
We focus on UDA for image classification when the SD has enough labeled data , and unlabeled data in the TD , where denotes the feature vector, refers to the sample label, having a total of K classes. It is assumed that the SD and TD features and label spaces are the same. The goal of DA is to locate a mapping h that will maximise the consistency between the mapped spaces of the SD data and the TD data . As a result, the model is able to build a more efficient classifier on the SD using labeled samples to anticipate the labels of the TD, i.e., .
3.2. CM-IKFC
The proposed CM-IKFC focuses on creating a discriminative subspace for reducing distributional changes between two domains. As seen in Figure 2, there are two main components of our model, named the K-means algorithm and IKFC. In CM-IKFC, first, we use the k-means algorithm [17] to cluster the data from the two domains in a learning subspace. After that, we apply pseudo-labels to the target samples by comparing the clustered centroid of the TD with the clustered centroid of the SD. In this method, the distributions of the SD and TD are both considered when deciding on pseudo-labels. Finally, the KFC is improved by utilizing normalized parameters and weighed schemes to rebuild the scatter matrices between different classes and within the same class. As a result, it has the capability to alter the function known as the kernel scatter difference discriminant. CM-IKFC applies the IKFC constraint to increase inter-class discrepancy in both domains, while decreasing intra-class discrepancy. This encourages distribution shift reduction and cluster matching.
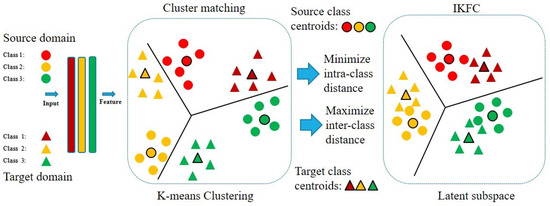
Figure 2.
The proposed CM-IKFC method architecture.
3.3. Domain Clustering
The K-means technique is utilised to cluster both domain samples and attach associated labels. The number of clusters is equal to the number of core classes K. The distance means for the K classes in the data set are determined using the distance as the metric and the initial centroid to describe each class. The Euclidean distance is the similarity index for a specific data set X with n multi-dimensional data points and the class K to be partitioned. The clustering objectives reduce the sum of the squares of the different data types [34].
In this context, if a data point belongs to cluster K, then the value of is set to 1; otherwise, it is set to 0. The variable represents the center of the cluster, i represents the total number of data points, K denotes the cluster number, and represents the squared distance between a data point and the cluster center .
It is a two-step minimization problem. We start by minimizing e in relation to and treating as fixed. Then, we minimize e w.r.t. and regard as fixed. Technically, we distinguish e with respect to first and then update cluster assignments. After that, we differentiate e concerning and recompute the centroids based on the cluster assignments from the initial phase as follows:
It means that the data point should be assigned to the cluster that is the closest to it, based on its sum of squared distance from the centroid of the cluster, and the assignment should be made using the following formula:
This requires the centroids of all of the clusters to be recalculated so that they reflect the new assignments.
Initially, the cluster center is chosen at random, drawn from the sample set. Every sample point is grouped to form a cluster that represents the center point that is nearest to it. Then, all sample points are combined, and the core of each cluster is its own center. The preceding procedures are performed until the cluster’s center point is constant or until the specified number of iterations have been completed. The algorithm output fluctuates depending on the center point selected, causing instabilities. The K value chosen sets the center point, which serves as the algorithm’s target. The results of clustering directly affect aspects such as local or global optimality.
3.4. Cluster Matching
To calculate the UDA’s conditional distribution, each target sample is labeled along with having a pseudo-label. In contrast to traditional methods, to allocate the pseudo-labels, a classifier that has been trained on the SD is employed. This task takes all these domain distributions into account. In such scenarios, it becomes possible to obtain pertinent information regarding the sample distribution structure of the target data. To accomplish this objective, there are several pre-existing clustering algorithms that can be suitable options. Without sacrificing the generalizability of our approach, we chose to employ the well-established K-means algorithm in this study for the purpose of obtaining cluster prototypes. Therefore, the ensuing formula can be expressed as follows [21]:
where represent the projection matrix. denotes the cluster centroids of the target data. is the cluster indicator matrix for the target data. This matrix is defined as if the cluster label of is j, and otherwise.
Next, we conduct the computation of class centroids for the source data and class centroid matching of the SD and TD. When we have the cluster prototypes of the target data, we may reframe the distribution discrepancy reduction issue as the class centroid matching problem. This is possible once we receive the cluster prototypes. It is important to keep in mind that the class centroids of the source data may be precisely determined by computing the mean value of the sample features that belong to the same class. In this study, we used the straightforward and time-saving technique of searching for the closest neighbor to find a solution to the issue of matching class centroids. To be more specific, we looked for the class centroid that was geographically closest to each target cluster centroid, and we tried to find a way to reduce the total distance between each pair of class centroids. In conclusion, the formula for class centroid matching between two domains reads as follows [21]:
where the matrix is a fixed matrix that is utilized to calculate the class centroids of the source data in the transformed space with each element if , and otherwise.
3.5. KFDA
KFDA is an effective nonlinear FDA technique, in which the kernel function is applied to handle the issues of nonlinear optimization. The KFDA is widely used in several fields, due to its effectiveness. The numerical principle is evaluated as follows.
Suppose is the dataset, which consists of K classes in a d-dimensional real space , where samples belong to the j th class, .
FDA is employed for the purpose of finding the optimal projection vectors w that minimize the within-class scatter among different samples. The vector that optimizes the Fisher discriminant function provides FDA as
where represents the within-class scatter matrix and represents the scatter matrix between classes. FDA primarily relies on linear techniques, posing a challenge when attempting to distinguish samples that exhibit nonlinear separability.
The utilization of a kernel trick in the KFDA leads to a notable enhancement in the classification capability of the FDA when dealing with samples that are nonlinearly separable. To accommodate nonlinear scenarios, the function transforms the samples from a lower-dimensional space into a higher-dimensional feature space. Note that is the i th projection value in the class . denotes the mean vector of the entire population, and represents the mean vector of class . In the feature space F, we define the total scatter matrix , the within-class scatter matrix , and the between-class scatter matrix as [35]:
The development of KFDA may be traced back to the following improvement in the kernel Fisher criteria function:
where the various optimal projection vectors are represented by v. Directly calculating the ideal discriminant vector v is not feasible, due to the large dimension of feature space F and the infinite dimension. Applying the kernel technique is one approach to resolve this issue, as is shown below [36]:
Any solution v must exist inside the feature space F, as stated by the notion of reproducing a kernel [26], which spans as follows:
By projecting any test samples into w in F, the following equation is obtained:
The kernel between-class scatter matrix and within-class scatter matrix in F may be defined as follows [37]:
We know that , , are in a semi-definite symmetrical matrix. The fisher criterion function in the feature space F is defined as [38]:
In accordance with the characteristics of the generalized Rayleigh quotient, the optimum solution vector w may be found by increasing the value of the criteria function in (19) until it is equal to the solution of the generalized characteristic equation in the following manner:
3.6. IKFC
The scatter difference discriminant function [39] was constructed in this study in response to the ill-posed issue of the discriminant criteria function (19):
The within-class scatter matrix singular issue is substantially resolved by this approach.
The basic concept of the weighted kernel maximum scatter difference discriminant analysis is that a class is designated as a margin class if it is significantly distant from the center. In this instance, the margin class is distinguished from other classes using the best discriminant vectors produced by maximizing the kernel scatter difference criteria function, since the class variance is greatest in this direction. The class with a greater distance from the center plays a significant part in the process of maximizing the kernel scatter difference criteria function. These projection vectors not only cannot separate classes, other than the margin class, but also cause neighboring classes in the feature space to overlap. The between-class scatter matrix is redefined in response to this issue in the manner described below [38]:
where ; is the distance between ith class and center. represents the weighted function. In order to reduce the impact of margin classes, we employed a strategy where the larger value of was assigned a smaller weight. To achieve this, we defined a weighted function . Additionally, we assigned a weight to the within-class scatter matrix. Here, . By employing these methods, we obtained the following result.
The weight’s objective was to bring all of the training samples belonging to a certain class closer together to the class’s center, and so further reducing the amount of large overlapping occurring across classes. The following is a definition of the weighted kernel scatter difference discriminant function in the feature space:
The column vector is of dimension N. By applying the Regeneration Kernel Theory and Equations (14)–(22), we obtain the following result:
In the given context, and are referred to as the weighted kernel total scatter matrix, weighted kernel within-class scatter matrix, and weighted kernel between-class scatter matrix, respectively. It is important to note that these matrices are semi-definite and symmetrical, with dimensions of . Moving on, we can infer that Equation (22) can be equivalently expressed in the following forms:
The expression can be rewritten as , where represents a unit matrix. Using the Expansion Rayleigh Quotient, we derive the following information.
3.7. Selecting a Normalized Parameter
A normalized parameter was used because the characteristic equation is difficult to solve. If represents a non-singular matrix, then is an optimal vector which is obtained by maximizing Equation (19), which is comparable to the feature vector corresponding to the top m greatest eigenvalues, as described in the article by [40]. Equation (20) may also be written as
where represents the singular matrix. It is not always possible to just use Equation (32). Furthermore, employing a regularized method improves the stability of numerical methods.
where, represents a small, positive number, and indicates the identity matrix. Then, Equation (20) can be written as
While KFDA is employed to solve applied problems, the parameter is determined based on experience or experimental results. In this, a normalized parameter was used and the value regarded as a function of :
where, function f is stable, and the value of the function tends to zero in Equation (36), the is the best classification parameter,
In Algorithm 1, the whole optimization of CM-IKFC is presented.
| Algorithm 1 CM-IKFC |
|
4. Experiments and Analysis
We evaluated the CM-IKFC method using benchmarks, including Office-31, ImageCLEF, and Office-Home, for object classification. We compared CM-IKFC with state-of-the-art DA methods. To enable an accurate comparison, original or state-of-the-art papers were used to obtain the results. The research findings showed how well the proposed CM-IKFC handled the DA problem.
4.1. Benchmark Datasets
The research used three well-known benchmark datasets: Office-31, ImageCLEF, and Office-Home. Each dataset is briefly described below, and Table 2 provides a quick rundown of each dataset’s specifics.

Table 2.
Description of the benchmark datasets.
The Office-31 [41], a frequently used evaluation dataset for visual DA, is made up of 4652 images and 31 classes from the following three different domains: images gathered from the (1) Amazon site (Amazon domain), (2) digital SLR photo (DSLR domain), and (3) web camera (Webcam domain) under various conditions, as shown in Figure 3. The dataset’s distribution across domains is shown in Table 2 with 2817 images belonging to the Amazon domain, 795 images to the Webcam domain, and 498 images to the DSLR domain.

Figure 3.
Images of (a) Amazon (b) DSLR (c) Webcam from office-31 dataset.
The Office–Home [42] poses significant challenges when utilizing it for the examination of the DA model. The 65 categories contain more than 15,500 images of things used every day in homes and offices. The four distinct domains are artistic images (Ar), clip art (Cl), product images (Pr), and real-world images (Rw), as shown in Figure 4. Backgrounds and appearances in these photos are very different. It is more difficult to transfer data between domains because there are many more categories than in Office-31. We examined each technique on each of the 12 adaptation tasks.
Figure 4.
Images of (a) Artistic (b) Clip Art (c) Product and (d) Real World from Office–Home datasets.
The ImageCLEF [43] dataset has 31 categories and 3 domains, namely, Pascal (P), Caltech (C) and ImageNet (I), as shown in Figure 5. We set up six DA tasks: IC, I→P, PI, C→I, P→C, C→P.

Figure 5.
Images of (a) Caltech (b) Imagnet (c) Pascal from ImageCLEF dataset.
4.2. Implementation Details
The model was implemented using the PyTorch framework. In every experiment, the projection matrix dimension was always 100. Twenty iterations were the most that could be carried out. We used K-means algorithms for clustering, so the value of K was set according to the classes in the datasets. Specifically, the values of K on the Office-31, Office-Home and ImageCLEF datasets were set as 31, 65, and 31, respectively. Furthermore, we set the parameter = 0.2 analytically. The following section analyzes the impact of the trade-off parameter.
4.3. Baseline Methods
To evaluate the effectiveness of our proposed strategy in an experimental setting, we looked at both conventional and state-of-the-art DA methodologies, such as DAN [44], DANN [45], CyCADA [46], JDDA [47], CDAN [48], HAFN [15], SAFN [15], DMP [49], ADDA [50], JAN [51] and rRevGrad+ CAT [31]. We evaluated the method with other domain adaptation techniques. For the purpose of classifying target samples, ResNet-50 [52] simply utilizes the classification model trained on the SD. Multi-mode structures are used by MADA [53] to achieve proper alignment of different data distributions, based on numerous domain discriminators.
4.4. Results and Analysis
In order to demonstrate the efficacy of CM-IKFC, this section presents the classification accuracy achieved on the benchmark datasets. Additionally, we conducted several experiments to investigate how and why our CM-IKFC model successfully addressed domain adaptability. The bold values in the tables represent the highest accuracy achieved for the specific task, indicating superior performance.
The experimental data confirmed the model’s efficacy in this research. The classification results of our model on six UDA tasks from the Office-31 dataset, are shown in Table 3. The source-only model performed satisfactorily for D⇆W tasks because the domain gap was minimal. When compared to other models, our method’s accuracy improved more significantly for the challenging A⇆W and A⇆D adaptation tasks. For instance, our approach considerably outperformed all the current adaptation techniques on A→D, W→A, and D→A, especially when compared to CyCADA [46], which had an equal number of class-based discriminators. Our suggested CM-IKFC model outperformed other approaches in the majority of domain adaptation tasks and also improved average performance by 2.47%. In the six experiments, CM-IKFC produced the four best results and none of the poorest results. This demonstrates how well K-means cluster matching and the IKFC work with UDA.

Table 3.
Results (%) comparison of proposed and existing methodologies for Office-31.
In this study, we describe how the use of IKFC enhanced the performance of our proposed approach, CM-IKFC, in comparison to the base KFC. To demonstrate this improvement, we conducted an experiment where we compared the performance of our proposed approach, CM-IKFC, with that of the KFC-based method without the IKFC extension. The results presented in Table 3, demonstrate that the use of the IKFC criterion significantly enhanced performance by increasing inter-class variability and decreasing intra-class variation. As a result, we observed a substantial improvement in the accuracy of pseudo-labels for TD samples. These findings comprehensively explain how the IKFC criterion was integrated into the KFC to improve its effectiveness. Specifically, the inclusion of a normalized parameter enabled the IKFC criterion to solve the characteristic equation more accurately, leading to a significant improvement in the classification performance of our proposed approach.
The experiment’s results for the office–home dataset are presented in Table 4. Compared to other methods, CM-IKFC outperformed some traditional methods and performed better on 8 of the 12 cross-domain tasks. The average classification accuracy obtained by CM-IKFC was 68.50%, and, compared with the baseline model, it displayed an improvement in accuracy of 1.3% on average, proving that the process of incremental hardening of prediction labels improves the discriminative information therein. Overall, the majority of tasks achieved excellent results.

Table 4.
Results (%) comparison of proposed and existing methodologies for Office–Home.
On the ImageCLEF dataset, Table 5 displays the experimental results of this method and the related comparison methods. In domain adaptation tasks, such as I→P, P→I, C→I, and P→C, CM-IKFC achieved the four best accuracies and none of the six domain adaptation trials’ poorest performances. This demonstrates that CM-IKFC produces greater improvements on challenging DA tasks. The proposed model achieved an average accuracy result of 89.8%, an improvement of 0.7% in comparison with the other baseline methods. We found, through our experiments on all three datasets, that good results with fewer classes were achieved, as seen with the average accuracy of Office-31 and ImageCLEF’s being higher than Office–Home.

Table 5.
Results (%) comparison of proposed and existing methodologies for ImageCLEF.
The proposed method is well-suited for UDA in image classification tasks. However, it may not be applicable to other types of data. The performance of the method can be affected by high-dimensional input data, and it may be necessary to employ feature selection or dimensionality reduction techniques. Additionally, the method requires similar feature distributions between the SD and TD, as large differences may compromise its performance. These limitations should be taken into consideration when applying the method. The information provided is helpful in understanding the restrictions associated with this approach.
4.5. Effectiveness of the Parameter Tuning
Finally, we examined the consequences of the parameter . In order to take the parametric sensitivities into account, we chose 4 transfer tasks from each trial. as we tuned the parameter over the range of {0.1, 0.2, 0.3, 0.5, 0.8, 1.0}. In Figure 6, the outcomes are displayed. It is clear that the results of several trials differed from one another. The performance levels in the Office-31 and Office-Home experiments rose gradually, peaked when the trade-off parameter was around 0.2, and then declined as grew. The ImageCLEF experiment showed that it performed best when was around 0.3 and degraded as the parameter increased. This pattern showed that the ideal varied depending on the transfer task; for instance, the ideal for task A-W from the Office-31 experiment was 0.2, although it was around 0.3 for other tasks within the same experiment. We selected 0.2 for Office–Home and Office-31 and 0.3 for the ImageCLEF experiment in our experimental settings because the parameters were suitable for most tasks.
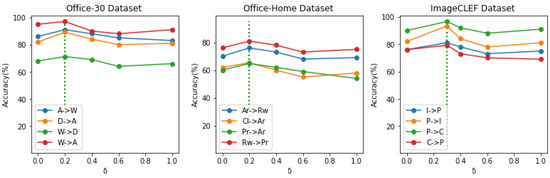
Figure 6.
Parameter Sensitivity Analysis comprising of four tasks from each experiment, assessed using various parameter values. For our study, the vertical green dotted line was the ideal parameter.
5. Conclusions
The purpose of UDA is to reduce distribution discrepancy when data is being transferred data from a labeled SD to an unlabeled TD. The new CM-IKFC approach proposed creates a proper pseudo-label for every target sample. Specifically, the samples are clustered by utilizing K-Means clustering in both domains. In the TD, the clusters are matched by using cluster matching, and then this is extended in the training phase by suggesting an IKFC. This ensures that the updated images’ semantic architectures and class transitions are preserved. Furthermore, because the characteristic equation is difficult to solve, to improve the KFC, a normalized parameter is utilized. In all domains, this CM-IKFC minimizes intra-class variability while boosting inter-class variants. The results from several experiments showed that, on a variety of image benchmark datasets, CM-IKFC was superior to state-of-the-art UDA methods.
Author Contributions
Conceptualization, S.K (Siraj Khan), M.A. and S.A.C.; methodology, S.K. (Siraj Khan) and M.A.; software, S.K. (Siraj Khan); validation, S.K. (Siraj Khan), M.A., B.A., S.K. (Salabat Khan) and M.A.; formal analysis, S.K. (Siraj Khan) and S.A.C.; investigation, M.A.; resources, S.K. (Salabat Khan), A.M., S.A.C. and B.A.; data curation, S.K. (Siraj Khan), B.A., S.K. (Salabat Khan) and A.M.; writing—original draft preparation, S.K. (Siraj Khan) and M.A.; writing—review and editing, S.K (Siraj Khan), S.A.C., B.A., S.K. (Salabat Khan) and M.A.; visualization, S.K. (Siraj Khan), M.A., S.A.C., S.K. (Salabat Khan) and A.M.; supervision, M.A.; project administration, S.K. (Siraj Khan), A.M. and S.A.C.; funding acquisition, S.A.C. All authors have read and agreed to the published version of the manuscript.
Funding
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R239), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data can be made available on request.
Acknowledgments
The authors would like to thank the support of the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University. This work was supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R239), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia. Also, the authors would like to thank Prince Sultan University for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Xie, D.; Deng, C.; Li, C.; Liu, X.; Tao, D. Multi-task consistency-preserving adversarial hashing for cross-modal retrieval. IEEE Trans. Image Process. 2020, 29, 3626–3637. [Google Scholar] [CrossRef] [PubMed]
- Kouw, W.M.; Loog, M. An introduction to domain adaptation and transfer learning. arXiv 2018, arXiv:1812.11806. [Google Scholar]
- Wang, M.; Deng, W. Deep visual domain adaptation: A survey. Neurocomputing 2018, 312, 135–153. [Google Scholar] [CrossRef]
- Wilson, G.; Cook, D.J. A survey of unsupervised deep domain adaptation. ACM Trans. Intell. Syst. Technol. (TIST) 2020, 11, 1–46. [Google Scholar] [CrossRef]
- Liang, J.; Hu, D.; Wang, Y.; He, R.; Feng, J. Source data-absent unsupervised domain adaptation through hypothesis transfer and labeling transfer. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 8602–8617. [Google Scholar] [CrossRef]
- Ren, C.X.; Liu, Y.H.; Zhang, X.W.; Huang, K.K. Multi-source unsupervised domain adaptation via pseudo target domain. IEEE Trans. Image Process. 2022, 31, 2122–2135. [Google Scholar] [CrossRef]
- Khan, S.; Asim, M.; Khan, S.; Musyafa, A.; Wu, Q. Unsupervised domain adaptation using fuzzy rules and stochastic hierarchical convolutional neural networks. Comput. Electr. Eng. 2023, 105, 108547. [Google Scholar] [CrossRef]
- Al-gaashani, M.S.; Shang, F.; Muthanna, M.S.; Khayyat, M.; Abd El-Latif, A.A. Tomato leaf disease classification by exploiting transfer learning and feature concatenation. IET Image Process. 2022, 16, 913–925. [Google Scholar] [CrossRef]
- Abbas, F.; Yasmin, M.; Fayyaz, M.; Abd Elaziz, M.; Lu, S.; El-Latif, A.A.A. Gender classification using proposed CNN-based model and ant colony optimization. Mathematics 2021, 9, 2499. [Google Scholar] [CrossRef]
- Khan, S.; Guo, Y.; Ye, Y.; Li, C.; Wu, Q. Mini-batch Dynamic Geometric Embedding for Unsupervised Domain Adaptation. Neural Process. Lett. 2023, 1, 1–18. [Google Scholar] [CrossRef]
- Zhang, L.; Lan, M.; Zhang, J.; Tao, D. Stagewise unsupervised domain adaptation with adversarial self-training for road segmentation of remote-sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Long, M.; Wang, J.; Ding, G.; Sun, J.; Yu, P.S. Transfer feature learning with joint distribution adaptation. In Proceedings of the IEEE international Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 2200–2207. [Google Scholar]
- Zhuang, F.; Qi, Z.; Duan, K.; Xi, D.; Zhu, Y.; Zhu, H.; Xiong, H.; He, Q. A comprehensive survey on transfer learning. Proc. IEEE 2020, 109, 43–76. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Hao, S.; Feng, W.; Shen, Z. Balanced distribution adaptation for transfer learning. In Proceedings of the 2017 IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 18–21 November 2017; pp. 1129–1134. [Google Scholar]
- Xu, R.; Li, G.; Yang, J.; Lin, L. Larger norm more transferable: An adaptive feature norm approach for unsupervised domain adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1426–1435. [Google Scholar]
- Liu, S.; Lin, G.; Qu, L.; Zhang, J.; De Vel, O.; Montague, P.; Xiang, Y. CD-VulD: Cross-domain vulnerability discovery based on deep domain adaptation. IEEE Trans. Dependable Secur. Comput. 2020, 19, 438–451. [Google Scholar] [CrossRef]
- Abasi, A.K.; Khader, A.T.; Al-Betar, M.A.; Naim, S.; Alyasseri, Z.A.A.; Makhadmeh, S.N. A novel hybrid multi-verse optimizer with K-means for text documents clustering. Neural Comput. Appl. 2020, 32, 17703–17729. [Google Scholar] [CrossRef]
- Li, R.; Cao, W.; Wu, S.; Wong, H.S. Generating target image-label pairs for unsupervised domain adaptation. IEEE Trans. Image Process. 2020, 29, 7997–8011. [Google Scholar] [CrossRef]
- Das, D.; Lee, C.G. Sample-to-sample correspondence for unsupervised domain adaptation. Eng. Appl. Artif. Intell. 2018, 73, 80–91. [Google Scholar] [CrossRef]
- Guan, D.; Huang, J.; Xiao, A.; Lu, S.; Cao, Y. Uncertainty-aware unsupervised domain adaptation in object detection. IEEE Trans. Multimed. 2021, 24, 2502–2514. [Google Scholar] [CrossRef]
- Tian, L.; Tang, Y.; Hu, L.; Ren, Z.; Zhang, W. Domain adaptation by class centroid matching and local manifold self-learning. IEEE Trans. Image Process. 2020, 29, 9703–9718. [Google Scholar] [CrossRef]
- Xie, S.; Zheng, Z.; Chen, L.; Chen, C. Learning semantic representations for unsupervised domain adaptation. In Proceedings of the International conference on machine learning, Vienna, Austria, 25–31 July 2020; pp. 5423–5432. [Google Scholar]
- Zou, Y.; Yu, Z.; Kumar, B.; Wang, J. Unsupervised domain adaptation for semantic segmentation via class-balanced self-training. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 289–305. [Google Scholar]
- Zhang, X.; Ge, Y.; Qiao, Y.; Li, H. Refining pseudo labels with clustering consensus over generations for unsupervised object re-identification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3436–3445. [Google Scholar]
- Dong, X.; Shen, J.; Shao, L. Rethinking Clustering-Based Pseudo-Labeling for Unsupervised Meta-Learning. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 169–186. [Google Scholar]
- Mika, S.; Ratsch, G.; Weston, J.; Scholkopf, B.; Mullers, K.R. Fisher discriminant analysis with kernels. In Proceedings of the Neural Networks for Signal Processing IX: Proceedings of the 1999 IEEE Signal Processing Society Workshop (Cat. No. 98th8468), Madison, WI, USA, 25 August 1999; pp. 41–48. [Google Scholar]
- Billings, S.A.; Lee, K.L. Nonlinear Fisher discriminant analysis using a minimum squared error cost function and the orthogonal least squares algorithm. Neural Netw. 2002, 15, 263–270. [Google Scholar] [CrossRef]
- Liu, J.; Zhao, F.; Liu, Y. Learning kernel parameters for kernel Fisher discriminant analysis. Pattern Recognit. Lett. 2013, 34, 1026–1031. [Google Scholar] [CrossRef]
- Fung, G.; Dundar, M.; Bi, J.; Rao, B. A fast iterative algorithm for fisher discriminant using heterogeneous kernels. In Proceedings of the Twenty-First International Conference on Machine Learning, Banff, AB, Canada, 4–8 July 2004; p. 40. [Google Scholar]
- Khemchandani, R.; Chandra, S. Learning the optimal kernel for Fisher discriminant analysis via second order cone programming. Eur. J. Oper. Res. 2010, 203, 692–697. [Google Scholar] [CrossRef]
- Deng, Z.; Luo, Y.; Zhu, J. Cluster alignment with a teacher for unsupervised domain adaptation. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Repblic of Korea, 27 October–2 November 2019; pp. 9944–9953. [Google Scholar]
- Chang, H.; Zhang, F.; Ma, S.; Gao, G.; Zheng, H.; Chen, Y. Unsupervised domain adaptation based on cluster matching and Fisher criterion for image classification. Comput. Electr. Eng. 2021, 91, 107041. [Google Scholar] [CrossRef]
- Meng, M.; Wu, Z.; Liang, T.; Yu, J.; Wu, J. Exploring fine-grained cluster structure knowledge for unsupervised domain adaptation. IEEE Trans. Circuits Syst. Video Technol. 2022, 32, 5481–5494. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, C.; Feng, Z.; Ye, J.f. Review of K-means clustering algorithm. Electron. Des. Eng. 2012, 20, 21–24. [Google Scholar]
- Ghojogh, B.; Karray, F.; Crowley, M. Fisher and kernel Fisher discriminant analysis: Tutorial. arXiv 2019, arXiv:1906.09436. [Google Scholar]
- Hofmann, T.; Schölkopf, B.; Smola, A.J. Kernel methods in machine learning. Ann. Stat. 2008, 36, 1171–1220. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, H.; Ma, S. Improving kernel Fisher discriminant analysis for face recognition. IEEE Trans. Circuits Syst. Video Technol. 2004, 14, 42–49. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Huang, C. An improved kernel Fisher discriminant analysis for face recognition. In Proceedings of the 2009 International Conference on Computational Intelligence and Security, Washington, DC, USA, 11–14 December 2009; Volume 1, pp. 353–357. [Google Scholar]
- Tang, H.; Fang, T.; Shi, P.F. Laplacian linear discriminant analysis. Pattern Recognit. 2006, 39, 136–139. [Google Scholar] [CrossRef]
- Wang, J.; Li, Q.; You, J.; Zhao, Q. Fast kernel Fisher discriminant analysis via approximating the kernel principal component analysis. Neurocomputing 2011, 74, 3313–3322. [Google Scholar] [CrossRef]
- Saenko, K.; Kulis, B.; Fritz, M.; Darrell, T. Adapting visual category models to new domains. In Proceedings of the European Conference on Computer Vision, Heraklion, Greece, 5–11 September 2010; pp. 213–226. [Google Scholar]
- Venkateswara, H.; Eusebio, J.; Chakraborty, S.; Panchanathan, S. Deep hashing network for unsupervised domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5018–5027. [Google Scholar]
- Ionescu, B.; Müller, H.; Villegas, M.; García Seco de Herrera, A.; Eickhoff, C.; Andrearczyk, V.; Dicente Cid, Y.; Liauchuk, V.; Kovalev, V.; Hasan, S.A.; et al. Overview of ImageCLEF 2018: Challenges, datasets and evaluation. In Proceedings of the International Conference of the Cross-Language Evaluation Forum for European Languages, Avignon, France, 10–14 September 2018; pp. 309–334. [Google Scholar]
- Long, M.; Cao, Y.; Wang, J.; Jordan, M. Learning transferable features with deep adaptation networks. In Proceedings of the International Conference on Machine Learning. PMLR, Lille, France, 6–11 July 2015; pp. 97–105. [Google Scholar]
- Ajakan, H.; Germain, P.; Larochelle, H.; Laviolette, F.; Marchand, M. Domain-adversarial neural networks. arXiv 2014, arXiv:1412.4446. [Google Scholar]
- Hoffman, J.; Tzeng, E.; Park, T.; Zhu, J.Y.; Isola, P.; Saenko, K.; Efros, A.; Darrell, T. Cycada: Cycle-consistent adversarial domain adaptation. In Proceedings of the International Conference on Machine Learning. Pmlr, Stockholm, Sweden, 10–15 July 2018; pp. 1989–1998. [Google Scholar]
- Chen, C.; Chen, Z.; Jiang, B.; Jin, X. Joint domain alignment and discriminative feature learning for unsupervised deep domain adaptation. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 3296–3303. [Google Scholar]
- Long, M.; Cao, Z.; Wang, J.; Jordan, M.I. Conditional adversarial domain adaptation. In Proceedings of the 32nd Annual Conference Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; Volume 31, pp. 1640–1650. [Google Scholar]
- Luo, Y.W.; Ren, C.X.; Ge, P.; Huang, K.K.; Yu, Y.F. Unsupervised domain adaptation via discriminative manifold embedding and alignment. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; Volume 34, pp. 5029–5036. [Google Scholar]
- Tzeng, E.; Hoffman, J.; Saenko, K.; Darrell, T. Adversarial discriminative domain adaptation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7167–7176. [Google Scholar]
- Long, M.; Zhu, H.; Wang, J.; Jordan, M.I. Deep transfer learning with joint adaptation networks. In Proceedings of the International Conference on Machine Learning. PMLR, Sydney, Australia, 6–11 August 2017; pp. 2208–2217. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Pei, Z.; Cao, Z.; Long, M.; Wang, J. Multi-adversarial domain adaptation. In Proceedings of the Thirty-second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).