An Efficient Stress–Strength Reliability Estimate of the Unit Gompertz Distribution Using Ranked Set Sampling

Abstract

In this paper, the estimation of the stress–strength reliability is taken into account when the stress and strength variables have unit Gompertz distributions with a similar scale parameter. The consideration of the unit Gompertz distribution in this context is because of its intriguing symmetric and asymmetric properties that can accommodate various histogram proportional-type data shapes. As the main contribution, the reliability estimate is determined via seven frequentist techniques using the ranked set sampling (RSS) and simple random sampling (SRS). The proposed methods are the maximum likelihood, least squares, weighted least squares, maximum product spacing, Cramér–von Mises, Anderson–Darling, and right tail Anderson–Darling methods. We perform a simulation work to evaluate the effectiveness of the recommended RSS-based estimates by using accuracy metrics. We draw the conclusion that the reliability estimates in the maximum product spacing approach have the lowest value compared to other approaches. In addition, we note that the RSS-based estimates are superior to those obtained by a comparable SRS approach. Additional results are obtained using two genuine data sets that reflect the survival periods of head and neck cancer patients.

1. Introduction

In many practical contexts, we have to deal with the uncertainty of bounded problems. In particular, we commonly encounter quantitative variables that fall within the range of $(0,1)$, such as proportions or percentages. For addressing bounded data sets in various disciplines, several probability distributions have been developed. Recent popular ones include the unit Birnbaum–Saunders distribution (see ref. [1]), the unit Weibull distribution (see ref. [2]), the unit Gompertz distribution (UGD) (see ref. [3]), the unit-inverse Gaussian distribution (see ref. [4]), the unit Burr XII distribution (see ref. [5]), the unit Gamma/Gompertz distribution (see ref. [6]), the unit generalized log Burr XII distribution (see ref. [7]), the unit exponentiated half logistic distribution (see ref. [8]), the unit generalized inverse Weibull distribution (see ref. [9]), the another unit Burr XII distribution (see ref. [10]), the unit xgamma distribution (see ref. [11]), the extreme left-skewed unit distribution (see ref. [12]), the unit-power Burr X distribution (see ref. [13]), the unit inverse exponentiated Weibull distribution (see ref. [14]), and the unit log–log distribution (see ref. [15]).

For the purposes of this paper, a retrospective on the UGD is necessary. To begin, its probability density function (PDF) is indicated as:

$$g\left(w\right)=\phi {\tau }_1{w}_{}^{-\phi -1}\exp \left[-{\tau }_1\left(w_{}^{-\phi }-1\right)\right],$$

(1)

for $w\in (0,1)$, and $g\left(w\right)=0$ for $w\notin (0,1)$, where ${\tau }_1>0$ is the shape parameter and $\phi >0$ is the scale parameter. Hence, a random variable W with this distribution can be written as $W\sim$ UGD$({\tau }_1,\phi )$. The followings are the related cumulative distribution function (CDF) and hazard function (HF):

$$G\left(w\right)=\exp \left[-{\tau }_1\left(w_{}^{-\phi }-1\right)\right],$$

(2)

for $w\in (0,1)$, $G\left(w\right)=0$ for $w\le 1$, and $G\left(w\right)=1$ for $w>1$, and

$$\vartheta \left(w\right)=\frac{\phi {\tau }_1{w}_{}^{-\phi -1}\exp \left[-{\tau }_1\left(w_{}^{-\phi }-1\right)\right]}{1-\exp \left[-{\tau }_1\left(w_{}^{-\phi }-1\right)\right]},$$

for $w\in (0,1)$, and $\vartheta \left(w\right)=0$ for $w\notin (0,1)$, respectively. In order to understand the modeling capabilities of the UGD, plots of the PDF and HF are represented in Figure 1 for some choices of parameters.

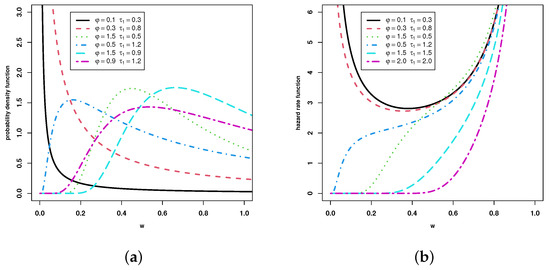
Figure 1. Various plots of the PDF (subfigure (a)) and HF (subfigure (b)) of the UGD.

In this figure, we observe diverse symmetric and asymmetric shapes. In particular, the PDF can be decreasing or unimodal, and the HF can be J-shaped, growing, or in the form of an upside-down. These impressive panels of shapes demonstrate a functional versatility that is attractive in the fit of proportional-type data. The UGD stands out from most of its direct competitors in this aspect. A number of its features (moments, quantiles, etc.) were examined by ref. [3]. The UGD has comparable behavior to certain well-known probability distributions, such as the beta and Kumaraswamy distributions, in terms of real-data application (see ref. [3]). The authors mentioned that the UGD may be applied to the study of skewed data and may be useful in the fields of industrial reliability, environmental sciences, and survival analysis. In addition, the UGD is involved in current reliability estimation problems. For instance, based on it, the issue of assessing multicomponent stress–strength reliability under progressive type II censoring was explored by ref. [16]. According to ref. [17], the reliability estimation in a multicomponent stress–strength based on the UGD was taken into consideration. In their discussion, ref. [18] used record values and inter-record periods for the inference of the UGD, along with a concrete application. Reference [19] addressed the applicability of actual data for the UGD under dual generalized order statistics. There is, however, a lot to do with the UGD from a statistical perspective. In this spirit and with the motivation to describe our main findings, the ranked set sampling (RSS) needs to be presented.

For a first description, the RSS is acknowledged as a valuable sampling strategy (i) to achieve observational economy and (ii) to enhance the accuracy and efficiency of the estimation in situations where the variable under evaluation is expensive to measure or challenging to obtain yet cheap and simple to rank. The notion of the RSS was initially put forth in ref. [20], and ref. [21] reinforced it with mathematical theory. Even with a ranking error, RSS is more effective than simple random sampling (SRS), according to the study in ref. [22]. To give more details, the RSS of the n units to be measured is produced using the following process: First, $n^2$ units are chosen at random from the population and divided into n groups of n units. The lowest-ranking unit from the first sample is used for measurement, while the other units are not. From a subsequent sample of size n, only the unit ranked second-smallest is selected for measurement. After repeating this procedure, the largest ranking unit of the n-th sample of size n is determined. We call this technique one cycle of a ranked set sample of size n. To create an RSS of size $n_{}^{†}=an$, the cycle is then repeated a number of times. In this context, the terms $“n”$ and $“a”$ denote the set size and cycle count, respectively. The set size n should be mentioned as a significant component of the RSS process. According to ref. [23], set sizes larger than five would likely not considerably boost the RSS’s effectiveness since they would undoubtedly result in too many ranking mistakes. In order to properly rank sets of n units, the set size n is often fixed between two and five (see ref. [23]).

Applications of the RSS in different fields have been considered by several authors. In an east Texas pine-hardwood forest, ref. [24] used the RSS to estimate the weights of browsing and herbage. The use of the RSS to determine the volume of trees in a forest was covered by ref. [25]. Reference [26] used the RSS to estimate the mean of forest, grassland, and other vegetation resources. The application of the RSS in environmental chemistry was investigated in ref. [27]. Reference [28] investigated how well the RSS estimated milk output using data from 402 sheep. Reference [29] estimated the average olive yields in a field in the west of Jordan using the multistage RSS. Using agricultural production information from the United States Department of Agriculture, ref. [30] studied the application of the RSS in determining the mean and median of a population. The RSS approach was considered by ref. [31] in market and consumer surveys. Using actual data on body measurement, ref. [32] employed the RSS approach to obtain the population means and ratio. The authors utilized information on the height and weight of 507 people. The RSS was applied in a study on fisheries by ref. [33].

On the other hand, in the literature, there has been much discussion on the issue of drawing conclusions regarding the stress–strength (S-S) model $R^{◊◊}=P(Q<W).$ Here, Q stands for the stress, W for the strength, and $R^{◊◊}$ is a measure of system reliability. When the stress exceeds the system’s capacity, it is clear that the system will malfunction; otherwise, it will continue to function. In several fields, including engineering, statistics, and biostatistics, the S-S model is widely used. The following are some real-world examples: structures, the aging of concrete pressure vessels, the degeneration of rocket motors, and fatigue failure of aircraft structures (see ref. [34]). Historically, ref. [35] was the one who initially considered the S-S model. Many academics have looked at the estimation of the S-S reliability for varied independent distributions; see, for example, refs. [36,37,38,39].

Current discussions on the RSS and its modification techniques have included statistical inferences about the S-S reliability. In Refs. [40,41], the estimation of the S-S reliability via the RSS for independent random samples from the exponential and Weibull distributions, respectively, was the main topic. Using an independent Lindley distribution, an estimate of $R^{◊◊}$ has been provided in ref. [42]. The inferences for the S-S reliability of Burr type X distributions based on the RSS were discussed in ref. [43]. For more recent studies, the reader can refer to refs. [44,45,46,47,48,49,50,51].

In this paper, despite the fact that alternative frequentist methods can sometimes yield estimates that are better than the maximum likelihood (ML) method, little attention has been devoted to using them to estimate the S-S reliability based on the RSS. This is why, in addition to the ML method, we seek to apply frequentist estimation methods in this study. The suggested frequentist estimation methods include the maximum product spacing (MPS), least squares (LS), weighted LS (WLS), Cramér–von-Mises (CV), Anderson–Darling (AD), and right tail AD (RTAD) methods. In this research, we concentrate on seven alternative estimation techniques to estimate $R^{◊◊}=P(Q<W)$, when Q and W are independent random variables that follow the UGD and analyze the behavior of the various estimates for various sample sizes and parameter values via the SRS and RSS. The findings are validated using actual data sets.

The structure of the work is as follows: in Section 2, we provide the ML estimate (MLE) of the S-S reliability. The reliability estimate based on the LS and WLS techniques is provided in Section 3. We derive the estimate in Section 4 by employing the MPS technique. In Section 5, the S-S reliability estimate is generated utilizing the AD, RTAD, and CV approaches. Both simulation research and its application to actual scenarios are discussed in Section 6 and Section 7, with comparisons between the RSS estimates and their SRS counterparts. Section 8 concludes the argument in the paper.

2. Maximum Likelihood Estimate of ${\mathit{R}}^{◊◊}$

In this section, we look at the estimation of $R^{◊◊}=P(Q<W)$, when both stress Q and strength W are modeled by random variables with UGDs defined with a common known scale parameter. The SRS and RSS are considered.

Hence, let $W\sim$ UGD$({\tau }_1,\phi )$ and $Q\sim$ UGD$({\tau }_2,\phi )$ be independent random variables, with W of PDF $f_W\left(w\right)$ and Q of CDF $G_Q\left(q\right)$. Then, the expression of $R^{◊◊}$ is

$$R^{◊◊}={\int }_0^1{G}_Q\left(w\right)f_W\left(w\right)dw={\tau }_1\phi {\int }_0^1{w}^{-\phi -1}\exp \left[-({\tau }_1+{\tau }_2)\left(w^{-\phi }-1\right)\right]dw=\frac{{\tau }_1}{{\tau }_1+{\tau }_2}.$$

(3)

In light of this, the S-S reliability is a function of ${\tau }_1$ and ${\tau }_2$. In accordance with the MLE’s invariance property, an efficient estimate of $R^{◊◊}$ is constructed by inserting the MLEs of ${\tau }_1$ and ${\tau }_2$ in (3).

2.1. MLE Based on the RSS

Let $W_{l_1\left(l_1\right)d_1}$ be the order statistics (OS) of the $l_1$-th sample, $l_1=(1,2,\dots ,n_w)$, in the $d_1$-th cycle ($d_1=1,2,\dots ,a_w$) from the UGD$({\tau }_1,\phi )$. Let $Q_{l_2\left(l_2\right)d_2}$ be the OS of the $l_2$-th sample, $l_2=(1,2,\dots ,n_q)$, in the $d_2$-th cycle ($d_2=1,2,\dots ,a_q$) from the the UGD$({\tau }_2,\phi ).$ Here, $n_1^{†}=n_w^{}{a}_w$, and $n_2^{†}=n_q{a}_q$ are the sample sizes of $W_{l_1\left(l_1\right)d_1}$, and $Q_{l_2\left(l_2\right)d_2}$, respectively, where $n_w^{}$ and $n_q^{}$ are the set sizes and $a_w$, $a_q$ are the cycle numbers.

For the purpose of convenience, we refer to $W_{l_1\left(l_1\right)d_1}$ and $Q_{l_2\left(l_2\right)d_2}$, respectively, as $W_{l_1{d}_1}$ and $Q_{l_2{d}_2}$ throughout the remainder of the work. The PDFs of $W_{l_1{d}_1}$ and $Q_{l_2{d}_2}$ are precisely the PDFs of the $l_1$-th and $l_2$-th OS assuming that the ordering of the observations is perfect. The PDF of $W_{l_1{d}_1}$, for ${\tau }_1,\phi >0$, is provided by:

$$\begin{array}{c}{g}_{W_{l_1{d}_1}}\left(w_{l_1{d}_1}\right)=\frac{n_w^{}!}{(l_1-1)!(n_w^{}-l_1)!}g\left(w_{l_1{d}_1}\right){\left[G\left(w_{l_1{d}_1}\right)\right]}^{l_1-1}{\left[1-G\left(w_{l_1{d}_1}\right)\right]}^{n_w^{}-l_1}\hfill \\ =\frac{n_w^{}!{\tau }_1\phi }{(l_1-1)!(n_w^{}-l_1)!}{w}_{l_1{d}_1}^{-\phi -1}\exp \left[-{\tau }_1{l}_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]{\left[1-\exp \left[-{\tau }_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]\right]}^{n_w^{}-l_1},\hfill \end{array}$$

with $w_{l_1{d}_1}\in (0,1)$. It should be noted that a similar process is used to produce the PDF of $Q_{l_2{d}_2}.$ For the sake of brevity, we will not copy it here. The likelihood function (LF) of the stress Q and the strength W based on the RSS with the perfect ranking assumption is expressed as follows:

$$\begin{array}{c}{L}^{\circ \circ }({\tau }_1,{\tau }_2)\propto {\displaystyle \prod _{l_1=1}^{n_w}}{\displaystyle \prod _{d_1=1}^{a_w}}{\tau }_1\phi w_{l_1{d}_1}^{-\phi -1}\exp \left[-{\tau }_1{l}_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]{\left[1-\exp \left[-{\tau }_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]\right]}^{n_w^{}-l_1}\hfill \\ \times {\displaystyle \prod _{l_2=1}^{n_q}}{\displaystyle \prod _{d_2=1}^{a_q}}{\tau }_2\phi q_{l_2{d}_2}^{-\phi -1}\exp \left[-{\tau }_2{l}_2\left(q_{l_2{d}_2}^{-\phi }-1\right)\right]{\left[1-\exp \left[-{\tau }_2\left(q_{l_2{d}_2}^{-\phi }-1\right)\right]\right]}^{n_q^{}-l_2}.\hfill \end{array}$$

(4)

The log-LF of (4) based on the RSS, is then provided by:

$$\begin{array}{c}{\ell }^{\circ \circ }\propto a_w{n}_w^{}\log \left({\tau }_1\phi \right)-{\displaystyle \sum _{l_1=1}^{n_w^{}}}{\displaystyle \sum _{d_1=1}^{a_w}}\left[{\tau }_1{l}_1\left(w_{l_1{d}_1}^{-\phi }-1\right)+(\phi +1)\log w_{l_1{d}_1}\right]+{\displaystyle \sum _{l_1=1}^{n_w^{}}}{\displaystyle \sum _{d_1=1}^{a_w}}(n_w^{}-l_1)\log \left[1-\exp \left[-{\tau }_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]\right]\hfill \\ +a_q{n}_q^{}\log \left({\tau }_2\phi \right)-{\displaystyle \sum _{l_2=1}^{n_q^{}}}{\displaystyle \sum _{d_2=1}^{a_q}}\left[{\tau }_2{l}_2\left(q_{l_2{d}_2}^{-\phi }-1\right)+(\phi +1)\log q_{l_2{d}_2}\right]+{\displaystyle \sum _{l_2=1}^{n_q^{}}}{\displaystyle \sum _{d_2=1}^{a_q}}(n_q^{}-l_2)\log \left[1-\exp \left[-{\tau }_2\left(q_{l_2{d}_2}^{-\phi }-1\right)\right]\right].\hfill \end{array}$$

The MLEs of ${\tau }_1$ and ${\tau }_2$, denoted by ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_2$, respectively, are obtained by maximizing this function (with respect to ${\tau }_1$ and ${\tau }_2$). To achieve this aim, a differentiable approach is also possible.

Thus, we consider

$$\frac{\partial {\ell }^{\circ \circ }}{\partial {\tau }_1}=\frac{n_1^{†}}{{\tau }_1}-\sum _{l_1=1}^{n_w^{}}\sum _{d_1=1}^{a_w}{l}_1\left(w_{l_1{d}_1}^{-\phi }-1\right)+\sum _{l_1=1}^{n_w^{}}\sum _{d_1=1}^{a_w}\frac{(n_w^{}-l_1)\left(w_{l_1{d}_1}^{-\phi }-1\right)}{\exp \left[{\tau }_1\left(w_{l_1{d}_1}^{-\phi }-1\right)\right]-1},$$

(5)

and

$$\frac{\partial {\ell }^{\circ \circ }}{\partial {\tau }_2}=\frac{n_2^{†}}{{\tau }_2}-\sum _{l_2=1}^{n_q^{}}\sum _{d_2=1}^{a_q}{l}_2\left(q_{l_2{d}_2}^{-\phi }-1\right)+\sum _{l_2=1}^{n_q^{}}\sum _{d_2=1}^{a_q}\frac{(n_q^{}-l_2)\left(q_{l_2{d}_2}^{-\phi }-1\right)}{\exp \left[{\tau }_2\left(q_{l_2{d}_2}^{-\phi }-1\right)\right]-1}.$$

(6)

By equating the equations in (5) and (6) to zero and solving the obtained system, it is possible to derive ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_2$. Consequently, the MLE of $R^{◊◊}$ based on the RSS is given by:

$${\widehat{R}}^{◊◊}=\frac{{\widehat{\tau }}_1}{{\widehat{\tau }}_1+{\widehat{\tau }}_2}.$$

Hence, the MLE ${\widehat{R}}^{◊◊}$ depends only on ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_2$.

2.2. MLE Based on the SRS

Here, the MLE of $R^{◊◊}$ is obtained under the SRS. Let $W_{i_1}$, $i_1=(1,2,\dots ,n_1^{†})$ and $Q_{i_2}$, $i_2=(1,2,\dots ,n_2^{†})$ be a two independent SRS from the UGD$({\tau }_1,\phi )$ and UGD$({\tau }_2,\phi )$, respectively. The LF of the two observed samples is given by:

$$L_1^{\circ \circ }({\tau }_1,{\tau }_2)={\displaystyle \prod _{i_1=1}^{n_1^{†}}}{\tau }_1\phi w_{i_1}^{-\phi -1}\exp \left[-{\tau }_1\left(w_{i_1}^{-\phi }-1\right)\right]{\displaystyle \prod _{i_2=1}^{n_2^{†}}}{\tau }_2\phi q_{i_2}^{-\phi -1}\exp \left[-{\tau }_2\left(q_{i_2}^{-\phi }-1\right)\right].$$

(7)

The log-LF of (7) based on the SRS is then provided by:

$${\ell }_1^{\circ \circ }=n_1^{†}\log \left({\tau }_1\phi \right)-\sum _{i_1=1}^{n_1^{†}}\left[(\phi +1)\log w_{i_1}+{\tau }_1\left(w_{i_1}^{-\phi }-1\right)\right]+n_2^{†}\log \left({\tau }_2\phi \right)-\sum _{i_2=1}^{n_2^{†}}\left[(\phi +1)\log q_{i_2}+{\tau }_2\left(q_{i_2}^{-\phi }-1\right)\right].$$

The MLEs for ${\tau }_1$ and ${\tau }_2$, say ${\widehat{\tau }}_{11}$ and ${\widehat{\tau }}_{22}$, respectively, are obtained by maximizing this function. To this end, a differentiable approach is also possible. Thus, we consider

$$\frac{\partial {\ell }_1^{\circ \circ }}{\partial {\tau }_1}=\frac{n_1^{†}}{{\tau }_1}-\sum _{i_1=1}^{n_1^{†}}\left(w_{i_1}^{-\phi }-1\right),\frac{\partial {\ell }_1^{\circ \circ }}{\partial {\tau }_2}=\frac{n_2^{†}}{{\tau }_2}-\sum _{i_2=1}^{n_2^{†}}\left(q_{i_2}^{-\phi }-1\right).$$

(8)

The MLEs are given as the solution of the non-linear equations in (8) after equating them with zero using the numerical technique. As a result, the MLE ${\widehat{\widehat{R}}}^{◊◊}$ of $R^{◊◊}$ based on the SRS is obtained by inserting ${\widehat{\tau }}_{11}$ and ${\widehat{\tau }}_{22}$ in (3), according to the invariance property as below:

$${\widehat{\widehat{R}}}^{◊◊}=\frac{{\widehat{\tau }}_{11}}{{\widehat{\tau }}_{11}+{\widehat{\tau }}_{22}}.$$

3. LS and WLS Estimates of ${\mathit{R}}^{◊◊}$

For estimating the unknown parameters, the LS and WLS procedures are well known (see ref. [52]). Here, the two methods for determining the estimate of $R^{◊◊}=P(Q<W)$ are given.

Let $W_{1:n_1^{†}}\dots ,W_{n_1^{†}:n_1^{†}}$ be an OS forming a RSS of size $n_1^{†}=n_w^{}{a}_w$ from the UGD$({\tau }_1,\phi ).$ Also, let $Q_{1:n_2^{†}}\dots ,Q_{n_2^{†}:n_2^{†}}$ be an OS forming a RSS of size $n_2^{†}=n_q^{}{a}_q$ from the UGD$({\tau }_2,\phi ).$ Here, $n_w^{}$ and $n_q^{}$ are the set sizes and $a_w$ and $a_q$ are the cycle numbers. The LS estimate (LSE) ${\widehat{\tau }}_1^L$ of ${\tau }_1$ is obtained by minimizing ${\displaystyle \sum _{j_1=1}^{n_1^{†}}}{\left[G\left(w_{(j_1:n_1^{†})}\right)-\frac{j_1}{n_1^{†}+1}\right]}^2$, that is

$$\sum _{j_1=1}^{n_1^{†}}{\left[\exp \left[-{\tau }_1\left(w_{(j_1:n_1^{†})}^{-\phi }-1\right)\right]-\frac{j_1}{n_1^{†}+1}\right]}^2.$$

Hence, ${\widehat{\tau }}_1^L$ is the solution of the following equation:

$$\sum _{j_1=1}^{n_1^{†}}\left[\left[\exp \left[-{\widehat{\tau }}_1^L\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)\right]\right]-\frac{j_1}{n_1^{†}+1}\right]\exp \left[-{\widehat{\tau }}_1^L\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)\right]\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)=0.$$

(9)

Similarly, the LSE ${\widehat{\tau }}_2^L$ of ${\tau }_2$ is obtained by solving the following equation:

$$\sum _{j_2=1}^{n_2^{†}}\left[\left[\exp \left[-{\widehat{\tau }}_2^L\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)\right]\right]-\frac{j_2}{n_2^{†}+1}\right]\exp \left[-{\widehat{\tau }}_2^L\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)\right]\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)=0.$$

(10)

Hence, the LSE ${\widehat{R}}^L{}^{◊◊}$ of $R^{◊◊}$ based on the RSS is obtained by putting produced ${\widehat{\tau }}_1^L$ and ${\widehat{\tau }}_2^L$ from (9) and (10) in (3). Furthermore, the WLS estimate (WLSE) ${\widehat{\tau }}_1^W$ of ${\tau }_1$ is obtained by minimizing

$$\sum _{j_1=1}^{n_1^{†}}\frac{{(n_1^{†}+1)}^2(n_1^{†}+2)}{j_1(n_1^{†}-j_1+1)}{\left[\exp \left[-{\tau }_1\left(w_{(j_1:n_1^{†})}^{-\phi }-1\right)\right]-\frac{j_1}{n_1^{†}+1}\right]}^2.$$

Hence, ${\widehat{\tau }}_1^W$ is the solution of the following equation:

$$\sum _{j_1=1}^{n_1^{†}}\frac{{(n_1^{†}+1)}^2(n_1^{†}+2)}{j_1(n_1^{†}-j_1+1)}\left[\left[\exp \left[-{\widehat{\tau }}_1^W\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)\right]\right]-\frac{j_1}{n_1^{†}+1}\right]\exp \left[-{\widehat{\tau }}_1^W\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)\right]\left(w_{j_1:n_1^{†}}^{-\phi }-1\right)=0.$$

(11)

Similarly, the WLSE ${\widehat{\tau }}_2^W$ of ${\tau }_2$ is obtained by solving the following equation:

$$\sum _{j_2=1}^{n_2^{†}}\frac{{(n_2^{†}+1)}^2(n_2^{†}+2)}{j_2(n_2^{†}-j_2+1)}\left[\left[\exp \left[-{\widehat{\tau }}_2^W\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)\right]\right]-\frac{j_2}{n_2^{†}+1}\right]\exp \left[-{\widehat{\tau }}_2^W\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)\right]\left(q_{j_2:n_2^{†}}^{-\phi }-1\right)=0.$$

(12)

Hence, the WLSE ${\widehat{R}}^{W◊◊}$ of $R^{◊◊}$ based on the RSS is obtained by putting the determined estimates from (11) and (12) in (3).

Additionally, using the above similar procedure, the LSEs ${\widehat{\tau }}_{11}^L$ and ${\widehat{\tau }}_{22}^L$ of ${\tau }_1$ and ${\tau }_2$, respectively, based on the SRS $W_{\left(1\right)},W_{\left(2\right)},\dots ,W_{\left(n_1^{†}\right)}$ and $Q_{\left(1\right)},Q_{\left(2\right)},\dots ,Q_{\left(n_2^{†}\right)}$ of sizes $n_1^{†}$ and $n_2^{†}$, respectively, are obtained by solving numerically the following nonlinear equations:

$$\sum _{i_1=1}^{n_1^{†}}\left[\left[\exp \left[-{\widehat{\tau }}_{11}^L\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]\right]-\frac{i_1}{n_1^{†}+1}\right]\exp \left[-{\widehat{\tau }}_{11}^L\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]\left(w_{\left(i_1\right)}^{-\phi }-1\right)=0,$$

(13)

and

$$\sum _{i_2=1}^{n_2^{†}}\left[\left[\exp \left[-{\widehat{\tau }}_{22}^L\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]\right]-\frac{i_2}{n_2^{†}+1}\right]\exp \left[-{\widehat{\tau }}_{22}^L\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]\left(q_{\left(i_2\right)}^{-\phi }-1\right)=0.$$

(14)

In order to determine the LSE ${\widehat{\widehat{R}}}^{L◊◊}$ of $R^{◊◊}$ based on the SRS, we insert ${\widehat{\tau }}_{11}^L$ and ${\widehat{\tau }}_{22}^L$ that generated from (13) and (14) in (3). In a similar way, the WLSEs ${\widehat{\tau }}_{11}^W$ and ${\widehat{\tau }}_{22}^W$ of ${\tau }_1$ and ${\tau }_2$, respectively, based on the SRS $W_{\left(1\right)},W_{\left(2\right)},\dots ,W_{\left(n_1^{†}\right)}$ and $Q_{\left(1\right)},Q_{\left(2\right)},\dots ,Q_{\left(n_2^{†}\right)}$ of sizes $n_1^{†}$ and $n_2^{†}$, respectively, are obtained by solving numerically the following nonlinear equations:

$$\sum _{i_1=1}^{n_1^{†}}\frac{{(n_1^{†}+1)}^2(n_1^{†}+2)}{i_1(n_1^{†}-i_1+1)}\left[\left[\exp \left[-{\widehat{\tau }}_{11}^W\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]\right]-\frac{i_1}{n_1^{†}+1}\right]\exp \left[-{\widehat{\tau }}_{11}^W\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]\left(w_{\left(i_1\right)}^{-\phi }-1\right)=0,$$

(15)

and

$$\sum _{i_2=1}^{n_2^{†}}\frac{{(n_2^{†}+1)}^2(n_2^{†}+2)}{i_2(n_2^{†}-i_2+1)}\left[\left[\exp \left[-{\widehat{\tau }}_{22}^W\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]\right]-\frac{i_2}{n_2^{†}+1}\right]\exp \left[-{\widehat{\tau }}_{22}^W\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]\left(q_{\left(i_2\right)}^{-\phi }-1\right)=0.$$

(16)

As a result, putting ${\widehat{\tau }}_{11}^W$ and ${\widehat{\tau }}_{22}^W$ generated from (15) and (16) in (3) yields the WLSE ${\widehat{\widehat{R}}}^{W◊◊}$ of $R^{◊◊}$ based on the SRS.

4. Maximum Product Spacing Estimate of ${\mathit{R}}^{◊◊}$

Reference [53] proposed the MPS method for the parameter estimation as an alternative to the ML method. Separately, ref. [54] first suggested it as a reasonable approximation for the Kullback-Leibler information measure. In this section, the MPS estimate (MPSE) of $R^{◊◊}$ is discussed using the RSS and SRS.

Let $W_{1:n_1^{†}}\dots ,W_{n_1^{†}:n_1^{†}}$ be an OS forming an RSS of size $n_1^{†}=n_w^{}{a}_w$ from the UGD$({\tau }_1,\phi ).$ Here, the spacing of a random sample of size $n_1^{†}=n_w^{}{a}_w$ is defined as $D_{j_1}\left({\tau }_1\right)=G(w_{(j_1:n_1^{†})})-G(w_{(j_1-1:n_1^{†})})$, $j_1=1,2,\dots ,n_1^{†}$, $G\left(w_{\left(0\right)}\right)=0,G(w_{(n_1^{†}+1:n_1^{†})})=1.$ The desired estimate ${\widehat{\tau }}_1^M$ of ${\tau }_1$ is computed by maximizing the geometric mean of spacings $\left({\left[{\displaystyle \prod _{j_1=1}^{n_1^{†}+1}}{D}_{j_1}\left({\tau }_1\right)\right]}^{1/\phantom{1(n_1^{†}+1)}(n_1^{†}+1)}\right).$ Alternatively, we maximize ${(n_1^{†}+1)}^{-1}{\displaystyle \sum _{j_1=1}^{n_1^{†}+1}}\log \left(D_{j_1}\left({\tau }_1\right)\right)$ and compute the desired estimate of ${\tau }_1$ from the following equation:

$$\frac{1}{n_1^{†}+1}\sum _{j_1=1}^{n_1^{†}+1}\frac{1}{D_{j_1}\left({\tau }_1\right)}\left\{\exp \left[-{\widehat{\tau }}_1^M\left(w_{(j_1-1:n_1^{†})}^{-\phi }-1\right)\right]\left(w_{(j_1-1:n_1^{†})}^{-\phi }-1\right)-\exp \left[-{\widehat{\tau }}_1^M\left(w_{(j_1:n_1^{†})}^{-\phi }-1\right)\right]\left(w_{(j_1:n_1^{†})}^{-\phi }-1\right)\right\}=0.$$

(17)

Next, let $Q_{(1:n_2^{†})}\dots ,Q_{(n_2^{†}:n_2^{†})}$ be an OS forming a RSS of size $n_2^{†}=n_q^{}{a}_q$ from the UGD$({\tau }_2,\phi ).$ Let us define $D_{j_2}\left({\tau }_2\right)=G\left(q_{(j_2:n_2^{†})}\right)-G\left(q_{(j_2-1:n_2^{†})}\right)$, $j_2=1,2,\dots ,n_2^{†}$, $G\left(q_{\left(0\right)}\right)=0,G\left(q_{(n_2^{†}+1:n_2^{†})}\right)=1.$ The desired estimate ${\widehat{\tau }}_2^M$ of ${\tau }_2$ is obtained from the following equation:

$$\frac{1}{n_2^{†}+1}\sum _{j_2=1}^{n_2^{†}+1}\frac{1}{D_{j_2}\left({\tau }_2\right)}\left\{\exp \left[-{\widehat{\tau }}_2^M\left(q_{(j_2-1:n_2^{†})}^{-\phi }-1\right)\right]\left(q_{(j_2-1:n_2^{†})}^{-\phi }-1\right)-\exp \left[-{\widehat{\tau }}_2^M\left(q_{(j_2:n_2^{†})}^{-\phi }-1\right)\right]\left(q_{(j_2:n_2^{†})}^{-\phi }-1\right)\right\}=0.$$

(18)

Thus, it is possible to determine the MPSE ${\widehat{R}}^{M◊◊}$ of $R^{◊◊}$ after inserting ${\widehat{\tau }}_1^M$ and ${\widehat{\tau }}_2^M$ produced from (17) and (18) in (3).

Secondly, the MPSE ${\widehat{\widehat{R}}}^{M◊◊}$ is then provided based on the SRS. Using the above similar procedure, the MPEs ${\widehat{\tau }}_{11}^M$ and ${\widehat{\tau }}_{22}^M$ of ${\tau }_1$ and ${\tau }_2$, respectively, from the SRS $W_{\left(1\right)},W_{\left(2\right)},\dots ,W_{\left(n_1^{†}\right)}$ and $Q_{\left(1\right)},Q_{\left(2\right)},\dots ,Q_{\left(n_2^{†}\right)}$ of sizes $n_1^{†}$ and $n_2^{†}$, respectively, are obtained. The uniform spacing is defined by $D_{i_1}\left({\tau }_1\right)=G\left(w_{\left(i_1\right)}\right)-G\left(w_{(i_1-1)}\right),i_1=1,\dots ,n_1^{†}$ with $G\left(w_{\left(0\right)}\right)=0,G\left(w_{\left(n_1^{†}\right)}\right)=1$, for the strength W. In addition, for the stress Q, the uniform spacing is $D_{i_2}\left({\tau }_2\right)=G\left(q_{\left(i_2\right)}\right)-G\left(q_{(i_2-1)}\right),i_2=1,\dots ,n_2^{†}$ with $G\left(q_{\left(0\right)}\right)=0,G\left(q_{\left(n_2^{†}\right)}\right)=1$. Hence, the MPSEs ${\widehat{\tau }}_{11}^M$ and ${\widehat{\tau }}_{22}^M$ are obtained by maximizing ${(n_1^{†}+1)}^{-1}{\displaystyle \sum _{i_1=1}^{n_1^{†}+1}}\log \left(D_{i_1}\left({\tau }_1\right)\right)$ and ${(n_2^{†}+1)}^{-1}{\displaystyle \sum _{i_2=1}^{n_2^{†}+1}}\log \left(D_{i_2}\left({\tau }_2\right)\right)$, respectively. As a result, the desired estimates of ${\tau }_1$ and ${\tau }_2$ are obtained by solving the following equations:

$$\frac{1}{n_1^{†}+1}\sum _{i_1=1}^{n_1^{†}+1}\frac{1}{D_{i_1}\left({\tau }_1\right)}\left\{\exp \left[-{\widehat{\tau }}_{11}^M\left(w_{(i_1-1)}^{-\phi }-1\right)\right]{\widehat{\tau }}_{11}^M\left(w_{(i_1-1)}^{-\phi }-1\right)-\exp \left[-{\widehat{\tau }}_{11}^M\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]{\widehat{\tau }}_{11}^M\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right\}=0,$$

(19)

and

$$\frac{1}{n_2^{†}+1}\sum _{i_2=1}^{n_2^{†}+1}\frac{1}{D_{i_2}\left({\tau }_2\right)}\left\{\exp \left[-{\widehat{\tau }}_{22}^M\left(q_{(i_2-1)}^{-\phi }-1\right)\right]{\widehat{\tau }}_{22}^M\left(q_{(i_2-1)}^{-\phi }-1\right)-\exp \left[-{\widehat{\tau }}_{22}^M\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]{\widehat{\tau }}_{22}^M\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right\}=0.$$

(20)

Consequently, ${\widehat{\widehat{R}}}^{M◊◊}$ is derived after putting ${\widehat{\tau }}_{11}^M$ and ${\widehat{\tau }}_{22}^M$ produced from (19) and (20) in (3).

5. Other Estimation Methods

The minimizing of the test statistics between the empirical CDF and theoretical CDF may be used to support the proposal of a number of estimating methods. Here, we take into account the AD, RTAD, and CV methods to obtain the estimate of $R^{◊◊}$.

5.1. Estimates of $R^{◊◊}$ Based on the RSS

Suppose that $W_{(1:n_1^{†})}\dots ,W_{(n_1^{†}:n_1^{†})}$ is an OS forming a RSS of size $n_1^{†}=n_w^{}{a}_w$ from the UGD$({\tau }_1,\phi ).$ Also, let $Q_{(1:n_2^{†})}\dots ,Q_{(n_2^{†}:n_2^{†})}$ be an OS forming a RSS of size $n_2^{†}=n_q^{}{a}_q$ from the UGD$({\tau }_2,\phi ).$

$${\mathbb{C}}_1=\frac{-1}{12n_1^{†}}+\sum _{j_1=1}^{n_1^{†}}{\left[G\left(w_{(j_1:n_1^{†})}\right)-\frac{2j_1-1}{2n_1^{†}}\right]}^2=\frac{-1}{12n_1^{†}}+\sum _{j_1=1}^{n_1^{†}}{\left[\exp \left[-{\tau }_1\left(w_{(j_1:n_1^{†})}^{-\phi }-1\right)\right]-\frac{2j_1-1}{2n_1^{†}}\right]}^2,$$

(21)

and

$${\mathbb{C}}_2=\frac{-1}{12n_2^{†}}+\sum _{j_2=1}^{n_2^{†}}{\left[G\left(q_{(j_2:n_2^{†})}\right)-\frac{2j_2-1}{2n_2^{†}}\right]}^2=\frac{-1}{12n_2^{†}}+\sum _{j_2=1}^{n_2^{†}}{\left[\exp \left[-{\tau }_2\left(q_{(j_2:n_2^{†})}^{-\phi }-1\right)\right]-\frac{2j_2-1}{2n_2^{†}}\right]}^2.$$

(22)

After inserting the results of ${\widehat{\tau }}_1^C$ and ${\widehat{\tau }}_2^C$ from (21) and (22) in (3), the estimate ${\widehat{R}}^{C◊◊}$ based on the CV technique is consequently provided.

The AD estimates (ADEs) ${\widehat{\tau }}_1^A$ and ${\widehat{\tau }}_2^A$ of ${\tau }_1$ and ${\tau }_2$, respectively, are produced after minimizing the following functions:

$$\begin{array}{c}{A}_1=-n_1^{†}-\frac{1}{n_1^{†}}{\displaystyle \sum _{j_1=1}^{n_1^{†}}}(2j_1-1)\left[\log G\left(w_{(j_1:n_1^{†})}\right)+\log \left[1-G\left(w_{(n_1^{†}-j_1+1:n_1^{†})}\right)\right]\right]\hfill \\ =-n_1^{†}-\frac{1}{n_1^{†}}{\displaystyle \sum _{j_1=1}^{n_1^{†}}}(2j_1-1)\left\{\left[{\tau }_1\left(1-w_{(j_1:n_1^{†})}^{-\phi }\right)\right]+\log \left[1-\exp \left[-{\tau }_1\left(w_{{}_{(n_1^{†}-j_1+1:n_1^{†})}}^{-\phi }-1\right)\right]\right]\right\},\hfill \end{array}$$

and

$$\begin{array}{c}{A}_2=-n_2^{†}-\frac{1}{n_2^{†}}{\displaystyle \sum _{j_2=1}^{n_2^{†}}}(2j_2-1)\left[\log G\left(q_{(j_2:n_2^{†})}\right)+\log \left[1-G\left(q_{(n_2^{†}-j_2+1:n_2^{†})}\right)\right]\right]\hfill \\ =-n_2^{†}-\frac{1}{n_2^{†}}{\displaystyle \sum _{j_2=1}^{n_2^{†}}}(2j_2-1)\left\{\left[{\tau }_2\left(1-q_{(j_2:n_2^{†})}^{-\phi }\right)\right]+\log \left[1-\exp \left[-{\tau }_2\left(q_{{}_{(n_2^{†}-j_2+1:n_2^{†})}}^{-\phi }-1\right)\right]\right]\right\}.\hfill \end{array}$$

The reliability estimate ${\widehat{R}}^{A◊◊}$ based on the AD method is provided after putting the produced ${\widehat{\tau }}_1^A$ and ${\widehat{\tau }}_2^A$ in (3).

The RTAD estimates (RTADEs) ${\widehat{\tau }}_1^{TA}$ and ${\widehat{\tau }}_2^{TA}$ of ${\tau }_1$ and ${\tau }_2$, respectively, are produced after minimizing the following functions:

$$\begin{array}{c}T{A}_1=\frac{n_1^{†}}{2}-2{\displaystyle \sum _{j_1=1}^{n_1^{†}}}G\left(w_{(j_1:n_1^{†})}\right)-\frac{1}{n_1^{†}}{\displaystyle \sum _{j_1=1}^{n_1^{†}}}(2j_1-1)\left[\log G\left(w_{(n_1^{†}-j_1+1:n_1^{†})}\right)\right]\hfill \\ =\frac{n_1^{†}}{2}-2{\displaystyle \sum _{j_1=1}^{n_1^{†}}}\exp \left[-{\tau }_1\left(w_{{}_{(j_1:n_1^{†})}}^{-\phi }-1\right)\right]+\frac{1}{n_1^{†}}{\displaystyle \sum _{j_1=1}^{n_1^{†}}}(2j_1-1)\left[{\tau }_1\left(w_{{}_{(n_1^{†}-j_1+1:n_1^{†})}}^{-\phi }-1\right)\right],\hfill \end{array}$$

and

$$\begin{array}{c}T{A}_2=\frac{n_2^{†}}{2}-2{\displaystyle \sum _{j_2=1}^{n_2^{†}}}G\left(q_{(j_2:n_2^{†})}\right)-\frac{1}{n_2^{†}}{\displaystyle \sum _{j_2=1}^{n_2^{†}}}(2j_2-1)\left[\log G\left(q_{(n_2^{†}-j_2+1:n_2^{†})}\right)\right]\hfill \\ =\frac{n_2^{†}}{2}-2{\displaystyle \sum _{j_2=1}^{n_2^{†}}}\exp \left[-{\tau }_2\left(q_{{}_{(j_2:n_2^{†})}}^{-\phi }-1\right)\right]+\frac{1}{n_2^{†}}{\displaystyle \sum _{j_2=1}^{n_2^{†}}}(2j_2-1)\left[{\tau }_2\left(q_{{}_{(n_2^{†}-j_2+1:n_2^{†})}}^{-\phi }-1\right)\right].\hfill \end{array}$$

The reliability estimate ${\widehat{R}}^{TA◊◊}$ based on the RTAD method is provided after putting ${\widehat{\tau }}_1^{TA}$ and ${\widehat{\tau }}_2^{TA}$ in (3).

5.2. Estimates of $R^{◊◊}$ Based on the SRS

Here, the CVE, ADE, and RTADE of $R^{◊◊}$ are obtained under the SRS. Let $W_{i_1}$, $i_1=(1,2,\dots ,n_1^{†})$ be a SRS from the UGD$({\tau }_1,\phi )$, and suppose that $Q_{i_2}$, $i_2=(1,2,\dots ,n_2^{†})$ is a SRS from the UGD$({\tau }_2,\phi )$, respectively, all independent. With the minimization of the following functions, the CVEs ${\widehat{\tau }}_{11}^C$ and ${\widehat{\tau }}_{22}^C$ of ${\tau }_1$ and ${\tau }_2$, respectively, are generated:

$${\mathbb{C}}_1^{\prime }=\frac{-1}{12n_1^{†}}+{\displaystyle \sum _{i_1=1}^{n_1^{†}}}{\left[\exp \left[-{\tau }_1\left(w_{\left(i_1\right)}^{-\phi }-1\right)\right]-\frac{2i_1-1}{2n_1^{†}}\right]}^2,$$

and

$${\mathbb{C}}_2^{\prime }=\frac{-1}{12n_2^{†}}+{\displaystyle \sum _{i_2=1}^{n_2^{†}}}{\left[\exp \left[-{\tau }_2\left(q_{\left(i_2\right)}^{-\phi }-1\right)\right]-\frac{2i_2-1}{2n_2^{†}}\right]}^2.$$

Consequently, the reliability estimate ${\widehat{\widehat{R}}}^{C◊◊}$ based on the CV method is obtained after putting ${\widehat{\tau }}_{11}^C$ and ${\widehat{\tau }}_{22}^C$ in (3). The ADEs ${\widehat{\tau }}_{11}^A$ and ${\widehat{\tau }}_{22}^A$ of ${\tau }_1$ and ${\tau }_2$, respectively, are produced after minimizing the following functions:

$$A_1^{\prime }=-n_1^{†}-\frac{1}{n_1^{†}}{\displaystyle \sum _{i_1=1}^{n_1^{†}}}(2i_1-1)\left\{\left[{\tau }_1\left(1-w_{\left(i_1\right)}^{-\phi }\right)\right]+\log \left[1-\exp \left[-{\tau }_1\left(w_{{}_{(n_1^{†}-i_1+1)}}^{-\phi }-1\right)\right]\right]\right\},$$

and

$$A_2^{\prime }=-n_2^{†}-\frac{1}{n_2^{†}}{\displaystyle \sum _{i_2=1}^{n_2^{†}}}(2i_2-1)\left\{\left[{\tau }_2\left(1-q_{\left(i_2\right)}^{-\phi }\right)\right]+\log \left[1-\exp \left[-{\tau }_2\left(q_{{}_{(n_2^{†}-i_2+1)}}^{-\phi }-1\right)\right]\right]\right\}.$$

The reliability estimate ${\widehat{\widehat{R}}}^{A◊◊}$ based on the AD method is provided after putting ${\widehat{\tau }}_{11}^A$ and ${\widehat{\tau }}_{22}^A$ in (3).

The RTADEs ${\widehat{\tau }}_{11}^{TA}$ and ${\widehat{\tau }}_{22}^{TA}$ of ${\tau }_1$ and ${\tau }_2$, respectively, are produced after minimizing the following functions:

$$T{A}_1^{\prime }=\frac{n_1^{†}}{2}-2{\displaystyle \sum _{i_1=1}^{n_1^{†}}}\exp \left[-{\tau }_1\left(w_{{}_{\left(i_1\right)}}^{-\phi }-1\right)\right]+\frac{1}{n_1^{†}}{\displaystyle \sum _{i_1=1}^{n_1^{†}}}(2i_1-1)\left[{\tau }_1\left(w_{{}_{(n_1^{†}-i_1+1)}}^{-\phi }-1\right)\right],$$

and

$$T{A}_2^{\prime }=\frac{n_2^{†}}{2}-2{\displaystyle \sum _{i_2=1}^{n_2^{†}}}\exp \left[-{\tau }_2\left(q_{{}_{\left(i_2\right)}}^{-\phi }-1\right)\right]+\frac{1}{n_2^{†}}{\displaystyle \sum _{i_2=1}^{n_2^{†}}}(2i_2-1)\left[{\tau }_2\left(q_{{}_{(n_2^{†}-i_2+1)}}^{-\phi }-1\right)\right].$$

The reliability estimate ${\widehat{\widehat{R}}}^{TA◊◊}$ based on the RTAD method is provided after putting ${\widehat{\tau }}_{11}^{TA}$ and ${\widehat{\tau }}_{22}^{TA}$ in (3).

6. Numerical Evaluation

Through the use of MathCAD software, version 14.0 we conduct a simulation study in this section to assess how well the suggested methods for estimating $R^{◊◊}$ under the RSS and SRS perform. We obtain the absolute bias (AB) and mean squared error (MSE) criteria for different estimates. Additionally, the $R^{◊◊}$ estimates’ relative efficiencies (REs) are provided, which are defined as follows:

$$RE\left(R^{◊◊}\right)=\frac{{\mathrm{MSE}}_{\mathrm{SRS}}({\widehat{\widehat{R}}}^{◊◊})}{{\mathrm{MSE}}_{RSS}\left({\widehat{R}}^{◊◊}\right)}.$$

• The parameter values are chosen as $({\tau }_1,{\tau }_2)=(3,2),(0.8,2),(5,2),(3,0.2),\phi =2$, and the true value of $R^{◊◊}$ is determined as $R^{◊◊}=$ 0.2857, 0.6000, 0.7143, and 0.9375, respectively.
• The observed RSS $w_{1d_1}\dots ,w_{n_w{d}_1},d_1=1,\dots .,a_w$ from the strength and $q_{1d_2},\dots .q_{n_q{d}_2}$, $d_2=1,\dots ,a_q$, from the stress having the set sizes: $(n_w,n_q)=$ (2,2), (2,3), (3,3), (3,4), (4,4), (4,5), (5,5), with the cycle numbers $a_w=a_q=10$. The sample sizes are $(n_1^{†},n_2^{†})=(n_w{a}_w,n_q{a}_q)=$ (20,20), (20,30), (30,40), (40.40),(40,50), (50,50).
• In view of the SRS, the observed SRS $w_1\dots ,w_{n_1^{†}}$, $q_1\dots ,q_{n_2^{†}}$, are drawn from strength and stress with sample sizes $(n_1^{†},n_2^{†})=$ (20,20), (20,30), (30,40), (40.40), (40,50), (50,50).
• Using the inverse transformation method, 1000 random samples are created from the strength $W\sim$UGD$({\tau }_1,\phi )$, and stress $Q\sim$UGD$({\tau }_2,\phi )$.
• Different estimation techniques, along with the selected sample scheme, were used to determine the MLE, MPSE, LSE, WLSE, CVE, ADE, and RTADE, namely, ${\widehat{R}}^{◊◊},{\widehat{R}}^{M◊◊}$, ${\widehat{R}}^{L◊◊}$, ${\widehat{R}}^{W◊◊},{\widehat{R}}^{C◊◊},{\widehat{R}}^{A◊◊},{\widehat{R}}^{TA◊◊}$ based on the RSS, and ${\widehat{\widehat{R}}}^{◊◊}$, ${\widehat{\widehat{R}}}^{L◊◊}$, ${\widehat{\widehat{R}}}^{W◊◊}$, ${\widehat{\widehat{R}}}^{M◊◊}$, ${\widehat{\widehat{R}}}^{C◊◊}$, ${\widehat{\widehat{R}}}^{A◊◊}$, ${\widehat{\widehat{R}}}^{TA◊◊}$ based on the SRS.
• The AB, MSE, and RE of the different $R^{◊◊}$ estimates are summarized in Table 1, Table 2 and Table 3 and described graphically in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.
  Table 1. Measures of different $R^{◊◊}$ estimates for the UGD under the RSS.

  ${\mathit{R}}^{◊◊}$	$({\mathit{n}}_{\mathit{w}}^{},{\mathit{n}}_{\mathit{q}}^{})$	$({\mathit{n}}_1^{†},{\mathit{n}}_2^{†})$	RSS
  			Measures	ML	MPS	LS	WLS	CV	AD	RTAD
  0.28570	(2,2)	(20,20)	AB	0.00984	0.00526	0.00824	0.00645	0.00735	0.00842	0.00743
  			MSE	0.00584	0.00518	0.00605	0.00598	0.00672	0.00636	0.00954
  	(2,3)	(20,30)	AB	0.00865	0.00515	0.00764	0.00532	0.00634	0.00804	0.00694
  			MSE	0.00484	0.00496	0.00573	0.00554	0.00582	0.00563	0.00832
  	(3,3)	(30,30)	AB	0.00724	0.00456	0.00698	0.00486	0.00597	0.00784	0.00617
  			MSE	0.00421	0.00441	0.00513	0.00496	0.00524	0.00503	0.00785
  	(3,4)	(30,40)	AB	0.00736	0.00414	0.00615	0.00443	0.00524	0.00705	0.00585
  			MSE	0.00384	0.00327	0.00475	0.00425	0.00495	0.00486	0.00715
  	(4,4)	(40,40)	AB	0.00635	0.00385	0.00595	0.00419	0.00492	0.00674	0.00516
  			MSE	0.00284	0.00224	0.00386	0.00326	0.00406	0.00396	0.00625
  	(4,5)	(40,50)	AB	0.00574	0.00313	0.00553	0.00394	0.00421	0.00618	0.00497
  			MSE	0.00214	0.00196	0.00314	0.00273	0.00374	0.00304	0.00535
  	(5,5)	(50,50)	AB	0.00527	0.00265	0.00428	0.00316	0.00407	0.00544	0.00421
  			MSE	0.00197	0.00115	0.00245	0.00207	0.00274	0.00235	0.00432
  0.60000	(2,2)	(20,20)	AB	0.00743	0.00498	0.00072	0.00039	0.00434	0.00084	0.00583
  			MSE	0.00477	0.0039	0.0054	0.00498	0.00611	0.00468	0.00783
  	(2,3)	(20,30)	AB	0.00718	0.00402	0.00034	0.00032	0.00343	0.00027	0.00924
  			MSE	0.00347	0.00303	0.00386	0.00374	0.00423	0.00345	0.00531
  	(3,3)	(30,30)	AB	0.00722	0.00186	0.00035	0.00021	0.0011	0.0003	0.00356
  			MSE	0.00235	0.00219	0.00262	0.0024	0.00281	0.00235	0.00345
  	(3,4)	(30,40)	AB	0.00662	0.0038	0.00026	0.00085	0.00314	0.00025	0.0044
  			MSE	0.00186	0.00174	0.00211	0.00197	0.00225	0.00189	0.00287
  	(4,4)	(40,40)	AB	0.00149	0.00437	0.00014	0.00022	0.001	0.00012	0.00215
  			MSE	0.00118	0.00125	0.00146	0.00136	0.00158	0.00129	0.00167
  	(4,5)	(40,50)	AB	0.00099	0.00972	0.0028	0.00236	0.00011	0.0032	0.00189
  			MSE	0.00094	0.00086	0.00128	0.0012	0.00095	0.00119	0.0011
  	(5,5)	(50,50)	AB	0.00119	0.00355	0.00011	0.00011	0.00098	0.0001	0.00316
  			MSE	0.00075	0.00071	0.0011	0.001	0.00107	0.00099	0.00097
  0.71430	(2,2)	(20,20)	AB	0.00865	0.00122	0.00029	0.00206	0.00887	0.00012	0.00815
  			MSE	0.00385	0.00354	0.00422	0.00396	0.00465	0.0038	0.00578
  	(2,3)	(20,30)	AB	0.00656	0.00137	0.00118	0.00204	0.00823	0.00012	0.00952
  			MSE	0.00259	0.00244	0.00303	0.00279	0.003	0.00253	0.00395
  	(3,3)	(30,30)	AB	0.00216	0.00143	0.00158	0.00001	0.00448	0.00257	0.0043
  			MSE	0.00185	0.00163	0.0019	0.00178	0.00205	0.00165	0.0022
  	(3,4)	(30,40)	AB	0.00227	0.01319	0.0021	0.00114	0.00288	0.00248	0.00254
  			MSE	0.0015	0.00131	0.00167	0.00152	0.00165	0.00147	0.00161
  	(4,4)	(40,40)	AB	0.00862	0.00487	0.00222	0.00338	0.00658	0.0011	0.00659
  			MSE	0.0012	0.00114	0.00122	0.00124	0.00143	0.00123	0.0014
  	(4,5)	(40,50)	AB	0.0025	0.00112	0.00064	0.00111	0.00471	0.00039	0.00569
  			MSE	0.00101	0.00082	0.0011	0.00108	0.00116	0.0011	0.0011
  	(5,5)	(50,50)	AB	0.00213	0.01059	0.0012	0.00221	0.00479	0.00012	0.00539
  			MSE	0.00082	0.00063	0.00099	0.00084	0.00097	0.00084	0.00086
  0.93750	(2,2)	(20,20)	AB	0.00274	0.00148	0.00646	0.00468	0.00128	0.00441	0.00191
  			MSE	0.00077	0.00052	0.00093	0.00084	0.00083	0.00077	0.00127
  	(2,3)	(20,30)	AB	0.00149	0.00129	0.00605	0.00453	0.00047	0.00411	0.00203
  			MSE	0.00049	0.00036	0.00058	0.00066	0.00058	0.00056	0.00069
  	(3,3)	(30,30)	AB	0.0015	0.00113	0.0048	0.00307	0.00046	0.00335	0.00168
  			MSE	0.00034	0.0003	0.00048	0.00041	0.00038	0.00052	0.00046
  	(3,4)	(30,40)	AB	0.00019	0.0011	0.00488	0.00368	0.00069	0.00338	0.00204
  			MSE	0.00026	0.00021	0.00034	0.00029	0.0003	0.00041	0.00026
  	(4,4)	(40,40)	AB	0.00094	0.00946	0.00365	0.0023	0.00034	0.00256	0.00083
  			MSE	0.00015	0.00012	0.00027	0.00022	0.00025	0.00034	0.00017
  	(4,5)	(40,50)	AB	0.00108	0.00855	0.00303	0.00183	0.00018	0.00184	0.00069
  			MSE	0.00013	0.0001	0.00021	0.00018	0.00019	0.00019	0.00014
  	(5,5)	(50,50)	AB	0.00163	0.00702	0.00247	0.00108	0.0007	0.00119	0.00015
  			MSE	0.00009	0.00007	0.00018	0.00016	0.00016	0.00015	0.00011

  Table 2. Measures of different $R^{◊◊}$ estimates for the UGD under the SRS.

  ${\mathit{R}}^{◊◊}$	$({\mathit{n}}_1^{†},{\mathit{n}}_2^{†})$	SRS
  		Measures	ML	MPS	LS	WLS	CV	AD	RTAD
  0.28570	(20,20)	AB	0.17519	0.16174	0.70317	0.03157	0.26093	0.68545	0.27421
  		MSE	0.04012	0.03529	0.1537	0.06734	0.2734	0.47193	0.18969
  	(20,30)	AB	0.0155	0.08533	0.00692	0.15086	0.06247	0.68119	0.03833
  		MSE	0.03795	0.02963	0.1251	0.04891	0.27865	0.44683	0.1861
  	(30,30)	AB	0.01155	0.01964	0.00495	0.1309	0.04692	0.5967	0.02273
  		MSE	0.03158	0.02953	0.17423	0.03795	0.18737	0.4159	0.13309
  	(30,40)	AB	0.00786	0.00738	0.00375	0.12996	0.01081	0.30458	0.01076
  		MSE	0.02984	0.02638	0.14688	0.03057	0.13454	0.3966	0.11841
  	(40,40)	AB	0.00516	0.00628	0.00175	0.11865	0.01036	0.31973	0.01107
  		MSE	0.02315	0.02057	0.13789	0.02395	0.09834	0.28643	0.10976
  	(40,50)	AB	0.00428	0.00416	0.00462	0.11579	0.00972	0.28663	0.01087
  		MSE	0.01976	0.01863	0.12788	0.02064	0.09012	0.21727	0.10107
  	(50,50)	AB	0.00397	0.00267	0.00246	0.10546	0.00171	0.21865	0.01025
  		MSE	0.01765	0.01456	0.11956	0.01965	0.07966	0.19753	0.09674
  0.60000	(20,20)	AB	0.16002	0.13942	0.38944	0.13881	0.12924	0.37839	0.2296
  		MSE	0.03454	0.02722	0.15278	0.04306	0.05375	0.14373	0.07758
  	(20,30)	AB	0.15797	0.13129	0.38094	0.1309	0.12695	0.37826	0.21932
  		MSE	0.03334	0.02279	0.11157	0.04075	0.04296	0.14344	0.06812
  	(30,30)	AB	0.15625	0.13065	0.35707	0.13	0.12106	0.37306	0.18365
  		MSE	0.02932	0.02111	0.13672	0.03384	0.03406	0.13996	0.05182
  	(30,40)	AB	0.14254	0.12985	0.35202	0.12101	0.09539	0.37205	0.15646
  		MSE	0.02769	0.02039	0.13388	0.027	0.02869	0.13431	0.04696
  	(40,40)	AB	0.1479	0.11533	0.39135	0.15334	0.10949	0.38588	0.13785
  		MSE	0.0204	0.01768	0.12339	0.02076	0.02234	0.11897	0.02834
  	(40,50)	AB	0.13747	0.11036	0.38623	0.14828	0.10107	0.37535	0.12876
  		MSE	0.01887	0.01526	0.11963	0.01946	0.01974	0.11223	0.01936
  	(50,50)	AB	0.11556	0.10785	0.31877	0.12854	0.10096	0.32765	0.11876
  		MSE	0.01505	0.01288	0.11546	0.01624	0.01583	0.11056	0.01758
  0.71430	(20,20)	AB	0.14297	0.12973	0.27983	0.17008	0.15636	0.2394	0.23269
  		MSE	0.02638	0.01974	0.07833	0.03225	0.02796	0.06102	0.05619
  	(20,30)	AB	0.1322	0.11779	0.27176	0.12216	0.10126	0.24578	0.20279
  		MSE	0.02006	0.01498	0.05396	0.02298	0.02145	0.05146	0.04489
  	(30,30)	AB	0.11959	0.12683	0.27559	0.12866	0.11089	0.2472	0.12942
  		MSE	0.01765	0.01282	0.04602	0.01516	0.01954	0.04177	0.02913
  	(30,40)	AB	0.11096	0.11965	0.22987	0.12098	0.10944	0.22875	0.11987
  		MSE	0.01588	0.01095	0.03987	0.01304	0.01698	0.03864	0.02226
  	(40,40)	AB	0.10875	0.11258	0.21877	0.11877	0.07861	0.21545	0.11543
  		MSE	0.01499	0.00995	0.02397	0.01087	0.01515	0.03265	0.01995
  	(40,50)	AB	0.10087	0.10998	0.18763	0.10258	0.05789	0.20966	0.10976
  		MSE	0.01268	0.00734	0.02065	0.00955	0.01341	0.02968	0.01592
  	(50,50)	AB	0.08446	0.05676	0.16868	0.08634	0.03668	0.18443	0.10025
  		MSE	0.01086	0.00575	0.01065	0.00785	0.01135	0.02267	0.01299
  0.93750	(20,20)	AB	0.07436	0.09124	0.93698	0.11872	0.2761	0.87643	0.58189
  		MSE	0.02577	0.01244	0.04794	0.03022	0.02426	0.05289	0.04265
  	(20,30)	AB	0.20656	0.22591	0.93733	0.24662	0.71968	0.9375	0.24549
  		MSE	0.0175	0.0111	0.03217	0.02135	0.02084	0.04142	0.04047
  	(30,30)	AB	0.14405	0.20795	0.93725	0.43749	0.41608	0.98324	0.1437
  		MSE	0.01226	0.00928	0.02844	0.01315	0.01211	0.03079	0.01935
  	(30,40)	AB	0.23887	0.32184	0.99743	0.61278	0.51933	0.98764	0.05003
  		MSE	0.00968	0.00754	0.02117	0.01181	0.01056	0.02763	0.01138
  	(40,40)	AB	0.13043	0.23449	0.93731	0.2402	0.49519	0.9375	0.04162
  		MSE	0.00684	0.0045	0.01922	0.01006	0.00999	0.01953	0.00854
  	(40,50)	AB	0.20397	0.27371	0.76449	0.22049	0.70024	0.84536	0.17623
  		MSE	0.0061	0.00381	0.01254	0.00906	0.00845	0.01176	0.00796
  	(50,50)	AB	0.15677	0.21486	0.79876	0.28434	0.61279	0.87534	0.11587
  		MSE	0.00425	0.00275	0.01008	0.00885	0.00795	0.01056	0.00715

  Table 3. RE of different $R^{◊◊}$ estimates of the UGD.

  ${\mathit{R}}^{◊◊}$	$({\mathit{n}}_{\mathit{w}}^{},{\mathit{n}}_{\mathit{q}}^{})$	$({\mathit{n}}_1^{†},{\mathit{n}}_2^{†})$	RE
  			ML	MPS	LS	WLS	CV	AD	RTAD
  0.28570	(2,2)	(20,20)	6.86986	6.81801	25.40496	11.26087	40.68452	74.16785	19.88365
  	(2,3)	(20,30)	7.84091	5.97379	21.83246	8.82852	47.87801	79.3659	22.36779
  	(3,3)	(30,30)	7.50119	6.69615	33.96296	7.65121	35.75763	82.6839	16.95414
  	(3,4)	(30,40)	7.77083	8.06728	30.92211	7.19294	27.1798	81.60494	16.56084
  	(4,4)	(40,40)	8.15141	9.18304	35.7228	7.3454	24.22167	72.33081	17.5616
  	(4,5)	(40,50)	9.23364	9.5051	40.72611	7.56044	24.09626	71.46967	18.89234
  	(5,5)	(50,50)	8.95939	12.66087	48.80122	9.49275	29.07409	84.05532	22.39398
  0.60000	(2,2)	(20,20)	7.24109	6.97949	28.29259	8.64659	8.79705	30.71154	9.90805
  	(2,3)	(20,30)	9.60807	7.52145	28.90415	10.89572	10.15603	41.57681	12.82863
  	(3,3)	(30,30)	12.4766	9.63927	52.18321	14.11176	12.121	59.55745	15.02029
  	(3,4)	(30,40)	14.8871	11.71839	63.45024	13.70558	12.75111	71.06349	16.36237
  	(4,4)	(40,40)	17.28814	14.144	84.5137	15.26471	14.13924	92.22481	16.92951
  	(4,5)	(40,50)	20.07447	17.84795	93.46406	16.21833	20.78211	94.31429	17.60364
  	(5,5)	(50,50)	20.12032	18.23654	104.96364	16.243	14.79215	111.67677	18.12062
  0.71430	(2,2)	(20,20)	6.85195	5.57627	18.56161	8.14394	6.0129	16.05789	9.72145
  	(2,3)	(20,30)	7.74517	6.13811	17.80858	8.23656	7.15	20.33992	11.36456
  	(3,3)	(30,30)	9.54054	7.86503	24.22105	8.51685	9.53171	25.31515	13.24091
  	(3,4)	(30,40)	10.58667	8.36031	23.87545	8.58092	10.28848	26.28571	13.81141
  	(4,4)	(40,40)	12.4875	8.72807	19.64754	8.7621	10.5972	26.54472	14.24065
  	(4,5)	(40,50)	12.55149	8.95537	18.77582	8.83796	11.56379	26.98	14.47545
  	(5,5)	(50,50)	13.24756	9.13365	10.76061	9.34881	11.70103	26.99214	15.1
  0.93750	(2,2)	(20,20)	33.46753	23.92308	51.54839	35.97024	29.23012	68.68831	33.57953
  	(2,3)	(20,30)	35.71429	30.84444	55.4569	32.35152	35.93264	73.96964	58.64638
  	(3,3)	(30,30)	36.05882	30.92333	59.25	32.07561	31.85526	59.20981	42.06522
  	(3,4)	(30,40)	37.24615	35.90524	62.25	40.7069	35.20667	67.39268	43.78077
  	(4,4)	(40,40)	45.59333	37.51833	71.19778	45.74091	39.96	57.45294	50.23529
  	(4,5)	(40,50)	46.92308	38.14	59.72857	50.33333	44.47368	61.89474	56.88571
  	(5,5)	(50,50)	47.26667	39.34286	56	55.3125	49.70938	70.37333	64.96364

  

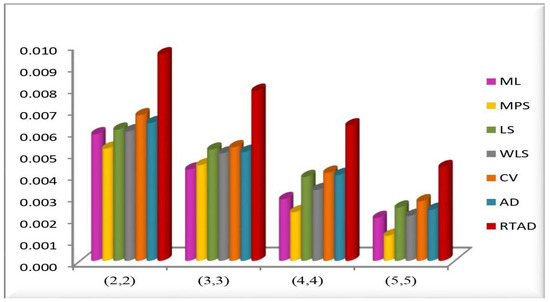  Figure 2. MSE of the $R^{◊◊}$ estimates for all the methods at $R^{◊◊}=0.60000$ in the RSS.
  

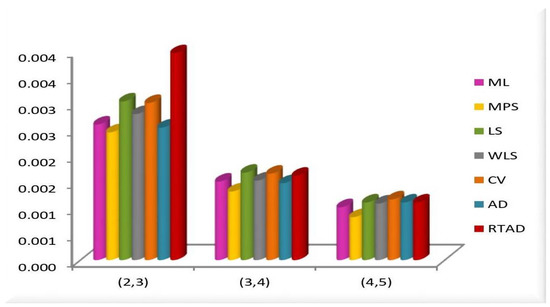  Figure 3. MSE of the $R^{◊◊}$ estimates for all the methods at $R^{◊◊}=0.71430$ in the RSS.
  

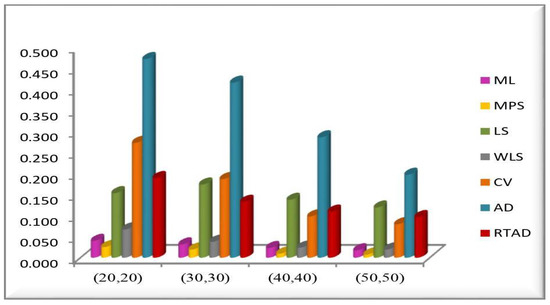  Figure 4. MSE of the $R^{◊◊}$ estimates for all the methods at $R^{◊◊}=0.28570$ in the SRS.
  

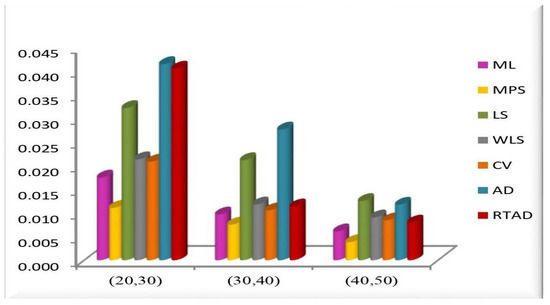  Figure 5. MSE of the $R^{◊◊}$ estimates for all the methods at $R^{◊◊}=0.93750$ in the SRS.
  

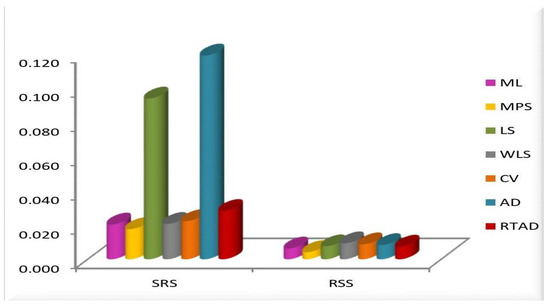  Figure 6. MSE of the $R^{◊◊}$ estimates for all the methods at $(n_w^{},n_q^{})=(4,4),(n_1^{†},n_2^{†})=(40,40)$ and $R^{◊◊}=0.60000$.
  

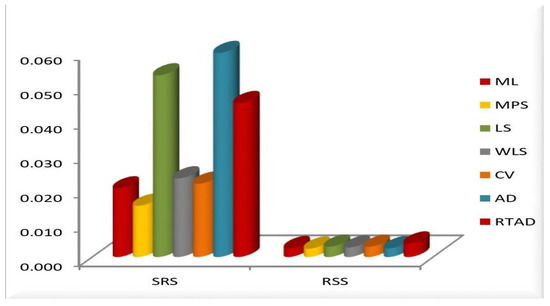  Figure 7. MSE of the $R^{◊◊}$ estimates for all the methods at $(n_w^{},n_q^{})=(2,3),(n_1^{†},n_2^{†})=(20,30)$ and $R^{◊◊}=0.71430$.
  

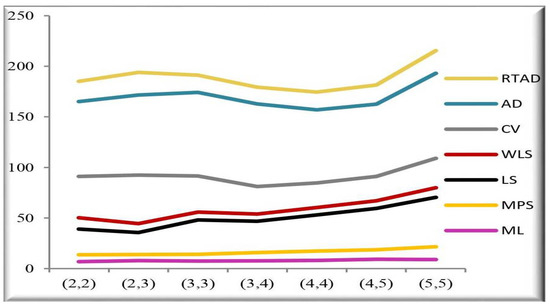  Figure 8. RE of the $R^{◊◊}$ estimates at $R^{◊◊}=0.28570$ for different $(n_w^{},n_q^{})$ at $a_w=a_q=10$.
  

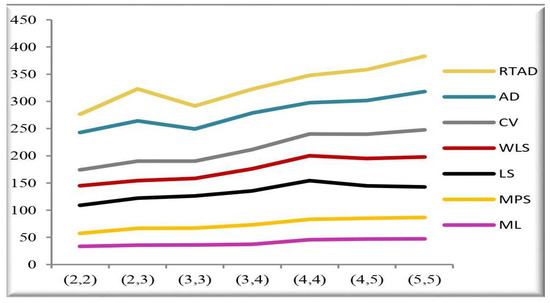  Figure 9. RE of the $R^{◊◊}$ estimates at $R^{◊◊}=0.93750$ for different $(n_w^{},n_q^{})$ at $a_w=a_q$ = 10.

We note the following based on the measurement values in these tables and figures.

• All the reliability estimates based on the RSS are more efficient than the others based on the SRS in most situations (see Table 1 and Table 2).
• For a variety of $n_1^{†}$, and $n_2^{†}$, the MSEs of all the estimates under the RSS are often lower than those under the SRS (see Table 1 and Table 2).
• In the majority of the cases, as seen in Figure 2, the MSEs of the $R^{◊◊}$ estimates decrease as $n_w$ and $n_q$ increase.
• The MSE of the $R^{◊◊}$ estimates for the RTAD method has the highest values (see Figure 2 and Figure 3).
• The MSE of the $R^{◊◊}$ estimates for the MPS method has the smallest values, as seen in Figure 2 and Figure 3.
• In the majority of the time, the MSEs of the $R^{◊◊}$ estimates decrease as $(n_1^{†},n_2^{†})$ increases, also the $R^{◊◊}$ estimates from the MPS method typically take the lowest values when using the SRS (see Table 2 and Figure 4 and Figure 5).
• For both sampling methods, the MSEs of the $R^{◊◊}$ estimates for the MPS method have the lowest values. While the MSEs of the $R^{◊◊}$ estimates for the AD method take the highest values in the SRS, the highest values are given to the MSEs of the estimates for the RTAD method in the RSS scheme.
• Figure 6 and Figure 7 show that the RSS is preferable to the SRS with respect to MSE measures in most cases.
• Figure 8 and Figure 9 show that the RTAD is the most efficient method for $R^{◊◊}$ at the true values $R^{◊◊}=0.2857,0.9375$ and $a_w=a_q=10.$
• The RE increases as $n_w$ and $n_q$ increase (Figure 8 and Figure 9).
• The MSE always decreases as $n_w$ and $n_q$ increase, indicating that the estimates are all consistent.
• The estimates become more accurate as $n_1^{†}$ and $n_2^{†}$ increase, indicating that they are asymptotically unbiased.
• The MSE always decreases as the true value of $R^{◊◊}$ increases, indicating that the estimates are all consistent.

7. Real Data Applications

Two data sets that ref. [55] proposed were considered in this section. The data collection includes two groups of head and neck cancer patients. The survival times of 58 head and neck cancer patients treated with radiation are shown in the data set for the first group, whereas the survival times of 44 patients treated with radiotherapy plus chemotherapy are shown in the data set for the second group. The information is as follows:

Data set I ($\mathit{W}$): 523, 583, 594, 14.48, 16.1, 22.7, 34, 41.55, 42, 45.28, 49.4, 84, 91, 160, 160, 165, 108, 112, 129, 133, 133, 139, 140, 140, 146, 149, 154, 157, 146, 149, 154, 157, 160, 160, 165, 173, 176, 218, 6.53, 7, 10.42, 225, 241, 248, 273, 277, 297, 405, 417, 53.62, 63, 64, 83, 420, 440, 1101, 1146, 1417.

Data set II ($\mathit{Q}$): 25.87, 31.98, 37, 41.35, 47.38, 55.46, 58.36, 63.47, 319, 339, 432, 469, 68.46, 78.26, 173, 179, 194, 195, 74.47, 81.43, 84, 92, 519, 633, 725, 94, 110, 112, 119, 127, 130, 133, 140, 146, 12.2, 23.56, 23.74, 155, 159, 209, 249, 281, 817, 1776.

We divide the data by 2000 to have values between 0 and 1. The Kolmogorov-Smirnov (K-S) goodness-of-fit test is used to fit each of the two data sets individually using the UGD. The UGD fits the data sets, according to the K-S test (K-ST) and the accompanying p-value. It is noted that for Data sets I and II, the K-ST of the UGD has values of 0.16913 and 0.070689, respectively, with p-values of 0.07245 and 0.9694.

The initial PDF shapes are reported utilizing the non-parametric kernel density estimation approach in Figure 10 and Figure 11 for both data sets. From Figure 10 and Figure 11, we can see that the shape of the PDF is asymmetric for both data sets. The normality condition is checked via the QQ plot; see Figure 10 and Figure 11. The outliers can also be spotted using the box plot; see Figure 10 and Figure 11. Henceforth, we can say that there are outliers in both data sets. Figure 12 and Figure 13 display the estimated CDF (ECDF), estimated PDF (EPDF), PP—plots, and estimated survival function (ESF) for the UGD. Thanks to its asymmetric properties, the UGD is an appropriate model for fitting these data.

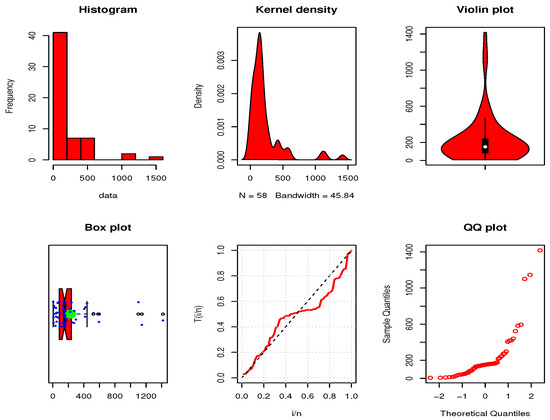
Figure 10. Some basic non-parametric plots for Data set I.

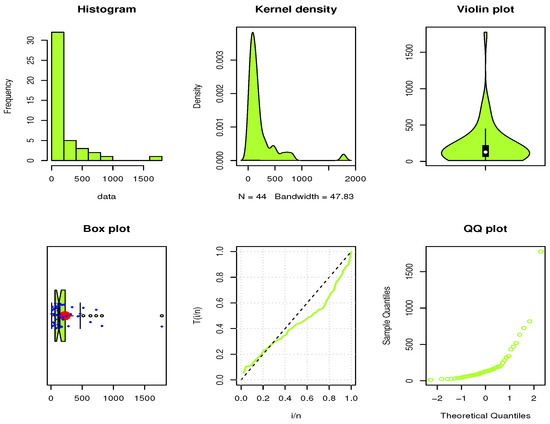
Figure 11. Some basic non-parametric plots for Data set II.

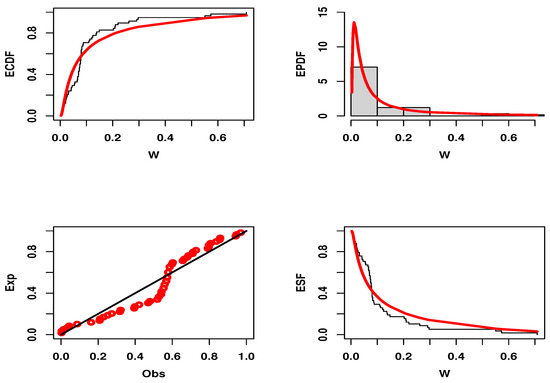
Figure 12. ECDF, EPDF, PP plots and ESF of the UGD for Data set I.

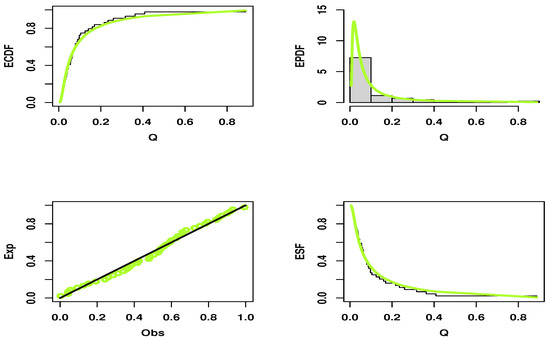
Figure 13. ECDF, EPDF, PP plots and ESF of the UGD for Data set II.

In the earlier sections, it was assumed that stress and strength random variables followed the UGD with the same scale parameter and that the estimates of $R^{◊◊}$ were then examined. Consequently, in order to estimate it using actual data, we also need to see if the specifications of their second scale are the same.

First, it is assumed that $W\sim UGD({\tau }_1,{\phi }_1)$ and $Q\sim UGD({\tau }_2,{\phi }_2)$. We perform the following tests of the hypothesis: $H_0:{\phi }_1={\phi }_2\mathrm{vs}{H}_1:{\phi }_1\ne {\phi }_2$.

The associated likelihood function, based on the SRS, is given by:

$$\begin{array}{c}{L}_1({\tau }_1,{\phi }_1,{\tau }_2,{\phi }_2)={\displaystyle \prod _{l_1=1}^{n_1^{†}}}{\tau }_1{\phi }_1{w}_{l_1}^{-{\phi }_1-1}\exp \left[-{\tau }_1\left(w_{l_1}^{-{\phi }_1}-1\right)\right]\hfill \\ \times {\displaystyle \prod _{l_2=1}^{n_2^{†}}}{\tau }_2{\phi }_2{q}_{l_2}^{-{\phi }_2-1}\exp \left[-{\tau }_2\left(q_{l_2}^{-{\phi }_2}-1\right)\right].\hfill \end{array}$$

The MLEs of ${\tau }_1,{\phi }_1,{\tau }_2$ and ${\phi }_2$ are as follows: ${\widehat{\tau }}_1=0.11552,{\widehat{\phi }}_1=0.33684,{\widehat{\tau }}_2=1.11884$ and ${\widehat{\phi }}_2=0.48394$, and the log-likelihood value is $\log L_1({\tau }_1,{\phi }_1,{\tau }_2,{\phi }_2)=-68.040.$

Second, suppose that $W\sim UGD({\tau }_1,\phi )$ and $Q\sim UGD({\tau }_2,\phi ),$ also, as the same steps in the above, the corresponding LF is given by:

$$\begin{array}{c}{L}_2({\tau }_1,{\tau }_2,\phi )={\displaystyle \prod _{l_1=1}^{n_1^{†}}}{\tau }_1\phi w_{l_1}^{-\phi -1}\exp \left[-{\tau }_1\left(w_{l_1}^{-\phi }-1\right)\right]\hfill \\ \times {\displaystyle \prod _{l_2=1}^{n_2^{†}}}{\tau }_2\phi q_{l_2}^{-\phi -1}\exp \left[-{\tau }_2\left(q_{l_2}^{-\phi }-1\right)\right].\hfill \end{array}$$

The MLEs of ${\tau }_1,{\tau }_2$ and $\phi$ are as follows: ${\widehat{\tau }}_1=0.23668{\widehat{\tau }}_2=0.18232$ and $\widehat{\phi }=0.22347$ and the log-likelihood value is $\log L_2({\tau }_1,{\tau }_2,\phi )=-68.223.$

Then the likelihood ratio statistic is constructed as follows:

$$LR=-2\log \left(\frac{L_2({\tau }_1,{\tau }_2,\phi )}{L_1({\tau }_1,{\phi }_1,{\tau }_2,{\phi }_2)}\right),$$

that is, $-2\left(\log L_2({\tau }_1,{\tau }_2,\phi )-\log L_1({\tau }_1,{\phi }_1,{\tau }_2,{\phi }_2\right))=0.366.$ As a result, the null hypothesis cannot be rejected. Therefore, in this case, the assumption of ${\phi }_1={\phi }_2$ is justified. Thus, both tests accept the null hypothesis that each data set is drawn from the UGD with the same scale parameter.

Then, using the suggested estimating methods for real data sets, we acquire various estimates of $R^{◊◊}$. We observe that the MPS method cannot be used to estimate the parameters and reliability of Data set I because they have equal values $D_{j_1}\left({\tau }_1\right)=G\left(w_{(j_1:n_1^{†})}\right)-G\left(w_{(j_1-1:n_1^{†})}\right)$, $D_{i_1}\left({\tau }_1\right)=G\left(w_{\left(i_1\right)}\right)-G\left(w_{(i_1-1)}\right)$, $i_1=1,\dots ,n_1^{†}$ based on the strength W, are equal to zero at most observation in both RSS and SRS. A similar observation is found for the second data set. Thus, different methods of estimation under different criteria are used to determine the estimated parameters, CV test (CVT), AD test (ADT), K-ST, and p-values for the proposed model. They are presented in Table 4 and Table 5 for the two real data sets, respectively. Therefore, the only estimates in Table 4 and Table 5 are the ML, LS, WLS, CV, AD, and RTAD estimates.

Table 4. Different estimates of ${\tau }_1,{\tau }_2,\phi$ and $R^{◊◊}$ for Data sets I and II under the RSS and SRS.

Sampling	Parameter	ML	LS	WLS	CV	AD	RTAD
RSS	${\tau }_1$	0.0985	0.0364	0.02502	0.01995	0.08008	0.01273
	${\tau }_2$	0.0658	0.0215	0.01479	0.01095	0.0517	0.00782
	$\phi$	0.8061	1.1919	1.3158	1.42399	0.88302	1.57378
	$R^{◊◊}$	0.59954	0.62828	0.62844	0.64563	0.60768	0.61925
SRS	${\tau }_1$	0.0999	0.05228	0.04501	0.01016	0.1442	0.006
	${\tau }_2$	0.06654	0.02944	0.02361	0.00536	0.09	0.00367
	$\phi$	0.8119	1.05798	1.10582	1.6	0.69261	1.83009
	$R^{◊◊}$	0.60021	0.63978	0.65594	0.65453	0.61571	0.62078

Table 5. Goodness of fit measures by different estimation methods for Data sets I and II under the RSS and SRS.

Data	Method	Design	CVT	ADT	K-ST	p-Value
Data I (W)	ML	RSS	0.31307	1.77129	0.80208	0.19792
		SRS	0.35676	1.97197	0.83753	0.16247
	LS	RSS	0.58241	3.02593	0.59506	0.40494
		SRS	0.81977	4.03263	0.6442	0.3558
	WLS	RSS	0.68988	3.51439	0.64709	0.35291
		SRS	0.85842	4.21798	0.66789	0.33211
	CV	RSS	0.80507	4.03447	0.46013	0.5399
		SRS	1.19579	5.85561	0.8254	0.1746
	AD	RSS	0.31975	1.80642	0.80061	0.19939
		SRS	0.46097	2.52828	0.80468	0.19532
	RTAD	RSS	0.92209	4.56446	0.54294	0.45706
		SRS	1.33812	6.5031	0.6411	0.3589
Data II (Q)	ML	RSS	0.09068	0.52067	0.85594	0.14406
		SRS	0.11648	0.69209	0.92817	0.07183
	LS	RSS	0.17787	24.00754	0.44851	0.55149
		SRS	1.20519	25.88331	0.89192	0.10808
	WLS	RSS	0.24755	24.41183	0.52657	0.47343
		SRS	1.22362	26.32725	0.90168	0.09832
	CV	RSS	0.32337	24.82667	0.56885	0.43115
		SRS	0.57053	25.14119	0.94204	0.05796
	AD	RSS	0.07759	23.39339	0.16622	0.83378
		SRS	0.15845	23.91292	0.89778	0.10222
	RTAD	RSS	0.46001	2.58214	0.71077	0.28923
		SRS	0.78925	4.15739	0.94517	0.05483

From these data, we suppose a SRS of size $(n_1^{†},n_2^{†})=(20,20)$, whereas for the RSS, a small set size of $(n_w^{},n_q^{})=(2,2)$ is considered with cycles count being $a_w=a_q=10$. It is interesting to observe that the RSS and SRS are contrasted using the same quantity of measurement units. We determine the estimates of the parameters and reliability in each design using the preceding techniques with a perfect ranking. We use the previous criteria measures, i.e., CVT, ADT, K-ST, and p-value, to compare the different estimates from the two data sets.

The findings in Table 4 and Table 5 illustrate that the $R^{◊◊}$ estimates, via the RSS, are better than their equivalents in the SRS in terms of the smallest values of CVT, ADT, K-ST, and largest values of P–values, using the ML, LS, WLS, CV, AD, and RTAD methods.

8. Summary and Conclusions

In this paper, various estimation techniques for estimating the S-S reliability when both stress and strength random variables have the unit Gompertz distribution based on the RSS and SRS are covered. The methods that have been suggested include the maximum likelihood, least squares, weighted least squares, maximum product spacing, Cramér–von Mises, Anderson–Darling, and right tail Anderson–Darling methods. To assess the effectiveness of the proposed estimates based on both sampling designs, a simulation research is conducted. According to the results, for all the estimating techniques taken into consideration, the RSS estimates outperform the SRS estimates in terms of MSE, absolute bias, and efficiency values. The estimates based on the MPS have the smallest MSE for both sampling techniques. The reliability estimates based on the AD and RTAD methods have the largest MSE based on the SRS and RSS, respectively. Two real data sets that indicate the survival times of head and neck cancer patients have been used to provide further findings. Future research might look at the inference in a multicomponent S-S model based on the different RSS modifications.