Abstract
Tetrahedrane-derived compounds consist of n crossed quadrilaterals and possess complex three-dimensional structures with high symmetry and dense spatial arrangements. As a result, these compounds hold great potential for applications in materials science, catalytic chemistry, and other related fields. The Kirchhoff index of a graph G is defined as the sum of resistive distances between any two vertices in G. This article focuses on studying a type of tetrafunctional compound with a linear crossed square chain shape. The Kirchhoff index and degree Kirchhoff index of this compound are calculated, and a detailed analysis and discussion is conducted. The calculation formula for the Kirchhoff index is obtained based on the relationship between the Kirchhoff index and Laplace eigenvalue, and the number of spanning trees is derived for linear crossed quadrangular chains. The obtained formula is validated using Ohm’s law and Cayley’s theorem. Asymptotically, the ratio of Kirchhoff index to Wiener index approaches one-fourth. Additionally, the expression for the degree Kirchhoff index of the linear crossed quadrangular chain is obtained through the relationship between the degree Kirchhoff index and the regular Laplace eigenvalue and matrix decomposition theorem.
1. Introduction
The Kirchhoff index and the degree Kirchhoff index are important graph invariants that have been studied extensively in the field of graph theory. They have applications in various fields, including chemistry, physics, and computer science.
In 1993, Klein and Randi put forward the concept of resistive distance on graphs [1]. Various resistance distance calculation formulas such as classical algebraic formulas, probability formulas, combinatorial formulas and functional formulas are deduced one after another. The Kirchhoff index and degree Kirchhoff index discussed in this paper are defined using the resistance distance [2,3]. The Kirchhoff index refers to the sum of the resistance distances between all disordered point pairs in the graph, and it is also known as the total effective resistance [4]. Its research is of great significance in various aspects. For example, in chemistry, it describes the structural characteristics of molecules. In physics, it reflects the scale and connectivity of the network. Mathematically, the Kirchhoff index also occupies an important position. However, direct calculation of the resistance distance and Kirchhoff index is still very difficult, so it is necessary to obtain the Kirchhoff index formula. In the last two decades, many researchers have developed closed-form formulas for Kirchhoff indices for certain types of graphs [5,6,7,8,9,10]. In their study [5], Li et al. aimed to determine the normalized Laplacian spectrum of using new methods of decomposition theorem and elementary operations that were not previously stated in the existing literature. They then derived explicit formulas for both the degree Kirchhoff index and the number of spanning trees with respect to . These findings can offer valuable insights into the fundamental properties of a particular system and contribute to the development of more advanced materials or applications. Wang et al. investigated the Kirchhoff index of cyclopolyanenes in the literature [6]. They found that the ratio of the Kirchhoff index to the winner index of cyclopolyanenes was approximately 1/3. In their study [7], Liu et al. utilized the recursive method to compute the Kirchhoff index and degree-based Kirchhoff index of random cyclooctane chains. In their study [8], the authors utilized spectral graph theory to derive an exact formula for the Kirchhoff index of hypercube networks. Yang et al. studied the Nordhaus–Gaddum-type Kirchhoff index [9]. In another study [10], the authors proposed exact formulas for calculating the expected values of a random polyomino chain to construct the multiplicative and additive degree Kirchhoff indices. Additionally, they thoroughly examined the highest degree of the expected values through these indices. These formulas can potentially have applications in materials science and other related fields, providing insights into the fundamental properties of electric and heat conductivity in such systems. There is an inseparable relationship between the Kirchhoff index of the graph and the Laplace eigenvalue of the graph, and its value can be obtained by the Laplacian eigenvalue of the graph. In reference [11], Liu et al. used Laplace’s characteristic polynomial decomposition theorem to deduce the Kirchhoff index of a linear crossed quadrangular chain. Chen Haiyan and Zhang Fuji gave a new graph parameter based on resistance distance in 2007: degree Kirchhoff index [12]. It is closely related to the regular Laplacian spectrum, which can not only handle the spectral problem of the irregular graph very well, but also has a very close relationship with the random walk on the graph.
Studies on these indices have greatly extended their applications in different fields such as drug design, materials science, and network analysis. In their study [13], Liu et al. began by determining the normalized Laplacian spectra of . They then obtained the multiplicative degree Kirchhoff index and complexity corresponding to . Finally, by comparing these indices with the Wiener index and Gutman index, the researchers observed that the multiplicative degree Kirchhoff index of is nearly one-quarter of its Gutman Wiener index. In their work [14], Feng et al. investigated the Kirchhoff index of phenylenes. In another work [15], they studied the Kirchhoff index and the number of spanning trees of linear pentagonal derivation chains. Meanwhile the authors of [16] compared the winner index and Kirchhoff index of random pentane chains and obtained some conclusions. Yang studied the upper and lower bounds of the Kirchhoff index of planar graphs and fullerene graphs in the literature [17]. In another study [18], the authors derived closed-form formulas for the degree Kirchhoff index of pentagonal cylinders and Möbius chains. Additionally, they investigated the Gutman index and Schultz index of these graphs. These findings shed light on the fundamental properties of these structures, potentially contributing to the development of more advanced materials or applications. Despite their significance, there has been a limited understanding of the Kirchhoff index and the degree Kirchhoff index for complex molecular systems, especially for linear crossed quadrilateral chains. To address this knowledge gap, we aim to investigate the Kirchhoff index and the degree Kirchhoff index of linear crossed quadrilateral chains, which can provide insights into the structural and chemical properties of these systems. Our work builds on previous studies on the Kirchhoff index and the degree Kirchhoff index of other types of molecular systems. This paper deduced the Kirchhoff index of a linear crossed quadrangular chain, counted the formula of spanning tree, obtained its Wiener index, and pointed out that the limit of the ratio of its Kirchhoff index to its Wiener index is one-fourth.
The rest of this paper is organized as follows. Section 2 provides a brief overview of the methods used to calculate the Kirchhoff index and the degree Kirchhoff index. In Section 3 and Section 4, we present our results on the Kirchhoff index and the degree Kirchhoff index of linear crossed quadrilateral chains. Finally, we summarize our findings and discuss their implications in Section 5.
2. Preparations
The linear crossed quadrangular chains studied in this paper are all related to an undirected graph. The vertex set and edge set of graph G are expressed by V and E. A binary set consisting of a point set and an edge set is called graph G, namely [8]. The difference between the degree diagonal matrix D and the adjacency matrix A of a graph G is called the Laplacian matrix L of the graph, namely . The degree diagonal matrix D is a diagonal matrix that represents the degrees of each vertex in the graph G. Specifically, the diagonal elements of D are equal to the degree of each vertex, where the degree of a vertex is defined as the number of edges that are incident to the vertex. On the other hand, the adjacency matrix A is a matrix that represents the connections between vertices in the graph. The element of A is equal to 1 if there exists an edge between vertices i and j in the graph G, and 0 otherwise.
Definition 1
([19]). The normal Laplace matrix is defined as follows:
where denotes the degree of vertex and represents the normal Laplacian matrix of graph G.
Definition 2
([19]). Let the unit resistance be each edge of graph G, then the sum of the resistance distances of all pairs of vertices is called the Kirchhoff index of the graph G.
where represents the resistance distance between vertices i and j.
Definition 3
([20]). The sum of the distances between all point pairs is defined as the Wiener index, namely
where represents the shortest past between vertex and in graph G.
Lemma 1
([21]). Let be the corresponding Laplace and normal Laplace matrix, then the Laplace and normal Laplace decomposition theorem is
Lemma 2
([22]). Suppose a graph G is a simple graph, which has m edges and n vertices, then the intrinsic relationship between the number of spanning trees and the normal Laplace eigenvalues of graph G is
where denotes a spanning tree of graph G.
Lemma 3
([22]). Let G be a simple connected graph with m vertices and n edges. The relationship between the Kirchhoff index of a graph G and its normalized Laplacian eigenvalues is given by:
where is the eigenvalue of matrix .
Lemma 4
([5]). Let G be a simple connected graph with m vertices and n edges. The relationship between the degree Kirchhoff index of a graph G and its normalized Laplacian eigenvalues is given by:
where is the eigenvalue of matrix .
For symbols, definitions and lemmas that are not explained in the text, please refer to [20]. Let denote the characteristic polynomial of a matrix M of order n. Linear crossed quadrilateral chains can be obtained by adding edges to linear quadrilateral chains; that is, adding two pairs of sides to each quadrilateral, as shown in Figure 1.
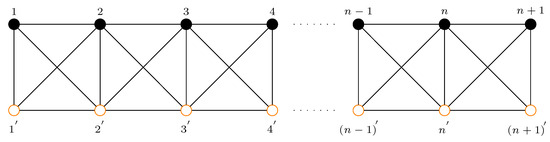
Figure 1.
Linear crossed quadrilateral chain.
It could be obtained from the graph that is an automorphic [23], and . So Laplacian and normal Laplacian matrices could be represented by the following block matrices: , and we have , . From the unitary transformation, we have , where is the transpose of P.
Thus,
3. Kirchhoff Indexes for Linear Crossed Quadrilateral Chains
According to the definition of Laplacian matrix, we could obtain the block matrix and as follows.
where . .
where , . From the formula, we can obtain
where , .
Suppose and are the roots of and , respectively. Note that if , . In other words, 0 is the eigenvalue of . From Lemma 3, we can obtain the following lemma.
Lemma 5.
Assume that is a linear crossed quadrilateral chain, then
According to the matrix , it is not difficult to obtain
Then, according to Lemma 3, we will focus on computing , where is the eigenvalue of matrix . Then, we obtain
From the above equation, we can conclude that are the roots of the following equation:
According to Vieta’s theorem [5], we can get
Two facts are given as follows [24].
Fact 1.
.
Proof.
For the convenience of description, the i-order main sub-matrix of matrix is expressed as . Let , then . To obtain the n-order main sub-matrix, we eliminate the last row and last column of . Afterward, we compute and obtain for . Further calculations reveal that .
Note that is equal to the sum of the determinants of all major submatrices of order n of matrix , namely,
where
Let . According to the structure of the symmetric matrix , we have , therefore
□
Fact 2.
.
Proof.
Note that is equal to the sum of the determinants of all major submatrices of order of matrix , namely,
where . If , we can get , so, . Note that
□
From Facts 1 and 2, the following equation can be obtained:
By substituting Formulas (21), (12) into (11), we can obtain the following theorem:
Theorem 1.

Assuming is a linear crossed quadrilateral chain, its Kirchhoff index is
Through calculation, we can obtain the partial value of the Kirchhoff index of the linear crossed quadrangular chain, as follows in Table 1.

Table 1.
Partial values of Kirchhoff indexes for linear crossed quadrilateral chains.
In the above table, we list the Kirchhoff indexes of , . Next, let us calculate the number of spanning trees.
Theorem 2.

Let be a linear crossed quadrilateral chains of length n. The number of distinct spanning trees of , denoted by , is given by the formula
Proof.
The number of spanning trees is calculated below in Table 2.Based on Lemma 2, we obtain
Then,
Based on the aforementioned analysis, we can obtain the value of .
□

Table 2.
Partial value of the number of spanning trees for a linearly crossed quadrilateral chain.
Experimental results have confirmed that when , the linear crossed quadrilateral chain forms a structure. According to Ohm’s law
we find the sum of the resistance distances of is 3, which represents the Kirchhoff index. According to Theorem 1, we can calculate the Kirchhoff index as follows: Using the Cayley formula, we can determine the number of spanning trees for : By applying Formula (24), the number of spanning trees for can also be derived as follows: Next, we can explore the ratio of the Kirchhoff index of to its Wiener index.
Theorem 3.
Assuming is a linear crossed quadrilateral chain, then
Proof.
For distance , when we calculate and discuss the Wiener index of , the choice of point i can be divided into the following two cases:
The first vertex of :
The vertex of , Therefore, we can conclude
Combining the expressions of and , we can get
□
4. Degree Kirchhoff Index of Linear Crossing Quadrilateral Chains
In this section, we first give the normal Laplace spectrum of and then solve the degree Kirchhoff index of . According to the definition of the normal Laplace matrix, we can conclude
, a diagonal matrix of order . Suppose and are the roots of and , respectively. Note that if , . In other words, 0 is an eigenvalue of . From Lemma 4, we can obtain the following lemma.
Lemma 6.
Suppose is a linear crossed quadrilateral chain, then
According to the matrix , it is not difficult to obtain
Next, we will concentrate on computing . are the eigenvalues of matrix . In that case, we can conclude
From the above equation, we can conclude that is the root of the following equation
Based on Vieta’s theorem, we can obtain
Two facts are given as follows.
Fact 3.
Proof.
The i-order principal submatrix of matrix is denoted as . Let , then and we can obtain ,
Note that is equal to the sum of the determinants of all major submatrices of order n of matrix , namely,
where,
Let . Since the similarity transformation does not change the determinant of the square matrix, we can conclude , then
□
Fact 4.
Proof.
Note that is equal to the sum of the determinants of all major submatrices of order of matrix , namely,
where
In summary, we can obtain
Based on Formula (29), all possible values of i and j are as follows.
By derivation, it is not difficult to obtain the following:
Case 1:
Case 2:
Case 3:
Case 4:
It is observed that Cases 3 and 4 are equal.
To sum up, the sum of the determinants of all primary and submatrices of order is
□
From Facts 3 and 4, the following equation can be obtained:
Substituting Formulas (30) and (43) into Formula (29), the following theorem can be obtained.
Theorem 4.

Assuming is a linear crossed quadrilateral chain. Its degree Kirchhoff index is
In Table 3 below, we list the degree Kirchhoff index of , .

Table 3.
Partial values of Kirchhoff indexes for linear crossed quadrilateral chain degrees.
5. Discussion
This article focuses on studying a type of tetrafunctional compound with a linear crossed square chain shape and its Kirchhoff index. The Kirchhoff index is an essential parameter for measuring electric and heat conductivity in materials science. The newly derived formula provides a more efficient way to calculate the Kirchhoff index of crossed quadrangular chains than previous methods. The proposed approach could potentially be extended to other graph structures, lending it great practical significance.
One limitation of this study is that it only applies to linear crossed quadrangular chains. More extensive graphs require further investigation. Another potential direction is to explore the relationship between the Kirchhoff index and other topological indices of graphs. Additionally, numerical simulations and experimental verification would help validate the theoretical results obtained in this study.
There are several potential areas for future work on this topic. Firstly, extending the proposed method to other complex structures would be a fruitful avenue for research. Secondly, investigating the interdependence between the Kirchhoff index and other parameters, such as the degree and diameter of the network, remains a crucial question. Thirdly, applying the Kirchhoff index to analyze the properties of real-world networks, such as social, transportation, and biological systems, would have significant implications in various fields. Finally, numerical simulations and empirical experiments are needed to confirm the theoretical results. Overall, the current research presents valuable insights into the fundamental characteristics of electric and heat conductivity in synthetic and natural systems, which could have broad implications for numerous applications.
6. Conclusions
In this research, we studied the Kirchhoff index in the context of a type of tetrafunctional compound with a linear crossed square chain shape. We utilized matrix theory and Laplace’s characteristic polynomial decomposition theorem to derive a precise formula for calculating the Kirchhoff index of a linear crossed quadrangular chain. Through comparative analysis with the Kirchhoff index obtained by applying Ohm’s law and the number of spanning trees calculated using Cayley’s theorem, we verified the accuracy of our formula.
Our findings reveal that the ratio of Kirchhoff index to Wiener index tends towards one-fourth in the asymptotic limit. This sheds new light on the relationship between the Kirchhoff index and other topological indices of graphs, such as the Wiener index. Overall, this study presents a new formula for calculating the Kirchhoff index of a specific type of tetrafunctional compound with a linear crossed square chain shape. This formula could potentially have applications in materials science and related fields, providing insights into the fundamental characteristics of electric and heat conductivity in such systems.
Author Contributions
Methodology, K.Z.; writing—original draft preparation, D.Z. and Y.Z.; supervision, X.L. and Z.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Natural Science Fund of Chizhou University Quality Engineering Project (2022XXSKC09), Chizhou University introduces doctoral research startup project (CZ2022YJRC08), Anhui Provincial Course Ideological and Political Education Teaching Team of 2020, Chizhou University Center for Applied Mathematics Research, Innovation and Entrepreneurship Training Program for college students in Anhui Province (S202211306114, S202211306134, 202211306105); Chizhou university research focus projects (CZ2023ZRZ04).
Data Availability Statement
The data is available within the manuscript.
Conflicts of Interest
The authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Klein, D.J.; Randi, M. Resistance distance. J. Math. Chem. 1993, 12, 81–95. [Google Scholar] [CrossRef]
- Ye, L. On the Kirchhoff index of some toroidal lattices. Linear Multilinear Algebra 2011, 59, 645–650. [Google Scholar] [CrossRef]
- Jing, Z.; JiaBao, L.; Sakander, H. Resistance distance-based graph invariants and the number of spanning trees of linear crossed octagonal graphs. Appl. Math. Comput. 2020, 63, 1865–2085. [Google Scholar]
- Wenrui, W. Kirchhoff Index and Degree Kirchhoff Index of Complete Multipartite Graph; Anhui University: Hefei, China, 2016. [Google Scholar]
- Liu, J.B.; Zhao, J.; Zhu, Z.; Cao, J. On the Normalized Laplacian and the Number of Spanning Trees of Linear Heptagonal Networks. Mathematics 2019, 7, 314. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, W. Kirchhoff Index of Cyclopolyacenes. Z. Naturforschung A 2010, 65, 865–870. [Google Scholar] [CrossRef]
- Liu, H.; WU, R.; You, L. Three Types of Kirchhoff Indices in the Random Cyclooctane Chains. J. South China Norm. Univ. 2021, 53, 96–103. [Google Scholar]
- Guanghui, W.; Jiabao, L.; Jinde, C.; XiangFeng, P.; Ahmed, E. The Kirchhoff Index of Hypercubes and Related Complex Networks. Discret. Dyn. Nat. Soc. 2007, 2013, 543189. [Google Scholar]
- Yang, Y.; Zhang, H. and Klein, Douglas J. New Nordhaus-Gaddum-type results for the Kirchhoff index. J. Math. Chem. 2011, 49, 1587–1598. [Google Scholar] [CrossRef]
- Mitsuhashi, H.; Morita, H.; Sato, I. Kirchhoff Index and Additive Kirchhoff Index Based on Multiplicative Degree for a Random Polyomino Chain. Symmetry 2023, 15, 718. [Google Scholar]
- Brualdi, R.A.; Ryser, H.J. Combinatorial Matrix Theory; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Huang, J.; Li, S.; Li., X. The normalized Laplacian, degree—Kirchhoff index and spanning trees of the linear polyomino chains. Appl. Math. Utation 2016, 289, 324–334. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, Q.; Cai, Z.; Hayat, S. On the Laplacians and Normalized Laplacians for Graph Transformation with Respect to the Dicyclobutadieno Derivative of [n] Phenylenes. Polycycl. Aromat. Compd. 2022, 42, 1413–1434. [Google Scholar] [CrossRef]
- Feng, Z.; Huang, S.; Yan, L. On the Kirchhoff Indices and the Numbers of Spanning Trees of Two Types of Molecular Graphs. Polycycl. Aromat. Compd. 2022, 42, 316–331. [Google Scholar] [CrossRef]
- Tu, Y.; Ma, X.; Zhang, Y.; Ren, J. On the Laplacian, the Kirchhoff Index, and the Number of Spanning Trees of the Linear Pentagonal Derivation Chain. Axioms 2022, 11, 278. [Google Scholar] [CrossRef]
- Wei, S.L.; Shiu, W.C.; Ke, X.L.; Huang, J.W. Comparison of the Wiener and Kirchhoff Indices of Random Pentachains. J. Math. 2021, 2021, 7523214. [Google Scholar] [CrossRef]
- Massimo, F.; Yang, Y.J. Some Bounds for the Kirchhoff Index of Graphs. Abstr. Appl. Anal. 2013, 2014, 1085–3375. [Google Scholar]
- Sahir, M.A.; Nayeem, S.M.A. On the degree-Kirchhoff index, Gutman index and the Schultz index of pentagonal cylinder/Möbius chain. arXiv 2023, arXiv:2302.07170. [Google Scholar]
- Aouchiche, M.; Hansen, P. Distance spectra of graphs: A survey. Linear Algebra Its Appl. 2014, 458, 301–386. [Google Scholar] [CrossRef]
- Muthuraman, S.; Rajkumar, R. Spectral analysis of weighted neighborhood networks. Discret. Math. Algorithms Appl. 2022, 2022, 2250141. [Google Scholar] [CrossRef]
- Jia, Y.; Du, J.; Zhang, W. Proceedings of the 2018 Chinese Intelligent Systems Conference Volume II; Springer: Singapore, 2019. [Google Scholar]
- Li, Z.; Xie, Z.; Li, J.; Pan, Y. Resistance distance-based graph invariants and spanning trees of graphs derived from the strong prism of a star. Appl. Math. Comput. 2020, 382, 125335. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, Z. Spectra, Hitting Times and Resistance Distances of q- Subdivision Graphs. Comput. J. 2019, 64, 76–92. [Google Scholar] [CrossRef]
- Pan, Y.; Liu, C.; Li, J. Kirchhoff Indices and Numbers of Spanning Trees of Molecular Graphs Derived from Linear Crossed Polyomino Chain. Polycycl. Aromat. Compd. 2022, 42, 218–225. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).