Sweeping Surfaces Due to Conjugate Bishop Frame in 3-Dimensional Lie Group

Abstract

In this work, we present a new Bishop frame for the conjugate curve of a curve in the 3-dimensional Lie group ${\mathbb{G}}_3$. With the help of this frame, we derive a parametric representation for a sweeping surface and show that the parametric curves on this surface are curvature lines. We then examine the local singularities and convexity of this sweeping surface and establish the sufficient and necessary conditions for it to be a developable ruled surface. Additionally, we provide detailed explanations and examples of its applications.

1. Introduction

The mutual appearances of algebra and geometry, which are two considerable topics of mathematics, are composed Lie groups in two shapes: as a Lie group, and as a differentiable manifold. Thus, the algebraic and geometric structure of Lie groups must be consistent with a specific technique. The treatise of Lie groups is great to the mutual new track to geometry. Therefore, there are considerable results on curves and surfaces in the 3-dimensional Lie group [1,2,3,4,5,6,7,8].

In the Euclidean 3-space, a sweeping surface is a surface that is traced from a section curve positioned over a path, which acts as the spine curve. Sweeping is an essential and famous tool that is utilized for geometric modeling. This idea depends on taking several geometrical topics (such as generators) that are moved along the spine curve (trajectory) in space. This evolution includes the movement in space with the deformation of intrinsic properties resulting in the sweep object. The type of the sweep objects is based on choosing both generators and trajectories. Therefore, sweeping the curve through another curve creates the sweeping surface. Many familiar names of sweeping surfaces are known such as tubular surface, pipe surface, string, as well as canal surface [9,10,11,12,13,14,15]. A considerable fact about sweeping surfaces is that they can be developable ruled surfaces [15]. Developable ruled surfaces are vastly applied in the industrial manufacturing of some non-expandable materials, such as leather, cloth, metal plate, etc. There can also be seen in modern automotive design, aircraft wing design and upper design. There are three types of developable ruled surfaces: cylinders, cones and tangent surfaces [15,16,17,18,19,20]. However, to the authors’ knowledge, there is no work devoted to discussing the conceptions of sweeping surfaces with conjugate curve of a curve in the 3-dimensional Lie group ${\mathbb{G}}_3$.

In this work, the geometry and kinematics of a sweeping surface with a conjugate curve of a curve is offered based on Bishop frame in 3-dimensional Lie group ${\mathbb{G}}_3$. The relations among the curvature lines and singularities of this surface are expressed in simple form with geometrical reasoning and demonstration. Then, we derived the sufficient and necessary conditions for the the sweeping surfaces to be a developable ruled surfaces. We also investigated the uniqueness and the singularities of such developable surfaces. Meanwhile, some examples are offered and explained in detail.

Hopefully, these results will drive a connection with the similarities among the theory of the sweeping surfaces in Euclidean 3-space and, with that, in the 3-dimensional Lie group.

2. Preliminaries

In this section, we present important concepts that we will employ in this paper (see [1,2,3,4,5,6,7,8,9,10]). Let $\mathbb{G}$ be a Lie group with a bi-invariant metric $<,>$, and ∇ be the Levi-Civita connection of $\mathbb{G}$. If $\mathfrak{g}$ indicates the Lie algebra of $\mathbb{G}$, then $\mathfrak{g}$ is isomorphic to $T_e\mathbb{G}$ where e is the identity (the neutral) element of $\mathbb{G}$. For any vector fields x, y, $\mathit{z}\in$$\mathfrak{g}$, we obtain:

$$<\mathit{x},[\mathit{y},\mathit{z}]>=-<\mathit{y},[\mathit{x},\mathit{z}]>,$$

and

$${\nabla }_{\mathit{x}}\mathit{y}=\frac{1}{2}[\mathit{x},\mathit{y}].$$

(1)

Let $\mathit{\gamma }:I\subset \mathbb{R}\to \mathbb{G}$ be an arc-length smooth curve (unit speed curve), and {${\mathit{e}}_1$, ${\mathit{e}}_2,\dots ,{\mathit{e}}_n$} be an orthonormal basis of $\mathfrak{g}$. In this case, any two vector fields x and y can be written as $\mathit{x}={\displaystyle \sum _{i=1}^n}{x}_i{\mathit{e}}_i$, and $\mathit{y}={\displaystyle \sum _{i=1}^n}{y}_i{\mathit{e}}_i$, where $y_i$, $x_i$: $I\to \mathbb{R}$ are smooth functions. The Lie bracket of x and y is

$$[\mathit{x},\mathit{y}]=\stackrel{n}{\underset{i,i=1}{\Sigma }}{x}_i{y}_j[{\mathit{e}}_i,{\mathit{e}}_j],$$

and the directional derivative of x on the curve $\mathit{\gamma }$ is as follows

$${\nabla }_{\mathit{t}}{\mathit{x}:=\mathit{x}}^{\prime }+\frac{1}{2}[\mathit{t},\mathit{x}];\left({}^{\prime }=\frac{d}{ds}\right),$$

(2)

where ${\mathit{t}=\mathit{\gamma }}^{\prime }=\frac{d\mathit{\gamma }}{ds}$, and ${\mathit{x}}^{\prime }=\stackrel{n}{\underset{i=1}{\Sigma }}{x}_i^{\prime }{\mathit{e}}_i$, where $x_i^{\prime }=\frac{d{x}_i}{ds}$. Note that if x is the left-invariant vector field to the curve, then ${\mathit{x}}^{\prime }=0$.

Let {$\mathit{t}\left(s\right)$, $\mathit{n}\left(s\right)$, $\mathit{b}\left(s\right)$, $\kappa \left(s\right)$, $\tau \left(s\right)$} denote the Serret–Frenet apparatus of the curve $\mathit{\gamma }\left(s\right)$ in ${\mathbb{G}}_3$; then it is easy to see that $\kappa \left(s\right)=∥{\mathit{x}}^{\prime }∥$ (see for details [1,2,3,4,5,6,7]).

Definition 1. 

There exists a differentiable function ${\tau }_G$ named Lie torsion realized by:

$${\tau }_G\left(s\right)=\frac{1}{2}<\mathit{t},[\mathit{n},\mathit{b}]>,$$

(3)

or

$${\tau }_G\left(s\right)=\frac{1}{2{\kappa }^2\tau }<{\mathit{t}}^{\prime \prime },[\mathit{t},{\mathit{t}}^{\prime }]>+\frac{1}{4{\kappa }^2\tau }{∥[\mathit{t},{\mathit{t}}^{\prime }]∥}^2.$$

(4)

Proposition 1. 

Consider $\mathit{\gamma }\left(s\right)$ to be an arc-length parametrized curve in ${\mathbb{G}}_3$. Then the following holds:

$$\begin{array}{ccc}\hfill [\mathit{t},\mathit{n}]=<\mathit{t},[\mathit{n},\mathit{b}]>\mathit{b}=& & 2{\tau }_G\left(s\right)\mathit{b},\hfill \\ \hfill [\mathit{b},\mathit{t}]=<[\mathit{b},\mathit{t}],\mathit{n}>\mathit{b}=& & 2{\tau }_G\left(s\right)\mathit{n},\hfill \\ \hfill [\mathit{n},\mathit{b}]=<[\mathit{n},\mathit{b}],\mathit{t}>\mathit{b}=& & 2{\tau }_G\left(s\right)\mathit{t}.\hfill \end{array}$$

Via Equation (2) and Proposition 1, the Serret–Frenet formula is

$${\nabla }_{\mathit{t}}\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right):=\left(\begin{array}{c}{\mathit{t}}^{\prime }\hfill \\ {\mathit{n}}^{\prime }\hfill \\ {\mathit{b}}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \hfill & 0\hfill \\ -\kappa \hfill & 0\hfill & \tau -{\tau }_G\hfill \\ 0\hfill & -\left(\tau -{\tau }_G\right)\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right),$$

(5)

where $\mathit{t}(s{)=\mathit{\gamma }}^{\prime }\left(s\right),$$\kappa \left(s\right)=∥{\nabla }_{\mathit{t}}\mathit{t}∥=∥{\mathit{t}}^{\prime }∥$, and $\tau \left(s\right)=∥{\nabla }_{\mathit{t}}\mathit{b}∥-{\tau }_G$ (see [1,2,3]).

Remark 1. 

Let $\mathbb{G}$ be a 3-dimensional Lie group with a bi-invariant metric. Then the following holds:

(1) If $\mathbb{G}$ is the special orthogonal group $\mathbb{SO}$(3), then ${\tau }_G=1/2$;

(2) If $\mathbb{G}$ is the special unitary group $\mathbb{SU}$(2), then ${\tau }_G=1$;

(3) If $\mathbb{G}$ is a commutative (Abelian) group, then ${\tau }_G=0$.

Lemma 1. 

For the unit speed curve $\mathit{\gamma }=\mathit{\gamma }\left(s\right)$, there is a unit speed conjugate mate curve $\mathit{\varphi }\left(s\right)=\int \mathit{b}(s)ds$ and the pair $\left\{\mathit{\gamma }\right(s)$, $\mathit{\varphi }\left(s\right)\}$ is named the conjugate pair [21].

Let $\{{\mathit{e}}_1\left(s\right)$, ${\mathit{e}}_2\left(s\right)$, ${\mathit{e}}_3\left(s\right)\}$ be the Serret–Frenet of $\mathit{\varphi }\left(s\right)$, then [21]:

$${\mathit{e}}_1\left(s\right)=\mathit{b}\left(s\right),{\mathit{e}}_2\left(s\right)=-\mathit{n}\left(s\right),\mathrm{and}{\mathit{e}}_3\left(s\right)=\mathit{t}\left(s\right).$$

(6)

The Serret–Frenet equations are as follows:

$$\left(\begin{array}{c}{\mathit{e}}_1^{{}^{\prime }}\hfill \\ {\mathit{e}}_2^{{}^{\prime }}\hfill \\ {\mathit{e}}_3^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \left(\tau -{\tau }_G\right)\hfill & 0\hfill \\ -\left(\tau -{\tau }_G\right)\hfill & 0\hfill & \kappa \hfill \\ 0\hfill & -\kappa \hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right)=\mathit{\omega }\times \left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right),$$

(7)

where $\mathit{\omega }\left(s\right)=\kappa \left(s\right){\mathit{e}}_1\left(s\right)+\left(\tau -{\tau }_G\right){\mathit{e}}_3\left(s\right)$ is the Darboux vector.

Definition 2. 

A movable frame $\{{\mathit{\upsilon }}_1,$${\mathit{\upsilon }}_2$, ${\mathit{\upsilon }}_3\}$ along the space curve, is named a rotation minimizing frame (RMF) or Bishop frame, with respect to ${\mathit{\upsilon }}_i$ ($i=1,$$2,$ 3) if its Darboux vector ω fulfills $<{\mathit{\omega },\mathit{\upsilon }}_i>=0$.

In view of Definition 2, the set $\{{\mathit{e}}_1\left(s\right)$, ${\mathit{e}}_2\left(s\right)$, ${\mathit{e}}_3\left(s\right)\}$ is RMF with respect to ${\mathit{e}}_2\left(s\right)$, but not with respect to the tangent ${\mathit{e}}_1\left(s\right)$ and the binormal ${\mathit{e}}_3\left(s\right)$. However, one can readily gain such an RMF from it. New normal plane vectors (${\mathit{\xi }}_1$,${\mathit{\xi }}_2$) are recognized through a rotation of (${\mathit{e}}_2$,${\mathit{e}}_3$) via

$$\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \end{array}\right)=\left(\begin{array}{ccc}1\hfill & 0\hfill & 0\hfill \\ 0\hfill & cos\psi \hfill & sin\psi \hfill \\ 0\hfill & -sin\psi \hfill & cos\psi \hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{e}}_2\hfill \\ {\mathit{e}}_3\hfill \end{array}\right),$$

(8)

with a certain angle $\psi \left(s\right)\ge 0$. Here, the set $\{{\mathit{e}}_1\left(s\right),$ ${\mathit{\xi }}_1\left(s\right)$, ${\mathit{\xi }}_2\left(s\right)\}$ is an RMF or conjugate Bishop frame (CBF). Then, we have

$$\left(\begin{array}{c}{\mathit{e}}_1^{{}^{\prime }}\hfill \\ {\mathit{\xi }}_1^{{}^{\prime }}\hfill \\ {\mathit{\xi }}_2^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & {\Gamma }_1\left(s\right)\hfill & -{\Gamma }_2\left(s\right)\hfill \\ -{\Gamma }_1\left(s\right)\hfill & 0\hfill & 0\hfill \\ {\Gamma }_2\left(s\right)\hfill & 0\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \end{array}\right)=\mathit{\varpi }\left(s\right)\times \left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \end{array}\right),$$

(9)

where $\mathit{\varpi }\left(s\right)={\Gamma }_2\left(s\right){\mathit{\xi }}_1\left(s\right)+{\Gamma }_1\left(s\right){\mathit{\xi }}_2\left(s\right)$ is the Darboux vector. One can show that

$$\left.\begin{array}{c}{\Gamma }_1\left(s\right)=\left(\tau -{\tau }_G\right)cos\psi ,{\Gamma }_2\left(s\right)=\left(\tau -{\tau }_G\right)sin\psi ,\hfill \\ \psi \left(s\right)={tan}^{-1}\left(\frac{{\Gamma }_2}{{\Gamma }_1}\right);{\Gamma }_1\left(s\right)\ne 0,\hfill \\ \psi \left(s\right)={\psi }_0-\underset{s_0}{\stackrel{s}{\int }}\kappa \left(s\right)ds,\mathrm{with}{\psi }_0=\psi \left(s_0\right).\hfill \end{array}\right\}$$

(10)

3. Sweeping Surfaces with Conjugate Bishop Frame

The conception of a sweeping surface is realized kinematically by a planar curve, movable through space such that the activity of any point on the surface is constantly orthogonal to the plane [8]. By utilizing the conjugate Bishop frame, the sweeping surface family that passes through $\mathit{\varphi }\left(s\right)$ is parametrized by

$$M:\mathit{q}(s,u)=\mathit{\varphi }\left(s\right)+A\left(s\right)\mathit{x}\left(u\right)=\mathit{\varphi }\left(s\right)+f\left(u\right){\mathit{\xi }}_1\left(s\right)+g\left(u\right){\mathit{\xi }}_2\left(s\right),$$

(11)

where $\mathit{p}\left(u\right)$ is the planar profile (cross-section) curve specified by $\mathit{p}\left(u\right)=(0,$${f\left(u\right),g\left(u\right))}^T$, the symbol ‘T’ appears as transposition, with the other parameter $u\in I\subseteq \mathbb{R}$. The orthogonal matrix $A\left(s\right)=\{{\mathit{e}}_1\left(s\right),{\mathit{\xi }}_1\left(s\right)$,${\mathit{\xi }}_2\left(s\right)\}$ designates the CBF over $\mathit{\varphi }\left(s\right)$. $\mathit{p}\left(u\right)$ is in the 2D or 3D space, which progress among the spine curve $\mathit{\varphi }\left(s\right)$ through sweeping. Evidently, the sweeping way leaves the designer with one degree of freedom, as it is still conceivable to rotate the Bishop frame.

Remark 2. 

Clearly, if $\mathit{\varphi }\left(s\right)$ is a circle, then the sweeping surface is a torus. If, on the other hand, $\mathit{\varphi }\left(s\right)$ is a straight line, the sweeping surface is a circular cylinder, having $\mathit{\varphi }\left(s\right)$ as a symmetry axis.

We now resolve the connection through regularity of $\mathit{\varphi }\left(s\right)$ and of the matching sweeping surface. However, we can put the profile curve p(u) as a unit speed curve, that is, ${\stackrel{.}{f}}^2+{\stackrel{.}{g}}^2=1$. In what follows, we employ a “dot” to indicate the differentiation regarding the arc-length parameter of the profile curve $\mathit{p}\left(u\right)$. Then, the tangent vectors and the unit normal vector to the surface, respectively, are:

$$\left.\begin{array}{c}{\mathit{q}}_s(s,u)=(1-f{\Gamma }_1+g{\Gamma }_2){\mathit{e}}_1,\\ {\mathit{q}}_u(s,u)=\stackrel{.}{f}{\mathit{\xi }}_1+\stackrel{.}{g}{\mathit{\xi }}_2,\end{array}\right\}$$

(12)

and

$$\mathbf{N}(s,u):=\frac{{\mathit{q}}_u\times {\mathit{q}}_s}{∥{\mathit{q}}_u\times {\mathit{q}}_s∥}=\stackrel{.}{g}{\mathit{\xi }}_1-\stackrel{.}{f}{\mathit{\xi }}_2.$$

(13)

Equation (13) shows that the surface normal $\mathit{N}(s,u)$ is lying in the osculating plane of the spine curve $\mathit{\gamma }\left(s\right)$, for it is orthogonal to b. Thus, the surface normal and the normal of the profile curve $\mathit{p}\left(u\right)$ are identical.

Proposition 2. 

Let p be a point in the osculating plane of the spine curve $\mathit{\varphi }\left(s\right)$. The tangent vector of its trajectory $\mathit{\varphi }\left(s\right)+A\left(s\right)\mathit{p}\left(u\right)$, that is traced by the Bishop frame, is constantly parallel to the binormal vector b.

From Equation (12) the coefficients of the first fundamental form $g_{11}$, $g_{12}$ and $g_{22}$ are

$$\left.\begin{array}{c}{g}_{11}=<{\mathit{q}}_{\mathit{s}},{\mathit{q}}_{\mathit{s}}>={(1-f{\Gamma }_1+g{\Gamma }_2)}^2,\hfill \\ g_{12}=<{\mathit{q}}_s,{\mathit{q}}_u>=0,g_{22}=<{\mathit{q}}_u,{\mathit{q}}_u>=1.\hfill \end{array}\right\}$$

Furthermore, we have

$$\left.\begin{array}{c}{\mathit{q}}_{ss}=\left(-f{\Gamma }_1^{{}^{\prime }}+g{\Gamma }_2^{{}^{\prime }}\right){\mathit{e}}_1+(1-f{\Gamma }_1+g{\Gamma }_2)({\Gamma }_1{\mathit{\xi }}_1-{\Gamma }_2{\mathit{\xi }}_2),\hfill \\ {\mathit{q}}_{su}=(-\stackrel{.}{f}{\Gamma }_1+\stackrel{.}{g}{\Gamma }_2){\mathit{e}}_1,\hfill \\ {\mathit{q}}_{uu}=\stackrel{..}{f}{\mathit{\xi }}_1+\stackrel{..}{g}{\mathit{\xi }}_2.\hfill \end{array}\right\}$$

(14)

Then, the second fundamental forms $h_{11}$, $h_{12}$, and $h_{22}$ are

$$\left.\begin{array}{c}{h}_{11}=<{\mathit{q}}_{ss},\mathit{N}>=(1-f{\Gamma }_1+g{\Gamma }_2)({\Gamma }_1\stackrel{.}{g}+\stackrel{.}{f}{\Gamma }_2),\hfill \\ h_{12}=<{\mathit{q}}_{su},\mathit{N}>=0,h_{22}=<{\mathit{q}}_{uu},\mathit{N}>=\stackrel{.}{g}\stackrel{..}{f}-\stackrel{.}{f}\stackrel{..}{g}.\hfill \end{array}\right\}$$

Hence, the u and s curves of M are curvature lines, that is, $g_{12}=0$ and $h_{12}=0$. Thus, the isoparametric curve

$$\pi \left(u\right):\mathit{\zeta }\left(u\right):=\mathit{q}(u,s_0)=\mathit{\gamma }\left(s_0\right)+f\left(u\right){\mathit{\xi }}_1\left(s_0\right)+g\left(u\right){\mathit{\xi }}_2\left(s_0\right),$$

(15)

is a planar unit speed curvature line. Equation (15) realizes a one-parameter family of planes in ${\mathbb{G}}_3$. The unit tangent vector to $\mathit{\zeta }\left(u\right)$ is

$${\mathit{t}}_{\zeta }\left(u\right)=\stackrel{.}{f}\left(u\right){\mathit{\xi }}_1\left(s_0\right)+\stackrel{.}{g}\left(u\right){\mathit{\xi }}_2\left(s_0\right).$$

Thus, the unit principal normal vector of the curve $\mathit{\zeta }\left(u\right)$ is given by

$${\mathit{n}}_{\zeta }\left(u\right)={\mathit{t}}_{\zeta }\left(u\right)\times {\mathit{e}}_1\left(s_0\right)=\stackrel{.}{g}{\mathit{\xi }}_1-\stackrel{.}{f}{\mathit{\xi }}_2=\mathit{N}(s_0,u).$$

(16)

So, the surface normal $\mathit{N}(s_0,u)$ is parallel to the principal normal ${\mathit{n}}_{\zeta }\left(u\right)$, that is, the curve $\mathit{\zeta }\left(u\right)$ is a geodesic planar curvature line. Surfaces whose parametric curves are curvature lines have various applications in geometric design [12,13,14]. In the case of sweeping surfaces, one has to calculate the offset surfaces ${\mathit{q}}_{\rho }(u,s)=\mathit{q}(u,s)+\rho \mathit{n}(s_0,u)$ of a given surface $\mathit{q}(u,s)$ at a certain distance $\rho$. Consequently, the offsetting procedure for a sweeping surface can be turned into the offsetting of a planar profile curve, which is far easier to deal with. Hence, we can state the following proposition:

Proposition 3. 

Consider a sweeping surface Equation (11). Let ${\mathit{p}}_{\rho }\left(u\right)$ be the planar offset of the profile $\mathit{p}\left(u\right)$ at distance ρ. Then the offset surface ${\mathit{q}}_{\rho }(u,s)$ is still a sweeping surface, traced by the spine curve $\mathit{\varphi }\left(s\right)$ and profile curve ${\mathit{p}}_{\rho }\left(u\right)$.

3.1. Singularity and Convexity

Singularities and convexity are useful for the ownerships of sweeping surfaces and are analyzed in the following: M has singular points if and only if

$$∥{\mathit{q}}_u\times {\mathit{q}}_s∥=1-f{\Gamma }_1+g{\Gamma }_2=0,$$

from which we find

$$\chi \left(s\right)-fcos\psi +gsin\psi =0,$$

(17)

where $\chi \left(s\right)={\left(\tau -{\tau }_G\right)}^{-1}$ is the radius of curvature of $\mathit{\varphi }\left(s\right)$. From Equation (17), it follows that singular points only happen when

$$f=\chi \left(s\right)cos\psi ,\mathrm{and}g=-\chi \left(s\right)sin\psi .$$

(18)

Then, there is only one singular (striction) curve given by

$$c\left(s\right)=\mathit{\varphi }\left(s\right)+\chi \left(s\right)\left(cos\psi {\mathit{\xi }}_1\left(s\right)-sin\psi {\mathit{\xi }}_2\left(s\right)\right).$$

(19)

Note that, the singular points happen at the intersection through the profile curve $\mathit{p}=\mathit{p}\left(u\right)$, and the curvature axis (spinning axis), that is,

$$L\left(u\right)=\left\{\right(f,g)\mid \chi (s)-fcos\psi +gsin\psi =0\}.$$

Thus, the sweeping surface has a 2nd order contact with the revolution surface forming by rotating the profile curve $\mathit{p}=\mathit{p}\left(u\right)$ around $L\left(u\right)$. Hence, we attain the following corollary:

Corollary 1. 

The sweeping surface M Equation (11), has singular points if the following condition

$$\chi \left(s\right)-fcos\psi +gsin\psi =0,$$

is satisfied for all s, and u.

In Computer Aided Geometric Design, the conditions that warrant the convexity of a surface are wanted in various applications (such as manufacturing of sculptured surfaces, or layered manufacturing). In the case of the sweeping surface, however, the convexity can be controlled with the assistance of the differential geometric properties. Therefore, we research the Gaussian curvature $K(s,u)={ϵ}_1{ϵ}_2$; ${ϵ}_i(s,u)$ ($i=1,2$) are the principal curvatures, as follows: Since $g_{12}=h_{12}=0$, the value of one principal curvature is:

$${ϵ}_1(s_0,u)=\frac{∥\stackrel{.}{\mathit{p}}\times \stackrel{..}{\mathit{p}}∥}{{∥\stackrel{.}{\mathit{p}}∥}^2}=\stackrel{.}{f}\stackrel{..}{g}-\stackrel{.}{g}\stackrel{..}{f}.$$

(20)

The curvature of the isoparametric s-curves (u-constant) is:

$$ϵ(s,u_0)=\frac{∥{\mathit{q}}_s\times {\mathit{q}}_{ss}∥}{{∥{\mathit{q}}_s∥}^2}=\frac{1}{\chi \left(s\right)-fcos\psi +gsin\psi }.$$

(21)

Furthermore, from Equations (8) and (16), we have:

$$\mathit{N}(s,u)=cos\phi {\mathit{e}}_2+sin\phi {\mathit{e}}_3,\mathrm{with}\phi (s,u)={tan}^{-1}\left(\frac{\stackrel{.}{g}sin\psi -\stackrel{.}{f}cos\psi }{\stackrel{.}{g}cos\psi +\stackrel{.}{f}sin\psi }\right).$$

(22)

In view of Meusnier’s Theorem, ${ϵ}_2(s,u)$ is linked with $ϵ(s,u)$ as [9,10]:

$${ϵ}_2(s,u)=ϵ(s,u)cos\phi .$$

(23)

Hence, the Gaussian curvature $K(s,u)$ can be created as:

$$K(s,u)={ϵ}_1(s,u)ϵ(s,u)cos\phi .$$

(24)

We now attempt to locate the curves on M that are created by parabolic points, that is, points with $K(s,u)=0$. These curves separate elliptic ($K>0$, locally convex) and hyperbolic ($K<0$, hence non-convex) parts of the surface. Then, from Equation (24), it follows that:

$$K(s,u)=0\iff {ϵ}_1(s,u)ϵ(s,u)cos\phi =0.$$

(25)

Then, there exists three cases which define parabolic points:

Case (1) exists when ${ϵ}_1=0$. If ${ϵ}_1=0$, the profile curve $\mathit{p}=\mathit{p}\left(u\right)$ turns into a straight line; from Equation (20), it can be seen that

$${ϵ}_1=0\iff \stackrel{.}{\mathit{p}}\times \stackrel{..}{\mathit{p}}=\mathbf{0}\iff \stackrel{.}{\mathit{p}}\Vert \stackrel{..}{\mathit{p}},$$

which shows that an inflection or flat point $\mathit{p}=\mathit{p}\left(u\right)$ forms a parabolic curve $s=$ const. on parts of the sweeping surface.

Case (2) exists when $ϵ(s,u)=0$. This leads to an inflection or flat point of the spine curve, producing an isoparametric parabolic curve $u=$ const. on the sweeping surface.

Case (3) exists when $\phi =\pi /2$. Owing to Equation (22), these parabolic curves are qualified by

$$\stackrel{.}{g}cos\psi +\stackrel{.}{f}sin\psi =0.$$

(26)

is satisfied for all s, and u. In this case, the spine curve $\mathit{\varphi }$ is not only a curvature line but also an asymptotic curve on the sweeping surface. By integration of Equation (26), the following can be gained

$$gcos\psi +fsin\psi =\sigma \left(s\right),$$

where $\sigma =\sigma \left(s\right)$ is an arbitrary function. Then we have the relations

$$f=\sigma \left(s\right)sin\psi ,g=\sigma \left(s\right)cos\psi .$$

(27)

When Equation (27) is utilized for Equation (11), we find that the parabolic curve is

$$z\left(s\right)=\mathit{\varphi }\left(s\right)+\sigma \left(s\right)\left(sin\psi {\mathit{\xi }}_1\left(s\right)+cos\psi {\mathit{\xi }}_2\left(s\right)\right).$$

(28)

From the above analysis, the following conclusions can be reached.

Corollary 2. 

Let M be a sweeping surface Equation (11) with spine and profile curves having non-vanishing curvatures anywhere. Then, M has only one parabolic curve if and only if the spine curve is an asymptotic and curvature line.

Example 1. 

Given the circle

$$\mathit{\gamma }\left(s\right)=(coss,sins,0),0\le s\le 2\pi .$$

Via Lemma 1, Equations (6) and (9), for this curve,

$$\begin{array}{ccc}\hfill \mathit{t}(s)& =& (-sins,coss,0),\mathit{n}(s)=(-coss,-sins,0),\hfill \\ \hfill \mathit{b}(s)& =& (0,0,1),\mathit{\varphi }\left(s\right)=(0,0,s),\hfill \\ \hfill \kappa \left(s\right)& =& 1,\tau \left(s\right)=0,{\tau }_G\left(s\right)=\frac{1}{2},\psi \left(s\right)=-s,\hfill \\ \hfill {\Gamma }_1\left(s\right)& =& \frac{1}{2}coss,{\Gamma }_2\left(s\right)=\frac{1}{2}sins.\hfill \end{array}$$

The CBF $\{{\mathit{e}}_1\left(s\right)$, ${\mathit{\zeta }}_1\left(s\right)$, ${\mathit{\zeta }}_2\left(s\right)$} is

$$\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 0\hfill & 1\hfill \\ -sins\hfill & -coss\hfill & 0\hfill \\ coss\hfill & -sins\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right).$$

Then,

$${\mathit{e}}_1=\left(1,0,0\right),{\mathit{\xi }}_1=\left(0,1,0\right),{\mathit{\xi }}_2=\left(0,0,1\right).$$

If $\mathit{p}\left(u\right)=(cosu,sinu,0)$, then the sweeping surface in $\mathbb{SO}$(3) with the spine curve $\mathit{\varphi }\left(s\right)$ is given by

$$M:\mathit{q}(s,t)=\left(cosu,sinu,s\right).$$

where $0\le s$, $u\le 2\pi$ (Figure 1).

Example 2. 

Given a helix

$$\mathit{\gamma }\left(s\right)=\frac{1}{\sqrt{2}}(coss,sins,s),0\le s\le 2\pi .$$

For this curve,

$$\begin{array}{ccc}\hfill \mathit{t}\left(s\right)& =& \frac{1}{\sqrt{2}}(-sins,coss,1),\mathit{n}\left(s\right)=(-coss,-sins,0),\hfill \\ \hfill \mathit{b}\left(s\right)& =& \frac{1}{\sqrt{2}}(sins,-coss,1),\mathit{\varphi }\left(s\right)=\frac{1}{\sqrt{2}}(-coss,-sins,s),\hfill \\ \hfill \kappa \left(s\right)& =& \tau \left(s\right)=\frac{1}{\sqrt{2}},{\tau }_G\left(s\right)=0,\psi \left(s\right)=-\frac{s}{\sqrt{2}},\hfill \\ \hfill {\Gamma }_1\left(s\right)& =& -\frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}},{\Gamma }_2\left(s\right)=-\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}.\hfill \end{array}$$

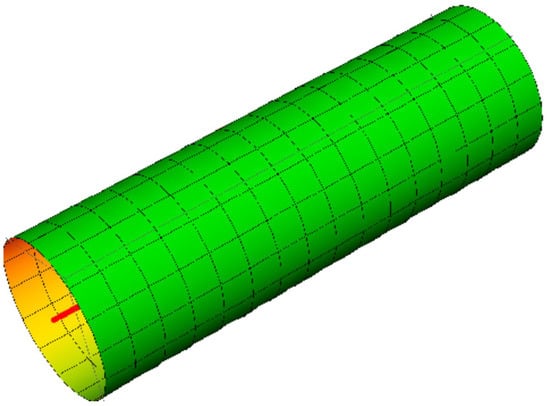
Figure 1. M withits spine curve $\mathit{\varphi }\left(s\right)$.

The CBF $\{{\mathit{e}}_1\left(s\right)$, ${\mathit{\zeta }}_1\left(s\right)$, ${\mathit{\zeta }}_2\left(s\right)$} is

$$\left(\begin{array}{c}{\mathit{e}}_1\hfill \\ {\mathit{\xi }}_1\hfill \\ {\mathit{\xi }}_2\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 0\hfill & 1\hfill \\ -sin\frac{s}{\sqrt{2}}\hfill & -cos\frac{s}{\sqrt{2}}\hfill & 0\hfill \\ cos\frac{s}{\sqrt{2}}\hfill & -sin\frac{s}{\sqrt{2}}\hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathit{t}\hfill \\ \mathit{n}\hfill \\ \mathit{b}\hfill \end{array}\right).$$

Then,

$$\begin{array}{ccc}\hfill {\mathit{\xi }}_1& =& \left(\begin{array}{c}{\mathit{\xi }}_{11}\hfill \\ {\mathit{\xi }}_{12}\hfill \\ {\mathit{\xi }}_{13}\hfill \end{array}\right)=\left(\begin{array}{c}\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}sins+cosscos\frac{s}{\sqrt{2}}\hfill \\ -\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}coss+sinscos\frac{s}{\sqrt{2}}\hfill \\ -\frac{1}{\sqrt{2}}sin\frac{s}{\sqrt{2}}\hfill \end{array}\right),\hfill \\ \hfill {\mathit{\xi }}_2& =& \left(\begin{array}{c}{\mathit{\xi }}_{21}\hfill \\ {\mathit{\xi }}_{22}\hfill \\ {\mathit{\xi }}_{23}\hfill \end{array}\right)=\left(\begin{array}{c}-\frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}sins+cosssin\frac{s}{\sqrt{2}}\hfill \\ \frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}coss+sinssin\frac{s}{\sqrt{2}}\hfill \\ \frac{1}{\sqrt{2}}cos\frac{s}{\sqrt{2}}\hfill \end{array}\right).\hfill \end{array}$$

In view of the Equation (19), the singular curve is (Figure 2):

$$\mathit{c}\left(s\right)=\left(\left(-\frac{1}{\sqrt{2}}+1\right)coss,\left(-\frac{1}{\sqrt{2}}+1\right)sins,\frac{s}{\sqrt{2}}\right).$$

If $\mathit{p}\left(u\right)=(cosu,sinu,0)$, the sweeping surface in the commutative (Abelian) group with the spine curve $\mathit{\varphi }\left(s\right)$ is given by

$$M:\mathit{q}(s,u)=\frac{1}{\sqrt{2}}(-coss,-sins,s)+\left(\begin{array}{c}{\mathit{\xi }}_{11}\hfill \\ {\mathit{\xi }}_{12}\hfill \\ {\mathit{\xi }}_{13}\hfill \end{array}\right)cosu+\left(\begin{array}{c}{\mathit{\xi }}_{21}\hfill \\ {\mathit{\xi }}_{22}\hfill \\ {\mathit{\xi }}_{23}\hfill \end{array}\right)sinu,$$

which has various singularities on the striction curve (blue), see Figure 3; $0\le s$, $u\le 2\pi$.

Figure 2. $\mathit{c}\left(u\right)$ has no singular points.

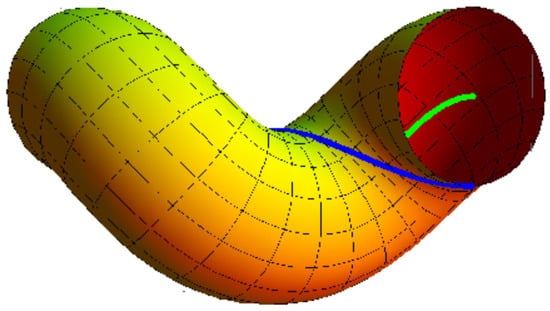
Figure 3. M has singularities along $\mathit{c}\left(s\right)$.

3.2. Developable Surfaces

Developable surface can be simply realized as a special case of the ruled surface. The significance of the developable surface lies in the reality that it is utilized in many sectors of manufacturing and engineering, including modeling of apparel, automobile combinations, and ship hulls (see, e.g., [8,9,10,11]). Then, we check the case where the profile curve $\mathit{p}=\mathit{p}\left(u\right)$ is turned into a line; that is, $\mathit{p}\left(u\right)=(0,0,u)$. Then, Equation (11) turns into

$$d:\mathit{x}(s,u)=\mathit{\varphi }\left(s\right)+u{\mathit{\xi }}_2\left(s\right),u\in \mathbb{R}.$$

(29)

It is evident that d is a developable ruled surface; that is,

$$\det ({\mathit{\varphi }}^{{}^{\prime }}\left(s\right),{\mathit{\xi }}_2\left(s\right),{\mathit{\xi }}_2^{{}^{\prime }}\left(s\right))=0.$$

Via Proposition 2, all tangent vectors ${\mathit{x}}_s(s,u)$ are parallel to $\mathit{b}\left(s\right)$. The rulings of d are curvature lines as well.

Proposition 4. 

If the profile curve $\mathit{p}\left(u\right)$ turns into a straight line, then the sweeping surface is a developable surface.

From Equation (11), we also have the following developable surface

$$d^{\perp }:{\mathit{x}}^{\perp }(s,u)=\mathit{\varphi }\left(s\right)+u{\mathit{\zeta }}_1\left(s\right),u\in \mathbb{R}.$$

(30)

Simply, we can show that $\mathit{x}(s,0)=\mathit{\varphi }\left(s\right)$ (${\mathit{x}}^{\perp }(s,0)=\mathit{\varphi }\left(s\right)$), $0\le s\le L$; that is, the surface d ($d^{\perp }$) interpolates the curve $\mathit{\varphi }\left(s\right)$. Also, since

$${\mathit{x}}_s\times {\mathit{x}}_u:=\left(1+u{\Gamma }_2\right){\mathit{\zeta }}_1\left(s\right),$$

(31)

then, $d^{\perp }$ is the normal developable surface of d along $\mathit{\varphi }\left(s\right)$. Thus, the surface d ($d^{\perp }$) interpolates the curve $\mathit{\varphi }\left(s\right)$, and $\mathit{\varphi }\left(s\right)$ is a curvature line of d ($d^{\perp }$).

Theorem 1. 

Let M be the sweeping surface Equation (11). Then,

(1) the developable surfaces d and $d^{\perp }$ interrelated along $\mathit{\varphi }\left(s\right)$ at a right angle,

(2) the curve $\mathit{\varphi }\left(s\right)$ is a mutual curvature line of d and $d^{\perp }$.

Theorem 2. 

(Existence and uniqueness). Under the above notions, there exists a unique developable surface Equation (29).

Proof. 

For the existence, we have the developable Equation (29). However, since d is a ruled surface, we may assume that

$$\left.\begin{array}{c}d:\mathit{x}(s,u)=\mathit{\varphi }\left(s\right)+u\mathit{e}\left(s\right),u\in \mathbb{R},\hfill \\ \\ \mathit{e}\left(s\right)=r_1\left(s\right){\mathit{\xi }}_1+r_2\left(s\right){\mathit{\xi }}_2+r_3\left(s\right)\mathit{b},\hfill \\ \\ {∥\mathit{e}\left(s\right)∥}^2=r_1^2+r_2^2+r_3^2=1,{\mathit{e}}^{{}^{\prime }}\left(s\right)\ne \mathbf{0}.\hfill \end{array}\right\}$$

(32)

It can be seen that d is developable if and only if

$$det({\mathit{\varphi }}^{{}^{\prime }},{\mathit{e},\mathit{e}}^{{}^{\prime }})=0\iff r_1{r}_2^{{}^{\prime }}-r_2{r}_1^{{}^{\prime }}-r_3\left(\tau -{\tau }_G\right)\left(r_{1}cos\psi +r_{2}sin\psi \right)=0.$$

(33)

However, as in Equation (31), we have:

$$\left({\mathit{x}}_s\times {\mathit{x}}_u\right)\left(s,u\right)=-\omega \left(s,u\right){\mathit{\xi }}_1,$$

(34)

where $\omega =\omega \left(s,u\right)$ is a regular function. Further, the normal vector ${\mathit{x}}_s\times {\mathit{x}}_u$ at the point $(s,0)$ is

$$\left({\mathit{x}}_s\times {\mathit{x}}_u\right)(s,0)=-r_2{\mathit{\xi }}_1+r_1{\mathit{\xi }}_2.$$

(35)

Thus, from Equations (34) and (35), one finds that:

$$r_1=0,\mathrm{and}{r}_2=\omega \left(s,0\right),$$

(36)

Thus, Equation (33) shows that $r_2{r}_3\left(\tau -{\tau }_G\right)sin\psi =0$, this is equivalent to $r_2{r}_3=0$, with $\tau -{\tau }_G\ne 0$. If $(s,0)$ is a regular point (i.e., $\omega \left(s,0\right)\ne 0$), then $r_2\left(s\right)\ne 0$, and $r_3=0$. This means that $e\left(s\right)\Vert {\mathit{\xi }}_2\left(s\right)$.

Now, if d has a singular point at $(s_0,0)$, then $\omega \left(s_0,0\right)=r_1\left(s_0\right)=r_3\left(s_0\right)=0$, and $\mathit{e}\left(s_0\right)=r_2\left(s_0\right){\mathit{\xi }}_2\left(s_0\right)$. Let the singular point $\mathit{\varphi }\left(s_0\right)$ be in the closure of the set of points where d is developable along $\mathit{\varphi }\left(s\right)$, which is regular, then there exists a point $\mathit{\varphi }\left(s\right)$ in any neighborhood of $\mathit{\varphi }\left(s_0\right)$ such that the uniqueness of d holds at $\mathit{\varphi }\left(s\right)$. Passing to the limit $s\to s_0$ is the uniqueness of the developable at $s_0$. Suppose that J$\subseteq I$ is an open interval such that d is singular at $\mathit{\varphi }\left(s\right)$ for any $s\in J$. Then, $x(s,u)=\mathit{\varphi }\left(s\right)+u{r}_2\left(s\right){\mathit{\xi }}_2\left(s\right)$ for any $s\in J$. This means that $r_1\left(s\right)=r_3\left(s\right)=0$ for $s\in J$. It obeys that

$$\left(x_s\times x_u\right)(s,u)=\left(\tau -{\tau }_G\right)u{r}_2^2\left(cos\psi {\xi }_2+sin\psi {\xi }_1\right).$$

Thus, $\left({\mathit{x}}_s\times {\mathit{x}}_u\right)\Vert {\mathit{\xi }}_1\left(s\right)$ if and only if $\psi =\pi /2$ for any $s\in J$. In this case, $\mathit{e}\left(s\right)=\pm {\mathit{\xi }}_2$. This means that uniqueness holds. □

As an implementation, such as flank milling or cylindrical milling, through the movement of the type-2 Bishop frame, we put a cylindrical cutter which is linked with this frame. Then, the equation of a group of cylindrical cutters, which is located by the movement of cylindrical cutter over $\mathit{\varphi }\left(s\right)$, can be shown as follows:

$$d_{\rho }:\overline{\mathit{x}}(s,u)=\mathit{x}(s,u)+\rho {\mathit{\xi }}_1\left(s\right),$$

(37)

where $\rho$ indicates the cylindrical cutter radius. The surface $d_{\rho }$ is an offset of the surface $x(s,u)$. The equation of $d_{\rho }$, can then be written as

$$d_{\rho }:\overline{\mathit{x}}(s,u)=\mathit{\varphi }\left(s\right)+u{\mathit{\xi }}_2\left(s\right)+\rho {\mathit{\xi }}_1\left(s\right).$$

(38)

The vector normal is:

$${\mathit{n}}_{\rho }(s,0)=\frac{{\overline{\mathit{x}}}_s\times {\overline{\mathit{x}}}_u}{∥{\overline{\mathit{x}}}_s\times {\overline{\mathit{x}}}_u∥}={\mathit{\xi }}_1(s).$$

(39)

From Equation (38), we also have:

$$d:\mathit{x}(s,u)=\overline{\mathit{x}}(s,u)-\rho {\mathit{\xi }}_1\left(s\right).$$

(40)

Thus, partial derivative ${\overline{\mathit{x}}}_s(s,u)$ can be gained as follows:

$${\overline{\mathit{x}}}_s(s,u)={\mathit{x}}_s(s,u)-\left(\rho \mathit{\varpi }\right)\times {\mathit{\xi }}_1,$$

(41)

which shows the vector ${\overline{\mathit{x}}}_s(s,u)$ is orthogonal to ${\mathit{\xi }}_1$. Additionally, the vector ${\mathit{\xi }}_1$ is orthogonal to the tool axis vector $\mathit{b}\left(s\right)$. As a result of this equation, the envelope surface of the cylindrical cutter and the developable surface $\mathit{x}(s,u)$ have a mutual normal vector, and the distance between the two surfaces is equal to the radius of the cylindrical cutter, denoted by $\rho$.

Proposition 5. 

Let d be the developable surface Equation (29), and if $d_{\rho }$ being the envelope surface of the cylindrical cutter at distance ρ, then the two developable surfaces d and $d_{\rho }$ are offset developable surfaces.

We designate $\Gamma \left(s\right)$ to represent ${\Gamma }_i\left(s\right)$$(i=1,$ 2), and by using Theorem 4.1 in [20], we can give the following:

Theorem 3. 

Let d($d^{\perp }$) be the developable surface Equations (29) and (30). Then,

(1) Surface d($d^{\perp }$) is locally diffeomorphic to Cuspidal edge at $(s_0,u_0)$ if and only if $\Gamma \left(s_0\right)=0$, and ${\Gamma }^{\prime }\left(s_0\right)\ne 0$.

(2) Surface d($d^{\perp }$) is locally diffeomorphic to Swallowtail at $(s_0,t_0)$ iff ${\Gamma }^{-1}\left(s_0\right)\ne 0$, ${\Gamma }^{\prime }\left(s_0\right)=0$, and ${\left({\Gamma }^{-1}\left(s_0\right)\right)}^{\prime \prime }\ne 0$.

Example 3. 

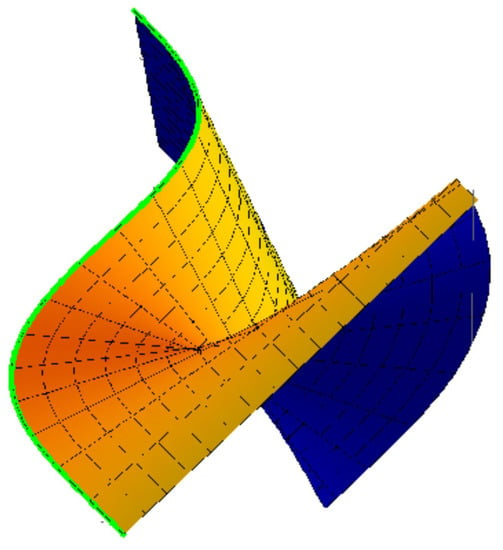
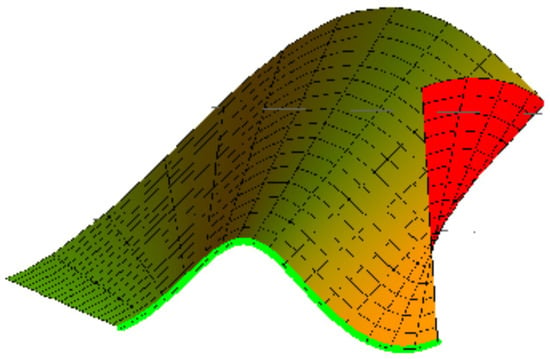
Based on Example 2, we have: (1) If $s_0=0$, then ${\Gamma }_2\left(s_0\right)=0$, and ${\Gamma }_2^{{}^{\prime }}\left(s_0\right)\ne 0$. The developable surface

$$d^{\perp }:{\mathit{x}}^{\perp }(s,u)=(-\frac{1}{\sqrt{2}}coss+u{\xi }_{21},-\frac{1}{\sqrt{2}}sins+u{\xi }_{21},\frac{1}{\sqrt{2}}s+u{\xi }_{21}).$$

is locally diffeomorphic to Cuspidal edge, see Figure 4; $0\le s\le 2$, and $-3\le u\le 3.$

Figure 4. Locally diffeomorphic to Cuspidal edge.

(2) If $s_0=0$, then ${\Gamma }_1\left(s_0\right)\ne 0$, ${\Gamma }_1^{\prime }\left(s_0\right)=0$, and ${\left({\Gamma }_1^{-1}\left(s_0\right)\right)}^{\prime \prime }\ne 0$. The developable surface

$$d:x(s,u)=\frac{1}{\sqrt{2}}(-coss+u{\xi }_{11},-sins+u{\xi }_{12},s+u{\xi }_{13}).$$

is locally diffeomorphic to Swallowtail, see Figure 5; $0\le s\le 2\pi$, and $-3\le u\le 3$.

Figure 5. Locally diffeomorphic to Swallowtail.

Notice that the developable surfaces d and $d^{\perp }$ intersect along $\mathit{\varphi }\left(s\right)$ at $\pi /2$, as can be seen in Figure 6.

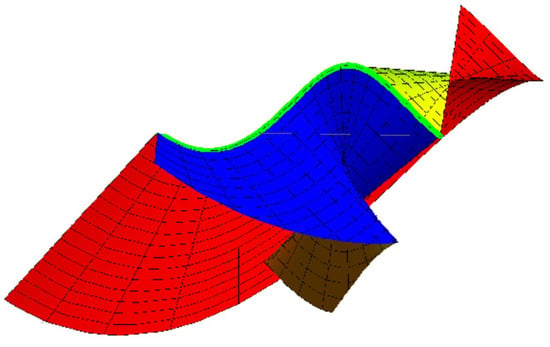
Figure 6. $d\cup d^{\perp }$.

4. Conclusions

A sweeping surface is a surface that is traced from a section curve positioned along a path, which acts as the spine curve, and it has symmetrical properties. In this study, we have parametrized sweeping surfaces with the conjugate mate curve of a spatial curve in the 3-dimensional Lie group ${\mathbb{G}}_3$. We showed that the parametric curves on these surfaces are curvature lines. Additionally, we derived sufficient and necessary conditions for this surface to be a developable ruled surface. In particular, we focused on the discussion of the singularities of this developable. Furthermore, we provide some representative examples.

There are several opportunities for further work. The authors plan to extend the study to different spaces and examine the classification of singularities as in [20,21,22,23,24,25,26,27,28].