p-Numerical Semigroups of Generalized Fibonacci Triples

Abstract

For a nonnegative integer p, we give explicit formulas for the p-Frobenius number and the p-genus of generalized Fibonacci numerical semigroups. Here, the p-numerical semigroup $S_p$ is defined as the set of integers whose nonnegative integral linear combinations of given positive integers $a_1,a_2,\dots ,a_k$ are expressed in more than p ways. When $p=0$, $S_0$ with the 0-Frobenius number and the 0-genus is the original numerical semigroup with the Frobenius number and the genus. In this paper, we consider the p-numerical semigroup involving Jacobsthal polynomials, which include Fibonacci numbers as special cases. We can also deal with the Jacobsthal–Lucas polynomials, including Lucas numbers accordingly. An application on the p-Hilbert series is also provided. There are some interesting connections between Frobenius numbers and geometric and algebraic structures that exhibit symmetry properties.

1. Introduction

Given the set of positive integers $A:=\{a_1,a_2,\dots ,a_k\}$ ($k\ge 2$), for a nonnegative integer p, let $S_p$ be the set of integers whose nonnegative integral linear combinations of given positive integers $a_1,a_2,\dots ,a_k$ are expressed in more than p ways. For some backgrounds of the number of representations, see, e.g., [1,2,3,4,5]. For a set of nonnegative integers ${\mathbb{N}}_0$, the set ${\mathbb{N}}_0\backslash S_p$ is finite if and only if $gcd(a_1,a_2,\dots ,a_k)=1$. Then there exists the largest integer $g_p\left(A\right):=g\left(S_p\right)$ in ${\mathbb{N}}_0\backslash S_p$, which is called the p-Frobenius number. The cardinality of ${\mathbb{N}}_0\backslash S_p$ is called the p-genus and is denoted by $n_p\left(A\right):=n\left(S_p\right)$. The sum of the elements in ${\mathbb{N}}_0\backslash S_p$ is called the p-Sylvester sum and is denoted by $s_p\left(A\right):=s\left(S_p\right)$. This kind of concept is a generalization of the famous Diophantine problem of Frobenius ([6,7,8]) since $p=0$ is the case when the original Frobenius number $g\left(A\right)=g_0\left(A\right)$, the genus $n\left(A\right)=n_0\left(A\right)$ and the Sylvester sum $s\left(A\right)=s_0\left(A\right)$ are recovered. $S_p$ can then be called the p-numerical semigroup. Strictly speaking, when $p\ge 1$, $S_p$ does not include 0, since the integer 0 has only one representation, so it satisfies simply additivity and the set $S_p\cup \left\{0\right\}$ becomes a numerical semigroup. For numerical semigroups, we refer to [9,10,11].

Additionally, there exist different extensions of the Frobenius number and genus, even in terms of the number of representations called denumerant. For example, some consider $S_p^{*}$ as the set of integers whose nonnegative integral linear combinations of given positive integers $a_1,a_2,\dots ,a_k$ are expressed in exactly p ways (see, e.g., [12,13]). Consequently, the corresponding p-Frobenius number $g_p^{*}\left(A\right)$ is the largest integer that has exactly p distinct representations. However, in this case, $g_p^{*}\left(A\right)$ does not necessarily increase as p increases. For example, when $A:=\{2,5,7\}$, $g_{17}^{*}(2,5,7)=43>g_{18}^{*}(2,5,7)=42$. In addition, for some p, $g_p^{*}$ may not exist. For example, $g_{22}^{*}(2,5,7)$ does not exist because there is no positive integer whose number of representations is exactly 22. Similarly, the p-genus may be also defined in different ways. For example, $n_p^{*}\left(A\right)$ can be defined as the cardinality of $[{\ell }_p\left(A\right),g_p\left(A\right)+1]\backslash S_p\left(A\right)$, where ${\ell }_p\left(A\right)$ is the least element of $S_p\left(A\right)$. However, in our definition of $n_p\left(A\right)$ as the cardinality of $[0,g_p\left(A\right)+1]\backslash S_p\left(A\right)$, one can use the convenient formula arising from the p-Apéry set in order to obtain $n_p\left(A\right)$. See the next section for detail.

In [14], numerical semigroups generated by $\{a,a+b,a{F}_{k-1}+b{F}_k\}$ are considered. Using a technique of Johnson [15], the Frobenius numbers of such semigroups are found as a generalization of the result by Marin et al. [16].

In this paper, for a positive integer v, we treat with Jacobsthal polynomials $J_n\left(v\right)$, defined by the recurrence relation $J_n\left(v\right)=J_{n-1}\left(v\right)+v{J}_{n-2}\left(v\right)$ ($n\ge 2$) with $J_0\left(v\right)=0$ and $J_1\left(v\right)=1$ (see, e.g., [17] (Chapter 44)). When $v=1$, $F_n=J_n\left(1\right)$ are Fibonacci numbers. When $v=2$, $J_n=J_n\left(2\right)$ are Jacobsthal numbers. Then, we give explicit formulas of p-Frobenius numbers for $A:=\{a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\}$, where a and b are positive integers with $gcd(a,b)=1$ and $a,k\ge 3$. If $a=J_i\left(v\right)$ and $b=J_{i+1}\left(v\right)$, then by $v{J}_i\left(v\right)J_{k-1}\left(v\right)+J_{i+1}\left(v\right)J_k\left(v\right)=J_{i+k}\left(v\right)$, we get $A=\{J_i\left(v\right),J_{i+2}\left(v\right),J_{i+k}\left(v\right)\}$. Hence, the results in [18] are recovered as special cases. In addition, if $v=1$, the results in [16,19] are recovered as special cases.

For $k=2$, that is, the case of two variables, closed formulas are explicitly given for $g_0\left(A\right)$ ([8]), $n_0\left(A\right)$ ([6]) and $s_0\left(A\right)$ ([20]; its extension [21]). However, for $k\ge 3$, the Frobenius number cannot be given by any set of closed formulas which can be reduced to a finite set of certain polynomials ([22]). For $k=3$, various algorithms have been devised for finding the Frobenius number ([15,23,24]). Some inexplicit formulas for the Frobenius number in three variables can be seen in [25]. Even in the original case of $p=0$, it is very difficult to give a closed explicit formula of any general sequence for three or more variables (see, e.g., [24,26,27,28]). Indeed, it is even more difficult when $p>0$. However, finally, we have succeeded in obtaining the p-Frobenius number in triangular numbers [29] and repunits [30] as well as Fibonacci and Lucas triplets [19] and Jacobsthal triples [18] quite recently.

It is well-known that the Fibonacci sequence exhibits a certain symmetry property known as self-similarity, where the pattern of the sequence repeats itself in smaller and smaller scales. There are some interesting connections between Frobenius numbers and geometric and algebraic structures that exhibit symmetry properties ([31,32,33]), some of which are found in this paper. In the context of Lotka–Volterra models, the Frobenius number may be relevant in determining the stability of equilibria or the number of limit cycles in the system. This can in turn affect the occurrence of bifurcations. In addition, the Frobenius number may be used in models that seek to predict the behavior of financial markets based on historical data.

The structure of the paper is as follows. In Section 2, we prepare a concept for the p-Apéry set and convenient formulas using its elements, which we will use afterwards. In Section 3, we prove the main theorem about the p-Frobenius number on Jacobsthal polynomials. We first set up the structure of the p-Apéry set when $p=0$ and, based on it, we determine the structures of the p-Apéry set when $p=1,2,\dots$. Once the structure of the p-Apéry set is known, the formula prepared in Section 2 is used to find the p-Frobenius number. By looking at the tables in Section 3, one will have a better understanding of how the p-Frobenius number is found. In Section 4, by using the structure of the p-Apéry set discussed in Section 3 and the formula prepared in Section 2, we find the p-genus. In a similar manner, we can also find the p-Sylvester number but we leave it out as the result will only be complicated. In Section 4, we show the corresponding results with respect to the Jacobsthal–Lucas polynomials. In Section 5, we give an application concerning the p-Hilbert series that play an important role in the numerical semigroup. In Section 6, we discuss future works.

2. Preliminaries

We introduce the Apéry set (see [34]) below in order to obtain the formulas for $g_p\left(A\right)$, $n_p\left(A\right)$ and $s_p\left(A\right)$ technically. Without loss of generality, we assume that $a_1=min\left(A\right)$.

Definition 1.

Let p be a nonnegative integer. For a set of positive integers $A=\{a_1,a_2,\dots ,a_k\}$ with $gcd\left(A\right)=1$ and $a_1=min\left(A\right)$ we denote by

$${\mathrm{Ap}}_p\left(A\right)={\mathrm{Ap}}_p(a_1,a_2,\dots ,a_k)=\{m_0^{\left(p\right)},m_1^{\left(p\right)},\dots ,m_{a_1-1}^{\left(p\right)}\},$$

the p-Apéry set of A, where $m_i^{\left(p\right)}$ is the least positive integer of $S_p\left(A\right)$, satisfying $m_i^{\left(p\right)}\equiv i(mod{a}_1)$$(0\le i\le a_1-1)$ (that is, $m_i^{\left(p\right)}\in S_p\left(A\right)$ and $m_i^{\left(p\right)}-a_1\notin S_p\left(A\right)$). Note that $m_0^{\left(0\right)}$ is defined to be 0.

It follows that, for each p,

$${\mathrm{Ap}}_p\left(A\right)\equiv \{0,1,\dots ,a_1-1\}\left(\mathrm{mod}{a}_1\right).$$

Even though it is hard to find any explicit form of $g_p\left(A\right)$ as well as $n_p\left(A\right)$ and $s_p\left(A\right)$ when $k\ge 3$, by using convenient formulas established in [35,36], we can obtain such values for some special sequences $(a_1,a_2,\dots ,a_k)$ after finding any regular structure of $m_j^{\left(p\right)}$ is hard enough in general. One of the applicable formulas is on the power sum

$$s_p^{\left(\mu \right)}\left(A\right):=\sum _{n\in {\mathbb{N}}_0\backslash S_p\left(A\right)}{n}^{\mu }$$

by using Bernoulli numbers $B_n$ defined by the generating function

$$\frac{x}{e^x-1}=\sum _{n=0}^{\infty }{B}_n\frac{x^n}{n!},$$

and another applicable formula is on the weighted power sum ([37,38])

$$s_{\lambda ,p}^{\left(\mu \right)}\left(A\right):=\sum _{n\in {\mathbb{N}}_0\backslash S_p\left(A\right)}{\lambda }^n{n}^{\mu }$$

by using Eulerian numbers $⟨\genfrac{}{}{0pt}{}{n}{m}⟩$ appearing in the generating function

$$\sum _{k=0}^{\infty }{k}^n{x}^k=\frac{1}{{(1-x)}^{n+1}}\sum _{m=0}^{n-1}⟨\genfrac{}{}{0pt}{}{n}{m}⟩x^{m+1}(n\ge 1)$$

with $0^0=1$ and $⟨\genfrac{}{}{0pt}{}{0}{0}⟩=1$. Here, $\mu$ is a nonnegative integer and $\lambda \ne 1$. From these formulas, many useful expressions are yielded as special cases. Some useful ones are given as follows. Formulas (2) and (3) are entailed from $s_{\lambda ,p}^{\left(0\right)}\left(A\right)$ and $s_{\lambda ,p}^{\left(1\right)}\left(A\right)$, respectively.

Lemma 1.

Let k, p and μ be integers with $k\ge 2$, $p\ge 0$ and $\mu \ge 1$. Assume that $gcd(a_1,a_2,\dots ,a_k)=1$. We have

$$\begin{array}{cc}\hfill g_p(a_1,a_2,\dots ,a_k)& =\left(\underset{0\le j\le a_1-1}{max}{m}_j^{\left(p\right)}\right)-a_1,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill n_p(a_1,a_2,\dots ,a_k)& =\frac{1}{a_1}\sum _{j=0}^{a_1-1}{m}_j^{\left(p\right)}-\frac{a_1-1}{2},\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill s_p(a_1,a_2,\dots ,a_k)& =\frac{1}{2a_1}\sum _{j=0}^{a_1-1}{\left(m_j^{\left(p\right)}\right)}^2-\frac{1}{2}\sum _{j=0}^{a_1-1}{m}_j^{\left(p\right)}+\frac{a_1^2-1}{12}.\hfill \end{array}$$

(3)

Remark 1.

When $p=0$, the formulas (1)–(3) reduce to the formulas by Brauer and Shockley [39] [Lemma 3], Selmer [40] [Theorem], and Tripathi [41] [Lemma 1] (there was a typo but it was corrected in [42]), respectively:

$$\begin{array}{cc}\hfill g(a_1,a_2,\dots ,a_k)& =\left(\underset{0\le j\le a_1-1}{max}{m}_j\right)-a_1,\hfill \\ \hfill n(a_1,a_2,\dots ,a_k)& =\frac{1}{a_1}\sum _{j=0}^{a_1-1}{m}_j-\frac{a_1-1}{2},\hfill \\ \hfill s(a_1,a_2,\dots ,a_k)& =\frac{1}{2a_1}\sum _{j=0}^{a_1-1}{\left(m_j\right)}^2-\frac{1}{2}\sum _{j=0}^{a_1-1}{m}_j+\frac{a_1^2-1}{12},\hfill \end{array}$$

where $m_j=m_j^{\left(0\right)}$ ($1\le j\le a_1-1$) with $m_0=m_0^{\left(0\right)}=0$.

3. Main Results

Determine integers q and r by $a=q{J}_k\left(v\right)+r$ with $0\le r<J_k\left(v\right)$. The function $⌊x⌋$ denotes the largest integer that does not exceed x.

Theorem 1.

Let a and b be positive integers with $a\ge 3$ and $gcd(a,b)=1$. Then, for a positive integer $k\ge 3$, and $0\le p\le ⌊a/J_k\left(v\right)⌋$ we have

$$\begin{array}{cc}\hfill & g_p\left(a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}(a-1)b+a\left(v(r-1)-1\right)+\frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}+p\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill & \\ ifa<J_k\left(v\right)or(va+b)r>va\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right);\hfill & \\ (a-r-1)b+va(J_k\left(v\right)-J_{k-1}\left(v\right)-1)-a+\frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}\hfill & \\ +p\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)ifa\ge J_k\left(v\right)and(va+b)r<va\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right),\hfill \end{array}\right.\hfill \end{array}$$

where $r=a-⌊a/J_k\left(v\right)⌋J_k\left(v\right)$.

For example, if $k=3$ and $v=1$, then for $0\le p\le ⌊a/2⌋$ we have

$$\begin{array}{cc}\hfill & g_p(a,a+b,a{F}_2+b{F}_3)\hfill \\ \hfill & =\left\{\begin{array}{cc}(a-1)b+{\displaystyle \frac{a(a-3)}{2}}+p(a+2b)\hfill & \mathrm{if}a\mathrm{is}\mathrm{odd};\hfill \\ (a-1)b+{\displaystyle \frac{a(a-2)}{2}}+p(a+2b)\hfill & \mathrm{if}a\mathrm{is}\mathrm{even}.\hfill \end{array}\right.\hfill \end{array}$$

3.1. The Case $p=0$

In this triple $\{a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\}$, we can use the similar framework to one in [18] to construct the elements of the p-Apéry set. Nevertheless, it is very important to see that such a framework is not always possible. For example, referring to [29] may call for a different structure. No structure has been analyzed for most other triples, so no explicit formula has been found for them.

Consider the expression

$$t_{y,z}:=y(va+b)+z\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right).$$

We see that $q=⌊a/J_k\left(v\right)⌋$. Then all the elements in the 0-Apéry set are represented as in Table 1.

Table 1. ${\mathrm{Ap}}_0(a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))$.

$t_{0,0}$	⋯	⋯	⋯	$t_{J_k\left(v\right)-1,0}$
$t_{0,1}$	⋯	⋯	⋯	$t_{J_k\left(v\right)-1,1}$
⋮				⋮
$t_{0,q-1}$	⋯	⋯	⋯	$t_{J_k\left(v\right)-1,q-1}$
$t_{0,q}$	⋯	$t_{r-1,q}$

Since $t_{i+1,j}-t_{i,j}\equiv b(moda)$ and $t_{0,j+1}-t_{J_k\left(v\right)-1,j}\equiv b(moda)$, the sequence

$$\begin{array}{cc}\hfill & t_{0,0},t_{1,0},\dots ,t_{J_k\left(v\right)-1,0},t_{0,1},t_{1,1},\dots ,t_{J_k\left(v\right)-1,1},\dots \hfill \\ \hfill & t_{0,q-1},t_{1,q-1},\dots ,t_{J_k\left(v\right)-1,q-1},t_{0,q},\dots ,t_{r-1,q}\hfill \end{array}$$

is equivalent to the sequence ${\{\ell b(moda)\}}_{\ell =0}^{a-1}$ in a way that keeps this order completely. Since $gcd(a,b)=1$ (otherwise, $gcd\left(A\right)>1$), all the elements appearing in Table 1 constitute a complete residue system modulo $a\left(=q{J}_k\left(v\right)+r\right)$.

It is clear that the largest element in ${\mathrm{Ap}}_0\left(A\right)$, where $A:=\{a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\}$, is $t_{r-1,q}$ or $t_{J_k\left(v\right)-1,q-1}$. If $a<J_k\left(v\right)$, by $q=0$, the largest element is $t_{r-1,q}=t_{a-1,q}$. Otherwise, by $q>0$, compare two values. The inequality $t_{r-1,q}>t_{J_k\left(v\right)-1,q-1}$ holds if and only if $(va+b)r>va\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$. Hence, if $(va+b)r>va\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$, then by Lemma 1 (1) we have

$$\begin{array}{cc}\hfill g_0\left(A\right)& =t_{r-1,q}-a\hfill \\ \hfill & =(a-1)b+a\left(v(r-1)-1\right)+\frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}.\hfill \end{array}$$

If $(va+b)r<va\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$, then we have

$$\begin{array}{cc}\hfill g_0\left(A\right)& =t_{J_k\left(v\right)-1,q-1}-a\hfill \\ \hfill & =(a-r-1)b+va(J_k\left(v\right)-J_{k-1}\left(v\right)-1)-a+\frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}.\hfill \end{array}$$

Note that $(va+b)r\ne vs.a\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$ because $gcd(a,b)=1$.

3.2. The Case $p=1$

We assume that $a\ge J_k\left(v\right)$ from now on. If $a<J_k\left(v\right)$, the situation becomes more and more complicated by requiring a lot of case-by-case discussion for $p\ge 1$. So, the discussion that follows does not apply.

All the elements in ${\mathrm{Ap}}_1\left(A\right)$ can be determined from those in ${\mathrm{Ap}}_0\left(A\right)$. Only those elements that have the same residue modulo a as those in the top row of ${\mathrm{Ap}}_0\left(A\right)$ are arranged in order in the form of filling gaps under the same block. Elements that have the same residue modulo a as the other elements of ${\mathrm{Ap}}_0\left(A\right)$ are arranged in a row shift up to the immediately adjacent block. This is shown in Table 2.

Table 2. ${\mathrm{Ap}}_1\left(A\right)$ from ${\mathrm{Ap}}_0\left(A\right)$.

This fact is supported by the congruence relationships

$$\begin{array}{cc}\hfill t_{y,z}& \equiv t_{y+J_k\left(v\right),z-1}(moda)\hfill \\ \hfill & (0\le y\le J_k\left(v\right)-1,0\le z\le q-1;0\le y\le r-1,z=q),\hfill \\ \hfill t_{y,0}& \equiv t_{y+r,q}(moda)(0\le y\le J_k\left(v\right)-r-1),\hfill \\ \hfill t_{J_k\left(v\right)-r+y,0}& \equiv t_{y,q+1}(moda)(0\le y\le r-1).\hfill \end{array}$$

In addition, each element of ${\mathrm{Ap}}_1\left(A\right)$ has two representations in terms of a, $va+b$ and $va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)$, because

$$\begin{array}{cc}\hfill t_{y+J_k\left(v\right),z-1}& =\left(y+J_k\left(v\right)\right)(va+b)+(z-1)\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =v\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)a+y(va+b)+z\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right),\hfill \\ \hfill t_{y+r,q}& =(y+r)(va+b)+q\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =\left(va+b-q\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)\right)a+y(va+b),\hfill \\ \hfill t_{y,q+1}& =y(va+b)+(q+1)\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =\left(va+b-(q+1)v^2{J}_{k-2}\left(v\right)\right)a+\left(y+J_k\left(v\right)-r\right)(va+b).\hfill \end{array}$$

Notice that $(va+b-q\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)>0$ and $va+b-(q+1)v^2{J}_{k-2}\left(v\right)>0$ because $a=q{J}_k\left(v\right)+r$ and $J_k\left(v\right)=J_{k-1}\left(v\right)+v{J}_{k-2}\left(v\right)$.

There are four candidates to take the largest value in ${\mathrm{Ap}}_1\left(A\right)$:

$$t_{r-1,q+1},t_{J_k\left(v\right)-1,q},t_{J_k\left(v\right)+r-1,q-1},t_{2J_k\left(v\right)-1,q-2}.$$

However, since $2vs.a{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)>va{J}_k\left(v\right)$, we can see that $t_{r-1,q+1}>t_{J_k\left(v\right)+r-1,q-1}$ and $t_{J_k\left(v\right)-1,q}>t_{2J_k\left(v\right)-1,q-2}$. In addition, $t_{r-1,q+1}>t_{J_k\left(v\right)-1,q}$ if and only if $(va+b)r>va\left(J_k\left(v\right)-J_{k-2}\left(v\right)\right)$. Hence, if $(va+b)r>a\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$, then by Lemma 1 (1) we have

$$\begin{array}{cc}\hfill g_1\left(A\right)& =t_{r-1,q+1}-a\hfill \\ \hfill & =(a-1)b+a\left(v(r-1)-1\right)+{\displaystyle \frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}}+\left(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right).\hfill \end{array}$$

If $(va+b)r<a\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)$, then we have

$$\begin{array}{cc}\hfill g_1\left(A\right)& =t_{J_k\left(v\right)-1,q}-a\hfill \\ \hfill & =(a-r-1)b+va(J_k\left(v\right)-J_{k-1}\left(v\right)-1)-a\hfill \\ \hfill & +\frac{va(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}+(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)).\hfill \end{array}$$

3.3. The Case $p\ge 2$

When $p\ge 2$, in a similar manner, each element of ${\mathrm{Ap}}_p\left(A\right)$ is determined by the corresponding element with the same residue modulo a in ${\mathrm{Ap}}_{p-1}\left(A\right)$. In each block with a lateral length of $J_k\left(v\right)$, the elements in the top row in ${\mathrm{Ap}}_{p-1}\left(A\right)$ are arranged in order to fill the gap below the left-most block in ${\mathrm{Ap}}_p\left(A\right)$. The other elements of ${\mathrm{Ap}}_{p-1}\left(A\right)$ are shifted directly to the right block by one in ${\mathrm{Ap}}_p\left(A\right)$.

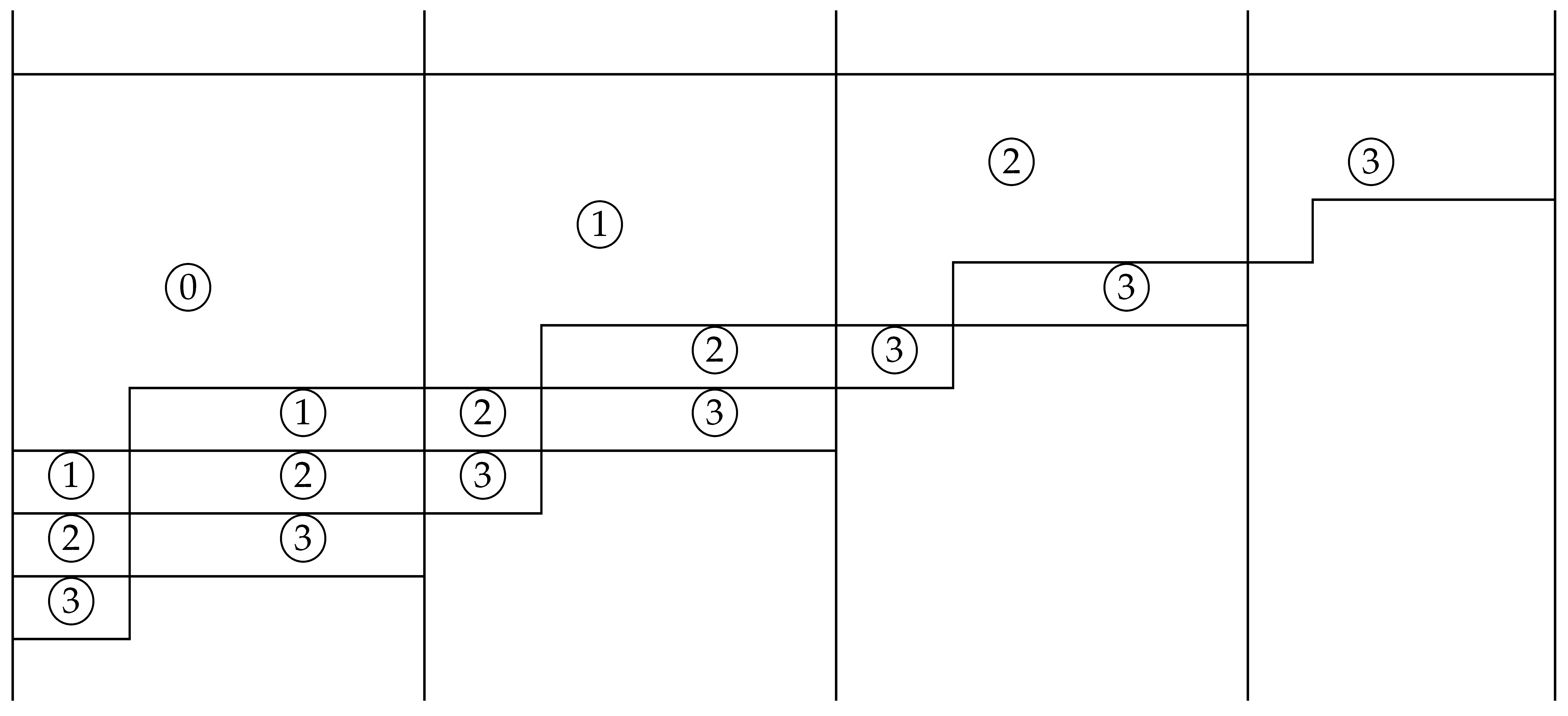
In Table 3, denotes the area of elements in Ap_n(A). Here, each $m_j^{\left(n\right)}$, satisfying $m_j^{\left(n\right)}\equiv j (\mathrm{mod} a)(0\le j\le a-1)$, can be expressed in at least n + 1 ways but $m_j^{\left(n\right)}-a$ in at most n ways. Each element of Ap₃(A) existing in the second block to the fourth block corresponds to each element having the same residue of Ap₂(A) existing in the block immediately to the left thereof in a form of shifting up one step. The J_k(v) elements of Ap₃(A) existing over two rows (or one row) at the bottom of the first block correspond to the J_k(v) elements with the same residue of Ap₂(A) at the top of the third block. Therefore, since all the elements in Ap₂(A) form a complete remainder system, so is Ap₃(A). It can be shown that all the elements of Ap₃(A) have exactly four ways of being expressed in terms of a, va + b and vaJ_k−1(v) + bJ_k(v). Within each region of Ap₃(A), one of the two leftmost (lower left) elements t_r−1,q+3 and t_{Jk(v)−1,q+2} is the largest so, by comparing these elements, the largest element of Ap₃(A) can be determined.

Table 3. ${\mathrm{Ap}}_p\left(A\right)$ ($p=0,1,2,3$) for $q\ge 3$.

Such a structure of ${\mathrm{Ap}}_p\left(A\right)$ continues as long as $p\le ⌊a/J_k\left(v\right)⌋=q$. Eventually, the largest element in ${\mathrm{Ap}}_p\left(A\right)$ is $t_{r-1,q+p}$ or $t_{J_k\left(v\right)-1,q+p-1}$. However, when $p=⌊a/J_k\left(v\right)⌋+1$, this kind of regularity is broken. Therefore, regularity cannot be maintained even for the largest value of ${\mathrm{Ap}}_p\left(A\right)$. Therefore, Theorem 1 is proved. Table 4 shows the arrangement of the p-Apéry sets ($p=0,1,\dots ,5$) when $⌊a/J_k\left(v\right)⌋=5$. One can see that there will be a deficiency in the arrangement of the lower left for the 6-Apéry set.

Table 4. ${\mathrm{Ap}}_p\left(A\right)$ ($p=⌊a/J_k\left(v\right)⌋$).

See [18,19], etc. for a detailed explanation that the elements located within the entire specified areas actually constitute the elements of the p-Apéry set. That is, they form a complete residue system modulo a and each element is represented by a, $va+b$, $va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)$ in at least $p+1$ ways. The rough structure is similar to that in [18,19], though the structures of the p-Apéry set in other cases are not necessarily similar or have not been known yet.

4. $\mathit{p}$-Genus

The elements of ${\mathrm{Ap}}_p\left(A\right)$ in the area of the $2p$ staircase parts are

$$\begin{array}{cc}\hfill & t_{0,q+p},\dots ,t_{r-1,q+p},t_{r,q+p-1},\dots ,t_{J_k\left(v\right)-1,q+p-1},\hfill \\ \hfill & t_{J_k\left(v\right),q+p-2},\dots ,t_{J_k\left(v\right)+r-1,q+p-2},t_{J_k\left(v\right)+r,q+p-3},\dots ,t_{2J_k\left(v\right)-1,q+p-3},\hfill \\ \hfill & t_{2J_k\left(v\right),q+p-4},\dots ,t_{2J_k\left(v\right)+r-1,q+p-4},t_{2J_k\left(v\right)+r,q+p-5},\dots ,t_{3J_k\left(v\right)-1,q+p-5},\hfill \\ \hfill & \dots \hfill \\ \hfill & t_{(p-1)J_k\left(v\right),q-p+2},\dots ,t_{(p-1)J_k\left(v\right)+r-1,q-p+2},t_{(p-1)J_k\left(v\right)+r,q-p+1},\dots ,t_{p{J}_k\left(v\right)-1,q-p+1}\hfill \end{array}$$

in order from the lower left and the elements of ${\mathrm{Ap}}_p\left(A\right)$ in the right-most main area are

$$\begin{array}{cc}\hfill & t_{p{J}_k\left(v\right),0},\dots ,t_{p{J}_k\left(v\right)+r-1,0},t_{p{J}_k\left(v\right)+r,0},\dots ,t_{(p+1)J_k\left(v\right)-1,0},\hfill \\ \hfill & t_{p{J}_k\left(v\right),1},\dots ,t_{p{J}_k\left(v\right)+r-1,1},t_{p{J}_k\left(v\right)+r,1},\dots ,t_{(p+1)J_k\left(v\right)-1,1},\hfill \\ \hfill & \dots \hfill \\ \hfill & t_{p{J}_k\left(v\right),q-p-1},\dots ,t_{p{J}_k\left(v\right)+r-1,q-p-1},t_{p{J}_k\left(v\right)+r,q-p-1},\dots ,t_{(p+1)J_k\left(v\right)-1,q-p-1},\hfill \\ \hfill & t_{p{J}_k\left(v\right),q-p},\dots ,t_{p{J}_k\left(v\right)+r-1,q-p}.\hfill \end{array}$$

Hence, by $a=q{J}_k\left(v\right)+r$, we have

$$\begin{array}{cc}\hfill & \sum _{w\in {\mathrm{Ap}}_p\left(A\right)}w\hfill \\ \hfill & =\sum _{i=0}^{p-1}\sum _{j=0}^{r-1}{t}_{i{J}_k\left(v\right)+j,q+p-2i}+\sum _{i=0}^{p-1}\sum _{j=0}^{J_k\left(v\right)-r-1}{t}_{i{J}_k\left(v\right)+r+j,q+p-2i-1}\hfill \\ \hfill & +\sum _{i=0}^{J_k\left(v\right)-1}\sum _{j=0}^{q-p-1}{t}_{p{J}_k\left(v\right)+i,j}+\sum _{i=0}^{r-1}{t}_{p{J}_k\left(v\right)+i,q-p}\hfill \\ \hfill & =\frac{a}{2}\left(-v(a-r^2)+b(a-1)+v\left((a+r)q-a+r\right)J_{k-1}\left(v\right)+v(a-r)J_k\left(v\right)\right)\hfill \\ \hfill & +\frac{p}{2}a{J}_k\left(v\right)\left(2(va+b)-v(J_k\left(v\right)-J_{k-1}\left(v\right)\right)-\frac{p^2}{2}avs.J_k\left(v\right)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right).\hfill \end{array}$$

(4)

Thus, by Lemma 1 (2), we obtain that

$$\begin{array}{cc}\hfill & n_p(a,va+b,a{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))\hfill \\ \hfill & =\frac{1}{a}\sum _{w\in {\mathrm{Ap}}_p\left(A\right)}w-\frac{a-1}{2}\hfill \\ \hfill & =\frac{1}{2}\left(-v(a-r^2)+b(a-1)+v\left((a+r)q-a+r\right)J_{k-1}\left(v\right)+v(a-r)J_k\left(v\right)\right)\hfill \\ \hfill & +\frac{p}{2}a{J}_k\left(v\right)\left(2(va+b)-v(J_k\left(v\right)-J_{k-1}\left(v\right)\right)\hfill \\ \hfill & -\frac{p^2}{2}avs.J_k\left(v\right)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)-\frac{a-1}{2}\hfill \\ \hfill & =\frac{1}{2}(-v(a-r^2)+(a-1)(b-1)+\frac{v(a+r)(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}\hfill \\ \hfill & +v(a-r)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right))\hfill \\ \hfill & +\frac{p}{2}a{J}_k\left(v\right)\left(2(va+b)-v(J_k\left(v\right)-J_{k-1}\left(v\right)\right)-\frac{p^2}{2}avs.J_k\left(v\right)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right).\hfill \end{array}$$

Theorem 2.

Let a and b be coprime integers. Then, for a positive integer $k\ge 3$ and $0\le p\le ⌊a/J_k\left(v\right)⌋$ we have

$$\begin{array}{cc}\hfill & n_p\left(a,a+b,a{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =\frac{1}{2}(-v(a-r^2)+(a-1)(b-1)+\frac{v(a+r)(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}\hfill \\ \hfill & +v(a-r)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right))\hfill \\ \hfill & +\frac{p}{2}a{J}_k\left(v\right)\left(2(va+b)-v(J_k\left(v\right)-J_{k-1}\left(v\right)\right)-\frac{p^2}{2}avs.J_k\left(v\right)\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right),\hfill \end{array}$$

where $r=a-⌊a/J_k\left(v\right)⌋J_k\left(v\right)$.

p-Sylvester Sum

In this subsection, we shall show a closed formula for the Sylvester sum. By $a=q{J}_k\left(v\right)+r$, we have

$$\begin{array}{cc}\hfill & \sum _{w\in {\mathrm{Ap}}_p\left(A\right)}{w}^2\hfill \\ \hfill & =\sum _{i=0}^{p-1}\sum _{j=0}^{r-1}{\left(t_{i{J}_k\left(v\right)+j,q+p-2i}\right)}^2+\sum _{i=0}^{p-1}\sum _{j=0}^{J_k\left(v\right)-r-1}{\left(t_{i{J}_k\left(v\right)+r+j,q+p-2i-1}\right)}^2\hfill \\ \hfill & +\sum _{i=0}^{J_k\left(v\right)-1}\sum _{j=0}^{q-p-1}{\left(t_{p{J}_k\left(v\right)+i,j}\right)}^2+\sum _{i=0}^{r-1}{\left(t_{p{J}_k\left(v\right)+i,q-p}\right)}^2\hfill \\ \hfill & =\frac{a}{6}({(va+b)}^2+(va+b)(2vs.r^2-3ab-3vs.r^2)+2ab(ab+3vs.r^2)\hfill \\ \hfill & +v^{2}a\left(2q^2(a+2r)-(a-r)(3q-1)\right)J_{k-1}{\left(v\right)}^2\hfill \\ \hfill & -3v(a-r)(va+b-b(a-r))J_k\left(v\right)+v(a-r)(2vs.a+b)J_k{\left(v\right)}^2\hfill \\ \hfill & +v\left(3\right(a-r\left)\right((a-r)(va-b)+va+b)+q(a+r\left)\right(4ab-3(va+b))\hfill \\ \hfill & +2q{r}^2(3vs.a-b)-(a-r)(3vs.a+b)J_k\left(v\right)\left)J_{k-1}\left(v\right)\right)\hfill \\ \hfill & +\frac{ap}{6}(6((va+b)(ab+v{r}^2)-{(va+b)}^2-b^2)J_k\left(v\right)\hfill \\ \hfill & +3v\left((va+b)(2r+1)+2vs.a^2\right)J_k{\left(v\right)}^2-v(2vs.a-b)J_k{\left(v\right)}^3\hfill \\ \hfill & +v(6(a^2-r^2)(av+b)+3((va+b)(2r-1)-4vs.a^2)J_k\left(v\right)\hfill \\ \hfill & +(5vs.a-b)J_k{\left(v\right)}^2)J_{k-1}\left(v\right)+3v^{2}a\left(2a-J_k\left(v\right)\right)J_{k-1}{\left(v\right)}^2)\hfill \\ \hfill & +\frac{a{p}^2}{2}(\left(v(va+b)(2a+1)+2b^2-v(2vs.a+b)J_k\left(v\right)\right)J_k{\left(v\right)}^2\hfill \\ \hfill & -v\left(2a(va-b)+av+b\right)J_{k-1}\left(v\right)J_k\left(v\right)+v^{2}a{J}_{k-1}{\left(v\right)}^2(2a-J_k{\left(v\right)}^2))\hfill \\ \hfill & -\frac{2av(va+b)p^3}{3}\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right){\left(J_k\left(v\right)\right)}^2.\hfill \end{array}$$

Thus, by Lemma 1 (3), together with ${\sum }_{w\in {\mathrm{Ap}}_p\left(A\right)}w$ in (4), we obtain that

$$\begin{array}{cc}\hfill & s_p\left(a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\right)\hfill \\ \hfill & =\frac{1}{2a}\sum _{w\in {\mathrm{Ap}}_p\left(A\right)}{w}^2-\frac{1}{2}\sum _{w\in {\mathrm{Ap}}_p\left(A\right)}w+\frac{a^2-1}{12}\hfill \\ \hfill & =\frac{1}{12}((a-r)v(2av+b)J_k{\left(v\right)}^2-(a-r)v(3(va+b-b(a-r)+a)\hfill \\ \hfill & +(3vs.a+b)J_{k-1}\left(v\right))J_k\left(v\right)+v^{2}a(a-r)J_{k-1}{\left(v\right)}^2\hfill \\ \hfill & +3(a-r)v\left(va+b+(a-r)(va-b)+a\right)J_{k-1}\left(v\right)\hfill \\ \hfill & +3\left(v{r}^2(va+b)+va{r}^2(2b-1)-v{a}^2(b-1)-ab(a+b-1)\right)\hfill \\ \hfill & +{(va+b)}^2+(a^2-1)+2\left(v{r}^3(va-b)+a^2{b}^2\right)\hfill \\ \hfill & +\frac{2v^{2}a(a-r)(a^2+ar-2r^2)J_{k-1}{\left(v\right)}^2}{J_k{\left(v\right)}^2}-\frac{3v^{2}a{(a-r)}^2{J}_{k-1}{\left(v\right)}^2}{J_k\left(v\right)}\hfill \\ \hfill & +\frac{v(a-r)J_{k-1}\left(v\right)}{J_k\left(v\right)}(4ab(2a+3r)+2r^2(3v-b)\hfill \\ \hfill & -3(a^2+r(v+b+1))-3a(va+b)\left)\right)\hfill \\ \hfill & +\frac{p}{12}(-v(2vs.a-b)J_k{\left(v\right)}^3+3v\left(-(2r-1)(va+b)+a(2vs.a+1)\right)J_k{\left(v\right)}^2\hfill \\ \hfill & +6(va+b)\left(v{r}^2-(va+b)+a(b-1)\right)J_k\left(v\right)\hfill \\ \hfill & +v(5vs.a-b)J_{k-1}\left(v\right)J_k{\left(v\right)}^2\hfill \\ \hfill & +3v\left(-(2r-1)(va+b)+a(4vs.a+1)\right)J_{k-1}\left(v\right)J_k\left(v\right)\hfill \\ \hfill & +6v(a^2-r^2)(va+b)J_{k-1}\left(v\right)+3v^{2}a\left(2a-J_k\left(v\right)\right)J_{k-1}{\left(v\right)}^2)\hfill \\ \hfill & +\frac{p^2}{4}(v\left(a(2vs.a-2b+1)+va+b-(3vs.a+b)J_k\left(v\right)\right)J_{k-1}\left(v\right)J_k\left(v\right)\hfill \\ \hfill & +\left(v(2a+1)(va+b)+va+2b^2-v(2vs.a+b)J_k\left(v\right)\right)J_k{\left(v\right)}^2\hfill \\ \hfill & +v^{2}a{J}_{k-1}{\left(v\right)}^2{J}_k{\left(v\right)}^2)\hfill \\ \hfill & -\frac{v(va+b)p^3}{3}\left(J_k\left(v\right)-J_{k-1}\left(v\right)\right)J_k{\left(v\right)}^2.\hfill \end{array}$$

Here, again $q=⌊a/J_k\left(v\right)⌋$ and $r=a-q{J}_k\left(v\right)$.

5. Jacobsthal–Lucas Polynomials

The same discussion as Jacobsthal polynomials can be applied to Jacobsthal–Lucas polynomials $j_n\left(v\right)$. Here, $j_n\left(v\right)=j_{n-1}\left(v\right)+j_{n-2}\left(v\right)$ ($n\ge 2$) with $j_0\left(v\right)=2$ and $j_1\left(v\right)=1$ (see, e.g., [17], Chapter 44). When $v=1$, $L_n=j_n\left(1\right)$ are Lucas numbers. When $v=2$, $j_n=j_n\left(2\right)$ are Jacobsthal–Lucas numbers. Similarly, determine integers q and r by $a=q{j}_k\left(v\right)+r$ with $0\le r<j_k\left(v\right)$. If $a=j_i\left(v\right)$ and $b=j_{i+1}\left(v\right)$, then the numerical semigroup $⟨j_i\left(v\right),j_{i+2}\left(v\right),j_{i+k}\left(v\right)⟩$ in [18] can be reduced as a special case.

Theorem 3.

Let a and b be positive integers with $gcd(a,b)=1$ and $a\ge 3$. Then, for a positive integer $k\ge 3$ and $0\le p\le ⌊a/j_k\left(v\right)⌋$ we have

$$\begin{array}{cc}\hfill & g_p\left(a,va+b,va{j}_{k-1}\left(v\right)+b{j}_k\left(v\right)\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}(a-1)b+a\left(v(r-1)-1\right)+\frac{va(a-r)j_{k-1}\left(v\right)}{j_k\left(v\right)}+p\left(va{j}_{k-1}\left(v\right)+b{j}_k\left(v\right)\right)\hfill & \\ ifa<j_k\left(v\right)or(va+b)r>va\left(j_k\left(v\right)-j_{k-1}\left(v\right)\right);\hfill & \\ (a-r-1)b+va(j_k\left(v\right)-j_{k-1}\left(v\right)-1)-a+\frac{va(a-r)j_{k-1}\left(v\right)}{j_k\left(v\right)}\hfill & \\ +p\left(va{j}_{k-1}\left(v\right)+b{j}_k\left(v\right)\right)\hfill & \\ ifa\ge j_k\left(v\right)and(va+b)r<va\left(j_k\left(v\right)-j_{k-1}\left(v\right)\right),\hfill \end{array}\right.\hfill \end{array}$$

where $r=a-⌊a/j_k\left(v\right)⌋j_k\left(v\right)$.

Theorem 4.

Let a and b be coprime integers. Then, for a positive integer $k\ge 3$ and $0\le p\le ⌊a/j_k\left(v\right)⌋$ we have

$$\begin{array}{cc}\hfill & n_p\left(a,a+b,a{j}_{k-1}\left(v\right)+b{j}_k\left(v\right)\right)\hfill \\ \hfill & =\frac{1}{2}(-v(a-r^2)+(a-1)(b-1)+\frac{v(a+r)(a-r)j_{k-1}\left(v\right)}{j_k\left(v\right)}\hfill \\ \hfill & +v(a-r)\left(j_k\left(v\right)-j_{k-1}\left(v\right)\right))\hfill \\ \hfill & +\frac{p}{2}a{j}_k\left(v\right)\left(2(va+b)-v(j_k\left(v\right)-j_{k-1}\left(v\right)\right)-\frac{p^2}{2}avs.j_k\left(v\right)\left(j_k\left(v\right)-j_{k-1}\left(v\right)\right),\hfill \end{array}$$

where $r=a-⌊a/j_k\left(v\right)⌋j_k\left(v\right)$.

6. $\mathit{p}$-Hilbert Series

There are some applications, due to the p-Apéry set. One of them is on the p-Hilbert series ([36]) of $S_p\left(A\right)$, which is defined by

$$H_p(A;x):=H(S_p;x)=\sum _{s\in S_p\left(A\right)}{x}^s,$$

When $p=0$, the 0-Hilbert series is the original Hilbert series, which plays an important role in the numerical semigroup (see, e.g., [9]). In addition, the p-gaps generating function is defined by

$${\mathsf{\Psi }}_p(A;x)=\sum _{s\in {\mathbb{N}}_0\backslash S_p\left(A\right)}{x}^s,$$

satisfying $H_p(A;x)+{\mathsf{\Psi }}_p(A;x)=1/(1-x)$ ($\left|x\right|<1$). Moreover, according to the same arguments of Chapter 5 in [9], we can express the p-Hilbert series as

$$H_p(A;x)=\frac{1}{1-x^a}\sum _{w\in {\mathrm{Ap}}_p(A;a)}{x}^w,$$

(5)

where $a=min\left\{A\right\}$.

When $A=\{a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)\}$, similarly to (4), we have

$$\begin{array}{cc}\hfill & \sum _{w\in {\mathrm{Ap}}_p\left(A\right)}{x}^w\hfill \\ \hfill & =\sum _{i=0}^{p-1}\sum _{j=0}^{r-1}{x}^{t_{i{J}_k\left(v\right)+j,q+p-2i}}+\sum _{i=0}^{p-1}\sum _{j=0}^{J_k\left(v\right)-r-1}{x}^{t_{i{J}_k\left(v\right)+r+j,q+p-2i-1}}\hfill \\ \hfill & +\sum _{i=0}^{J_k\left(v\right)-1}\sum _{j=0}^{q-p-1}{x}^{t_{p{J}_k\left(v\right)+i,j}}+\sum _{i=0}^{r-1}{x}^{t_{p{J}_k\left(v\right)+i,q-p}}\hfill \\ \hfill & =\frac{(1-x^{r(va+b)})(x^{2p(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{p(va+b)J_k\left(v\right)})}{x^{(p-q-2)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}(1-x^{va+b})(x^{2(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{(va+b)J_k\left(v\right)})}\hfill \\ \hfill & +\frac{(x^{r(va+b)}-x^{(va+b)J_k\left(v\right)})(x^{2p(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{p(va+b)J_k\left(v\right)})}{x^{(p-q-1)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}(1-x^{va+b})(x^{2(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{(va+b)J_k\left(v\right)})}\hfill \\ \hfill & +\frac{(x^{p(va+b)J_k\left(v\right)}-x^{(p+1)(va+b)J_k\left(v\right)})(1-x^{(q-p)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)))})}{(1-x^{va+b})(1-x^{va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)})}\hfill \\ \hfill & +\frac{x^{pvs.a(J_k\left(v\right)-J_{k-1}\left(v\right))+q(va{J}_{k-1}+b{J}_k\left(v\right))}(1-x^{r(va+b)})}{1-x^{va+b}}.\hfill \end{array}$$

Therefore, by (5)

$$\begin{array}{cc}\hfill & H_p\left(a,va+b,va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right);x\right)\hfill \\ \hfill & =\frac{1}{1-x^a}(\frac{(1-x^{r(va+b)})(x^{2p(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{p(va+b)J_k\left(v\right)})}{x^{(p-q-2)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}(1-x^{va+b})(x^{2(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{(va+b)J_k\left(v\right)})}\hfill \\ \hfill & +\frac{(x^{r(va+b)}-x^{(va+b)J_k\left(v\right)})(x^{2p(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{p(va+b)J_k\left(v\right)})}{x^{(p-q-1)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}(1-x^{va+b})(x^{2(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right))}-x^{(va+b)J_k\left(v\right)})}\hfill \\ \hfill & +\frac{(x^{p(va+b)J_k\left(v\right)}-x^{(p+1)(va+b)J_k\left(v\right)})(1-x^{(q-p)(va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)))})}{(1-x^{va+b})(1-x^{va{J}_{k-1}\left(v\right)+b{J}_k\left(v\right)})}\hfill \\ \hfill & +\frac{x^{pvs.a(J_k\left(v\right)-J_{k-1}\left(v\right))+q(va{J}_{k-1}+b{J}_k\left(v\right))}(1-x^{r(va+b)})}{1-x^{va+b}}).\hfill \end{array}$$

7. Future Works

In this paper, as well as in [18,19,29,30], the p-numerical semigroup with three variables has been studied. However, that with four variables is very difficult to deal with. In fact, even for $p=0$, no algorithm to calculate the Frobenius number has been discovered yet.

In [43], the numerical semigroup of $A:=(a,a+b,2a+3b,\dots ,F_{2k-1}a+F_{2k}b)$ is studied for relatively prime integers a and b when $p=0$:

$$g_0\left(A\right)=a\left(⌊\frac{F_{2k-1}(a-1)}{F_{2k}}⌋-1\right)+(a-1)b$$

and

$$n_0\left(A\right)=\sum _{y=1}^{a-1}⌊\frac{F_{2k-1}y}{F_{2k}}⌋+\frac{(a-1)(b-1)}{2}.$$

However, for $p\ge 1$, it is very difficult to find an explicit formula for the case with more than three variables. One wants to study a more general number ${\mathcal{U}}_n$, satisfying ${\mathcal{U}}_n=u{\mathcal{U}}_{n-1}+v{\mathcal{U}}_{n-2}$, but nothing is known even for the numerical semigroup of Pell numbers $P_n$, satisfying $P_n=2P_{n-1}+P_{n-2}$ ($n\ge 2$) with $P_0=0$ and $P_1=1$, because the structure is rather different.