The Quasi-Boundary Regularization Method for Recovering the Initial Value in a Nonlinear Time–Space Fractional Diffusion Equation

Abstract

In this paper, we consider the inverse problem for identifying the initial value problem of the time–space fractional nonlinear diffusion equation. The uniqueness of the solution is proved by taking the fixed point theorem of Banach compression, and the ill-posedness of the problem is analyzed through the exact solution. The quasi-boundary regularization method is chosen to solve the ill-posed problem, and the error estimate between the regularization solution and the exact solution is given. Moreover, several numerical examples are chosen to prove the effectiveness of the quasi-boundary regularization method. Finally, our method can be used to solve high dimensional time–space fractional nonlinear diffusion equation, especially in cylindrical and spherical symmetric regions.

1. Introduction

In recent years, the time-fractional equation has been popular in the field of anomalous diffusion and mechanics, the continuous random walk phenomenon [1], option pricing [2], and superdiffusion and subdiffusion phenomena [3]. The time-fractional equation has an advantage in describing genetic diffusion because of the memory property of its derivative. When the initial conditions, boundary conditions and source terms are known, this problem is called the direct problem. However, in practice, when some initial conditions, boundary conditions and source terms are unknown, we need some additional data to identify them, which is called the inverse problem. For the direct problem, until now, scholars have already done a great deal of work, see [4,5,6,7]. For the inverse problem, there is also a large quantity of research results. For identifying an initial value problem, in [8], the authors used the quasi-boundary regularization method to solve the initial value problem of the time-fractional diffusion equation in spherically symmetric regions. In [9], Wang used the Tikhonov regularization method to solve a backward problem for the time-fractional diffusion equation in a general bounded domain. In [10], Wei made use of a modified quasi-boundary value method to consider the backward time-fractional diffusion equation with variable coefficients in a general bounded domain. In [11], Wei considered the inverse problem of the time-fractional diffusion equation and analyzed the optimal error bound of the problem. In [12], Wang took an iterative method to consider a backward time-fractional diffusion problem in a general bounded domain. For identifying a source term problem, in [13], Li et al. adopted the Tikhonov method to identify the time-dependent source for a multi-dimensional time-fractional diffusion equation from boundary Cauchy data. In [14], Zhang used the truncated method to identify an unknown source in the time-fractional diffusion equation. In [15], Liu et al. applied the strong maximum principle to consider an inverse source problem for the fractional diffusion equations. In [16], Ismailov took an eigenfunction expansion method for an inverse source problem of a time-fractional diffusion equation with nonlocal boundary conditions. For an inverse heat conduction problem, in [17], Xiong et al. applied the optimal regularization method to solve the heat conduction problem of the time-fractional diffusion equation. In [18], Babaei used a mollification regularization method to solve the inverse problems of the time-fractional diffusion equations under the unknown nonlinear boundary conditions. In [19], the authors used the Landweber iterative regularization method to identify the inverse source of the time-fractional diffuse-wave equations in spherically symmetric domains. The above references deal with the inverse problems of the linear and one-dimensional time-fractional diffusion equation. However, for the inverse problem of the high-dimensional and nonlinear time-fractional diffusion equation, there is little in the way of research results. In this paper, we consider the inverse problem to identify the initial value for the nonlinear time-fractional diffusion equation. The quasi-boundary regularization method is used to solve this inverse problem. The basic idea of the quasi-boundary regularization method is to construct the approximate solution of the original ill-posed problem by adding the perturbation term to the boundary conditions of the original equation, so that the original ill-posed problem becomes a well-posed problem. In this paper, the prior error estimation between the exact solution and the approximate solution of the nonlinear diffusion–heat equation is given under the quasi-boundary regularization method, which lays a foundation for the subsequent study of nonlinear ill-posed inverse problems.

It can be seen from the literature analysis that there are few papers on the initial value identification of time-fractional nonlinear diffusion equations with the fractional Laplacian operator. Here, we are prepared to discuss the following time-fractional diffusion equation:

$$\left\{\begin{array}{cc}{D}_t^{\alpha }u=-A^{\beta }u(x,t)+F(u(x,t),x,t),\hfill & x\in (0,\pi ),t\in (0,T),\hfill \\ u(0,t)=u(\pi ,t)=0,\hfill & t\in (0,T),\hfill \\ u(x,0)=f(x),\hfill & x\in (0,\pi ),\hfill \\ u(x,T)=g(x),\hfill & x\in (0,\pi ),\hfill \end{array}\right.$$

(1)

where $\frac{1}{2}\le \beta \le 1$ and $D_t^{\alpha }(·)$ is the Caputo fractional derivative of the order $\alpha (0<\alpha \le 1)$ defined by

$$D_t^{\alpha }u=\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}:=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }(1-\alpha )}{\int }_0^t\frac{u_{\tau }(x,\tau )}{{(t-\tau )}^{\alpha }}ds,\hfill & 0<\alpha <1,\hfill \\ u_t(x,t),\hfill & \alpha =1,\hfill \end{array}\right.$$

(2)

$\mathsf{\Gamma }(x)$ is a Gamma function. Furthermore, the Dirichlet–Laplacian operator A is expressed as the following formula:

$$\left\{\begin{array}{c}Af=-\Delta f=-\sum _{j=1}^d{\partial }_j^{2}f,\hfill \\ D(A)={\mathbb{L}}^2(\mathsf{\Omega })\bigcap {\mathbb{H}}_0^1(\mathsf{\Omega })\bigcap {\mathbb{W}}^{2,2},\hfill \end{array}\right.$$

(3)

where ${\mathbb{W}}^{m,p}(\mathsf{\Omega })$ is a Sobolev space. $A^{\beta }$ which will be detailed in Section 2 stands for the fractional Laplace operator. The inverse problem is that we would like to restore the unknown initial value $u(x,0)$ by using the measurement of the final time $g(x)=u(x,T)$. We assume that the exact measurable data $g(x)$ and the noise measurable data $g^{\delta }(x)$ satisfy

$$\parallel g^{\delta }{-g\parallel }_{L^2(0,\pi )}\le \delta ,$$

(4)

where $\parallel ·\parallel$ is the $L^2$ norm throughout the paper and $\delta >0$ is the noise level.

There is little work on an initial value identification problem for a time-fractional nonlinear diffusion equation with a fractional Laplacian. In [20], Varlamov talked about a fractional diffusion system with power nonlinearity. In [21], Bogdan et al. derived estimates for a heat kernel of a fractional Laplacian. They only studied the existence and uniqueness of the strong solutions considering systems. In [22], Hu et al. studied the finite difference method for parabolic equations of the Caputo type with fractional Laplace operators. In [23], Xiong took a kind of fractional Tikhonov method to resolve an initial value identification problem for a time-fractional diffusion equation with a fractional Laplacian. In [24], Yu et al. used the Adomian decomposition method to construct explicit solutions of the nonlinear Caputo type time–space fractional diffusion equation. In [25], Zhuang adopted numerical methods for the variable-order time-fractional diffusion equation with a nonlinear source term. In [26], Fan applied the Fourier truncated regularization method with a nonlinear source to solve the inverse problem of the time-fractional diffusion equation. In [27], Tuan utilized the improved kernel function method on a backward problem for nonlinear fractional diffusion equations. In this paper, we use the quasi-boundary regularization method to solve the inversion problem of the unknown initial values. The quasi-boundary regularized method is an effective method to deal with the ill-posed problem [28,29]. The article is written as follows. In the second section, we will give some useful results. In the third section, we analyze the ill-posedness of this problem and give the uniqueness of solution. In the fourth section, we choose the quasi-boundary regularization method to solve the above inverse problem, and give the error estimate between the approximate solution and the exact solution. In the fifth section, we present numerical results of the approximate solution and the exact solution. In the sixth section, we give a brief conclusion.

2. Preliminary Results

For sake of solving problem (1), in the following, we give some useful definitions and theorems.

First, we introduce a positive self-adjoint operator ${(-\Delta )}^{\beta }$. Here, the fractional Dirichlet–Laplacian operator ${(-\Delta )}^{\beta }$ is represented by the following spectral theorem.

Definition 1

([23]). Let $\psi \in {\mathbb{L}}^2(\mathsf{\Omega })$, for every $\frac{1}{2}\le \beta \le 1$,

$$A^{\beta }\psi ={(-\Delta )}^{\beta }\psi =\sum _{n=1}^{\infty }{\lambda }_n^{\beta }<\psi ,{\phi }_n>{\phi }_n(x),if\beta \ne 0.$$

(5)

$$D(A^{\beta })=\{\psi \in {\mathbb{L}}^2(\mathsf{\Omega }):\parallel A^{\beta }\psi {\parallel }_{{\mathbb{L}}^2(\mathsf{\Omega })}<+\infty \},if\beta >0.$$

(6)

Suppose ${\left\{{\lambda }_n\right\}}_{n\in \mathbb{N}}\in \mathbb{R}$ and ${\left\{{\phi }_n(x)\right\}}_{n\in \mathbb{N}}\in D(A)$ are defined as eigenvalues and eigenfunctions of A; ${\lambda }_n$ satisfies ${\lambda }_n\ge {\lambda }_{n-1}\ge \cdots \ge {\lambda }_2\ge {\lambda }_1>0$; then we obtain the following lemma.

Lemma 1

([23]). Set $\psi ={\sum }_{n=1}^{\infty }{\psi }_n{\phi }_n(x)$; here ${\psi }_n=<\psi ,{\phi }_n>$ is the Fourier coefficient of ψ; we assume that

$$\sum _{n=1}^{\infty }{\psi }_n^2{\lambda }_n^{2\beta }<+\infty .$$

(7)

Then $\psi \in D(A^{\beta })$, we have

$$A^{\beta }\psi =\sum _{n=1}^{\infty }{\lambda }_n^{\beta }{\psi }_n{\phi }_n(x).$$

(8)

Definition 2

([5]). The Mittag–Leffler function is

$$E_{\alpha ,\gamma }(z)=\sum _{k=0}^{\infty }\frac{z^k}{\mathsf{\Gamma }(\alpha k+\gamma )},z\in \mathbb{C},$$

(9)

where $\alpha >0$ and $\gamma \in \mathbb{R}$ are arbitrary constants.

Lemma 2

([27]). Let $\alpha \in (0,1)$ then $0<E_{\alpha ,1}(-z)<1$ for any $z>0$. Moreover, there exist three positive constants $M_{1,\alpha }^{-},M_{1,\alpha }^{+},M_{2,\alpha }^{+}$ such that

$$\frac{M_{1,\alpha }^{-}}{1+z}\le E_{\alpha ,1}(-z)\le \frac{M_{1,\alpha }^{+}}{1+z},E_{\alpha ,\alpha }(-z)\le \frac{M_{2,\alpha }^{+}}{1+z}.$$

(10)

If $\alpha \in [{\alpha }_0,{\alpha }_1]$, for any $0<{\alpha }_0<{\alpha }_1<1$, then the constants $M_{1,\alpha }^{-},M_{1,\alpha }^{+},M_{2,\alpha }^{+}$ can be chosen which depend only on ${\alpha }_0,{\alpha }_1$.

Lemma 3

([9]). For any ${\lambda }_n^{\beta }\ge {\lambda }_1^{\beta }>0$, there exist constants $\underline{C},\overline{C}>0$ which are only dependent on $\alpha ,T,{\lambda }_1^{\beta }$, satisfying

$$\frac{\underline{C}}{{\lambda }_n^{\beta }}\le E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })\le \frac{\overline{C}}{{\lambda }_n^{\beta }}.$$

(11)

3. Existence, Uniqueness and Ill-Posedness of the Mild Solution

Definition 3

([27]). The function u is called a mild solution of Problem (1) if $u\in L^{\infty }(0,T;L^2(0,\pi ))$ and satisfies

$$\begin{array}{cc}\hfill u(x,t)& =\sum _{n=1}^{\infty }\frac{E_{\alpha ,1}(-{\lambda }_n^{\beta }{t}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)\hfill \\ \hfill & +\sum _{n=1}^{\infty }\left({\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(t-s)}^{\alpha })<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill & -\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,1}(-{\lambda }_n^{\beta }{t}^{\alpha })E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x).\hfill \end{array}$$

(12)

where $g_n=<g,{\phi }_n>$ stands for its Fourier coefficient.

We use some notation to simplify the mild solution representation.

$$u(x,t)=\sum _{n=1}^{\infty }\frac{E_{\alpha ,1}(-{\lambda }_n^{\beta }{t}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)+G_{1}u(x,t)+G_{2}u(x,t),$$

(13)

where

$$G_{1}u(x,t)=-\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,1}(-{\lambda }_n^{\beta }{t}^{\alpha })E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x),$$

$$G_{2}u(x,t)=\sum _{n=1}^{\infty }\left({\int }_0^t{(t-s)}^{\alpha -1}{E}_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(t-s)}^{\alpha })<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x).$$

According to problem (1), the initial value $u(x,0)=f(x)$, which is

$$\begin{array}{cc}\hfill u(x,0)& =\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)+G_{1}u(x,0)+G_{2}u(x,0)\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)\hfill \\ \hfill & -\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x)+0.\hfill \end{array}$$

Consequently,

$$\begin{array}{cc}\hfill f(x)& =\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)\hfill \\ \hfill & -\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x).\hfill \end{array}$$

(14)

Theorem 1

([27]). We assume F satisfies ${\parallel F(v(·,t))-F(w(·,t))\parallel }_{L^2(0,\pi )}\le K(t){\parallel v(·,t)-w(·,t)\parallel }_{L^2(0,\pi )}$, $K(t)$ is a bounded function, the integral ${\int }_0^T{(T-t)}^{-2}{K}^2(t)dt$ converges to ${|\mathsf{\Psi }(T)|}^2$ and

$$L(\alpha ,T)=(\frac{M_{2,\alpha }^{+}}{\underline{C}}|\mathsf{\Psi }(T)|+\underset{0\le t\le T}{sup}|K(t)|\mathcal{A})<1,$$

where $\mathcal{A}={\sum }_{n=1}^{\infty }\frac{1}{{\lambda }_n^{\beta }}$. Then there is a unique weak solution for (1).

Next, we clarify the instability of the mild solution. For the noisy measurement date $g^{\delta }(x)$, the corresponding solution to the initial value with such noisy final data can be represented as

$$f^{\delta }(x)=u^{\delta }(x,0)=\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n^{\delta }{\phi }_n(x)+G_1{u}^{\delta }(x,0).$$

(15)

This implies that

$$\begin{array}{cc}\hfill {\displaystyle \parallel f^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}}& \le \parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}(g_n^{\delta }-g_n){\phi }_n(x){\parallel }_{L^2(0,\pi )}+{\parallel G_{1}u(x,0)-G_1{u}^{\delta }(x,0)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& ={\left(\sum _{n=1}^{\infty }{\left(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}(g_n^{\delta }-g_n)\right)}^2\right)}^{\frac{1}{2}}+{\parallel G_{1}u(x,0)-G_1{u}^{\delta }(x,0)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& \le \underset{n\ge 1}{sup}|\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}|\delta +\parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& \le \underset{n\ge 1}{sup}|\frac{{\lambda }_n^{\beta }}{\underline{C}}|\delta +\parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )},\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & \parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )}^2\hfill \\ \hfill & =\parallel -\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s))-F(·,s,u^{\delta }(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}^2\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\sum _{n=1}^{\infty }{\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s))-F(·,s,u^{\delta }(·,s)),{\phi }_n>ds\right)}^2\hfill \\ \hfill & \le |\frac{M_{2,\alpha }^{+}}{\underline{C}}{|}^2\sum _{n=1}^{\infty }{\left({\int }_0^T{(T-s)}^{-1}<F(·,s,u(·,s))-F(·,s,u^{\delta }(·,s)),{\phi }_n>ds\right)}^2\hfill \\ \hfill & \le |\frac{M_{2,\alpha }^{+}}{\underline{C}}{|}^2{\int }_0^T{(T-s)}^{-2}{K}^2(s){\parallel u(·,s)-u^{\delta }(·,s)\parallel }_{L^2(0,\pi )}^{2}ds\hfill \\ \hfill & =J,\hfill \end{array}$$

$$\parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )}^2\le J.$$

(16)

If we pick $s=0$ in J, then

$$\begin{array}{cc}\hfill J& =|\frac{M_{2,\alpha }^{+}}{\underline{C}}{|}^2{\int }_0^T{T}^{-2}{K}^2(0){\parallel u(·,0)-u^{\delta }(·,0)\parallel }_{L^2(0,\pi )}^{2}ds\hfill \\ \hfill & \le |\frac{M_{2,\alpha }^{+}}{\underline{C}}{|}^2{|\mathsf{\Psi }(T)|}^2{\parallel f(·)-f^{\delta }(·)\parallel }_{L^2(0,\pi )}^2.\hfill \end{array}$$

(17)

Combining (16) and (17), we obtain

$$\parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )}\le \frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T){\parallel f(·)-f^{\delta }(·)\parallel }_{L^2(0,\pi )}.$$

(18)

To sum up,

$$\begin{array}{cc}\hfill \parallel f^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}& \le \underset{n\ge 1}{sup}|\frac{{\lambda }_n^{\beta }}{\underline{C}}|\delta +\parallel G_{1}u(x,0)-G_1{u}^{\delta }{(x,0)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill & \le \underset{n\ge 1}{sup}|\frac{{\lambda }_n^{\beta }}{\underline{C}}|\delta +\frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T){\parallel f(·)-f^{\delta }(·)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill & \le \underset{n\ge 1}{sup}|\frac{{\lambda }_n^{\beta }}{(1-\frac{M_{2,\alpha }^{+}}{\underline{C}})\underline{C}}|\delta ,\hfill \end{array}$$

where $0<1-\frac{M_{2,\alpha }^{+}}{\underline{C}}<1$.

Therefore, we can conclude that

$$\underset{n\to \infty }{lim}\parallel f^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}\le \underset{n\to \infty }{lim}|\frac{{\lambda }_n^{\beta }}{(1-\frac{M_{2,\alpha }^{+}}{\underline{C}})\underline{C}}|\delta =\infty .$$

Hence, the problem of recovering the initial value in (1) is ill-posed.

4. The Quasi-Boundary Regularization Method and the Convergence Rate

In this section, we will use the quasi-boundary regularization method to solve problem (1). The convergence rate between the regularization solution and the exact solution is obtained based on some mathematical analysis.

Set $u_{\mu }^{\delta }(x,t)$ to be the solution of the following regularization problem

$$\left\{\begin{array}{cc}{D}_t^{\alpha }{u}_{\mu }^{\delta }=-A^{\beta }{u}_{\mu }^{\delta }(x,t)+F(u_{\mu }^{\delta }(x,t),x,t),\hfill & x\in (0,\pi ),t\in (0,T),\hfill \\ u_{\mu }^{\delta }(0,t)=u_{\mu }^{\delta }(\pi ,t)=0,\hfill & t\in (0,T),\hfill \\ u_{\mu }^{\delta }(x,0)=f^{\delta }(x),\hfill & x\in (0,\pi ),\hfill \\ u_{\mu }^{\delta }(x,T)+\mu u_{\mu }^{\delta }(x,0)=g^{\delta }(x),\hfill & x\in (0,\pi ),\hfill \end{array}\right.$$

(19)

where $\mu >0$ is the regularization parameter.

According to problem (19), we can obtain the regularization solution $f_{\mu }^{\delta }(x)$:

$$\begin{array}{cc}\hfill f_{\mu }^{\delta }(x)& =\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{g}_n^{\delta }{\phi }_n(x)\hfill \\ \hfill & -\sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }^{\delta }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill & =\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{g}_n^{\delta }{\phi }_n(x)+G_1{u}_{\mu }^{\delta }(x,0).\hfill \end{array}$$

(20)

Moreover, the error estimates between the quasi-boundary regular solution and the exact solution are given by the following theorem. Before giving out the error estimation, we need to define the a priori boundary of the initial value $f(x)$,

$${\parallel f(x)\parallel }_{H^{\beta p}(0,\pi )}:=(\sum _{n=1}^{\infty }{\lambda }_n^{\beta p}|<f(x),{\phi }_n(x)>{{|}^2)}^{\frac{1}{2}}\le E,$$

(21)

where ${\parallel ·\parallel }_{H^{\beta p}(0,\pi )}$ is the Hilbert space equipped with norm.

Theorem 2.

Let the exact solution $f(x)$ be given by (14) and the regular solution $f_{\mu }^{\delta }(x)$ be given by (20). Suppose that $f(x)$ satisfies the a priori bounded condition (21) and the noise assumption (4) holds, then we have

$$\mu =\left\{\begin{array}{c}{(\frac{\delta }{E})}^{\frac{2}{p+2}},0<p<2,\hfill \\ {(\frac{\delta }{E})}^{\frac{1}{2}},p\ge 2,\hfill \end{array}\right.$$

(22)

$$\parallel f_{\mu }^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}\le \left\{\begin{array}{c}{C}_2{\delta }^{\frac{p}{p+2}}{E}^{\frac{2}{p+2}},0<p<2,\hfill \\ C_3{\delta }^{\frac{1}{2}}{E}^{\frac{1}{2}},p\ge 2,\hfill \end{array}\right.$$

(23)

where $C_2=\frac{1+C_1}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}|\mathsf{\Psi }(T)|}$, $C_3=\frac{2}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}|\mathsf{\Psi }(T)|}$.

Proof. 

According to the triangle inequality, we have

$$\parallel f_{\mu }^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}\le \parallel f_{\mu }^{\delta }(x)-f_{\mu }{(x)\parallel }_{L^2(0,\pi )}+{\parallel f_{\mu }(x)-f(x)\parallel }_{L^2(0,\pi )}.$$

(24)

Firstly, we give the estimate for the first term of (24).

$$\begin{array}{cc}\hfill {\displaystyle }& \parallel f_{\mu }^{\delta }(x)-f_{\mu }{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& =\parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{g}_n^{\delta }{\phi }_n(x)+G_1{u}_{\mu }^{\delta }(x,0)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle }& -\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{g}_n{\phi }_n(x)-G_1{u}_{\mu }{(x,0)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& =\parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(g_n^{\delta }-g_n){\phi }_n(x)+(G_1{u}_{\mu }^{\delta }(x,0)-G_1{u}_{\mu }(x,0)){\parallel \parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& \le \parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(g_n^{\delta }-g_n){\phi }_n(x){\parallel }_{L^2(0,\pi )}+\parallel \sum _{n=1}^{\infty }{G}_1{u}_{\mu }^{\delta }(x,0)-G_1{u}_{\mu }(x,0){\parallel \parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& =H_1+H_2.\hfill \end{array}$$

Next, we estimate $H_1$,

$$\begin{array}{cc}\hfill {\displaystyle H_1}& =\parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(g_n^{\delta }-g_n){\phi }_n(x){\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle }& ={\left(\sum _{n=1}^{\infty }{\left(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(g_n^{\delta }-g_n)\right)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill {\displaystyle }& \le \underset{n\ge 1}{sup}|\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }|{\left(\sum _{n=1}^{\infty }{(g_n^{\delta }-g_n)}^2\right)}^{\frac{1}{2}}\hfill \\ \hfill {\displaystyle }& \le {\mu }^{-1}\delta .\hfill \end{array}$$

Thus

$$H_1\le {\mu }^{-1}\delta .$$

(25)

Like the (18) proof, $H_2$ has the following conclusion:

$$H_2\le \frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T){\parallel f_{\mu }^{\delta }(x)-f_{\mu }(x)\parallel }_{L^2(0,\pi )}.$$

(26)

Combining (25) and (26), we obtain

$$\parallel f_{\mu }^{\delta }(x)-f_{\mu }{(x)\parallel }_{L^2(0,\pi )}\le \frac{1}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T)}{\mu }^{-1}\delta .$$

(27)

Secondly, we give the second term of (24).

$$\begin{array}{cc}\hfill {\displaystyle }& \parallel f_{\mu }{(x)-f(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle =}& \parallel \sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{g}_n{\phi }_n(x)-\sum _{n=1}^{\infty }\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n{\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle +}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle =}& \parallel \sum _{n=1}^{\infty }\frac{-\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })(E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu )}{g}_n{\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle +}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle =}& \parallel \sum _{n=1}^{\infty }\frac{-\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n\hfill \\ \hfill {\displaystyle -}& {\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds){\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left(\frac{\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle +}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle \le }& \parallel \sum _{n=1}^{\infty }\frac{-\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n\hfill \\ \hfill {\displaystyle -}& {\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle +}& \parallel \sum _{n=1}^{\infty }\left(\frac{\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle +}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle =}& \parallel \sum _{n=1}^{\infty }\frac{-\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{\lambda }_n^{-\frac{\beta p}{2}}{\lambda }_n^{\frac{\beta p}{2}}(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n\hfill \\ \hfill {\displaystyle -}& {\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle +}& \parallel \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u_{\mu }(·,s)),{\phi }_n>ds\right){\phi }_n(x)\hfill \\ \hfill {\displaystyle -}& \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }<F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle \le }& (\sum _{n=1}^{\infty }(\frac{-\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{\lambda }_n^{-\frac{\beta p}{2}}{\lambda }_n^{\frac{\beta p}{2}}(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n\hfill \\ \hfill {\displaystyle -}& {\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds){)}^2{)}^{\frac{1}{2}}\hfill \\ \hfill {\displaystyle +}& \parallel \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u_{\mu }(·,s))-F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n{(x)\parallel }_{L^2(0,\pi )}\hfill \\ \hfill {\displaystyle \le }& \underset{n\ge 1}{sup}|\frac{\mu }{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })+\mu }{\lambda }_n^{-\frac{\beta p}{2}}|(\sum _{n=1}^{\infty }({\lambda }_n^{\frac{\beta p}{2}}(\frac{1}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}{g}_n\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle -}& {\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u(·,s)),{\phi }_n>ds){)}^2{)}^{\frac{1}{2}}+Y\hfill \\ \hfill {\displaystyle \le }& \underset{n\ge 1}{sup}|\frac{\mu {\lambda }_n^{1-\frac{\beta p}{2}}}{\underline{C}+\mu {\lambda }_n^{\beta p}}|E+Y\hfill \\ \hfill {\displaystyle =}& \underset{n\ge 1}{sup}|A(n)|E+Y,\hfill \end{array}$$

where $A(n)=\frac{\mu {\lambda }_n^{1-\frac{\beta p}{2}}}{\underline{C}+\mu {\lambda }_n^{\beta p}}$ and

$$Y=\parallel \sum _{n=1}^{\infty }\left({\int }_0^T{(T-s)}^{\alpha -1}\frac{E_{\alpha ,\alpha }(-{\lambda }_n^{\beta }{(T-s)}^{\alpha })}{E_{\alpha ,1}(-{\lambda }_n^{\beta }{T}^{\alpha })}<F(·,s,u_{\mu }(·,s))-F(·,s,u(·,s)),{\phi }_n>ds\right){\phi }_n(x)\parallel .$$

Let $s={\lambda }_n^{\frac{\beta }{2}},s>0$, we can obtain the function $a(s)=\frac{\mu s^{2-p}}{\underline{C}+\mu s^2}$.

When $0<p<2$, because of both ${lim}_{s\to 0}=0$ and ${lim}_{s\to \infty }=0$, so

$$a(s)\le \underset{s\in (0,\infty )}{sup}a(s)\le a(s_0),$$

where $s_0\in (0,\infty )$ and $s_0$ satisfies $a^{\prime }(s_0)=0$.

If $s_0$ satisfies the equation $a^{\prime }(s_0)=0$, we obtain

$$s_0={(\frac{(2-p)\underline{C}}{\mu p})}^{\frac{1}{2}}.$$

Then

$$a(s)\le a_{s_0}=\frac{\mu {(\frac{(2-p)\underline{C}}{\mu p})}^{\frac{2-p}{2}}}{1+\mu \frac{(2-p)\underline{C}}{\mu p}}=\frac{{(\frac{(2-p)\underline{C}}{p})}^{\frac{2-p}{2}}}{\underline{C}+\frac{(2-p)\underline{C}}{p}}{\mu }^{\frac{p}{2}}=C_1{\mu }^{\frac{p}{2}}.$$

When $p\ge 2$,

$$a(s)=\frac{\mu s^{2-p}}{\underline{C}+\mu s^2}\le \mu .$$

According to the above calculation, we can obtain

$$A(n)\le \left\{\begin{array}{c}{C}_1{\mu }^{\frac{p}{2}},0<p<2,\hfill \\ \mu ,p\ge 2,\hfill \end{array}\right.$$

where $C_1=\frac{{(\frac{(2-p)\underline{C}}{p})}^{\frac{2-p}{2}}}{\underline{C}+\frac{(2-p)\underline{C}}{p}}$.

□

Like the proof of (18), Y has the following conclusion:

$$Y\le \frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T){\parallel f_{\mu }(x)-f(x)\parallel }_{L^2(0,\pi )}.$$

(28)

Consequently,

$$\parallel f_{\mu }(x)-f(x)\parallel \le \left\{\begin{array}{c}\frac{C_1}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T)}{\mu }^{\frac{p}{2}}E,0<p<2,\hfill \\ \frac{1}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}\mathsf{\Psi }(T)}\mu E,p\ge 2.\hfill \end{array}\right.$$

(29)

By (27) and (29), we can obtain

$$\mu =\left\{\begin{array}{c}{(\frac{\delta }{E})}^{\frac{2}{p+2}},0<p<2,\hfill \\ {(\frac{\delta }{E})}^{\frac{1}{2}},p\ge 2.\hfill \end{array}\right.$$

(30)

Combining (27), (29) with (30), we obtain

$$\parallel f_{\mu }^{\delta }{(x)-f(x)\parallel }_{L^2(0,\pi )}\le \left\{\begin{array}{c}{C}_2{\delta }^{\frac{p}{p+2}}{E}^{\frac{2}{p+2}},0<p<2,\hfill \\ C_3{\delta }^{\frac{1}{2}}{E}^{\frac{1}{2}},p\ge 2,\hfill \end{array}\right.$$

(31)

where $C_2=\frac{1+C_1}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}|\mathsf{\Psi }(T)|}$, $C_3=\frac{2}{1-\frac{M_{2,\alpha }^{+}}{\underline{C}}|\mathsf{\Psi }(T)|}$.

5. Numerical Examples

In this section, we will give numerical examples to prove the effectiveness and stability of the quasi-boundary regularization method. First, we will select three numerical examples and discretize the original formula. Next, Matlab software is used for numerical simulation on the basis of certain mathematical analysis.

We solve the following direct problem to obtain the final data $g(x)$:

$$\left\{\begin{array}{cc}{D}_t^{\alpha }u=-A^{\beta }u(x,t)+F(u(x,t),x,t),\hfill & (0,\pi )\times (0,T),\hfill \\ u(0,t)=u(\pi ,t)=0,\hfill & (0,T),\hfill \end{array}\right.$$

(32)

Through solving the above equation by a finite difference method, we obtain the “exact” $g(x)$. The time step and the space step are defined as $\Delta x=\pi /M$ and $\Delta t=T/N$, respectively. Thus, the time grid node and the space grid node are, respectively, defined as $t_n=n\Delta t(n=0,1,2,\dots ,N)$ and $x_i=i\Delta x(i=0,1,2,\dots ,M)$. In addition, the approximate value of the unknown function is denoted as $u_i^n\approx u(x_i,t_n)$.

We generate the noise-contaminated data by adding a random perturbation, i.e.,

$$g^{\delta }(x)=g(x)+\epsilon ·g(x)(2·rand(size(g))-1),$$

(33)

where $size(g)$ represents the size of g in space, the function $rand(·)$ generates arrays of random numbers whose elements are normally distributed with mean 0, variance ${\sigma }^2=1$ and the noise level is:

$$\delta =\parallel g^{\delta }-g\parallel =\sqrt{\frac{1}{M+1}\sum _{i=1}^{M+1}{(g_i-g_i^{\delta })}^2}.$$

(34)

The absolute error level is defined as:

$$e_a=\sqrt{\frac{1}{M+1}\sum {(f(x)-f^{\delta }(x))}^2},$$

(35)

In the following example, we let $T=1,\beta =0.5$, $F(u(x,t),x,t)=u(x,t)$, $M=100,$ $N=50$ and the noise level $\epsilon =0.01,0.005,0.001$.

From Table 1, fixing $\epsilon =0.01$, we can see that the relative error increases as $\alpha$ increases. On the other hand, from Table 2, fixing $\alpha =0.25$, we can see that the relative error increases as $\epsilon$ increases.

Table 1. Numerical results of Example 1 for different $\alpha$ with $\epsilon =0.01$.

$\mathit{\alpha }$	0.05	0.10	0.15	0.20	0.25
$e_a$	0.0278	0.0538	0.0787	0.1086	0.1399

Table 2. Numerical results of Example 1 for different $\epsilon$ with $\alpha =0.25$.

$\mathit{\epsilon }$	0.0001	0.0002	0.0004	0.0006	0.0008
$e_a$	0.1280	0.1281	0.1283	0.1284	0.1285

To illustrate our method, we consider the following test functions:

Example 1.

Consider smooth function

$$f(x)=sin(x).$$

Example 2.

Consider piecewise smooth function

$$f(x)=\left\{\begin{array}{c}2x,0<x<\frac{\pi }{2},\hfill \\ 2(\pi -x),\frac{\pi }{2}<x<\pi .\hfill \end{array}\right.$$

Example 3.

Consider non-smooth function

$$f(x)=\left\{\begin{array}{c}0,0<x<\frac{\pi }{3},\hfill \\ 1,\frac{\pi }{3}<x<\frac{2\pi }{3},\hfill \\ 0,\frac{2\pi }{3}<x<\pi .\hfill \end{array}\right.$$

Figure 1 is a comparison between exact solution $f(x)$ of the relative error level $ϵ=0.01,0.005,0.001$ under Example 1 (smooth function) and its approximate solution $f_{\mu }^{\delta }(x)$ under $\alpha =0.05,0.15,0.25$. Figure 2 is a comparison between exact solution $f(x)$ of the relative error level $ϵ=0.01,0.005,0.001$ under Example 2 (piecewise smooth function) and its approximate solution $f_{\mu }^{\delta }(x)$ under $\alpha =0.05,0.15,0.25$. Figure 3 is a comparison between exact solution $f(x)$ of the relative error level $ϵ=0.01,0.005,0.001$ under Example 3 (non-smooth function) and its approximate solution $f_{\mu }^{\delta }(x)$ under $\alpha =0.05,0.15,0.25$.

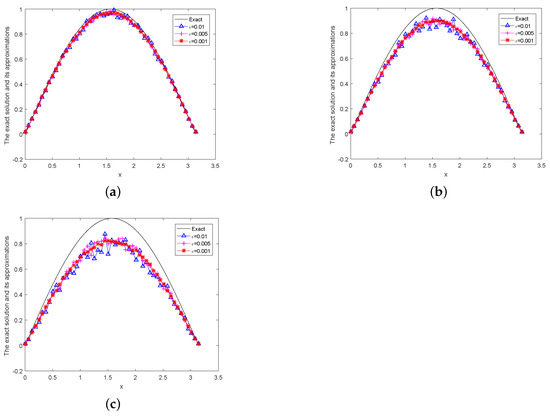
Figure 1. The exact $f(x)$ and regularization solution $f_{\mu }^{\delta }(x)$ is given by a posteriori parameter choice rule for Example 1, (a) $\alpha =0.05$, (b) $\alpha =0.15$, (c) $\alpha =0.25$.

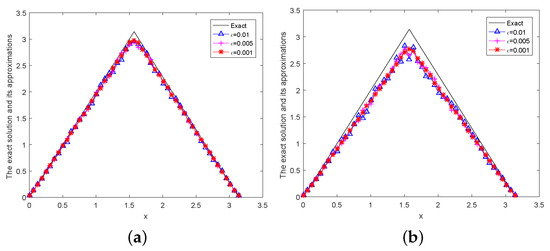
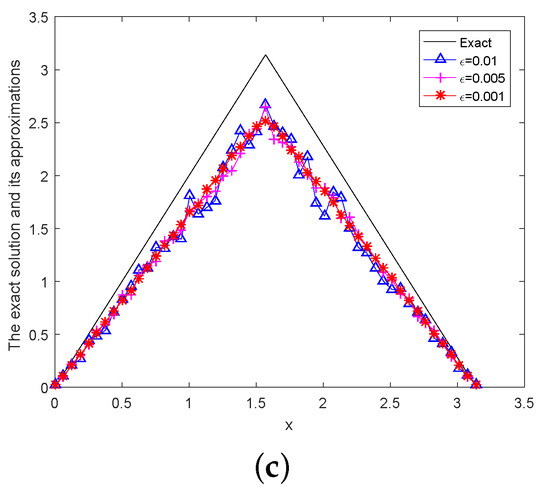
Figure 2. The exact $f(x)$ and regularization solution $f_{\mu }^{\delta }(x)$ is given by a posteriori parameter choice rule for Example 2, (a) $\alpha =0.05$, (b) $\alpha =0.15$, (c) $\alpha =0.25$.

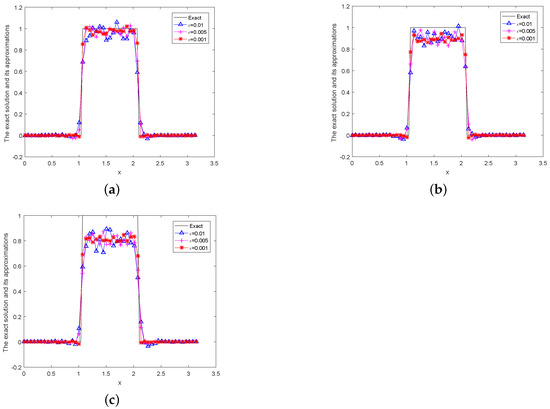
Figure 3. The exact $f(x)$ and regularization solution $f_{\mu }^{\delta }(x)$ is given by a posteriori parameter choice rule for Example 3, (a) $\alpha =0.05$, (b) $\alpha =0.15$, (c) $\alpha =0.25$.

From the above numerical results, we can obtain the conclusion that the quasi-boundary regularization method is effective in solving this problem; the smaller $\epsilon ,\alpha$ the better the numerical results.

6. Conclusions

In this paper, we consider an identification initial value problem for a time-fractional nonlinear diffusion–heat equation with a fractional Laplacian. We talk about the uniqueness and the ill-posedness of the inverse problem. We take on the quasi-boundary method to solve this problem. Based on the properties of the Mittag–Leffler function and the trigonometric inequality, the error estimate between the regularization solution and the exact solution is obtained. Furthermore, we give out numerical examples to show the quasi-boundary method is effective in solving the problem.