Omnidimensional Convex Polytopes

Abstract

The study shows that the volumes and surfaces of n-balls, n-simplices, and n-orthoplices are holomorphic functions of n, which makes those objects omnidimensional, that is well defined in any complex dimension. Applications of these formulas to the omnidimensional polytopes inscribed in and circumscribed about n-balls reveal previously unknown properties of these geometric objects. In particular, for $0<n<1$, the volumes of the omnidimensional polytopes are larger than those of circumscribing n-balls, and both their volumes and surfaces are smaller than those of inscribed n-balls. The surface of an n-simplex circumscribing a unit diameter n-ball is spirally convergent to zero with real n approaching negative infinity but first has a local maximum at $n=-3.5$. The surface of an n-orthoplex circumscribing a unit diameter n-ball is spirally divergent with real n approaching negative infinity but first has a local minimum at $n=-1.5$, where its real and imaginary parts are equal to each other; similarly, is its volume, where the similar local minimum occurs at $n=-3.5$. Reflection functions for volumes and surfaces of these polytopes inscribed in and circumscribed about n-balls are proposed. Symmetries of products and quotients of the volumes in complex dimensions n and $-n$ and of the surfaces in complex dimensions n and $2-n$ are shown to be independent of the metric factor and the gamma function. Specific symmetries also hold between the volumes and surfaces in dimensions $n=-1/2$ and $n=1/2$.

1. Introduction

The notion of a dimension n is intuitively defined as a natural number of coordinates of a point within Euclidean space ${\mathbb{R}}^n$. However, this is not the only possible definition [1,2] of a dimension of a set. For example, analytic continuations from positive dimensions [2,3,4,5] can define negative dimensions [6]. Fractional (or fractal), including negative [7], dimensions are consistent with experimental results and enable the examination of transport parameters in multiphase fractal media [8,9]. This renders dimension n real, or at least a rational number. Complex [2], including complex fractional [10], dimensions can also be considered. Complex geodesic paths, for example, emerge in the presence of black hole singularities [11] and in entropic motion on curved statistical manifolds [12]. Complex wavelengths occur in Maxwell–Boltzmann, and Fermi–Dirac statistics on black hole event horizons [13]. Fractional derivatives of complex functions can describe different physical phenomena [14]. For example, it was recently shown [15] that the magnetic monopole motion in a 3-simplicial spin ice crystal lattice is limited to a fractal cluster.

In n-dimensional space, n-dimensional objects have $(n-1)$-dimensional surfaces which have a dimension of volume in $(n-1)$-dimensional space. However, this sequence has a singularity at $n=-1$. A 0-dimensional point in 0-dimensional space has a vanishing $(-1)$-surface being a vanishing volume of the $(-1)$-dimensional void. But the surface of the $(-1)$-dimensional void is not $(-2)$-dimensional. It is undefined. This discontinuity hints that thinking about dimension in terms of a point on a number axis, where negative dimensions are analytic continuations from positive ones, may be misleading. Thinking of a dimension as a point on a number semiaxis, similar to a point on a radius with $(-n)$-dimension corresponding to n-dimension seems more appropriate. Considering the dimension of a set as the length exponent at which that set can be measured makes the negative dimensions refer to densities as positive ones refer to quantities [5]. Thus, the $(-2)$-dimensional pressure, for example, considered in terms of density (e.g., in units of N/m${}^2$) corresponds to a 2-dimensional area (in units of m${}^2$) that it acts upon. Following the same logic, gravitational force $F=GMm/R^2$ acting towards an inside of a 2-dimensional equipotential surface is $(-2)$-dimensional, whereas centripetal force $F=m{V}^2/R^1$ acting towards an outside of a 1-dimensional curve is $(-1)$-dimensional.

The notion of distance intuitively defines how far apart two points are. Thus, intuition suggests that it is a non-negative quantity. However, intuition can be misleading (e.g., in aviation, where relying on a sense of orientation [i.e., relying on intuition] can be fatal), and the Euclidean distance admits not only the principal, non-negative, square root but also a negative one. This fact, taken plainly, violates the nonnegativity axiom of the metric. However, diffuse metrics [16], including the Łukaszyk–Karmowski metric [17], are known to violate the identity of the indiscernibles axiom of the metric. This hints that axiomatizing distance as a non-negative quantity may also be misleading. Complex effects (bivalence) extend real effects (classically one value), just as quantum theory extends classical physics.

Prior research [18] presented novel recurrence relations for volumes and surfaces of the three polytopes present in all natural dimensions [19]. It was also conjectured in the prior research [18] that they were continuous for $n\in \mathbb{R}$ within domains of their definitions, whereas the starting points for fractional dimensions can be provided, e.g., using spline interpolation between two (or three, in the case of n-balls) subsequent integer dimensions. The present study shows that these recurrence relations allow removing indefiniteness present in known formulas, thus making them holomorphic functions of a complex dimension n and omnidimensional (i.e., well-defined $\forall n\in \mathbb{C}$).

Refs. [13,20,21,22] outline the framework for the physical explanation of the observed results.

The paper is structured as follows. Section 2 summarizes known formulas and recurrence relations for volumes and surfaces of n-balls and regular, convex n-polytopes. Section 3 shows that these formulas and recurrence relations can be extended to all complex dimensions. Section 4 examines the properties of the omnidimensional, regular, convex polytopes inscribed in and circumscribed about n-balls and their reflection functions. Section 5 presents metric-independent relations between volumes and surfaces of these polytopes and n-balls, whereas Section 6 presents particular symmetries between volumes and surfaces for $\left|n\right|=1/2$. Section 7 concludes and discusses the findings of this study, hinting at their possible applications.

2. Known Formulas

It is known that the volume of an n-ball (B) is

$$V{\left(n\right)}_B=\frac{{\pi }^{n/2}}{\mathsf{\Gamma }(n/2+1)}{R}^n,$$

(1)

where $\mathsf{\Gamma }:\mathbb{C}\to \mathbb{C}$ is the Euler’s gamma function, $n\in \mathbb{C}\backslash \{n=-2k-2$, $k\in {\mathbb{N}}_0\}$, and R denotes the n-ball radius. As the gamma function is meromorphic, volumes of n-balls are complex in complex dimensions. The volume of an n-ball can be expressed [23] in terms of the volume of an $(n-2)$-ball of the same radius as a recurrence relation

$$V{\left(n\right)}_B=\frac{2\pi R^2}{n}V{(n-2)}_B,$$

(2)

where $V{\left(0\right)}_B:=1$ and $V_1{\left(R\right)}_B:=2R$. The relation (2) can be extended [18] into negative dimensions as

$$V{\left(n\right)}_B=\frac{n+2}{2\pi R^2}V{(n+2)}_B,$$

(3)

solving Equation (2) for $V(n-2)$ and assigning a new n as the previous $n-2$. A radius recurrence relation [18] (We choose the notation $f\left(n\right)$ over $f_n$, as $n\in \mathbb{C}$)

$$f\left(n\right):=\frac{2}{n}f(n-2),$$

(4)

where $n\in \mathbb{C}$, $f\left(0\right):=1$ and $f\left(1\right):=2$, allow for expressing the volume n-ball as

$$V{\left(n\right)}_B:=f\left(n\right){\pi }^{⌊n/2⌋}{R}^n,$$

(5)

where “$⌊x⌋$” is the floor function that yields the greatest integer less than or equal to its argument x. The relation (4) can be, analogously as Equation (2), extended [18] into negative dimensions as

$$f\left(n\right)=\frac{n+2}{2}f(n+2),$$

(6)

which allows us to define $f(-1)=f\left(0\right):=1$ to initiate the sequences (4) or (6). The known [23] surface of an n-ball is

$$S{\left(n\right)}_B=\frac{n}{R}V{\left(n\right)}_B.$$

(7)

We note in passing that in this study S(n) denotes the (n − 1)-dimensional surface of an n-dimensional object (that is a property of this object), and not the n-dimensional surface of the (n + 1)-dimensional object, as it is commonly defined in the literature.

The known volume of an n-cube (C) is

$$V{\left(n\right)}_C=A^n,$$

(8)

where $n\in \mathbb{C}$ and A is the edge length. The known surface of an n-cube is

$$S{\left(n\right)}_C=2n{A}^{n-1},$$

(9)

where $n\in \mathbb{C}$.

The known [24,25] volume of a regular n-simplex (S) is

$$V{\left(n\right)}_S=\frac{\sqrt{n+1}}{n!\sqrt{2^n}}{A}^n,$$

(10)

where $n\in \mathbb{N}$. Equation (10) can be written [18] as a recurrence relation

$$V{\left(n\right)}_S=AV{(n-1)}_S\sqrt{\frac{n+1}{2n^3}},$$

(11)

with $V{\left(0\right)}_S:=1$, to remove the indefiniteness of the factorial for $n<1$. Equation (11) can be solved for $V(n-1)$. Assigning new n as the previous $n-1$, yields [18]

$$V{\left(n\right)}_S=\frac{V{(n+1)}_S}{A}\sqrt{\frac{2{(n+1)}^3}{n+2}},$$

(12)

which also removes the singularity for $n=0$ present in the volume (10). An n-simplex has $n+1$$(n-1)$-facets [23]. Therefore, its surface is

$$S{\left(n\right)}_S=(n+1)V{(n-1)}_S.$$

(13)

The known [23] volume of an n-orthoplex (O) is

$$V{\left(n\right)}_O=\frac{\sqrt{2^n}}{n!}{A}^n,$$

(14)

where $n\in {\mathbb{N}}_0$.

Equation (14) can be written [18] as a recurrence relation

$$V{\left(n\right)}_O=AV{(n-1)}_O\frac{\sqrt{2}}{n},$$

(15)

where $n\ne 0$ and $V{\left(0\right)}_O:=1$, to remove the indefiniteness of the factorial for $n<0$. Solving Equation (15) for $V(n-1)$ and assigning new n as the previous $n-1$, yields [18]

$$V{\left(n\right)}_O=V{(n+1)}_O\frac{n+1}{A\sqrt{2}},$$

(16)

which also removes singularity for $n=0$ present in Equation (15). Any n-orthoplex has $2^n$ facets [23], which are regular $(n-1)$-simplices. Therefore, its surface is

$$S{\left(n\right)}_O=2^{n}V{(n-1)}_S.$$

(17)

3. Holomorphizing Known Formulas

The known formulas presented in the preceding section can be extended to all complex dimensions. We note that volumes and surfaces of n-cubes are already defined $\forall n\in \mathbb{C}$ and thus are holomorphic. We also note that a square root is bivalued in the complex domain and by choosing complex analysis, we enter into bivalence by its very nature ($A^n=A^{2n/2}=\sqrt{A^{2n}}\stackrel{?}{=}\pm A^n$). Therefore, volumes and surfaces of n-balls and regular, convex n-polytopes are also bivalued in complex dimensions n. We call the branch with positive values in positive real dimensions the principal branch.

Theorem 1.

The volume of an n-ball is a holomorphic, bivalued function of a complex dimension n.

Proof. 

First, we note that the initial bivalued values for the radius recurrence relations (4) and (6) are $f(-1)=f\left(0\right):=\pm 1$, $V{\left(0\right)}_B:=\pm 1$ and $V_1{\left(R\right)}_B:=\pm 2R$. Then, we note that the recurrence relations (3) and (5) correspond to each other

$$\begin{array}{cc}\hfill & V{\left(n\right)}_B=\frac{n+2}{2\pi R^2}V{(n+2)}_B=\frac{n+2}{2}f(n+2){\pi }^{⌊n/2⌋}{R}^n,\hfill \\ \hfill & V{(n+2)}_B=\pi f(n+2){\pi }^{⌊n/2⌋}{R}^{n+2},\hfill \end{array}$$

(18)

which, after setting $\tilde{n}:=n+2$, yields

$$V{\left(\tilde{n}\right)}_B=f\left(\tilde{n}\right){\pi }^{1+⌊(\tilde{n}-2)/2⌋}{R}^{\tilde{n}}=f\left(\tilde{n}\right){\pi }^{⌊\tilde{n}/2⌋}{R}^{\tilde{n}}.$$

(19)

Comparing the non-recurrence general n-ball volume (1), which is bivalued for $n\in \mathbb{C}$ and valid within the domain of the gamma function, with the recurrence relation (3)

$$V{\left(n\right)}_B=\pm \frac{{\pi }^{n/2}}{\mathsf{\Gamma }(n/2+1)}{R}^n=\frac{n+2}{2\pi R^2}V{(n+2)}_B$$

(20)

yields

$$\begin{array}{c}\hfill V{(n+2)}_B=\pm \frac{2{\pi }^{n/2+1}}{(n+2)\mathsf{\Gamma }(n/2+1)}{R}^{n+2}.\end{array}$$

(21)

Setting $\tilde{n}:=n+2$ yields

$$\begin{array}{cc}\hfill V{\left(\tilde{n}\right)}_B& =\pm \frac{2{\pi }^{\tilde{n}/2}}{m\mathsf{\Gamma }(\tilde{n}/2)}{R}^m=\pm \frac{{\pi }^{\tilde{n}/2}}{\frac{\tilde{n}}{2}\mathsf{\Gamma }(\tilde{n}/2)}{R}^{\tilde{n}}=\hfill \\ & =\pm \frac{{\pi }^{\tilde{n}/2}}{\mathsf{\Gamma }(m/2+1)}{R}^{\tilde{n}},\hfill \end{array}$$

(22)

which recovers Equation (1), as $\frac{n}{2}\mathsf{\Gamma }\left(\frac{n}{2}\right)=\mathsf{\Gamma }\left(\frac{n}{2}+1\right)$, $\forall n\in \mathbb{C}\backslash \{n=-2k$, $k\in {\mathbb{N}}_0\}$. Thus, we have proved that the recurrence relations (2), (3), and (5) correspond to the general n-ball volume (22) within this domain.

However, now we can use any of the backward recurrence relations (3) or (5) with (6) to determine the values of the n-ball volume outside this domain: $\forall n+2\in \mathbb{C}$ we can find $V{\left(n\right)}_B$.

On the other hand

$$\underset{n\to -2k-2,k\in {\mathbb{N}}_0}{lim}\pm \frac{{\pi }^{n/2}{R}^n}{\mathsf{\Gamma }(n/2+1)}=\frac{a}{\infty }=0,$$

(23)

so the poles of the meromorphic gamma function $\mathsf{\Gamma }(n/2+1)$ present in Equation (22), now defined in the sense of a limit of a function, vanish, which completes the proof. □

Corollary 1.

The surface of an n-ball is a holomorphic, bivalued function of a complex dimension n.

Proof. 

If the volume of an n-ball is a holomorphic, bivalued function by Theorem 1, then, using Equation (7), the surface of an n-ball is also a holomorphic function.

Using Equations (22) and (7) the surface of an n-ball is given by

$$S{\left(n\right)}_B=\pm \frac{n{\pi }^{n/2}}{\mathsf{\Gamma }(n/2+1)}{R}^{n-1}.$$

(24)

□

Theorem 2.

The volume of a regular n-simplex is a holomorphic, bivalued function of a complex dimension n.

Proof. 

Expressing the factorial in the volume of a regular n-simplex (10) by the gamma function extends its domain of applicability to complex dimensions

$$\begin{array}{cc}\hfill V{\left(n\right)}_S& =\pm \frac{\sqrt{n+1}}{n!\sqrt{2^n}}{A}^n=\pm \frac{{(1+n)}^{1/2}}{\mathsf{\Gamma }(n+1)2^{n/2}}{A}^n.\hfill \end{array}$$

(25)

On the other hand, comparing the volume (25) with the recurrence relation (12)

$$\pm \frac{\sqrt{n+1}}{\mathsf{\Gamma }(n+1)2^{n/2}}{A}^n=\frac{V{(n+1)}_S}{A}\sqrt{\frac{2{(n+1)}^3}{n+2}}$$

(26)

yields

$$\begin{array}{c}\hfill V{(n+1)}_S=\pm \frac{\sqrt{n+1}\sqrt{n+2}}{\mathsf{\Gamma }(n+1)2^{(n+1)/2}\sqrt{{(n+1)}^3}}{A}^{n+1},\end{array}$$

(27)

which, after setting $\tilde{n}:=n+1$, yields

$$\begin{array}{cc}\hfill V{\left(\tilde{n}\right)}_S=& \pm \frac{\sqrt{\tilde{n}}\sqrt{\tilde{n}+1}}{\mathsf{\Gamma }\left(\tilde{n}\right)2^{\tilde{n}/2}\sqrt{{\tilde{n}}^3}}{A}^{\tilde{n}}=\hfill \\ \hfill =& \pm \frac{\sqrt{\tilde{n}+1}}{\mathsf{\Gamma }(\tilde{n}+1)2^{\tilde{n}/2}}{A}^{\tilde{n}}\frac{\tilde{n}\sqrt{\tilde{n}}}{\sqrt{{\tilde{n}}^3}}=\hfill \\ \hfill =& \pm \frac{\sqrt{\tilde{n}+1}}{\mathsf{\Gamma }(\tilde{n}+1)2^{\tilde{n}/2}}{A}^{\tilde{n}},\hfill \end{array}$$

(28)

and recovers the volume (25) as $n\mathsf{\Gamma }\left(n\right)=\mathsf{\Gamma }(n+1)\forall n\in \mathbb{C}\backslash \{n=-k,k\in {\mathbb{N}}_0\}$ and $n\sqrt{n}/\sqrt{n^3}=\pm 1$ (cf. Appendix A).Thus, we have proved that the recurrence relation (12) corresponds to the generalized n-simplex volume (25) within this domain.

However, now we can use the recurrence relation (12) to determine the values of the n-simplex volume outside this domain: $\forall n+1\in \mathbb{C}$ we can find $V{\left(n\right)}_S$. For example, even though $n\sqrt{n}/\sqrt{n^3}$ is undefined for $n=0$, we can determine that $V{\left(0\right)}_S=\pm 1$ using the recurrence relation (12) with $V{\left(1\right)}_S=\pm A$ obtained from the volume (25).

On the other hand,

$$\underset{n\to -k-1,k\in {\mathbb{N}}_0}{lim}\pm \frac{2^{-n/2}{A}^n\sqrt{n+1}}{\mathsf{\Gamma }(n+1)}=\frac{a}{\infty }=0,$$

(29)

so the poles of the meromorphic gamma function $\mathsf{\Gamma }(n+1)$ present in the volume (25), now defined in the sense of a limit of a function, vanish, which completes the proof. □

For $n\in \mathbb{R}\backslash \mathbb{Z}\cap \{n\in \mathbb{R}:n<-1$}, the n-simplex volume (25) is imaginary.

Corollary 2.

The surface of a regular n-simplex is a holomorphic, bivalued function of a complex dimension n.

Proof. 

If the volume of a regular n-simplex is a holomorphic, bivalued function by Theorem 2, then its surface, using Equation (13), is also a holomorphic, bivalued function.

Using (13) and (25), the surface of a regular n-simplex is given by (cf. Appendix A)

$$\begin{array}{cc}\hfill S{\left(n\right)}_S& =\pm \frac{n^{3/2}(n+1)}{\mathsf{\Gamma }(n+1)2^{(n-1)/2}}{A}^{n-1}\frac{(n-1)\sqrt{n-1}}{\sqrt{{(n-1)}^3}}=\hfill \\ & =\pm \frac{n^{3/2}(1+n)}{\mathsf{\Gamma }(n+1)2^{(n-1)/2}}{A}^{n-1}.\hfill \end{array}$$

(30)

□

Again, even though $(n-1)\sqrt{n-1}/\sqrt{{(n-1)}^3}$ is undefined for $n=1$, we can determine that $S{\left(1\right)}_S=\pm 2$ directly from Equation (13) knowing that $V{\left(0\right)}_S=\pm 1$.

For $n\in \mathbb{R}\backslash \mathbb{Z}:n<0$, the n-simplex surface (30) is imaginary.

Theorem 3.

The volume of an n-orthoplex is a bivalued, holomorphic function of a complex dimension n.

Proof. 

Expressing the factorial in the volume of an n-orthoplex (14) with the gamma function extends the domain of applicability of Equation (14) to complex dimensions

$$\begin{array}{c}\hfill V{\left(n\right)}_O=\pm \frac{\sqrt{2^n}}{n!}{A}^n=\pm \frac{\sqrt{2^n}}{\mathsf{\Gamma }(n+1)}{A}^n.\end{array}$$

(31)

On the other hand, comparing Equation (31) with the recurrence relation (16)

$$\begin{array}{c}\hfill \pm \frac{\sqrt{2^n}}{\mathsf{\Gamma }(n+1)}{A}^n=V{(n+1)}_O\frac{n+1}{A\sqrt{2}},\end{array}$$

(32)

yields

$$V{(n+1)}_O=\pm \frac{2^{(n+1)/2}}{(n+1)\mathsf{\Gamma }(n+1)}{A}^{n+1},$$

(33)

whereas setting $\tilde{n}=n+1$ in Equation (33) yields

$$V{\left(\tilde{n}\right)}_O=\pm \frac{\sqrt{2^{\tilde{n}}}}{\tilde{n}\mathsf{\Gamma }\left(\tilde{n}\right)}{A}^{\tilde{n}}=\pm \frac{2^{\tilde{n}/2}}{\mathsf{\Gamma }(\tilde{n}+1)}{A}^{\tilde{n}},$$

(34)

which recovers n-orthoplex volume (14), as $n\mathsf{\Gamma }\left(n\right)=\mathsf{\Gamma }(n+1)$$\forall n\in \mathbb{C}\backslash \{n=-k,k\in {\mathbb{N}}_0\}$. Thus, we have proved that the recurrence relation (16) corresponds to the general n-orthoplex volume (31) within this domain.

However, now we can use the recurrence relation (16) to determine the values of the n-orthoplex volume outside this domain: $\forall n+1\in \mathbb{C}$ we can find $V{\left(n\right)}_O$. On the other hand

$$\underset{n\to -k-1,k\in {\mathbb{N}}_0}{lim}\pm \frac{2^{n/2}{A}^n}{\mathsf{\Gamma }(n+1)}=\frac{a}{\infty }=0,$$

(35)

so the poles of the meromorphic gamma function $\mathsf{\Gamma }(n+1)$ present in (31), now defined in the sense of a limit of a function, vanish, which completes the proof. □

Corollary 3.

The surface of an n-orthoplex is a holomorphic, bivalued function of a complex dimension n.

Proof. 

If the volume of a regular n-simplex is a holomorphic, bivalued function by Theorem 2, then, using Equation (17), the surface of an n-orthoplex is a holomorphic, bivalued function.

Using Equations (17) and (31), the surface of an n-orthoplex is given by

$$S{\left(n\right)}_O=\pm \frac{n^{3/2}{2}^{(n+1)/2}}{\mathsf{\Gamma }(n+1)}{A}^{n-1}.$$

(36)

□

For $n\in \mathbb{R}\backslash \mathbb{Z}:n<0$, n-orthoplex bivalued surface (36) is imaginary.

Thus, the volumes and surfaces of n-balls, n-simplices, and n-orthoplices, shown in Figure 1 and Figure 2 for $n\in \mathbb{R}$, are holomorphic functions of n, which makes those objects omnidimensional. They can be explicitly expressed in terms of the complex dimension (cf. Appendix B).

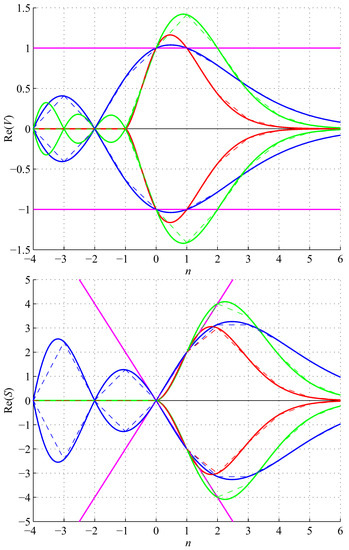
Figure 1. Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), n-cubes (pink), and unit diameter n-balls (blue), along with the integer recurrence relations (dashed lines) for $n\in \left[-4,6\right]$.

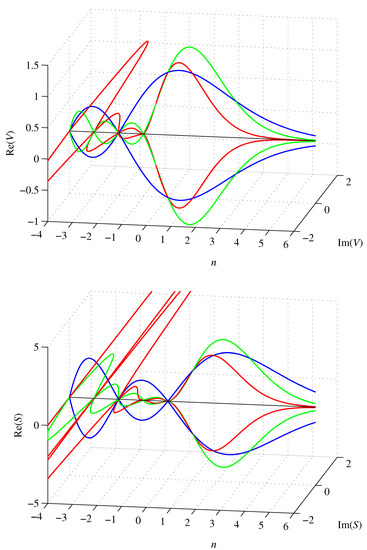
Figure 2. Graphs of volumes (V) and surfaces (S) of unit edge length regular n-simplices (red), n-orthoplices (green), and unit diameter n-balls (blue) for $n\in \mathbb{R}:n\in \left[-4,6\right]$.

4. Omnidimensional Polytopes Inscribed in and Circumscribed about $\mathit{n}$-Balls

First, we will introduce the definition of a reflection function.

Definition 1.

For each function $F:\mathbb{C}\to \mathbb{C}$ of a complex argument n given by the formula

$$F\left(n\right)=\pm \prod _{j=1}^l{(a_j+b_{j}n)}^{(c_j+d_{j}n)/2}g\left(n\right),$$

(37)

where $j=1,2,\dots ,l\in \mathbb{N}$, $a_j,b_j,c_j,d_j\in \mathbb{R}:a_j\ge 0,b_j>0$, and $g\left(n\right)$ is some nonzero function of n, we define its reflection function

$$\tilde{F}\left(n\right):=\pm i^{c+dn}\prod _{j=1}^l{(-a_j-b_{j}n)}^{(c_j+d_{j}n)/2}g\left(n\right),$$

(38)

where

$$c:=\sum _{j=1}^l{c}_j\mathit{and}d:=\sum _{j=1}^l{d}_j\ne 0.$$

(39)

Theorem 4.

The same branches of functions $F\left(n\right)$ (37) and $\tilde{F}\left(n\right)$ (38) are equal to each other for $n\le 0$ or for $n\in \mathbb{Z}$ such that $sin\left(\frac{c+dn}{2}\pi \right)=0$, with c, d defined by (39).

Proof. 

For $n\in \mathbb{R}$, the functions (37) and (38) can be expressed as

$$\begin{array}{cc}\hfill F\left(n\right)& =\pm \prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2+i{\theta }_n(c_j+d_{j}n)/2}g\left(n\right)=\hfill \\ \hfill & =\pm e^{i{\theta }_n({\sum }_{j=1}^l{c}_j+n{\sum }_{j=1}^l{d}_j)/2}\hfill \\ \hfill & \prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right)=\hfill \\ \hfill & =\pm e^{i{\theta }_n(c+dn)/2}\prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right),\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill \tilde{F}\left(n\right)& =\pm i^{c+dn}\hfill \\ \hfill & \prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2-i{\theta }_{-n}(c_j+d_{j}n)/2}g\left(n\right)=\hfill \\ \hfill & =\pm e^{-i{\theta }_{-n}({\sum }_{j=1}^l{c}_j+n{\sum }_{j=1}^l{d}_j)/2}\hfill \\ \hfill & \prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right)=\hfill \\ \hfill & =\pm i^{c+dn}{e}^{-i{\theta }_{-n}(c+dn)/2}\hfill \\ \hfill & \prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right),\hfill \end{array}$$

(41)

where ${\theta }_n=\mathrm{atan}2(0,n)$, and ${\theta }_{-n}=\mathrm{atan}2(-0,-n)$, as ${lim}_{y\to 0^{-}}\mathrm{atan}2(y,x)=-\pi$ and ${lim}_{y\to 0^{+}}\mathrm{atan}2(y,x)=\pi$ for $x<0$.

Without loss of generality, we consider positive branches of $F\left(n\right)$ (40) and $\tilde{F}\left(n\right)$ (41)

$$\begin{array}{cc}\hfill & e^{i{\theta }_n(c+dn)/2}\prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right)=\hfill \\ \hfill =& i^{c+dn}{e}^{-i{\theta }_{-n}(c+dn)/2}\prod _{j=1}^l{e}^{(c_j+d_{j}n)ln(a_j+b_{j}n)/2}g\left(n\right),\hfill \\ \hfill & e^{i{\theta }_n(c+dn)/2}=i^{c+dn}{e}^{-i{\theta }_{-n}(c+dn)/2}\iff \hfill \\ \hfill & e^{i({\theta }_n+{\theta }_{-n})(c+dn)/2}=i^{c+dn}.\hfill \end{array}$$

(42)

We note here that $\forall n\in \mathbb{R}$, such that $n\ne 0$

$${\theta }_n+{\theta }_{-n}=\left\{\begin{array}{cc}\pi ,\hfill & n<0\hfill \\ -\pi ,\hfill & n>0\hfill \end{array}\right.,$$

(43)

so that

$$\begin{array}{cc}\hfill & e^{i({\theta }_n+{\theta }_{-n})(c+dn)/2}=\hfill \\ \hfill =& \left\{\begin{array}{cc}{e}^{i\pi (c+dn)/2}=\cos \left(\frac{c+dn}{2}\pi \right)+isin\left(\frac{c+dn}{2}\pi \right),\hfill & n<0\hfill \\ e^{-i\pi (c+dn)/2}=\cos \left(\frac{c+dn}{2}\pi \right)-isin\left(\frac{c+dn}{2}\pi \right),\hfill & n>0,\hfill \end{array}\right.\hfill \end{array}$$

(44)

and that $\forall n\in \mathbb{C}$ and for the principal value of $\theta$

$$i^n=\cos \left(\frac{n}{2}\pi \right)+isin\left(\frac{n}{2}\pi \right).$$

(45)

Therefore,

$$\begin{array}{cc}\hfill & i^{c+dn}=\cos \left(\frac{c+dn}{2}\pi \right)+isin\left(\frac{c+dn}{2}\pi \right)=\hfill \\ \hfill =& \left\{\begin{array}{cc}\cos \left(\frac{c+dn}{2}\pi \right)+isin\left(\frac{c+dn}{2}\pi \right),\hfill & n<0\hfill \\ \cos \left(\frac{c+dn}{2}\pi \right)-isin\left(\frac{c+dn}{2}\pi \right),\hfill & n>0\hfill \end{array}\right.\iff \hfill \\ \hfill \iff & F\left(n\right)=\tilde{F}\left(n\right)\mathrm{under}\mathrm{the}\mathrm{condition}\hfill \\ \hfill & \forall n<0\vee \forall n\in \mathbb{Z}:sin\left(\frac{c+dn}{2}\pi \right)=0.\hfill \end{array}$$

(46)

□

Each regular, omnidimensional polytope discussed in Section 3 can be inscribed in and circumscribed about an n-ball. This section presents their volumes, surfaces, and reflection functions (38). Particular values of their volumes and surfaces are listed in Table 1 and Table 2. Unless stated otherwise, $n\in \mathbb{R}$ and $k\in \mathbb{N}$. Unit diameter n-balls are assumed.

Table 1. Particular volumes of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).

n	$-3/2$	−1	$-1/2$	0	$1/2$	1	$3/2$
$V_B$	0.331	$2/\pi \approx 0.637$	$0.867$	1	$1.039$	1	$0.908$
$V_{SIB}$	$\frac{i{3}^{3/4}}{\sqrt{\pi }}\approx i1.286$	0	$\frac{1-i}{\sqrt{2\pi }}\approx 0.399\left(1-i\right)$	1	$\frac{3^{3/4}}{\sqrt{\pi }}\approx 1.286$	1	$\frac{5^{5/4}}{3^{7/4}\sqrt{\pi }}\approx 0.617$
$V_{SCB}$	$\frac{2^{3/2}}{3^{3/4}\sqrt{\pi }}\approx 0.7$	0	$\frac{1-i}{\sqrt{\pi }}\approx 0.564\left(1-i\right)$	1	$\frac{3^{3/4}}{\sqrt{2\pi }}\approx 0.909$	1	$\frac{5^{5/4}}{3^{1/4}{2}^{3/2}\sqrt{\pi }}\approx 1.133$
$V_{OIB}$	$\frac{-1}{2\sqrt{\pi }}\approx -0.282$	0	$\frac{1}{\sqrt{\pi }}\approx 0.564$	1	$\frac{2}{\sqrt{\pi }}\approx 1.128$	1	$\frac{4}{3\sqrt{\pi }}\approx 0.752$
$V_{OCB}$	$\frac{1+i}{2^{3/4}{3}^{3/4}\sqrt{\pi }}\approx 0.147\left(1+i\right)$	0	$\frac{1-i}{2^{1/4}\sqrt{\pi }}\approx 0.474\left(1-i\right)$	1	$\frac{2^{3/4}}{\sqrt{\pi }}\approx 0.949$	1	$\frac{2^{5/4}}{3^{1/4}\sqrt{\pi }}\approx 1.02$
$V_{CIB}$	$\frac{\left(i-1\right)3^{3/4}}{2^{5/4}}\approx 0.958\left(i-1\right)$	i	$\frac{\left(1+i\right)}{2^{3/4}}\approx 0.595\left(1+i\right)$	1	$2^{1/4}\approx 1.189$	1	$\frac{2^{3/4}}{3^{3/4}}\approx 0.738$
$V_{CCB}$	1	1	1	1	1	1	1

Table 2. Particular surfaces of omnidimensional polytopes inscribed in and circumscribed about unit diameter n-balls (principal branch).

n	$-3/2$	−1	$-1/2$	0	$1/2$	1	$3/2$
$S_B$	$-0.992$	$-4/\pi \approx -1.273$	$-0.867$	0	$1.039$	2	$2.723$
$S_{SIB}$	$\frac{-i{3}^{11/4}}{2\sqrt{\pi }}\approx -5.787i$	0	$\frac{1+i}{\sqrt{\pi }{2}^{3/2}}\approx 0.199\left(1+i\right)$	0	$\frac{3^{3/4}}{2\sqrt{\pi }}\approx 0.643$	2	$\frac{3^{1/4}{5}^{5/4}}{2\sqrt{\pi }}\approx 2.776$
$S_{SCB}$	$\frac{-2^{3/2}{3}^{1/4}}{\sqrt{\pi }}\approx -2.1$	0	$\frac{i-1}{\sqrt{\pi }}\approx 0.564\left(i-1\right)$	0	$\frac{3^{3/4}}{\sqrt{2\pi }}\approx 0.909$	2	$\frac{3^{3/4}{5}^{5/4}}{2^{3/2}\sqrt{\pi }}\approx 3.4$
$S_{OIB}$	$\frac{3^{3/2}i}{2^{3/2}\sqrt{\pi }}\approx 1.036i$	0	$\frac{-i}{\sqrt{2\pi }}\approx -0.399i$	0	$\frac{\sqrt{2}}{\sqrt{\pi }}\approx 0.798$	2	$\frac{2^{3/2}\sqrt{3}}{\sqrt{\pi }}\approx 2.764$
$S_{OCB}$	$\frac{-\left(1+i\right)3^{1/4}}{2^{3/4}\sqrt{\pi }}\approx -0.442\left(1+i\right)$	0	$\frac{\left(i-1\right)}{2^{1/4}\sqrt{\pi }}\approx 0.474\left(i-1\right)$	0	$\frac{2^{3/4}}{\sqrt{\pi }}\approx 0.949$	2	$\frac{2^{5/4}{3}^{3/4}}{\sqrt{\pi }}\approx 3.059$
$S_{CIB}$	$\frac{\left(1+i\right)3^{9/4}}{2^{7/4}}\approx 3.521\left(1+i\right)$	2	$\frac{1-i}{2^{5/4}}\approx 0.42\left(1-i\right)$	0	$2^{-1/4}\approx 0.841$	2	$3^{3/4}{2}^{1/4}\approx 2.711$
$S_{CCB}$	$-3$	$-2$	$-1$	0	1	2	3

4.1. Regular n-Simplices Inscribed in n-Balls

The diameter $D_{BCS}$ of an n-ball circumscribing a regular n-simplex ($BCS$) is known [25] to be

$$D_{BCS}=\pm \frac{\sqrt{2n}}{\sqrt{n+1}}A,$$

(47)

where A is the edge length. Hence, the edge length $A_{SIB}$ of a regular n-simplex inscribed ($SIB$) in an n-ball (B) with a diameter D is

$$A_{SIB}=\pm \frac{\sqrt{n+1}}{\sqrt{2n}}D,$$

(48)

so that the regular n-simplex volume (25) becomes

$$V{\left(n\right)}_{SIB}=\pm \frac{{(1+n)}^{(1+n)/2}{n}^{-n/2}{2}^{-n}}{\mathsf{\Gamma }(1+n)}{D}^n.$$

(49)

For $n\notin \mathbb{Z}:n<-1$, the inscribed n-simplex volume (49) is imaginary and divergent with n approaching negative infinity. It is complex for $-1<n<0$, with the real part equaling the imaginary part for $n=-1/2$. It is zero for $n=-k$, and for $0<n<1$, it is larger than the volume of the circumscribing n-ball. The volume (49) does not have a reflection function (38), as d in the definition (39) vanishes.

Similarly, the surface (30) of a regular inscribed n-simplex with edge length A given by Equation (48) is

$$S{\left(n\right)}_{SIB}=\pm \frac{{(1+n)}^{(1+n)/2}{n}^{(4-n)/2}{2}^{1-n}}{\mathsf{\Gamma }(1+n)}{D}^{n-1},$$

(50)

as shown in Figure 4. For $n\notin \mathbb{Z}:n<-1$ the inscribed n-simplex surface (50) is imaginary and divergent with n approaching negative infinity. It is complex for $-1<n<0$, with the real part equaling the imaginary part for $n=-1/2$. It is zero for $n=-k$, $k\in {\mathbb{N}}_0$. The surface (50) does not have a reflection function (38), as d in the definition (39) vanishes.

Volumes (49) and surfaces (50) of n-simplices inscribed in n-balls are shown in Figure 3 and Figure 4.

Figure 3. Graphs of $V{\left(n\right)}_{SIB}$ (red) and $V{\left(n\right)}_B$ (blue) for $n\in \left[-6,6\right]$.

Figure 4. Graphs of $S{\left(n\right)}_{SIB}$ (red) and $S{\left(n\right)}_B$ (blue) for $n\in \left[-6,6\right]$.

4.2. Regular n-Simplices Circumscribed about n-Balls

The diameter $D_{BIS}$ of an n-ball inscribed in a regular n-simplex ($BIS$) is known [25] to be

$$D_{BIS}=\pm \frac{\sqrt{2}}{\sqrt{n}\sqrt{n+1}}A,$$

(51)

where A is the edge length. Hence, the edge length $A_{SCB}$ of a regular n-simplex circumscribed ($SCB$) about an n-ball (B) with a diameter D is

$$A_{SCB}=\pm \frac{\sqrt{n}\sqrt{n+1}}{\sqrt{2}}D,$$

(52)

so that its volume (25) becomes

$$V{\left(n\right)}_{SCB}=\pm \frac{{(1+n)}^{(1+n)/2}{n}^{n/2}{2}^{-n}}{\mathsf{\Gamma }(1+n)}{D}^n.$$

(53)

For $n<0$, the volume (53) is complex with a nonzero imaginary part, whereas both branches are left-handed spirals converging to zero with n approaching negative infinity. For $0<n<1$, the volume (53) is smaller than the volume of an inscribed n-ball. It is zero for $n=-k$, and real for $n=-(2k+1)/2$, where it amounts to

$$\begin{array}{cc}\hfill & V{\left(\frac{-\left(2k+1\right)}{2}\right)}_{SCB}=\hfill \\ \hfill & =\pm \frac{i^{2k}{2}^{\left(4k+1\right)/2}{\left(2k-1\right)}^{\left(1-2k\right)/4}}{\mathsf{\Gamma }\left(\frac{1-2k}{2}\right){\left(2k+1\right)}^{\left(1+2k\right)/4}}\approx \hfill \\ \hfill & \approx \pm \{0.7,0.5618,0.4251,0.3172,0.2353,\dots \}.\hfill \end{array}$$

(54)

Furthermore, for $n=-1/2$ and $n=-(2k+3)/4$, the real part of the volume (53) equals the imaginary part in modulus. For $n=-1/2$, $V{(-1/2)}_{SCB}=\pm (1-i)/\sqrt{\pi }\approx \pm 0.5642(1-i)$. Otherwise, it amounts to

$$\begin{array}{cc}\hfill & V{\left(\frac{-\left(2k+3\right)}{4}\right)}_{SCB}=\hfill \\ \hfill & =\pm \frac{(1+i)i^k{2}^{\left(6k+3\right)/4}{\left(2k-1\right)}^{\left(1-2k\right)/8}}{\mathsf{\Gamma }\left(\frac{1-2k}{4}\right){\left(2k+3\right)}^{\left(2k+3\right)/8}}\approx \hfill \\ \hfill & \approx \pm \left\{-0.3549,-0.3359,0.2996,0.2626,-0.2283,\dots \right\}\hfill \\ \hfill & (1+i)i^k.\hfill \end{array}$$

(55)

The reflection function (38) of the volume (53) is

$$\tilde{V}{\left(n\right)}_{SCB}=\pm \frac{i^{1+2n}{(-1-n)}^{(1+n)/2}{(-n)}^{n/2}{2}^{-n}}{\mathsf{\Gamma }(1+n)}{D}^n,$$

(56)

and the volumes (56) and (53) are equal for $n=(2k+1)/2,k\in {\mathbb{N}}_0$.

Similarly, the surface (30) of a regular circumscribed n-simplex with edge length $A_{SCB}$ (52) is

$$S{\left(n\right)}_{SCB}=\pm \frac{{\left(1+n\right)}^{\left(1+n\right)/2}{n}^{\left(2+n\right)/2}{2}^{1-n}}{\mathsf{\Gamma }\left(1+n\right)}{D}^{n-1}.$$

(57)

The surface (57) is zero for $n=-k$, $k\in {\mathbb{N}}_0$, and for $0<n<1$, it is smaller than the surface of the inscribed n-ball. The surface (57) is complex for $n<0$, with both branches being left-handed spirals converging towards zero with n approaching negative infinity. However, it is initially divergent to achieve a modulus maximum of about 2.9757 at $n\approx -3.4997$ (numerically calculated; numerical calculations were performed in this study using Euler gamma function of complex argument defined for |n| < 172) and a real maximum of about $2.976$ at $n=-3.5$. For $n=-(2k+1)/2$ the imaginary part of the surface (57) vanishes and it amounts to

$$\begin{array}{cc}\hfill & S{\left(\frac{-\left(2k+1\right)}{2}\right)}_{SCB}=\hfill \\ \hfill & =\mp \frac{i^{2k}{2}^{\left(4k+1\right)/2}{\left(2k-1\right)}^{\left(1-2k\right)/4}}{\mathsf{\Gamma }\left(\frac{1-2k}{2}\right){\left(2k+1\right)}^{\left(2k-3\right)/4}}\approx \hfill \\ \hfill & \approx \mp \{2.1,2.809,\underline{2.976},2.854,2.588,\dots \}.\hfill \end{array}$$

(58)

The real part of the surface (57) is equal to the imaginary part in modulus for $n=-1/2$ ($S{(-1/2)}_{SCB}=\pm (-1+i)/\sqrt{\pi }$) and $n=-(2k+3)/4$

$$\begin{array}{cc}\hfill & S{\left(\frac{-\left(2k+3\right)}{4}\right)}_{SCB}=\hfill \\ \hfill & =\mp \frac{(1+i)i^k{2}^{\left(6k-1\right)/4}{\left(2k-1\right)}^{\left(1-2k\right)/8}}{\mathsf{\Gamma }\left(\frac{1-2k}{4}\right){\left(2k+3\right)}^{\left(2k-5\right)/8}}\approx \hfill \\ \hfill & \approx \mp \left\{-0.8973,-1.1755,1.3484,1.4443,\right.\hfill \\ \hfill & \left.-\underline{1.4842},-1.4828,\dots \right\}\left(1+i\right)i^k.\hfill \end{array}$$

(59)

The reflection function (38) of the surface (57) is

$$\begin{array}{cc}\hfill & \tilde{S}{\left(n\right)}_{SCB}=\hfill \\ \hfill & \pm \frac{i^{3+2n}{(-n)}^{\left(2+n\right)/2}{\left(-1-n\right)}^{\left(1+n\right)/2}{2}^{1-n}}{\mathsf{\Gamma }\left(1+n\right)}{D}^{n-1},\hfill \end{array}$$

(60)

and it equals the volume (53) for $n=(2k+1)/2,k\in {\mathbb{N}}_0$.

Volumes (53) and surfaces (57) of n-simplices circumscribed about n-balls are shown in Figure 5 and Figure 6.

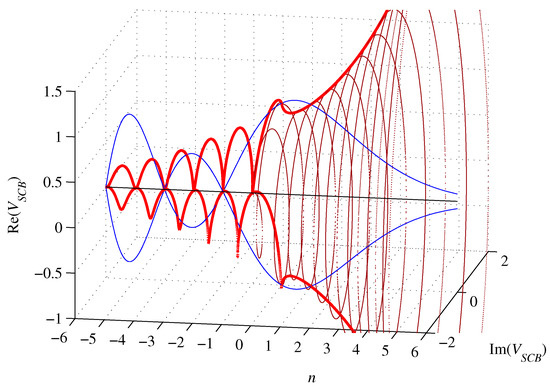
Figure 5. Graphs of $V{\left(n\right)}_{SCB}$ (red), $V{\left(n\right)}_B$ (blue), and $\tilde{V}{\left(n\right)}_{SCB}$ (dark red), for $n\in \left[-6,6\right]$.

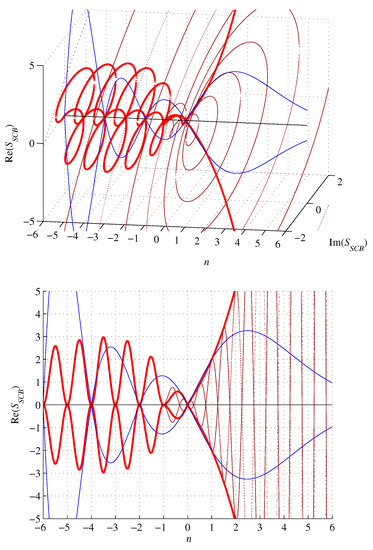
Figure 6. Graphs of $S{\left(n\right)}_{SCB}$ (red), $S{\left(n\right)}_B$ (blue), and $\tilde{S}{\left(n\right)}_{SCB}$ (dark red), for $n\in \left[-6,6\right]$.

4.3. n-Orthoplices Inscribed in n-Balls

The diameter $D_{BCO}$ of an n-ball circumscribing an n-orthoplex ($BCO$) is known [26] to be

$$D_{BCO}=\pm \sqrt{2}A,$$

(61)

where A is the edge length. Hence, the edge length $A_{OIB}$ of an n-orthoplex inscribed in an n-ball ($OIB$) with a diameter D is

$$A_{OIB}=\pm \frac{1}{\sqrt{2}}D,$$

(62)

so that its volume (31) becomes

$$V{\left(n\right)}_{OIB}=\pm \frac{1}{\mathsf{\Gamma }\left(n+1\right)}{D}^n.$$

(63)

The inscribed n-orthoplex volume (63) is real, vanishes for $n=-k$, and for $0<n<1$ it is larger than the volume of the circumscribing n-ball. It does not have a reflection function, as Equation (63) does not satisfy the definition (37).

Similarly, the surface (36) of the inscribed n-orthoplex with the edge length A given by Equation (62) becomes

$$S{\left(n\right)}_{OIB}=\pm \frac{2n^{3/2}}{\mathsf{\Gamma }\left(n+1\right)}{D}^{n-1}.$$

(64)

For $n\notin \mathbb{Z}:n<0$, the inscribed n-orthoplex surface (64) is imaginary and oscillatory divergent with n approaching negative infinity, and for $n=-k$ it vanishes. It also does not have a reflection function ($d=0$ in the definition (39)).

Volumes (63) and surfaces (64) of n-orthoplices inscribed in n-balls are shown in Figure 7 and Figure 8.

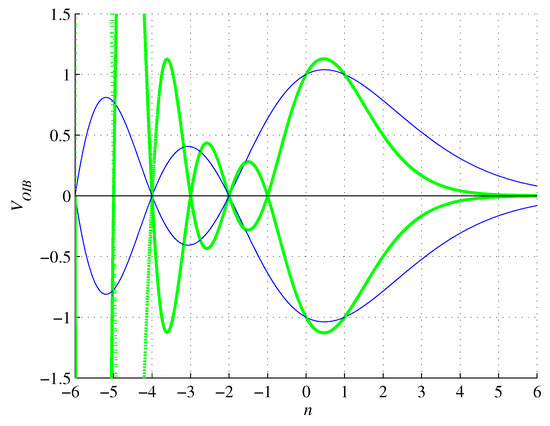
Figure 7. Graphs of $V{\left(n\right)}_{OIB}$ (green) and $V{\left(n\right)}_B$ (blue), for $n\in \left[-6,6\right]$.

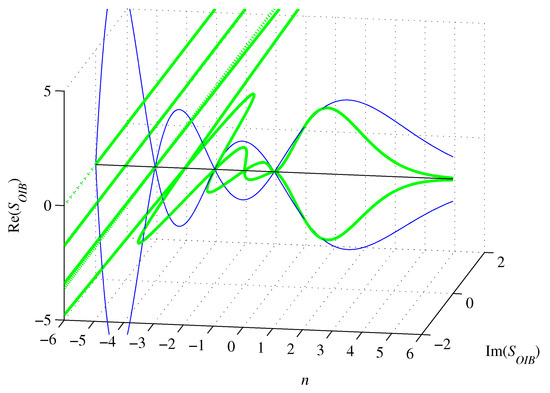
Figure 8. Graphs of $S{\left(n\right)}_{OIB}$ (green) and $S{\left(n\right)}_B$ (blue), for $n\in \left[-6,6\right]$.

4.4. n-Orthoplices Circumscribed about n-Balls

The diameter $D_{BIO}$ of an n-ball inscribed in an n-orthoplex ($BIO$) is known [26] to be

$$D_{BIO}=\pm \sqrt{\frac{2}{n}}A,$$

(65)

where A is the edge length. Hence, the edge length $A_{OCB}$ of an n-orthoplex circumscribed about an n-ball ($OCB$) with a diameter D is

$$A_{OCB}=\pm \sqrt{\frac{n}{2}}D,$$

(66)

so that its volume (31) becomes

$$V{\left(n\right)}_{OCB}=\pm \frac{n^{n/2}}{\mathsf{\Gamma }\left(n+1\right)}{D}^n,$$

(67)

as shown in Figure 9.

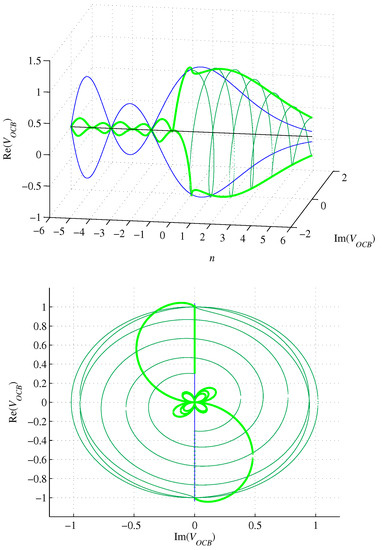
Figure 9. Graphs of $V{\left(n\right)}_{OCB}$ (green), $V{\left(n\right)}_B$ (blue), and $\tilde{V}{\left(n\right)}_{OCB}$ (dark green), for $n\in \left[-6,6\right]$.

The circumscribed n-orthoplex volume (67) is complex for $n<0$. It oscillates and is initially convergent to achieve a modulus minimum of about 0.1181 at $n\approx -3.4976$ (numerically computed) and then becomes divergent with n approaching negative infinity. For $n=-k$, it vanishes. For $0<n<1$, it is smaller than the volume of an inscribed n-ball. For $n=-(2k+1)/2$, $k\in {\mathbb{N}}_0$ the real part of the volume (67) equals the imaginary part in modulus, achieving a local minimum at $n=-3.5$ and amounts to

$$\begin{array}{cc}\hfill & V{\left(\frac{-\left(2k+1\right)}{2}\right)}_{OCB}=\hfill \\ \hfill & =\pm \frac{(1+i)i^k{2}^{\left(2k-1\right)/4}}{\mathsf{\Gamma }\left(\frac{1-2k}{2}\right){\left(2k+1\right)}^{\left(2k+1\right)/4}}\approx \hfill \\ \hfill & \approx \pm \left\{0.4744,-0.1472,0.0952,-\underline{0.0835},\right.\hfill \\ \hfill & \left.0.0888,-0.1084,\dots \right\}\left(1+i\right)i^k.\hfill \end{array}$$

(68)

The reflection function (38) of the volume (67) is

$$\tilde{V}{\left(n\right)}_{OCB}=\pm i^n\frac{{(-n)}^{n/2}}{\mathsf{\Gamma }\left(n+1\right)}{D}^n,$$

(69)

and it equals the volume (67) for $n=2k$, $k\in {\mathbb{N}}_0$.

Similarly, the surface (36) of a circumscribed n-orthoplex with the edge length A given by Equation (66) becomes

$$S{\left(n\right)}_{OCB}=\pm \frac{2n^{(2+n)/2}}{\mathsf{\Gamma }\left(n+1\right)}{D}^{n-1},$$

(70)

as shown in Figure 10.

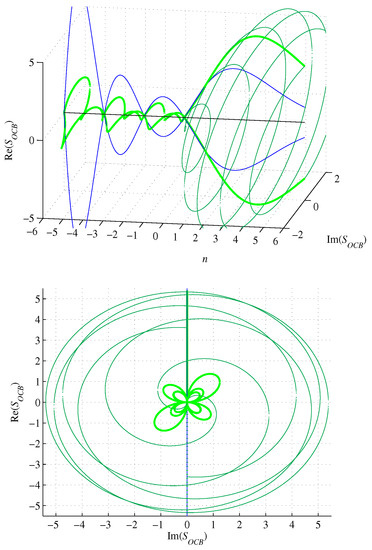
Figure 10. Graphs of $S{\left(n\right)}_{OCB}$ (green), $S{\left(n\right)}_B$ (blue), and $\tilde{S}{\left(n\right)}_{OCB}$ (dark green), for $n\in \left[-6,6\right]$.

The circumscribed n-orthoplex surface (70) is complex for $n<0$. It oscillates and is initially convergent to achieve a modulus minimum of about 0.6244 at $n\approx -1.5$ (numerical) and then becomes divergent with n approaching negative infinity. For $n=-k$, it vanishes. For $0<n<1$, it is smaller than the surface of an inscribed n-ball. Furthermore, its real part equals the imaginary part in modulus for $n=-(2k+1)/2$, $k\in {\mathbb{N}}_0$. It achieves a local minimum at $n=-1.5$ and amounts to

$$\begin{array}{cc}\hfill & S{\left(\frac{-\left(2k+1\right)}{2}\right)}_{OCB}=\hfill \\ \hfill & =\pm \frac{-(1+i)i^k{2}^{\left(2k-1\right)/4}{\left(2k+1\right)}^{\left(3-2k\right)/4}}{\mathsf{\Gamma }\left(\frac{1-2k}{2}\right)}\approx \hfill \\ \hfill & \approx \pm \left\{-0.4744,\underline{0.4415},-0.4759,0.5846,\right.\hfill \\ \hfill & \left.-0.7989,\dots \right\}(1+i)i^k.\hfill \end{array}$$

(71)

The reflection function (38) of the surface (70) is

$$\tilde{S}{\left(n\right)}_{OCB}=\pm \frac{i^{2+n}2{(-n)}^{(2+n)/2}{D}^{n-1}}{\mathsf{\Gamma }\left(n+1\right)},$$

(72)

and it equals the surface (70) for $n=2k$, $k\in {\mathbb{N}}_0$.

Volumes (67), (69) and surfaces (70), (72) of n-orthoplices inscribed in n-balls are shown in Figure 9 and Figure 10.

4.5. n-Cubes Inscribed in and Circumscribed about n-Balls

The edge length $A_{CCB}$ of an n-cube circumscribed about an n-ball ($CCB$) corresponds to the diameter D of this n-ball. Thus, the volume of this cube is simply

$$V{\left(n\right)}_{CCB}=\pm D^n,$$

(73)

and the surface is

$$S{\left(n\right)}_{CCB}=\pm 2n{D}^{n-1}.$$

(74)

However, the edge length $A_{CIB}$ of an n-cube inscribed in an n-ball ($CIB$) of diameter D is

$$A{\left(n\right)}_{CIB}=\pm D{n}^{-1/2},$$

(75)

which is singular for $n=0$ and complex for $n<0$, rendering [18] the volume

$$V{\left(n\right)}_{CIB}=\pm n^{-n/2}{D}^n,$$

(76)

and the surface

$$S_{CIB}=\pm 2n^{\left(3-n\right)/2}{D}^{n-1},$$

(77)

of an n-cube inscribed in an n-ball.

The reflection functions (38) of the volume (76) and surface (77) are [18]

$$\tilde{V}{\left(n\right)}_{CIB}=\pm i^{-n}{(-n)}^{-n/2}{D}^n,$$

(78)

$$\tilde{S}{\left(n\right)}_{CIB}=\pm 2i^{3-n}{(-n)}^{\left(3-n\right)/2}{D}^{n-1}.$$

(79)

The volumes (76) and (78) are equal [18] for $n=2k$, $k\in {\mathbb{N}}_0$, and the surfaces (77) and (79) are equal for $n=2k-1$, $k\in \mathbb{N}$, as shown in Figure 11 and Figure 12.

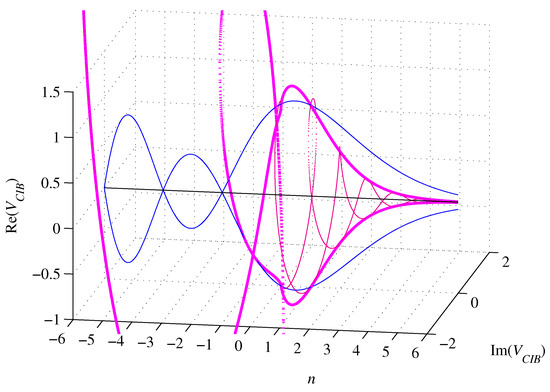
Figure 11. Graphs of $V{\left(n\right)}_{CIB}$ (pink), $V{\left(n\right)}_B$ (blue), and $\tilde{V}{\left(n\right)}_{CIB}$ (dark pink), for $n\in \left[-6,6\right]$.

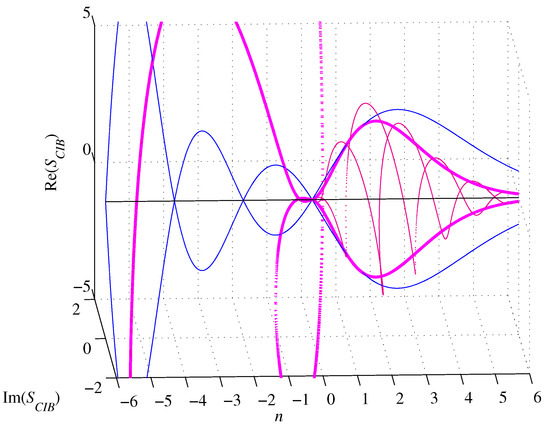
Figure 12. Graphs of $S{\left(n\right)}_{CIB}$ (pink), $S{\left(n\right)}_B$ (blue), and $\tilde{S}{\left(n\right)}_{CIB}$ (dark pink), for $n\in \left[-6,6\right]$.

The volume (76) and the surface (77) are complex if $n<0$ and divergent, with n approaching negative infinity. For $0<n<1$, the volume (76) is larger than the volume of a circumscribing n-ball.

5. Metric-Independent Relations

The following metric-independent relations hold, for $n\in \mathbb{C}:n\ne 0$, between volumes of n-balls (22)

$$V{\left(n\right)}_{B}V{(-n)}_B=\pm \frac{2sin\left(\pi n/2\right)}{\pi n},$$

(80)

n-simplices (25)

$$V{\left(n\right)}_{S}V{(-n)}_S=\pm \frac{{\left(1+n\right)}^{1/2}{\left(1-n\right)}^{1/2}sin\left(\pi n\right)}{\pi n},$$

(81)

n-orthoplices (31) and n-orthoplices inscribed in n-balls (63)

$$V{\left(n\right)}_{O}V{(-n)}_O=V{\left(n\right)}_{OIB}V{(-n)}_{OIB}=\pm \frac{sin\left(\pi n\right)}{\pi n},$$

(82)

n-simplices inscribed in n-balls (49)

$$V{\left(n\right)}_{SIB}V{(-n)}_{SIB}=\pm \frac{{\left(1+n\right)}^{\left(1+n\right)/2}{\left(1-n\right)}^{\left(1-n\right)/2}{\left(n\right)}^{\left(-n\right)/2}{\left(-n\right)}^{\left(n\right)/2}sin\left(\pi n\right)}{\pi n},$$

(83)

n-simplices circumscribed about n-balls (53)

$$V{\left(n\right)}_{SCB}V{(-n)}_{SCB}=\pm \frac{{\left(1+n\right)}^{\left(1+n\right)/2}{\left(1-n\right)}^{\left(1-n\right)/2}{\left(n\right)}^{\left(n\right)/2}{\left(-n\right)}^{\left(-n\right)/2}sin\left(\pi n\right)}{\pi n},$$

(84)

and n-orthoplices circumscribed about n-balls (67)

$$V{\left(n\right)}_{OCB}V{(-n)}_{OCB}=\pm \frac{{\left(n\right)}^{\left(n\right)/2}{\left(-n\right)}^{\left(-n\right)/2}sin\left(\pi n\right)}{\pi n},$$

(85)

where we used Euler’s reflection formula, $\mathsf{\Gamma }\left(\tilde{n}\right)\mathsf{\Gamma }(1-\tilde{n})=\pi /sin\pi \tilde{n}$, with $\tilde{n}:=n+1$, and $\mathsf{\Gamma }\left(n\right)=(n-1)\mathsf{\Gamma }(n-1)$

$$\begin{array}{cc}\hfill \mathsf{\Gamma }\left(n+1\right)\mathsf{\Gamma }\left(-n+1\right)& =\mathsf{\Gamma }\left(\tilde{n}\right)\mathsf{\Gamma }\left(2-\tilde{n}\right)=\mathsf{\Gamma }\left(\tilde{n}\right)\mathsf{\Gamma }\left(1-\tilde{n}\right)\left(1-\tilde{n}\right)=\hfill \\ \hfill & =\frac{\pi }{sin\left(\pi \tilde{n}\right)}(1-\tilde{n})=-\frac{\pi n}{sin\left[\pi \left(n+1\right)\right]}=\frac{\pi n}{sin\left(\pi n\right)},\hfill \end{array}$$

(86)

as well as (for $n\in \mathbb{C}:n\ne 1$), between surfaces of n-balls (24)

$$S{\left(n\right)}_{B}S{(2-n)}_B=\pm 4sin\left(\pi n/2\right),$$

(87)

n-simplices (30),

$$S{\left(n\right)}_{S}S{(2-n)}_S=\pm \frac{n^{1/2}\left(n+1\right){\left(2-n\right)}^{1/2}\left(3-n\right)sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(88)

n-orthoplices (36)

$$S{\left(n\right)}_{O}S{(2-n)}_O=\pm \frac{4n^{1/2}{\left(2-n\right)}^{1/2}sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(89)

n-simplices inscribed in n-balls (50)

$$S{\left(n\right)}_{SIB}S{(2-n)}_{SIB}=\pm \frac{n^{\left(2-n\right)/2}{\left(n+1\right)}^{\left(n+1\right)/2}{\left(2-n\right)}^{n/2}{\left(3-n\right)}^{\left(3-n\right)/2}sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(90)

n-simplices circumscribed about n-balls (57)

$$S{\left(n\right)}_{SCB}S{(2-n)}_{SCB}=\pm \frac{n^{n/2}{\left(n+1\right)}^{\left(n+1\right)/2}{\left(2-n\right)}^{\left(2-n\right)/2}{\left(3-n\right)}^{\left(3-n\right)/2}sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(91)

n-orthoplices inscribed in n-balls (64)

$$S{\left(n\right)}_{OIB}S{(2-n)}_{OIB}=\pm \frac{4n^{1/2}{\left(2-n\right)}^{1/2}sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(92)

n-orthoplices circumscribed about n-balls (70)

$$S{\left(n\right)}_{OCB}S{(2-n)}_{OCB}=\pm \frac{4n^{n/2}{\left(2-n\right)}^{\left(2-n\right)/2}sin\left(\pi n\right)}{\pi \left(1-n\right)},$$

(93)

and n-cubes inscribed in n-balls (77) ($\forall n\in \mathbb{C}$)

$$S{\left(n\right)}_{CIB}S{(2-n)}_{CIB}=\pm 4n^{\left(3-n\right)/2}{\left(2-n\right)}^{\left(1+n\right)/2},$$

(94)

where we again used $\tilde{n}=n+1$, $\mathsf{\Gamma }\left(n\right)=(n-1)\mathsf{\Gamma }(n-1)$, and Euler’s reflection formula

$$\begin{array}{cc}\hfill & \mathsf{\Gamma }\left(n+1\right)\mathsf{\Gamma }\left(3-n\right)=\mathsf{\Gamma }\left(\tilde{n}\right)\mathsf{\Gamma }\left(1-\tilde{n}\right)\left(1-\tilde{n}\right)\left(2-\tilde{n}\right)\left(3-\tilde{n}\right)=\hfill \\ \hfill & =\frac{\pi }{sin\left(\pi \tilde{n}\right)}\left(1-\tilde{n}\right)\left(2-\tilde{n}\right)\left(3-\tilde{n}\right)=-\frac{\pi n\left(1-n\right)\left(2-n\right)}{sin\left[\pi \left(n+1\right)\right]}=\frac{\pi n\left(1-n\right)\left(2-n\right)}{sin\left(\pi n\right)}.\hfill \end{array}$$

(95)

These relations are independent of the distance values D (or A) and their particular form, whether negative ($D<0$), complex ($D=a+bi$, $a,b\in \mathbb{R}$), or purely imaginary ($a=0$). Furthermore, the relations (80)–(85) and (87)–(93) are independent of the gamma function. Relations (80)–(85) are shown in Figure 13. The imaginary part of the surface relations (88)–(94) vanishes for $0<n<2$.

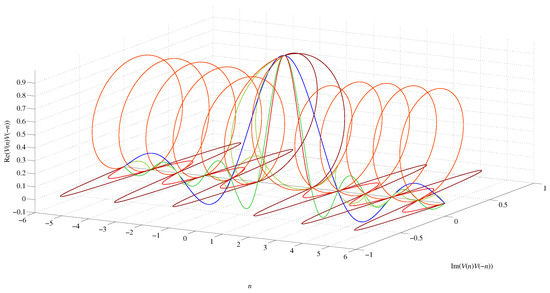
Figure 13. Volume metric and gamma function independent relations. $V{\left(n\right)}_{B}V{(-n)}_B$ (blue), $V{\left(n\right)}_{S}V{(-n)}_S$ (red), $V{\left(n\right)}_{SIB}V{(-n)}_{SIB}$ (dark red), $V{\left(n\right)}_{SCB}V{(-n)}_{SCB}$ (orange-red), $V{\left(n\right)}_{O}V{(-n)}_O=V{\left(n\right)}_{OIB}V{(-n)}_{OIB}$ (lime green), $V{\left(n\right)}_{OCB}V{(-n)}_{OCB}$ (yellow-green), for $n\in \mathbb{R}:n\in \left[-6,6\right]$.

Moreover, for $n\in \mathbb{C}:n\ne 0$, the following both metric and gamma function independent relations can be obtained between volumes (73), (76) and surfaces (74), (77) of circumscribed and inscribed n-cubes

$$V{\left(n\right)}_{CCB}=\pm n^{n/2}V{\left(n\right)}_{CIB},S{\left(n\right)}_{CCB}=\pm n^{\left(n-1\right)/2}S{\left(n\right)}_{CIB},$$

(96)

between volumes (53), (49) and surfaces (57), (50) of circumscribed and inscribed n-simplices

$$V{\left(n\right)}_{SCB}=\pm n^{n}V{\left(n\right)}_{SIB},S{\left(n\right)}_{SCB}=\pm n^{n-1}S{\left(n\right)}_{SIB},$$

(97)

and between volumes (67), (63) and surfaces (70), (64) of circumscribed and inscribed n-orthoplices

$$V{\left(n\right)}_{OCB}=\pm n^{n/2}V{\left(n\right)}_{OIB},S{\left(n\right)}_{OCB}=\pm n^{\left(n-1\right)/2}S{\left(n\right)}_{OIB}.$$

(98)

Notably, the ratio of the volume $V{\left(n\right)}_{CCB}$ of an n-cube circumscribed about an n-ball to the volume $V{\left(n\right)}_{CIB}$ of an n-cube inscribed in an n-ball (96) is the same as the ratio of the volume $V{\left(n\right)}_{OCB}$ of an n-orthoplex circumscribed about an n-ball to the volume $V{\left(n\right)}_{OIB}$ of an n-orthoplex inscribed in an n-ball (98), and the same holds for the ratio of their surfaces, $S{\left(n\right)}_{CCB}/S{\left(n\right)}_{CIB}=S{\left(n\right)}_{OCB}/S{\left(n\right)}_{OIB}$. This is unsurprising: as an n-cube is dual to an n-orthoplex, these ratios remain invariant.

Curiously, analogous symmetries do not hold for the reflection functions (38) of these volumes or surfaces, as neither the inscribed volumes $V{\left(n\right)}_{SIB}$, $V{\left(n\right)}_{OIB}$, nor the circumscribed volume $V{\left(n\right)}_{CCB}$, nor the corresponding inscribed surfaces $S{\left(n\right)}_{SIB}$, $S{\left(n\right)}_{OIB}$, nor circumscribed surface $S{\left(n\right)}_{CCB}$, have the reflection functions.

6. Volume-Surface Symmetries

Furthermore, the following particular symmetries between $n=-1/2$ and $n=1/2$ hold for (22), (24); (25), (30); (31), (36); (49), (50); (53), (57); (63), (64); (67), (70); (76), (77); and (73), (74)

$$V{\left(-1/2\right)}_B=\mp S{\left(-1/2\right)}_{B}D,V{\left(1/2\right)}_B=\pm S{\left(1/2\right)}_{B}D,$$

(99)

$$V{\left(-1/2\right)}_S=\pm S{\left(-1/2\right)}_{S}Ai2\sqrt{2},V{\left(1/2\right)}_S=\pm S{\left(1/2\right)}_{S}A2\sqrt{\frac{2}{3}},$$

(100)

$$V{\left(-1/2\right)}_O=\pm 2iS{\left(-1/2\right)}_{O}A,V{\left(1/2\right)}_O=\pm 2S{\left(1/2\right)}_{O}A,$$

(101)

$$V{\left(-1/2\right)}_{SIB}=\pm 2S{\left(-1/2\right)}_{SIB}D,V{\left(1/2\right)}_{SIB}=\pm 2S{\left(1/2\right)}_{SIB}D,$$

(102)

$$V{\left(-1/2\right)}_{SCB}=\mp S{\left(-1/2\right)}_{SCB}D,V{\left(1/2\right)}_{SCB}=\pm S{\left(1/2\right)}_{SCB}D,$$

(103)

$$V{\left(-1/2\right)}_{OIB}=\pm i\sqrt{2}S{\left(-1/2\right)}_{OIB}D,V{\left(1/2\right)}_{OIB}=\pm \sqrt{2}S{\left(1/2\right)}_{OIB}D,$$

(104)

$$V{\left(-1/2\right)}_{OCB}=\mp S{\left(-1/2\right)}_{OCB}D,V{\left(1/2\right)}_{OCB}=\pm S{\left(1/2\right)}_{OCB}D,$$

(105)

$$V{\left(-1/2\right)}_{CIB}=\pm \sqrt{2}S{\left(-1/2\right)}_{CIB}^{*}D,V{\left(1/2\right)}_{CIB}=\pm \sqrt{2}S{\left(1/2\right)}_{CIB}D,$$

(106)

$$V{\left(-1/2\right)}_{CCB}=\mp S{\left(-1/2\right)}_{CCB}D,V{\left(1/2\right)}_{CCB}=\pm S{\left(1/2\right)}_{CCB}D,$$

(107)

where “*” denotes a complex conjugate.

Furthermore, if $A=D$

$$S{\left(3\right)}_{OIB}=\pm S{\left(3\right)}_S,S{\left(2\right)}_{OIB}=\pm S{\left(2\right)}_{CIB}.$$

(108)

7. Discussion

The volumes and surfaces of n-balls, n-simplices, and n-orthoplices have been defined in any complex dimension. As these geometric objects occur, along with n-cubes, in all natural dimensions [19], this result makes them omnidimensional, i.e., present in any complex dimension.

Applications of these formulas to the omnidimensional polytopes inscribed in and circumscribed about n-balls revealed previously unknown properties of these geometric objects. In particular, for $0<n<1$, the omnidimensional polytopes’ volumes are larger than those of circumscribing n-balls, while their volumes and surfaces are smaller than those of inscribed n-balls.

Reflection functions for volumes and surfaces of these polytopes inscribed in and circumscribed about n-balls are proposed.

Symmetries of products (80)–(85), (87)–(94) and quotients (96)–(98) of volumes of these circumscribed and inscribed omnidimensional polytopes and n-balls in complex dimensions n and $-n$ and of surfaces in complex dimensions n and $2-n$ are shown to be independent of the metric factor and the gamma function.

Specific symmetries also hold between volumes and surfaces in dimensions $n=-1/2$ and $n=1/2$.

The results of this study could be applied in linguistic statistics, where the dimension in the distribution for frequency dictionaries is chosen to be negative [3], and in fog computing, where an n-simplex is related to a full mesh pattern, an n-orthoplex is linked to a quasi-full mesh structure, and an n-cube is referred to as a certain type of partial mesh layout [27]. Further possible applications include molecular physics and crystallography. Perhaps the results of this study are also related to the 2-dimensional quantum hall effect.

One can also investigate the properties of the examined geometric objects extending these concepts to quaternions. This can help us discover many interesting mathematical properties and physical phenomena. One of the challenges certainly involves characterizing all types of symmetries introduced by Definition 1.