Starlike Functions Associated with Secant Hyperbolic Function

Abstract

Motivated by the recent work on the symmetric domains, this article investigates certain features of symmetric domain which are caused by the secant hyperbolic functions. Geometric characteristics of analytic functions associated with secant hyperbolic functions are discussed, which include the inclusion results, structural formula, certain sharp radii results such as radius of starlikeness and convexity of order $\alpha .$ It also finds a radius for ratios of analytic functions associated with Euler numbers.

1. Introduction

Denoted by ${\mathcal{A}}_m$, the class of functions $\mathsf{f}\left(\varsigma \right)=\varsigma +a_{m+1}{\varsigma }^{m+1}+a_{m+2}{\varsigma }^{m+2}+\cdots ,$ analytic in $\mathbb{D}=\{\varsigma \in \mathbb{C}:|\varsigma |<1\}$ and ${\mathcal{A}}_1=\mathcal{A}$ denote the class of analytic functions having the series form

$$\mathsf{f}\left(\varsigma \right)=\varsigma +\underset{m=2}{\sum ^{\infty }}{a}_m{\varsigma }^m,\varsigma \in \mathbb{D}.$$

(1)

The subclass $\mathcal{S}$ of $\mathcal{A}$ contains univalent functions (one to one) in $\mathbb{D}$. Moreover, ${\mathcal{S}}^{*}$ and $\mathcal{C}$ represent classes of starlike and convex functions in $\mathbb{D}$, respectively. These classes are defined for the functions $\mathsf{f}$ analytically by the relation $Re\left(\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)/\mathsf{f}\left(\varsigma \right)\right)>0$ and $Re\left(1+\varsigma {\mathsf{f}}^{″}\left(\varsigma \right)/{\mathsf{f}}^{\prime }\left(\varsigma \right)\right)>0$ in $\mathbb{D}$, respectively. A function $\mathsf{f}$ analytic in $\mathbb{D}$ is subordinated by analytic function $\mathsf{g}$ denoted by $\mathsf{f}\prec$g if there exists a Schwarz function w which maps $\mathbb{D}$ to itself with $w\left(0\right)=0$ such that $\mathsf{f}\left(\varsigma \right)=\mathsf{g}\left(w\left(\varsigma \right)\right)$. If $\mathsf{g}$ is univalent in $\mathbb{D}$ and $\mathsf{f}\left(0\right)=\mathsf{g}\left(0\right)$, then $\mathsf{f}\left(\mathbb{D}\right)\subset \mathsf{g}\left(\mathbb{D}\right)$.

The concept of subordination was applied by Ma and Minda [1] to introduce generalized subclasses ${\mathcal{S}}^{*}\left(\mathrm{\Psi }\right)$ and $\mathcal{C}\left(\mathrm{\Psi }\right)$ of starlike and convex functions, respectively, which are analytically defined as:

$${\mathcal{S}}^{*}\left(\mathrm{\Psi }\right):=\left\{\mathsf{f}\in \mathcal{A}:\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \mathrm{\Psi }\left(\varsigma \right)\right\},$$

and

$$\mathcal{C}\left(\mathrm{\Psi }\right):=\left\{\mathsf{f}\in \mathcal{A}:1+\frac{\varsigma {\mathsf{f}}^{″}\left(\varsigma \right)}{{\mathsf{f}}^{\prime }\left(\varsigma \right)}\prec \mathrm{\Psi }\left(\varsigma \right)\right\}.$$

The function $\mathrm{\Psi }$ is an analytic and univalent in $\mathbb{D}$. It maps $\mathbb{D}$ onto the convex set in $\mathbb{C}$ with $\mathrm{\Psi }\left(0\right)=1$ and $Re\left\{{\mathrm{\Psi }}^{\prime }\left(\varsigma \right)\right\}>0$ in $\mathbb{D}.$ The classes ${\mathcal{S}}^{*}\left(\mathrm{\Psi }\right)$ and $\mathcal{C}\left(\mathrm{\Psi }\right)$ unify many subclasses of ${\mathcal{S}}^{*}$ and $\mathcal{C}$. We write a few of these by taking the particular $\mathrm{\Psi }$. The classes ${\mathcal{S}}^{*}[a,b]:={\mathcal{S}}^{*}\left((1+a\varsigma )/(1+b\varsigma )\right)$ and $\mathcal{C}[a,b]:=\mathcal{C}\left((1+a\varsigma )/(1+b\varsigma )\right),$$-1\le b<a\le 1$ represent the Janowski starlike and Janowski convex functions [2]. By choosing $a=1-2\gamma$ and $b=-1,$ the classes ${\mathcal{S}}^{*}[a,b]$ and $\mathcal{C}[a,b]$ reduce to the starlike and convex functions of order $\gamma \in \left[0,1\right)$. The class $\mathcal{S}{\mathcal{S}}_{\beta }^{*}:={\mathcal{S}}^{*}{\left[(1+\varsigma )/(1-\varsigma )\right]}^{\beta }$ represents the strongly starlike functions of order $\beta \in \left(0,1\right].$ The class ${\mathcal{S}}_s^{*}:={\mathcal{S}}^{*}(1+sin\left(\varsigma \right))$ serves as the class of starlike functions related with sine function [3]. Sokół and Stankiewicz [4] defined the class ${\mathcal{S}}_L^{*}:={\mathcal{S}}^{*}\left(\sqrt{1+\varsigma }\right)$. The class ${\mathcal{S}}_L^{*}\left(\gamma \right)$ performs as a subclass of ${\mathcal{S}}_L^{*}$ with order $\gamma$ [5]. Similarly, the class ${\mathcal{S}}^{*}\left(\sqrt{2}-(\sqrt{2}-1)\sqrt{\frac{1-\varsigma }{1+2(\sqrt{2}-1)\varsigma }}\right)$ is represented by ${\mathcal{S}}_{RL}^{*}$ [6]. The class ${\mathcal{S}}_C^{*}:={\mathcal{S}}^{*}\left(1+\frac{4\varsigma }{3}+\frac{2{\varsigma }^2}{3}\right)$ is a subclass of ${\mathcal{S}}^{*}$ related to a cardioid [7]. The class ${\mathcal{S}}_l^{*}\left(1+\sqrt{2}\varsigma +\frac{{\varsigma }^2}{2}\right)$ is a class related with limacon [8,9,10]. The class ${\mathcal{S}}_e^{*}={\mathcal{S}}^{*}\left(e^{\varsigma }\right)$ was defined by Mendiratta et al. [11]. The class ${\mathcal{S}}_{cos}^{*}={\mathcal{S}}^{*}(cos\left(\varsigma \right))$ represents the starlike functions related to the cosine function; see [12,13]. The class ${\mathcal{S}}_{\mathrm{\Delta }}^{*}:={\mathcal{S}}^{*}\left(\varsigma +\sqrt{1+{\varsigma }^2}\right)$ was introduced and studied in [14], while the class ${\mathcal{BS}}^{*}\left(\gamma \right):={\mathcal{S}}^{*}\left(1+\varsigma /\left(1-\gamma {\varsigma }^2\right)\right),\gamma \in [0,1]$ was given by Kargar et al. [15]. For some more recent work in the same direction, we refer to [16,17,18,19,20,21,22] and the references therein.

Recently, some authors have explored the geometry of certain generating functions for well-known numbers and connected them with certain subclasses of $\mathcal{S}$. For instance, Sokół [23] defined a subclass of ${\mathcal{S}}^{*}$ by using Fibonacci numbers. Some applications of these numbers were given by Dziok et al. [24,25]. Certain coefficient bounds for starlike functions related to generalized telephone numbers were given by Deniz [26]; also see [27]. A subclass of ${\mathcal{S}}^{*}$ related with Bell numbers was studied in [28,29]. The subclasses of ${\mathcal{S}}^{*}$ and $\mathcal{C}$ related to Bernoulli numbers were studied by Raza et al. [30].

Motivated by the given above progress, we take the function

$${\mathrm{\Psi }}_E\left(\varsigma \right)=sech\left(\varsigma \right)=\frac{2}{e^{\varsigma }+e^{-\varsigma }}=\sum _{m=0}^{\infty }\frac{E_m}{m!}{\varsigma }^m,$$

where the Euler’s numbers $E_m$ satisfy the relation $E_{2m+1}=0,$$m=0,1,2,\cdots .$ It is clear that $E_0=1,E_2=-1,$ $E_4=5$ and $E_6=-61.$ The numbers $E_m$ are closely connected with other well-known numbers such as the Genocchi numbers, the Bernoulli numbers, the Stirling numbers of two kinds, the tangent numbers, the Riemann zeta function and the Euler polynomials, and therefore are very useful in number theory and combinatorics; see [31,32,33,34] and references therein.

The generating function ${\mathrm{\Psi }}_E$ of Euler numbers is univalent in $\mathbb{D}$ with $Re\left\{{\mathrm{\Psi }}_E\left(\varsigma \right)\right\}>0$ in $\mathbb{D}.$ Therefore, by using the function ${\mathrm{\Psi }}_E,$ we define the class ${\mathcal{S}}_E^{*}$ in $\mathbb{D}$ as follows:

$${\mathcal{S}}_E^{*}:=\left\{\mathsf{f}\in \mathcal{A}:\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec {\mathrm{\Psi }}_E\left(\varsigma \right)\right\}.$$

The function ${\mathrm{\Psi }}_E$ is symmetric about the real axis, as given in Figure 1.

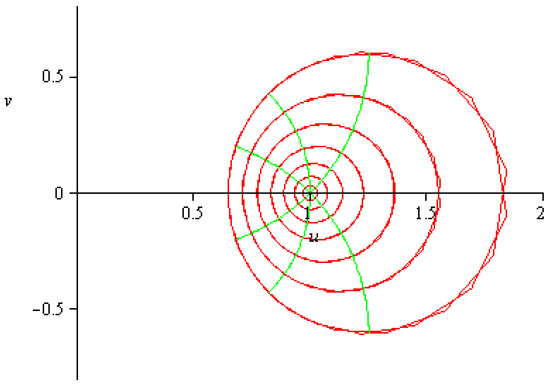
Figure 1. Graph of ${\mathrm{\Psi }}_E$.

In other words, let $\mathsf{p}\left(\varsigma \right)\prec {\mathrm{\Psi }}_E\left(\varsigma \right).$ Then $\mathsf{f}$ is in the class ${\mathcal{S}}_E^{*}$ if and only if it can be written as

$$\mathsf{f}\left(\varsigma \right)=\varsigma exp\left({\int }_0^{\varsigma }\frac{\mathsf{p}\left(t\right)-1}{t}dt\right).$$

(2)

Now we provide few examples in the class ${\mathcal{S}}_E^{*}.$ Consider

$${\mathsf{p}}_1\left(\varsigma \right)=1+\frac{\varsigma }{3},{\mathsf{p}}_2\left(\varsigma \right)=\frac{4+2\varsigma }{4+\varsigma },{\mathsf{p}}_3\left(\varsigma \right)=1+\frac{\varsigma }{6}.$$

Since the function ${\mathrm{\Psi }}_E\left(\varsigma \right)$ is univalent in $\mathbb{D}$ with ${\mathsf{p}}_i\left(0\right)={\mathrm{\Psi }}_E\left(0\right)=1,$$\left(i=1,2,3\right)$ and ${\mathsf{p}}_i\left(\mathbb{D}\right)\subset {\mathrm{\Psi }}_E\left(\mathbb{D}\right),$ therefore ${\mathsf{p}}_i\left(\varsigma \right)\prec {\mathrm{\Psi }}_E\left(\varsigma \right).$

We intend to prove that the following functions are in the class ${\mathcal{S}}_E^{*}$.

$${\mathsf{f}}_1\left(\varsigma \right)=\varsigma e^{\frac{\varsigma }{3}},{\mathsf{f}}_2\left(\varsigma \right)=\varsigma +\frac{{\varsigma }^2}{4},{\mathsf{f}}_3\left(\varsigma \right)=\varsigma e^{\frac{\varsigma }{6}}$$

We also intend to establish connections of newly defined class ${\mathcal{S}}_E^{*}$ of analytic functions associated with secant hyperbolic functions with many other classes of analytic functions. These connections are given by radii problems and inclusion results. We emphasize and thoroughly study the radii problems for starlikeness and convexity of the class ${\mathcal{S}}_E^{*}$. For that, we need the following classes of analytic functions and certain established results which are given below in Section 2. All the proved results are sharp, which is justified by giving suitable extremal functions.

The class $\mathcal{M}\left(\beta \right)$ is defined for the functions $\mathsf{f}\in \mathcal{A}$ such that $Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)<\gamma ,\gamma >1$. The class ${\mathcal{P}}_m[a,b]$ for $-1\le b<a\le 1$ is defined as

$${\mathcal{P}}_m[a,b]:=\left\{\mathsf{p}\left(\varsigma \right)=1+\sum _{k=m}^{\infty }{c}_k{\varsigma }^k:\mathsf{p}\left(\varsigma \right)\prec \frac{1+a\varsigma }{1+b\varsigma }\right\}.$$

In particular, ${\mathcal{P}}_m[1-2\gamma .-1]:={\mathcal{P}}_m\left(\gamma \right)$ for $\gamma \in \left[0,1\right),{\mathcal{P}}_m:={\mathcal{P}}_m\left(0\right)$ and ${\mathcal{P}}_1=\mathcal{P}$, the well-known classes having functions with positive real parts in $\mathbb{D}$. Any function $\mathsf{p}\in \mathcal{P}$ has the series form

$$\mathsf{p}\left(\varsigma \right)=1+\sum _{m=1}^{\infty }{q}_m{\varsigma }^m,\varsigma \in \mathbb{D}.$$

(3)

Let ${\mathcal{S}}_{E,m}^{*}={\mathcal{A}}_m\cap {\mathcal{S}}_E^{*},{\mathcal{S}}_m^{*}[a,b]={\mathcal{A}}_m\cap {\mathcal{S}}^{*}[a,b]$ and ${\mathcal{M}}_m\left(\gamma \right):={\mathcal{A}}_m\cap \mathcal{M}\left(\gamma \right).$ Ali et al. [35] studied the classes ${\mathcal{S}}_m$ and ${\mathcal{CS}}_m\left(\gamma \right).$ These are defined as

$${\mathcal{S}}_m:=\{\mathsf{f}\in {\mathcal{A}}_m:\frac{\mathsf{f}\left(\varsigma \right)}{\varsigma }\in {\mathcal{P}}_m\}$$

and

$${\mathcal{CS}}_m\left(\gamma \right):=\left[\mathsf{f}\in {\mathcal{A}}_m:\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}\in {\mathcal{P}}_m,\mathsf{g}\in {\mathcal{S}}_m^{{}_{*}}\left(\gamma \right)\right].$$

2. Preliminary Results

We utilize the following results in our study.

Lemma 1.

[36] If $\mathsf{p}\in {\mathcal{P}}_m\left(\gamma \right)$, then, for $\left|\varsigma \right|=s$,

$$\left|\frac{\varsigma {\mathsf{p}}^{\prime }\left(\varsigma \right)}{\mathsf{p}\left(\varsigma \right)}\right|\le \frac{2(1-\gamma )m{s}^m}{(1-s^m)(1+(1-2\gamma )s^m)}.$$

Lemma 2.

[37] If $\mathsf{p}\in {\mathcal{P}}_m[a,b]$, then, for $\left|\varsigma \right|=s,$

$$\left|\mathsf{p}\left(\varsigma \right)-\frac{1-ab{s}^{2m}}{1-b^2{s}^{2m}}\right|\le \frac{(a-b)s^m}{1-b^2{s}^{2m}}.$$

In particular, if $\mathsf{p}\in {\mathcal{P}}_m\left(\gamma \right)$, then, for $\left|\varsigma \right|=s,$

$$\left|\mathsf{p}\left(\varsigma \right)-\frac{(1+(1-2\gamma ))s^{2m}}{1-s^{2m}}\right|\le \frac{2(1-\gamma )s^m}{1-s^{2m}}.$$

3. Starlikeness and Convexity

Firstly, we study the starlikeness and strong starlikeness of order $\gamma$ and order $\beta$, respectively, for the class ${\mathcal{S}}_E^{*}$. We start with the following result, which is useful in proving our inclusion results.

Lemma 3.

Let ${\mathrm{\Psi }}_E\left(\varsigma \right)=sech\left(\varsigma \right).$ Then for $s\in \left(0,1\right),$

$$\underset{\left|\varsigma \right|=s}{min}Re{\mathrm{\Psi }}_E\left(\varsigma \right)={\mathrm{\Psi }}_E\left(s\right)=\underset{\left|\varsigma \right|=s}{min}\left|{\mathrm{\Psi }}_E\left(\varsigma \right)\right|=sech\left(s\right),$$

and

$$\underset{\left|\varsigma \right|=s}{max}Re{\mathrm{\Psi }}_E\left(\varsigma \right)=sec\left(s\right)=\underset{\left|\varsigma \right|=s}{max}\left|{\mathrm{\Psi }}_E\left(\varsigma \right)\right|.$$

Proof. 

For $\varsigma =s{e}^{iy},y\in \left[0,2\pi \right]$ and $0<s<1,$ the function

$$Re{\mathrm{\Psi }}_E\left(\varsigma \right)=\frac{cos\left(ssin\left(y\right)\right)cosh\left(cos\left(y\right)\right)}{{\left[sinh(scos(y\left)\right)\right]}^2+{\left[cos(ssin(y\left)\right)\right]}^2}$$

has minimum value at $y=0$ and $\pi$ and maximum at $y=\pi /2.$ Hence,

$$\underset{\left|\varsigma \right|=s}{min}Re{\mathrm{\Psi }}_E\left(\varsigma \right)={\mathrm{\Psi }}_E\left(s\right)=sech\left(s\right),$$

and

$$\underset{\left|\varsigma \right|=s}{max}Re{\mathrm{\Psi }}_E\left(\varsigma \right)=sec\left(s\right).$$

Additionally, the function

$$\frac{{\left[cos(ssin(y\left)\right)cosh(scos(y\left)\right)\right]}^2+{\left[sin(ssin(y\left)\right)sinh(scos(y\left)\right)\right]}^2}{{\left[{\left(sinh(scos(y\left)\right)\right)}^2+{\left(cos(ssin(y\left)\right)\right)}^2)\right]}^2}$$

has minimum value at $y=0$ and $\pi$ and maximum at $y=\pi /2.$ Hence, we conclude that

$$\underset{\left|\varsigma \right|=s}{min}\left|{\mathrm{\Psi }}_E\left(\varsigma \right)\right|={\mathrm{\Psi }}_E\left(s\right)=sech\left(s\right),$$

and

$$\underset{\left|\varsigma \right|=s}{max}\left|{\mathrm{\Psi }}_E\left(\varsigma \right)\right|=sec\left(s\right).$$

□

Theorem 1.

The class ${\mathcal{S}}_E^{*}$ satisfies the following inclusion:

1.

${\mathcal{S}}_E^{*}\subset {\mathcal{S}}^{*}\left(\gamma \right),$ for $0\le \gamma \le sech\left(1\right),$

2.

${\mathcal{S}}_E^{*}\subset \mathcal{M}($γ) for $\gamma \ge sec\left(1\right),$

3.

${\mathcal{S}}_E^{*}\subset {\mathcal{SS}}^{*}\left(\beta \right),$ whenever ${\beta }_0\le \beta \le 1,$ where ${\beta }_0\approx 0.7949056270.$

Proof. 1.

Let $\mathsf{f}\in {\mathcal{S}}_E^{*}.$ Then we can write

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec sech\left(\varsigma \right).$$

By using Lemma 3, we conclude that

$$\underset{\left|\varsigma \right|=1}{min}Re(sech\left(\varsigma \right))<Re\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}<\underset{\left|\varsigma \right|=1}{max}Re(sech\left(\varsigma \right)),$$

Hence,

$$sech\left(1\right)<Re\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}<sec\left(1\right).$$

(4)

Thus, ${\mathcal{S}}_E^{*}\subset {\mathcal{S}}^{*}\left(\gamma \right),$ where $0\le \gamma \le sech\left(1\right).$

2. Result follows from (4).

3. Let $\mathsf{f}\in {\mathcal{S}}_E^{*}.$ Then,

$$\begin{array}{ccc}\hfill \left|arg\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right|& <& \underset{\left|\varsigma \right|=1}{max}arg\left(sech\left(\varsigma \right)\right)=\hfill \\ & & \underset{\left|\varsigma \right|=1}{max}\left\{-arctan\left(\frac{sin(sin(y\left)\right)sinh(cos(y\left)\right)}{cos(sin(y\left)\right)cosh(cos(y\left)\right)}\right)\right\}.\hfill \end{array}$$

Let

$$h\left(y\right)=-arctan\left(\frac{sin(sin(y\left)\right)sinh(cos(y\left)\right)}{cos(sin(y\left)\right)cosh(cos(y\left)\right)}\right).$$

Then, $h^{\prime }\left(y\right)=0$ has two roots in $[0,\pi ],$ namely

$$y_0\approx 0.9583580911\mathrm{and}{y}_1\approx 2.183234562.$$

A simple computation shows that $h^{″}\left(y_1\right)=-1.979302776.$ Therefore, we conclude that $max\left(h\left(y\right)\right)=h\left(y_1\right)=0.5060526392$. Thus,

$$\mathsf{f}\in {\mathcal{SS}}^{*}\left(\frac{2}{\pi }h\left(y_1\right)\right).$$

□

Theorem 2.

The ${\mathcal{S}}^{*}\left(\gamma \right)$-radii, for ${\mathcal{S}}_E^{*}$ is $s_0=arcsech\left(\gamma \right)$ with $sech\left(1\right)\le \gamma <1.$

Proof. 

Since $\mathsf{f}\in {\mathcal{S}}_E^{*},$ then by using Lemma 3, we have

$$sech\left(s\right)\le Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)\le sec\left(s\right).$$

Hence,

$$Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)\ge sech\left(s\right)\ge \gamma$$

for $s=arcsech\left(\gamma \right).$ Thus, the radius $s_0$ of ${\mathcal{S}}^{*}\left(\gamma \right)$ for ${\mathcal{S}}_E^{*}$ is the positive and smallest root $s_0\in (0,1)$ of the equation $sech\left(s\right)-\gamma =0.$ □

Theorem 3.

The $\mathcal{C}\left(\gamma \right)$-radius for the class ${\mathcal{S}}_E^{*}$ is $s_0,$ where $s_0$ is the positive and smallest root of the equation

$$(1-s^2)cos\left(s\right)\left[sech\left(s\right)-\gamma \right]-ssinh\left(s\right)=0.$$

Proof. 

Since $\mathsf{f}\in {\mathcal{S}}_E^{*},$ therefore for an analytic function $\omega$ with $\omega \left(0\right)=0$ and $\left|\omega \left(\varsigma \right)\right|\le \left|\varsigma \right|$, we can write

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=sech\left(\omega \left(\varsigma \right)\right).$$

(5)

By taking logarithmic differentiation of (5) it follows that

$$1+\frac{\varsigma {\mathsf{f}}^{″}\left(\varsigma \right)}{{\mathsf{f}}^{\prime }\left(\varsigma \right)}=sech\left(\omega \left(\varsigma \right)\right)-\frac{\varsigma {\omega }^{\prime }\left(\varsigma \right)sinh\left(\omega \left(\varsigma \right)\right)}{cosh\left(\omega \left(\varsigma \right)\right)}.$$

(6)

From (6), we may write

$$Re\left(1+\frac{\varsigma {\mathsf{f}}^{″}\left(\varsigma \right)}{{\mathsf{f}}^{\prime }\left(\varsigma \right)}\right)\ge Re(sech\left(\omega \left(\varsigma \right)\right))-\frac{|sinh\left(\omega \left(\varsigma \right)\right)\left|\right|\varsigma {\omega }^{\prime }\left(\varsigma \right)|}{|cosh\left(\omega \left(\varsigma \right)\right)|}.$$

(7)

For the minimum value, we assume $\omega \left(\varsigma \right)=\mathcal{R}{e}^{iy}$ with $\mathcal{R}\le \left|\varsigma \right|=s,-\pi \le y\le \pi .$ A simplification shows that

$$Re\left(sech\left(\omega \left(\varsigma \right)\right)\right)=\frac{cos(\mathcal{R}sin(y\left)\right)cosh(\mathcal{R}cos(y\left)\right)}{{\left[sinh(\mathcal{R}cos(y)\right]}^2+{\left[cos(\mathcal{R}sin(y\left)\right)\right]}^2}=\mathrm{\Phi }\left(y\right).$$

Since $\mathrm{\Phi }\left(y\right)=\mathrm{\Phi }(-y),$ therefore we only consider $y\in [0,\pi ]$ and the equation ${\mathrm{\Phi }}^{\prime }\left(y\right)=0$ has namely $0,\pi /2$ and $\pi$ roots. It implies that

$$min\left\{\mathrm{\Phi }\left(0\right),\mathrm{\Phi }(\pi /2),\mathrm{\Phi }\left(\pi \right)\right\}=\mathrm{\Phi }\left(0\right)=\mathrm{\Phi }\left(\pi \right)=sech\left(\mathcal{R}\right),$$

and

$$max\left\{\mathrm{\Phi }\left(0\right),\mathrm{\Phi }(\pi /2),\mathrm{\Phi }\left(\pi \right)\right\}=\mathrm{\Phi }\left(\frac{\pi }{2}\right)=sec\left(\mathcal{R}\right).$$

This implies that

$$Re(sech\left(\omega \left(\varsigma \right)\right)))\ge sech\left(\mathcal{R}\right)\ge sech\left(s\right).$$

(8)

Now consider

$$|cosh\left(R{e}^{iy}\right){|}^2={\left[cos\left(\mathcal{R}sin\left(y\right)\right)cosh\left(\mathcal{R}cos\left(y\right)\right)\right]}^2+{\left[sin\left(\mathcal{R}sin\left(y\right)\right)sinh\left(\mathcal{R}cos\left(y\right)\right)\right]}^2={\mathrm{\Phi }}_1\left(y\right).$$

We see that the equation ${\mathrm{\Phi }}_1^{\prime }\left(y\right)=0$ has $0,\pm \frac{\pi }{2}$ and $\pm \pi$ roots. Since ${\mathrm{\Phi }}_1\left(y\right)={\mathrm{\Phi }}_1(-y),$ therefore we take $y\in [0,\pi ].$ It is easy to see that ${\mathrm{\Phi }}_1\left(0\right)={\mathrm{\Phi }}_1\left(\pi \right)={cosh}^2\left(\mathcal{R}\right)$ and ${\mathrm{\Phi }}_1\left(\frac{\pi }{2}\right)={cos}^2\left(\mathcal{R}\right).$ Now

$$max\left\{{\mathrm{\Phi }}_1\left(0\right),{\mathrm{\Phi }}_1(\pi /2),{\mathrm{\Phi }}_1\left(\pi \right)\right\}={\mathrm{\Phi }}_1\left(0\right)={\mathrm{\Phi }}_1\left(\pi \right)={cosh}^2\left(\mathcal{R}\right).$$

Therefore,

$$cos\left(s\right)\le cos\left(\mathcal{R}\right)\le |cosh\left(\mathcal{R}{e}^{iy}\right)|\le cosh\left(\mathcal{R}\right)\le 1.$$

(9)

Additionally, it is easy to see that

$$|sinh\left(\mathcal{R}{e}^{iy}\right)|\le sinh\left(\mathcal{R}\right)\le sinh\left(s\right).$$

(10)

Using (8), (9) and (10) along with the result due to Nehari [38] for Schwarz function $\omega$ such that

$$|{\omega }^{\prime }\left(\varsigma \right)|\le \frac{1-{\left|\omega \left(\varsigma \right)\right|}^2}{1-{\left|\varsigma \right|}^2}=\frac{1-{\mathcal{R}}^2}{1-{\left|\varsigma \right|}^2}\le \frac{1}{1-{\left|\varsigma \right|}^2},$$

we have

$$Re\left(1+\frac{\varsigma {\mathsf{f}}^{″}\left(\varsigma \right)}{{\mathsf{f}}^{\prime }\left(\varsigma \right)}\right)\ge sech\left(s\right)-\frac{ssinh\left(s\right)}{(1-s^2)cos\left(s\right)}\ge \gamma$$

for $(1-s^2)cos\left(s\right)\left[sech\left(s\right)-\gamma \right]-ssinh\left(s\right)\ge 0.$ Thus, the $\mathcal{C}\left(\gamma \right)$-radius $s_0$ for the class ${\mathcal{S}}_E^{*}$ is the root of the equation

$$(1-s^2)cos\left(s\right)\left[sech\left(s\right)-\gamma \right]-ssinh\left(s\right)=0.$$

□

Corollary 1.

The $\mathcal{C}$ radius for ${\mathcal{S}}_E^{*}$ is $s_0\approx 0.623081.$

4. Inclusion Results

This section deals with inclusion results for the class ${\mathcal{S}}_E^{*}$ and certain subclasses of starlike functions.

Theorem 4.

For ${\mathcal{S}}_E^{*}$, the following inclusion relations hold:

1.

${\mathcal{S}}_L^{*}\left(\gamma \right)\subset {\mathcal{S}}_E^{*}$, for $\gamma \ge sech\left(1\right),$

2.

${\mathcal{S}}_{q_c}^{*}\subset {\mathcal{S}}_E^{*}$, for $0<c\le 1-{\left[sech\left(1\right)\right]}^2,$

3.

${\mathcal{S}}^{*}[1-\gamma ,0]\subset {\mathcal{S}}_E^{*}$, for $sech\left(1\right)\le \gamma \le 1.$

Proof. 1.

To show the function $\mathsf{f}\in {\mathcal{S}}_L^{*}\left(\gamma \right)$ lies in the class ${\mathcal{S}}_E^{*}$, we use the result ([5], Lemma 2.1), that gives

$$\gamma <Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)<\gamma +(1-\gamma )\sqrt{2}.$$

Let $\mathsf{f}\in {\mathcal{S}}_L^{*}\left(\gamma \right)$. Then,

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \gamma +\left(1-\gamma \right)\sqrt{1+\varsigma },0\le \gamma <1.$$

The function $\mathsf{f}\in {\mathcal{S}}_E^{*}$ if either $\gamma \ge sech\left(1\right)$ or $\gamma +(1-\gamma )\sqrt{2}\le sec\left(1\right).$ Thus, $\mathsf{f}\in {\mathcal{S}}_E^{*}$ for $\gamma \ge sech\left(1\right).$

2. Let $\mathsf{f}\in {\mathcal{S}}_{q_c}^{*}(0<c\le 1).$ Then $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \sqrt{1+c\varsigma }$ and

$$\sqrt{1-c}<Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)<\sqrt{1+c}.$$

We see that $\sqrt{1+c}<\sqrt{2}<sec\left(1\right).$ Thus, the function $\mathsf{f}\in {\mathcal{S}}_E^{*}$ if $\sqrt{1-c}\ge sech\left(1\right)$. This gives $c\le 1-{\left[sech\left(1\right)\right]}^2.$

3. Proceeding as in part (ii), we see that the function $\mathsf{f}\in {\mathcal{S}}^{*}[1-\gamma ,0]$ lies in the class ${\mathcal{S}}_E^{*}$ if

$$sech\left(1\right)\le \gamma <Re\left(\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\right)<2-\gamma \le sec\left(1\right),$$

which holds for $\gamma \ge sech\left(1\right).$ □

5. Radius Problems

In the following result, we establish the radius for the smallest and largest disks with center $(\lambda ,0)$ such that the domain ${\mathrm{\Delta }}_E:=sech\left(\mathbb{D}\right)$ contains the largest disk and is contained in the smallest disk.

Lemma 4.

Let $sech\left(1\right)<\lambda <sec\left(1\right)$. Then,

$$\{\omega \in \mathbb{C}:\left|\omega -\lambda \right|<s_{\lambda }\}\subseteq {\mathrm{\Delta }}_E\subseteq \{\omega \in :\left|\omega -\lambda \right|<{\mathcal{R}}_{\lambda }\},$$

where

$$s_{\lambda }=\left\{\begin{array}{c}\lambda -sech\left(1\right),sech\left(1\right)<\lambda \le \frac{1}{2}\left(sech\left(1\right)+sec\left(1\right)\right),\\ Section\left(1\right)-\lambda ,\frac{1}{2}\left(sech\left(1\right)+sec\left(1\right)\right)\le \lambda <sec\left(1\right),\end{array}\right.$$

and ${\mathcal{R}}_{\lambda }$ be given by

$${\mathcal{R}}_{\lambda }=\left\{\begin{array}{c}sec\left(1\right)-\lambda ,sech\left(1\right)<\lambda \le {\lambda }^{*},\\ \sqrt{l\left(y_{\lambda }\right),}{\lambda }^{*}<\lambda \le {\lambda }^{**},\\ \lambda -sech\left(1\right),{\lambda }^{**}\le \lambda <sec\left(1\right),\end{array}\right.$$

where ${\lambda }^{*}\approx 1.2448601986$ and ${\lambda }^{**}\approx 1.27292765302578.$

Proof. 

Firstly, we consider the distance of any point on the boundary ${\mathrm{\Delta }}_E$ to $(\lambda ,0)$. The square of this distance is given as

$$l\left(t\right)={\left(\lambda -\frac{cosh(cos(y\left)\right)cos(sin(y\left)\right)}{{\left[cos(sin(y\left)\right)\right]}^2+{\left[sinh(cos(y\left)\right)\right]}^2}\right)}^2+{\left(\frac{sinh(cos(y\left)\right)sin(sin(y\left)\right)}{{\left[cos(sin(y\left)\right)\right]}^2+{\left[sinh(cos(y\left)\right)\right]}^2}\right)}^2$$

(11)

To obtain the radius for the largest disk in ${\mathrm{\Delta }}_E$, we only prove that ${\displaystyle \underset{0\le y\le \pi }{min}}\sqrt{l\left(y\right)}=s_{\lambda }$. Since $l\left(y\right)=l(-y)$, therefore we take $0\le y\le \pi$. We have the following cases:

Case 1. When $sech\left(1\right)<\lambda \le {\lambda }^{*},$ the equation $l^{\prime }\left(y\right)=0$ has 0, $\frac{\pi }{2}$ and $\pi$ roots. Moreover, the function $l^{\prime }$ is positive when $y\in \left(0,\frac{\pi }{2}\right)$ and negative for $y\in \left(\frac{\pi }{2},\pi \right).$ Hence, we conclude that minimum of l exists at 0 and $\pi .$ This implies that

$$\underset{0\le y\le \pi }{min}\sqrt{l\left(y\right)}=\sqrt{l\left(0\right)}=\sqrt{l\left(\pi \right)}=\lambda -sech\left(1\right).$$

Case 2. When ${\lambda }^{*}<\lambda \le {\lambda }^{**},$ the equation $l^{\prime }\left(y\right)=0$ has 0, $y_{{\lambda }_1}$, $\frac{\pi }{2}$, $y_{{\lambda }_2}$ and $\pi$ roots. Here the roots $y_{{\lambda }_1}$ and $y_{{\lambda }_2}$ depend upon $\lambda .$ Furthermore, the function $l^{\prime }$ is increasing for $t\in \left(0,y_{{\lambda }_1}\right),$ decreasing for $y\in \left(y_{{\lambda }_1},\frac{\pi }{2}\right),$ increasing for $y\in \left(\frac{\pi }{2},y_{{\lambda }_2}\right)$ and again decreasing for $y\in \left(y_{{\lambda }_2},\pi \right).$ Therefore,

$$\underset{0\le y\le \pi }{min}\sqrt{l\left(y\right)}=min\left\{\sqrt{l\left(0\right)},\sqrt{l\left(\frac{\pi }{2}\right)},\sqrt{l\left(\pi \right)}\right\}.$$

We also observe from the graph of the function l that when ${\lambda }^{*}<\lambda \le \left(sech\left(1\right)+sec\left(1\right)\right)/2$, the function l has minimum value at 0 and $\pi .$ This implies that

$$\underset{0\le y\le \pi }{min}\sqrt{l\left(y\right)}=min\left\{\sqrt{l\left(0\right)},\sqrt{l\left(\frac{\pi }{2}\right)},\sqrt{l\left(\pi \right)}\right\}=\sqrt{l\left(0\right)}=\sqrt{l\left(\pi \right)}=\lambda -sech\left(1\right).$$

Additionally, we see that when $\left(sech\left(1\right)+sec\left(1\right)\right)/2\le \lambda \le {\lambda }^{**},$

$$\underset{0\le y\le \pi }{min}\sqrt{l\left(y\right)}=min\left\{\sqrt{l\left(0\right)},\sqrt{l\left(\frac{\pi }{2}\right)},\sqrt{l\left(\pi \right)}\right\}=l\left(\frac{\pi }{2}\right)=sec\left(1\right)-\lambda .$$

Case 3. When ${\lambda }^{**}<\lambda \le sec\left(1\right),$ the equation $l^{\prime }\left(y\right)=0$ has 0, $\frac{\pi }{2}$ and $\pi$ roots. Moreover, the function $l^{\prime }$ is negative when $y\in \left(0,\frac{\pi }{2}\right)$ and positive for $y\in \left(\frac{\pi }{2},\pi \right).$ Hence, we conclude that

$$\underset{0\le y\le \pi }{min}\sqrt{l\left(y\right)}=\sqrt{l\left(\frac{\pi }{2}\right)}=sec\left(1\right)-\lambda .$$

Using the same argument, we obtain the result for ${\mathcal{R}}_{\lambda }$. □

Theorem 5.

1.

A function $\mathsf{f}\left(\varsigma \right)=\varsigma +\nu {\varsigma }^2$ is in ${\mathcal{S}}_E^{*}$ if and only if $\left|\nu \right|\le \frac{1-sech\left(1\right)}{2-sech\left(1\right)},$

2.

The function $\mathsf{f}\left(\varsigma \right)=\frac{\varsigma }{{(1-\nu \varsigma )}^2}\in {\mathcal{S}}_E^{*}$ if and only if $\left|\nu \right|\le \frac{1-sech\left(1\right)}{1+sech\left(1\right)}.$

Proof. 1.

If $\mathsf{f}\in {\mathcal{S}}_E^{*}\subset {\mathcal{S}}^{*}$, so we have $\left|\nu \right|\le \frac{1}{2}$. Using Lemma 2 for $\omega =\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=\frac{1+2\nu \varsigma }{1+\nu \varsigma }$, it will map $\mathbb{D}$ onto the disc

$$\left|\omega -\frac{1-2{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}\right|<\frac{\left|\nu \right|}{1-{\left|\nu \right|}^2}.$$

As $\left|\nu \right|\le \frac{1}{2}$, so we have $\frac{1-2{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}<sech\left(1\right)$ and $\frac{\left|\nu \right|}{1-{\left|\nu \right|}^2}\le \frac{1-2{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}-sech\left(1\right)$, which gives

$$\left|\nu \right|\le \frac{1-sech\left(1\right)}{2-sech\left(1\right)}.$$

Conversely, if $\left|\nu \right|\le \frac{1-sech\left(1\right)}{2-sech\left(1\right)}$, then

$$\frac{\left|\nu \right|}{1-{\left|\nu \right|}^2}\le \frac{1-2{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}-sech\left(1\right).$$

In view of Lemma 4, we see that $\mathsf{f}\in {\mathcal{S}}_E^{*}$.

2. If $\nu =1$, then $\frac{\varsigma }{{(1-\varsigma )}^2}$ does not belong to the class $\mathsf{f}\in {\mathcal{S}}_E^{*}$, so $\nu \ne 1$. Then, by using Lemma 2 the following bilinear transformation $\omega =\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=\frac{1+\nu \varsigma }{1-\nu \varsigma }$ maps $\mathbb{D}$ onto the disc, where $\mathsf{f}\left(\varsigma \right)=\frac{\varsigma }{{(1-\nu \varsigma )}^2}$.

$$\left|\omega -\frac{1+{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}\right|\le \frac{2\left|\nu \right|}{1-{\left|\nu \right|}^2}$$

with diameter end points $x_L=\frac{1-\left|\nu \right|}{1+\left|\nu \right|}$ and $x_{\mathcal{R}}=\frac{1+\left|\nu \right|}{1-\left|\nu \right|}$. If $\mathsf{f}\in {\mathcal{S}}_E^{*}$, then $x_L\ge sech\left(1\right)$, after simplifying it gives us $\left|\nu \right|\le \frac{1-sech\left(1\right)}{1+sech\left(1\right)}$. Conversely, if $\left|\nu \right|\le \frac{1-sech\left(1\right)}{1+sech\left(1\right)}$, then in the light of Lemma 4, we have

$$\frac{1+{\left|\nu \right|}^2}{1-{\left|\nu \right|}^2}<sec\left(1\right),$$

and

$$\lambda +\frac{2\left|\nu \right|}{1-{\left|\nu \right|}^2}=\frac{1+\left|\nu \right|}{1-\left|\nu \right|}<sec\left(1\right).$$

From the above equation, it is clear that

$$\frac{2\left|\nu \right|}{1-{\left|\nu \right|}^2}\le Section\left(1\right)-\lambda .$$

See the sharpness of the result in Figure 2. □

Figure 2. Graph of $\frac{1+\nu z}{1-\nu z}$ for $\left|\nu \right|\le -\frac{-1+\mathit{sech}\left(1\right)}{1+\mathit{sech}\left(1\right)}$ to be contained in $S_E^{*}$.

Theorem 6.

The ${\mathcal{S}}_E^{*}$ radii for the classes ${\mathcal{S}}_L^{*}$, ${\mathcal{S}}_{RL}^{*}$, ${\mathcal{S}}_C^{*}$, ${\mathcal{S}}_{lim}^{*}$, $\mathcal{BS}\left(\gamma \right)$, ${\mathcal{SL}}^{*}\left(\gamma \right)$ and $\mathcal{W}$ are given as follows.

1.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_L^{*}\right)=1-{sech\left(1\right)}^2\approx 0.58002$,

2.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_{RL}^{*}\right)=\frac{(2-3sech\left(1\right)+{sech\left(1\right)}^2)2\sqrt{2}+5-8sech\left(1\right)+3{sech\left(1\right)}^2}{(2-2sech\left(1\right)+{sech\left(1\right)}^2)2\sqrt{2}+5-8sech\left(1\right)+2{sech\left(1\right)}^2}\approx 0.63147$,

3.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_C^{*}\right)=\frac{2-\sqrt{6sech\left(1\right)-2}}{2}\approx 0.31291$,

4.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_{lim}^{*}\right)=\sqrt{2}\left(1-\sqrt{sech\left(1\right)}\right)\approx 0.27576$,

5.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_L^{*}\left(\gamma \right)\right)=\frac{1-2\gamma +2\gamma sech\left(1\right)-{sech\left(1\right)}^2}{{(sech\left(1\right)-1)}^2},$

6.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left(\mathcal{BS}\left(\gamma \right)\right)=\frac{2\left(1-sech\left(1\right)\right)}{1+\sqrt{1+4sech\left(1\right)-8{sech\left(1\right)}^2+4{sech\left(1\right)}^3}},$

7.

${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left(\mathcal{W}\right)=\frac{1-sech\left(1\right)}{1+\sqrt{2-2sech\left(1\right)+{sech\left(1\right)}^2}}.$

Proof. 1.

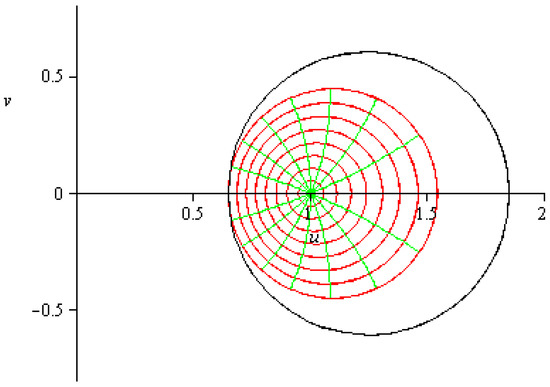
For the functions $\mathsf{f}\in {\mathcal{S}}_L^{*}$, we have $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \sqrt{1+\varsigma }$. Thus, for $\left|\varsigma \right|=s$, we have by Lemma 4,

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le 1-\sqrt{1-s}\le 1-sech\left(1\right),$$

whenever the inequality $s\le 1-{sech\left(1\right)}^2$ holds. The sharpness is obtained for the function

$${\mathsf{f}}_0\left(\varsigma \right)=\frac{4\varsigma exp(2\sqrt{1+\varsigma }-2)}{{(1+\sqrt{1+\varsigma })}^2},$$

which is in class ${\mathcal{S}}_L^{*}$. Since $\frac{\varsigma {\mathsf{f}}_0^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_0\left(\varsigma \right)}=\sqrt{1+\varsigma }=sech\left(1\right)$ at point $\varsigma ={\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_L^{*}\right),$(see Figure 3).

Figure 3. $S_E^{*}$ radius for ${\mathcal{S}}_L^{*}$ (left figure), ${\mathcal{S}}_{RL}^{*}$ (right figure).

2. For functions $\mathsf{f}\in {\mathcal{S}}_{RL}^{*}$, we have

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \sqrt{2}-(\sqrt{2}-1)\sqrt{\frac{1-\varsigma }{1+2(\sqrt{2}-1)\varsigma }}.$$

This implies that

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le 1-\sqrt{2}+(\sqrt{2}-1)\sqrt{\frac{1+s}{1-2(\sqrt{2}-1)s}}\le 1-sech\left(1\right),$$

provided

$$s\le \frac{(2-3sech\left(1\right)+{sech\left(1\right)}^2)2\sqrt{2}+5-8sech\left(1\right)+3{sech\left(1\right)}^2}{(2-2sech\left(1\right)+{sech\left(1\right)}^2)2\sqrt{2}+5-8sech\left(1\right)+2{sech\left(1\right)}^2}.$$

For sharpness, we consider the function ${\mathsf{f}}_1$ given as

$${\mathsf{f}}_1\left(\varsigma \right)=\varsigma exp\left({\int }_0^{\varsigma }\frac{q_1\left(t\right)-1}{1}dt\right),$$

where

$$q_1\left(\varsigma \right)=\sqrt{2}-(\sqrt{2}-1)\sqrt{\frac{1-\varsigma }{1+2(\sqrt{2}-1)\varsigma }}.$$

At point $\varsigma ={\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_{RL}^{*}\right)$, we have

$$\frac{\varsigma {\mathsf{f}}_1^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_1\left(\varsigma \right)}=\sqrt{2}-(\sqrt{2}-1)\sqrt{\frac{1-\varsigma }{1+2(\sqrt{2}-1)\varsigma }}=sech\left(1\right),$$

(see Figure 3).

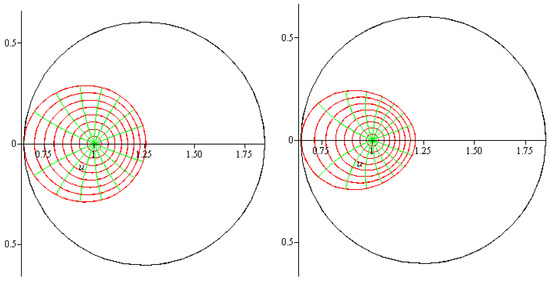
3. For the functions $\mathsf{f}\in {\mathcal{S}}_C^{*}$, we have $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec 1+\frac{4\varsigma }{3}+\frac{2{\varsigma }^2}{3}$. Thus, for $\left|\varsigma \right|=s$, we have by Lemma 4,

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{4s}{3}-\frac{2s^2}{3}\le 1-sech\left(1\right),$$

whenever the inequality $s\le \frac{2-\sqrt{6sech\left(1\right)-2}}{2}$ holds. Consider the function

$${\mathsf{f}}_2\left(\varsigma \right)=\varsigma exp\frac{4\varsigma +{\varsigma }^{\mathsf{2}}}{3}.$$

Since $\frac{\varsigma {\mathsf{f}}_2^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_2\left(\varsigma \right)}=1+\frac{4\varsigma }{3}+\frac{2{\varsigma }^2}{3}$, so $\mathsf{f}\in {\mathcal{S}}_C^{*}$ and at point $\varsigma =-{\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_C^{*}\right),$ we have $\frac{\varsigma {\mathsf{f}}_2^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_2\left(\varsigma \right)}=sech\left(1\right)$. Hence, the result is sharp, see Figure 4 (left).

Figure 4. $S_E^{*}$ radius for ${\mathcal{S}}_C^{*}$ (left figure), ${\mathcal{S}}_{lim}^{*}$ (centered figure), ${\mathcal{S}}_{\mathcal{L}}^{*}\left(0\right)$ (right figure).

4. For the functions $\mathsf{f}\in {\mathcal{S}}_{lim}^{*}$, we have $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec 1+\sqrt{2}\varsigma +\frac{{\varsigma }^2}{2}$. Thus, for $\left|\varsigma \right|=s$, we have by Lemma 4,

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \sqrt{2}s-\frac{s^2}{2}\le 1-sech\left(1\right),$$

whenever the inequality $s\le \sqrt{2}\left(1-\sqrt{sech\left(1\right)}\right)$ holds. Consider the function

$${\mathsf{f}}_3\left(\varsigma \right)=\varsigma e^{\sqrt{2}\varsigma +\frac{{\varsigma }^2}{4}}.$$

Since $\frac{\varsigma {\mathsf{f}}_3^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_3\left(\varsigma \right)}=1+\sqrt{2}\varsigma +\frac{{\varsigma }^2}{2}$, so $\mathsf{f}\in {\mathcal{S}}_C^{*}$ and at point $\varsigma =-{\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_C^{*}\right),$ we have $\frac{\varsigma {\mathsf{f}}_3^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_3\left(\varsigma \right)}=sech\left(1\right)$. Hence, the result is sharp, see Figure 4 (centered).

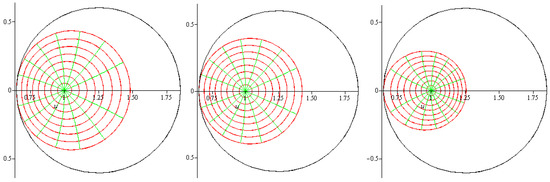
5. Let $\mathsf{f}\in {\mathcal{S}}_L^{*}\left(\gamma \right)$. Then $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\prec \gamma +(1-\gamma )\sqrt{1+\varsigma }$. Now we have

$$\begin{array}{ccc}\hfill \left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|& \le & \left|\gamma +(1-\gamma )\sqrt{1+\varsigma }-1\right|\hfill \\ & \le & (1-\gamma )(1-\sqrt{1-s})\hfill \\ & \le & 1-sech\left(1\right).\hfill \end{array}$$

This holds for

$$s\le \frac{1-2\gamma +2\gamma sech\left(1\right)-{sech\left(1\right)}^2}{{(sech\left(1\right)-1)}^2}.$$

The sharpness can be obtained for ${\mathsf{f}}_4$, given by the relation

$$\frac{\varsigma {\mathsf{f}}_4^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_4\left(\varsigma \right)}=\gamma +(1-\gamma )\sqrt{(1+\varsigma )}$$

and

$$\frac{\varsigma {\mathsf{f}}_4^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_4\left(\varsigma \right)}=sech\left(1\right),$$

for $\varsigma =\frac{1-2\gamma +2\gamma sech\left(1\right)-{sech\left(1\right)}^2}{{(sech\left(1\right)-1)}^2}.$ For $\gamma =0$, the sharpness is shown in Figure 4 (right).

6. For $\mathsf{f}\in \left(\mathcal{BS}\right(\gamma )$, we have $\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)/\mathsf{f}\left(\varsigma \right)\prec 1+\varsigma /(1-\gamma {\varsigma }^2),$ which gives

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{s}{1-\gamma s^2},$$

for $\left|\varsigma \right|<s.$ By using Lemma 4, we obtain $s/(1-\gamma s^2)\le 1-sech\left(1\right)$ and it simplifies to $s\le \frac{-2\left(-1+sech\left(1\right)\right)}{1+\sqrt{1+4sech\left(1\right)-8{sech\left(1\right)}^2+4{sech\left(1\right)}^3}},$ for $0<\gamma <1.$ Take the function ${\mathsf{f}}_5$ given by

$${\mathsf{f}}_5\left(\varsigma \right)=\varsigma {\left(\frac{1+\sqrt{\gamma }\varsigma }{1-\sqrt{\gamma }\varsigma }\right)}^{1/\left(2\sqrt{\gamma }\right)}.$$

At $\varsigma =-{\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left(\mathcal{BS}\left(\gamma \right)\right),$ the quantity $\varsigma {\mathsf{f}}_5^{\prime }\left(\varsigma \right)/{\mathsf{f}}_5\left(\varsigma \right)=sech\left(1\right)$ is obtained.

7. Let $\mathsf{f}\in \mathcal{W}$. Then $\frac{\mathsf{f}\left(\varsigma \right)}{\varsigma }\in \mathcal{P}$, for all $\varsigma \in \mathbb{D}$. Let us define function $\mathsf{p}\in \mathcal{P}$ such that $\mathsf{p}\left(\varsigma \right)=\mathsf{f}\left(\varsigma \right)/\varsigma$. Then,

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=1+\frac{\varsigma {\mathsf{p}}^{\prime }\left(\varsigma \right)}{\mathsf{p}\left(\varsigma \right)}.$$

Thus, we have

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{2s}{1-s^2}.$$

By using Lemmas 1 and 4, the function $\mathsf{f}\in {\mathcal{S}}_E^{*}$ for $\left|\varsigma \right|<s$ if $2s/(1-s^2)<1-sech\left(1\right)$. This simplifies to $s\le \frac{1-sech\left(1\right)}{1+\sqrt{2-2sech\left(1\right)+{sech\left(1\right)}^2}}.$ Sharpness can be seen for the function ${\mathsf{f}}_6\left(\varsigma \right)=\varsigma (1+\varsigma )/(1-\varsigma )$. For this function, we have

$$\frac{\varsigma {\mathsf{f}}_6^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_6\left(\varsigma \right)}=sech\left(1\right)\mathrm{at}\varsigma =\frac{1-sech\left(1\right)}{1+\sqrt{2-2sech\left(1\right)+{sech\left(1\right)}^2}}.$$

□

Theorem 7.

Let $-1\le b<a\le 1$, with $b<0$. Let

$${\mathcal{R}}_1=min\left(1,\frac{\sqrt{-b\left[2a-bsech\left(1\right)-bsec\left(1\right)\right]\left[-2+sech\left(1\right)+sec\left(1\right)\right]}}{b\left[bsech\left(1\right)+bsec\left(1\right)-2a\right]}\right).$$

$${\mathcal{R}}_2=min\left(1,\frac{1-sech\left(1\right)}{a-bsech\left(1\right)}\right)$$

and

$${\mathcal{R}}_3=min\left(1,\frac{sec\left(1\right)-1}{a-bsec\left(1\right)}\right).$$

Then, ${\mathcal{S}}_E^{*}$ radius for ${\mathcal{S}}^{*}[a,b]$ is given by

$${\mathcal{R}}_{{\mathcal{S}}_E^{*}}\left({\mathcal{S}}_E^{*}[a,b]\right)=\left\{\begin{array}{c}{\mathcal{R}}_2,if{\mathcal{R}}_2\le {\mathcal{R}}_1,\\ {\mathcal{R}}_3,if{\mathcal{R}}_2>{\mathcal{R}}_1.\end{array}\right.$$

Proof. 

Let $\mathsf{f}\in {\mathcal{S}}^{*}[a,b]$, then by Lemmas 2 and 4, we have

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-\frac{1-ab{s}^2}{1-b^2{s}^2}\right|\le \frac{(a-b)s}{1-b^2{s}^2}.$$

We have to determine the numbers ${\mathcal{R}}_1,{\mathcal{R}}_2$ and ${\mathcal{R}}_3$. Now $s\le {\mathcal{R}}_1$, if and only if $\frac{1-ab{s}^2}{1-b^2{s}^2}\le \frac{sech\left(1\right)+sec\left(1\right)}{2}$. This yields us $s\le \frac{\sqrt{-b\left[2a-bsech\left(1\right)-bsec\left(1\right)\right]\left[-2+sech\left(1\right)+sec\left(1\right)\right]}}{b\left[bsech\left(1\right)+bsec\left(1\right)-2a\right]}$. Similarly $s\le {\mathcal{R}}_2$ if and only if

$$\frac{(a-b)s}{1-b^2{s}^2}\le \frac{1-ab{s}^2}{1-b^2{s}^2}-sech\left(1\right).$$

The above equation gives us $s\le \frac{1-sech\left(1\right)}{a-bsech\left(1\right)}$. Also $s\le {\mathcal{R}}_3$ if and only if

$$\frac{(a-b)s}{1-b^2{s}^2}\le Section\left(1\right)-\frac{1-ab{s}^2}{1-b^2{s}^2}.$$

A simple calculation yields

$$s\le \frac{sec\left(1\right)-1}{a-bsec\left(1\right)b}.$$

□

Theorem 8.

The ${\mathcal{S}}_{E,m}^{*}$-radius for ${\mathcal{S}}_m$ is

$${\mathcal{R}}_{\left({\mathcal{S}}_{E,m}^{*}\right)}\left({\mathcal{S}}_m\right):={\left(\frac{1-sech\left(1\right)}{m+\sqrt{m^2+1-2sech\left(1\right)+{\left[sech\left(1\right)\right]}^2}}\right)}^{\frac{1}{m}}.$$

Proof. 

Take the function h$:\mathbb{D}\to \mathbb{C}$ given by h$\left(\varsigma \right)=\frac{\mathsf{f}\left(\varsigma \right)}{\varsigma }$. Then h$\in {\mathcal{P}}_m$ and $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1=\frac{\varsigma {\mathsf{h}}^{\prime }\left(\varsigma \right)}{\mathsf{h}\left(\varsigma \right)}.$ Applying Lemma 1, it will give us the following disc

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{2m{s}^m}{1-s^{2m}}.$$

By Lemma 4, the above disc is contained in ${\mathrm{\Delta }}_E$ if

$$\frac{2m{s}^m}{1-s^{2m}}\le 1-sech\left(1\right),$$

which gives

$$s\le \mathcal{R}:={\left(-\frac{-1+sech\left(1\right)}{m+\sqrt{m^2+1-2sech\left(1\right)+sech{\left(1\right)}^2}}\right)}^{\frac{1}{m}}.$$

Consider the function ${\mathsf{f}}_1$ defined by ${\mathsf{f}}_1\left(\varsigma \right)=\frac{\varsigma (1+{\varsigma }^m)}{1-{\varsigma }^m}$. It is easy to check that $Re\frac{{\mathsf{f}}_1\left(\varsigma \right)}{\varsigma }>0$ in $\mathbb{D}$. Thus, ${\mathsf{f}}_1\in {\mathcal{S}}_m$ and

$$\frac{\varsigma {\mathsf{f}}_1^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_1\left(\varsigma \right)}-1=\frac{2m{\varsigma }^m}{1-{\varsigma }^{2m}}.$$

Furthermore, the function ${\mathsf{f}}_1$ gives the sharpness as at $\varsigma ={\mathcal{R}}_{\left({\mathcal{S}}_E^{*}\right)}\left({\mathcal{S}}_m\right)$, we have

$$\frac{\varsigma {\mathsf{f}}_1^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_1\left(\varsigma \right)}-1=\frac{2m{\varsigma }^m}{1-{\varsigma }^{2m}}=1-sech\left(1\right).$$

□

Theorem 9.

Let

$${\mathcal{R}}_1={\left(\frac{\sqrt{\left(2-4\gamma +sech\left(1\right)+sec\left(1\right)\right)\left(-2+sec\left(1\right)+sech\left(1\right)\right)}}{2-4\gamma +sech\left(1\right)+sec\left(1\right)}\right)}^{\frac{1}{m}},$$

$${\mathcal{R}}_2={\left(\frac{1-sech\left(1\right)}{1+m-\gamma +\sqrt{m\left(m-2\gamma +2\right)+{\gamma }^2-2\gamma sech\left(1\right)+{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}},$$

and

$${\mathcal{R}}_3={\left(\frac{1-sec\left(1\right)}{\gamma -1-m-\sqrt{m\left(m-2\gamma +2\right)+{\gamma }^2+{sec\left(1\right)}^2-2\gamma sec\left(1\right)}}\right)}^{\frac{1}{m}}.$$

Then ${\mathcal{S}}_{E,m}^{*}$-radius for ${\mathcal{CS}}_m\left(\gamma \right)$ is given by

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{CS}}_m\left(\gamma \right)\right)=\left\{\begin{array}{c}{\mathcal{R}}_2,if{\mathcal{R}}_2\le {\mathcal{R}}_1,\\ {\mathcal{R}}_3,if{\mathcal{R}}_2>{\mathcal{R}}_1.\end{array}\right.$$

Proof. 

Let $\mathsf{f}\in {\mathcal{CS}}_m\left(\gamma \right)$ and define $\mathsf{h}\left(\varsigma \right)=\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}$, where $\mathsf{g}\in {\mathcal{S}}_m^{{}_{*}}\left(\gamma \right)$. Then $\mathsf{h}\in {\mathcal{P}}_m.$ Therefore,

$$\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=\frac{\varsigma {\mathsf{g}}^{\prime }\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}+\frac{\varsigma {\mathsf{h}}^{\prime }\left(\varsigma \right)}{\mathsf{h}\left(\varsigma \right)}.$$

Using Lemma 2, we have

$$\left|\frac{\varsigma {\mathsf{g}}^{\prime }\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}-\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}\right|\le \frac{2(1-\gamma )s^m}{1-s^{2m}}.$$

Therefore,

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}\right|\le \frac{2(1+m-\gamma )s^m}{1-s^{2m}}.$$

For $0\le \gamma <1$ and $0<s<1$, we are going to find the values of ${\mathcal{R}}_1,{\mathcal{R}}_2$ and ${\mathcal{R}}_3$. Here, $s\le {\mathcal{R}}_1$ if and only if

$$\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}\le \frac{sech\left(1\right)+sec\left(1\right)}{2}.$$

This yields us

$$s\le {\left(\frac{\sqrt{\left(2-4\gamma +sech\left(1\right)+sec\left(1\right)\right)\left(-2+sec\left(1\right)+sech\left(1\right)\right)}}{2-4\gamma +sech\left(1\right)+sec\left(1\right)}\right)}^{\frac{1}{m}}.$$

Next, we determine ${\mathcal{R}}_2$ such that $s\le {\mathcal{R}}_2$ if and only if

$$\frac{2(1+m-\gamma )s^m}{1-s^{2m}}\le \frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}-sech\left(1\right),$$

provided

$$s\le {\left(\frac{1-sech\left(1\right)}{1+m-\gamma +\sqrt{2m+m^2-2m\gamma +{\gamma }^2-2\gamma sech\left(1\right)+{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}.$$

We determine ${\mathcal{R}}_3$ such that $s\le {\mathcal{R}}_3$ if and only if

$$\frac{2(1+m-\gamma )s^m}{1-s^{2m}}\le Section\left(1\right)-\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}$$

provided

$$s\le {\left(\frac{1-sec\left(1\right)}{\gamma -1-m-\sqrt{2m+m^2-2m\gamma +{\gamma }^2+{sec\left(1\right)}^2-2\gamma sec\left(1\right)}}\right)}^{\frac{1}{m}}.$$

□

Theorem 10.

The class ${\mathcal{S}}_m^{*}[a,b]$ is in the class ${\mathcal{S}}_{E,m}^{*}$ if either of the following relations is satisfied.

1.

$2(1-b^2)sech\left(1\right)<2\left(1-ab\right)\le \left(sec\left(1\right)+sech\left(1\right)\right)(1-b^2)$ and $(1-b)sech\left(1\right)\le (1-a),$

2.

$\left(sec\left(1\right)+sech\left(1\right)\right)(1-b^2)<2\left(1-ab\right)<2sec\left(1\right)(1-b^2)$ and $(1+a)\le (1+b)sec\left(1\right).$

Proof. 

From the definition of the class ${\mathcal{S}}_m^{*}[a,b]$, we have $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\in {\mathcal{P}}_m[a,b].$ By using Lemma 2, we can write

$$\left|\mathsf{p}\left(\varsigma \right)-\frac{1-ab}{1-b^2}\right|\le \frac{a-b}{1-b^2}.$$

The above relation gives us a disc with center $\left(1-ab\right)/\left(1-b^2\right)$ and radius $\left(a-b\right)/\left(1-b^2\right).$ In view of Lemma 4, we have to show that

$$\left|\mathsf{p}\left(\varsigma \right)-\frac{1-ab}{1-b^2}\right|\le s=\left\{\begin{array}{c}\frac{1-ab}{1-b^2}-sech\left(1\right),sech\left(1\right)<\frac{1-ab}{1-b^2}\le \frac{sec\left(1\right)+sech\left(1\right)}{2},\\ sec\left(1\right)-\frac{1-ab}{1-b^2},\frac{sec\left(1\right)+sech\left(1\right)}{2}\le \frac{1-ab}{1-b^2}<sec\left(1\right).\end{array}\right.$$

This implies that

$$\frac{a-b}{1-b^2}\le s=\left\{\begin{array}{c}\frac{1-ab}{1-b^2}-sech\left(1\right),sech\left(1\right)<\frac{1-ab}{1-b^2}\le \frac{sec\left(1\right)+sech\left(1\right)}{2},\\ sec\left(1\right)-\frac{1-ab}{1-b^2},\frac{sec\left(1\right)+sech\left(1\right)}{2}\le \frac{1-ab}{1-b^2}<sec\left(1\right).\end{array}\right.$$

which is equivalent to either

$$\frac{a-b}{1-b^2}\le \frac{1-ab}{1-b^2}-sech\left(1\right)\mathrm{and}sech\left(1\right)<\frac{1-ab}{1-b^2}\le \frac{sec\left(1\right)+sech\left(1\right)}{2}$$

or

$$\frac{a-b}{1-b^2}\le sec\left(1\right)-\frac{1-ab}{1-b^2}\mathrm{and}\frac{sec\left(1\right)+sech\left(1\right)}{2}\le \frac{1-ab}{1-b^2}<sec\left(1\right).$$

Simple calculations establish the required result. □

Theorem 11.

The ${\mathcal{S}}_{E,m}^{*}$-radius for ${\mathcal{M}}_m\left(\gamma \right)$ is given by

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{M}}_m\left(\gamma \right)\right)={\left(\frac{sech\left(1\right)-1}{1-2\gamma +sech\left(1\right)}\right)}^{\frac{1}{m}}.$$

The result is sharp.

Proof. 

Let $\mathsf{f}\in {\mathcal{M}}_m\left(\gamma \right).$ Then by using Lemma 2, we have

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}\right|\le \frac{2(\gamma -1)s^m}{1-s^{2m}}.$$

Clearly $\lambda :=\frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}<\frac{sec\left(1\right)+sech\left(1\right)}{2}$ for $\gamma >1$, Then from Lemma 4, it follows that

$$\frac{2(\gamma -1)s^m}{1-s^{2m}}\le \frac{1+(1-2\gamma )s^{2m}}{1-s^{2m}}-sech\left(1\right).$$

provided

$$s\le {\left(\frac{sech\left(1\right)-1}{1-2\gamma +sech\left(1\right)}\right)}^{\frac{1}{m}}.$$

Consider the function $\mathsf{f}$ given by

$$\mathsf{f}\left(\varsigma \right)=\frac{\varsigma }{{(1-{\varsigma }^m)}^{\frac{2(1-\gamma )}{m}}}.$$

since $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}=\frac{1+(1-2\gamma ){\varsigma }^m}{1-{\varsigma }^m}=sech\left(1\right)$, at point $\varsigma ={\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{M}}_m\left(\gamma \right)\right).$ Hence, the sharpness is obtained. □

6. Radius Problems for Ratios of Analytic Functions

In this section, we find radii problems of class ${\mathcal{S}}_{E,m}^{*}$ for some ratios of analytic functions.

Consider the function

$${\mathcal{F}}_1=\left\{\mathsf{f}\in {\mathcal{A}}_m:Re\left(\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}\right)>0\mathrm{and}Re\left(\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }\right)>0,\mathsf{g}\in {\mathcal{A}}_m\right\}.$$

Theorem 12.

The sharp ${\mathcal{S}}_{E,m}^{*}$-radii for the functions in the class ${\mathcal{F}}_1$ is

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_1\right)={\left(\frac{1-sech\left(1\right)}{2m+\sqrt{4m^2+1-2sech\left(1\right)+{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}.$$

Proof. 

Let $\mathsf{f}\in {\mathcal{F}}_1$. Then we define functions $\mathsf{p},\mathsf{h}:\mathbb{D}\to \mathbb{C}$ given by $\mathsf{p}\left(\varsigma \right)=\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }$ and $\mathsf{h}\left(\varsigma \right)=\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}$. Then, $\mathsf{p},\mathsf{h}\in {\mathcal{P}}_m$. Since $\mathsf{f}\left(\varsigma \right)=\varsigma \mathsf{p}\left(\varsigma \right)\mathsf{h}\left(\varsigma \right)$, and therefore from Lemmas 1 and 4, it follows that

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{4m{s}^m}{1-s^{2m}}\le 1-sech\left(1\right),$$

for $s\le {\left(\frac{1-sech\left(1\right)}{2m+\sqrt{4m^2+1-2sech\left(1\right)+{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}={\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_1\right)$. For the sharpness, consider the functions

$${\mathsf{f}}_{*}\left(\varsigma \right)=\varsigma {\left(\frac{1+{\varsigma }^m}{1-{\varsigma }^m}\right)}^2\mathrm{and}{\mathsf{g}}_{*}\left(\varsigma \right)=\varsigma \left(\frac{1+{\varsigma }^m}{1-{\varsigma }^m}\right).$$

Thus, clearly

$$Re\left(\frac{{\mathsf{f}}_{*}\left(\varsigma \right)}{{\mathsf{g}}_{*}\left(\varsigma \right)}\right)>0\mathrm{and}Re\left(\frac{{\mathsf{g}}_{*}\left(\varsigma \right)}{\varsigma }\right)>0.$$

This shows that ${\mathsf{f}}_{*}\in {\mathcal{F}}_1$. Now at $\varsigma ={\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_1\right)e^{\frac{i\pi }{m}}$

$$\frac{\varsigma {\mathsf{f}}_{*}^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_{*}\left(\varsigma \right)}=1+\frac{4m{\varsigma }^m}{1-{\varsigma }^{2m}}=sech\left(1\right).$$

This guarantees sharpness. □

Next, consider the class ${\mathcal{F}}_2$ of functions $\mathsf{f}\in {\mathcal{A}}_m$ satisfying the inequality

$$Re\left(\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}\right)>0$$

for some $\mathsf{g}\in {\mathcal{A}}_m$ with

$$Re\left(\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }\right)>\frac{1}{2}.$$

Theorem 13.

The sharp ${\mathcal{S}}_{E,m}^{*}$-radii for the functions in the class ${\mathcal{F}}_2$ is

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_2\right)={\left(\frac{2(1-sech(1\left)\right)}{3m+\sqrt{9m^2+4m-4msech\left(1\right)+4-8sech\left(1\right)+4{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}$$

Proof. 

Let $\mathsf{f}\in {\mathcal{F}}_2$. Then, we introduce functions $\mathsf{p},\mathsf{h}:\mathbb{D}\to \mathbb{C}$ by $\mathsf{p}\left(\varsigma \right)=\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }$ and $\mathsf{h}\left(\varsigma \right)=\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}$. Then, $\mathsf{p}\in {\mathcal{P}}_m$ and $\mathsf{h}\in {\mathcal{P}}_m\left(\frac{1}{2}\right)$. Since $\mathsf{f}\left(\varsigma \right)=\varsigma \mathsf{p}\left(\varsigma \right)\mathsf{h}\left(\varsigma \right)$, it follows from Lemma 1 that

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|=\left|\frac{\varsigma {\mathsf{p}}^{\prime }\left(\varsigma \right)}{\mathsf{p}\left(\varsigma \right)}-\frac{\varsigma {\mathsf{h}}^{\prime }\left(\varsigma \right)}{\mathsf{h}\left(\varsigma \right)}\right|=\frac{m{s}^m(3+s^m)}{1-s^{2m}}.$$

By Lemma 4 $\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}\in {\mathrm{\Delta }}_E$ if $\frac{m{s}^m(3+s^m)}{1-s^{2m}}\le 1-sech\left(1\right)$, provided

$$s\le {\left(\frac{2(1-sech(1\left)\right)}{3m+\sqrt{9m^2+4m-4msech\left(1\right)+4-8sech\left(1\right)+4{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}.$$

Consider the functions

$${\mathsf{f}}_{**}\left(\varsigma \right)=\frac{\varsigma (1+{\varsigma }^m)}{{(1-{\varsigma }^m)}^2}\mathrm{and}{\mathsf{g}}_{**}\left(\varsigma \right)=\frac{\varsigma }{1-{\varsigma }^m}.$$

Then clearly $Re\left(\frac{{\mathsf{f}}_{**}\left(\varsigma \right)}{{\mathsf{g}}_{**}\left(\varsigma \right)}\right)>0$ and $Re\left(\frac{{\mathsf{g}}_{**}\left(\varsigma \right)}{\varsigma }\right)>\frac{1}{2}$ and hence $\mathsf{f}\in {\mathcal{F}}_2$. □

Let ${\mathcal{F}}_3$ represent functions $\mathsf{f}\in {\mathcal{A}}_m$, satisfying

$$\left|\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}-1\right|<1$$

for $\mathsf{g}\in {\mathcal{A}}_m$ and

$$Re\left(\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }\right)>0.$$

Theorem 14.

The sharp ${\mathcal{S}}_{E,m}^{*}$-radii for the function in the class ${\mathcal{F}}_3$ is

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_3\right)={\left(\frac{2(1-sech(1\left)\right)}{3m+\sqrt{9m^2+4m-4msech\left(1\right)+4-8sech\left(1\right)+4{sech\left(1\right)}^2}}\right)}^{\frac{1}{m}}.$$

Proof. 

Let $\mathsf{f}\in {\mathcal{F}}_3$. Then we define functions $\mathsf{p},\mathsf{h}$ by $\mathsf{p}\left(\varsigma \right)=\frac{\mathsf{g}\left(\varsigma \right)}{\varsigma }$ and $\mathsf{h}\left(\varsigma \right)=\frac{\mathsf{g}\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}$. Then, $\mathsf{p}\in {\mathcal{P}}_m$. We see that $\left|\frac{1}{\mathsf{h}\left(\varsigma \right)}\right|<1$ if and only if $Re\left(\mathsf{h}\left(\varsigma \right)\right)>\frac{1}{2}$ and hence $\mathsf{h}\in \mathcal{P}\left(\frac{1}{2}\right)$. By using Lemma 1, we have

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-1\right|\le \frac{3m{s}^m+m{s}^{2m}}{1-s^{2m}}.$$

The remaining part of the proof is same as of Theorem 13. For sharpness, we consider a functions given by

$${\mathsf{f}}_0\left(\varsigma \right)=\frac{\varsigma {(1+{\varsigma }^m)}^2}{1-{\varsigma }^m}\mathrm{and}{\mathsf{g}}_0\left(\varsigma \right)=\frac{\varsigma (1+{\varsigma }^m)}{1-{\varsigma }^m},$$

where ${\mathsf{f}}_0\in {\mathcal{F}}_3$. Now at $\varsigma ={\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_3\right)e^{\frac{i\pi }{m}}$, we have

$$\frac{\varsigma {\mathsf{f}}_0^{\prime }\left(\varsigma \right)}{{\mathsf{f}}_0\left(\varsigma \right)}-1=\frac{3m{\varsigma }^m+m{\varsigma }^{2m}}{1-{\varsigma }^{2m}}=1-sech\left(1\right).$$

This confirms the sharpness of the result. □

Let ${\mathcal{F}}_4$ be the class of functions $\mathsf{f}\in {\mathcal{A}}_m$ satisfying the inequality

$$\left|\frac{\mathsf{f}\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}-1\right|<1$$

for some convex function $\mathsf{g}\in {\mathcal{A}}_m.$

Theorem 15.

Let

$$\begin{array}{ccc}\hfill {\mathcal{R}}_1& =& {\left(\frac{\sqrt{\left(sech\left(1\right)+sec\left(1\right)\right)\left(-2+sech\left(1\right)+sec\left(1\right)\right)}}{sech\left(1\right)+sec\left(1\right)}\right)}^{\frac{1}{m}},\hfill \\ \hfill {\mathcal{R}}_2& =& {\left(-\frac{2(-1+sech(1\left)\right)}{m+1+\sqrt{m^2+6m+1-4msech\left(1\right)+4{sech\left(1\right)}^2-4sech\left(1\right)}}\right)}^{\frac{1}{m}}\hfill \end{array}$$

and

$${\mathcal{R}}_3={\left(\frac{sec\left(1\right)-1}{m+sec\left(1\right)}\right)}^{\frac{1}{m}}.$$

Then ${\mathcal{S}}_{E,m}^{*}$-radii for the functions in the class ${\mathcal{F}}_4$ is

$${\mathcal{R}}_{{\mathcal{S}}_{E,m}^{*}}\left({\mathcal{F}}_4\right)=\left\{\begin{array}{c}{\mathcal{R}}_2,if{\mathcal{R}}_2\le {\mathcal{R}}_1,\\ {\mathcal{R}}_3,if{\mathcal{R}}_2>{\mathcal{R}}_1.\end{array}\right.$$

Proof. 

Let $\mathsf{f}\in {\mathcal{F}}_4$. Define functions $\mathsf{h}$ as $\mathsf{h}\left(\varsigma \right)=\frac{\mathsf{g}\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}$ on open unit disk, where $\mathsf{g}\in {\mathcal{A}}_m$ is convex function. Since every convex function is starlike of order half, therefore using Lemma 1, we can write

$$\left|\frac{\varsigma {\mathsf{g}}^{\prime }\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}-\frac{1}{1-s^{2m}}\right|\le \frac{s^m}{1-s^{2m}}.$$

Here, $\mathsf{h}\in {\mathcal{P}}_m\left(\frac{1}{2}\right)$. Using Lemma 4, we have

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-\frac{1}{1-s^{2m}}\right|=\left|\frac{\varsigma {\mathsf{g}}^{\prime }\left(\varsigma \right)}{\mathsf{g}\left(\varsigma \right)}-\frac{1}{1-s^{2m}}\right|+\left|\frac{\varsigma {\mathsf{h}}^{\prime }\left(\varsigma \right)}{\mathsf{h}\left(\varsigma \right)}\right|\le \frac{s^m}{1-s^{2m}}+\frac{m{s}^m}{1-s^m}.$$

This gives us

$$\left|\frac{\varsigma {\mathsf{f}}^{\prime }\left(\varsigma \right)}{\mathsf{f}\left(\varsigma \right)}-\frac{1}{1-s^{2m}}\right|\le \frac{(1+m)s^m+m{s}^{2m}}{1-s^{2m}}.$$

Here we find the result by determining the three numbers ${\mathcal{R}}_1,{\mathcal{R}}_2$ and ${\mathcal{R}}_3$. We have $r\le {\mathcal{R}}_1$, if and only if $\frac{1}{1-s^{2m}}\le \frac{sech\left(1\right)+sec\left(1\right)}{2}$. This yields us $s\le {\left(\frac{\sqrt{\left(sech\left(1\right)+sec\left(1\right)\right)\left(-2+sech\left(1\right)+sec\left(1\right)\right)}}{sech\left(1\right)+sec\left(1\right)}\right)}^{\frac{1}{m}}$. We determine ${\mathcal{R}}_2$, such that $s\le {\mathcal{R}}_2$, if and only if $\frac{(1+m)s^m+m{s}^{2m}}{1-s^{2m}}\le \frac{1}{1-s^{2m}}-sech\left(1\right).$ The positive root of the above inequality is

$$s^m=\frac{2(1-sech(1\left)\right)}{m+1+\sqrt{m^2+6m+1-4msech\left(1\right)+4{sech\left(1\right)}^2-4sech\left(1\right)}}.$$

Next, we determine ${\mathcal{R}}_3$ such that $s\le {\mathcal{R}}_3$ if and only if

$$\frac{(1+m)s^m+m{s}^{2m}}{1-s^{2m}}\le Section\left(1\right)-\frac{1}{1-s^{2m}},$$

The positive root of the above inequality is

$$s^m=\frac{sec\left(1\right)-1}{m+sec\left(1\right)}.$$

□

7. Conclusions

In this article, we have linked the generating function for Euler numbers with a class of starlike functions. We have also linked this class with various subclasses of univalent functions by inclusion and radius results. All the radii problems are sharp. This work covers the study of class ${\mathcal{S}}_E^{*}$ regarding its connection with other classes of analytic functions. Its certain interesting characteristics are yet to be explored, which includes coefficient estimates such as coefficient bounds, Hankel determinants, inverse coefficients and logarithmic coefficients for class ${\mathcal{S}}_E^{*}$.