Heat and Mass Transport in Casson Nanofluid Flow over a 3-D Riga Plate with Cattaneo-Christov Double Flux: A Computational Modeling through Analytical Method

Abstract

This work examines the non-Newtonian Cassonnanofluid’s three-dimensional flow and heat and mass transmission properties over a Riga plate. The Buongiorno nanofluid model, which is included in the present model, includes thermo-migration and random movement of nanoparticles. It also took into account the Cattaneo–Christov double flux processes in the mass and heat equations. The non-Newtonian Casson fluid model and the boundary layer approximation are included in the modeling of nonlinear partial differential systems. The homotopy technique was used to analytically solve the system’s governing equations. To examine the impact of dimensionless parameters on velocities, concentrations, temperatures, local Nusselt number, skin friction, and local Sherwood number, a parametric analysis was carried out. The velocity profile is augmented in this study as the size of the modified Hartmann number increases. The greater thermal radiative enhances the heat transport rate. When the mass relaxation parameter is used, the mass flux values start to decrease.

1. Introduction

A new fluid with better performance is valuable for accomplishing in industrial technologies. Choi and Eastman [1] were the first who coined the word nanofluid and showed that the dispersion of nanosized particles increased the thermal physical properties of an ordinary fluid. Recently, various applications have been used in cooling transformers, heat change, food processing, and many others. “In the presence of partial slip, nanofluid past a stretching surface with boundary layer flow was explored by Das [2] and it is realized that the thermophoretic force escalates the heat transfer rate. Kuznetsov and Nield [3] investigated the nanofluid model with Brownian motion and thermophoresis and the heat transfer rate diminished due to these effects. Hamad et al. [4] acquired the results of MHD nanofluid flow on a flat plate. The two nanoparticles namely $Cu$ and $Ag$ have a greater cooling concert, according to the researchers. The impact of non-Newtonian nanofluid flow on a stretching sheet (SS) was investigated by Nadeem and co-workers [5], who discovered that the nanopartical volume fraction (NPVF) reinforced the greater amount of the thermophoresis variable. Khan and Pop [6] studied the 2D flow of a nanoliquid owing to an SS using a numerical approach and identified that the presence of the BM parameter controls the heat. Sajid et al. [7] probed the cross non-Newtonian hybrid nanofluid flow with heat sink/source and thermal radiation. They investigated the novel tetra hybrid Tiwari and Das nanofluid model on blood flow arteries. The influence of Reiner–Philippoff hybrid nanofluid flow over a non-linear heat source/sink and mathematical Fourier heat law was delved by Sajid et al. [8]. They solved the problem numerically by employing the Galerkin method of finite elements. Hassan et al. [9] analytically proposed the boundary layer problem due to a SS.

Flows of fluid due to a permeable space are significant in various chemical, manufacturing, biological and industrial systems, such as crude oil purification, water development in reservoirs, grain stockpiling, and blood flow. A relevant analysis of Darcy–Forchheimer fluid flow can be carried out by attempts ([10,11,12,13,14,15]). These analyses incorporate the Darcy law to consider the permeable medium. However, the stability of this law for smaller velocity is inappropriate in plenty of practical conditions where the permeable medium has weak porosity separation near the wall area and a significant flow rate. The viscous and inertial forces have been given by the Darcy–Forchheimer (DF) model. Consequently, this model accurately described the fluid flow and heat transport as the permeable medium. Zubair et al. [16] deliberated the prominent features of Darcy–Forchheimer time flow of nanomaterials using Cattaneo–Christov heat diffusion (CCHD) theory and the speed of liquid increases when elevating the inertia coefficient. The second law analysis with DF model for MHD nanoliquid flow past a SS was conducted by Abbas et al. [17]. Ahmad et al. [18] presented the 3D couple stress MHD flow nanoliquid for DF model due to an exponentially SS. Their outcome explores that the speed of fluid upsurges with enhancing the inertia parameter.

A survey of non-Newtonian fluids in the modern era has paid particular attention to the current engineers and researchers owing various prominent features in the industrial area. The complexity of non-Newtonian fluid has made it difficult to explain all relations in one constitutive expression. So, the non-Newtonian fluid is prominent from viscous material. It is lesser than the order of differential system in the non-Newtonian fluid. A lot of models have been presented with their different properties. One of the non-Newtonian models is known as CF. This model is explained as human blood flow at a low shear rate and explained viscoelastic fluid with prominent features. Thamaraikannan et al. [19] investigated the MHD Casson fluid flow past a porous channel with the effect of body acceleration. Chemically reactive CF induced by exponentially inclined permeability was carried out by Reddy [20]. Hayat et al. [21] explored the chemically reactive flow of CNF over a heated SS with a heat sink/source. They discovered that when mass Biot number is present, the fluid concentration and its associated BL thickness rise. Casson nanofluid was assessed by Aboehashari et al. [22] using heat and mass transport characteristics owing to a stretched surface.

The Riga plate (RP) is a well-known actuator made out of magnets and electrodes that stay there and alternately generate Lorentz’s force, which quickly decreases with distance. Zubaidi et al. [23] explored the nanofluid flow over a RP. Chemical reaction and viscosity dissipation in a nanofluid’s mixed convective flow on a Riga plate was delved by Vaidya et al. [24]. They noticed that when the modified Hartmann number increased, the velocity profile grew and the temperature profile shrinks. Rafique et al. [25] numerically investigated the micropolar nanofluid flow over a Riga plate. They found that the fluid speed was bolstered as the modified Hartmann number improved. Riga plate with convective boundary conditions on a nanofluid under radial SS was scrutinized by Prasad et al. [26]. They noted that the modified Hartmann number improves the speed profile and slumps the temperature distribution. Darvesh et al. [27] probed the infinite shear rate of the Cross-fluid viscosity model, which is then coupled with the Riga plate and they used the Keller Box method. Recently, the Riga plate model of a nanofluid with a non-Fourier heat flux was numerically inspected by Divya et al. [28]. They found that a rise in the modified Hartmann number leads to weaken the skin friction coefficient.

Influenced by the above-mentioned investigations and applications recently, many researchers are attributing attention to revealing the thermal effect of nanoliquid flow with Cattaneo–Christov flux due to a Darcy–Forchheimer porous medium. However, the investigations over this flow over a Riga plate have not yet begun. To fill this gap the authors examined the Casson nanofluid flow over a 3-D Riga plate with a Cattaneo–Christov flux Darcy–Forchheimer porous medium. The results of this study are helpful in different engineering applications such as glass blowing, the spinning of fibers and the continuous casting of metals.

2. Flow Analysis

We consider the Cattaneo–Christov theory in a $3\mathrm{D}$ Casson nano-liquid flow past a permeable Riga surface. The surface was considered with x and y directions with velocities $u \left(x\right)=ax$ and $v \left(y\right)=by$, respectively. Let $T_W$ and $C_W$ are represented by the surface of temperature and concentration which are always larger than the ambient temperature and concentration represented by $T_{\infty }$ and $C_{\infty }$. The nanofluid formulation was the physical properties of thermophoresis and Brownian movement parameters. Porous medium was tackled through the Darcy–Forchheimer model. The lower plate was considered as heated with hotter fluid $T_f$ and creates a heat transport coefficient $h_c$. The known fluid behaves as heat-generating or absorbing. The flow geometry is given in Figure 1 and the governing equations are taken from [29,30]:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0$$

(1)

$$\left[u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}\right]=\upsilon \left[\left(\frac{\beta +1}{\beta }\right)\frac{{\partial }^{2}u}{\partial z^2}\right]-\left[\frac{\upsilon }{k_1}u\right]-\left[F{u}^2\right]+\frac{\pi j_0{M}_{0}exp\left(-\frac{\pi }{e}z\right)}{8\rho }$$

(2)

$$\left[u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}\right]=\upsilon \left[\left(\frac{\beta +1}{\beta }\right)\frac{{\partial }^{2}v}{\partial z^2}\right]-\left[\frac{\upsilon }{k_1}v\right]-\left[F{v}^2\right]$$

(3)

$$\begin{array}{l}\rho c_p\left[u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=K\frac{{\partial }^{2}T}{\partial z^2}+\tau \left[D_B\frac{\partial C}{\partial z}\frac{\partial T}{\partial z}+\frac{D_T}{T_{\infty }}{\left(\frac{\partial T}{\partial z}\right)}^2\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-{\lambda }_E[\frac{{\partial }^{2}T}{\partial x^2}{u}^2+\frac{{\partial }^{2}T}{\partial y^2}{v}^2+\frac{{\partial }^{2}T}{\partial z^2}{w}^2+\frac{{\partial }^{2}T}{\partial x\partial y}2uv+\frac{{\partial }^{2}T}{\partial y\partial z}2vw+\frac{{\partial }^{2}T}{\partial x\partial z}2uw+\frac{\partial u}{\partial x}\frac{\partial T}{\partial x}u+\frac{\partial u}{\partial y}\frac{\partial T}{\partial x}v\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+\frac{\partial u}{\partial z}\frac{\partial T}{\partial z}w+\frac{\partial v}{\partial x}\frac{\partial T}{\partial x}u+\frac{\partial v}{\partial y}\frac{\partial T}{\partial x}v+\frac{\partial v}{\partial z}\frac{\partial T}{\partial z}w+\frac{\partial w}{\partial x}\frac{\partial T}{\partial x}u+\frac{\partial w}{\partial y}\frac{\partial T}{\partial x}v+\frac{\partial w}{\partial z}\frac{\partial T}{\partial z}w]+\frac{Q_0}{\rho c_p}\left(T-T_{\infty }\right)\end{array}$$

(4)

$$\begin{array}{l}u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}=D_B\frac{{\partial }^{2}C}{\partial z^2}+\frac{D_T}{T_{\infty }}\frac{{\partial }^{2}T}{\partial z^2}-{\lambda }_c[\frac{{\partial }^{2}C}{\partial x^2}{u}^2+\frac{{\partial }^{2}C}{\partial y^2}{v}^2+\frac{{\partial }^{2}C}{\partial z^2}{w}^2+\frac{{\partial }^{2}C}{\partial x\partial y}2uv+\frac{{\partial }^{2}C}{\partial y\partial z}2vw+\frac{{\partial }^{2}C}{\partial x\partial z}2uw+\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\frac{\partial u}{\partial x}\frac{\partial C}{\partial x}u+\frac{\partial u}{\partial y}\frac{\partial C}{\partial x}v+\frac{\partial u}{\partial z}\frac{\partial C}{\partial z}w+\frac{\partial v}{\partial x}\frac{\partial C}{\partial x}u+\frac{\partial v}{\partial y}\frac{\partial C}{\partial x}v+\frac{\partial v}{\partial z}\frac{\partial C}{\partial z}w+\frac{\partial w}{\partial x}\frac{\partial C}{\partial x}u+\frac{\partial w}{\partial y}\frac{\partial C}{\partial x}v+\frac{\partial w}{\partial z}\frac{\partial C}{\partial z}w]\end{array}$$

(5)

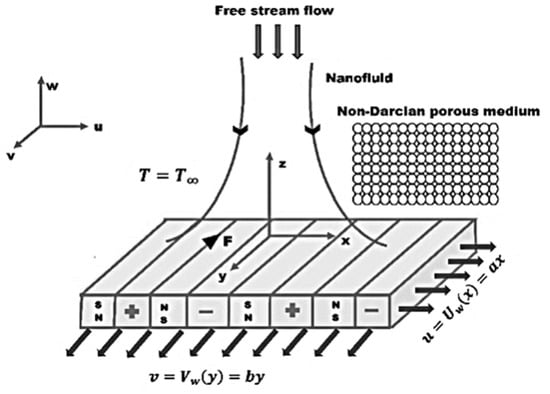
Figure 1. Physical geometry.

The boundary points are

$$\begin{array}{l}\left\{u\left(x,y,0\right)=ax, v\left(x,y,0\right)=by, w\left(x,y,0\right)=0,-k\frac{\partial T}{\partial z}\left(x,y,0\right)=h_f\left[T_f\left(x,y,0\right)-T\left(x,y,0\right)\right], C\left(x,y,0\right)=C_w\left(x\right)\right\}\\ \hspace{1em}\hspace{1em}\hspace{1em}\left\{u\left(x,y,\infty \right)\to 0, v\left(x,y,\infty \right)\to 0, \frac{\partial u}{\partial z}\left(x,y,\infty \right)\to 0,\frac{\partial v}{\partial z}\left(x,y,\infty \right)\to 0,T\left(x,y,\infty \right)\to T_{\infty }, C\left(x,y,\infty \right)\to C_{\infty }\right\}\end{array}$$

(6)

Now, we state the symmetry transformations [31]:

$$\begin{array}{l}u=ax{f}^{\prime }\left(\eta \right), \eta ={\left(\frac{a}{\nu }\right)}^{0.5}z, v=ay{g}^{\prime }\left(\eta \right), w=-\sqrt{a\nu }\left[f\left(\eta \right)+g\left(\eta \right)\right], \theta \left(\eta \right)=\frac{T-T_{\infty }}{T_f-T_{\infty }},\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} \varphi \left( \eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }}\end{array}$$

(7)

With the help of Equation (7), Equations (2)–(5) will be reduced to the following form

$$\left(1+\frac{1}{\beta }\right)f^{‴}-{f^{\prime }}^2+\left[f+g\right]f^{″}-\lambda f^{\prime }-Fr{f^{\prime }}^2+Ha{e}^{-d_1\eta }=0$$

(8)

$$\left(1+\frac{1}{\beta }\right)g^{‴}-{g^{\prime }}^2+\left[f+g\right]g^{″}-\lambda g^{\prime }-Fr{g^{\prime }}^2=0$$

(9)

$$\begin{array}{l}\frac{1}{Pr}{\theta }^{″}+\left[f+g\right]{\theta }^{\prime }-\Gamma \left[{\left[f+g\right]}^2\right]{\theta }^{″}+\left[f+g\right]\left[f^{\prime }+g^{\prime }\right]{\theta }^{\prime }\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{{\theta }^{\prime }}^2+Hg\theta =0\end{array}$$

(10)

$${\varphi }^{″}+Le\left[f+g\right]{\varphi }^{\prime }-Le{\Gamma }_C\left[{\left[f+g\right]}^2\right]{\varphi }^{″}+Le\left[f+g\right]\left[f^{\prime }+g^{\prime }\right]{\varphi }^{\prime }+\frac{Nt}{Nb}{\theta }^{″}=0$$

(11)

The boundary conditions are,

$$\begin{array}{l}f\left(0\right)=0, g\left(0\right)=0,\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} f^{\prime }\left(0\right)=1,g^{\prime }\left(0\right)=ϵ,f^{\prime }(\infty )=0,g^{\prime }(\infty )=0,f^{″}(\infty )=0,g^{″}(\infty )=0,{\theta }^{\prime }\left(0\right)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} =-Bi\left(1-\theta \left(0\right)\right),\theta (\infty )=0,\varphi \left(0\right)=1,\varphi (\infty )=0\end{array}$$

(12)

Here, the non-dimensional variables are defined as

$$\begin{array}{l}\lambda =\frac{\nu }{k_{1}a},Fr=\frac{C_b}{\sqrt{k_1}},Ha=\frac{\pi j_0{M}_0}{8a^{3}x\rho },d_1=-\frac{\pi }{ b}\sqrt{\frac{\nu }{a}},Pr=\frac{\nu }{{\alpha }_m},\Gamma ={\lambda }_{E}a,Nb=\frac{\tau D_B}{\nu }\left(C_w-C_{\infty }\right),Nt=\frac{\tau D_T}{\nu T_{\infty }}\left(T_f-T_{\infty }\right),\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}Hg=\frac{Q_0}{\rho c_{p}a},{\Gamma }_C={\lambda }_{C}a, and Le=\frac{{\alpha }_m}{D_B}\end{array}$$

The engineering concerns “skin friction”, “local Nusselt number (LNN)”, and “local Sherwood number (LSN)” are defined below:

$$R{e}^{0.5}C{f}_x=\left(1+\frac{1}{\beta }\right)f^{″}\left(0\right)=\mathrm{skin}\mathrm{friction}\mathrm{in}\mathrm{x}-\mathrm{direction}$$

$$R{e}^{0.5}C{f}_y=\left(1+\frac{1}{\beta }\right)g^{″}\left(0\right)=\mathrm{skin}\mathrm{friction}\mathrm{in}\mathrm{y}-\mathrm{direction}$$

$$R{e}^{-0.5}N{u}_x=-{\theta }^{\prime }\left(0\right)=\mathrm{local}\mathrm{Nusselt}\mathrm{number}$$

$$R{e}^{-0.5}S{h}_x=-{\varphi }^{\prime }\left(0\right)=\mathrm{local}\mathrm{Sherwood}\mathrm{number}$$

3. Solution Process

The transformed nonlinear ODE Equations (8)–(11) with the boundary conditions in Equation (12) are solved using HAM technique. This techniques used solve highly non-linear problems. The advantage of this method is to freely fix initial approximations and linear operators. The flow chart of this method is illustrated in Figure 2.

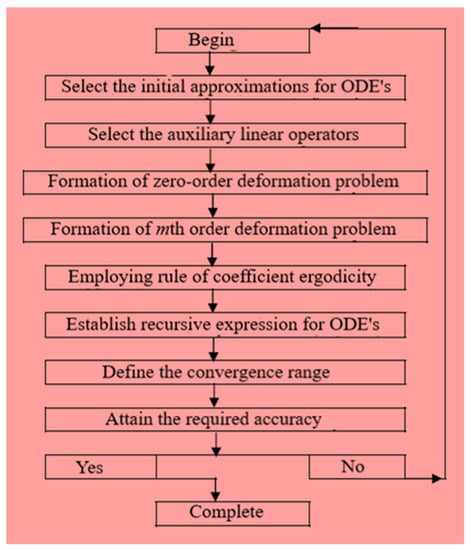
Figure 2. Flow chart of HAM.

The convergences values are of $h_f, h_g, h_{\theta }$ and $h_{\varphi }$ are plotted in Figure 3. The range of convergence is $-1.4\le h_f, h_g\le 0.0$, and $-1.75\le h_{\theta }, h_{\varphi }\le 0.1$. Table 1 observes the order of $f^{″}\left(0\right)$, $g^{″}\left(0\right)$, ${\theta }^{\prime }\left(0\right)$, and ${\varphi }^{\prime }\left(0\right)$ are $15\mathrm{th}$ order.

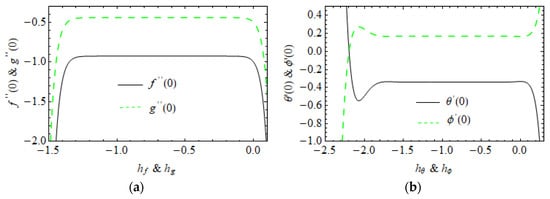
Figure 3. The $h-$ curves of (a) $f^{″}\left(0\right)$, $g^{″}\left(0\right)$ and (b) ${\theta }^{\prime }\left(0\right)$, ${\varphi }^{\prime }\left(0\right)$.

Table 1. HAM order.

Order	$-{\mathit{f}}^{″}\left(0\right)$	$-{\mathit{g}}^{″}\left(0\right)$	$-{\mathsf{\theta }}^{\prime }\left(0\right)$	$-{\mathsf{\varphi }}^{\prime }\left(0\right)$
1	0.918333	0.435833	0.333333	0.166667
5	0.925136	0.440945	0.340580	0.170290
10	0.925015	0.441018	0.339931	0.169966
15	0.925015	0.441018	0.339958	0.169979
20	0.925015	0.441018	0.339958	0.169979
25	0.925015	0.441018	0.339958	0.169979
30	0.925015	0.441018	0.339958	0.169979
35	0.925015	0.441018	0.339958	0.169979
40	0.925015	0.441018	0.339958	0.169979

4. Correlation Analysis

For analyzing the concert of a thermal system design, the system of equations is required. The acquired numerical data are utilized to generate the system of equations using linear regression analysis. The skin friction, heat and mass relationship equations:

$$R{e}^{0.5}C{f}_x=-1.840454+0.428572\ast Ha-0.525588\ast \lambda +0.262804\ast \beta -0.340727\ast Fr$$

$$R{e}^{0.5}C{f}_y=-0.765295-0.014398\ast Ha-0.307248\ast \lambda +0.099039\ast \beta -0.093480\ast Fr$$

$$\frac{Nu}{\sqrt{Re}}=0.343840+0.002102\ast Ha-0.004278\ast \lambda -0.001629\ast \beta -0.001564\ast Fr$$

$$\frac{Sh}{\sqrt{Re}}=-0.171920-0.001051\ast Ha+0.002139\ast \lambda +0.000814\ast \beta +0.000782\ast Fr$$

For $Ha=\left[0.0, 0.3\right], \lambda =\left[0.0, 0.2\right], \beta =\left[1, 2\right]$ and $Fr\in \left[0,1\right]$ with maximum error is 0.028.

5. Computational Results and Discussion

In this section, the investigation is taken to scrutinize an essential description of the different dimensional factors on velocity along $x$ and $y$ directions, temperature, and concentration of nanoparticles. Table 2 elucidates the comparison analysis of $N{u}_x$ for numerous parameters from Muhammad et al. [31]. This table ensures the accuracy of obtained results and the precision of numerical computation utilized in this analysis. It is noted that there is an outstanding achievement with the earlier publication. Table 3 provides the characteristics of $\Gamma ,{\Gamma }_c$, Nb, Nt, Bi and Hg on ${Nu}_x$ and ${Sh}_x$ for CNF and VNF. It is realized that the HTG grows when mounting the size of $\Gamma ,{\Gamma }_c$ and Bi and it decays when improving the size of $Nt$ and Hg for both fluids. Furtherer more, the LNN remains fixed when changing the $Nb$ values, see Muhammad et al. [31]. The LSN decays when varying the size of $\Gamma ,{\Gamma }_c$, $Nt$ and Bi and it rise when changing the values of $Nb$ and Hg for both fluids.

Table 2. Comparison of local Nusselt number with Muhammad et al. [31].

$\mathsf{\lambda }$	$\mathit{F}\mathit{r}$	$\mathit{c}$	$\mathit{B}\mathit{i}$	$\mathit{N}\mathit{t}$	$\mathit{N}\mathit{b}$	$\mathit{P}\mathit{r}$	$\mathit{S}\mathit{c}$	$\mathit{N}{\mathit{u}}_{\mathit{x}}$
								Present Study	Muhammad et al. [31]
0.0	0.1	0.2	0.3	0.2	0.5	1	1	0.204499	0.20448
0.2								0.202543	0.20248
0.5								0.199988	0.19970
0.2	0	0.2	0.3	0.2	0.5	1	1	0.202832	0.20278
	0.2							0.202261	0.20220
	0.4							0.201715	0.20164
0.2	0.1	0	0.3	0.2	0.5	1	1	0.194819	0.19458
		0.3						0.205636	0.20560
		0.5						0.201081	0.21080
0.2	0.1	0.2	0.2	0.2	0.5	1	1	0.151507	0.15148
			0.5					0277074	0.27696
			1					0.382155	0.38194
0.2	0.1	0.2	0.3	0	0.5	1	1	0.203088	0.20306
				0.5				0.201711	0.20159
				1				0.200281	0.20004
0.2	0.1	0.2	0.3	0.2	0	1	1	0.202543	0.20248
					0.5			0.202543	0.20248
					1			0.202543	0.20248
0.2	0.1	0.2	0.3	0.2	0.5	0	1	0.167990	0.16685
						0.5		0.202543	0.20248
						1		0.219363	0.21949
0.2	0.1	0.2	0.3	0.2	0.5	1	0	0.202752	0.20271
							0.5	0.202543	0.20248
							1	0.202395	0.20234

Table 3. The LNN and LSN for different combinations of $\Gamma , {\Gamma }_C, Nb, Nt, Bi$ and $Hg$ for both fluids.

$\Gamma$	${\Gamma }_{\mathit{C}}$	$\mathit{N}\mathit{b}$	$\mathit{N}\mathit{t}$	$\mathit{B}\mathit{i}$	${\mathit{H}}_{\mathit{g}}$	CNF		VNF
						$\mathit{N}{\mathit{u}}_{\mathit{x}}$	$\mathit{S}{\mathit{h}}_{\mathit{x}}$	$\mathit{N}{\mathit{u}}_{\mathit{x}}$	$\mathit{S}{\mathit{h}}_{\mathit{x}}$
0.0	0.1	0.2	0.1	0.5	−0.5	0.338869	−0.169434	0.336420	−0.168210
0.1						0.339958	−0.169979	0.337334	−0.168667
0.2						0.341138	−0.170569	0.338314	−0.169157
0.3						0.342452	−0.171226	0.339365	−0.169683
0.4						0.344002	−0.172001	0.340503	−0.170252
0.1	0	0.2	0.1	0.5	−0.5	0.339957	−0.169978	0.337336	−0.168668
	0.1					0.339958	−0.169979	0.337334	−0.168667
	0.2					0.339965	−0.169982	0.337332	−0.168666
	0.3					0.339981	−0.169990	0.337332	−0.168666
	0.4					0.340014	−0.170007	0.337336	−0.168662
0.1	0.1	0.5	0.1	0.5	−0.5	0.339958	−0.067992	0.337334	−0.067467
		1				0.339958	−0.033996	0.337334	−0.033733
		1.5				0.339958	−0.022664	0.337334	−0.022489
		2				0.339958	−0.016998	0.337334	−0.016867
		2.5				0.339958	−0.013598	0.337334	−0.013493
0.1	0.1	0.2	0	0.5	−0.5	0.340194	0.000000	0.337581	0.000000
			0.3			0.339483	−0.509225	0.336838	−0.505257
			0.5			0.339004	−0.847509	0.336338	−0.840845
			0.8			0.338277	−1.353110	0.335581	−1.342320
			1			0.337788	−1.688940	0.335071	−1.675360
0.1	0.1	0.2	0.1	0.5	−0.5	−0.938068	0.469034	−0.958026	0.479013
				0.3		−0.417310	0.208655	−0.421272	0.210636
				0		0.000000	0.000000	0.000000	0.000000
				0.5		0.233960	−0.116980	0.232716	−0.116358
				0.3		0.339958	−0.169979	0.337334	−0.168667
0.1	0.1	0.2	0.1	0.5	−0.5	0.339958	−0.169979	0.337334	−0.168667
					−0.3	0.329027	−0.164513	0.325349	−0.162675
					0	0.305975	−0.152987	0.298929	−0.149465
					0.5	0.265742	−0.132871	0.244510	−0.122255
					0.3	0.209128	−0.104564	0.133063	−0.066530

Figure 4a,b display the velocity $f^{\prime }\left(\eta \right)$ and $g^{\prime }\left(\eta \right)$ against the various value of Casson fluid parameter $\beta$ on $\lambda =0.2$ and $\lambda =0$. It is noted that the augmentation of $\beta$ produces a reduction in velocity profile and boundary layer thickness. The influence of $Ha$ on $f^{\prime }\left(\eta \right)$ and $g^{\prime }\left(\eta \right)$ is employed in Figure 4c,d on $\lambda =0.2$ and $\lambda =0$. The larger value of $Ha$ increases the velocity profile in both directions. The existence of a modified Hartman number enhanced the motion of Casson fluid. Also, the larger fluid velocity attains when $\lambda =0.0 \mathrm{than}\mathrm{the}$ $\lambda =0.2$ when varing $\beta$ and Ha values in both directions. Moreover, the Riga plate is an electromagnetic device that pushes the movement of the flow in a specific direction. Figure 5a,b illustrates the intensification of the temperature with the rising value of Biot number $Bi$ on RP, SP, porous RP and non-porous RP. The Biot number is the leading function of temperature distribution in the case of $Ha=\left(0.0, 0.3\right)$ and $\lambda =\left(0.0, 0.2\right).$ Physically, enhancing the value of $Bi$ obtained stronger heat convection at the wall of the surface. The impact of $Hg$ on the temperature field on heated RP and SP is exposed in Figure 5c. The temperature field enlarges for greater values of $Hg$. Additionally, heat has been induced due to a greater value of $Hg$, which is the reason the temperature profile is enlarged in the sense of heating RP and SP. In contrast, an opposite trend is observed in Figure 5d for cooling RP and SP. The impact of $Nt$ on $\theta \left(\eta \right)$ for fluid heat generating and absorbing on a RP is examined in Figure 5e and seen that the $\theta \left(\eta \right)$ develops when raising the Nt values. Thermophoresis attained through a temperature difference produces a faster flow that moves away from the stretching sheet. The temperature inside the surface increases due to faster flow, resulting in an amelioration of the temperature profile. Figure 5f elucidates the thermal relaxation time $\Gamma$ on temperature distribution on heated and cooled RP. It is detected that the temperature field and corresponding thermal layer thickness depreciated by the enhancing value of $\Gamma$ on heated RP. A larger value of $\Gamma$ results in particles of materials needing extra time to transport heat near its particles which is responsible for the lessening of the thermal layer. The opposite behavior getting for cooled RP.

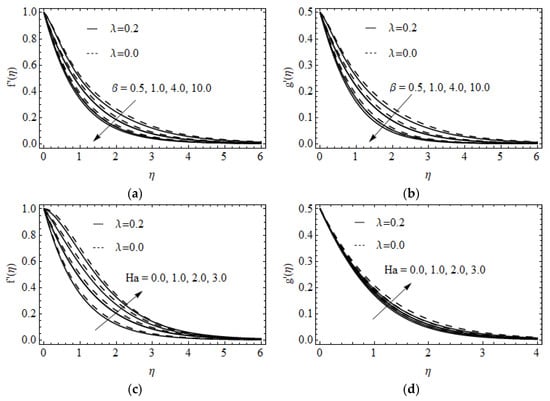
Figure 4. The $x$-direction (a,c) and $y$-direction (b,d) velocity for various values of $\beta$ and $Ha$ for porous and non-porous RP.

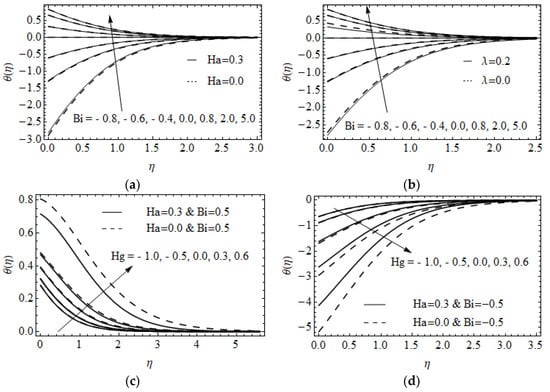
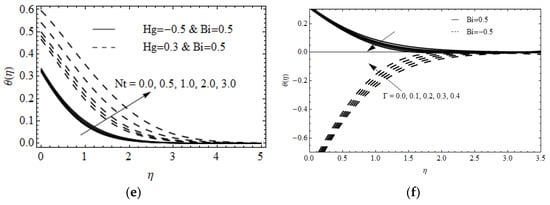
Figure 5. The variations of $\theta \left(\eta \right)$ for various values of $Bi$ (a,b) over RP and SP (a), porous and non-porous RP (b), $Hg$ (c,d) for convective heating (c) and cooling (d) RP and SP, $Nt$ (e) for heat generating and absorption and $\Gamma$ (f) for convective heating and cooling RP.

Figure 6a,b reveals the influence of Biot number $Bi$ on $\varphi \left(\eta \right)$ for the case of $\left(Ha=0.0, Ha=0.3\right)$ and $\left(\lambda =0.0, \lambda =0.2\right)$, it is clear from the figure that the concentration of nanoparticles and its corresponding layer thickness are accelerated due to the larger value of $Bi$ for all cases. The variation of $Hg$ on $\varphi \left(\eta \right)$ for heated and cooled RP and SP was displayed in Figure 6c,d. Increasing the value of $Hg$ leads to accelerate in $\varphi \left(\eta \right)$ due to heated RP and a reduction cooled RP. The effect of $Nb$ on $\varphi \left(\eta \right)$ on fluid heat generating and absorbing on heated and cooled RP is shown in Figure 6e,f. It is seen that $\varphi \left(\eta \right)$ decays when strengthening the $Nb$ in headed RP and the opposite trend attains in cooled RP for both fluid heat generating and absorbing cases. The variation of $Ha$ and $\lambda$ for CNF and VNF on the drag friction coefficient in the $x$, and $y$ directions were presented in Figure 7a,b. In Figure 7a shows that the $C{f}_x$ climbs with an enhancement in $Ha$ and it is suppresses for a higher size of $\lambda$ and $C{f}_y$ diminishes with an improvement in $Ha$ and $\lambda$ for both fluids, see Figure 7b. Figure 8a displays the LNN $N{u}_x$ for $Ha$ and $\lambda$. The growth of $Ha$ escalates the LNN and it decays for larger quantity of $\lambda$. On the contrary, Figure 8b presents that the LNN $N{u}_x$ and $N{u}_x$ is a lessening function of $Hg$ and $Nt$. The contour plot of LNN for Pr and $\lambda$ for CNF and VNF was illustrated in Figure 8c,d. The LSN for various values of $\lambda \&Ha$ and $Nt\&Hg$ for both fluids were displayed in Figure 9a,b. It is seen that the LSN improves when enhancing the values of $\lambda$ and Hg. The opposite nature attains for Ha and Nt. The impact of Nb and Nt on LSN for heated and cooled RP was displayed in Figure 9c,d. The quite opposite nature occurs in heating and cooling cases. The contour plot of LSN for various values of ${\Gamma }_c$ and Le for both fluids was addressed in Figure 9e,f.

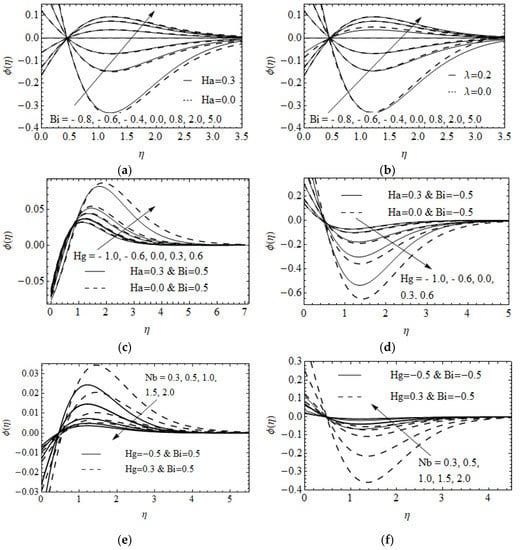
Figure 6. The variations of $\varphi \left(\eta \right)$ for different values of Bi (a,b) for SP and RP(a), porous and non-porous RP (b), Hg (c,d) for convective heating RP and SP (c) and convective cooling RP and SP (d), Nb (e,f) for convective heating with heat generation and absorption (e) and convective cooling with heat generation and absorption (f).

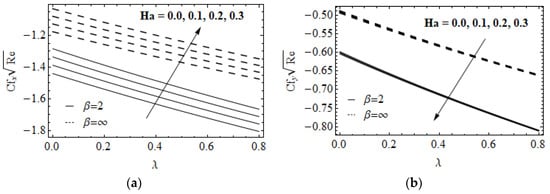
Figure 7. The Skin friction in $x$-direction (a) and $y$-direction (b) with different values of $Ha$ and $\lambda$ for both fluids.

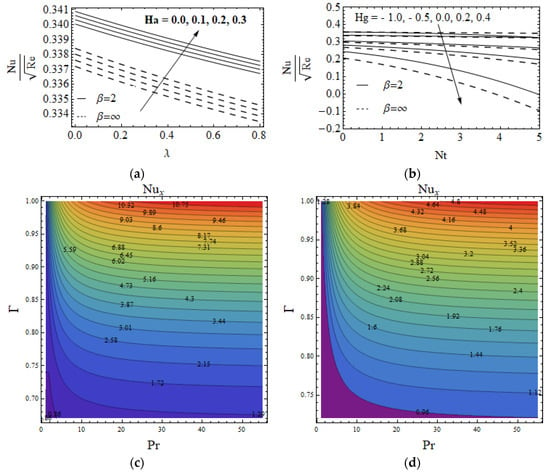
Figure 8. The $N{u}_x$ variations Ha&$\lambda \left(a\right), Hg\&Nt\left(b\right)\mathrm{for}\mathrm{both}\mathrm{fluids}\mathrm{and} Pr\&\Gamma \left(c,d\right)$ for Casson nanofluid (c) and viscous nanoluid (d).

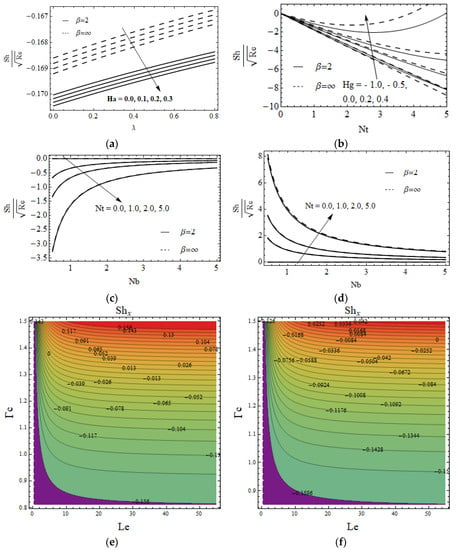
Figure 9. The ${Sh}_x$ for $\lambda \&Ha \left(a\right)$ and $Nt\&Hg$ (b) for both fluids and $Nb\&Nt$ with $Bi=0.5\left(c\right)$ and $Bi=-0.5\left(d\right)$, $Le\&{\Gamma }_C$ for Casson nanofluid (e) and viscous nanofluid (f).

6. Conclusions

The Darcy–Forchheimer flow of the 3-D Casson nanofluid owing to the Riga plate was investigated using the Cattaneo–Christov dual diffusion theory. In addition, the homotopy technique was used for the solution process. The most important finding is highlighted below.

• The skin friction rate in $x-$ direction enhances and in $y-$ direction decays when enhancing the modified Hartman number.
• The larger skin friction rate occurs in viscous nanofluid than the Casson nanofluid.
• Thermal layer thickness amplifies with an augmented value of $Bi$.
• A larger value of $Hg$ upsurges in the thermal layer in the case of $Bi=0.5$ while the thermal layer reduces with a larger value of $Hg$ for $Bi=-0.5$.
• The thermal relaxation parameter improves the local Nusselt number for both fluids.
• In the future, we will extend this work with the Tiwari and Das model with a hybrid nanofluid case.