Abstract
In gauge mediation models with multiple spurion fields breaking SUSY and the R-symmetry separately, we show that it is possible to generate gaugino masses in one loop if the R-charge arrangement satisfies a certain condition. The resulting gaugino masses are calculated and suppressed by a power of the messenger’s mass scale. We present two simple examples to demonstrate this possibility and discuss possible phenomenology implications.
1. Introduction
Gauge mediation [1,2,3,4] provides a mechanism to mediate spontaneous supersymmetry (SUSY) breaking effects from the SUSY breaking hidden sector to the visible supersymmetric standard model (SSM) sector, giving rise to soft terms for sparticle masses and coupling constants that may be tested at the LHC or other future experiments. Although recent experimental results have excluded many SUSY models [5], there are still some unexplored corners of the parameter space where models compatible with experiments can be constructed.
In gauge mediation models, SUSY breaking fields in the hidden sector [6] are coupled to messenger fields, which are nontrivial representations of the standard model (SM) gauge symmetries. The hidden sector is effectively described by a Wess–Zumino model, which possesses F-term spontaneous SUSY breaking [7,8]. A chiral superfield X, named the SUSY breaking spurion, obtains a vacuum expectation value (VEV) for its auxiliary field component after spontaneous SUSY breaking. To build a natural SUSY breaking model in the hidden sector, it is necessary to introduce R-symmetry that restricts the possible terms appearing in the superpotential [9]. The R-charge assignment of fields determines the generic form of the superpotential, which has R-charge 2. SUSY or SUSY breaking vacua can be obtained by a proper R-charge assignment satisfying certain conditions [10,11,12,13,14,15,16,17,18,19,20]. SUSY-breaking effects are transferred to the visible sector through the coupling of messenger fields. In gauge mediation models, the R-symmetry also needs to be spontaneously broken to generate Majorana gaugino masses, which do not respect the R-symmetry. The R-symmetry is effectively spontaneously broken by the VEV of the scalar component of a chiral superfield Y with a nonzero R-charge, which is named the R-symmetry breaking spurion. In a simple model of the hidden sector, the SUSY-breaking and R-symmetry breaking spurions are usually considered to be aligned, and X is identified with Y. The scalar component of X, or the SUSY-breaking pseudo-modulus [21,22,23], obtains a VEV at the loop level by including quantum corrections [24,25], or through the inclusion of D-terms [26,27]. Thus, X has the VEV
Sparticle masses are generated through the gauge mediation mechanism. Among them, the gauginos obtain Majorana masses from one-loop diagrams with messengers in the loop. Up to an overall factor, the magnitude of gaugino masses is
where is the fine structure constant of the gauge group labeled by the index s.
It is also possible to build models with R-symmetry breaking before considering quantum corrections, or at the tree level [28,29]. Such a model can be effectively described as the misalignment between X and Y fields. A naive guess for gaugino masses would be
However, as shown in previous literature [30], the simplest type of tree-level R-symmetry breaking model does not have a one-loop diagram for the gaugino masses with R-charge conservation at all vertices, unless the R-charges of X and Y are identical and the assumption of misalignment becomes invalid. Thus, generic tree-level R-symmetry breaking models in the simplest cases fail to generate gaugino masses and are not favored phenomenologically.
In this work, we investigate the possibility of bypassing the previous no-go statement [30] in more general models. We show that with multiple Xs, Ys, and messenger fields, gaugino masses can be generated at the one-loop level if the R-charge assignment of fields satisfies certain conditions. The resulting gaugino masses from one-loop Feynman diagram calculations are always suppressed by a power of the messenger mass scale, whose exponent depends on the number of X fields, although the detailed gaugino mass spectrum requires more careful calculation. We present two simple examples to demonstrate this possibility. Finally, we discuss possible implications for model building and phenomenology.
2. Gaugino Masses from One Spurion
This section reviews previous results of ordinary gauge mediation, which will later be generalized to models with multiple misaligned spurions. We start from the superfield formulation of the SUSY Lagrangian
and expand it to component fields. Ignoring the details of SUSY breaking and R-symmetry breaking mechanisms, the SUSY breaking sector is described by a spurion field X with the VEV (1) breaking both SUSY and the R-symmetry. The R-charge of Grassmann numbers is set to 1 in the superfield formulation, so the superpotential W has R-charge 2 to make the Lagrangian R-invariant. In simple models, X usually has R-charge 2, and couples to messenger fields through the cubic interaction in the superpotential
where the messenger fields and have opposite R-charges and are conjugated to each other as SM gauge symmetry representations. Expanding the superpotential part of the SUSY Lagrangian in the component fields, the nonzero VEV of X gives quadratic vertices to messenger fields:
Messengers are nontrivial representations of SM gauge symmetries coupled to vector superfields in the kinetic part of the Lagrangian, where are gauge symmetry group generators; we use the Einstein summation convention for repeating indices throughout this work. Expanding the kinetic part of the SUSY Lagrangian in the component fields, the gauge coupling gives the cubic vertices between messenger fields and gauginos:
where are the SSM gauginos , and the gauge coupling strength is related to the fine structure constant of the gauge group labeled by the index s:
Similar vertices from gauge coupling between and V also exist. The Feynman rules of these vertexes are shown in Figure 1. Gauginos obtain Majorana masses of the magnitude (2) from the one-loop Feynman diagram shown in Figure 2, where the R-charges of messenger component fields are labeled.
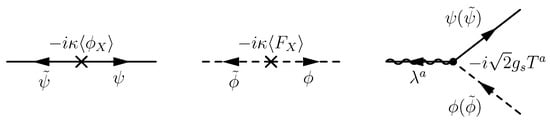
Figure 1.
Messenger coupling vertices related to gaugino masses.
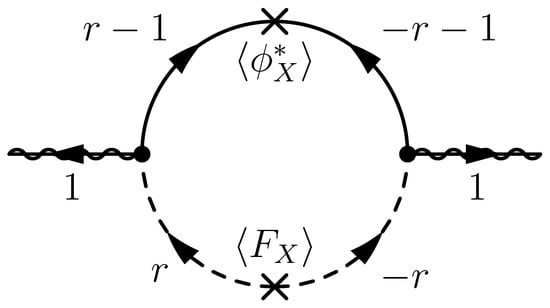
Figure 2.
A one-loop diagram for gaugino masses with R-charges labeled.
The messenger sector can be generalized to have more than two messenger fields, and include explicit mass terms [31,32]. The corresponding superpotential is
where each term with nonzero or must have R-charges of fields added up to 2. Messenger fields with and without tilde on their symbols are conjugated to each other as SM gauge symmetry representations. The messenger mass matrix
is not diagonal and depends on the VEV of X. It alters the quadratic vertices and the propagators of messengers in the loop, making the one-loop calculation more complicated. One can instead do the calculation using the wave-function renormalization method [33], and the resulting gaugino masses are given as in [31]:
As a consequence of the R-symmetric superpotential (9), the determinant of the messenger mass matrix has the identity
Then (11) becomes
which agrees with the magnitude (2). In particular, a model with a classically stable pseudo-modulus space always gives in the identity (12), and the gaugino mass (13) becomes zero. To obtain a nonzero gaugino mass at one loop, the classically stable vacuum condition must be relaxed. So the SUSY breaking pseudo-modulus space must have a classically unstable region that the stabilized vacuum—after including quantum corrections—should avoid. This type of classical instability also means that there must be some vacuum or runaway direction with lower potential energy than the SUSY breaking vacuum. Thus, we reached an additional argument for the necessity of metastable SUSY breaking [34,35], which complements the argument of metastability from non-perturbative effects explicitly breaking the R-symmetry [36,37]. Note that both the wave-function renormalization result (11) and the messenger mass matrix identity (11) are based on the assumption of a single spurion X, which breaks both SUSY and the R-symmetry. Thus, this argument of metastability from classical instability of the pseudo-modulus space does not work for the following cases with multiple misaligned spurions.
3. Gaugino Masses from Misaligned Spurions
This section generalizes the gauge mediation formulation in the previous section to tree-level R-symmetry breaking models; the essential concept is the misalignment between the SUSY breaking spurion X and the R-symmetry breaking spurion Y. Instead of (1), we have the VEVs
Here, we suppose that in a generalized model, there may be multiple X and Y fields with different R-charges, and . It is a common feature of previously known examples of SUSY breaking models with tree-level R-symmetry breaking [28,29,34]. Both X and Y fields couple to messenger fields through cubic interactions in the superpotential
where each term with a nonzero coefficient or must have R-charges of fields added up to 2. Messenger fields with and without tilde on their symbols are conjugate with each other as SM gauge symmetry representations. Expanding the superpotential part of the SUSY Lagrangian in component fields, the nonzero VEVs of the Xs and Ys give quadratic vertices to messenger fields:
Moreover, the gauge coupling in the kinetic part of the SUSY Lagrangian gives the cubic vertices between messenger fields and gauginos:
Similar vertices from gauge coupling between and V also exist. The Feynman rules of these vertexes are shown in Figure 3. Note that a quadratic vertex may mix messenger fields with different indices, but a cubic vertex always connects a gaugino with fermion and scalar components of the same messenger superfield. One can insert multiple quadratic vertices into both the fermion part and the scalar part of the loop, and gauginos may obtain Majorana masses from the one-loop Feynman diagram shown in Figure 4. If the diagram does exist, R-charge conservation should be satisfied at each vertex. Thus, the R-charges of messengers can be determined by , , and r, which is the R-charge of the first messenger connecting to the gaugino on the left of the loop diagram. The resulting R-charges of messenger component fields are labeled in Figure 4. Then R-charge conservation at the vertex connecting messengers to the gaugino on the right of the loop diagram leads to the condition
where the sum is over the vertices or the vertices in the loop diagram. Noticing the arrow directions of messenger field propagators and pairs of messengers with and without tilde connected to quadratic vertices, both the fermion part and the scalar part of the loop diagram in Figure 4 must have odd numbers of vertices inserted. Thus both and must be odd numbers.
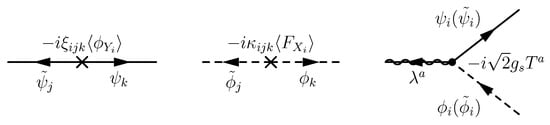
Figure 3.
Messenger coupling vertices related to gaugino masses from misaligned spurions.
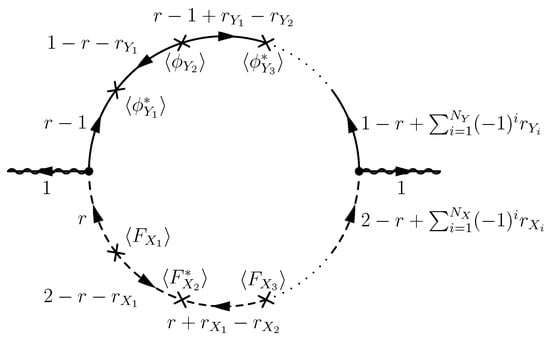
Figure 4.
A possible one-loop diagram for gaugino masses from misaligned spurions with R-charges labeled.
To obtain the magnitude of gaugino masses from the one-loop Feynman diagram shown in Figure 4, we simplify the coefficients of cubic interactions in the superpotential (15) to just two universal parameters and . We assume for simplicity that all VEVs of Xs and Ys are at the universal scales and , and all messengers obtain masses at the universal scale . Notice that all Feynman rules of quadratic vertices can be set to real by proper complex phase rotations of messenger fields. Now, we are interested in the regime so that an effective field theory calculation can be done to give soft masses from the SUSY breaking effect. Using the two-component spinor techniques for quantum field theory developed in [38], a straightforward calculation of the one-loop diagram in Figure 4 gives:
Following the standard procedure in quantum field theory textbooks [39], the integration can be done by introducing a Feynman parameter x and performing a Wick rotation:
Plugging this result into (20) and setting , we obtain the one-loop contribution to gaugino masses with the awkward integration and sum expressions. Note that all integrations over the Feynman parameter x in the sum are finite. Neglecting an overall factor, it is easy to obtain the magnitude of gaugino masses:
which is always suppressed by a power of the messenger mass scale.
For models with only one vertex and one vertex inserted in the loop in Figure 4, it seems that (22) gives the magnitude of gaugino masses
However, the condition (19) in this case means . The R-symmetry requires X and Y to share the same set of coupling terms with messengers. There is no distinction between X and Y in terms of R-charges. Therefore, the misaligned VEVs in (14) are not generic, and the scalar component of X may also obtain a VEV to break the R-symmetry in a generic model. This is just the no-go statement obtained in [30]: The simplest tree-level R-symmetry breaking model, if it successfully generates gaugino masses in gauge mediation, is generically accompanied by same magnitude of loop-level R-symmetry breaking, which also contributes to the gaugino masses. To generate gaugino masses from misaligned SUSY breaking and R-symmetry breaking spurions in a generic model, it is necessary to have multiple s or multiple s inserted in the loop in Figure 4, satisfying the condition (19).
4. Examples
This section presents simple examples to demonstrate the possibility of generating gaugino masses with multiple spurions satisfying the condition (19). Noticing that both and must be odd numbers, the simplest model has either three vertices or three vertices inserted in the loop. One can further simplify the model by allowing different vertices to come from the same X or Y as long as they are not next to each other. Therefore, the simplest model may be constructed with one X field and two Y fields, or two X fields and one Y field.
4.1. The Model
In the first example, we have one SUSY breaking spurion, X, and two R-symmetry breaking spurions, and . The couplings between X, Ys, and messenger fields are described by the superpotential
which is compatible with the R-charge assignment:
where the free parameters r, , and may be fixed by some mechanism in the ultraviolet theory, such as anomaly cancellation when the R-symmetry is gauged in supergravity. According to (22), the one-loop Feynman diagram shown in Figure 5 gives the magnitude of gaugino masses
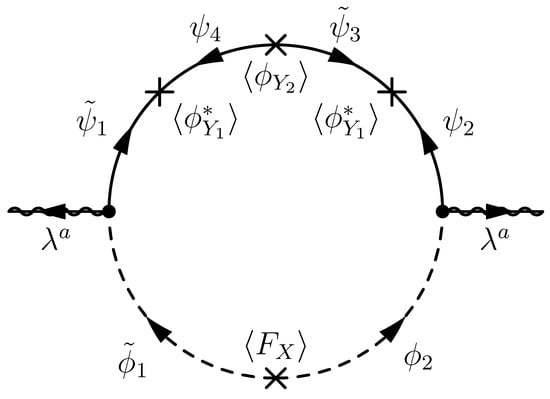
Figure 5.
A one-loop diagram for gaugino masses in the model.
If there are explicit messenger mass terms in a model, the mass coefficients can be viewed as VEVs of some Y fields with R-charges 0, which do not violate the R-symmetry of the model. Thus, some vertices in the loop in Figure 5 can be replaced by explicit mass insertions, and the model may be built with only one X field and one Y field. If we replace the two vertices with masses in the loop, we have the superpotential
with the R-charge assignment
We can also replace the one vertex with a mass in the loop, then we have the superpotential
with the R-charge assignment
The one-loop Feynman diagrams for gaugino masses in these two variations of the model are shown in Figure 6. Both of them give the same magnitudes of gaugino masses as (26) if we assume , and the explicit messenger masses are at the universal scale M.
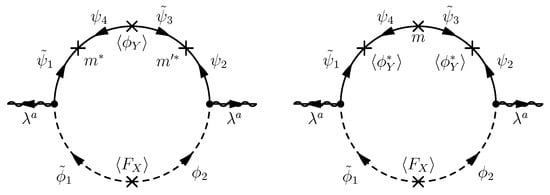
Figure 6.
One-loop diagrams for gaugino masses in two variations of the model.
4.2. The Model
In the second example, we have two SUSY breaking spurions, and , and one R-symmetry breaking spurion, Y. The couplings between the Xs, Ys, and messenger fields are described by the superpotential
which is compatible with the R-charge assignment:
where the free parameters r, , and may be fixed by some mechanism in the ultraviolet theory. According to (22), the one-loop Feynman diagram shown in Figure 7 gives the magnitude of gaugino masses
which is suppressed by a higher power of M because of multiple insertions in the loop of Figure 7.
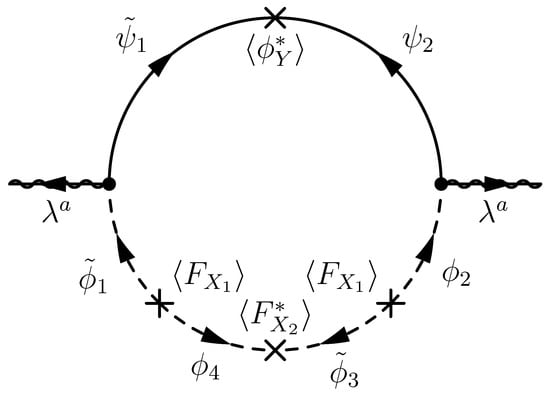
Figure 7.
A one-loop diagram for gaugino masses in the model.
5. Conclusions
In this study, we demonstrated that it is feasible to generate gaugino masses using multiple SUSY breaking and R-symmetry breaking spurions with a suitable R-charge arrangement that satisfies the condition (19). The magnitude of the resulting gaugino masses (22) is suppressed by a power of the messenger mass scale M. The exponent of M in the denominator depends on , the number of quadratic vertices inserted in the scalar part of the loop diagram shown in Figure 4. Specifically, models with one SUSY breaking spurion X always result in gaugino masses of the magnitude , provided that all VEVs of Ys and all messenger masses are at the universal scale M. In realistic models, there may be some hierarchy among the VEVs of different Xs and Ys, as well as coefficients of different cubic interactions in the superpotential. Messenger masses must be determined from the eigenvalues of the messenger mass matrix, and the mass eigenstates are typically not aligned with the R-charge eigenstates of messengers. Moreover, there may be more than one combination of Xs and Ys that satisfies the condition (19), corresponding to multiple different loop diagrams that contribute to the gaugino masses. Thus, the actual gaugino masses necessitate more detailed calculations that depend on the model’s details.
The misalignment between SUSY breaking and R-symmetry breaking spurions may arise not only in tree-level R-symmetry breaking models [28,29,34], but also in models with separate SUSY breaking and R-symmetry breaking sectors. Recently found counter-examples to the Nelson–Seiberg theorem show the possibility of R-symmetry breaking spurions that do not break SUSY [12,13,15,18]. Thus, there may be more freedom to manipulate the mass spectrum of gauginos, as well as other SUSY breaking soft terms, by independently adjusting the SUSY breaking and R-symmetry breaking effects in different sectors. Gaugino masses are suppressed by a higher power of the messenger mass scale M in models that require multiple insertions in the one-loop diagrams to satisfy the condition (19). On the other hand, sfermion masses from two-loop diagrams do not suffer from such suppression, thus may remain heavy. This splitting of sparticle masses gives rise to the split-SUSY scenario [40,41,42], which has gained attention and development in the era of null discoveries from LHC and dark matter searches [43,44,45,46].
The multiple spurions in our assumption could just be artifacts of the R-symmetry, that one single SUSY breaking or R-symmetry breaking spurion is a linear combination of spurions with different R-charges. This is the usual situation of tree-level R-symmetry breaking models [28,29,34] with a single sector possessing both SUSY breaking and R-symmetry breaking. An alternative possibility is to have multiple sectors, where each one independently breaks SUSY or the R-symmetry. The multiple decoupled SUSY breaking sectors correspondingly yield to multiple massless goldstini [47], which could lead to interesting phenomenologies, such as models for goldstini dark matter [48,49].
Author Contributions
Conceptualization, T.L. and Z.S.; Methodology, T.L. and Z.S.; Formal analysis, Y.F., T.L., L.R. and Z.S.; Writing—original draft, Z.S.; Writing—review & editing, Y.F., T.L., L.R. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key Research and Development Program of China: Grant Number 2020YFC2201504; National Natural Science Foundation of China: Grant Number 11875062, Grant Number 11947302, Grant Number 12047503, Grant Number 12275333; Key Research Program of the Chinese Academy of Sciences: Grant Number XDPB15; Scientific Instrument Developing Project of the Chinese Academy of Sciences: Grant Number YJKYYQ20190049; International Partnership Program of Chinese Academy of Sciences for Grand Challenges: Grant Number 112311KYSB20210012; National Natural Science Foundation of China: Grant Number 11305110.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
We thank Michael Dine, Feihu Liu, Muyang Liu, and Dimitri Polyakov for the helpful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Martin, S.P. A Supersymmetry primer. Adv. Ser. Direct. High Energy Phys. 1998, 18, 1–98. [Google Scholar]
- Giudice, G.F.; Rattazzi, R. Theories with gauge mediated supersymmetry breaking. Phys. Rept. 1999, 322, 419–499. [Google Scholar] [CrossRef]
- Meade, P.; Seiberg, N.; Shih, D. General Gauge Mediation. Prog. Theor. Phys. Suppl. 2009, 177, 143–158. [Google Scholar] [CrossRef]
- Kitano, R.; Ooguri, H.; Ookouchi, Y. Supersymmetry Breaking and Gauge Mediation. Ann. Rev. Nucl. Part. Sci. 2010, 60, 491–511. [Google Scholar] [CrossRef]
- Particle Data Group; Zyla, P.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2022, 2022, 083C01. [Google Scholar]
- Intriligator, K.A.; Seiberg, N. Lectures on supersymmetry breaking. Class. Quant. Grav. 2007, 24, S741–S772. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. A Lagrangian Model Invariant Under Supergauge Transformations. Phys. Lett. B 1974, 49, 52–54. [Google Scholar] [CrossRef]
- Wess, J.; Zumino, B. Supergauge Invariant Extension of Quantum Electrodynamics. Nucl. Phys. B 1974, 78, 1–13. [Google Scholar] [CrossRef]
- Nelson, A.E.; Seiberg, N. R symmetry breaking versus supersymmetry breaking. Nucl. Phys. B 1994, 416, 46–62. [Google Scholar] [CrossRef]
- Sun, Z. Low energy supersymmetry from R-symmetries. Phys. Lett. B 2012, 712, 442–444. [Google Scholar] [CrossRef]
- Kang, Z.; Li, T.; Sun, Z. The Nelson-Seiberg theorem revised. J. High Energy Phys. 2013, 12, 93. [Google Scholar] [CrossRef]
- Sun, Z.; Tan, Z.; Yang, L. A counterexample to the Nelson-Seiberg theorem. J. High Energy Phys. 2020, 10, 72. [Google Scholar] [CrossRef]
- Amariti, A.; Sauro, D. On the Nelson-Seiberg theorem: Generalizations and counter-examples. arXiv 2020, arXiv:2005.02076. [Google Scholar]
- Li, Z.; Sun, Z. The Nelson-Seiberg theorem generalized with nonpolynomial superpotentials. Adv. High Energy Phys. 2020, 2020, 3701943. [Google Scholar] [CrossRef]
- Sun, Z.; Tan, Z.; Yang, L. A sufficient condition for counterexamples to the Nelson-Seiberg theorem. J. High Energy Phys. 2021, 2021, 175. [Google Scholar] [CrossRef]
- Li, Z.; Sun, Z. Nonexistence of supersymmetry breaking counterexamples to the Nelson-Seiberg theorem. J. High Energy Phys. 2021, 10, 170. [Google Scholar] [CrossRef]
- Brister, J.; Sun, Z.; Yang, G. A formal notion of genericity and term-by-term vanishing superpotentials at supersymmetric vacua from R-symmetric Wess-Zumino models. J. High Energy Phys. 2021, 12, 199. [Google Scholar] [CrossRef]
- Brister, J.; Sun, Z. Novel counterexample to the Nelson-Seiberg theorem. Phys. Rev. D 2022, 106, 085009. [Google Scholar] [CrossRef]
- Brister, J.; Kou, S.; Li, Z.; Sun, Z. A brute-force search for R-symmetric Wess-Zumino models. arXiv 2022, arXiv:2204.05767. [Google Scholar]
- Sun, Z. Supersymmetry and R-symmetries in Wess-Zumino models: Properties and model dataset construction. arXiv 2022, arXiv:2207.13933. [Google Scholar]
- Ray, S. Some properties of meta-stable supersymmetry-breaking vacua in Wess-Zumino models. Phys. Lett. B 2006, 642, 137–141. [Google Scholar]
- Sun, Z. Continuous degeneracy of non-supersymmetric vacua. Nucl. Phys. B 2009, 815, 240–255. [Google Scholar] [CrossRef]
- Sun, Z. Vacuum statistics and parameter tuning for F-term supersymmetry breaking. J. High Energy Phys. 2011, 2011, 107. [Google Scholar] [CrossRef]
- Shih, D. Spontaneous R-symmetry breaking in O’Raifeartaigh models. J. High Energy Phys. 2008, 2008, 091. [Google Scholar] [CrossRef]
- Curtin, D.; Komargodski, Z.; Shih, D.; Tsai, Y. Spontaneous R-symmetry Breaking with Multiple Pseudomoduli. Phys. Rev. D 2012, 85, 125031. [Google Scholar] [CrossRef]
- Azeyanagi, T.; Kobayashi, T.; Ogasahara, A.; Yoshioka, K. Runaway, D term and R-symmetry Breaking. Phys. Rev. D 2012, 86, 095026. [Google Scholar]
- Vaknin, T. New phases in O’Raifeartaigh-like models and R-symmetry breaking. J. High Energy Phys. 2014, 2014, 4. [Google Scholar] [CrossRef]
- Carpenter, L.M.; Dine, M.; Festuccia, G.; Mason, J.D. Implementing General Gauge Mediation. Phys. Rev. D 2009, 79, 035002. [Google Scholar] [CrossRef]
- Sun, Z. Tree level spontaneous R-symmetry breaking in O’Raifeartaigh models. J. High Energy Phys. 2009, 2009, 002. [Google Scholar] [CrossRef]
- Liu, F.; Liu, M.; Sun, Z. No-go for tree-level R-symmetry breaking. Eur. Phys. J. C 2017, 77, 745. [Google Scholar] [CrossRef]
- Cheung, C.; Fitzpatrick, A.L.; Shih, D. (Extra)ordinary gauge mediation. J. High Energy Phys. 2008, 2008, 054. [Google Scholar] [CrossRef]
- Marques, D. Generalized messenger sector for gauge mediation of supersymmetry breaking and the soft spectrum. J. High Energy Phys. 2009, 2009, 038. [Google Scholar] [CrossRef]
- Giudice, G.F.; Rattazzi, R. Extracting supersymmetry breaking effects from wave function renormalization. Nucl. Phys. B 1998, 511, 25–44. [Google Scholar] [CrossRef]
- Komargodski, Z.; Shih, D. Notes on SUSY and R-Symmetry Breaking in Wess-Zumino Models. J. High Energy Phys. 2009, 2009, 093. [Google Scholar] [CrossRef]
- Abel, S.A.; Jaeckel, J.; Khoze, V.V. Gaugino versus Sfermion Masses in Gauge Mediation. Phys. Lett. B 2010, 682, 441–445. [Google Scholar] [CrossRef]
- Intriligator, K.A.; Seiberg, N.; Shih, D. Dynamical SUSY breaking in meta-stable vacua. J. High Energy Phys. 2006, 2006, 021. [Google Scholar] [CrossRef]
- Intriligator, K.A.; Seiberg, N.; Shih, D. Supersymmetry breaking, R-symmetry breaking and metastable vacua. J. High Energy Phys. 2007, 2007, 017. [Google Scholar] [CrossRef]
- Dreiner, H.K.; Haber, H.E.; Martin, S.P. Two-component spinor techniques and Feynman rules for quantum field theory and supersymmetry. Phys. Rept. 2010, 494, 1–196. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Addison-Wesley: Boston, MA, USA, 1995; ISBN 978-0-201-50397-5. [Google Scholar]
- Arkani-Hamed, N.; Dimopoulos, S. Supersymmetric unification without low energy supersymmetry and signatures for fine-tuning at the LHC. J. High Energy Phys. 2005, 2005, 073. [Google Scholar] [CrossRef]
- Giudice, G.F.; Romanino, A. Split supersymmetry. Nucl. Phys. B 2004, 699, 65–89, Erratum: Nucl. Phys. B 2005, 706, 487. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Dimopoulos, S.; Giudice, G.F.; Romanino, A. Aspects of split supersymmetry. Nucl. Phys. B 2005, 709, 3–46. [Google Scholar] [CrossRef]
- Harigaya, K.; Ibe, M.; Yanagida, T.T. A Closer Look at Gaugino Masses in Pure Gravity Mediation Model/Minimal Split SUSY Model. J. High Energy Phys. 2013, 12, 016. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Yang, J.M. Split supersymmetry under GUT and current dark matter constraints. Eur. Phys. J. C 2014, 74, 3121. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Yang, J.M. A split SUSY model from SUSY GUT. J. High Energy Phys. 2015, 2015, 050. [Google Scholar] [CrossRef]
- Ahmed, W.; Mansha, A.; Li, T.; Raza, S.; Roy, J.; Xu, F.Z. The upper bounds on supersymmetry breaking scales in split supersymmetry from the Higgs mass and electroweak vacuum stability. Prog. Theor. Exp. Phys. 2020, 2020, 043B08. [Google Scholar] [CrossRef]
- Cheung, C.; Nomura, Y.; Thaler, J. Goldstini. J. High Energy Phys. 2010, 2010, 073. [Google Scholar] [CrossRef]
- Cheng, H.C.; Huang, W.C.; Low, I.; Menon, A. Goldstini as the decaying dark matter. J. High Energy Phys. 2011, 2011, 19. [Google Scholar] [CrossRef]
- Cao, J.; Du, X.; Li, Z.; Wang, F.; Zhang, Y. Explaining The XENON1T Excess With Light Goldstini Dark Matter. arXiv 2020, arXiv:2007.09981. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).