Multiple Multi-Orbit Pairing Algebras in Nuclei

Abstract

The algebraic group theory approach to pairing in nuclei is an old subject and yet it continues to be important in nuclear structure, giving new results. It is well known that for identical nucleons in the shell model approach with j − j coupling, pairing algebra is SU(2) with a complementary number-conserving Sp(N) algebra and for nucleons with good isospin, it is SO(5) with a complementary number-conserving Sp(2Ω) algebra. Similarly, with L − S coupling and isospin, the pairing algebra is SO(8). On the other hand, in the interacting boson models of nuclei, with identical bosons (IBM-1) the pairing algebra is SU(1, 1) with a complementary number-conserving $SO(\mathcal{N})$ algebra and for the proton–neutron interacting boson model (IBM-2) with good F-spin, it is SO(3, 2) with a complementary number-conserving SO(Ω^B) algebra. Furthermore, in IBM-3 and IBM-4 models several pairing algebras are possible. With more than one j or ℓ orbit in shell model, i.e., in the multi-orbit situation, the pairing algebras are not unique and we have the new paradigm of multiple pairing [SU(2), SO(5) and SO(8)] algebras in shell models and similarly there are multiple pairing algebras [SU(1, 1), SO(3, 2) etc.] in interacting boson models. A review of the results for multiple multi-orbit pairing algebras in shell models and interacting boson models is presented in this article with details given for multiple SU(2), SO(5), SU(1, 1) and SO(3, 2) pairing algebras. Some applications of these multiple pairing algebras are discussed. Finally, multiple SO(8) pairing algebras in shell model and pairing algebras in IBM-3 model are briefly discussed.

1. Introduction

Pairing is one of the most important concepts in nuclear structure physics and its fingerprints are seen clearly in binding energies of nuclei, ground state spins, odd-even effects, beta decay, double beta decay, orbit occupancies and so on [1,2]. Very early Bohr, Mottelson and Pines [3] suggested the use of BCS theory for pairing in nuclei and all the subsequent developments in this direction are well reviewed in [4,5,6]. Focusing on nuclear shell model [7,8], algebraic group theory approach to pairing has started receiving attention following Racah’s seniority quantum number [9,10]. For identical nucleons in a single-j shell, pair state is coupled to angular momentum zero and the corresponding pair creation operators are unique. The pair-creation operator, pair-annihilation operator and the number operator generate the $SU(2)$ pairing algebra. The eigenstates of the pairing Hamiltonian, that is a product of pair-creation and pair-annihilation operators, carry the $SU(2)$ quasi-spin or seniority quantum number. There are several single-j shell nuclei that are known to carry seniority quantum number (v) as a good or useful quantum number; see [7] and also [11,12,13,14] and references therein for full details of quasi-spin and seniority for identical particles and their applications. Even when single-j shell seniority is a broken symmetry, seniority quantum number is useful as it provides a basis for constructing shell model Hamiltonian matrices [15]. Pairing symmetry with nucleons occupying several j-orbits is more complex and less well understood from the point of view of its goodness or usefulness in nuclei. Restricting to nuclei with identical valence nucleons (protons or neutrons), and say these nucleons occupy several-j orbits, then it is possible to consider the pair-creation operator to be a sum of the single-j shell pair-creation operators with arbitrary phases and for each choice there will be quasi-spin $SU(2)$ algebra giving multi-orbit or generalized seniority quantum number v. With r number of orbits there will be $2^{r-1}$ number of $SU(2)$ pairing algebras. With $2\mathrm{\Omega }={\sum }_j(2j+1)$, the spectrum generating algebra (SGA) is $U(2\mathrm{\Omega })$ and the pairing $SU(2)$ algebra is complementary to the $Sp(2\mathrm{\Omega })$ algebra in $U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })$ with v denoting the irreducible representations (irreps) of $Sp(2\mathrm{\Omega })$ that belong to a given number m of identical nucleons [m denotes the irrep of $U(2\mathrm{\Omega })$]. The usefulness or goodness of these multiple pairing algebras is not well known except a special situation that was studied long ago by Arvieu and Moszkowski (AM) [16] in the context of surface delta interaction. We will discuss this in detail in Section 2. In addition, pair states with linear superposition of single-j shell pair states with arbitrary coefficients are used in generating low-lying states of nuclei, such as Sn isotopes, with good generalized seniority [7], and they are also employed in the so called broken pair model [17]. On the other hand, these are also used in providing a microscopic basis for the interacting boson model [18]. Going beyond all these, there are also attempts to solve and apply more general pairing Hamiltonian’s by Pan Feng et al. [19] and also a pair shell model was developed by Arima and Zhao [20].

In the interacting boson models [21,22,23], the $SO({\mathcal{N}}^B)$ algebras in the SGA $U({\mathcal{N}}^B)$ are well known. For example $SO(6)$ in $sd$IBM-1, $SO(15)$ and $SO(14)$ in $sdg$IBM-1 and so on. However, what is not often emphasized is that the $SO({\mathcal{N}}^B)$ algebras correspond to pairing for bosons. In fact, for identical bosons in single ℓ shell (for example d orbit in $sd$IBM, g in $sdg$IBM) or in multi-ℓ situation (for example $sd$, $sdg$ etc.), the pairing algebra is the non-compact $SU(1,1)$ algebra and the better known $SO({\mathcal{N}}^B)$ algebras are complementary algebras (see Section 3 ahead) [21,24]. However, just as the situation with identical fermions, here also there will be multiple $SU(1,1)$ pairing algebras (with r number of ℓ orbits, there will be $2^{r-1}$ number of algebras) and for each of these there will be a complementary $SO({\mathcal{N}}^B)$ algebra. These multiple multi-orbit pairing algebras and their applications are described in Section 3.

Pairing in identical fermion systems is easy to deal with as the algebra is $SU(2)$. However, the situation changes if we consider nucleons with isospin (T) degree of freedom. Here, the algebra changes to the more complex $SO(5)$ algebra that generates seniority (v) and in addition also reduced isospin (t) [25,26]. Another important result is that the $SO(5)$ contains only isovector pair-creation and -annihilation operators (an unsatisfactory aspect of the $SO(5)$ pairing algebra of shell model is that it does not contain isoscalar pair operators). With isospin, in a single-j orbit the SGA is $U(4\mathrm{\Omega })$ with $2\mathrm{\Omega }=(2j+1)$. The $Sp(2\mathrm{\Omega })$ algebra in $U(4\mathrm{\Omega })\supset [U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })]\otimes S{U}_T(2)$ is complementary to $SO(5)$ with $(v,t)$ uniquely labeling the $Sp(2j+1)$ irreps. For the first papers on single-j shell pairing with isospin see [25,26,27,28,29,30,31]. Similarly, for the technical work on the more complicated $SO(5)$ algebra [for example, deriving analytical formulas for the Wigner and Racah coefficients for $SO(5)$] see [30,32,33,34,35,36,37,38] and for recent applications see [39,40,41,42,43,44,45,46] and references therein. Although many of the single-j shell results extend to the multi-j shell situation with $(2j+1)$ replaced by $2\mathrm{\Omega }={\sum }_j(2j+1)$, a crucial aspect of the multi-j shell $SO(5)$ pairing algebra is that there will be multiple $SO(5)$ algebras (also the corresponding multiple $Sp(2\mathrm{\Omega })$ algebras) as the pair-creation operator here is no longer unique. Section 4 describes these multiple $SO(5)$ isovector pairing and seniority $Sp(2\mathrm{\Omega })$ multi-j algebras with isospin in nuclei and their applications.

Parallel to pairing in shell model with isospin is the pairing with F-spin in interacting boson models. Making a distinction between proton bosons and neutron bosons and treating them as projections of a fictitious (F) spin $1/2$ object, we have $pn$IBM or IBM-2 with F-spin degree of freedom (F-spin in IBM is mathematically similar to isospin in shell model). As we present in Section 5, the pairing algebra changes from $SU(1,1)$ to more complicated $SO(3,2)$ algebra [47]. More importantly, in the multi-ℓ situation there will be multiple $SO(3,2)$ algebras and for each of these there will be a complementary $SO({\mathrm{\Omega }}^B)$ algebra. In Section 5 multiple multi-orbit $SO(3,2)$ pairing algebras with F-spin in IBMs are discussed.

Going further, interestingly multiple pairing algebras appear also in the $LST$ pairing $SO(8)$ algebra in shell model and also in the isospin invariant IBM-3 model and spin-isospin invariant IBM-4 model; see [48,49,50,51,52,53,54] for $SO(8)$ algebra and [21,55,56] for IBM-3 and IBM-4. In Section 6 we will briefly describe multiple $SO(8)$ pairing algebras in shell model and the pairing algebras in IBM-3.

Before proceeding further, let us stress that the most important aspect of pairing algebras is the complementarity between the pairing algebras with number non-conserving generators and the shell model/IBM algebras with only number-conserving generators [57]. A general mathematical theory describing this complementarity is due to Neergard [58,59,60,61] and this is based on Howe’s general duality theorem [62,63]. It is important to mention that the first proof of complementarity is due to Helmers [28] and later work is due to Rowe et al. [64]. We will not discuss these more mathematically rigorous results in this paper.

Many of the results in Section 2, Section 3 and Section 4 are presented in two conference proceedings [65,66]. Furthermore, the present article complements the results obtained for multiple $SU(3)$ algebras in nuclei as reported in [67,68,69].

2. Multiple Multi-Orbit Pairing Algebras in Shell Model: Identical Nucleons

With identical nucleons (protons or neutrons) in a single-j shell, the pair-creation operator $S_{+}$ and annihilation operator $S_{-}={(S_{+})}^{†}$ and the number operator [$\widehat{n}$ or more appropriately $\widehat{n}-N/2$ with $N=(2j+1)$, generate remarkably the quasi-spin $SU(2)$ algebra. The quasi-spin quantum number Q and its z-component $M_Q$ can be used to label many (m)-particle states. On the other hand, the SGA is $U(N)$ and the $Sp(N)$ subalgebra of $U(N)$ is ‘complementary’ to the quasi-spin $SU(2)$ algebra. The seniority quantum number v that labels the states according to $Sp(2j+1)$ algebra [v labels $Sp(N)$ irreps] corresponds to Q and similarly, particle number m that labels the irreps of $U(2j+1)$ corresponds to $M_Q$. Seniority quantum number gives number of particles that are not in zero coupled pairs. Thus, the classification of states given by $(Q,M_Q)$ with number non-conserving operators, is the same as the one given by the shell model chain $U(N)\supset Sp(N)$ which contains only number-conserving operators. More importantly, this solves the pairing Hamiltonian $H_p=-S_{+}{S}_{-}$ and allows one to extract m dependence of many particle matrix elements of a given operator. All these are well known [7].

All the single-j shell results extend to the multi-j shell situation i.e., for identical particles occupying several-j orbits, with $(2j+1)$ replaced by $2\mathrm{\Omega }={\sum }_j(2j+1)$. In this situation, v is called generalized seniority. A new result that appears for the multi-j situation is that there will be multiple quasi-spin (or $Sp(2\mathrm{\Omega })$) algebras with the pair-creation operator here being a sum of single-j pair-creation operators with different phases; $S_{+}={\sum }_j{\alpha }_j{S}_{+}(j)$; ${\alpha }_j=\pm 1$. Then, clearly with r number of j-orbits, there will be $2^{r-1}$ number of quasi-spin $SU(2)$ and the corresponding $2^{r-1}$$Sp(2\mathrm{\Omega })$ algebras. Section 2.1 and Section 2.2 give details of these multiple multi-orbit pairing $SU(2)$ and the complementary $Sp(N)$ algebras. The complementarity is established at the level of quadratic Casimir invariants of various group algebras that appear here. These multiple multi-j quasi-spin algebras (one for each ${\alpha }_j$ choice) play an important role in deciding selection rules for electric and magnetic multi-pole operators. This is the topic of Section 2.3. Correlations between realistic interactions and pairing interactions that correspond to various multiple pairing algebras are studied in Section 2.4. Applications of multi-j seniority describing data in certain nuclei is presented in Section 2.5 with results drawn from [7,70,71,72,73]. Finally, a summary is given in Section 2.6.

2.1. Multiple Multi-Orbit Pairing $SU(2)$ Algebras

Let us say there are m number of identical fermions (protons or neutrons) in j orbits $j_1$, $j_2$, …, $j_r$. Now, it is possible to define a generalized pair-creation operator $S_{+}$ as

$${\displaystyle S_{+}=\sum _j{\alpha }_j{S}_{+}(j);S_{+}(j)=\sum _{m>0}{(-1)}^{j-m}{a}_{jm}^{†}{a}_{j-m}^{†}=\frac{{\displaystyle \sqrt{2j+1}}}{2}{\left(a_j^{†}{a}_j^{†}\right)}^0.}$$

(1)

Here, ${\alpha }_j$ are free parameters and assumed to be real. The m used for number of particles should not be confused with the m in $jm$. Given the $S_{+}$ operator, the corresponding pair-annihilation operator $S_{-}$ is

$${\displaystyle S_{-}={\left(S_{+}\right)}^{†}=\sum _j{\alpha }_j{S}_{-}(j);S_{-}(j)={\left(S_{+}(j)\right)}^{†}=-\frac{{\displaystyle \sqrt{2j+1}}}{2}{\left({\tilde{a}}_j{\tilde{a}}_j\right)}^0.}$$

(2)

Note that $a_{jm}={(-1)}^{j-m}{\tilde{a}}_{j-m}$. The operators $S_{+}$, $S_{-}$ and $S_0$,

$${\displaystyle S_0=\frac{\widehat{n}-\mathrm{\Omega }}{2};\mathrm{\Omega }=\sum _j{\mathrm{\Omega }}_j,{\mathrm{\Omega }}_j=(2j+1)/2,}$$

(3)

form the generalized quasi-spin SU(2) algebra [hereafter called $S{U}_Q(2)$] only if

$${\alpha }_j^2=1\mathrm{for} \mathrm{all}j.$$

(4)

Note that $\widehat{n}={\sum }_{jm}{a}_{jm}^{†}{a}_{jm}$, is the number operator. With Equation (4) we have,

$$\left[S_0,S_{\pm }\right]=\pm S_{\pm },\left[S_{+},S_{-}\right]=2S_0.$$

(5)

Thus, in the multi-orbit situation for each

$$\left\{{\alpha }_{j_1},{\alpha }_{j_2},\dots ,{\alpha }_{j_r}\right\}$$

with ${\alpha }_{j_i}=\pm 1$ there is a $S{U}_Q(2)$ algebra defined by the operators in Equations (1)–(3). For example, say we have three j orbits $j_1$, $j_2$ and $j_3$. Then, without loss of generality we can choose ${\alpha }_1=+1$ and then $({\alpha }_2,{\alpha }_3)$ can take values $(+1,+1)$, $(+1,-1)$, $(-1,+1)$, $(-1,-1)$ giving four pairing $S{U}_Q(2)$ algebras. Similarly, with four j orbits, there will be eight $S{U}_Q(2)$ algebras and in general for r number of j orbits there will $2^{r-1}$ number of $S{U}_Q(2)$ algebras. The consequences of having these multiple pairing $S{U}_Q(2)$ algebras will be investigated in the following. Before going further let us mention that the $S{U}_Q(2)$ here should not be confused with the quantum group $S{U}_q(2)$ of Biedenharn and Macfarlane [74,75] (see also [76]).

Though well known, for later use and for completeness, some of the results of the $S{U}_Q(2)$ algebra are that the $S^2=S_{+}{S}_{-}-S_0+S_0^2$ operator and the $S_0$ operator in Equation (3) define the quasi-spin s and its z-component $m_s$ with $S^2\left|s{m}_s\right.⟩=s(s+1)\left|s{m}_s\right.⟩$ and $S_0\left|s{m}_s\right.⟩=m_s\left|s{m}_s\right.⟩$. Furthermore, from Equation (3) we have $m_s=(m-\mathrm{\Omega })/2$; the m here is number of particles. Moreover, it is possible to introduce the so called seniority quantum number v such that $s=(\mathrm{\Omega }-v)/2$ giving,

$$\begin{array}{ccc}\hfill s& =& \left(\mathrm{\Omega }-v\right)/2,m_s=\left(m-\mathrm{\Omega }\right)/2,\hfill \\ \hfill v& =& m,m-2,\dots ,0\mathrm{or}1\mathrm{for}m\le \mathrm{\Omega }\hfill \\ & =& \left(2\mathrm{\Omega }-m\right),\left(2\mathrm{\Omega }-m\right)-2,..,0\mathrm{or}1\mathrm{for}m\ge \mathrm{\Omega }.\hfill \end{array}$$

(6)

Note that the total number of single particle states is $N=2\mathrm{\Omega }$ and therefore for $m>\mathrm{\Omega }$ one has fermion holes rather than particles. With the pairing Hamiltonian $H_p$ given by

$$H_p=-G{S}_{+}{S}_{-}$$

(7)

where G being the pairing strength, the following results will provide a meaning to the seniority quantum number “v”,

$$\begin{array}{ccc}\hfill {⟨S_{+}{S}_{-}⟩}^{s{m}_s}& =\hfill & {⟨S_{+}{S}_{-}⟩}^{mv}=⟨m,v,\beta \mid S_{+}{S}_{-}\mid m,v,\beta ⟩\hfill \\ & =\hfill & \frac{1}{4}(m-v)(2\mathrm{\Omega }-m-v+2),\hfill \end{array}$$

(8)

$$\left|m,v,\beta ⟩\right.=\sqrt{\frac{{\displaystyle \left(\mathrm{\Omega }-v-p\right)!}}{{\displaystyle \left(\mathrm{\Omega }-v\right)!p!}}}{\left(S_{+}\right)}^{\frac{{\displaystyle m-v}}{{\displaystyle 2}}}\left|v,v,\beta ⟩\right.;p=\frac{(m-v)}{2}.$$

(9)

with these, it is clear that for a given v and m there are $(m-v)/2$ zero coupled pairs in eigenstates of $H_p$. Thus, v gives the number of particles that are not coupled to angular momentum zero. In Equation (9), $\beta$ is an extra label that is required to specify a ${(j_1,j_2,\dots ,j_r)}^m$ state completely.

Before going further, an important result (to be used later) that follows from Equations (1) and (2) is,

$$\begin{array}{ccc}\hfill 4S_{+}{S}_{-}& =& {\displaystyle 4\sum _j{S}_{+}(j)S_{-}(j)+\sum _{j_1>j_2}{\alpha }_{j_1}{\alpha }_{j_2}}\hfill \\ & \times & {\displaystyle \sum _k\sqrt{2k+1}\left\{{\left[{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}^k{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}^k\right]}^0+{\left[{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}^k{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}^k\right]}^0\right\}.}\hfill \end{array}$$

(10)

2.2. Multiple Multi-Orbit Complementary $Sp(N)$ Algebras

In the ${(j_1,j_2,\dots ,j_r)}^m$ space, often it is more convenient to start with the $U(N)$ algebra generated by the one-body operators $u_q^k(j_1,j_2)$,

$$u_q^k(j_1,j_2)={\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k.$$

(11)

The total number of generators is obviously $N^2$ and $N=2\mathrm{\Omega }$. All m fermion states will be antisymmetric and therefore belong uniquely to the irrep $\left\{1^m\right\}$ of $U(N)$. The quadratic Casimir invariant of $U(N)$ is easily given by

$${\displaystyle C_2(U(N))=\sum _{j_1,j_2}{(-1)}^{j_1-j_2}\sum _k{u}^k(j_1,j_2)·u^k(j_2,j_1),}$$

(12)

with eigenvalues

$${⟨C_2(U(N))⟩}^m=m(N+1-m);N=2\mathrm{\Omega }.$$

(13)

Equation (13) can be proved by writing the one and two-body parts of $C_2(U(N))$ and then showing that the one-body part is $2\mathrm{\Omega }\widehat{n}$ and the two-body part will have two-particle matrix elements diagonal with all of them having value $-2$.

More importantly, $U(N)\supset Sp(N)$ and the $Sp(N)$ algebra is generated by the $N(N+1)/2$ number of generators $u_q^k(j,j)$ with k=odd only and $V_q^k(j_1,j_2)$, $j_1>j_2$ where

$$V_q^k(j_1,j_2)={\left[\mathcal{N}(j_1,j_2,k)\right]}^{1/2}\left[{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k+X(j_1,j_2,k){\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^k\right],{\left\{X(j_1,j_2,k)\right\}}^2=1.$$

(14)

The quadratic Casimir invariant of $Sp(N)$ is given by,

$${\displaystyle C_2(Sp(N))=2\sum _j\sum _{k=odd}{u}^k(j,j)·u^k(j,j)+\sum _{j_1>j_2;k}{V}^k(j_1,j_2)·V^k(j_1,j_2).}$$

(15)

The $Sp(N)$ algebra will be complementary to the quasi-spin $SU(2)$ algebra defined for a given set of $\left\{{\alpha }_{j_1},{\alpha }_{j_2},\dots ,{\alpha }_{j_r}\right\}$ provided

$$\mathcal{N}(j_1,j_2,k)={(-1)}^{k+1}{\alpha }_{j_1}{\alpha }_{j_2},X(j_1,j_2,k)={(-1)}^{j_1+j_2+k}{\alpha }_{j_1}{\alpha }_{j_2}.$$

(16)

Using Equations (12) and (14)–(16) along with Equation (10) it is easy to derive the following important relation,

$$C_2(U(N))-C_2(Sp(N))=4S_{+}{S}_{-}-\widehat{n}.$$

(17)

Now, Equations (8), (13) and (17) will give

$${⟨C_2(Sp(N)⟩}^{m,v}=v(2\mathrm{\Omega }+2-v)$$

(18)

and this proves that the seniority quantum number v corresponds to the $Sp(N)$ irrep $⟨1^v⟩$.

In summary, given the $S{U}_Q(2)$ algebra generated by $\{S_{+},S_{-},S_0\}$ operators for a given set of $\left\{{\alpha }_{j_1},{\alpha }_{j_2},\dots ,{\alpha }_{j_r}\right\}$ with ${\alpha }_{j_i}=+1$ or $-1$, there is a complementary (↔) $Sp(N)$ subalgebra of $U(N)$ generated by

$$\begin{array}{c}Sp(N):u^k(j,j)={\left(a_j^{†}{\tilde{a}}_j\right)}_q^{k}withk=odd,\hfill \\ V_q^k(j_1,j_2)={\left[{(-1)}^{k+1}{\alpha }_{j_1}{\alpha }_{j_2}\right]}^{1/2}\left[{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k+{(-1)}^{j_1+j_2+k}{\alpha }_{j_1}{\alpha }_{j_2}{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^k\right]with{j}_1>j_2.\hfill \end{array}$$

(19)

As the $Sp(N)$ generators are one-body operators and that $Sp(N)\leftrightarrow S{U}_Q(2)$, there will be special selection rules for electro-magnetic transition operators connecting m fermion states with good seniority. These are well known for a special choice of $\alpha$’s [7] and their relation to the multiple $SU(2)$ algebras or equivalently to the $\left\{{\alpha }_{j_1},{\alpha }_{j_2},\dots ,{\alpha }_{j_r}\right\}$ set is the topic of the next Section.

2.3. Selection Rules and Matrix Elements for Electro-Magnetic Transitions

Electro-magnetic (EM) operators are essentially one-body operators (two and higher-body terms are usually not considered). In order to derive selection rules and matrix elements for allowed transitions, let us consider the commutator of $S_{+}$ with ${\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k$. Firstly we have easily,

$$\left[S_{+}(j),{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k\right]=-{\delta }_{j,j_2}{\left(a_{j_1}^{†}{a}_{j_2}^{†}\right)}_q^k.$$

(20)

This gives

$$\begin{array}{c}\left[S_{+},{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k+X{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^k\right]\hfill \\ =-{\alpha }_{j_2}{\left(a_{j_1}^{†}{a}_{j_2}^{†}\right)}_q^k\left\{1-X{\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+k}\right\}\hfill \\ =0\mathrm{if}X={\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+k}\hfill \\ \ne 0\mathrm{if}X=-{\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+k}.\hfill \end{array}$$

(21)

Note that the commutator being zero implies that the operator is a scalar $T_0^0$ with respect to $S{U}_Q(2)$ and otherwise it will be a quasi-spin vector $T_0^1$. In either situation the $S_z$ component of T is zero as a one-body operator can not change particle number. Thus, for $j_1\ne j_2$ we have

$$\begin{array}{c}{U}_q^k(j_1,j_2)={\mathcal{N}}_u\left\{{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k+{\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+k}{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^k\right\}\to T_0^0,\hfill \\ W_q^k(j_1,j_2)={\mathcal{N}}_w\left\{{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^k-{\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+k}{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^k\right\}\to T_0^1.\hfill \end{array}$$

(22)

Here ${\mathcal{N}}_u$ and ${\mathcal{N}}_w$ are some constants. Similarly, for $j_1=j_2$ we have

$$\begin{array}{c}{\left(a_j^{†}{\tilde{a}}_j\right)}_q^k\mathrm{with}k\mathrm{odd}\to T_0^0,\hfill \\ {\left(a_j^{†}{\tilde{a}}_j\right)}_q^k\mathrm{with}k\mathrm{even}\to T_0^1\mathrm{except\; for}k=0.\hfill \end{array}$$

(23)

The results in Equation (22) are easy to understand as $U_q^k$ in Equation (22) is to within a factor same as $V_q^k$ of Equation (19) and therefore a generator of $Sp(N)$. Hence it cannot change the v quantum number of a m-particle state. Moreover, as $Sp(N)\leftrightarrow S{U}_Q(2)$, clearly $U_q^k$ will be a $S{U}_Q(2)$ scalar. Similarly turning to Equation (23), as ${\left(a_j^{†}{\tilde{a}}_j\right)}_q^k$ with k odd are generators of $Sp(N)$ and hence they are also $S{U}_Q(2)$ scalars.

The general form of electric and magnetic multi-pole operators $T^{EL}$ and $T^{ML}$ respectively with $L=1,2,3,\dots$ is, with $X=E$ or M,

$$\begin{array}{ccc}\hfill T_q^{XL}& =& {\displaystyle \sum _{j_1,j_2}{ϵ}_{j_1,j_2}^{XL}{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^L}\hfill \\ & =& {\displaystyle \sum _j{ϵ}_{j,j}^{XL}{\left(a_j^{†}{\tilde{a}}_j\right)}_q^L+\sum _{j_1>j_2}{ϵ}_{j_1,j_2}^{XL}\left[{\displaystyle {\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^L+\frac{{ϵ}_{j_2,j_1}^{XL}}{{ϵ}_{j_1,j_2}^{XL}}{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^L}\right].}\hfill \end{array}$$

(24)

Therefore, ${ϵ}_{j_2,j_1}^{XL}/{ϵ}_{j_1,j_2}^{XL}$ along with Equations (22) and (23) will determine the selection rules. Then,

$$\begin{array}{c}{\displaystyle \frac{{ϵ}_{j_2,j_1}^{XL}}{{ϵ}_{j_1,j_2}^{XL}}={\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+L}\to T_0^0\mathrm{w.r.t.}S{U}_Q(2),}\hfill \\ {\displaystyle \frac{{ϵ}_{j_2,j_1}^{XL}}{{ϵ}_{j_1,j_2}^{XL}}=-{\alpha }_{j_1}{\alpha }_{j_2}{(-1)}^{j_1+j_2+L}\to T_0^1\mathrm{w.r.t.}S{U}_Q(2).}\hfill \end{array}$$

(25)

Thus, the $S{U}_Q(2)$ tensorial nature of $T^{XL}$ depends on the ${\alpha }_i$ choice. For $T_0^0$ we have $v\to v$ and for $T_0^1$ we have $v\to v,v\pm 2$ transitions. It is well known [7,16] that for $T^{EL}$ and $T^{ML}$ operators,

$${\displaystyle \frac{{ϵ}_{j_2,j_1}^{EL}}{{ϵ}_{j_1,j_2}^{EL}}=-{(-1)}^{{\ell }_1+{\ell }_2+j_1+j_2+L},\frac{{ϵ}_{j_2,j_1}^{ML}}{{ϵ}_{j_1,j_2}^{ML}}={(-1)}^{{\ell }_1+{\ell }_2+j_1+j_2+L}.}$$

(26)

In Equation (26) ${\ell }_i$ is the orbital angular momentum of the $j_i$ orbit. Therefore, combining results in Equations (22)–(26) together with parity selection rule will give seniority selection rules, in the multi-orbit situation, for electro-magnetic transition operators when the observed states carry seniority quantum number as a good quantum number. The selection rules with the choice ${\alpha }_{j_i}={(-1)}^{{\ell }_i}$ for all i are as follows.

• $T^{EL}$ with L even will be $T_0^1$ w.r.t. $S{U}_Q(2)$.
• $T^{EL}$ with L odd will be $T_0^1$ w.r.t. $S{U}_Q(2)$. However, if all j orbits have same parity, then $T^{EL}$ with L odd will not exist. Therefore here, for the transitions to occur, we need minimum two orbits of different parity.
• $T^{ML}$ with L odd will be $T_0^0$ w.r.t. $S{U}_Q(2)$.
• $T^{ML}$ with L even will be $T_0^0$ w.r.t. $S{U}_Q(2)$. However, if all j orbits have same parity, then $T^{ML}$ with L even will not exist. Therefore here, for the transitions to occur, we need minimum two orbits of different parity.
• For $T_0^0$ only $v\to v$ transitions are allowed while for $T_0^1$ both $v\to v$ and $v\to v\pm 2$ transition are allowed. For both m is not changed.

The above rules were given already by Arvieu and Moszkowski [16] and described by Talmi [7]. As stated by Arvieu and Moszkowski, they have introduced the choice ${\alpha }_i={(-1)}^{{\ell }_i}$ “for convenience” and then found that it will make surface delta interaction a $S{U}_Q(2)$ scalar. It is important to note that for $S{U}_Q(2)$ generated by ${\alpha }_i\ne {(-1)}^{{\ell }_i}$, the above rules (1)–(4) will be violated and then Equation (25) has to be applied. This is a new result and it was reported first in [65] (see also [77]). A similar result applies to interacting boson models as presented in Section 3.

Applying the Wigner–Eckart theorem for the many particle matrix elements in good seniority states, the number dependence of the matrix elements of $T_0^0$ and $T_0^1$ operators is easily determined. For fermions we simply need $SU(2)$ Wigner coefficients [78]. Results for fermion systems are given for example in [7]. For completeness we will give these here,

$$\begin{array}{c}⟨m,v,\alpha \mid T_0^0\mid m,v^{\prime },\beta ⟩={\delta }_{v,v^{\prime }}⟨v,v,\alpha \mid T_0^0\mid v,v,\beta ⟩,\hfill \\ {\displaystyle ⟨m,v,\alpha \mid T_0^1\mid m,v,\beta ⟩=\frac{\mathrm{\Omega }-m}{\mathrm{\Omega }-v}⟨v,v,\alpha \mid T_0^1\mid v,v,\beta ⟩,}\hfill \\ {\displaystyle ⟨m,v,\alpha \mid T_0^1\mid m,v-2,\beta ⟩=\sqrt{{\displaystyle \frac{(2\mathrm{\Omega }-m-v+2)(m-v+2)}{4(\mathrm{\Omega }-v+1)}}}⟨v,v,\alpha \mid T_0^1\mid v,v-2,\beta ⟩.}\hfill \end{array}$$

(27)

Before turning to applications, within the shell model context it is necessary to conform that a realistic pairing operator do respect the condition ${\alpha }_i={(-1)}^{{\ell }_i}$. In order to test this, we will use correlation coefficient between operators as defined in French’s spectral distribution method [79].

2.4. Correlation between Operators and Phase Choice in the Pairing Operator

Given an operator $\mathcal{O}$ acting in m particle spaces and assumed to be real, its m particle trace is ${⟨⟨\mathcal{O}⟩⟩}^m={\sum }_{\alpha }⟨m,\alpha \mid \mathcal{O}\mid m,\alpha ⟩$ where $\left|m,\alpha \right.⟩$ are m-particle states. Similarly, the m-particle average is ${⟨\mathcal{O}⟩}^m={\left[d(m)\right]}^{-1}{⟨⟨\mathcal{O}⟩⟩}^m$ where $d(m)$ is m-particle space dimension. In m particle spaces it is possible to define, using the spectral distribution method of French [79,80], a geometry [80,81] with norm (or size or length) of an operator $\mathcal{O}$ given by $\mid \mid \mathcal{O}\mid {\mid }_m=\sqrt{{⟨\tilde{\mathcal{O}}\tilde{\mathcal{O}}⟩}^m}$; $\tilde{\mathcal{O}}$ is the traceless part of $\mathcal{O}$. With this, given two operators ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$, the correlation coefficient

$${\displaystyle \zeta ({\mathcal{O}}_1,{\mathcal{O}}_2)=\frac{{⟨\widetilde{{\mathcal{O}}_1}\widetilde{{\mathcal{O}}_2}⟩}^m}{\mid \mid {\mathcal{O}}_1\mid {\mid }_m\mid \mid {\mathcal{O}}_2\mid {\mid }_m},}$$

(28)

gives the cosine of the angle between the two operators. Thus, ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$ are same within a normalization constant if $\zeta =1$ and they are orthogonal to each other if $\zeta =0$ [79,81]. The most recent application of norms and correlation coefficients, defined above, to understand the structure of effective interactions is due to Draayer et al. [82,83,84].

Clearly, in a given shell model space, given a realistic effective interaction Hamiltonian H, the $\zeta$ in Equation (28) can be used as a measure for its closeness to the pairing Hamiltonian $H_P=S_{+}{S}_{-}$ with $S_{+}$ defined by Equation (1) for a given set of ${\alpha }_j$’s. Evaluating $\zeta (H,H_P)$ for all possible ${\alpha }_j$ sets, it is possible to identify the ${\alpha }_j$ set that gives maximum correlation of $H_p$ with H. Following this, $\zeta (H,H_P)$ is evaluated for effective interactions in (${}^0{f}_{7/2}$, ${}^0{f}_{5/2}$, ${}^1{p}_{3/2}$, ${}^1{p}_{1/2}$), (${}^0{f}_{5/2}$, ${}^1{p}_{3/2}$, ${}^1{p}_{1/2}$, ${}^0{g}_{9/2}$) and (${}^0{g}_{7/2}$, ${}^1{d}_{5/2}$, ${}^1{d}_{3/2}$, ${}^2{s}_{1/2}$, ${}^0{h}_{11/2}$) spaces using GXPF1 [85], JUN45 [86] and jj55-SVD [87] interactions respectively. As we are considering only identical particle systems and also as we are interested in studying the correlation of H’s with $H_P$’s, only the $T=1$ part of the interactions is considered (dropped are the $T=0$ two-body matrix elements and also the single particle energies). With this $\zeta (H,H_P)$ are calculated in the three spaces for different values of the particle number m and for all possible choices of ${\alpha }_j$’s defining $S_{+}$ and hence $H_P$. Results are given in Table 1. It is clearly seen that the choice ${\alpha }_j={(-1)}^{{\ell }_i}$ gives the largest value for $\zeta$ and hence it should be the most preferred choice. This is a significant result justifying the choice made by AM [16], although the magnitude of $\zeta$ is not more than $0.3$. Thus, realistic H are far, on a global m-particle space scale, from the simple pairing Hamiltonian. However, it is likely that the generalized pairing quasi-spin or sympletic symmetry may be an effective symmetry for low-lying state and some special high-spin states [12]. Evidence for this will be discussed in Section 2.5.

Table 1. Correlation coefficient $\zeta$ between the $T=1$ part of a realistic interaction and the pairing Hamiltonian $H_p$ for various particle numbers (m) in three different shell model spaces. The single particle (sp) orbits for these three spaces are given in column #1. The range of m values used is given in column #3. The phases ${\alpha }_j$ for each orbit in the generalized pair-creation operator are given in column #4 (the order is the same as the sp orbits listed in column #1). The variation in $\zeta$ with particle number m is given in column #5. Results for the phase choices that give $\left|\zeta \right|<0.15$ for all m values are not shown in the table. See Section 2.4 for further discussion.

Sp Orbits	Interaction	m	${\mathit{\alpha }}_{\mathit{j}}$	$\mathit{\zeta }(\mathit{H},{\mathit{H}}_{\mathit{p}})$
0$g_{7/2}$, 1$d_{5/2}$, 1$d_{3/2}$, 2$s_{1/2}$, 0$h_{11/2}$	jj55-SVD	2–30	$(+,+,+,+,-)$	$0.33$–$0.11$
			$(+,+,+,-,-)$	$0.26$–$0.09$
			$(+,+,-,+,-)$	$0.17$–$0.06$
0$f_{5/2}$, 1$p_{3/2}$, 1$p_{1/2}$, 0$g_{9/2}$	jun45	2–20	$(+,+,+,-)$	$0.42$–$0.21$
			$(+,+,-,-)$	$0.27$–$0.13$
			$(+,-,+,-)$	$0.15$–$0.07$
0$f_{7/2}$, 1$p_{3/2}$, 0$f_{5/2}$, 1$p_{1/2}$	gxpf1	2–18	$(+,+,+,+)$	$0.36$–$0.33$
			$(+,+,+,-)$	$0.22$–$0.20$

Before turning to applications of multiple pairing algebras, it is useful to add that in principle the spectral distribution method can be used to study the mixing of seniority quantum number in the eigenstates generated by a given Hamiltonian by using the so called partial variances [11,79]. The $v_i\to v_f$ partial variances, with $v_i\ne v_f$, are defined by

$${\displaystyle {\sigma }^2(m,v_i\to m,v_f)={\left[d(m,v_i)\right]}^{-1}\sum _{\alpha ,\beta }{\left|⟨m,v_f,\beta \mid H\mid m,v_i,\alpha ⟩\right|}^2.}$$

(29)

In Equation (29), $d(m,v)$ is the dimension of the $(m,v)$ space. It is important to note that the partial variances can be evaluated without constructing the H matrices but by using the propagation equations. These are available both for fermion and boson systems; see [88,89,90]. However, propagation equations for the more realistic ${\sigma }^2(m,v_i,J\to m,v_f,J)$ partial variances are not yet available.

2.5. Applications

In order to understand the variation of $B(EL)$ [similarly $B(ML$)] for fermion systems, for states with good seniority, some numerical examples are shown in Figure 1 and Figure 2. Firstly, consider an electric multi-pole (of multi-polarity L) transition between two states with same v value. Then, the $B(EL)\propto {[(\mathrm{\Omega }-m)/(\mathrm{\Omega }-v)]}^2$ as seen from the second equation in Equation (27). Note that, with ${\alpha }_{j_i}={(-1)}^{{\ell }_i}$, the $T^{EL}$ operators are $T_0^1$ w.r.t. $S{U}_Q(2)$. Assuming $v=2$, variation of $B(EL)$ with particle number m is shown for three different values of $\mathrm{\Omega }$ and m varying from 2 to $2\mathrm{\Omega }-2$ in Figure 1. It is clearly seen that $B(EL)$ decrease up to mid-shell and then again increases, i.e., $B(EL)$ vs m is an inverted parabola. The parabolas shift depending on the value of $\mathrm{\Omega }$. In addition, shown in Figure 1 is also the variation with m for states with $v=1$ and 4. Assuming the ground $0^{+}$ and first excited $2^{+}$ states of a nucleus belong to $v=0$ and $v=2$ respectively, $B(E2;2^{+}\to 0^{+})$ variation with particle number is calculated using the third equation in Equation (27) giving $B(E2)\propto (2\mathrm{\Omega }-m-v+2)(m-v+2)/4(\mathrm{\Omega }-v+1)$. The variation of $B(E2)$ is that it will increase up to mid-shell and then decrease; i.e., the $B(E2;2^{+}\to 0^{+})$ vs m is a parabola. This is shown in Figure 2 for three different values of $\mathrm{\Omega }$ and again one sees a shift in the parabolas with $\mathrm{\Omega }$ changing. Similar is the result for more general $B(EL)$ transitions, assuming that the transitions are from states with a v value to those with $v-2$; see the lower panel in Figure 2.

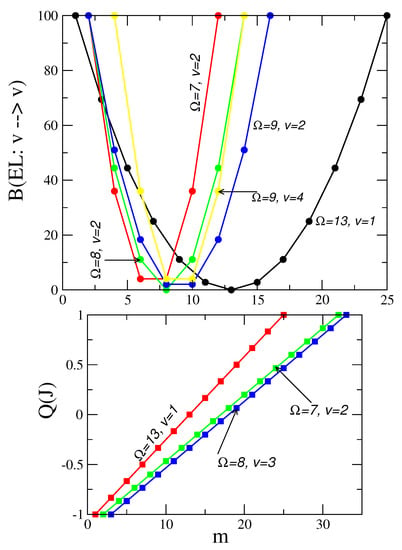
Figure 1. Upper panel shows variation of $B(EL)$ with particle number m for five different values of $\mathrm{\Omega }$ and seniority v for $v\to v$ transitions. Similarly, lower panel shows variation of quadrupole moment $Q(J)$ with particle number m and for three different values of $\mathrm{\Omega }$. The quadrupole moments are for states with seniority v. These results, useful in shell model description, are obtained by applying the second formula in Equation (27). The $B(EL)$ values are scaled such that the maximum value is 100 and similarly, $|Q(J)|$ is scaled such that the maximum value is 1. Thus, the $B(EL)$ and $Q(J)$ in the figure are not in any units. See Section 2.5 for further discussion.

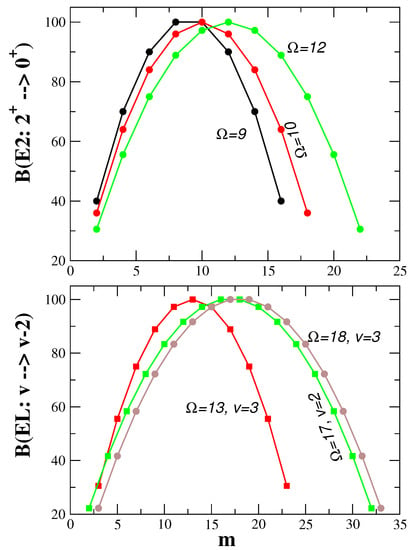
Figure 2. Upper panel shows variation of $B(E2;v=2,2^{+}\to v=0,0^{+})$ with particle number m for three different values of $\mathrm{\Omega }$. Similarly, lower panel shows variation of $B(EL)$ with particle number m for transitions between states with v to states with $v-2$. These results, useful in shell model description, are obtained by applying the third formula in Equation (27). The $B(EL)$ and $B(E2)$ values are scaled such that the maximum value is 100 and therefore they are not in any units. See Section 2.5 for further discussion.

First examples for the goodness of generalized seniority in nuclei are Sn isotopes. Note that for Sn isotopes the valence nucleons are neutrons with Z = 50, a magic number. From Equation (8) it is easy to see that the spacing between the first $2^{+}$ state (it will have $v=2$) and the ground state $0^{+}$ (it will have $v=0$) will be independent of m, i.e., the spacing should be same for all Sn isotopes and this is well verified by experimental data [7]. Going beyond this, recently $B(E2;2_1^{+}\to 0_1^{+})$ data for ${}^{104}$Sn to ${}^{130}$Sn are analyzed using the results in Equation (27), i.e., the results in Figure 2. Data show a dip at ${}^{116}$Sn and they are close to adding two displaced parabolas; see Figure 1 in [71]. This is understood by employing ${}^0{g}_{7/2}$, ${}^1{d}_{5/2}$, ${}^1{d}_{3/2}$ and ${}^2{s}_{1/2}$ orbits for neutrons in ${}^{104}$Sn to ${}^{116}$Sn with $\mathrm{\Omega }=10$ and ${}^{100}$Sn core. Similarly, ${}^1{d}_{5/2}$, ${}^1{d}_{3/2}$, ${}^2{s}_{1/2}$ and ${}^0{h}_{11/2}$ orbits with $\mathrm{\Omega }=12$ and ${}^{108}$Sn core for ${}^{116}$Sn to ${}^{130}$Sn. Then, the $B(E2)$ vs m structure follows from Figure 2 by shifting appropriately the centers of the two parabolas in the figure and defining properly the beginning and end points. It is also shown in [71] that shell model calculations with an appropriate effective interaction in the above orbital spaces reproduce the results from the simple formulas given by seniority description and the experimental data.

In addition to $B(E2;2^{+}\to 0^{+})$ data, there is now good data available for $B(E2)$’s and $B(E1)$’s for some high-spin isomer states in even Sn isotopes. These are: $B(E2;{10}^{+}\to 8^{+})$ data for ${}^{116}$Sn to ${}^{130}$Sn and $B(E2;{15}^{-}\to {13}^{-})$ for ${}^{120}$Sn to ${}^{128}$Sn and $B(E1;{13}^{-}\to {12}^{+})$ in ${}^{120}$Sn to ${}^{126}$Sn. The states ${10}^{+}$ and $8^{+}$ are interpreted to be $v=2$ states while ${15}^{-}$, ${13}^{-}$ and ${12}^{+}$ are $v=4$ states. Therefore, all these transitions are $v\to v$ transitions and their variation with m will be as shown in Figure 1. This is well verified by data [70] by assuming that the active sp orbits are ${}^0{h}_{11/2}$, ${}^1{d}_{3/2}$ and ${}^2{s}_{1/2}$ with $\mathrm{\Omega }=9$ (see also Figure 1 with $\mathrm{\Omega }=9$). The results with $\mathrm{\Omega }=8$ and $\mathrm{\Omega }=7$, obtained by dropping ${}^2{s}_{1/2}$ and ${}^1{d}_{3/2}$ orbits respectively, are not in good accord with the data. In all this and in the analysis in [72,73], it is assumed that the $\alpha$ and $\beta$ in Equation (27) are independent of m, i.e., they remain same for a given isotopic chain.

In summary, both the $B(E2;2^{+}\to 0^{+})$ data and the $B(E2)$ and $B(E1)$ data for high-spin isomer states are explained by assuming goodness of generalized seniority with the choice ${\beta }_j={(-1)}^{{\ell }_j}$ but with effective $\mathrm{\Omega }$ values. Although the sp orbits (and hence $\mathrm{\Omega }$ values) used are different for the low-lying levels and the high-spin isomer states, the good agreements between data and effective generalized seniority description on one hand and the correlation coefficients presented in Section 2.4 on the other show that for Sn isotopes generalized seniority is possibly an ‘emergent symmetry’or a “partial dynamical symmetry (PDS)” (see [14] for PDS). Let us add that although detailed nuclear structure calculations are possible for Sn isotopes [91], generalized seniority gives simple explanation for trends seen in some of the observables.

Going beyond Sn isotopes, with some further assumptions, near constancy of the energies of $2_1^{+}$ and $3_1^{-}$ levels and also $B(E2;2_1^{+}\to 0_1^{+})$ and $B(E3;3_1^{-}\to 0_1^{+})$ using Equation (27) for $B(EL)$’s in Cd and Te isotopes are explained well [72]. In this study, neutrons in ${}^0{g}_{7/2}$, ${}^0{h}_{11/2}$, ${}^1{d}_{5/2}$, ${}^1{d}_{3/2}$ and ${}^2{s}_{1/2}$ orbits in various combinations, depending on their occupancy, giving $\mathrm{\Omega }=9-12$ are employed. Further, more recently Equation (27) is applied successfully to explain empirical data on g-factors, quadrupole moments and $B(E2)$ values for the $13/2^{+}$, ${12}^{+}$ and $33/2^{+}$ isomers in Hg, Pb and Po isotopes. See Figure 1 for variation of quadrupole moments $Q(J)$ with particle number m [this is obtained using the second formula in Equation (27)] and the decrease as we move towards mid-shell region is seen in data [73]. In addition, $B(E2;2_1^{+}\to 0_1^{+})$ values in these isotopes are also explained [73]. In this study used are Equation (27) and neutrons in the single particle orbits ${}^0{h}_{9/2}$, ${}^0{i}_{13/2}$, ${}^1{f}_{7/2}$, ${}^2{p}_{3/2}$ and ${}^1{f}_{5/2}$ giving $\mathrm{\Omega }=13$, 17 and 18 depending on the occupancy of these orbits [73].

2.6. Summary

In this section presented are results on multiple multi-orbit pairing $SU(2)$ and the complementary $SO(N)$ algebras in $j-j$ coupling shell model for identical nucleons. The relationship between quasi-spin tensorial nature of one-body transition operators and the phase choices in the multi-orbit pair-creation operator is presented. As pointed out in Section 2.1 and Section 2.2, some of the results here are known before for some special situations. Selection rules for EM transition strengths as determined by multiple multi-orbit pairing algebras are presented in Section 2.3. In Section 2.4, results for the correlation coefficient between the pairing operator with different choices for phases in the generalized pair-creation operator and realistic effective interactions are presented. It is found that the choice advocated by AM [16] gives maximum correlation though its absolute value, no more than 0.3, is small. Applications using particle number variation in electromagnetic transition strengths, of multiple pairing algebras are briefly discussed in Section 2.5 drawing from the recent analysis by Maheswari and Jain [70,71,72,73]. Generalized seniority with phase choice advocated by AM appear to describe $B(E2)$ and $B(E1)$ data in Sn isotopes both for low-lying states and high-spin isomeric states. This agreement also appears to extend to Cd, Te, Hg, Pb and Po isotopes. Though deviations from the results obtained using AM choice is a signature for multiple multi-orbit pairing algebras, direct experimental evidence for the multiple pairing algebras is not yet available. This requires examination of data where EM selection rules are violated.

3. Multiple Multi-Orbit Pairing Algebras in Interacting Boson Models: Identical Boson Systems

3.1. Multiple Quasi-Spin $S{U}_Q(1,1)$ and Complementary $SO(\mathcal{N})$ Pairing Algebras

Going beyond the shell model, also within the interacting boson models, i.e., for example in $sd$, $sp$, $sdg$ and $sdpf$ IBM’s, again it is possible to have multiple pairing algebras as we have several ℓ orbits in these models but with bosons [21,22,23,55,56,92,93,94]. Here, as is well known, the pairing algebra is $S{U}_Q(1,1)$ instead of $S{U}_Q(2)$ [95]. Let us consider IBM with identical bosons carrying angular momentum ${\ell }_1$, ${\ell }_2$, …, ${\ell }_r$ and the parity of an ${\ell }_i$ orbit is ${(-1)}^{{\ell }_i}$. Now, again it is possible to define a generalized boson pair-creation operator $S_{+}^B$ as

$${\displaystyle S_{+}^B=\sum _{\ell }{\beta }_{\ell }{S}_{+}^B(\ell );S_{+}^B(\ell )=\frac{1}{2}\sum _m{(-1)}^m{b}_{\ell m}^{†}{b}_{\ell -m}^{†}=\frac{{\displaystyle \sqrt{2\ell +1}}}{2}{(-1)}^{\ell }{\left(b_{\ell }^{†}{b}_{\ell }^{†}\right)}^0=\frac{1}{2}{b}_{\ell }^{†}·b_{\ell }^{†}.}$$

(30)

Here, ${\beta }_{\ell }$ are free parameters and assumed to be real. Given the $S_{+}^B$ operator, the corresponding pair-annihilation operator $S_{-}^B$ is

$${\displaystyle S_{-}^B={\left(S_{+}^B\right)}^{†}=\sum _{\ell }{\beta }_{\ell }{S}_{-}^B(\ell );S_{-}^B(\ell )={\left(S_{+}^B(\ell )\right)}^{†}={(-1)}^{\ell }\frac{{\displaystyle \sqrt{2\ell +1}}}{2}{\left({\tilde{b}}_{\ell }{\tilde{b}}_{\ell }\right)}^0=\frac{1}{2}{\tilde{b}}_{\ell }·{\tilde{b}}_{\ell }.}$$

(31)

Note that $b_{\ell m}={(-1)}^{l-m}{\tilde{b}}_{\ell -m}$. The operators $S_{+}^B$, $S_{-}^B$ and $S_0^B$, with ${\widehat{n}}^B={\sum }_{\ell m}{a}_{\ell m}^{†}{a}_{\ell m}$ the number operator,

$${\displaystyle S_0^B=\frac{{\widehat{n}}^B+{\mathrm{\Omega }}^B}{2};{\mathrm{\Omega }}^B=\sum _{\ell }{\mathrm{\Omega }}_{\ell }^B,{\mathrm{\Omega }}_{\ell }^B=(2\ell +1)/2}$$

(32)

form the generalized quasi-spin SU(1,1) algebra [hereafter called $S{U}_Q^B(1,1)$—the $S{U}_Q(1,1)$ here should not be confused with the quantum group $S{U}_q(1,1)$ of Kulish [96] only if

$${\beta }_{\ell }^2=1\mathrm{for\; all}\ell .$$

(33)

with Equation (33) we have,

$$\left[S_0^B,S_{\pm }^B\right]=\pm S_{\pm }^B,\left[S_{+}^B,S_{-}^B\right]=-2S_0^B.$$

(34)

Thus, in the multi-orbit situation for each

$$\left\{\beta \right\}=\left\{{\beta }_{{\ell }_1},{\beta }_{{\ell }_2},\dots ,{\beta }_{{\ell }_r}\right\};{\beta }_{{\ell }_i}=\pm 1,$$

(35)

there is a $S{U}_Q^B(1,1)$ algebra defined by the operators in Equations (30)–(32). Thus, in general for r number of ℓ orbits there will $2^{r-1}$ number of $S{U}_Q^B(1,1)$ algebras. Let us mention that ${(S^B)}^2={(S_0^B)}^2-S_0^B-S_{+}^B{S}_{-}^B$ and $S_0^B=({\widehat{n}}^B+{\mathrm{\Omega }}^B)/2$ provide the quasi-spin s and the $S_0$ quantum number $m_s$ giving the basis $\left|s,m_s\right.⟩$ [56,92],

$$\begin{array}{c}{(S^B)}^2\left|s,m_s,\gamma \right.⟩=s(s-1)\left|s,m_s,\gamma \right.⟩,S_0\left|s,m_s,\gamma \right.⟩=m_s\left|s,m_s,\gamma \right.⟩;\hfill \\ m_s=s,s+1,s+2,\dots \hfill \\ \Rightarrow \hfill \\ s=({\mathrm{\Omega }}^B+{\omega }^B)/2,m_s=({\mathrm{\Omega }}^B+N^B)/2,{\omega }^B=N^B,N^B-2,\cdots ,0or1,\hfill \\ S_{+}^B{S}_{-}^B\left|s,m_s,\gamma \right.⟩=S_{+}^B{S}_{-}^B\left|N^B,{\omega }^B,\gamma \right.⟩=\frac{1}{4}(N^B-{\omega }^B)({\omega }^B+N^B+2{\mathrm{\Omega }}^B-2)\left|N^B,{\omega }^B,\gamma \right.⟩.\hfill \end{array}$$

(36)

Here, $N^B$ is number of bosons and $\gamma$ is an additional label needed for complete specification of a state with $N^B$ number of bosons.

Just as for fermions, corresponding to each of the $2^{r-1}$ $S{U}_Q^B(1,1)$ algebras there will be, in the ${({\ell }_1,{\ell }_2,\dots ,{\ell }_r)}^{N^B}$ space, a $SO(\mathcal{N})$ subalgebra of $U(\mathcal{N})$ with $\mathcal{N}=2{\mathrm{\Omega }}^B={\sum }_{\ell }(2\ell +1)$. The $U(\mathcal{N})$ algebra is generated by the ${\mathcal{N}}^2$ number of operators

$$u_q^k({\ell }_1,{\ell }_2)={\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^k.$$

(37)

As all the $N^B$ boson states need to be symmetric, they belong uniquely to the irrep $\left\{N^B\right\}$ of $U(\mathcal{N})$. The quadratic Casimir invariant of $U(\mathcal{N})$ is easily given by

$${\displaystyle C_2(U(\mathcal{N}))=\sum _{{\ell }_1,{\ell }_2}{(-1)}^{{\ell }_1+{\ell }_2}\sum _k{u}^k({\ell }_1,{\ell }_2)·u^k({\ell }_2,{\ell }_1),}$$

(38)

with eigenvalues

$${⟨C_2(U(\mathcal{N}))⟩}^{N^B}=N^B(N^B+\mathcal{N}-1).$$

(39)

More importantly, $U(\mathcal{N})\supset SO(\mathcal{N})$ and the $\mathcal{N}(\mathcal{N}-1)/2$ generators of $SO(\mathcal{N})$ are [55],

$$\begin{array}{c}SO(\mathcal{N}):u_q^k(\ell ,\ell )\mathrm{with}kodd,\hfill \\ V_q^k({\ell }_1,{\ell }_2)={\left\{{(-1)}^{{\ell }_1+{\ell }_2}Y({\ell }_1,{\ell }_2,k)\right\}}^{1/2}\left[{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^k+Y({\ell }_1,{\ell }_2,k){\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^k\right];\hfill \\ Y({\ell }_1,{\ell }_2,k)={(-1)}^{k+1}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}.\hfill \end{array}$$

(40)

Just as for fermion systems, the $S{O}^{(\beta )}(\mathcal{N})$ defined by Equation (40) is complementary to the quasi-spin $S{U}_Q^{B:(\beta )}(1,1)$ defined by Equations (30)–(32) and this follows from the following relations that are proved in [55],

$$\begin{array}{c}4S_{+}^B{S}_{-}^B=C_2(U(\mathcal{N}))-{\widehat{n}}^B-C_2(SO(\mathcal{N})),\hfill \\ \\ {\displaystyle C_2(SO(\mathcal{N}))=\sum _{\ell }{C}_2(SO({\mathcal{N}}_{\ell }))+\sum _{{\ell }_i<{\ell }_j}\sum _k{V}^k\left({\ell }_i,{\ell }_j\right)·V^k\left({\ell }_i,{\ell }_j\right);}\hfill \\ \\ {\displaystyle C_2(SO({\mathcal{N}}_{\ell }))=2\sum _{k=\mathrm{odd}}{u}^k(\ell ,\ell )·u^k(\ell ,\ell );}\hfill \\ \\ ⟹{⟨C_2(SO(\mathcal{N}))⟩}^{N^B,{\omega }^B}={\omega }^B({\omega }^B+\mathcal{N}-2).\hfill \end{array}$$

(41)

In the last step we have used Equations (36) and (39). Thus, the irreps of $S{O}^{(\beta )}(\mathcal{N})$ are labeled by the symmetric irreps $\left[{\omega }^B\right]$ with

$${\omega }^B=N^B,N^B-2,\dots ,0or1.$$

(42)

In summary, we have established at the level of quadratic Casimir invariants that there are multiple $S{U}^B(1,1)$ algebras each with a complementary number-conserving $SO(\mathcal{N})$ algebra when we have identical bosons in several ℓ orbits. An important property is that the spectrum in the symmetry limit, generated by

$$H_P^B=G_B{S}_{+}^B{S}_{-}^B,$$

will not depend on $\left\{\beta \right\}$; see Equation (36). However, the eigenfunctions do depend on $\left\{\beta \right\}$ and a method to construct the eigenfunctions is given in Appendix A. Now, as an example, we will consider the dependence on $\left\{\beta \right\}$ giving selection rules for EM transitions.

3.2. Selection Rules and Matrix Elements for One-Body Transition Operators

Given a general one-body operator

$$\begin{array}{c}{\displaystyle T_q^k=\sum _{{\ell }_1,{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^k{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^k}\hfill \\ {\displaystyle =\sum _{\ell }{ϵ}_{\ell ,\ell }^k{\left(b_{\ell }^{†}{\tilde{b}}_{\ell }\right)}_q^k+\sum _{{\ell }_1>{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^k\left[{\displaystyle {\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^k+\frac{{ϵ}_{{\ell }_2,{\ell }_1}^k}{{ϵ}_{{\ell }_1,{\ell }_2}^k}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^k}\right],}\hfill \end{array}$$

(43)

as $SO(\mathcal{N})\leftrightarrow S{U}_B(1,1)$, it should be clear from the generators in Equation (40) that the diagonal ${\left(b_{\ell }^{†}{\tilde{b}}_{\ell }\right)}_q^k$ parts will be $S{U}_Q^B(1,1)$ scalars $T_0^0$ for k odd and vectors $T_0^1$ for k even (except for $k=0$). Similarly, the off diagonal parts

$$\left[{\displaystyle {\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^k+\frac{{ϵ}_{{\ell }_2,{\ell }_1}^k}{{ϵ}_{{\ell }_1,{\ell }_2}^k}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^k}\right]$$

will be $S{U}_Q^B(1,1)$ scalars $T_0^0$ or vectors $T_0^1$,

$${\displaystyle \frac{{ϵ}_{{\ell }_2,{\ell }_1}^k}{{ϵ}_{{\ell }_1,{\ell }_2}^k}={(-1)}^{k+1}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}\to T_0^0,\frac{{ϵ}_{{\ell }_2,{\ell }_1}^k}{{ϵ}_{{\ell }_1,{\ell }_2}^k}={(-1)}^k{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}\to T_0^1.}$$

(44)

Thus, the selection rules for the boson systems are similar to those for the fermion systems. Results in Equations (40) and (44) together with a condition for the seniority tensorial structure will allow us to write proper forms for the EM operators in boson systems. Let us say that $S_{+}^B$ is given by

$${\displaystyle S_{+}^B=\sum _{\ell }\frac{{\beta }_{\ell }}{2}{b}_{\ell }^{†}·b_{\ell }^{†};{\beta }_{\ell }=+1\mathrm{or}-1.}$$

(45)

If we impose the condition that the $T^{E,L=even}$ and $T^{M,L=odd}$ operators are $T_0^1$ and $T_0^0$ w.r.t. $S{U}_Q^B(1,1)$, just as the fermion operators are w.r.t. $S{U}_Q(2)$ (see Section 2), then

$$\begin{array}{c}{\displaystyle T^L=\sum _{\ell }{ϵ}_{\ell ,\ell }^L{\left(b_{\ell }^{†}{\tilde{b}}_{\ell }\right)}_q^L+\sum _{{\ell }_1>{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^L\left[{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^L+{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^L\right];}\hfill \\ \Rightarrow \hfill \\ T^{EL}\to T_0^1,T^{ML}\to T_0^0.\hfill \end{array}$$

(46)

Note that for ${\ell }_1\ne {\ell }_2$, parity selection rule implies that ${(-1)}^{{\ell }_1+{\ell }_2}$ must be $+1$. Similarly, the parity changing $T^{E,L=odd}$ and $T^{M,L=even}$ operators are,

$$\begin{array}{c}{\displaystyle T^L=\sum _{{\ell }_1>{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^L\left[{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^L-{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^L\right];}\hfill \\ \Rightarrow \hfill \\ T^{EL}\to T_0^1,T^{ML}\to T_0^0.\hfill \end{array}$$

(47)

Note that for ${\ell }_1\ne {\ell }_2$, parity selection rule implies that ${(-1)}^{{\ell }_1+{\ell }_2}$ must be $-1$ and therefore here we need orbits of different parity as in $sp$ and $sdpf$ IBM’s. On the other hand, if we impose the condition that $T^{EL}$ is $T_0^0$ w.r.t. $S{U}_Q^B(1,1)$, then

$$\begin{array}{c}{\displaystyle T^{E,L=even}=\sum _{{\ell }_1>{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^L\left[{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^L-{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^L\right];{(-1)}^{{\ell }_1+{\ell }_2}=+1,}\hfill \\ {\displaystyle T^{E,L=odd}=\sum _{{\ell }_1>{\ell }_2}{ϵ}_{{\ell }_1,{\ell }_2}^L\left[{\left(b_{{\ell }_1}^{†}{\tilde{b}}_{{\ell }_2}\right)}_q^L+{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{\left(b_{{\ell }_2}^{†}{\tilde{b}}_{{\ell }_1}\right)}_q^L\right];{(-1)}^{{\ell }_1+{\ell }_2}=-1}\hfill \\ \Rightarrow \hfill \\ T^{EL}\to T_0^0.\hfill \end{array}$$

(48)

Similarly, $T^{ML}$ can be chosen to be $T_0^1$ w.r.t. $S{U}_Q^B(1,1)$. Examples for $sd$, $sp$, $sdg$ and $sdpf$ systems are discussed ahead.

Applying the Wigner–Eckart theorem for the many particle matrix elements in good seniority states, the number dependence of the matrix elements of $T_0^0$ and $T_0^1$ operators is easily determined. Here, we need $S{U}^{(}1,1)$ Wigner coefficients. Using $SU(1,1)$ algebra (see for example [95]), we have

$$\begin{array}{c}⟨N^B,{\omega }^B,\alpha \mid T_0^0\mid N^B,{\omega }^B,\beta ⟩=⟨{\omega }^B,{\omega }^B,\alpha \mid T_0^0\mid {\omega }^B,{\omega }^B,\beta ⟩,\hfill \\ {\displaystyle ⟨N^B,{\omega }^B,\alpha \mid T_0^1\mid N^B,{\omega }^B,\beta ⟩=\frac{{\mathrm{\Omega }}^B+N^B}{{\mathrm{\Omega }}^B+{\omega }^B}⟨{\omega }^B,{\omega }^B,\alpha \mid T_0^1\mid {\omega }^B,{\omega }^B,\beta ⟩,}\hfill \\ ⟨N^B,{\omega }^B,\alpha \mid T_0^1\mid N^B,{\omega }^B-2,\beta ⟩=\hfill \\ {\displaystyle \sqrt{{\displaystyle \frac{(2{\mathrm{\Omega }}^B+N^B+{\omega }^B-2)(N^B-{\omega }^B+2)}{4({\mathrm{\Omega }}^B+{\omega }^B-1)}}}⟨{\omega }^B,{\omega }^B,\alpha \mid T_0^1\mid {\omega }^B,{\omega }^B-2,\beta ⟩.}\hfill \end{array}$$

(49)

Note the well-established $\mathrm{\Omega }\to -\mathrm{\Omega }$ symmetry between the fermion and boson system formulas in Equations (27) and (49); see also [55,56,90]. Moreover, $T_0^1$ generates both $v({\omega }^B)\to v({\omega }^B)$ and $v({\omega }^B)\to v({\omega }^B)\pm 2$ transitions while $T_0^0$ only $v({\omega }^B)\to v({\omega }^B)$ transitions for fermion (boson) systems. The later matrix elements are independent of number of particles. Equation (49) is useful only when ${\omega }^B<<N^B$. In Figure 3, variation of $B(EL)$ for boson systems with boson number assuming ${\omega }^B=2$ for both ${\omega }^B\to {\omega }^B$ and ${\omega }^B\to {\omega }^B-2$ transitions are shown by employing the last two equations in Equation (49). The $B(EL)$ values increase with $N^B$ and this variation is quite different from the variation seen in Figure 1 and Figure 2 for fermion systems. However, for boson system such as those described by IBM, it is well known that the low-lying states correspond to highest seniority (${\omega }^B=N^B$) and therefore, Equation (49) will not give, for example, $B(EL)$ trends in yrast levels.

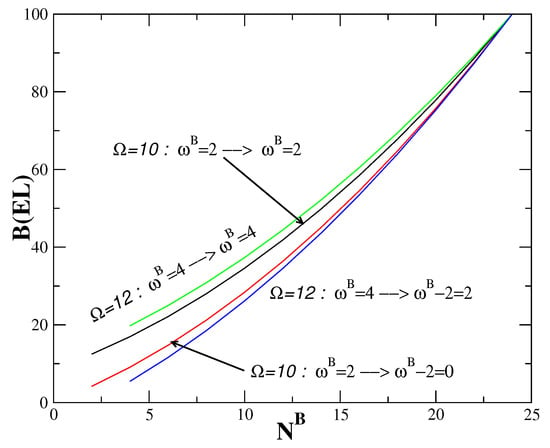
Figure 3. Variation of $B(EL)$ with particle number $N^B$ for ${\omega }^B\to {\omega }^B$ and ${\omega }^B\to {\omega }^B-2$ for transitions for two values of ${\mathrm{\Omega }}^B$ and seniority ${\omega }^B$. Results are for boson systems and they are obtained by applying the last two equations in Equation (49). The $B(EL)$ values are scaled such that the maximum value is 100 and therefore they are not in any units. See Section 3.2 for further discussion.

3.3. Applications to EM Transition Operators

3.3.1. $sd$IBM

In the applications to interacting boson models, let us first consider the $SO(6)$ limit of $sd$IBM. Then, we have $U(6)\supset SO(6)$ and the complementary $SU(1,1)$ algebra corresponds to the $sd$ pair $S_{+}=s^{†}{s}^{†}\pm d^{†}·d^{†}$. Arima and Iachello [21] used the choice $S_{+}=s^{†}{s}^{†}-d^{†}·d^{†}$. The corresponding $SU(1,1)$ we denote as $S{U}^{(-)}(1,1)$. Similarly, the $SU(1,1)$ with $S_{+}=s^{†}{s}^{†}+d^{†}·d^{†}$ is denoted by $S{U}^{(+)}(1,1)$. Corresponding to the two $SU(1,1)$ algebras, there will be two $SO(6)$ algebras as pointed out first in [97]. Their significance is seen in quantum chaos studies [98,99]. For illustration, let us consider the tensorial structure of the $E2$ operator. Following the discussion in Section 3.2, the $E2$ transition operator will be $T_0^0$ w.r.t. $S{U}^{(-)}(1,1)$ if we choose $T^{E2}=\alpha {(s^{†}\tilde{d}+d^{†}\tilde{s})}_{\mu }^2$ where $\alpha$ is a constant. This is the choice made in [21] and this operator will not change the seniority quantum number (called $\sigma$ in [21]) defining the irreps of $SO(6)$ that is complementary to $S{U}^{(-)}(1,1)$. However, if we demand that the $T^{E2}$ operator should be $T_0^1$ w.r.t. $S{U}^{(-)}(1,1)$, then we have $T^{E2}={\alpha }_1{(d^{†}\tilde{d})}_{\mu }^2+i{\alpha }_2{(s^{†}\tilde{d}-d^{†}\tilde{s})}_{\mu }^2$. This operator will have both $\sigma \to \sigma$ and $\sigma \to \sigma \pm 2$ transitions. On the other hand, $T^{E2}={\alpha }_1{(d^{†}\tilde{d})}_{\mu }^2+{\alpha }_2{(s^{†}\tilde{d}+d^{†}\tilde{s})}_{\mu }^2$ will be a mixture of $T_0^0$ and $T_0^1$ operators.

Employing $T^{E2}=\alpha {(s^{†}\tilde{d}+d^{†}\tilde{s})}_{\mu }^2$, analytical formulas for $B(E2)$’s in the two $SO(6)$ limits are derived in [97]. Used is $U(6)\supset S{O}^{(\pm )}(6)\supset SO(5)\supset SO(3)$ giving the basis states $\left|N,\sigma ,\tau ,L\right.⟩$ where $\sigma$ and $\tau$ are $SO(6)$ and $SO(5)$ irreps with $\sigma =N,N-2,\dots ,0$ or 1 and $\tau =0,1,\dots ,\sigma$. The $\tau \to L$ rules are well known [21]. For the low-lying levels $\sigma =N$ and for these the following formula was derived in [97],

$$\begin{array}{c}B{(E2;N,N,\tau +1,L_i\to N,N,\tau ,L_f)}_{S{O}^{(+)}(6)}\hfill \\ ={\left({\displaystyle \frac{\tau +2}{N+1}}\right)}^{2}B{(E2;N,N,\tau +1,L_i\to N,N,\tau ,L_f)}_{S{O}^{(-)}(6)}\hfill \end{array}$$

(50)

and for example [21],

$$\begin{array}{c}B{(E2;N,N,\tau +1,L_i=2\tau +2\to N,N,\tau ,L_f=2\tau )}_{S{O}^{(-)}(6)}\hfill \\ {\displaystyle ={\alpha }^2\frac{(N-\tau )(N+\tau +4)(\tau +1)(4\tau +5)}{(2\tau +5)}.}\hfill \end{array}$$

(51)

Thus, $B(E2)$s carry the signature of multiple $SO(6)$ algebras in IBM.

3.3.2. $sp$IBM

In the second example we will consider the $sp$ boson model, also called vibron model with applications to diatomic molecules [100] and two-body clusters in nuclei [101,102]. Just as in $sd$IBM, here we have $U(4)\supset SO(4)$ and there will be two $SO(4)$ algebras with $S_{+}=s^{†}{s}^{†}+\beta p^{†}·p^{†}$; $\beta =\pm 1$. The general form of the $E1$ operator (to lowest order) in this model is $T^{E1}={ϵ}_{sp}{\left(s^{†}\tilde{p}\pm p^{†}\tilde{s}\right)}_{\mu }^1$. With $S{U}^{(+)}(1,1)$ defined by $S_{+}=s^{†}{s}^{†}+p^{†}·p^{†}$, from Equation (47) we see that $T^{E1}=iϵ{\left(s^{†}\tilde{p}-p^{†}\tilde{s}\right)}_{\mu }^1$ will be $T_0^1$ w.r.t. $S{U}^{(+)}(1,1)$. Similarly, with $S{U}^{(-)}(1,1)$ defined by $S_{+}=s^{†}{s}^{†}-p^{†}·p^{†}$, from Equation (46) we see that $T^{E1}=ϵ{\left(s^{†}\tilde{p}+p^{†}\tilde{s}\right)}_{\mu }^1$ will be $T_0^1$ w.r.t. $S{U}^{(-)}(1,1)$. If the definitions of $T^{E1}$ are interchanged, then they will be $T_0^0$ w.r.t. the corresponding $SU(1,1)$ algebras. These results are described and applied in [100,103,104].

3.3.3. $sdg$IBM

In the third example we will consider the $sdg$ interacting boson model [22] and there is new interest in this model in the context of quantum phase transitions (QPT) [105]. With s, d and g bosons, the generalized pair operator here is $S_{+}=s^{†}{s}^{†}\pm d^{†}·d^{†}\pm g^{†}·g^{†}$ giving four $S{U}^{(+,\pm ,\pm )}(1,1)$ algebras and the corresponding $S{O}^{(+,\pm ,\pm )}(15)$ algebras in $U(15)\supset SO(15)$; the superscripts in $S{U}^{(+,\pm ,\pm )}(1,1)$ and similarly in $SO(15)$ are the signs of the s, d and g pair operators in $S_{+}$. In QPT studies, Van Isacker et al. [105] have chosen the operators ${(s^{†}\tilde{d}+d^{†}\tilde{s})}_{\mu }^2$ and ${(s^{†}\tilde{g}+g^{†}\tilde{s})}_{\mu }^4$ to be $SO(15)$ scalars. Then, from Equation (44) it is seen that the $SO(15)$ will correspond to the $S{U}^{(+,-,-)}(1,1)$ algebra with $H_p=S_{+}{S}_{-}$ where $S_{+}=s^{†}{s}^{†}-d^{†}·d^{†}-g^{†}·g^{†}$. Note that here the $sd$-part is the same as the one used by Arima and Iachello (see the $sd$IBM discussion above). In another recent study, the $E2$ operator in $sdg$IBM was chosen to be [106]

$$T^{E2}={\alpha }_1{(d^{†}\tilde{d})}_{\mu }^2+{\alpha }_2{(g^{†}\tilde{g})}_{\mu }^2+{\alpha }_3{(s^{†}\tilde{d}+d^{†}\tilde{s})}_{\mu }^2+{\alpha }_4{(d^{†}\tilde{g}+g^{†}\tilde{d})}_{\mu }^2.$$

With respect to the $S{U}^{(+,-,-)}(1,1)$ above, this operator will be a mixture of $T_0^0$ and $T_0^1$ operators. However, w.r.t. $S{U}^{(+,+,+)}(1,1)$, it will be a pure $T_0^1$ operator. It should be clear that with different choices of $SU(1,1)$ algebras (there are four of them), the QPT results for transition to rotational $SU(3)$ limit in $sdg$IBM will be different. It is important to investigate this going beyond the results presented in [105]. Moreover, it will be useful to extend Equation (50) to $sdg$IBM with the four $SO(15)$ (or $SU(1,1)$) algebras and test these using, say, the $B(E2)$ and $B(E4)$ data for Pd isotopes (they are examined using a different model in [107]).

3.3.4. $sdpf$IBM

In the final example, let us consider the $sdpf$ model [23,93,94] applied recently with good success in describing $E1$ strength distributions in Nd, Sm, Gd and Dy isotopes [108] and also spectroscopic properties (spectra, and $E2$ and $E1$ strengths) of even–even ${}^{98-110}$Ru isotopes [109]. Note that the parities of the p and f orbit are negative. In $sdpf$IBM, following the results in Section 3.1 and Section 3.2, there will be eight generalized pairs $S_{+}$ and the algebra complementary to the $SU(1,1)$ is $SO(16)$ in $U(16)\supset SO(16)$. Keeping the $SO(6)$ pair structure, as chosen by Arima and Iachello, of $sd$IBM intact we will have four $S_{+}$ pairs, $S_{+}=s^{†}{s}^{†}-d^{†}·d^{†}\pm p^{†}·p^{†}\pm f^{†}·f^{†}$ giving $S{U}^{(+,-,\pm ,\pm )}(1,1)$ and correspondingly four $S{O}^{(+,-,\pm ,\pm )}(16)$ algebras. For each of the four choices, one can write down the $T^{E2}$ and $T^{E1}$ operators that transform as $T_0^0$ or $T_0^1$ w.r.t. $SU(1,1)$. In [23], $S{U}^{(+,-,-,-)}(1,1)$ is employed. Then, the $E2$ and $E1$ operators employed in [23,108,109] will be mixture of $T_0^0$ and $T_0^1$ w.r.t. to $S{U}^{(+,-,-,-)}(1,1)$. For example, the $E1$ operator used is

$$T^{E1}={\alpha }_{sp}{\left(s^{†}\tilde{p}+p^{†}\tilde{s}\right)}_{\mu }^1+{\alpha }_{pd}{\left(p^{†}\tilde{d}+d^{†}\tilde{p}\right)}_{\mu }^1+{\alpha }_{df}{\left(d^{†}\tilde{f}+f^{†}\tilde{d}\right)}_{\mu }^1.$$

(52)

The first term in the operator will be $T_0^1$ and the remaining two terms will be $T_0^0$ w.r.t. $S{U}^{(+,-,-,-)}(1,1)$. However if we use ${\alpha }_{sp}{\left(s^{†}\tilde{p}-p^{†}\tilde{s}\right)}_{\mu }^1$ in the above, then the whole operator will be $T_0^0$. It will be interesting to employ the $H_p=S_{+}{S}_{-}$ with $S_{+}$ given above (there will be four choices) in the analysis made in [109] and confront the data.

3.4. Application to QPT

Quantum phase transitions (QPT) are studied in $sd$IBM in great detail using the $U(5)$, $SU(3)$ and $SO(6)$ algebras of this model [110]. This topic continues to be important with new investigations and experimental tests [111,112]. For example, with recent interest in $sdg$ [105] and $sdpf$ [108,109] IBM’s, it will be interesting to study QPT and order–chaos transitions in these models, in a systematic way, employing Hamiltonians that interpolate the different pairing algebras in these models. Such studies for the simpler $sd$ and $sp$ IBM’s are available; see [98,99,110]. Construction of the Hamiltonian matrix for the interpolating Hamiltonians is straightforward as described briefly in Appendix A. As an example, results for the spectra for a $sdg$IBM system are shown in Figure 4. The SGA for $sdg$IBM is $U(15)$ and the generalized pairing algebra here is $SO(15)$ in $U(15)\supset SO(15)$. Dividing the space into $sd$ and g spaces, there will be two $SO(15)$ algebras and therefore it is possible to consider a Hamiltonian that interpolates the three symmetry limits

$$\begin{array}{c}I.U(15)\supset U_{sd}(6)\oplus U_g(9)\supset S{O}_{sd}(6)\oplus S{O}_g(9)\supset K,\hfill \\ II.U(15)\supset S{O}^{(+)}(15)\supset S{O}_{sd}(6)\oplus S{O}_g(9)\supset K,\hfill \\ III.U(15)\supset S{O}^{(-)}(15)\supset S{O}_{sd}(6)\oplus S{O}_g(9)\supset K.\hfill \end{array}$$

(53)

Figure 4. Energy spectra for 50 bosons and $({\omega }_{sd}^B,{\omega }_g^B)=(0,0)$ in $sdg$IBM with the Hamiltonian given by Equation (54). In each panel, energy spectra are shown as a function of the parameter $\xi$ taking values from 0 to 1. Results are shown in the figures for $x=1$, $0.8$, $0.5$, $0.2$, 0, $-0.2$, $-0.5$, $-0.8$ and $-1$. Note that $x=1$ and $-1$ correspond to the two $SO(15)$ or $SU(1,1)$ algebras in the model. In the figures, energies are not in any units. See Section 3.4 for further discussion.

The algebra K will not play any role in our present discussion. Note that the $U(15)$ irrep is given by total number of bosons $N^B$ in the system. Number of $sd$ bosons $N_{sd}^B$ and number g bosons $N_g^B$ label the irreps of $U_{sd}(6)$ and $U_g(9)$ respectively. The $SO(15)$ label ${\omega }^B=N^B,N^B-2,\dots$. Similarly, the $S{O}_{sd}(6)$ and $S{O}_g(9)$ labels are ${\omega }_{sd}^B$ and ${\omega }_g^B$ respectively. The rules for ${\omega }^B\to ({\omega }_{sd}^B,{\omega }_g^B)$ are well known [113]. Employed in the calculations is the interpolating Hamiltonian

$$H_{sdg}=\left[(1-\xi )/N^B\right]{\widehat{n}}_g+\left[(\xi /{(N^B)}^2\right]\left[4(S_{+}^{sd}+x{S}_{+}^g)(S_{-}^{sd}+x{S}_{-}^g)-N^B(N^B+13)\right]$$

(54)

where $S_{+}^{sd}$ is the $S_{+}$ operator for the $sd$ boson system and $S_{+}^g$ for the g boson system. Results are presented in Figure 4 for a $sdg$ system with 50 bosons and $({\omega }_{sd}^B,{\omega }_g^B)=(0,0)$. Figure clearly shows order–chaos–order transition as we have two $SO(15)$ or $SU(1,1)$ algebras in the model both giving the same spectrum for $\xi =1$ and $x=\pm 1$. Let us add that QPT here was studied in the past by varying $\xi$ with $x=1$ (equivalently $x=-1$) and it is shown that the transition point is $\xi =0.2$ [114,115]. Going further, it is possible to extend the two level results in Figure 4 using the four $SU(1,1)$ or $SO(15)$ algebras in s, d and g space. Then we have in place of $(S_{+}^{sd}+x{S}_{+}^g)$, the operator $(S_{+}^s\pm x{S}_{+}^d\pm y{S}_{+}^g)$. Explorations using this will give further insights in QPT and the role of multiple pairing algebras in IBM.

Finally, turning to fermion systems, just as using Equations (53) and (54) for QPT in IBM, it is also possible to use in a two orbit identical nucleon example (with $\mathrm{\Omega }={\mathrm{\Omega }}_1+{\mathrm{\Omega }}_2$), a Hamiltonian interpolating between the following three algebras

$$\begin{array}{c}I.U(2\mathrm{\Omega })\supset S{p}^{(+)}(2\mathrm{\Omega })\supset Sp(2{\mathrm{\Omega }}_1)\oplus Sp(2{\mathrm{\Omega }}_2)\supset R\hfill \\ II.U(2\mathrm{\Omega })\supset S{p}^{(-)}(2\mathrm{\Omega })\supset Sp(2{\mathrm{\Omega }}_1)\oplus Sp(2{\mathrm{\Omega }}_2)\supset R\hfill \\ III.U(2\mathrm{\Omega })\supset U(2{\mathrm{\Omega }}_1)\oplus U(2{\mathrm{\Omega }}_2)\supset Sp(2{\mathrm{\Omega }}_1)\oplus Sp(2{\mathrm{\Omega }}_2)\supset R\hfill \end{array}$$

(55)

A study using these and their extensions will give insights into QPT in shell model spaces.

3.5. Summary

In this section, multiple pairing algebras $SU(1,1)$ and the better known complementary $SO(\mathcal{N})$ algebras in multi-orbit interacting boson models, with identical bosons, such as $sd$, $sp$, $sdg$ and $sdpf$ IBM’s are presented. The relationship between quasi-spin tensorial nature of one-body transition operators and the phase choices in the multi-orbit pair creation operator is derived for identical boson systems described by interacting boson models. All these results are presented in Section 3.1 and Section 3.2. As pointed out in these Sections, some of the results here are known before for some special situations. Turning to applications to interacting boson model description of collective states, imposing specific tensorial structure with respect to pairing $SU(1,1)$ algebras is possible as discussed with various examples in Section 3.3. It will be interesting to derive results for B(E2)’s (say in $sdg$ and $sdpf$ IBM’s) and B(E1)’s (in $sdpf$ IBM) with fixed tensorial structure for the transition operator but with wavefunctions that correspond to different $SU(1,1)$ algebras. Such an exercise was carried out before only for $sd$IBM as discussed in Section 3.3.1. Finally, an application to QPT in nuclei is presented in Section 3.4.

4. Multiple Multi-Orbit Pairing Algebras in Shell Model with Isospin

Going beyond identical nucleon (fermion) and interacting boson systems considered in Section 2 and Section 3, now we will consider pairing algebras for nucleons with isospin. As already mentioned in the introduction (Section 1), with isospin the pairing algebra is $SO(5)$. In Section 4.1 the pairing $SO(5)$ and the complementary seniority and reduced isospin generating $Sp(2\mathrm{\Omega })$ algebras are described for multi-j situation giving their generators and the quadratic Casimir operators. With r number of j orbits, there will be $2^{r-1}$ number of $SO(5)$ algebras and for each of these there will be a corresponding $Sp(2\mathrm{\Omega })$ algebra as shown in Section 4.1. Section 4.2 gives a brief discussion of the irrep reductions and also the formulas for constructing many-particle matrix elements of the pairing Hamiltonian generating multiple $SO(5)$ algebras. In Section 4.3 presented are three applications. Finally, Section 4.4 gives a summary.

4.1. Multiple Multi-j Shell $SO(5)$ and $Sp(2\mathrm{\Omega })$ Algebras

4.1.1. Number-Conserving Group Chain with $Sp(2\mathrm{\Omega })$ Generating Seniority and Reduced Isospin

Let us consider a system of m nucleons in r number of spherical j orbits $(j_1,j_2,\dots ,j_r)$ with $\mathrm{\Omega }$ defined by

$${\displaystyle 2\mathrm{\Omega }=\sum _{k=1}^r(2j_k+1);2{\mathrm{\Omega }}_{j_k}=(2j_k+1).}$$

(56)

In addition, let us consider the one-body operators $u_{m_k,m_t}^{k,t}(j_1,j_2)$ in terms of the single particle creation and annihilation operators in angular momentum j and isospin t spaces,

$$u_{m_k,m_t}^{k,t}(j_1,j_2)={\left(a_{j_1\frac{1}{2}}^{†}{\tilde{a}}_{j_2\frac{1}{2}}\right)}_{m_k,m_t}^{k,t}$$

(57)

where ${\tilde{a}}_{j-m,\frac{1}{2}-m_t}={(-1)}^{j-m+\frac{1}{2}-m_t}{a}_{jm,\frac{1}{2}{m}_t}$. Using angular momentum algebra it is easy to prove that the $16{\mathrm{\Omega }}^2$ number of operators $u^{k,t}(j_1,j_2)$ form a closed algebra (note that $t=0,1$) and this is the SGA $U(4\mathrm{\Omega })$. Moreover, we have the subalgebra

$$U(4\mathrm{\Omega })\supset U(2\mathrm{\Omega })\otimes S{U}_T(2).$$

(58)

The operators $u_{m_k,0}^{k,0}(j_1,j_2)$ ($4{\mathrm{\Omega }}^2$ in number) generate $U(2\mathrm{\Omega })$. Similarly, $S{U}_T(2)$ is generated by isospin T with $T_{\mu }^1$ given by

$${\displaystyle T_{\mu }^1=\sum _{j=j_1,j_2,\dots ,j_r}\sqrt{{\displaystyle \frac{2j+1}{2}}}{\left(a_{j\frac{1}{2}}^{†}{\tilde{a}}_{j\frac{1}{2}}\right)}_{\mu }^{0,1}.}$$

(59)

It is easy to prove that the $T_{\mu }^1$ commute with $u_{m_k,0}^{k,0}(j_1,j_2)$ operators giving Equation (58). Let us add that the number operator is given by

$${\displaystyle \widehat{n}=\sum _{j=j_1,j_2,\dots ,j_r}\sqrt{2(2j+1)}{\left(a_{j\frac{1}{2}}^{†}{\tilde{a}}_{j\frac{1}{2}}\right)}^{0,0}.}$$

(60)

Note that $\{T_{\mu }^1,\widehat{n}\}$ generate $U_T(2)$. Following the known results for the multi-j shell identical nucleon systems [65] and those for nucleons in a single-j shell with isospin, it is easy to recognize that $U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })$ and the generators of $Sp(2\mathrm{\Omega })$ are

$$\begin{array}{ccc}\hfill Sp(2\mathrm{\Omega })& :& u_{\mu ,0}^{k,0}(j,j);k=\mathrm{odd}\hfill \\ & & V_{\mu ,0}^{k,0}(j_1,j_2)={\mathcal{N}}^{1/2}(j_1,j_2,k)\left[u_{\mu ,0}^{k,0}(j_1,j_2)+X(j_1,j_2,k)u_{\mu ,0}^{k,0}(j_2,j_1)\right];j_1>j_2.\hfill \end{array}$$

(61)

By simple counting, it is seen that the number of generators in Equation (61) is $(2\mathrm{\Omega })(2\mathrm{\Omega }+1)/2$ as required for $Sp(2\mathrm{\Omega })$. An important task now is to find the conditions on $X(j_1,j_2,k)$ so that the generators in Equation (61) form $Sp(2\mathrm{\Omega })$ algebra that is complementary to the pairing $SO(5)$ algebra; normalization factor $\mathcal{N}(j_1,j_2,k)$ is determined such that the quadratic Casimir operator gives eigenvalues in standard form. Before we turn to this, a few other remarks are in order.

Firstly, $Sp(2\mathrm{\Omega })$ contains angular momentum algebra $SO(3)$ generated by $J_{\mu }^1$ where

$${\displaystyle J_{\mu }^1=\sum _j\sqrt{j(j+1)(2j+1)}{u}_{\mu ,0}^{1,0}.}$$

(62)

with this, we have the decomposition, with only number-conserving operators,

$$U(4\mathrm{\Omega })\supset \left[U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })\supset S{O}_J(3)\right]\otimes S{U}_T(2)$$

(63)

All m nucleon states transform as the antisymmetric irrep $\left\{1^m\right\}$ of $U(4\mathrm{\Omega })$. Similarly, the irreps of $U(2\mathrm{\Omega })$ will be two columned irreps $\left\{2^{m_1}{1}^{m_2}\right\}$ in Young tableaux notation with $2m_1+m_2=m$ and $T=m_2/2$. Thus, the $U(2\mathrm{\Omega })$ irreps are labeled by $(m,T)$. Given a two-column irrep of $U(2\mathrm{\Omega })$, the $Sp(2\mathrm{\Omega })$ irreps also will be at most two-columned, denoted by $⟨2^{v_1}{1}^{v_2}⟩$ in Young tableaux notation. Then, $v=2v_1+v_2$ is the seniority quantum number and $t=v_2/2$ is called reduced isospin. Group theory allows us to obtain $\left\{2^{m_1}{1}^{m_2}\right\}\to ⟨2^{v_1}{1}^{v_2}⟩\to J$ reductions [116]. Examples are presented ahead in Section 4.2. In order to understand better the complicated $Sp(2\mathrm{\Omega })$ algebra, the $(v,t)$ quantum numbers and their relation to pairing, we will turn to the complementary multi-j shell $SO(5)$ algebra.

4.1.2. Multiple $SO(5)$ Pairing Algebras with Isospin

Consider the angular momentum zero coupled isovector pair-creation operator $A_{\mu }^1(j)$ for nucleons in a single-j shell,

$${\displaystyle A_{\mu }^1(j)=\frac{{\displaystyle \sqrt{2j+1}}}{2}{\left(a_{j\frac{1}{2}}^{†}{a}_{j\frac{1}{2}}^{†}\right)}_{0,\mu }^{0,1}}$$

(64)

and its hermitian adjoint ${\left[A_{\mu }^1(j)\right]}^{†}$,

$${\displaystyle {\left[A_{\mu }^1(j)\right]}^{†}=\frac{{\displaystyle \sqrt{2j+1}}}{2}{(-1)}^{\mu }{\left({\tilde{a}}_{j\frac{1}{2}}{\tilde{a}}_{j\frac{1}{2}}\right)}_{0,-\mu }^{0,1}.}$$

(65)

Now, with nucleons in $(j_1,j_2,\dots ,j_r)$ orbits, pair-creation operator can be taken as a linear combination of the single-j shell pair-creation operators but with different phases giving the generalized pairing operator to be,

$${\displaystyle {\mathcal{A}}_{\mu }^1(\beta )=\sum _{p=1}^r{\beta }_{j_p}{A}_{\mu }^1(j_p);\left\{\beta \right\}=\{{\beta }_{j_1},{\beta }_{j_2},\dots ,{\beta }_{j_r}\}=\{\pm 1,\pm 1,\dots \}.}$$

(66)

Similarly, the corresponding generalized pair-annihilation operator is

$${\displaystyle {\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}=\sum _{p=1}^r{\beta }_{j_p}{\left[A_{\mu }^1(j_p)\right]}^{†}.}$$

(67)

Using angular momentum algebra, it is easy to derive the commutators for the operators ${\mathcal{A}}_{\mu }^1(\beta )$, ${\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}$, $T_{\mu }^1$ and $Q_0=[\widehat{n}-2\mathrm{\Omega }]/2$. The results are independent of $\left\{\beta \right\}$ when ${\beta }_{j_p}=\pm 1$ as in Equation (66),

$$\begin{array}{c}{\displaystyle \left[{\mathcal{A}}_{\mu }^1,{({\mathcal{A}}_{-{\mu }^{\prime }}^1)}^{†}\right]=\sqrt{2}{(-1)}^{{\mu }^{\prime }}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩T_{\mu +{\mu }^{\prime }}^1+{\delta }_{\mu ,-{\mu }^{\prime }}(-Q_0),}\hfill \\ \left[{\mathcal{A}}_{\mu }^1,Q_0\right]=-{\mathcal{A}}_{\mu }^1,\hfill \\ {\displaystyle \left[{\mathcal{A}}_{\mu }^1,T_{{\mu }^{\prime }}^1\right]=\sqrt{2}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩{\mathcal{A}}_{\mu +{\mu }^{\prime }}^1,}\hfill \\ {\displaystyle \left[T_{\mu }^1,T_{{\mu }^{\prime }}^1\right]=-\sqrt{2}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩T_{\mu +{\mu }^{\prime }}^1,}\hfill \\ \left[T_{\mu }^1,Q_0\right]=0.\hfill \end{array}$$

(68)

All the commutators that are not given above can be obtained by taking hermitian conjugates on both sides of the above formulas. Furthermore, we have dropped $\left\{\beta \right\}$ for brevity and because the results are independent of $\left\{\beta \right\}$. Equation (68) shows that the ten operators ${\mathcal{A}}_{\mu }^1(\beta )$, ${\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}$, $T_{\mu }^1$ and $Q_0$ (equivalently $\widehat{n}$) form a pairing $S{O}^{(\beta )}(5)$ algebra for each $\{(\beta )\}$ set. Without loss of generality we can choose ${\beta }_{j_1}=+1$ and then the remaining ${\beta }_{j_p}$ will be $\pm 1$. Thus, there will be $2^{r-1}$$SO(5)$ algebras. Then, with two j orbits we have two $SO(5)$ algebras $S{O}^{(+,+)}(5)$ and $S{O}^{(+,-)}(5)$, with three we have four $SO(5)$ algebras $S{O}^{(+,+,+)}(5)$, $S{O}^{(+,+,-)}(5)$, $S{O}^{(+,-,+)}(5)$ and $S{O}^{(+,-,-)}(5)$, with four j orbits there will be eight $SO(5)$ algebras and so on.

Before proceeding further, let us define isovector pairing Hamiltonians $H_p(\beta )$ for each $\beta$ set,

$${\displaystyle H_p(\beta )=-G\sum _{\mu }{\mathcal{A}}_{\mu }^1(\beta ){\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}.}$$

(69)

Here, G is the pairing strength. Then, the non-zero two-body matrix elements of $H_p(\beta )$ are,

$${\displaystyle ⟨(j_f{j}_f)J=0,T=1\mid H_p(\beta )\mid (j_i{j}_i)J=0,T=1⟩=-\frac{G}{2}\sqrt{(2j_i+1)(2j_f+1)}{\beta }_{j_i}{\beta }_{j_f}}$$

(70)

and typically $G\sim 27/A$. We can prove that the quadratic Casimir invariant of $S{O}^{(\beta )}(5)$ is,

$${\displaystyle {\mathcal{C}}_2(S{O}^{(\beta )}(5))=2\sum _{\mu }{\mathcal{A}}_{\mu }^1(\beta ){\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}+T^2+Q_0(Q_0-3).}$$

(71)

and this commutes with all the ten generators of $S{O}^{(\beta )}(5)$. This is used to identify the complementary $S{p}^{(\beta )}(2\mathrm{\Omega })$ algebras as described below.

4.1.3. Multiple $S{O}^{(\beta )}(5)$ Algebras and the Complementary $S{p}^{(\beta )}(2\mathrm{\Omega })$ Algebras

With the generators of $U(2\mathrm{\Omega })$, $Sp(2\mathrm{\Omega })$ and $S{U}_T(2)$ given in Section 4.1.1, the quadratic Casimir invariants of these algebras are

$$\begin{array}{ccc}\hfill {\mathcal{C}}_2(U(2\mathrm{\Omega }))& =& {\displaystyle 2\sum _{j_1,j_2,k}{(-1)}^{j_1-j_2}{u}^{k,0}(j_1,j_2)·u^{k,0}(j_2,j_1),}\hfill \\ \hfill {\mathcal{C}}_2(Sp(2\mathrm{\Omega }))& =& {\displaystyle 4\sum _j\sum _{k=odd}{u}^{k,0}(j,j)·u^{k,0}(j,j)}\hfill \\ & & {\displaystyle +2\sum _{j_1>j_2,k}{V}^{k,0}(j_1,j_2)·V^{k,0}(j_1,j_2),}\hfill \\ \hfill {\mathcal{C}}_2(U_T(2))& =& {\displaystyle \sum _{j_1,j_2;t=0,1}\sqrt{(2j_1+1)(2j_2+1)}{u}^{0,t}(j_1,j_1)·u^{0,t}(j_2,j_2).}\hfill \end{array}$$

(72)

Starting with these it is easy to prove that

$$\begin{array}{c}{\mathcal{C}}_2(U(2\mathrm{\Omega }))+{\mathcal{C}}_2(U_T(2))=\widehat{n}(2+2\mathrm{\Omega }),\hfill \\ {\displaystyle {\mathcal{C}}_2(U_T(2))=\frac{{\widehat{n}}^2}{2}+2T^2.}\hfill \end{array}$$

(73)

More importantly, carrying out considerable amount of angular momentum algebra, we are able to prove that, if the following conditions hold

$$\mathcal{N}(j_1,j_2,k)={(-1)}^{k+1}{\beta }_{j_1}{\beta }_{j_2},X(j_1,j_2,k)={(-1)}^{j_1+j_2+k}{\beta }_{j_1}{\beta }_{j_2},$$

(74)

then we have the equality

$${\displaystyle {\mathcal{C}}_2(U(2\mathrm{\Omega }))-{\mathcal{C}}_2(Sp(2\mathrm{\Omega }))=4\sum _{\mu }{\mathcal{A}}_{\mu }^1(\beta ){\left[{\mathcal{A}}_{\mu }^1(\beta )\right]}^{†}-\widehat{n}.}$$

(75)

Thus, there is a $S{p}^{(\beta )}(2\mathrm{\Omega })$ that corresponds to the pairing Hamiltonians $H_p(\beta )$ or the $S{O}^{(\beta )}(5)$ algebra. More explicitly, we have the important relation, combining Equations (71)–(73) and (75),

$${\mathcal{C}}_2(S{O}^{(\beta )}(5))=-\frac{1}{2}{\mathcal{C}}_2(S{p}^{(\beta )}(2\mathrm{\Omega }))+\mathrm{\Omega }(\mathrm{\Omega }+3).$$

(76)

The Equation (76) establishes that the multiple $S{O}^{(\beta )}(5)$ algebras with number non-conserving generators and $S{p}^{(\beta )}(2\mathrm{\Omega })$ algebras with only number-conserving generators are complementary provided Equation (74) is satisfied along with Equation (66). As mentioned in the introduction, more formal mathematical proofs for all these are given recently by Neergard [58,59,60,61]. It is also important to add that the expressions for Casimir invariants, in a different form, are given by Racah very early [10,117].

Given the $Sp(2j+1)$ irrep $⟨2^{v_1}{1}^{v_2}⟩$ or equivalently $(v,t)$, the eigenvalues of ${\mathcal{C}}_2(Sp(2j+1))$ are given by (see for example [56,118])

$${⟨{\mathcal{C}}_2(Sp(2j+1))⟩}^{v,t}=2\left[\mathrm{\Omega }(\mathrm{\Omega }+3)-\left(\mathrm{\Omega }-\frac{v}{2}\right)\left(\mathrm{\Omega }-\frac{v}{2}+3\right)-t(t+1)\right].$$

(77)

Further, $SO(5)$ irreps are labeled by $({\omega }_1,{\omega }_2)$ with ${\omega }_1$ and ${\omega }_2$ both integers or half integers and ${\omega }_1\ge {\omega }_2\ge 0$ [56,116,118]. Then, the eigenvalues of ${\mathcal{C}}_2(SO(5))$ are

$${⟨{\mathcal{C}}_2(SO(5))⟩}^{({\omega }_1,{\omega }_2)}={\omega }_1({\omega }_1+3)+{\omega }_2({\omega }_2+1).$$

(78)

Using this and Equations (76) and (78) show that $({\omega }_1,{\omega }_2)$ are equivalent to $(v,t)$,

$${\omega }_1=\mathrm{\Omega }-\frac{v}{2},{\omega }_2=t,$$

(79)

Moreover, Equations (69), (71) (76) and (77) will give the eigenvalues of the isovector pairing Hamiltonian $H_p^{(\beta )}$ as

$${\displaystyle {⟨H_p^{(\beta )}⟩}^{m,T;v,t}=-\frac{G}{4}\left[(m-v)\left(2\mathrm{\Omega }+3-\frac{m+v}{2}\right)-2T(T+1)+2t(t+1)\right].}$$

(80)

Note that $S{O}^{(\beta )}(5)\supset [SO(3)\supset SO(2)]\otimes U(1)$ subalgebra with $SO(3)$ generating T, $SO(2)$ generating $M_T$ ($T_z$ quantum number (N-Z)/2) and $U(1)$ generating particle number or $H_1=(m-2\mathrm{\Omega })/2$. Then, the eigenstates of $H_p^{(\beta )}$ are

$$\left|{\mathsf{\Psi }}_{H_p^{(\beta )}}\right.⟩\Rightarrow \left|(\mathrm{\Omega }-\frac{v}{2},t),H_1=\frac{m-2\mathrm{\Omega }}{2},T,M_T=\frac{N-Z}{2},\alpha \right.⟩.$$

(81)

In Equation (81), $\alpha$ are additional labels that may be needed for complete classification of the eigenstates. Though the labels in Equation (81) do not depend on $(\beta )$, explicit structure of the wavefunctions do depend on $(\beta )$; see Section 4.3. Thus, they will effect various selection rules and matrix elements of certain transition operators (see Section 4.3). Finally, with $SO(5)$ algebra it is possible to factorize $(m,T)$ dependence of various matrix elements and this is the most important application of $SO(5)$ pairing algebra [7,33,42].

4.2. Classification of Symmetry Adopted States and Their Construction

4.2.1. Classification of States

The first important question to be addressed, in applications of $SO(5)/Sp(2\mathrm{\Omega })$, is enumeration of the irrep labels in Equation (81). To this end we will use $[U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })]\otimes S{U}_T(2)$. Rules for enumerating the $U(2\mathrm{\Omega })$ irreps $\left\{2^a{1}^b\right\}$ allowed for a given $Sp(2\mathrm{\Omega })$ irrep $⟨2^{v_1}{1}^{v_2}⟩$ are well known [116,119,120,121] and used for example in [53]. The allowed $\left\{2^a{1}^b\right\}$ irreps are given by the $U(2\mathrm{\Omega })$ Kronecker product of the irrep $\left\{2^{v_1}{1}^{v_2}\right\}$ with all allowed $\left\{2^{2r}{1}^{2s}\right\}$ type irreps. All final irreps $\left\{2^a{1}^b\right\}$ are irreps for m nucleons with $m=2a+b$ and $T=b/2$ (where appropriate, we need to use particle-hole equivalence of $U(2\mathrm{\Omega })$ irreps). Let us consider $v=0$ states and then $t=0$ and $⟨2^{v_1}{1}^{v_2}⟩=⟨0⟩$. Therefore, for $(v,t)=(0,0)$ we have

$$\begin{array}{ccc}\hfill \left\{2^a{1}^b\right\}& =& \left\{2^{2r}{1}^{2s}\right\}\Rightarrow m=4r+2s,T=s\hfill \\ \hfill \hspace{1em}\hspace{1em}\Rightarrow & & {\displaystyle T=\frac{m}{2}-2r=\frac{m}{2},\frac{m}{2}-2,\frac{m}{2}-4,\dots }\hfill \end{array}$$

(82)

Note that here m is even. For $v=1$ we have $t=\frac{1}{2}$ and then $⟨2^{v_1}{1}^{v_2}⟩=⟨1⟩$. Therefore, for $(v,t)=(1,\frac{1}{2})$ we have

$$\begin{array}{ccc}\hfill \left\{2^a{1}^b\right\}& =& \left\{2^{2r}{1}^{2s}\right\}\times \left\{1\right\}=\left\{2^{2r}{1}^{2s+1}\right\}\oplus {\left\{2^{2r+1}{1}^{2s-1}\right\}}_{s\ge 1},\hfill \\ \hfill \left\{2^{2r}{1}^{2s+1}\right\}& \Rightarrow & m=4r+2s+1,T=s+\frac{1}{2}\hfill \\ & \Rightarrow & {\displaystyle T=\frac{m}{2}-2r=\frac{m}{2},\frac{m}{2}-2,\frac{m}{2}-4,\dots ,}\hfill \\ \hfill \left\{2^{2r+1}{1}^{2s-1}\right\}& \Rightarrow & m=4r+2s+1,T=s-\frac{1}{2}\hfill \\ & \Rightarrow & {\displaystyle T=\frac{m}{2}-2r-1=\frac{m}{2}-1,\frac{m}{2}-3,\frac{m}{2}-5,\dots .}\hfill \end{array}$$

(83)

Note that m is odd here. Results in Equations (82) and (83) are given in [7] and in many other papers by using quite different methods. Proceeding further with $v=2$, there are two irreps $⟨2⟩$ and $⟨1^2⟩$ and they correspond to $(v,t)=(2,0)$ and $(2,1)$ respectively. Then, for $(v,t)=(2,0)$ we have

$$\begin{array}{ccc}\hfill \left\{2^a{1}^b\right\}& =& \left\{2^{2r}{1}^{2s}\right\}\times \left\{2\right\}=\left\{2^{2r+1}{1}^{2s}\right\}\Rightarrow m=4r+2s+2,T=s\hfill \\ & \Rightarrow & {\displaystyle T=\frac{m}{2}-2r-1=\frac{m}{2}-1,\frac{m}{2}-3,\frac{m}{2}-5,\dots .}\hfill \end{array}$$

(84)

Finally, for $(v,t)=(2,1)$ we have

$$\begin{array}{ccc}\hfill \left\{2^a{1}^b\right\}& =& \left\{2^{2r}{1}^{2s}\right\}\times \left\{1^2\right\}={\left\{2^{2r+1}{1}^{2s}\right\}}_{s\ge 1}\oplus \left\{2^{2r}{1}^{2s+2}\right\}\oplus {\left\{2^{2r+2}{1}^{2s-2}\right\}}_{s\ge 1},\hfill \\ \hfill \left\{2^{2r+1}{1}^{2s}\right\}& \Rightarrow & m=4r+2s+2,T=s=\frac{m}{2}-2r-1,\hfill \\ \hfill \left\{2^{2r}{1}^{2s+2}\right\}& \Rightarrow & m=4r+2s+2,T=s+1=\frac{m}{2}-2r,\hfill \\ \hfill \left\{2^{2r+2}{1}^{2s-2}\right\}& \Rightarrow & m=4r+2s+2,T=s-1=\frac{m}{2}-2r-2.\hfill \end{array}$$

(85)

Note that here m is even and $r=0,1,2,\dots$. A significant result that follows from Equation (85) is that here there will be T multiplicity. Moreover, in Equations (82)–(85) we need to apply particle-hole relation where appropriate (see Table 1, Table 2, Table 3 and Table 4 for examples).

Table 2. Allowed T values for $m=8$, 6, 4, 2 and 0 number of nucleons in an orbit for $(v,t)=(0,0)$, $(2,0)$ and $(2,1)$. Results in column 3 are for $\mathrm{\Omega }=6$ and in column 6 are for $\mathrm{\Omega }=5$. See Section 4.2.1 for further discussion.

$\mathrm{\Omega }=6$			$\mathrm{\Omega }=5$
$\mathit{m}$	$(\mathit{v},\mathit{t})$	$\mathit{T}$	$\mathit{m}$	$(\mathit{v},\mathit{t})$	$\mathit{T}$
8	$(0,0)$	0, $2^2$	8	$(0,0)$	0, 1, 2
	$(2,0)$	1, 3		$(2,0)$	1, 3
	$(2,1)$	0, 1, $2^3$, 3		$(2,1)$	0, $1^2$, $2^2$, 3
6	$(0,0)$	1, 3	6	$(0,0)$	1, 2
	$(2,0)$	0, 2		$(2,0)$	0, 2
	$(2,1)$	$1^2$, 2, 3		$(2,1)$	$1^2$, $2^2$
4	$(0,0)$	0, 2	4	$(0,0)$	0, 2
	$(2,0)$	1		$(2,0)$	1
	$(2,1)$	0, 1, 2		$(2,1)$	0, 1, 2
2	$(0,0)$	1	2	$(0,0)$	1
	$(2,0)$	0		$(2,0)$	0
	$(2,1)$	1		$(2,1)$	1
0	$(00)$	0	0	$(0,0)$	0

Table 3. Basis states for a $m=8$ system with $T=0$ and positive parity. Quantum numbers are shown for seniorities in the two orbits $v_1$ and $v_2\le 2$. See Section 4.2.1 for further discussion.

$\#$	$\left|({\mathit{v}}_1,{\mathit{t}}_1){\mathit{m}}_1,{\mathit{T}}_1:({\mathit{v}}_2,{\mathit{t}}_2){\mathit{m}}_2,{\mathit{T}}_2;\mathit{T}=0\right.⟩$
1	$\left|(0,0),8,0:(0,0)0,0;0\right.⟩$
2	$\left|(2,1),8,0:(0,0)0,0;0\right.⟩$
3	$\left|(0,0),6,1:(0,0)2,1;0\right.⟩$
4	$\left|(0,0),6,1:(2,1)2,1;0\right.⟩$
5	$\left|(2,1),6,1_a:(0,0)2,1;0\right.⟩$
6	$\left|(2,1),6,1_b:(0,0)2,1;0\right.⟩$
7	$\left|(2,1),6,1_a:(2,1)2,1;0\right.⟩$
8	$\left|(2,1),6,1_b:(2,1)2,1;0\right.⟩$
9	$\left|(2,0),6,0:(2,0)2,0;0\right.⟩$
10	$\left|(0,0),4,0:(0,0)4,0;0\right.⟩$
11	$\left|(0,0),4,0:(2,1)4,0;0\right.⟩$
12	$\left|(2,1),4,0:(0,0)4,0;0\right.⟩$
13	$\left|(2,1),4,0:(2,1)4,0;0\right.⟩$
14	$\left|(2,0),4,1:(2,0)4,1;0\right.⟩$
15	$\left|(2,0),4,1:(2,1)4,1;0\right.⟩$
16	$\left|(2,1),4,1:(2,0)4,1;0\right.⟩$
17	$\left|(2,1),4,1:(2,1)4,1;0\right.⟩$
18	$\left|(0,0),4,2:(0,0)4,2;0\right.⟩$
19	$\left|(0,0),4,2:(2,1)4,2;0\right.⟩$
20	$\left|(2,1),4,2:(0,0)4,2;0\right.⟩$
21	$\left|(2,1),4,2:(2,1)4,2;0\right.⟩$
22	$\left|(0,0),2,1:(0,0)6,1;0\right.⟩$
23	$\left|(0,0),2,1:(2,1)6,1_a;0\right.⟩$
24	$\left|(0,0),2,1:(2,1)6,1_b;0\right.⟩$
25	$\left|(2,1),2,1:(0,0)6,1;0\right.⟩$
26	$\left|(2,1),2,1:(2,1)6,1_a;0\right.⟩$
27	$\left|(2,1),2,1:(2,1)6,1_b;0\right.⟩$
28	$\left|(2,0),2,0:(2,0)6,0;0\right.⟩$
29	$\left|(0,0),0,0:(0,0)8,0;0\right.⟩$
30	$\left|(0,0),0,0:(2,1)8,0;0\right.⟩$

In reality, when pairing is important, often it is sufficient to enumerate the allowed T values for a given $(v,t)$ and m with seniority $v=0$, 1 and 2. However, the procedure used above extends to any v. For example, for the $(m=6,\mathrm{\Omega }=6)$ system, for $v=4$ the $\left\{2^{2r}{1}^{2s}\right\}=\left\{1^2\right\}$ only. Therefore, for $(v,t)=(4,0)$ we have $\left\{2^a{1}^b\right\}=\left\{1^2\right\}\times \left\{2^2\right\}=\left\{2^2{1}^2\right\}$ giving $T=1$ only. For $(v,t)=(4,1)$ we have $\left\{1^2\right\}\times \left\{{21}^2\right\}=\left\{2^3\right\}+\left\{2^2{1}^2\right\}+\left\{{21}^4\right\}$ giving $T=0$, 1 and 2. Similarly, for $(v,t)=(4,2)$ we have $\left\{1^2\right\}\times \left\{1^4\right\}=\left\{1^6\right\}+\left\{{21}^4\right\}+\left\{2^2{1}^2\right\}$ giving $T=1$, 2 and 3. Finally, for $v=6$ we have $(v,t)=(6,0)\to T=0$, $(v,t)=(6,1)\to T=1$, $(v,t)=(6,2)\to T=2$ and $(v,t)=(6,3)\to T=3$. In the same manner, for $m=4$ with $v=4$ we have $(v,t)=(4,0)\to T=0$, $(v,t)=(4,1)\to T=1$ and $(v,t)=(4,2)\to T=2$.

Table 2 gives some examples for the basis state quantum numbers for $m=8$, 6, 4, 2 and 0. Considered are systems with $\mathrm{\Omega }=5$ and 6. These results are obtained using the formulas in Equations (82)–(85). It is useful to note that in the table $T^x$ means T is appearing x number of times. In some of the results in the table we have applied particle hole equivalence. For example for $m=8$, $\mathrm{\Omega }=6$ and $(v,t)=(00)$ in Equation (82) for $r=0$ and $s=4$, the $U(12)$ irrep $\left\{1^8\right\}$ goes to $\left\{1^4\right\}$ due to $p-h$ equivalence giving $T=2$ instead of 4. Similarly, for $m=8$, $\mathrm{\Omega }=5$ and $(v,t)=(00)$ the $U(10)$ irrep $\left\{1^8\right\}$ goes to $\left\{1^2\right\}$ giving $T=1$ instead of $T=4$ and for $m=6$, the $\left\{1^6\right\}$ goes to $\left\{1^4\right\}$ giving $T=2$ instead of 6. In addition for some other $(v,t)$, the restrictions on s in Equation (85) apply. Given the results in Table 2, the basis states with positive parity and $T=0$ for an example of eight nucleons in two-orbits, with the first orbit having ${\mathrm{\Omega }}_1=6$ with −ve parity and second orbit having ${\mathrm{\Omega }}_2=5$ with positive parity, will be 30 in number. These are listed in Table 3.

4.2.2. Construction of Many-Particle Pairing H Matrix with Multiple $SO(5)$ Algebras

In order to probe the role of multiple pair $S{O}^{(\beta )}(5)$ algebras with isospin, we need to obtain the eigenstates of the pairing Hamiltonian ${\mathcal{H}}_p$ as a function of $\left\{\beta \right\}$’s. A convenient basis for constructing the ${\mathcal{H}}_p$ matrix is the product basis defined by the single-j shell $SO(5)$ basis. We will illustrate this using two j-orbits, say $j_1$ and $j_2$. Hereafter, we call the corresponding spaces a and b respectively (or 1 and 2). Then, the basis states are,

$$\begin{array}{ccc}\hfill {\mathsf{\Psi }}_{ab}(T{M}_T)& =& \left|({\omega }_1^a{\omega }_2^a){\beta }^a{H}^a{T}^a,({\omega }_1^b{\omega }_2^b){\beta }^b{H}^b{T}^b;T{M}_T\right.⟩\hfill \\ & \leftrightarrow & \left|(v_1,t_1){\beta }_1{m}_1{T}_1,(v_2,t_2){\beta }_2{m}_2{T}_2;T{M}_T\right.⟩\hfill \end{array}$$

(86)

Given m number of nucleons with nucleons $m_1$ in number in the first orbit and $m_2$ in the second orbit, $m=m_1+m_2$. Then, with ${\mathrm{\Omega }}_1=j_1+\frac{1}{2}$ and ${\mathrm{\Omega }}_2=j_2+\frac{1}{2}$, we have $H^a=\frac{m_1}{2}-{\mathrm{\Omega }}_1$ and $H^b=\frac{m_2}{2}-{\mathrm{\Omega }}_2$. Similarly $T^a$ and $T^b$ are the isospins in the two spaces respectively. Furthermore, the ${\beta }^r$ (or ${\beta }_r$) labels are additional labels that are required as discussed in [33,35]; see Equation (90) ahead. In the second line in Equation (86), we used the equivalent and often simpler $(v_i,t_i)$ labels and $m_i$ instead of $H^a$ (or $H^b$). Now, a general pairing Hamiltonian is,

$$\begin{array}{c}{\displaystyle {\mathcal{H}}_p(\xi ,\alpha )=\frac{(1-\xi )}{m}{\widehat{n}}_2-\frac{\xi }{m^2}\left\{{\displaystyle 4\sum _{\mu }{\mathcal{A}}_{\mu }^1(\alpha ){\left[{\mathcal{A}}_{\mu }^1(\alpha )\right]}^{†}}\right\};}\hfill \\ {\mathcal{A}}_{\mu }^1(\alpha )=A_{\mu }^1(j_1)+\alpha A_{\mu }^1(j_2)\hfill \end{array}$$

(87)

Here ${\widehat{n}}_2$ is the number operator for the second orbit and $\xi$ and $\alpha$ are parameters changing from 0 to 1 and $+1$ to $-1$ respectively. Note that for $\xi =1$ and $\alpha =+1$ we have a $S{O}^{(+)}(5)$ algebra in the total two-orbit space and similarly for $\xi =1$ and $\alpha =-1$ the $S{O}^{(-)}(5)$ algebra. This follows from the results in Section 4.1.

The diagonal matrix elements of ${\mathcal{H}}_p$ in the basis defined by Equation (86) follow easily from Equations (79) and (80) and they will be independent of the $\beta$ labels. With ${\widehat{n}}_2$ giving $m_2$ in the chosen basis, we have

$$\begin{array}{c}⟨(v_1,t_1){\beta }_1{m}_1{T}_1,(v_2,t_2){\beta }_2{m}_2{T}_2;T{M}_T\mid {\mathcal{H}}_p(\xi ,\alpha )\mid (v_1,t_1){\beta }_1{m}_1{T}_1,(v_2,t_2){\beta }_2{m}_2{T}_2;T{M}_T⟩\hfill \\ {\displaystyle =\frac{(1-\xi )}{m}{m}_2-\frac{\xi }{m^2}\left[A+{\alpha }^{2}B\right];}\hfill \\ A=\left\{(m_1-v_1)\left(2{\mathrm{\Omega }}_1+3-\frac{m_1+v_1}{2}\right)-2T_1(2T_1+1)+2t_1(t_1+1)\right\},\hfill \\ B=\left\{(m_2-v_2)\left(2{\mathrm{\Omega }}_2+3-\frac{m_2+v_2}{2}\right)-2T_2(2T_2+1)+2t_2(t_2+1)\right\}.\hfill \end{array}$$

(88)

Similarly, off-diagonal matrix elements follow from the $SO(5)\supset [S{O}_T(3)\supset SO(2)]\otimes U(1)$ tensorial structure of $A_{\mu }^1(j)$ and ${\left[A_{\mu }^1(j)\right]}^{†}$ operators. The general tensorial form is $T_{H_1,T,M_T}^{({\omega }_1,{\omega }_2)}$. Then, $A_{\mu }^1(j)$ tensorial structure in the j-space is $T_{1,1,\mu }^{(11)}$ and ${\left[A_{\mu }^1(j)\right]}^{†}$ tensorial structure within a phase factor is $T_{-1,1,-\mu }^{(11)}$. Now, the off-diagonal matrix elements of ${\mathcal{H}}_p$ are first written in terms of the product of the reduced matrix elements of $A^1(j_1)$ and ${\left[A^1(j_2)\right]}^{†}$ in the $j_1$ and $j_2$ spaces. Then, applying the Wigner–Eckart theorem using the $SO(5)\supset SO(3)\otimes U(1)$ reduced Wigner coefficients and the formula

$$⟨({\omega }_1{\omega }_2)\mid \mid T^{(11)}\mid \mid ({\omega }_1{\omega }_2)⟩={\left[({\omega }_1({\omega }_1+3)+{\omega }_2({\omega }_2+1)\right]}^{1/2}$$

as described in detail in [33] (see Equation (14) of this paper) will finally give,

$$\begin{array}{c}⟨({\omega }_1^a{\omega }_2^a){\beta }_f^a{H}_f^a{T}_f^a,({\omega }_1^b{\omega }_2^b){\beta }_f^b{H}_f^b{T}_f^b;T{M}_T\mid {\mathcal{H}}_p(\zeta ,\alpha )\hfill \\ \mid ({\omega }_1^a{\omega }_2^a){\beta }_i^a{H}_i^a{T}_i^a,({\omega }_1^b{\omega }_2^b){\beta }_i^b{H}_i^b{T}_i^b;T{M}_T⟩=-\left({\displaystyle \frac{4\xi }{m^2}}\right)(\alpha )\hfill \\ \times {\left[({\omega }_1^a({\omega }_1^a+3)+{\omega }_2^a({\omega }_2^a+1)\right]}^{1/2}{\left[({\omega }_1^b({\omega }_1^b+3)+{\omega }_2^b({\omega }_2^b+1)\right]}^{1/2}\hfill \\ {\displaystyle \times {(-1)}^{T_f^a+T_f^b+T+1}\sqrt{(2T_f^a+1)(2T_f^b+1)}\left\{\begin{array}{ccc}T& T_f^b& T_f^a\\ 1& T_i^a& T_i^b\end{array}\right\}}\hfill \\ \times ⟨({\omega }_1^a{\omega }_2^a){\beta }_i^a{H}_i^a{T}_i^a(11)1,1\mid \mid ({\omega }_1^a{\omega }_2^a){\beta }_f^a{H}_f^a{T}_f^a⟩\hfill \\ \times ⟨({\omega }_1^b{\omega }_2^b){\beta }_i^b{H}_i^b{T}_i^b(11)-1,1\mid \mid ({\omega }_1^b{\omega }_2^b){\beta }_f^b{H}_f^b{T}_f^b⟩.\hfill \end{array}$$

(89)

Note that $H_i^a=\frac{m_1}{2}-{\mathrm{\Omega }}_1$, $H_i^b=\frac{m_2}{2}-{\mathrm{\Omega }}_2$, $H_f^a=\frac{m_1+2}{2}-{\mathrm{\Omega }}_1$ and $H_f^b=\frac{m_2-2}{2}-{\mathrm{\Omega }}_2$. Similarly, the $⟨----\mid \mid ----⟩$ are the $SO(5)\supset SO(3)\otimes U(1)$ reduced Wigner coefficients.

For the $m=6$ system considered in the next section, the needed Wigner coefficients follow from Tables III in [33] and Table A.1 of [35]. It is important to mention that the $\beta$ labels are not needed for the $SO(5)$ irreps of the type $(\omega ,0)$. For the $(\omega ,1)$ irreps used is the $\beta$ label as defined in [35]. This gives for example for $T\le 1$, in the convention used in [35],

$$\begin{array}{c}\mathrm{for}(\omega ,1)\mathrm{irrep}\hfill \\ H_1=-\omega ,T=1\to \beta =2\hfill \\ H_1=-\omega +1,T=0\to \beta =1\hfill \\ H_1=-\omega +1,T=1\to \beta =0\hfill \\ H_1=-\omega +2,T=1^2\to \beta =1,2\hfill \\ H_1=-\omega +3,T=0\to \beta =1\hfill \\ H_1=-\omega +3,T=1\to \beta =0\hfill \end{array}$$

(90)

Finally, Equation (89) can be extended to three or more orbits by using isospin T couplings. Thus, ${\mathcal{H}}_p$ construction is possible with multiple $S{O}^{(\beta })(5)$ algebras provided all the needed Wigner coefficients in Equation (89) are known. It is useful to add that the basis defined by Equation (86), with multi-orbit extension was employed in the Rochester–Oak Ridge shell model code [15].

4.3. Applications of Multiple $SO(5)$ and $Sp(2\mathrm{\Omega })$ Algebras

4.3.1. Selection Rules for Electromagnetic Transitions

Electromagnetic transition operators $T^{EL}$ and $T^{ML}$ are one-body operators and selection rules for these follow from their $SO(5)\supset [S{O}_T(3)\supset SO(2)]\otimes U(1)$ tensorial structure. The general tensorial form is $T_{H_1,T,M_T}^{({\omega }_1,{\omega }_2)}$. Firstly, the creation operators transform as $T_{\frac{1}{2},\frac{1}{2},\pm \frac{1}{2}}^{(\frac{1}{2},\frac{1}{2})}$. Similarly, the annihilation operator with an appropriate phase factor transforms as $T_{-\frac{1}{2},\frac{1}{2},\pm \frac{1}{2}}^{(\frac{1}{2},\frac{1}{2})}$. Therefore the $SO(5)$ tensorial structure of one-body operators (they will be of the form $a^{†}a$) is given by $({\omega }_1,{\omega }_2)$ where

$$({\omega }_1,{\omega }_2)=\left(\frac{1}{2},\frac{1}{2}\right)\times \left(\frac{1}{2},\frac{1}{2}\right)=(11)\oplus (10)\oplus (00).$$

(91)

Note that $(11)$ irrep is ten-dimensional, $(10)$ five-dimensional and $(00)$ is one-dimensional. The general formula for $SO(5)$ dimensions is [116,118],

$${\displaystyle d({\omega }_1{\omega }_2)=\frac{({\omega }_1-{\omega }_2+1)({\omega }_1+{\omega }_2+2)(2{\omega }_1+3)(2{\omega }_2+1)}{6}.}$$

(92)

Clearly, the 10 $S{O}^{(\beta )}(5)$ generators transform as the $(11)$ irrep of $S{O}^{(\beta )}(5)$ but not as the $(11)$ irrep of another $S{O}^{({\beta }^{\prime })}(5)$ with $\beta \ne {\beta }^{\prime }$.

With $X=E$ or M, the general form of electric and magnetic multi-pole operators, ignoring the isospin part, is

$$\begin{array}{ccc}\hfill T_q^{XL}& =& {\displaystyle \sum _{j_1,j_2}{ϵ}_{j_1,j_2}^{XL}{\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^L}\hfill \\ & =& {\displaystyle \sum _j{ϵ}_{j,j}^{XL}{\left(a_j^{†}{\tilde{a}}_j\right)}_q^L+\sum _{j_1>j_2}{ϵ}_{j_1,j_2}^{XL}\left[{\displaystyle {\left(a_{j_1}^{†}{\tilde{a}}_{j_2}\right)}_q^L+\frac{{ϵ}_{j_2,j_1}^{XL}}{{ϵ}_{j_1,j_2}^{XL}}{\left(a_{j_2}^{†}{\tilde{a}}_{j_1}\right)}_q^L}\right].}\hfill \end{array}$$

(93)

As the electric $T^{EL}$ and magnetic $T^{ML}$L-th multi-pole transition operators are one-body operators, their $SO(5)$ tensorial character is $(11)\oplus (10)\oplus (00)$. Action of the $(00)$ part on a $SO(5)$ irrep $({\omega }_1{\omega }_2)$ is simple. The $(10)$ and $(11)$ parts acting on a state with $SO(5)$ irrep $({\omega }_1{\omega }_2)$ will generate states with $SO(5)$ irreps $({\omega }_1^f{\omega }_2^f)$ and the rules for enumerating the allowed $({\omega }_1^f{\omega }_2^f)$ correspond to the Kronecker product

$$({\omega }_1,{\omega }_2)\times (a,b)\to \sum ({\omega }_1^f,{\omega }_2^f)\oplus ;(a,b)=(1,0),(1,1).$$

For the irreps of interest for the examples considered in Section 4.2, Section 4.3.2 and Section 4.3.3 the following results for Kronecker products will suffice and they follow from the rules given in [116,119,120],

$$\begin{array}{ccc}\hfill (\omega ,0)\times (1,0)& \to & (\omega -1,0)\oplus (\omega +1,0)\oplus (\omega ,1),\hfill \\ \hfill (\omega ,1)\times (1,0)& \to & (\omega +1,1)\oplus {(\omega ,2)}_{\omega \ge 2}\oplus (\omega ,1)\oplus (\omega ,0)\oplus {(\omega -1,1)}_{\omega \ge 2},\hfill \\ \hfill (\omega ,0)\times (1,1)& \to & (\omega +1,1)\oplus (\omega ,1)\oplus (\omega ,0)\oplus {(\omega -1,1)}_{\omega \ge 2},\hfill \\ \hfill (2,1)\times (1,1)& \to & (1,0)\oplus (1,1)\oplus (2,0)\oplus {(2,1)}^2\oplus (2,2)\hfill \\ & \oplus & (3,0)\oplus (3,1)\oplus (3,2),\hfill \\ \hfill (4,1)\times (1,1)& \to & (3,0)\oplus (3,1)\oplus (3,2)\oplus (4,0)\oplus {(4,1)}^2\oplus (4,2)\hfill \\ & \oplus & (5,0)\oplus (5,1)\oplus (5,2).\hfill \end{array}$$

(94)

These can be changed easily into the rules for $(v,t)\times (a,b)\to (v^f,t^f)$.

With $H_1=0$ for one-body operators, a isoscalar $T_q^{XL}$ will be $(11)\oplus (00)$; the $(10)$ irrep gives only isovector operators. Thus, isoscalar $EM$ transition that involve states with different $(v,t)$ will be generated purely by the $(11)$ irrep part of $T^{XL}$. Further, Equations (61), (74) and (93) show that it is possible for $T^{EL}$ and $T^{ML}$ to be generators of $S{p}^{(\beta )}(2\mathrm{\Omega })$ depending on ${ϵ}_{j_2,j_1}^{XL}/{ϵ}_{j_1,j_2}^{XL}$. Then, they will preserve $(v,t)$ or $({\omega }_1{\omega }_2)$ quantum numbers (note that the group generators when acting on group irreps will not change the irrep labels). With these, we have the following results.

• The isovector parts of $T^{EL}$ and $T^{ML}$ will not be $S{p}^{(\beta )}(2\mathrm{\Omega })$ scalars as the generators of this algebra consists of only isoscalar operators.
• The $T^{EL}$ with L even (they preserve parity) will not be generators of any $S{p}^{(\beta )}(2\mathrm{\Omega })$ as $u^{k=even,t=0}(j,j)$ are not generators. In addition, even for L odd [they change parity and hence we need $j_f({\ell }_f)\ne j_i({\ell }_i)]$, the $T^{EL}$ will not be generators of $S{p}^{(\beta )}(2\mathrm{\Omega })$; see Equation (26).
• The isoscalar part of $T^{ML}$ with L odd (they preserve parity) can be $S{p}^{(\beta )}(2\mathrm{\Omega })$ scalars. Firstly, the first part of $T^{ML}$ as given by Equation (93) consists of only the generators of $S{p}^{(\beta )}(2\mathrm{\Omega })$ as L is odd. The second part also consists of only the generators provided one uses the Arvieu and Moszkowski [7,16] choice of ${\beta }_{j(\ell )}={(-1)}^{\ell }$ for the $j(\ell )$ orbits; see Equation (26).
• The $T^{ML}$ with L even will change parity and hence the $T^{ML}$ involve only the second part in Equation (93). Clearly, the isoscalar $T^{ML}$ will be $S{p}^{(\beta )}(2\mathrm{\Omega })$ scalars if ${\beta }_{j(\ell )}={(-1)}^{\ell }$ for the $j(\ell )$ orbits.

With the phase choice ${\beta }_{j(\ell )}={(-1)}^{\ell }$, the selection rule from the generators that they will not change $(v,t)$ or $({\omega }_1{\omega }_2)$ irreps can be used for $ML$ transitions in experimental tests. Moreover, if in an energy region high seniority v states occur with the immediate states below it having seniority $v^{\prime }<<v$, then all EL and ML transitions will be forbidden to these levels as EL and ML transitions can change seniority only by units of 2, i.e., transition for $v\to v\pm 2$ states only allowed. In addition, the $(m,T)$ dependence of, say, magnetic moments and $B(E2)$’s can be written down using the $SO(5)$ Wigner coefficients listed in [33,34,35]; see Ref. [7] for some examples.

4.3.2. Energy Levels and Order–Chaos Transitions

In the second application, let us consider a two level system with first level having ${\mathrm{\Omega }}_1=6$ with −ve parity and the second level having ${\mathrm{\Omega }}_2=5$ with +ve parity. This is appropriate for nuclei in A = 56–80 region so that the ($1p_{3/2}$, $0f_{5/2}$, $1p_{1/2}$) orbits with degenerate single particle levels giving the ${\mathrm{\Omega }}_1=6$ orbit (we will call it orbit #1 or (a) and $0g_{9/2}$ giving the ${\mathrm{\Omega }}_2=5$ orbit (we will call it orbit #2 or (b). In our numerical calculations we use the system with six nucleons in the above two orbits and without any restriction on $v_i$ in any of the two orbits. Then, the number of +ve parity basis states for $m=6$ and $T=0$ with all allowed $v_i$, $i=1,2$ ($v_i\le 6$) will be 24 and these are listed in Table 4. It is important to note that the $m=6$ basis states are multiplicity free.

Table 4. Basis states for the $m=6$ system with $T=0$ and for all allowed $v_1$ and $v_2$. Here, ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=5$. See Section 4.3.2 for further discussion.

$\#$	$\left|({\mathit{v}}_1,{\mathit{t}}_1){\mathit{m}}_1,{\mathit{T}}_1:({\mathit{v}}_2,{\mathit{t}}_2){\mathit{m}}_2,{\mathit{T}}_2;\mathit{T}=0\right.⟩$
1	$\left|(6,0),6,0:(0,0)0,0;0\right.⟩$
2	$\left|(4,1),6,0:(0,0)0,0;0\right.⟩$
3	$\left|(2,0),6,0:(0,0)0,0;0\right.⟩$
4	$\left|(4,0),4,0:(2,0)2,0;0\right.⟩$
5	$\left|(4,1),4,1:(0,0)2,1;0\right.⟩$
6	$\left|(4,1),4,1:(2,1)2,1;0\right.⟩$
7	$\left|(2,1),4,0:(2,0)2,0;0\right.⟩$
8	$\left|(2,0),4,1:(0,0)2,1;0\right.⟩$
9	$\left|(2,0),4,1:(2,1)2,1;0\right.⟩$
10	$\left|(2,1),4,1:(0,0)2,1;0\right.⟩$
11	$\left|(2,1),4,1:(2,1)2,1;0\right.⟩$
12	$\left|(0,0),4,0:(2,0)2,0;0\right.⟩$
13	$\left|(0,0),2,1:(4,1)4,1;0\right.⟩$
14	$\left|(2,0),2,0:(4,0)4,0;0\right.⟩$
15	$\left|(2,1),2,1:(4,1)4,1;0\right.⟩$
16	$\left|(2,0),2,0:(0,0)4,0;0\right.⟩$
17	$\left|(2,0),2,0:(2,1)4,0;0\right.⟩$
18	$\left|(2,1),2,1:(2,0)4,1;0\right.⟩$
19	$\left|(2,1),2,1:(2,1)4,1;0\right.⟩$
20	$\left|(0,0),2,1:(0,0)4,1;0\right.⟩$
21	$\left|(0,0),2,1:(2,1)4,1;0\right.⟩$
22	$\left|(0,0),0,0:(6,0)6,0;0\right.⟩$
23	$\left|(0,0),0,0:(4,1)6,0;0\right.⟩$
24	$\left|(0,0),0,0:(2,0)6,0;0\right.⟩$

Table 4. Basis states for the $m=6$ system with $T=0$ and for all allowed $v_1$ and $v_2$. Here, ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=5$. See Section 4.3.2 for further discussion.

$\#$	$\left|({\mathit{v}}_1,{\mathit{t}}_1){\mathit{m}}_1,{\mathit{T}}_1:({\mathit{v}}_2,{\mathit{t}}_2){\mathit{m}}_2,{\mathit{T}}_2;\mathit{T}=0\right.⟩$
1	$\left|(6,0),6,0:(0,0)0,0;0\right.⟩$
2	$\left|(4,1),6,0:(0,0)0,0;0\right.⟩$
3	$\left|(2,0),6,0:(0,0)0,0;0\right.⟩$
4	$\left|(4,0),4,0:(2,0)2,0;0\right.⟩$
5	$\left|(4,1),4,1:(0,0)2,1;0\right.⟩$
6	$\left|(4,1),4,1:(2,1)2,1;0\right.⟩$
7	$\left|(2,1),4,0:(2,0)2,0;0\right.⟩$
8	$\left|(2,0),4,1:(0,0)2,1;0\right.⟩$
9	$\left|(2,0),4,1:(2,1)2,1;0\right.⟩$
10	$\left|(2,1),4,1:(0,0)2,1;0\right.⟩$
11	$\left|(2,1),4,1:(2,1)2,1;0\right.⟩$
12	$\left|(0,0),4,0:(2,0)2,0;0\right.⟩$
13	$\left|(0,0),2,1:(4,1)4,1;0\right.⟩$
14	$\left|(2,0),2,0:(4,0)4,0;0\right.⟩$
15	$\left|(2,1),2,1:(4,1)4,1;0\right.⟩$
16	$\left|(2,0),2,0:(0,0)4,0;0\right.⟩$
17	$\left|(2,0),2,0:(2,1)4,0;0\right.⟩$
18	$\left|(2,1),2,1:(2,0)4,1;0\right.⟩$
19	$\left|(2,1),2,1:(2,1)4,1;0\right.⟩$
20	$\left|(0,0),2,1:(0,0)4,1;0\right.⟩$
21	$\left|(0,0),2,1:(2,1)4,1;0\right.⟩$
22	$\left|(0,0),0,0:(6,0)6,0;0\right.⟩$
23	$\left|(0,0),0,0:(4,1)6,0;0\right.⟩$
24	$\left|(0,0),0,0:(2,0)6,0;0\right.⟩$

Using the basis states in Table 4, the matrix for ${\mathcal{H}}_p$ defined by Equation (87) is constructed using Equation (88) for the diagonal matrix elements and Equation (89) for the off-diagonal matrix elements. The $SO(5)\supset SO(3)\otimes U(1)$ Wigner coefficients needed are all available from Table III in [33] and Table A.1 in [35]. As we are using all allowed $(v_i{t}_i)$ states in the ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=5$ space for six nucleons ($m=6$) with $T=0$, diagonalization of ${\mathcal{H}}_p(\xi =1,\alpha =\pm 1)$ will give eigenvalues that must be same as those given by Equation (80) with $(\mathrm{\Omega }=11,m=6,T=0)$ and $(v,t)=(6,0)$, $(4,1)$ and $(2,0)$. The eigenvalues are 0, $-1.222$ and $-2.333$ respectively. Thus, there will be degeneracies in the spectrum. There are two states with eigenvalue $-2.333$ and $(v,t)=(2,0)$, nine with eigenvalue $-1.222$ and $(v,t)=(4,1)$ and thirteen with eigenvalue 0 and $(v,t)=(6,0)$. It is easy to see that the wavefunctions are of the form $\left|(v_1,t_1)(v_2,t_2)(v,t)\gamma ,m=6,T=0\right.⟩$ where $\gamma$ are additional labels. Therefore, a sum of ${\mathcal{C}}_2(S{O}^{(a)}(5))$ and ${\mathcal{C}}_2(S{O}^{(b)}(5))$ will remove some of the degeneracies in the spectrum without changing the eigenvectors. Following this, we have added the term $-(\xi /m^2)[{\mathcal{C}}_2(S{O}^{(a)}(5))+\frac{3}{4}{\mathcal{C}}_2(S{O}^{(b)}(5))]$ to ${\mathcal{H}}_p(\xi ,\alpha )$, i.e., used the modified Hamiltonian

$$\begin{array}{c}{\displaystyle {\mathcal{H}}_p^{mod}(\xi ,\alpha )=\frac{(1-\xi )}{m}{\widehat{n}}_2-\frac{\xi }{m^2}\left\{{\displaystyle 4\sum _{\mu }{\mathcal{A}}_{\mu }^1(\alpha ){\left[{\mathcal{A}}_{\mu }^1(\alpha )\right]}^{†}+{\mathcal{C}}_2(S{O}^a(5))+\frac{3}{4}{\mathcal{C}}_2(S{O}^b(5))}\right\}}\hfill \end{array}$$

(95)

and calculated the eigenvalues for the $(m=6,T=0)$ system. Shown in Figure 5 are the energies of the 24 states as a function of $\xi$ for nine $\alpha$ values. In Table 5 the wavefunctions structure for $\alpha =\pm 1$ (with $\xi =1$) is shown for all the 24 wavefunctions. With the $\alpha$ dependence shown in the Table, clearly the two $S{O}^{(+)}(5)$ and $S{O}^{(-)}(5)$ limits generate different results for EM transition strengths, two nucleon transfer (TNT) strengths etc. Some TNT examples are discussed in the next subsection.

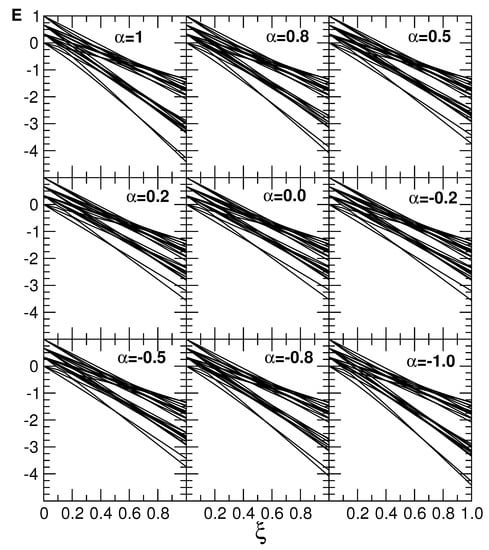
Figure 5. Energy spectra generated by the pairing Hamiltonian ${\mathcal{H}}_p^{mod}$ in Equation (95) as a function of $\xi$ and $\alpha$. Note that the energies (E) are unitless. Results are for a two-orbit system with $(m=6,T=0)$. See Section 4.3.2 for further discussion.

Table 5. Eigenvalues (E) and eigenstates ($\mathsf{\Psi }$) for the $m=6$ system with $T=0$ and positive parity. Eigenstates are given as an expansion in the basis states given in Table 4. As stated in the text, eigenstates are of the form $\left|m(v_1{t}_1)(v_2{t}_2)(vt)T=0\right.⟩$. See Section 4.3.2 for further discussion.

E	$\mathsf{\Psi }$
$-4.417$	$\left|6(0,0)(2,0)(2,0)T=0\right.⟩=\sqrt{\frac{13}{35}}\left|4(0,0)0:2(2,0)0;0\right.⟩-\alpha \sqrt{\frac{16}{35}}\left|2(0,0)1:4(2,0)1;0\right.⟩+\sqrt{\frac{6}{35}}\left|0(0,0)0:6(2,0)0;0\right.⟩$
$-4.278$	$\left|6(2,0)(0,0)(2,0)T=0\right.⟩=\sqrt{\frac{11}{42}}\left|6(2,0)0:0(0,0)0;0\right.⟩-\alpha \sqrt{\frac{20}{42}}\left|4(2,0)1:2(0,0)1;0\right.⟩+\sqrt{\frac{11}{42}}\left|2(2,0)0:4(0,0)0;0\right.⟩$
$-3.347$	$\left|6(0,0)(2,1)(4,1)T=0\right.⟩=\left|2(0,0)1:4(2,1)1;0\right.⟩$
$-3.306$	$\left|6(0,0)(2,0)(4,1)T=0\right.⟩=\sqrt{\frac{26}{55}}\left|4(0,0)0:2(2,0)0;0\right.⟩+\alpha \sqrt{\frac{2}{55}}\left|2(0,0)1:4(2,0)1;0\right.⟩-\sqrt{\frac{27}{35}}\left|0(0,0)0:6(2,0)0;0\right.⟩$
$-3.222$	$\left|6(2,1)(0,0)(4,1)T=0\right.⟩=\left|4(2,1)1:2(0,0)1;0\right.⟩$
$-3.167$	$\left|6(2,0)(0,0)(4,1)T=0\right.⟩=\sqrt{\frac{1}{2}}\left|6(2,0)0:2(0,0)0;0\right.⟩-\sqrt{\frac{1}{2}}\left|2(2,0)0:4(0,0)0;0\right.⟩$
$-3.139$	$\left|6(0,0)(4,1)(4,1)T=0\right.⟩=\sqrt{\frac{6}{11}}\left|2(0,0)1:4(4,1)1;0\right.⟩-\alpha \sqrt{\frac{5}{11}}\left|0(0,0)0:6(4,1)0;0\right.⟩$
$-3.014$	$\left|6(2,1)(2,1)(4,1)T=0\right.⟩=\sqrt{\frac{6}{11}}\left|4(2,1)1:2(2,1)1;0\right.⟩-\alpha \sqrt{\frac{5}{11}}\left|2(2,1)1:4(2,1)1;0\right.⟩$
$-2.972$	$\left|6(2,1)(2,0)(4,1)T=0\right.⟩=\sqrt{\frac{7}{11}}\left|4(2,1)0:2(2,0)0;0\right.⟩-\alpha \sqrt{\frac{4}{11}}\left|2(2,1)1:4(2,0)1;0\right.⟩$
$-2.958$	$\left|6(2,0)(2,1)(4,1)T=0\right.⟩=\sqrt{\frac{5}{11}}\left|4(2,0)1:2(2,1)1;0\right.⟩-\alpha \sqrt{\frac{6}{11}}\left|2(2,0)0:4(2,1)0;0\right.⟩$
$-2.889$	$\left|6(4,1)(0,0)(4,1)T=0\right.⟩=\sqrt{\frac{6}{11}}\left|6(4,1)0:0(0,0)0;0\right.⟩-\alpha \sqrt{\frac{5}{11}}\left|4(4,1)1:2(0,0)1;0\right.⟩$
$-2.083$	$\left|6(0,0)(2,0)(6,0)T=0\right.⟩=\sqrt{\frac{12}{77}}\left|4(0,0)0:2(2,0)0;0\right.⟩+\alpha \sqrt{\frac{39}{77}}\left|2(0,0)1:4(2,0)1;0\right.⟩+\sqrt{\frac{26}{77}}\left|0(0,0)0;6(2,0)0\right.⟩$
$-1.944$	$\left|6(2,0)(0,0)(6,0)T=0\right.⟩=\sqrt{\frac{5}{21}}\left|6(2,0)0:0(0,0)0;0\right.⟩+\alpha \sqrt{\frac{11}{21}}\left|4(2,0)1:2(0,0)1;0\right.⟩+\sqrt{\frac{5}{21}}\left|2(2,0)0:4(0,0)0;0\right.⟩$
$-1.917$	$\left|6(0,0)(4,1)(6,0)T=0\right.⟩=\sqrt{\frac{5}{11}}\left|2(0,0)1:4(4,1)1;0\right.⟩+\alpha \sqrt{\frac{6}{11}}\left|0(0,0)0:6(4,1)0;0\right.⟩$
$-1.792$	$\left|6(2,1)(2,1)(6,0)T=0\right.⟩=\sqrt{\frac{5}{11}}\left|4(2,1)1:2(2,1)1;0\right.⟩+\alpha \sqrt{\frac{6}{11}}\left|2(2,1)1:4(2,1)1;0\right.⟩$
$-1.750$	$\left|6(2,1)(2,0)(6,0)T=0\right.⟩=\sqrt{\frac{4}{11}}\left|4(2,1)0:2(2,0)0;0\right.⟩+\alpha \sqrt{\frac{7}{11}}\left|2(2,1)1:4(2,0)1;0\right.⟩$
$-1.736$	$\left|6(2,0)(2,1)(6,0)T=0\right.⟩=\sqrt{\frac{6}{11}}\left|4(2,0)1:2(2,1)1;0\right.⟩+\alpha \sqrt{\frac{5}{11}}\left|2(2,0)0:4(2,1)0;0\right.⟩$
$-1.708$	$\left|6(0,0)(6,0)(6,0)T=0\right.⟩=\left|0(0,0)0:6(6,0)0;0\right.⟩$
$-1.667$	$\left|6(4,1)(0,0)(6,0)T=0\right.⟩=\sqrt{\frac{5}{11}}\left|6(4,1)0:0(0,0)0;0\right.⟩+\alpha \sqrt{\frac{6}{11}}\left|4(4,1)1:2(0,0)1;0\right.⟩$
$-1.583$	$\left|6(2,1)(4,1)(6,0)T=0\right.⟩=\left|2(2,1)1:4(4,1)1;0\right.⟩$
$-1.486$	$\left|6(2,0)(4,0)(6,0)T=0\right.⟩=\left|2(2,0)0:4(4,0)0;0\right.⟩$
$-1.458$	$\left|6(4,1)(2,1)(6,0)T=0\right.⟩=\left|4(4,1)1:2(2,1)1;0\right.⟩$
$-1.361$	$\left|6(4,0)(2,0)(6,0)T=0\right.⟩=\left|4(4,0)0:2(2,0)0;0\right.⟩$
$-1.333$	$\left|6(6,0)(0,0)(6,0)T=0\right.⟩=\left|6(6,0)0:0(0,0)0;0\right.⟩$

As seen from Figure 5, clearly by changing $(\xi ,\alpha )$ it is possible to study order–chaos–order transitions as the spectrum for $\alpha =+1$ and $\alpha =-1$ is identical. The QPT here is smoothed as we have a fermion system and the particle number is not large. It is easy to see that as we change $\xi$ and $\alpha$, there is transition among the following three group chains

$$\begin{array}{c}I.U(4\mathrm{\Omega })\supset U(4{\mathrm{\Omega }}_1)\oplus U(4{\mathrm{\Omega }}_2)\supset \left[Sp(2{\mathrm{\Omega }}_1)\otimes S{U}_{T_1}(2)\right]\oplus \left[Sp(2{\mathrm{\Omega }}_2)\otimes S{U}_{T_2}(2)\right]\hfill \\ \supset K\otimes S{U}_T(2)\hfill \\ II.U(4\mathrm{\Omega })\supset S{p}^{(+)}(2\mathrm{\Omega })\otimes S{U}_T(2)\supset \left[Sp(2{\mathrm{\Omega }}_1)\oplus Sp(2{\mathrm{\Omega }}_2)\right]\otimes S{U}_T(2)\hfill \\ \supset K\otimes S{U}_T(2)\hfill \\ III.U(4\mathrm{\Omega })\supset S{p}^{(-)}(2\mathrm{\Omega })\otimes S{U}_T(2)\supset \left[Sp(2{\mathrm{\Omega }}_1)\oplus Sp(2{\mathrm{\Omega }}_2)\right]\otimes S{U}_T(2)\hfill \\ \supset K\otimes S{U}_T(2)\hfill \end{array}$$

(96)

The algebra K above will not play any role when we use the Hamiltonian in Equation (95). Further analysis of the QPT involving the three limits in Equation (96) is important and this needs to be addressed in future.

4.3.3. Two-Nucleon Transfer

In order to bring out explicitly the role of multiple $SO(5)$ algebras, we will consider in this Subsection two-particle transfer. As an example let us consider removal of a isovector pair from the lowest state (see Table 5) of the $(m=6,T=0)$ system considered in Section 4.3.2 and this will generate some of the states of the $(m=4,T=1)$ system. To study the transfer strengths, we have diagonalized ${\mathcal{H}}_p^{mod}(\xi =1,\alpha =\pm 1)$ in $(m=4,T=1)$ space and the basis states here are 14 in number; see Table 6. Then, the eigenstates (see Table 7) belong to $(v,t)=(21)$, $(20)$ and $(41)$ irreps of $S{O}^{(\pm )}(5)$ in the four-nucleon space. There are three, two and nine states respectively with these irreps [the corresponding eigenvalues are $-2.75$, $-2.5$ and 0 respectively if we drop the ${\mathcal{C}}_2(SO(5))$ parts in Equation (95)]. The transition operator is chosen to be

$$P^1(\beta )={\left[A_{\mu }^1(1)\right]}^{†}+\beta {\left[A_{\mu }^1(2)\right]}^{†}$$

(97)

and $(1)$ and $(2)$ here correspond to the ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=5$ spaces. Acting with the operator P on the $(m=6,T=0)$ ground state (gs) will generate states #4 and #7 in Table 7 of the $(m=4,T=1)$ system. From Table 5 we have,

$$\begin{array}{ccc}\hfill \left|(m=6,T=0)gs\right.⟩& =& \sqrt{\frac{13}{35}}\left|4(0,0)0:2(2,0)0;T=0\right.⟩-\alpha \sqrt{\frac{16}{35}}\left|2(0,0)1:4(2,0)1;T=0\right.⟩\hfill \\ & +& \sqrt{\frac{6}{35}}\left|0(0,0)0:6(2,0)0;T=0\right.⟩\hfill \end{array}$$

(98)

Table 6. Basis states for the $m=4$ system with $T=1$ and for all allowed $v_1$ and $v_2$. Here, ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=5$. See Section 4.3.3 for further discussion.

$\#$	$\left|({\mathit{v}}_1,{\mathit{t}}_1){\mathit{m}}_1,{\mathit{T}}_1:({\mathit{v}}_2,{\mathit{t}}_2){\mathit{m}}_2,{\mathit{T}}_2;\mathit{T}=1\right.⟩$
1	$\left|(2,0),4,1:(0,0)0,0;1\right.⟩$
2	$\left|(2,1),4,1:(0,0)0,0;1\right.⟩$
3	$\left|(4,1),4,1:(0,0)0,0;1\right.⟩$
4	$\left|(2,0),2,0:(2,1)2,1;1\right.⟩$
5	$\left|(2,0),2,0:(0,0)2,1;1\right.⟩$
6	$\left|(2,1),2,1:(2,0)2,0;1\right.⟩$
7	$\left|(2,1),2,1:(2,1)2,1;1\right.⟩$
8	$\left|(2,1),2,1:(0,0)2,1;1\right.⟩$
9	$\left|(0,0),2,1:(2,0)2,0;1\right.⟩$
10	$\left|(0,0),2,1:(2,1)2,1;1\right.⟩$
11	$\left|(0,0),2,1:(0,0)2,1;1\right.⟩$
12	$\left|(0,0),0,0:(2,0)4,1;1\right.⟩$
13	$\left|(0,0),0,0:(2,1)4,1;1\right.⟩$
14	$\left|(0,0),0,0:(4,1)4,1;1\right.⟩$

Table 7. Eigenvalues (E) and eigenstates ($\mathsf{\Psi }$) for the $m=4$ system with $T=1$ and positive parity. Eigenstates are given as an expansion in the basis states given in Table 6. As stated in the text, eigenstates are of the form $\left|m(v_1{t}_1)(v_2{t}_2)(vt)T=1\right.⟩$. See Section 4.3.3 for further discussion.

#	E	$\mathsf{\Psi }$
$1$	$-8$	$\left|4(0,0)(0,0)(2,1)T=1\right.⟩=\left|2(0,0)1:2(0,0)1;T=1\right.⟩$
$2$	$-7.531$	$\left|4(0,0)(2,1)(2,1)T=1\right.⟩=\sqrt{\frac{6}{11}}\left|2(0,0)1:2(2,1)1;T=1\right.⟩-\alpha \sqrt{\frac{5}{11}}\left|0(0,0)0:4(2,1)1;T=1\right.⟩$
$3$	$-7.25$	$\left|4(2,1)(0,0)(2,1)T=1\right.⟩=\sqrt{\frac{6}{11}}\left|4(2,1)1:0(0,0)0;T=1\right.⟩+\alpha \sqrt{\frac{5}{11}}\left|2(2,1)1:2(0,0)1;T=1\right.⟩$
$4$	$-7.188$	$\left|4(0,0)(2,0)(2,0)T=1\right.⟩=\sqrt{\frac{3}{5}}\left|2(0,0)1:2(2,0)0;T=1\right.⟩+\alpha \sqrt{\frac{2}{5}}\left|0(0,0)0:4(2,0)1;T=1\right.⟩$
$5$	$-6.875$	$\left|4(2,0)(0,0)(2,0)T=1\right.⟩=\sqrt{\frac{1}{2}}\left|4(2,0)1;0(0,0)0\right.⟩+\alpha \sqrt{\frac{1}{2}}\left|2(2,0)0;2(0,0)1\right.⟩$
$6$	$-4.781$	$\left|4(0,0)(2,1)(4,1)T=1\right.⟩=\sqrt{\frac{5}{11}}\left|2(0,0)1:2(2,1)1;T=1\right.⟩+\alpha \sqrt{\frac{6}{11}}\left|0(0,0)0:4(2,1)1;T=1\right.⟩$
$7$	$-4.688$	$\left|4(0,0)(2,0)(4,1)T=1\right.⟩=\sqrt{\frac{2}{5}}\left|2(0,0)1:2(2,0)0;T=1\right.⟩-\alpha \sqrt{\frac{3}{5}}\left|0(0,0)0:4(2,0)1;T=1\right.⟩$
$8$	$-4.5$	$\left|4(2,1)(0,0)(4,1)T=1\right.⟩=\sqrt{\frac{5}{11}}\left|4(2,1)1:0(0,0)0;T=1\right.⟩-\alpha \sqrt{\frac{6}{11}}\left|2(2,1)1:2(2,0)1;T=1\right.⟩$
$9$	$-4.375$	$\left|4(2,0)(0,0)(4,1)T=1\right.⟩=\sqrt{\frac{1}{2}}\left|4(2,0)1:0(0,0)0;T=1\right.⟩-\alpha \sqrt{\frac{1}{2}}\left|2(2,0)0:2(0,0)1;T=1\right.⟩$
$10$	$-4.313$	$\left|4(0,0)(4,1)(4,1)T=1\right.⟩=\left|0(0,0)0:4(4,1)1;T=1\right.⟩$
$11$	$-4.031$	$\left|4(2,1)(2,1)(4,1)T=1\right.⟩=\left|2(2,1)1:2(2,1)1:T=1\right.⟩$
$12$	$-3.938$	$\left|4(2,1)(2,0)(4,1)T=1\right.⟩=\left|2(2,1)1:2(2,0)0;T=1\right.⟩$
$13$	$-3.906$	$\left|4(2,0)(2,1)(4,1)T=1\right.⟩=\left|2(2,0)0:2(2,1)1;T=1\right.⟩$
$14$	$-3.75$	$\left|4(4,1)(0,0)(4,1)T=0\right.⟩=\left|4(4,1)1:0(0,0)0;T=1\right.⟩$

As both ${\left[A_{\mu }^1(i)\right]}^{†}$ operators will not change $(v_1,t_1)$ and $(v_2,t_2)$ in Equation (98), clearly only the states #4 and #7 listed in Table 7 will be generated by the action of $P^1(\beta )$. Then, the transfer strengths are given by

$$\begin{array}{c}S(m=6,T=0:gs\to m=4,T=1:\#X)=\hfill \\ {\left|⟨m=4,T=1:X\mid \mid P^1(\beta )\mid \mid m=6,T=0:gs⟩\right|}^2;X=4,7.\hfill \end{array}$$

(99)

As all the states appearing in Equation (99) contain the $\alpha$ parameter [$\alpha =+1$ for $S{O}^{(+)}(5)$ and $\alpha =-1$ for $S{O}^{(-)}(5)$], the two-particle transfer strengths carry information about $\alpha$, i.e., multiple $SO(5)$ algebras. With the states having the structure $\left|(T_1{T}_2)T\right.⟩$, the reduced matrix elements in Equation (99) will be sum of the reduced matrix elements of ${\left[A^1(1)\right]}^{†}$ and ${\left[A^1(2)\right]}^{†}$ in the ${\mathrm{\Omega }}_1$ and ${\mathrm{\Omega }}_2$ spaces respectively (each multiplied by a factor as follows from Equations (7.1.7) and (7.1.8) in [78]). Formula for the reduced matrix elements of ${\left[A^1(i)\right]}^{†}$ is [33],

$$\begin{array}{c}⟨({\omega }_1{\omega }_2)H_f,T_f\mid \mid {\left[A^1\right]}^{†}\mid \mid ({\omega }_1{\omega }_2)H_i,T_i⟩={\left[({\omega }_1({\omega }_1+3)+{\omega }_2({\omega }_2+1)\right]}^{1/2}\hfill \\ {\displaystyle \times {(-1)}^{T_i+T_f+1}\sqrt{2T_i+1}⟨({\omega }_1{\omega }_2)H_f,T_f(11)1-1\mid \mid ({\omega }_1{\omega }_2)H_i,T_i⟩}\hfill \end{array}$$

(100)

All the $SO(5)$ Wigner coefficients in Equation (100) are available in [33]. Using these and carrying out all the simplifications will give

$$\begin{array}{c}{\displaystyle S(m=6,T=0:gs\to m=4,T=1:\#4)=\frac{21}{25}{\left[3+2\beta \alpha \right]}^2,}\hfill \\ {\displaystyle S(m=6,T=0:gs\to m=4,T=1:\#7)=\frac{2}{175}{\left[1-\beta \alpha \right]}^2.}\hfill \end{array}$$

(101)

It is clearly seen that for $\beta =\alpha$, the transition from $(m=6,T=0)gs$ to state #7 of $(m=4,T=1)$ system is forbidden. This is due to the fact that for $\beta =\alpha$, the transfer operator $P^1(\beta )$ is a generator of $S{O}^{(\alpha =\beta ))}(5)$ and the six-particle state belongs to $({\omega }_1{\omega }_2)=(2,0)$ irrep while the four-particle state belongs to $({\omega }_1{\omega }_2)=(4,1)$ irrep; see Table 5 and Table 7. Equation (101) clearly shows that the two-particle transfer strengths depend on $\alpha$ (i.e., they are different for $\alpha =+$ and $-1$) in the situation $\beta \ne \alpha$. Finally, it is also possible to consider $pp$, $nn$ and $pn$ pairs in the ground states of a $(m,T)$ system and study their $\alpha$ dependence; see [39,40] for the importance of such a study.

4.4. Summary

Multiple multi-orbit pairing $SO(5)$ and the complementary $Sp(2\mathrm{\Omega })$ algebras with isospin degree of freedom for nucleons are described in this section. The complementarity is established at the level of quadratic Casimir operators. Besides giving some details of these algebras in Section 4.1, described in Section 4.2 are the methods for obtaining the irrep labels for $SO(5)\supset [S{O}_T(3)\supset S{O}_{M_T}(2)]\otimes U(1)$ algebra, i.e., the allowed values of T for a given m of $U(1)$ and $(v,t)$ of $SO(5)$. Tables are given for some particle numbers of interest. In addition, a method to construct symmetry defined Hamiltonian matrix in a two space example is also given. In this situation there will be two $SO(5)$ algebras and the wavefunctions that correspond to the two $SO(5)$ algebras are tabulated explicitly in two examples. Going further, in Section 4.3 three applications of multiple $SO(5)$ algebras are described and these are: (i) selection rules for EM operators; (ii) a simple Hamiltonian generating order–chaos–order transitions; (iii) two nucleon transfer strength. Further exploration of these and other examples will give us more signatures that are useful in finding empirical examples for multiple $SO(5)$ algebras in nuclei.

5. Multiple Pairing Algebras in Proton–Neutron Interacting Boson Model with Fictitious ($\mathbf{F}$) Spin

For a two-species boson systems (such as the proton–neutron interacting boson model ($pn$IBM or IBM2) [21]), it is possible to introduce a fictitious (F) spin for the bosons such that the two projections of F represent the two species. Then, for N bosons the total fictitious spin F takes values $N/2$, $N/2-1$, …, 0 or $1/2$. For such a system with N number of bosons occupying orbits with angular momentum $({\ell }_1,{\ell }_2,\dots ,{\ell }_r)$ and the Hamiltonian preserving F-spin, the SGA is $U(2{\mathrm{\Omega }}^B)\supset U({\mathrm{\Omega }}^B)\otimes S{U}_F(2)$ with $S{U}_F(2)$ generating F-spin and ${\mathrm{\Omega }}^B={\sum }_{\ell }(2\ell +1)$. For example, for $pn-sd$IBM, $pn-sdg$IBM and $pn-sdpf$IBM we have ${\mathrm{\Omega }}^B=6$, 15 and 16 respectively. There is good evidence that heavy nuclei preserve F-spin [21,122,123,124,125]. Here below we will show that they are multiple pairing algebras for boson systems with F-spin and consider some of their applications. It is important to stress that although we consider pairing algebras for bosons, their physical interpretation is different as is well known in the example of the $SO(6)$ limit of IBM-1 [21].

5.1. Multiple Pairing $SO(3,2)$ Algebras with F-Spin

Let us consider a system of N bosons in r number of spherical ℓ orbits $({\ell }_1,{\ell }_2,\dots ,{\ell }_r)$ and each boson carrying F-spin $1/2$ degree of freedom. Then, total number of degrees of freedom for a singe boson is $2{\mathrm{\Omega }}^B$ where ${\mathrm{\Omega }}^B={\sum }_{\ell }$${\mathrm{\Omega }}_{\ell }^B$ and ${\mathrm{\Omega }}_{\ell }^B=(2\ell +1)$. Now, it is easy to see that the $4{({\mathrm{\Omega }}^B)}^2$ number of one-body operators $U_{m_k,m_{f_0}}^{k,f_0}({\ell }_1,{\ell }_2)$, with $f_0=0$ and 1,

$$U_{m_k,m_{f_0}}^{k,f_0}({\ell }_1,{\ell }_2)={\left(b_{{\ell }_1\frac{1}{2}}^{†}{\tilde{b}}_{{\ell }_2\frac{1}{2}}\right)}_{m_k,m_{f_0}}^{k,f_0}$$

(102)

where $b^{†}$ and b are single boson creation and annihilation operators in angular momentum and F-spin spaces, generate the SGA $U(2{\mathrm{\Omega }}^B)$. Note that ${\tilde{b}}_{\ell m,\frac{1}{2}{m}_f}={(-1)}^{\ell +m+\frac{1}{2}+m_f}{b}_{\ell -m,\frac{1}{2}-m_f}$. Moreover, with good F-spin symmetry, we have the subalgebra

$$U(2{\mathrm{\Omega }}^B)\supset U({\mathrm{\Omega }}^B)\otimes S{U}_F(2).$$

(103)

The operators $U_{m_k,0}^{k,0}({\ell }_1,{\ell }_2)$ [${({\mathrm{\Omega }}^B)}^2$ in number] generate $U({\mathrm{\Omega }}^B)$. Similarly, $S{U}_F(2)$ is generated by F-spin operator $\widehat{F}$ where

$${\displaystyle F_{\mu }^1=\sum _{\ell }\sqrt{{\displaystyle \frac{2\ell +1}{2}}}{\left(b_{\ell \frac{1}{2}}^{†}{\tilde{b}}_{\ell \frac{1}{2}}\right)}_{\mu }^{0,1}.}$$

(104)

In addition, the number operator $\widehat{N^B}$ and the total angular momentum operator $\widehat{L}$ are given by

$$\begin{array}{c}{\displaystyle \widehat{N^B}=\sum _{\ell }\sqrt{2(2\ell +1)}{\left(b_{\ell \frac{1}{2}}^{†}{\tilde{b}}_{\ell \frac{1}{2}}\right)}^{0,0},}\hfill \\ {\displaystyle L_{\mu }^1=\sum _{\ell }\sqrt{\ell (\ell +1)(2\ell +1)}{\left(b_{\ell \frac{1}{2}}^{†}{\tilde{b}}_{\ell \frac{1}{2}}\right)}_{\mu }^{1,0}.}\hfill \end{array}$$

(105)

Note that $\{\widehat{F},\widehat{N^B}\}$ generate $U_F(2)$. It is useful to note that all N boson states transform as the symmetric irrep $\left\{N\right\}$ of $U(2{\mathrm{\Omega }}^B)$ and the irreps of $U({\mathrm{\Omega }}^B)$ will be two-rowed, given by $\{N_1,N_2\}$, $N_1\ge N_2$ in Young tableaux notation with $N_1+N_2=N$ and $F=(N_1-N_2)/2$. Thus, the $U({\mathrm{\Omega }}^B)$ irreps are labeled by $(N_1,N_2)$ or $(N,F)$.

Turning to pairing, for boson systems with F-spin and a single ℓ orbit, the pair-creation operator with angular momentum zero and F-spin 1 is $B_{\mu }^1(\ell )$ where

$${\displaystyle B_{\mu }^1(\ell )=\sqrt{\frac{2\ell +1}{2}}{\left(b_{\ell \frac{1}{2}}^{†}{b}_{\ell \frac{1}{2}}^{†}\right)}_{0,\mu }^{0,1}}$$

(106)

and its hermitian adjoint ${\left[B_{\mu }^1(\ell )\right]}^{†}$ is,

$${\displaystyle {\left[B_{\mu }^1(\ell )\right]}^{†}=\sqrt{\frac{2\ell +1}{2}}{(-1)}^{1-\mu }{\left({\tilde{b}}_{\ell \frac{1}{2}}{\tilde{b}}_{\ell \frac{1}{2}}\right)}_{0,-\mu }^{0,1}.}$$

(107)

Now, with bosons in $({\ell }_1,{\ell }_2,\dots ,{\ell }_r)$ orbits, the pair-creation operator can be taken as a linear combination of the single-ℓ shell pair-creation operators but with different phases giving the generalized pairing operator (it is no longer unique) to be,

$${\displaystyle {\mathcal{B}}_{\mu }^1(\beta )=\sum _{\ell }{\beta }_{\ell }{B}_{\mu }^1(\ell );\left\{\beta \right\}=\{{\beta }_{{\ell }_1},{\beta }_{{\ell }_2},\dots ,{\beta }_{{\ell }_r}\}=\{\pm 1,\pm 1,\dots \}.}$$

(108)

The corresponding generalized pair-annihilation operator is

$${\displaystyle {\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}=\sum _{\ell }{\beta }_{\ell }{\left[B_{\mu }^1(\ell )\right]}^{†}.}$$

(109)

Using straightforward but lengthy angular momentum algebra, it is easy to derive the commutators for the operators ${\mathcal{B}}_{\mu }^1(\beta )$, ${\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}$, $F_{\mu }^1$ and $Q_0=[\widehat{N^B}+{\mathrm{\Omega }}^B]/2$. Note the difference in $Q_0$ for fermions. The results are independent of $\left\{\beta \right\}$ when ${\beta }_{{\ell }_p}=\pm 1$ as in Equation (108),

$$\begin{array}{c}\left[{\mathcal{B}}_{\mu }^1,{({\mathcal{B}}_{-{\mu }^{\prime }}^1)}^{†}\right]=2\left[{\displaystyle \sqrt{2}{(-1)}^{{\mu }^{\prime }}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩F_{\mu +{\mu }^{\prime }}^1+{\delta }_{\mu ,-{\mu }^{\prime }}(-Q_0)}\right],\hfill \\ \left[{\mathcal{B}}_{\mu }^1,Q_0\right]=-{\mathcal{B}}_{\mu }^1,\hfill \\ {\displaystyle \left[{\mathcal{B}}_{\mu }^1,F_{{\mu }^{\prime }}^1\right]=\sqrt{2}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩{\mathcal{B}}_{\mu +{\mu }^{\prime }}^1,}\hfill \\ {\displaystyle \left[F_{\mu }^1,F_{{\mu }^{\prime }}^1\right]=-\sqrt{2}⟨1\mu 1{\mu }^{\prime }\mid 1,\mu +{\mu }^{\prime }⟩F_{\mu +{\mu }^{\prime }}^1,}\hfill \\ \left[F_{\mu }^1,Q_0\right]=0.\hfill \end{array}$$

(110)

Equation (110) shows that the ten operators ${\mathcal{B}}_{\mu }^1(\beta )$, ${\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}$, $F_{\mu }^1$ and $Q_0$ (equivalently $\widehat{N^B}$) form an algebra for each $\left\{\beta \right\}$ set and this is the non-compact Lie algebra $S{O}^{(\beta )}(3,2)$. This was pointed out for the first time for bosons with F-spin by Lerma et al. [47]. Some mathematical details of $SO(3,2)$ algebra are given [118] and references therein. Without loss of generality we can choose ${\beta }_{{\ell }_1}=+1$ and then the remaining ${\beta }_{{\ell }_p}$ will be $\pm 1$. Thus, there will be $2^{r-1}$$SO(3,2)$ algebras. Then, with two ℓ orbits we have two $SO(3,2)$ algebras $S{O}^{(+,+)}(3,2)$ and $S{O}^{(+,-)}(3,2)$, with three ℓ orbits we have four $SO(3,2)$ algebras $S{O}^{(+,+,+)}(3,2)$, $S{O}^{(+,+,-)}(3,2)$, $S{O}^{(+,-,+)}(3,2)$ and $S{O}^{(+,-,-)}(3,2)$, with four ℓ orbits there will be eight $SO(3,2)$ algebras and so on. Before proceeding further, let us introduce the pairing Hamiltonians $H_p(\beta )$ for bosons,

$${\displaystyle H_p^B(\beta )=G_B\sum _{\mu }{\mathcal{B}}_{\mu }^1(\beta ){\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}}$$

(111)

where $G_B$ is the pairing strength. Now we will consider the complementary $SO(\mathrm{\Omega })$ algebra for further results.

5.2. Complementary $SO({\mathrm{\Omega }}^B)$ Algebras

Starting with the SGA $U(2{\mathrm{\Omega }}^B)\supset U({\mathrm{\Omega }}^B)\otimes S{U}_F(2)$, it is easy to recognize that $U({\mathrm{\Omega }}^B)\supset SO({\mathrm{\Omega }}^B)$ and the generators of $SO({\mathrm{\Omega }}^B)$ are

$$\begin{array}{ccc}\hfill SO({\mathrm{\Omega }}^B)& :& U_{\mu }^{k,0}(\ell ,\ell )\mathrm{with}k\mathrm{odd},\hfill \\ & & V_{\mu }^{k,0}({\ell }_1,{\ell }_2)={\mathcal{N}}^{1/2}({\ell }_1,{\ell }_2,k)\left[U_{\mu }^{k,0}({\ell }_1,{\ell }_2)+X({\ell }_1,{\ell }_2,k)U_{\mu }^{k,0}({\ell }_2,{\ell }_1)\right],{\ell }_1>{\ell }_2\hfill \end{array}$$

(112)

with $\mathcal{N}$ and X determined such that $SO({\mathrm{\Omega }}^B)$ is complementary to the pairing $SO(3,2)$ algebra. Towards this end we will define the quadratic Casimir operators (${\mathcal{C}}_2$) of the various algebras involved and then we will use the formulas for their eigenvalues as given for example in [118]. The quadratic Casimir invariants of $U({\mathrm{\Omega }}^B)$, $U_F(2)$ and $SO({\mathrm{\Omega }}^B)$ are

$$\begin{array}{ccc}\hfill {\mathcal{C}}_2(U({\mathrm{\Omega }}^B))& =& {\displaystyle 2\sum _{{\ell }_1,{\ell }_2,k}{(-1)}^{{\ell }_1-{\ell }_2}{U}^{k,0}({\ell }_1{\ell }_2)·U^{k,0}({\ell }_2{\ell }_1),}\hfill \\ \hfill {\mathcal{C}}_2(U_F(2))& =& {\displaystyle \sum _{{\ell }_1,{\ell }_2;f=0,1}\sqrt{(2{\ell }_1+1)(2{\ell }_2+1))}{U}^{0,f}({\ell }_1{\ell }_1)·U^{0,f}({\ell }_2{\ell }_2)=\frac{{(\widehat{N^B})}^2}{2}+2{\widehat{F}}^2,}\hfill \\ \hfill {\mathcal{C}}_2(SO({\mathrm{\Omega }}^B))& =& {\displaystyle 4\sum _{\ell ;k=odd}{U}^{k,0}(\ell \ell )·U^{k,0}(\ell \ell )+2\sum _{{\ell }_1>{\ell }_2;k}{V}^{k,0}({\ell }_1{\ell }_2)·V^{k,0}({\ell }_1{\ell }_2).}\hfill \end{array}$$

(113)

Using angular momentum algebra and Equation (113) the following important relations are derived,

$$\begin{array}{c}{\mathcal{C}}_2(U({\mathrm{\Omega }}^B))-{\mathcal{C}}_2(U_F(2))=\widehat{N^B}({\mathrm{\Omega }}^B-2),\hfill \\ {\displaystyle {\mathcal{C}}_2(U({\mathrm{\Omega }}^B))-{\mathcal{C}}_2(SO({\mathrm{\Omega }}^B))=\widehat{N^B}+2\sum _{\mu }{\mathcal{B}}_{\mu }^1(\beta ){\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}}\hfill \end{array}$$

(114)

and the second equality above is valid only when

$$X({\ell }_1,{\ell }_2,k)={(-1)}^{{\ell }_1+{\ell }_2+1+k}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}.$$

(115)

Note that for proper scaling for the Casimir operators, also needed is

$$\mathcal{N}({\ell }_1,{\ell }_2,k)={(-1)}^{k+1}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}.$$

with ${\beta }_{\ell }$ defining the generalized pair ${\mathcal{B}}_{\mu }^1(\beta )$, we have from Equations (114) and (115) the correspondence

$$SO({\mathrm{\Omega }}^B)\to S{O}^{(\beta )}({\mathrm{\Omega }}^B)\leftrightarrow S{O}^{(\beta )}(3,2)$$

and $\left[U({\mathrm{\Omega }}^B)\supset S{O}^{(\beta )}({\mathrm{\Omega }}^B)\right]\otimes S{U}_F(2)$ solves the pairing Hamiltonian given by Equation (111). With the $U({\mathrm{\Omega }}^B)$ irreps labeled by $(N_1,N_2)$ or $(N,F)$, the $S{O}^{(\beta )}({\mathrm{\Omega }}^B)$ irreps are labeled by $\left[{\sigma }_1,{\sigma }_2\right]$ with ${\sigma }_1\ge {\sigma }_2$ or by $(\sigma ,f)$ where $\sigma ={\sigma }_1+{\sigma }_2$ and $f=({\sigma }_1-{\sigma }_2)/2$. Then, $\sigma$ is seniority, like quantum number, and f is reduced F-spin. With these, the $SO({\mathrm{\Omega }}^B)$ symmetry algebra and the corresponding basis states are

$$\begin{array}{c}SO({\mathrm{\Omega }}^B):U(2{\mathrm{\Omega }}^B)\supset \left[U({\mathrm{\Omega }}^B)\supset S{O}^{(\beta )}({\mathrm{\Omega }}^B)\right]\otimes \left[S{U}_F(2)\supset U_{M_F}(1)\right],\hfill \\ \mathrm{Basis\; states}::\left|(N,F,M_F),(\sigma ,f),\alpha \right.⟩\leftrightarrow \left|N;\{N_1,N_2\}\left[{\sigma }_1,{\sigma }_2\right]M_F,\alpha \right.⟩.\hfill \end{array}$$

(116)

where $\alpha$ are additional labels needed for complete specification of the basis states and $M_F$ is $F_z$ eigenvalue with $-F\le M_F\le F$. Note that sometimes $M_F$ is included in $\alpha$. Formulas for the eigenvalues of the $U({\mathrm{\Omega }}^B)$ and $S{O}^{(\beta )}({\mathrm{\Omega }}^B)$ are well known [56,118,121],

$$\begin{array}{ccc}\hfill {⟨{\mathcal{C}}_2(U({\mathrm{\Omega }}^B))⟩}^{m,F}& =& {\displaystyle \frac{N(2{\mathrm{\Omega }}^B+N-4)}{2}+2F(F+1),}\hfill \\ \\ \hfill {⟨{\mathcal{C}}_2(S{O}^{(\beta )}({\mathrm{\Omega }}^B))⟩}^{\sigma ,f}& =& {\displaystyle \frac{\sigma (2{\mathrm{\Omega }}^B+\sigma -6)}{2}+2f(f+1).}\hfill \end{array}$$

(117)

The first formula here also follows easily from the first equality in Equation (114). Using Equations (111), (114) and (117) we have

$$\begin{array}{ccc}\hfill {⟨{\displaystyle \sum _{\mu }{\mathcal{B}}_{\mu }^1(\beta ){\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}}⟩}^{N,F,\sigma ,f}& =& {(G_B)}^{-1}{⟨H_p^B(\beta )⟩}^{N,F,\sigma ,f}\hfill \\ & =& {\displaystyle \frac{1}{4}(N-\sigma )(2{\mathrm{\Omega }}^B-6+N+\sigma )+F(F+1)-f(f+1).}\hfill \end{array}$$

(118)

Thus, the pairing Hamiltonian $H_p^B$ is solvable by the $SO({\mathrm{\Omega }}^B)$ symmetry (pairing eigenvalues do not depend on $(\beta )$ and $M_F$). In order to establish the above correspondence with $S{O}^{(\beta )}(3,2)$ algebra, we will rewrite the second formula in Equation (117) as

$$\begin{array}{c}{\displaystyle \frac{1}{2}{⟨{\mathcal{C}}_2(S{O}^{(\beta )}({\mathrm{\Omega }}^B))⟩}^{({\omega }_1^B,{\omega }_2^B)}=\left[{\omega }_1^B({\omega }_1^B-3)+{\omega }_2^B({\omega }_2^B+1)\right]-\frac{{\mathrm{\Omega }}^B}{2}\left({\displaystyle \frac{{\mathrm{\Omega }}^B}{2}-3}\right);}\hfill \\ {\displaystyle {\omega }_1^B=\frac{{\mathrm{\Omega }}^B+\sigma }{2},{\omega }_2^B=f.}\hfill \end{array}$$

(119)

with these we can identify the subalgebra of $SO(3,2)$ algebra, the corresponding irrep labels (basis states) and the quadratic Casimir operator of $SO(3,2)$,

$$\begin{array}{c}SO(3,2):SO(3,2)\supset \left[S{U}_F(2)\supset U_{M_F}(1)\right]\otimes U_{Q_0}(1),\hfill \\ \mathrm{Basis\; states}:\left|({\omega }_1^B,{\omega }_2^B),Q_0=\frac{{\mathrm{\Omega }}^B+N}{2},F,M_F\right.⟩,\hfill \\ {\mathcal{C}}_2(S{O}^{(\beta )}(3,2))=-{\mathcal{B}}_{\mu }^1(\beta ){\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†}+F^2+Q_0(Q_0-3),\hfill \\ {⟨{\mathcal{C}}_2(S{O}^{(\beta )}(3,2)⟩}^{({\omega }_1^B,{\omega }_2^B)}=\left[{\omega }_1^B({\omega }_1^B-3)+{\omega }_2^B({\omega }_2^B+1)\right].\hfill \end{array}$$

(120)

Then, we have the formula

$${⟨{(G_B)}^{-1}{H}_p^B(\beta )⟩}^{({\omega }_1^B,{\omega }_2^B),Q_0,F}=Q_0(Q_0-3)+F(F+1)-\left[{\omega }_1^B({\omega }_1^B-3)+{\omega }_2^B({\omega }_2^B+1)\right].$$

(121)

It is important to note that Equations (119) and (77) are related by $\mathrm{\Omega }\to -\mathrm{\Omega }$ symmetry. Finally, for obtaining the spectrum generated by $H_p^B(\beta )$ we need $(N,F)\to (\sigma ,f)$ reductions or the set of $(N,F)$ allowed for a given $(\sigma ,f)$ or $({\omega }_1^B,{\omega }_2^B)$. We will turn to this now.

5.3. Irreducible Representations

For labeling the eigenstates of $H_P^B(\beta )$, for a N boson system we need the irrep reductions $(N,F)\to (\sigma ,f)$. A simple method for this is to use the results for Kronecker products (denoted by × below) of the irreps of $U({\mathrm{\Omega }}^B)$ and similarly for $SO({\mathrm{\Omega }}^B)$. The rules for these follow from the Schur functions theory as given in [116,119,120] and for the present purpose the simplified results given for example in [56,113] will be adequate (see also Section 3). Given a two-rowed irrep $\{N_1,N_2\}$ of $U({\mathrm{\Omega }}^B)$, it can be expanded in terms of Kronecker products involving only symmetric irreps,

$$\{N_1,N_2\}=\left\{N_1\right\}\times \left\{N_2\right\}-\{N_1+1\}\times \{N_2-1\};\left\{0\right\}=1and\{-a\}=0.$$

(122)

Similarly, the Kronecker product of any two symmetric $SO({\mathrm{\Omega }}^B)$ irreps, with ${\mathrm{\Omega }}^B\ge 5$, will give

$${\displaystyle \left[P\right]\times \left[Q\right]=\sum _{k=0}^Q\sum _{r=0}^{Q-k}[P-Q+k+2r,k];P\ge Q.}$$

(123)

Equations (122) and (123) along with the well known result from the pairing algebra for identical boson systems [65],

$$\left\{N\right\}\to \left[\sigma \right]=\left[N\right],\left[N-2\right],\dots ,\left[0\right]or\left[1\right]$$

(124)

will give the reductions for any $(N,F)$ to $(\sigma ,f)$’s. Note that $\left\{N\right\}$ in Equation (124) is the symmetric irrep of $U({\mathrm{\Omega }}^B)$ with $F=N/2$ and similarly $\left[\sigma \right]$ is a symmetric irrep of $SO({\mathrm{\Omega }}^B)$ with $f=\sigma /2$. Using Equations (122)–(124) we obtain for example

$$\begin{array}{c}{\displaystyle \{N-1,1\}⟶\left[{\sigma }_1,{\sigma }_2\right]=\sum _{r=0}^{[N/2]-1}\left[N-2r-1,1\right]\oplus \sum _{r=0}^{[(N-1)/2]-1}\left[N-2r-2,0\right],}\hfill \\ \\ {\displaystyle \{N-2,2\}⟶\left[{\sigma }_1,{\sigma }_2\right]=\sum _{r=0}^{[N/2]-2}\left[N-2r-2,2\right]\oplus \sum _{r=0}^{[(N-1)/2]-2}\left[N-2r-3,1\right]\oplus }\hfill \\ {\displaystyle \left[N-2,0\right]\oplus \left[N-2-2[(N-2)/2],0\right]\oplus \sum _{r=0}^{[(N)/2]-3}{\left[N-2r-4,0\right]}^2.}\hfill \end{array}$$

(125)

In these equations $[X/2]$ is the integer part of $X/2$ and there is multiplicity (i.e., some irreps appear more than once) in the $\{N-2,2\}$ reductions. For $F<N/2-2$, numerical results for the reductions can be obtained easily using Equations (122)–(124) as they are easy to program. Table 8 gives results for $(N,F=N/2-3)$ and Table 9 gives results for $(N,F=N/2-4)$.

Table 8. $U({\mathrm{\Omega }}^B)$ irreps $\{\mathcal{N},3\}$ reductions to $SO({\mathrm{\Omega }}^B)$ irreps $[{\sigma }_1,{\sigma }_2]$ for $\mathcal{N}=3$ to 15 and ${\mathrm{\Omega }}^B\ge 5$. The $SO({\mathrm{\Omega }}^B)$ irreps are given as $\alpha \left[{\sigma }_1{\sigma }_2\right]$ where $\alpha$ is the multiplicity. Note that $N=\mathcal{N}+3$, $F=(\mathcal{N}-3)/2=N/2-3$, $\sigma ={\sigma }_1+{\sigma }_2$ and $f=({\sigma }_1-{\sigma }_2)/2$. See Section 5.3 for further discussion.

$\left\{33\right\}$

1[ 1 1] 1[ 3 1] 1[ 3 3]

$\left\{43\right\}$

1[ 1 0] 1[ 2 1] 1[ 3 0] 1[ 3 2] 1[ 4 1] 1[ 4 3]

$\left\{53\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 1[ 4 0] 1[ 3 3] 1[ 4 2] 1[ 5 1] 1[ 5 3]

$\left\{63\right\}$ 1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 1[ 5 0] 1[ 4 3] 1[ 5 2]

1[ 6 1] 1[ 6 3]

$\left\{73\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 2[ 4 0] 1[ 3 3] 1[ 4 2] 2[ 5 1] 1[ 6 0]

1[ 5 3] 1[ 6 2] 1[ 7 1] 1[ 7 3]

$\left\{83\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 2[ 5 0] 1[ 4 3] 1[ 5 2]

2[ 6 1] 1[ 7 0] 1[ 6 3] 1[ 7 2] 1[ 8 1] 1[ 8 3]

$\left\{93\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 2[ 4 0] 1[ 3 3] 1[ 4 2] 2[ 5 1] 2[ 6 0]

1[ 5 3] 1[ 6 2] 2[ 7 1] 1[ 8 0] 1[ 7 3] 1[ 8 2] 1[ 9 1] 1[ 9 3]

$\left\{103\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 2[ 5 0] 1[ 4 3] 1[ 5 2]

2[ 6 1] 2[ 7 0] 1[ 6 3] 1[ 7 2] 2[ 8 1] 1[ 9 0] 1[ 8 3] 1[ 9 2]

1[10 1] 1[10 3]

$\left\{113\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 2[ 4 0] 1[ 3 3] 1[ 4 2] 2[ 5 1] 2[ 6 0]

1[ 5 3] 1[ 6 2] 2[ 7 1] 2[ 8 0] 1[ 7 3] 1[ 8 2] 2[ 9 1] 1[10 0]

1[ 9 3] 1[10 2] 1[11 1] 1[11 3]

$\left\{123\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 2[ 5 0] 1[ 4 3] 1[ 5 2]

2[ 6 1] 2[ 7 0] 1[ 6 3] 1[ 7 2] 2[ 8 1] 2[ 9 0] 1[ 8 3] 1[ 9 2]

2[10 1] 1[11 0] 1[10 3] 1[11 2] 1[12 1] 1[12 3]

$\left\{133\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 2[ 4 0] 1[ 3 3] 1[ 4 2] 2[ 5 1] 2[ 6 0]

1[ 5 3] 1[ 6 2] 2[ 7 1] 2[ 8 0] 1[ 7 3] 1[ 8 2] 2[ 9 1] 2[10 0]

1[ 9 3] 1[10 2] 2[11 1] 1[12 0] 1[11 3] 1[12 2] 1[13 1] 1[13 3]

$\left\{143\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 2[ 5 0] 1[ 4 3] 1[ 5 2]

2[ 6 1] 2[ 7 0] 1[ 6 3] 1[ 7 2] 2[ 8 1] 2[ 9 0] 1[ 8 3] 1[ 9 2]

2[10 1] 2[11 0] 1[10 3] 1[11 2] 2[12 1] 1[13 0] 1[12 3] 1[13 2]

1[14 1] 1[14 3]

$\left\{153\right\}$

1[ 1 1] 1[ 2 0] 2[ 3 1] 2[ 4 0] 1[ 3 3] 1[ 4 2] 2[ 5 1] 2[ 6 0]

1[ 5 3] 1[ 6 2] 2[ 7 1] 2[ 8 0] 1[ 7 3] 1[ 8 2] 2[ 9 1] 2[10 0]

1[ 9 3] 1[10 2] 2[11 1] 2[12 0] 1[11 3] 1[12 2] 2[13 1] 1[14 0]

1[13 3] 1[14 2] 1[15 1] 1[15 3]

Table 9. $U({\mathrm{\Omega }}^B)$ irreps $\{\mathcal{N},4\}$ reductions to $SO({\mathrm{\Omega }}^B)$ irreps $[{\sigma }_1,{\sigma }_2]$ for $\mathcal{N}=4$ to 14 and ${\mathrm{\Omega }}^B\ge 5$. The $SO({\mathrm{\Omega }}^B)$ irreps are given as $\alpha \left[{\sigma }_1{\sigma }_2\right]$ where $\alpha$ is the multiplicity. Note that $N=\mathcal{N}+4$, $F=(\mathcal{N}-4)/2=N/2-4$, $\sigma ={\sigma }_1+{\sigma }_2$ and $f=({\sigma }_1-{\sigma }_2)/2$. See Section 5.3 for further discussion.

$\left\{44\right\}$

1[ 0 0] 1[ 2 0] 1[ 2 2] 1[ 4 0] 1[ 4 2] 1[ 4 4]

$\left\{54\right\}$

1[ 1 0] 1[ 2 1] 1[ 3 0] 1[ 3 2] 1[ 4 1] 1[ 5 0] 1[ 4 3] 1[ 5 2]

1[ 5 4]

$\left\{64\right\}$

1[ 0 0] 2[ 2 0] 1[ 2 2] 1[ 3 1] 2[ 4 0] 2[ 4 2] 1[ 5 1] 1[ 6 0]

1[ 4 4] 1[ 5 3] 1[ 6 2] 1[ 6 4]

$\left\{74\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 2[ 5 0] 1[ 4 3] 2[ 5 2]

1[ 6 1] 1[ 7 0] 1[ 5 4] 1[ 6 3] 1[ 7 2] 1[ 7 4]

$\left\{84\right\}$

1[ 0 0] 2[ 2 0] 1[ 2 2] 1[ 3 1] 3[ 4 0] 2[ 4 2] 2[ 5 1] 2[ 6 0]

1[ 4 4] 1[ 5 3] 2[ 6 2] 1[ 7 1] 1[ 8 0] 1[ 6 4] 1[ 7 3] 1[ 8 2]

1[ 8 4]

$\left\{94\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 3[ 5 0] 1[ 4 3] 2[ 5 2]

2[ 6 1] 2[ 7 0] 1[ 5 4] 1[ 6 3] 2[ 7 2] 1[ 8 1] 1[ 9 0] 1[ 7 4]

1[ 8 3] 1[ 9 2] 1[ 9 4]

$\left\{104\right\}$

1[ 0 0] 2[ 2 0] 1[ 2 2] 1[ 3 1] 3[ 4 0] 2[ 4 2] 2[ 5 1] 3[ 6 0]

1[ 4 4] 1[ 5 3] 2[ 6 2] 2[ 7 1] 2[ 8 0] 1[ 6 4] 1[ 7 3] 2[ 8 2]

1[ 9 1] 1[10 0] 1[ 8 4] 1[ 9 3] 1[10 2] 1[10 4]

$\left\{114\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 3[ 5 0] 1[ 4 3] 2[ 5 2]

2[ 6 1] 3[ 7 0] 1[ 5 4] 1[ 6 3] 2[ 7 2] 2[ 8 1] 2[ 9 0] 1[ 7 4]

1[ 8 3] 2[ 9 2] 1[10 1] 1[11 0] 1[ 9 4] 1[10 3] 1[11 2] 1[11 4]

$\left\{124\right\}$

1[ 0 0] 2[ 2 0] 1[ 2 2] 1[ 3 1] 3[ 4 0] 2[ 4 2] 2[ 5 1] 3[ 6 0]

1[ 4 4] 1[ 5 3] 2[ 6 2] 2[ 7 1] 3[ 8 0] 1[ 6 4] 1[ 7 3] 2[ 8 2]

2[ 9 1] 2[10 0] 1[ 8 4] 1[ 9 3] 2[10 2] 1[11 1] 1[12 0] 1[10 4]

1[11 3] 1[12 2] 1[12 4]

$\left\{134\right\}$

1[ 1 0] 1[ 2 1] 2[ 3 0] 1[ 3 2] 2[ 4 1] 3[ 5 0] 1[ 4 3] 2[ 5 2]

2[ 6 1] 3[ 7 0] 1[ 5 4] 1[ 6 3] 2[ 7 2] 2[ 8 1] 3[ 9 0] 1[ 7 4]

1[ 8 3] 2[ 9 2] 2[10 1] 2[11 0] 1[ 9 4] 1[10 3] 2[11 2] 1[12 1]

1[13 0] 1[11 4] 1[12 3] 1[13 2] 1[13 4]

$\left\{144\right\}$

1[ 0 0] 2[ 2 0] 1[ 2 2] 1[ 3 1] 3[ 4 0] 2[ 4 2] 2[ 5 1] 3[ 6 0]

1[ 4 4] 1[ 5 3] 2[ 6 2] 2[ 7 1] 3[ 8 0] 1[ 6 4] 1[ 7 3] 2[ 8 2]

2[ 9 1] 3[10 0] 1[ 8 4] 1[ 9 3] 2[10 2] 2[11 1] 2[12 0] 1[10 4]

1[11 3] 2[12 2] 1[13 1] 1[14 0] 1[12 4] 1[13 3] 1[14 2] 1[14 4]

For boson systems, it is well known that the states with $F=N/2$ will be lowest in energy and then those with $F=N/2-1$ [21]. In order to obtain this ordering, it is necessary to add Majorana interaction (M) term as recognized in IBM studies. Then, $H_p^B(\beta )$ changes to

$$\begin{array}{c}{H}^B(G^B,a^B)=H_p^B(\beta )+M;\hfill \\ {\displaystyle H_p^B(\beta )=G_B\sum _{\mu }{\mathcal{B}}_{\mu }^1(\beta ){\left[{\mathcal{B}}_{\mu }^1(\beta )\right]}^{†},M=a^B\left[{\displaystyle \frac{{\widehat{N}}_B}{2}\left({\displaystyle \frac{{\widehat{N}}_B}{2}+1}\right)-{\widehat{F}}^2}\right]}\hfill \end{array}$$

(126)

with ${\widehat{F}}^2$ eigenvalues being $F(F+1)$. See [21,126] for details regarding the Majorana term M. The $H^B(G^B,a^B)$ eigenvalues E for some states with $F=N/2$ and $F=N/2-1$ are,

$$\begin{array}{c}E(N;\left\{N\right\}\left[N\right]\alpha )=0,\hfill \\ E(N;\left\{N\right\}\left[N-2\right]\alpha )=G^B(2N+2),\hfill \\ E(N;\left\{N\right\}\left[N-4\right]\alpha )=G^B(4N),\hfill \\ E(N;\{N-1,1\}\left[N-1,1\right]\alpha )=a^{B}N,\hfill \\ E(N;\{N-1,1\}\left[N-2\right]\alpha )=G^B(N+2)+a^{B}N,\hfill \\ E(N;\{N-1,1\}\left[N-3,1\right]\alpha )=G^B(2N)+a^{B}N,\hfill \\ E(N;\{N-1,1\}\left[N-4\right]\alpha )=G^B(3N)+a^{B}N.\hfill \end{array}$$

(127)

These show the important result that for $G^B>0$ and $a^B>0$, the states with $F=N/2$ will be lowest in energy and the states with $F=N/2-1$ will lie at energy $a^{B}N$ above the $F=N/2$ states and they will be next higher states. If $a^B=0$, the $F=N/2$ states will not be separated from $F=N/2-1$ states. The states with $F=N/2-1$ are called mixed symmetry states [21]. From Equation (127), it is clear that the formulas for irrep reductions given in Equations (124) and (125) and the results in Table 8 and Table 9 are sufficient for most applications.

5.4. Applications

5.4.1. Selection Rules

In the symmetry limit, selection rules for EM transitions follow from Equations (112) and (115). It is easy to see that only the isoscalar part of the EM operators will have selection rules. General form of the isoscalar part of EM operators is, with $X=E$ or M,

$${\displaystyle T^{XL}=\sum _{\ell }{x}_{\ell }^L{U}_{\mu }^{L,0}(\ell ,\ell )+\sum _{{\ell }_1>{\ell }_2}{y}_{{\ell }_1,{\ell }_2}^L{V}_{\mu }^{L,0}({\ell }_1,{\ell }_2).}$$

(128)

Therefore, isoscalar part of EL operators with L even will be $S{O}^{(\beta )}({\mathrm{\Omega }}^B)$ generators and therefore connect only states having the same $({\sigma }_1,{\sigma }_2)$ [or $({\omega }_1^B,{\omega }_2^B)$] provided we choose the operators such that $x_{\ell }^L=0$ for all ℓ and $V^{L,0}$ in Equation (128) are such that Equation (115) is satisfied. This is indeed the choice made for quadrupole ($L=2$) transition operator in IBM-2 studies [21,124,125]. However, for $ML$ operators with L-even, due to parity selection rule $U^{L,0}$ will not exist. Therefore, they will connect only states having the same $({\sigma }_1,{\sigma }_2)$ [or $({\omega }_1^B,{\omega }_2^B)$] provided we choose the operators such that $V^{L,0}$ in Equation (128) satisfy Equation (115). Turning to EM operators with L odd, both EL and ML operators with L odd will connect only states having the same $({\sigma }_1,{\sigma }_2)$ [or $({\omega }_1^B,{\omega }_2^B)$] provided we choose the operators such that $V^{L,0}$ in Equation (128) satisfy Equation (115). This is due the fact that $U^{L,0}$ with L odd (they are needed only for ML operators while they do not exist for EL operators due to parity selection rule) are generators of $S{O}^{(\beta )}({\mathrm{\Omega }}^B)$. It is important to add that the selection rules for the isoscalar part of EM operators will be violated if the $\beta$ in $S{O}^{\beta }({\mathrm{\Omega }}^B)$ are not same as the $\left\{\beta \right\}$ needed for defining $V^{L,0}$ in Equation (128) via Equation (115). These selection rules may provide some tests of the multiple pairing algebras with good F-spin in interacting boson models ($sd$, $sdg$, $sdf$, $sdpf$ etc) of nuclei.

5.4.2. H Matrix Construction

Results for electromagnetic transition strengths, as generated by multiple multi-orbit pairing algebras, can be obtained by developing the Wigner–Racah algebra for $SO(3,2)$ and following the same procedure that is adopted in Section 4 for multiple multi-orbit $SO(5)$ algebras with isospin in shell model. It may be possible in future to follow the methods used in Refs. [30,31,32,33,34,35,36,37,38] to obtain $SO(3,2)$ Wigner and Racah coefficients. As these group theory results, to our knowledge, are not available, an alternative is to construct the H matrix in a convenient basis and obtain the eigenfuctions generated for different choices of $\beta$ in Equations (108) and (111). To this end, one can use the $M_F$ basis, i.e., a basis with proton ($\pi$) and neutron ($\nu$) bosons. We will use the notation $\left|\pi \right.⟩=\left|F=\frac{1}{2},M_F=\frac{1}{2}\right.⟩$ and $\left|\nu \right.⟩=\left|F=\frac{1}{2},M_F=-\frac{1}{2}\right.⟩$. More explicitly, for a system of interacting bosons with sp angular momenta ${\ell }_1,{\ell }_2,\dots$, a convenient basis is

$$\begin{array}{c}\left|{\mathrm{\Phi }}^B(L)\right.⟩=\left|\prod _{r=1,2,\dots }\left\{\left|{\varphi }^{\pi }({\ell }_r:L_r^{\pi }){\varphi }^{\nu }({\ell }_r:L_r^{\nu })\right.⟩\right\}\Delta L\right.⟩;\hfill \\ {\varphi }^{\rho }({\ell }_r:L_r^{\rho })=\left|N_{{\ell }_r:\rho }^B{\omega }_{{\ell }_r:\rho }^B{\alpha }_r^{\rho }{L}_r^{\rho }\right.⟩,\rho =\pi ,\nu .\hfill \end{array}$$

(129)

Here, ${\sum }_{\ell }{N}_{\ell :\pi }^B=N_{\pi }^B$ is number of proton bosons, ${\sum }_{\ell }{N}_{\ell :\nu }^B=N_{\nu }^B$ is number of neutron bosons giving $N^B=N_{\pi }^B+N_{\nu }^B$ the total number of bosons. Similarly, ${\omega }_{\ell :\pi }^B$ and ${\omega }_{\ell :\nu }^B$ being the ℓ boson seniorities in $\pi$ and $\nu$ spaces. For a given nucleus $(N_{\pi }^B,N_{\nu }^B)$ or $(N,M_F=N_{\pi }^B-N_{\nu }^B)$ are preserved. Similarly, $L_r^{\rho }$ are the angular momentum of the $N_{{\ell }_r:\rho }^B$ number of bosons with sp angular momentum ${\ell }_r$. Further, L is the total angular momentum obtained by vector addition of all $L_r^{\rho }$. In addition, ${\alpha }_r^{\rho }$ and $\Delta$ are additional labels needed for complete specification of the basis states.

For example, the pairing Hamiltonian ${(G_B)}^{-1}{H}_p^B(\beta )$ in terms of $\pi$ and $\nu$ bosons is

$$\begin{array}{c}{(G_B)}^{-1}{H}_p^B(\beta )=\left\{{\displaystyle 2\sum _{{\ell }_1,{\ell }_2,\rho =\pi ,\nu }{(-1)}^{{\ell }_1+{\ell }_2}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{S}_{+}^{\rho }({\ell }_1)S_{-}^{\rho }({\ell }_2)}\right\}\hfill \\ +\left\{{\displaystyle \sum _{{\ell }_1,{\ell }_2;L}\sqrt{(2{\ell }_1+1)(2{\ell }_2+1)(2L+1)}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2}{\left[{\left(b_{{\ell }_1\pi }^{†}{\tilde{b}}_{{\ell }_2\pi }\right)}^L{\left(b_{{\ell }_1\nu }^{†}{\tilde{b}}_{{\ell }_2\nu }\right)}^L\right]}^0}\right\}\hfill \end{array}$$

(130)

The $S_{+}(\ell )$ and $S_{-}(\ell )$ operators appearing above are as defined by Equations (30) and (31). Following the results in Appendix A, it is easy to write the matrix element of the terms involving $S_{+}$ and $S_{-}$ in the basis given by Equation (129). For the Second term in Equation (130) we need the reduced matrix elements of $b_{\ell }^{†}$ and tables, formulas and computer programmes for these are available for $\ell =1$ (p bosons), 2 (d bosons), 3 (f) bosons and 4 (g) bosons; see for example [21,100,127,128,129]. Let us add that it is possible to consider a more general H with the basis given in Equation (129), for example by adding splitting of single ℓ-orbit energies. Without explicit matrix construction, energy eigenvalues are obtained in [47] by employing the so called Richardson–Gaudin (RG) equations. Studied in [47] are energy spectra in $sd$, $sdg$ and $sdf$ boson systems (however, in this study multiple pairing algebras with F-spin are not considered). Let us add that it may be possible also to use in proton–neutron spaces the methods developed by Feng Pan et al. [19]. Further investigations using these approaches or by constructing the H matrix explicitly will give new insights into multiple pairing algebras in interacting boson models with F-spin but this is for future.

Going beyond $sd$IBM-2, in $sdg$IBM-2, $sdf$IBM-2, $sdpf$IBM-2 and so on, there will be many pairing algebras. For example, in $sdg$IBM-2 the SGA is $U(30)$ and the first pairing algebra corresponds to $SO(15)$ in

$$U(30)\supset [U(15)\supset SO(15)]\otimes S{U}_F(2)$$

with pair operator

$$B_{\mu }^1(sdg)=B_{\mu }^1(s)\pm B_{\mu }^1(d)\pm B_{\mu }^1(g).$$

The $SO(15)$ can be decomposed further into three subalgebras

$$\begin{array}{c}SO(15)\supset S{O}_{dg}(14)\supset S{O}_d(5)\oplus S{O}_g(9),\hfill \\ SO(15)\supset S{O}_{sd}(6)\oplus S{O}_g(9)\supset S{O}_d(5)\oplus S{O}_g(9),\hfill \\ SO(15)\supset S{O}_{sg}(10)\oplus S{O}_d(5)\supset S{O}_d(5)\oplus S{O}_g(9).\hfill \end{array}$$

There are $SO(3,2)$ algebras corresponding to all these $SO(n)$ algebras. It is important to recognize that the choice of the four signs in $B_{\mu }^1(sdg)$ will uniquely fix the sign choices of the pair-creation operators that correspond to the various $SO(n)$ algebras in the three $SO(15)$ subalgebras given above. Investigations of these various multiple pair algebras may prove to be useful.

5.5. Summary

Multiple multi-orbit pairing $SO(3,2)$ and the complementary $SO({\mathrm{\Omega }}^B)$ algebras with F-spin in the proton–neutron interacting boson models of nuclei are described in this Section. The complementarity is established at the level of quadratic Casimir operators. Besides giving some details of these algebras in Section 5.1 and Section 5.2, described in Section 5.3 are the methods for obtaining the irrep labels for $U(2{\mathrm{\Omega }}^B)\supset [U({\mathrm{\Omega }}^B)\supset SO({\mathrm{\Omega }}^B)]\otimes S{U}_F(2)$ algebra, i.e., the allowed values of $({\sigma }_1,{\sigma }_2)$ of $SO({\mathrm{\Omega }}^B)$ for a given $(N,F)$. Results for $F=N/2$, $N/2-1$, $N/2-2$, $N/2-3$ and $N/2-4$ are presented. Going further, in Section 5.4 some possible applications of multiple $SO(3,2)$ algebras are described. Further explorations using group theory approach as in Section 4 but extended to $SO(3,2)$, by explicit matrix construction, using the RG method employed in [47]) or by extending the methods developed by Feng Pan are expected to give us signatures that are useful in finding empirical examples for multiple $SO(3,2)$ algebras in nuclei.

6. Multiple Pairing Algebras with $\mathit{L}-\mathit{S}$ Coupling in Shell Model and in IBM with Isospin $\mathit{T}=\mathbf{1}$ Degree of Freedom

In the shell model with $L-S$ coupling, a $L=0$ coupled nucleon pair carries spin-isospin degrees of freedom $(ST)=(10)$ and $(01)$. With this, the pairing algebra is $SO(8)$ as established first in [48]. More importantly, with nucleons occupying several ℓ-orbits, there will be multiple $SO(8)$ algebras and each of them contains both isoscalar and isovector pair-creation operators unlike only isovector pair operator in the $SO(5)$ pairing algebra for nucleons in j orbits (see Section 4). The $SO(8)$ algebra is complex with three subalgebra chains as discussed ahead in Section 6.1. In addition, in Section 6.2 we will describe briefly the various pairing algebras in the interacting boson model with the bosons carrying isospin $T=1$ degree of freedom (called IBM-3 or IBM-T [21,56]). Here also, there will be multiple pairing algebras for $sd$, $sdg$, $sdf$, $sdpf$, … boson systems. As the algebras appearing in this Section are quite complex, the presentation will be brief without too many details. We hope that the discussion here will prompt many investigations of these algebras in future.

6.1. Multiple $SO(8)$ Pairing Algebras in Shell Model

6.1.1. $SO(8)$ and Its Three Subalgebras

In the shell model, in the situation that nucleons occupy ℓ orbits (i.e., they occupy both $j=\ell \pm \frac{1}{2}$ orbits), then the nucleon pair coupled to orbital angular momentum zero, due to antisymmetry, carries spin-isospin degrees of freedom $(ST)=(10)$ and $(01)$. With this, the isoscalar and isovector pair-creation operators $D_{\mu }^{†}(\ell )$ and $P_{\mu }^{†}(\ell )$ respectively are

$${\displaystyle D_{\mu }^{†}(\ell )=\sqrt{{\displaystyle \frac{2\ell +1}{2}}}{\left(a_{\ell \frac{1}{2}\frac{1}{2}}^{†}{a}_{\ell \frac{1}{2}\frac{1}{2}}^{†}\right)}_{0,\mu ,0}^{0,1,0},P_{\mu }^{†}(\ell )=\sqrt{{\displaystyle \frac{2\ell +1}{2}}}{\left(a_{\ell \frac{1}{2}\frac{1}{2}}^{†}{a}_{\ell \frac{1}{2}\frac{1}{2}}^{†}\right)}_{0,0,\mu }^{0,0,1}}$$

(131)

with $\mu =-1,0,+1$. Note that we are using $(L,S,T)$ order in Equation (131). For the multi-orbit case, we have generalized isoscalar and isovector pair operators $D_{\mu }^{†}$ and $P_{\mu }^{†}$ as linear combinations of single orbit operators except for phase factors giving

$${\displaystyle D_{\mu }^{†}=\sum _{\ell }{\beta }_{\ell }{D}_{\mu }^{†}(\ell ),P_{\mu }^{†}=\sum _{\ell }{\beta }_{\ell }{P}_{\mu }^{†}(\ell );{\beta }_{\ell }=+1\mathrm{or}-1.}$$

(132)

Now, the isoscalar plus isovector pairing Hamiltonian in $LS$-coupling is

$${\displaystyle H_p^{LST}(x)=-(1-x)\sum _{\mu }{P}_{\mu }^{†}{P}_{\mu }-(1+x)\sum _{\mu }{D}_{\mu }^{†}{D}_{\mu }.}$$

(133)

Note that $P_{\mu }={(P_{\mu }^{†})}^{†}$ and $D_{\mu }={(D_{\mu }^{†})}^{†}$. Most significant result here is that the twelve operators $(D_{\mu }^{†}$, $P_{\mu }^{†}$, $D_{\mu }$, $P_{\mu }$), the six spin and isospin generators ($S_{\mu }^1$, $T_{\mu }^1$), the number operator $\widehat{n}$ [or $Q_0=\frac{\widehat{n}}{2}-\mathrm{\Omega }$, $\mathrm{\Omega }=\sum (2\ell +1)$] and the nine ${(\sigma \tau )}_{\mu ,{\mu }^{\prime }}^{1,1}$ operators, a total of 28 operators generate a $SO(8)$ algebra independent of the ${\beta }_{\ell }$ in Equation (132) [48,53] (note that the $SO(8)$ algebra appearing here is different from the $SO(8)$ appearing in the schematic model for monopole and quadrupole pairing in nuclei by Ginocchio [130]). Thus, there are multiple $SO(8)$ algebras in shell model and the number is $2^{r-1}$ for r number of ℓ orbits. Going further, each $SO(8)$ algebra admits three subalgebra chains and the pairing Hamiltonian in Equation (133) is diagonal in the basis defined by these subalgebra chains for $x=0,1,-1$. These are [48,53],

$$\begin{array}{ccc}\hfill x=0& :& SO(8)\supset S{O}_{ST}(6)\supset S{O}_S(3)\otimes S{O}_T(3),\hfill \\ \hfill x=1& :& SO(8)\supset \left[S{O}_S(5)\supset S{O}_S(3)\right]\otimes S{O}_T(3),\hfill \\ \hfill x=-1& :& SO(8)\supset \left[S{O}_T(5)\supset S{O}_T(3)\right]\otimes S{O}_S(3).\hfill \end{array}$$

(134)

Noted that $S{O}_{ST}(6)\supset S{O}_S(3)\otimes S{O}_T(3)$ above is the same as the well known $S{U}_{ST}(4)\supset S{U}_S(2)\otimes S{U}_T(2)$ spin-isospin supermultiplet algebra [131]. By varying the parameter x in Equation (133), it is possible to study the competition between isoscalar and isovector pairing. It is important to recognize that $H_p^{LST}(x)$ contains only the generators of $SO(8)$ and therefore for all x values, the eigenstates will carry $SO(8)$ quantum numbers. It is well known that $SO(8)$ irreps contain four numbers and they can be recasted into a seniority quantum number v and three other numbers. It is useful to add that the shell model SGA is $U(4\mathrm{\Omega })$ and the three subalgebra chains of this SGA that are in one-to-one correspondence with the chains in Equation (134) are

$$\begin{array}{ccc}\hfill x=0& :& U(4\mathrm{\Omega })\supset \left[U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })\right]\otimes [S{O}_{ST}(6)\supset S{O}_S(3)\otimes S{O}_T(3)]\hfill \\ \hfill x=1& :& U(4\mathrm{\Omega })\supset \left[U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })\supset SO(\mathrm{\Omega })\otimes S{U}_T(2)\right]\otimes S{U}_S(2)\hfill \\ \hfill x=-1& :& U(4\mathrm{\Omega })\supset \left[U(2\mathrm{\Omega })\supset Sp(2\mathrm{\Omega })\supset SO(\mathrm{\Omega })\otimes S{U}_S(2)\right]\otimes S{U}_T(2).\hfill \end{array}$$

(135)

Using group theory, all the irrep labels for the algebras in Equation (135) can be determined and by correspondence, the irrep labels of the algebras in Equation (134). See [53,54] for details. Most importantly, for the $SO(8)$ seniority $v=0$ a convenient set of basis states for a given number m of nucleons and a given value of $\mathrm{\Omega }$ are the $SO(6)$ basis states, i.e., the states given by the chain with $x=0$ above. These states are labeled by

$$\left|{\mathrm{\Phi }}_{SO(6)}^{(ST)}\right.⟩=\left|\mathrm{\Omega },N,\omega ,(S,T),\alpha \right.⟩.$$

The various quantum numbers appearing here are given by (assuming m is even) [49,53,54],

$$\begin{array}{c}N=m/2ifm\le 2\mathrm{\Omega },N=(4\mathrm{\Omega }-m)/2\mathrm{if}m>2\mathrm{\Omega },\hfill \\ \omega =N,N-2,N-4,\dots ,0or1,\hfill \\ S+T=\omega ,\omega -2,\dots ,0or1.\hfill \end{array}$$

(136)

For the $SO(8)\supset S{O}_{ST}(6)\supset S{O}_S(3)\otimes S{O}_T(3)$ limit, for the above $SO(8)$ seniority $v=0$ basis states, the Wigner–Racah algebra was developed in [49]. Further, the algebra is also available for $v=1$ and $v=2$ states; see [49,52]. Using these, spectra and two-nucleon and $\alpha$ transfer strengths are studied in some detail using H with $SO(8)$ pairing and considering only $SO(8)$ seniority $v=0$ in [50,51]. The $SO(8)$ algebra was also applied to study some aspects of double $\beta$-decay matrix elements in [132] and in the study of some aspects of IBM-4 (interacting boson model with spin-isospin degrees of freedom) in [133,134].

6.1.2. Two-Nucleon Transfer in a Two-Orbit System

With our interest in this article being on multiple $SO(8)$ algebras, here below we will consider the simpler two-orbit situation and present some results for two-nucleon transfer that distinguishes the two $SO(8)$ algebras. Note that with two orbits there will be two $SO(8)$ algebras, with three orbits there will be four $SO(8)$ algebras and so on.

Let us consider two orbits with $\mathrm{\Omega }$ taking values say ${\mathrm{\Omega }}_1$ for the first orbit and ${\mathrm{\Omega }}_2$ for the second orbit. Given that there are say m number of nucleons in these orbits, we can distribute them in these orbits in all possible ways. Then, $m=m_1+m_2$ with $m_1$ number of nucleons in orbit #1 and $m_2$ in orbit #2. For each $(m_1,m_2)$ we can generate the $SO(6)$ basis states in spaces 1 and 2 using Equation (136). Table 10 gives an example with ${\mathrm{\Omega }}_1=6$, ${\mathrm{\Omega }}_2=4$ and $m=8$ with total $(S,T)=(0,0)$. Note that the basis states are of the form,

$$\left|{\mathrm{\Phi }}_{S{O}_1(6)\oplus S{O}_2(6)}^{(ST)}\right.⟩=\left|\left\{\left|{\mathrm{\Omega }}_1,N_1,{\omega }_1,(S_1,T_1),{\alpha }_1\right.⟩\left|{\mathrm{\Omega }}_2,N_2,{\omega }_2,(S_2,T_2),{\alpha }_2\right.⟩\right\}{\alpha }_{12}(S,T)\right.⟩$$

(137)

and here one is restricting the $SO(8)$ seniorities $v_1$ and $v_2$ in the two spaces to $v_1=0$ and $v_2=0$. With $m=m_1+m_2$, the $N_1$ above is defined by $({\mathrm{\Omega }}_1,m_1)$ following Equation (136) and similarly the $N_2$ by $({\mathrm{\Omega }}_2,m_2)$. Finally, the $\alpha$ labels in Equation (137) will not play any role in the results presented here. Using the above basis and the algebra given in [49,131], it is possible to construct the H matrix for the isoscalar plus isovector pairing Hamiltonian,

$$H_p(x,\beta )=-(1-x)\left[\left(P_1^{†}+\beta P_2^{†}\right)\left(P_1+\beta P_2\right)\right]-(1+x)\left[\left(D_1^{†}+\beta D_2^{†}\right)\left(D_1+\beta D_2\right)\right].$$

(138)

Table 10. $SO(6)$ limit quantum numbers for the basis states in a two-orbit example with ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=4$. Shown are the quantum numbers for eight nucleons ($m=8$) with total $(S,T)=(0,0)$. Note that the $SO(8)$ seniorities for the nucleons in the two orbits are zero. See Section 6.1.2 for further discussion.

#	${\mathit{N}}_1$	${\mathit{\omega }}_1$	${\mathit{S}}_1$	${\mathit{T}}_1$	${\mathit{N}}_2$	${\mathit{\omega }}_2$	${\mathit{S}}_2$	${\mathit{T}}_2$
1	0	0	0	0	4	4	0	0
2	0	0	0	0	4	2	0	0
3	0	0	0	0	4	0	0	0
4	1	1	0	1	3	3	0	1
5	1	1	0	1	3	1	0	1
6	1	1	1	0	3	3	1	0
7	1	1	1	0	3	1	1	0
8	2	2	0	2	2	2	0	2
9	2	2	1	1	2	2	1	1
10	2	2	2	0	2	2	2	0
11	2	2	0	0	2	2	0	0
12	2	2	0	0	2	0	0	0
13	2	0	0	0	2	2	0	0
14	2	0	0	0	2	0	0	0
15	3	3	0	1	1	1	0	1
16	3	3	1	0	1	1	1	0
17	3	1	0	1	1	1	0	1
18	3	1	1	0	1	1	1	0
19	4	4	0	0	0	0	0	0
20	4	2	0	0	0	0	0	0
21	4	0	0	0	0	0	0	0

Adding the splitting of the energies of the two orbits and restricting to $\beta =+1$, spectra, two nucleon transfer strengths and $\alpha$ transfer strengths are studied in two-orbit examples in [51] and the systems studied are found to exhibit several interesting phase transitions. As our interest is in multiple $SO(8)$ algebras, we have analyzed the eigenvalues and eigenvectors for various $(ST)$ values as generated by $H_p(x,\beta )$ for $x=0,\pm 1$ and $\beta =\pm 1$ using ${\mathrm{\Omega }}_1=6$, ${\mathrm{\Omega }}_2=4$ and $m=8$. The results are as follows. Firstly, as is well known, the eigenvalues do not depend on $\beta$ and this is seen in the calculated results. For $x=0$, the eigevalues with respect to the eigenvalue of $(ST)={(00)}_1$ state for ${(ST)}_i={(02)}_1$, ${(04)}_1$, ${(00)}_2$, ${(02)}_2$, ${(04)}_2$, ${(01)}_1$ and ${(10)}_1$ are 38, 48, 6, 48, 58, 46 and 46 respectively. Further, for $x=1$, they are 42, 76, 20, 42, 76, 42 and 22. Similarly, for $x=-1$ they are 6, 20, 20, 26, 40, 22 and 42. These eigenvalues, all independent of $\beta =\pm 1$, clearly show that the spectrum in isospin space, as expected [53], for $x=-1$ is rotational and for $x=+1$ close to vibrational (see the spacing between $T=0$, 2 and 4 states). However, the eigenfunctions do depend on $\beta$. In order to exhibit this feature, we have studied two-nucleon transfer strengths in a simple example as described below.

Two nucleon transfer strength for adding a pair of two nucleons coupled to $(S_0{T}_0)=(01)$ to the ground state of a $m=6$ system with the two orbits as above and $(S_i{T}_i)=(01)$ generating $m=8$ states with ${(S_f{T}_f)}_i={(00)}_i$ are calculated using ${\left\{T^{(01)}\right\}}^{†}=P^{†}=(P_1^{†}+P_2^{†})$ as the transfer operator. Then, the transfer strength is given by

$$S(m=6,(01)\to m=8,{(00)}_i)={\left|⟨m=8,{(00)}_i\mid \mid P_1^{†}+P_2^{†}\mid \mid m=6,{(01)}_1⟩\right|}^2.$$

(139)

Note that $⟨\mid \mid \mid \mid ⟩$ is the reduced matrix element with respect to both spin and isospin. For calculating S, first the eigenstates of $m=6$ system are obtained using the Hamiltonian given by Equation (138) for both $\beta =+1$ and $-1$. The basis states for the $m=6$ states are given in Table 11. Note that the eigenfunctions for $m=8$ system are linear combination of the basis states in Table 10 and similarly, for $m=6$ in terms of the states in Table 11. These are obtained by diagonalizing the $H_p(x,\beta =\pm 1)$ matrices in m = 8 and m = 6 basis spaces. Now, using angular momentum algebra, it is easy to see that all we need are the reduced matrix elements of $P_1^{†}$ in the first orbit basis states and $P_2^{†}$ in the second orbit basis states. From [49,51], we have following result (for an orbit with $\mathrm{\Omega }$):

$$\begin{array}{c}⟨N^f=N^i+1,{\omega }^f={\omega }^i\pm 1,(00)\mid \mid P^{†}\mid \mid N^i,{\omega }^i,(01)⟩\hfill \\ =f(\mathrm{\Omega },\mathrm{\Omega }-N^i,\mathrm{\Omega }-N^f,{\omega }^i,{\omega }^f){⟨\begin{array}{cc}\left\{{\omega }^i,{\omega }^i\right\}& \left\{1,1\right\}\\ (01)& (01)\end{array}\mid \mid \begin{array}{c}\left\{{\omega }^f,{\omega }^f\right\}\\ (00)\end{array}⟩}_{SU(4)}.\hfill \end{array}$$

(140)

Formulas for the f factors here are given in [49] and similarly, formulas for the $SU(4)$ coefficients are given in [131]. Using Equations (139) and (140) and the wavefunctions obtained for $m=6$ and $m=8$ systems in the basis states given in Table 10 and Table 11, the transfer strengths are obtained. The strength to the first $(00)$ state of the $m=8$ system with $x=0$ for $\beta =+1$ is found to be 25 times the strength to the first $(00)$ state for $\beta =-1$. Similarly, it is 25 times also for the second $(00)$ states. Thus, two nucleon transfer, distinguishes multiple $SO(8)$ algebras. Further, for $x=-1$ the transfer strength for $\beta =+1$ is found to be 25 times the strength to the first $(00)$ state for $\beta =-1$. However, for the second $(00)$ state the ratio is zero. Further, for $x=+1$, the strength to the first $(00)$ state for $\beta =+1$ and $-1$ are same and so is the result for the second $(00)$ state. It is possible to extend this study to a general x value and also for $(10)$ transfer as well as for two nucleon removal strengths. Further, using the formulation described in [51], it possible to study $\alpha$ transfer strengths as a function of $\beta$.

Table 11. $SO(6)$ limit quantum numbers for the basis states in a two orbit example with ${\mathrm{\Omega }}_1=6$ and ${\mathrm{\Omega }}_2=4$. Shown are the quantum numbers for six nucleons ($m=6$) with total $(S,T)=(0,1)$. Note that the $SO(8)$ seniorities for the nucleons in the two orbits are zero. See Section 6.1.2 for further discussion.

#	${\mathit{N}}_1$	${\mathit{\omega }}_1$	${\mathit{S}}_1$	${\mathit{T}}_1$	${\mathit{N}}_2$	${\mathit{\omega }}_2$	${\mathit{S}}_2$	${\mathit{T}}_2$
1	0	0	0	0	3	3	0	1
2	0	0	0	0	3	1	0	1
3	1	1	0	1	2	2	0	2
4	1	1	0	1	2	2	0	0
5	1	1	0	1	2	0	0	0
6	1	1	1	0	2	2	1	1
7	2	2	0	2	1	1	0	1
8	2	2	1	1	1	1	1	0
9	2	2	0	0	1	1	0	1
10	2	0	0	0	1	1	0	1
11	3	3	0	1	0	0	0	0
12	3	1	0	1	0	0	0	0

6.2. Multiple Pairing Algebras in IBM-3

Interacting boson model with the bosons carrying angular momentum $({\ell }_1,{\ell }_2,\dots )$ and isospin $T=1$ (or an intrinsic spin 1) degree of freedom, the SGA is $U(3\mathrm{\Omega })$, $\mathrm{\Omega }={\sum }_{\ell }(2\ell +1)$. This model is called IBM-3 or IBM-T. For nuclei, it is possible to consider IBM-3 with $sd$, $sdg$, $sdf$ and $sdpf$ bosons. The $sd$ boson version was investigated with applications in the past [42,43,44,135,136,137]. Interestingly, IBM-3 admits two types of pairing algebras and they are related to $U(3\mathrm{\Omega })\supset SO(3\mathrm{\Omega })$ and $U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })$. These are first discussed in [138] for systems with several ${\ell }_i$ orbits but with ${\ell }_i=0$. Here, we will consider briefly the general $({\ell }_1,{\ell }_2,\dots )$ systems.

6.2.1. Multiple $SU(1,1)$ Pairing Algebras with $U(3\mathrm{\Omega })\supset SO(3\mathrm{\Omega })$

Denoting isospin by t for a single boson, we have $t=1$ in IBM-3. With bosons carrying angular momentum $({\ell }_1,{\ell }_2,\dots ,{\ell }_r)$, single boson creation operator is $b_{\ell ,m:t,m_t}^{†}$ and then the generators of the SGA $U(3\mathrm{\Omega })$ are

$$u_{q,\mu }^{L,k}({\ell }_i,{\ell }_j)={\left(b_{{\ell }_i,1}^{†}{\tilde{b}}_{{\ell }_j,1}\right)}_{q,\mu }^{L,k};i,j=1-r.$$

(141)

Note that ${\tilde{b}}_{\ell ,m,1,m_t}={(-1)}^{\ell +m+1+m_t}{b}_{\ell ,-m,1,-m_t}$. Ahead we will use the definition

$${\displaystyle A^{L,k}·B^{L,k}={(-1)}^{L+k}\sqrt{(2L+1)(2k+1)}{\left(A^{L,k}{B}^{L,k}\right)}^{0,0}.}$$

Going further, clearly we have $U(3\mathrm{\Omega })\supset SO(3\mathrm{\Omega })$ and the generator of $SO(3\mathrm{\Omega })$ are

$$\begin{array}{c}{u}_{q,\mu }^{L,k}({\ell }_i,{\ell }_i)\mathrm{with}L+k=\mathrm{odd};\hfill \\ V_{q,\mu }^{L,k}({\ell }_i,{\ell }_j)={\left[\alpha (i,j){(-1)}^{{\ell }_i+{\ell }_j+L+k}\right]}^{1/2}\left\{u_{q,\mu }^{L,k}({\ell }_i,{\ell }_j)+\alpha (i,j){(-1)}^{L+k}{u}_{q,\mu }^{L,k}({\ell }_j,{\ell }_i)\right\};i>j,\hfill \end{array}$$

(142)

with the ${\alpha }_{i,j}$ determined by the pairing algebra as we will show now. In the $3\mathrm{\Omega }$ space, the pair-creation operator $S_{+}$ is

$${\displaystyle S_{+}=\sum _{\ell }{\beta }_{\ell }{S}_{+}(\ell );S_{+}(\ell )=\frac{1}{2}{b}_{\ell ,t=1}^{†}·b_{\ell ,t=1}^{†},{\beta }_{\ell }=\pm 1.}$$

(143)

The operators $\{S_{+},S_{-},S_0\}$ with $S_{-}={(S_{+})}^{†}$ and ${\displaystyle S_0=\frac{\mathrm{\Omega }+\widehat{n}}{2}}$ for each $\left\{\beta \right\}=\{{\beta }_1,{\beta }_2,\dots \}$ set, generate a $SU(1,1)$ pairing algebra and this is in correspondence with the $SO(3\mathrm{\Omega })$ generated by the operators in Equation (142) satisfying

$$\alpha ({\ell }_i,{\ell }_j)=-{\beta }_{{\ell }_i}{\beta }_{{\ell }_j}.$$

(144)

Thus, we have in IBM-3 multiple pairing $SU(1,1)$ algebras with corresponding $SO(3\mathrm{\Omega })$ algebras. These first class of pairing algebras are clearly established at the level of quadratic Casimir operators. The following are easily proved [55] given Equations (141)–(144),

$$\begin{array}{c}4S_{+}{S}_{-}=\widehat{n}(\widehat{n}+3\mathrm{\Omega }-2)-{\mathcal{C}}_2(SO(3\mathrm{\Omega })),\hfill \\ \\ {\displaystyle {\mathcal{C}}_2(SO(3\mathrm{\Omega }))=\sum _{L+k=odd;\ell }{u}^{L,k}(\ell ,\ell )·u^{L,k}(\ell ,\ell )+\sum _{i<j}\sum _{L,k}{V}^{L,k}({\ell }_i,{\ell }_j)·V^{L,k}({\ell }_i,{\ell }_j),}\hfill \\ \\ {\displaystyle {\mathcal{C}}_2(U(3\mathrm{\Omega }))=\sum _{i,j}\sum _{L,k}{(-1)}^{{\ell }_i+{\ell }_j}{u}^{L,k}({\ell }_i,{\ell }_j)·u^{L,k}({\ell }_j,{\ell }_i).}\hfill \end{array}$$

(145)

Following the results presented in Section 3, given m number of bosons, the $SO(3\mathrm{\Omega })$ irreps [equivalently the irreps of $SU(1,1)$] are labeled by $\omega$ with $\omega =m,m-2,\dots$, 0 or 1. With this, the eigenvalues of the Casimir operators are,

$$\begin{array}{ccc}\hfill {⟨{\mathcal{C}}_2(U(3\mathrm{\Omega }))⟩}^{m,\omega }& =& m(m+3\mathrm{\Omega }-1),\hfill \\ \hfill {⟨{\mathcal{C}}_2(SO(3\mathrm{\Omega }))⟩}^{m,\omega }& =& \omega (\omega +3\mathrm{\Omega }-2),\hfill \\ \hfill {⟨4S_{+}{S}_{-}⟩}^{m,\omega }& =& (m-\omega )(m+\omega +3\mathrm{\Omega }-2)\hfill \end{array}$$

(146)

Given several ℓ orbits, they can be grouped in different ways giving $3\mathrm{\Omega }=3{\mathrm{\Omega }}_1+3{\mathrm{\Omega }}_2+\dots$ and we can define again pairing $SU(1,1)\sim SO(3{\mathrm{\Omega }}_i)$ algebras in each $3{\mathrm{\Omega }}_i$ space. For example with $sdg$IBM-3, we have $\mathrm{\Omega }=15$ and the SGA is $U(45)$. With this first we have $SU(1,1)\sim S{O}_{sdg}(45)$ pairing algebra and there will be four of these algebras as seen from Equation (143). Further, we have $S{O}_{sd}(18)$, $S{O}_{sg}(30)$, $S{O}_{dg}(42)$ algebras (two each) besides $S{O}_d(15)$ and $S{O}_g(27)$ algebras in $sdg$IBM-3. All these are pairing algebras with a corresponding $SU(1,1)$ algebra for each of them. Thus, in IBM-3 there will be large number of $SU(1,1)$ class of pairing algebras. It is challenging to investigate the various structures that they generate.

6.2.2. Multiple $Sp(6)$ Pairing Algebras with $U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })$

In order to identify the second class of pairing algebras, let us first decompose the space into orbital part and isospin part giving $U(3\mathrm{\Omega })\supset [U(\mathrm{\Omega }\supset SO(\mathrm{\Omega })]\otimes [SU(3)\supset S{O}_T(3)]$ algebra. Generators of $U(\mathrm{\Omega })$, $SO(\mathrm{\Omega })$, $SU(3)$ (and $U(3)$) and $S{O}_T(3)$ are identified following the results in [55],

$$\begin{array}{c}{\displaystyle U(\mathrm{\Omega }):h_q^L({\ell }_1,{\ell }_2)=\sqrt{3}{u}_{q,0}^{L,0}({\ell }_1,{\ell }_2)}\hfill \\ SO(\mathrm{\Omega }):u_{q,0}^{L,0}(\ell ,\ell ),L=\mathrm{odd},V_q^L({\ell }_i,{\ell }_j)\mathrm{with}i<j\hfill \\ V_q^L({\ell }_1,{\ell }_2)={\mathcal{N}}^{1/2}\left\{u_{q,0}^{L,0}({\ell }_1,{\ell }_2)+\alpha ({\ell }_1,{\ell }_2){(-1)}^L{u}_{q,0}^{L,0}({\ell }_2,{\ell }_1)\right\}\hfill \\ {\displaystyle U(3):g_{\mu }^k=\sum _{\ell }\sqrt{(2\ell +1)}{u}_{0,\mu }^{0,k}(\ell ,\ell );k=0,1,2}\hfill \\ SU(3):g_{\mu }^k,k=1,2\hfill \\ {\displaystyle S{O}_T(3):T_{\mu }^1=\sqrt{2}{g}_{\mu }^1}\hfill \\ {\displaystyle U(1):\widehat{n}=\sum _{\ell }\sqrt{3(2\ell +1)}{u}_{0,0}^{0,0}(\ell ,\ell ).}\hfill \end{array}$$

(147)

Note that $\alpha ({\ell }_1,{\ell }_2)=\pm 1$ and these are fixed by identifying the pairing algebra that is complementary to the $SO(\mathrm{\Omega })$ algebra. For a pair coupled to angular momentum zero, symmetric nature of the wavefunctions with respect to $U(3\mathrm{\Omega })$ show that the isospin K of the pairs will be $K=0,2$ ($K=1$ is forbidden due to symmetry). Therefore, we have six pair-creation operators given by

$${\displaystyle P_{\mu }^K=\sum _{\ell }{\beta }_{\ell }\sqrt{(2\ell +1)}{\left(b_{\ell 1}^{†}{b}_{\ell 1}^{†}\right)}_{0,\mu }^{0,K};K=0,2,{\beta }_{\ell }=\pm 1.}$$

(148)

Now, the 21 operators $P_{\mu }^{0,2}$, ${\left[P_{\mu }^{0,2}\right]}^{†}$, $g_{\mu }^{1,2}$ and $\widehat{n}$ generate the $Sp(6)$ pairing algebra for each $\left\{\beta \right\}$ set. Thus, we have multiple $Sp(6)$ pairing algebras and they will be complementary to the $SO(\mathrm{\Omega })$ algebras given above provided

$$\mathcal{N}={(-1)}^{L+1}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2},\alpha ({\ell }_1,{\ell }_2)={(-1)}^{{\ell }_1+{\ell }_2+1}{\beta }_{{\ell }_1}{\beta }_{{\ell }_2},{\ell }_1\ne {\ell }_2.$$

(149)

with this we have the important relation,

$$\begin{array}{ccc}\hfill H_p& =& {\displaystyle \sum _{K=0,2;\mu }{P}_{\mu }^K{\left(P_{\mu }^K\right)}^{†}}\hfill \\ & =& {\mathcal{C}}_2(U(\mathrm{\Omega }))-{\mathcal{C}}_2(SO(\mathrm{\Omega }))-\widehat{n}.\hfill \end{array}$$

(150)

The quadratic Casimir operators appearing here are given by

$$\begin{array}{ccc}\hfill {\mathcal{C}}_2(U(\mathrm{\Omega }))& =& {\displaystyle \sum _{{\ell }_1,{\ell }_2,L}{(-1)}^{{\ell }_1+{\ell }_2}{h}^L({\ell }_1,{\ell }_2)·h^L({\ell }_2,{\ell }_1),}\hfill \\ \hfill {\mathcal{C}}_2(SO(\mathrm{\Omega })& =& {\displaystyle 2\sum _{\ell ,L=odd}{u}^L(\ell ,\ell )·u^L(\ell ,\ell )+\sum _{{\ell }_1<{\ell }_2,L}{V}^L({\ell }_1,{\ell }_2)·V^L({\ell }_1,{\ell }_2).}\hfill \end{array}$$

(151)

Besides these, ${\mathcal{C}}_2(U(3))={\sum }_{k=0,1,2}{g}^k·g^k$, ${\mathcal{C}}_2(SU(3))=(3/2){\sum }_{k=1,2}{g}^k·g^k$ and ${\mathcal{C}}_2(S{O}_T(3))=2g^1·g^1$. Finally, given m number of bosons, the irreps of $U(\mathrm{\Omega })$ will be three-rowed Young tableux $\{f_1,f_2,f_3\}$ with $f_1\ge f_2\ge f_3\ge 0$ and $f_1+f_2+f_3=m$. Similarly, the $U(3)$ irreps are labeled by the same $\left\{f\right\}=\{f_1,f_2,f_3\}$ and those of $SU(3)$ then are $(\lambda ,\mu )=(f_1-f_2,f_2-f_3)$. Given a three-rowed $U(\mathrm{\Omega })$ irrep, the $SO(\mathrm{\Omega })$ irreps will be also maximum three-rowed and denoted by $\left[\omega \right]=[{\omega }_1,{\omega }_2,{\omega }_3]$. With this we have the states $\left|m,\left\{f\right\},\left[\omega \right]:(\lambda ,\mu )T{m}_T\right.⟩$ and the reductions for $\left\{f\right\}\to \left[\omega \right]$ and $(\lambda ,\mu )\to T$ follow from the rules given in [53,116,119,135,139]. It is important to recognize that the $Sp(6)$ algebra we have is a non-compact $Sp(6,R)$ algebra [118]. The irreps of $Sp(6)$ are labeled by three numbers $⟨{\lambda }_1,{\lambda }_2,{\lambda }_3⟩$ and they will be in correspondence with $[{\omega }_1,{\omega }_2,{\omega }_3]$ via Equation (150). Moreover, with $Sp(6)$ pairing we have the algebra $Sp(6)\supset [SU(3)\supset S{O}_T(3)]\otimes U(1)$. This algebra need to be analyzed in detail in future. Finally, by grouping the ℓ orbits in different ways, it is easy to recognize that there will be large number of $Sp(6)$ algebras in IBM-3. For example, in $sdg$IBM-3 there will be $Sp(6)$ algebras that correspond to $U_{sd}(18)\supset [U_{sd}(6)\supset S{O}_{sd}(6)]\otimes [SU(3)\supset S{O}_{T_{sd}}(3)]$, $U_{sg}(30)\supset [U_{sg}(10)\supset S{O}_{sg}(10)]\otimes [SU(3)\supset S{O}_{T_{sg}}(3)]$ and so on.

6.3. Summary

Multiple $SO(8)$ pairing algebras appear with $LS$-coupling in shell model and they allow for both isoscalar and isovector pairing terms in the Hamiltonian. The $SO(8)$ algebra generates three subalgebras with each having a correspondence with a algebra chain that starts with the SGA $U(4\mathrm{\Omega })$. In Section 6.1 these are briefly discussed along with a method to construct H matrices in a two-orbit example assuming $SO(8)$ seniority zero in the two-orbits. Using this system, it is shown that two-nucleon transfer distinguishes the two $SO(8)$ pairing algebras possible although the energy spectra are same. More detailed investigations of the multiple $SO(8)$ pairing algebras are possible by developing further the corresponding Wigner–Racah algebra. An alternative is to employ nuclear shell model codes as attempted in [140,141] or use the Richardson–Gaudin method as discussed in [142]. Turning to boson systems, described briefly in Section 6.2 are the two different types of pairing algebras in IBM-3 (or IBM-T). The first one operates in the total $3\mathrm{\Omega }$ space giving $SU(1,1)$ pairing algebra in correspondence with the $U(3\mathrm{\Omega })\supset SO(3\mathrm{\Omega })$ algebra. The other one is a $Sp(6)$ pairing algebra in correspondence with $SO(\mathrm{\Omega })$ in the direct product subalgebra $U(3\mathrm{\Omega })\supset [U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })]\otimes [SU(3)\supset S{O}_T(3)]$. In the multi-orbit situation (as in $sd$, $sdg$, $sdpf$ etc.), there will be multiple $SU(1,1)$ and $Sp(6)$ pairing algebras. These algebras need to be investigated in further. Let us mention that the $SO(8)$ and IBM-3 pairing algebras are important for heavy N = Z nuclei.

7. Conclusions and Future Outlook

Pairing plays a central role in nuclear structure and it is essential for many exotic processes such as for example double beta decay. From the point of view of symmetries, pairing algebras are a topic of investigation for many decades. In shell model for identical nucleons, the pairing algebra is $SU(2)$ and similarly for nucleons with isospin it is $SO(5)$. Furthermore, $LS$ coupling gives $SO(8)$ pairing algebra. In the same way, pairing algebra for identical bosons in the interacting boson models is the non-compact $SU(1,1)$ algebra and F-spin gives $SO(3,2)$ algebra. However, in the multi-orbit situation the pairing algebras are not unique and recently it is recognized that we have the new paradigm of multiple multi-orbit pairing algebras $SU(2)$, $SO(5)$ and $SO(8)$ within shell model and $SU(1,1)$, $SO(3,2)$ and $Sp(6)$ within interacting boson models. In the present paper, a review of the results for multiple multi-orbit pairing algebras in shell model and interacting boson models is presented. In Section 2 results are presented for $SU(2)$ pairing algebra for identical nucleon systems in shell model and in Section 3 for $SU(1,1)$ pairing algebra for identical bosons in interacting boson models. Similarly, in Section 4 and Section 5 results are presented for $SO(5)$ pairing algebra for nucleons with isospin in shell model and $SO(3,2)$ pairing algebra for bosons with F-spin in the interacting boson models. As seen from the results presented in Section 2, Section 3, Section 4 and Section 5, clearly a given set of multiple pairing algebras generate the same spectrum but different results for properties such as EM transition strengths, two-nucleon transfer strengths and so on that depend on the wavefunctions. In the final Section 6, the more complex multiple $SO(8)$ pairing algebras in shell model with $LS$-coupling and the two classes of pairing algebras in interacting boson models with isospin $T=1$ degree of freedom are briefly described. Here the algebras need much more further development. Summarizing, Table 12 gives the list of main cases of complementary algebras described in the present review. Let us add that, although we have discussed only IBM-1, IBM-2, and IBM-3 models, it is also possible to consider multiple pairing algebras in IBM-4, interacting boson model with spin–isospin degrees of freedom [21,55,56]. The algebras here will be much more complex and they will be discussed elsewhere. In addition, multiple multi-orbit pairing algebras each generating a pairing Hamiltonian and combining this with the quadrupole–quadrupole ($Q.Q$) Hamiltonians generated by multiple $SU(3)$ algebras (both in shell model and interacting bosons models [67,68,69]) will give multiple pairing plus $Q.Q$ Hamiltonians. Nuclear structure studies using these new class of pairing plus $Q.Q$ interactions will be interesting. Finally, it is our hope that the results presented in this review will lead to much further work on multiple pairing and also multiple $SU(3)$ algebras in future.

Table 12. Summary of pairing algebras considered in this article. See Section 2, Section 3, Section 4, Section 5 and Section 6 for details. Note that SGA stands for spectrum generating algebra.

Model	Nature of Constituents	SGA	Pairing Algebra	Complementary Number-Conserving Algebra
$j-j$ coupling	identical nucleons	$U(N)$	$SU(2)$	$Sp(N)$ in
shell model				$U(N)\supset Sp(N)$
Interacting	identical bosons	$U(\mathrm{\Omega })$	$SU(1,1)$	$SO(\mathrm{\Omega })$
boson models (IBM-1)				in $U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })$
$j-j$ coupling	nucleons	$U(2\mathrm{\Omega })$	$SO(5)$	$Sp(\mathrm{\Omega })$ in $U(2\mathrm{\Omega })\supset$
shell model	with isospin			$\left[U(\mathrm{\Omega })\supset Sp(\mathrm{\Omega })\right]\otimes S{U}_T(2)$
Interacting	bosons with	$U(2\mathrm{\Omega })$	$SO(3,2)$	$SO(\mathrm{\Omega })$ in $U(2\mathrm{\Omega })\supset$
boson models (IBM-2)	F-spin			$\left[U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })\right]\otimes S{U}_F(2)$
$L-S$ coupling	nucleons	$U(4\mathrm{\Omega })$	$SO(8)$ with;	$SO(\mathrm{\Omega })$ in
shell model	with isospin		3 limits-Equation (134)	3 limits-Equation (135)
Interacting	bosons with	$U(3\mathrm{\Omega })$	$SU(1,1)$	$SO(3\mathrm{\Omega })$
boson models (IBM-3)	isospin $T=1$			in $U(3\mathrm{\Omega })\supset SO(3\mathrm{\Omega })$
			$Sp(6)$	$SO(\mathrm{\Omega })$ in $U(3\mathrm{\Omega })\supset$
				$\left[U(\mathrm{\Omega })\supset SO(\mathrm{\Omega })\right]\otimes \left[SU(3)\supset S{O}_T(3)\right]$