1. Introduction
In some sense, we have a closed-form solution of the Schrodinger equation for the hydrogen molecule, but, beyond this, there are no closed-form solutions for any other molecule. However, with the aid of numerical techniques, we can solve the molecular problem with a great degree of accuracy. As more and more larger molecules are considered, techniques tend to have limitations. Many clever approaches result in all sorts of approximation schemes, which work well for some systems but not for others. Paousek and Aliev [
1] have shown that the general molecular Hamiltonian to is given by,
where
is the momentum of electrons and
is the momentum of the nuclei. It does not lend itself to a description of the stationary states of a polyatomic molecule. Although the Hamiltonian is of a simple form, the numerical integration of the Hamiltonian in terms of the space-fixed coordinates of the atomic nuclei and electrons is extremely difficult, even for the simplest of molecular systems [
2,
3,
4].
A classical description of such a system of atomic nuclei and electrons sometimes reveals translation and rotation motion in space. The atomic nuclei can vibrate around the configuration given by the electronic structure of the molecule, and the electron also can move around the atomic nuclei. As a result, a quantum mechanical description of these motions should yield vibrational, rotational, and electronic energy levels and the corresponding wave function of the Schrodinger equation for this system. The task, however, of getting the information from a full Schrodinger wave equation is almost impossible, therefore, other techniques must be explored [
1,
2,
3,
4].
One approach is to develop a classical model of its translation, overall rotation, the vibration of the atomic nuclei, and the electronic motions. This is achieved by replacing the laboratory or the space-fixed coordinates of the atomic nuclei and electrons with new coordinate systems suitable for describing the individual types of motion mentioned above [
3,
4]. The Hamiltonian is developed in the new coordinates
, which are the coordinates of the electrons concerning a moving x,y,z axis system fixed to a molecule. The Euler angles
define the orientation of the x,y,z axis system with respect to the X, Y, Z axis system. The coordinates
are the vibrational displacement vectors of the system atomic nuclei for the x, y, z axis system [
1,
2,
3,
4,
5]. Next, we make the Born–Oppenheimer approximation (BOA) to obtain a Hamiltonian for the electronic state and a Hamiltonian for vibrational–rotational states for given electronic states. Furthermore, Born–Oppenheimer-like approximations allow for the separation of the vibrational motions from the rotational motion [
1,
2,
3,
4,
5,
6,
7,
8].
The BOA allows the molecular Hamiltonian to be separated into the electronic part and its rovibrational Hamiltonian. The rovibrational Hamiltonian is given by
where
and
is the rotational Hamiltonian, and
is a harmonic oscillator Hamiltonian. The wavefunction for the molecule is given by,
Here, we can exploit the spatial symmetry of the molecule in the molecular system. A symmetry operation is a geometrical action that leaves the position of the atoms unchanged. There are five types of geometry operations: Identity (1), reflection (σ), rotation (
), rotation–reflection (
), and inversion (
). Each symmetry operation, excluding the identity, is associated with a symmetry element [
1,
2,
3,
4,
8,
9]. The symmetry operation is the actual action, while the symmetry element is the point, line, or plane about which the action occurs. Therefore, our goal in this paper is to illustrate how symmetry analysis can calculate genuine vibrations and classify the spectra according to the point group irreps. Thus, spectral decomposition is a powerful tool that will aid in determining the eigenvectors and the eigenvalues if the symmetry group is known. Harter [
3,
8] has detailed descriptions of the procedure for such a computation. We will outline how to utilize this method to perform calculations on a tetrahedral molecule. The key in this approach is to determine the projectors associated with the particular group symmetries.
2. Commuting Observable and Symmetry Projectors
Symmetry groups are classified into two categories: Abelian and Non-Abelian. The neat thing about Abelian groups is that we can write all the class operators as a combination of a single set of idempotent projectors. However, this is not the case for Non-Abelian groups. For the very simple fact that every group operator does not commute. All is not lost because we can find a set of mutually commuting operators. We describe how to do this by following the procedure outlined by Harter [
3,
8]. Moreover, similar approaches have been described in [
4,
7,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18].
- A.
Class algebra and all-commuting operator. We create the class structure of the group. This allows us to create communicative algebra. Each class sum commutes with each other and with every operator in the entire group algebra. In other words, the
cg’s are mutually commuting with respect to themselves and all-commuting with respect to the whole group.
. Harter [
3,
8] showed that an all-commuting operator C =
Cg g that is, one that commutes with all h in the group, is a combination of class sums
cg. All commutation (C h = h C) implies,
- B.
Characters and all-commuting projectors. We construct the projectors by solving the minimal equation of the group,
where
are called the All-Commuting Class Idempotent (ACCI), and
and
are eigenvalues from the minimal equation. We can expand the original class operators in terms of all commuting idempotent [
3] i.e.,
where
is the eigenvalue such that
. By knowing the character table of the group, (5) can be obtained from,
Next, we acquire the inverse of (7), which must satisfy the completeness and spectral decomposition relation, i.e.,
The way we performed the spectral decomposition will depend on whether the group is Abelian or Non-Abelian. For Abelian grouping, an element
must satisfy a minimal equation
where there exists
orthogonal idempotents
. We must choose another element
of the group that would yield
. Both sets must satisfy the completeness and the spectral decomposition equation,
We then multiply (9) by
, which may result in the splitting of
into a sum of operators
,
This set of nonzero terms
will also satisfy orthonormality and completeness relations. Therefore, the spectral decomposition of
and
,
- C.
Maximal sets of commuting operators (MSOCO). These are the independent operators of the group that can be diagonalized at once. They are not unique since there are numerous sets of operators that compete to be part of a specialized set called an MSOCO (Maximal Set of Commuting Operators or Observables
(MSOCO) [
3,
8]. The number of operators is the
rank of the
group. As an example, shown in [
8], the rank of
D3 turns out to be four. Furthermore, the set diagram of
D3 in
Figure 1 shows the class sum algebra of all-commuting operators at the center of the diagram.
The D
3 dimension determines the number of orthogonal irreducible representations (irreps) in the algebra (the irreps
A1,
A2, and
E and the three all-commuting projectors
of the center are uniquely defined; no others exist). A rank of four implies another member of the
MSOCO. The rank can be obtained by simply summing down the column of the character table (13). From the first column of the character table, we are able to tell how each irrep will split.
The other member of the rank-4 MSOCO is not uniquely chosen; one choice is the operator
picked in
Figure 1 (other choices are shown in the figure). By choosing this operator to be diagonal, we are selecting a particular way to “split” the
idempotent and build a particular set of
E-irreps. Furthermore, the number of operators needed depends on the order of group. Thus, in the case of D
3 there are six projectors needed. In general, the number of operators needed is given by,
In the case of tetrahedral symmetry, the rank is 10 but only 5 irreps are possible: and total number operators is 24. However, is not vibrational mode and, thus, only 15 operators are necessary.
- D.
Computing irreducible projectors. To compute the irreducible projectors of a non-communicating group we must consider the projectors of its subgroups. The key is finding the non-commutative spectral decomposition of the entire Non-Albelian group. Unlike Abelian, Non-Abelian will consist of nilpotent and idempotent projectors. Nilpotent projectors are important for expanding operators that do not commute. Each of the all-commuting idempotents can be split into irreducible idempotents, i.e.,
, then
remains un-split. We use the subgroup idempotent to split
. Suppose that
where
and
are the irreps of
and
, respectively, such that
are projectors of
and
are projectors of
, then idempotent of both
and
satisfy the completeness relation,
such that:
Hater [
3] refers to this as one times one (
trick. Thus, a single projector such that
will split as,
Every subgroup will give a different splitting. For octahedral [
3], the all-commuting idempotent
splits when multiplied by six idempotents of
:
Let’s consider D
3 symmetry a much simpler group with rank 4 and three irreps see (13). Of the three irreps only
splits. Since C
2 is a subgroup of D
3 we use it decompose
into the irreducible projectors
and
shown below,
Now using the (
trick with the completeness relation gives,
Next,
1 is wrapped around any operator
g of the
D3 algebra to give the following generalized
Spectral Decomposition of the form shown in (22),
Thus, this result in (21) in which the
and
are unchanged because they are all-commuting,
The remaining four terms are the
E-projectors multiplied by irreps as seen by comparing (24)
(23) is the form of a generalized non-commutative spectral decomposition of an entire Non-Abelian group. D3’s decomposition differs from the commutative C6. D3 has two nilpotent projectors and along with four ordinary (idempotent) projectors , , , and . Other Non-Abelian groups have other numbers of these two kinds of P’s.
All commutative groups can be reduced to orthogonal idempotents that satisfy simple orthogonality relations given in [
4],
A more general formulation spectral decomposition comes from writing (12) as,
and (25) replaced by the generalized projector orthonormality relation for non-commutative projectors,
To obtain generalized projectors, the decomposition (26) must be inverted. The result which will be proved below is the famous Wigner–Weyl projection formula,
where
oG = 6 is the order of the group D
3 and
is the m-irrep dimension, (
,
, and
). Again, these numbers vary from group to group. For Abelian groups, irrep dimensions are always one (
).
Let us summarize the first set of six irrep projectors which will be used in a band theory model below,
The element
is outside of the CSOCO can be used to determine the two non-zero nilpotent projectors
PExy and
PEyx since the idempotents
PExx and
PEyy from (29) are orthogonal. A commuting operator would permit the two projectors to annihilate [
8]. The key is to choose any operator such as
,
,
, or
outside of the
CSOCO, as shown in
Figure 1. This will give all the needed projectors. At this stage, we use the projector to find eigenvalues and eigenvectors,
Suppose that we have the normalized eigenfunction
, then the vector product is
gives,
Given this and the irrep
P-operators in (29), the
D3-symmetry projected states are obtained easily,
The E-matrices
we can derive from the projector states for example
; This comes about by computing the operator
acts on the column element
and
(i.e.,
and
),
We compute the following products,
,
,
, and
. In general,
and
Thus, from (33)–(36) we found all reduce regular representation for our
example as shown by (37),
Each bra or ket is an operation of P-operator on the “first” state |1. Note the use of conjugation:.
3. Rovibrational Hamiltonian and Wavefunctions
In (2), we write down the rovibrational Hamiltonian for a molecular system. This is synonymous with that described by Bunker and Jensen [
4]. Bunker and Jensen [
4] showed that invoking the harmonic oscillator approximation leads to the rigid-rotor harmonic oscillator Hamiltonian for a rotational–vibrational motion. Consequently, our Hamiltonian is given by,
where
This is then treated as a quantum oscillator, as em-modes are quantized to give quantum field theory. The quantum theory of vibrational modes has the same traditional classical roots as quantum field theory. We will use canonical variables, which are defined by
Next, we write the canonical variables in ordinary coordinates.
Using the completeness relation gives
where
We can then write annihilation and creation operators in terms of symmetry coordinates since
We can consider how to symmetrize the wavefunction for the rovibrational Hamiltonian. Dijon group [
19,
20] define a compact form that can be expressed as,
We consider the form for the vibration and rotation as describe by ref. [
9,
10],
where
and
or similarly in spherical harmonics by Wormer [
21]
- A.
Rotational Wavefunction
To
we must consider the overall external symmetry
. This then correlated with the internal symmetry
. Knowing
gives a correlation induced between the irrep
and that of
. The characters of R
3 are given by,
We derive the character of
from its outer product in relation to
in (51).
The frequency
of the irreducible representation of
subduced to
is given by:
where
is the irrep label of the point group of the composite rigid body. With
the Equation (53) and we can use character table (54) to find the induced representation,
Therefore, we give the correlation between
and
as (55),
We construct symmetrize rotational wave function as follows
We must compute how
J split under a subduction
. For instance, if
, which is tetrahedral symmetry, and that we the splitting at
, then the split is
. We build the corresponding wavefunction
and
as outlined by Harter [
3] for octahedral symmetry. From (56) we have,
The local symmetry of
has a projector
,
We need the tetragonal (
) projectors
of
and only those for which
Thus, we find the induced representation
of
by performing a correlation between the character tables of
and
:
Using columns 1 and Ii
I of
table from (54) gives,
It is clear from (62) that
correlates with the tetrahedral component
and
. Therefore, we have
and
. This tells us that we must use the third row of the tetragonal D-matrix for
symmetry irrep, however, in the case of E symmetry irrep, it said both the first and third could be used. Therefore, consider
and repeat correlation with
symmetry group, as shown by (63). We find that
correlates with E and
correlates with
. Both suggest that the last rows in
and
D-matrices are needed (57), depending on the D-function of
and symmetry irreps coset leaders. Let’s choose the following coset leaders. We can write each coset leader in terms of its Euler angle rotation.
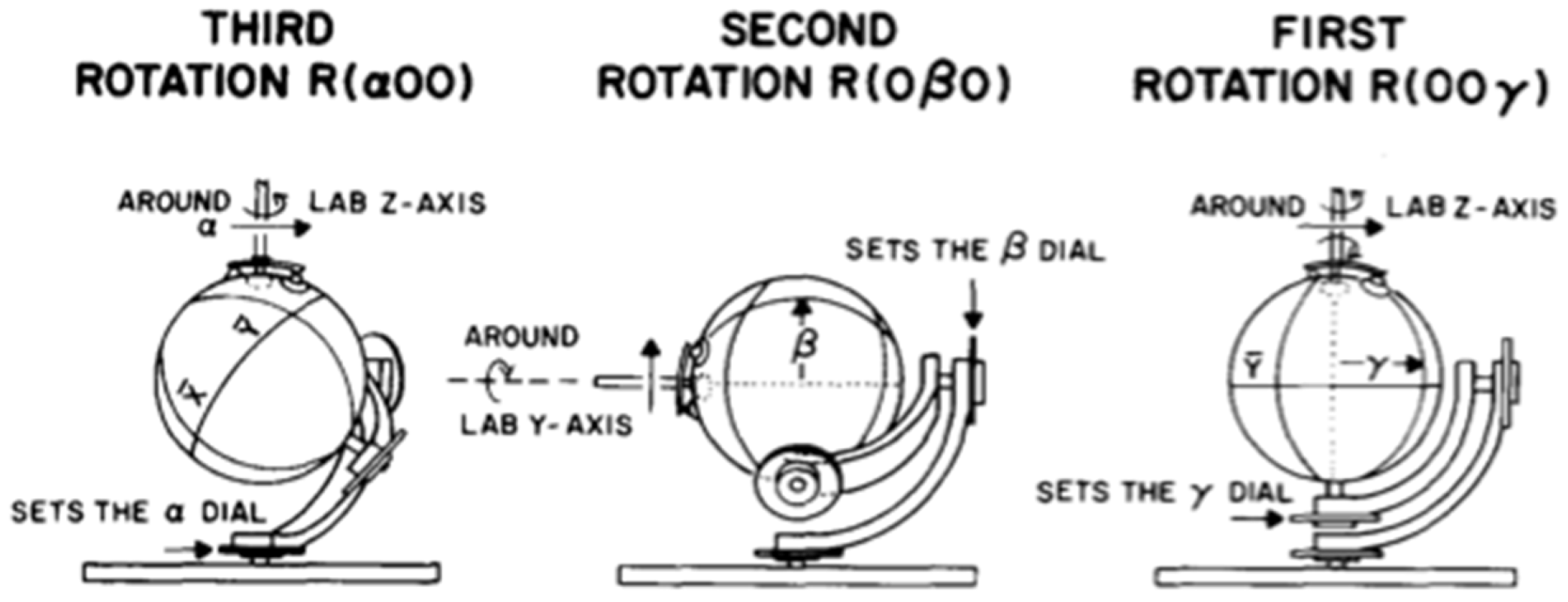
Figure 2. shows the Euler machine designed and built by Harter to perform these operations [
3,
14]. There are sequenced pivot bearings connecting each frame to its neighbor. One of the three Euler angles
is displayed on each bearing’s indicator and dial.
Harter [
3] showed that the ordered rotation sequence of lab-based operations orients the body into position relative to the lab, i.e.,
There are steps we must perform to find
. As shown in
Figure 3,
is a rotation around the z-axis,
around y-axis, and
rotation around z-axis. The first move is to zero the azimuth angle
with the z-crank, and, then, zero the polar angle
with the crank, finally the
rotation is given by the z crank
. To complete this operation, we return
to its original position by doing the reserve operation
. This allows us to create the expression between Euler rotations and Darboux rotations,
We obtain the Euler angles from Darboux angles [
2] as described by (66):
Here we find all following for our coset leaders written in their polar form:
We could have also us the follow alternative sets of cosets leaders:
By using (66) we found the Euler representation (56) leading cosets:
Thus, we proceed with the example by finding the representation components of
for each coset leader by taking only the first column of the
matrix (49), therefore,
We evaluate (70) for the coset leaders, and we have
Now, we use Equation (54) through (71) to determine our orbital states (72).
By applying spherical harmonics, we have,
By combining (72) and (73), we acquire the same result for the rotational tensor given in [
3].
- B.
Vibrational Wavefunction
Consider the vibration Hamiltonian expanded in terms of raising
and lowering
operators,
Suppose
is an eigenstate of H then
as such:
Furthermore,
is the spectroscopy notation for
, such that in methane
for
,
for
,
for
for
. There, E label
has a triple degenerate:
(77) is exactly the same as Alvarez-Bajo et al. [
10], i.e.,
, therefore, we can say
4. Concrete Example: Symmetry Analysis of Methane
The chemical formula for methane is CH
4.; there are four hydrogen atoms bonded to one carbon atom. The ground state methane (CH
4) molecule has T
d symmetry, i.e., tetrahedral point group symmetry. Imagine a cube that has four hydrogen atoms placed at four of its corners laying diagonally at equal distances with a carbon atom at the center. These atoms are connected to each other via springs. Thus, the tetrahedral symmetry is shown in
Figure 4.
The position of Hydrogen atoms or Y atoms will be represented with symmetry coordinates.
Figure 4. shows a set of bases for the Y atoms. We will use these base sets to do the symmetry analysis of XY
4. The vibrational modes will be calculated, and they can be simulated on a computer to understand the dynamics of XY
4 molecules better.
There are twelve bases stated describing the Y atom in XY
4 and three bases stated for the X atom. Bases set of Y atoms in
Figure 4. are labeled by set selected symmetry operators in
Figure 5,
The symmetry operations for an object with
symmetry is given by the following in
Figure 6.
Although (a) and (b) make up
point symmetry, the symmetry operations of (a) moves the four
atoms to the same place that the symmetry operations in (b) would. Consequently, the symmetry operation in (a) and (b) of the two cosets of twelve in
base vectors of the X atom are,
The eigenvectors are then obtained from the group projectors
. When the particular symmetry is known, the eigenvectors or near-eigenvectors
are very easily found,
There exists a local symmetry of
that preserves each coordinate vector
so
. It has a projector
,
Thus, it spans an induced representation
of
. The full
labeled orbit is given by a 12-dimensional induced representation
. The character tables of
,
and
and using columns 1 and Ii
1 of
table gives (63). However, by considering the sub-group chain
, we find the symmetry characteristic of the energy levels in
as shown by
Figure 5. We start with the
character table:
Then, we determine the correlation
between the
character table (60) and the
character table (85),
Next, we obtain the correlation between
and
,
From (79)–(88), we construct the following energy level correlation diagram (see
Figure 7), which shows symmetry splitting for the subgroup chain
. This gives the eigenvectors:
Irrep matrix
are determined from irrep idempotent
by constructing the normalize element
. In
Appendix A we list the trigonal and tetrahedral bases
and
matrices. We demonstrate in
Section 2 how to compute
for
matrices, however, for more details consult red. 3. In (89) the element of
are used to find the eigenvectors.
The projected near eigenvectors corresponding to
are given below,
The
and
eigenvectors are written in the trigonal bases (see
Appendix A.4,
Appendix A.5 and
Appendix A.6) and are related to the subgroup chain
by the unitary transformation,
Applying the transformation to the irrep matrices of the
chain gives the irrep matrices for the
chain (see
Appendix A.1,
Appendix A.2 and
Appendix A.3). As a result, we find the eigenvectors in a new bases which is given by,
In
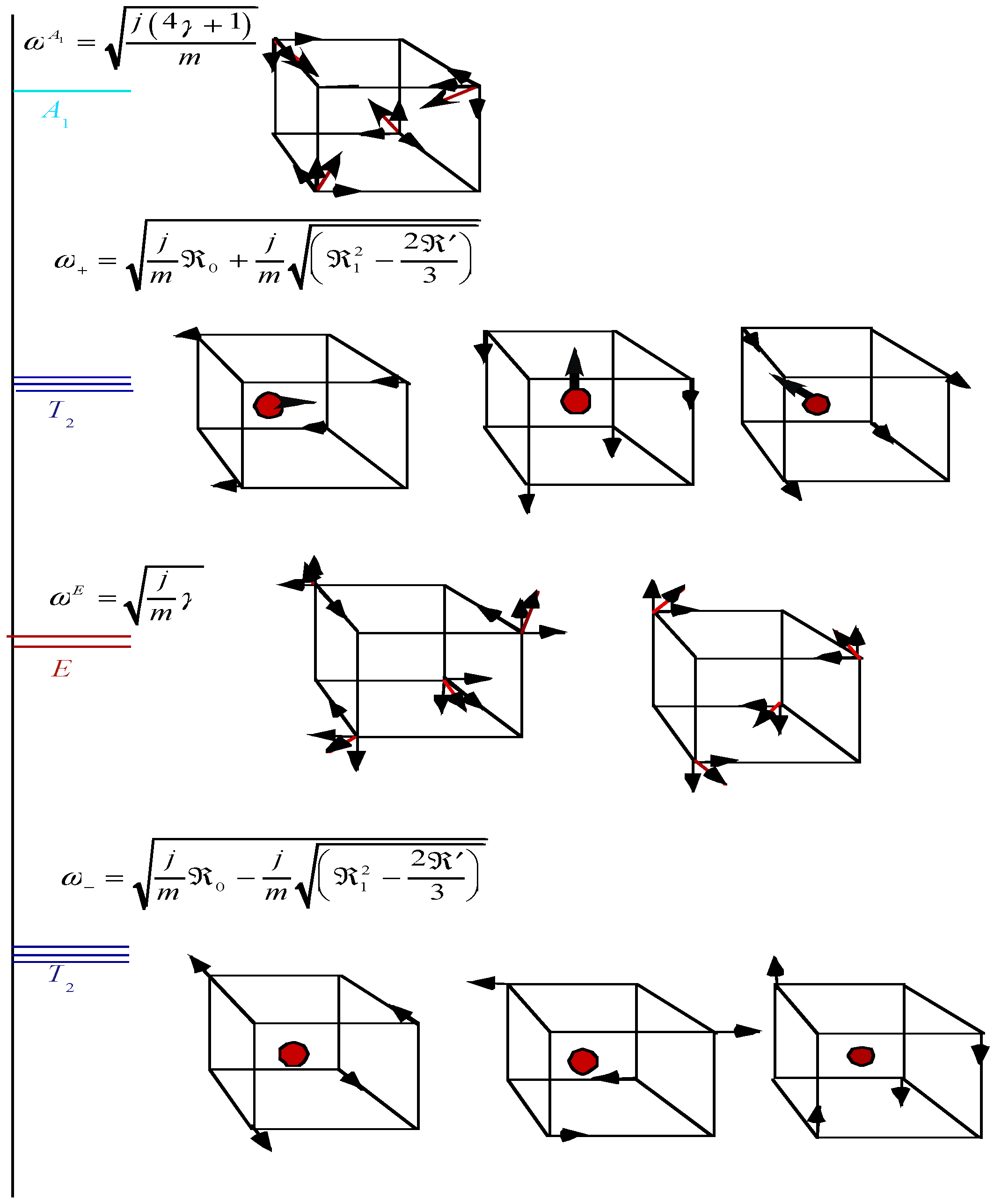
Figure 8, we display all the genuine vibrations of XY
4. Now, we consider the energy eigenvalues using those bases for XY
4 molecule.
4.1. Solving the Equation of Motion
From the
symmetry projection operators, we can construct the eigenstates and use them to partially solve the equation of motion (94),
The number of elements we need for the force matrix is considerably less than (15)
2 = 225 due to symmetry considerations. Only 18 elements are needed for the force matrix. Because of the non-genuine vibration of the
mode, it will acquire in general (82), which simplifies to a block matrix form (96). To compute the F-matrix we must obtain the component
by computing the product of the projections of each spring on the coordinate axis
and
for all spring and summing products.
which implies a force matrix given by,
Notice in the force matrix, only the first column must be written down. Thus, with our eigenvectors applied to this first row we obtain the eigenfrequencies:
T
1 mode has an eigenfrequency of zero corresponding to a pure classical rotation. Since
XY4 is spherically symmetric, the following rotational Hamiltonian can describe
modes (see
Figure 9),
4.2. Non-Genuine Vibration
There are two
modes for the H atoms and one for the C atom. Thus, there are six eigenfrequencies since the dimension of
is three (see
Figure 8). The
are not all genuine vibrations, but two vibrational modes are mixed with one translation mode. By using the above
eigenvectors and the
bases to transform each Q matrix where Q = F or Q = m, we acquire a block diagonal form,
Note, there are nine eigenvalues and one for each j = 1, 2, 3 three 3 × 3 Γ-matrices, since by symmetry each 3 × 3 matrix is the same. By solving one of them we determine all nine eigenvalues of three triply degenerate levels. (103) gives the matrix element calculation for (102),
First, we consider
in (102) to give the force matrix as
Next, by making Q = m in (103) through (107) and Q = M to give,
As a result, we have the following acceleration matrix,
We solved the eigenvalue equation,
Solving (112), we have following eigenvalues
The corresponding eigenvectors can be written as
This procedure could be carried out using 2 × 2 matrices instead of 3 × 3 matrices since one of the
modes is a pure translation. By excluding that mode, we only need to solve a 2 × 2 matrix. For the translation, both the X atom and the four
atoms should move by the same amount. As a result, we have,
We illustrate
in
Figure 10 where the translation of H atoms or the Y atoms and X-atom for states that are in the
direction.
The translational mode and two vibrational modes of
are now isolated (see
Figure 10). This was achieved by taking linear combinations of the
modes.
A
mode that is orthogonal to (95) must be a genuine vibration, i.e.,
(120) gives the genuine vibration from the non-genuine vibrations. We illustrate (120) pictorially in
Figure 11.
We just need to find the overlap matrix between the next
mode, namely
, and
i.e.,
with eigenvalues,
and the eigensolution
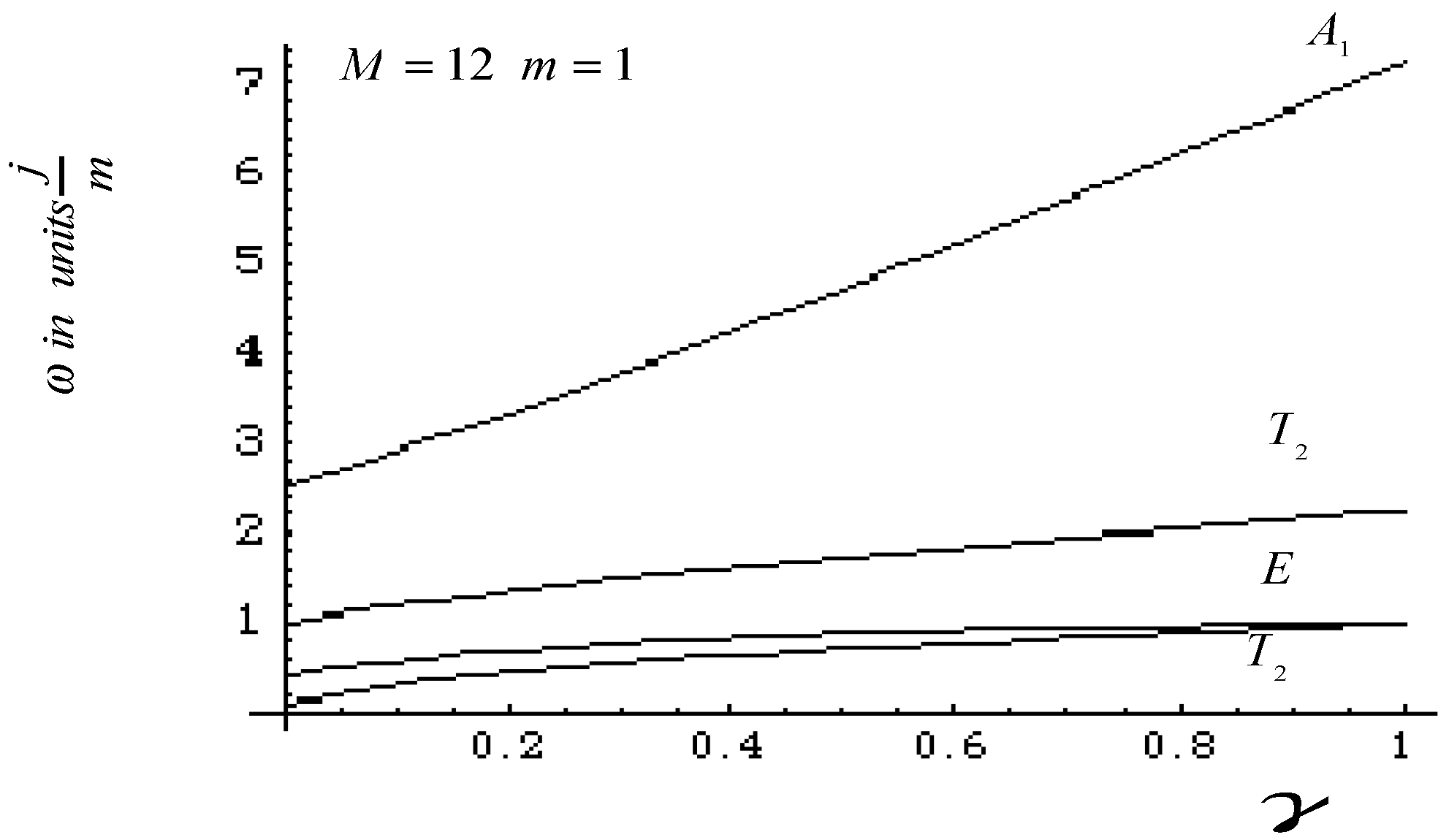
Figure 12 shows how the frequency of vibration is affected as the ratio of the spring coupling increases.
For the CH
4 molecular parameters values
,
,
, and
, (113) gives the following acceleration,
where we found the eigenvalues to be
;
and the eigenvectors of the vibration for the
mode are,
Table 1 shows the observed with the computed in units of cm
−1. A
1 mode, and two
modes compare with observed frequency. We obtain computed frequency by using the force constants of
,
, and
, respectively. However, the E-mode does not compare well.
In the analysis of
, we see that only the
moves the X atom. This means there is a coupling between the X and Y atoms through the j spring. It is evident that this is the case since the
modes repel each other, as shown in
Figure 12. In
Figure 12, there is a clustering of (E,
) modes which is more pronounced when the strength of the j spring and mass ratio of X and Y atom increases. For better results with the
molecule, we would need to consider bending forces for a more precise agreement.