Multi Polar q-Rung Orthopair Fuzzy Graphs with Some Topological Indices

Abstract

The importance of symmetry in graph theory has always been significant, but in recent years, it has become much more so in a number of subfields, including but not limited to domination theory, topological indices, Gromov hyperbolic graphs, and the metric dimension of graphs. The purpose of this monograph is to initiate the idea of a multi polar q-rung orthopair fuzzy graphs (m-$\mathfrak{PqROPFG})$ as a fusion of multi polar fuzzy graphs and q-rung orthopair fuzzy graphs. Moreover, for a vertex of multi polar q-rung orthopair fuzzy graphs, the degree and total degree of the vertex are defined. Then, some product operations, inclusive of direct, Cartesian, semi strong, strong lexicographic products, and the union of multi polar q-rung orthopair fuzzy graphs (m-$\mathfrak{PqROPFG}s)$, are obtained. Also, at first we define some degree based fuzzy topological indices of m-$\mathfrak{PqROPFG}$. Then, we compute Zareb indices of the first and second kind, Randic indices, and harmonic index of a m-$\mathfrak{PqROPFG}$.

1. Introduction

The theory of a fuzzy subset of a set was put forward in 1965 by Zadeh [1]. He generalized crisp set by providing membership grades to each member of the set from the interval $[0,1]$. Since than, the fuzzy set theory has developed into a robust discipline of research in different fields inclusive of graph theory, social science, decision making, medical field, management, artificial intelligence and engineering. The technique that offers coherence in the ranking of alternatives under multiple criterion is familiar as Multi criteria decision making (MCDM). Through these processes decision makers provides a feasible decision while considering a set multiple criteria. To fulfil their requirements and pursue an optimal alternative, this technique helps them in the hierarchy of short listed alternatives. Being inspired by the idea of bi-polar fuzzy sets which was established by Zhang $\left(1994\right)$ [2,3], Chen et al. $\left(2014\right)$ [4] proposed an augmentation of fuzzy set known as m-polar fuzzy set. In an m-polar fuzzy set the assessment of the membership grade of a member with m different attributes lies in ${[0,1]}^m,$ and all its respective membership grades are captured by following the same procedure. He indicated that 2-polar fuzzy sets and bipolar fuzzy sets are cryptographic mathematical ideas and that can acquire compactly one from the corresponding one [4]. In real world problems the data are sporadically collected from i agents $(i⩾2)$ this is the concept behind “multipolar information”. For example, in neurobiology, a lot of information is gathered by multi-polar neurons from other neurons in the brain. Some characteristics of m-polar fuzzy sets and several algebraic operations were introduced by Naeem et al. [5]. Multi-polar technology is designed to meet the needs of wide-ranging systems in information technology. In the last decades, the focus of many researchers has been shifted to imperfect, uncertain and vague information related problems. With the intention of dealing with such problems, Atanassov [6] put forward an augmentation of the fuzzy set by virtue of the membership and the non-membership functions, familiar as intuitionistic fuzzy set (IFS). Yager [7] established the notion of Pythagorean fuzzy set (PFS) as an extended form of Atanassov’s intuitionistic fuzzy set. Subtraction and division over Pythagorean fuzzy numbers are presented by Peng [8]. He also explored their characteristics such as boundedness, idempotency and monotonicity. Hashmi and Riaz [9] introduced an innovative idea of Pythagorean m-polar fuzzy sets and a few fundamental operations on these sets. In 2019, Hashmi [10] expressed the concept of m-polar neutrosophic set. Yager [11] in $2017,$ established the concept of q-rung orthopair fuzzy sets (q-ROFS), which is abstraction of (IFS) and (PFS). For the q-ROFSs, the membership and non-membership function need to fulfil the following condition $⟨{\left(\mu \left(\varsigma \right)\right)}^q+{\left(\upsilon \left(\varsigma \right)\right)}^q⟩⩽1,$ where $q⩾1$ and $\mu \left(\varsigma \right)\in [0,1]$, $\upsilon \left(\varsigma \right)\in$$[0,1]$ here the span of information expression is determined by parameter q. The span of information expression becomes larger as q increases. q-ROFSs came up with more flexibility to make assessments with reference to membership and non-membership functions as in contrast with IFSs and PFSs. Ali [12] studied the uncertainty index $H_{\mathcal{F}}\left(\varsigma \right)$ which depends on the orbit where the point ($\mu \left(\varsigma \right),\upsilon \left(\varsigma \right)$) is situated. In 2021, Riaz et al. [13], introduced a hybrid model of the m-polar fuzzy set and q-rung orthopair fuzzy set, familiar as m-polar q-rung orthopair fuzzy set. Toward uncertainty, a q-ROmPFS is more elastic and superior approach as compared with the prior approaches of intuitionistic m-polar fuzzy sets and Phythagorean m-polar fuzzy sets.

Graphs are diagrammatical representations of decision making problems. By utilizing this convenient appliance vertices and edges are used to demonstrate the decision-making objects and their relationships. In 1973, Kaufmann [14] initiated the rudimentary notion of fuzzy graph. Some advanced concepts of fuzzy graphs were discovered by Rosenfeld [15] in 1975. Rosenfeld also discussed the fuzzy relations between fuzzy sets. Bhattacharya $\left(1987\right)$ [16] defined certain concepts of fuzzy cut vertices and fuzzy bridges with reference to connectivity. Mordeson and Nair [17] explored a number of new ideas of fuzzy graphs. Nagoorani and Latha [18,19] investigated irregular fuzzy graphs and degree and order of intuitionistic fuzzy graphs. Many new ideas, comprising of bipolar fuzzy graphs, irregular bipolar fuzzy graphs, bipolar fuzzy digraph in decision support system, m-polar fuzzy graphs, m-polar fuzzy line graphs and certain metrics in m-polar fuzzy graphs were established by Akram et al. [20,21,22,23,24,25,26]. With different representation, numerous different types of graphs have been initiated for decision-making information, such as Pythagorean fuzzy graph [27] and single-valued neutrosophic graphs [28]. In 2014 Samanta [29] introduced m-step neighbourhood graph which is generalization of fuzzy competition graph. Based on q-ROFSs, a new form of graph has been created by Habib et al. [30] in $2019,$ which is named as q-rung orthopair fuzzy graph (q-ROFG). Rashmanlou and others in [31,32,33,34] added some interesting results to generalized fuzzy graphs.

Product operations of graphs are large and essential part of graph theory. Mordeson and Peng [35,36] defined a number of product operations on fuzzy graphs. Later, for different kinds of product operations of fuzzy graphs, the degree of the vertices was obtained by Nirmala in 2012 [37]. Sahoo and Pal [38,39] defined product operations on IFGs and also estimated the degree of vertex in IFGs. The number of product operations on fuzzy hypergraphs were introduced by Gong and Wang [38]. On interval-valued fuzzy graphs Rashmanlou et al. [40] established product operations and degree of a vertex for these graphs was also investigated. Single-valued neutrosophic graphs SVNGs were initiated by Naz et al. [28] in the scenario of multi-criteria decision-making, also several product operations on SVNGs were obtained. Latterly, Akram et al. [27] explored product operations for Pythagorean fuzzy graphs and for a vertex in PFGs the degree and total degree were defined. In 2019, Songyi et al. [41] defined product operations on q-ROPFGs.

In mathematical chemistry its topology branch is known as chemical graph theory which deals with the combination of graph theory and chemistry. For a chemical phenomena we applied graph theory to its mathematical model in chemical graph theory. The graph invariant of a graph which is a numerical parameter is known as a topological index as the topology of the graph is characterized with the help of this numeric value. Topological indices are utilized in the advancement of (QSAR) Quantative Structure Activity Relationships. These indices play important role to demonstrate the properties of molecules or biological activities which are correlated with their chemical structure. Several indices were initiated due to their application in chemistry such as Zagreb indices, Randic, Harmonic and Gutman indices but the first developed topological index is the Wiener index or Wiener number. In $1997,$ It was Xu [42] who introduced the application of fuzzy graph in chemical sciences. In 2019, Mordeson et al. [43] defined connectivity index and Wiener index in fuzzy graphs. Naeem [44] developed some connectivity indices in the context of IFG in 2021. He introduced two kinds of connectivity index and average connectivity index in the environment of IFGs. Kalathian et al. [45] developed fuzzy Zagreb indices of first and second kind, fuzzy Randic index and fuzzy Harmonic index. Some topological indices for intuitionistic fuzzy graph were presented by Dinar et al. [46] in 2023.

2. Preliminaries

This section presents a study of some rudimentary notions that will be beneficial to understand the current monograph.

Definition 1 ([1]). 

For a set of discourse $\mathfrak{U},$ a fuzzy set $\mathfrak{B}$ is expressed in a well known format,

$$\mathfrak{B}=\left\{⟨\varsigma ,{\mu }_{\mathfrak{B}}\left(\varsigma \right)⟩:\varsigma \in \mathfrak{U}\right\},$$

where membership function of fuzzy set $\mathfrak{B}$ is portryed by ${\mu }_{\mathfrak{B}}\left(\varsigma \right):\mapsto \left[0,1\right].$

Definition 2 ([4]). 

An m-polar fuzzy set $\left(MPFS\right)$ on a non empty set $\mathfrak{U}$ is a mapping $\mathfrak{A}:$$\mathfrak{U}$${\to [0,1]}^m,$ for a natural number m. $m\left(\mathfrak{U}\right)$ is used to denote the set of all m-polar fuzzy set on $\mathfrak{U}.$ Where $1=(1,1,\dots ,1)$ is the largest value in ${[0,1]}^m$ and the smallest value in ${[0,1]}^m$ is $0=(0,0,\dots ,0).$

Definition 3 ([6]). 

Let $\mathfrak{U}$ be a universe of discourse. Then a set $\mathfrak{C}$ is considered as intuitionistic fuzzy set if $\mathfrak{C}$ is a mapping in the form $\mathfrak{C}=\left\{⟨\varsigma ;{\mu }_{\mathfrak{C}}\left(\varsigma \right),{\upsilon }_{\mathfrak{C}}\left(\varsigma \right)⟩:\varsigma \in \mathfrak{U}\right\},$ where, ${\mu }_{\mathfrak{C}}\left(\varsigma \right)$ and ${\upsilon }_{\mathfrak{C}}\left(\varsigma \right)$ are taken from the interval $\left[0,1\right]$. These are used to define the membership grade and non-memembership grade of the element $\varsigma \in \mathfrak{U}$, respectively, to the set $\mathfrak{C}$ with $0\le {\mu }_{\mathfrak{C}}\left(\varsigma \right)+{\upsilon }_{\mathfrak{C}}\left(\varsigma \right)\le 1$ for each $\varsigma \in \mathfrak{U}.$

Definition 4 ([11]). 

On a set of discourse $\mathfrak{U}$. We define a set $\mathfrak{A}$ for $q\ge 1,$ in the given format

$$\mathfrak{A}=\left\{⟨\varsigma ,({\mu }_{\mathfrak{A}}\left(\varsigma \right),({\upsilon }_{\mathfrak{A}}\left(\varsigma \right)⟩:0\le {\left({\mu }_{\mathfrak{A}}\left(\varsigma \right)\right)}^q+{\left({\upsilon }_{\mathfrak{A}}\left(\varsigma \right)\right)}^q\le 1:\varsigma \in \mathfrak{U}\right\},$$

$\mathfrak{A}$ is familiar as q-rung orthopair fuzzy set (q-ROPFS). We take ${\mu }_{\mathfrak{A}}\left(\varsigma \right)$ and ${\upsilon }_{\mathfrak{A}}\left(\varsigma \right)$ from the interval $\left[0,1\right]$ and these values are used to porty the membership grade and non-membership grade of $\varsigma \in \mathfrak{U}.$

Definition 5. 

A set $\mathcal{F}$ on a set of discourse $\mathfrak{U}$ is introduced as an multi polar q-rung orthopair fuzzy set (m-$\mathfrak{PqROPFs}$) if it is established in the following form,

$$\mathcal{F}=\left\{⟨\varsigma ,({\mu }_{\mathcal{F}}^1\left(\varsigma \right),{\mu }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\varsigma \right)),({\upsilon }_{\mathcal{F}}^1\left(\varsigma \right),{\upsilon }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\varsigma \right))⟩:\varsigma \in \mathfrak{U}\right\},$$

where ${\mu }_{\mathcal{F}}^1\left(\varsigma \right)\ge {\mu }_{\mathcal{F}}^2\left(\varsigma \right)\ge \dots \ge {\mu }_{\mathcal{F}}^m\left(\varsigma \right),$${\upsilon }_{\mathcal{F}}^1\left(\varsigma \right)\le {\upsilon }_{\mathcal{F}}^2\left(\varsigma \right)\le \dots \le {\upsilon }_{\mathcal{F}}^m\left(\varsigma \right),$$0\le {\left({\mu }_{\mathcal{F}}^i\left(\varsigma \right)\right)}^q+{\left({\upsilon }_{\mathcal{F}}^i\left(\varsigma \right)\right)}^q\le 1,$ $q\ge 1$ and $\mathfrak{i}=1,2,\dots ,m.$ Here we take ${\mu }_{\mathcal{F}}^i\left(\varsigma \right)$ and ${\upsilon }_{\mathcal{F}}^i\left(\varsigma \right)$ in descending and ascending order, respectively, but it is not necessary condition for m-$\mathfrak{PqROPFs}.$

We denote multi polar q-rung orthopair fuzzy set

$$\mathcal{F}=\left\{⟨\varsigma ,({\mu }_{\mathcal{F}}^1\left(\varsigma \right),{\mu }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\varsigma \right),({\upsilon }_{\mathcal{F}}^1\left(\varsigma \right),{\upsilon }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\varsigma \right))⟩:\varsigma \in \mathfrak{U}\right\},$$

by $\mathcal{F}=\left\{⟨\varsigma ,{\mu }_{\mathcal{F}}\left(\varsigma \right),{\upsilon }_{\mathcal{F}}\left(\varsigma \right)⟩:\varsigma \in j\right\},$ where ${\mu }_{\mathcal{F}}\left(\varsigma \right)=({\mu }_{\mathcal{F}}^1\left(\varsigma \right),{\mu }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\varsigma \right))$ and ${\upsilon }_{\mathcal{F}}\left(\varsigma \right)=({\upsilon }_{\mathcal{F}}^1\left(\varsigma \right),{\upsilon }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\varsigma \right)).$

Example 1. 

Let $\mathfrak{U}=\{a,b,c\}$ be a universe of discourse. The 2-polar 3-rung orthopair fuzzy set $\mathcal{F}$ is given below:

$$\mathcal{F}=\left(\frac{((0.7,0.6),\left(0.8,0.9\right))}{a},\frac{(\left(0.9,0.7\right),\left(0.5,0.8\right))}{b},\frac{(\left(0.8,0.6\right),\left(0.7,0.9\right))}{c}\right).$$

Definition 6. 

Consider two multi polar q-rung orthopair fuzzy sets $\mathfrak{L}$ and $\mathfrak{S}$ on a set $\mathfrak{U},$ given below:

$$\begin{array}{cc}\hfill \mathfrak{L}& =\left\{⟨\varsigma :({\mu }_{\mathfrak{L}}^1\left(\varsigma \right),{\mu }_{\mathfrak{L}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathfrak{L}}^m\left(\varsigma \right)),({\upsilon }_{\mathfrak{L}}^1\left(\varsigma \right),{\upsilon }_{\mathfrak{L}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathfrak{L}}^m\left(\varsigma \right))⟩:\varsigma \in \mathfrak{U}\right\},\hfill \\ \hfill and\mathfrak{S}& =\left\{⟨\varsigma :({\mu }_{\mathfrak{S}}^1\left(\varsigma \right),{\mu }_{\mathfrak{S}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathfrak{S}}^m\left(\varsigma \right)),({\upsilon }_{\mathfrak{S}}^1\left(\varsigma \right),{\upsilon }_{\mathfrak{S}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathfrak{S}}^m\left(\varsigma \right))⟩:\varsigma \in \mathfrak{U}\right\}.\hfill \end{array}$$

Some relations and operations are defined below:

(i) 

Inclusion

$$\begin{array}{cc}\hfill \mathfrak{L}& \subset \mathfrak{S}\iff {\mu }_{\mathfrak{L}}^i\left(\varsigma \right)\le {\mu }_{\mathfrak{S}}^i\left(\varsigma \right)and{\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)\ge {\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right);i=1,2,\dots ,mand\varsigma \in \mathfrak{U}\hfill \\ \hfill \mathfrak{L}& =\mathfrak{S}\iff \mathfrak{L}\subset \mathfrak{S}and\mathfrak{S}\subset \mathfrak{L}.\hfill \end{array}$$

(ii) 

Complement

$$\overline{\mathfrak{L}}=\{⟨\varsigma :({\upsilon }_{\mathfrak{L}}^m\left(\varsigma \right),{\upsilon }_{\mathfrak{L}}^{m-1}\left(\varsigma \right),\dots ,{\upsilon }_{\mathfrak{L}}^1\left(\varsigma \right)),({\mu }_{\mathfrak{L}}^m\left(\varsigma \right),{\mu }_{\mathfrak{L}}^{m-1}\left(\varsigma \right),\dots ,{\mu }_{\mathfrak{L}}^1\left(\varsigma \right))⟩:\varsigma \in \mathfrak{U}\}.$$

(iii) 

Union $(\mathfrak{L}\cup \mathfrak{S}):$ In $(\mathfrak{L}\cup \mathfrak{S})$ we obtained the membership and non-membership grades by following way:

$$\begin{array}{cc}\hfill {\mu }_{\mathfrak{L}\cup \mathfrak{S}}^i\left(\varsigma \right)& ={\mu }_{\mathfrak{L}}^i\left(\varsigma \right)\vee {\mu }_{\mathfrak{S}}^i\left(\varsigma \right),\hfill \\ \hfill {\upsilon }_{\mathfrak{L}\cup \mathfrak{S}}^i\left(\varsigma \right)& ={\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)\wedge {\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right),i=1,2,\dots ,mand\varsigma \in \mathfrak{U}.\hfill \end{array}$$

(iv) 

Intersection $(\mathfrak{L}\cap \mathfrak{S}):$ In $(\mathfrak{L}\cap \mathfrak{S})$ we obtained the membership and non-membership grades by following way:

$$\begin{array}{cc}\hfill {\mu }_{\mathfrak{L}\cap \mathfrak{S}}^i\left(\varsigma \right)& ={\mu }_{\mathfrak{L}}^i\left(\varsigma \right)\wedge {\mu }_{\mathfrak{S}}^i\left(\varsigma \right),\hfill \\ \hfill {\upsilon }_{\mathfrak{L}\cap \mathfrak{S}}^i\left(\varsigma \right)& ={\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)\vee {\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right),i=1,2,\dots ,mand\varsigma \in \mathfrak{U}.\hfill \end{array}$$

(v) 

Addition $(\mathfrak{L}\oplus \mathfrak{S}$$):$ In $(\mathfrak{L}\oplus \mathfrak{S}$) we obtained the membership and non-membership grades by following way:

$$\begin{array}{cc}\hfill {\mu }_{\mathfrak{L}\oplus \mathfrak{S}}^i\left(\varsigma \right)& ={\mu }_{\mathfrak{L}}^i\left(\varsigma \right)+{\mu }_{\mathfrak{S}}^i\left(\varsigma \right)-{\mu }_{\mathfrak{L}}^i\left(\varsigma \right)·{\mu }_{\mathfrak{S}}^i\left(\varsigma \right),\hfill \\ \hfill {\upsilon }_{\mathfrak{L}\oplus \mathfrak{S}}^i\left(\varsigma \right)& ={\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)·{\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right),i=1,2,\dots ,mand\varsigma \in \mathfrak{U}.\hfill \end{array}$$

(vi) 

Multiplication $(\mathfrak{L}\otimes \mathfrak{S}):$ In $(\mathfrak{L}\otimes \mathfrak{S}$) the membership and non-membership grades are obtained as:

$$\begin{array}{cc}\hfill {\mu }_{\mathfrak{L}\otimes \mathfrak{S}}^i\left(\varsigma \right)& ={\mu }_{\mathfrak{L}}^i\left(\varsigma \right)·{\mu }_{\mathfrak{S}}^i\left(\varsigma \right),\hfill \\ \hfill {\upsilon }_{\mathfrak{L}\otimes \mathfrak{S}}^i\left(\varsigma \right)& ={\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)+{\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right)-{\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)·{\upsilon }_{\mathfrak{S}}^i\left(\varsigma \right),i=1,2,\dots ,mand\varsigma \in \mathfrak{U}.\hfill \end{array}$$

(vii) 

Alpha-beta cut $\left[({\alpha }_i,{\beta }_i)\text{-}cut\right]:$ Let

$$\mathfrak{L}=\left\{⟨\varsigma :({\mu }_{\mathfrak{L}}^1\left(\varsigma \right),{\mu }_{\mathfrak{L}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathfrak{L}}^m\left(\varsigma \right)),({\upsilon }_{\mathfrak{L}}^1\left(\varsigma \right),{\upsilon }_{\mathfrak{L}}^2\left(\varsigma \right),...,{\upsilon }_{\mathfrak{L}}^m\left(\varsigma \right)⟩:\varsigma \in \mathfrak{U}\right\}$$

be a m-$\mathfrak{PqROPFs}.$ Let ${\alpha }_i,{\beta }_i\in [0,1]$ such that $0\le {\alpha }_i^q+{\beta }_i^q\le 1.$ Then $({\alpha }_i,{\beta }_i)$-cut of $\mathfrak{L}$ is defined as a crisp set and it is constructed in the following form

$${\mathfrak{L}}^{({\alpha }_i,{\beta }_i)}=\left\{\varsigma \in \mathfrak{U}:{\mu }_{\mathfrak{L}}^i\left(\varsigma \right)\ge {\alpha }_i,{\upsilon }_{\mathfrak{L}}^i\left(\varsigma \right)\le {\beta }_i,i=1,2,\dots ,m\right\},$$

where ${\alpha }_i,{\beta }_i\in [0,1],$$0\le {\alpha }_i^q+{\beta }_i^q\le 1$ and $q\ge 1.$

Theorem 1. 

For any three m-$\mathfrak{PqROPFs}$$\mathfrak{D},\mathfrak{S}$ and $\mathfrak{J}.$

1. 

$\mathfrak{D}\otimes \mathfrak{S}=\mathfrak{S}\otimes \mathfrak{D};$

2. 

$(\mathfrak{D}\otimes \mathfrak{S})\otimes \mathfrak{J}=\mathfrak{D}\otimes (\mathfrak{S}\otimes \mathfrak{J});$

3. 

$\mathfrak{D}\otimes (\mathfrak{S}\cup \mathfrak{J})=(\mathfrak{D}\otimes \mathfrak{S})\cup (\mathfrak{D}\otimes \mathfrak{J});$

4. 

$\mathfrak{D}\otimes (\mathfrak{S}\cap \mathfrak{J})=(\mathfrak{D}\otimes \mathfrak{S})\cap (\mathfrak{D}\otimes \mathfrak{J});$

5. 

$\mathfrak{D}\otimes (\mathfrak{S}\oplus \mathfrak{J})⊑(\mathfrak{D}\otimes \mathfrak{S})\oplus (\mathfrak{D}\otimes \mathfrak{J});$

6. 

$\mathfrak{D}\otimes (\mathfrak{S}\otimes \mathfrak{J})\supseteq (\mathfrak{D}\otimes \mathfrak{S})\otimes (\mathfrak{D}\otimes \mathfrak{J}).$

Proof. 

Straightforward. □

3. Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 7. 

An m-$\mathfrak{PqROPFs}$ℜ in $\mathfrak{U}\times \mathfrak{U}$ is considered to be a m-polar q-rung orthopair fuzzy relation in $\mathfrak{U}$ expressed by

$$\Re =\left\{⟨\eta \varsigma ,({\mu }_{\mathcal{F}}^1\left(\eta \varsigma \right),{\mu }_{\mathcal{F}}^2\left(\eta \varsigma \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\eta \varsigma \right)),({\upsilon }_{\mathcal{F}}^1\left(\eta \varsigma \right),{\upsilon }_{\mathcal{F}}^2\left(\eta \varsigma \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\eta \varsigma \right))⟩:\eta \varsigma \in \mathfrak{U}\times \mathfrak{U}\right\}$$

where ${\mu }_{\Re }^i\left(\eta \varsigma \right):\mathfrak{U}\times \mathfrak{U}\to \left[0,1\right]$ and ${\upsilon }_{\Re }^i\left(\eta \varsigma \right):\mathfrak{U}\times \mathfrak{U}\to \left[0,1\right]$ represents the membership and non-membership function of $\Re ,$ respectively, such that $0\le$${\left({\mu }_{\Re }^i\left(\eta \varsigma \right)\right)}^q+{\left({\upsilon }_{\Re }^i\left(\eta \varsigma \right)\right)}^q\le 1,$$q\ge 1$ and $i=1,2,\dots ,m,$ for all $\eta \varsigma \in \mathfrak{U}\times \mathfrak{U}.$

Definition 8. 

An multi polar q-rung orthopair fuzzy graph (m-$\mathfrak{PqROPFG}$) of a graph $\mathfrak{G}=(\mathcal{L},\mathcal{M})$ (where $\mathcal{L}$ is the set of vertices and $\mathcal{M}$ is the set of edges) is defined as an ordered pair $\mathbb{G}=\left(\mathcal{F},\Re \right)$, (where $\mathcal{F}$ and ℜ are, respectively, the m-$\mathfrak{PqROPFs}$ on $\mathcal{L}$ and $\mathcal{M}$), if following conditions are satisfied:

(i) 

${\mu }_{\Re }^i\left(\eta \varsigma \right)\le min\{{\mu }_{\mathcal{F}}^i\left(\eta \right),{\mu }_{\mathcal{F}}^i\left(\varsigma \right)\},$

(ii) 

${\upsilon }_{\Re }^i\left(\eta \varsigma \right)\le max\{{\upsilon }_{\mathcal{F}}^i\left(\eta \right),{\upsilon }_{\mathcal{F}}^i\left(\varsigma \right)\},$

for all $\eta ,\varsigma \in \mathcal{L},$$q\ge 1$ and $i=1,2,\dots ,m.$

Example 2. 

Consider a graph $\mathfrak{G}=(\mathcal{L},\mathcal{M}),$ where $\mathcal{L}=\left\{r,s,t\right\}$ and $\mathcal{M}=\left\{rs,st,rt\right\}.$ Let $\mathcal{F}$ and ℜ be the 3-polar 3-rung orthopair fuzzy vertex set and the 3-polar 3-rung orthopair fuzzy edge set defined on $\mathcal{L}$ and $\mathcal{M},$ respectively:

$\mathcal{F}=⟨\frac{(\left(0.7,0.6,0.5\right),(0.8,0.9,0.9))}{r},\frac{\left(\right(0.8,0.7,0.6),(0.7,0.8,0.9\left)\right)}{s},\frac{(\left(0.9,0.8,0.7\right),(0.5,0.7,0.8))}{t}⟩,$

$\Re =⟨\frac{\left(\right(0.6,0.5,0.4),(0.7,0.7,0.8\left)\right)}{rs},\frac{\left(\right(0.7,0.6,0.5),(0.6,0.7,0.8\left)\right)}{st},\frac{\left(\right(0.6,0.4,0.3),(0.6,0.8,0.9\left)\right)}{rt}⟩.$

It is easy to find by direct calculation that $\mathbb{G}=(\mathcal{F},\Re )$ in Figure 1 is a m-$\mathfrak{PqROPFG}.$

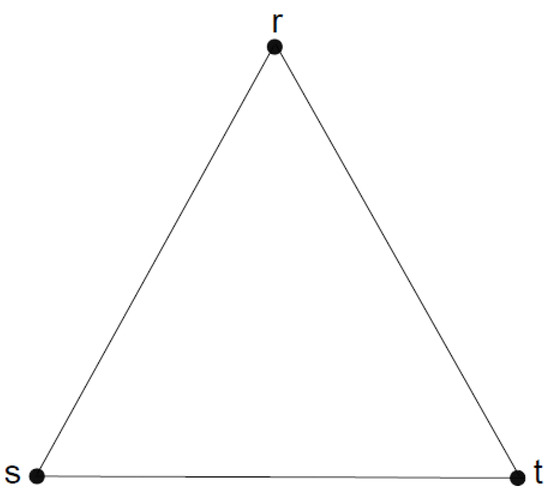
Figure 1. 3-polar 3-rung fuzzy graph.

Definition 9. 

Let $\mathbb{G}=\left(\mathcal{F},\Re \right)$ be multi polar q–rung orthopair fuzzy graph of a graph $\mathfrak{G}=\left(\mathcal{L},\mathcal{M}\right).$ Then we define the degree and total degree of a vertex η in graph $\mathbb{G}$ as

$$\begin{array}{cc}\hfill d_{{}_{\mathbb{G}}}\left(\eta \right)& =((d_{\mu }^1\left(\eta \right),d_{\mu }^2\left(\eta \right),\dots ,d_{\mu }^m\left(\eta \right)),(d_{\upsilon }^1\left(\eta \right),d_{\upsilon }^2\left(\eta \right),\dots ,d_{\upsilon }^m\left(\eta \right)))and,\hfill \\ \hfill t{d}_{{}_{\mathbb{G}}}\left(\eta \right)& =((t{d}_{\mu }^1\left(\eta \right),t{d}_{\mu }^2\left(\eta \right),\dots ,t{d}_{\mu }^m\left(\eta \right)),(t{d}_{\upsilon }^1\left(\eta \right),t{d}_{\upsilon }^2\left(\eta \right),\dots ,t{d}_{\upsilon }^m\left(\eta \right)))\hfill \end{array}$$

respectively. Where,

$$d_{\mu }^i\left(\eta \right)=\sum _{\eta ,\varsigma \in \mathcal{L},\eta \ne \varsigma }{\mu }_{\Re }^i\left(\eta \varsigma \right),d_{\upsilon }^i\left(\eta \right)=\sum _{\eta ,\varsigma \in \mathcal{L},\eta \ne \varsigma }{\upsilon }_{\Re }^i\left(\eta \varsigma \right),$$

$$t{d}_{\mu }^i\left(\eta \right)=\sum _{\eta ,\varsigma \in \mathcal{L},\eta \ne \varsigma }\left({\mu }_{\Re }^i\left(\eta \varsigma \right)\right)+{\mu }_{\mathcal{F}}^i\left(\eta \right),t{d}_{\upsilon }^i\left(\eta \right)=\sum _{\eta ,\varsigma \in \mathcal{L},\eta \ne \varsigma }\left({\upsilon }_{\Re }^i\left(\eta \varsigma \right)\right)+{\upsilon }_{\mathcal{F}}^i\left(\varsigma \right),$$

for $i=1,2,3,\dots ,m.$

Example 3. 

Consider a 3-polar 3-rung orthopair fuzzy graph $\mathbb{G}=\left(\mathcal{F},\Re \right)$ given in Figure 1. The degree of vertex r is $d_{\mathbb{G}}\left(r\right)=((1.2,0.9,0.7),(1.3,1.6,1.8))$ and the total degree of vertex r is $t{d}_{\mathbb{G}}\left(r\right)=((1.9,1.5,1.2),(2.1,2.5,2.7)).$

4. Some Product Operations of Multi Polar q-Rung Orthopair Fuzzy Graphs

This section deals with some product operations of m-$\mathfrak{PqROPFGs}.$ We analyze direct, Cartesian, semi strong, strong and lexicographic products of m-$\mathfrak{PqROPFGs}$.

4.1. Direct Product of Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 10. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of the graphs ${\mathfrak{G}}_1=({\mathcal{L}}_1,{\mathcal{M}}_1)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right)$, respectively. Then, the direct product of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ is expressed as ${\mathbb{G}}_1\times {\mathbb{G}}_2=\left({\mathcal{F}}_1\times {\mathcal{F}}_2,{\Re }_1\times {\Re }_2\right),$ and defined as:

(i) 

$\left\{\begin{array}{c}\hfill \left({\mu }_{{\mathcal{F}}_1}^i\times {\mu }_{{\mathcal{F}}_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right)={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\\ \hfill \left({\upsilon }_{{\mathcal{F}}_1}^i\times {\upsilon }_{{\mathcal{F}}_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right)={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\end{array}\right.$

for all $\left({\varsigma }_1,{\varsigma }_2\right)\in {\mathcal{L}}_1{\times L}_2$ and $i=1,2,3,\dots ,m.$

(ii) 

$\left\{\begin{array}{c}\hfill \left({\mu }_{{\Re }_1}^i\times {\mu }_{{\Re }_{{}_2}}^i\right)\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)={\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ \hfill \left({\upsilon }_{{\Re }_1}^i\times {\upsilon }_{{\Re }_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)={\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $=1,2,3,\dots ,m$.

Proposition 1. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of the graphs ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right)$, respectively. Then, ${\mathbb{G}}_1\times {\mathbb{G}}_2$ represents the direct product of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2,$ and it is a m-$\mathfrak{PqROPFG}$ of ${\mathfrak{G}}_1\times$${\mathfrak{G}}_2.$

Definition 11. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ Then, the degree of vertex $\left({\varsigma }_1,{\varsigma }_2\right)\in {\mathcal{L}}_1{\times L}_2$ is defined as:

$${\left(d\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=({\left(d_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right),{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)),$$

where,

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1\times {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1\times {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1\times {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\times {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\times {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\times {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

and

$$\begin{array}{cc}\hfill d_{{\mu }_1\times {\mu }_2}^i({\varsigma }_1,{\varsigma }_2)& =\sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}\left({\mu }_{{\Re }_1}^i\times {\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & =\sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill d_{{\upsilon }_1\times {\upsilon }_2}^i({\varsigma }_1,{\varsigma }_2)& =\sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}\left({\upsilon }_{{\Re }_1}^i\times {\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & =\sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 2. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If ${\mu }_{{\Re }_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\Re }_2}^i\le {\upsilon }_{{\Re }_1}^i,$ then $d_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_2\right)\right|d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)$ and if ${\mu }_{{\Re }_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\Re }_1}^i\le {\upsilon }_{{\Re }_2}^i,$ then $d_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_1\right)\right|d_{{\mathbb{G}}_2}\left({\varsigma }_2\right)$ for all $\left({\varsigma }_1,{\varsigma }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2.$ Where the number of vertices adjacent to ${\varsigma }_2$ in ${\mathbb{G}}_2$ is represented by $\left|N\left({\varsigma }_2\right)\right|={\displaystyle {\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}}1$, similarly $\left|N\left({\varsigma }_1\right)\right|={\displaystyle {\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}}1$ shows the number of vertices adjacent to ${\varsigma }_1$ in ${\mathbb{G}}_1.$

Proof. 

By definition of degree of vertex in ${\mathbb{G}}_1\times {\mathbb{G}}_2,$ we have

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1\times {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1\times {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1\times {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\times {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\times {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\times {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill d_{{\mu }_1\times {\mu }_2}^i({\varsigma }_1,{\varsigma }_2)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i\times {\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),(\sin \mathrm{ce}{\mu }_{{\Re }_2}^i\ge {\mu }_{{\Re }_1}^i)\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & =\left|N\left({\varsigma }_2\right)\right|{\left(d^i\right)}_{{\mu }_{{}_1}}\left({\varsigma }_1\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill d_{{\upsilon }_1\times {\upsilon }_2}^i({\varsigma }_1,{\varsigma }_2)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i\times {\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),(\sin \mathrm{ce}{\upsilon }_{{\Re }_2}^i\le {\upsilon }_{{\Re }_1}^i)\hfill \\ \hfill & =\left|N\left({\varsigma }_2\right)\right|{\left(d^i\right)}_{{\upsilon }_1}\left({\varsigma }_1\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$ Hence, ${\left(d\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_2\right)\right|{\left(d\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right).$ In similar manner we can show that if ${\mu }_{{\Re }_{{}_1}}^i\ge {\mu }_{{\Re }_{{}_2}}^i,{\upsilon }_{{\Re }_{{}_1}}^i\le {\upsilon }_{{\Re }_2}^i,$ then ${\left(d\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_1\right)\right|{\left(d\right)}_{{\mathbb{G}}_{{}_1}}\left({\varsigma }_2\right).$ □

Definition 12. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ Then, for vertex $\left({\varsigma }_1,{\varsigma }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ the total degree is defined as:

$${\left(td\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=({\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right),{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)),$$

where,

$${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1\times {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1\times {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1\times {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_1\times {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_1\times {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_1\times {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

and,

$$\begin{array}{cc}\hfill t{d}_{{\mu }_1\times {\mu }_2}^i({\varsigma }_1,{\varsigma }_2)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\mu }_{{\Re }_1}^i\times {\mu }_{{}_{{\Re }_2}}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +({\mu }_{{\mathcal{F}}_1}^i\times {\mu }_{{\mathcal{F}}_2}^i)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill t{d}_{{\upsilon }_1\times {\upsilon }_2}^i({\varsigma }_1,{\varsigma }_2)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i\times {\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +({\upsilon }_{{\mathcal{F}}_1}^i\times {\upsilon }_{{\mathcal{F}}_2}^i)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_{{}_1}}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_{{}_2}}^i\left({\varsigma }_2{\eta }_2\right)+{\upsilon }_{{}_{{\mathcal{F}}_1}}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 3. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If

1. 

${\mu }_{{\Re }_2}^i\ge {\mu }_{{\Re }_1}^i,$ then ${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_2\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

2. 

${\upsilon }_{{\Re }_2}^i\le {\upsilon }_{{\Re }_1}^i,$ then ${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_2\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

3. 

${\mu }_{{\Re }_1}^i\ge {\mu }_{{\Re }_2}^i,$ then ${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_1\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

4. 

${\upsilon }_{{\Re }_1}^i\le {\upsilon }_{{\Re }_1}^i,$ then ${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_1\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

for all $\left({\varsigma }_1,{\varsigma }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m,$ where ${\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)=(d_{{\mu }_1}^1\left({\varsigma }_1\right),d_{{\mu }_1}^2\left({\varsigma }_1\right),$$\dots ,d_{{\mu }_1}^m\left({\varsigma }_1\right))$ and ${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)=(d_{{\upsilon }_1}^1\left({\varsigma }_1\right),d_{{\upsilon }_1}^2\left({\varsigma }_1\right),...,d_{{\upsilon }_1}^m\left({\varsigma }_1\right)).$

Proof. 

By using Definition 12 and Theorem 2 the proof is straightforward. □

Example 4. 

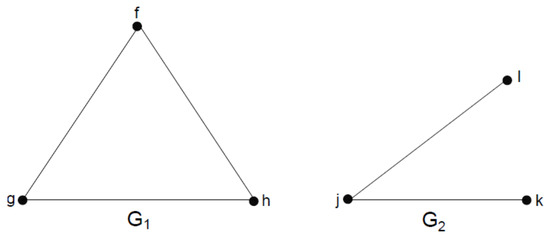
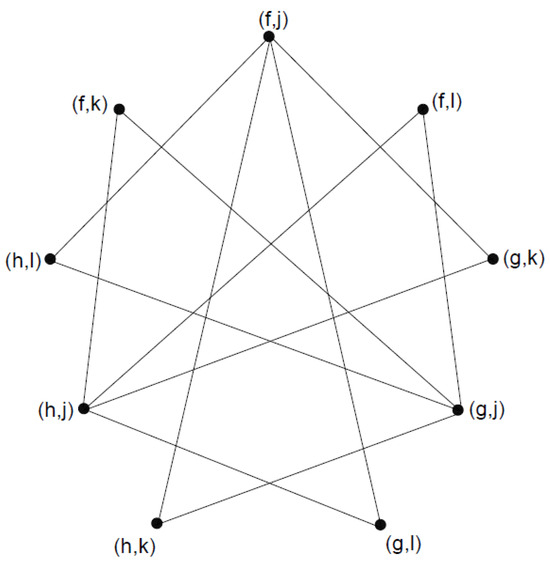
Consider two 3-polar 3-rung orthopair fuzzy graphs ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ on vertex sets ${\mathcal{L}}_1=\{f,g,h\}$ and ${\mathcal{L}}_2=\{j,k,l\},$ respectively, as represented in Figure 2, Table 1 and Table 2. Then, the direct product ${\mathbb{G}}_1\times {\mathbb{G}}_2$ is given in Figure 3, Table 3 and Table 4.

Figure 2. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1),{\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$.

Table 1. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1)$.

$\mathcal{L}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
f	$(0.7,0.6,0.5)$	$(0.7,0.8,0.8)$	$fg$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
g	$(0.8,0.7,0.5)$	$(0.6,0.8,0.9)$	$gh$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.9)$
h	$(0.9,0.8,0.6)$	$(0.6,0.7,0.8)$	$fh$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$

Table 2. ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$.

$\mathcal{L}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
j	$(0.9,0.8,0.7)$	$(0.5,0.6,0.7)$	$jk$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
k	$(0.8,0.7,0.6)$	$(0.7,0.8,0.9)$	$jl$	$(0.8,0.7,0.5)$	$(0.6,0.6,0.8)$
l	$(0.9,0.7,0.5)$	$(0.6,0.7,0.9)$

Figure 3. Direct product (${\mathbb{G}}_1\times {\mathbb{G}}_2$).

Table 3. Vertex set (${\mathbb{G}}_1\times {\mathbb{G}}_2$).

$\mathcal{L}({\mathbb{G}}_1\times {\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\times {\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$	$\left({\mathit{\upsilon }}_{{\mathcal{F}}_{{}_1}}^{\mathit{i}}\times {\mathit{\upsilon }}_{{\mathcal{F}}_2}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)$
$(f,j)$	$(0.7,0.6,0.5)$	$(0.7,0.8,0.8)$
$(g,j)$	$(0.8,0.7,0.5)$	$(0.6,0.8,0.9)$
$(h,j)$	$(0.9,0.8,0.6)$	$(0.6,0.7,0.8)$
$(f,k)$	$(0.7,0.6,0.5)$	$(0.7,0.8,0.9)$
$(g,k)$	$(0.8,0.7,0.5)$	$(0.7,0.8,0.9)$
$(h,k)$	$(0.8,0.7,0.6)$	$(0.7,0.8,0.9)$
$(f,l)$	$(0.7,0.6,0.5)$	$(0.7,0.8,0.9)$
$(g,l)$	$(0.8,0.7,0.5)$	$(0.6,0.8,0.9)$
$(h,l)$	$(0.9,0.7,0.5)$	$(0.6,0.7,0.9)$

Table 4. Edge set (${\mathbb{G}}_1\times {\mathbb{G}}_2$).

$\mathcal{M}({\mathbb{G}}_1\times {\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\times {\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}\times {\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$
$(f,j)(g,k)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,j)(g,l)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,j)(h,k)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,j)(h,l)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,l)(g,j)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,l)(h,j)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,k)(g,j)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(f,k)(h,j)$	$(0.6,0.5,0.4)$	$(0.7,0.7,0.8)$
$(g,j)(h,l)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.9)$
$(g,j)(h,k)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.9)$
$(g,l)(h,j)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.9)$
$(g,k)(h,j)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.9)$

Since ${\mu }_{{\Re }_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\Re }_2}^i\le {\upsilon }_{{\Re }_1}^i,$ so by Theorem 2, we have

${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left(f,j\right)=\left|N\left(j\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_{{}_1}}\left(f\right)=(2.4,2,1.6),$

${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left(f,j\right)=\left|N\left(j\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(f\right)=(2.8,2.8,3.2).$

Therefore, $d_{{}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}}\left(f,j\right)$ $=\left(\right(2.4,2,1.6),(2.8,2.8,3.2\left)\right).$

In addition, by Theorem 3, we have

${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left(f,j\right)=\left|N\left(j\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\mu }_{{\mathcal{F}}_1}^i\left(f\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(j\right)=(3.1,2.6,2.1),$

${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}\left(f,j\right)=\left|N\left(j\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left(f\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(j\right)=(3.5,3.6,4).$

Therefore, $t{d}_{{\mathbb{G}}_1\times {\mathbb{G}}_2}(f,j)=((3.1,2.6,2.1),(3.5,3.6,4)).$

Similarly, for all the vertices in ${\mathbb{G}}_1\times {\mathbb{G}}_2$ we can find the degree and total degree.

4.2. Cartesian Product of Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 13. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then, for ${\mathbb{G}}_1$ and ${\mathbb{G}}_2,$${\mathbb{G}}_1\square {\mathbb{G}}_2=({\mathcal{F}}_1\square {\mathcal{F}}_2,{\Re }_1\square {\Re }_2)$ represents the Cartesian product and it is defined as:

(i) 

$\left\{\begin{array}{c}({\mu }_{{\mathcal{F}}_1}^i\square {\mu }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\\ ({\upsilon }_{{\mathcal{F}}_1}^i\square {\upsilon }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\end{array}\right.$

for all $({\varsigma }_{{}_1},{\varsigma }_{{}_2})\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

(ii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i\square {\mu }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\mu }_{{\mathcal{F}}_{{}_1}}^i\left(\varsigma \right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ ({\upsilon }_{{\Re }_1}^i\square {\upsilon }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all $\varsigma \in {\mathcal{L}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$, and $i=1,2,3,\dots ,m$.

(iii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i\square {\mu }_{{\Re }_2}^i)\left(({\varsigma }_1,z)({\eta }_1,z)\right)={\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(z\right)\\ ({\upsilon }_{{\Re }_1}^i\square {\upsilon }_{{\Re }_2}^i)\left(({\varsigma }_1,z)({\eta }_1,z)\right)={\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(z\right),\end{array}\right.$

for all $z\in {\mathcal{L}}_2$, ${\varsigma }_1{\eta }_1$$\in {\mathcal{M}}_1$ and $i=1,2,3,\dots ,m$.

Proposition 2. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_1,{\Re }_1\right)$ be the m-$\mathfrak{PqROPFG}s$ of the graphs ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then, ${\mathbb{G}}_1\square {\mathbb{G}}_2$ the Cartesian product is a m-$\mathfrak{PqROPFG}.$

Definition 14. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$. Then, the degree of vertex $({\varsigma }_{{}_1},{\varsigma }_{{}_2})\in {\mathcal{L}}_1\times$ ${\mathcal{L}}_2$ is defined as:

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1\square {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1\square {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1\square {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\square {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\square {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\square {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1\square {\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\mu }_{{\Re }_1}^i\square {\mu }_{{\Re }_2}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill +& {\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill {\left(d^i\right)}_{{\upsilon }_1\square {\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\upsilon }_{{\Re }_1}^i\square {\upsilon }_{{\Re }_2}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 4. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$. If ${\mu }_{{\mathcal{F}}_{{}_1}}^i\ge {\mu }_{{\Re }_2}^i$, ${\upsilon }_{{\mathcal{F}}_{{}_1}}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_{{}_2}}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\mathcal{F}}_{{}_2}}^i\le {\upsilon }_{{\Re }_1}^i,$ then, $d_{{\mathbb{G}}_1\square {\mathbb{G}}_2}({\varsigma }_1,{\varsigma }_2)=d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right)$ for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1$×${\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

Proof. 

By definition of vertex degree of ${\mathbb{G}}_1$□${\mathbb{G}}_2$, we have

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1\square {\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\mu }_{{\Re }_1}^i\square {\mu }_{{\Re }_2}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_{{}_1}}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_{{}_2}}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill (\mathrm{by}\mathrm{using}{\mu }_{{\mathcal{F}}_1}^i& \ge {\mu }_{{\Re }_2}^{i}and{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i)\hfill \\ \hfill & ={\left(d^i\right)}_{{\mu }_2}\left({\varsigma }_2\right)+{\left(d^i\right)}_{{\mu }_1}\left({\varsigma }_1\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\upsilon }_1\square {\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i\square {\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill (\mathrm{by}\mathrm{using}{\upsilon }_{{\mathcal{F}}_1}^i& \le {\upsilon }_{{\Re }_2}^{i}and{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_1}^i)\hfill \\ \hfill & ={\left(d^i\right)}_{{\upsilon }_2}\left({\varsigma }_2\right)+{\left(d^i\right)}_{{\upsilon }_1}\left({\varsigma }_1\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$ Hence $d_{{\mathbb{G}}_1\square {\mathbb{G}}_2}({\varsigma }_1,{\varsigma }_2)=d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right).$ □

Definition 15. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ Then, for any vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1$×${\mathcal{L}}_2$, the total degree is defined as:

$${\left(td\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=({\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right),{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)),$$

where,

$${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1\square {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1\square {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1\square {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_1\square {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_1\square {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_1\square {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

and,

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1\square {\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\mu }_{{\Re }_1}^i\square {\mu }_{{\Re }_2}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill +& ({\mu }_{{\mathcal{F}}_1}^i\square {\mu }_{{\mathcal{F}}_2}^i)(\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_{{}_2}}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_{{}_1}}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill {\left(t{d}^i\right)}_{{\upsilon }_1\square {\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}({\upsilon }_{{\Re }_1}^i\square {\upsilon }_{{\Re }_2}^i)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill +& ({\upsilon }_{{\mathcal{F}}_1}^i\square {\upsilon }_{{\mathcal{F}}_2}^i)(\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_{{}_1}}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill +& {\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 5. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If

(i) 

${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,$ then

${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

(ii) 

${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i,$ then

${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right);$ for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and for $i=1,2,3,\dots ,m.$

Proof. 

By definition of vertex total degree of ${\mathbb{G}}_1\square {\mathbb{G}}_2,$

(i)

If ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$,${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i$

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1\square {\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\left(t{d}^i\right)}_{{\mu }_1}\left({\varsigma }_1\right)+{\left(t{d}^i\right)}_{{\mu }_{{}_2}}\left({\varsigma }_2\right)-{\mu }_{{\mathcal{F}}_{{}_1}}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

(ii)

If ${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i$

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\upsilon }_1\square {\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill =& {\left(t{d}^i\right)}_{{\upsilon }_1}\left({\varsigma }_1\right)+{\left(t{d}^i\right)}_{{\upsilon }_{{}_2}}\left({\varsigma }_2\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

□

Example 5. 

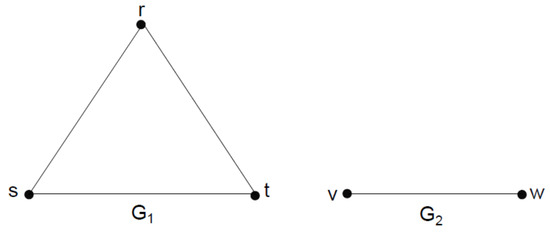
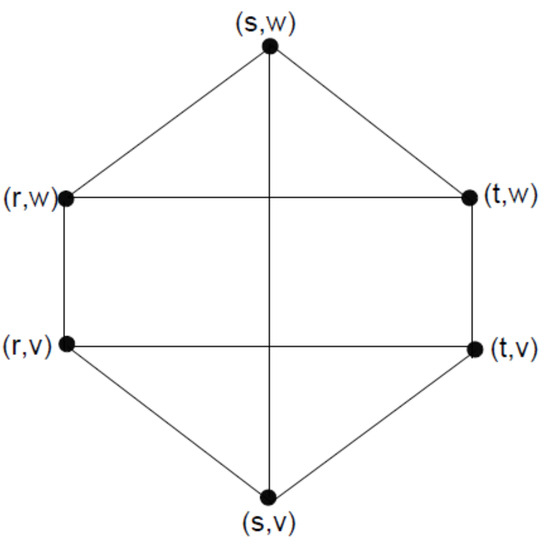
Consider two 3-polar 3-rung orthopair fuzzy graphs ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ on vertex sets ${\mathcal{L}}_1=\{r,s,t\}$ and ${\mathcal{L}}_2=\{v,w\}$, respectively, given in Figure 4, Table 5 and Table 6, where ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i.$ Then, their Cartesian product ${\mathbb{G}}_1\square {\mathbb{G}}_2$ is presented in Figure 5, Table 7 and Table 8.

Figure 4. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1),{\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

Table 5. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1$).

$\mathcal{L}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
r	$(0.8,0.7,0.6)$	$(0.7,0.7,0.8)$	$rs$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
s	$(0.9,0.6,0.6)$	$(0.6,0.7,0.8)$	$st$	$(0.8.0.6,0.6)$	$(0.7,0.7,0.8)$
t	$(0.9,0.8,0.7)$	$(0.5,0.6,0.7)$	$tr$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$

Table 6. ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

$\mathcal{L}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{\mathcal{F}2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
v	$(0.8,0.8,0.7)$	$(0.6,0.6,0.8)$	$vw$	$(0.7,0.6,0.6)$	$(0.7,0.7,0.8)$
w	$(0.8,0.7,0.7)$	$(0.7,0.7,0.8)$

Figure 5. Cartesian product ${\mathbb{G}}_1\square {\mathbb{G}}_2$).

Table 7. Vertex set (${\mathbb{G}}_1\square {\mathbb{G}}_2$).

$\mathcal{L}({\mathbb{G}}_1$□${\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\square$${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}\square {\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)$
$(r,v)$	$(0.8,0.7,0.6)$	$(0.6,0.7,0.8)$
$(r,w)$	$(0.8,0.7,0.6)$	$(0.5,0.6,0.7)$
$(s,v)$	$(0.8,0.6,0.6)$	$(0.6,0.7,0.8)$
$(s,w)$	$(0.8,0.6,0.6)$	$(0.6,0.7,0.8)$
$(t,v)$	$(0.8,0.8,0.7)$	$(0.6,0.7,0.8)$
$(t,w)$	$(0.8,0.7,0.7)$	$(0.5,0.6,0.7)$

Table 8. Edge set (${\mathbb{G}}_1\square {\mathbb{G}}_2$).

$\mathcal{M}({\mathbb{G}}_1$□${\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\square$${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})({\mathit{\varsigma }}_{\mathit{w}},{\mathit{\varsigma }}_{\mathit{q}})$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}\square {\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)({\mathit{\varsigma }}_{\mathit{w}},{\mathit{\varsigma }}_{\mathit{q}})$
$(r,v)(s,v)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(r,v)(t,v)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(r,v)(r,w)$	$(0.7,0.6,0.6)$	$(0.7,0.7,0.8)$
$(r,w)(s,w)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(r,w)(t,w)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(s,v)(s,w)$	$(0.7,0.6,0.6)$	$(0.7,0.7,0.8)$
$(s,v)(t,v)$	$(0.8,0.6,0.6)$	$(0.7,0.7,0.8)$
$(t,v)(t,w)$	$(0.7,0.6,0.6)$	$(0.7,0.7,0.8)$
$(s,w)(t,w)$	$(0.8,0.6,0.6)$	$(0.7,0.7,0.8)$

with the help of Theorem 4, we obtain

${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left(r,v\right)={\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(r\right)+{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left(v\right)=(2.1,1.8,1.6),$

${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left(r,v\right)={\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(r\right)+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(v\right)=(2.1,2.1,2.4).$

Therefore, $d_{{}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}}\left(r,v\right)=((2.1,1.8,1.6),(2.1,2.1,2.4)).$

In addition, by Theorem 5, we have

${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left(r,v\right)={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(r\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(v\right)-{\mu }_{{\mathcal{F}}_1}^i\left(r\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(v\right)=(2.9,2.5,2.2),$

${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left(r,v\right)={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(r\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(v\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(r\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left(v\right)=(2.8,2.8,3.2).$

Therefore, $t{d}_{{\mathbb{G}}_1\square {\mathbb{G}}_2}\left(r,v\right)=((2.9,2.5,2.2),(2.8,2.8,3.2)).$

Similarly, for all the vertices in ${\mathbb{G}}_1\square {\mathbb{G}}_2$ the degree and total degree can be found.

4.3. Semi Strong Product of Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 16. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of the graph ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right)$, respectively. Then, ${\mathbb{G}}_1·{\mathbb{G}}_2=({\mathcal{F}}_1·{\mathcal{F}}_2,{\Re }_1·{\Re }_2)$ denoted the semi-strong product of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ and defined as:

(i) 

$\left\{\begin{array}{c}({\mu }_{{\mathcal{F}}_1}^i·{\mu }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\\ ({\upsilon }_{{\mathcal{F}}_1}^i·{\upsilon }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\end{array}\right.$

for all $({\varsigma }_{{}_1},{\varsigma }_{{}_2})\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

(ii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i·{\mu }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ ({\upsilon }_{{\Re }_1}^i·{\upsilon }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all $\varsigma \in {\mathcal{L}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $i=1,2,3,\dots ,m$.

(iii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i·{\mu }_{{\Re }_2}^i)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ ({\upsilon }_{{\Re }_1}^i·{\upsilon }_{{\Re }_2}^i)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $i=1,2,3,\dots ,m$.

Proposition 3. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of the graph ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then, ${\mathbb{G}}_1·{\mathbb{G}}_2$ is the semi-strong product of ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ and it is a m-$\mathfrak{PqROPFG}.$

Definition 17. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$. Then, the degree of vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ is defined as:

$${\left(d_{\mu }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1·{\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1·{\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1·{\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\cdot {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\cdot {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\cdot {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1·{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i·{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill {\left(d^i\right)}_{{\upsilon }_1\cdot {\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i·{\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 6. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$, ${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$, ${\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i,{\upsilon }_{{\Re }_1}^i\ge {\upsilon }_{{\Re }_2}^i,$ then, $d_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}({\varsigma }_1,{\varsigma }_2)=\left|N\left({\varsigma }_2\right)\right|d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right),$ for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

Proof. 

By definition of vertex degree of ${\mathbb{G}}_1·{\mathbb{G}}_2$, we have

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1·{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i·{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill \mathrm{by}\mathrm{using}{\mu }_{{\mathcal{F}}_1}^i& \ge {\mu }_{{\Re }_2}^{i}and{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i\hfill \\ \hfill & ={\left(d^i\right)}_{{\mu }_2}\left({\varsigma }_2\right)+\left|N\left({\varsigma }_2\right)\right|{\left(d^i\right)}_{{\mu }_1}\left({\varsigma }_1\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$ Analogously, it can be proved that ${\left(d_{\upsilon }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=\left|N\left({\varsigma }_2\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)$ $+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_{{}_2}}\left({\varsigma }_2\right).$ Hence, $d_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}({\varsigma }_1,{\varsigma }_2)=\left|N\left({\varsigma }_2\right)\right|d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right).$ □

Definition 18. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ Then, for vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ the total degree is determined as:

$${\left(t{d}_{\mu }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1·{\mu }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1·{\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1·{\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_{1·}{\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_{1·}{\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_{1·}{\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1·{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i·{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +({\mu }_{{\mathcal{F}}_1}^i·{\mu }_{{\mathcal{F}}_2}^i)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill {\left(t{d}^i\right)}_{{\upsilon }_1·{\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i·{\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +\left({\upsilon }_{{\mathcal{F}}_1}^i·{\upsilon }_{{\mathcal{F}}_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 7. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If

(i) 

${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$ and ${\mu }_{{\Re }_1}^i\ge {\mu }_{{\Re }_2}^i,$ then, ${\left(t{d}_{\mu }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=\left(\left|N\left({\varsigma }_2\right)\right|\right){\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_{{}_2}}\left({\varsigma }_2\right)+(1-\left|N\left({\varsigma }_2\right)\right|){\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

(ii) 

${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\upsilon }_{{\Re }_1}^i\le {\upsilon }_{{\Re }_2}^i,$ then, ${\left(t{d}_{\upsilon }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left({\varsigma }_1,{\varsigma }_2\right)=\left(\left|N\left({\varsigma }_2\right)\right|\right){\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_{{}_2}}\left({\varsigma }_2\right)+(1-\left|N\left({\varsigma }_2\right)\right|){\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2.$

Proof. 

By definition of vertex total degree of ${\mathbb{G}}_1·{\mathbb{G}}_2,$

(i) ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$ and ${\mu }_{{\Re }_1}^i\ge {\mu }_{{\Re }_2}^i$

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1·{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & =\left|N\left({\varsigma }_2\right)\right|{\left(t{d}^i\right)}_{{\mu }_1}\left({\varsigma }_1\right)+{\left(t{d}^i\right)}_{{\mu }_{{}_2}}\left({\varsigma }_2\right)+(1-\left|N\left({\varsigma }_2\right)\right|){\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$ Analogously, $\left(ii\right)$ can be proved. □

Example 6. 

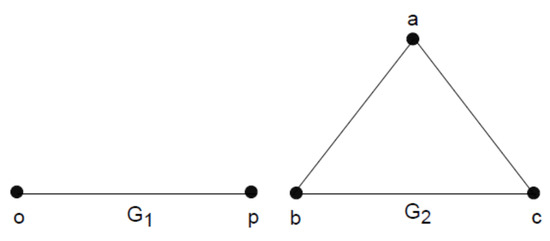
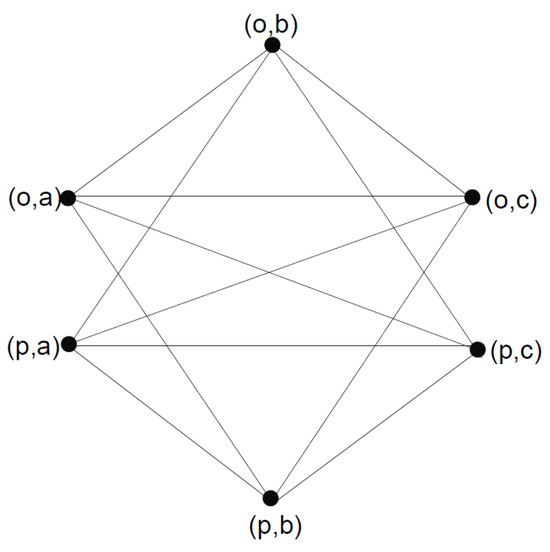
Consider ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1)$ and ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$ be two 3-polar 3-rung orthopair fuzzy graphs be visible in Figure 6, Table 9 and Table 10, where ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i,{\upsilon }_{{\Re }_1}^i\ge {\upsilon }_{{\Re }_2}^i.$ Then, their semi-strong product ${\mathbb{G}}_1·{\mathbb{G}}_2$ is shown in Figure 7, Table 11 and Table 12.

Figure 6. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1),{\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

Table 9. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1$).

$\mathcal{L}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{\mathcal{F}1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
o	$(0.9,0.6,0.5)$	$(0.6,0.7,0.8)$	$op$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
p	$(0.8,0.7,0.6)$	$(0.7,0.7,0.8)$

Table 10. ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

$\mathcal{L}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
a	$(0.7,0.6,0.6)$	$(0.6,0.6,0.8)$	$ab$	$(0.7,0.5,0.5)$	$(0.7,0.7,0.8)$
b	$(0.8,0.7,0.5)$	$(0.7,0.7,0.8)$	$bc$	$(0.8,0.6,0.4)$	$(0.7,0.7,0.8)$
c	$(0.9,0.8,0.6)$	$(0.6,0.7,0.7)$	$ac$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$

Figure 7. Semi strong product (${\mathbb{G}}_1·{\mathbb{G}}_2$).

Table 11. Vertex set (${\mathcal{F}}_1·{\mathcal{F}}_2$).

$\mathcal{L}({\mathbb{G}}_1·{\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}·{\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$	$({\mathit{\upsilon }}_{{\mathcal{F}}_{{}_1}}^{\mathit{i}}·{\mathit{\upsilon }}_{{\mathcal{F}}_{{}_2}}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$
$(o,a)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
$(o,b)$	$(0.8,0.7,0.5)$	$(0.7,0.7,0.8)$
$(o,c)$	$(0.9,0.6,0.5)$	$(0.6,0.7,0.8)$
$(p,a)$	$(0.8,0.7,0.6)$	$(0.7,0.7,0.8)$
$(p,b)$	$(0.8,0.7,0.5)$	$(0.7,0.7,0.8)$
$(p,c)$	$(0.8,0.7,0.6)$	$(0.7,0.7,0.8)$

Table 12. Edge set (${\Re }_1·{\Re }_2$).

$\mathcal{M}({\mathbb{G}}_1·{\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}·{\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$	$({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}·{\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}})\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$
$(o,a)(o,b)$	$(0.7,0.5,0.5)$	$(0.7,0.7,0.8)$
$(o,a)(o,c)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(o,a)(p,c)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,a)(p,b)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,b)(o,c)$	$(0.8,0.6,0.4)$	$(0.7,0.7,0.8)$
$(o,b)(p,c)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,b)(p,a)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,c)(p,a)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,c)(p,b)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(p,c)(p,a)$	$(0.7,0.6,0.5)$	$(0.7,0.7,0.8)$
$(p,c)(p,b)$	$(0.8,0.6,0.4)$	$(0.7,0.7,0.8)$
$(p,b)(p,a)$	$(0.7,0.5,0.5)$	$(0.7,0.7,0.8)$

Thus, by using Table 9, Table 10, Table 11 and Table 12 and Theorem 6, we have

${\left(d_{\mu }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(o,a\right)=\left|N\left(a\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left(a\right)=(2.8,2.1,1.8),$

${\left(d_{\upsilon }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(a,o\right)=\left|N\left(o\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(a\right)+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(o\right)=(2.8,2.8,3.2).$

Therefore, $d_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(a,o\right)=((2.8,2.1,1.8),(2.8,2.8,3.2)).$

In addition, by Theorem 7, we have ${\left(t{d}_{\mu }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(o,a\right)=\left|N\left(a\right)\right|{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(a\right)+(1-\left|N\left(a\right)\right|){\mu }_{{\mathcal{F}}_1}^i\left(o\right)-{\mu }_{{\mathcal{F}}_1}^i\left(o\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(a\right)=(3.5,2.7,2.3),$

${\left(t{d}_{\upsilon }\right)}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(o,a\right)=\left|N\left(a\right)\right|{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(a\right)+(1-\left|N\left(a\right)\right|){\upsilon }_{{\mathcal{F}}_1}^i\left(o\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(o\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left(a\right)=(3.5,3.5,4).$

Therefore, $t{d}_{{}_{{\mathbb{G}}_1·{\mathbb{G}}_2}}\left(o,a\right)=\left((3.5,2.7,2.3)\right),(3.5,3.5,4)).$

Similarly, for all the vertices in ${\mathbb{G}}_1·{\mathbb{G}}_2$ we can find their degree and total degree.

4.4. Strong Product of Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 19. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then ${\mathbb{G}}_1⊠{\mathbb{G}}_2=({\mathcal{F}}_1⊠{\mathcal{F}}_2,{\Re }_1⊠{\Re }_2)$ represents the strong product of these two m-$\mathfrak{PqROPFG}s$ and defined as:

(i) 

$\left\{\begin{array}{c}({\mu }_{{\mathcal{F}}_1}^i⊠{\mu }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\\ ({\upsilon }_{{\mathcal{F}}_1}^i⊠{\upsilon }_{{\mathcal{F}}_2}^i)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\end{array}\right.$

for all $({\varsigma }_{{}_1},{\varsigma }_{{}_2})\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

(ii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_2)(\varsigma ,{\eta }_2))\right)={\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ ({\upsilon }_{{\Re }_1}^i⊠{\upsilon }_{{\Re }_2}^i)\left((\varsigma ,{\varsigma }_2)(\varsigma ,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all $\varsigma \in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $i=1,2,3,\dots ,m$.

(iii) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i)\left(({\varsigma }_{{}_1},z)({\eta }_1,z)\right)={\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(z\right)\\ ({\upsilon }_{{\Re }_1}^i⊠{\upsilon }_{{\Re }_2}^i)\left(({\varsigma }_1,z)({\eta }_1,z)\right)={\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(z\right),\end{array}\right.$

for all $z\in {\mathcal{L}}_2$, ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$ and $i=1,2,3,\dots ,m$.

(iv) 

$\left\{\begin{array}{c}({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i({\varsigma }_2,{\eta }_2)\\ ({\upsilon }_{{\Re }_1}^i⊠{\upsilon }_{{\Re }_2}^i)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i({\varsigma }_2,{\eta }_2),\end{array}\right.$

for all ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $i=1,2,3,\dots ,m$.

Proposition 4. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then, ${\mathbb{G}}_1⊠{\mathbb{G}}_2$ the strong product is a m-$\mathfrak{PqROPFG}.$

Definition 20. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ The degree of vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ is defined as:

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1⊠{\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1⊠{\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1⊠{\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1⊠{\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1⊠{\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1⊠{\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1⊠{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill {\left(d^i\right)}_{{\upsilon }_1⊠{\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i⊠{\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right).\hfill \end{array}$$

Theorem 8. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$, ${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$, ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i$, ${\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i,$${\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i,{\upsilon }_{{\Re }_1}^i\ge {\upsilon }_{{\Re }_2}^i$, then $d_{{}_{{}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}}}({\varsigma }_1,{\varsigma }_2)=(1+\left|N\left({\varsigma }_2\right)\right|)d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right)$ for all $({\varsigma }_1,{\varsigma }_2)$$\in {\mathcal{L}}_1\times {\mathcal{L}}_2$, where $\left|N\left({\varsigma }_2\right)\right|$ is total number of vertices adjscent to ${\varsigma }_2$ in ${\mathbb{G}}_2.$

Proof. 

By definition of vertex degree of ${\mathbb{G}}_1$⊠${\mathbb{G}}_2$, we have

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1⊠{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill \mathrm{Sin}\mathrm{ce}{\mu }_{{\mathcal{F}}_1}^i& \ge {\mu }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^{i}and{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i\hfill \\ \hfill & =(1+\left|N\left({\varsigma }_2\right)\right|){\left(d^i\right)}_{{\mu }_1}\left({\varsigma }_1\right)+{\left(d^i\right)}_{{\mu }_2}\left({\varsigma }_2\right).\hfill \\ \hfill & \mathrm{Analogously},\mathrm{it}\mathrm{is}\mathrm{easy}\mathrm{to}\mathrm{show}\mathrm{that}\hfill \\ \hfill {\left(d^i\right)}_{{\upsilon }_1⊠{\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& =(1+\left|N\left({\varsigma }_2\right)\right|){\left(d^i\right)}_{{\upsilon }_1}\left({\varsigma }_1\right)+{\left(d^i\right)}_{{\upsilon }_2}\left({\varsigma }_2\right),\hfill \\ \hfill \mathrm{Hence}{d}_{G_1⊠G_2}\left({\varsigma }_1,{\varsigma }_2\right)& =(1+\left|N\left({\varsigma }_2\right)\right|)d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right).\hfill \end{array}$$

□

Definition 21. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ The total degree of vertex $({\varsigma }_1,{\varsigma }_2)$$\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ is defined as:

$${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1⊠{\mu }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1⊠{\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1⊠{\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_1⊠{\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_1⊠{\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_1⊠{\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1⊠{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i⊠{\mu }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +\left({\mu }_{{\mathcal{F}}_1}^i⊠{\mu }_{{\mathcal{F}}_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & +{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill {\left(t{d}^i\right)}_{{\upsilon }_1⊠{\upsilon }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i⊠{\upsilon }_{{\Re }_2}^i\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +\left({\upsilon }_{{\mathcal{F}}_1}^i⊠{\upsilon }_{{\mathcal{F}}_2}^i\right)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

Theorem 9. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If

(i) ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i,$ then ${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right)+(1+\left|N\left({\varsigma }_2\right)\right|){\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_{{}_1}}\left({\varsigma }_1\right)-\left|N\left({\varsigma }_2\right)\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

(ii) ${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i,{\mu }_{{\Re }_1}^i\ge {\mu }_{{\Re }_2}^i,$ then ${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_{{}_2}}\left({\varsigma }_2\right)+(1+\left|N\left({\varsigma }_2\right)\right|){\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)-\left|N\left({\varsigma }_2\right)\right|{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$

for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2.$

Proof. 

For any vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2,$

(i) ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i$

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1⊠{\mu }_2}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+\hfill \\ \hfill & {\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill \sin \mathrm{ce}{\mu }_{{\mathcal{F}}_1}^i& \ge {\mu }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)+(1+\left|N({\varsigma }_{2)}\right|){\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +\left|N({\varsigma }_{2)}\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-\left|N({\varsigma }_{2)}\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)+(1+\left|N({\varsigma }_{2)}\right|)({\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right))-\left(\left|N({\varsigma }_{2)}\right|\right){\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\left(t{d}^i\right)}_{{\mu }_{{}_2}}\left({\varsigma }_2\right)+\left|1+N\left({\varsigma }_2\right)\right|{\left(t{d}^i\right)}_{{\mu }_{{}_1}}\left({\varsigma }_1\right)-\left|N({\varsigma }_{2)}\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

Analogously $,\left(ii\right)$ is easy to prove. □

Example 7. 

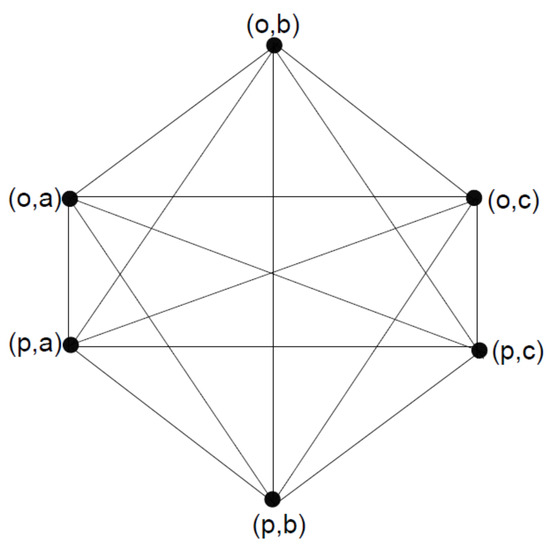
Consider ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1)$ and ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$ be two 3-polar 3-rung orthopair fuzzy graphsas in example 34, where ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\mathcal{F}}_2}^i\ge {\upsilon }_{{\Re }_1}^i,{\mu }_{{\Re }_1}^i\le {\mu }_{{\Re }_2}^i,{\upsilon }_{{\Re }_1}^i\ge {\upsilon }_{{\Re }_2}^i$ and their strong product ${\mathbb{G}}_1⊠{\mathbb{G}}_2$ is shown in Figure 8. The vertex set of ${\mathbb{G}}_1⊠{\mathbb{G}}_2$ is same as given in Table 11 and edge set of ${\mathbb{G}}_1⊠{\mathbb{G}}_2$ is Table 12 with three additional edges given in the Table 13.

Figure 8. Strong product (${\mathbb{G}}_1⊠{\mathbb{G}}_2$).

Table 13. Additional edges for Edge set (${\Re }_1⊠{\Re }_2$).

$\mathcal{M}({\mathbb{G}}_1⊠{\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}⊠{\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}⊠{\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}}\right)({\mathit{\varsigma }}_{\mathit{p}},{\mathit{\varsigma }}_{\mathit{q}})$
$(o,a)(p,a)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,b)(p,b)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$
$(o,c)(p,c)$	$(0.7,0.5,0.4)$	$(0.7,0.7,0.8)$

Thus, by using Table 9, Table 10, Table 11, Table 12 and Table 13 and Theorem 8, we can find

${\left(d_{\mu }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left(o,a\right)=\left|1+N\left(a\right)\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left(a\right)=(3.5,2.6,2.2),$

${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left(o,a\right)=\left|1+N\left(a\right)\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(a\right)=(3.5,3.5,4).$

Therefore, $d_{G_1⊠G_2}\left(l,p\right)=\left((3.5,2.6,2.2)(3.5,3.5,4)\right).$

By using Theorem 9, we can prove ${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left(o,a\right)=\left|1+N\left(a\right)\right|{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(a\right)-\left|N\left(a\right)\right|{\mu }_{{\mathcal{F}}_1}^i\left(o\right)-{\mu }_{{\mathcal{F}}_1}^i\left(o\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(a\right)=(4.2,3.2,2.7),$

${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left(o,a\right)=\left|1+N\left(a\right)\right|{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(o\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(a\right)-\left|N\left(a\right)\right|{\upsilon }_{{\mathcal{F}}_1}^i\left(o\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(o\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left(a\right)=(4.1,4.2,4.8).$

Therefore, $t{d}_{{\mathbb{G}}_1⊠{\mathbb{G}}_2}\left(l,p\right)=((4.2,3.2,2.7),(4.1,4.2,4.8)).$

Similarly, for all the vertices in ${\mathbb{G}}_1⊠{\mathbb{G}}_2$ the degree and total degree can be calculated.

4.5. The Lexicographic Product of Multi Polar q-Rung Orhopair Fuzzy Graphs

Definition 22. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$$=({\mathcal{F}}_1\left[{\mathcal{F}}_2\right],{\Re }_1\left[{\Re }_2\right])$ denotes the lexicographic product of these two m-$\mathfrak{PqROPFG}s$ and it is defined as follows:

(i) 

$\left\{\begin{array}{c}\left({\mu }_{{\mathcal{F}}_1}^i\left[{\mu }_{{\mathcal{F}}_2}^i\right]\right)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\\ \left({\upsilon }_{{\mathcal{F}}_1}^i\left[{\upsilon }_{{\mathcal{F}}_2}^i\right]\right)({\varsigma }_{{}_1},{\varsigma }_{{}_2})={\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\end{array}\right.$

for all $({\varsigma }_{{}_1},{\varsigma }_{{}_2})\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

(ii) 

$\left\{\begin{array}{c}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\\ \left({\upsilon }_{{\Re }_1}^i\left[{\upsilon }_{{\Re }_2}^i\right]\right)\left((\varsigma ,{\varsigma }_{{}_2})(\varsigma ,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right),\end{array}\right.$

for all $\varsigma \in {\mathcal{L}}_1$, ${\varsigma }_2{\eta }_2\in {\mathcal{M}}_2$ and $i=1,2,3,\dots ,m$.

(iii) 

$\left\{\begin{array}{c}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left(({\varsigma }_{{}_1},z)({\eta }_1,z)\right)={\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(z\right)\\ \left({\upsilon }_{{\Re }_1}^i\left[{\upsilon }_{{\Re }_2}^i\right]\right)\left(({\varsigma }_1,z)({\eta }_1,z)\right)={\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(z\right),\end{array}\right.$

for all $z\in {\mathcal{L}}_2$, ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$ and $i=1,2,3,\dots ,m$.

(iv) 

$\left\{\begin{array}{c}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\wedge {\mu }_{{\Re }_1}^i({\varsigma }_1,{\eta }_1)\\ \left({\upsilon }_{{\Re }_1}^i\left[{\upsilon }_{{\Re }_2}^i\right]\right)\left(({\varsigma }_{{}_1},{\varsigma }_2)({\eta }_1,{\eta }_2)\right)={\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\vee {\upsilon }_{{\Re }_1}^i({\varsigma }_1,{\eta }_1),\end{array}\right.$

for all ${\varsigma }_1{\eta }_1\in {\mathcal{M}}_1$, ${\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

Proposition 5. 

For two m-$\mathfrak{PqROPFG}s,$${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ the lexicographic product ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$ is a m-$\mathfrak{PqROPFG}.$

Definition 23. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ The degree of any vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ is defined as:

$${\left(d_{\mu }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1\left[{\mu }_2\right]}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1\left[{\mu }_2\right]}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1\left[{\mu }_2\right]}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\left[{\upsilon }_2\right]}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\left[{\upsilon }_2\right]}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\left[{\upsilon }_2\right]}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1\left[{\mu }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill {\left(d^i\right)}_{{\upsilon }_1\left[{\upsilon }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i\left[{\upsilon }_{{\Re }_2}^i\right]\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Theorem 10. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$. If ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i$, then $d_{{}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}}({\varsigma }_1,{\varsigma }_2)=\left|{\mathcal{L}}_2\right|d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right)$ for all $({\varsigma }_1,{\varsigma }_2)$$\in {\mathcal{L}}_1\times {\mathcal{L}}_2,$ where $\left|{\mathcal{L}}_2\right|$ represents the number of total vertices in ${\mathbb{G}}_2.$

Proof. 

For any vertex $({\varsigma }_1,{\varsigma }_2)$$\in {\mathcal{L}}_1\times {\mathcal{L}}_2,$

$$\begin{array}{cc}\hfill {\left(d^i\right)}_{{\mu }_1\left[{\mu }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+({\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1+{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2}}1){\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right),\hfill \\ \hfill (\sin \mathrm{ce}{\mu }_{{\mathcal{F}}_1}^i& \ge {\mu }_{{\Re }_2}^{i}and{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i)\hfill \\ \hfill & ={\left(d^i\right)}_{{\mu }_2}\left({\varsigma }_2\right)+\left|{\mathcal{L}}_2\right|{\left(d^i\right)}_{{\mu }_1}\left({\varsigma }_1\right),\hfill \\ \hfill & \mathrm{analogously},\mathrm{we}\mathrm{can}\mathrm{show}\mathrm{that}\hfill \\ \hfill {\left(d_{\upsilon }\right)}_{{}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}}({\varsigma }_1,{\varsigma }_2)& =\left|{\mathcal{L}}_2\right|{\left(d^i\right)}_{{\upsilon }_1}\left({\varsigma }_1\right)+{\left(d^i\right)}_{{\upsilon }_2}\left({\varsigma }_2\right),\hfill \\ \hfill \mathrm{hence},d_{{}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}}({\varsigma }_1,{\varsigma }_2)& =\left|{\mathcal{L}}_2\right|d_{{\mathbb{G}}_1}\left({\varsigma }_1\right)+d_{{\mathbb{G}}_2}\left({\varsigma }_2\right).\hfill \end{array}$$

□

Definition 24. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPF}\mathfrak{gs}.$ The degree of any vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ is defined as:

$${\left(t{d}_{\mu }\right)}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1\left[{\mu }_2\right]}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1\left[{\mu }_2\right]}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1\left[{\mu }_2\right]}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_1\left[{\upsilon }_2\right]}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_1\left[{\upsilon }_2\right]}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_1\left[{\upsilon }_2\right]}^m({\varsigma }_1,{\varsigma }_2)),$$

where,

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1\left[{\mu }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\mu }_{{\Re }_1}^i\left[{\mu }_{{\Re }_2}^i\right]\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +\left({\mu }_{{\mathcal{F}}_1}^i\left[{\mu }_{{\mathcal{F}}_2}^i\right]\right)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1\eta \right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill {\left(t{d}^i\right)}_{{\upsilon }_1\left[{\upsilon }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{\begin{array}{c}\left({\varsigma }_1,{\varsigma }_2\right),\left({\eta }_1,{\eta }_2\right)\in {\mathcal{L}}_1\times {\mathcal{L}}_2\\ \left({\varsigma }_1,{\varsigma }_2\right)\ne \left({\eta }_1,{\eta }_2\right)\end{array}}}\left({\upsilon }_{{\Re }_1}^i\left[{\upsilon }_{{\Re }_2}^i\right]\right)\left(\left({\varsigma }_1,{\varsigma }_2\right)\left({\eta }_1,{\eta }_2\right)\right)\hfill \\ \hfill & +\left({\upsilon }_{{\mathcal{F}}_1}^i\left[{\upsilon }_{{\mathcal{F}}_2}^i\right]\right)\left({\varsigma }_1,{\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\upsilon }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\vee {\mu }_{{\Re }_1}^i\left({\varsigma }_1\eta \right)+{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

Theorem 11. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ If

(i) ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,$ then

$${\left(t{d}_{\mu }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left({\varsigma }_2\right)+\left|{\mathcal{L}}_2\right|{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_{{}_1}}\left({\varsigma }_1\right)-(\left|{\mathcal{L}}_2\right|-1){\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$$

(ii) ${\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i,$ then

$${\left(t{d}_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left({\varsigma }_1,{\varsigma }_2\right)={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_{{}_2}}\left({\varsigma }_2\right)+\left|{\mathcal{L}}_2\right|{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left({\varsigma }_1\right)-(\left|{\mathcal{L}}_2\right|-1){\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right);$$

for all $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

Proof. 

For any vertex $({\varsigma }_1,{\varsigma }_2)\in {\mathcal{L}}_1\times {\mathcal{L}}_2,$

(i) ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i$

$$\begin{array}{cc}\hfill {\left(t{d}^i\right)}_{{\mu }_1\left[{\mu }_2\right]}\left({\varsigma }_1,{\varsigma }_2\right)& ={\displaystyle \sum _{{\varsigma }_1={\eta }_1\in {\mathcal{L}}_1,{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2\in {\mathcal{L}}_2,{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\mathcal{F}}_2}^i\left({\eta }_2\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\wedge {\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_1={\eta }_1}}1·{\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2}}1·{\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\displaystyle \sum _{{\varsigma }_2{\eta }_2\in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left({\varsigma }_2{\eta }_2\right)+{\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right)+({\displaystyle \sum _{{\varsigma }_2={\eta }_2}}1+{\displaystyle \sum _{{\varsigma }_2\ne {\eta }_2}}1){\displaystyle \sum _{{\varsigma }_1{\eta }_1\in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left({\varsigma }_1{\eta }_1\right)\hfill \\ \hfill & +\left|{\mathcal{L}}_2\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)-\left|{\mathcal{L}}_2\right|{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)+{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right),\hfill \\ \hfill & ={\left(t{d}^i\right)}_{{\mu }_2}\left({\varsigma }_2\right)+\left|{\mathcal{L}}_2\right|{\left(t{d}^i\right)}_{{\mu }_{{}_1}}\left({\varsigma }_1\right)-(\left|{\mathcal{L}}_2\right|-1){\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\hfill \\ \hfill & -{\mu }_{{\mathcal{F}}_1}^i\left({\varsigma }_1\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left({\varsigma }_2\right).\hfill \end{array}$$

Analogously, $\left(ii\right)$ can be proved. □

Example 8. 

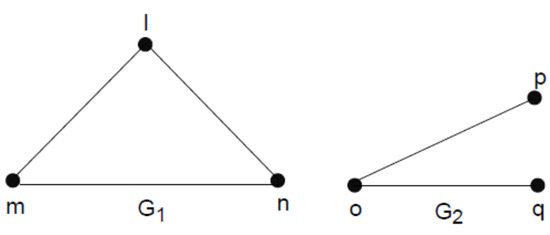
Consider ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two 3-polar 3-rung orthopair fuzzy graphs shown in Figure 9, Table 14 and Table 15, where ${\mu }_{{\mathcal{F}}_1}^i\ge {\mu }_{{\Re }_2}^i,{\upsilon }_{{\mathcal{F}}_1}^i\le {\upsilon }_{{\Re }_2}^i$ and ${\mu }_{{\mathcal{F}}_2}^i\ge {\mu }_{{\Re }_1}^i,{\upsilon }_{{\mathcal{F}}_2}^i\le {\upsilon }_{{\Re }_1}^i$ and their lexicographic product is shown in Figure 10 and Table 16.

Figure 9. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1),{\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

Table 14. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1)$.

$\mathcal{L}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
l	$(0.8,0.7,0.6)$	$(0.5,0.6,0.7)$	$lm$	$(0.6,0.4,0.3)$	$(0.6,0.7,0.8)$
m	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$	$nl$	$(0.7.0.6,0.5)$	$(0.6,0.7,0.8)$
n	$(0.9,0.8,0.7)$	$(0.5,0.6,0.7)$	$mn$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$

Table 15. ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$.

$\mathcal{L}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
o	$(0.9,0.8,0.7)$	$(0.6,0.7,0.8)$	$op$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
p	$(0.7,0.6,0.5)$	$(0.4,0.6,0.7)$	$oq$	$(0.7,0.5,0.3)$	$(0.6,0.7,0.8)$
q	$(0.8,0.7,0.5)$	$(0.4,0.5,0.6)$

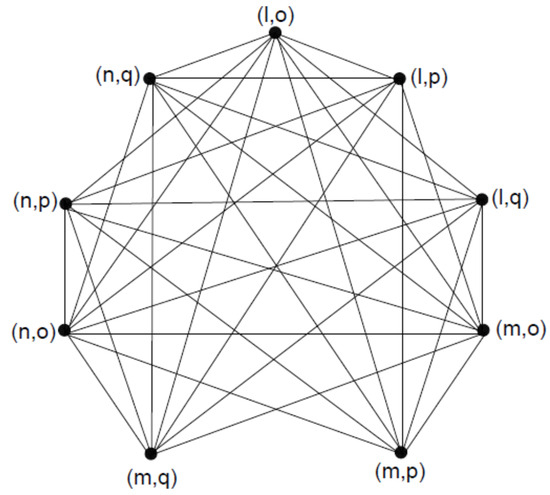
Figure 10. Lexicographic product ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$.

Table 16. Edge set ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$.

$\mathcal{M}\left({\mathbb{G}}_1\left[{\mathbb{G}}_2\right]\right)$	$\left({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left[{\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\right]\right)(\mathit{n},\mathit{o})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left[{\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\right]\right)(\mathit{n},\mathit{o})({\mathit{\varsigma }}_{\mathit{j}},{\mathit{\varsigma }}_{\mathit{k}})$
$(n,o)(m,q)$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
$(n,o)(m,p)$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
$(n,o)(m,o)$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
$(n,o)(l,q)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
$(n,o)(l,p)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
$(n,o)(l,o)$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
$(n,o)(n,q)$	$(0.7,0.5,0.3)$	$(0.6,0.7,0.8)$
$(n,o)(n,p)$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$

Now we find degree of vertex $(n,o)$. We have

$\left({\mu }_{{\mathcal{F}}_1}^i\left[{\mu }_{{\mathcal{F}}_2}^i\right]\right)(n,o)=(0.9,0.8,0.7)$ and

$\left({\upsilon }_{{\mathcal{F}}_1}^i\left[{\upsilon }_{{\mathcal{F}}_2}^i\right]\right)(n,o)=(0.6,0.7,0.8)$. We have total 33 number of edges in edge set of ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$ but here we take only those edges which are adjacent with vertex $(n,o)$ in Table 16.

Thus with the help of Theorem 10 and using Table 14, Table 15 and Table 16, we obtain

${\left(d_{\mu }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left(n,o\right)=\left|{\mathcal{L}}_2\right|{\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(n\right)+{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left(o\right)=(5.2,4.3,3.4),$

${\left(d_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left(n,o\right)=\left|{\mathcal{L}}_2\right|{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(n\right)+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(o\right)=(4.8,5.6,6.4).$

Therefore, $d_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left(n,o\right)=((5.2,4.3,3.4),(4.8,5.6,6.4)).$ In addition, we must have the following results by using Theorem 11,

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left(n,o\right)& =\left|{\mathcal{L}}_2\right|{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(n\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(o\right)-(\left|{\mathcal{L}}_2\right|-1){\mu }_{{\mathcal{F}}_1}^i\left(n\right)-{\mu }_{{\mathcal{F}}_1}^i\left(n\right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(o\right)\hfill \\ \hfill & =(6.1,5.1,4.1),\hfill \\ \hfill {\left(t{d}_{\upsilon }\right)}_{{}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}}\left(n,o\right)& =\left|{\mathcal{L}}_2\right|{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(n\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(o\right)-(\left|{\mathcal{L}}_2\right|-1){\upsilon }_{{\mathcal{F}}_1}^i\left(n\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(n\right)\wedge {\upsilon }_{{\mathcal{F}}_2}^i\left(o\right)\hfill \\ \hfill & =(5.4,6.3,7.2).\hfill \end{array}$$

Therefore, $t{d}_{{}_{{\mathbb{G}}_1\left[{\mathbb{G}}_2\right]}}\left(n,o\right)=((6.1,5.1,4.1),(5.4,6.3,7.2)).$

In similar way, for all the vertices in ${\mathbb{G}}_1\left[{\mathbb{G}}_2\right]$ the degree and total degree of these vertices can be calculated.

5. Union of Multi Polar q-Rung Orthopair Fuzzy Graphs

Definition 25. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s$ of the graphs ${\mathfrak{G}}_1=\left({\mathcal{L}}_1,{\mathcal{M}}_1\right)$ and ${\mathfrak{G}}_2=\left({\mathcal{L}}_2,{\mathcal{M}}_2\right),$ respectively. Then, the union ${\mathbb{G}}_1\cup {\mathbb{G}}_2=$$\left({\mathcal{F}}_1\cup {\mathcal{F}}_2,{\Re }_1\cup {\Re }_2\right)$ is defined as follows:

(i) 

$({\mu }_{{\mathcal{F}}_1}^i\cup {\mu }_{{\mathcal{F}}_2}^i)\left(\varsigma \right)=\left\{\begin{array}{c}{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_1-{\mathcal{L}}_2\\ {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_2-{\mathcal{L}}_1\\ {\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_1\cap {\mathcal{L}}_2,\end{array}\right.$

(ii) 

$({\upsilon }_{{\mathcal{F}}_1}^i\cup \left({\upsilon }_{{\mathcal{F}}_2}^i\right)\left(\varsigma \right)=\left\{\begin{array}{c}({\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_1-{\mathcal{L}}_2\\ ({\upsilon }_{{\mathcal{F}}_2}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_2-{\mathcal{L}}_1\\ ({\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge ({\upsilon }_{{\mathcal{F}}_2}^i\left(\varsigma \right)if\varsigma \in {\mathcal{L}}_1\cap {\mathcal{L}}_2,\end{array}\right.$

(iii) 

(${\mu }_{{\Re }_1}^i\cup {\mu }_{{\Re }_2}^i)\left(\varsigma \eta \right)=\left\{\begin{array}{c}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_1-{\mathcal{M}}_2\\ {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_2-{\mathcal{M}}_1\\ {\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\vee {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2,\end{array}\right.$

(iv) 

$({\upsilon }_{{\Re }_1}^i\cup {\upsilon }_{{\Re }_2}^i)\left(\varsigma \eta \right)=\left\{\begin{array}{c}{\upsilon }_{{\Re }_1}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_1-{\mathcal{M}}_2\\ {\upsilon }_{{\Re }_2}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_2-{\mathcal{M}}_1\\ {\upsilon }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\upsilon }_{{\Re }_2}^i\left(\varsigma \eta \right)if\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2,\end{array}\right.$

for $i=1,2,3,\dots ,m.$

Theorem 12. 

If ${\mathbb{G}}_1$ and ${\mathbb{G}}_2$ are m-$\mathfrak{PqROPFG}s$ of ${\mathfrak{G}}_1$ and ${\mathfrak{G}}_2,$ respectively, Then the union ${\mathbb{G}}_1\cup {\mathbb{G}}_2$ is a m-$\mathfrak{PqROPFG}$ of ${\mathfrak{G}}_1\cup {\mathfrak{G}}_2$, where ${\mathcal{F}}_1,{\mathcal{F}}_2,{\Re }_1$ and ${\Re }_2$ are the m-$\mathfrak{PqROPFS}s$ of ${\mathcal{L}}_1,{\mathcal{L}}_2,{\mathcal{M}}_1$ and ${\mathcal{M}}_2$, respectively, and ${\mathcal{L}}_1\cap {\mathcal{L}}_2=\varphi .$

Definition 26. 

Let ${\mathbb{G}}_1=\left({\mathcal{F}}_1,{\Re }_1\right)$ and ${\mathbb{G}}_2=\left({\mathcal{F}}_2,{\Re }_2\right)$ be two m-$\mathfrak{PqROPFG}s.$ For any vertex $\varsigma \in {\mathcal{L}}_1\cup {\mathcal{L}}_2$ and $i=1,2,3,\dots ,m,$ the degree of vertex $\varsigma \in {\mathcal{L}}_1\cup {\mathcal{L}}_2,$ is defined as

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\mu }_1\cup {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\mu }_1\cup {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\mu }_1\cup {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(d_{{\upsilon }_1\cup {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),d_{{\upsilon }_1\cup {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,d_{{\upsilon }_1\cup {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

and total degree is defined as

$${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\mu }_1\cup {\mu }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\mu }_1\cup {\mu }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\mu }_1\cup {\mu }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

$${\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left({\varsigma }_1,{\varsigma }_2\right)=(t{d}_{{\upsilon }_1\cup {\upsilon }_2}^1({\varsigma }_1,{\varsigma }_2),t{d}_{{\upsilon }_1\cup {\upsilon }_2}^2({\varsigma }_1,{\varsigma }_2),\dots ,t{d}_{{\upsilon }_1\cup {\upsilon }_2}^m({\varsigma }_1,{\varsigma }_2)),$$

Here, we consider three cases.

Case 1. 

Either $\varsigma \in {\mathcal{L}}_1-{\mathcal{L}}_2$ or $\varsigma \in {\mathcal{L}}_2-{\mathcal{L}}_1$. Then, no edge incident at ς lies in ${\mathcal{M}}_1\cap {\mathcal{M}}_2.$ Thus, for $\varsigma \in {\mathcal{L}}_1-{\mathcal{L}}_2$ and $i=1,2,3,\dots ,m.$

$$\begin{array}{cc}\hfill {\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)={\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right),{\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left(\varsigma \eta \right)={\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right),\hfill \\ \hfill {\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\left(t{d}_{\mu }^i\right)}_{{}_{{\mathbb{G}}_1}}\left(\varsigma \right),{\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right).\hfill \end{array}$$

For $\varsigma \in {\mathcal{L}}_2-{\mathcal{L}}_1$ and $i=1,2,3,\dots ,m.$

$$\begin{array}{cc}\hfill {\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)={\left(d_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right),{\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2}}{\upsilon }_{{\Re }_2}^i\left(\varsigma \eta \right)={\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right),\hfill \\ \hfill {\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\left(t{d}_{\mu }^i\right)}_{{}_{{\mathbb{G}}_2}\left(\varsigma \right)},{\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right).\hfill \end{array}$$

Case 2. 

If $\varsigma \in {\mathcal{L}}_1\cap {\mathcal{L}}_2$ but no edge insident at ς lies in ${\mathcal{M}}_1\cap {\mathcal{M}}_2.$ Then, any edge incident at ς is either in ${\mathcal{M}}_1-{\mathcal{M}}_2$ or in ${\mathcal{M}}_2-{\mathcal{M}}_1.$ For $i=1,2,3,\dots ,m$ we have,

$$\begin{array}{cc}\hfill {\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cup {\mathcal{M}}_2}}({\mu }_{{\Re }_1}^i\cup {\mu }_{{\Re }_2}^i)\left(\varsigma \eta \right),\hfill \\ \hfill & ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right),\hfill \\ \hfill & ={\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(d_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right).\hfill \end{array}$$

Similarly, ${\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right),$

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cup {\mathcal{M}}_2}}({\mu }_{{\Re }_1}^i\cup {\mu }_{{\Re }_2}^i)\left(\varsigma \eta \right)+{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right),\hfill \\ \hfill & ={\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(d_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)+{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right),\hfill \\ \hfill & ={\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right).\hfill \end{array}$$

Similarly, ${\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(\varsigma \right).$

Case 3. 

If $\varsigma \in {\mathcal{L}}_1\cap {\mathcal{L}}_2$ and some edges incident at ς are in ${\mathcal{M}}_1\cap {\mathcal{M}}_2.$ Then, for $i=1,2,3,\dots ,m,$

$$\begin{array}{cc}\hfill {\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)& ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cup {\mathcal{M}}_2}}({\mu }_{{\Re }_1}^i\cup {\mu }_{{\Re }_2}^i)\left(\varsigma \eta \right)\hfill \\ \hfill & -{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1-{\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2-{\mathcal{M}}_1}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\vee {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right),\hfill \\ \hfill & ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1-{\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2-{\mathcal{M}}_1}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\vee {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)\hfill \\ \hfill & +{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right),\hfill \\ \hfill & ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1-{\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2-{\mathcal{M}}_1}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)\hfill \\ \hfill & -{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right),\hfill \\ \hfill & ={\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)+{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_2}}{\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)\hfill \\ \hfill & ={\left(d_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(d_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right).\hfill \end{array}$$

Similarly, ${\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(d_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left(\varsigma \eta \right)\vee {\upsilon }_{{\Re }_2}^i(\varsigma \eta$).

In addition,

$${\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(t{d}_{\mu }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\mu }_{{\Re }_1}^i\left(\varsigma \eta \right)\wedge {\mu }_{{\Re }_2}^i\left(\varsigma \eta \right)-{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right),$$

$${\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(\varsigma \right)={\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_1}\left(\varsigma \right)+{\left(t{d}_{\upsilon }^i\right)}_{{\mathbb{G}}_2}\left(\varsigma \right)-{\displaystyle \sum _{\varsigma \eta \in {\mathcal{M}}_1\cap {\mathcal{M}}_2}}{\upsilon }_{{\Re }_1}^i\left(\varsigma \eta \right)\vee {\upsilon }_{{\Re }_2}^i\left(\varsigma \eta \right)-{\mu }_{{\mathcal{F}}_1}^i\left(\varsigma \right)\vee {\mu }_{{\mathcal{F}}_2}^i\left(\varsigma \right).$$

Example 9. 

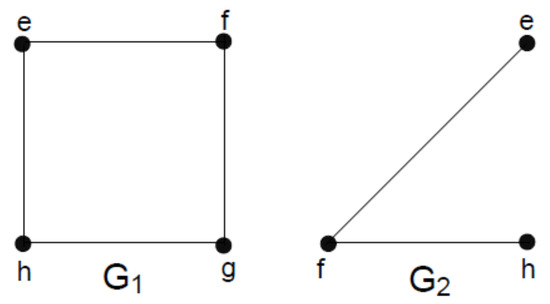
Consider ${\mathbb{G}}_1=\left(P_1,Q_1\right)$ and ${\mathbb{G}}_2=\left(P_2,Q_2\right)$ be two 3-polar 3-rung orthopair fuzzy graphs on vertex sets ${\mathcal{L}}_1=\left\{e,f,g,h\right\}$ and ${\mathcal{L}}_2=\left\{e,f,h\right\},$ respectively, as shown in Figure 11, Table 17 and Table 18. In addition, their union ${\mathbb{G}}_1\cup {\mathbb{G}}_2$ is shown in Figure 12, Table 19 and Table 20, since $f\in {\mathcal{L}}_1\setminus {\mathcal{L}}_2$.

Figure 11. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1),{\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2$).

Table 17. ${\mathbb{G}}_1=({\mathcal{F}}_1,{\Re }_1)$.

$\mathcal{L}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_1\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_1}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
e	$(0.8,0.6,0.5)$	$(0.7,0.8,0.9)$	$ef$	$(0.7,0.6,0.4)$	$(0.6,0.7,0.8)$
f	$(0.9,0.7,0.6)$	$(0.5,0.6,0.8)$	$fg$	$(0.7,0.5,0.3)$	$(0.6,0.7,0.7)$
g	$(0.8,0.5,0.4)$	$(0.7,0.7,0.8)$	$gh$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
h	$(0.9,0.8,0.7)$	$(0.6,0.7,0.8)$	$eh$	$(0.8,0.5,0.4)$	$(0.7,0.7,0.8)$

Table 18. ${\mathbb{G}}_2=({\mathcal{F}}_2,{\Re }_2)$.

$\mathcal{L}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{{\mathcal{F}}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left({\mathbb{G}}_2\right)$	${\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{{\mathit{\Re }}_2}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
e	$(0.9,0.8,0.6)$	$(0.6,0.7,0.8)$	$ef$	$(0.6,0.5,0.4)$	$(0.5,0.7,0.9)$
f	$(0.7,0.6,0.5)$	$(0.6,0.8,0.9)$	$fh$	$(0.6,0.4,0.3)$	$(0.5,0.7,0.8)$
h	$(0.8,0.7,0.6)$	$(0.5,0.8,0.9)$

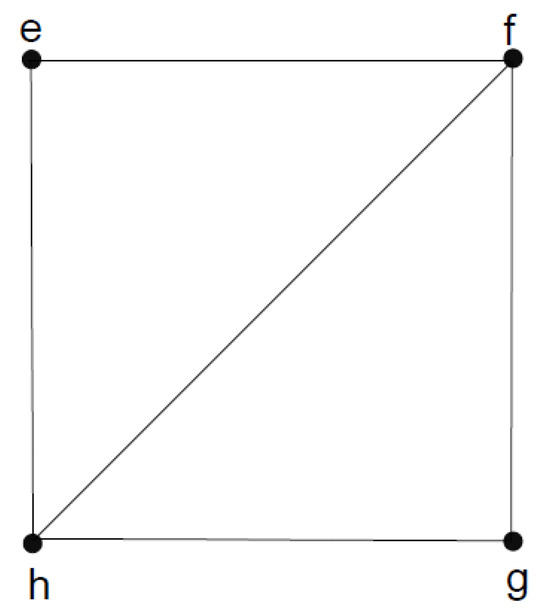
Figure 12. Union ${\mathbb{G}}_1\cup {\mathbb{G}}_2$.

Table 19. Vertex set (${\mathcal{F}}_1\cup {\mathcal{F}}_2$).

$\mathcal{L}({\mathbb{G}}_1\cup {\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathcal{F}}_1}^{\mathit{i}}\cup {\mathit{\mu }}_{{\mathcal{F}}_2}^{\mathit{i}})\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\left({\mathit{\upsilon }}_{{\mathcal{F}}_{{}_1}}^{\mathit{i}}\cup {\mathit{\upsilon }}_{{\mathcal{F}}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}}\right)$
e	$(0.9,0.8,0.6)$	$(0.6,0.7,0.8)$
f	$(0.9,0.7,0.6)$	$(0.5,0.6,0.8)$
g	$(0.8,0.5,0.4)$	$(0.7,0.7,0.8)$
h	$(0.9,0.8,0.7)$	$(0.5,0.7,0.8)$

Table 20. Edge set $({\Re }_1\cup {\Re }_2)$.

$\mathcal{M}({\mathbb{G}}_1\cup {\mathbb{G}}_2)$	$({\mathit{\mu }}_{{\mathit{\Re }}_1}^{\mathit{i}}\cup {\mathit{\mu }}_{{\mathit{\Re }}_2}^{\mathit{i}})\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	$\left({\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_1}}^{\mathit{i}}\cup {\mathit{\upsilon }}_{{\mathit{\Re }}_{{}_2}}^{\mathit{i}}\right)\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
$ef$	$(0.7,0.6,0.4)$	$(0.5,0.7,0.8)$
$fg$	$(0.7,0.5,0.3)$	$(0.6,0.7,0.7)$
$gh$	$(0.6,0.5,0.4)$	$(0.6,0.7,0.8)$
$eh$	$(0.8,0.5,0.4)$	$(0.7,0.7,0.8)$
$fh$	$(0.6,0.4,0.3)$	$(0.5,0.7,0.8)$

Since $g\in {\mathcal{L}}_1-{\mathcal{L}}_{2,}$ thus,

$${\left(d_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)={\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(g\right)=(1.3,1,0.7),{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)={\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(g\right)=(1.2,1.4,1.5).$$

Therefore,$d_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)=d_{{\mathbb{G}}_1}\left(g\right)=((1.3,1,0.7),(1.2,1.4,1.5)).$

$${\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(g\right)=(2.1,1.5,1.1),{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(g\right)=(1.9,2.1,2.3).$$

Therefore,$t{d}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(g\right)=d_{{\mathbb{G}}_1}\left(g\right)=((2.1,1.5,1.1),(1.9,2.1,2.3)).$

Since $h\in {\mathcal{L}}_1\cap {\mathcal{L}}_2$ but no edge concide with h lies in ${\mathcal{M}}_1\cap {\mathcal{M}}_2,$

$$\begin{array}{cc}\hfill {\left(d_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(h\right)& ={\left(d_{\mu }\right)}_{{\mathbb{G}}_1}\left(h\right)+{\left(d_{\mu }\right)}_{{\mathbb{G}}_2}\left(h\right)=(2,1.4,1.1),\hfill \\ \hfill {\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(l\right)& ={\left(d_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(l\right)+{\left(d_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(l\right)=(1.8,2.1,2.4).\hfill \end{array}$$

Therefore,$d_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(h\right)=d_{{\mathbb{G}}_1}\left(h\right)+d_{{\mathbb{G}}_2}\left(h\right)=((2,1.4,1.1),(1.8,2.1,2.4)).$

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(h\right)& ={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(h\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(h\right)-{\mu }_{{\mathcal{F}}_1}^i\left(h\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(h\right)=(2.9,2.2,1.8),\hfill \\ \hfill {\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(h\right)& ={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(h\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(h\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(h\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(h\right)=(2.3,2.8,3.2).\hfill \end{array}$$

Therefore,$t{d}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(h\right)=((2.9,2.2,1.8),(2.3,2.8,3.2)).$

Since $f\in {\mathcal{L}}_1\cap {\mathcal{L}}_2$ and $ef\in {\mathcal{M}}_1\cap {\mathcal{M}}_2,$ thus,

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)& ={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(f\right)-{\mu }_{{\Re }_1}^i\left(ef\right)\wedge {\mu }_{{\Re }_2}^i\left(ef\right)=(2,1.5,1),\hfill \\ \hfill {\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)& ={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(f\right)-{\upsilon }_{{\Re }_1}^i\left(ef\right)\vee {\upsilon }_{{\Re }_2}^i\left(ef\right)=(1.6,2.1,2.3).\hfill \end{array}$$

Therefore,$t{d}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)=((2,1.5,1),(1.6,2.1,2.3)).$

$$\begin{array}{cc}\hfill {\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)& ={\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\left(t{d}_{\mu }\right)}_{{\mathbb{G}}_2}\left(f\right)-{\mu }_{{\Re }_1}^i\left(ef\right)\wedge {\mu }_{{\Re }_2}^i\left(ef\right)-{\mu }_{{\mathcal{F}}_1}^i\left(f\right)\wedge {\mu }_{{\mathcal{F}}_2}^i\left(f\right),\hfill \\ \hfill & =(2.9,2.2,1.6),\hfill \\ \hfill {\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)& ={\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_1}\left(f\right)+{\left(t{d}_{\upsilon }\right)}_{{\mathbb{G}}_2}\left(f\right)-{\upsilon }_{{\Re }_1}^i\left(ef\right)\vee {\upsilon }_{{\Re }_2}^i\left(ef\right)-{\upsilon }_{{\mathcal{F}}_1}^i\left(f\right)\vee {\upsilon }_{{\mathcal{F}}_2}^i\left(f\right),\hfill \\ \hfill & =(2.1,2.7,3.1).\hfill \end{array}$$

Therefore, $t{d}_{{\mathbb{G}}_1\cup {\mathbb{G}}_2}\left(f\right)=((2.9,2.2,1.6),(2.1,2.7,3.1)).$

6. Some Topological Indices for Multi Polar q-Rung Orthopair Fuzzy Graphs

The physicochemical properties of molecular structures are well described with a numeric value which is known as Topological index. Topological indices of a graph have a wide range of implication in network design, theoretical chemistry, data transmission, etc. In fuzzy graphs these topological indices play very important role and have thorough implications. We named them modified topological indices as these are new in fuzzy graphs. In $2020,$ Kalathian et al. [45] established several toplogical indices of fuzzy graphs inclusive of Zagreb indices of two kinds, Randic index, and Harmonic index. Further these indices are cumputed for IFG by Dinar et al. [46] in 2023. Firstly in this part of the monograph we introduce the topological indices of multi polar q-rung fuzzy graphs and then computed these indices in an example.

Definition 27. 

Let $\mathfrak{S}=(\mathcal{F},\Re )$ be the multi polar q-rung orthopair fuzzy graph of $\mathfrak{G}=(\mathcal{L},\mathcal{M}),$ where

$$\mathcal{F}=\left\{⟨\varsigma ,({\mu }_{\mathcal{F}}^1\left(\varsigma \right),{\mu }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\varsigma \right)),({\upsilon }_{\mathcal{F}}^1\left(\varsigma \right),{\upsilon }_{\mathcal{F}}^2\left(\varsigma \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\varsigma \right))⟩:\varsigma \in X\right\},$$

$$\Re =\left\{⟨\varsigma \eta ,({\mu }_{\mathcal{F}}^1\left(\varsigma \eta \right),{\mu }_{\mathcal{F}}^2\left(\varsigma \eta \right),\dots ,{\mu }_{\mathcal{F}}^m\left(\varsigma \eta \right)),({\upsilon }_{\mathcal{F}}^1\left(\varsigma \eta \right),{\upsilon }_{\mathcal{F}}^2\left(\varsigma \eta \right),\dots ,{\upsilon }_{\mathcal{F}}^m\left(\varsigma \eta \right))⟩:\varsigma \eta \in X\times X\right\}.$$

Then the first Zagreb index is represnted by ${\mathcal{M}}_1\left(\mathfrak{S}\right)$ and defined as

$${\mathcal{M}}_1\left(\mathfrak{S}\right)=({\mathcal{M}}_1^1\left(\mathfrak{S}\right),{\mathcal{M}}_1^2\left(\mathfrak{S}\right),\dots ,{\mathcal{M}}_1^m\left(\mathfrak{S}\right)),$$

where,

$$\begin{array}{cc}\hfill {\mathcal{M}}_1^i\left(\mathfrak{S}\right)& =\sum _{\varsigma \in \mathcal{L}}\left[\left({\left({\mu }_{\mathcal{F}}^i\left(\varsigma \right)\right)}^2{\left(d_{\mu }^i\left(\varsigma \right)\right)}^2\right)+\left({\left({\upsilon }_{\mathcal{F}}^i\left(\varsigma \right)\right)}^2{\left(d_{\upsilon }^i\left(\varsigma \right)\right)}^2\right)\right],\hfill \\ \hfill & =\sum _{\varsigma \in \mathcal{L}}{\left(\left({\mu }_{\mathcal{F}}^i\left(\varsigma \right)\right)\left(d_{\mu }^i\left(\varsigma \right)\right)\right)}^2+\sum _{\varsigma \in \mathcal{L}}{\left(\left({\upsilon }_{\mathcal{F}}^i\left(\varsigma \right)\right)\left(d_{\upsilon }^i\left(\varsigma \right)\right)\right)}^2,\hfill \\ \hfill & =\mu ({\mathcal{M}}_1^i\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^i\left(\mathfrak{S}\right)\right),\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Definition 28. 

Let $\mathfrak{S}=(\mathcal{F},\Re )$ be the multi polar q-rung orthopair fuzzy graph of $\mathfrak{G}=(\mathcal{L},\mathcal{M}).$ ${\mathcal{M}}_2\left(\mathfrak{S}\right)$ represnts the second Zagreb index which is defined as

$$\begin{array}{cc}\hfill {\mathcal{M}}_2\left(\mathfrak{S}\right)& =({\mathcal{M}}_2^1\left(\mathfrak{S}\right),{\mathcal{M}}_2^2\left(\mathfrak{S}\right),\dots ,{\mathcal{M}}_2^m\left(\mathfrak{S}\right)),\hfill \\ \hfill {\mathcal{M}}_2^i\left(\mathfrak{S}\right)& =\sum _{\varsigma \eta \in \mathcal{M}}[{\mu }_{\mathcal{F}}^i\left(\varsigma \right).{\mu }_{\mathcal{F}}^i\left(\eta \right).d_{\mu }^i\left(\varsigma \right).d_{\mu }^i\left(\eta \right)]+\sum _{\varsigma \eta \in \mathcal{M}}[{\upsilon }_{\mathcal{F}}^i\left(\varsigma \right).{\upsilon }_{\mathcal{F}}^i\left(\eta \right).d_{\upsilon }^i\left(\varsigma \right).d_{\upsilon }^i\left(\eta \right)],\hfill \\ \hfill {\mathcal{M}}_2\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_2^i\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_2^i\left(\mathfrak{S}\right)\right).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Definition 29. 

Let $\mathfrak{S}=(\mathcal{F},\Re )$ be the multi polar q-rung orthopair fuzzy graph of $\mathfrak{G}=(\mathcal{L},\mathcal{M}).$ The Randic index is denoted by $R(\mathfrak{S})$ and defined as

$$R(\mathfrak{S})=\left(R^1\right(\mathfrak{S}),R^2\left(\mathfrak{S}\right),\dots ,R^m(\mathfrak{S}\left)\right),$$

where,

$$\begin{array}{cc}\hfill R^i\left(\mathfrak{S}\right)& =\sum _{\varsigma \eta \in \mathcal{M}}\frac{1}{\sqrt{({\mu }_{\mathcal{F}}^i\left(\varsigma \right).{\mu }_{\mathcal{F}}^i\left(\eta \right).d_{\mu }^i\left(\varsigma \right).d_{\mu }^i\left(\eta \right))}}+\sum _{\varsigma \eta \in \mathcal{M}}\frac{1}{\sqrt{({\upsilon }_{\mathcal{F}}^i\left(\varsigma \right).{\upsilon }_{\mathcal{F}}^i\left(\eta \right).d_{\upsilon }^i\left(\varsigma \right).d_{\upsilon }^i\left(\eta \right))}},\hfill \\ \hfill R^i\left(\mathfrak{S}\right)& =\mu \left(R^i\right(\mathfrak{S}\left)\right)+\upsilon (R^i\left(\mathfrak{S}\right)).\hfill \end{array}$$

for $i=1,2,3,\dots ,m.$

Definition 30. 

Let $\mathfrak{S}=(\mathcal{F},\Re )$ be the multi polar q-rung orthopair fuzzy graph of $\mathfrak{G}=(\mathcal{L},\mathcal{M}).$ The Harmonic index is represented by $H\left(\mathfrak{S}\right)$ and defined as

$$H(\mathfrak{S})=\left(H^1\right(\mathfrak{S}),H^2\left(\mathfrak{S}\right),\dots ,H^m(\mathfrak{S}\left)\right),$$

where,

$$\begin{array}{cc}\hfill H^i\left(\mathfrak{S}\right)& =\sum _{\varsigma \eta \in \mathcal{M}}\left(\frac{2}{\left({\mu }_{\mathcal{F}}^i\left(\varsigma \right).{\mu }_{\mathcal{F}}^i\left(\eta \right)\right)(d_{\mu }^i\left(\varsigma \right)+d_{\mu }^i\left(\eta \right))}\right)+\sum _{\varsigma \eta \in \mathcal{M}}\left(\frac{2}{\left({\upsilon }_{\mathcal{F}}^i\left(\varsigma \right).{\upsilon }_{\mathcal{F}}^i\left(\eta \right)\right)\left(d_{\upsilon }^i\left(\varsigma \right)+d_{\upsilon }^i\left(\eta \right)\right)}\right),\hfill \\ \hfill H^i\left(\mathfrak{S}\right)& {=\mu (H}^i\left(\mathfrak{S}{\left)\right)+\upsilon (H}^i\right(\mathfrak{S})),\hfill \end{array}$$

for$i=1,2,3,\dots ,m.$

Example 10. 

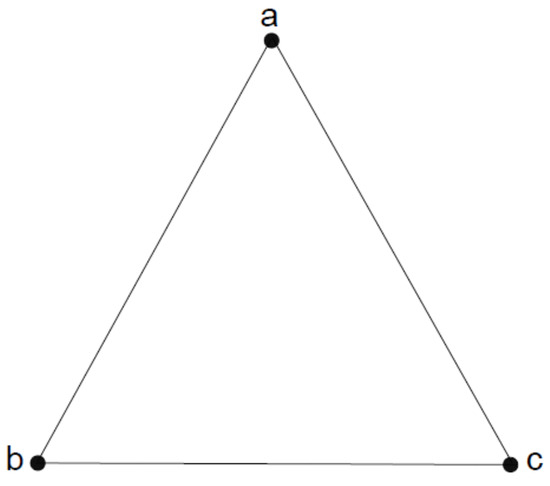
Consider $\mathfrak{S}=\left(\mathcal{F},\Re \right)$ be a 3-polar 3-rung orthopair fuzzy graph of $\mathfrak{G}=(\mathcal{L},\mathcal{M}),$ where $\mathcal{L}=\{a,b,c\}$ and $\mathcal{M}=\{ab,bc,ac\}$ are vertex set and edge set, respectively, as given in the Figure 13 and Table 21. Then we find the first and second kind of Zagreb indices, Randic index and Harmonic index of this graph.

Figure 13. $\mathfrak{S}=\left(\mathcal{F},\Re \right)$.

Table 21. $\mathfrak{S}=\left(\mathcal{F},\Re \right)$.

$\mathcal{L}\left(\mathfrak{S}\right)$	${\mathit{\mu }}_{\mathcal{F}}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	${\mathit{\upsilon }}_{\mathcal{F}}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}\right)$	$\mathcal{M}\left(\mathfrak{S}\right)$	${\mathit{\mu }}_{\mathit{\Re }}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$	${\mathit{\upsilon }}_{\mathit{\Re }}^{\mathit{i}}\left({\mathit{\varsigma }}_{\mathit{j}}{\mathit{\varsigma }}_{\mathit{k}}\right)$
a	$(0.7,0.6,0.5)$	$(0.8,0.9,0.9)$	$ab$	$(0.6,0.5,0.4)$	$(0.7,0.8,0.8)$
b	$(0.8,0.7,0.6)$	$(0.7,0.8,0.9)$	$bc$	$(0.7,0.6,0.5)$	$(0.6,0.7,0.8)$
c	$(0.9,0.8,0.7)$	$(0.6,0.7,0.8)$	$ac$	$(0.5,0.4,0.3)$	$(0.7,0.8,0.9)$

By direct calculation, we have

$$\begin{array}{cc}\hfill d\left(a\right)& =\left(\right(1.1,0.9,0.7),(1.4,1.6,1.7\left)\right),\hfill \\ \hfill d\left(b\right)& =\left(\right(1.3,1.1,0.9),(1.3,1.5,1.6\left)\right),\hfill \\ \hfill d\left(c\right)& =\left(\right(1.2,1,0.8),(1.3,1.5,1.7\left)\right).\hfill \end{array}$$

Now by using definition, we calculate first Zagreb index

$${\mathcal{M}}_1\left(\mathfrak{S}\right)=({\mathcal{M}}_1^1\left(\mathfrak{S}\right),{\mathcal{M}}_1^2\left(\mathfrak{S}\right),{\mathcal{M}}_1^3\left(\mathfrak{S}\right)),$$

where,

$$\begin{array}{cc}\hfill {\mathcal{M}}_1^1\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_1^1\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right)\right),\hfill \\ \hfill \mu ({\mathcal{M}}_1^1(\mathfrak{S}\left)\right)& {=(\mu }^1\left(a\right).d_{\mu }^1{\left(a\right))}^2+{(\mu }^1\left(b\right).d_{\mu }^1\left(b\right){{)}^2+{(\mu }^1\left(c\right).d_{\mu }^1\left(c\right))}^2,\hfill \\ \hfill \mu ({\mathcal{M}}_1^1\left(\mathfrak{S}\right))& ={\left(0.77\right)}^2+{\left(1.04\right)}^2+{\left(1.08\right)}^2,\hfill \\ \hfill \mu ({\mathcal{M}}_1^1\left(\mathfrak{S}\right))& =2.8409.\hfill \\ \hfill \upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right))& =\left(\upsilon \right(a).d_{\upsilon }{\left(a\right))}^2+\left(\upsilon \right(b).d_{\upsilon }{\left(b\right))}^2+\left(\upsilon \right(c{).d_{\upsilon }\left(c\right))}^2,\hfill \\ \hfill \upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right))& ={\left(1.12\right)}^2+{\left(0.91\right)}^2+{\left(0.78\right)}^2,\hfill \\ \hfill \upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right))& =2.6909,\hfill \end{array}$$

hence, ${\mathcal{M}}_1^1(\mathfrak{S})=\mu ({\mathcal{M}}_1^1\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right)\right)$ and in similar mannar we calculate ${\mathcal{M}}_1^2\left(\mathfrak{S}\right)$ and ${\mathcal{M}}_1^3\left(\mathfrak{S}\right)$,

$$\begin{array}{cc}\hfill {\mathcal{M}}_1^1\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_1^1\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^1\left(\mathfrak{S}\right)\right)=2.8409+2.6909=5.5318,\hfill \\ \hfill {\mathcal{M}}_1^2\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_1^2\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^2\left(\mathfrak{S}\right)\right)=1.5245+4.6161=6.1406,\hfill \\ \hfill {\mathcal{M}}_1^3\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_1^3\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_1^3\left(\mathfrak{S}\right)\right)=0.7277+6.2641=6.9916,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{M}}_1\left(\mathfrak{S}\right)& =({\mathcal{M}}_1^1\left(\mathfrak{S}\right),{\mathcal{M}}_1^2\left(\mathfrak{S}\right),{\mathcal{M}}_1^3\left(\mathfrak{S}\right)),\hfill \\ \hfill {\mathcal{M}}_1\left(\mathfrak{S}\right)& =(5.5318,6.1406,6.9916).\hfill \end{array}$$

We also observed that

$$\begin{array}{cc}\hfill \mu ({\mathcal{M}}_1\left(\mathfrak{S}\right))=(\mu & ({\mathcal{M}}_1^1\left(\mathfrak{S}\left)\right)\ge \mu ({\mathcal{M}}_1^2(\mathfrak{S}\left)\right)\ge \mu ({\mathcal{M}}_1^3\left(\mathfrak{S}\right))\right),\hfill \\ \hfill \mu ({\mathcal{M}}_1\left(\mathfrak{S}\right))=& (2.8409\ge 1.5245\ge 0.7277),and\hfill \\ \hfill \upsilon ({\mathcal{M}}_1\left(\mathfrak{S}\right))=(\upsilon & ({\mathcal{M}}_1^1\left(\mathfrak{S}\left)\right)\le \upsilon ({\mathcal{M}}_1^2(\mathfrak{S}\left)\right)\le \upsilon ({\mathcal{M}}_1^3\left(\mathfrak{S}\right))\right),\hfill \\ \hfill \upsilon ({\mathcal{M}}_1\left(\mathfrak{S}\right))=& (2.6909\le 4.6161\le 6.2641),\hfill \end{array}$$

Now we calculate second Zagreb index by using definition,

$$\begin{array}{cc}\hfill {\mathcal{M}}_2^1\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_2^1\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_2^1\left(\mathfrak{S}\right)\right)=2.7556+2.6060=5.3582,\hfill \\ \hfill {\mathcal{M}}_2^2\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_2^2\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_2^2\left(\mathfrak{S}\right)\right)=1.4638+4.5=5.9638,\hfill \\ \hfill {\mathcal{M}}_2^3\left(\mathfrak{S}\right)& =\mu ({\mathcal{M}}_2^3\left(\mathfrak{S}\left)\right)+\upsilon ({\mathcal{M}}_2^3\left(\mathfrak{S}\right)\right)=0.6874+6.2424=6.9298,\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{M}}_2\left(\mathfrak{S}\right)=& ({\mathcal{M}}_2^1\left(\mathfrak{S}\right),{\mathcal{M}}_2^2\left(\mathfrak{S}\right),{\mathcal{M}}_2^3\left(\mathfrak{S}\right)),\hfill \\ \hfill {\mathcal{M}}_2\left(\mathfrak{S}\right)=& (5.3582,5.9638,6.9298).\hfill \end{array}$$

Also we have,

$$\begin{array}{cc}\hfill \mu ({\mathcal{M}}_2\left(\mathfrak{S}\right))=(\mu & ({\mathcal{M}}_2^1\left(\mathfrak{S}\left)\right)\ge \mu ({\mathcal{M}}_2^2\left(\mathfrak{S}\right)\right)\ge \mu ({\mathcal{M}}_2^3\left(\mathfrak{S}\right)\left)\right),\hfill \\ \hfill \left({\mathcal{M}}_2\left(\mathfrak{S}\right)\right)=& (2.7556\ge 1.4638\ge 0.6874),and\hfill \\ \hfill \upsilon ({\mathcal{M}}_2\left(\mathfrak{S}\right))=(\upsilon & ({\mathcal{M}}_2^1\left(\mathfrak{S}\left)\right)\le \upsilon ({\mathcal{M}}_2^2\left(\mathfrak{S}\right)\right)\le \upsilon ({\mathcal{M}}_2^3\left(\mathfrak{S}\right)\left)\right),\hfill \\ \hfill \left({\mathcal{M}}_2\left(\mathfrak{S}\right)\right)=& (2.6060\le 4.5\le 6.2424).\hfill \end{array}$$

Now by using definition we calculate Randic index

$$\begin{array}{cc}\hfill R^1\left(\mathfrak{S}\right)& =\mu (R^1\left(\mathfrak{S}\left)\right)+\upsilon (R^1\right(\mathfrak{S}\left)\right)=3.1576+3.2473=6.4049,\hfill \\ \hfill R^2\left(\mathfrak{S}\right)& =\mu (R^2\left(\mathfrak{S}\left)\right)+\upsilon (R^2\right(\mathfrak{S}\left)\right)=4.3464+2.4649=6.8113,\hfill \\ \hfill R^3\left(\mathfrak{S}\right)& =\mu (R^3\left(\mathfrak{S}\left)\right)+\upsilon (R^3\right(\mathfrak{S}\left)\right)=6.3775+2.0815=8.459,\hfill \end{array}$$

$$\begin{array}{cc}\hfill R(\mathfrak{S})& =\left(R^1\right(\mathfrak{S}),R^2\left(\mathfrak{S}\right),R^3(\mathfrak{S}\left)\right),\hfill \\ \hfill R(\mathfrak{S})& =(6.4049,6.8113,8.459).\hfill \end{array}$$

where we have,

$$\begin{array}{cc}\hfill \mu (R(\mathfrak{S}\left)\right)& =\left(\mu \right(R^1\left(\mathfrak{S}\left)\right)\le \mu (R^2\right(\mathfrak{S}\left)\right)\le \mu (R^3(\mathfrak{S}\left)\right),\hfill \\ \hfill \mu (R(\mathfrak{S}\left)\right)& =(3.1576\le 4.3464\le 6.3775),and\hfill \\ \hfill \upsilon (R(\mathfrak{S}\left)\right)& =\left(\upsilon \right(R^1\left(\mathfrak{S}\left)\right)\ge \upsilon (R^2\right(\mathfrak{S}\left)\right)\ge \upsilon (R^3(\mathfrak{S}\left)\right),\hfill \\ \hfill \upsilon (R(\mathfrak{S}\left)\right)& =(3.2473\ge 2.4649\ge 2.0815).\hfill \end{array}$$

Finally we find Harmonic index by using definition

$$\begin{array}{cc}\hfill H^1\left(\mathfrak{S}\right)& {=\mu (H}^1(\mathfrak{S}{\left)\right)+\upsilon (H}^1(\mathfrak{S}\left)\right)=3.9794+4.6975=8.6769,\hfill \\ \hfill H^2\left(\mathfrak{S}\right)& {=\mu (H}^2\left(\mathfrak{S}{\left)\right)+\upsilon (H}^2\right(\mathfrak{S}\left)\right)=6.2745+3.1106=9.3851,\hfill \\ \hfill H^3\left(\mathfrak{S}\right)& {=\mu (H}^3(\mathfrak{S}{\left)\right)+\upsilon (H}^3(\mathfrak{S}\left)\right)=10.7773+2.4069=13.1842,\hfill \end{array}$$

$$\begin{array}{cc}\hfill H(\mathfrak{S})=& \left(H^1\left(\mathfrak{S}\right),H^2\left(\mathfrak{S}\right),H^3\right(\mathfrak{S}\left)\right),\hfill \\ \hfill H(\mathfrak{S})=& (8.6769,9.3851,13.1842).\hfill \end{array}$$

We observed that,

$$\begin{array}{cc}\hfill \mu (H(\mathfrak{S}\left)\right)=(\mu & \left(H^1\right(\mathfrak{S}\left)\right)\le \mu (H^2\left(\mathfrak{S}\left)\right)\le \mu (H^3\right(\mathfrak{S}\left)\right),\hfill \\ \hfill \mu (H(\mathfrak{S}\left)\right)=& (3.9794\le 6.2745\le 10.7773),and\hfill \\ \hfill \upsilon (H(\mathfrak{S}\left)\right)=(\upsilon & \left(H^1\right(\mathfrak{S}\left)\right)\ge \upsilon (H^2\left(\mathfrak{S}\left)\right)\ge \upsilon (H^3\right(\mathfrak{S}\left)\right),\hfill \\ \hfill \upsilon (H(\mathfrak{S}\left)\right)=& (4.6975\ge 3.1106\ge 2.4069).\hfill \end{array}$$

Theorem 13. 

If two m-$\mathfrak{SqROSSG}s$$\mathfrak{S}=({\mathcal{F}}_{\mathfrak{S}},{\Re }_{\mathfrak{S}})$ and $\mathfrak{Q}=({\mathcal{F}}_{\mathfrak{Q}},{\Re }_{\mathfrak{Q}})$ are isomorphic to each other, then these graphs have equal topological indices values.

Proof. 

Let $\mathfrak{S}=({\mathcal{F}}_{\mathfrak{S}},{\Re }_{\mathfrak{S}})$ and $\mathfrak{Q}=({\mathcal{F}}_{\mathfrak{Q}},{\Re }_{\mathfrak{Q}})$ be two isomorphic m-$\mathfrak{SqROSSG}s.$ Then there we have an identity function, $I_{\mathcal{F}}:{\mathcal{F}}_{\mathfrak{S}}\left(t\right)\to {\mathcal{F}}_{\mathfrak{Q}}\left(s\right)$ for every $t\in {\mathcal{L}}_{\mathfrak{S}}$ there exist $s\in {\mathcal{L}}_{\mathfrak{Q}}$ as well as for each $t_j{t}_k\in {\Re }_{\mathfrak{S}}$ there exist $s_j{s}_k\in {\Re }_{\mathfrak{Q}}$ such that $I_{\Re }:{\Re }_{\mathfrak{S}}\left(t_j{t}_k\right)\to {\Re }_{\mathfrak{Q}}\left(s_j{s}_k\right)(i.e.)$ for vertices and edges of $\mathfrak{S}=({\mathcal{F}}_{\mathfrak{S}},{\Re }_{\mathfrak{S}})$ each membership value coincides with the values of graph $\mathfrak{Q}=({\mathcal{F}}_{\mathfrak{Q}},{\Re }_{\mathfrak{Q}})$. Therefore, we conclude that, with same membership values for equal collection of vertices and edges the graph structures may differ but there topological indices values are equal. □

Corollary 1. 

If the topological values of two $m-\mathfrak{SqROSSG}s$ $\mathfrak{S}=({\mathcal{F}}_{\mathfrak{S}},{\Re }_{\mathfrak{S}})$ and $\mathfrak{Q}=({\mathcal{F}}_{\mathfrak{Q}},{\Re }_{\mathfrak{Q}})$ are same, then the two m-$\mathfrak{SqROSSG}s$ need not to be isomorphic.

Corollary 2. 

Let $\mathfrak{S}=({\mathcal{F}}_{\mathfrak{S}},{\Re }_{\mathfrak{S}})$ and $\mathfrak{Q}=({\mathcal{F}}_{\mathfrak{Q}},{\Re }_{\mathfrak{Q}})$ be the m-$\mathfrak{SqROSSG}s.$ Then the union of two m-$\mathfrak{SqROSSG}s$$\mathfrak{S}\cup \mathfrak{Q}$ is

(i) 

$\left(M_1^i(\mathfrak{S}\cup \mathfrak{Q})\right)\ge max\{\left(M_1^i\left(\mathfrak{S}\right)\right),\left(M_1^i\left(\mathfrak{Q}\right)\right)\},$

(ii) 

$\left(M_2^i(\mathfrak{S}\cup \mathfrak{Q})\right)\ge max\{\left(M_2^i\left(\mathfrak{S}\right)\right),\left(M_2^i\left(\mathfrak{Q}\right)\right)\},$

(iii) 

$\left(R^i(\mathfrak{S}\cup \mathfrak{Q})\right)\ge min\{\left(R^i\left(\mathfrak{S}\right)\right),\left(R^i\left(\mathfrak{Q}\right)\right)\},$

(iv) 

$\left(H^i(\mathfrak{S}\cup \mathfrak{Q})\right)\ge min\{\left(H^i\left(\mathfrak{S}\right)\right),\left(H^i\left(\mathfrak{Q}\right)\right)\},$

for $i=1,2,3,\dots ,m.$

Proof. 

We can prove these results with the help of Example 9. □

7. Conclusions

In this monograph we have demonstrated several rudimentary operations on m-$\mathfrak{FqROFFG}s$ together with their essential results. Firstly, for a vertex in m-$\mathfrak{FqROFFG},$ we have defined the degree of vertex then we calculated its total degree. For product operations on m-$\mathfrak{FqROFFG}s,$ these degrees permit to comprehend their characteristics. Secondly, product operations on m-$\mathfrak{FqROFFG}s,$ inclusive direct, Cartesian, semi-strong, strong and lexicographic products, are obtained. Thirdly, using degree and total degree of vertex we have defined some general theorems under the obtained product operations on m-$\mathfrak{FqROFFG}s$. More specifically, in product operations on m-$\mathfrak{FqROFFG}s$ the relationship between the degree and total degree of a vertex and the collection of adjoining vertices is analyzed with the help of these theorems. Finally, we have defined some degree based topological indices for m-$\mathfrak{FqROFFG}s$ and calculated these indices in an example. Due to vast range of implementation in various fields of sciences such as molecular science, medication, computer science, etc., the utilization of topological indices in fuzzy graphs are obtaining attraction. We can define and calculate already existed different topological indices for m-$\mathfrak{FqROFFG}s$. In our upcoming work we can extend the application of m-$\mathfrak{FqROFFG}s$ to chemical structures.