Multi-Attribute Group Decision-Making Methods Based on Entropy Weights with q-Rung Picture Uncertain Linguistic Fuzzy Information

Abstract

This paper introduces a new concept called q-rung picture uncertain linguistic fuzzy sets (q-RPULSs). These sets provide a reliable and comprehensive method for describing complex and uncertain decision-making information. In addition, q-RPULSs help to integrate the decision maker’s quantitative assessment ideas with qualitative assessment information. For the q-RPUL multi-attribute group decision-making problem with unknown weight information, an entropy-based fuzzy set method for q-rung picture uncertainty language is proposed. The method considers the interrelationships among attributes and builds a q-rung picture uncertain language model. In addition, the q-RPULMSM operator and its related properties are discussed in this paper. This operator enables the fusion of q-RPULSs and helps to reach consensus in decision-making scenarios. To demonstrate the validity of the methodology, we provide a real case study involving commodity selection. Based on this case study, the reasonableness and superiority of the method are evaluated, highlighting the practical advantages and applicability of q-RPULSs in decision-making processes.

1. Introduction

MAGDM is a vital process that involves decision makers evaluating and prioritizing alternatives while considering various attributes [1]. The goal is to select the most advantageous option from a range of available programs. This process plays a significant role in modern decision-making science and is widely applied in fields such as engineering, economics, and management. The use of mathematical models [2] based on partial differential equations allows us to model physically relevant quantities. A new method to optimize the hyperparameters was proposed by Effat Jalaeian Zaferani et al. [3]. Due to the complexity of real-world issues and the unpredictable nature of decision-making environments, traditional mathematical models based on binary logic are no longer adequate for accurately representing the attribute values associated with potential solutions during the decision-making process. Therefore, the researchers introduced some fuzzy sets.

FSs made significant progress with the pioneering work of Zadeh [4]. FSs have emerged as a crucial tool for representing imprecise and uncertain information. Ataanassov [5] further contributed to the field by building upon Zadeh’s work. In addition to fuzzy sets, Zadeh introduced intuitionistic fuzzy sets, which enhance the theoretical framework by representing uncertain information and phenomena more effectively. Intuitionistic fuzzy sets incorporate both subordination and non-subordination dimensions, surpassing classical fuzzy sets in this aspect. However, it is important to note that intuitionistic fuzzy sets must satisfy the non-boundedness condition, which restricts their practical application and scope. To overcome this limitation, Yager [6] proposed Pythagorean fuzzy sets, which strictly adhere to the condition that the sum of the squares of the positive and negative ratings must not exceed 1. This breakthrough led to extensive research on solving multi-attribute group decision-making (MAGDM) problems using Pythagorean fuzzy sets. Zhang et al. [7] introduced generalized Pythagorean fuzzy Bonferroni mean operators, which are valuable in capturing the interrelationships among Pythagorean fuzzy numbers and finding practical utility in decision-making. Furthermore, Garg [8] explored the practical applications of Pythagorean fuzzy sets in MAGDM by presenting logarithmic operator laws and aggregation operators specifically tailored for them. Xu et al. [9] introduced a set of Pythagorean fuzzy intersection Muirhead averaging operators as a solution to handle the intersection between Pythagorean membership and non-membership, while also effectively capturing the interrelationships among multiple Pythagorean fuzzy numbers. Despite the abundant research conducted on Pythagorean fuzzy sets, these sets possess certain limitations, particularly when employed in complex decision problems. In certain scenarios, it is observed that the quadratic sum of the positive and negative ratings do not surpass 1, while the sum of the cubic or higher powers exceeds 1. To overcome this limitation, Yager [10] proposed q-rung orthogonal fuzzy sets. The constraint in q-rung orthogonal fuzzy sets is that the summation of the q-th powers of the positive and negative ratings should not exceed 1. Liu and Wang [11] subsequently devised straightforward weighted average operators to consolidate generalized orthogonal fuzzy numbers and successfully employed these operators in the realm of multi-attribute group decision-making (MAGDM). Liu [12] introduced the generalized orthogonal fuzzy Bonferroni mean value operator as a means to amalgamate the interrelationships among q-rung orthogonal fuzzy numbers.

However, in reality, decision-making problems can be excessively complex. We may encounter situations where human voters provide different types of answers in a poll, such as yes, no, reject, or abstain. Under such scenarios, the fuzzy set proof presented above is not sufficient. Thus, Cuong and Kreinovich [13] have made significant contributions by introducing picture fuzzy sets (PFSs). They have conducted extensive research on the fundamental operations and properties of PFSs. PFSs are distinguished by their positive, neutral, and negative degrees of membership, while adhering to the constraint that the cumulative sum of the positive evaluation, neutral evaluation, and negative evaluation must not surpass 1. Thong and Soncite [14,15] have developed various fuzzy clustering algorithms using fuzzy sets of images. These algorithms have been successfully applied to weather forecasting and project selection. However, there are limitations of these methods. For example, they are no longer used when dealing with the sum of positive, neutral, and negative ratings exceeding 1. To address this issue, Li et al. [16] proposed a new method using q-RPFSs with the constraint that the sum of the q powers of positive, neutral, and negative ratings must be equal to or less than one. This advancement in the unique constraint form of q-RPFSs effectively addresses the inherent limitations of q-level generalized orthogonal fuzzy sets and graphical fuzzy sets. Pinar et al. [17] proposed the q-RPF-KNN algorithm, which computes the distance between test instances and training instances. Comparing with other KNN algorithms, the results are more perfect. Akram et al. [18] utilized 2TLCq-RPFSs to solve the problem of optimal machine selection. Tahir et al. [19] introduced T-spherical fuzzy sets and applied them to medical diagnosis. While previous approaches are unable to comprehensively address quantitative and qualitative decision-making and the intricate relationships between multiple parameters, our proposed method and operators aim to fill this important gap. By introducing innovative methods, we aim to provide decision makers with an integrated framework that considers both quantitative and qualitative aspects of decision-making.

In certain scenarios, decision makers often prioritize quantitative decisions over qualitative ones due to constraints such as time limitations and limited expertise. This tendency to incorporate both quantitative and qualitative assessment information is particularly evident in real-world MAGDM problems. In such complex decision-making scenarios, it is crucial to consider not only the numerical values associated with the attributes but also the qualitative aspects. By recognizing the importance of both quantitative and qualitative factors, decision makers can ensure a more comprehensive and balanced assessment of options in MAGDM problems. Decision makers recognize the need to consider and integrate both types of information provided by stakeholders in order to make informed and well-rounded decisions. The utilization of linguistic variables as valuable tools in expressing the qualitative evaluations of decision makers has demonstrated its effectiveness. Li et al. [16] introduced a q-rung picture linguistic set in order to select a suitable enterprise resource planning system. Consequently, a fusion of ULVs and q-rung picture fuzzy sets has been employed to accurately capture the evaluations of decision makers. Singh et al. [20] used the LDULFPEWG operator to select the best microgrid scheme. In order to analyze the conditions of the anomalous aluminum electrolyzer, zhu et al. [21] studied the PUL-DUCG model and achieved satisfactory results. As a result, this research introduces a novel concept known as q-RPULSs. This integration enhances the representation of decision makers’ evaluations, providing a comprehensive and robust framework. To illustrate, let us examine a situation in which a professor is evaluating the research capabilities of a graduate student.

Researchers have introduced a range of operators employed to aggregate the decision matrix, facilitating the derivation of comprehensive attribute values for each alternative. Subsequently, by ranking the alternatives based on the scores of the comprehensive attributes, researchers are able to identify the optimal solution. This approach enables efficient decision-making in scenarios involving multiple attributes, ensuring a comprehensive and well-informed selection process by effectively considering the correlation between any pair of input parameters. In the realm of multi-attribute decision-making, information aggregation operators hold significant prominence and have garnered considerable attention from scholars. Noteworthy operators include the Bonferroni mean (BM) operator [22], the Heronian mean (HM) operator [23,24], and the Maclaurin symmetric mean (MSM) operator [25]. The interrelationships between two input parameters are effectively captured by the Bonferroni mean (BM) operator, which was originally introduced by Bonferroni [22]. Fatma et al. [26] proposed the picture fuzzy Bonferroni mean, which was chosen to match the company’s enterprise resource planning system. Liu et al. [12] proposed the q-rung orthopair fuzzy Bonferroni mean operator, which solves the project investment problem. Similarly, the HM aggregation operator, introduced by Gleb et al. [27], shares similar characteristics with the BM operator, allowing for the consideration of correlations among any pair of input parameters. Liu et al. [28] proposed a intuitionistic uncertain linguistic arithmetic Heronian mean operator and applied it to project investment. Sumera et al. [29] proposed a generalized 2-tuple linguistic bipolar fuzzy Heronian mean operator and its application to battery selection. Nevertheless, the BM operator and the HM operator do not have the ability to account for interrelationships among multiple parameters. As a consequence, this restriction may introduce biases and inaccuracies in the evaluation results when dealing with complex real-world problems. To tackle this issue, Maclaurin [25] proposed a solution by introducing the MSM operator. The MSM operator offers the capability of considering the correlation among multiple input parameters, thereby enhancing the accuracy and dependability of the evaluation outcomes. Subsequent advancements led Detemple and Robertson [30] to develop an extended version of the MSM operator. Building upon the strengths of the MSM operator, researchers have conducted extensive studies that have yielded numerous noteworthy results. Wang et al. [31] proposed the IFPMSM operator and applied it to air quality evaluation.

The above-described method focuses on scenarios where complete attribute weight information is known but, in many real-world MAGDM problems, attribute weights are often unknown. Therefore, a novel MAGDM approach is proposed for dealing with MAGDM problems under q-RPULSs with unknown weight information. This study aims to address this issue as follows: (1) Recognizing that the Maclaurin symmetric mean (MSM) operator can consider interrelationships amongst multiple attributes; introducing q-RPULSs of the MSM operator to effectively handle extreme evaluations of decision makers. (2) Proposing a new MAGDM technique for the q-RPUL multi-attribute group decision-making problem that accounts for unknown attribute weights. The rest of this paper is organized as follows: Section 2 reviews and discusses fundamental concepts and theories comprehensively. Section 3 introduces several MSM operators designed for q-rung picture uncertain linguistic sets (q-RPULSs), including the q-rung picture uncertain language Maclaurin symmetric averaging operator (q-RPULMSM) and the q-rung picture uncertain language weighted Maclaurin symmetric averaging operator (q-RPULWMSM). Furthermore, this section extensively examines the properties of these operators. Section 4 describes the aggregation method for problem-solving. Section 5 showcases the performance of the method by applying it to a real-world scenario or simulation, and provides empirical evidence of its utility. Finally, in Section 6, conclusions are drawn based on the key findings and results obtained from the study.

Table 1. Fuzzy sets and operators.

Abbreviation	Full Name
MAGDM	multi-attribute group decision-making
FSs	fuzzy sets
IFSs	intuitionistic fuzzy sets
PyFSs	Pythagorean fuzzy sets
PFSs	picture fuzzy sets
q-ROFs	q-rung orthopair fuzzy sets
q-ROULSs	q-rung orthopair uncertain linguistic sets
q-RPULSs	q-rung picture uncertain linguistic sets
q-RPFSs	q-rung picture fuzzy sets
ULVs	uncertain linguistic variables
MSM	Maclaurin symmetric mean
q-RPULMSM	q-rung picture uncertain linguistic Maclaurin symmetric mean
q-RPULWMSM	q-rung picture uncertain linguistic weighted Maclaurin symmetric mean
2TLCq-RPFSs	2-tuple linguistic complex q-rung picture fuzzy sets
LDULFPEWG	linear diophantine uncertain linguistic fuzzy power Einstein-weighted geometric
TSULWA	T-spherical uncertain linguistic weighted averaging
T-SFWGMSM	T-spherical fuzzy weighted geometric Maclaurin symmetric mean
q-RPFDHM	q-rung picture fuzzy dual Heronian mean
q-RPULA	q-rung picture uncertain linguistic averaging
PULMSM	picture uncertain linguistic Maclaurin symmetric mean
q-RPULBM	q-rung picture uncertain linguistic Bonferroni mean
SPULMSM	spherical picture uncertain linguistic Maclaurin symmetric mean
RAM	random access memory

is provided to assist in better understanding the fuzzy sets and operators mentioned in this article.

2. Preliminaries

In this section, we provide a brief introduction to various types of fuzzy sets, including ULSs, PFSs, q-ROFSs, q-RPLSs, q-ROULSs, and q-RPFSs, and their corresponding operations. In addition, we discuss in depth an important tool applicable to fuzzy set theory, namely MSM. Furthermore, we introduce the novel concept of q-RPULSs and provide scoring functions and distance measures that can be employed to evaluate q-RPULSs.

Definition 1

([32]). One can describe the representation of a PFS $C_{HT}$ in a nonempty fixed set X as follows:

$$C_{HT}=\{<x,u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)>|x\in X\}$$

(1)

In this context, the term “positive rating” $u_{C_{HT}}$ denotes the rating to which x belongs positively to $C_{HT}$, while the term “neutrality rating” ${\eta }_{C_{HT}}$ signifies the degree to which x has neutral association with $C_{HT}$. Additionally, the term “negative rating” $v_{C_{HT}}$ indicates the degree to which x has a negative association with $C_{HT}$. The degrees of affiliation mentioned above adhere to the following conditions: $0\le u_{C_{HT}}(x)+{\eta }_{C_{HT}}(x)+v_{C_{HT}}(x)\le 1$. Moreover, refusal rating, denoted as ${\pi }_A(x)$, can be determined by ${\pi }_{C_{HT}}(x)=(1-(u_{C_{HT}}(x)+{\eta }_{C_{HT}}(x)+v_{C_{HT}}(x)))$.

The triplets $(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))$ are called picture fuzzy numbers (PFNs) and play a significant role in representing uncertainty and fuzziness in PFSs.

Definition 2

([17]). Let us define a q-ROFS on a nonempty fixed set X as follows:

$$C_{HT}=\{<x,u_{C_{HT}}(x),v_{C_{HT}}(x)>|x\in X\}$$

(2)

Here, $u_{C_{HT}}$ and $v_{C_{HT}}$ represent affiliation and non-affiliation of x to $C_{HT}$, respectively. It is necessary for the following condition to hold for every x in X: $x\in X$: $0\le (u_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q)\le 1,(q\ge 1)$. Additionally, the degree of refusal rating is calculated as:

$${\pi }_{C_{HT}}(x)={(1-(u_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q))}^{\frac{1}{q}}.$$

(3)

To provide a more convenient representation, we can refer to the notation $<u_{C_{HT}}(x),v_{C_{HT}}(x)>$ as a q-ROFN.

Definition 3

([17]). We can define a q-RPFS on set of positive real numbers X in the following manner:

$$C_{HT}=\{<x,u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)>|x\in X\}$$

(4)

In this definition, we ensure that $0\le (u_{C_{HT}}{(x)}^q+{\eta }_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q)\le 1$ for each element x in X. The values $u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)$ belong to the range [0, 1] and represent the positive, neutral, and negative ratings of x to the q-RPFS. Additionally, we can calculate the refusal rating ${\pi }_A(x)$ using the expression ${\pi }_{C_{HT}}(x)={(1-(u_{C_{HT}}{(x)}^q+{\eta }_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q))}^{\frac{1}{q}}$.

For simplicity, we refer to each triplet $(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))$ as a q-RPFN.

Definition 4

([16]). We can define a q-RPLS $C_{HT}$ on an ordinary fixed set X:

$$C_{HT}=\{<x,s_{\varphi (x)},(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))]>|x\in X\}$$

(5)

Here, the term $s_{\varphi (x)}$ belongs to S and $s_{\varphi (x)}$ represents the linguistic term interval in S. The triplet $u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)$ represents the positive, neutral, and negative ratings of the element x in the q-RPULS. These membership degrees satisfy the conditions that $0\le (u_{C_{HT}}{(x)}^q+{\eta }_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q)\le 1$ and $u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)\in [0,1]$ are within the range [0, 1]. For convenience, we can refer to the notation $<s_{\varphi (x)},(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))>$ as the q-RPLS. To simplify the notation further, we may write it as $<s_{\varphi },(u,\eta ,v)>$.

Definition 5

([33]). Linguistic term set $S=\{s_0,s_1,\dots ,s_{t-1}\}$ is composed of k elements, where k is an odd number. Generally, t = 3, 5, 7, 9. For example, t equals 5, $S=\{s_0,s_1,s_2,s_3,s_4\}=\{very poor,poor,good,very good,excellent\}.$

Definition 6

([34]). We can define a q-ROULS $C_{HT}$ on an ordinary fixed set X:

$$C_{HT}=\{<x,[s_{\varphi (x)},s_{\psi (x)}],(u_{C_{HT}}(x),v_{C_{HT}}(x))]>|x\in X\}$$

(6)

Here, the terms $s_{\varphi (x)},s_{\psi (x)}$ belong to S and $s_{\varphi (x)},s_{\psi (x)}$ represents the linguistic term interval in S. The $u_{C_{HT}}(x),v_{C_{HT}}(x)$ represents the positive and negative ratings of the element x in the q-ROULS. These membership degrees satisfy the conditions that $0\le (u_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q)\le 1$ and $u_{C_{HT}}(x),v_{C_{HT}}(x)\in [0,1]$ are within the range [0, 1]. For convenience, we can refer to the notation $<[s_{\varphi (x)},s_{\psi (x)}],(u_{C_{HT}}(x),v_{C_{HT}}(x))>$ as the q-ROULS. To simplify the notation further, we may write it as $<[s_{\varphi },s_{\psi }],(u,v)>$.

Definition 7.

We can define a q-RPULS $C_{HT}$ on an ordinary fixed set X:

$$C_{HT}=\{<x,[s_{\varphi (x)},s_{\psi (x)}],(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))]>|x\in X\}$$

(7)

Here, the terms $s_{\varphi (x)},s_{\psi (x)}$ belong to S and $s_{\varphi (x)},s_{\psi (x)}$ represents the linguistic term interval in S. The triplet $u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)$ represents the positive, neutral, and negative ratings of the element x in the q-RPULS. These membership degrees satisfy the conditions that $0\le (u_{C_{HT}}{(x)}^q+{\eta }_{C_{HT}}{(x)}^q+v_{C_{HT}}{(x)}^q)\le 1$ and $u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x)\in [0,1]$ are within the range [0, 1]. For convenience, we can refer to the notation $<[s_{\varphi (x)},s_{\psi (x)}],(u_{C_{HT}}(x),{\eta }_{C_{HT}}(x),v_{C_{HT}}(x))>$ as the q-RPULS. To simplify the notation further, we may write it as $<[s_{\varphi },s_{\psi }],(u,\eta ,v)>$.

Definition 8.

Let $a_1=<[s_{{\varphi }_1},s_{{\psi }_1}],(u_1,{\eta }_1,v_1)>$ and $a_2=<[s_{{\varphi }_2},s_{{\psi }_2}],(u_2,{\eta }_2,v_2)>$ be two q-RPULSs, and consider a positive real number m, where in several fundamental operations:

1. 

${\alpha }_1\oplus {\alpha }_2$ = $<[s_{{\varphi }_1+{\varphi }_2},s_{{\psi }_1+{\psi }_2}],({(u_1^q+u_2^q-u_1^q{u}_2^q)}^{\frac{1}{q}},{\eta }_1{\eta }_2,v_1{v}_2)>$;

2. 

${\alpha }_1\otimes {\alpha }_2$= $<[s_{{\varphi }_1{\varphi }_2},s_{{\psi }_1{\psi }_2}],(u_1{u}_2,{({\eta }_1^q+{\eta }_2^q-{\eta }_1^q{\eta }_2^q)}^{\frac{1}{q}},{(v_1^q+v_2^q-v_1^q{v}_2^q)}^{\frac{1}{q}})>$;

3. 

$m{\alpha }_1=<[s_{m{\varphi }_1},s_{m{\psi }_1}],({(1-{(1-u_1^q)}^m)}^{\frac{1}{q}},{\eta }_1^m,v_1^m)>$;

4. 

${\alpha }_1^m=<[s_{{\varphi }_1^m},s_{{\psi }_1^m}],(u_1^m,{(1-{(1-{\eta }_1^q)}^m)}^{\frac{1}{q}},{(1-{(1-v_1^q)}^m)}^{\frac{1}{q}})>$.

By utilizing Definition 8 as a foundation, we can obtain the following rules.

Theorem 1.

Let ${\Gamma }_1=<[s_{{\varphi }_1},s_{{\psi }_1}],(u_1,{\eta }_1,v_1)>$ and ${\Gamma }_2=<[s_{{\varphi }_2},s_{{\psi }_2}],(u_2,{\eta }_2,v_2)>$ be two q-RPULSs, and $\lambda ,{\lambda }_1,{\lambda }_2>0$; then:

1. 

${\Gamma }_1\oplus {\Gamma }_2={\Gamma }_2\oplus {\Gamma }_1$;

2. 

${\Gamma }_1\otimes {\Gamma }_2={\Gamma }_2\otimes {\Gamma }_1$;

3. 

$\lambda ({\Gamma }_1\oplus {\Gamma }_2)=\lambda {\Gamma }_1\oplus \lambda {\Gamma }_2$

4. 

${({\Gamma }_1\otimes {\Gamma }_2)}^{\lambda }={\Gamma }_1^{\lambda }\otimes {\Gamma }_2^{\lambda }$

5. 

${\lambda }_1\Gamma \oplus {\lambda }_2\Gamma =({\lambda }_1+{\lambda }_2)\Gamma$

6. 

${\Gamma }^{{\lambda }_1}\otimes {\Gamma }^{{\lambda }_2}={\Gamma }^{({\lambda }_1+{\lambda }_2)}$

7. 

${({\Gamma }^{{\lambda }_1})}^{{\lambda }_2}={\Gamma }^{{\lambda }_1{\lambda }_2}$

Definition 9.

Consider a q-RPULS denoted as $\Gamma =<[s_{\varphi },s_{\psi }],(u,\eta ,v)>$. Let us introduce a score function $S(\Gamma )$ and an exact function $A(\Gamma )$ defined with respect to Γ.

$$S(\Gamma )=\frac{\varphi +\psi }{4}\frac{(u^q+1-{\eta }^q-v^q)}{3}$$

(8)

$$A(\Gamma )=\frac{\varphi +\psi }{2}(u^q+{\eta }^q+v^q)$$

(9)

The comparative law for q-RPULSs is as follows:

Definition 10

([35]). Let ${\Gamma }_1=<[s_{{\varphi }_1},s_{{\psi }_1}],(u_1,{\eta }_1,v_1)>$ and ${\Gamma }_2=<[s_{{\varphi }_2},s_{{\psi }_2}],(u_2,{\eta }_2,v_2)>$ be two q-RPULSs; then:

• If $({\Gamma }_1)<S({\Gamma }_2)$, then ${\Gamma }_1<{\Gamma }_2$;
• If $({\Gamma }_1)>S({\Gamma }_2)$, then ${\Gamma }_1>{\Gamma }_2$;
• If $({\Gamma }_1)=S({\Gamma }_2)$, then

  1. 

  If $A({\Gamma }_1)<A({\Gamma }_2)$, then ${\Gamma }_1<{\Gamma }_2$;

  2. 

  If $A({\Gamma }_1)>A({\Gamma }_2)$, then ${\Gamma }_1>{\Gamma }_2$;

  3. 

  If $A({\Gamma }_1)=A({\Gamma }_2)$, then ${\Gamma }_1={\Gamma }_2$.

Definition 11

([36]). Let ${\Gamma }_1=<[s_{{\varphi }_1},s_{{\psi }_1}],(u_1,{\eta }_1,v_1)>$ and ${\Gamma }_2=<[s_{{\varphi }_2},s_{{\psi }_2}],(u_2,{\eta }_2,v_2)>$ be two q-RPULSs, and $q\ge 1$; then, the q-RPUL distance measure between them is defined as:

$$\begin{array}{c}\hfill d({\Gamma }_1,{\Gamma }_2)=\frac{1}{4(t-1)}(|u_1^q{\varphi }_1-u_2^q{\varphi }_2|+|{\eta }_1^q{\varphi }_1-{\eta }_2^q{\varphi }_2|+|v_1^q{\varphi }_1-v_2^q{\varphi }_2|+|{\pi }_1^q{\varphi }_1-{\pi }_2^q{\varphi }_2|\\ \hfill +|u_1^q{\psi }_1-u_2^q{\psi }_2|+|{\eta }_1^q{\psi }_1-{\eta }_2^q{\psi }_2|+|v_1^q{\psi }_1-v_2^q{\psi }_2|+|{\pi }_1^q{\psi }_1-{\pi }_2^q{\psi }_2|).\end{array}$$

(10)

Definition 12

([37,38]). Suppose we have a collection of crisp numbers represented as ${\xi }_i$ (where i = 1, 2, …, n), then the $MS{M}^{(k)}$ operator is the following:

$$MS{M}^{(k)}={(\frac{\begin{array}{c}{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\xi }_{i_j}\end{array}}{C_n^k})}^{\frac{1}{k}}$$

(11)

In the given context, where k is a parameter with a range of values 1, 2, …, n, and i = 1, 2, …, n, the notation $C_n^k=\frac{n!}{k!(n-k)!}$.

Theorem 2.

The significant features of $MS{M}^{(k)}$ are as follows:

1. 

Idempotency. If ${\sigma }_i(i=1,2,\dots ,n)$ = σ for all i, then $MS{M}^{(k)}=(\sigma ,\sigma ,\dots ,\sigma )=\sigma$;

2. 

Monotonicity. If ${\sigma }_i\le {\zeta }_i$ for all i, then $MS{M}^{(k)}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)\le MS{M}^{(k)}({\zeta }_1,{\zeta }_2,\dots ,{\zeta }_n)$;

3. 

Boundedness. $min({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)\le MS{M}^{(k)}({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)\le max({\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n)$.

3. The q-Rung Picture Uncertain Linguistic Set Aggregation Operators

3.1. The q-Rung Picture Uncertain Linguistic Set Aggregation Maclaurin Symmetric Mean Operators

We will discuss the development of fuzzy arithmetic aggregation operators using the concept of q-rung picture uncertain linguistic sets in this section. Some examples of these operators include the q-RPULMSM operator and the q-RPULWMSM operator.

Definition 13.

Let $h_l=<[s_{{\varphi }_l},s_{{\psi }_l}],(u_l,{\eta }_l,v_l)>$ be the set of q-RPULSs, then the q-RPULMSM operator is defined as:

$$q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)={(\frac{{⨁}_{1\le l_1<\dots <l_k\le n}{⨂}_{j=1}^k{h}_{l_j}}{C_n^k})}^{\frac{1}{k}}.$$

(12)

By applying the computational laws of q-RPULN, we can derive the subsequent results for the q-RPULMSM operator:

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)& =<[s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\varphi }_{l_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\psi }_{l_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k{u}_{l_j}^q)}^{\frac{1}{C_n^k}})}^{\frac{1}{qk}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-v_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}}).\hfill \end{array}$$

(13)

Proof. 

Based on the above definition, we can derive

$$\underset{j=1}{\overset{k}{⨂}}{h}_{l_j}=<[s_{{\prod }_{j=1}^k{\varphi }_{l_j}},s_{{\prod }_{j=1}^k{\psi }_{l_j}}],(\prod _{j=1}^k{u}_{l_j},{(1-\prod _{j=1}^k(1-{\eta }_{l_j}))}^{\frac{1}{q}},{(1-\prod _{j=1}^k(1-v_{l_j}))}^{\frac{1}{q}})>.$$

(14)

Furthermore,

$$\begin{array}{cc}\hfill \underset{1\le l_1<\dots <l_k\le n}{⨁}\underset{j=1}{\overset{k}{⨂}}{h}_{l_j}& =<[s_{{({\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\varphi }_{l_j})}^{\frac{1}{k}}},s_{{({\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\psi }_{l_j})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le l_1<\dots <l_k\le n}(1-\prod _{j=1}^k{u}_{l_j}^q))}^{\frac{1}{q}},\hfill \\ \hfill & \prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{l_j}^q))}^{\frac{1}{q}},\hfill \\ \hfill & \prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-v_{l_j}^q))}^{\frac{1}{q}})>.\hfill \end{array}$$

(15)

Thus,

$$\begin{array}{cc}\hfill \frac{{⨁}_{1\le l_1<\dots <l_k\le n}{⨂}_{j=1}^k{h}_{l_j}}{C_n^k}& =<[s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\varphi }_{l_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\psi }_{l_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k{u}_{l_j}^q)}^{\frac{1}{C_n^k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-v_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{q}})>.\hfill \end{array}$$

(16)

Therefore,

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)& =<[s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\varphi }_{l_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le l_1<\dots <l_k\le n}{\prod }_{j=1}^k{\psi }_{l_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k{u}_{l_j}^q)}^{\frac{1}{C_n^k}})}^{\frac{1}{qk}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le l_1<\dots <l_k\le n}{(1-\prod _{j=1}^k(1-v_{l_j}^q))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}}).\hfill \end{array}$$

(17)

□

Theorem 3.

This theorem establishes that, if $h_l$ = <[$s_{\varphi l}$, $s_{\psi l}$], ($u_l$, ${\eta }_l$, $v_l$)> (l = 1, 2, …, n) represents a set of q-RPULNs, then the $q-RPULMS{M}^{(k)}$ operator possesses the following rules:

1. 

Idempotency. If all $h_l=h=<[s_{\varphi },s_{\psi }],(u,\eta ,v)>$ are equal for all l, then $q-RPULMS{M}^{(k)}$ = $(h,h,\dots ,h)=h$.

2. 

Monotonicity. Let $h_l=<[s_{{\varphi }_l},s_{{\psi }_l}],(u_l,{\eta }_l,v_l)>$ and $g_j=<[s_{{\varphi }_j},s_{{\psi }_j}],(u_j,{\eta }_j,v_j)>(l,j=1,2,\dots ,n)$ be two sets of q-RPULSs; if $s_{{\varphi }_l}\le s_{{\varphi }_j},s_{{\psi }_l}\ge s_{{\psi }_j},u_i\le u_j,{\eta }_l\ge {\eta }_j,v_l\ge v_j$, then

$q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)\le q-RPULMS{M}^{(k)}(g_1,g_2,\dots ,g_n)$.

3. 

Boundedness. Let $h_i=<[s_{{\varphi }_i},s_{{\psi }_i}],(u_i,{\eta }_i,v_i)>(i=1,2,\dots ,n)$ be a set of q-RPULNs and

$h^{+}=([max(s_{{\varphi }_i}),min(s_{{\psi }_i})],max(u_i),min({\eta }_i),min(v_i))$,

$h^{-}=([min(s_{{\varphi }_i}),max(s_{{\psi }_i})],min(u_i),max({\eta }_i),max(v_i))$; then,

$h^{-}\le q-RPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n)\le h^{+}$.

4. 

Permutation Invariance. Let $h_i$ be a permutation of $h_i^{*}$ for all i; therefore,

$q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)=q-RPULMS{M}^{(k)}(h_1^{*},h_2^{*},\dots ,h_n^{*})$

Proof 1. Let $h_l=h$ for each i; then,

$$\begin{gathered} q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)={(\frac{{⨁}_{1\le l_1<\dots <l_k\le n}{⨂}_{j=1}^k{h}_{l_j}}{C_n^k})}^{\frac{1}{k}}={(\frac{{⨁}_{1\le l_1<\dots <l_k\le n}{⨂}_{j=1}^{k}h}{C_n^k})}^{\frac{1}{k}}= \\ {(\frac{{⨁}_{1\le l_1<\dots <l_k\le n}{h}^k}{C_n^k})}^{\frac{1}{k}}=(\frac{{⨁}_{1\le l_1<\dots <l_k\le n}h}{C_n^k})=h \end{gathered}$$

Proof 2. Consider $u_l\le u_j$; we can obtain ${\prod }_{m=1}^k{u}_{l_m}^q\le {\prod }_{m=1}^k{u}_{j_m}^q$; then, $1-{\prod }_{m=1}^k{u}_{l_m}^q\ge 1-{\prod }_{m=1}^k{u}_{j_m}^q$; therefore’ $1-{\prod }_{1\le l_1<\dots <l_k\le n}{(1-{\prod }_{m=1}^k{u}_{l_m}^q)}^{\frac{1}{C_n^k}}{{)}^{\frac{1}{qk}}\le 1-{\prod }_{1\le l_1<\dots <l_k\le n}{(1-{\prod }_{m=1}^k{u}_{j_m}^q)}^{\frac{1}{C_n^k}})}^{\frac{1}{qk}}$. ${\eta }_l\ge {\eta }_j$, $v_l\ge v_j$ are similar to $u_l\le u_j$, so we omit them. Therefore, $q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)\le q-RPULMS{M}^{(k)}(g_1,g_2,\dots ,g_n)$

Proof 3. From proof 1, 2, we have

$h^{-}=q-RPULMS{M}^{(k)}(h^{-},h^{-},\dots ,h^{-})\le q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)$,

$q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)\le q-RPULMS{M}^{(k)}(h^{+},h^{+},\dots ,h^{+})$; then,

$h^{-}\le q-RPULMS{M}^{(k)}(h_1,h_2,\dots ,h_n)\le h^{+}$. Moreover, we will delve into specific instances of the q-RPULMSM operator by considering various parameter values assigned to k and q.

Case 1: When k = 1, the q-RPULMSM operator simplifies to the q-RPULA operator.

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n)& =<[s_{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\varphi }_{i_j}}{n})},s_{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\psi }_{i_j}}{n})}],\hfill \\ \hfill & ({(1-\prod _{1\le i_1\le n}{(1-\prod _{j=1}^1{u}_{i_j}^q)}^{\frac{1}{C_n^1}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1\le n}{(1-\prod _{j=1}^1(1-{\eta }_{i_j}^q))}^{\frac{1}{C_n^1}})}^{\frac{1}{1}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1\le n}{(1-\prod _{j=1}^1(1-v_{i_j}^q))}^{\frac{1}{C_n^1}})}^{\frac{1}{1}})}^{\frac{1}{q}})>\hfill \\ \hfill & =q-RPULA(a_1,a_2,\dots ,a_n).\hfill \end{array}$$

(18)

Case 2: When k = 2, the q-RPULMSM operator transforms into the q-RPULBM operator.

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n)& ={(\frac{{\sum }_{1\le i_1<i_2\le n{\prod }_{j=1}^2{a}_{i_j}}}{C_n^2})}^{\frac{1}{2}}={(\frac{2{\sum }_{1\le i_1<i_2\le n{\prod }_{j=1}^2{a}_{i_1}{a}_{i_2}}}{n(n-1)})}^{\frac{1}{2}}\hfill \\ \hfill & ={(\frac{{\sum }_{i,j=1,i\ne j{a}_{i_1}{a}_{i_2}}}{n(n-1)})}^{\frac{1}{2}}=q-RPULB{M}^{1,1}(a_1,a_2,\dots ,a_n).\hfill \end{array}$$

(19)

Case 3: When q = 1, the q-RPULMSM operator simplifies to the PULMSM operator.

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n)& =<[s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\varphi }_{i_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\psi }_{i_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k{u}_{i_j})}^{\frac{1}{C_n^k}})}^{\frac{1}{k}},\hfill \\ \hfill & (1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{i_j}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}}),\hfill \\ \hfill & (1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-v_{i_j}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}}))>\hfill \\ \hfill & =PULMS{M}^{(k)}(a_1,a_2,\dots ,a_n).\hfill \end{array}$$

(20)

Case 4: When q = 2, the q-RPULMSM operator can be simplified to the SPULMSM operator.

$$\begin{array}{cc}\hfill q-RPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n)& =<[s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\varphi }_{i_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{\psi }_{i_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k{u}_{i_j}^2)}^{\frac{1}{C_n^k}})}^{\frac{1}{2k}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{i_j}^2))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{2}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-v_{i_j}^2))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{2}})>\hfill \\ \hfill & =SPULMS{M}^{(k)}(a_1,a_2,\dots ,a_n).\hfill \end{array}$$

(21)

Definition 14.

Let $a_i=<[s_{{\varphi }_i},s_{{\psi }_i}],(u_i,{\eta }_i,v_i)>$ be the set of q-RPULSs; $w={(w_1,w_2,\dots ,w_n)}^T$ is a weight vector and satisfies $w_i\in [0,1]$ and ${\sum }_{i=1}^n=1,wherek=1,2,\dots ,n;$ then, the q-RPULWMSM operator is defined as:

$$q-RPULWMS{M}^{(k)}(a_1,a_2,\dots ,a_n)={(\frac{{⨁}_{1\le i_1<\dots <i_k\le n}{⨂}_{j=1}^k{w}_{i_j}{a}_{i_j}}{C_n^k})}^{\frac{1}{k}}.$$

(22)

We can deduce the following outcomes for the q-RPULWMSM operator by utilizing the computational laws of q-RPULN:

$$\begin{array}{cc}\hfill q-RPFWMS{M}^{(k)}(a_1,a_2,\dots ,a_n)& =<[s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{w}_{i_j}{\varphi }_{i_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{w}_{i_j}{\psi }_{i_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{(1-u_{i_j}^q)}^{w_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{qk}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{i_j}^{q{w}_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-v_{i_j}^{q{w}_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}})>.\hfill \end{array}$$

(23)

Theorem 4.

Let $h_i=<[s_{{\varphi }_i},s_{{\psi }_i}],(u_i,{\eta }_i,v_i)>$ be the set of q-RPULSs; then, the following properties of $q-RPULWMS{M}^{(k)}$ are obtained:

1. 

Idempotency. If all $h_i=h=<[s_{\varphi },s_{\psi }],(u,\eta ,v)>$ are equal for all i, then $q-RPULWMS{M}^{(k)}$ = $(h,h,\dots ,h)=h$;

2. 

Monotonicity. Let $h_i=<[s_{{\varphi }_i},s_{{\psi }_i}],(u_i,{\eta }_i,v_i)>$ and $g_j=<[s_{{\varphi }_j},s_{{\psi }_j}],(u_j,{\eta }_j,v_j)>(i,j=1,2,\dots ,n)$ be two sets of q-RPULSs; if $s_{{\varphi }_i}\le s_{{\varphi }_j},s_{{\psi }_i}\ge s_{{\psi }_j},u_i\le u_j,{\eta }_i\ge {\eta }_j,v_i\ge v_j$, then

$q-RPULWMS{M}^{(k)}(h_1,h_2,\dots ,h_n)\le q-RPULWMS{M}^{(k)}(g_1,g_2,\dots ,g_n)$;

3. 

Boundedness. Let $h_i=<[s_{{\varphi }_i},s_{{\psi }_i}],(u_i,{\eta }_i,v_i)>(i=1,2,\dots ,n)$ be a set of q-RPULNs and

$h^{+}=([max(s_{{\varphi }_i}),min(s_{{\psi }_i})],max(u_i),min({\eta }_i),min(v_i))$,

$h^{-}=([min(s_{{\varphi }_i}),max(s_{{\psi }_i})],min(u_i),max({\eta }_i),max(v_i))$; then,

$h^{-}\le q-RPULWMS{M}^{(k)}(a_1,a_2,\dots ,a_n)\le h^{+}$.

4. 

Commutativity. Let $h_i$ be a permutation of $h_i^{*}$ for all i; therefore,

$q-RPULWMS{M}^{(k)}(h_1,h_2,\dots ,h_n)=q-RPULWMS{M}^{(k)}(h_1^{*},h_2^{*},\dots ,h_n^{*})$

The proof for the q-RPFWMSM theorem follows a similar approach to that of Theorem 3; thus, it has been excluded in this context.

3.2. A Method to Determine the Attribute Weights Based on Entropy

Definition 15.

Let q-RPULSs(X) denote the set of all q-RPULSs in the universe of discourse X. Let $a_1=<[s_{{\varphi }_1},s_{{\psi }_1}],(u_1,{\eta }_1,v_1)>$ and $a_2=<[s_{{\varphi }_2},s_{{\psi }_2}],(u_2,{\eta }_2,v_2)>$ be two q-RPULSs. Here are a few more properties that an entropy function G must satisfy on q-RPULSs:

1. 

G($a_1$) = 0, if and only if $a_1$ is a crisp set;

2. 

G($a_1$) = 1 if and only if $s_{{\varphi }_1}=s_{{\psi }_1}$, $u_1={\eta }_1=v_1$;

3. 

G($a_1$) ≤ G($a_2$), if and only if $u_1\le u_2$, ${\eta }_1\ge {\eta }_2$ and $v_1\ge v_2$;

4. 

G($a_1$) = G($a_1^c$).

Based on the given axiom, we will now introduce a measure of entropy for q-RPULSs. Let $a=<[s_{\varphi },s_{\psi }],(u,\eta ,v)>$ be a q-RPULFN; then, the entropy measure of a is defined as

$$G(a)=1-d(a,a^c)$$

(24)

where d(a,$a^c$) is distance measure.

Using the entropy measure for q-RPULSs, we propose a novel approach to ascertain the weights of aggregated q-RPULSs. Let $a_i(i=1,2,\dots ,n)$ be a collection of q-RPULSs; then, the weight of $a_i$ is given as

$${\lambda }_i=\frac{1-E(a_i)}{n-{\sum }_{i=1}^{n}E(a_i)}$$

(25)

4. MAGDM Methods Based on q-RPULMSM Operator

This section presents techniques for solving the MAGDM problem using the q-RPULWMSM operator. For MAGDM questions, let $H=H_1,H_2$,…,$H_n$ be an attribute collection; $W=w_1,w_2$,…,$w_n$ is a vector of weights for attribute $L_j(j=1,2,\dots ,n)$, where $w_j\ge 0$, ${\sum }_{j=1}^n{w}_j=1$. Suppose that $H^e={[a_{ij}^e]}_{m\times n}$ is the decision matrix and that the decision maker is required to represent his/her evaluation value using a q-RPULN, which can be expressed as $a_{ij}^e=<[s_{{\varphi }_{ij}^e},s_{{\psi }_{ij}^e}],(u_{ij}^e,{\eta }_{ij}^e,v_{ij}^e)>$. The main steps in using the proposed operator for the MAGDM problem are as follows:

Step 1: To normalize the original decision matrix, we can utilize two attributes: a benefit attribute and a cost attribute. The normalization process follows the steps outlined below:

$$a_{ij}^e=<[s_{{\varphi }_{ij}^e},s_{{\psi }_{ij}^e}],(u_{ij}^e,{\eta }_{ij}^e,v_{ij}^e)>=\left\{\begin{array}{c}<[s_{{\varphi }_{ij}^e},s_{{\psi }_{ij}^e}],(u_{ij}^e,{\eta }_{ij}^e,v_{ij}^e)>,G_j\in J_1\\ <[s_{{\varphi }_{ij}^e},s_{{\psi }_{ij}^e}],(v_{ij}^e,{\eta }_{ij}^e,u_{ij}^e)>,G_j\in J_2\end{array}\right\}$$

(26)

where $J_1$ and $J_2$ denote benefit-type attributes and cost-type attributes, respectively.

Step 2: Compute the Sup($a_{il},a_{im}$) by

$$Sup(a_{il},a_{im})=1-d(a_{il},a_{im}),$$

(27)

where Sup($a_{il},a_{im}$) symbolize support values for $a_{il}$ from $a_{im},l,m=1,2,\dots ,n;$$l\ne m$.

Step 3: Compute $Q(a_{ij})$ by

$$Q(a_{ij})=\sum _{l,m=1,l\ne m}^{n}Sup(a_{il},a_{im}),$$

(28)

Step 4: Compute the weight of $L_j(j=1,2,\dots ,n)$ based on the entropy measure; the result is below:

$${\lambda }_i=\frac{1-G(a_i)}{n-{\sum }_{i=1}^{n}G(a_i)}$$

(29)

Step 5: Compute the power weights $w_{ij}$ using the below method.

$$w_{ij}=\frac{{\lambda }_i(1+Q(a_{ij}))}{{\sum }_{i=1}^n{\lambda }_i(1+Q(a_{ij}))},$$

(30)

Step 6: Aggregate all attribute values $a_{ij}(j=1,2,\dots ,n)$ using the q-RPULWMSM operator to obtain a composite value $a_i$.

$$\begin{array}{cc}\hfill a_i=q-RPULWMS{M}^{(k)}(a_{i1},a_{i2},\dots ,a_{in})& =<[s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{w}_{i_j}{\varphi }_{i_j}}{C_n^k})}^{\frac{1}{k}}},s_{{(\frac{{\sum }_{1\le i_1<\dots <i_k\le n}{\prod }_{j=1}^k{w}_{i_j}{\psi }_{i_j}}{C_n^k})}^{\frac{1}{k}}}],\hfill \\ \hfill & ({(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{(1-u_{i_j}^q)}^{w_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{qk}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-{\eta }_{i_j}^{q{w}_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}},\hfill \\ \hfill & {(1-{(1-\prod _{1\le i_1<\dots <i_k\le n}{(1-\prod _{j=1}^k(1-v_{i_j}^{q{w}_{i_j}}))}^{\frac{1}{C_n^k}})}^{\frac{1}{k}})}^{\frac{1}{q}})>.\hfill \end{array}$$

(31)

where w is a vector of weights for the attribute.

Step 7: Use the value of the score function $S(a_i)$ calculated in Equation (7).

Step 8: By utilizing the sequence of the overall values to arrange alternatives, select the optimal one.

5. Numerical Example and Comparative Analysis

5.1. Evaluation Steps for the q-RPULWMSM Operator

This example is adopted from He and Zhang [39]. To verify the validity of this method, an example is used for calculation, comparison, and analysis. The annual “618” e-commerce shopping festival is the day of national consumers and the e-commerce platform of the carnival; the major e-commerce platforms launch the most favorable activities of the year. In this context, a college student plans to go to Taobao Mall to buy computers, for example, after the initial screening, but is still indecisive about four computers; respectively, $A_1$ is an Asus computer, $A_2$ is a Lenovo computer, $A_3$ is a Dell computer, and $A_4$ is an Apple computer. The student developed four selection indicators based on his preferences: $C_1$ is price; $C_2$ is range; $C_3$ is chip processing power; and $C_4$ is RAM. Each decision maker is asked to evaluate the four items in terms of the four attributes using q-RPULNs. Therefore, the decision matrix $A^e={[a_{ij}^e]}_{m\times n}$ follows from

Table 2. The q-RPULSs decision matrix.

	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$
$A_1$	<[s${}_5$, $s_5$], (0.5, 0.4, 0.1)>	<[s${}_2$, $s_3$], (0.8, 0.1, 0.1)>	<[s${}_5$, $s_6$], (0.4, 0.3, 0.2)>	<[s${}_3$, $s_4$], (0.1, 0.8, 0.1)>
$A_2$	<[s${}_4$, $s_5$], (0.7, 0.1, 0.1)>	<[s${}_5$, $s_5$], (0.1, 0.7, 0.2)>	<[s${}_3$, $s_4$], (0.1, 0.7, 0.2)>	<[s${}_4$, $s_4$], (0.7, 0.1, 0.1)>
$A_3$	<[s${}_3$, $s_4$], (0.8, 0.1, 0.1)>	<[s${}_4$, $s_4$], (0.1, 0.8, 0.1)>	<[s${}_4$, $s_5$], (0.1, 0.8, 0.1)>	<[s${}_4$, $s_5$], (0.6, 0.2, 0.1)>
$A_4$	<[s${}_6$, $s_6$], (0.7, 0.1, 0.1)>	<[s${}_2$, $s_3$], (0.7, 0.2, 0.1)>	<[s${}_3$, $s_4$], (0.1, 0.7, 0.1)>	<[s${}_3$, $s_3$], (0.1, 0.8, 0.1)>

:

Step 1: Since all attributes are benefit attributes, normalization is not required.

Step 2: Calculate the Sup($a_{il},a_{im}$) (l, m = 1, 2, 3, 4; i = 1, 2, 3, 4; $l\ne m$). Let q = 3. Therefore, the result of calculation is as follows.

$$\begin{gathered} S^{12}=S^{21}=(0.6826,0.6990,0.6604,0.7064); \\ {S}^{13}=S^{31}=(0.8839,0.7136,0.6188,0.5928); \\ {S}^{14}=S^{41}=(0.6297,0.9584,0.7794,0.4954); \\ {S}^{23}=S^{32}=(0.5951,0.8751,0.9584,0.7745); \\ {S}^{24}=S^{42}=(0.7040,0.6888,0.6224,0.7754); \\ {S}^{34}=S^{43}=(0.5591,0.7550,0.6214,0.9026). \end{gathered}$$

Step 3: According to Equation (28), calculate $Q(a_{ij})$; the result is below.

$$Q=\left[\begin{array}{cccc}2.1962& 2.3710& 2.0586& 1.7946\\ 1.9817& 2.2629& 2.2412& 2.2563\\ 2.0381& 2.3437& 2.1986& 2.2699\\ 1.8910& 2.4022& 2.0232& 2.1734\end{array}\right]$$

Step 4: Calculate the weght of $L_j(j=1,2,\dots ,n)$ based on the entropy measure of q-RPULSs as the following formula:

According to Equation (24), we seek the entropy measure as follows:

$$G(a_{ij})=\left[\begin{array}{cccc}0.8967& 0.7871& 0.9487& 1.0000\\ 0.7435& 0.9942& 0.9959& 0.7720\\ 0.7019& 1.0000& 1.0000& 0.8387\\ 0.6580& 0.8575& 1.0000& 1.0000\end{array}\right]$$

According to Equation (29), calculate the weight based on the entropy measure; the result is the following:

$${\lambda }_{ij}=\left[\begin{array}{cccc}0.2811& 0.5793& 0.1396& 0.0000\\ 0.5188& 0.0117& 0.0083& 0.4612\\ 0.6489& 0.0000& 0.0000& 0.3511\\ 0.7059& 0.2941& 0.0000& 0.0000\end{array}\right]$$

Step 5: Calculate the power weights $w_{ij}$, q = 3 and k = 2; the result is the following:

$$w_{ij}=\left[\begin{array}{cccc}0.2741& 0.5957& 0.1302& 0.0000\\ 0.4968& 0.0123& 0.0086& 0.4823\\ 0.6319& 0.0000& 0.0000& 0.3680\\ 0.6710& 0.3289& 0.0000& 0.0000\end{array}\right]$$

Step 6: Aggregate all attribute values $a_{ij}(j=1,2,\dots ,n)$ using Equation (31) to obtain a composite value $a_i$; the result is the following:

$$\begin{gathered} a_1=<[s_{2.5693},s_{3.1356}],(0.3240,0.0271,0.0070)>, \\ {a}_2=<\left[s_{2.8837},s_{3.2217}\right],(0.2540,0.0202,0.0051)>, \\ {a}_3=<\left[s_{2.3624},s_{3.0498}\right],(0.2610,0.0000,0.0000)>, \\ {a}_4=<\left[s_{2.3014},s_{2.8187}\right],(0.3040,0.0000,0.0000)>. \end{gathered}$$

Step 7: Use the value of the score function $S(a_i)$ calculated in Equation (8). The result is the following:

$$S(a_1)=0.4916,S(a_2)=0.5171,S(a_3)=0.4590,S(a_4)=0.4387.$$

Step 8: Rank the four alternative options.

$$A_2>A_1>A_3>A_4$$

.

Therefore, Lenovo computers $A_2$ best fit that college student’s choices.

5.2. Comparative Analysis and Discussion

We compare our proposed method with other methods in this section. These methods consist of the TSULWA operator introduced by Wang et al. [36], the T-SFWGMSM operator proposed by Liu et al. [40], and the q-RPFDHM operator presented by He et al. [41]. The comparison results are available in

Table 3. Compared with other methods.

Methods	Score Values	Ranking
q-RPULWMSM	$S(a_1)$ = 0.4916, $S(a_2)$ = 0.5171, $S(a_3)$ = 0.4590, $S(a_4)$ = 0.4387.	$A_2>A_1>A_3>A_4$
TSULWA [36]	$S(a_1)$ = 0.4416, $S(a_2)$ = 0.4671, $S(a_3)$ = 0.4590, $S(a_4)$ = 0.4364.	$A_2>A_3>A_1>A_4$
T-SFWGMSM [40]	$S(a_1)$ = 0.4334, $S(a_2)$ = 0.4571, $S(a_3)$ = 0.4532, $S(a_4)$ = 0.4236.	$A_2>A_3>A_1>A_4$
q-RPFDWHM [41]	$S(a_1)$ = 0.4853, $S(a_2)$ = 0.4951, $S(a_3)$ = 0.4590, $S(a_4)$ = 0.4596.	$A_2>A_1>A_4>A_3$

.

By examining the table, we can observe that the most favorable alternative among all the methods is represented by $A_2$. This outcome serves as evidence to support the validity and practicality of the method introduced. Moreover, the ranking outcomes presented in this study diverge from other methods such as [36,40,41], primarily due to the limitations of these methods. These previous methods only account for the interaction between two parameters and overlook the correlation between multiple parameters. Operators such as q-RPULWMSM have the following characteristics:

• Q-rung picture uncertain linguistic sets (q-RPULSs) incorporate qualitative and quantitative aspects of decision-making, while also utilizing linguistic terms that are easily comprehensible and relatable to people’s perception.
• The MSM operator provides a powerful tool to account for the interdependence of multiple input parameters, resulting in the improved accuracy and reliability of evaluation results.
• A novel solution is put forward for the issue of MAGDM with unknown attribute weights.

The parameter q is a key factor in determining the final rankings of alternative goods. To evaluate the influence of the parameter q on the experimental outcomes, we conducted the aforementioned example using different values of q (starting from k = 2). The resulting rankings for various q values are depicted in Figure 1.

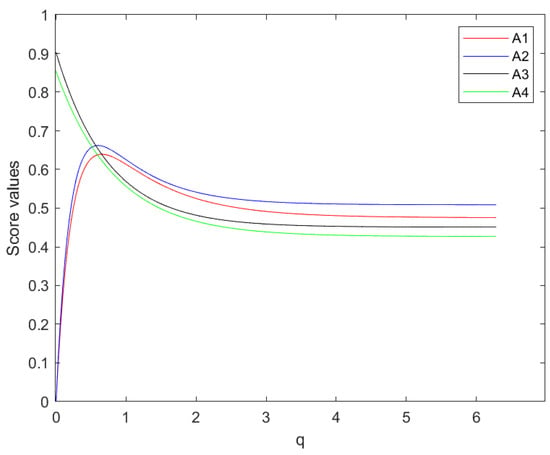
Figure 1 illustrates that employing the q-RPULWMSM operator yields distinct scores for different q values. However, despite the variability in scores, the final outcome consistently favors alternative $A_2$. In practical decision-making scenarios, selecting an optimal q value depends on the decision maker’s personal preferences and judgment. The q value in the q-RPULWMSM operator allows the decision maker to customize the weighting of attributes and their interactions according to their individual priorities and the specific context of the decision. This flexibility empowers the decision maker to adjust the level of significance assigned to the relationship between attributes and fine-tune the evaluation process to better reflect their preferences and requirements. By having the freedom to choose the q value, the decision maker can tailor the decision model to their unique needs, resulting in more effective and personalized decision outcomes. Through thorough analysis, it is evident that the method introduced in this paper exhibits remarkable adaptability and effectiveness when compared to existing problem-solving approaches.

6. Conclusions

This paper introduces a new approach to address the MAGDM problem. It combines the q-RPULSs method with the MSM operator, resulting in the q-RPULMSM operator. This operator not only considers qualitative and quantitative decision-making but also captures comprehensive information, avoids information loss, and considers the neutrality of the decision maker and the interrelationships among multiple attributes. To handle the issue of unknown attribute weights, the entropy measure is employed. Consequently, we propose a comprehensive approach to solve the MAGDM problem, and provide a numerical example to demonstrate its superiority and accuracy.

While our proposed method has several advantages over existing approaches, it also has limitations. One drawback is its reliance on limited decision-maker data. In real-world scenarios, there may be more attributes involved, requiring the use of multiple methods and metrics for evaluation. Therefore, future research will focus on integrating complex decision-making problems with big data to overcome these limitations.