On Fractional Ostrowski-Mercer-Type Inequalities and Applications

Abstract

The objective of this research is to study in detail the fractional variants of Ostrowski–Mercer-type inequalities, specifically for the first and second order differentiable s-convex mappings of the second sense. To obtain the main outcomes of the paper, we leverage the use of conformable fractional integral operators. We also check the numerical validations of the main results. Our findings are also validated through visual representations. Furthermore, we provide a detailed discussion on applications of the obtained results related to special means, q-digamma mappings, and modified Bessel mappings.

1. Introduction

In 1937, Alexandar Markowich Ostrowski [1] discovered an integral inequality known as the Ostrowski inequality, stated as:

Let $\psi :\mathcal{I}=[\mu ,\kappa ]\subseteq \mathbb{R}\to \mathbb{R}$ (Real numbers) be a differentiable mapping on the interior of $\mathcal{I}$ such that $\psi$ is integrable on $[\mu ,\kappa ]$, where $\mu ,\kappa \in \mathcal{I}$ with $\mu <\kappa$. If $\left|{\psi }^{\prime }\left(\lambda \right)\right|\le M$ for all $\lambda \in (\mu ,\kappa )$ and $M>0$, then

$$\begin{array}{c}\hfill \left|\psi (\mathit{\ell })-\frac{1}{\kappa -\mu }\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\le M\left(\kappa -\mu \right)\left[\frac{1}{4}+\frac{{\left(\mathit{\ell }-\frac{\mu +\kappa }{2}\right)}^2}{{\left(\kappa -\mu \right)}^2}\right],\end{array}$$

holds for all $\mathit{\ell }\in [\mu ,\kappa ]$, and $\frac{1}{4}$ is the best possible constant.

Ostrowski’s inequality provides an approximation of the difference between mapping values and their integral average over a given interval. For more than 5000 years, inequalities have been seen in wide applications. The oldest was recorded in ancient Chinese mathematics, called the He Chengtian inequality [2]. By utilizing this inequality, He Chengtian calculated the approximate values of the fractional day of a moon and a year. Over the course of time, researchers have broadened the scope of convex mappings, leading to the discovery of various variants of the Hermite–Hadamard inequality, see [3,4,5,6,7,8,9,10,11,12,13,14].

The class of convex mappings is regarded as cornerstone of the theory of inequalities with a wide range of applications in many areas of mathematics such as in numerical integration, special means and special functions.

A mapping $\psi :\mathcal{I}\to \mathbb{R}$ is said to be convex, if

$$\begin{array}{c}\hfill \psi \left(\lambda \mu +(1-\lambda )\kappa \right)\le \lambda \psi \left(\mu \right)+\left(1-\lambda \right)\psi \left(\kappa \right),\forall \mu ,\kappa \in \mathcal{I},\lambda \in [0,1].\end{array}$$

(1)

One of the prolific results concerning to the convexity property of the mappings is Jensen’s inequality (see [15]) interpreted as:

For a convex mapping $\psi :\mathcal{I}=[\mu ,\kappa ]\subseteq \mathbb{R}\to \mathbb{R}$, we have

$$\begin{array}{c}\hfill \psi \left(\sum _{j=1}^n{\wp }_j{\gamma }_j\right)\le \sum _{j=1}^n{\wp }_j\psi \left({\gamma }_j\right),\end{array}$$

where $0<{\gamma }_1\le {\gamma }_2\le ···\le {\gamma }_n$ and $\wp =\left({\wp }_1,{\wp }_2,···,{\wp }_n\right)$ are non-negative weights with ${\displaystyle \sum _{i=1}^n}{\wp }_i=1$, ${\gamma }_j\in [\mu ,\kappa ]$, ${\wp }_j\in [0,1]$ and $j=1,···,n$.

A new variant of Jensen’s inequality known as Jensen–Mercer inequality was introduced by Mercer [16] in 2003, stated as:

For a convex mapping $\psi :\mathcal{I}=[\mu ,\kappa ]\subseteq \mathbb{R}\to \mathbb{R}$, we have

$$\begin{array}{c}\hfill \psi \left(\mu +\kappa -\sum _{j=1}^n{\wp }_j{\gamma }_j\right)\le \psi \left(\mu \right)+\psi \left(\kappa \right)-\sum _{j=1}^n{\wp }_j\psi \left({\gamma }_j\right),\end{array}$$

for all ${\gamma }_j\in [\mu ,\kappa ]$, ${\wp }_j\in [0,1]$ and $j=1,···,n$.

Kian and Moslehian [17] obtained the Hermite–Hadamard–Jensen–Mercer inequality for convex mappings, as follows:

For a convex mapping $\psi :[\mu ,\kappa ]\subseteq \mathbb{R}\to \mathbb{R}$ and ${\varphi }_1,{\varphi }_2\in [\mu ,\kappa ]$, we have

$$\begin{array}{cc}\hfill \psi \left(\mu +\kappa -\frac{{\phi }_1+{\phi }_2}{2}\right)& \le \frac{1}{{\phi }_2-{\phi }_1}\underset{{\phi }_1}{\overset{{\phi }_2}{\int }}\psi \left(\mu +\kappa -\lambda \right)d\lambda \hfill \\ \hfill & \le \frac{\psi \left(\mu +\kappa -{\phi }_1\right)+\psi \left(\mu +\kappa -{\phi }_2\right)}{2}\hfill \\ \hfill & \le \psi \left(\mu \right)+\psi \left(\kappa \right)-\frac{\psi \left({\phi }_1\right)+\psi \left({\phi }_2\right)}{2}.\hfill \end{array}$$

For more work on Jensen–Mercer-type inequalities, see [18,19,20,21,22].

Over time, the researchers have extended the definition of convex mappings to obtain different variants of Hermite–Hadamard inequality. The concept of s-Breckner convex mappings, or s-convex mappings in the second sense $(0<s\le 1)$, was introduced by Breckner [23] in 1978; this is a generalized class of convex mappings such that for $s=1$, it reduces back to convexity.

A mapping $\psi :[0,\infty )\to \mathbb{R}$ is said to be s-convex mapping in the second sense, when

$$\begin{array}{c}\hfill \psi \left(\lambda \mu +(1-\tau )\kappa \right)\le {\lambda }^s\psi \left(\mu \right)+{(1-\lambda )}^s\psi \left(\kappa \right),\end{array}$$

(2)

holds for all $\mu ,\kappa \in [0,\infty )$, $s\in (0,1]$ and $\lambda \in [0,1]$. The geometrical aspect of s-convexity $(0<s<1)$ is that a curved chord joining any two points always lies above the mapping’s graph. The inequality (2) is identical to the inequality (1), when $s=1$.

Cortez and Hernández [24] have proved Jensen–Mercer inequality for s-convex mapping $\psi :\mathcal{I}=[0,\infty )\to \mathbb{R}$ with $(0<s\le 1)$ as follows:

$$\begin{array}{c}\hfill \psi \left(\mu +\kappa -\sum _{j=1}^n{\wp }_j{\gamma }_j\right)\le \psi \left(\mu \right)+\psi \left(\kappa \right)-\sum _{j=1}^n{\wp }_j^s\psi \left({\gamma }_j\right),\end{array}$$

for all ${\gamma }_j\in \mathcal{I}$, ${\wp }_j\in [0,1]$ and $j=1,···,n$.

For s-convex mapping, $\psi :[\mu ,\kappa ]\subseteq \mathbb{R}\to \mathbb{R}$, ${\varphi }_1,{\varphi }_2\in [\mu ,\kappa ]$ and $s\in (0,1]$, the Hermite–Hadamard–Jensen–Mercer inequality is given in [24] as follows:

$$\begin{array}{cc}\hfill \psi \left(\mu +\kappa -\frac{{\phi }_1+{\phi }_2}{2}\right)& \le \frac{1}{{\phi }_2-{\phi }_1}\underset{{\phi }_1}{\overset{{\phi }_2}{\int }}\psi \left(\mu +\kappa -\lambda \right)d\lambda \hfill \\ \hfill & \le \psi \left(\mu \right)+\psi \left(\kappa \right)-\frac{\psi \left({\phi }_1\right)+\psi \left({\phi }_2\right)}{s+1}.\hfill \end{array}$$

Fractional calculus, dealing with integrals and derivatives of arbitrary real order, has significantly contributed to the characterization of diverse real materials, such as polymers. The fractional models are more adequate than the previous used models of integer orders, see [25,26,27]. In addition to classical derivatives, fractional order derivatives offer superior capabilities in describing the memory and hereditary characteristics of diverse processes. In [28], Podlubny discussed various applications of fractional derivatives. Riemann, Liouville, Grünwald and other researchers defined the fractional derivatives in several ways given in [28,29].

To investigate the characteristics of fractional differentiability and local scaling, the fractional derivatives were not suitable because of their non-local nature [30]. By renormalization of the Riemann–Liouville definition, Kolwankar and Gangal [30,31] proposed the idea of local fractional derivatives. The calculus of fractal space-time is studied with the help of local fractional derivatives. In addition, two-scale fractal theory is utilized to study problems involving porous media and unsmooth boundaries [32,33,34]. Moreover, the fractional derivatives are also utilized to find the approximate solutions of the fractional differential equations, see [35,36].

Probably the most frequently used definition of fractional integrals is due to B. Riemann and J. Liouville, commonly known as the Riemann–Liouville fractional integrals, defined as follows:

Let $\psi$ be an integrable mapping on $[\mu ,\kappa ]$. Then, the left and right sided Reimann–Liouville fractional integrals $I_{{\mu }^{+}}^{\omega }\psi$ and $I_{{\kappa }^{-}}^{\omega }\psi$ of order $\nu >0$ with $\mu \ge 0$ are defined by:

$$\begin{array}{c}\hfill I_{{\mu }^{+}}^{\nu }\psi \left(y\right)=\frac{1}{\mathrm{\Gamma }\left(\nu \right)}{\int }_{\mu }^y{(y-\lambda )}^{\nu -1}\psi \left(\lambda \right)d\lambda ,y>\mu ,\end{array}$$

(3)

and

$$\begin{array}{c}\hfill I_{{\kappa }^{-}}^{\nu }\psi \left(y\right)=\frac{1}{\mathrm{\Gamma }\left(\nu \right)}{\int }_y^{\kappa }{(\lambda -y)}^{\nu -1}\psi \left(\lambda \right)d\lambda ,y<\kappa ,\end{array}$$

(4)

where $\mathrm{\Gamma }\left(\nu \right)$ is the gamma mapping defined as:

$$\begin{array}{c}\hfill \mathrm{\Gamma }\left(\nu \right)=\underset{0}{\overset{\infty }{\int }}{\lambda }^{\nu -1}{e}^{-\lambda }d\lambda ,Re\left(\nu \right)>0.\end{array}$$

For more details, see [37].

When the fractional operators are closely examined, various features such as singularity, locality, generalization and differences in their kernel structures become apparent. Although generalizations and inferences are the foundations of mathematical methods, the new fractional operators add new features to solutions, particularly for the time memory effect. In the literature, there are various fractional operators with local, nonlocal, singular and non-singular kernels, [38,39,40,41]. Jarad et al. [42] defined conformable fractional integrals and derivatives with two parameters and kernels, which are helpful to the better understanding of the complexity of fractional variational problems, optimal control problems and modelling of complex systems.

For an integrable mapping $\psi$ on $[\mu ,\kappa ]$, the left and right-conformable fractional integrals ${}_{\mu }^{\nu }{I}^{\omega }\psi$ and ${}^{\nu }{I}_{\kappa }^{\omega }\psi$ of order $\nu \in \mathbb{C}$ (Complex numbers), $Re\left(\nu \right)>0$, $\omega \in (0,1]$ are defined as:

$$\begin{array}{c}\hfill {}_{\mu }^{\nu }{I}^{\omega }\psi \left(y\right)=\frac{1}{\mathrm{\Gamma }\left(\nu \right)}{\int }_{\mu }^y{\left(\frac{{\left(y-\mu \right)}^{\omega }-{\left(\lambda -\mu \right)}^{\omega }}{\omega }\right)}^{\nu -1}\frac{\psi \left(\lambda \right)}{{(\lambda -\mu )}^{1-\omega }}d\lambda ,y>\mu ,\end{array}$$

(5)

and

$$\begin{array}{c}\hfill {}^{\nu }{I}_{\kappa }^{\omega }\psi \left(y\right)=\frac{1}{\mathrm{\Gamma }\left(\nu \right)}{\int }_y^{\kappa }{\left(\frac{{\left(\kappa -y\right)}^{\omega }-{\left(\kappa -\lambda \right)}^{\omega }}{\omega }\right)}^{\nu -1}\frac{\psi \left(\lambda \right)}{{(\kappa -\lambda )}^{1-\omega }}d\lambda ,y<\kappa .\end{array}$$

(6)

When $\omega =1$ in (5) and (6), then they coincides with (3) and (4), respectively. They also coincide with the Hadamard fractional integral [43] by setting $\mu =0$ and $\omega \to 0$ in (5) and $\kappa =0$ and $\omega \to 0$ in (6). In addition, by choosing $\mu =0$ in (5) and $\kappa =0$ in (6), we have the generalized fractional integrals [44].

Let us recall beta mapping or Euler integral of the first kind with two variables defined by:

$$\begin{array}{c}\hfill \mathrm{B}({\mu }_1,{\kappa }_1)=\underset{0}{\overset{1}{\int }}{t}^{{\mu }_1-1}{(1-t)}^{{\kappa }_1-1}dt,Re\left({\mu }_1\right)>0,Re\left({\kappa }_1\right)>0.\end{array}$$

(7)

In terms of gamma mapping, it is defined as:

$$\begin{array}{c}\hfill \mathrm{B}({\mu }_1,{\kappa }_1)=\frac{\mathrm{\Gamma }\left({\mu }_1\right)\mathrm{\Gamma }\left({\kappa }_1\right)}{\mathrm{\Gamma }\left({\mu }_1+{\kappa }_1\right)}.\end{array}$$

Some properties of beta function are:

• The beta function is symmetric i.e., $B\left({\mu }_1,{\kappa }_1\right)=B\left({\kappa }_1,{\mu }_1\right)$.
• $B\left({\mu }_1+1,{\kappa }_1\right)=B\left({\mu }_1,{\kappa }_1\right)\frac{{\mu }_1}{{\mu }_1+{\kappa }_1}$.
• $B\left({\mu }_1,{\kappa }_1+1\right)=B\left({\mu }_1,{\kappa }_1\right)\frac{{\kappa }_1}{{\mu }_1+{\kappa }_1}$.
• $B\left({\mu }_1,{\kappa }_1\right)=B\left({\mu }_1+1,{\kappa }_1\right)+B\left({\mu }_1,{\kappa }_1+1\right)$.

The motivation of this paper is to establish several new fractional variants of Ostrowski–Mercer-type inequalities using the first and the second order s-convex mappings of second sense. To achieve this goal, we employ conformable fractional integral operators. The main results’ relevance has also been analyzed numerically and graphically. In addition, we also demonstrate some applications to means, q-digamma mappings, and modified Bessel mappings.

2. Ostrowski–Mercer-Type Inequalities for the First Order Differentiable $\mathit{s}$-Convex Mappings

In this section, we first establish a key lemma for the first differentiable mappings involving conformable fractional integrals. Then, by utilizing this result, we obtain several inequalities for the first order differentiable mappings whose absolute values are s-convex in the second sense.

Lemma 1.

Let $\psi :[\mu ,\kappa ]\to \mathbb{R}$ be a differentiable mapping on $({\phi }_1,{\phi }_2)$ and ${\psi }^{\prime }$ is integrable mapping on $[{\phi }_1,{\phi }_2]$, then for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$, ${\phi }_1,{\phi }_2\in [\mu ,\kappa ]$, $\omega \in (0,1]$ and $Re\left(\nu \right)>0$, the following identity holds:

$$\begin{array}{cc}\hfill & {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\hfill \\ \hfill & ={\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & -{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau .\hfill \end{array}$$

(8)

Proof. 

Consider

$$\begin{array}{cc}\hfill & {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & -{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & ={\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{Y}_1-{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{Y}_2.\hfill \end{array}$$

(9)

Applying integration by parts, we have

$$\begin{array}{cc}\hfill & Y_1=\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & ={\left.{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\frac{\psi \left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_1}\right|}_0^1\hfill \\ \hfill & -\nu \underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu -1}\frac{\psi \left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_1}{\left(1-\tau \right)}^{\omega -1}d\tau \hfill \\ \hfill & =\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)}{\mathit{\ell }-{\phi }_1}-\frac{\nu }{\mathit{\ell }-{\phi }_1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu -1}\psi \left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right){\left(1-\tau \right)}^{\omega -1}d\tau \hfill \\ \hfill & =\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)}{\mathit{\ell }-{\phi }_1}-\frac{\nu }{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu +1}}\hfill \\ \hfill & \underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}{\left(\frac{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega }-{\left(\mathit{\ell }+\mu -{\phi }_1-\lambda \right)}^{\omega }}{\omega }\right)}^{\nu -1}\psi \left(\lambda \right){\left(\mathit{\ell }+\mu -{\phi }_1-\lambda \right)}^{\omega -1}d\lambda \hfill \\ \hfill & =\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)}{\mathit{\ell }-{\phi }_1}-\frac{\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu +1}}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right).\hfill \end{array}$$

(10)

Similarly,

$$\begin{array}{cc}\hfill & Y_2=\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & ={\left.{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\frac{\psi \left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_2}\right|}_0^1\hfill \\ \hfill & -\nu \underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu -1}\frac{\psi \left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_2}{\left(1-\tau \right)}^{\omega -1}d\tau \hfill \\ \hfill =& -\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)}{{\phi }_2-\mathit{\ell }}+\frac{\nu }{{\phi }_2-\mathit{\ell }}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu -1}\psi \left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right){\left(1-\tau \right)}^{\omega -1}d\tau \hfill \\ \hfill =& -\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)}{{\phi }_2-\mathit{\ell }}+\frac{\nu }{{\phi }_2-\mathit{\ell }}\hfill \\ \hfill & \underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}{\left(\frac{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega }-{\left({\phi }_2-\mathit{\ell }-\left(\kappa -\lambda \right)\right)}^{\omega }}{\omega }\right)}^{\nu -1}\psi \left(\lambda \right){\left({\phi }_2-\mathit{\ell }-\left(\kappa -\lambda \right)\right)}^{\omega -1}d\lambda \hfill \\ \hfill & =-\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)}{{\phi }_2-\mathit{\ell }}+\frac{\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu +1}}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right).\hfill \end{array}$$

(11)

Now using (10) and (11) in (9) and multiply with ${\omega }^{\nu }$, we obtain

$$\begin{array}{cc}\hfill & ={\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right).\hfill \end{array}$$

(12)

The proof is completed. □

Remark 1.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ and $\omega =1$ in Lemma 1, we obtain Lemma 2 in [1].

Remark 2.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $\nu =1$ in Lemma 1, we obtain Lemma 1 in [3].

Theorem 1.

For a differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if $\left|{\psi }^{\prime }\right|$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$. Then, under the assumptions of Lemma 1, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left\{\frac{1}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|\right]\right.\hfill \\ \hfill & \left.-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\psi }^{\prime }\left|{\phi }_1\right|+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left\{\frac{1}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|\right]\right.\hfill \\ \hfill & \left.-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\psi }^{\prime }\left|{\phi }_2\right|+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}.\hfill \end{array}$$

(13)

where

$$\begin{array}{cc}\hfill {\mathcal{C}}_1\left(s,\nu ,\omega \right)& =\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\tau }^{s}d\tau ,\hfill \\ \hfill {\mathcal{C}}_2\left(s,\nu ,\omega \right)& =\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\left(1-\tau \right)}^{s}d\tau ,\hfill \end{array}$$

and the beta mapping $B(·,·)$ is defined in (7).

Proof. 

Using Lemma 1 and the Jensen–Mercer inequality with the s-convexity of $\left|{\psi }^{\prime }\right|$ on $[\mu ,\kappa ]$, we obtain

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & =\left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \right.\hfill \\ \hfill & \left.-{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left\{{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|-\left[{\tau }^s{\psi }^{\prime }\left|{\phi }_1\right|+{\left(1-\tau \right)}^s{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left\{{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|-\left[{\tau }^s{\psi }^{\prime }\left|{\phi }_2\right|+{\left(1-\tau \right)}^s{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}d\tau \hfill \end{array}$$

Since

$$\begin{array}{cc}\hfill \underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau & =\frac{1}{{\omega }^{\nu }}\frac{\mathrm{\Gamma }\left(1+\nu \right)\mathrm{\Gamma }\left(1+\frac{1}{\omega }\right)}{\mathrm{\Gamma }\left(1+\nu +\frac{1}{\omega }\right)}\hfill \\ \hfill & =\frac{1}{{\omega }^{\nu }}\frac{\nu \mathrm{\Gamma }\left(\nu \right)\frac{1}{\omega }\mathrm{\Gamma }\left(\frac{1}{\omega }\right)}{\nu +\frac{1}{\omega }\mathrm{\Gamma }\left(\nu +\frac{1}{\omega }\right)}=\frac{\nu }{{\omega }^{\nu }\left(\omega \nu +1\right)}B\left(\nu ,\frac{1}{\omega }\right)\hfill \\ \hfill & =\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right).\hfill \end{array}$$

Which implies

$$\begin{array}{cc}\hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left\{\frac{1}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|\right]\right.\hfill \\ \hfill & \left.-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\psi }^{\prime }\left|{\phi }_1\right|+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left\{\frac{1}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|\right]\right.\hfill \\ \hfill & \left.-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\psi }^{\prime }\left|{\phi }_2\right|+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}.\hfill \end{array}$$

(14)

The proof is completed. □

Remark 3.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ and $\omega =1$ in Theorem 1, we obtain Theorem 7 in [1].

Remark 4.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$, and $s=1$ in Theorem 1, we obtain Theorem 2 in [4].

Corollary 1.

If we set ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $\nu =1$ in Theorem 1, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-\mu \right)}^2\left\{\frac{1}{2}\left({\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|\right)-\left[\frac{1}{s+2}{\psi }^{\prime }\left|\mu \right|+\frac{1}{2+3s+s^2}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}\hfill \\ \hfill & +{\left(\kappa -\mathit{\ell }\right)}^2\left\{\frac{1}{2}\left({\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|\right)-\left[\frac{1}{s+2}{\psi }^{\prime }\left|\kappa \right|+\frac{1}{2+3s+s^2}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}.\hfill \end{array}$$

Corollary 2.

If we set $\omega =1$ and $\nu =1$ in Theorem 1, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right.\hfill \\ \hfill & \left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2\left\{\frac{1}{2}\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|\right]-\left[\frac{1}{s+2}{\psi }^{\prime }\left|{\phi }_1\right|+\frac{1}{2+3s+s^2}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\left\{\frac{1}{2}\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|\right]\right.\left.-\left[\frac{1}{s+2}{\psi }^{\prime }\left|{\phi }_2\right|+\frac{1}{2+3s+s^2}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}.\hfill \end{array}$$

Corollary 3.

If we set $\omega =1$, $\nu =1$ and $s=1$ in Theorem 1, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right.\hfill \\ \hfill & \left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2\left\{\frac{1}{2}\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\mu \right|\right]-\left[\frac{1}{3}{\psi }^{\prime }\left|{\phi }_1\right|+\frac{1}{6}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\left\{\frac{1}{2}\left[{\psi }^{\prime }\left|\mathit{\ell }\right|+{\psi }^{\prime }\left|\kappa \right|\right]\right.\left.-\left[\frac{1}{3}{\psi }^{\prime }\left|{\phi }_2\right|+\frac{1}{6}{\psi }^{\prime }\left|\mathit{\ell }\right|\right]\right\}.\hfill \end{array}$$

Corollary 4.

By considering $\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|\le \mathcal{M}$ in Theorem 1, we obtain

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le M\left[\frac{2}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)-\left\{{\mathcal{C}}_1\left(s,\nu ,\omega \right)+{\mathcal{C}}_2\left(s,\nu ,\omega \right)\right\}\right]\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right\}.\hfill \end{array}$$

Corollary 5.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$ in Corollary 4, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-\mu \right)}^{\nu }+{\left(\kappa -\mathit{\ell }\right)}^{\nu }\right\}\psi \left(\mathit{\ell }\right)-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\right.\hfill \\ \hfill & \left.\left\{\frac{1}{{\left(\mathit{\ell }-\mu \right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }}^{\omega }\psi \left(\mu \right)\right)+\frac{1}{{\left(\kappa -\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le M\left[\frac{2}{{\omega }^{v+1}}B\left(\nu +1,\frac{1}{\omega }\right)-\left\{{\mathcal{C}}_1\left(s,\nu ,\omega \right)+{\mathcal{C}}_2\left(s,\nu ,\omega \right)\right\}\right]\left\{{\left(\mathit{\ell }-\mu \right)}^{\nu +1}+{\left(\kappa -\mathit{\ell }\right)}^{\nu +1}\right\}.\hfill \end{array}$$

Remark 5.

If we set $\omega =1$ and $\nu =1$ in Corollary 5, we obtain Theorem 2 in [5].

Remark 6.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $s=1$ in Corollary 4, we obtain Corollary 1 in [1].

Theorem 2.

For a differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{\prime }\right|}^q$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ and $p,q>1$. Then, under the assumptions of Lemma 1, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\frac{1}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\frac{1}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}},\hfill \end{array}$$

(15)

where $\frac{1}{p}=1-\frac{1}{q}$ and $B(·,·)$ is the beta mapping defined in (7).

Proof. 

Using Lemma 1 and the Hölder inequality for integrals, we have

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right)}^{\frac{1}{p}}{\left(\underset{0}{\overset{1}{\int }}{\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right)}^{\frac{1}{p}}{\left(\underset{0}{\overset{1}{\int }}{\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right)}^{\frac{1}{q}}.\hfill \end{array}$$

(16)

Now, by applying the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{\prime }\right|}^q$, we have

$$\begin{array}{cc}\hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\frac{1}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\frac{1}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}.\hfill \end{array}$$

(17)

The proof is completed. □

Remark 7.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ and $\omega =1$ in Theorem 2, we obtain Theorem 8 in [1].

Remark 8.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$, and $s=1$ in Theorem 2, we obtain Theorem 3 in [4].

Corollary 6.

If we set $\omega =1$ and $\nu =1$ in Theorem 2, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}.\hfill \end{array}$$

(18)

Corollary 7.

If we set $\omega =1$, $\nu =1$ and $s=1$ in Theorem 2, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{2}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}\hfill \\ \hfill & {\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{2}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}.\hfill \end{array}$$

Corollary 8.

If we set ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $\nu =1$ in Theorem 2, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-\mu \right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}{\left(\frac{s}{s+1}\left[{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\kappa -\mathit{\ell }\right)}^2{\left(\frac{1}{p+1}\right)}^{\frac{1}{p}}{\left(\frac{s}{s+1}\left[{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right)}^{\frac{1}{q}}.\hfill \end{array}$$

Corollary 9.

By considering $\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|\le \mathcal{M}$ in Theorem 2, we obtain

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le \frac{\mathcal{M}}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}{\left(\frac{2s}{s+1}\right)}^{\frac{1}{q}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Corollary 10.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$ in Corollary 9, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-\mu \right)}^{\nu }+{\left(\kappa -\mathit{\ell }\right)}^{\nu }\right\}\psi \left(\mathit{\ell }\right)-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{\frac{1}{{\left(\mathit{\ell }-\mu \right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }}^{\omega }\psi \left(\mu \right)\right)+\frac{1}{{\left(\kappa -\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le \frac{\mathcal{M}}{{\omega }^{\nu }}{\left(\frac{1}{\omega }B\left(p\nu +1,\frac{1}{\omega }\right)\right)}^{\frac{1}{p}}{\left(\frac{2s}{s+1}\right)}^{\frac{1}{q}}\left[{\left(\mathit{\ell }-\mu \right)}^{\nu +1}+{\left(\kappa -\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Remark 9.

If we set $\omega =1$ and $\nu =1$ in Corollary 10, we obtain Theorem 3 in [5].

Remark 10.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $s=1$ in Corollary 9, we obtain Corollary 2 in [1].

Theorem 3.

For a differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{\prime }\right|}^q$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ and $q>1$. Then, under the assumptions of Lemma 1, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\left\{\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q\right)-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\left\{\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q\right)-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right)}^{\frac{1}{q}},\hfill \end{array}$$

(19)

where $B(·,·)$ is the beta mapping defined by (7) and ${\mathcal{C}}_1\left(s,\nu ,\omega \right)$ and ${\mathcal{C}}_2\left(s,\nu ,\omega \right)$ are defined in Theorem 1.

Proof. 

Using Lemma 1, power mean inequality and the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{\prime }\right|}^q$, we have

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau \right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right)}^{\frac{1}{q}}\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\left\{\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q\right)-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}\hfill \\ \hfill & {\left(\left\{\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\left({\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q\right)-\left[{\mathcal{C}}_1\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\mathcal{C}}_2\left(s,\nu ,\omega \right){\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right)}^{\frac{1}{q}}.\hfill \end{array}$$

(20)

The proof is completed. □

Remark 11.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ and $\omega =1$ in Theorem 3, we obtain Theorem 9 in [1].

Remark 12.

By setting ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$, and $s=1$ in Theorem 3, we obtain Theorem 4 in [4].

Corollary 11.

If we set ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $\nu =1$ in Theorem 3, we obtain

$$\begin{array}{cc}\hfill & \left|\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-\mu \right)}^2{\left(\frac{1}{2}\right)}^{1-\frac{1}{q}}{\left(\frac{s}{2s+4}{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q+\frac{3s+s^2}{4+6s+2s^2}{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right)}^{\frac{1}{q}}\hfill \\ \hfill & +{\left(\kappa -\mathit{\ell }\right)}^2{\left(\frac{1}{2}\right)}^{1-\frac{1}{q}}{\left(\frac{s}{2s+4}{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q+\frac{3s+s^2}{4+6s+2s^2}{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right)}^{\frac{1}{q}}.\hfill \end{array}$$

Corollary 12.

By considering $\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|\le \mathcal{M}$ in Theorem 3, we obtain

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le \mathcal{M}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}{\left[\frac{2}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)-\left\{{\mathcal{C}}_1\left(s,\nu ,\omega \right)+{\mathcal{C}}_2\left(s,\nu ,\omega \right)\right\}\right]}^{\frac{1}{q}}\hfill \\ \hfill & \left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Corollary 13.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$ in Corollary 12, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-\mu \right)}^{\nu }+{\left(\kappa -\mathit{\ell }\right)}^{\nu }\right\}\psi \left(\mathit{\ell }\right)-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{\frac{1}{{\left(\mathit{\ell }-\mu \right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }}^{\omega }\psi \left(\mu \right)\right)+\frac{1}{{\left(\kappa -\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le \mathcal{M}{\left(\frac{1}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)\right)}^{1-\frac{1}{q}}{\left[\frac{2}{{\omega }^{\nu +1}}B\left(\nu +1,\frac{1}{\omega }\right)-\left\{{\mathcal{C}}_1\left(s,\nu ,\omega \right)+{\mathcal{C}}_2\left(s,\nu ,\omega \right)\right\}\right]}^{\frac{1}{q}}\hfill \\ \hfill & \left[{\left(\mathit{\ell }-\mu \right)}^{\nu +1}+{\left(\kappa -\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Remark 13.

If we set $\omega =1$ and $\nu =1$ in Corollary 13, we obtain Theorem 4 in [5].

Remark 14.

Taking ${\phi }_1=\mu ,{\phi }_2=\kappa$, $\omega =1$ and $s=1$ in Corollary 12, we obtain Corollary 3 in [1].

Theorem 4.

For a differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{\prime }\right|}^q$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ with $p,q>1$ and $\frac{1}{p}+\frac{1}{q}=1$. Then, under the assumptions of Lemma 1, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p{\omega }^{\nu p+1}}\right.B\left(\nu p+1,\frac{1}{\omega }\right)\hfill \\ \hfill & \left.+\frac{1}{q}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p{\omega }^{\nu p+1}}B\left(\nu p+1,\frac{1}{\omega }\right)\right.\hfill \\ \hfill & \left.+\frac{1}{q}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right].\hfill \end{array}$$

(21)

Proof. 

Taking modulus of Lemma 1 and using Young’s inequality, i.e., $xy\le \frac{1}{p}{x}^p+\frac{1}{q}{y}^q$ (equality holds when $x^p=y^q$), we have

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau +\frac{1}{q}\underset{0}{\overset{1}{\int }}{\left|{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }pd\tau +\frac{1}{q}\underset{0}{\overset{1}{\int }}{\left|{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q}d\tau \right]\hfill \end{array}$$

Now, applying the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{\prime }\right|}^q$, we obtain

$$\begin{array}{cc}\hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q}\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu p}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q}\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}d\tau \right]\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p{\omega }^{\nu p+1}}\right.B\left(\nu p+1,\frac{1}{\omega }\right)\hfill \\ \hfill & \left.+\frac{1}{q}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mu \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_1\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p{\omega }^{\nu p+1}}B\left(\nu p+1,\frac{1}{\omega }\right)\right.\hfill \\ \hfill & \left.+\frac{1}{q}\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^q-\frac{1}{s+1}\left[{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^q+{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^q\right]\right\}\right].\hfill \end{array}$$

(22)

The proof is completed. □

Corollary 14.

By considering $\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|\le \mathcal{M}$ in Theorem 4, we obtain

$$\begin{array}{cc}\hfill & \left|{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu -\nu }}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)-\frac{{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu -\nu }}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right|\hfill \\ \hfill & \le \left\{\frac{1}{p{\omega }^{\nu p+1}}B\left(\nu p+1,\frac{1}{\omega }\right)+\frac{2{\mathcal{M}}^q}{q}\frac{s}{s+1}\right\}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Remark 15.

If we set $\omega =1$ and $s=1$ in Theorem 4, we obtain Theorem 5 in [4].

3. Ostrowski–Mercer-Type Inequalities for the Twice Differentiable $\mathbf{s}$-Convex Mappings

In this section, we first establish a key result for the twice differentiable mappings involving conformable fractional integrals. Then, by utilizing this result, we obtain several inequalities for the twice differentiable mappings whose absolute values are s-convex in the second sense.

Lemma 2.

Let $\psi :[\mu ,\kappa ]\to \mathbb{R}$ be twice differentiable mapping on $({\phi }_1,{\phi }_2)$ and ${\psi }^{″}$ is integrable mapping on $[{\phi }_1,{\phi }_2]$, then for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$, ${\phi }_1,{\phi }_2\in [\mu ,\kappa ]$, $\omega \in (0,1]$ and $Re\left(\nu \right)>0$, the following identity holds:

$$\begin{array}{cc}\hfill & \left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & -{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\hfill \\ \hfill & ={\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & -{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau .\hfill \end{array}$$

(23)

Proof. 

Consider

$$\begin{array}{cc}\hfill & {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & -{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & ={\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{Y}_1-{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{Y}_2.\hfill \end{array}$$

(24)

Applying integration by parts, we have

$$\begin{array}{cc}\hfill & Y_1=\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & =\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\left.\frac{{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_1}\right|}_0^1\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\frac{{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_1}d\tau .\hfill \end{array}$$

Since we have proved in Lemma 1:

$$\begin{array}{cc}\hfill & \underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }{\psi }^{\prime }\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & =\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)}{\mathit{\ell }-{\phi }_1}-\frac{\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu +1}}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right).\hfill \end{array}$$

Which implies

$$\begin{array}{cc}\hfill & =-\frac{{\psi }^{\prime }\left(\mu \right)}{\mathit{\ell }-{\phi }_1}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau \hfill \\ \hfill & +\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)}{\mathit{\ell }-{\phi }_1}-\frac{\mathrm{\Gamma }\left(\nu +1\right)}{{\left(\mathit{\ell }-{\phi }_1\right)}^{\omega \nu +1}}\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right).\hfill \end{array}$$

(25)

Similarly,

$$\begin{array}{cc}\hfill & Y_2=\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)d\tau \hfill \\ \hfill & =\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\left.\frac{{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)}{\mathit{\ell }-{\phi }_2}\right|}_0^1\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }\frac{{\psi }^{\prime }\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)}{{\phi }_2-\mathit{\ell }}d\tau \hfill \\ \hfill & =-\frac{{\psi }^{\prime }\left(\kappa \right)}{{\phi }_2-\mathit{\ell }}\underset{0}{\overset{1}{\int }}{\left(\frac{1-{\left(1-\tau \right)}^{\omega }}{\omega }\right)}^{\nu }d\tau -\frac{1}{{\omega }^{\nu }}\frac{\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)}{{\phi }_2-\mathit{\ell }}\hfill \\ \hfill & +\frac{\mathrm{\Gamma }\left(\nu +1\right)}{{\left({\phi }_2-\mathit{\ell }\right)}^{\omega \nu +1}}\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right).\hfill \end{array}$$

(26)

Now using (25) and (26) in (24) and multiplying by ${\omega }^{\nu }$, we obtain

$$\begin{array}{cc}\hfill & \left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & -{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}.\hfill \end{array}$$

(27)

The proof is completed. □

Theorem 5.

For a twice differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if $\left|{\psi }^{″}\right|$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$. Then, under the assumptions of Lemma 2, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[{\mathcal{C}}_3\left(\nu ,\omega \right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\mu \right|\right\}-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right){\psi }^{″}\left|{\phi }_1\right|+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[{\mathcal{C}}_3\left(\nu ,\omega \right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\kappa \right|\right\}-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right){\psi }^{″}\left|{\phi }_2\right|+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right],\hfill \end{array}$$

(28)

where

$$\begin{array}{cc}\hfill {\mathcal{C}}_3\left(\nu ,\omega \right)& =\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau ,\hfill \\ \hfill {\mathcal{C}}_4\left(s,\nu ,\omega \right)& =\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\tau }^{s}d\tau \hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\mathcal{C}}_5\left(s,\nu ,\omega \right)& =\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\left(1-\tau \right)}^{s}d\tau .\hfill \end{array}$$

Proof. 

Using Lemma 2 and the Jensen–Mercer inequality with the s-convexity of $\left|{\psi }^{″}\right|$, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\mu \right|-\left[{\tau }^s{\psi }^{″}\left|{\phi }_1\right|+{\left(1-\tau \right)}^s{\psi }^{″}\left|\mathit{\ell }\right|\right]\right\}d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\kappa \right|-\left[{\tau }^s{\psi }^{″}\left|{\phi }_2\right|+{\left(1-\tau \right)}^s{\psi }^{″}\left|\mathit{\ell }\right|\right]\right\}d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[{\mathcal{C}}_3\left(\nu ,\omega \right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\mu \right|\right\}-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right){\psi }^{″}\left|{\phi }_1\right|+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[{\mathcal{C}}_3\left(\nu ,\omega \right)\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\kappa \right|\right\}-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right){\psi }^{″}\left|{\phi }_2\right|+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right].\hfill \end{array}$$

(29)

The proof is completed. □

Corollary 15.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ with $\omega =1$ and $\nu =1$ in Theorem 5

$$\begin{array}{cc}\hfill & \left|\left\{\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)\right\}+\frac{1}{2}\left\{\left(\kappa -\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-\mu \right){\psi }^{\prime }\left(\mu \right)\right\}-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-\mu \right)}^2\left[\left\{\left(\frac{1}{3}-\frac{1}{\left(s+1\right)\left(s+3\right)}\right){\psi }^{″}\left|\mu \right|+\left(\frac{1}{3}-\frac{1}{2\left(s+1\right)}+\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right]\hfill \\ \hfill & +{\left(\kappa -\mathit{\ell }\right)}^2\left[\left\{\left(\frac{1}{3}-\frac{1}{\left(s+1\right)\left(s+3\right)}\right){\psi }^{″}\left|\kappa \right|+\left(\frac{1}{3}-\frac{1}{2\left(s+1\right)}+\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right].\hfill \end{array}$$

Corollary 16.

If we set $\omega =1$ and $\nu =1$ in Theorem 5, we obtain

$$\begin{array}{cc}\hfill & |\left\{\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\hfill \\ \hfill & +\frac{1}{2}\left\{\left({\phi }_2-\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-{\phi }_1\right){\psi }^{\prime }\left(\mu \right)\right\}-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2\left[\frac{1}{3}\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\mu \right|\right\}-\left\{\frac{1}{\left(s+1\right)\left(s+3\right)}{\psi }^{″}\left|{\phi }_1\right|+\left(\frac{1}{2\left(s+1\right)}-\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\left[\frac{1}{3}\left\{{\psi }^{″}\left|\mathit{\ell }\right|+{\psi }^{″}\left|\kappa \right|\right\}-\left\{\frac{1}{\left(s+1\right)\left(s+3\right)}{\psi }^{″}\left|{\phi }_2\right|+\left(\frac{1}{2\left(s+1\right)}-\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\psi }^{″}\left|\mathit{\ell }\right|\right\}\right].\hfill \end{array}$$

Corollary 17.

By considering $\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|\le {\mathcal{M}}_1$ in Theorem 5, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\mathcal{M}}_1\left[2{\mathcal{C}}_3\left(\nu ,\omega \right)-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right)+{\mathcal{C}}_5\left(s,\nu ,\omega \right)\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\mathcal{M}}_1\left[2{\mathcal{C}}_3\left(\nu ,\omega \right)-\left\{{\mathcal{C}}_4\left(s,\nu ,\omega \right)+{\mathcal{C}}_5\left(s,\nu ,\omega \right)\right\}\right].\hfill \end{array}$$

Theorem 6.

For a twice differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{″}\right|}^{q_1}$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ and $p_1,q_1>1$. Then, under the assumptions of Lemma 2, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left({\mathcal{C}}_6\left(\nu ,\omega \right)\right)}^{\frac{1}{p_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right],\hfill \end{array}$$

(30)

where

$$\begin{array}{c}\hfill {\mathcal{C}}_6\left(\nu ,\omega \right)=\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau ,\end{array}$$

and $\frac{1}{p_1}=1-\frac{1}{q_1}$.

Proof. 

Using Lemma 2 and the Hölder inequality for integrals, we have

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{\frac{1}{p_1}}{\left(\underset{0}{\overset{1}{\int }}{\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{\frac{1}{p_1}}{\left(\underset{0}{\overset{1}{\int }}{\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right)}^{\frac{1}{q_1}}.\hfill \end{array}$$

Now, by applying the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{″}\right|}^{q_1}$, we have

$$\begin{array}{cc}\hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{\frac{1}{p_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{\frac{1}{p_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & \le {\left({\mathcal{C}}_6\left(\nu ,\omega \right)\right)}^{\frac{1}{p_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

(31)

The proof is completed. □

Corollary 18.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ with $\omega =1$ and $\nu =1$ in Theorem 30

$$\begin{array}{cc}\hfill & \left|\left\{\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)\right\}+\frac{1}{2}\left\{\left(\kappa -\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-\mu \right){\psi }^{\prime }\left(\mu \right)\right\}-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\frac{1}{3}\right)}^{\frac{1}{p_1}}\left[{\left(\mathit{\ell }-\mu \right)}^2{\left(\frac{s}{s+1}\left\{{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right\}\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & \left.+{\left(\kappa -\mathit{\ell }\right)}^2{\left(\frac{s}{s+1}\left\{{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right\}\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

Corollary 19.

If we set $\omega =1$ and $\nu =1$ in Theorem 30, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\frac{1}{2}\left\{\left({\phi }_2-\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-{\phi }_1\right){\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\frac{1}{3}\right)}^{\frac{1}{p_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^2{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & \left.+{\left({\phi }_2-\mathit{\ell }\right)}^2{\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

Corollary 20.

By considering $\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|\le {\mathcal{M}}_1$ in Theorem 30, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left({\mathcal{C}}_6\left(\nu ,\omega \right)\right)}^{\frac{1}{p_1}}{\mathcal{M}}_1{\left(\frac{2s}{s+1}\right)}^{\frac{1}{q_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Theorem 7.

For a twice differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{″}\right|}^{q_1}$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ and $q_1>1$. Then, under the assumptions of Lemma 2, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left({\mathcal{C}}_3\left(\nu ,\omega \right)\right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & \left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\left\{{\mathcal{C}}_3\left(\nu ,\omega \right)\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}\right)-\left[{\mathcal{C}}_4\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left.{\left(\left\{{\mathcal{C}}_3\left(\nu ,\omega \right)\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}\right)-\left[{\mathcal{C}}_4\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

(32)

where ${\mathcal{C}}_3\left(\nu ,\omega \right)$, ${\mathcal{C}}_4\left(s,\nu ,\omega \right)$ and ${\mathcal{C}}_5\left(s,\nu ,\omega \right)$ are defined in Theorem 5.

Proof. 

Using Lemma 2, power mean inequality and the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{″}\right|}^{q_1}$, we have

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right){\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}{\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)d\tau \right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & {\left(\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left\{{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{\prime }\left(\kappa \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{\prime }\left({\phi }_2\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{\prime }\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right)}^{\frac{1}{q_1}}\hfill \\ \hfill & \le {\left({\mathcal{C}}_3\left(\nu ,\omega \right)\right)}^{1-\frac{1}{q_1}}\hfill \\ \hfill & \left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}{\left(\left\{{\mathcal{C}}_3\left(\nu ,\omega \right)\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}\right)-\left[{\mathcal{C}}_4\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left.{\left(\left\{{\mathcal{C}}_3\left(\nu ,\omega \right)\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}\right)-\left[{\mathcal{C}}_4\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\mathcal{C}}_5\left(s,\nu ,\omega \right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

(33)

The proof is completed. □

Corollary 21.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ with $\omega =1$ and $\nu =1$ in Theorem 7

$$\begin{array}{cc}\hfill & \left|\left\{\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)\right\}+\frac{1}{2}\left\{\left(\kappa -\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-\mu \right){\psi }^{\prime }\left(\mu \right)\right\}-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le {\left(\frac{1}{3}\right)}^{1-\frac{1}{q_1}}\left[{\left(\mathit{\ell }-\mu \right)}^2{\left(\left\{\left(\frac{1}{3}-\frac{1}{s^2+4s+3}\right){\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}+\left(\frac{1}{3}-\frac{1}{1+s}+\frac{2\mathrm{\Gamma }\left(1+s\right)}{\mathrm{\Gamma }\left(4+s\right)}\right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right\}\right)}^{\frac{1}{q_1}}\right.\hfill \\ \hfill & +{\left(\kappa -\mathit{\ell }\right)}^2\left.{\left(\left\{\left(\frac{1}{3}-\frac{1}{s^2+4s+3}\right){\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}+\left(\frac{1}{3}-\frac{1}{1+s}+\frac{2\mathrm{\Gamma }\left(1+s\right)}{\mathrm{\Gamma }\left(4+s\right)}\right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right\}\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

Corollary 22.

If we set $\omega =1$ and $\nu =1$ in Theorem 7, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\frac{1}{2}\left\{\left({\phi }_2-\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-{\phi }_1\right){\psi }^{\prime }\left(\mu \right)\right\}\left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\frac{1}{3}\right)}^{1-\frac{1}{q_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^2\right.\hfill \\ \hfill & {\left(\left\{\frac{1}{3}\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}\right)-\left[\frac{1}{s^2+4s+3}{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+\left(\frac{1}{1+s}-\frac{2\mathrm{\Gamma }\left(1+s\right)}{\mathrm{\Gamma }\left(4+s\right)}\right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\hfill \\ \hfill & \left.{\left(\left\{\frac{1}{3}\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}\right)-\left[\frac{1}{s^2+4s+3}{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+\left(\frac{1}{1+s}-\frac{2\mathrm{\Gamma }\left(1+s\right)}{\mathrm{\Gamma }\left(4+s\right)}\right){\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right)}^{\frac{1}{q_1}}\right].\hfill \end{array}$$

Corollary 23.

By considering $\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|\le {\mathcal{M}}_1$ in Theorem 7, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left({\mathcal{C}}_3\left(\nu ,\omega \right)\right)}^{1-\frac{1}{q_1}}{\mathcal{M}}_1{\left\{2{\mathcal{C}}_3\left(\nu ,\omega \right)-{\mathcal{C}}_4\left(s,\nu ,\omega \right)-{\mathcal{C}}_5\left(s,\nu ,\omega \right)\right\}}^{\frac{1}{q_1}}\left[{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right].\hfill \end{array}$$

Theorem 8.

For a twice differentiable mapping $\psi :[\mu ,\kappa ]\to \mathbb{R}$ on $(\mu ,\kappa )$ and if ${\left|{\psi }^{″}\right|}^{q_1}$ is an s-convex mapping in the second sense on $[\mu ,\kappa ]$ with $p_1,q_1>1$ and $\frac{1}{p_1}+\frac{1}{q_1}=1$. Then, under the assumptions of Lemma 2, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right].\hfill \end{array}$$

(34)

Proof. 

Taking modulus of Lemma 2 and using Young’s inequality, i.e., $xy\le \frac{1}{p_1}{x}^{p_1}+\frac{1}{q_1}{y}^{q_1}$ (equality holds when $x^{p_1}=y^{q_1}$), we have

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\underset{0}{\overset{1}{\int }}\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|d\tau \hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau +\frac{1}{q_1}\underset{0}{\overset{1}{\int }}{\left|{\psi }^{″}\left(\mathit{\ell }+\mu -\left[\tau {\phi }_1+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau +\frac{1}{q_1}\underset{0}{\overset{1}{\int }}{\left|{\psi }^{″}\left(\mathit{\ell }+\kappa -\left[\tau {\phi }_2+\left(1-\tau \right)\mathit{\ell }\right]\right)\right|}^{q_1}d\tau \right]\hfill \end{array}$$

Now, applying the Jensen–Mercer inequality with the s-convexity of ${\left|{\psi }^{″}\right|}^{q_1}$, we obtain

$$\begin{array}{cc}\hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\underset{0}{\overset{1}{\int }}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\left[{\tau }^s{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left(1-\tau \right)}^s{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}d\tau \right]\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau \right.\hfill \\ \hfill & \left.+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right].\hfill \end{array}$$

(35)

The proof is completed. □

Corollary 24.

Setting ${\phi }_1=\mu ,{\phi }_2=\kappa$ with $\omega =1$ and $\nu =1$ in Theorem 8

$$\begin{array}{cc}\hfill & \left|\left\{\left(\kappa -\mu \right)\psi \left(\mathit{\ell }\right)\right\}+\frac{1}{2}\left\{\left(\kappa -\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-\mu \right){\psi }^{\prime }\left(\mu \right)\right\}-\underset{\mu }{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right|\hfill \\ \hfill & \le \left\{{\left(\mathit{\ell }-\mu \right)}^2+{\left(\kappa -\mathit{\ell }\right)}^2\right\}\left[\frac{\sqrt{\pi }\mathrm{\Gamma }\left(1+p_1\right)}{2^{p_1+1}{p}_1\mathrm{\Gamma }\left(\frac{3}{2}+p_1\right)}+\frac{s}{q_1\left(s+1\right)}\left({\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}\right)\right]\hfill \end{array}$$

Corollary 25.

If we set $\omega =1$ and $\nu =1$ in Theorem 8, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{\left(\mathit{\ell }-{\phi }_1\right)\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\frac{1}{2}\left\{\left({\phi }_2-\mathit{\ell }\right){\psi }^{\prime }\left(\kappa \right)-\left(\mathit{\ell }-{\phi }_1\right){\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}\psi \left(\lambda \right)d\lambda +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}\psi \left(\lambda \right)d\lambda \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2\left[\frac{\sqrt{\pi }\mathrm{\Gamma }\left(1+p_1\right)}{2^{p_1+1}{p}_1\mathrm{\Gamma }\left(\frac{3}{2}+p_1\right)}+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mu \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_1\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right]\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\left[\frac{\sqrt{\pi }\mathrm{\Gamma }\left(1+p_1\right)}{2^{p_1+1}{p}_1\mathrm{\Gamma }\left(\frac{3}{2}+p_1\right)}+\frac{1}{q_1}\left\{{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\kappa \right)\right|}^{q_1}-\frac{1}{s+1}\left[{\left|{\psi }^{″}\left({\phi }_2\right)\right|}^{q_1}+{\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|}^{q_1}\right]\right\}\right].\hfill \end{array}$$

Corollary 26.

By considering $\left|{\psi }^{″}\left(\mathit{\ell }\right)\right|\le {\mathcal{M}}_1$ in Theorem 8, we obtain

$$\begin{array}{cc}\hfill & \left|\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }\psi \left(\mathit{\ell }+\mu -{\phi }_1\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }\psi \left(\mathit{\ell }+\kappa -{\phi }_2\right)\right\}\right.\hfill \\ \hfill & +\underset{0}{\overset{1}{\int }}{\left(1-{\left(1-\tau \right)}^{\omega }\right)}^{\nu }d\tau \left\{{\left({\phi }_2-\mathit{\ell }\right)}^{\nu }{\psi }^{\prime }\left(\kappa \right)-{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu }{\psi }^{\prime }\left(\mu \right)\right\}\hfill \\ \hfill & \left.-{\omega }^{\nu }\mathrm{\Gamma }\left(\nu +1\right)\left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu -\omega \nu }\left({}^{\nu }{I}_{\mathit{\ell }+\mu -{\phi }_1}^{\omega }\psi \left(\mu \right)\right)+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu -\omega \nu }\left({}_{\mathit{\ell }+\kappa -{\phi }_2}^{\nu }{I}^{\omega }\psi \left(\kappa \right)\right)\right\}\right|\hfill \\ \hfill & \le \left\{{\left(\mathit{\ell }-{\phi }_1\right)}^{\nu +1}+{\left({\phi }_2-\mathit{\ell }\right)}^{\nu +1}\right\}\left[\frac{1}{p_1}\underset{0}{\overset{1}{\int }}{\left(\underset{\tau }{\overset{1}{\int }}{\left(\frac{1-{\left(1-x\right)}^{\omega }}{\omega }\right)}^{\nu }dx\right)}^{p_1}d\tau +\frac{2{{\mathcal{M}}_1}^{q_1}}{q_1}\frac{s}{s+1}\right].\hfill \end{array}$$

4. Numerical Examples and Visual Analysis

Throughout this section, for the numerical verification, the following assumptions will be considered:

Suppose $\psi \left(\tau \right)={\tau }^s$ with $s=0.5,\omega =0.5$, $[\mu ,\kappa ]=[1,5]$, $[{\phi }_1,{\phi }_2]=[2,4]$, $\mathit{\ell }=3$, $\nu =1$ and $(p,q,p_1,q_1=2)$.

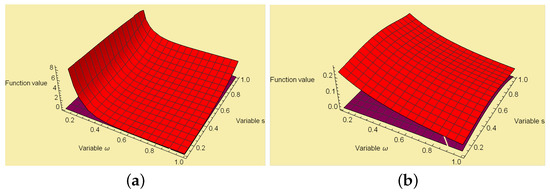
Now from Theorem 1, we have $0.04834<0.40370$ and from Theorem 5, we have $0.04377<0.10530$. This proves the numerical validation of these results.

Next in Figure 1, we present the graphical visualization of Theorems 1 and 5. For this we consider the above mentioned assumptions and $s\in (0,1]$ and $\omega \in (0,1]$.

Figure 1. In the above figures, the yellow and purple surfaces show the right and left sides of inequalities (a) (13) and (b) (28), respectively. Clearly one can see that the inequalities (13) and (28) hold good by varying both the parameters s and $\omega$.

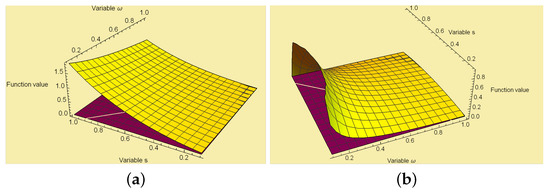
Now from Theorem 2, we have $0.04834<0.27498$ and from Theorem 6, we have $0.04377<0.13139$. This proves the numerical validation of these results.

In Figure 2, we present the graphical visualization of Theorems 2 and 6. For this we consider the above mentioned assumptions and $s\in (0,1]$ and $\omega \in (0,1]$.

Figure 2. In the above figures, the green and purple surfaces show the right and left sides of inequalities (a) (15) and (b) (30), respectively. Clearly one can see that the inequalities (15) and (30) hold good by varying both the parameters s and $\omega$.

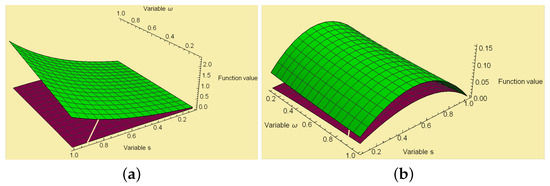
Now from Theorem 3, we have $0.04834<0.12172$ and from Theorem 7, we have $0.04377<0.09022$. This proves the numerical validation of these results.

Next in Figure 3, we present the graphical visualization of Theorems 3 and 7. For this we consider the above mentioned assumptions and $s\in (0,1]$ and $\omega \in (0,1]$.

Figure 3. In the above figures, the pink and purple surfaces show the right and left sides of inequalities (a) (19) and (b) (32), respectively. Clearly one can see that the inequalities (19) and (32) hold good by varying both the parameters s and $\omega$.

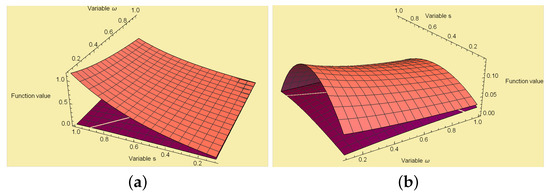
Now from Theorem 4, we have $0.04834<0.78191$ and from Theorem 8, we have $0.04377<0.28330$. This proves the numerical validation of these results.

Now in Figure 4, we present the graphical visualization of Theorems 4 and 8. For this we consider the above mentioned assumptions and $s\in (0,1]$ and $\omega \in (0,1]$.

Figure 4. In the above figures, the red and purple surfaces show the right and left sides of inequalities (a) (21) and (b) (34), respectively. Clearly one can see that the inequalities (21) and (34) hold good by varying both the parameters s and $\omega$.

5. Applications

In this section, we will discuss some applications of our results.

5.1. Special Means

For positive real numbers ${\phi }_1,{\phi }_2,{\phi }_1\ne {\phi }_2$, the following means are well known in the literature:

• The arithmetic mean

  $$\begin{array}{c}\hfill A({\phi }_1,{\phi }_2)=\frac{{\phi }_1+{\phi }_2}{2},{\phi }_1,{\phi }_2\in \mathcal{R}.\end{array}$$
• The generalized log mean

  $$\begin{array}{c}\hfill L_n({\phi }_1,{\phi }_2)={\left(\frac{{{\phi }_2}^{n+1}-{{\phi }_1}^{n+1}}{(n+1)({\phi }_2-{\phi }_1)}\right)}^{\frac{1}{n}},n\in \mathcal{R}\setminus \left\{-1,0\right\},{\phi }_1,{\phi }_2>0\end{array}$$

Proposition 1.

If $\mu ,\kappa \in \mathbb{R},\mu <\kappa$ and $s\in (0,1]$. Then, for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$ and ${\phi }_1,{\phi }_2\in [\mu ,\kappa ]$, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right){\left(2A\left(\mathit{\ell },\mu \right)-{\phi }_1\right)}^s+\left({\phi }_2-\mathit{\ell }\right){\left(2A\left(\mathit{\ell },\kappa \right)-{\phi }_2\right)}^s\right.\hfill \\ \hfill & \left.-\left\{\left(\mathit{\ell }-{\phi }_1\right)L_s^s(\mathit{\ell }+\mu -{\phi }_1,\mu )+\left({\phi }_2-\mathit{\ell }\right)L_s^s(\mathit{\ell }+\kappa -{\phi }_2,\kappa )\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{2}s\left\{A\left({\mathit{\ell }}^{s-1},{\mu }^{s-1}\right)-\frac{2}{s+2}A\left({{\phi }_1}^{s-1},\frac{{\mathit{\ell }}^{s-1}}{s+1}\right)\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{2}s\left\{A\left({\mathit{\ell }}^{s-1},{\kappa }^{s-1}\right)-\frac{2}{s+2}A\left({{\phi }_2}^{s-1},\frac{{\mathit{\ell }}^{s-1}}{s+1}\right)\right\}.\hfill \end{array}$$

Proof. 

Setting $\psi \left(\lambda \right)={\lambda }^s$ in Corollary 2, we obtain the desired inequality. □

Proposition 2.

If $\mu ,\kappa \in \mathbb{R},\mu <\kappa$ and $s\in (0,1]$. Then, for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$ and ${\phi }_1,{\phi }_2\in [\mu ,\kappa ]$, the following inequality holds:

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right){\left(2A\left(\mathit{\ell },\mu \right)-{\phi }_1\right)}^s+\left({\phi }_2-\mathit{\ell }\right){\left(2A\left(\mathit{\ell },\kappa \right)-{\phi }_2\right)}^s\right.\hfill \\ \hfill & +\frac{s}{2}\left\{\left({\phi }_2-\mathit{\ell }\right){\kappa }^{s-1}-\left(\mathit{\ell }-{\phi }_1\right){\mu }^{s-1}\right\}\hfill \\ \hfill & \left.-\left\{\left(\mathit{\ell }-{\phi }_1\right)L_s^s(\mathit{\ell }+\mu -{\phi }_1,\mu )+\left({\phi }_2-\mathit{\ell }\right)L_s^s(\mathit{\ell }+\kappa -{\phi }_2,\kappa )\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^{2}s\left(s-1\right)\left\{\frac{2}{3}A\left({\mathit{\ell }}^{s-2},{\mu }^{s-2}\right)-\left(\frac{1}{\left(s+1\right)\left(s+3\right)}{\phi }_1^{s-2}+\left(\frac{1}{2\left(s+1\right)}-\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\mathit{\ell }}^{s-2}\right)\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^{2}s\left(s-1\right)\left\{\frac{2}{3}A\left({\mathit{\ell }}^{s-2},{\kappa }^{s-2}\right)-\left(\frac{1}{\left(s+1\right)\left(s+3\right)}{\phi }_2^{s-2}+\left(\frac{1}{2\left(s+1\right)}-\frac{\mathrm{\Gamma }\left(s+1\right)}{\mathrm{\Gamma }\left(s+4\right)}\right){\mathit{\ell }}^{s-2}\right)\right\}.\hfill \end{array}$$

Proof. 

Setting $\psi \left(\lambda \right)={\lambda }^s$ in Corollary 16, we obtain the desired inequality. □

5.2. $\mathfrak{q}$-Digamma Mapping

For $0<\mathfrak{q}<1$, the $\mathfrak{q}$-digamma mapping ${\zeta }_{\mathfrak{q}}$ is given in [45,46] as follows:

$$\begin{array}{cc}\hfill {\zeta }_{\mathfrak{q}}\left(\gamma \right)& =-ln\left(1-\mathfrak{q}\right)+ln\mathfrak{q}\sum _{j=0}^{\infty }\frac{{\mathfrak{q}}^{k+\gamma }}{1-{\mathfrak{q}}^{k+\gamma }}\hfill \\ \hfill & =-ln\left(1-\mathfrak{q}\right)+ln\mathfrak{q}\sum _{j=1}^{\infty }\frac{{\mathfrak{q}}^{k\gamma }}{1-{\mathfrak{q}}^k}.\hfill \end{array}$$

For $\mathfrak{q}>1$ and $\gamma >0$, the $\mathfrak{q}$-digamma mapping ${\zeta }_{\mathfrak{q}}$ can be defined as follows:

$$\begin{array}{cc}\hfill {\zeta }_{\mathfrak{q}}\left(\gamma \right)& =-ln\left(\mathfrak{q}-1\right)+ln\mathfrak{q}\left[\gamma -\frac{1}{2}-\sum _{j=0}^{\infty }\frac{{\mathfrak{q}}^{-\left(k+\gamma \right)}}{1-{\mathfrak{q}}^{-\left(k+\gamma \right)}}\right]\hfill \\ \hfill & =-ln\left(\mathfrak{q}-1\right)+ln\mathfrak{q}\left[\gamma -\frac{1}{2}-\sum _{j=1}^{\infty }\frac{{\mathfrak{q}}^{-\left(k\gamma \right)}}{1-{\mathfrak{q}}^{-\left(k\gamma \right)}}\right].\hfill \end{array}$$

Proposition 3.

Let $0<\mu <\kappa$, $\mathfrak{p},\mathfrak{q}>1$, $0<\mathfrak{q}<1$ and ${\mathfrak{q}}^{-1}=1-{\mathfrak{p}}^{-1}$. Then, for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$ and ${\phi }_1,{\phi }_1\in [\mu ,\kappa ]$, we have

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right){\zeta }_{\mathfrak{q}}\left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right){\zeta }_{\mathfrak{q}}\left(\mathit{\ell }+\kappa -{\phi }_2\right)\right.\hfill \\ \hfill & \left.-\left\{\underset{\mu }{\overset{\mathit{\ell }+\mu -{\phi }_1}{\int }}{\zeta }_{\mathfrak{q}}\left(\gamma \right)d\gamma +\underset{\mathit{\ell }+\kappa -{\phi }_2}{\overset{\kappa }{\int }}{\zeta }_{\mathfrak{q}}\left(\gamma \right)d\gamma \right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2{\left(\frac{1}{\mathfrak{p}+1}\right)}^{\frac{1}{\mathfrak{p}}}\hfill \\ \hfill & {\left({\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\mathit{\ell }\right)\right|}^{\mathfrak{q}}+{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\mu \right)\right|}^{\mathfrak{q}}-\frac{1}{2}\left[{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left({\phi }_1\right)\right|}^{\mathfrak{q}}+{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\mathit{\ell }\right)\right|}^{\mathfrak{q}}\right]\right)}^{\frac{1}{\mathfrak{q}}}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2{\left(\frac{1}{\mathfrak{p}+1}\right)}^{\frac{1}{\mathfrak{p}}}\hfill \\ \hfill & {\left({\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\mathit{\ell }\right)\right|}^{\mathfrak{q}}+{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\kappa \right)\right|}^{\mathfrak{q}}-\frac{1}{2}\left[{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left({\phi }_2\right)\right|}^{\mathfrak{q}}+{\left|{{\zeta }_{\mathfrak{q}}}^{\prime }\left(\mathit{\ell }\right)\right|}^{\mathfrak{q}}\right]\right)}^{\frac{1}{\mathfrak{q}}}.\hfill \end{array}$$

Proof. 

The assertion can be obtained immediately by using Corollary 7 with the $\psi :\gamma \to {\zeta }_{\mathfrak{q}}\left(\gamma \right)$ is a completely monotone mapping on $(0,\infty )$ for all $\gamma >0$ and consequently, ${\psi }^{\prime }\left(\gamma \right):={{\zeta }_{\mathfrak{q}}}^{\prime }\left(\gamma \right)$ is convex. □

5.3. Modified Bessel Function

In [46], the modified Bessel mapping of the first kind ${\xi }_{\omega }\left(\gamma \right)$ is given as follows:

$$\begin{array}{c}\hfill {\xi }_{\omega }\left(\gamma \right)=\sum _{n=0}^{\infty }\frac{{\left(\frac{\gamma }{2}\right)}^{\omega +2n}}{n!\mathrm{\Gamma }\left(\omega +n+1\right)},\end{array}$$

where $\gamma \in \mathbb{R}$ and $\omega <-1$.

The modified Bessel mapping of the second kind ${\varrho }_{\omega }\left(\gamma \right)$ (see [46]) is given as follows:

$$\begin{array}{c}\hfill {\varrho }_{\omega }\left(\gamma \right)=\frac{\pi }{2}\frac{{\gamma }_{-\omega }\left(\gamma \right)-{\gamma }_{\omega }\left(\gamma \right)}{sin\omega \pi }.\end{array}$$

The mapping ${\mathcal{B}}_{\omega }\left(\gamma \right):\mathbb{R}\to [1,\infty )$ can be defined as follows:

$$\begin{array}{c}\hfill {\mathcal{B}}_{\omega }\left(\gamma \right)=2^{\omega }\mathrm{\Gamma }\left(\omega +1\right){\gamma }^{-\omega }{\varrho }_{\omega }\left(\gamma \right),\end{array}$$

where $\mathrm{\Gamma }$ is the gamma mapping.

In [46], the following derivative formulas of $B_{\omega }\left(\gamma \right)$ are given as follows:

$$\begin{array}{c}\hfill {{\mathcal{B}}_{\omega }}^{\prime }\left(\gamma \right)=\frac{\gamma }{2\left(\omega +1\right)}{\mathcal{B}}_{\omega +1}\left(\gamma \right),\end{array}$$

(36)

and

$$\begin{array}{c}\hfill {{\mathcal{B}}_{\omega }}^{″}\left(\gamma \right)=\frac{{\gamma }^2{\mathcal{B}}_{\omega +2}\left(\gamma \right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\gamma \right)}{2\left(\omega +1\right)}.\end{array}$$

(37)

Proposition 4.

Let $0<\mu <\kappa$ and $\omega >-1$. Then, for all $\mathit{\ell }\in [{\phi }_1,{\phi }_2]$ and ${\phi }_1,{\phi }_1\in [\mu ,\kappa ]$, we have

$$\begin{array}{cc}\hfill & \left|\left(\mathit{\ell }-{\phi }_1\right)\frac{\left(\mathit{\ell }+\mu -{\phi }_1\right)}{2\left(\omega +1\right)}{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }+\mu -{\phi }_1\right)+\left({\phi }_2-\mathit{\ell }\right)\right.\frac{\left(\mathit{\ell }+\kappa -{\phi }_2\right)}{2\left(\omega +1\right)}{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }+\kappa -{\phi }_2\right)\hfill \\ \hfill & \left.-\left\{\left({\mathcal{B}}_{\omega }\left(\mathit{\ell }+\mu -{\phi }_1\right)-{\mathcal{B}}_{\omega }\left(\mu \right)\right)+\left({\mathcal{B}}_{\omega }\left(\kappa \right)-{\mathcal{B}}_{\omega }\left(\mathit{\ell }+\kappa -{\phi }_2\right)\right)\right\}\right|\hfill \\ \hfill & \le {\left(\mathit{\ell }-{\phi }_1\right)}^2\left\{\frac{1}{2}\left[\frac{{\mathit{\ell }}^2{\mathcal{B}}_{\omega +2}\left(\mathit{\ell }\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }\right)}{2\left(\omega +1\right)}+\frac{{\mu }^2{\mathcal{B}}_{\omega +2}\left(\mu \right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\mu \right)}{2\left(\omega +1\right)}\right]\right.\hfill \\ \hfill & \left.-\left[\frac{1}{3}\left(\frac{{\left({\phi }_1\right)}^2{\mathcal{B}}_{\omega +2}\left({\phi }_1\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left({\phi }_1\right)}{2\left(\omega +1\right)}\right)+\frac{1}{6}\left(\frac{{\mathit{\ell }}^2{\mathcal{B}}_{\omega +2}\left(\mathit{\ell }\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }\right)}{2\left(\omega +1\right)}\right)\right]\right\}\hfill \\ \hfill & +{\left({\phi }_2-\mathit{\ell }\right)}^2\left\{\frac{1}{2}\left[\frac{{\mathit{\ell }}^2{\mathcal{B}}_{\omega +2}\left(\mathit{\ell }\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }\right)}{2\left(\omega +1\right)}+\frac{{\mathit{\ell }}^2{\mathcal{B}}_{\omega +2}\left(\kappa \right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\kappa \right)}{2\left(\omega +1\right)}\right]\right.\hfill \\ \hfill & \left.-\left[\frac{1}{3}\left(\frac{{\left({\phi }_2\right)}^2{\mathcal{B}}_{\omega +2}\left({\phi }_2\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left({\phi }_2\right)}{2\left(\omega +1\right)}\right)+\frac{1}{6}\left(\frac{{\mathit{\ell }}^2{\mathcal{B}}_{\omega +2}\left(\mathit{\ell }\right)}{4\left(\omega +1\right)\left(\omega +2\right)}+\frac{{\mathcal{B}}_{\omega +1}\left(\mathit{\ell }\right)}{2\left(\omega +1\right)}\right)\right]\right\}.\hfill \end{array}$$

Proof. 

Using Corollary 3 to the mapping $\psi :\gamma ={{\mathcal{B}}_{\omega }}^{\prime }\left(\gamma \right),\gamma >0$ (Note that all assumptions are satisfied) and the identities (36) and (37). □

6. Conclusions

To summarize, this research study introduces new fractional versions of Ostrowski–Mercer-type inequalities by using the first and the second order differentiable s-convex mappings, achieved by using the conformable fractional integral operators. The significance and applicability of our main results have been discussed thoroughly by numerical examples and graphical analysis. We have also discussed the applications of our outcomes pertaining to special means, q-digamma functions, and modified Bessel functions. We hope that this study will inspire interested readers working in this field.