Abstract
This paper presents an initial proposal for the utilization of mediative fuzzy logic in control problems. Mediative fuzzy logic (MFL) was originally proposed with the idea of modeling situations in which there exists contradictory knowledge among several experts in an application domain. In this situation, a mediative solution may be a better choice in this particular decision-making situation. In this paper, we are extending the concept of fuzzy control to the realm of MFL for situations in which we have two or more control experts, and the design of the fuzzy controller has to be based on their knowledge. In this situation, we are taking advantage of the symmetrical nature of membership functions in reducing the complexity of designing the fuzzy controllers. The goal of this study was to improve control results by combining the knowledge of several experts, which MFL is aimed at executing. The initial architecture of mediative fuzzy control for type-1 fuzzy logic is presented, and an illustrative example is used to better comprehend the proposed approach. Later, we extend type-1 MFL to the realms of type-2 and type-3 fuzzy logic, and we also provide a comparative study that exhibits that the type-3 version surpasses the type-2 and type-1 versions of mediative fuzzy control. The idea of utilizing type-2 and type-3 is to improve the capabilities of the fuzzy controller in handling uncertainty coming from noise in the control process.
1. Introduction
In computational intelligence, it is well known that fuzzy systems can successfully be applied in a plethora of areas, such as control, diagnosis and prediction. Originally, fuzzy sets (now called type-1) were put forward by Lotfi Zadeh in 1965 [1]. Later, fuzzy logic and fuzzy systems were also proposed by Zadeh, and many applications followed, mainly in control [2].
The concept of mediative fuzzy logic (MFL) was originally proposed by the authors in 2005 [3], and was later illustrated with an application to control a parameter in the human evolutionary algorithm [4]. This initial proposal was only for type-1 fuzzy logic and was viewed as an extension of intuitionistic fuzzy logic. Later, other authors have applied this concept to several medical problems, such as heart disease diagnosis [5,6], diabetes diagnosis [7], prediction of the COVID-19 pandemic [8] and others [9]. In summary, most of the existing works utilizing MFL have been carried out in relation to the medical diagnosis area, where the knowledge of several medical experts is combined to improve the diagnosis. However, even with these developments, the extension of mediative fuzzy logic to the realm of fuzzy control has remained an open problem, which can be viewed as a research gap in this area. The only similar work we can mention on this line of research is the recently outlined proposal of type-3 intuitionistic fuzzy logic (IFL) in [10], as the type-3 mediative fuzzy system could be thought of as a generalization of that work. This was the motivation for undertaking this work, in which we are putting forward the extension of mediative fuzzy logic to the realm of fuzzy control with the expectation that this will provide us with even more powerful tools to solve complex and uncertain decision-making problems. Since MFL was initially proposed for type-1, it is natural to think about its extension to the realms of type-2 and type-3, and, in this sense, this is how the existing research gap that motivated our work was identified. The research gap consists of the nonexistent applications of MFL in the area of control that would consider the knowledge of several control experts, as well as the combination of MFL with type-2 or type-3 that have also not yet been proposed in the literature. The extensions of mediative fuzzy control to the level of type-2, and after that to the level of type-3, were proposed in this work. We can mention that, recently, type-3 fuzzy logic has been utilized (with relative success) to handle uncertainty coming from sensor measurements, such as in control problems and other application areas [11,12,13,14,15,16,17,18,19]. The main idea in these type-3 applications was to model the intrinsic uncertainty of real problems in an improved manner, which comes from the noise in real data. However, the uncertainty from expert knowledge was not considered. As a consequence, we are proposing an initial approach for a mediative type-3 fuzzy controller in this work, which we expect will be able to handle both kinds of uncertainty, coming from the noise in the control process and from the contradictory knowledge of the experts. In summary, the main contribution is the proposal of combining MFL with type-1, type-2 and type-3 fuzzy logic, which have not been previously proposed in the literature. In addition, an illustrative example is utilized to show that the proposed mediative fuzzy control approach has the potential of having good performance in the control area. Finally, a comparative study shows that the type-3 and MFL surpasses all the other variants of MFL, as well as the intuitionistic and conventional controllers.
The primary finding of this work is that MFL can help improve the control results by combining the knowledge of several experts, by handling the uncertainty in the knowledge of the experts. Another important finding is that MFL, in conjunction with the ideas of type-2 and type-3 fuzzy logic, can also improve the capabilities of the controllers in handling the uncertainty in the real control process (due to the external noise of dynamic changes in the environment). If we could mention a limitation of the proposed methods with MFL, it would be that we need to have availability for at least two experts in a particular control application area.
The rest of the article is structured as follows: Section 2 recalls the definitions of mediative fuzzy logic, Section 3 outlines the definition of fuzzy control, Section 4 puts forward the proposal for mediative fuzzy control, Section 5 illustrates the proposal with an example, and Section 6 offers the conclusions reached after performing this research work.
2. Mediative Fuzzy Logic for Type-1 Controller
Since the knowledge offered by the experts has large variations and is contradictory to some degree, we proposed the utilization of a contradiction fuzzy set to estimate a mediation result. MFL was proposed as an extension of IFL (in the sense of [20]). MFL relies on type-1 fuzzy logic with the capability of managing contradiction; therefore, it is an intuitionistic and paraconsistent system.
A traditional fuzzy set in X [21] is given by
where µA(x) has values in [0, 1]. In this expression, µA(x) is the membership function (MF) that assigns a membership to each x. This fuzzy set is now called type-1.
A = {⟨x, µA(x)⟩ | x ∈ X},
An intuitionistic fuzzy set B [10,20] is given by
where µB(x), νB(x) are the membership and non-membership degrees of x ∈ X to a set B in X, 0 ≤ µB(x), νB(x) ≤ 1 and
B = {⟨x, µB(x), νB(x)⟩ | x ∈ X},
0 ≤ µB(x) + νB(x) ≤ 1.
Now consider the following equation:
where, here, πB defines the uncertainty degree. The key idea is that uncertainty in real problems is captured by π.
πB(x) = 1 − μB(x) − νB(x),
The inference in intuitionistic systems has to consider MFs and non-membership functions (NMFs). In this case, it is supposed that the output is a mixture of two systems (MF and NMF).
The IFS output of an intuitionistic system is computed with the following expression [22]:
where FSµ is the output utilizing MFs (µ), and FSν is the output utilizing NMFs (ν). In this case, Equation (6) for π = 0 reduces to a type-1 system; however, the results change accordingly, for different π values.
IFS = (1 − π)FSµ + πFSν
In a similar way, a contradiction fuzzy set C in X can be expressed by
where μC(x) represents the agreement MF, and νC(x) is the non-agreement MF [4].
ζC(x) = min(μC(x), νC(x))
We are utilizing agreement and non-agreement instead of membership and non-membership because we believe that these labels are more appropriate when there are contradictions.
We originally proposed three expressions for computing the inference at the system’s output, and these are [4]
where MFS stands for the output of the mediative fuzzy system. In this case, when ζ = 0, the system’s output reduces to an intuitionistic output or, when π = 0, it reduces to a type-1 output.
MFS = (1 − π − ζ/2)FSµ + (π + ζ/2)FSν
MFS = min(((1 − π)FSµ + πFSν), (1 − ζ/2))
MFS = ((1 − π)FSµ + πFSν)) (1 − ζ/2)
3. Proposed Mediative Type-1 Fuzzy Controller
Fuzzy control is based on the original ideas of fuzzy sets and fuzzy logic proposed by Zadeh [1,2]. The first fuzzy controller was designed by Mamdani by utilizing fuzzy rules (containing knowledge from the experts) and fuzzy reasoning to obtain the outputs. The main idea was that by using linguistic variables and values, the control tasks could be performed in a similar way to expert humans. The main components of a Mamdani fuzzy system are as follows: fuzzifier, fuzzy rules, inferences and defuzzification. Furthermore, many fuzzy controllers have been designed and implemented in this way. Fuzzy control was very successful and has been utilized in many real-world problems [23].
In this paper, we are proposing an extension to the concept of fuzzy control by utilizing the MFL concept, which would be useful when the knowledge of several experts is considered in designing the fuzzy controllers. Of course, when several experts are considered, there exists the possibility of contradictory knowledge, and, in this situation, mediative fuzzy logic would be helpful in modeling this contradictory part. For this reason, we propose the following architecture of the mediative fuzzy controller (Figure 1), where we consider two fuzzy controllers (one for membership and the other for non-membership), and then the aggregation of the outputs is performed with Equation (7) to obtain the final output.
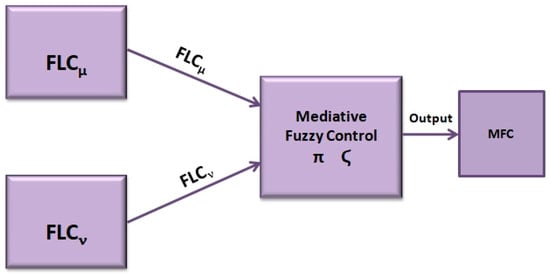
Figure 1.
Proposed architecture for the mediative fuzzy controller.
4. Mediative Type-2 Fuzzy Controller
This section describes the initial approach for combining type-2 fuzzy logic with mediative fuzzy logic for control applications. Type-2 fuzzy logic was proposed as a way to handle uncertainty in real-world problems, for example, in the noise in control applications. Mediative fuzzy logic (MFL) was originally put forward to manage contradictory knowledge among several experts in the design of fuzzy systems. As a consequence, we propose the type-2 fuzzy mediative controller as a better approach to handle both kinds of uncertainty, namely due to noise and contradiction.
The main architecture of the mediative type-2 fuzzy controller would be similar to Figure 2, with a need to change the blocks of type-1 for type-2, and then by applying Equation (7) for combining the results. The idea is that, with the type-2 fuzzy controller, we could handle uncertainty in fuzzy control due to noise or perturbations, while the mediative controller could manage the uncertainty caused by the contradictory knowledge from the experts.
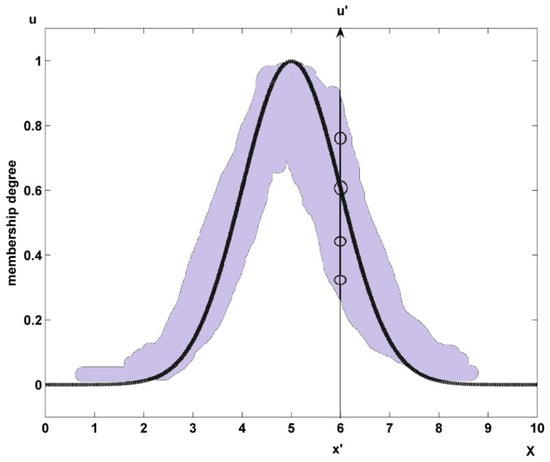
Figure 2.
Type-2 membership function as a blurred type-1 MF.
Fuzzy rules in mediative type-2 fuzzy control are the same as in type-1 because the knowledge of the experts should be same; the difference resides in the form of the membership functions (MFs), which now have a footprint of uncertainty (FOU) [24]. In Figure 2, we illustrate the form of a type-2 MF in which the shaded area is the FOU.
A typical structure of a type-2 fuzzy system is depicted in Figure 3. The output processor generates a type-1 fuzzy set output (from the type reducer) or a number (from the defuzzifier). This structure is similar to the one for type-1; however, the main difference lies in the utilization of type reduction for converting type-2 fuzzy sets into type-1 sets. Of course, all operations with type-2 fuzzy sets are generalized versions of their type-1 counterparts [24].
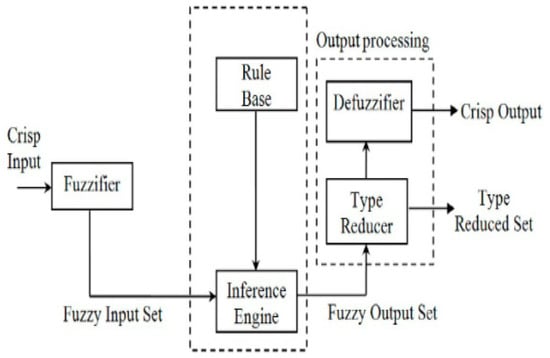
Figure 3.
Structure of a type-2 fuzzy system.
The structure in Figure 3 refers to a Mamdani style of inference; however, there also exist Sugeno kinds of fuzzy models, which would be a slightly different at the output of the fuzzy system [25].
5. Mediative Type-3 Fuzzy Controller
This section considers elevating the type of fuzzy logic to the realm of type-3 for providing even higher capabilities of handling uncertainty to the fuzzy controllers [25]. This is due to the recent evidence that the type-3 fuzzy controllers have been able to outperform type-2 in some complex control problems [26,27]. Therefore, in this sense, it will be expected that a combination of type-3 and MFL would be valuable in handling uncertainty coming from noise as well as due to contradictory knowledge.
The main architecture of a mediative type-3 fuzzy controller would be similar to Figure 1, but by changing the blocks of type-1 for type-3, and then by applying Equation (7) for combining the results.
Fuzzy rules in the mediative type-3 fuzzy controller are the same as in type-2 because the knowledge of the experts should be same; the difference resides in the form of the membership functions, which now have a new form for the footprint of uncertainty (FOU). In Figure 4, we illustrate the form of a type-3 MF in which the shaded area is the FOU. In addition, Figure 5 illustrates a typical structure for a type-3 fuzzy system based on vertical cuts [26].
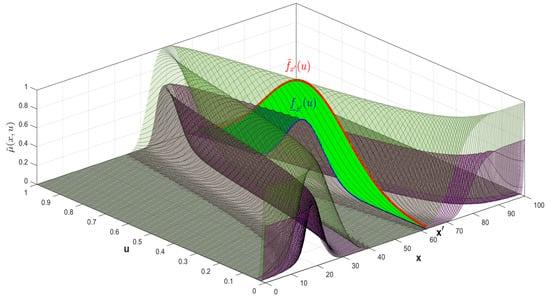
Figure 4.
Illustration of an interval type-3 membership function.
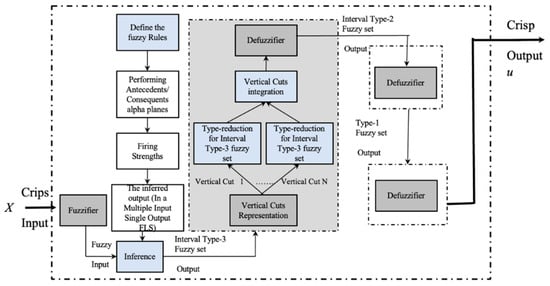
Figure 5.
Structure of a type-3 fuzzy system.
By comparing Figure 5 for type-3 with Figure 3 for type-2 fuzzy sets, we can notice that the most notable difference is in the type-reduction process, which involves using multiple fuzzy systems (corresponding to the vertical cuts) and then aggregating the results and defuzzification to obtain an interval type-2 fuzzy set. After this, the process is completed similarly to type-2, which is performed by reducing the fuzzy set to type-1 and then by performing traditional defuzzification to obtain a crisp number. Of course, all operations on type-3 fuzzy sets are an extension of the type-2 fuzzy operations; more details are outlined in the reference [26].
6. Illustrative Example
Air vehicles, such as airplanes and helicopters, have complex dynamics because of the nonlinear aerodynamic forces and uncertain effects of air flows. Therefore, the control of these vehicles is very difficult and is a challenge for any kind of controller [28]. The control systems’ design for stability of air vehicles is a very important topic. For flight control systems, Feedback Inc. designed a laboratory platform called twin rotor multi-input multi-output system (TRMS), which is illustrated in Figure 6. TRMS is similar to a helicopter, which has two rotors that are the tail rotor and main rotor, and the rotors generate, respectively, vertical (pitch angle) and horizontal torques (yaw) [28].
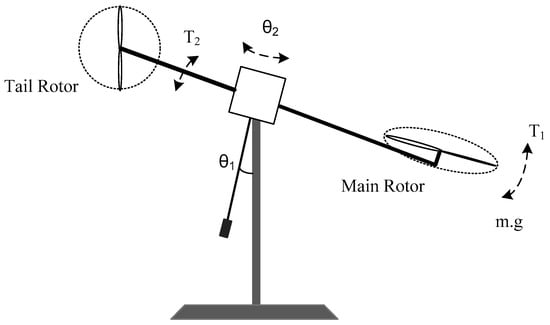
Figure 6.
Twin rotor MIMO systems from Feedback Inc.
The equations of the helicopter are nonlinear multi-input and multi-output systems in which the tail rotor and main rotor models are, respectively, expressed as
where ϴ1 and ϴ2 are the angles which are changed by the main and tail motors. TRMS uses the DC motors to generate the torques which have nonlinear characteristics and are expressed as
where τ1 and τ2 are dependent on the DC motor voltage, and are expressed as
where u1 and u2 are, respectively, the main motor and tail rotor voltages, and k1, k2, T11, T10 and T20 are motor parameters.
There are also fraction forces, and these forces generate fractional torques that are, respectively, expressed as
where and are fraction constants. In the TRMS, the gyroscopic torque, gravity torque and cross reaction torque are, respectively, formulated as
where KGY, T0 and Tp are system parameters in the TRMS model.
An intuitionistic fuzzy controller was proposed in [28], and more details about the nature of the fuzzy rules and MFs can be found there. Following this process, a fuzzy rule base, which is based on an if-then structure is defined for both rotors; more details are described in [28]. Both the error and change of error linguistic variables were granulated in five linguistic values: negative big (NB), negative (N), zero (Z), positive (P) and positive big (PB). Also, the output variable is granulated in the same way. The parameters for the antecedents are presented in Table 1 and Table 2 for the error and change of error variables, respectively. The parameters for the consequences are shown in Table 3.

Table 1.
MF antecedent parameters for the error variable for the main and tail rotors.

Table 2.
MF antecedent parameters for the change of error variable for the main and tail rotors.

Table 3.
MF consequent parameters for the main and tail rotors (same for both outputs).
In Table 1, Table 2 and Table 3, we show the parameters of the MFs for the linguistic values, which utilize three parameters (a, b, c) for the triangular MFs and four parameters (a, b, c, d) for the trapezoidal MFs. For obtaining the NMFs, we needed to define a π value that is appropriate, which, in this case, we found with trial and error to be 0.1. For extending fuzzy sets to type-2 and type-2 MFs, we utilize the parameters (LowerScale) and (LowerLag), which provides the FOU for these types of fuzzy systems; for more details, please check [26]. Based on the MFs and non-MFs proposed in [28], we present the results for the mediative type-1 fuzzy controller that can be viewed as an extension of the intuitionistic controller presented in [28]. In this case, we needed to find the ζ value, which represents the level of contradiction of the experts, and we found the appropriate value to be 0.05. We can now utilize Equation (7) to combine the outputs of the fuzzy systems (for MFs and NMFs) and finally compute the mediative output for each case (type-1, type-2 and type-3).
The tracking performance of the pitch and yaw angles of the twin rotor system in the conventional control method are shown in Table 4 for different reference signals. The test criterion is a performance index called the integral square error (ISE). In Table 2, we show a comparison of the mediative with respect to the intuitionistic and proportional integral derivative (PID) controller. Trom Table 4, we can clearly notice that the mediative controller (with type-1) produces lower errors than the intuitionistic and PID controllers, which is a positive sign of the potential advantage of using MFL in conjunction with type-1 fuzzy logic. This shows that our initial claim that MFL could improve the results is valid because the mediative results (last column) show a lower error in all signals.

Table 4.
Comparison of results of the proposed controller with respect to previous works.
Now, we show the simulation results for the mediative type-2 and type-3 fuzzy controllers, in which we only change the form of the MFs (which are three-dimensional), while the fuzzy control rules remain the same. In Table 5, we compare the results of mediative type-1, type-2 and type-3 fuzzy controls of the helicopter problem. In this table, it is evident that the mediative type-3 fuzzy controller is able to outperform the mediative versions of the type-2 and type-1 fuzzy controllers, with this also showing that our initial claim that the type-3 fuzzy controller would be able to improve results is also true.

Table 5.
Comparison of results of the mediative type-3 fuzzy controller with respect to the type-2 and type-1 fuzzy controllers.
The previous results were obtained by designing all versions of the fuzzy controllers with trial and error, which means that the parameterization was performed with manual tuning (based on the original type-1 versions of [28]). As a future work, we will consider the optimization of parameters with the help of metaheuristic algorithms, such as particle swarm optimization, genetic algorithm or the grey wolf algorithm. Even with this limitation of this work, we can state that our claim that, along with MFL, we could model the uncertainty of the expert knowledge and, in this way, improve the control results that were shown to be true with the results from Table 4 and Table 5. In addition, our claim that type-3 could also help to model the uncertainty coming from the noise in the control process can be verified to be true with the results from Table 5 (last column), in which the mediative type-3 fuzzy controller achieves the lowest errors.
7. Conclusions
This article has outlined an initial proposal for the utilization of mediative fuzzy logic in control problems. Mediative fuzzy logic was originally proposed with the idea of modeling situations in which there exists contradictory knowledge among several experts in an application domain. In this situation, a mediative solution may be a better choice in this particular decision-making situation. In this work, we are extending the concept of the fuzzy controller to the realm of MFL for situations in which we have two or more control experts, and the design of the fuzzy controller has to be based on their knowledge. The architecture of a mediative fuzzy controller was presented, and an illustrative example is used to better comprehend the proposed approach. In addition, we have also considered the extension of mediative fuzzy logic to the realms of type-2 and type-3 fuzzy logic to increase our ability to handle higher levels of uncertainty in controllers. Simulation results show that the mediative type-3 fuzzy controller is the best option for this kind of problem. We can justify that our claims are true based on the results obtained in the illustrative example, particularly in Table 4 and Table 5, which show that the utilization of MFL which helps to improve our results. In addition, the utilization of type-3 fuzzy logic in conjunction with MFL produces the best results, as it is able to handle both kinds of uncertainty (coming from knowledge contradiction and from the noise in the controllers). As a future work, we will continue constructing the basis for mediative fuzzy controllers, and, later, their applications in different control problems, such as the ones discussed in [29,30,31,32]. The optimization of the mediative fuzzy controllers with metaheuristics (such as particle swarm optimization, genetic algorithms or others) could be considered as a future research direction, and it is expected that the results could be improved even further. Finally, it is also possible to consider other application areas for utilizing MFL in conjunction with type-2 or type-3 fuzzy logic, such as medical diagnosis, plant monitoring or pattern recognition.
Author Contributions
Conceptualization and writing—review and editing, O.C.; formal analysis, methodology and validation, P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank TecNM and Conacyt for their support during the realization of this research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Knowledge representation in Fuzzy Logic. In IEEE Transactions on Knowledge Data Engineering; Springer: Boston, MA, USA, 1989; Volume 1, p. 89. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Rodríguez Días, A.; Sepúlveda, R. Reducing the cycling problem in evolutionary algorithms. In Proceedings of the ICAI-2005, Las Vegas, NV, USA, 27–30 June 2005; pp. 426–432. [Google Scholar]
- Montiel, O.; Castillo, O.; Melin, P.; Sepulveda, R. Mediative fuzzy logic: A new approach for contradictory knowledge management. Soft Comput. 2008, 12, 251–256. [Google Scholar] [CrossRef]
- Iancu, I. Heart disease diagnosis based on mediative fuzzy logic. Artif. Intell. Med. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- Dhiman, N.; Sharma, M.K. Mediative Sugeno’s-TSK Fuzzy Logic Based Screening Analysis to Diagnosis of Heart Disease. Appl. Math. 2019, 10, 448–467. [Google Scholar] [CrossRef][Green Version]
- Sharma, M.K.; Dhiman, N.; Mishra, V.N. Mediative Fuzzy Logic of Sugeno-Tsk Model for the Diagnosis of Diabetes. J. Phys. Conf. Ser. 2021, 1724, 012028. [Google Scholar] [CrossRef]
- Sharma, M.K.; Dhiman, N.; Vandana Mishra, V.N. Mediative fuzzy logic mathematical model: A contradictory management prediction in COVID-19 pandemic. Appl. Soft Comput. 2021, 105, 107285. [Google Scholar] [CrossRef]
- Sharma, M.K.; Dhiman, N.; Mishra, L.N.; Mishra, V.N.; Sahani, S.K. Mediative Fuzzy Extension Technique and Its Consistent Measurement in the Decision Making of Medical Application. Math. Probl. Eng. 2021, 2021, 1–9. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. Towards Interval Type-3 Intuitionistic Fuzzy Sets and Systems. Mathematics 2022, 10, 4091. [Google Scholar] [CrossRef]
- Qasem, S.N.; Ahmadian, A.; Mohammadzadeh, A.; Rathinasamy, S.; Pahlevanzadeh, B. A type-3 logic fuzzy system: Optimized by a correntropy based Kalman filter with adaptive fuzzy kernel size. Inform. Sci. 2021, 572, 424–443. [Google Scholar] [CrossRef]
- Mohammadzadeh, A.; Sabzalian, M.H.; Zhang, W. An interval type-3 fuzzy system and a new online fractional-order learning algorithm: Theory and practice. IEEE Trans. Fuzzy Syst. 2020, 28, 1940–1950. [Google Scholar] [CrossRef]
- Liu, Z.; Mohammadzadeh, A.; Turabieh, H.; Mafarja, M.; Band, S.S.; Mosavi, A. A New Online Learned Interval Type-3 Fuzzy Control System for Solar Energy Management Systems. IEEE Access 2021, 9, 10498–10508. [Google Scholar] [CrossRef]
- Singh, D.; Verma, N.K.; Ghosh, A.K.; Malagaudanavar, A.K. An Approach Towards the Design of Interval Type-3 TS Fuzzy System. IEEE Trans. Fuzzy Syst. 2021, 30, 3880–3893. [Google Scholar] [CrossRef]
- Wang, J.H.; Tavoosi, J.; Mohammadzadeh, A.; Mobayen, S.; Asad, J.H.; Assawinchaichote, W.; Skruch, P. Non-Singleton Type-3 Fuzzy Approach for Flowmeter Fault Detection: Experimental Study in a Gas Industry. Sensors 2021, 21, 7419. [Google Scholar] [CrossRef] [PubMed]
- Alattas, K.A.; Mohammadzadeh, A.; Mobayen, S.; Aly, A.A.; Felemban, B.F. A New Data-Driven Control System for MEMSs Gyroscopes: Dynamics Estimation by Type-3 Fuzzy Systems. Micromachines 2021, 12, 1390. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Raise, A.; Mohammadzadeh, A.; Rathinasamy, S.; Band, S.S.; Mosavi, A. Deep learned recurrent type-3 fuzzy system: Application for renewable energy modeling/prediction. Energy Rep. 2021, 7, 8115–8127. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, C.; Mohammadzadeh, A. Type-3 Fuzzy Control of Robotic Manipulators. Symmetry 2023, 15, 483. [Google Scholar] [CrossRef]
- Huang, H.; Xu, H.; Chen, F.; Zhang, C.; Mohammadzadeh, A. An Applied Type-3 Fuzzy Logic System: Practical Matlab Simulink and M-Files for Robotic, Control, and Modeling Applications. Symmetry 2023, 15, 475. [Google Scholar] [CrossRef]
- Atanassov, K. Intuitionistic Fuzzy Sets: Theory and Applications; Springer: Heidelberg, Germany, 1999. [Google Scholar]
- Mendel, J.M.; Bob John, R.I. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A new method for fuzzy inference in intuitionistic fuzzy systems. In Proceedings of the International Conference NAFIPS 2003, Chicago, IL, USA, 24–26 July 2003; IEEE Press: Chicago, IL, USA; pp. 20–25. [Google Scholar]
- Melin, P.; Castillo, O. Adaptive intelligent control of aircraft systems with a hybrid approach combining neural networks, fuzzy logic and fractal theory. Appl. Soft Comput. 2003, 3, 353–362. [Google Scholar] [CrossRef]
- Mendel, J.M.; Hagras, H.; Tan, W.-W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control; Wiley and IEEE Press: Hoboken, NJ, USA, 2014. [Google Scholar]
- JMoreno, J.E.; Sanchez, M.A.; Mendoza, O.; Rodríguez-Díaz, A.; Castillo, O.; Melin, P.; Castro, J.R. Design of an interval Type-2 fuzzy model with justifiable uncertainty. Inf. Sci. 2020, 513, 206–221. [Google Scholar] [CrossRef]
- Castillo, O.; Castro, J.R.; Melin, P. Interval Type-3 Fuzzy Systems: Theory and Design, 1st ed.; Springer: Cham, Switzerland, 2022; pp. 45–67. [Google Scholar]
- Mendez, G.M.; Lopez-Juarez, I.; Montes-Dorantes, P.N.; Garcia, M.A. A New Method for the Design of Interval Type-3 Fuzzy Logic Systems with Uncertain Type-2 Non-Singleton Inputs (IT3 NSFLS-2): A Case Study in a Hot Strip Mill. IEEE Access 2023, 11, 44065–44081. [Google Scholar] [CrossRef]
- Castillo, O.; Kutlu, F.; Atan, O. Intuitionistic fuzzy control of twin rotor multiple input multiple output systems. J. Intell. Fuzzy Syst. 2020, 38, 821–833. [Google Scholar] [CrossRef]
- Nabipour, N.; Qasem, S.N.; Jermsittiparsert, K. Type-3 fuzzy voltage management in PV/hydrogen fuel cell/battery hybrid systems. Int. J. Hydrog. Energy 2020, 45, 32478–33249. [Google Scholar] [CrossRef]
- Taghieh, A.; Aly, A.A.; Felemban, B.F.; Althobaiti, A.; Mohammadzadeh, A.; Bartoszewicz, A. A Hybrid Predictive Type-3 Fuzzy Control for Time-Delay Multi-Agent Systems. Electronics 2022, 11, 63. [Google Scholar] [CrossRef]
- Vafaie, R.H.; Mohammadzadeh, A.; Piran, M. A new type-3 fuzzy predictive controller for MEMS gyroscopes. Nonlinear Dyn. 2021, 106, 381–403. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Mohammadzadeh, A.; Tavoosi, J.; Mobayen, S.; Safdar, R.; Assawinchaichote, W.; Vu, M.T.; Zhilenkov, A. Stability of Interval Type-3 Fuzzy Controllers for Autonomous Vehicles. Mathematics 2021, 9, 2742. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).