Benefits Evaluation Method of an Integrated Energy System Based on a Fuzzy Comprehensive Evaluation Method

Abstract

Building an integrated energy system (IES) is an excellent solution to environmental pollution and energy consumption currently. However, there are usually various IES configurations with different performances, and it is usually difficult for the decision-makers to select the most sustainable IES solution among multiple choices. In this paper, we attempt to design an evaluation method that considers the renewable energy and energy system model for evaluating the benefit of an IES. Firstly, this paper constructs an evaluation index system including four dimensions of technology, economy, environment, and society, based on the physical architecture of IES and its benefit influencing factors. It focuses on multiple energy sources or systems, and satisfies the overall evaluation of IES, resulting in accurate benefit evaluation results. Secondly, the subjective weight is determined by combining the triangular fuzzy number (TFN) and the analytic hierarchy process (AHP). The objective weight is determined by the entropy method. The combined weight is obtained by combining the subjective and objective weights, which solves the problem of the weight calculation error caused by the mutual influence between the indexes. Finally, the fuzzy comprehensive evaluation method is used to conduct the benefit evaluation of the IES, which solves the problem that the qualitative index cannot be calculated. This paper takes an IES project in a city in northern China as a case study. Through sensitivity analysis and comparative analysis, the reliability and feasibility of the evaluation results and proposed method are verified. The analysis results show that the model evaluation results are intuitive and consistent with reality, and the data information utilization rate is high.

1. Introduction

Energy is the foundation of social development and human survival, so solving the sustainability of the energy supply is the primary issue of current development. Fossil energy releases greenhouse gases to the environment during combustion. In recent years, the demand for energy in various countries has gradually increased. Huge energy consumption has caused many problems related to developmental delay and environmental damage, especially in economically backward countries. Therefore, countries began to intensify research on renewable energy and energy cascade utilization technology, and to adjust energy structures to respond to the growing shortage of energy [1,2].

In this context, the concept of IES came into being and was recognized by all countries in the world [3,4,5]. Indeed, IES is an energy system with unified planning and scheduling of various types of energy. It uses advanced information technology to integrate various types of resources, realizes collaborative management among all aspects, improves energy utilization efficiency, and promotes the sustainable development of energy [6,7]. It is different from the traditional energy system. The traditional system has no connection with each other in the planning and design of multi-energy systems and has poor system stability. The IES can not only improve the self-healing ability of the system to respond to emergencies but can also achieve the purpose of alleviating the energy supply pressure in peak periods [8].

At present, in the process of promoting regional integrated energy projects in China gradually, the main forms are heat and power cogeneration in the north and regional refrigeration projects in the south. The purpose of regional IES is to make full use of natural resources, build a low-carbon and sustainable energy supply structure, and improve the living environment of human settlements. Therefore, in a certain range, such as science and technology parks, residential areas, and commercial areas, to choose the appropriate energy system, through the optimal combination of appropriate technology and equipment, to achieve real regional energy conservation and emission reduction effect, has been a concern by scholars at home and abroad widely.

The benefits evaluation of IES, as a feedback link of project planning and construction, can promote the orderly progress of project construction [9]. Multiple energies in the IES are coupled with each other, which is characterized by strong nonlinearity and high dimension. Most studies only focus on a single energy variety or system, lacking the overall discussion of IES, and also have difficulty in obtaining index data when selecting indexes. Therefore, the benefit evaluation system of IES needs to be improved. In summary, the establishment of an evaluation index system and the reasonable selection of evaluation methods can provide theoretical guidance and a basis for the sustainable development of energy projects.

At present, the research on the benefit evaluation of integrated energy systems is not perfect, and further work is needed to propose a set of overall evaluation methods. The contributions in this paper are as follows:

• Considering the IES coupling between energy, this paper proposes an index system for the benefit evaluation of IES, which can objectively express the feature of the evaluation object;
• This paper proposes a combined weighting method. The TFN-AHP method is used to determine the subjective weight, and objective weights are determined by the entropy method. By combining the linear weighting method, the subjective and objective weights are integrated to determine the combined weights. It avoids the influence of subjective factors on the weights and solves the problem of weight calculation errors caused by the mutual influence between indexes;
• This paper proposes the fuzzy comprehensive evaluation method, which conducts the multi-criterion benefit evaluation of the IES. The transformation of the index from qualitative to quantitative is realized, and the problem of the uncertainty of the index is solved.

In conclusion, a method for evaluating the benefits of integrated energy systems is proposed in this paper, based on a fuzzy comprehensive evaluation. Section 2 summarizes and analyzes the current situation of domestic and foreign research. Section 3 constructs a multi-dimensional benefit evaluation index system and proposes the combination weighting method and fuzzy comprehensive evaluation method. Section 4 analyzes the evaluation results and method. Finally, Section 5 gives the conclusion of this paper.

2. Related Work

The benefits evaluation of IES is one of the important tools to promote project construction. At present, some achievements have been made in the research of IES benefit evaluation, which includes two parts, namely the index system and evaluation method.

2.1. Research on the Index System

The index system is composed of multiple evaluation indexes according to a certain logical structure. It is one of the most important tools for decision-makers to carry out the evaluation, and it is an indispensable link between evaluation methods and evaluated objects.

Katal and Fazerpur [10] discussed factors, such as economic benefits, technology, and the surrounding environment for the evaluated power plant. The social impact of the proposed power plant is ignored. Yang Kun [11] et al. constructed an evaluation index system for choosing the best energy supply system for universities. However, how the evaluation index system was constructed has not yet been explained, and many important indexes have been ignored. The literature [12] established the benefit evaluation index system of regional IES, based on the interests of the government, power grid, investment operators, and users, reflected the characteristics of the system in energy, environment, economy, security, reliability, and other aspects. Pilavachi [13] et al. evaluated the performance of various combined cooling, heating, and power (CCHP) systems in environmental, policy, and economic terms. However, the authors did not construct a well-structured system of evaluation criteria. The literature [14] discussed the concept of the energy internet and its interest relationship between subjects, and then established the energy internet evaluation index system covering the five factors of economy, energy, environment, society, and engineering. The literature [15] evaluated the comprehensive energy network investment, from two aspects of power supply investment benefit and heating investment benefit. The investment benefit index system includes three aspects, namely economic benefit, technical benefit, and service benefit.

The above analyses show that the research is still deficient. The existing index system is mostly aimed at single benefits, which cannot evaluate the overall benefit of the system. Some indexes are uncertain, and the data are difficult to obtain, which has a certain impact on the evaluation results. Thus, improvements in this aspect are needed.

2.2. Research on Evaluation Methods

Evaluation methods can be divided into two aspects, namely the index weighting and evaluation methods.

(1) The index weighting method includes subjective and objective methods. Subjective approaches depend on the experience and knowledge of the decision-maker. Common methods are Delphi, the analytic hierarchy process (AHP), and the method of minimum square sum [16]. The objective method is a quantitative method to determine the weight according to the correlation between indexes, including the entropy weight method [17], the mean square deviation method [18], the principal component analysis method (PCA) [19], etc. Subjective and objective methods are complementary and, therefore, the combination of the weights of these two methods is crucial for evaluation.

Pilavachi et al. [13] combined different weights of evaluation indexes in different aspects, such as economy, society, and technology to conduct a comprehensive evaluation of the combined heat and power system. Wu [20] et al. evaluated the CCHP systems of four typical buildings in different ecological environments in Japan. The authors weighted the selected indexes within each building type according to their relative importance pairwise. Jing et al. [21] evaluated the feasibility of CCHP-based solid oxide fuel cells in public buildings in China in terms of technology, ecology, and economy, based on the gray relational analysis (GRA) method and entropy method. Li Min [22] et al. evaluated a comprehensive benefit of the performance of the integrated triple power generation system including three types of the wineshop, dwelling, and office. The authors use only objective methods to determine the weight of the criteria. Pilavachi [23] et al. used the AHP method to evaluate 10 types of power plants using different energy sources, including fossil fuels, nuclear energy, renewable energy, etc. Zeng [24] took the same weight of the annual total cost-saving ration, primary energy-saving ratio, and CO₂ emission reduction ratio to evaluate the optimized CCHP system.

(2) The comprehensive evaluation method includes the fuzzy comprehensive evaluation method [25], TOPSIS [26], artificial neural network method (ANN) [27], gray comprehensive evaluation method [28], matter-element extension method [29], etc. The diversification and complication of evaluation indexes make modern research more and more required on evaluation methods. Many researchers improve the above basic evaluation methods or integrate various evaluation methods.

The literature [30] used agent-based technical diffusion modeling to promote more residential energy efficiency. The literature [31], through the real-time analysis and comprehensive evaluation of the CHP system based on residential PV/T, improved sustainable energy utilization and contributed to energy conservation and emission reduction. Wang et al. [32] constructed an evaluation system including the GRA method and optimal weighting method to evaluate various distributed triple power generation systems. Noorollahi Y et al. [33] evaluated the potential of a photovoltaic solar power plant in Khuzestan province through GIS-based AHP decision analysis and fuzzy Boolean logic. Wu et al. [20] obtained the weights of the selected indexes of four typical buildings through the AHP method and calculated the ranking of each building in different regions. The literature [34] applied the AHP method in studies of Japanese residential DES. Georgiou et al. [35] used the preference ranking organization method and AHP method to determine the optimal energy supply topology of the autonomous seawater desalination plant. Dong et al. [36] used the combined method of entropy, AHP, and the set pair analysis method to evaluate various DES with multiple indexes. Vishnupriyan et al. [37] evaluated the energy supply system based on the simplicity and consistency of AHP. Kaya and Kahraman [38] used the fuzzy VIsekriterijumsko KOmpromisno Rangiranje (VIKOR) method, and the AHP approach, to determine the best renewable energy alternatives and the best energy production locations in Istanbul.

Wang et al. [39] constructed an evaluation system for tobacco companies’ energy-saving and emission-reduction technologies based on the fuzzy comprehensive evaluation method. Li et al. [40] evaluated the operation status of high-energy consumption equipment through fuzzy comprehensive evaluation and the AHP method. Colak and Kaya [41] proposed a multi-index composite evaluation model to evaluate the performance of renewable energy alternatives in Turkey. The literature [42] proposed a two-stage dispatching model for isolated microgrids considering multiple stakeholders. In the real-time electricity pricing environment, its lower model and upper model realize the minimization of user cost and microgrid operation cost, respectively. The literature [43] established a comprehensive efficiency evaluation model, based on the cross-super-efficiency CCR model. Literature [44] overcome the limitations of the market value approach, the energy value evaluation method of IES based on energy value theory is proposed. The literature [45] proposed an integrated demand response (IDR) scheduling model due to chance-constrained programming, which enables IES to minimize system operating costs in an uncertain environment. In brief, the above analyses show that there are deficiencies in research on the evaluation method, as follows:

(1) Subjective methods can reflect people’s thoughts, but the weight results of the target are different by different decision makers. The weight explanatory of the objective method is weak, and it may appear contrary to the objective law;

(2) The accuracy of the method will be affected by the data samples. Different sample choices may produce different decision results. There are uncertainties in the evaluation of indexes, which means that the qualitative indexes cannot be solved.

Therefore, it is of great significance to study the scientific, universal, and comprehensive evaluation index system, and the reasonable evaluation method.

3. Benefit Evaluation Method of the Integrated Energy System

The benefits evaluation process is shown in Figure 1, and it mainly includes four sections. In Section 1, according to the principle of index construction, the benefit evaluation index system is constructed. Section 2 illustrates the subjective weight is decided by the TFN-AHP method, the entropy method for objective weight. The subjective and objective weights are integrated to determine the combined weight. Section 3 expounds on the fuzzy comprehensive evaluation method of benefits evaluation. Section 4 takes the IES project in a city in northern China as a case study, the comprehensive benefit of the system scheme is evaluated, and the sensitivity analysis and comparative analysis are implemented.

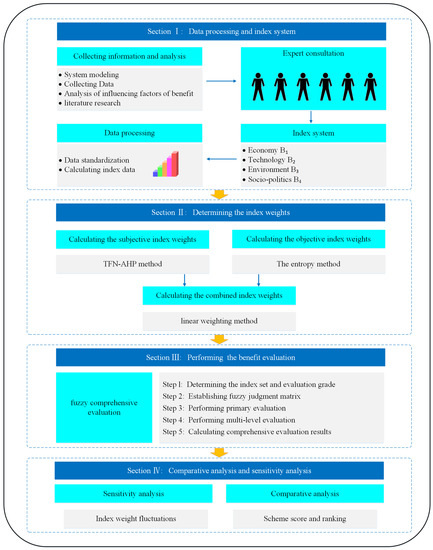
Figure 1. The flow of integrated energy system benefit evaluation.

3.1. Benefit Evaluation Index System

According to the principle of index construction [46,47], referring to the expert consultation, the internal performance characteristics of the IES, and relevant references [48,49,50], the three-layer evaluation index system is established as shown in Table 1. Each layer index is divided according to the subordinate relationship. The target layer is the comprehensive benefit of the IES. The second layer is secondary indexes, which include economic, technological, environmental, and social aspects. The bottom layer is third-grade indexes, reflecting the performance of the object in specific aspects, including quantitative and qualitative indexes to fully guarantee the objectivity of the evaluation work.

Table 1. Evaluation index system of the integrated energy system.

Target Layer	Secondary Indexes	Third-Grade Indexes	Type
Comprehensive benefit A	Economy B1	Initial investment (C11) Payback period (C12) System operating cost (C13) Equipment life (C14)	quantity
	Technology B2	Energy conversion efficiency (C21) Renewable energy utilization ratio (C22) Comprehensive energy utilization efficiency (C23) Primary energy utilization efficiency (C24)
	Environment B3	CO2 emission (C31) Nitrogen oxide emission (C32) SO2 emission (C33) PMX emission (C34)
	Socio-politics B4	Compatibility with political framework (C41) Social acceptability (C42) Space occupation (C43) Maintenance convenience (C44)	quality

3.2. Determination Method of Index Weight

The choice of weight directly affects the accuracy of the evaluation results. The index weighting method can be divided into two categories, namely subjective and objective methods. In this paper, the subjective weight is obtained by the TFN-AHP method, and the objective weight is obtained by the entropy method. Finally, the combined weight is determined by the linear weighting method. The steps of each method are detailed in this section, and the specific calculation flow is shown in Figure 2.

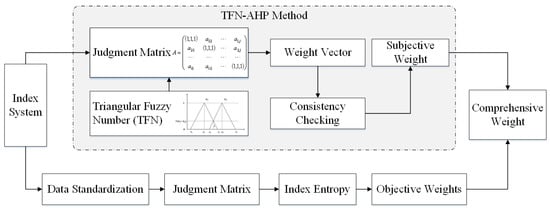
Figure 2. Calculation flow of index weight.

3.2.1. Evaluation Index Standardization

Bulleted lists look as follows:

Usually, indexes are divided into qualitative indexes and quantitative indexes. To facilitate comparative analysis of the indexes, there is a need to standardize this index, eliminate the influence of the unit of measurement on the original data, and transform it to the same dimensional value that can be added up directly.

(1) Standardization of qualitative indexes

Expert methods were used to quantify the qualitative indexes. Each qualitative index can be divided into five grades from A to E. Here, A is excellent, C is medium, and E is the worst. The relationship between score values and levels is shown in Figure 3. Then, we standardize the index data through quantitative index standardization methods, as shown in Equations (1) and (2);

Figure 3. Evaluation values of qualitative indexes.

(2) Standardization of quantitative indexes

Quantitative indexes can be used to evaluate IES, or expressed in numerical values. However, data often need to be standardized because their units and dimensions often differ. To standardize, the evaluation indexes are divided into two categories: “larger desirable response” and “smaller desirable response”.

For the “larger desirable response”, the original sequence can be standardized, as shown in the following Equation (1):

$$b_{ij}=\frac{e_{ij}-\underset{i}{\min }{e}_{ij}}{\underset{i}{\max }{e}_{ij}-\underset{i}{\min }{e}_{ij}}$$

(1)

For the “smaller desirable response”, the raw sequence can be standardized, as shown in the following Equation (2):

$$b_{ij}=\frac{\underset{i}{\max }{e}_{ij}-e_{ij}}{\underset{i}{\max }{e}_{ij}-\underset{i}{\min }{e}_{ij}}$$

(2)

In the formula, $i=1,2,\cdots ,n$, $j=1,2,\cdots ,m$, where $m$ is the number of options, and $n$ is the number of large desirable indexes. Additionally, $e_{ij}$ is the $i\text{-}th$ index value of the $j\text{-}th$ option, $\underset{i}{\min }{e}_{ij}$ is the minimum value of the $i\text{-}th$ index in all $j\text{-}th$ options, $\underset{i}{\max }{e}_{ij}$ is the maximum value of the $i\text{-}th$ index in all $j\text{-}th$ options, and $b_{ij}$ is the normalized value of $e_{ij}$.

3.2.2. Subjective Method Based on the TFN-AHP

The analytic hierarchy process (AHP) is an analysis and decision-making method. It combines network system theory and multi-objective comprehensive evaluation methods to obtain subjective weight. Triangle fuzzy number (TFN) is a numerical interval in the form $\left(x,y,z\right)$ [51,52]. In typical AHP methods, decision-makers must give an exact figure to measure the relative importance between these two indexes. However, it is difficult to determine the relative importance between the two indexes, resulting in uncertainty in the pairwise comparison matrix. In the TFN-AHP method, these uncertainties were included by the TFN. The computational steps of the TFN-AHP method are identical to those of the classical AHP method. The values in the TFN range from 1 to 9, as shown in Table 2. The steps of the TFN-AHP method are shown as follows.

Table 2. Index importance comparison scale.

Scale Value	Meaning
1	This represents that both elements have the same importance
3	One element is slightly more important than the other element
5	One element is significantly more important than the other element
7	One element is much more important than the other element
9	One element is more important than the other element
2, 4, 6, 8	The intermediate value of the above two adjacent judgments
inverse	$a_{ij}$ is judgment comparing factor i and j, then factor j and i is $a_{ij}=1/a_{ji}$

Step 1—Construct a fuzzy judgment matrix.

When comparing the importance of the $i\text{-}th$ element with the $j\text{-}th$ element, the relative importance is quantified as $a_{ij}$. If there are $n$ elements for comparison, a judgment matrix $A$ is formed, where $a_{ij}=1/a_{ji}$, $a_{ii}=1$. The judgment matrix $A$ is defined as shown in the following Equation (3):

$$A=\left(\begin{array}{cccc}\left(1,1,1\right)& a_{12}& \cdots & a_{1j}\\ a_{21}& \left(1,1,1\right)& \cdots & a_{2j}\\ \cdots & \cdots & \cdots & \cdots \\ a_{i1}& a_{i2}& \cdots & \left(1,1,1\right)\end{array}\right)$$

(3)

The number of triangular fuzzy $a_{ij}$, namely the average relative importance value, is expressed as ($x_{ij}$, $y_{ij}$, $z_{ij}$). Here, $y_{ij}$ is greater than $x_{ij}$, but less than $z_{ij}$. Accordingly, $a_{ji}$ is the value of the $a_{ij}$ symmetric position, obtained by $a_{ij}$ transformation, and expressed as ($1/z_{ij}$, $1/y_{ij}$, $1/x_{ij}$).

If there are $H$ experts to perform the evaluation, $a_{ij}$ is expressed as shown in the following Equation (4):

$$a_{ij}=\frac{1}{H}\left(a_{ij}^1+a_{ij}^2+\cdots +a_{ij}^h\right)$$

(4)

Among them, $a_{ij}^h$ ($x_{ij}^h$, $y_{ij}^h$, $z_{ij}^h$) is the triangular number from the $H$ expert, and $H=1,2,\cdots ,h$.

Step 2—Calculate the index weight.

(1) Calculate the fuzzy weight of the $i\text{-}th$ element, as shown in the following Equation (5):

$$G_i=\frac{{\displaystyle {\sum }_{j=1}^n{a}_{ij}}}{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{a}_{ij}}}}=\left(\frac{{\displaystyle {\sum }_{j=1}^n{a}_{ij}^x}}{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{a}_{ij}^z}}},\frac{{\displaystyle {\sum }_{j=1}^n{a}_{ij}^y}}{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{a}_{ij}^y}}},\frac{{\displaystyle {\sum }_{j=1}^n{a}_{ij}^z}}{{\displaystyle {\sum }_{i=1}^n{\displaystyle {\sum }_{j=1}^n{a}_{ij}^x}}}\right)$$

(5)

(2) Calculate the non-fuzzy weight.

The degree of probability $G_1$ is larger than $G_2$, as shown in Equation (6). The possibility of a TFN is larger than m TFNs, as shown in Equation (7).

$$V\left(G_1\ge G_2\right)=\{\begin{array}{l}1;y_1\ge y_2\\ \frac{x_2-z_1}{\left(y_1-z_1\right)-\left(y_2-x_2\right)};y_1\le y_2,z_1\ge x_2\\ 0;x_2\ge z_2\end{array}$$

(6)

$$V\left(G\ge G_1,G_2\cdots ,G_m\right)=\min V\left(G\ge G_i\right),i=1,2,\cdots ,m$$

(7)

Finally, based on the above equations, the non-fuzzy weight can be obtained, as shown in Equation (8), as follows:

$$M\left(C_i\right)=\min V\left(G_{C_i}\ge G_{C_m}\right)$$

(8)

where $C_i$ is the $i\text{-}th$ secondary index or third-grade index, and $i$ and $m$ are integers between 1 and $n$, but not equal to each other.

(3) Standardize non-fuzzy weight

The standardized weight of $C_i$, as shown in the following Equation (9):

$$w_i=\frac{M\left(C_i\right)}{{\displaystyle {\sum }_{i=1}^{n}M\left(C_i\right)}}, i=1,2,\cdots ,n$$

(9)

For the secondary index, it is calculated under the target layer, while for the third-grade index, it is calculated under the corresponding secondary index.

Step 3—Calculate the geometric mean of the element in the judgment matrix.

The fuzzy judgment matrix $A$ is deblurred to obtain the non-fuzzy judgment matrix $A^{\prime }$, as shown in Equation (10). After normalizing the row vector of the matrix $A^{\prime }$, the geometric mean $\omega$ of each row of the element is obtained, as shown in Equations (11) and (12).

$$A^{\prime }=\left(\begin{array}{cccc}1& y_{12}& \cdots & y_{1j}\\ y_{21}& 1& \cdots & y_{2j}\\ \cdots & \cdots & \cdots & \cdots \\ y_{i1}& y_{i2}& \cdots & 1\end{array}\right)$$

(10)

$${\tilde{w}}_i={\left({\displaystyle {\sum }_{j=1}^n{y}_{ij}}\right)}^{1/n}, i=1,2,\cdots ,n$$

(11)

$$\omega ={\left({\tilde{w}}_1,{\tilde{w}}_2,\cdots ,{\tilde{w}}_n\right)}^{{\rm T}}$$

(12)

Step 4—Consistency checking.

Define the consistency index as a $CI$, the maximum eigenvalue of the matrix as ${\lambda }_{\max }$, as shown in the following Equations (13) and (14):

$${\lambda }_{\max }={\displaystyle {\sum }_{i=1}^n\frac{{\left(A^{\prime }\omega \right)}_i}{n{\omega }_i}}$$

(13)

$$CI=\frac{{\lambda }_{\max }-n}{n-1}$$

(14)

The random test coefficient is defined as $CR$, as shown in Equation (15). When $CR\le 0.1$, the judgment matrix $A$ can pass the consistency checking. Otherwise, the parameters of the judgment matrix should be corrected, and the consistency should be verified.

$$CR=CI/RI$$

(15)

The average random consistency index $RI$ is shown in the equation, and the values are shown in Table 3.

Table 3. Judgment matrix stochastic consistency index.

n	1	2	3	4	5	6	7	8	9
RI	0	0	0.58	0.9	1.12	1.24	1.32	1.14	1.45

3.2.3. Objective Method Based on the Entropy Method

The entropy weight method determines the index weights based on the information given by the observations. Emphasizing the mathematical evaluation of data is an objective approach. The steps to determine the index weights are shown as follows:

Step 1—Determine the evaluation coefficient matrix $B$ as shown in Equation (16).

$$B=\left(\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1j}\\ b_{21}& b_{22}& \cdots & b_{2j}\\ \cdots & \cdots & \cdots & \cdots \\ b_{i1}& b_{i2}& \cdots & b_{ij}\end{array}\right)$$

(16)

Step 2—Normalize the evaluation coefficient matrix.

First, standardize the evaluation coefficient matrix $B$ representation, as shown in the following Equation (17):

$$B^{\prime }=\left(\begin{array}{cccc}{b^{\prime }}_{11}& {b^{\prime }}_{12}& \cdots & {b^{\prime }}_{1j}\\ {b^{\prime }}_{21}& {b^{\prime }}_{22}& \cdots & {b^{\prime }}_{2j}\\ \cdots & \cdots & \cdots & \cdots \\ {b^{\prime }}_{i1}& {b^{\prime }}_{i2}& \cdots & {b^{\prime }}_{ij}\end{array}\right)$$

(17)

Then, the normalized matrix $P_{ij}$ can be obtained, as shown in Equation (18), as follows:

$$P_{ij}=\frac{{b^{\prime }}_{ij}}{{\displaystyle {\sum }_{j=1}^n{b^{\prime }}_{ij}}}$$

(18)

Step 3—Calculate the information entropy $e_j$ of the $j\text{-}th$ index, as shown in the following Equations (19) and (20):

$$e_j=-\theta {\displaystyle {\sum }_{i=1}^n{P}_{ij}}\ln P_{ij}$$

(19)

$$\theta =\frac{1}{\ln n}$$

(20)

Step 4—Calculate the difference coefficient of the $j\text{-}th$ index. The difference coefficient is $g_j$, as shown in the following Equation (21):

$$g_j=1-e_j$$

(21)

Step 5—Calculate the weights $\omega$, as shown in the following Equation (22):

$${\omega }_j=\frac{g_j}{{\displaystyle {\sum }_{j=1}^n{g}_j}}$$

(22)

3.2.4. Combined Weight

Based on the TFN-AHP method and entropy method, the subjective weight and objective weight are combined, which not only considers the expert knowledge and experience but also excavates the internal laws of the data itself. This section uses linear weighting methods to determine the combined weights. Set the subjective weight $w_i=\left[w_1,w_2,w_3,\cdots ,w_n\right]$ and the objective weight is $w_j=\left[w_1,w_2,w_3,\cdots ,w_n\right]$, then the combined weight is $w_y$, as shown in the following Equation (23):

$$w_y=\lambda w_i+\left(1-\lambda \right)w_j$$

(23)

where $i=1,2,\cdots ,n;j=1,2,\cdots ,n$, the subjective and objective weight proportion is set to 1:1, that is $\lambda =0.5$, and the parameter $\lambda$ satisfies the $0\le \lambda \le 1$.

The combined method is used to combine the results of multiple single methods and eliminate the problems of one-sided and poor stability. This section combines subjective and objective weight, which avoids the excessive influence of subjective factors on weight effectively.

3.3. Fuzzy Comprehensive Evaluation Method

Fuzzy mathematics, as the core of the fuzzy comprehensive evaluation method, expands the scope from precision to fuzziness. It solves the fuzzy factors that are difficult to deal with, and provides theoretical support for the analysis of a large number of fuzzy things, by defining the level of membership degree of the evaluated object. A fuzzy comprehensive evaluation method can deal with the factors that cannot be calculated by an accurate mathematical model. It can also make the results more realistic and objective by eliminating the selectivity deviation, which is caused by the subjective experience of experts.

Step 1—Determine the index set and evaluation set.

The index set which has been set is divided according to the constructed index system level, that is $U=\left\{u_1,u_2,\cdots ,u_N\right\}$. The set $U_i=\left\{u_{i1},u_{i2},\cdots ,u_{i{k}_i}\right\}$, $i=1,2,\cdots ,N$, and it contains $k_i$ elements. The evaluation set $V=\left\{v_1,v_2,\cdots ,v_n\right\}$ is determined according to the evaluation situation and the evaluation needs, and $n$ is the number of evaluation grades.

Step 2—Construct a fuzzy judgment matrix.

There are h experts to participate in the evaluation, and the index set $U_i=\left\{u_{i1},u_{i2},\cdots ,u_{i{k}_i}\right\}$ according to the level of the evaluation set $V=\left\{v_1,v_2,\cdots ,v_n\right\}$ for evaluation, $V=\left\{v_1,v_2,v_3,v_4,v_5\right\}$ = {good, preferably, general, poor, bad}. The frequency of each index $u_{i{k}_i}$ belonging to each evaluation set $F_{i{k}_i}$ is calculated, to obtain the membership value of each index. The fuzzy judgment matrix of $U_i$ is $F_i=\left\{F_{i1},F_{i2},\cdots ,F_{i{k}_i}\right\}$.

Step 3—Primary evaluation.

For each index set $U_i=\left\{u_{i1},u_{i2},\cdots ,u_{i{k}_i}\right\}$, the corresponding fuzzy judgment matrix is $F_i=\left\{F_{i1},F_{i2},\cdots ,F_{i{k}_i}\right\}$. According to the weight $w_i$ of the index set $U_i$, the primary evaluation, is shown in Equation (24), as follows:

$$B_i=w_i{F}_i$$

(24)

Step 4—Multi-level evaluation.

The subset of weights corresponding to the index set $U=\left\{u_1,u_2,\cdots ,u_N\right\}$ is $w=\left\{w_1,w_2,\cdots ,w_N\right\}$, so the fuzzy judgment vector $B$ is shown in Equation (25), as follows:

$$B=\left(\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_N\end{array}\right)=\left(\begin{array}{c}{w}_1{F}_1\\ w_2{F}_2\\ ⋮\\ w_N{F}_N\end{array}\right)$$

(25)

Step 5—Calculate the comprehensive evaluation value.

The comprehensive evaluation value $P$ is calculated from the fuzzy judgment vector $B$ and evaluation set $V$, as shown in the following Equation (26):

$$P=VB$$

(26)

In summary, the multi-level fuzzy comprehensive evaluation process is shown in Figure 4.

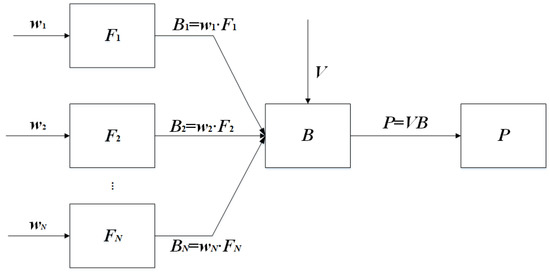
Figure 4. The multi-level fuzzy comprehensive evaluation process.

4. Case Study

4.1. Building Loads

This paper takes the multi-stage project of IES in a city in northern China as a case study. The project started planning and construction in 2015, and will end in 2030, with a planning phase taking place every five years. The total planned construction area of the second phase of the project is about 40,000 m². According to the project demand, the main interest is in meeting the cooling load, heat load, and power load. The summertime of the project is mainly concentrated from early June to the end of September, and the cooling season is 4 months. The wintertime is concentrated from mid-November to mid-March, and the heating season is 5 months. According to the feasibility data, the simulation of building loads, including power, cooling, and heating, is achieved by CloudPSS, which is a free simulation software platform (Development Team of Tsinghua University). The total cooling load in summer is about 4941 kW, and the heat load in winter is about 3491 kW. The daily load curve is shown in Figure 5. The three curves in the figure represent the building’s electric, cooling, and heat loads at different times of the day.

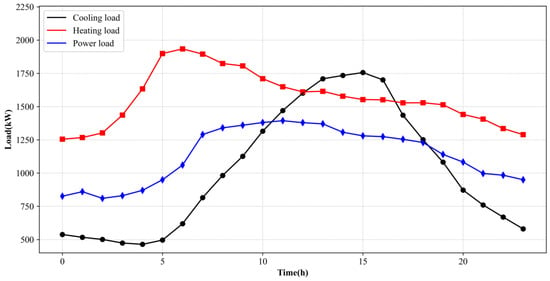
Figure 5. Electric/cold/heat load power curve diagram.

According to the local energy resources and energy supply situation, five energy supply system schemes are proposed, as shown in Table 4. The gas boilers in SC2 and SC3 are auxiliary equipment, and electricity for the public grid is generated primarily from coal. The main technical parameters of the system equipment are shown in Table 5.

Table 4. The energy supply system.

Number	System Scheme	Main Configuration
1	Separate production system	Electric chiller + gas boiler + power grid
2	CCHP system	Gas turbine + lithium bromide absorption unit + electric refrigerator + gas boiler + power grid
3	Optimized CCHP system	Electric refrigerator + gas boiler + power grid + gas turbine + absorption chiller + power chiller + exhaust treater + energy storage device
4	Solar collector system	Solar heat collection device + power grid
5	GSHP system	Ground source heat pump system

Table 5. Technical parameters of each equipment.

Equipment	Parameter	Value
Gas turbine	Rated generating power (kW)	5050
	Generating efficiency (%)	30
	Heating efficiency (%)	25
Absorption chiller	Refrigeration status rated refrigeration capacity (kW)	200
	The hot and cold ratio in the refrigeration state	3.5
	Heating state rated heat (kW)	200
	Heat exchange efficiency in the heating state (%)	80
	Electric Power (kW)	50
Exhaust-heat boiler	Rated heat supply capacity (kW)	200
	Heat transfer efficiency (%)	90
Electric compression Refrigeration machine	Rated Refrigeration Capacity (kW)	500
	Refrigeration energy efficiency ratio	6
Gas boiler	Rated heat supply capacity (kW)	200
	Heating efficiency (%)	90

4.2. Analysis of the Experimental Results

To evaluate the benefit of the schemes accurately, all schemes are evaluated by the proposed method in Section 3. The original data statistics of the 16 quantitative and qualitative indexes are shown in Table 6.

Table 6. Calculation results of the evaluation indexes of each scheme.

Index Number	Unit	Scheme 1	Scheme 2	Scheme 3	Scheme 4	Scheme 5
C11	Wan Yuan	3621	4745	5106	4275	4980
C12	year	6.3	9.7	9.3	5.6	8.4
C13	Wan yuan/year	3014.04	2536.21	1706.79	1789.48	1805.48
C14	year	20	30	30	25	30
C21	%	56	68	80	76	75
C22	%	0	28.32	39.68	35.77	32.22
C23	%	70	80.95	89.73	82.44	79.72
C24	%	46.7	76.1	81.5	62	75.6
C31	t/y	36,313.2	19,756	11,756	19,491.1	28,946
C32	t/y	1670.93	1175.79	1060.52	995	1106.75
C33	t/y	788.02	704.60	546.25	686.55	694.42
C34	t/y	280.41	169.76	122.97	112.90	142.54
C41	value	40	90	95	90	90
C42	value	70	90	95	90	80
C43	value	60	90	90	90	75
C44	value	50	90	95	90	80

The original index set is standardized by the method, and the results are shown in Table 7. To keep the data types consistent for easy calculation, the results retain four decimal places, and all the indexes are distributed within the 0–1 interval.

Table 7. Standardized values of the evaluation indexes.

Index Number	Scheme 1	Scheme 2	Scheme 3	Scheme 4	Scheme 5
C11	1.0000	0.2431	0.0000	0.5596	0.0848
C12	0.8292	0.0000	0.0976	1.0000	0.3170
C13	0.0000	0.3655	1.0000	0.9367	0.9245
C14	0.0000	1.0000	1.0000	0.5000	1.0000
C21	0.0000	0.5000	1.0000	0.8333	0.7916
C22	0.0000	0.7137	1.0000	0.9015	0.8119
C23	0.0000	0.5549	1.0000	0.6305	0.4927
C24	0.0000	0.8448	1.0000	0.4396	0.8304
C31	0.0000	0.3257	1.0000	0.3149	0.7000
C32	0.0000	0.2674	0.0969	1.0000	0.1653
C33	0.0000	0.6549	1.0000	0.5803	0.6128
C34	0.0000	0.6605	0.9398	1.0000	0.8230
C41	0.4000	0.9000	0.9500	0.9000	0.9000
C42	0.7000	0.9000	0.9500	0.8500	0.8000
C43	0.6000	0.9000	0.9000	0.9000	0.7500
C44	0.5000	0.9000	0.9500	0.9000	0.8000

After the hierarchical construction, the weights for each criterion layer were calculated using TFN-AHP. A pairwise comparison matrix is first established based on the ranking table given by the experts, as shown below. For example, the weight vectors of the secondary indexes B1, B2, B3, and B4 relative to the overall objective can be calculated as $W=\left(0.239,0.3397,0.1404,0.2808\right)$. At the same time, the $C{I}_A$, one that meets the requirements of consistency checking, is 0.01805. Similarly, the relative importance of the third-grade indexes to the secondary indexes is shown in the matrix below.

$\begin{array}{cc}A& \begin{array}{cccc}{B}_1& B_2& B_3& B_4\end{array}\\ \begin{array}{c}{B}_1\\ B_2\\ B_3\\ B_4\end{array}& \left(\begin{array}{cccc}1& \left(1/3,1/2,1\right)& \left(1/3,1/2,1\right)& \left(1/3,1/2,1\right)\\ \left(1,2,3\right)& 1& \left(1/3,1/2,1\right)& 1\\ \left(1,2,3\right)& \left(1,2,3\right)& 1& 1\\ \left(1,2,3\right)& 1& 1& 1\end{array}\right)\end{array}$ $\begin{array}{cc}{B}_1& \begin{array}{cccc}{C}_{11}& C_{12}& C_{13}& C_{14}\end{array}\\ \begin{array}{c}{C}_{11}\\ C_{12}\\ C_{13}\\ C_{14}\end{array}& \left(\begin{array}{cccc}1& \left(2,3,4\right)& \left(3,4,5\right)& \left(4,5,6\right)\\ \left(1/4,1/3,1/2\right)& 1& \left(1,2,3\right)& \left(2,3,4\right)\\ \left(1/5,1/4,1/3\right)& \left(1/3,1/2,1\right)& 1& 1\\ \left(1/6,1/5,1/4\right)& \left(1/4,1/3,1/2\right)& 1& 1\end{array}\right)\end{array}$

$\begin{array}{cc}{B}_2& \begin{array}{cccc}{C}_{21}& C_{22}& C_{23}& C_{24}\end{array}\\ \begin{array}{c}{C}_{21}\\ C_{22}\\ C_{23}\\ C_{24}\end{array}& \left(\begin{array}{cccc}1& \left(1,2,3\right)& 1& \left(2,3,4\right)\\ \left(1/3,1/2,1\right)& 1& \left(1/3,1/2,1\right)& 1\\ 1& \left(1,2,3\right)& 1& \left(1,2,3\right)\\ \left(1/4,1/3,1/2\right)& 1& \left(1/3,1/2,1\right)& 1\end{array}\right)\end{array}$ $\begin{array}{cc}{B}_3& \begin{array}{cccc}{C}_{31}& C_{32}& C_{33}& C_{34}\end{array}\\ \begin{array}{c}{C}_{31}\\ C_{32}\\ C_{33}\\ C_{34}\end{array}& \left(\begin{array}{cccc}1& \left(1/3,1/2,1\right)& \left(1/4,1/3,1/2\right)& 1\\ \left(1,2,3\right)& 1& \left(1/3,1/2,1\right)& \left(1,2,3\right)\\ \left(2,3,4\right)& \left(1,2,3\right)& 1& \left(2,3,4\right)\\ 1& \left(1/3,1/2,1\right)& \left(1/3,1/2,1\right)& 1\end{array}\right)\end{array}$

$\begin{array}{cc}{B}_4& \begin{array}{cccc}{C}_{41}& C_{42}& C_{43}& C_{44}\end{array}\\ \begin{array}{c}{C}_{41}\\ C_{42}\\ C_{43}\\ C_{44}\end{array}& \left(\begin{array}{cccc}1& \left(1,2,3\right)& \left(2,3,4\right)& \left(2,3,4\right)\\ \left(1/3,1/2,1\right)& 1& \left(1,2,3\right)& \left(1,2,3\right)\\ \left(1/4,1/3,1/2\right)& \left(1/3,1/2,1\right)& 1& \left(1/3,1/2,1\right)\\ \left(1/4,1/3,1/2\right)& \left(1/3,1/2,1\right)& \left(1,2,3\right)& 1\end{array}\right)\end{array}$

The subjective and objective weights are calculated separately, and each level is shown in Table 8. The weight of technical and economic indexes is the highest, followed by environmental indexes and social benefits indexes. The weights calculated by different methods are different. Therefore, it can reflect the importance of using a combination weighting method to obtain weight. The results of the combination weighting method are shown in Figure 6. Index weight comparison results are shown in Figure 7. The technical benefit index and economic benefit index accounted for 34% and 24% of the total weight, respectively, and play the most important role in the evaluation, which is consistent with the goal of the stable operation of the IES. The weight allocation meets the objective application requirements. It is proved that the combination weighting method proposed in this paper can integrate subjective and objective weights effectively, and can obtain more scientific and reasonable weight results.

Table 8. Subjective and objective weight values of indexes.

Secondary Indexes	Weight	Third-Grade Indexes	Subjective Weight	Objective Weight
B1	0.2390	C11	0.3628	0.3953
		C12	0.1630	0.2387
		C13	0.3260	0.2292
		C14	0.1479	0.1367
B2	0.3397	C21	0.1408	0.1868
		C22	0.2628	0.1325
		C23	0.4554	0.5976
		C24	0.1408	0.0830
B3	0.1404	C31	0.5485	0.6729
		C32	0.2349	0.1593
		C33	0.1164	0.1166
		C34	0.0999	0.0510
B4	0.2808	C41	0.4511	0.2745
		C42	0.2609	0.5087
		C43	0.1189	0.1223
		C44	0.1689	0.0942

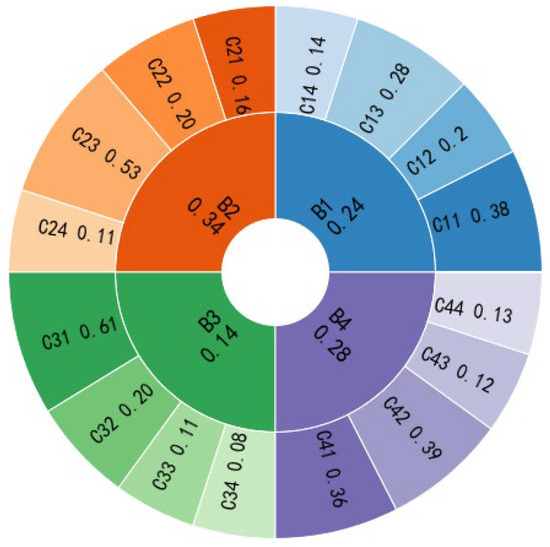
Figure 6. Evaluation index combination weight value.

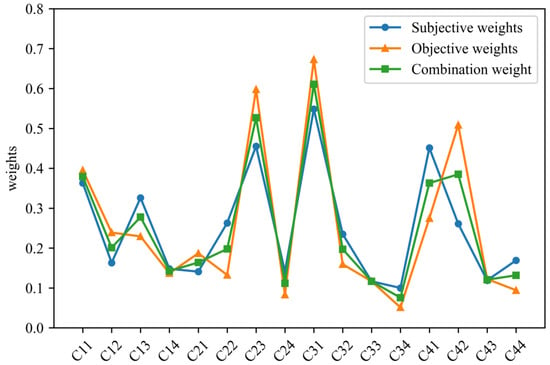
Figure 7. Comparison of index weight results.

From the index layer analysis, the compatibility with the political framework, CO₂ emission, comprehensive energy utilization efficiency, and the initial investment are the high subjective weight. It shows that the general understanding of experts is the same. The subordinate indexes of technical and economics are the indexes that experts pay more attention to. Additionally, the objective weights based on the data also reflect the same situation. The weight results can confirm that the IES should be based on ensuring stability, strengthening the consumption of renewable energy, improving the energy supply balance ability, optimizing the energy supply structure, improving energy utilization, and minimizing energy consumption. The consistency between the weighting results and the actual demand of the IES current stage is proven.

Due to the qualitative judgment of indexes, evaluation was performed using the fuzzy evaluation method. First, the index set is divided, according to the index system, and the corresponding secondary indexes and third-grade indexes set are divided into two levels. The secondary and third-grade index sets correspond to $U_1$, and $U_2$, respectively. The economic indexes correspond to $U_{21}$, the technical indexes correspond to $U_{22}$, the environmental indexes correspond to $U_{23}$, and the social indexes correspond to $U_{24}$. The evaluation set $F$ of the index is divided into five grades, namely $V=\left\{v_1,v_2,v_3,v_4,v_5\right\}$ = {good, preferably, general, poor, bad}, and the scoring table is shown in Table 9.

Table 9. Scoring table.

Score Segment	90–100	80–90	70–80	60–70	Below 60
Evaluation level	good	preferably	general	poor	bad

Questionnaires were conducted for each index set and rating scale, and the frequency of each index was normalized for different grades. Six experts were consulted in this paper (three electrical professional masters, and three experts in the field of integrated energy). The membership of each index is shown in Table 10. According to the calculation results of the index membership degree, the fuzzy judgment matrix corresponding to each index set is established. Additionally, we calculate the evaluation score layer by layer in ascending order.

Table 10. Evaluation index membership values.

Secondary Indexes	Third-Grade Indexes	Degree of Membership
B1	C11	(0, 0.17, 0.33, 0, 0.5)
	C12	(0.17, 0.5, 0.17, 0.17, 0)
	C13	(0.17, 0.33, 0.5, 0, 0)
	C14	(1, 0, 0, 0, 0)
B2	C21	(0.33, 0.5, 0.17, 0, 0)
	C22	(1, 0, 0, 0, 0)
	C23	(0.17, 0.33, 0.5, 0, 0)
	C24	(0.67, 0.33, 0, 0, 0)
B3	C31	(1, 0, 0, 0, 0)
	C32	(1, 0, 0, 0, 0)
	C33	(0.67, 0.17, 0.17, 0, 0)
	C34	(0.5, 0.5, 0, 0, 0)
B4	C41	(0.5, 0.5, 0, 0, 0)
	C42	(0.67, 0.33, 0, 0, 0)
	C43	(0.83, 0.17, 0, 0, 0)
	C44	(0.83, 0.17, 0, 0, 0)

The fuzzy judgment matrix of economic indexes is shown in Equation (27), as follows:

$$F_{21}=\left[\begin{array}{ccccc}0& 0.17& 0.33& 0& 0.5\\ 0.17& 0.5& 0.17& 0.17& 0\\ 0.17& 0.33& 0.5& 0& 0\\ 1& 0& 0& 0& 0\end{array}\right]$$

(27)

The fuzzy judgment vector of economic indexes $f_{11}={\omega }_{21}{}^T{F}_{21}=\left[0.2983,0.1689,0.2856,0.1502,0.1038\right]$ is obtained from the combined weight ${\omega }_{21}={\left[0.6107,0.1972,0.1166,0.0755\right]}^T$. Similarly, the judgment vector of technical, environmental, and social secondary indexes is shown in the following Equations (28)–(30):

$$f_{12}={\omega }_{22}{}^T{F}_{22}=\left[0.4686,0.3198,0.2032,0,0\right]$$

(28)

$$f_{13}={\omega }_{23}{}^T{F}_{23}=\left[0.7703,0.1456,0.0895,0,0\right]$$

(29)

$$f_{14}={\omega }_{24}{}^T{F}_{24}=\left[0.6487,0.3514,0,0,0\right]$$

(30)

Therefore, the fuzzy judgment matrix of the fuzzy judgment vector composition of each secondary index is shown in Equation (31), as follows:

$$F_1=\left[\begin{array}{ccccc}0.2983& 0.1689& 0.2856& 0.1502& 0.1038\\ 0.4686& 0.3198& 0.2032& 0& 0\\ 0.7703& 0.1456& 0.0895& 0& 0\\ 0.6487& 0.3514& 0& 0& 0\end{array}\right]$$

(31)

The total fuzzy judgment vector obtained by weight $\omega ={\left(0.2390,0.3397,0.1404,0.2808\right)}^T$ is shown in Equation (32), as follows:

$$A={\omega }^T{F}_1=\left[0.5977,0.2483,0.1191,0.0211,0.0146\right]$$

(32)

According to the evaluation set $V=\left[100,90,80,70,60\right]$, the evaluation results are converted into a percentage, as shown in Equation (33), as follows:

$$P=V{A}^T=93.490$$

(33)

The evaluation results concluded that the comprehensive benefit of SC3 is in a “good” state, and the final evaluation score was 93.490. The evaluation results of the five schemes are shown in Table 11, and the results of each index are shown in Figure 8. In Figure 8, the X-axis is the target layer and secondary indexes, and the Y-axis is the evaluation value.

Table 11. Results of the evaluation value of each scheme.

Number	SC1	SC2	SC3	SC4	SC5
Evaluation value	65.926	84.625	93.490	87.579	87.125

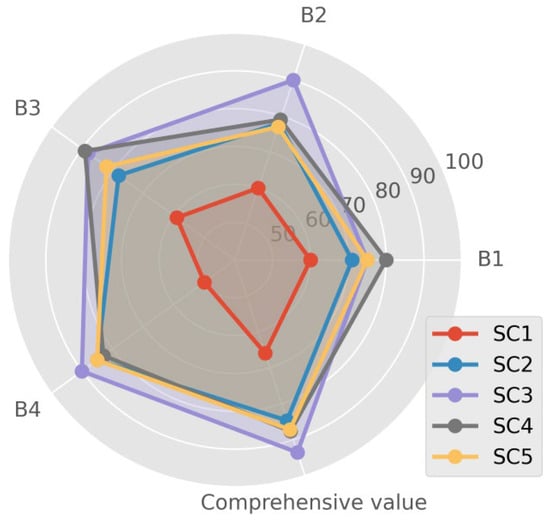
Figure 8. Results of the comprehensive benefit evaluation of each scheme.

The main influencing factors of the economy are the initial investment and operating cost. The best scheme is SC4, because of its low initial investment and less fuel consumption. On the other hand, SC1 is the worst system, although the initial investment is low, the operation and consumption cost is high. Furthermore, SC5 has a relatively low initial investment, and SC4 has a low annual energy consumption, heating operation cost, and a long system service life. Therefore, SC4 and 5 are slightly more advantageous than the previous three schemes. If the decision-makers focus on the economy, they should give priority to SC4 and 5.

The main influencing factors of technical performance are the renewable energy utilization ratio and comprehensive energy utilization efficiency. As shown in Figure 8, SC3 is the best solution for energy cascade utilization. The SC2, 4, and 5 scores are 78, 79, and 76, respectively, and SC1 is the worst at 60. Meeting the maximum load is the basic principle for selecting equipment. Inefficiencies in the power generation equipment and absorption chillers can lead to overall system inefficiencies when the system is operating at partial load. Here, SC3 has a high renewable energy utilization ratio, cooling performance coefficient, and thermal performance coefficient, and has obvious advantages over other schemes in energy saving and emission reduction.

The main influencing factor of environmental performance is the number of pollutants produced. Natural gas emits far fewer pollutants than coal burning. Therefore, from the perspective of the environment, SC3 and 4 are good, because of the high coefficient of refrigeration and heating performance, and fewer pollutant emissions. Therefore, from the environmental protection analysis, the priority should be to select SC3 and SC4. Traditional independent energy supply systems can lead to adverse environmental benefits.

Evaluation criteria for social benefits include compatibility with the political framework, social acceptability, space occupation, and maintenance convenience. The IES is a research hotspot in the field of energy. Although IES has bright advantages, such as environmental performance and energy cascade utilization, it also has many problems that prevent its large-scale promotion, such as a large initial investment and complex system.

In conclusion, the highest evaluation result is SC3, which is a multi-energy complementary system. It has high development prospects, so this scheme should be chosen.

4.3. Analysis of the Influencing Factors of the Evaluation Results

(1) Because different experts have different professional backgrounds, the evaluation of IES has subjective differences. In the relative importance of indexes, different experts have different evaluations. Thus, the comprehensive evaluation value of each expert is calculated separately, as shown in Table 12.

Table 12. Results of the subjective evaluation of the experts.

Number	Scheme 1	Scheme 2	Scheme 3	Scheme 4	Scheme 5
Expert 1	65.48	85.125	93.482	87.882	89.85
Expert 2	66.58	84.381	92.885	86.33	87.156
Expert 3	64.86	83.86	93.593	86.256	87.23
Expert 4	62.72	83.01	89.46	86.50	88.94
Expert 5	63.37	79.82	91.78	88.62	90.22
Expert 6	59.81	81.95	92.74	86.44	87.75
Fuzzy comprehensive method	65.926	84.625	93.490	87.579	88.925

As shown in Figure 9, the curve of the six experts’ evaluation, coincides with the fuzzy comprehensive evaluation curve. It indicates that different experts have similar evaluations of the same scheme. It also proves the scientific rationality of the fuzzy comprehensive evaluation method in this paper.

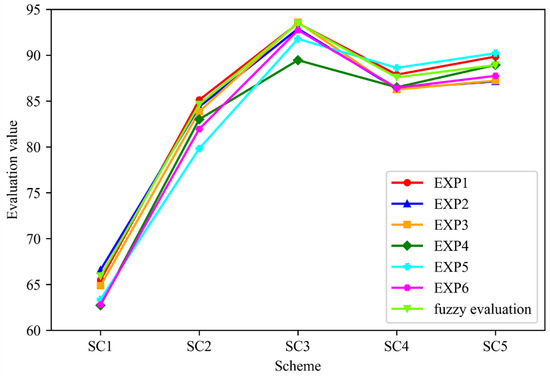
Figure 9. Expert evaluation value.

(2) This paper uses the fuzzy comprehensive evaluation method to analyze the benefits of the IES. The evaluation results obtained by different methods are compared respectively, and their influence on the evaluation results is analyzed.

By using the classical AHP method and sorting the relative importance of 16 indexes by experts, the subjective weight is obtained. The entropy method is used to calculate the objective weight of 80 index data. As shown in Figure 10, the evaluation results of three methods are given. It shows that different methods lead to different final results. The AHP method is basically consistent with the fuzzy comprehensive evaluation method, but the results of the entropy method are different. The result of the fuzzy comprehensive evaluation method is that SC3 is optimal, and the objective method is that SC5 is optimal. It can be concluded that the AHP results are similar to the results of the fuzzy comprehensive evaluation method, so the subjective method has a great influence on the comprehensive evaluation results.

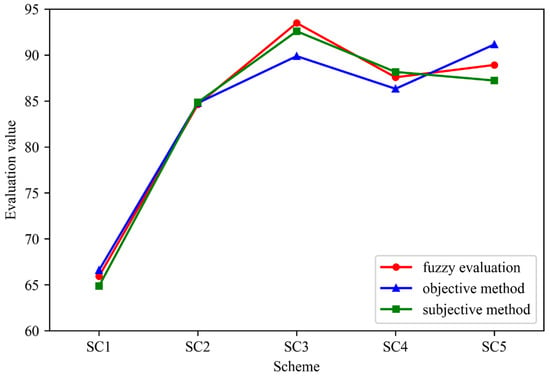
Figure 10. Comparison diagram of the evaluation results.

(3) The rationality and accuracy of the method used in this paper are further validified. This paper evaluates three different operation schemes that have been run in the first phase of the project and evaluates them by different methods. The evaluation results are shown in Figure 11.

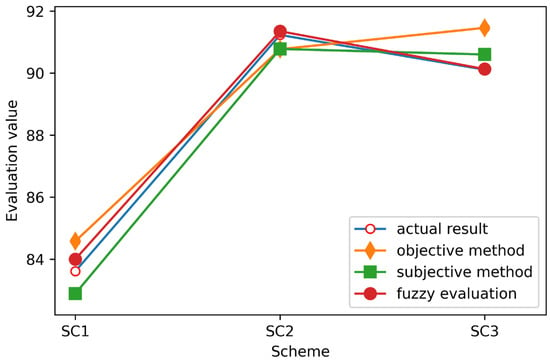
Figure 11. Evaluation results.

As shown in Figure 11, the actual result is the energy efficiency level of the actual operation of the scheme, the optimal result obtained by the objective evaluation method is SC3, the optimal result obtained by the subjective evaluation method is SC2, and the optimal result obtained by the fuzzy comprehensive evaluation method is SC2. The index comparison diagram of the operation of each scheme is shown in Figure 12. The analysis shows that with the increase in the proportion of renewable energy, the comprehensive benefits of the system show a significant upward trend. The sub-graphs (a) and (b) in Figure 12 prove that they have a positive impact on the integrated energy system benefits. The comprehensive energy efficiency index of SC2 is significantly better than that of SC1. Due to the high proportion of renewable energy in SC2, the utilization of traditional fossil energy is reduced, and the comprehensive energy efficiency is increased by 7.62% compared with SC1. Since the load data of each scheme are the same, to allow for reasonable comparison and to reduce the impact of initial investment cost on the evaluation results, the total cost analysis scheme is used to analyze the economic benefits. The total cost of SC2 is 6.4% and 2.8% lower than that of SC1 and SC3, respectively. The main reason is that the energy allocation of SC2 is more reasonable, and the energy efficiency is higher than that of other schemes. Therefore, the operation cost of SC2 is lower than that of other schemes, which effectively reduces the total cost and improves the overall system.

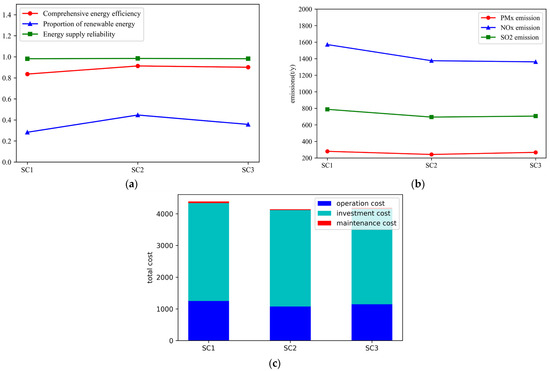
Figure 12. Comparison of each index. (a) Technical index; (b) Environmental index; (c) Economic index.

In summary, compared with other methods, the evaluation results of the method used in this paper are closer to the actual situation, and can objectively reflect the actual situation. Thus, it can be proved that the evaluation results of the method used in this paper are accurate and reasonable.

4.4. Sensitivity Analysis

To verify the robustness of the combined weight and fuzzy comprehensive evaluation method, the sensitivity analysis affected by the fluctuation of index weight is carried out in this section. The purpose of the analysis is to test whether the different values of the index weight lead to a qualitative change in the evaluation results. According to the original data of 16 index weights, each index weight increased by 10%, 20%, and 30%, and decreased by 10%, 20%, and 30%. This section selects three schemes for analysis, and the results are shown in Figure 13, Figure 14, Figure 15 and Figure 16.

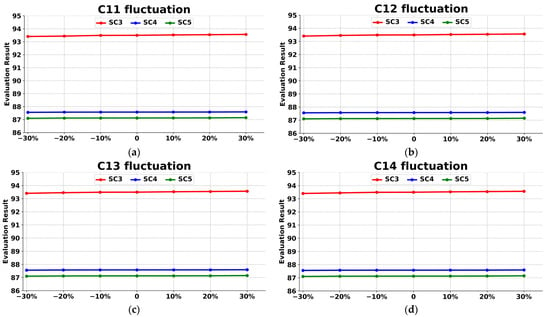
Figure 13. Sensitivity analysis of the economic indexes. (a) C₁₁ fluctuation; (b) C₁₂ fluctuation; (c) C₁₃ fluctuation; (d) C₁₄ fluctuation.

Figure 14. Sensitivity analysis of the technical indexes. (a) C₂₁ fluctuation; (b) C₂₂ fluctuation; (c) C₂₃ fluctuation; (d) C₂₄ fluctuation.

Figure 15. Sensitivity analysis of the environmental indexes. (a) C₃₁ fluctuation; (b) C₃₂ fluctuation; (c) C₃₃ fluctuation; (d) C₃₄ fluctuation.

Figure 16. Sensitivity analysis of the social indexes. (a) C₄₁ fluctuation; (b) C₄₂ fluctuation; (c) C₄₃ fluctuation; (d) C₄₄ fluctuation.

From the change in each index, the evaluation results increase with the gradual increase in the index. With the index $C_{12}$, $C_{23}$, $C_{24}$, and $C_{44}$ gradually fluctuating from small to large, the results appear as slight fluctuations. Changes in other indexes have no significant impact on the results. Therefore, the sensitivity fluctuation of the results obtained by this method is small, stable relatively, and has good robustness, so the evaluation results are objective and reliable.

5. Conclusions

This paper proposes an evaluation method of IES based on the fuzzy evaluation method and applies it to community energy system engineering examples. By summarizing the benefit evaluation method in this case, the following conclusions are drawn:

(1) This paper establishes the IES benefit evaluation index system from the four dimensions of economy, technology, environment, and socio-politics. This evaluation index system can meet the needs of the benefit evaluation of the IES project;

(2) This paper proposes the subjective and objective weights of the TFN-AHP method and entropy method and combines the linear weighting method to obtain the combined weight. The method can obtain more scientific and objective weight results, avoid the subjective factors for the weight calculation effectively, and ensure the rationality of the evaluation results;

(3) This paper proposes a fuzzy comprehensive evaluation method to evaluate the benefit of the IES. Taking an IES project in a city in northern China as a case, the benefits of different schemes are compared and analyzed horizontally, and the influence of different methods on the evaluation results is compared horizontally. At the same time, the sensitivity analysis affected by the fluctuation of index weight is carried out, to verify the stability of the method and the reliability of the evaluation results.