Error Estimates of a Symmetric Spectral Method for a Linear Volterra Integral Equation

Abstract

A symmetric spectral method is applied to investigate the two-dimensional Volterra integral equation with weakly singular kernels and delays. In this work, the solution of the equation we considered is assumed to be sufficiently smooth so that the spectral method can be applied naturally. Employing three couples of variable transformations, we apply the two-dimensional Gauss quadrature rule to approximate the weakly singular integral with delays and obtain the spectral discretization. Then we derive the convergence results of the proposed approximation scheme. We show that the errors of solution decay exponentially in both the infinity norm and weighted square norm. In the end, we carry out numerical experiments to verify the theoretical results.

1. Introduction

Volterra equations with weakly singular kernel and/or delay frequently appear in many areas of science and engineering, such as the reaction–diffusion study [1], memory problems [2], population growth models [3], the competitive system [4], a model for tumor growth [5] and so on. In view of the extensive applications, Volterra integral equations with weakly singular kernel and/or delay have drawn much attention in recent years.

The literature [6] is the pioneer work, in which the authors proposed a spectral Jacobi-collocation approximation for the linear Volterra integral equations of the second kind with weakly singular kernels under the sufficiently smooth solutions. While the underlying solution is not sufficiently smooth, this case was considered in [7] by the same authors one year later. In [8], D. Li et al. discussed the Volterra integro-differential equations which are derived by combining a time memory term in the flux and a delay parameter in the reaction term. It is well known that spectral methods enjoy exponential convergence and high-order accuracy. As a result, there are many references on numerically investigating Volterra equations by using spectral methods. The literature [9] investigated the convergence of the spectral methods for the weakly singular Volterra integro-differential equations with smooth solutions. After that, weakly singular Volterra integral equations with pantograph delays were studied in [10]. In [11], a kind of Legendre spectral scheme was put forward to solve nonlinear systems of Volterra integral equations. The literature [12] dealt with a fractional order collocation method for second kind Volterra integral equations with weakly singular kernels. Fractional pantograph equations were taken into account for their long time numerical behaviors in [13]. G. Deng et al. [14] developed high accurate pseudo-spectral Galerkin scheme for pantograph type Volterra integro-differential equations with singular kernels, but the underlying solution they considered was sufficiently smooth. Based on a simple change of variable, a novel numerical approach had been devoted to the time-fractional parabolic equations with non-smooth solutions in [15]. Liang and Brunner established the analogous convergence analysis for Volterra integral equations with weakly singular kernels for both uniform and graded meshes [16]. For a more detailed description of this subject, we refer the readers to the recent papers [17,18,19,20,21,22,23,24] and the references therein. For the two-dimensional Volterra equations, there are only a few introductions in [25,26]. To the best of our knowledge, none of the two papers refer to the two-dimensional Volterra integral equations with weakly singular kernels or delays. In this paper, we will use the spectral method to numerically solve the two-dimensional Volterra integral equation with weakly singular kernels and delays. The novelty of our work lies in applying the two-dimensional Gauss quadrature rule to approximate the weakly singular integral with delays and employing the spectral error analysis for the Jacobi spectral collocation method.

The two-dimensional Volterra integral equation with weakly singular kernels and delays we shall study is of the form:

$$\begin{array}{ccc}\hfill & & {\int }_0^{pX}{\int }_0^{qY}{(pX-S_1)}^{-\mu }{(qY-{\xi }_1)}^{-\rho }\tilde{K}(X,Y,S_1,{\xi }_1)U(S_1,{\xi }_1)d{\xi }_{1}d{S}_1\hfill \\ & & =U(X,Y)+G(X,Y),X\in [0,T],Y\in [0,\Gamma ],\hfill \end{array}$$

(1)

where $U(X,Y)$ is the unknown function, $\tilde{K},G$ are given functions and $0<\mu ,\rho ,p,q\le 1$ are given constants. $S_1$ and ${\xi }_1$ are two integral variables. All functions in the above equation are assumed to be sufficiently smooth. As we know, this kind of equation not only arises from biological systems, but also found applications in physics, chemistry and memory material. Without losing generality, we discuss the last model, where $U(X,Y)$ stands for the initial shape. A temporary shape that is fixed is well illustrated by the double integral, in which the weak terms express the memory characteristic and two parameters p and q depend on the degree of deformation of the specific material in the X-axis and Y-axis, respectively. The deformation of the specific material is described by $\tilde{K}$. In the end, the function $G(x,y)$ represents the external force.

In order to apply the theory of orthogonal polynomials, we need to employ some linear transformations. First, let $S_1=pS,{\xi }_1=q\xi$ and (1) become:

$$\begin{array}{ccc}\hfill & & pq{\int }_0^X{\int }_0^Y{(pX-pS)}^{-\mu }{(qY-q\xi )}^{-\rho }\tilde{K}(X,Y,pS,q\xi )U(pS,q\xi )d\xi dS\hfill \\ & & =U(X,Y)+G(X,Y).\hfill \end{array}$$

(2)

Then we make the changes of variables $X=\frac{T}{2}(1+x)$ and $Y=\frac{\Gamma }{2}(1+y),$ where $(x,y)\in \overline{\Omega }$ ($\Omega =(-1,1)\times (-1,1)$), and the above equation turns into:

$$\begin{array}{ccc}\hfill & & {\int }_0^{\frac{T}{2}(1+x)}{\int }_0^{\frac{\Gamma }{2}(1+y)}{\left(p\frac{T}{2}(1+x)-pS\right)}^{-\mu }{\left(q\frac{\Gamma }{2}(1+y)-q\xi \right)}^{-\rho }\overline{K}(x,y,pS,q\xi )U(pS,q\xi )d\xi dS\hfill \\ & & =u(x,y)+g(x,y),\hfill \end{array}$$

(3)

where

$$\begin{array}{ccc}\hfill & & u(x,y)=U\left(\frac{T}{2}(1+x),\frac{\Gamma }{2}(1+y)\right),\hfill \\ & & \overline{K}(x,y,pS,q\xi )=pq\tilde{K}\left(\frac{T}{2}(1+x),\frac{\Gamma }{2}(1+y),pS,q\xi \right),\hfill \\ & & g(x,y)=G\left(\frac{T}{2}(1+x),\frac{\Gamma }{2}(1+y)\right).\hfill \end{array}$$

Later, two linear transformations $S=\frac{T}{2}(1+s)$ and $\xi =\frac{\Gamma }{2}(1+\tau )(s,\tau \in [-1,1])$ are employed and (3) changes into:

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}(x,y,s,\tau )u(ps+p-1,q\tau +q-1)d\tau ds\hfill \\ & & =u(x,y)+g(x,y),\hfill \end{array}$$

(4)

where

$$\begin{array}{c}\hfill \widehat{K}(x,y,s,\tau )={\left(\frac{pT}{2}\right)}^{1-\mu }{\left(\frac{q\Gamma }{2}\right)}^{1-\rho }\tilde{K}\left(\frac{T}{2}(1+x),\frac{\Gamma }{2}(1+y),p\frac{T}{2}(1+s),q\frac{\Gamma }{2}(1+\tau )\right).\end{array}$$

Spectral discretization will be carried out below. We first introduce the two-dimensional collocation points. Then we apply some linear transformations to obtain an equivalent problem to get the high-order accuracy. At last, the Gauss integration formula and Lagrange interpolation polynomial are employed to gain the high precision numerical format.

Firstly, we denote the collocation points in two-dimensional space by ${\left\{(x_i,y_j)\right\}}_{i,j=0}^N$, where ${\left\{x_i\right\}}_{i=0}^N$ and ${\left\{y_j\right\}}_{j=0}^N$ are the Gauss points in one dimension, equipped with the weights ${\omega }_i^x$ and ${\omega }_j^y$, respectively. Equation (4) holds at the two-dimensional collocation points, namely

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^{x_i}{\int }_{-1}^{y_j}{(x_i-s)}^{-\mu }{(y_j-\tau )}^{-\rho }\widehat{K}(x_i,y_j,s,\tau )u(ps+p-1,q\tau +q-1)d\tau ds\hfill \\ & & =u(x_i,y_j)+g(x_i,y_j).\hfill \end{array}$$

(5)

To apply Gauss quadrature rule, we need to transfer the two integral intervals $[-1,x_i]$ and $[-1,y_j]$ into $[-1,1]$, respectively, by using the following changes of variables:

$$\begin{array}{c}\hfill s=s\left(\theta \right)=\frac{x_i+1}{2}\theta +\frac{x_i-1}{2},\tau =\tau \left(\eta \right)=\frac{y_j+1}{2}\eta +\frac{y_j-1}{2},\end{array}$$

(6)

where $i,j=1,2,\dots ,N,\theta ,\eta \in [-1,1]$, then (5) becomes:

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-\theta )}^{-\mu }{(1-\eta )}^{-\rho }\widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))u(ps\left(\theta \right)+p-1,q\tau \left(\eta \right)+q-1)d\eta d\theta \hfill \\ & & =u(x_i,y_j)+g(x_i,y_j),\hfill \end{array}$$

(7)

where

$$\begin{array}{c}\hfill \widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))={\left(\frac{x_i+1}{2}\right)}^{1-\mu }{\left(\frac{y_j+1}{2}\right)}^{1-\rho }\widehat{K}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right)).\end{array}$$

(8)

The Gauss integration formula tells that the integration term in (7) can be approximated by:

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-\theta )}^{-\mu }{(1-\eta )}^{-\rho }\widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))u(ps\left(\theta \right)+p-1,q\tau \left(\eta \right)+q-1)d\eta d\theta \hfill \\ & & \approx {\displaystyle \sum _{k,l=0}^N}\widehat{k}(x_i,y_j,s\left({\theta }_k\right),\tau \left({\eta }_l\right))u(ps\left({\theta }_k\right)+p-1,q\tau \left({\eta }_l\right)+q-1){\omega }_k^x{\omega }_l^y.\hfill \end{array}$$

$I^{N}u(x,y)$ denotes the Lagrange interpolation polynomial, i.e.,

$$I^{N}u(x,y)={\displaystyle \sum _{i,j=0}^N}u(x_i,y_j)F_{ij}(x,y),$$

where $F_{ij}(x,y)=F_i\left(x\right)F_j\left(y\right),F_i$ and $F_j$ stand for two Lagrange interpolation basis functions which are based on the collocation points ${\left\{x_i\right\}}_{i=0}^N$ and ${\left\{y_j\right\}}_{j=0}^N$, respectively. $I^{N}u$ satisfies

$$I^{N}u(x_i,y_j)=u(x_i,y_j).$$

Denote $u_{ij}\approx u(x_i,y_j)$ and $u^N(x,y)\approx u(x,y)$, where

$$\begin{array}{c}\hfill u^N(x,y)={\displaystyle \sum _{i,j=0}^N}{u}_{ij}{F}_{ij}(x,y).\end{array}$$

(9)

Then the spectral collocation method tells that all of the $u_{ij},i,j=0,...,N$ can be found by solving the following linear system

$$\begin{array}{ccc}\hfill & & {\displaystyle \sum _{i,j=0}^N}{u}_{ij}\left({\displaystyle \sum _{k,l=0}^N}\widehat{k}(x_i,y_j,s\left({\theta }_k\right),\tau \left({\eta }_l\right))F_i(ps\left({\theta }_k\right)+p-1)F_j(q\tau \left({\theta }_l\right)+q-1){\omega }_k^x{\omega }_l^y\right)\hfill \\ & & =u_{ij}+g(x_i,y_j).\hfill \end{array}$$

(10)

Define $U={\left(u_{ij}\right)}^T$ and $G={\left(g(x_i,y_j)\right)}^T$. We rewrite (10) as the following matrix form:

$$\begin{array}{c}\hfill AU=U+G,\end{array}$$

(11)

where

$$A_{ij}={\displaystyle \sum _{k,l=0}^N}\widehat{k}(x_i,y_j,s\left({\theta }_k\right),\tau \left({\eta }_l\right))F_i(ps\left({\theta }_k\right)+p-1)F_j(q\tau \left({\theta }_l\right)+q-1){\omega }_k^x{\omega }_l^y.$$

For any given $\widehat{k}$ and G, we can obtain the values of $u_{ij}(i,j=0,\dots ,N)$ by solving the matrix Equation (11). Meanwhile, the approximate solution $u^N(x,y)$ can also be obtained by the expression of (9).

Now we give the arrangement of the following sections. Three kinds of norms and seven lemmas are described in Section 2. Error estimates are proposed in Section 3. Section 4 contains numerical examples to confirm the theoretical analysis. At last, we end the paper with some conclusions.

2. Some Preliminaries

In this section, some elementary lemmas will be provided, which are important for establishing the error estimates in the subsequent section. Before giving the lemmas, we introduce three kinds of norms one by one.

The first kind of norm ${\parallel v\parallel }_{\infty }$ denotes the infinite norm in the usual sense, given by

$${\parallel v\parallel }_{\infty }=\mathrm{e}\mathrm{s}\mathrm{s}\underset{(x,y)\in \Omega }{sup}\left|v(x,y)\right|.$$

The second kind of norm ${\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}$ represents the weighted square norm which is endowed in the space:

$$\begin{array}{ccc}& & L_{{\omega }^{\alpha ,\beta }}^2(\Omega )=\left\{u:{\int }_{-1}^1{\int }_{-1}^1{\left|u(x,y)\right|}^2{\omega }^{\alpha ,\beta }(x,y)dydx<+\infty \right\},\hfill \end{array}$$

(12)

whose norm is defined as:

$${\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}={\left({\int }_{-1}^1{\int }_{-1}^1{\left|u(x,y)\right|}^2{\omega }^{\alpha ,\beta }(x,y)dydx\right)}^{\frac{1}{2}},$$

and the inner product is given by:

$${(u,v)}_{{\omega }^{\alpha ,\beta }}={\int }_{-1}^1{\int }_{-1}^{1}u(x,y)v(x,y){\omega }^{\alpha ,\beta }(x,y)dydx,$$

where ${\omega }^{\alpha ,\beta }(x,y)={(1-x)}^{\alpha }{(1+x)}^{\beta }{(1-y)}^{\alpha }{(1+y)}^{\beta },\alpha ,\beta \in (-1,0)$.

The third kind of norm is denoted as ${\parallel v\parallel }_{{\omega }^{\alpha ,\beta }}^m={\left({\displaystyle \sum _{k=0}^m}{\parallel {\partial }^{k}v\parallel }_{{\omega }^{\alpha ,\beta }}^2\right)}^{\frac{1}{2}},$ which is equipped in the space

$$H_{{\omega }^{\alpha ,\beta }}^m(\Omega )=\left\{v:{\partial }^{k}v\in L_{{\omega }^{\alpha ,\beta }}^2(\Omega ),0\le k\le m\right\},$$

along with the semi-norm

$$\begin{array}{ccc}& & {\left|v\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}={\left({\displaystyle \sum _{k=\min (\mathrm{m},\mathrm{N}+1)}^m}{\parallel {\partial }^{k}v\parallel }_{{\omega }^{\alpha ,\beta }}^2\right)}^{\frac{1}{2}}.\hfill \end{array}$$

(13)

Then, seven important lemmas will be introduced. They will play key roles in the sharp error estimates for the fully discrete scheme in the next section. Throughout the paper, C denotes a generic positive constant, not necessarily the same at different places, which is dependent on the given data and the solution, but independent of the number of collocation points.

Lemma 1

([27] Gronwall inequality). Suppose a nonnegative integrable function $E(x,y)$ satisfies

$$E(x,y)\le M{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }E(s,\tau )d\tau ds+G(x,y),(x,y)\in \Omega ,$$

(14)

where M is a non-negative constant and $G(x,y)$ is a non-negative integrable function too. Then we have ${\parallel E\parallel }_{\infty }\le C{\parallel G\parallel }_{\infty }$ and ${\parallel E\parallel }_{{\omega }^{\alpha ,\beta }}\le C{\parallel G\parallel }_{{\omega }^{\alpha ,\beta }}.$

Lemma 2

([28]). Define $\left|\right|I^N{\left|\right|}_{\infty }=\underset{(x,y)\in \overline{\Omega }}{max}{\displaystyle \sum _{i,j=0}^N}\left|F_i\left(x\right)F_j\left(y\right)\right|$ and it holds that:

$$\begin{array}{c}\hfill \left|\right|I^N{\left|\right|}_{\infty }=\left\{\begin{array}{cc}\mathcal{O}\left({log}^{2}N\right),\hfill & -1<\alpha ,\beta \le -\frac{1}{2},\hfill \\ \mathcal{O}\left(N^{2max(\alpha ,\beta )+1}\right),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(15)

Lemma 3

([29]). Assume ${\mathcal{P}}_N$ denotes a space in which the degrees of all polynomials not exceed N and the product $v\varphi$ is integrated by the Gauss quadrature formula, where $v\in H_{{\omega }^{\alpha ,\beta }}^m(\Omega )$ for some $m>1$ and $\varphi \in {\mathcal{P}}_N$. Then

$$\left|{(v,\varphi )}_{{\omega }^{\alpha ,\beta }}-{(v,\varphi )}_N\right|\le C{N}^{-m}{\left|v\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}{\parallel \varphi \parallel }_{{\omega }^{\alpha ,\beta }},$$

(16)

where

$${(v,\varphi )}_N={\displaystyle \sum _{i,j=0}^N}v({\theta }_i,{\eta }_j)\varphi ({\theta }_i,{\eta }_j){\omega }_i^x{\omega }_j^y.$$

Lemma 4

([29,30]). Assume that $u(x,y)\in H_{{\omega }^{\alpha ,\beta }}^m(\Omega )$ for $m>1$. Then we have the following estimates:

$$\begin{array}{ccc}& & \parallel u-I^N{u\parallel }_{\infty }\le C{N}^{4-m}{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N},\hfill \end{array}$$

(17)

$$\begin{array}{ccc}& & \parallel u-I^N{u\parallel }_{{\omega }^{\alpha ,\beta }}\le C{N}^{-m}{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}.\hfill \end{array}$$

(18)

Lemma 5

([31]). Assume $v(x,y)$ is a bounded function and there is:

$$\begin{array}{c}\hfill \underset{N}{sup}\parallel {\displaystyle \sum _{i,j=0}^N}v(x_i,y_j)F_{ij}(x,y){\parallel }_{{\omega }^{\alpha ,\beta }}\le C\underset{(x,y)\in \overline{\Omega }}{max}\left|v(x,y)\right|,\end{array}$$

(19)

where C is a constant independent of $v(x,y)$.

Lemma 6

([32,33]). For a nonnegative integer r and $\kappa \in (0,1)$, there exists a constant $C_{r,\kappa }>0$ such that for any function $v\in {\mathcal{C}}^{r,\kappa }\left(\overline{\Omega }\right)$, there is a polynomial function ${\mathcal{J}}_{N}v\in {\mathcal{P}}_N$ such that

$$\parallel v-{\mathcal{J}}_{N}v{\parallel }_{\infty }\le C_{r,\kappa }{N}^{-(r+\kappa )}{\parallel v\parallel }_{{\mathcal{C}}^{r,\kappa }\left(\overline{\Omega }\right)},$$

(20)

where

$$\begin{array}{ccc}& & {\parallel v\parallel }_{C^{r,\kappa }\left(\overline{\Omega }\right)}=\underset{\alpha \le r}{max}\underset{(x,y)\in \overline{\Omega }}{max}\left|{\partial }^{\alpha }v(x,y)\right|+\underset{\alpha \le r}{max}\underset{(x^{\prime },y^{\prime })\ne (x^{″},y^{″})\in \overline{\Omega }}{sup}\left|\frac{{\partial }^{\alpha }v(x^{\prime },y^{\prime })-{\partial }^{\alpha }v(x^{″},y^{″})}{{[{(x^{\prime }-x^{″})}^2+{(y^{\prime }-y^{″})}^2]}^{\kappa /2}}\right|.\hfill \end{array}$$

It is obvious that ${\mathcal{J}}_N$ is a linear operator from ${\mathcal{C}}^{r,\kappa }\left(\overline{\Omega }\right)$ into ${\mathcal{P}}_N$.

Lemma 7

([34]). For any continuous function v defined in $C\left(\right[-1,1]\times [-1,1\left]\right)$, assume ${\mathcal{M}}_v$ is defined by:

$$\left({\mathcal{M}}_v\right)(x,y)={\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{k}(x,y,s,\tau )v(s,\tau )d\tau ds.$$

(21)

For any different points $(x_1,y_1),(x_2,y_2)\in [-1,1]\times [-1,1]$ and $\delta \in (0,\min \{1-\mu ,1-\rho \left\}\right)$, it is valid that:

$$\frac{|\left({\mathcal{M}}_v\right)(x^{\prime },y^{\prime })-\left({\mathcal{M}}_v\right)(x^{″},y^{″})|}{{[{(x^{\prime }-x^{″})}^2+{(y^{\prime }-y^{″})}^2]}^{\kappa /2}}\le C\underset{(x,y)\in \overline{\Omega }}{max}\left|v(x,y)\right|.$$

(22)

That is to say:

$$\parallel {\mathcal{M}}_v{\parallel }_{{\mathcal{C}}^{0,\kappa }\left(\overline{\Omega }\right)}\le C\underset{(x,y)\in \overline{\Omega }}{max}\left|v(x,y)\right|.$$

(23)

3. Error Estimates

We present the error estimates for the numerical scheme (10) and derive that the proposed approximation possesses the desired exponential rate of convergence. Firstly, we carry out the error estimate in the sense of the $L^{\infty }$ norm.

Theorem 1.

Suppose $u(x,y)$ is the exact solution of (4), which is supposed to be sufficiently smooth, $u^N(x,y)$ is the approximate solution of $u(x,y)$ and the error function is denoted as $e(x,y)=u(x,y)-u^N(x,y)$. If $m>4$, then we claim that:

$$\begin{array}{ccc}\hfill & & {\parallel e\parallel }_{\infty }\le C{N}^{-m}\left\{\begin{array}{c}{\displaystyle {log}^{2}N\underset{(x,y)\in \overline{\Omega }}{max}|\widehat{k}{(x,y,s,\tau )|}_{{\omega }^{\alpha ,\beta }}^{m;N}{\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+N^4{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N},\alpha ,\beta \in (-1,-\frac{1}{2}],}\hfill \\ {\displaystyle N^{2max(\alpha ,\beta )+1}\underset{(x,y)\in \overline{\Omega }}{max}|\widehat{k}{(x,y,s,\tau )|}_{{\omega }^{\alpha ,\beta }}^{m;N}{\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+N^4{\left|u\right|}_{{\omega }^{\alpha ,\beta }(\Omega )}^{m;N},\mathrm{otherwise}.}\hfill \end{array}\right.\hfill \end{array}$$

(24)

Proof. 

Subtracting (10) from (7), we get that:

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-\theta )}^{-\mu }{(1-\eta )}^{-\rho }\widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))u(ps\left(\theta \right)+p-1,q\tau \left(\eta \right)+q-1)d\eta d\theta \hfill \\ \hfill & & -{\displaystyle \sum _{i,j=0}^N}{u}_{ij}\left({\displaystyle \sum _{k,l=0}^N}\widehat{k}(x_i,y_j,s\left({\theta }_k\right),\tau \left({\eta }_l\right))L_i(ps\left({\theta }_k\right)+p-1)L_j(q\tau \left({\eta }_l\right)+q-1){\omega }_k^x{\omega }_l^y\right)\hfill \\ & & =u(x_i,y_j)-u_{ij},\hfill \end{array}$$

(25)

and we can rewrite (25) into the following form:

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^1{\int }_{-1}^1{(1-\theta )}^{-\mu }{(1-\eta )}^{-\rho }\widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))e(ps\left(\theta \right)+p-1,q\tau \left(\eta \right)+q-1)d\eta d\theta +B(x_i,y_j)\hfill \\ & & =u(x_i,y_j)-u_{ij},\hfill \end{array}$$

(26)

by defining

$$\begin{array}{ccc}& & B(x_i,y_j)\hfill \\ & & ={\int }_{-1}^1{\int }_{-1}^1{(1-\theta )}^{-\mu }{(1-\eta )}^{-\rho }\widehat{k}(x_i,y_j,s\left(\theta \right),\tau \left(\eta \right))u_N(ps\left(\theta \right)+p-1,q\tau \left(\eta \right)+q-1)d\eta d\theta \hfill \\ & & -{\displaystyle \sum _{i,j=0}^N}{u}_{ij}\left({\displaystyle \sum _{k,l=0}^N}\widehat{k}(x_i,y_j,s\left({\theta }_k\right),\tau \left({\eta }_l\right))L_i(ps\left({\theta }_k\right)+p-1)L_j(q\tau \left({\theta }_l\right)+q-1){\omega }_k^x{\omega }_l^y\right).\hfill \end{array}$$

Noting (6), we have that

$$\begin{array}{ccc}\hfill & & {\int }_{-1}^{x_i}{\int }_{-1}^{y_j}{(x_i-s)}^{-\mu }{(y_j-\tau )}^{-\rho }\widehat{K}(x_i,y_j,s,\tau )e(ps+p-1,q\tau +q-1)d\tau ds+B(x_i,y_j)\hfill \\ & & =u(x_i,y_j)-u_{ij}.\hfill \end{array}$$

(27)

Multiplying $F_i\left(x\right)F_j\left(y\right)$ on both sides of (27), then summing up the indexes i and j from 0 to N, respectively, and the error equation can be obtained as:

$$\begin{array}{ccc}\hfill & & e(x,y)={\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}(x,y,s,\tau )e(ps+p-1,q\tau +q-1)d\tau ds+{\displaystyle \sum _{m=1}^3}{B}_m(x,y),\hfill \end{array}$$

here

$$\begin{array}{ccc}\hfill & & B_1(x,y)={\displaystyle \sum _{i,j=0}^N}B(x_i,y_j)F_i\left(x\right)F_j\left(y\right),\hfill \\ \hfill & & B_2(x,y)=u(x,y)-I^{N}u(x,y),\hfill \\ \hfill & & B_3(x,y)=I^N{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}(x,y,s,\tau )e(ps+p-1,q\tau +q-1)d\tau ds\hfill \\ \hfill & & -{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}(x,y,s,\tau )e(ps+p-1,q\tau +q-1)d\tau ds.\hfill \end{array}$$

As a result, we obtain that

$$\begin{array}{c}\hfill \left|e(x,y)\right|\le M{\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\left|e(ps+p-1,q\tau +q-1)\right|d\tau ds+{\displaystyle \sum _{m=1}^3}\left|B_m(x,y)\right|,\end{array}$$

(28)

along with

$$\begin{array}{c}\hfill M=\underset{\genfrac{}{}{0pt}{}{-1\le s\le x\le 1,}{-1\le \tau \le y\le 1}}{max}\left|\widehat{K}(x,y,s,\tau )\right|.\end{array}$$

Using Lemma 1, we get that

$$\begin{array}{c}\hfill {\left|\right|e\left|\right|}_{\infty }\le C\left(\left|\right|B_1{\left|\right|}_{\infty }+\left|\right|B_2{\left|\right|}_{\infty }+\left|\right|B_3{\left|\right|}_{\infty }\right).\end{array}$$

(29)

Applying Lemmas 2 and 3 yields:

$$\begin{array}{ccc}\hfill & & \left|\right|B_1{\left|\right|}_{\infty }\hfill \\ \hfill & & \le C\left|\right|I^N{\left|\right|}_{\infty }\underset{0\le i,j\le N}{max}\left|B(x_i,y_j)\right|\hfill \\ \hfill & & \le C\left|\right|I^N{\left|\right|}_{\infty }{N}^{-m}\underset{0\le i,j\le N}{max}|\widehat{k}(x_i,y_j,s,\tau ){|}_{{\omega }^{\alpha ,\beta }}^{m;N}{(\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+{\parallel e\parallel }_{\infty })\hfill \\ & & \le C{N}^{-m}\underset{0\le i,j\le N}{max}|\widehat{k}(x_i,y_j,s,\tau ){|}_{{\omega }^{\alpha ,\beta }}^{m;N}{(\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+{\parallel e\parallel }_{\infty })\left\{\begin{array}{c}{log}^{2}N,\alpha ,\beta \in (-1,-\frac{1}{2}],\hfill \\ N^{2max(\alpha ,\beta )+1},\mathrm{otherwise}.\hfill \end{array}\right.\hfill \end{array}$$

(30)

By using the estimate (17) in Lemma 4, we have that:

$$\begin{array}{c}\hfill \left|\right|B_2{\left|\right|}_{\infty }\le C{N}^{4-m}{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}.\end{array}$$

(31)

Following Lemmas 6 and 7, we arrive at:

$$\begin{array}{ccc}\hfill & & \parallel B_3{\parallel }_{\infty }\hfill \\ \hfill & & =\parallel (I-I^N){\mathcal{M}}_e{\parallel }_{\infty }\hfill \\ \hfill & & =\parallel (I-I^N){\mathcal{M}}_e-(I-I^N){\mathcal{J}}_N{\mathcal{M}}_e{\parallel }_{\infty }\hfill \\ \hfill & & =\parallel (I-I^N)({\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e){\parallel }_{\infty }\hfill \\ \hfill & & \le (1+||I^N{\left|\right|}_{\infty })\parallel {\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e{\parallel }_{\infty }\hfill \\ \hfill & & \le C\parallel I^N{\parallel }_{\infty }{N}^{-\kappa }{\parallel {\mathcal{M}}_e\parallel }_{C^{0,\kappa }\overline{(\Omega )}}\hfill \\ & & \le C\parallel I^N{\parallel }_{\infty }{N}^{-\kappa }{\parallel e\parallel }_{\infty },\hfill \end{array}$$

(32)

where in the second step of (32) we notice the fact that $(I-I^N){\mathcal{J}}_N{\mathcal{M}}_e={\mathcal{J}}_N{\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e=0$.

Combining (29)–(32), we can get the estimate for ${\left|\right|e\left|\right|}_{\infty }$ immediately. □

Next, we carry out the error analysis in $L_{{\omega }^{\alpha ,\beta }}^2$ space.

Theorem 2.

If the hypotheses given in Theorem 1 hold, then:

$$\begin{array}{c}\hfill {\left|\right|e\left|\right|}_{{\omega }^{\alpha ,\beta }}\le C{N}^{-m}\left(\underset{(x,y)\in \overline{\Omega }}{max}|\widehat{k}{(x,y,s,\tau )|}_{{\omega }^{\alpha ,\beta }}^{m;N}{\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}+N^{-\kappa }{\parallel e\parallel }_{\infty }\right).\end{array}$$

(33)

Proof. 

With the help of (28) and Gronwall inequality, we have that:

$$\begin{array}{c}\hfill {\left|\right|e\left|\right|}_{{\omega }^{\alpha ,\beta }}\le C\left(\left|\right|B_1{\left|\right|}_{{\omega }^{\alpha ,\beta }}+\left|\right|B_2{\left|\right|}_{{\omega }^{\alpha ,\beta }}+\left|\right|B_3{\left|\right|}_{{\omega }^{\alpha ,\beta }}\right).\end{array}$$

(34)

By virtue of Lemmas 1 and 5, we get that:

$$\begin{array}{ccc}\hfill & & \left|\right|B_1{\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & \le C\underset{(x,y)\in \overline{\Omega }}{max}\left|B(x,y)\right|\hfill \\ & & \le C{N}^{-m}\underset{0\le i,j\le N}{max}{\left|\widehat{k}(x_i,y_j,s,\tau )\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}\left({\parallel u\parallel }_{{\omega }^{\alpha ,\beta }}+{\parallel e\parallel }_{{\omega }^{\alpha ,\beta }}\right).\hfill \end{array}$$

(35)

Applying Lemma 4 results in:

$$\begin{array}{c}\hfill \left|\right|B_2{\left|\right|}_{{\omega }^{\alpha ,\beta }}\le C{N}^{-m}{\left|u\right|}_{{\omega }^{\alpha ,\beta }}^{m;N}.\end{array}$$

(36)

By using Lemmas 5–7, we find that:

$$\begin{array}{ccc}\hfill & & \left|\right|B_3{\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & =\left|\right|(I-I^N){\mathcal{M}}_e{\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & =\left|\right|(I-I^N)({\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e){\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & =\left|\right|I({\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e){\left|\right|}_{{\omega }^{\alpha ,\beta }}+\left|\right|I^N({\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e){\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & \le \left|\right|{\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e{\left|\right|}_{{\omega }^{\alpha ,\beta }}+\left|\right|I^N({\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e){\left|\right|}_{{\omega }^{\alpha ,\beta }}\hfill \\ \hfill & & \le C\left|\right|{\mathcal{M}}_e-{\mathcal{J}}_N{\mathcal{M}}_e{\left|\right|}_{\infty }\hfill \\ \hfill & & \le C{N}^{-\kappa }\left|\right|{\mathcal{M}}_e{\left|\right|}_{{\mathcal{C}}^{r,\kappa }\left(\overline{\Omega }\right)}\hfill \\ & & \le C{N}^{-\kappa }{\left|\right|e\left|\right|}_{\infty }.\hfill \end{array}$$

(37)

Together with (34)–(37), and we can get the desired estimate. □

4. Error Tests

In this section, two examples will be presented to confirm the theoretical analysis. We perform the computations by using Matlab software.

Example 1.

Let $p=q=1$, then (4) has the following form:

$$\begin{array}{c}\hfill {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }\widehat{K}(x,y,s,\tau )u(s,\tau )d\tau ds=u(x,y)+g(x,y).\end{array}$$

(38)

Here we choose $u(x,y)=2e^{-cos\left(xy\right)}$ as the exact solution and select

$$\widehat{K}(x,y,s,\tau )={(x-s)}^2(y-\tau )e^{cos\left(s\tau \right)},$$

to this end

$$g(x,y)=\frac{2{(x+1)}^{3-\mu }{(y+1)}^{2-\rho }}{(3-\mu )(2-\rho )}-2e^{-cos\left(xy\right)}.$$

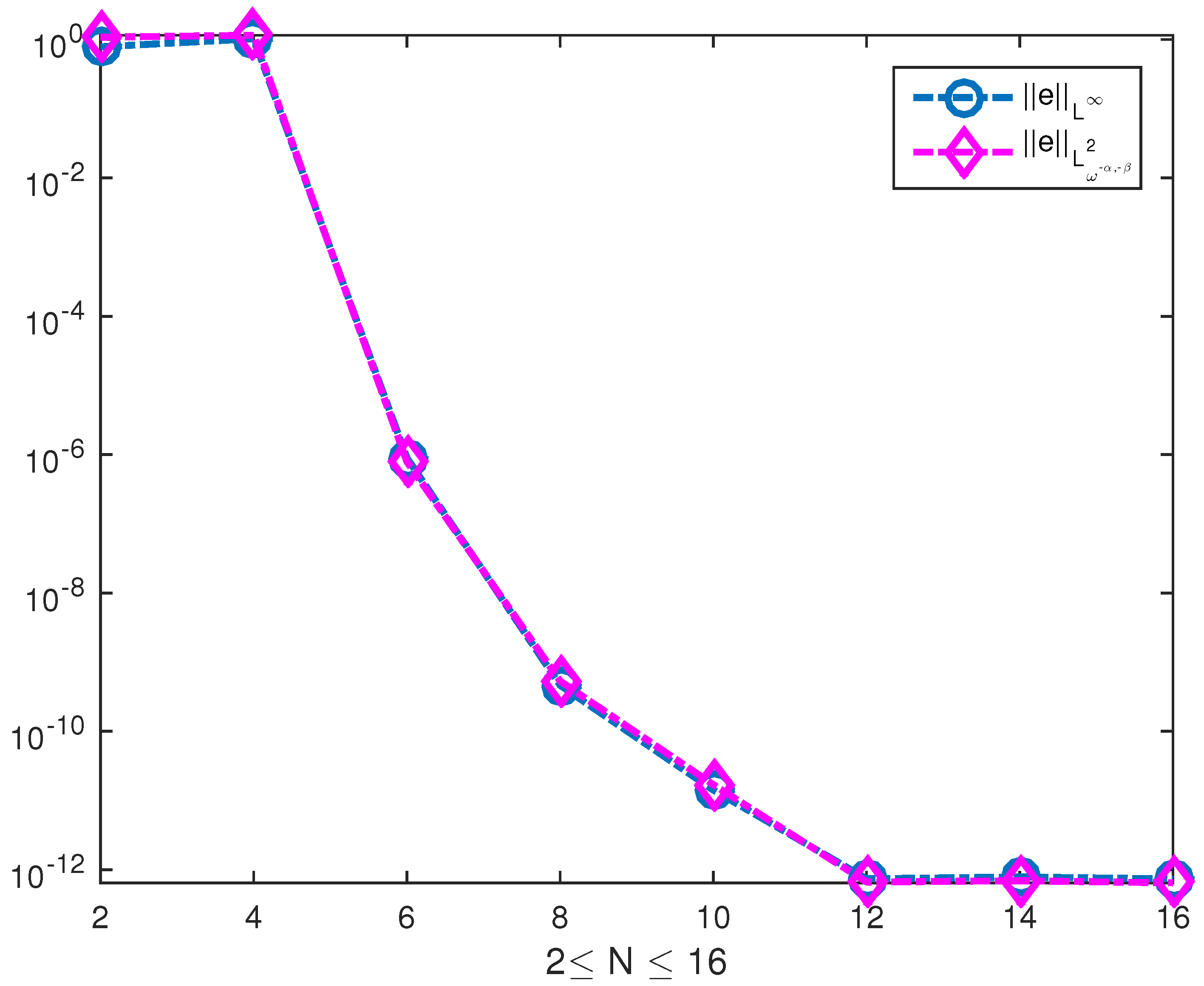
Let $\mu =0.5,\rho =1/3$, and we solve the matrix Equation (11), and the infinity error in $L^{\infty }$ norm and weighted square error in $L_{{\omega }^{\alpha ,\beta }}^2$ norm for different N which denotes the number of collocation points are listed in Table 1. To show the exponential rate of convergence more visually, Figure 1 exhibits the errors in the $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms versus N. From Table 1 and Figure 1, one can see that the spectral method achieves the exponential rate of convergence, illustrating a fact that the numerical simulations highly agree with the theoretical results.

Table 1. The infinity error and weighted square error for Example 1.

N	2	4	6	8
$L^{\infty }$-error	0.890754	0.813149	7.16 × 10${}^{-7}$	4.65 × 10${}^{-10}$
$L_{{\omega }^{\alpha ,\beta }}^2$-error	1.064346	0.888106	5.91 × 10${}^{-7}$	5.31 × 10${}^{-10}$
N	10	12	14	16
$L^{\infty }$-error	1.43 × 10${}^{-11}$	7.40 × 10${}^{-13}$	7.82 × 10${}^{-13}$	7.35 × 10${}^{-13}$
$L_{{\omega }^{\alpha ,\beta }}^2$-error	1.67 × 10${}^{-11}$	6.63 × 10${}^{-13}$	6.92 × 10${}^{-13}$	6.45 × 10${}^{-13}$

Figure 1. The errors in $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms for Example 1.

Example 2.

We consider a normal situation. We take:

$$u(x,y)=xy$$

and

$$\widehat{K}(x,y,s,\tau )=1$$

into Equation (4) and it becomes:

$$\begin{array}{c}\hfill {\int }_{-1}^x{\int }_{-1}^y{(x-s)}^{-\mu }{(y-\tau )}^{-\rho }(ps+p-1)(q\tau +q-1)d\tau ds=xy+g(x,y).\end{array}$$

(39)

By calculation, $g(x,y)$ is determined by:

$$g(x,y)=\left(\frac{p{(x+1)}^{2-\mu }}{(1-\mu )(2-\mu )}-\frac{{(x+1)}^{1-\mu }}{1-\mu }\right)\left(\frac{q{(y+1)}^{2-\rho }}{(1-\rho )(2-\rho )}-\frac{{(y+1)}^{1-\rho }}{1-\rho }\right)-xy.$$

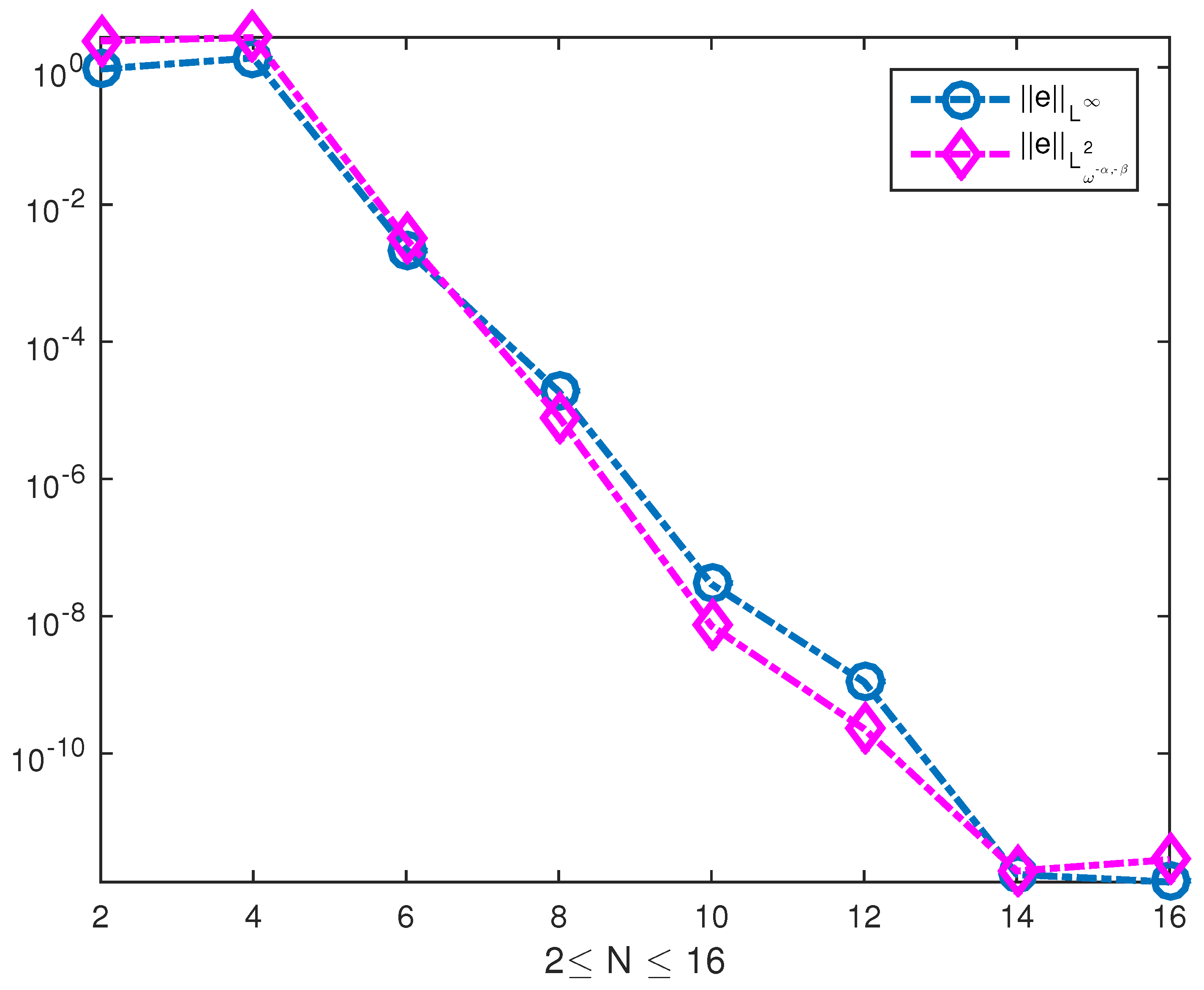
As the theoretical analysis shown, if four parameters $\mu ,\rho ,p,q$ are given, we can carry out the spectral numerical test to yield the approximate solution. Now we let $\mu =0.8,\rho =0.1,p=0.65,q=1/3$. Then we carry out the computation and get the errors in $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms. More information please see Table 2 and Figure 2. Again, we conclude that the spectral method exhibits the exponential rate of convergence. These simulations further confirm our theoretical results.

Table 2. The infinity error and weighted square error for Example 2.

N	2	4	6	8
$L^{\infty }$-error	1.126858	1.847336	3.18 × 10${}^{-3}$	1.01 × 10${}^{-5}$
$L_{{\omega }^{\alpha ,\beta }}^2$-error	1.777118	2.421684	4.59 × 10${}^{-3}$	7.04 × 10${}^{-6}$
N	10	12	14	16
$L^{\infty }$-error	1.34 × 10${}^{-7}$	4.30 × 10${}^{-10}$	1.85 × 10${}^{-12}$	1.34 × 10${}^{-12}$
$L_{{\omega }^{\alpha ,\beta }}^2$-error	5.19 × 10${}^{-8}$	8.30 × 10${}^{-11}$	2.02 × 10${}^{-12}$	2.84 × 10${}^{-12}$

Figure 2. The errors in $L^{\infty }$ and $L_{{\omega }^{\alpha ,\beta }}^2$ norms for Example 2.

5. Conclusions

In this paper, we have presented the error estimates for a weakly singular Volterra integral equation with delays in two-dimensional space. The main contribution of this work is that we have demonstrated rigorously that the errors of spectral approximations decay exponentially in both the $L^{\infty }$ norm and the $L_{{\omega }^{\alpha ,\beta }}^2$ norm, which is a desired feature for a spectral method. Two numerical examples verify the theoretical results and exhibit an improvement of accuracy over the existing method [35]. Next we will extend our work to two-dimensional Volterra integro-differential equations.