Abstract
A transient chaotic neural network (TCNN) is particularly useful for solving combinatorial optimization problems, and its hardware implementation based on memristors has attracted great attention recently. Although previously used filamentary memristors could provide the desired nonlinearity for implementing the annealing function of a TCNN, the controllability of filamentary switching still remains relatively poor, thus limiting the performance of a memristor-based TCNN. Here, we propose to use ferroelectric memristor to implement the annealing function of a TCNN. In the ferroelectric memristor, the conductance can be tuned by switching the lattice non-centrosymmetry-induced polarization, which is a nonlinear switching mechanism with high controllability. We first establish a ferroelectric memristor model based on a ferroelectric tunnel junction (FTJ), which exhibits the polarization-modulated tunnel conductance and the nucleation-limited-switching (NLS) behavior. Then, the conductance of the ferroelectric memristor is used as the self-feedback connection weight that can be dynamically adjusted. Based on this, a ferroelectric memristor-based transient chaotic neural network (FM-TCNN) is further constructed and applied to solve the traveling salesman problem (TSP). In 1000 runs for 10-city TSP, the FM-TCNN achieves a shorter average path distance, a 32.8% faster convergence speed, and a 2.44% higher global optimal rate than the TCNN.
1. Introduction
Combinatorial optimization is a branch of mathematical optimization which has wide applications in artificial intelligence, theoretical computer science, applied mathematics, and so on [1]. One of the most famous combinatorial optimization problems is the traveling salesman problem (TSP), which is ubiquitous in real-life scenarios such as supply chain management, aircraft routing, and job-shop scheduling. TSP aims to find the shortest route that visits every city exactly once and returns to the starting point, which is, however, an NP-hard problem that cannot be solved accurately. Swarm intelligence optimization algorithm [2,3] and artificial neural network [4,5] are the two mainstream methods to deal with TSP. Based on chaotic simulated annealing, Chen et al. proposed a transient chaotic neural network (TCNN) model to solve TSP in 1995 [6]. Compared with the Hopfield neural network (HNN) and chaotic neural network, TCNN shows stronger search ability. However, as the annealing processing of TCNN is determined by a damping factor, TCNN is easy to fall into local optimum when solving large-size TSP. In 2004, by adding decaying stochastic noise into TCNN, a noisy chaotic neural network (NCNN) was constructed [7]. The simulation results show that the NCNN achieved higher global optimal rate than TCNN when solving large-size TSP. Additionally, in order to provide the ability to characterize local features, Gauss wavelet self-feedback was introduced into TCNN [8], resulting in the reduction in local minima rate. However, these works all aimed to improve the global optimum rate by modifying the mathematical expression of annealing processing, while paying little attention to the physical implementation of annealing function or the whole algorithm.
Recently, memristor has attracted widespread interest on combinatorial optimization. Pershin et al. [9] showed that the memristive networks can efficiently solve shortest-path optimization problems thanks to its electrically programmable conductance, which shows potential as the hardware basis for implementing HNN or TCNN. For example, Fahimi et al. [10] proposed a weight annealing approach for HNN on a fabricated 20 × 20 analog-grade TiO memristive crossbar with the help of the designed mixed-signal accelerators. Liu et al. [11] proposed to use the conductance values of the Hewlett-Packard (HP) memristor, which can be adjusted dynamically according to the annealing algorithm, as the self-feedback connection weights in TCNN. Based on this, an HP memristor-based transient chaotic neural network (HPM-TCNN) was developed. Simulation results demonstrate that HPM-TCNN could quickly converge toward the global minimum, which was attributed to the efficient nonlinear annealing process stemming from the strong nonlinearity of the HP memristor. Moreover, Yang et al. [12] experimentally demonstrated the implementation of TCNN on a memristor crossbar, which realized high probability of global optimum and fast convergence by using the nonlinear long-term depression (LTD) processes of the diagonal memristors in the crossbar for annealing.
It is noteworthy that the memristors used so far for the implementation of TCNN are all filamentary memristors, which operate through the formation and rupture of conductive filaments. Although the filament formation/rupture is a nonlinear ion migration process, which can be well used to implement the annealing function, its intrinsic stochasticity may cause imprecise control of conductance, relatively poor endurance, and large device-to-device variation in filamentary memristors. This in turn limits the performance of a practical memristor-based TCNN. To address this issue, memristors with more controllable nonlinear switching dynamics are highly desirable.
A ferroelectric memristor emerges as a suitable candidate because its conductance change relies on the switching of lattice non-centrosymmetry-induced polarization, which is a purely electronic mechanism with strong nonlinearity and high controllability [13]. On one hand, the nonlinearity of polarization switching is fundamentally different from that of filament formation/rupture, offering an opportunity for the ferroelectric memristor to realize a more favorable annealing function. On the other hand, the high controllability of polarization switching enables the ferroelectric memristor to exhibit precise conductance control [14], high endurance [15], and small device-to-device variation [16]. These features make the ferroelectric memristor a promising building block for the hardware TCNN. However, it should be pointed out that although ferroelectric memristors have been widely investigated as synaptic devices for artificial neural networks [15,17] and convolutional neural networks [18], their use in the hardware implementation of TCNN has never been attempted.
In this study, we theoretically establish a ferroelectric memristor-based TCNN (FM-TCNN) model and demonstrate its high performance in solving combinatorial optimization problems such as the TSP. We first establish a single-neuron model with an annealing function implemented by a prototype ferroelectric memristor, i.e., ferroelectric tunnel junction (FTJ). The conductance of the ferroelectric memristor is used as the self-feedback connection weight. In addition, the conductance is adjusted by applying a voltage pulse whose amplitude depends linearly on the neuron output, resulting in the dynamical modulation of the self-feedback connection weight. It is shown that the neuron can successfully converge to the stable state from the chaotic state, and the convergence speed is modulated by the slope between the pulse amplitude and the neuron output. Then, the FM-TCNN model is applied to solve the TSP. It achieves shorter average path distance, higher convergence speed, and higher global optimal compared with TCNN and HPM-TCNN, demonstrating its effectiveness in solving combinatorial optimization problems.
The remainder of this paper is organized as follows. In Section 2, the ferroelectric memristor is modeled. The FM-TCNN model is described in Section 3. In Section 4, the application of FM-TCNN in solving TSP is carried out, and the experimental results are also discussed. The final section concludes this study.
2. Ferroelectric Memristor Model
A prototype ferroelectric memristor, i.e., FTJ, is used in this study. FTJ consists of an ultrathin ferroelectric film (i.e., the tunnel barrier) sandwiched between two different metal electrodes. The tunnel conductance depends on the average height of the tunnel barrier, which is modulated by the relative fraction of ferroelectric domains with polarization oriented toward one (or the other) electrode. More specifically, when all the domains are aligned downward, the barrier height at the ferroelectric/bottom (top) electrode interface is reduced (enhanced). The reverse scenario occurs when all the domains are aligned upward. Assuming that the bottom electrode has a larger screening length over dielectric constant than the top electrode, the polarization charge-induced barrier height modulation at the bottom interface is therefore more significant than that at the top interface. As a result, the FTJ exhibits the lowest (highest) average barrier height when all the domains aligned downward (upward), leading to the ON-state conductance (OFF-state conductance ).
As the domains are gradually switched from downward to upward (from upward to downward) through the application of voltage pulses, the device conductance (G) gradually evolves from to (from to ). To realize the gradual switching of domains, the number of domains underneath the electrode area is assumed to be sufficiently large. This can be achieved in two ways: (1) using sufficiently large electrodes and (2) using the domain engineering to reduce the domain size. For practical application, the second way is more favorable, because a small electrode area is always required for high integration density. Previous studies have demonstrated that the domain size can be reduced to be below 5 nm [19]. For a 130 nm technology node, the number of domains in an individual device can reach >670, which may be sufficiently large for ensuring the gradual switching of domains.
Using a simple model of parallel resistances, the relationship between G and the area fraction of downward domains S can be described below [20]:
where and have fixed values once a specific FTJ is used (here, and are used, which are extracted from the experimental data of a Pt/BaTiO3/Nb:SrTiO3 FTJ [21]), while S is a value between 0 and 1 depending on the amplitude and duration of the applied pulse.
To establish the relationship between S and the amplitude and duration of the applied pulse, the polarization switching kinetics need to be understood. It is widely accepted that the polarization switching in FTJ can be described by a nucleation-limited-switching (NLS) model [22]. In this model, the ferroelectric film is considered to consist of many different basic areas with independent switching kinetics. The switching time () in each basic area is governed by the domain nucleation, while the time for the domain growth can be neglected. Therefore, a distribution of exists, and a Lorentzian distribution function is assumed here [23]:
where is the mean switching time, and is the half-width at half-maximum. The dependence of on the applied electric field E (, where V is the voltage of the applied pulse, d is the ferroelectric film thickness, and symbol ‘’ means to take the absolute value.) follows the characteristic Merz’s law:
while the relationship between and E is given by
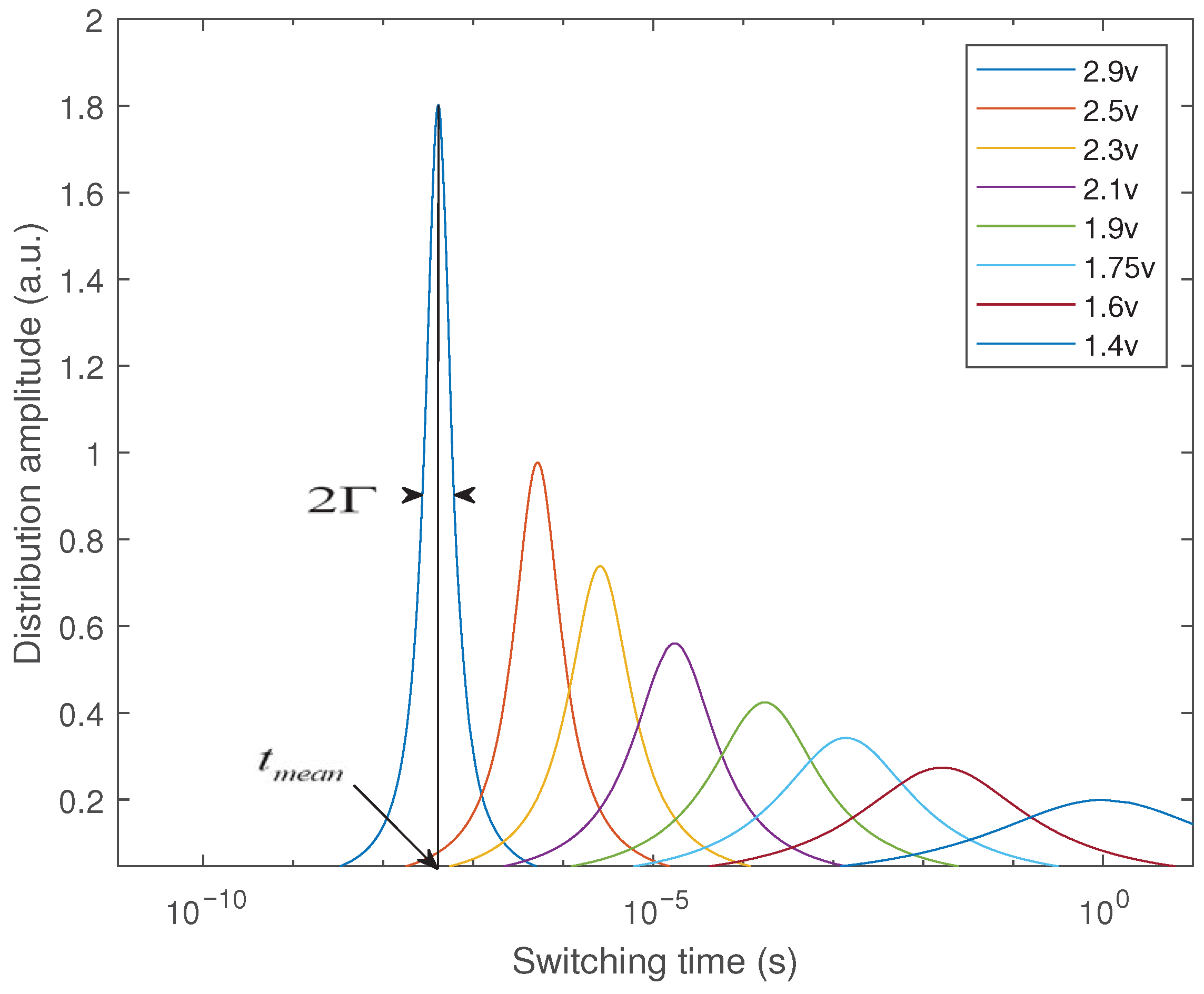
Simulations were performed using the experimental data given in ref. [21], where d = 2.8 nm and V varies in a certain range. Some examples of the simulated Lorentzian distribution of at different V are shown in Figure 1. It is seen that when V becomes larger, the switching occurs earlier and in a narrower time window, in good agreement with the experimental results [22,23,24].
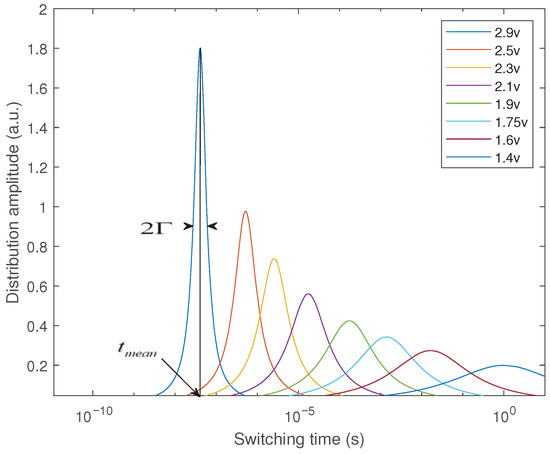
Figure 1.
Some examples of the Lorentzian distribution of switching time at different applied voltages.
Having obtained the Lorentzian distribution of , the area fraction of downward domains S can be approximated as a function of the amplitude V and duration t of the applied pulse
where ‘±’ relates to the sign of the applied pulse.
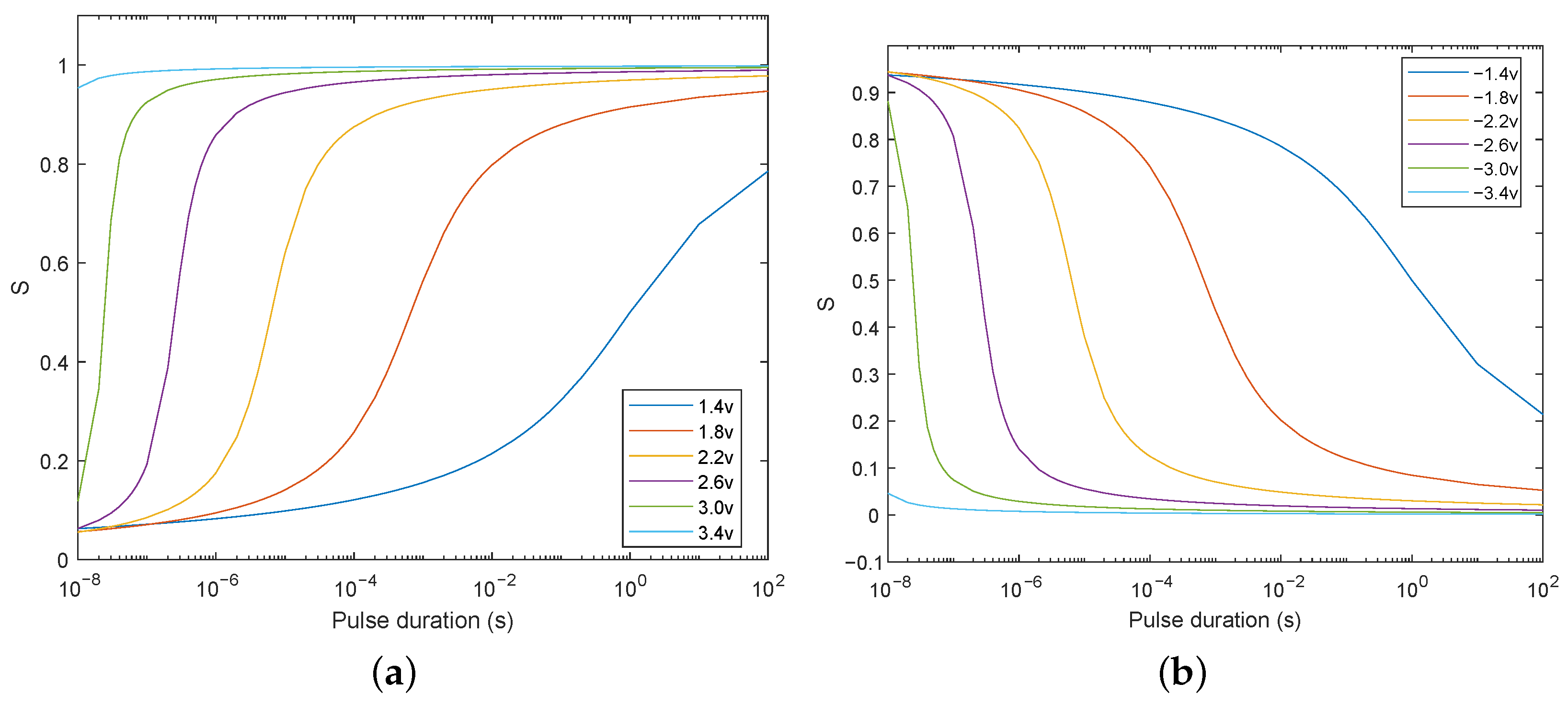
Using Equation (5) and the same set of and , the evolutions of S as a function of pulse duration t at different pulse amplitudes V are calculated and shown in Figure 2. When the applied pulse voltage is positive, as shown in Figure 2a, the larger the pulse duration, the larger the fraction of domains that can be switched downward (i.e., the closer S is to 1). In addition, under the same pulse duration, a larger pulse amplitude produces a larger fraction of downward domains. In contrast, as shown in Figure 2b, more domains are switched upward, i.e., S becomes closer to 0, with the increase in pulse amplitude and duration.
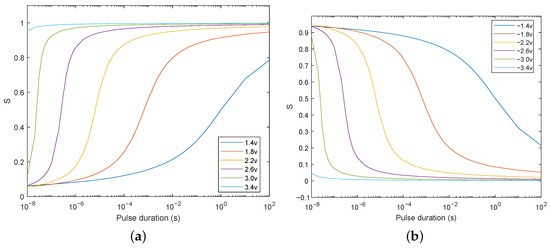
Figure 2.
Area fractions of downward domains as a function of pulse time at different pulse amplitude. (a) The applied pulse voltage is positive, and all the domains are initially aligned upward. (b) The applied pulse voltage is negative, and all the domains are initially aligned downward.
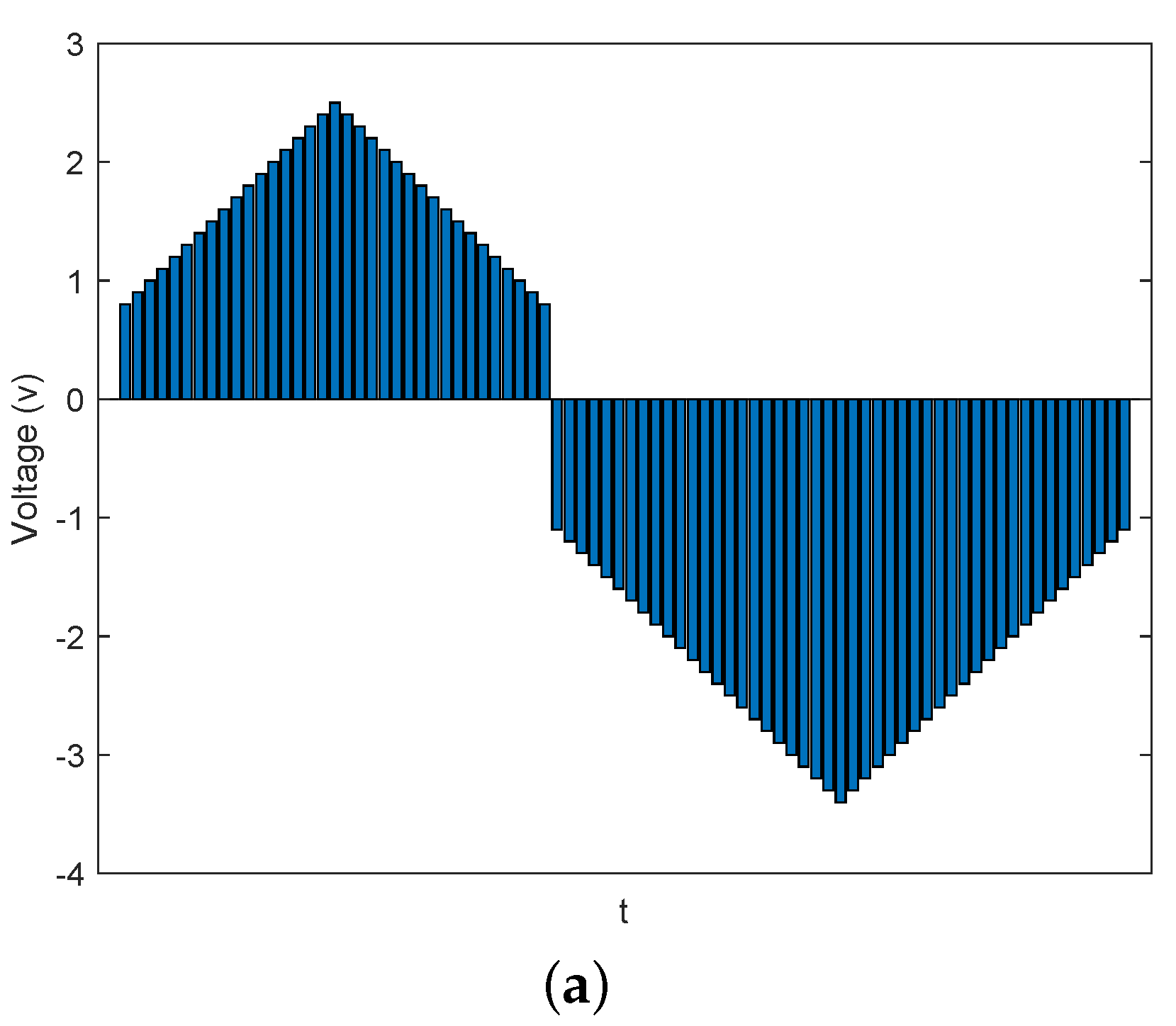
Then, a pulse train (see Figure 3a) consisting of consecutive pulses whose amplitudes vary from 0.8 v to 2.5 v (in increments of 0.1 v), from 2.4 v to 0.8 v (in decrements of 0.1 v), and subsequently vary from −1.1 v to −3.4 v (in decrements of 0.1 v), from 3.3 v to −1.1 v (in increments of 0.1 v), and finally back to 0 v, is applied to the FTJ, and the resulting evolution of S is investigated. Figure 3b shows the evolution of S as a function of pulse amplitude at different pulse durations. It is seen that S progressively increases toward a saturated value with the application of positive pulses and then progressively decreases toward the initial value, i.e., 0, with the application of negative pulses. Such hysteretic evolution of S agrees well with the hysteretic behavior of polarization switching. Additionally, Figure 3b also shows that, as the pulse duration increases, the saturated value of S after the application of positive pulses increases. This can be explained by the fact that positive pulses with longer duration can cause more domains to switch downward (see Figure 2a).
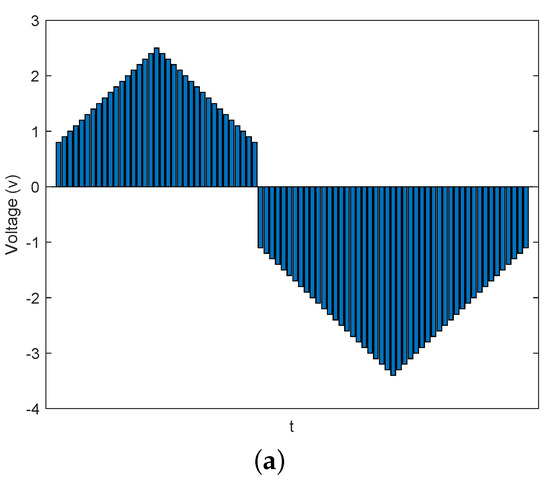
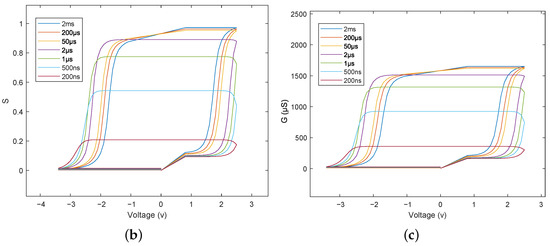
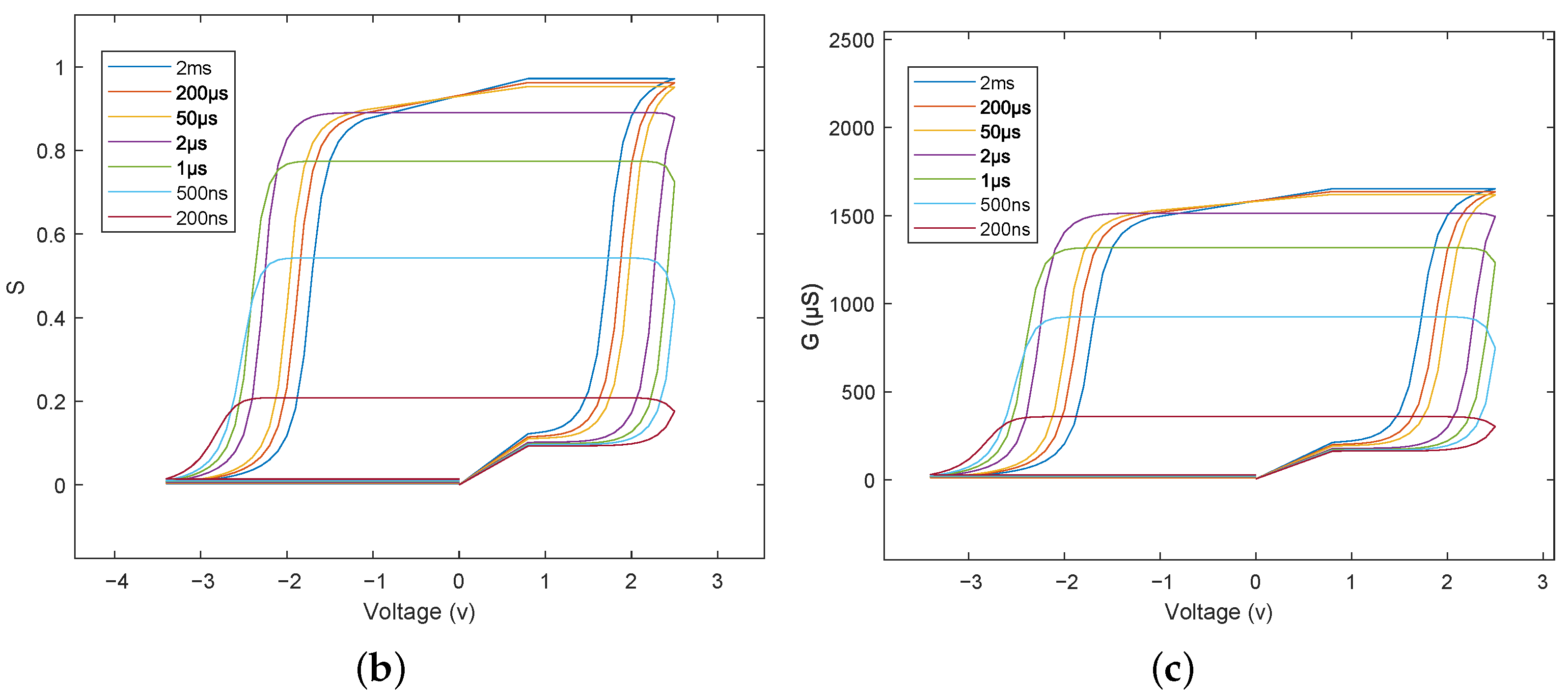
Figure 3.
Area fractions of downward domains as a function of pulse amplitude at different pulse durations. (a) Schematic illustration of the applied pulse train. Multiple (b) and (c) hysteresis loops obtained with the application of pulse trains, as schematically shown in (a), at different pulse durations.
Substituting the S values into Equation (1), we can obtain multiple hysteresis loops, as shown in Figure 3c. These hysteresis loops are in good agreement with those observed experimentally in FTJs [13,23,24], confirming the validity of our ferroelectric memristor model. Moreover, note that these loops are not fully closed, because the applied negative pulses are not sufficient to switch all the domains back to the upward direction. Therefore, S does not return exactly to 0 (not visible in Figure 3b), leading to the inconsistency between the initial and final G values.
3. The FM-TCNN
By introducing transiently chaotic dynamics into neural networks, Chen et al. proposed TCNN [6], which is governed by
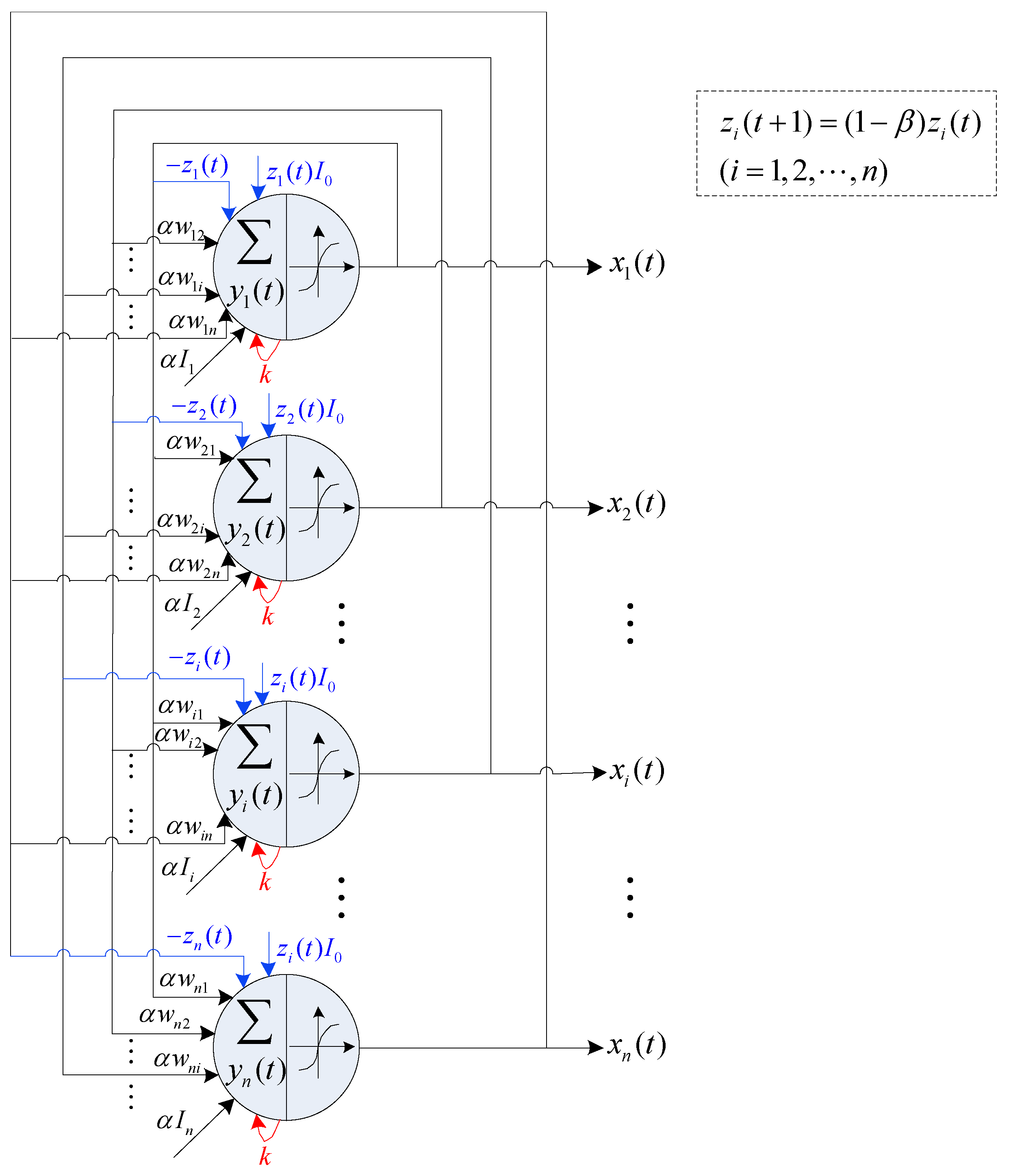
where are the output, the internal state, and the self-feedback connection weight of neuron i, respectively. is a steepness parameter of the output function. is a damping factor of nerve membrane. is a positive scaling parameter for inputs. is the connection weight from neuron j to neuron i. is the input bias of neuron i. is a positive parameter, and is a damping factor of the time-dependent , which is a critical factor for the annealing process. The structural diagram of TCNN is shown in Figure 4.
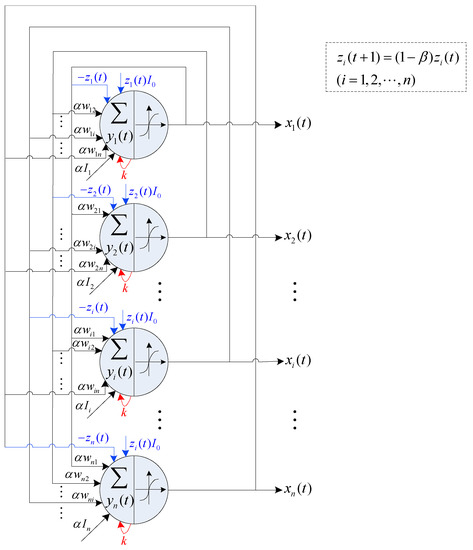
Figure 4.
Structural diagram of TCNN.
Due to the simulated annealing mechanism, the TCNN is an effective method to solve combinatorial optimization problems. As shown in Figure 5, the single neuron of TCNN can converge to the stable state from the chaotic state after a sufficient number of iterations. More importantly, the critical factor determines the chaotic attenuation speed. The larger the , the faster the chaos attenuates. In addition, with the different values of , the stabilized neuronal outputs are different.
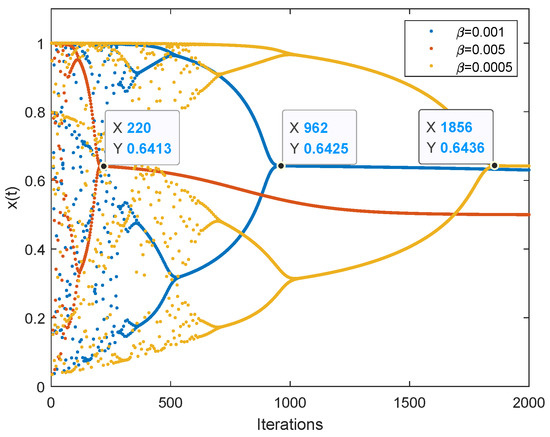
Figure 5.
Dynamic characteristics of a single neuron of TCNN. Here .
Then, the FTJ-based ferroelectric memristor model, as established in Section 2, is introduced into TCNN. Specifically, the conductance of the ferroelectric memristor is used as self-feedback connection weight for the annealing process. Equation (8) is therefore modified as:
where is a coefficient. In addition, the conductance is adjusted by an applied voltage pulse whose amplitude depends linearly on the neuron output:
where b is the slope and c is the intercept. The resultant conductance variation under the applied voltage pulse follows the FTJ’s behavioral model, i.e., Equations (1)–(5). Therefore, the self-feedback connection weight can be dynamically modified according to the neuron state. Combining Equations (1)–(7), (9), and (10), a ferroelectric memristor-based transiently chaotic neural network (FM-TCNN) is thus established.
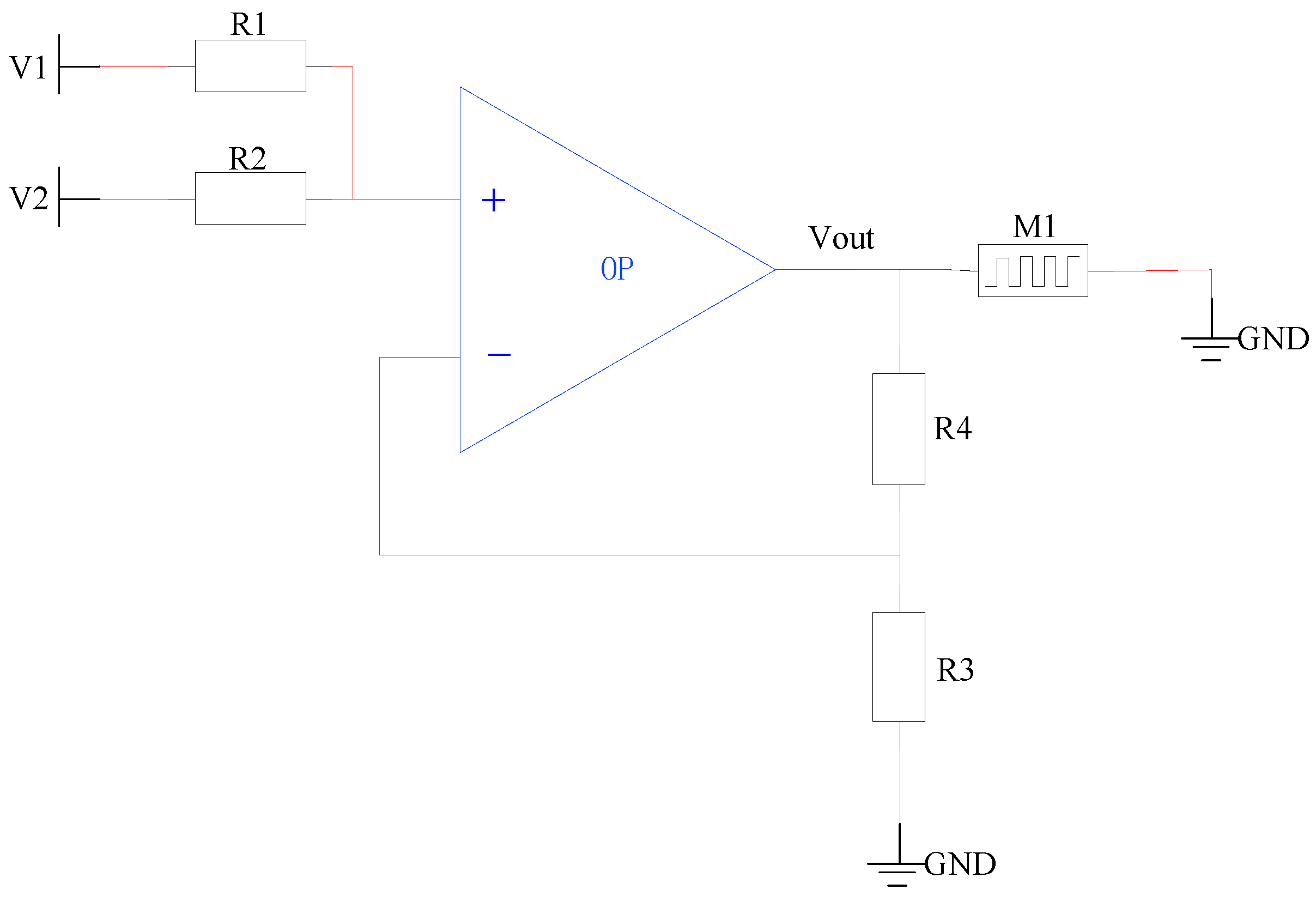
Note that Equation (10) can be implemented by an operational amplifier, as shown in Figure 6. Let R1 = bR2, R4 = bR3, V1 = c, and V2 = , thus Vout = . Then, the output voltage Vout of operational amplifier is applied to the FTJ-based ferroelectric memristor M1.
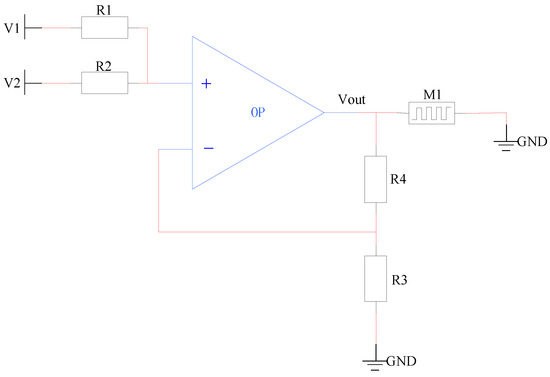
Figure 6.
The potential circuit implementation of Equation (10).
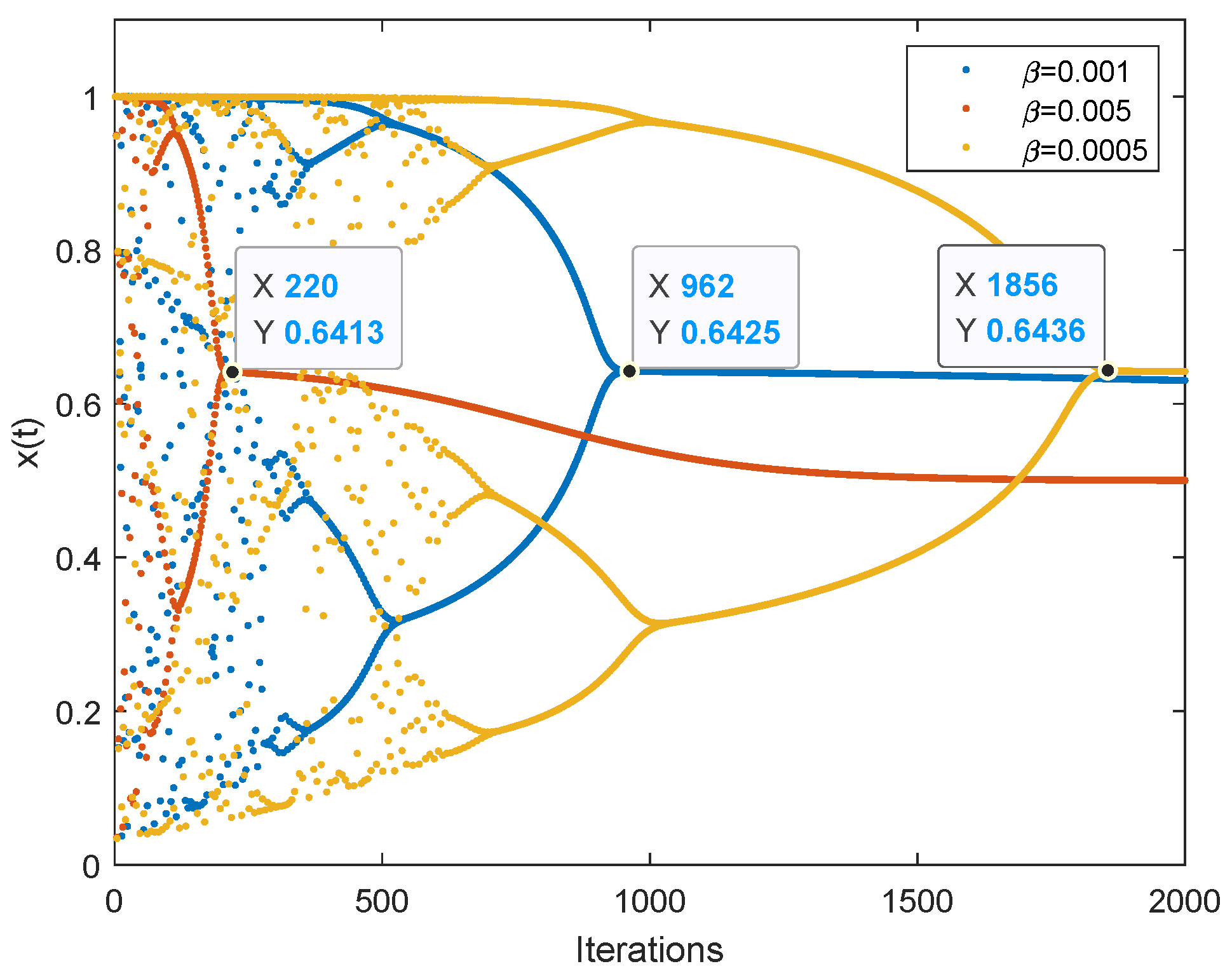
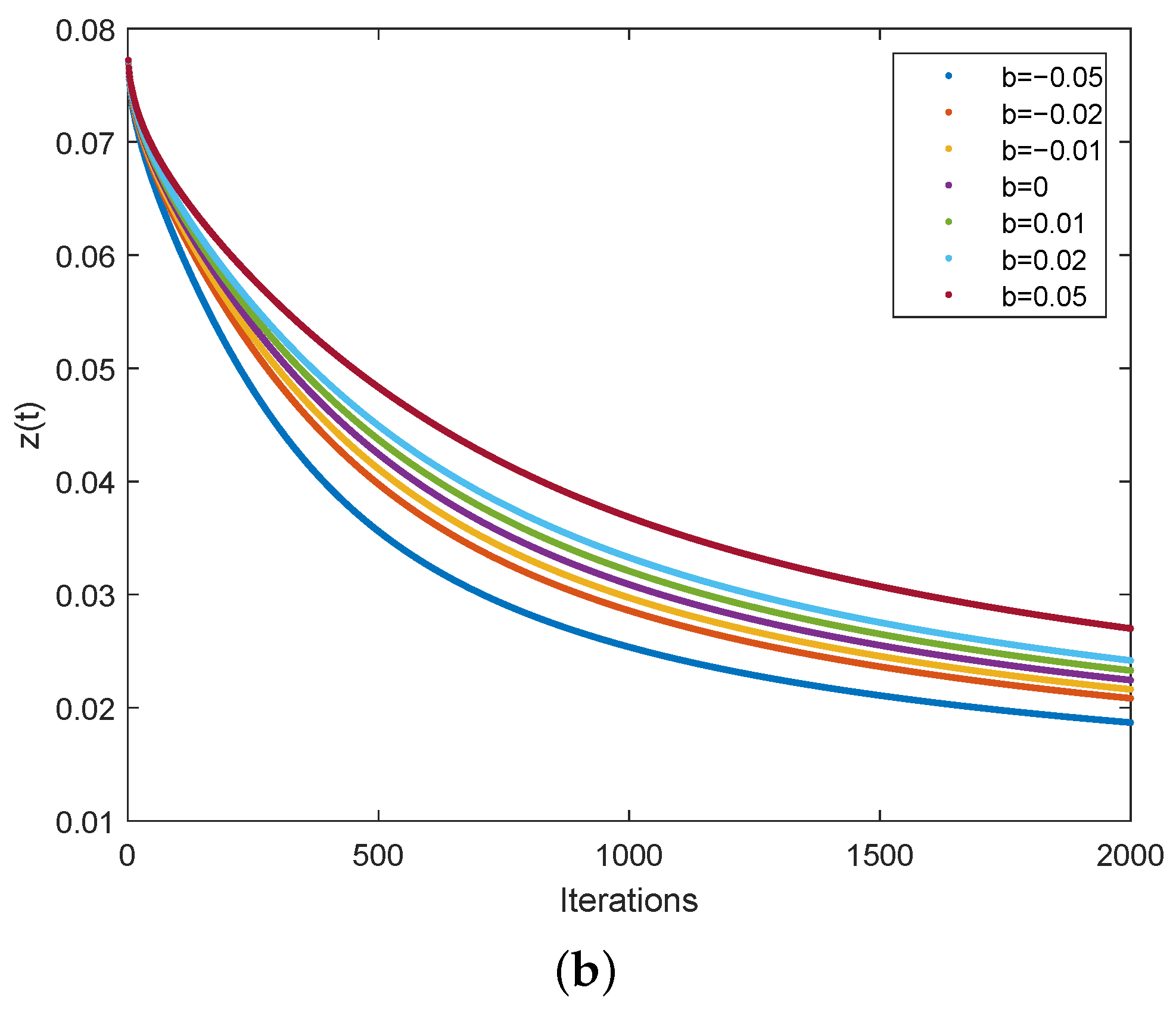
When , FM-TCNN degrades into a single-neuron model. The parameters are set as , and the others are the same as the TCNN single-neuron model. The iterations of are shown in Figure 7. We can see from Figure 7a that the neuron presents the chaotic state at the initial stage of iteration. Then, with the decrease in , as shown in Figure 7b, the neuron quickly enters the stable state. The greater the value of b, the slower decreases, and the slower the neuron stabilizes. What is more, the neuron stabilizes at the same value even when the values of b are different, which is quite different from the behavior of TCNN.
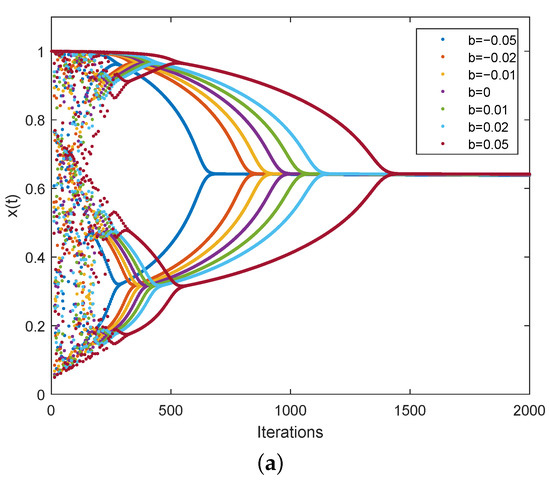
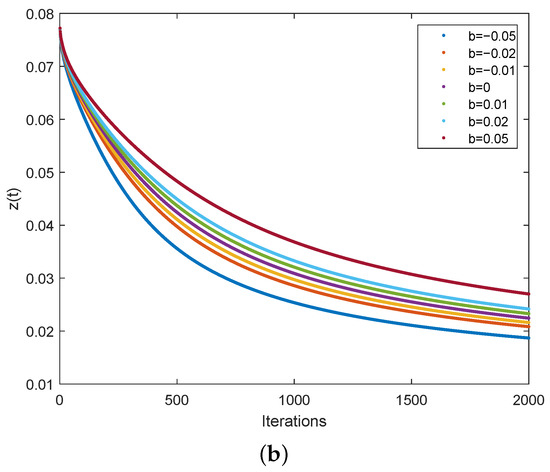
Figure 7.
Dynamic characteristics of a single neuron of FM-TCNN. (a) The iteration of . (b) The iteration of .
4. FM-TCNN for TSP
The TSP is one of the typical combinatorial optimization problems. Taking a city as a starting point, the traveling salesman must pass all the other cities and finally return to the starting point. The limitation is that each city can only be visited once. The goal of the TSP is to obtain the shortest path. Based on it, the energy function is first constructed as [6]:
where n is the number of cities, is the elements in matrix , , are weight parameters, and is the distance between city i and city k. Equation (11) consists of two parts. The first part is the limitation for the effective path, while the last part contains information concerning the total distance. It should be noted that the minimum energy state of the network means the optimal travel route for TSP. Moreover, note that for purely memristive circuits, the Lyapunov function is exactly quadratic, as Equation (11). Thus, searching the global minimization for the quadratic combinatorial optimization problems (e.g., the TSP) can be mapped directly at the circuit level [25,26].
Since the output of TSP is a matrix, the transient chaotic neural network for the TSP should change to have a double subscript. Thus, the FM-TCNN for n-city TSP can be obtain as
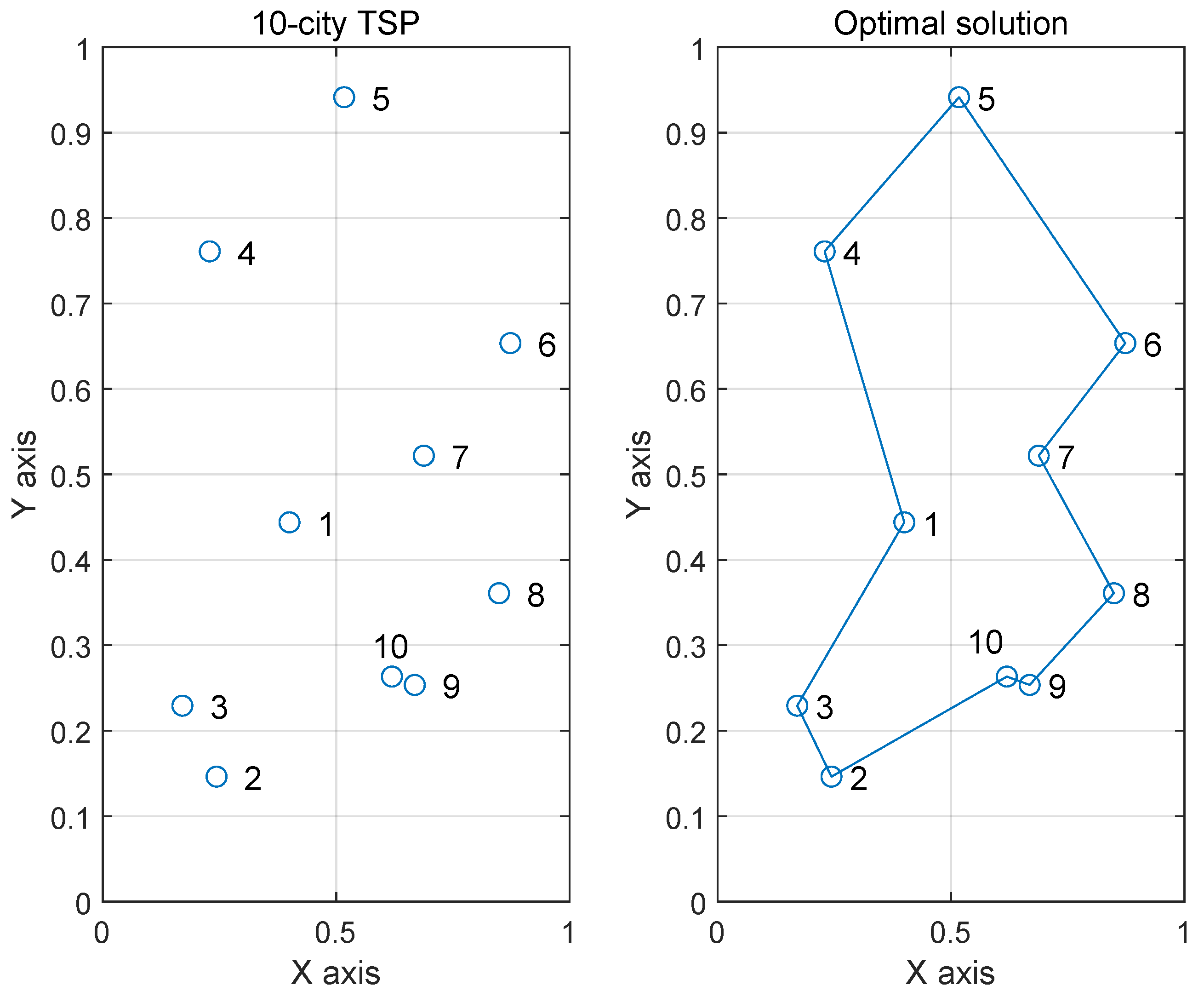
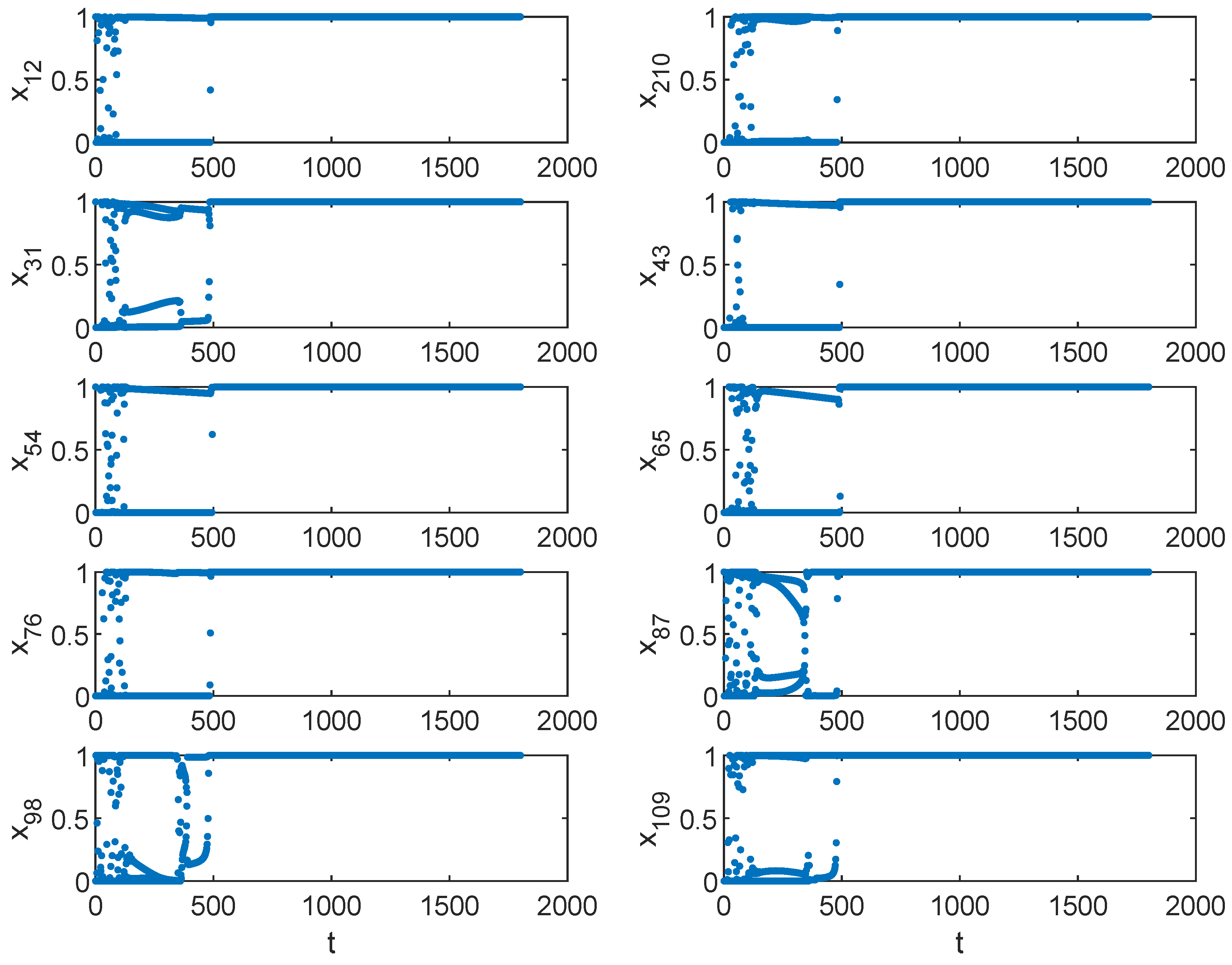
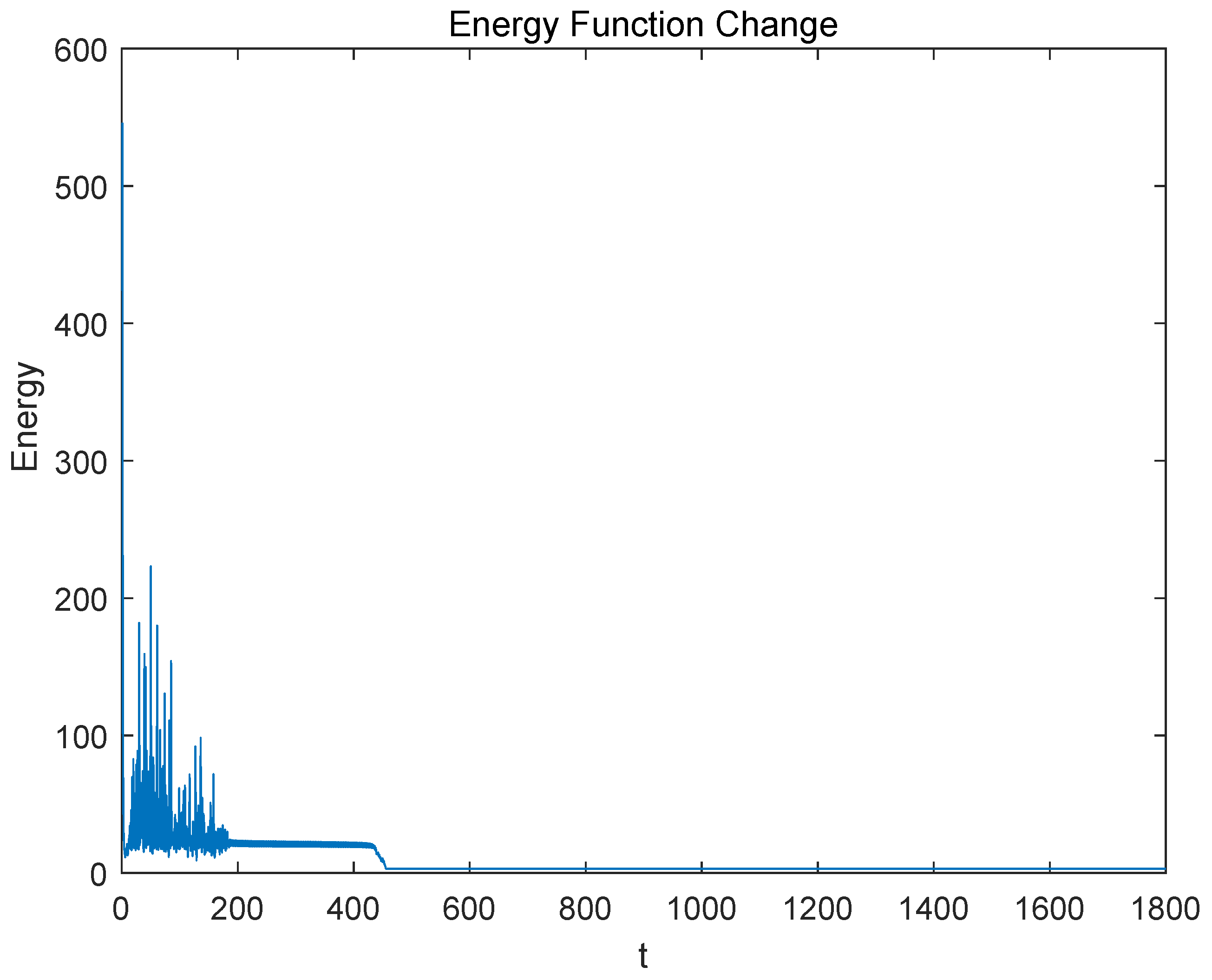
where the output of neuron in the network represents to visit city i in visiting order j. According to Equations (12)–(15), the self-feedback connection weights of different neurons are different; therefore, ferroelectric memristors are used for the 10-city TSP. The coordinates of the 10-city TSP and its optimal solution are shown in Figure 8. The initial values of are generated randomly in the range of . After iterating Equations (12)–(15) for 1800 times, the steady-state outputs can be obtained. A case of the elements in matrix X is that only and are equal to 1, as shown in Figure 9, and the rest are close to 0, indicating an optimal solution for the 10-city TSP as . We can see from Figure 9 that the neurons are explored in the whole phase space at the beginning of the iteration. Then, the neurons enter the periodic state after about 190 iterations and finally enter the stable state after about 500 iterations. As shown in Figure 10, the evolution of the energy function matches that of the neuron state, and it achieves the minimum after about 500 iterations. The tour length and the corresponding energy function of the optimal solution are approximately equal to 2.6907 and 2.9597, respectively.
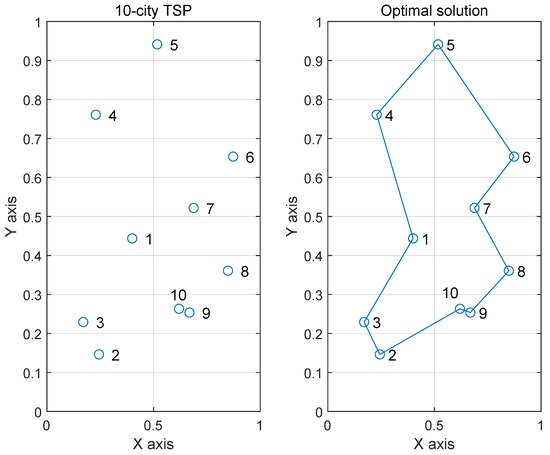
Figure 8.
The 10-city TSP coordinates and its optimal solution.
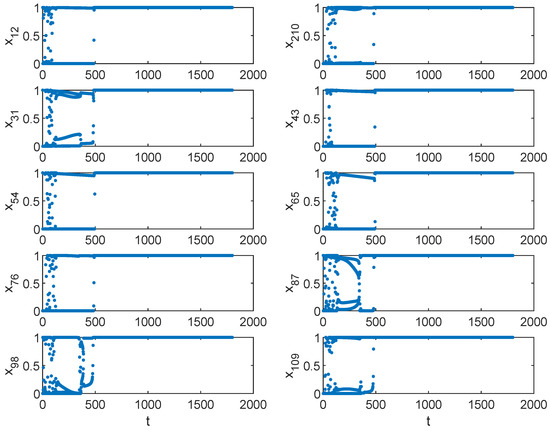
Figure 9.
Iterations of neuron outputs with steady-state values equal to 1 for the 10-city TSP. Here, .
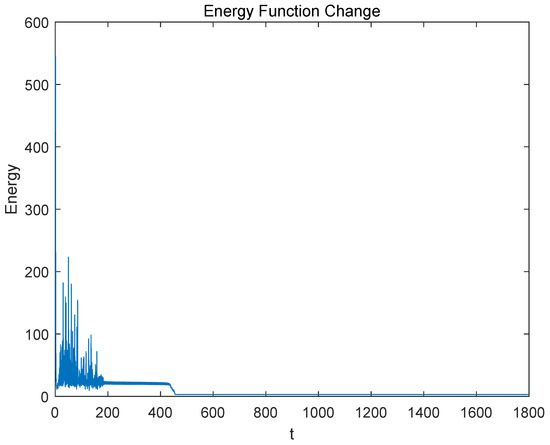
Figure 10.
Iteration of energy function.
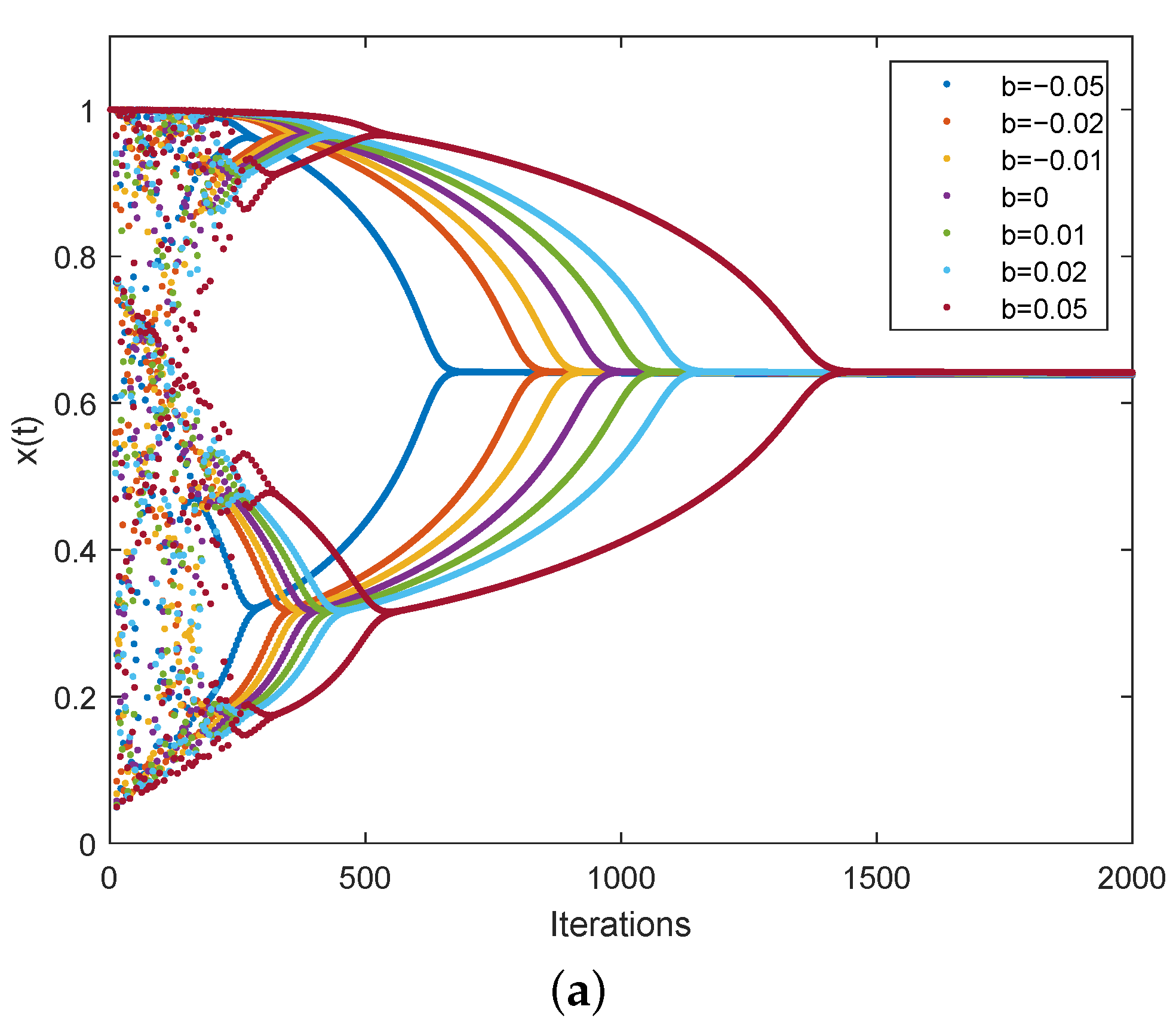
As discussed for Figure 7, the decreasing rate of and the speed of the neuron entering the steady state are determined by the parameter b. Thus, the influence of b on the performance of solving the 10-city TSP is first evaluated here. For each value of b, 1000 independent experiments are run. The iteration stops if the value of the energy function is less than 4 and the difference between the current energy function and the previous one is less than 0.001, or the number of iterations reaches 1800. The parameters are set as , and the others are the same as the FM-TCNN single-neuron model. The experimental results are shown in Table 1. It is seen that all the solutions are feasible in the investigated b range of . When b is negative, a negative disturbance is applied. Accelerated convergence can be achieved at the price of global optimum rate with decreasing b. By contrast, when b is positive, a positive disturbance is applied. The convergence speed reduces with increasing b. However, the global optimum rate reaches a peak value at and then decreases with increasing b. There is a clear trade-off between the convergence speed and global optimum rate. When , the proposed FM-TCNN achieves relatively good performance for the 10-city TSP, demonstrating its effectiveness in solving combinatorial optimization problems.

Table 1.
Experiment results of FM-TCNN with different values of b for 10-city TSP.
In addition, the performance comparison between TCNN [6], HPM-TCNN [11], and the proposed FM-TCNN is shown in Table 2. Note that the value in TCNN and the b and c values in HPM-TCNN have already been optimized. The FM-TCNN achieves the highest global optimum rates, which are 2.44% and 13.25% higher than those of the TCNN and HPM-TCNN, respectively. Meanwhile, the FM-TCNN achieves the shortest average path distance, which is the closest to the global optimum value of 2.6907. In addition, the FM-TCNN achieves the fewest average iterations for convergence, and its convergence speed is 32.8% faster than the TCNN. Therefore, the advantages of the FM-TCNN over TCNN and HPM-TCNN, in terms of global optimal rate, average path distance, and convergence speed, are well-verified. We believe that this should be attributed to the good nonlinear performance of the FTJ-based ferroelectric memristor.

Table 2.
Experiment results of TCNN, HPM-TCNN, and FM-TCNN for the 10-city TSP.
We further evaluate the performances of FM-TCNN for 30-city, 50-city, and 75-city TSPs, as shown in Table 3. The iteration times is set to 30,000. Parameters are the same as above, except b. Different values of b are tested, and 50 independent experiments are run for each value of b. The values of b which lead to the top five global optimal rates for the 30-city TSP are selected to be reported in Table 3. It is seen that it becomes more difficult for the FM-TCNN to find the global optimum when the number of cities increases. In addition, the feasible solution rate decreases with the number of cities. More specifically, for the 30-city TSP, the feasible solution rate is over 90%, and the best path length and average path length are close to the global optimum path length, while for the 50-city TSP and 75-city TSP, the gaps between the best path length, average path length, and global optimum path length are relatively large. Additionally, the feasible solution rates decrease dramatically and falls in the range of 60–80%. There is still room for improving the performance of the FM-TCNN on large-size TSPs. Nevertheless, for the same city scale, the best performance of the FM-TCNN can be achieved in a relatively wide range of b values. This enables us to effectively reduce the time for parameter adjustment when using the FM-TCNN.

Table 3.
Experiment results of FM-TCNN for differently sized TSPs.
5. Conclusions
In summary, an FM-TCNN is constructed by using a highly controllable nonlinear polarization switching process to implement the annealing function. A prototype ferroelectric memristor model based on FTJ is first established. Then, a single-neuron FM-TCNN model is developed by using the polarization-modulated conductance as the self-feedback connection weight. It is shown that the convergence speed of the neuron can be dynamical modulated by the slope between the pulse amplitude and the neuron output. Finally, the FM-TCNN model is applied to solve the TSP task. The effectiveness of FM-TCNN is well-verified, as it shows noticeable advantages over the TCNN and HPM-TCNN in terms of global optimal rate, average path distance, and convergence speed. Therefore, the FM-TCNN provides a promising route toward the hardware implementation of the TCNN. Additionally, as the ferroelectric memristor is an analog electrical device, it may also be used for implementing transient chaos in continuous-time neural networks, which warrants further investigation.
Author Contributions
Conceptualization, Z.L. and Z.F.; methodology, Z.F.; software, Z.L.; validation, Z.L. and Z.F.; formal analysis, Z.L.; investigation, Z.F.; writing—original draft preparation, Z.L.; writing—review and editing, Z.F.; visualization, Z.L.; supervision, Z.F.; project administration, Z.F.; funding acquisition, Z.L. and Z.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grants 61901304, U1932125, and 52172143. Zhen Fan would like to thank the support from Science and Technology Projects in Guangzhou (202201000008).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Korte, B.; Vygen, J. Combinatorial Optimization; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Saji, Y.; Barkatou, M. A Discrete Bat Algorithm Based on Lévy Flights for Euclidean Traveling Salesman Problem. Expert Syst. Appl. 2021, 172, 114639. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z. Ant Colony Optimization for Traveling Salesman Problem Based on Parameters Optimization. Appl. Soft Comput. 2021, 107, 107439. [Google Scholar] [CrossRef]
- Mele, U.J.; Gambardella, L.M.; Montemanni, R. A New Constructive Heuristic Driven by Machine Learning for the Traveling Salesman Problem. Algorithms 2021, 14, 267. [Google Scholar] [CrossRef]
- Ling, Z.; Tao, X.; Zhang, Y.; Chen, X. Solving Optimization Problems Through Fully Convolutional Networks: An Application to the Traveling Salesman Problem. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7475–7485. [Google Scholar] [CrossRef]
- Chen, L.; Aihara, K. Chaotic Simulated Annealing by a Neural Network Model with Transient Chaos. Neural Netw. 1995, 8, 915–930. [Google Scholar] [CrossRef]
- Wang, L.; Li, S.; Tian, F.; Fu, X. A Noisy Chaotic Neural Network for Solving Combinatorial Optimization Problems: Stochastic Chaotic Simulated Annealing. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2004, 34, 2119–2125. [Google Scholar] [CrossRef]
- Zhao, L.; Sun, M.; Cheng, J.; Xu, Y. A Novel Chaotic Neural Network With the Ability to Characterize Local Features and Its Application. IEEE Trans. Neural Netw. 2009, 20, 735–742. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Di Ventra, M. Self-Organization and Solution of Shortest-Path Optimization Problems with Memristive Networks. Phys. Rev. E 2013, 88, 013305. [Google Scholar] [CrossRef]
- Fahimi, Z.; Mahmoodi, M.R.; Nili, H.; Polishchuk, V.; Strukov, D.B. Combinatorial Optimization by Weight Annealing in Memristive Hopfield Networks. Sci. Rep. 2021, 11, 16383. [Google Scholar] [CrossRef]
- Liu, Y.A.; Yu, Q.; Hu, S.G.; Qiao, G.C.; Liu, Y. A Memristor-Based Transient Chaotic Neural Network Model and Its Application. J. Appl. Phys. 2019, 126, 114901. [Google Scholar] [CrossRef]
- Yang, K.; Duan, Q.; Wang, Y.; Zhang, T.; Yang, Y.; Huang, R. Transiently Chaotic Simulated Annealing Based on Intrinsic Nonlinearity of Memristors for Efficient Solution of Optimization Problems. Sci. Adv. 2020, 6, eaba9901. [Google Scholar] [CrossRef] [PubMed]
- Chanthbouala, A.; Garcia, V.; Cherifi, R.O.; Bouzehouane, K.; Fusil, S.; Moya, X.; Xavier, S.; Yamada, H.; Deranlot, C.; Mathur, N.D.; et al. A Ferroelectric Memristor. Nat. Mater. 2012, 11, 860–864. [Google Scholar] [CrossRef] [PubMed]
- Tian, B.; Liu, L.; Yan, M.; Wang, J.; Zhao, Q.; Zhong, N.; Xiang, P.; Sun, L.; Peng, H.; Shen, H.; et al. A Robust Artificial Synapse Based on Organic Ferroelectric Polymer. Adv. Electron. Mater. 2019, 5, 1800600. [Google Scholar] [CrossRef]
- Cheng, S.; Fan, Z.; Rao, J.; Hong, L.; Huang, Q.; Tao, R.; Hou, Z.; Qin, M.; Zeng, M.; Lu, X.; et al. Highly Controllable and Silicon-Compatible Ferroelectric Photovoltaic Synapses for Neuromorphic Computing. iScience 2020, 23, 101874. [Google Scholar] [CrossRef] [PubMed]
- Bégon-Lours, L.; Halter, M.; Pineda, D.D.; Bragaglia, V.; Popoff, Y.; la Porta, A.; Jubin, D.; Fompeyrine, J.; Offrein, B.J. A Back-End-Of-Line Compatible, Ferroelectric Analog Non-Volatile Memory. In Proceedings of the 2021 IEEE International Memory Workshop (IMW), Dresden, Germany, 16–19 May 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Cui, B.; Fan, Z.; Li, W.; Chen, Y.; Dong, S.; Tan, Z.; Cheng, S.; Tian, B.; Tao, R.; Tian, G.; et al. Ferroelectric Photosensor Network: An Advanced Hardware Solution to Real-Time Machine Vision. Nat. Commun. 2022, 13, 1707. [Google Scholar] [CrossRef] [PubMed]
- Kim, M.K.; Kim, I.J.; Lee, J.S. CMOS-compatible Compute-in-Memory Accelerators Based on Integrated Ferroelectric Synaptic Arrays for Convolution Neural Networks. Sci. Adv. 2022, 8, eabm8537. [Google Scholar] [CrossRef]
- Polking, M.J.; Han, M.G.; Yourdkhani, A.; Petkov, V.; Kisielowski, C.F.; Volkov, V.V.; Zhu, Y.; Caruntu, G.; Paul Alivisatos, A.; Ramesh, R. Ferroelectric order in individual nanometre-scale crystals. Nat. Mater. 2012, 11, 700–709. [Google Scholar] [CrossRef]
- Pantel, D.; Alexe, M. Electroresistance Effects in Ferroelectric Tunnel Barriers. Phys. Rev. B 2010, 82, 134105. [Google Scholar] [CrossRef]
- Li, J.; Ge, C.; Du, J.; Wang, C.; Yang, G.; Jin, K. Reproducible Ultrathin Ferroelectric Domain Switching for High-Performance Neuromorphic Computing. Adv. Mater. 2020, 32, 1905764. [Google Scholar] [CrossRef]
- Jo, J.Y.; Han, H.S.; Yoon, J.G.; Song, T.K.; Kim, S.H.; Noh, T.W. Domain Switching Kinetics in Disordered Ferroelectric Thin Films. Phys. Rev. Lett. 2007, 99, 267602. [Google Scholar] [CrossRef]
- Ma, C.; Luo, Z.; Huang, W.; Zhao, L.; Chen, Q.; Lin, Y.; Liu, X.; Chen, Z.; Liu, C.; Sun, H.; et al. Sub-Nanosecond Memristor Based on Ferroelectric Tunnel Junction. Nat. Commun. 2020, 11, 1439. [Google Scholar] [CrossRef] [PubMed]
- Boyn, S.; Grollier, J.; Lecerf, G.; Xu, B.; Locatelli, N.; Fusil, S.; Girod, S.; Carrétéro, C.; Garcia, K.; Xavier, S.; et al. Learning through Ferroelectric Domain Dynamics in Solid-State Synapses. Nat. Commun. 2017, 8, 14736. [Google Scholar] [CrossRef]
- Caravelli, F. Asymptotic Behavior of Memristive Circuits. Entropy 2019, 21, 789. [Google Scholar] [CrossRef] [PubMed]
- Caravelli, F.; Sheldon, F.C.; Traversa, F.L. Global Minimization via Classical Tunneling Assisted by Collective Force Field Formation. Sci. Adv. 2021, 7, eabh1542. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).