Pythagorean Fuzzy Partial Correlation Measure and Its Application

Abstract

The process of computing correlation among attributes of an ordinary database is significant in the analysis and classification of a data set. Due to the uncertainties embedded in data classification, encapsulating correlation techniques using Pythagorean fuzzy information is appropriate to curb the uncertainties. Although correlation coefficient between Pythagorean fuzzy data (PFD) is an applicable information measure, its output is not reliable because of the intrinsic effect of other interfering PFD. Due to the fact that the correlation coefficients in a Pythagorean fuzzy environment could not remove the intrinsic effect of the interfering PFD, the notion of Pythagorean fuzzy partial correlation measure (PFPCM) is necessary to enhance the measure of precise correlation between PFD. Because of the flexibility of Pythagorean fuzzy sets (PFSs), we are motivated to initiate the study on Pythagorean fuzzy partial correlation coefficient (PFPCC) based on a modified Pythagorean fuzzy correlation measure (PFCM). Examples are given to authenticate the choice of the modified PFCM in the computational process of PFPCC. For application, we discuss a case of pattern recognition and classification using the proposed PFPCC after computing the simple correlation coefficient between the patterns based on the modified correlation technique. To be precise, the contributions of the work include the enhancement of an existing PFCC approach, development of PFPCC using the enhanced PFCC, and the application of the developed PFPCC in pattern recognition and classifications.

1. Introduction

The variety of human decision-making goals requires the adoption of a multi-criteria decision making (MCDM) approach, especially in tasks relating to large-scale systems. Essential for the construction of MCDM is the modeling of appropriate relationship between the diverse components criteria in decision-making process. Humans are adept in linguistically expressing the appropriate relationship concerning the constituent criteria in numerous circumstances. Notwithstanding, the conception of fuzzy sets [1] offers a better setting for MCDM because of its capacity to provide a connection between mathematical modeling and linguistic expression. On the other hand, it is enough to say that modeling with fuzzy sets is insufficient since a fuzzy set considers merely the membership degree of the data under consideration.

Atanassov [2] developed the construct of intuitionistic fuzzy sets (IFSs) to alleviate the drawback of fuzzy sets in the modeling of practical problems. IFS is made up of membership degree (MD) $\eta$ and non-membership degree (NMD) $\theta$ with the likelihood of hesitation margin (HM) $\varrho$ where their aggregate is one and $\eta +\theta \le 1$. IFSs have been applied to discuss some contemporary problems such as appointment procedures [3] and emergency management [4]. Other assorted uses of IFSs are reported in [5,6,7,8,9,10]. Nonetheless, IFS is insufficient to explain certain problems in decision theory anytime the aggregate of MD and NMD exceeds one. As a result, Atanassov [11] developed IFSs of power 2 widely called Pythagorean fuzzy sets (PFSs) [12]. PFSs take a broad view of IFSs in which the aggregate of MD and NMD could exceeds one, and ${\eta }^2+{\theta }^2\le 1$. In short, every IFS can be presented as a PFS, but the reverse is not binding. Some properties and power average operators of PFSs were discussed in [13,14]. Due to the fact that PFS is more flexible compared to IFS, it has been used to solve several practical issues such as decision-making [15,16,17,18,19,20,21], pattern classifications [22,23,24,25,26], analysis of medical diagnostic process [27], etc., with sufficient reliability. The notion of PFSs has been extended to Pythagorean fuzzy soft sets and applied to sustainable supplier and decision making using operators such as Einstein aggregation, Einstein ordered weighted average, and Einstein-ordered weighted geometric [28,29,30].

In data analysis and classification, it is customary to deploy correlation measure whenever researchers want to find how two data sets are associated with each other. In the classical sense, the correlation coefficient is a useful tool to statisticians and other allied professionals for measuring the linear connection between any two data sets. The value of the correlation coefficient is positive every time two data sets are positively linearly related, and it is negative when there is no positive linear relation. On the other hand, every time the correlation coefficient is zero, it means there is no linear relationship, i.e., neither positive nor negative. Due to the complexities in ordinary data sets, the study if fuzzy data sets, intuitionistic fuzzy data sets or Pythagorean fuzzy data sets has become prominent, and as such, investigating such vague data sets is necessary. The discussions on correlation in fuzzy domain have been carried out [31,32], which have values akin to the correlation coefficient in the classical sense. Similarly, the idea of correlation measure in the intuitionistic fuzzy domain has been buttressed [33,34,35,36,37]. In the same vein, Pythagorean fuzzy correlation measures have been explored with some applications [38,39,40,41]. Among the studies on Pythagorean fuzzy correlation measures, it is only the work by Thao [39] that shows both linear relationship and direction of correlation; however, the study only considered MD and NMD of PFSs without taking into account HM.

Though the concept of correlation coefficient for PFD is an applicable information measure, its output is inaccurate as the measure cannot remove the intrinsic effect of other interfering PFD. Partial correlation coefficient (PCC) between any two fuzzy sets while keeping the other fuzzy sets constant has been studied in [42] using the correlation measure in [31]. Albeit, Hung and Wu [43] introduced fuzzy partial correlation measure based on empirical logit transformation. In addition, Hung [44] proposed PCC in intuitionistic fuzzy domain via the same approach [43] by considering only MD and NMD of IFSs. Partial correlation measure under Pythagorean fuzzy environment has not been studied. Because correlation coefficients under Pythagorean fuzzy environment could not remove the intrinsic effect of other PFD while measuring the correlation coefficient between two PFD, the notion of PFPCC is required to enhance the measure of exact correlation between PFD without interference. Sequel to this, we are motivated to develop partial correlation measure for PFD based on a modified PFCC [39], because of the suitability of PFSs to model uncertainties. To demonstrate the application of PFPCM, a case of pattern recognition of building materials is considered based on the introduced partial correlation coefficient between building patterns to enhance effective recognitions and classifications. To be specified, the contributions of the work include;

• enhancement of an existing PFCC approach to be used for the development of PFPCC,
• development of PFPCC using the enhanced PFCC,
• theoretical descriptions of the PFPCC for the sake of validation, and
• the application of the developed PFPCC in pattern recognition.

We delineate the paper as follows: Section 2 presents the concept of PFSs and its correlation coefficient measures, Section 3 discusses the PCC for PFD with some theoretical results, Section 4 addresses pattern recognitions and classifications via the proposed PCC for PFD, and Section 5 concludes the findings.

2. Preliminaries

This segment introduces the ideas of PFSs, PFCC approaches in [35,37,39], and a novel correlation coefficient measure.

2.1. Pythagorean Fuzzy Sets

Assume ℘ is a family of IFSs described within a non-empty set X.

Definition 1

([2]). Assume $C\subseteq \wp$ is an IFS, then the structure of C is described by

$$C=\{⟨x,{\eta }_C\left(x\right),{\theta }_C\left(x\right)⟩\mid x\in X\},$$

where ${\eta }_C,{\theta }_C:X\to [0,1]$ are MD and NMD of $x\in X$ for which

$$0\le {\eta }_C\left(x\right)+{\theta }_C\left(x\right)\le 1.$$

The hesitation margin for an IFS C in X is given by ${\varrho }_C\left(x\right)=1-{\eta }_C\left(x\right)-{\theta }_C\left(x\right)$.

Take ℓ to be a Pythagorean fuzzy space defined in a non-empty set X such that $\wp \subseteq \ell$.

Definition 2

([12]). A PFS represented by $C\subseteq \ell$ is a construct

$$C=\{⟨x,{\eta }_C\left(x\right),{\theta }_C\left(x\right)⟩\mid x\in X\},$$

where ${\eta }_C,{\theta }_C:X\to [0,1]$ are MD and NMD of $x\in X$ to C for which $0\le {\eta }_C^2\left(x\right)+{\theta }_C^2\left(x\right)\le 1$. The hesitation margin for a PFS C in X is given by

$${\varrho }_C\left(x\right)\in [0,1]=\sqrt{1-[{\left({\eta }_C\left(x\right)\right)}^2+{\left({\theta }_C\left(x\right)\right)}^2]}.$$

Definition 3

([12]). Assume $C,D\subseteq \ell$, then

(i) 

$C=D$ iff ${\eta }_C\left(x\right)={\eta }_D\left(x\right)$ ${\theta }_C\left(x\right)={\theta }_D\left(x\right)$ for every $x\in X$.

(ii) 

$C\subseteq D$ iff ${\eta }_C\left(x\right)\le {\eta }_D\left(x\right)$, ${\theta }_C\left(x\right)\ge {\theta }_D\left(x\right)$ for every $x\in X$.

(iii) 

$\overline{C}=\left\{⟨x,{\theta }_C\left(x\right),{\eta }_C\left(x\right)⟩\right|x\in X\}$, $\overline{D}=\left\{⟨x,{\theta }_D\left(x\right),{\eta }_D\left(x\right)⟩\right|x\in X\}$.

(iv) 

$C\cup D=\left\{⟨x,max\{{\eta }_C\left(x\right),{\eta }_D\left(x\right)\},min\{{\theta }_C\left(x\right),{\theta }_D\left(x\right)\}⟩\right|x\in X\}$.

(v) 

$C\cap D=\left\{⟨x,min\{{\eta }_C\left(x\right),{\eta }_D\left(x\right)\},max\{{\theta }_C\left(x\right),{\theta }_D\left(x\right)\}⟩\right|x\in X\}$.

Definition 4

([27]). Pythagorean fuzzy values (PFVs) also known as Pythagorean fuzzy pairs (PFPs) are described by the system $⟨x,y⟩$ where $x^2+y^2\le 1$ for $x,y\in [0,1]$. PFVs weigh the PFS in which x and y are taken to mean MD and NMD, respectively.

When the hesitation margins of PFSs are included in the PFVs of the PFSs, the PFVs become Pythagorean fuzzy data (PFD).

2.2. Simple Correlation Measures in Pythagorean Fuzzy Domain

We recall some correlation coefficient measures presented in Pythagorean fuzzy domain [35,37,39]. The choice of these approaches is because they show both linear relationship and direction of correlation. Suppose $C,D\subseteq \ell$ for $X=\{x_1,x_2,\cdots ,x_n\}$, $n\in (1,\infty )$ and let $\sigma (C,D)$ represents a PFCC of PFSs C and D. Then the definition of PFCC is as follows:

Definition 5

([39]). The correlation coefficient $\sigma (C,D)$ is a function $\sigma :PFS\times PFS\to [-1,1]$ which satisfies the following axioms:

(i) 

$\sigma (C,D)\in [-1,1]$,

(ii) 

$\sigma (C,D)=\sigma (D,C)$,

(iii) 

$\sigma (C,D)=1$ iff $C=D$.

When $\sigma (C,D)$ reaches 1, it means that C and D are near perfect positive correlation, and if $\sigma (C,D)$ reaches $-1$ then C and D are near perfect negative correlation. Whereas $\sigma (C,D)=1$ and $\sigma (C,D)=-1$ indicate perfect positive correlation and perfect negative correlation, respectively. The following are some PFCC techniques.

2.2.1. Thao’s Technique

The correlation coefficient $\sigma (C,D)$ (as given in [39]) is

$${\sigma }_1(C,D)={\displaystyle \frac{{\Sigma }_{i=1}^n{d}_i\left(C\right)d_i\left(D\right)}{{\left({\Sigma }_{i=1}^n{d}_i^2\left(C\right){\Sigma }_{i=1}^n{d}_i^2\left(D\right)\right)}^{\frac{1}{2}}}},$$

(1)

in which the deviations of C and D are

$$\left.\begin{array}{c}\hfill d_i\left(C\right)=({\eta }_C^2\left(x_i\right)-{\overline{{\eta }_C}}^2)-({\theta }_C^2\left(x_i\right)-{\overline{{\theta }_C}}^2)\\ \hfill d_i\left(D\right)=({\eta }_D^2\left(x_i\right)-{\overline{{\eta }_D}}^2)-({\theta }_D^2\left(x_i\right)-{\overline{{\theta }_D}}^2)\end{array}\right\},$$

(2)

for the means

$$\left.\begin{array}{c}\hfill \overline{{\eta }_C},\overline{{\eta }_D}={\displaystyle \frac{{\Sigma }_{i=1}^n{\eta }_C\left(x_i\right)}{n}},{\displaystyle \frac{{\Sigma }_{i=1}^n{\eta }_D\left(x_i\right)}{n}}\\ \hfill \overline{{\theta }_C},\overline{{\theta }_D}={\displaystyle \frac{{\Sigma }_{i=1}^n{\theta }_C\left(x_i\right)}{n}},{\displaystyle \frac{{\Sigma }_{i=1}^n{\theta }_D\left(x_i\right)}{n}}\end{array}\right\}.$$

(3)

2.2.2. Liu et al.’s Technique

The correlation coefficient $\sigma (C,D)$ (as given in [35]) is

$${\sigma }_2(C,D)={\displaystyle \frac{{\Sigma }_{i=1}^n{d}_i\left(C\right)d_i\left(D\right)}{{\left({\Sigma }_{i=1}^n{d}_i^2\left(C\right){\Sigma }_{i=1}^n{d}_i^2\left(D\right)\right)}^{\frac{1}{2}}}},$$

(4)

where the deviations of C and D are

$$\left.\begin{array}{c}\hfill d_i\left(C\right)=({\eta }_C\left(x_i\right)-\overline{{\eta }_C})-({\theta }_C\left(x_i\right)-\overline{{\theta }_C})\\ \hfill d_i\left(D\right)=({\eta }_D\left(x_i\right)-\overline{{\eta }_D})-({\theta }_D\left(x_i\right)-\overline{{\theta }_D})\end{array}\right\},$$

(5)

in which the means are same as (3).

2.2.3. Thao et al.’s Technique

The correlation coefficient $\sigma (C,D)$ (as given in [37]) is

$${\sigma }_3(C,D)={\displaystyle \frac{\varphi (C,D)}{{\left(\psi \left(C\right)\psi \left(D\right)\right)}^{\frac{1}{2}}}},$$

(6)

where

$$\left.\begin{array}{c}\hfill \psi \left(C\right)={\displaystyle \frac{1}{n-1}}{\Sigma }_{i=1}^n\left({({\eta }_C\left(s_i\right)-\overline{{\eta }_C})}^2+{({\theta }_C\left(s_i\right)-\overline{{\theta }_C})}^2\right)\\ \hfill \psi \left(D\right)={\displaystyle \frac{1}{n-1}}{\Sigma }_{i=1}^n\left({({\eta }_D\left(s_i\right)-\overline{{\eta }_D})}^2+{({\theta }_D\left(s_i\right)-\overline{{\theta }_D})}^2\right)\end{array}\right\},$$

$$\begin{array}{ccc}\hfill \varphi (C,D)& =& {\displaystyle \frac{1}{n-1}}{\Sigma }_{i=1}^n(({\eta }_C\left(s_i\right)-\overline{{\eta }_C})({\eta }_D\left(s_i\right)-\overline{{\eta }_D})\hfill \\ & +& ({\theta }_C\left(s_i\right)-\overline{{\theta }_C})({\theta }_D\left(s_i\right)-\overline{{\theta }_D})),\hfill \end{array}$$

in which the means are same as (3).

All these correlation measures discussed so far cannot provide a reliable interpretation because they do not consider the conventional parameters of PFS viz; MD, NMD, and HM. Thus, the need for an enhanced correlation measure.

2.2.4. Modified Technique

The modified version of (1) is

$$\tilde{\sigma }(C,D)={\displaystyle \frac{\tilde{\varphi }(C,D)}{{\left(\tilde{\psi }\left(C\right)\tilde{\psi }\left(D\right)\right)}^{\frac{1}{2}}}},$$

(7)

where $\tilde{\psi }\left(C\right)$, $\tilde{\psi }\left(D\right)$ are the variances of C and D defined by

$$\left.\begin{array}{c}\hfill \tilde{\psi }\left(C\right)={\displaystyle \frac{{\Sigma }_{i=1}^n{d}_i^2\left(C\right)}{n-1}}\\ \hfill \tilde{\psi }\left(D\right)={\displaystyle \frac{{\Sigma }_{i=1}^n{d}_i^2\left(D\right)}{n-1}}\end{array}\right\},$$

(8)

$\tilde{\varphi }(C,D)$ is the covariance of $(C,D)$ defined by

$$\tilde{\varphi }(C,D)={\displaystyle \frac{{\Sigma }_{i=1}^n{d}_i\left(C\right)d_i\left(D\right)}{n-1}},$$

(9)

in which the deviations of C and D are

$$\left.\begin{array}{c}\hfill d_i\left(C\right)=({\eta }_C^2\left(x_i\right)-{\overline{{\eta }_C}}^2)-({\theta }_C^2\left(x_i\right)-{\overline{{\theta }_C}}^2)-({\varrho }_C^2\left(x_i\right)-{\overline{{\varrho }_C}}^2)\\ \hfill d_i\left(D\right)=({\eta }_D^2\left(x_i\right)-{\overline{{\eta }_D}}^2)-({\theta }_D^2\left(x_i\right)-{\overline{{\theta }_D}}^2)-({\varrho }_D^2\left(x_i\right)-{\overline{{\varrho }_D}}^2)\end{array}\right\},$$

(10)

for the means

$$\left.\begin{array}{c}\hfill \overline{{\eta }_C},\overline{{\eta }_D}={\displaystyle \frac{{\Sigma }_{i=1}^n{\eta }_C\left(x_i\right)}{n}},{\displaystyle \frac{{\Sigma }_{i=1}^n{\eta }_D\left(x_i\right)}{n}}\\ \hfill \overline{{\theta }_C},\overline{{\theta }_D}={\displaystyle \frac{{\Sigma }_{i=1}^n{\theta }_C\left(x_i\right)}{n}},{\displaystyle \frac{{\Sigma }_{i=1}^n{\theta }_D\left(x_i\right)}{n}}\\ \hfill \overline{{\varrho }_C},\overline{{\varrho }_D}={\displaystyle \frac{{\Sigma }_{i=1}^n{\varrho }_C\left(x_i\right)}{n}},{\displaystyle \frac{{\Sigma }_{i=1}^n{\varrho }_D\left(x_i\right)}{n}}\end{array}\right\}.$$

(11)

We have $\tilde{\sigma }(C,D)=\tilde{\sigma }(D,C)$ because

$$\begin{array}{ccc}\hfill \tilde{\sigma }(C,D)& =& {\displaystyle \frac{\tilde{\varphi }(C,D)}{{\left(\tilde{\psi }\left(C\right)\tilde{\psi }\left(D\right)\right)}^{\frac{1}{2}}}}={\displaystyle \frac{\tilde{\varphi }(D,C)}{{\left(\tilde{\psi }\left(D\right)\tilde{\psi }\left(C\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& \tilde{\sigma }(D,C).\hfill \end{array}$$

Furthermore, $\tilde{\psi }\left(C\right)=\tilde{\varphi }(C,C)$ and $\tilde{\psi }\left(D\right)=\tilde{\varphi }(D,D)$. Certainly, (7) is more reliable than (1), (4) and (6) because it takes into account all parameters of PFSs under consideration.

2.2.5. Comparison for the PFCMs

Some numerical examples are considered to justify the upper hand of the modified PFCC technique in comparison to the existing PFCC techniques.

Example 1.

Take C and D as PFSs in $X=\{x_1,x_2,x_3\}$ in which

$$C=\{⟨x_1,0.1,0.2⟩,⟨x_2,0.2,0.1⟩,⟨x_3,0.3,0⟩\},$$

$$D=\{⟨x_1,0.3,0⟩,⟨x_2,0.2,0.2⟩,⟨x_3,0.1,0.6⟩\}.$$

By applying the correlation measures to find the PFCC between C and D, we obtain the following results:

$${\sigma }_1=-0.9080,{\sigma }_2=-0.9898,{\sigma }_3=-0.8800,\tilde{\sigma }=-0.7021.$$

Example 2.

Let $\ddot{C}$ and $\ddot{D}$ be PFSs in $X=\{x_1,x_2,x_3\}$, where

$$\ddot{C}=\{⟨x_1,0.8,0.6⟩,⟨x_2,0.3,0.6⟩,⟨x_3,0.4,0.6⟩\},$$

$$\ddot{D}=\{⟨x_1,0.54,0.72⟩,⟨x_2,0.54,0.27⟩,⟨x_3,0.54,0.36⟩\}.$$

By applying the correlation measures to find the PFCC between $\ddot{C}$ and $\ddot{D}$, we obtain the outputs as follows:

$${\sigma }_1=-1,{\sigma }_2=-1,{\sigma }_3=0,\tilde{\sigma }=-0.3235.$$

These results are represented in Table 1.

Table 1. Results for Comparison.

PFCCs	${\mathit{\sigma }}_1$	${\mathit{\sigma }}_2$	${\mathit{\sigma }}_3$	$\tilde{\mathit{\sigma }}$
Example 1	$-0.9080$	$-0.9898$	$-0.8800$	$-0.7021$
Example 2	$-1.0000$	$-1.0000$	$0.0000$	$-0.3235$

As seen in Table 1, it is certain that the PFCC methods satisfy the conditions of Definition 5, which make them appropriate PFCC. However, the enhanced PFCC yields outputs with better interpretations. From the results, the considered PFSs have weak correlations between each other corroborating the actual relation since one cannot completely establish either inclusive or equality properties between the PFSs. The modified technique produces the most precise outputs compare to the outputs from the techniques in [35,37,39]. In Example 2, the techniques in [35,39] put forward that a perfect negative correlation exists between the PFSs, whereas the modified technique stated otherwise because the PFSs are not totally dissimilar. The unreliability of the techniques in [35,39] is due to the omission of the $\varrho$ parameter. Similar unreliable interpretation follows from the technique in [37] for the same reason. However, the modified technique gives a reasonable value which corroborates the actual relation between the PFSs in Example 2. The modified technique is adopted for the partial correlation coefficient of PFSs due to its reliability over the techniques in [35,37,39].

3. Partial Correlation Coefficient of PFSs

Suppose we have random samples of three PFD C, D and E contain in ℓ. It is easy to find the relationship between C and D using (7). However, since C, D and E are PFD drawn from the same space ℓ, i.e., E could certainly impact the relationship between C and D. Therefore, if one is interested in finding the true relationship between C and D, then the influence of E must be kept constant just as in the case of implicit differentiation. To find such relationship between PFSs C and D, we introduce PFPCC as follows.

3.1. First-Order PFPCC

Definition 6.

The PFPCC for PFD C and D keeping PFD E constant is defined by

$${\tilde{\sigma }}^2(C,D|E)={\displaystyle \frac{{(\tilde{\sigma }(C,D)-\tilde{\sigma }(C,E)\tilde{\sigma }(D,E))}^2}{(1-{\tilde{\sigma }}^2(C,E))(1-{\tilde{\sigma }}^2(D,E))}}$$

(12)

or

$$\tilde{\sigma }(C,D|E)={\displaystyle \frac{\tilde{\sigma }(C,D)-\tilde{\sigma }(C,E)\tilde{\sigma }(D,E)}{{\left((1-{\tilde{\sigma }}^2(C,E))(1-{\tilde{\sigma }}^2(D,E))\right)}^{\frac{1}{2}}}},$$

(13)

where $\tilde{\sigma }(C,D)$, $\tilde{\sigma }(C,E)$ and $\tilde{\sigma }(D,E)$ can be computed by using (7).

We can say that the zero-order PCC of PFD is equivalent to simple correlation coefficient of PFD. Now, we consider some properties of first-order PCC of PFD as follows.

Theorem 1.

Suppose $C,D,E\subseteq \ell$ are PFD drawn from $X=\{x_1,\dots ,x_n\}$, $n\in ]1,\infty [$. Then $\tilde{\sigma }(C,D|E)=\tilde{\sigma }(D,C|E)$.

Proof. 

From (7), we see that $\tilde{\sigma }(C,D)=\tilde{\sigma }(D,C)$, and so

$$\begin{array}{ccc}\hfill \tilde{\sigma }(C,D|E)& =& {\displaystyle \frac{\tilde{\sigma }(C,D)-\tilde{\sigma }(C,E)\tilde{\sigma }(D,E)}{{\left((1-{\tilde{\sigma }}^2(C,E))(1-{\tilde{\sigma }}^2(D,E))\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{\tilde{\sigma }(D,C)-\tilde{\sigma }(D,E)\tilde{\sigma }(C,E)}{{\left((1-{\tilde{\sigma }}^2(D,E))(1-{\tilde{\sigma }}^2(C,E))\right)}^{\frac{1}{2}}}}\hfill \\ & =& \tilde{\sigma }(D,C|E).\hfill \end{array}$$

The result follows. □

Corollary 1.

With the same condition in Theorem 1, if C and E have a perfect positive linear relationship then $\tilde{\sigma }(C,D|E)=\tilde{\sigma }(D,C|E)=\infty$.

Proof. 

Suppose C and E have a perfect positive linear relationship, then $\tilde{\sigma }(C,E)=1$. The result follows by substitution. Similarly, if $\tilde{\sigma }(D,E)=1$, the result also holds. □

Proposition 1.

With the same condition in Theorem 1, a partial correlation coefficient $\tilde{\sigma }(C,D|E)$ becomes a simple correlation coefficient $\tilde{\sigma }(C,D)$ iff $\tilde{\sigma }(C,E)=\tilde{\sigma }(D,E)=0$.

Proof. 

Clearly, if $\tilde{\sigma }(C,E)=\tilde{\sigma }(D,E)=0$, then we have

$$\tilde{\sigma }(C,D|E)=\tilde{\sigma }(C,D)=\tilde{\sigma }(D,C)=\tilde{\sigma }(D,C|E).$$

The converse is straightforward. □

Proposition 2.

With the same condition in Theorem 1, the following statements are valid:

(i) 

If $\tilde{\sigma }(C,E)=0$, then

$$\tilde{\sigma }(C,D|E)={\displaystyle \frac{\tilde{\sigma }(C,D)}{{\left((1-{\tilde{\sigma }}^2(D,E))\right)}^{\frac{1}{2}}}}=\tilde{\sigma }(D,C|E).$$

Furthermore, if $\tilde{\sigma }(D,E)=0$, then

$$\tilde{\sigma }(C,D|E)={\displaystyle \frac{\tilde{\sigma }(C,D)}{{\left((1-{\tilde{\sigma }}^2(C,E))\right)}^{\frac{1}{2}}}}=\tilde{\sigma }(D,C|E).$$

(ii) 

If $\tilde{\sigma }(C,D)=0$, $\tilde{\sigma }(C,E)\ne 0$ and $\tilde{\sigma }(D,E)\ne 0$, then

$$\tilde{\sigma }(C,D|E)={\displaystyle \frac{-\tilde{\sigma }(C,E)\tilde{\sigma }(D,E)}{{\left((1-{\tilde{\sigma }}^2(C,E))(1-{\tilde{\sigma }}^2(D,E))\right)}^{\frac{1}{2}}}}.$$

Proof. 

The proofs are straightforward. □

3.2. nth-Order PFPCC

Suppose we have random samples of more than three PFD, the idea of nth-order PFPCC is naturally needed to find the linear relationship among them. Let $C_1,C_2,\cdots ,C_r,C_{r+1},\cdots ,C_{r+s}$ be PFD in X. Each of the PFD can be represented by

$$C_i=\left\{⟨x,{\eta }_{C_i}\left(x\right),{\theta }_{C_i}\left(x\right)⟩\right|x\in X\},$$

where ${\eta }_{C_i}\left(x\right),{\theta }_{C_i}\left(x\right):X\to [0,1]$ for $i=1,2,\cdots ,r+s$. We can also express $C_i$ as

$$C_i=\left\{⟨x_k,{\eta }_{C_1}\left(x_k\right),{\theta }_{C_1}\left(x_k\right),{\eta }_{C_2}\left(x_k\right),{\theta }_{C_2}\left(x_k\right)\cdots ,{\eta }_{C_{r+s}}\left(x_k\right),{\theta }_{C_{r+s}}\left(x_k\right)⟩\right|x_k\in X\}$$

for $k=1,2,\cdots ,n$.

We denote the covariances of PFD $C_1,C_2\cdots ,C_r,C_{r+1},C_{r+2},\cdots ,C_{r+s}$ as covariance matrix $\mathcal{M}$ defined by

$$\mathcal{M}=\left\{\varphi (C_i,C_j)\right|i=1,2,\cdots ,r+s,j=1,2,\cdots ,r+s\},$$

(14)

where

$$\varphi (C_i,C_j)={\displaystyle \frac{{\Sigma }_{k=1}^n{d}_k\left(C_i\right)d_k\left(C_j\right)}{n-1}}$$

(15)

is the covariance of $(C_i,C_j)$, in which

$$\left.\begin{array}{c}\hfill d_k\left(C_i\right)=({\eta }_{C_i}^2\left(x_k\right)-{\overline{{\eta }_{C_i}}}^2)-({\theta }_{C_i}^2\left(x_k\right)-{\overline{{\theta }_{C_i}}}^2)-({\varrho }_{C_i}^2\left(x_k\right)-{\overline{{\varrho }_{C_i}}}^2)\\ \hfill d_k\left(C_j\right)=({\eta }_{C_j}^2\left(x_k\right)-{\overline{{\eta }_{C_j}}}^2)-({\theta }_{C_j}^2\left(x_k\right)-{\overline{{\theta }_{C_j}}}^2)-({\varrho }_{C_j}^2\left(x_k\right)-{\overline{{\varrho }_{C_j}}}^2)\end{array}\right\}$$

(16)

are the deviations of $C_i$ and $C_j$, respectively.

Definition 7.

The PCC of $(C_i,C_j)$, $i,j=1,2,\cdots ,r$ by keeping $C_{r+1},C_{r+2},\cdots ,C_{r+s}$ constant can be derived as follows:

First, we partition $\mathcal{M}$ into four parts,

$$\mathcal{M}=\left[\begin{array}{cc}{\mathcal{M}}_{11}& {\mathcal{M}}_{12}\\ {\mathcal{M}}_{21}& {\mathcal{M}}_{22}\end{array}\right],$$

(17)

where ${\mathcal{M}}_{11}$ represents $r\times r$ covariance matrix of $(C_i,C_j)$ for $i,j=1,2,\cdots ,r$, ${\mathcal{M}}_{12}$ represents $r\times s$ covariance matrix of $(C_i,C_j)$ for $i=1,2,\cdots ,r$, $j=r+1,r+2,\cdots ,r+s$, ${\mathcal{M}}_{21}$ represents $s\times r$ covariance matrix of $(C_i,C_j)$ for $i=r+1,r+2,\cdots ,r+s$, $j=1,2,\cdots ,r$, ${\mathcal{M}}_{22}$ represents $s\times s$ covariance matrix of $(C_i,C_j)$ for $i,j=r+1,r+2,\cdots ,r+s$. Certainly, ${\mathcal{M}}_{12}$ and ${\mathcal{M}}_{21}$ transposes each other.

By muting the effect of $C_{r+1},C_{r+2},\cdots ,C_{r+s}$, the PCC of $(C_i,C_j)$ is defined by

$$\tilde{\sigma }\left((C_i,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))={\displaystyle \frac{\varphi \left((C_i,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))}{{\left(\varphi \left((C_i,C_i)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))\varphi \left((C_j,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))\right)}^{\frac{1}{2}}}},$$

(18)

where $i,j=1,2,\cdots ,r$ and $\varphi \left((C_i,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))$ is the $i,j$th element of partial covariance matrix of ${\mathcal{M}}_{11|2}={\mathcal{M}}_{11}-{\mathcal{M}}_{12}{\mathcal{M}}_{22}^{-1}{\mathcal{M}}_{21}$.

It follows that

$$\tilde{\sigma }\left((C_i,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))=\tilde{\sigma }\left((C_j,C_i)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))$$

since ${\mathcal{M}}_{11|2}$ is a symmetry matrix and

$$\varphi \left((C_i,C_j)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s}))=\varphi \left((C_j,C_i)\right|(C_{r+1},C_{r+2},\cdots ,C_{r+s})).$$

Theorem 2.

An nth-order PCC of PFD becomes a first-order partial correlation coefficient of PFD if $r=2$ and $s=1$.

Proof. 

Suppose $r=2$ and $s=1$. Then we have PFD $C_1$, $C_2$ and $C_3$. Our interest is to find the linear relationship between $C_1$ and $C_2$ by muting the effect of $C_3$. Since $r=2$ and $s=1$, $r+s=3$ and

$$\mathcal{M}=\left[\begin{array}{ccc}\varphi (C_1,C_1)& \varphi (C_1,C_2)& \varphi (C_1,C_3)\\ \varphi (C_2,C_1)& \varphi (C_2,C_2)& \varphi (C_2,C_3)\\ \varphi (C_3,C_1)& \varphi (C_3,C_2)& \varphi (C_3,C_3)\end{array}\right].$$

For simplicity sake, we write $\mathcal{M}$ as

$$\mathcal{M}=\left[\begin{array}{ccc}{\varphi }_{11}& {\varphi }_{12}& {\varphi }_{13}\\ {\varphi }_{21}& {\varphi }_{22}& {\varphi }_{23}\\ {\varphi }_{31}& {\varphi }_{32}& {\varphi }_{33}\end{array}\right],$$

which we partition into four parts as

$$\mathcal{M}=\left[\begin{array}{cc}\begin{array}{c}\hfill \left[\begin{array}{cc}{\varphi }_{11}& {\varphi }_{12}\\ {\varphi }_{21}& {\varphi }_{22}\end{array}\right]\end{array}& \begin{array}{c}\hfill \left[\begin{array}{c}{\varphi }_{13}\\ {\varphi }_{23}\end{array}\right]\end{array}\\ \begin{array}{c}\hfill \left[\begin{array}{cc}{\varphi }_{31}& {\varphi }_{32}\end{array}\right]\end{array}& \begin{array}{c}\hfill \left[\begin{array}{c}{\varphi }_{33}\end{array}\right]\end{array}\end{array}\right].$$

Clearly,

$${\mathcal{M}}_{11}=\left[\begin{array}{cc}{\varphi }_{11}& {\varphi }_{12}\\ {\varphi }_{21}& {\varphi }_{22}\end{array}\right],{\mathcal{M}}_{12}=\left[\begin{array}{c}{\varphi }_{13}\\ {\varphi }_{23}\end{array}\right],$$

$${\mathcal{M}}_{21}=\left[\begin{array}{cc}{\varphi }_{31}& {\varphi }_{32}\end{array}\right],{\mathcal{M}}_{22}=\left[\begin{array}{c}{\varphi }_{33}\end{array}\right],$$

where ${\mathcal{M}}_{11}$ represents the covariance matrix of $C_1$ and $C_2$, ${\mathcal{M}}_{12}$ represents the covariance matrix of $C_1$ and $C_3$, ${\mathcal{M}}_{21}$ represents the covariance matrix of $C_2$ and $C_3$, and ${\mathcal{M}}_{22}$ is the variance $C_3$.

Consequently, the PCC of $C_1$ and $C_2$ by keeping $C_3$ constant is

$$\tilde{\sigma }\left((C_1,C_2)\right|C_3)={\displaystyle \frac{\varphi \left((C_1,C_2)\right|C_3)}{{\left(\varphi \left((C_1,C_1)\right|C_3)\varphi \left((C_2,C_2)\right|C_3)\right)}^{\frac{1}{2}}}},$$

rewritten as

$${\tilde{\sigma }}_{12|3}={\displaystyle \frac{{\varphi }_{12|3}}{{\left({\varphi }_{11|3}{\varphi }_{22|3}\right)}^{\frac{1}{2}}}},$$

in which ${\varphi }_{12|3}$ is the element of ${\mathcal{M}}_{11|2}={\mathcal{M}}_{11}-{\mathcal{M}}_{12}{\mathcal{M}}_{22}^{-1}{\mathcal{M}}_{21}$. Observe that

$$\begin{array}{ccc}\hfill {\mathcal{M}}_{12}{\mathcal{M}}_{22}^{-1}{\mathcal{M}}_{21}& =& \left[\begin{array}{c}{\varphi }_{13}\\ {\varphi }_{23}\end{array}\right]{\left[\begin{array}{c}{\varphi }_{33}\end{array}\right]}^{-1}\left[\begin{array}{cc}{\varphi }_{31}& {\varphi }_{32}\end{array}\right]\hfill \\ & =& \left[\begin{array}{c}{\displaystyle \frac{{\varphi }_{13}}{{\varphi }_{33}}}\\ {\displaystyle \frac{{\varphi }_{23}}{{\varphi }_{33}}}\end{array}\right]\left[\begin{array}{cc}{\varphi }_{31}& {\varphi }_{32}\end{array}\right]\hfill \\ & =& \left[\begin{array}{cc}{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{33}}}& {\displaystyle \frac{{\varphi }_{13}{\varphi }_{32}}{{\varphi }_{33}}}\\ {\displaystyle \frac{{\varphi }_{23}{\varphi }_{31}}{{\varphi }_{33}}}& {\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{33}}}\end{array}\right].\hfill \end{array}$$

Thus,

$${\mathcal{M}}_{11|2}=\left[\begin{array}{cc}{\varphi }_{11}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{33}}}& {\varphi }_{12}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{32}}{{\varphi }_{33}}}\\ {\varphi }_{21}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{31}}{{\varphi }_{33}}}& {\varphi }_{22}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{33}}}\end{array}\right],$$

where

$${\varphi }_{11|3}={\varphi }_{11}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{33}}},{\varphi }_{12|3}={\varphi }_{12}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{32}}{{\varphi }_{33}}}$$

$${\varphi }_{21|3}={\varphi }_{21}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{31}}{{\varphi }_{33}}},{\varphi }_{22|3}={\varphi }_{22}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{33}}}.$$

Therefore,

$${\tilde{\sigma }}_{12|3}={\displaystyle \frac{{\varphi }_{12|3}}{{\left({\varphi }_{11|3}{\varphi }_{22|3}\right)}^{\frac{1}{2}}}},$$

becomes

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{12|3}& =& {\displaystyle \frac{{\varphi }_{12}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{32}}{{\varphi }_{33}}}}{{\left(\left({\varphi }_{11}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{33}}}\right)\left({\varphi }_{22}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{33}}}\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{{\displaystyle \frac{1}{{\left({\varphi }_{11}{\varphi }_{22}\right)}^{\frac{1}{2}}}}({\varphi }_{12}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{32}}{{\varphi }_{33}}})}{{\displaystyle \frac{1}{{\left({\varphi }_{11}{\varphi }_{22}\right)}^{\frac{1}{2}}}}{\left(\left({\varphi }_{11}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{33}}}\right)\left({\varphi }_{22}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{33}}}\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{{\displaystyle \frac{{\varphi }_{12}}{{\left({\varphi }_{11}{\varphi }_{22}\right)}^{\frac{1}{2}}}}-{\displaystyle \frac{{\varphi }_{13}}{{\left({\varphi }_{11}{\varphi }_{33}\right)}^{\frac{1}{2}}}}{\displaystyle \frac{{\varphi }_{23}}{{\left({\varphi }_{22}{\varphi }_{33}\right)}^{\frac{1}{2}}}}}{{\left(\left({\displaystyle \frac{{\varphi }_{11}}{{\varphi }_{11}}}-{\displaystyle \frac{{\varphi }_{13}{\varphi }_{31}}{{\varphi }_{11}{\varphi }_{33}}}\right)\left({\displaystyle \frac{{\varphi }_{22}}{{\varphi }_{22}}}-{\displaystyle \frac{{\varphi }_{23}{\varphi }_{32}}{{\varphi }_{22}{\varphi }_{33}}}\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{{\displaystyle \frac{{\varphi }_{12}}{{\left({\varphi }_{11}{\varphi }_{22}\right)}^{\frac{1}{2}}}}-{\displaystyle \frac{{\varphi }_{13}}{{\left({\varphi }_{11}{\varphi }_{33}\right)}^{\frac{1}{2}}}}{\displaystyle \frac{{\varphi }_{23}}{{\left({\varphi }_{22}{\varphi }_{33}\right)}^{\frac{1}{2}}}}}{{\left(\left({\displaystyle \frac{{\varphi }_{11}}{{\varphi }_{11}}}-{\displaystyle \frac{{\varphi }_{13}^2}{{\left({\varphi }_{11}^2{\varphi }_{33}^2\right)}^{\frac{1}{2}}}}\right)\left({\displaystyle \frac{{\varphi }_{22}}{{\varphi }_{22}}}-{\displaystyle \frac{{\varphi }_{23}^2}{{\left({\varphi }_{22}^2{\varphi }_{33}^2\right)}^{\frac{1}{2}}}}\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{{\tilde{\sigma }}_{12}-{\tilde{\sigma }}_{13}{\tilde{\sigma }}_{23}}{{\left(\right(1-{\tilde{\sigma }}_{13}^2\left)\right(1-{\tilde{\sigma }}_{23}^2\left)\right)}^{\frac{1}{2}}}}.\hfill \end{array}$$

Alternatively, it can be written as

$$\tilde{\sigma }\left((C_1,C_2)\right|C_3)={\displaystyle \frac{\tilde{\sigma }(C_1,C_2)-\tilde{\sigma }(C_1,C_3)\tilde{\sigma }(C_2,C_3)}{{\left((1-{\tilde{\sigma }}^2(C_1,C_3))(1-{\tilde{\sigma }}^2(C_2,C_3))\right)}^{\frac{1}{2}}}},$$

which is the first-order PCC of PFD as desired. □

Remark 1.

If $r=2$ and $s=2$, then the nth-order PCC of PFD becomes

$$\tilde{\sigma }\left((C_1,C_2)\right|(C_3,C_4))={\displaystyle \frac{\tilde{\sigma }\left((C_1,C_2)\right|C_4)-\tilde{\sigma }\left((C_2,C_3)\right|C_4)\tilde{\sigma }\left((C_1,C_3)\right|C_4)}{{\left((1-{\tilde{\sigma }}^2\left((C_2,C_3)\right|C_4))(1-{\tilde{\sigma }}^2\left((C_1,C_3)\right|C_4))\right)}^{\frac{1}{2}}}}$$

rewritten as

$${\tilde{\sigma }}_{12|34}={\displaystyle \frac{{\tilde{\sigma }}_{12|4}-{\tilde{\sigma }}_{23|4}{\tilde{\sigma }}_{13|4}}{{\left(\left(1-{\tilde{\sigma }}_{23|4}^2\right)\left(1-{\tilde{\sigma }}_{13|4}^2\right)\right)}^{\frac{1}{2}}}}.$$

Certainly, ${\tilde{\sigma }}_{12|34}={\tilde{\sigma }}_{12|43}$ since

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{12|34}& =& {\displaystyle \frac{{\tilde{\sigma }}_{12|4}-{\tilde{\sigma }}_{23|4}{\tilde{\sigma }}_{13|4}}{{\left(\left(1-{\tilde{\sigma }}_{23|4}^2\right)\left(1-{\tilde{\sigma }}_{13|4}^2\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\displaystyle \frac{{\tilde{\sigma }}_{12|3}-{\tilde{\sigma }}_{24|3}{\tilde{\sigma }}_{14|3}}{{\left(\left(1-{\tilde{\sigma }}_{24|3}^2\right)\left(1-{\tilde{\sigma }}_{14|3}^2\right)\right)}^{\frac{1}{2}}}}\hfill \\ & =& {\tilde{\sigma }}_{12|43}.\hfill \end{array}$$

4. Applicative Example in Pattern Recognitions and Classifications

The concept of pattern recognition is central to the recognition of patterns with the aid of a machine learning algorithm. The process of categorizing data using statistical information extracted from pattern and/or their representation is called pattern recognition. Alternatively, pattern recognition is a facility used to detect the classifications of data to produce information about a given data set or system. Although pattern recognition is applicable in diverse areas, the presence of fuzziness posed a huge setback. Consequently, encapsulating the idea of pattern recognition in the domain of PFSs is a welcome adventure.

Case Study

Here, we recognize and classify patterns of building materials in five feature space as random samples of PFAs using a Pythagorean fuzzy partial correlation measure. We compute the zero-order PCCs of the patterns, vis-a-vis the first and second PCCs of the patterns to determine the precise linear relationship among the building patterns.

Suppose the building patterns represented by PFAs $P_i$ for $i=1,2,\cdots ,n$ in the feature space $S=\{s_1,s_2,s_3,s_4,s_5\}$ are contained in Table 2.

Table 2. Pythagorean fuzzy pattern representations.

Feature Space
PFS	${\mathit{s}}_{\mathbf{1}}$	${\mathit{s}}_{\mathbf{2}}$	${\mathit{s}}_{\mathbf{3}}$	${\mathit{s}}_{\mathbf{4}}$	${\mathit{s}}_{\mathbf{5}}$
${\eta }_{P_1}$	0.8000	0.7000	0.9000	0.6000	0.8000
${\theta }_{P_1}$	0.1000	0.2000	0.0000	0.3000	0.1000
${\eta }_{P_2}$	0.9000	0.8000	0.8000	0.5000	0.7000
${\theta }_{P_2}$	0.1000	0.1000	0.1000	0.3000	0.2000
${\eta }_{P_3}$	0.5000	0.5000	0.9000	0.5000	0.7000
${\theta }_{P_3}$	0.3000	0.2000	0.0000	0.4000	0.1000
${\eta }_{P_4}$	0.7000	0.5000	0.9000	0.6000	0.8000
${\theta }_{P_4}$	0.2000	0.4000	0.1000	0.3000	0.0000

The HMs of $P_i$’s can be calculated using the formula in Definition 2.

By applying (7) to find the correlation coefficient between the building patterns, we obtain the Pythagorean fuzzy correlation coefficient matrix:

$$\begin{array}{cc}\begin{array}{c}{\hspace{1em}P}_1\hspace{1em}\hspace{1em}\hspace{1em}{\hspace{0.17em}P}_2\hspace{1em}\hspace{0.17em}{\hspace{1em}\hspace{0.17em}P}_3\hspace{1em}{\hspace{1em}\hspace{0.17em}P}_4\hspace{1em}\end{array}& \\ \left[\begin{array}{cccc}1& -0.1271& 0.1004& 0.1879\\ -0.1271& 1& -0.1361& -0.2556\\ 0.1004& -0.1361& 1& 0.2010\\ 0.1879& -0.2556& 0.2010& 1\end{array}\right]& \begin{array}{c}{P}_1\\ P_2\\ P_3\\ P_4\end{array}\end{array}$$

From this Pythagorean fuzzy correlation coefficient matrix, we observe that $\tilde{\sigma }(P_1,P_1)=1$, $\tilde{\sigma }(P_2,P_2)=1$, $\tilde{\sigma }(P_3,P_3)=1$, and $\tilde{\sigma }(P_4,P_4)=1$ in concord with Definition 5. Figure 1, Figure 2, Figure 3 and Figure 4 are plotted from the Pythagorean fuzzy correlation coefficient matrix.

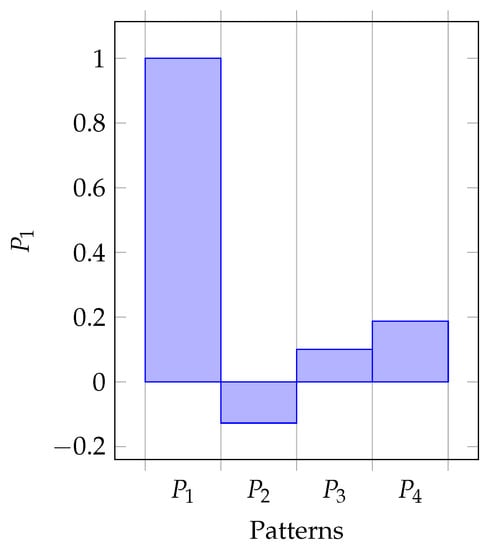
Figure 1. Pattern $P_1$ against other Patterns.

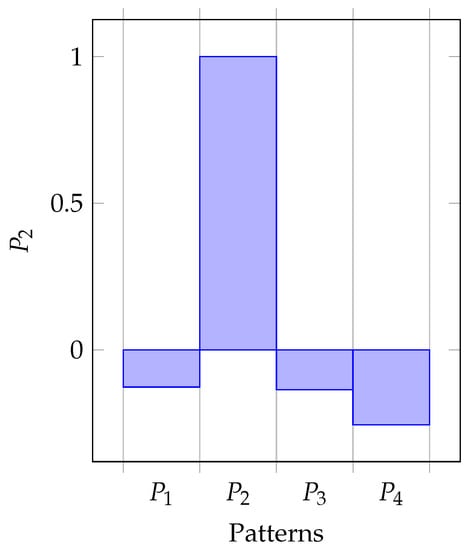
Figure 2. Pattern $P_2$ against other Patterns.

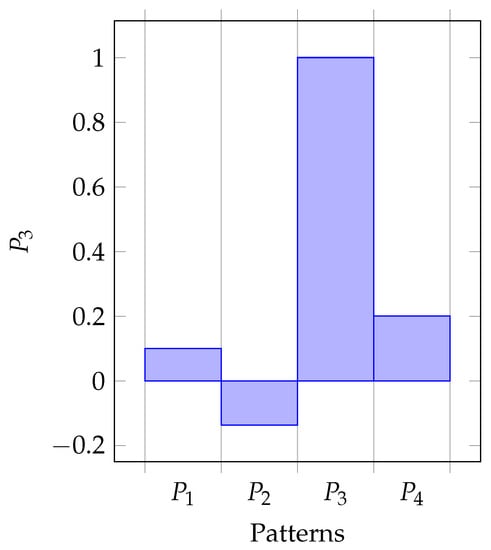
Figure 3. Pattern $P_3$ against other Patterns.

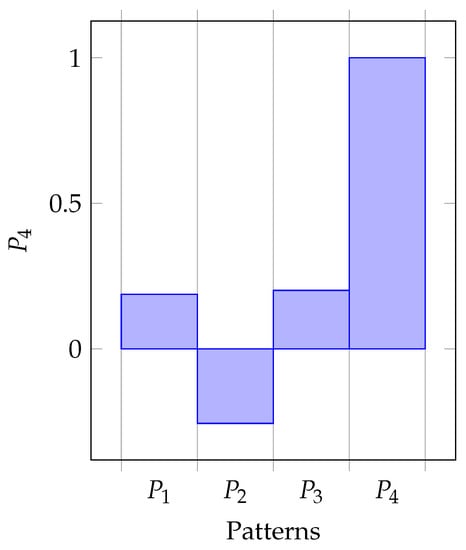
Figure 4. Pattern $P_4$ against other Patterns.

From the correlation coefficient matrix and Figure 1, Figure 2, Figure 3 and Figure 4, we observe that

$${\tilde{\sigma }}_{P_1{P}_4}\ge {\tilde{\sigma }}_{P_1{P}_3}\ge {\tilde{\sigma }}_{P_1{P}_2},{\tilde{\sigma }}_{P_2{P}_1}\ge {\tilde{\sigma }}_{P_2{P}_3}\ge {\tilde{\sigma }}_{P_2{P}_4},$$

$${\tilde{\sigma }}_{P_3{P}_4}\ge {\tilde{\sigma }}_{P_3{P}_1}\ge {\tilde{\sigma }}_{P_3{P}_2},{\tilde{\sigma }}_{P_4{P}_3}\ge {\tilde{\sigma }}_{P_4{P}_1}\ge {\tilde{\sigma }}_{P_4{P}_2},$$

which imply the following interpretations; pattern $P_1$ can be classified with pattern $P_4$ (since the correlation coefficient ${\tilde{\sigma }}_{P_1{P}_4}$ is the greatest), pattern $P_2$ can be classified with pattern $P_1$ (since the correlation coefficient ${\tilde{\sigma }}_{P_2{P}_1}$ is the greatest) and patterns $P_3$ and $P_4$ can be classified with each other (since the correlation coefficients ${\tilde{\sigma }}_{P_3{P}_4}$ and ${\tilde{\sigma }}_{P_4{P}_3}$ are the greatest in each cases). Certainly, the Pythagorean fuzzy correlation coefficient matrix is symmetric, i.e., ${\tilde{\sigma }}_{P_i{P}_{i+1}}={\tilde{\sigma }}_{P_{i+1}{P}_i}$ and each pattern is reflexive to itself, i.e., ${\tilde{\sigma }}_{P_i{P}_i}={\tilde{\sigma }}_{P_i{P}_i}=1$. The zero-order partial correlation coefficient results show that the four patterns have positive linear relationship with each other with the exceptions of ${\tilde{\sigma }}_{P_1{P}_2}$, ${\tilde{\sigma }}_{P_2{P}_3}$ and ${\tilde{\sigma }}_{P_2{P}_4}$.

To obtain an exact correlation among the building patterns, the first-order PCCs of $P_i$s are computed. The following values of the first-order PCCs between two patterns by muting the effect of another pattern are obtained by (12) using the corresponding zero-order partial correlation coefficients:

$${\tilde{\sigma }}_{P_1{P}_2|P_3}=-0.1151,{\tilde{\sigma }}_{P_1{P}_2|P_4}=-0.0833,$$

$${\tilde{\sigma }}_{P_1{P}_3|P_2}=0.0846,{\tilde{\sigma }}_{P_1{P}_3|P_4}=0.0651,$$

$${\tilde{\sigma }}_{P_1{P}_4|P_2}=0.1621,{\tilde{\sigma }}_{P_1{P}_4|P_3}=0.1721,$$

$${\tilde{\sigma }}_{P_2{P}_3|P_1}=-0.1250,{\tilde{\sigma }}_{P_2{P}_3|P_4}=-0.0895,$$

$${\tilde{\sigma }}_{P_2{P}_4|P_1}=-0.2378,{\tilde{\sigma }}_{P_2{P}_4|P_3}=-0.2352,$$

$${\tilde{\sigma }}_{P_3{P}_4|P_1}=0.1864,{\tilde{\sigma }}_{P_3{P}_4|P_2}=0.1735.$$

By associating these results with the simple correlation coefficients, we surmise that by removing the sway of another pattern from the simple correlation coefficients, the partial correlation coefficients either increase or decrease. By removing the effect of a pattern from the correlation between two patterns, it is observed that

(i)

Pattern $P_1$ has a negative sway on the correlation between patterns $(P_2,P_3)$, $(P_2,P_4)$ and a positive effect on the correlation of $(P_3,P_4)$.

(ii)

Pattern $P_2$ only has a positive sway on the correlation between patterns $(P_1,P_3)$, $(P_1,P_4)$ and $(P_3,P_4)$.

(iii)

Pattern $P_3$ has a negative effect on the correlation between patterns $\left(P_1{P}_2\right)$, $(P_2,P_4)$ and a positive effect on the correlation of $(P_1,P_4)$.

(iv)

Pattern $P_4$ has a negative influence on the correlation between patterns $(P_1,P_2)$, $(P_2,P_3)$ and a positive effect on the correlation of $(P_1,P_3)$.

By removing the effect of a pattern from the first-order partial correlations between patterns, we obtain:

$${\tilde{\sigma }}_{P_1{P}_2|P_3{P}_4}=-0.0780,{\tilde{\sigma }}_{P_1{P}_3|P_2{P}_4}=0.0581,$$

$${\tilde{\sigma }}_{P_1{P}_4|P_2{P}_3}=0.1502,{\tilde{\sigma }}_{P_2{P}_3|P_1{P}_4}=-0.0845,$$

$${\tilde{\sigma }}_{P_2{P}_4|P1P_3}=-0.2201,{\tilde{\sigma }}_{P_3{P}_4|P_1{P}_2}=0.1625,$$

While matching these results with the first-order PCCs between patterns, it is observed that when the impact of another pattern is muted from the first-order PCC, the second-order PCC between the patterns either increase or decrease, and the influences are

(i)

Pattern $P_1$ has a negative effect on the first-order partial correlations ${\tilde{\sigma }}_{P_2{P}_4|P_3}$, ${\tilde{\sigma }}_{P_2{P}_3|P_4}$ and a positive effect on ${\tilde{\sigma }}_{P_3{P}_4|P_2}$.

(ii)

Pattern $P_2$ only has a positive effect on the first-order partial correlations ${\tilde{\sigma }}_{P_1{P}_3|P_4}$, ${\tilde{\sigma }}_{P_1{P}_4|P_3}$ and ${\tilde{\sigma }}_{P_3{P}_4|P_1}$.

(iii)

Pattern $P_3$ has a negative impact on the first-order partial correlations ${\tilde{\sigma }}_{P_1{P}_2|P_4}$, ${\tilde{\sigma }}_{P_2{P}_4|P_1}$ and a positive effect on ${\tilde{\sigma }}_{P_1{P}_4|P_2}$.

(iv)

Pattern $P_4$ has a negative effect on the first-order partial correlation coefficients ${\tilde{\sigma }}_{P_1{P}_2|P_3}$, ${\tilde{\sigma }}_{P_2{P}_3|P_1}$ and a positive impact on ${\tilde{\sigma }}_{P_1{P}_3|P_2}$.

It is fascinating to know that Pattern $P_2$ possesses positive effect on both the simple correlations and the first-order partial correlations of the patterns. Roughly speaking, the index of a partial correlation coefficient of the patterns either increase or decrease when the effect of other pattern(s) is/are removed depending on the direction of the correlation.

The negative nature of the partial correlation coefficients ${\tilde{\sigma }}_{P_1{P}_2|P_3{P}_4}$, ${\tilde{\sigma }}_{P_2{P}_3|P_1{P}_4}$ and ${\tilde{\sigma }}_{P_2{P}_4|P_1{P}_3}$ suggest that the simple correlations between patterns $(P_1,P_2)$, $(P_2,P_3)$ and $(P_2,P_4)$ are really negative. Similarly, the positive nature of the partial correlation coefficients ${\tilde{\sigma }}_{P_1{P}_3|P_2{P}_4}$, ${\tilde{\sigma }}_{P_1{P}_4|P_2{P}_3}$ and ${\tilde{\sigma }}_{P_3{P}_4|P_1{P}_2}$ suggest that the simple correlations between patterns $(P_1,P_3)$, $(P_1,P_4)$ and $(P_3,P_4)$ are actually positive.

5. Conclusions

In this paper, the Pythagorean fuzzy partial correlation measure is initiated for the first time because of the flexibility of PFSs in decision-making. The concept of PCC for random fuzzy data [42] was extended to random PFD by considering all the descriptive parameters of PFSs. The simple correlation coefficient for PFD [39] was modified to include all the descriptive parameters of PFSs, and used in determining the Pythagorean fuzzy partial correlation coefficient between random PFD. Pythagorean fuzzy partial correlation measure is significant because it removes the influence of interfering PFD when measuring the correlation between any two random PFD. This ability of removing intrinsic influence of other PFD is beyond the capacity of a simple correlation coefficient for PFD. The applicability of the Pythagorean fuzzy partial correlation measure in the recognition of building patterns, where the patterns were represented by random PFD collected from a hypothetical survey was considered. From the analysis, it was discovered that whenever the impact of another pattern is removed, the index of the Pythagorean fuzzy partial correlation coefficient either increases or decreases subject to the linear relationship and direction of the correlation between the muted pattern and the considered patterns. The idea of PCC for PFD is beneficial because it shows the precise correlation between any two random PFD, and expresses the effect of the interfering PFD on the relationship. In future research, we could investigate the idea of Pythagorean fuzzy partial correlation coefficient based on multivariate correlation coefficients for random PFD with application in problems involving multiple criteria decision-making. To the best of our knowledge, the only limitation of the developed PFPCC is that it cannot be extended to some uncertain settings that are described with more than three parametric features such as picture fuzzy sets, spherical fuzzy sets, etc.