Generalized Interval-Valued q-Rung Orthopair Hesitant Fuzzy Choquet Operators and Their Application

Abstract

Hesitant fuzzy evaluation strategy related to the interval-valued membership and nonmembership degrees should be an appropriate choice due to the lack of experience, ability and knowledge of some decision experts. In addition, it is important to reasonably model the interrelationship of these experts. In this work, firstly, the generalized interval-valued q-rung orthopair hesitant fuzzy sets (GIVqROHFSs) are defined, and some operational rules with respect to GIVqROF numbers are discussed. Secondly, two types of operators, which are denoted as GIVqROHFCA and GIVqROHFCGM, are developed. Thirdly, the desired properties and relationships of two operators are studied. Furthermore, a new multiple attributes group decision making (MAGDM) approach is proposed. Finally, three experiments are completed to illustrate the rationality of the developed method and the monotonicity of this approach concerning the parameter in the GIVqROHFCGM operator and the GIVqROHFCA operator which meets symmetrical characteristics, and shows the superiority and reliability of this new method in solving the GIVqROHF problems. The main advantages of this work include three points: (1) extending hesitant fuzzy sets to the interval-valued q-rung orthopair fuzzy case and proposing two types of aggregation operators for the GIVqROHF information; (2) considering the interaction among decision makers and among attributes in decision problems, and dealing with this interrelationship by fuzzy measure; (3) introducing the new decision method for the GIVqROHF environment and enriching the mathematical tools to solve multiple attributes decision-making problems.

1. Introduction

In many problems of practical decision making or human cognition, a single value may not be completely suitable to present values of the nonmembership and membership (NMMDs) [1,2]. In view of these restrictions, HFSs are useful to model the hesitant uncertainty in MAGDM problems [3,4], and the fuzzy filters theory of Sheffer stroke algebras can be used to power bridges between fuzzy and hesitant fuzzy structures [5,6]. The membership of the hesitant fuzzy set includes several hesitant values on the unit interval [0, 1], which have an extension on the basis of different fuzzy forms in many practical decision-making problems such as the interval case [7], intuitionistic case [8], and Pythagorean case [9]. For instance, Deli introduced the MAGDM approach based on the GTHF-numbers and Bonferroni mean operator [10]; Liao et al. extended the ORESTE method to the hesitant fuzzy linguistic environment for the MAGDM problems [11]; Mishra et al. integrated the Shapley measure and hesitant fuzzy sets theory to propose the COPRAS method for the MAGDM process [12]; Wan et al. considered the multiplicative consistency of hesitant fuzzy preference relations and presented a mathematical program on the basis of the new consistency index of HFPR [13]; Shen et al. utilized the binary connection number theory to the probabilistic hesitant fuzzy MAGDM problems [14], and Liu et al. studied the distance measures of the probabilistic hesitant fuzzy element for the MAGDM methods [15]; Meng et al. analysed the time-sequence situation of hesitant degrees of people and introduced the concept of time-sequential hesitant fuzzy set for the MAGDM problems [16]. Kinds of extension of HFSs have been proposed for some MAGDM problems. The interval-valued hesitant fuzzy sets (IVHFSs) permit that degrees of the membership take interval values on [0, 1] which describe the intuitionistic differences among decision experts [17]. The intuitionistic hesitant fuzzy sets (IHFSs) involve the possible membership and nonmembership values which decision makers provide for accessing an alternative [18]. The interval-valued intuitionistic hesitant fuzzy sets (IVIHFSs) are another generation of HFSs, which allow membership degrees on an element to contain several interval-valued intuitionistic fuzzy numbers [19]. Pythagorean hesitant fuzzy sets, expanding the scope of the NMMDs on IHFSs, can manage the situation where the 2-power sum of NMMDs on an element is not greater than the unit one, and it is also an extension of IHFSs [20,21].

In addition, for one thing, the interval-valued intuitionistic fuzzy sets (IVIFSs) were proposed [22]. For another thing, the interval-valued Pythagorean fuzzy sets (IVPFSs) were defined to extend Pythagorean fuzzy sets (PFSs) [23,24]. Moreover, the interval-valued q-rung orthopair fuzzy sets (IVqROFSs), generalizing IVIFSs and IVPFSs, are efficient to describe fuzzy information in the practical MAGDM problems [25,26]. As a result, some researchers have studied some MAGDM problems under fuzzy surroundings which were modeled based on the IVPFSs and IVqROFSs. For instance, Liu et al. developed the new distance measures with respect to the IVPFSs for the IVPFS-based MAGDM approach [27]; Garg defined two new exponential operational laws of the IVPFSs and extended these rules to interval numbers situation for dealing with the MAGDM problems [28]; Rahman et al. provided more general aggregation operators for the IVPFS multiple-attribute group decision-making method [29]; Mu et al. proposed a new comparison rule about the IVPFNs based on the new comparison functions for the MAGDM problems [30]; Li et al. considered the IVPFS decision-making method on the basis of the set pair analysis and fuzzy integral theory [31]; Zhao et al. presented the IVPFS TODIM method for the green supplier selection in terms of the cumulative prospect theory [32]; Peng et al. introduced a new distance measure about the IVPFSs for the IVPFS emergency decision-making process [33]; Gao et al. extended the Archimedean Muirhead mean operator to the IVqROFS environment for the MAGDM analysis [34]; Garg developed the Possibility degree measure in regard to two IVqROFSs and introduced the corresponding MAGDM method [35]; Garg et al. pooled the aggregation operators, AHP and TOPSIS, to study the concept of complex IVqROFSs for the IVqROFS decision process [36].

Compared to the above fuzzy method, the MAGDM approaches with grey system theory were developed on the basis of another mathematical perspective. On the other hand, the grey system theory can describe the uncertain phenomena with the explicit denotation and ambiguous connotation, and it has been the mathematical tool that models hesitation and uncertainty of the incomplete information. For instance, Turanoglu et al. ranked the grey decoration materials in the light of the AHP and grey correlation with TOPSIS [37]; Alkharabsheh et al. extended the classical AHP approach to grey values environment for ranking the supply quality criteria [38]; Esangbedo et al. proposed a new weighting method based on the point-allocation approach and the grey system theory and developed the weighted sum model with grey numbers [39]. However, the uncertain situation, which is the clear connotation and unclear extension in the MAGDM problems, can be addressed by the fuzzy theory or extensions of this mathematical tool. Furthermore, owing to some influencing factors such as the capacities of information processing, limited attention of decision makers and the lack of data or knowledge during the practical MAGDM process, they cannot present a single IVqROF number for MNMDs of a considered element, and may give several possible IVqROF numbers. For instance, in order to obtain a desired evaluation result, a decision corporation demands decision experts to provide the degree values with respect to an attribute, and supposing that three cases are included, that is, some experts present $([0.8,0.95],[0.45,0.7])$, some provide $([0.45,0.65],[0.7,0.9])$ and the others assign $([0.7,0.85],[0.45,0.7])$, where they cannot change their opinions. It can easily be obtained that the sum of the maximal value within the membership and non-membership interval is more than or equal to the unit one, and the ones of their different powers are yet not less than the one, that is ${0.95}^4+{0.7}^4>1$, ${0.65}^3+{0.9}^3>1$ and ${0.85}^2+{0.7}^2>1$. It is shown that such a decision-making problem cannot be handled by the aforementioned MAGDM method, the fuzzy sets (FSs) theory [40] and extensions which involve the hesitant fuzzy sets (HFSs) theory [41], bipolar interval-valued neutrosophic sets (BIVNs) theory [42], dual hesitant fuzzy sets (DHFs) theory [43], interval-valued dual hesitant fuzzy sets (IVDHFs) theory [44], intuitionistic fuzzy sets theory [45], PFSs theory, interval-valued fuzzy sets (IVFSs) theory [46], IVIFSs theory, IVHFSs theory, IHFSs theory, IVIHFSs theory, PHFSs theory, IVPHFSs theory [47] and IVqROFSs theory [48]. Considering the concept of interval-valued q-rung dual fuzzy sets [49,50,51], the aforementioned hesitant fuzzy information may been modeled by an interval-valued q-rung dual fuzzy set (IVqRDHFS) $\left\{\{[0.8,0.95],[0.45,0.65],[0.7,0.85]\},\{[0.45,0.7]),[0.7,0.9]\}\right\}$, However, it is easily shown that the hesitant fuzzy information $([0.7,0.85],[0.45,0.7])$ is omitted, thus this situation results in loss of the useful information. From another perspective, the IVqRDHFS $\left\{\{[0.8,0.95],[0.45,0.65],[0.7,0.85]\},\{[0.45,0.7]),[0.7,0.9]\}\right\}$ may be presented by several IVqROFNs as follows:

$$\begin{array}{l}\{([0.8,0.95],[0.45,0.7]),([0.8,0.95],[0.7,0.9]),([0.45,0.65],[0.45,0.7]),\\ ([0.45,0.65],[0.7,0.9]),([0.7,0.85]\}\begin{array}{c},\end{array}[0.45,0.7]),([0.7,0.85]\},[0.7,0.9])\}\end{array}$$

According to this symbol, the hesitant fuzzy information in the above instance is contained, and the IVqRDHFS is justly a special case of a new type of hesitant fuzzy set which is characterized by several IVqROFSs. Therefore, the hesitant fuzzy sets should be extended to the IVqROFNs case. This paper takes the aim of the theory concerning the generalized interval-valued q-rung orthopair hesitant fuzzy sets (GIVqROHFSs) and the NMMDs set which may contain several possible IVqROFNs. In view of the previous instance, the NMMDs on an element can be described by the IVqROHFSs $\{([0.8,0.95],[0.45,0.7]),([0.45,0.65],[0.7,0.9]),([0.7,0.85],[0.45,0.7])\}$. In spite of the fact that the attribute values may be a set of IVqROFNs in the practical application of many MAGDM problems, there is a matter of great concern to the aggregation approach which can deal with the GIVqROHF information. Nevertheless, the existing fusion methods have encountered a great difficulty under the GIVqROHF environment, and decision methods in the above-mentioned references only account for the restriction that all of the input arguments or decision attributes in decision problems are independent, although the practical decision-making process always involves interactive characteristics among the alternatives or attributes under the uncertain decision environment. As a key characteristic case, the Choquet integral, which is a symmetric aggregation operator, can merge the interaction among alternatives or attributes into the decision process, and it is an efficient mathematical tool to incorporate interacting attributes under uncertain circumstances [52,53]. In general, the discrete Choquet integral, which is applied in the decision-making process, linearly expresses the mean of all reordered elements in discourse domain, and it coincides with the weighted mean or ordered weighted averaging (OWA) operator. Moreover, the Choquet integral-based aggregation methods can cope with the decision situation in which the correlation with each other exists [54,55]. Specifically, In the decision methods based on the Choquet operator, where attributes or experts can be dependent, thus, the non-additive fuzzy measure is possible to model the interrelationship among attributes or experts by defining a weight on each subset of attributes set or expert set. Consequently, it is very necessary that the Choquet integral is used to overcome the restriction of independence assumption among alternatives or attributes in MAGDM problems [56].

Motivated by the advantages of the Choquet integral theory applied in MAGDM methods, and the GIVqROHFSs theory, which is proposed in this paper, we assign two types of aggregation operators based on Choquet integration to handle the GIVqROHF information, and properties concerning these operators are studied. Moreover, a new decision method is presented for the GIVqROHF information processing, which considers the interaction among inputs or attributes of an alternative. In addition, an application is performed to manifest the performance of this new method.

According to the above, we organize contents (see Figure 1). Section 2 focuses on the basic knowledge involving the HFSs, fuzzy measure, Choquet integral and IVqROFSs. The concept of the GIVqROHFSs is proposed and some operational rules of the GIVqROHFSs are introduced in Section 3. The GIVqROHFCA and GIVqROHFCGM operators are developed in Section 4, and some properties of these two operators are discussed. By the proposed operators, Section 5 demonstrates a new MAGDM approach for processing the GIVqROHF information. The contents of Section 6 include an illustrative example and two number experiences such as sensitivity analysis and compared experience. Some remarks are presented in Section 7.

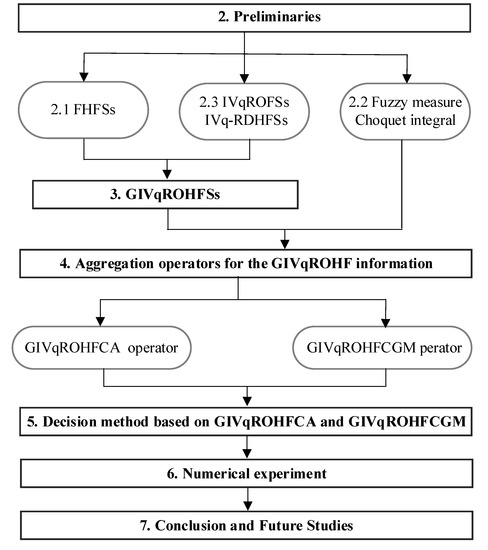
Figure 1. The visual chart of research framework in this work.

2. Preliminaries

The hesitant fuzzy sets (HFSs), fuzzy measure, Choquet integral and IVqROFSs are introduced in the following:

2.1. HFSs

Definition 1 ([1]).

Provided that$T$is a nonempty set and${\psi }_{\tilde{\tilde{X}}}^t$contains several real numbers on [0, 1] for any$t\in T$, a hesitant fuzzy set (HFS) is expressed by the following mathematical symbol:

$$\tilde{\tilde{X}}=\left\{\left(t,{\psi }_{\tilde{\tilde{X}}}^t\right)/t\in T\right\}$$

(1)

where${\psi }_{\tilde{\tilde{X}}}^t$represents membership degree values of$t\in T$to$\tilde{\tilde{X}}$, and it is simply denoted the symbol$\psi$which is called hesitant fuzzy element (HFE) [1].

If ${\psi }_k$ and ${\psi }_l$ are two HFEs, several operations are introduced as follows and all of the operational results between HFEs are also HFEs [19]:

$${\psi }_k\oplus {\psi }_l=\left\{t_k+t_l-t_k{t}_l\left|\begin{array}{l}{t}_k\in {\psi }_k\\ t_l\in {\psi }_l\end{array}\right.\right\}$$

$${\psi }_k\otimes {\psi }_l=\left\{t_k{t}_l\left|\begin{array}{l}{t}_k\in {\psi }_k\\ t_l\in {\psi }_l\end{array}\right.\right\}$$

$$k{\psi }_l=\{-{(1-t_l)}^k+1\left.\right|t_l\in {\psi }_l\}$$

$${\psi }_l{}^k=\{{(t_l)}^k\left.\right|t_l\in {\psi }_l\}$$

$${\psi }_l{}^c=\{1-t_l\left.\right|t_l\in {\psi }_l\}$$

The ranking relationship is introduced [19].

Definition 2 ([19]).

Provided that${\psi }_1$and${\psi }_2$are HFEs,$\#{\psi }_i$indicates the cardinal number of${\psi }_i$and the score function of${\psi }_i$is denoted as$v_s({\psi }_i)=({\displaystyle {\sum }_{t\in {\psi }_i}t})/\#{\psi }_i$, therefore

(1) 

$v_s({\psi }_1)<v_s({\psi }_2)\Rightarrow {\psi }_1<{\psi }_2$; (2)$v_s({\psi }_1)=v_s({\psi }_2)\Rightarrow {\psi }_1={\psi }_2$.

2.2. $\lambda$-Fuzzy Measure and Choquet Integral

Definition 3 ([57]).

$T$is a universe of discourse,$P(T)$is the power of$T$and$Y:P(T)\to [0,1]$is a mapping with conditions.

(1) 

$Y(\varphi )=0,Y(T)=1$.

(2) 

$\forall T_1,T_2\in P(T)$,$T_1\subseteq T_2\Rightarrow Y(T_1)\subseteq Y(T_2)$.

(3) 

$\forall T_1,T_2\in P(T)$,$T_1\cap T_2=\varphi$,$\lambda >-1\Rightarrow Y(T_1\cup T_2)=Y(T_1)+Y(T_2)+\lambda Y(T_1)Y(T_2)$.

We call$Y:P(T)\to [0,1]$ $\lambda$-fuzzy measure on$P(T)$.

When $T=\{t_1,t_2,\cdots ,t_n\}$ is a finite space, a $\lambda$-fuzzy measure $Y$ has the following equations:

$$Y(T)=\left\{\begin{array}{cc}(1/\lambda )\left({\displaystyle {\prod }_{i=1}^n[1+\lambda Y(\left\{t_i\right\})]-1}\right)& \lambda \ne 0\\ {\displaystyle {\sum }_{i=1}^{n}Y(\{t_i\})\begin{array}{ccccc}& & & & \end{array}}& \lambda =0\end{array}\right.$$

(2)

$$Y(T_1)=\left\{\begin{array}{cc}{\displaystyle {\prod }_{t_i\in T_1}[\lambda Y(\left\{t_i\right\})+1]}-1/\lambda & \lambda \ne 0\\ \begin{array}{ccccc}& & {\displaystyle {\sum }_{t_i\in T_1}Y(\{t_i\})}& & \end{array}& \lambda =0\end{array}\right.$$

(3)

$$1+\lambda ={\displaystyle {\prod }_{i=1}^n[1+\lambda Y(\left\{t_i\right\})]}$$

(4)

In MAGDM problems, $Y(\{t_i\})$ can indicate the importance of each decision expert or attribute, and $Y(T_1)$ can describe the interaction among decision experts or attributes [46].

Definition 4 ([58]).

Supposing that the conditions hold.

(1) 

$T=\{t_1,t_2,\cdots ,t_n\}$and$G:T\to R^{+}$is a positive real-valued function.

(2) 

$\{\kappa (1),\kappa (2),\cdots ,\kappa (n)\}$satisfies$G(t_{\kappa (1)})\ge G(t_{\kappa (2)})\ge \cdots \ge G(t_{\kappa (n)})$with$\kappa (l)\in \{1,2,\cdots ,n\}$.

(3) 

$X_{\kappa (m)}=\left\{t_{\kappa (l)}/l\le m\right\}$,$m\in \{1,2,\cdots ,n\}$and$X_{\kappa (0)}=\varphi$.

(4) 

$Y$is a$\lambda$-fuzzy measure on$P(T)$.

Choquet integral concerning$\lambda$-fuzzy measure$Y$is presented by:

$$(c){\displaystyle \int GdM={\displaystyle {\sum }_{l=1}^n\left(G(t_{\kappa (l)})\cdot [(Y(X_{\kappa (l)})-Y(X_{\kappa (l-1)})]\right)}}$$

(5)

The Choquet integral is a significant tool of information fusion in in MAGDM processes [40,41,45,59].

2.3. IVqROFSs and IVq-RDHFSs

Definition 5 [25].

Suppose that three conditions hold:

(1) 

$T$is a nonempty set,$q\ge 1$is a real number and$\forall t\in T$.

(2) 

For$0\le M^{t-}\le M^{t+}\le 1$,$0\le Z^{t-}\le Z^{t+}\le 1$and${(M^{t+})}^q+{(Z^{t+})}^q\le 1$.

(3) 

For$M^t=[M^{t-},M^{t+}]$and$Z^t=[Z^{t-},Z^{t+}]$.

An IVqROFS$\widetilde{\tilde{X_{\rho }}}$on$T$is structured:

$$\widetilde{\tilde{X_{\rho }}}=\left\{\begin{array}{c}\end{array}\left(t,\begin{array}{c}\end{array}{M}^t,Z^t\right)\left.\right|t\in T\right\}$$

(6)

where$Z_{}^t$and$M_{}^t$are, respectively, called the nonmembership and membership degree values of$\forall t\in T$to$\widetilde{\tilde{X_{\rho }}}$, and the ordered pair$(M^t,Z^t)$in$T$is called IVqROFN [60], which is simply denoted$(M,Z)$with the conditions$M=[M^{-},M^{+}]\subseteq [0,1]$,$Z=[Z^{-},Z^{+}]\subseteq [0,1]$.

IVqROFNs have some laws with respect to operations.

Definition 6 [61].

Supposing that${\mu }_k=(M_{{\mu }_k},Z_{{\mu }_k})$,$k=1,2$,$\mu =(M_{\mu },Z_{\mu })$are three IVqROFNs, then operation laws are presented:

(1) 

${\mu }_k\oplus {\mu }_l=\left(\left[\sqrt[q]{M_{{\mu }_k}^{-}{}^q+M_{{\mu }_l}^{-}{}^q-M_{{\mu }_k}^{-}{}^q\times M_{{\mu }_l}^{-}{}^q},\sqrt[q]{M_{{\mu }_k}^{+}{}^q+M_{{\mu }_l}^{+}{}^q-M_{{\mu }_k}^{+}{}^q\times M_{{\mu }_l}^{+}{}^q}\right],\left[Z_{{\mu }_k}^{-}\times Z_{{\mu }_l}^{-},Z_{{\mu }_k}^{+}\times Z_{{\mu }_l}^{+}\right]\right)$

(2) 

${\mu }_k\otimes {\mu }_l=\left(\left[M_{{\mu }_k}^{-}\times M_{{\mu }_l}^{-},M_{{\mu }_k}^{+}\times M_{{\mu }_l}^{+}\right],\left[\sqrt[q]{Z_{{\mu }_k}^{-}{}^q+Z_{{\mu }_l}^{-}{}^q-Z_{{\mu }_k}^{-}{}^q\times Z_{{\mu }_l}^{-}{}^q},\sqrt[q]{Z_{{\mu }_k}^{+}{}^q+Z_{{\mu }_l}^{+}{}^q-Z_{{\mu }_k}^{+}{}^q\times Z_{{\mu }_l}^{+}{}^q}\right]\right)$

(3) 

$m\mu =\left(\left[\sqrt[q]{-{\left(-M_{\mu }^{-}{}^q+1\right)}^m+1},\sqrt[q]{-{\left(-M_{\mu }^{+}{}^q+1\right)}^m+1}\right],\begin{array}{c}\end{array}\left[Z_{\mu }^{-}{}^m,Z_{\mu }^{+}{}^m\right]\right)$$m\in (0,+\infty )$

(4) 

${\mu }^m=\left(\left[M_{\mu }^{-}{}^m,M_{\mu }^{+}{}^m\right],\begin{array}{c}\end{array}\left[\sqrt[q]{-{\left(-Z_{\mu }^{-}{}^q+1\right)}^m+1},\sqrt[q]{-{\left(-Z_{\mu }^{+}{}^q+1\right)}^m+1}\right]\right)$, $m\in (0,+\infty )$

(5) 

${\mu }^c=\left(\left[Z_{{}^{\mu }}^{-},\begin{array}{c}\end{array}{Z}_{{}^{\mu }}^{+}\right],\left[M_{{}^{\mu }}^{-},\begin{array}{c}\end{array}{M}_{{}^{\mu }}^{+}\right]\right)$

(6) 

$\vee \left\{{\mu }_k,{\mu }_l\right\}=\left(\left[\vee \left\{M_{{}^{{\mu }_k}}^{-},M_{{}^{{\mu }_l}}^{-}\right\},\begin{array}{c}\end{array}\vee \left\{M_{{}^{{\mu }_k}}^{+},M_{{}^{{\mu }_l}}^{+}\right\}\right],\left\{\wedge \left\{Z_{{}^{{\mu }_k}}^{-},Z_{{}^{{\mu }_l}}^{-}\right\},\begin{array}{c}\end{array}\wedge \left\{Z_{{}^{{\mu }_k}}^{+},Z_{{}^{{\mu }_l}}^{+}\right\}\right\}\right)$

(7) 

$\wedge \left\{{\mu }_k,{\mu }_l\right\}=\left(\left[\wedge \left\{M_{{}^{{\mu }_k}}^{-},M_{{}^{{\mu }_l}}^{-}\right\},\begin{array}{c}\end{array}\wedge \left\{M_{{}^{{\mu }_k}}^{+},M_{{}^{{\mu }_l}}^{+}\right\}\right],\left\{\vee \left\{Z_{{}^{{\mu }_k}}^{-},Z_{{}^{{\mu }_l}}^{-}\right\},\begin{array}{c}\end{array}\vee \left\{Z_{{}^{{\mu }_k}}^{+},Z_{{}^{{\mu }_l}}^{+}\right\}\right\}\right)$

Theorem 7 [61].

From Definition 6, operational results of${\mu }_1\oplus {\mu }_2$,${\mu }_1\otimes {\mu }_2$,$m\mu$,${\mu }^m$,${\mu }^c$,${\mu }_1\vee {\mu }_2$and${\mu }_1\wedge {\mu }_2$are also IVqROFNs.

From the score and accuracy value with respect to IVqROFNs, an order relationship for them was presented.

Definition 8 [61].

Let${\mu }_1$and${\mu }_2$be IVqROFNs with${\mu }_k=\left([M_{{}^{{\mu }_k}}^{-},\begin{array}{c}\end{array}{M}_{{}^{{\mu }_k}}^{+}],\begin{array}{c}\end{array}[Z_{{}^{{\mu }_k}}^{-},\begin{array}{c}\end{array}{Z}_{{}^{{\mu }_k}}^{+}]\right)$, then the score value$v_s({\mu }_k)$and the accuracy value$v_h({\mu }_k)$have the form:

$$v_s({\mu }_k)=\left(M_{{}^{{\mu }_k}}^{+}{}^q+Z_{{}^{{\mu }_k}}^{+}{}^q-M_{{}^{{\mu }_k}}^{-}{}^q-Z_{{}^{{\mu }_k}}^{-}{}^q\right)/2$$

(7)

$$v_h({\mu }_k)=\left(M_{{}^{{\mu }_k}}^{+}{}^q+Z_{{}^{{\mu }_k}}^{+}{}^q+M_{{}^{{\mu }_k}}^{-}{}^q+Z_{{}^{{\mu }_k}}^{-}{}^q\right)/2$$

(8)

Consequently, the order relationship is presented as follows:

(1) $v_s({\mu }_1)<v_s({\mu }_2)\Rightarrow {\mu }_1<{\mu }_2$

(2) $v_s({\mu }_1)=v_s({\mu }_2)$, $v_h({\mu }_1)<v_h({\mu }_2)\Rightarrow {\mu }_1<{\mu }_2$

(3) $v_s({\mu }_1)=v_s({\mu }_2)$, $v_h({\mu }_1)=v_h({\mu }_2)\Rightarrow {\mu }_1={\mu }_2$

(4) $v_s({\mu }_1)=v_s({\mu }_2)$, $v_h({\mu }_1)>v_h({\mu }_2)\Rightarrow {\mu }_1>{\mu }_2$

Definition 9 [49].

Suppose that there exist the conditions:

(1) 

$T$,$T_1$ and$T_2$ are three nonempty sets,$q\ge 1$is a real number.

(2) 

For any$t\in T$,$t_1\in T_1$ and$t_2\in T_2$,

$$0\le M_{{}^{t_1}}^{t-}\le M_{{}^{t_1}}^{t+}\le 1, 0\le Z_{{}^{t_2}}^{t-}\le Z_{{}^{t_2}}^{t+}\le 1 and {\left(\underset{t_1\in T_1}{\max }\left\{M_{{}^{t_1}}^{t+}\right\}\right)}^q+{\left(\underset{t_2\in T_2}{\max }\left\{Z_{{}^{t_1}}^{t+}\right\}\right)}^q\le 1.$$

(3) 

For any$t\in T$, $M^t=\left\{[M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}]\left|t_1\in T_{t_1}\right.\right\}$and$Z^t=\left\{[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\left|t_2\in T_{t_2}\right.\right\}$.

An IVq-RDHFS$\widetilde{\tilde{X_{IVqD}}}$on$T$is characterized in the following symbol:

$$\widetilde{\tilde{X_{IVqD}}}=\left\{\begin{array}{c}\end{array}⟨t,\begin{array}{c}\end{array}{M}_{}^t,\begin{array}{c}\end{array}{Z}_{}^t⟩|t\in T\begin{array}{c}\end{array}\right\}$$

where$Z_{}^t$and$M_{}^t$are, respectively, called the nonmembership and membership degree values of$\forall t\in T$to$\widetilde{\tilde{X_{IVqD}}}$, and the ordered pair$\left\{M_{}^t,\begin{array}{c}\end{array}{Z}_{}^t\right\}$in$T$is called IVq-RDHFE [Z11].

3. GIVqROHFSs

The GIVqROHFSs, the key feature of which is a set of the membership degree with several possible IVqROFNs, is defined. Some basic operational laws with respect to GIVqROHFSs are studied.

Definition 10.

Let$t\in T=\{t_1,t_2,\cdots ,t_n\}$$(n<+\infty )$, $[M_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{M}_{{}^{\mu }}^{t+}]\subset [0,1]$, $[Z_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{\mu }}^{t+}]\subset [0,1]$ and${\left(M_{{}^{\mu }}^{t+}\right)}^q+{\left(Z_{{}^{\mu }}^{t+}\right)}^q\le 1$, an GIVqROHFS on$T$is presented by the symbol:

$$\widetilde{\tilde{X_{IVq}}}=\left\{\left(t,{\psi }_{\widetilde{\tilde{X_{IVq}}}}^t\right)/t\in T\right\}$$

(9)

where${\psi }_{\widetilde{\tilde{X_{IVq}}}}^t$consists of several IVqROFNs$\left\{\left.\left([M_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{M}_{{}^{\mu }}^{t+}],[Z_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{\mu }}^{t+}]\right)\right|\begin{array}{c}\end{array}\mu \in {\psi }_{\widetilde{\tilde{X_{IVq}}}}^t\right\}$ with condition${\left(M_{{}^{\mu }}^{t+}\right)}^q+{\left(Z_{{}^{\mu }}^{t+}\right)}^q\le 1$, which called an GIVqROHF element (GIVqROHFE), involving possible intervals of the MNMDs of$t\in T$to$\widetilde{\tilde{X_{IVq}}}$.

From Definition 10, there exist two considerations which need to be explained:

(1)

Provided that $\mu =([M_{\mu }^{-},M_{\mu }^{+}],[Z_{\mu }^{-},Z_{\mu }^{+}])\in {\psi }_{\widetilde{\tilde{X_{IVq}}}}^t$ satisfies the condition

$$(M_{\mu }^{+})+(Z_{\mu }^{+})\le 1 \mathrm{or} {(M_{\mu }^{+})}^2+{(Z_{\mu }^{+})}^2\le 1,$$

${\psi }_{\widetilde{\tilde{X_{IVq}}}}^t$, respectively, reduces to the IVIHFE. ${\psi }_{\widetilde{\tilde{X_{IVI}}}}^t=\left\{\left.\left([M_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{M}_{{}^{\mu }}^{t+}],[Z_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{\mu }}^{t+}]\right)\right|\begin{array}{c}\end{array}\mu \in {\psi }_{\widetilde{\tilde{X_{IVI}}}}^t\right\}$ with the condition $(M_{\mu }^{+})+(Z_{\mu }^{+})\le 1$ [37] or the IVPHFE. ${\psi }_{\widetilde{\tilde{X_{IVP}}}}^t=\left\{\left.\left([M_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{M}_{{}^{\mu }}^{t+}],[Z_{{}^{\mu }}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{\mu }}^{t+}]\right)\right|\begin{array}{c}\end{array}\mu \in {\psi }_{\widetilde{\tilde{X_{IVP}}}}^t\right\}$ with the condition ${(M_{\mu }^{+})}^2+{(Z_{\mu }^{+})}^2\le 1$ [33], that is, the GIVqROHFS is an extension of the IVIHFS and IVPHFS, therefore it is also a generation of the HFS, IVHFS and IHFS.

(2)

Let $\left\{\left\{[M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}]\left|t_1\in T_1\right.\right\},\begin{array}{c}\end{array}\left\{[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\left|t_2\in T_2\right.\right\}\right\}$ be an IVq-RDHFE, then one can obtain the GIVqROHFE $\left\{\left.\left([M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}],[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\right)\right|\begin{array}{c}\end{array}{t}_1\in T_1,t_2\in T_2\right\}$ which contains $T_1\times T_2$ pairs of intervals and does not make loss of information. On the contrary, when a GIVqROHFE $\left\{\left.\left([M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}],[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\right)\right|\begin{array}{c}\end{array}{t}_1\in T_1,t_2\in T_2\right\}$ is transformed into the IVq-RDHFE by the simple separation, due to the existence of the same membership degree interval and nonmembership degree interval in the interval pair set $\left\{\left.\left([M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}],[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\right)\right|\begin{array}{c}\end{array}{t}_1\in T_1,t_2\in T_{t_2}\right\}$, the following inequalities hold:

$$\left|\left\{[M_{{}^{t_1}}^{t-},\begin{array}{c}\end{array}{M}_{{}^{t_1}}^{t+}]\left|t_1\in T_1\right.\right\}\right|\le T_1,\left|\left\{[Z_{{}^{t_2}}^{t-},\begin{array}{c}\end{array}{Z}_{{}^{t_2}}^{t+}]\left|t_2\in T_2\right.\right\}\right|\le T_2$$

Therefore, it is inevitable to lose the useful information, moreover, the GIVqROHFS is also the extension of the IVq-RDHFS according to Definition 9 and Definition 10.

Definition 11.

Let${\psi }_k={\psi }_k(t)$and${\psi }_l={\psi }_l(t)$be two GIVqROHFEs with$m>0$, some operations among GIVqROHFEs are defined as follows:

$${\psi }_k\oplus {\psi }_l=\begin{array}{c}\end{array}\left\{\left(\left[\sqrt[q]{-\left(-M_{{\mu }_k}^{-}{}^q+1\right)\times \left(-M_{{\mu }_l}^{-}{}^q+1\right)+1},\sqrt[q]{-\left(-M_{{\mu }_k}^{+}{}^q+1\right)\times \left(-M_{{\mu }_l}^{+}{}^q+1\right)+1}\right],\left[Z_{{\mu }_k}^{-}\times Z_{{\mu }_l}^{-},Z_{{\mu }_k}^{+}\times Z_{{\mu }_l}^{+}\right]\right)/{\mu }_k\in {\psi }_k,{\mu }_l\in {\psi }_l\right\}$$

$${\psi }_k\otimes {\psi }_l=\begin{array}{c}\end{array}\left\{\left(\left[M_{{\mu }_k}^{-}\times M_{{\mu }_l}^{-},M_{{\mu }_k}^{+}\times M_{{\mu }_l}^{+}\right],\left[\sqrt[q]{-\left(-Z_{{\mu }_k}^{-}{}^q+1\right)\times \left(-Z_{{\mu }_l}^{-}{}^q+1\right)+1},\sqrt[q]{-\left(-Z_{{\mu }_k}^{+}{}^q+1\right)\times \left(-Z_{{\mu }_l}^{+}{}^q+1\right)+1}\right]\right)/{\mu }_k\in {\psi }_k,{\mu }_l\in {\psi }_l\right\}$$

$$m{\psi }_k=\left\{\left(\left[\sqrt[q]{-{\left(-M_{{\mu }_k}^{-}{}^q+1\right)}^m+1},\sqrt[q]{-{\left(-M_{{\mu }_k}^{+}{}^q+1\right)}^m+1}\right],\left[Z_{{\mu }_k}^{-}{}^m,Z_{{\mu }_k}^{+}{}^m\right]\right)/{\mu }_k\in {\psi }_k\right\},m\in (0,+\infty )$$

$${\psi }_k^m=\left\{{\mu }_k^m/{\mu }_k\in {\psi }_k\right\}=\left\{\left(\left[M_{{\mu }_k}^{-}{}^m,M_{{\mu }_k}^{+}{}^m\right],\left[\sqrt[q]{-{\left(-Z_{{\mu }_k}^{-}{}^q+1\right)}^m+1},\sqrt[q]{-{\left(-Z_{{\mu }_k}^{+}{}^q+1\right)}^m+1}\right]\right)/{\mu }_k\in {\psi }_k\right\},m\in (0,+\infty )$$

$${\psi }_k\cup {\psi }_l=\left\{\left(\left[\vee \left\{M_{{\mu }_k}^{-},M_{{\mu }_l}^{-}\right\},\vee \left\{M_{{\mu }_k}^{+},M_{{\mu }_l}^{+}\right\}\right],\left[\wedge \left\{Z_{{\mu }_k}^{-},Z_{{\mu }_l}^{-}\right\},\wedge \left\{Z_{{\mu }_k}^{+},Z_{{\mu }_l}^{+}\right\}\right]\right)/{\mu }_k\in {\psi }_k,{\mu }_l\in {\psi }_l\right\}$$

$${\psi }_k\cap {\psi }_l=\left\{\left(\left[\wedge \left\{M_{{\mu }_k}^{-},M_{{\mu }_l}^{-}\right\},\wedge \left\{M_{{\mu }_k}^{+},M_{{\mu }_l}^{+}\right\}\right],\left[\vee \left\{Z_{{\mu }_k}^{-},Z_{{\mu }_l}^{-}\right\},\vee \left\{Z_{{\mu }_k}^{+},Z_{{\mu }_l}^{+}\right\}\right]\right)/{\mu }_k\in {\psi }_k,{\mu }_l\in {\psi }_l\right\}$$

$${\psi }_k{}^c=\left\{\left(\left[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}\right],\left[M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}\right]\right)/{\mu }_k\in {\psi }_k\right\}$$

Theorem 12.

If${\psi }_k$and${\psi }_l$are two GIVqROHFEs and$m>0$, then${\psi }_k\oplus {\psi }_l$,${\psi }_k{}^m$,$m{\psi }_k$and${\psi }_k\otimes {\psi }_k$are GIVqROHFEs.

Proof of Theorem 12.

Let ${\psi }_k=\left\{\left([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}]\right)/{\mu }_k\in {\psi }_k)\right\}$, by Definition 10 and the definition of GIVqROFNs, we obtain $[M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}],[M_{{\mu }_l}^{-},M_{{\mu }_l}^{+}],[Z_{{\mu }_l}^{-},Z_{{\mu }_l}^{+}]\subset [0,1]$, $1-M_{{\mu }_k}^{+}{}^q\ge Z_{{\mu }_k}^{+}{}^q$ and $1-M_{{\mu }_l}^{+}{}^q\ge Z_{{\mu }_l}^{+}{}^q$.

(1) ${\psi }_k\oplus {\psi }_l$

$$0\le \sqrt[q]{-\left(-M_{{\mu }_k}^{-}{}^q+1\right)\times \left(-M_{{\mu }_l}^{-}{}^q+1\right)+1}\le \sqrt[q]{-\left(-M_{{\mu }_k}^{+}{}^q+1\right)\times \left(-M_{{\mu }_l}^{+}{}^q+1\right)+1}\le 1$$

$$0\le Z_{{\mu }_k}^{-}\times Z_{{\mu }_l}^{-}\le Z_{{\mu }_k}^{+}\times Z_{{\mu }_l}^{+}\le 1$$

$$-\left(-M_{{\mu }_k}^{+}{}^q+1\right)\times \left(-M_{{\mu }_l}^{+}{}^q+1\right)+1+Z_{{\mu }_k}^{+}{}^q\times Z_{{\mu }_l}^{+}{}^q\le -Z_{{\mu }_k}^{+}{}^q\times Z_{{\mu }_l}^{+}{}^q+1+Z_{{\mu }_k}^{+}{}^q\times Z_{{\mu }_l}^{+}{}^q=1$$

(2) ${\psi }_k\otimes {\psi }_l$

$$0\le M_{{\mu }_k}^{-}\times M_{{\mu }_l}^{-}\le M_{{\mu }_k}^{+}\times M_{{\mu }_l}^{+}\le 1$$

$$0\le \sqrt[q]{1-\left(1-Z_{{\mu }_k}^{-}{}^q\right)\times \left(1-Z_{{\mu }_l}^{-}{}^q\right)}\le \sqrt[q]{1-\left(1-Z_{{\mu }_k}^{+}{}^q\right)\times \left(1-Z_{{\mu }_l}^{+}{}^q\right)}\le 1$$

$$M_{{\mu }_k}^{+}{}^q\times M_{{\mu }_l}^{+}{}^q+1-\left(1-Z_{{\mu }_k}^{+}{}^q\right)\times \left(1-Z_{{\mu }_l}^{+}{}^q\right)\le M_{{\mu }_k}^{+}{}^q\times M_{{\mu }_l}^{+}{}^q+1-M_{{\mu }_k}^{+}{}^q\times M_{{\mu }_l}^{+}{}^q=1$$

(3) $m{\psi }_k$ $(m>0)$

$$0\le \sqrt[q]{-{\left(-M_{{\mu }_k}^{-}{}^q+1\right)}^m+1}\le \begin{array}{c}\end{array}\sqrt[q]{-{\left(-M_{{\mu }_k}^{+}{}^q+1\right)}^m+1}\begin{array}{c}\le 1\end{array},0\le Z_{{\mu }_k}^{-}{}^m\le Z_{{\mu }_k}^{+}{}^m\le 1$$

$$-{\left(-M_{{\mu }_k}^{+}{}^q+1\right)}^m+1+Z_{{\mu }_k}^{+}{}^{mq}\le -Z_{{\mu }_k}^{+}{{}^q}^m+1+Z_{{\mu }_k}^{+}{{}^m}^q=1$$

(4) ${\psi }_k^m$ $(m>0)$

$$0\le M_{{\mu }_k}^{-}{}^m\le M_{{\mu }_k}^{+}{}^m\le 1,0\le \sqrt[q]{-{\left(-Z_{{\mu }_k}^{-}{}^q+1\right)}^m+1}\le \begin{array}{c}\end{array}\sqrt[q]{-{\left(-Z_{{\mu }_k}^{+}{}^q+1\right)}^m+1}\begin{array}{c}\le 1\end{array}$$

$$M_{{\mu }_k}^{+}{}^{mq}-{\left(-Z_{{\mu }_k}^{+}{}^q+1\right)}^m+1\le M_{{\mu }_k}^{+}{{}^m}^q-M_{{\mu }_k}^{+}{{}^q}^m+1=1$$

Therefore, ${\psi }_k\oplus {\psi }_l$, ${\psi }_k{}^m$, $m{\psi }_k$ and ${\psi }_k\otimes {\psi }_l$ are GIVqROHFEs. □

Theorem 13.

If${\psi }_k$and${\psi }_l$are two GIVqROHFEs and$m>0$, then GIVqROHFEs have properties.

$${\psi }_k\oplus {\psi }_l={\psi }_l\oplus {\psi }_k,$$

$$(ml){\psi }_k=m(l{\psi }_k)$$

$$m{\psi }_k\oplus m{\psi }_l=m({\psi }_k\oplus {\psi }_l)$$

$${\psi }_l\otimes {\psi }_k={\psi }_k\otimes {\psi }_l$$

$${\psi }_l\otimes {\psi }_k={\psi }_k\otimes {\psi }_l$$

$${\psi }_k{}^{ml}={\left[{({\psi }_k)}^m\right]}^l$$

$${({\psi }_k)}^{m+l}={\psi }_k{}^m\otimes {\psi }_k{}^l$$

$$m{\psi }_k\oplus l{\psi }_k=(m+l){\psi }_k$$

$${\psi }_k{}^c\otimes {\psi }_l{}^c={\left[({\psi }_k)\oplus ({\psi }_l)\right]}^c$$

$${\psi }_k{}^c\oplus {\psi }_l{}^c={\left[({\psi }_k)\otimes ({\psi }_l)\right]}^c$$

$${\left[({\psi }_k)\cap ({\psi }_l)\right]}^c={\psi }_k{}^c\cup {\psi }_l{}^c$$

$${\left[({\psi }_k)\cup ({\psi }_l)\right]}^c={\psi }_k{}^c\cap {\psi }_l{}^c$$

$${({\psi }_k{}^c)}^m={(m{\psi }_k)}^c$$

$$m({\psi }_k{}^c)={({\psi }_k{}^m)}^c$$

For the proof of Theorem 13, refer to the Appendix A.

In order to rank the GIVqROHFEs, the comparison rules are presented as follows:

Definition 14.

Suppose that${\psi }_k=\left\{\left([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}]\right)/{\mu }_k\in {\psi }_k\right\}$$(k=1,2)$are GIVqROHFEs. The score function of${\psi }_k$is defined:

$$V_S({\psi }_k)=\left({\displaystyle {\sum }_{{\mu }_k\in {\psi }_k}{v}_s({\mu }_k)}\right)/\#{\psi }_k$$

(10)

where the cardinal number of${\psi }_k$is denoted as the symbol$\#{\psi }_k$.

The accuracy of${\psi }_k$is an equation:

$$V_H({\psi }_k)=\left({\displaystyle {\sum }_{{\mu }_k\in {\psi }_k}{v}_h({\mu }_k)}\right)/\#{\psi }_k$$

(11)

${\psi }_1$ and ${\psi }_2$ can be compared by the following order relation:

(1) $V_H({\psi }_1)<V_H({\psi }_2)\Rightarrow {\psi }_1<{\psi }_2$

(2) $V_S({\psi }_1)=V_S({\psi }_2)$, $V_H({\psi }_1)<V_H({\psi }_2)\Rightarrow {\psi }_1<{\psi }_2$

(3) $V_S({\psi }_1)=V_S({\psi }_2)$, $V_H({\psi }_1)=V_H({\psi }_2)\Rightarrow {\psi }_1={\psi }_2$

(4) $V_S({\psi }_1)=V_S({\psi }_2)$, $V_H({\psi }_1)>V_H({\psi }_2)\Rightarrow {\psi }_1>{\psi }_2$

According to the above Definition 14, Theorem 15 can be proven.

Theorem 15.

If$\psi =\left\{([M_{\mu }^{-},M_{\mu }^{+}],[Z_{\mu }^{-},Z_{\mu }^{+}])/\mu \in \psi \right\}$is a GIVqROHFE and$m>0$, then the following inequalities hold:

(1)$\psi \ge {\psi }^m,\begin{array}{c}m\in (1,+\infty \end{array})$; (2)$\psi \le {\psi }^m,m\in (0,1]$; (3)$\psi \le m\psi ,\begin{array}{c}\begin{array}{c}m\in (1,+\infty \end{array})\end{array}$; (4)$\psi \ge m\psi ,m\in (0,1]$

Proof of Theorem 15.

Since $\psi =\left\{\mu \left.\right|\mu \in \psi \right\}=\left\{([M_{\mu }^{-},M_{\mu }^{+}],[Z_{\mu }^{-},Z_{\mu }^{+}])/\mu \in \psi \right\}$ is a GIVqROFE, we have:

$$M_{\mu }^{-},M_{\mu }^{+},Z_{\mu }^{-},Z_{\mu }^{+}\in [0,1],{(M_{\mu }^{+})}^q+{(Z_{\mu }^{+})}^q\in [0,1]$$

$${\psi }^m=\left\{{\mu }^m/\mu \in \psi \right\}=\left\{\left(\left[{(M_{\mu }^{-})}^m,{(M_{\mu }^{+})}^m\right],\left[\sqrt[q]{-{\left(-Z_{\mu }^{-}{}^q+1\right)}^m+1},\sqrt[q]{-{\left(-Z_{\mu }^{+}{}^q+1\right)}^m+1}\right]\right)/\mu \in \psi \right\}$$

When $\begin{array}{c}m>1\end{array}$, $M_{\mu }^{-}{}^q\ge M_{\mu }^{-}{{}^m}^q$, $M_{\mu }^{+}{}^q\ge M_{\mu }^{+}{{}^m}^q$, ${(Z_{\mu }^{-})}^q\le -{\left[-{(Z_{\mu }^{-})}^q+1\right]}^m+1$ and ${(Z_{\mu }^{+})}^q\le -{\left[-{(Z_{\mu }^{+})}^q+1\right]}^m+1$. Thus, for any $\mu \in \psi$, $\begin{array}{c}m>1\end{array}$

$$\begin{array}{l}{v}_s(\mu )=\left(M_{\mu }^{-}{}^q+M_{\mu }^{+}{}^q-Z_{\mu }^{-}{}^q-Z_{\mu }^{+}{}^q\right)/2\\ \ge \frac{1}{2}\left(M_{\mu }^{-}{{}^m}^q+M_{\mu }^{+}{{}^m}^q-\left(1-{\left(1-Z_{\mu }^{-}{}^q\right)}^m\right)-\left(1-{\left(1-Z_{\mu }^{+}{}^q\right)}^m\right)\right)=v_s({\mu }^m)\end{array}$$

By the equation $\#\psi =\#{\psi }^m$, $V_S(\psi )=\frac{{\displaystyle {\sum }_{\mu \in \psi }{v}_s(\mu )}}{\#\psi }$ and $V_S({\psi }^m)=\frac{{\displaystyle {\sum }_{\mu \in \psi }{v}_s({\mu }^m)}}{\#{\psi }^m}$, we have $V_S(\psi )\ge V_S({\psi }^m)$. According to Definition 14, if $V_S(\psi )>V_S({\psi }^m)$ $(\begin{array}{c}m>1\end{array})$, then $\psi >{\psi }^m$.

If $V_S(\psi )=\left({\displaystyle {\sum }_{\mu \in \psi }{v}_s(\mu )}\right)/\#\psi =\left({\displaystyle {\sum }_{\mu \in \psi }{v}_s({\mu }^m)}\right)/\#{\psi }^m=V_S({\psi }^m)$, then we obtain the following results:

For any $\mu \in \psi$, $v_s(\mu )=\left(M_{\mu }^{-}{}^q+M_{\mu }^{+}{}^q-Z_{\mu }^{-}{}^q-Z_{\mu }^{+}{}^q\right)/2=\left(M_{\mu }^{-}{{}^m}^q+M_{\mu }^{+}{{}^m}^q+{\left(1-Z_{\mu }^{-}{}^q\right)}^m-2+{\left(1-Z_{\mu }^{+}{}^q\right)}^m\right)/2=v_s({\mu }^m)$

From the conditions $M_{\mu }^{-}{}^q\ge M_{\mu }^{-}{{}^m}^q$, $M_{\mu }^{+}{}^q\ge M_{\mu }^{+}{{}^m}^q$, $Z_{\mu }^{-}{}^q\le 1-{\left(1-Z_{\mu }^{-}{}^q\right)}^m$ and $Z_{\mu }^{+}{}^q\le 1-{\left(1-Z_{\mu }^{+}{}^q\right)}^m$, we have:

$$\begin{gathered} 0\le M_{\mu }^{-}{}^q+M_{\mu }^{+}{}^q-M_{\mu }^{-}{{}^m}^q-M_{\mu }^{+}{{}^m}^q=Z_{\mu }^{-}{}^q+Z_{\mu }^{+}{}^q+{\left(1-Z_{\mu }^{-}{}^q\right)}^m-2+{\left(1-Z_{\mu }^{+}{}^q\right)}^m\le 0, \\ {M}_{\mu }^{-}{}^q+M_{\mu }^{+}{}^q=M_{\mu }^{-}{{}^m}^q+M_{\mu }^{+}{{}^m}^q,Z_{\mu }^{-}{}^q+{\left(1-Z_{\mu }^{-}{}^q\right)}^m+{\left(1-Z_{\mu }^{+}{}^q\right)}^m=2-Z_{\mu }^{+}{}^q \end{gathered}$$

Therefore, for any $\mu \in \psi$,

$$v_h(\mu )=\frac{W_{\mu }^{-}{}^q+Z_{\mu }^{-}{}^q+W_{\mu }^{+}{}^q+Z_{\mu }^{+}{}^q}{2}=\left(M_{\mu }^{-}{{}^m}^q+M_{\mu }^{+}{{}^m}^q+2-{\left(1-Z_{\mu }^{-}{}^q\right)}^m-{\left(1-Z_{\mu }^{+}{}^q\right)}^m\right)/2=v_h({\mu }^m)$$

Consequently, $V_H(\psi )=\left({\displaystyle {\sum }_{\mu \in \psi }{v}_h(\mu )}\right)/\#\psi =\frac{{\displaystyle {\sum }_{\mu \in \psi }{v}_h({\mu }^m)}}{\#{\psi }^m}=V_H({\psi }^m)$, i.e., $\psi ={\psi }^m\begin{array}{c},m\in (1,+\infty \end{array})$. □

From the order relationship of GIVqROHFEs, (1) $\psi >{\psi }^m,(\begin{array}{c}m>1\end{array})$ is proven. By the similar inference, the other inequalities (2), (3) and (4) can be proven, which is omitted in this paper.

4. Aggregation Operators for the GIVqROHF Information

The GIVqROHFCA and GIVqROHFCGM Operators

Definition 16.

Let${\psi }_k=\left\{([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}])\left.\right|{\mu }_k\in {\psi }_k\right\}$be a GIVqROHFE with $k\in \left\{1,2,\cdots ,n\right\}$, $Y$ is a fuzzy measure on the power of $\{{\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\}$, and a permutation $\{\delta (1),\cdots ,\delta (k),\cdots ,\delta (n)\}$ of $\{1,\cdots ,k,\cdots ,n\}$ satisfies:

$${\psi }_{\delta (1)}\ge {\psi }_{\delta (2)}\ge \cdots \ge {\psi }_{\delta (n)},\lambda >0,X_{\delta (0)}=\varphi ,X_{\delta (i)}=\{{\psi }_{\delta (j)}\left.\right|j\le i\}$$

(1) 

A GIVqROHFCA operator is modeled.

$$GIVqROHFC{A}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)={\left({{\displaystyle \oplus }}_{k=1}^n{\psi }_{\delta (k)}^{\lambda }\left[Y(X_{\delta (k)})-Y(X_{\delta (k-1)})\right]\right)}^{1/\lambda }$$

(12)

(2) 

A GIVqROHFCGM operator is a kind of following form.

$$GIVqROHFCG{M}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)=\frac{1}{\lambda }\left({{\displaystyle \otimes }}_{k=1}^n{\left(\lambda {\psi }_{\delta (k)}\right)}^{\left(Y(X_{\delta (k)})-Y(X_{\delta (k-1)})\right)}\right)$$

(13)

From Definition 16, one can obtain a GIVqROHFS on the finite set $\left\{1,2,\cdots ,n\right\}$ which may present $n$ attributes or $n$ experts in multiple-attribute group decision making. Moreover, the GIVqROHF information, which needs generally to be considered in many practical problems, is characterized by this GIVqROHFS. On the basis of the above Definition 16, we discuss several cases of the GIVqROHFCA and GIVqROHFCGM operator:

(1)

If $\lambda =1$, the GIVqROHFCA and GIVqROHFCGM operator, respectively, reduce to the basic GIVqROHFCA operator abbreviated as IVqROHFCA and the basic GIVqROHFCGM operator with the symbol IVqROHFCGM.

$$IVqROHFCA({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)=\left({{\displaystyle \oplus }}_{k=1}^n({\psi }_{\delta (k)}^{}Y(X_{\delta (k)})-{\psi }_{\delta (k)}^{}Y(X_{\delta (k-1)}))\right)$$

(14)

$$IVqROHFCGM({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)=\left({{\displaystyle \otimes }}_{k=1}^n{({\psi }_{\delta (k)})}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}\right)$$

(15)

(2)

If $\forall k\in \{1,2,\cdots ,n\}$ $Y(\{{\psi }_{\delta (k)}\})=Y(X_{\delta (k)})-Y(X_{\delta (k-1)})$, the GIVqROHFCA operator is called the generalized IVqROHF weighted averaging (GIVqROHFWA) operator.

(3)

For a given $k$, $Y(X_{\delta (k)})-Y(X_{\delta (k-1)})$ is an invariant constant $w_i$ for any permutation of $\{1,2,\cdots ,n\}$, the GIVqROHFCA operator degenerates the generalized IVqROHF ordered weighted averaging (GIVqROHFOWA) operator. Especially, when $Y(X_{\delta (k)})-Y(X_{\delta (k-1)})=1/n$ for any $k$, a GIVqROHFCA operator is a generalized IVqROHF mathematical averaging (GIVqROHFMA) operator.

Theorem 17.

Suppose that${\psi }_k=\left\{\left([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}]\right)/{\mu }_k\in {\psi }_k\right\}$is a GIVqROHFE with$k\in \left\{1,2,\cdots ,n\right\}$, then their aggregated values with respect to the GIVqROHFCA operator and the GIVqROHFCGM operator are both GIVqROHFEs which have the form:

$$\begin{array}{l}GIVqROHFC{A}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)=\sqrt[\lambda ]{{{\displaystyle \oplus }}_{k=1}^n\left[{\psi }_{\delta (k)}^{\lambda }Y(X_{\delta (k)})-{\psi }_{\delta (k)}^{\lambda }Y(X_{\delta (k-1)})\right]}\\ =\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left(-M_{{\mu }_{\delta (k)}}^{-}{}^{q\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}},\\ \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left(-M_{{\mu }_{\delta (k)}}^{+}{}^{q\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{i=1}^n{\left[-{\left(-Z_{{\mu }_{\delta (k)}}^{-}{}^q+1\right)}^{\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1},\\ \sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{i=1}^n{\left[-{\left(-Z_{{\mu }_{\delta (k)}}^{-}{}^q+1\right)}^{\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k\in \left\{1,2,\cdots ,n\right\}\end{array}\right\}\end{array}$$

(16)

$$\begin{array}{l}GIVqROHFCG{M}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)=\frac{1}{\lambda }\left({{\displaystyle \otimes }}_{k=1}^n{\left[\lambda {\psi }_{\delta (k)}\right]}^{(M(T_{\delta (k)})-M(T_{\delta (k-1)}))}\right)\\ =\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(-M_{{\mu }_{\delta (k)}}^{-}{}^q+1\right)}^{\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1},\\ \sqrt[q]{1-\sqrt[\lambda ]{1-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(-M_{{\mu }_{\delta (k)}}^{+}{}^q+1\right)}^{\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}}}\end{array}\right]\\ \left[\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left(-Z_{{\mu }_{\delta (k)}}^{-}{}^{q\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}},\\ \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left(-Z_{{\mu }_{\delta (k)}}^{+}{}^{q\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k\in \left\{1,2,\cdots ,n\right\}\end{array}\right\}\end{array}$$

(17)

For the proof of Theorem 17, refer to the Appendix A.

The GIVqROHFCA operator involves some properties such as idempotency, symmetry and boundedness.

Proposition 1 (Idempotency).

If$\psi =\left\{\left([M_{\mu }^{-},M_{\mu }^{+}],[Z_{\mu }^{-},Z_{\mu }^{+}]\right)\left.\right|\mu \in \psi \right\}$is a GIVqROHFE then

$$GIVqROHFC{A}_{\lambda }(\psi ,\psi ,\cdots ,\psi )={\left({{\displaystyle \oplus }}_{k=1}^n\left[Y(X_{\delta (k)})-Y(X_{\delta (k-1)})\right]{\psi }_{}^{\lambda }\right)}^{1/\lambda }=\psi$$

(18)

Proof of Proposition 1.

According to the operational properties of the GIVqROHFEs, $Y(X_{\delta (0)})=\varphi$ and $M(\{{\psi }_1,{\psi }_2,\cdots ,{\psi }_n\})=1$,

$$\begin{gathered} GIVqROHFC{A}_{\lambda }(\psi ,\psi ,\cdots ,\psi )={\left({{\displaystyle \oplus }}_{k=1}^n{\psi }_{}^{\lambda }(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))\right)}^{1/\lambda } \\ =\sqrt[\lambda ]{{\psi }_{}^{\lambda }{\displaystyle {\sum }_{i=1}^n(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}=\sqrt[\lambda ]{{\psi }_{}^{\lambda }}=\psi \end{gathered}$$

 □

Proposition 2 (Symmetry).

If${\psi }_k=\left\{([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}])\left.\right|{\mu }_k\in {\psi }_k\right\}$is a GIVqROHFE with$k\in \left\{1,2,\cdots ,n\right\}$, and a permutation$\{\delta (1),\delta (2),\cdots ,\delta (n)\}$of this sequence is provided, then

$$GIVqROHFC{A}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)=GIVqROHFC{A}_{\lambda }({\psi }_{\delta (1)},{\psi }_{\delta (2)},\cdots ,{\psi }_{\delta (n)})$$

(19)

Proof of Proposition 2.

Since the order of ${\psi }_1,\cdots ,{\psi }_k,\cdots {\psi }_n$ is invariant, supposing that ${\psi }_{\delta (1)}\ge \cdots \ge {\psi }_{\delta (k)}\ge \cdots \ge {\psi }_{\delta (n)}$. Therefore,

$$\begin{array}{l}GIVqROHFC{A}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)=\sqrt[\lambda ]{{{\displaystyle \oplus }}_{k=1}^n(Y(X_{\delta (k)}){\psi }_{\sigma (k)}^{\lambda }-Y(X_{\delta (k-1)}){\psi }_{\sigma (k)}^{\lambda })}\\ =GIVqROHFC{A}_{\lambda }({\psi }_{\delta (1)},{\psi }_{\delta (2)},\cdots ,{\psi }_{\delta (n)})\end{array}$$

 □

Proposition 3 (Boundedness).

If$n$ GIVqROHFEs${\psi }_k=\left\{\left([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}]\right)/{\mu }_k\in {\psi }_k\right\}$$k=1,2,\cdots ,n$satisfy${\psi }_{\delta (1)}\ge \cdots \ge {\psi }_{\delta (k)}\ge \cdots \ge {\psi }_{\delta (n)}$with any permutation$\{\delta (1),\delta (2),\cdots ,\delta (n)\}$concerning$\{1,2,\cdots ,n\}$, and

$$\begin{array}{l}{\psi }_{\max }=\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(\underset{j}{\max }\left\{M_{{\mu }_{\delta (j)}}^{-}\right\}\right)}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}},\\ \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(\underset{j}{\max }\left\{M_{{\mu }_{\delta (j)}}^{+}\right\}\right)}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(\underset{j}{\min }\{Z_{{\mu }_{\delta (j)}}^{-}\})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1},\\ \sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(\underset{j}{\min }\{Z_{{\mu }_{\delta (j)}}^{-}\})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k=1,2,\cdots ,n\end{array}\right\}\\ {\psi }_{\min }=\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(\underset{j}{\min }\left\{M_{{\mu }_{\delta (j)}}^{-}\right\}\right)}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}},\\ \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{\left(\underset{j}{\min }\left\{M_{{\mu }_{\delta (j)}}^{+}\right\}\right)}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(\underset{j}{\max }\{Z_{{\mu }_{\delta (j)}}^{-}\})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1},\\ \sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(\underset{j}{\max }\{Z_{{\mu }_{\delta (j)}}^{-}\})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k=1,2,\cdots ,n\end{array}\right\}\end{array}$$

(20)

Then ${\psi }_{\min }\le GIVqROHFC{A}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)\le {\psi }_{\max }$. □

Proof of Proposition 3.

By the method of mathematical analysis, when $x\in (0,1)$,

$$d\left({(1-x^{q\lambda })}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}\right)/dx=\begin{array}{c}\begin{array}{l}\left[{(1-x^{q\lambda })}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}\right]\times \left(-q\lambda x^{q\lambda -1}\right)\\ \times \left[Y(X_{\delta (k)})-Y(X_{\delta (k-1)})\right]<0\end{array}\end{array}$$

$$\begin{array}{l}d\left({(1-{(1-x^q)}^{\lambda })}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}\right)/dx\\ =\left({(1-{(1-x^q)}^{\lambda })}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}\right)\times (-\lambda {(1-x^q)}^{\lambda -1})\times (-qx)\times (Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))>0\end{array}$$

In other words, the function ${(1-x^{q\lambda })}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}$ is decreasing on $x$, and ${\left[1-{(1-x^q)}^{\lambda }\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}$ is increasing on $x$.

Thus,

$$\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{(\underset{j}{\max }\{M_{{\mu }_{\delta (j)}}^{-}\})}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\\ \ge \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{(M_{{\mu }_{\delta (k)}}^{-})}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}$$

$$\begin{array}{l}\sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{(\underset{j}{\max }\{M_{{\mu }_{\delta (j)}}^{+}\})}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\\ \ge \sqrt[\lambda q]{-{\displaystyle {\prod }_{k=1}^n{\left[-{(M_{{\mu }_{\delta (k)}}^{+})}^{q\lambda }+1\right]}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\end{array}$$

$$\begin{array}{l}\sqrt[q]{1-\sqrt[\lambda ]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-{\left[1-{(\underset{j}{\min }\{Z_{{\mu }_{\delta (j)}}^{-}\})}^q\right]}^{\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}}}\\ \begin{array}{cc}& \end{array}\le \sqrt[q]{1-\sqrt[\lambda ]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-{\left[1-{(Z_{{\mu }_{\delta (k)}}^{-})}^q\right]}^{\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}}}\end{array}$$

$$\begin{array}{l}\sqrt[q]{1-\sqrt[\lambda ]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-{\left[1-{(\underset{j}{\min }\{Z_{{\mu }_{\delta (j)}}^{+}\})}^q\right]}^{\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}}}\\ \begin{array}{cc}& \end{array}\le \sqrt[q]{1-\sqrt[\lambda ]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-{\left[1-{(Z_{{\mu }_{\delta (k)}}^{+})}^q\right]}^{\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}}}\end{array}$$

On the basis of the inference method of Theorem 13, we obtain:

$${\psi }_{\min }\le GIVqROHFC{A}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)\le {\psi }_{\max }$$

 □

Theorem 18.

If${\psi }_k=\left\{\left([M_{{\mu }_k}^{-},M_{{\mu }_k}^{+}],[Z_{{\mu }_k}^{-},Z_{{\mu }_k}^{+}]\right)/{\mu }_k\in {\psi }_k\right\}$$k\in \{1,2,\cdots ,n\}$are$n$ GIVqROHFEs and$\lambda >0$, then the GIVqROHFCA operator$GIVqROHFC{A}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)$is increasing with respect to$\lambda$, and the GIVqROHFGM operator$GIVqROHFCG{M}_{\lambda }({\psi }_1,{\psi }_2,\cdots ,{\psi }_n)$is decreasing with respect to$\lambda$.

Proof of Theorem 18.

By Theorem 3.8 in [60], we obtain that the following formulas are increasing with respect to $\lambda$:

$$\begin{gathered} \sqrt[\lambda q]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-M_{{\mu }_{\delta (k)}}^{-}{}^{q\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}} \sqrt[\lambda q]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-M_{{\mu }_{\delta (k)}}^{+}{}^{q\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}} \\ \sqrt[\lambda q]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-Z_{{\mu }_{\delta (k)}}^{-}{}^{q\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}} \sqrt[\lambda q]{1-{\displaystyle {\prod }_{k=1}^n{\left(1-Z_{{\mu }_{\delta (k)}}^{+}{}^{q\lambda }\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}} \end{gathered}$$

Moreover, the following formulas are decreasing with respect to $\lambda$:

$$\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(M_{{\mu }_{\delta (k)}}^{-})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}$$

$$\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(M_{{\mu }_{\delta (k)}}^{+})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}$$

$$\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(Z_{{\mu }_{\delta (k)}}^{-})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}$$

$$\sqrt[q]{-\sqrt[\lambda ]{-{\displaystyle {\prod }_{k=1}^n{\left(-{\left[-{(Z_{{\mu }_{\delta (k)}}^{+})}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1}$$

Thus, according to Definition 14,

$$\begin{array}{l}{V}_S\left(GIVqROHFC{A}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)\\ =\frac{\#{\left(GIVqROHFC{A}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)}^{-1}}{2}{\displaystyle \sum _{\begin{array}{l}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k=1,\cdots ,n\end{array}}\left[\begin{array}{l}\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-M_{{\mu }_{\delta (k)}}^{-}{{}^q}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}}+1}\\ +\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-Z_{{\mu }_{\delta (k)}}^{-}{{}^q}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}-1\end{array}\right]}\\ +\frac{\#{\left(GIVqROHFC{A}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)}^{-1}}{2}{\displaystyle \sum _{\begin{array}{l}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k=1,\cdots ,n\end{array}}\left[\begin{array}{l}\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-M_{{\mu }_{\delta (k)}}^{+}{{}^q}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\\ +\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-Z_{{\mu }_{\delta (k)}}^{+}{{}^q}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}-1\end{array}\right]}\end{array}$$

The above equation is increasing with respect to $\lambda$, which illustrates that the GIVqROHFCA operator is increasing concerning $\lambda$.

Furthermore, $V_S\left(GIVqROHFCG{M}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)$

$$\begin{array}{l}=\frac{\#{\left(GIVqROHFCG{M}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)}^{-1}}{2}{\displaystyle \sum _{\begin{array}{l}{\mu }_{\delta (k)}\in {\psi }_{\delta (k)}\\ k=1,\cdots ,n\end{array}}\left[\begin{array}{l}-\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-{\left[-{\left(M_{{\mu }_{\delta (k)}}^{-}\right)}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\\ -\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-{\left[-{\left(Z_{{\mu }_{\delta (k)}}^{-}\right)}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1\end{array}\right]}\\ +\frac{\#{\left(GIVqROHFCG{M}_{\lambda }\left({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n\right)\right)}^{-1}}{2}{\displaystyle \sum _{{\mu }_{\delta (k)}\in {\psi }_{\delta (k)},k=1,\cdots ,n}\left[\begin{array}{l}-\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-{\left[-{\left(M_{{\mu }_{\delta (k)}}^{+}\right)}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}\\ -\sqrt[\lambda ]{-{\displaystyle \prod _{k=1}^n{\left(-{\left[-{\left(Z_{{\mu }_{\delta (k)}}^{+}\right)}^q+1\right]}^{\lambda }+1\right)}^{(Y(X_{\delta (k)})-Y(X_{\delta (k-1)}))}+1}}+1\end{array}\right]}\end{array}$$

Therefore, it is decreasing on $\lambda$, which demonstrates that the GIVqROHFCGM operator is decreasing concerning $\lambda$. □

Theorem 19.

If${\psi }_k$$k\in \{1,2,\cdots ,n\}$are$n$ GIVqROHFEs and$\lambda >0$, then the GIVqROHFCA, IVqROHFCA, GIVqROHFGM and GIVqROHFGM operators have order relations.

$$\left(1\right) IVqROHFCGM({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)\le GIVqROHFC{A}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)$$

(21)

$$\left(2\right) GIVqROHFCG{M}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)\le GIVqROHFC{A}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)$$

(22)

$$\left(3\right) GIVqROHFCG{M}_{\lambda }({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)\le IVqROHFCA({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)$$

(23)

$$\left(4\right) IVqROHFCGM({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)\le IVqROHFCA({\psi }_1,\cdots ,{\psi }_k,\cdots ,{\psi }_n)$$

(24)

For the proof of Theorem 19, refer to the Appendix A.

5. A New Decision Method Based on GIVqROHFCA and GIVqROHFCGM Operators

In some decision problems with high uncertainty, due to the lack of experience, ability and knowledge, decision experts may hesitate to present their own evaluation regarding each alternative, and there does not exist sufficient information for the single-valued membership and nonmembership degrees; therefore, hesitant fuzzy evaluation strategy related to the interval-valued membership and nonmembership degrees should be a good choice. In addition, the experts are not independent, but interactive in decision making, consequently, it is important to reasonably model these interrelationships in efficient decision making. As a result, an approach is presented by using the proposed GIVqROHFCA and GIVqROHFCGM operators, which can handle some MAGDM problems under the GIVqROHF environment. In the whole framework model of this approach: (1) for each alternative, the hesitant evaluation of decision expert with respect to all attributes is defined as a GIVqROHF set on attribute set which can present the GIVqROHF information; (2) for each attribute, the hesitant assessment from all experts is modeled as a GIVqROHF set on expert set which may indicate the GIVqROHF uncertainty; (3) the basic operation unit of the GIVqROHFCA and GIVqROHFCGM operators is the GIVqROHFE, which is the basic composition unit of the aforementioned two types of GIVqROHFSs. For convenience, some symbols are denoted in Table 1.

Table 1. Illustration of a MAGDM problem with the GIVqROHF information.

Symbols	Illustration
$Y_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_1$	$n_1$ alternatives
$C_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_2$	$n_2$ attributes
${\vartheta }_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_2$	$\lambda$-Fuzzy measure value of attribute $C_i$
$D_i\begin{array}{c}\end{array}i=1,2,\cdots ,l$	$l$ decision experts
$g_i\begin{array}{c}\end{array}i=1,2,\cdots ,l$	$\lambda$-Fuzzy measure value of decision expert $D_i$
${\psi }_{ij}^m=\{{\mu }_{ij}^m\left.\right|{\mu }_{ij}^m\in {\psi }_{ij}^m\}$	The GIVqROHFE that $Y_i$ satisfies $C_j$ from $D_m$
${\mu }_{ij}^m=([M_{{\mu }_{ij}}^{m-},M_{{\mu }_{ij}}^{m+}],[Z_{{\mu }_{ij}}^{m-},Z_{{\mu }_{ij}}^{m+}])$	The possible IVqROF membership and non-membership degree that $Y_i$ satisfies $C_j$ from $D_m$
${\zeta }^m={({\psi }_{ij}^m)}_{n_1\times n_2}$	A GIVqROHF decision profile from $D_m$
${\eta }^m={({\eta }_{ij}^m)}_{n_1\times n_2}$	A normalized GIVqROHF decision profile from $D_m$
${\xi }_{ij}^m=([M_{{\xi }_{ij}}^{m-},M_{{\xi }_{ij}}^{m+}],[Z_{{\xi }_{ij}}^{m-},Z_{{\xi }_{ij}}^{m+}])$	The normalized possible IVqROF membership and non-membership degree that $Y_i$ satisfies $C_j$ from $D_m$
${\eta }_{ij}^m={\psi }_{ij}^m$	The normalized GIVqROHFE that $Y_i$ satisfies benefit attribute $C_j$ from $D_m$
${\eta }_{ij}^m={({\psi }_{ij}^m)}^c$	The normalized GIVqROHFE that $Y_i$ satisfies cost attribute $C_j$ from $D_m$
${({\psi }_{ij}^m)}^c=$$\left\{([Z_{{\mu }_{ij}}^{m-},Z_{{\mu }_{ij}}^{m+}],[M_{{\mu }_{ij}}^{m-},M_{{\mu }_{ij}}^{m+}])\left.\right|{\mu }_{ij}^m\in {\psi }_{ij}^m\right\}$	Inverse operation of the GIVqROHFE
${\lambda }_1$	The parameter of the GIVqROHFCA operator
${\lambda }_2$	The parameter of the GIVqROHFCGM operator
${\gamma }_1$	The parameter of $\lambda$-Fuzzy measure with respect to decision experts
${\gamma }_2$	The parameter of $\lambda$-Fuzzy measure with respect to attributes
$\#{\eta }_i$	The number of elements in GIVqROHFE ${\eta }_i$
$\#{\eta }_{ij}^m$	The number of elements in GIVqROHFE ${\eta }_{ij}^m$
$\#{\eta }_{ij}$	The number of elements in GIVqROHFE ${\eta }_{ij}$
$\{\delta (1),\delta (2),\cdots ,\delta (i)\}$	A permutation of $\{1,2,\cdots ,i\}$

Based on the above symbols, several steps are involved to describe the new method (see Figure 2).

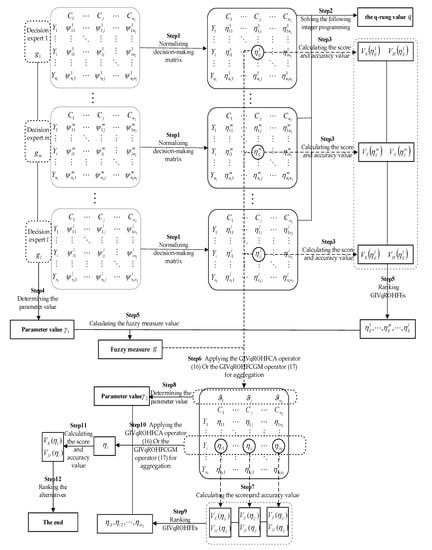
Figure 2. The visual chart of decision steps based on GIVqROHFCA and GIVqROHFCGM operators.

• Step 1. Obtaining the normalized decision-making matrix ${\eta }^m={({\eta }_{ij}^m)}_{n_1\times n_2}$ from the decision profile ${\zeta }^m={({\psi }_{ij}^m)}_{n_1\times n_2}$.

  $$\begin{gathered} {\eta }^m={({\eta }_{ij}^m)}_{n_1\times n_2}={\left(\{{\xi }_{ij}^m\left.\right|{\xi }_{ij}^m\in {\eta }_{ij}^m\}\right)}_{n_1\times n_2} \\ ={\left(\left\{([M_{{\xi }_{ij}}^{m-},M_{{\xi }_{ij}}^{m+}],[Z_{{\xi }_{ij}}^{m-},Z_{{\xi }_{ij}}^{m+}])\left.\right|{\xi }_{ij}^m\in {\eta }_{ij}^m\right\}\right)}_{n_1\times n_2} \end{gathered}$$
• Step 2. Solving the following integer programming to determining the q-rung value $q$.

  $$\begin{array}{c}\begin{array}{c}\begin{array}{cc}\min & q\end{array}\end{array}\\ \begin{array}{cc}s.t.& \left\{\begin{array}{l}0\le {(M_{{\xi }_{ij}}^{m+})}^q+{(Z_{{\xi }_{uj}}^{m+})}^q\le 1\\ q\in \{1,2,\cdots \}\\ i\in \{1,2,\cdots ,n_1\}\\ j\in \{1,2,\cdots ,n_2\}\\ m\in \{1,2,\cdots ,l\}\end{array}\right.\end{array}\end{array}$$
• Step 3. Calculating values of the score function $V_S({\eta }_{ij}^m)\begin{array}{c}\end{array}m=1,2,\cdots ,l$

  $$\begin{array}{l}{V}_S({\eta }_{ij}^m)=\left({\displaystyle {\sum }_{{\xi }_{ij}^m\in {\eta }_{ij}^m}{v}_s({\xi }_{ij}^m)}\right)/\#{\eta }_{ij}^m\\ \begin{array}{cc}& \end{array}=\left(\frac{1}{2}{\displaystyle {\sum }_{{\xi }_{ij}^m\in {\eta }_{ij}^m}[M_{{\xi }_{ij}}^{m-}{}^q+M_{{\xi }_{ij}}^{m+}{}^q-Z_{{\xi }_{ij}}^{m-}{}^q-Z_{{\xi }_{ij}}^{m+}{}^q]}\right)/\#{\eta }_{ij}^m\begin{array}{c}\end{array}m=1,2,\cdots ,l\end{array}$$

  (25)

  and the values of the accuracy function $V_H({\eta }_{ij}^m)\begin{array}{c}\end{array}m=1,2,\cdots ,l$

  $$\begin{array}{l}{V}_H({\eta }_{ij}^m)=\left({\displaystyle {\sum }_{{\xi }_{ij}^m\in {\eta }_{ij}^m}{v}_h({\xi }_{ij}^m)}\right)/\#{\eta }_{ij}^m\\ \begin{array}{cc}& \end{array}=\left(\frac{1}{2}{\displaystyle {\sum }_{{\xi }_{ij}^m\in {\eta }_{ij}^m}[M_{{\xi }_{ij}}^{m-}{}^q+Z_{{\xi }_{ij}}^{m-}{}^q+M_{{\xi }_{ij}}^{m+}{}^q+Z_{{\xi }_{ij}}^{m+}{}^q]}\right)/\#{\eta }_{ij}^m\begin{array}{c}\end{array}m=1,2,\cdots ,l\end{array}$$

  (26)
• Step 4. Determining the $\lambda$-fuzzy measure value $g_i$ of the decision expert $D_i\begin{array}{c}\end{array}i=1,2,\cdots ,l$, and solving the following equation to obtain the parameter value.

  $${\gamma }_1+1={\displaystyle {\prod }_{i=1}^l[1+{\gamma }_1{g}_i]}\mathrm{or}{\gamma }_1+1={\displaystyle {\prod }_{i=1}^l[1+{\gamma }_1{g}_i]}$$

  (27)

  where ${\gamma }_1$ is determined by numerical calculation method.
• Step 5. Ranking $l$ GIVqROHFEs ${\eta }_{ij}^1,{\eta }_{ij}^2,\cdots ,{\eta }_{ij}^l$ such that ${\eta }_{ij}^{\delta (1)}\ge \cdots \ge {\eta }_{ij}^{\delta (k)}\ge \cdots \ge {\eta }_{ij}^{\delta (l)}$, combining the ordered decision experts $X_{\delta (p)}=\{D_{\delta (1)},\cdots ,D_{\delta (k)},\cdots ,D_{\delta (p)},\}\begin{array}{c}\end{array}p\in \{1,2,\cdots ,l\}$ and calculating $\lambda$-fuzzy measure value $g(X_{\delta (p)}),\begin{array}{c}\end{array}p=1,2,\cdots ,l$ as the following formula:

  $$g(X_{\delta (p)})=\left\{\begin{array}{cc}\frac{1}{{\gamma }_1}\left({\displaystyle {\prod }_{s=1}^p[1+{\gamma }_1{g}_{\delta (s)}]-1}\right)& {\gamma }_1\ne 0\\ {\displaystyle {\sum }_{s=1}^p{g}_{\delta (s)}}\begin{array}{ccc}& & \end{array}& {\gamma }_1=0\end{array}\right.$$

  (28)
• Step 6. Applying the GIVqROHFCA operator (16) Or the GIVqROHFCGM operator (17) in order to obtain the the collective GIVqROHF matrix $\eta ={({\eta }_{ij})}_{n_1\times n_2}$ with the following form:

  $${\eta }_{ij}=\{([M_{{\xi }_{ij}}^{-},M_{{\xi }_{ij}}^{+}],[Z_{{\xi }_{ij}}^{-},Z_{{\xi }_{ij}}^{+}])\left.\right|{\xi }_{ij}\in {\eta }_{ij}\}$$

  $$\begin{array}{l}{\eta }_{ij}=GIVqROHFC{A}_{{\lambda }_1}\left({\eta }_{ij}^1,{\eta }_{ij}^2,\cdots ,{\eta }_{ij}^l\right)\\ \text{=}\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[{\lambda }_{1}q]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(M_{{\xi }_{ij}}^{\delta (s)-})}^q{}^{{\lambda }_1})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}},\\ \sqrt[{\lambda }_{1}q]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(M_{{\xi }_{ij}}^{\delta (s)+})}^q{}^{{\lambda }_1})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[q]{1-\sqrt[{\lambda }_1]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(1-{(Z_{{\xi }_{ij}}^{\delta (s)-})}^q)}^{{\lambda }_1})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}}},\\ \sqrt[q]{1-\sqrt[{\lambda }_1]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(1-{(Z_{{\xi }_{ij}}^{\delta (s)+})}^q)}^{{\lambda }_1})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}}}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\xi }_{ij}^{\delta (s)}\in {\eta }_{ij}^{\delta (s)}\\ s=1,2,\cdots ,l\end{array}\right\}\end{array}$$

  (29)

  $$\begin{array}{l}{\eta }_{ij}=GIVqROHFCG{M}_{{\lambda }_2}\left({\eta }_{ij}^1,{\eta }_{ij}^2,\cdots ,{\eta }_{ij}^l\right)\\ \text{=}\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[q]{1-\sqrt[{\lambda }_2]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(1-{(M_{{\xi }_{ij}}^{\delta (s)-})}^q)}^{{\lambda }_2})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}}},\\ \sqrt[q]{1-\sqrt[{\lambda }_2]{1-{\displaystyle {\prod }_{s=1}^l{(1-{(1-{(M_{{\xi }_{ij}}^{\delta (s)+})}^q)}^{{\lambda }_2})}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[{\lambda }_{2}q]{1-{\displaystyle {\prod }_{s=1}^l{\left(1-{(Z_{{\xi }_{ij}}^{\delta (s)-})}^q{}^{\lambda }\right)}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}},\\ \sqrt[{\lambda }_{2}q]{1-{\displaystyle {\prod }_{s=1}^l{\left(1-{(Z_{{\xi }_{ij}}^{\delta (s)+})}^q{}^{\lambda }\right)}^{(g(X_{\delta (s)})-g(X_{\delta (s-1)}))}}},\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\xi }_{ij}^{\delta (s)}\in {\eta }_{ij}^{\delta (s)}\\ s=1,2,\cdots ,l\end{array}\right\}\end{array}$$

  (30)
• Step 7. Calculating the values of $V_S({\eta }_{ij})$ to obtain score values of ${\eta }_{ij}\begin{array}{c}\end{array}j=1,2,\cdots ,n_2$

  $$V_S({\eta }_{ij})=\frac{1}{2}\frac{{\displaystyle {\sum }_{{\xi }_{ij}\in {\eta }_{ij}}[M_{{\xi }_{ij}}^{-}{}^q-Z_{{\xi }_{ij}}^{-}{}^q+M_{{\xi }_{ij}}^{+}{}^q-Z_{{\xi }_{ij}}^{+}{}^q]}}{\#{\eta }_{ij}}$$

  (31)

  and the values of the accuracy function $V_H({\eta }_{ij})\begin{array}{c}\end{array}j=1,2,\cdots ,n_2$

  $$V_H({\eta }_{ij})=\frac{1}{2}\frac{{\displaystyle {\sum }_{{\xi }_{ij}\in {\eta }_{ij}}[W_{{\xi }_{ij}}^{-}{}^q+Z_{{\xi }_{ij}}^{-}{}^q+W_{{\xi }_{ij}}^{+}{}^q+Z_{{\xi }_{ij}}^{+}{}^q]}}{\#{\eta }_{ij}}$$

  (32)
• Step 8. Provide the $\lambda$-fuzzy measure value ${\vartheta }_i$ of the attribute $C_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_2$, and solving the equation as follows:

  $${\gamma }_2+1={\displaystyle {\prod }_{i=1}^{n_2}[1+{\gamma }_2{\vartheta }_i]}\mathrm{or}{\gamma }_2+1={\displaystyle {\prod }_{i=1}^{n_2}[1+{\gamma }_2{\vartheta }_i]}$$

  (33)
• Step 9. Ranking $n$ GIVqROHFEs ${\eta }_{i1},{\eta }_{i2},\cdots ,{\eta }_{i{n}_2}$ such that:

  $${\eta }_{i\delta (1)}\ge \cdots \ge {\eta }_{i\delta (k)}\ge \cdots \ge {\eta }_{i\delta (n_2)},$$

  yielding the ordered attributes set $X_{\delta (i)}=\{C_{\delta (1)},\cdots ,C_{\delta (k)},\cdots ,C_{\delta (i)},\}\begin{array}{c}\end{array}i\in \{1,2,\cdots ,n_1\}$ and $\lambda$-fuzzy measure value $\vartheta (X_{\delta (i)}),\begin{array}{c}\end{array}i=1,2,\cdots ,n_1$ as the following formula:

  $$\vartheta (X_{\sigma (i)})=\left\{\begin{array}{cc}\frac{1}{{\gamma }_2}\left({\displaystyle {\prod }_{s=1}^i[1+{\gamma }_2{\vartheta }_{\delta (s)}]-1}\right)& {\gamma }_2\ne 0\\ {\displaystyle {\sum }_{s=1}^i{\vartheta }_{\delta (s)}}\begin{array}{ccc}& & \end{array}& {\gamma }_2=0\end{array}\right.$$

  (34)
• Step 10. Applying the GIVqROHFCA operator (16) or the GIVqROHFCGM operator (17) In order to derive the collective value ${\eta }_i=\{([M_{{\xi }_i}^{-},M_{{\xi }_i}^{+}],[Z_{{\xi }_i}^{-},Z_{{\xi }_i}^{+}])\left.\right|{\xi }_i\in {\eta }_i\}$ of the alternative $P_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_1$.

  $$\begin{array}{l}{\eta }_i=GIVqROHFC{A}_{{\lambda }_1}\left({\eta }_{i1},{\eta }_{i2},\cdots ,{\eta }_{i{n}_2}\right)\\ \text{=}\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[{\lambda }_{1}q]{1-{\displaystyle {\prod }_{s=1}^{n_2}{(1-{(M_{{\xi }_{i\delta (s)}}^{-})}^q{}^{{\lambda }_1})}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}},\\ \sqrt[{\lambda }_{1}q]{1-{\displaystyle {\prod }_{s=1}^{n_2}{(1-{(M_{{\xi }_{i\delta (s)}}^{+})}^q{}^{{\lambda }_1})}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[q]{1-\sqrt[{\lambda }_1]{1-{\displaystyle {\prod }_{s=1}^{n_2}{(1-{(1-{(Z_{{\xi }_{i\delta (s)}}^{-})}^q)}^{{\lambda }_1})}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}},\\ \sqrt[q]{1-\sqrt[{\lambda }_1]{1-{\displaystyle {\prod }_{s=1}^{n_2}{(1-{(1-{(Z_{{\xi }_{i\delta (s)}}^{+})}^q)}^{{\lambda }_1})}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\xi }_{i\delta (s)}\in {\eta }_{i\delta (s)}\\ s=1,2,\cdots ,n_2\end{array}\right\}\end{array}$$

  (35)

  $$\begin{array}{l}{\eta }_i=GIVqROHFCG{M}_{{\lambda }_2}\left({\eta }_{i1},{\eta }_{i2},\cdots ,{\eta }_{i{n}_2}\right)\\ \text{=}\left\{\left(\begin{array}{l}\left[\begin{array}{l}\sqrt[q]{1-\sqrt[{\lambda }_2]{1-{\displaystyle {\prod }_{s=1}^{n_2}{\left(1-{\left[1-{(M_{{\xi }_{i\delta (s)}}^{-})}^q\right]}^{{\lambda }_2}\right)}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}},\\ \sqrt[q]{1-\sqrt[{\lambda }_2]{1-{\displaystyle {\prod }_{s=1}^{n_2}{\left(1-{\left[1-{(M_{{\xi }_{i\delta (s)}}^{+})}^q\right]}^{{\lambda }_2}\right)}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}}\end{array}\right],\\ \left[\begin{array}{l}\sqrt[{\lambda }_{2}q]{1-{\displaystyle {\prod }_{s=1}^{n_2}{\left(1-{(Z_{{\xi }_{i\delta (s)}}^{-})}^q{}^{\lambda }\right)}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}},\\ \sqrt[{\lambda }_{2}q]{1-{\displaystyle {\prod }_{s=1}^{n_2}{\left(1-{(Z_{{\xi }_{i\delta (s)}}^{+})}^q{}^{\lambda }\right)}^{(\vartheta (X_{\delta (s)})-\vartheta (X_{\delta (s-1)}))}}}\end{array}\right]\end{array}\right)\left.\begin{array}{l}\\ \\ \\ \\ \\ \\ \\ \end{array}\right|\begin{array}{c}{\xi }_{i\delta (s)}\in {\eta }_{i\delta (s)}\\ s=1,2,\cdots ,n_2\end{array}\right\}\end{array}$$

  (36)
• Step 11. By Definition (13), calculating the score value $V_S({\eta }_i)$ of $Y_i$

  $$V_S({\eta }_i)=\frac{1}{2}\frac{{\displaystyle {\sum }_{{\xi }_i\in {\eta }_i}[Z_{{\xi }_i}^{+}{}^q+{(M_{{\xi }_i}^{+})}^q-Z_{{\xi }_i}^{-}{}^q-M_{{\xi }_i}^{-}{}^q]}}{\#{\eta }_i}$$

  (37)

  and the accuracy value $V_H({\eta }_i)$ of $P_i\begin{array}{c}\end{array}i=1,2,\cdots ,n_1$

  $$V_H({\eta }_i)=\frac{1}{2}\frac{{\displaystyle {\sum }_{{\xi }_i\in {\eta }_i}[M_{{\xi }_i}^{+}{}^q+Z_{{\xi }_i}^{+}{}^q+M_{{\xi }_i}^{-}{}^q+Z_{{\xi }_i}^{-}{}^q]}}{\#{\eta }_i}$$

  (38)

  arrange all of the alternatives by the score value or accuracy value.
• Step 12. End.

In the above Steps 2 and 4, we can obtain the $\lambda$-fuzzy measure value $g_i$ and ${\vartheta }_i$ by experience of people at an organization or corporation. In addition, the fuzzy measure can also be determined by mathematical programming method [57] or machine learning method [62,63].

6. Numerical Experiment

6.1. An Example for the New MAGDM Approach

An example is presented to demonstrate the method of Section 5. We take into account a problem of energy project selection with respect to the energy development strategy that was involved in [64]. According to Table 1, the structured representation of the selected decision problem is described in Table 2. In this example: (1) For Table 3, Table 4, Table 5 and Table 6, four decision experts provided the evaluation value with several possible GIVqROHFNs for each alternative; specifically, ${\zeta }^m={({\psi }_{ij}^m)}_{4\times 4},m=1,2,3,4$ is the generalized interval-valued q-rung orthopair hesitant fuzzy decision matrix which is evaluated by the decision expert $D_m$ that the alternative $Y_i$ satisfies the attribute $C_j$; (2) Considering that the attribute $C_1$ and $C_4$ are the cost attributes, and the attribute $C_2$ and $C_3$ are the benefit attributes, the standardized process of the original matrix should be completed in order to obtain Table 7, Table 8, Table 9 and Table 10, which, respectively, are the standardized matrix of the corresponding matrix of Table 3, Table 4, Table 5 and Table 6, that is, ${\eta }^m$ is the normalized version of ${\zeta }^m$; (3) For any pair $(Y_i,c_j)$, according to the GIVqROHFCA operator, the GIVqROHF assessments from four experts need to be ranked, and the corresponding results can be seen in Table 11; (4) The $\lambda$-fuzzy measure value $g_i$ and ${\vartheta }_i$ is determined by the experience of people at the higher levels of government or corporation, where the weight of each expert and the interaction among the ordered experts are presented by $g_i$ listed in Table 12, and the weight of any attribute and the interrelationship degree among the ordered attributes are represented by ${\vartheta }_i$ shown in Table 13; (5) From the GIVqROHFCA operator, for any pair $(Y_i,c_j)$, the collective results based on four experts and the aggregated GIVqROHF matrix in terms of four attributes, respectively, are displayed in Table 14 and Table 15.

Table 2. Illustration of an energy project problem with the GIVqROHF information.

Symbols		Illustration
$Y_1,Y_2,Y_3,Y_4$		$4$ alternatives
$C_1,C_2,C_3,C_4$	$C_1$	technological attribute (cost)
	$C_2$	economical attribute (benefit)
	$C_3$	sociopolitical attribute (benefit)
	$C_4$	environmental attribute (cost)
${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$	${\vartheta }_1$	0.20
	${\vartheta }_2$	0.35
	${\vartheta }_3$	0.50
	${\vartheta }_4$	0.15
$D_i\begin{array}{c}\end{array}i=1,2,3,4$		$4$ decision experts
$g_1,g_2,g_3,g_4$	$g_1$	0.25
	$g_2$	0.50
	$g_3$	0.35
	$g_4$	0.10
$\begin{array}{l}{\zeta }^m={({\psi }_{ij}^m)}_{4\times 4}\\ m=1,2,3,4\end{array}$	${\zeta }^1$	matrix from $D_1$ (Table 3)
	${\zeta }^2$	matrix from $D_2$ (Table 4)
	${\zeta }^3$	matrix from $D_3$ (Table 5)
	${\zeta }^4$	matrix from $D_4$ (Table 6)
$\begin{array}{l}{\eta }^m={({\eta }_{ij}^m)}_{4\times 4}\\ m=1,2,3\end{array}$	${\eta }^1$	normalized matrix from $D_1$ (Table 7)
	${\eta }^2$	normalized matrix from $D_2$ (Table 8)
	${\eta }^3$	normalized matrix from $D_3$ (Table 9)
	${\eta }^4$	normalized matrix from $D_4$ (Table 10)
${\lambda }_1$		1
${\lambda }_2$		1

Table 3. The GIVqROHF decision matrix ${\zeta }^1$ from the decision expert $D_1$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.3, 0.4], [0.6, 0.7]) ([0.4, 0.5], [0.5, 0.7])}	{([0.7, 0.8], [0.2, 0.4])}	{([0.3, 0.5], [0.7, 0.8])}	{([0.6, 0.9], [0.2, 0.3]) ([0.7, 0.9], [0.3, 0.4])}
$Y_2$	{([0.3, 0.5], [0.5, 0.6]) ([0.4, 0.5], [0.6, 0.7])}	{([0.2, 0.5], [0.6, 0.7])}	{([0.3, 0.6], [0.2, 0.5]) ([0.7, 0.8], [0.3, 0.5])}	{([0.3, 0.7], [0.4, 0.5])}
$Y_3$	{([0.5, 0.6], [0.4, 0.6])}	{([0.8, 0.9], [0.3, 0.4]) ([0.7, 0.9], [0.2, 0.3])}	{([0.3, 0.7], [0.4, 0.4])}	{([0.4, 0.6], [0.3, 0.6]) ([0.3, 0.5], [0.4, 0.6]) ([0.5, 0.6], [0.4, 0.7])}
$Y_4$	{([0.3, 0.6], [0.5, 0.7])}	{([0.3, 0.7], [0.3, 0.4])}	{([0.3, 0.8], [0.2, 0.3])}	{([0.6, 0.8], [0.2, 0.3])}

Table 4. The GIVqROHF decision matrix ${\zeta }^2$ from the decision expert $D_2$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.2, 0.4], [0.7, 0.8]) ([0.3, 0.5], [0.6, 0.8])}	{([0.8, 0.9], [0.1, 0.4])}	{([0.3, 0.4], [0.4, 0.6])}	{([0.5, 0.6], [0.2, 0.4])}
$Y_2$	{([0.2, 0.5], [0.7, 0.8])}	{([0.4, 0.7], [0.5, 0.7])}	{([0.4, 0.5], [0.4, 0.5])}	{([0.4, 0.5], [0.2, 0.5])}
$Y_3$	{([0.6, 0.6], [0.4, 0.4]) ([0.3, 0.6], [0.5, 0.6]) ([0.4, 0.6], [0.4, 0.4])}	{([0.6, 0.9], [0.1, 0.2]) ([0.7, 0.8], [0.1, 0.3])}	{([0.4, 0.5], [0.5, 0.6])}	{([0.7, 0.9], [0.3, 0.3])}
$Y_4$	{([0.5, 0.7], [0.6, 0.7])}	{([0.5, 0.7], [0.5, 0.6])}	{([0.8, 0.9], [0.2, 0.4]) ([0.9, 0.9], [0.1, 0.2])}	{([0.6, 0.9], [0.2, 0.2]) ([0.7, 0.8], [0.1, 0.2])}

Table 5. The GIVqROHF decision matrix ${\zeta }^3$ from the decision expert $D_3$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.3, 0.5], [0.6, 0.8])}	{([0.6, 0.7], [0.2, 0.5])}	{([0.3, 0.5], [0.6, 0.7])}	{([0.6, 0.7], [0.3, 0.5])}
$Y_2$	{([0.3, 0.6], [0.5, 0.7])}	{([0.3, 0.6], [0.6, 0.8])}	{([0.3, 0.4], [0.5, 0.6])}	{([0.3, 0.4], [0.1, 0.4])}
$Y_3$	{([0.7, 0.7], [0.5, 0.5])}	{([0.6, 0.8], [0.2, 0.3])}	{([0.5, 0.6], [0.6, 0.7])}	{([0.8, 0.9], [0.3, 0.4])}
$Y_4$	{([0.4, 0.6], [0.7, 0.8]) ([0.4, 0.6], [0.5, 0.6])}	{([0.4, 0.7], [0.4, 0.6])}	{([0.7, 0.9], [0.3, 0.4])}	{([0.6, 0.8], [0.2, 0.3])}

Table 6. The GIVqROHF decision matrix ${\zeta }^4$ from the decision expert $D_4$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.3, 0.4], [0.7, 0.8])}	{([0.5, 0.7], [0.3, 0.5]) ([0.4, 0.6], [0.2, 0.4]) ([0.6, 0.7], [0.3, 0.4])}	{([0.4, 0.6], [0.6, 0.8])}	{([0.7, 0.8], [0.4, 0.6])}
$Y_2$	{([0.4, 0.6], [0.6, 0.7])}	{([0.4, 0.6], [0.7, 0.8]) ([0.2, 0.4], [0.7, 0.9])}	{([0.2, 0.4], [0.5, 0.7]) ([0.3, 0.5], [0.5, 0.6])}	{([0.2, 0.4], [0.2, 0.5])}
$Y_3$	{([0.7, 0.8], [0.5, 0.6])}	{([0.6, 0.7], [0.3, 0.4])}	{([0.4, 0.5], [0.7, 0.8])}	{([0.7, 0.9], [0.3, 0.5])}
$Y_4$	{([0.3, 0.4], [0.7 0.9]) ([0.4, 0.5], [0.5, 0.7])}	{([0.5, 0.7], [0.5, 0.6])}	{([0.7, 0.8], [0.3, 0.5])}	{([0.6, 0.7], [0.1, 0.3])}

Table 7. The normalized GIVqROHF decision matrix ${\eta }^1$ from the decision expert $D_1$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.6, 0.7], [0.3, 0.4]) ([0.5, 0.7], [0.4, 0.5])}	{([0.7, 0.8], [0.2, 0.4])}	{([0.3, 0.5], [0.7, 0.8])}	{([0.2, 0.3], [0.6, 0.9]) ([0.3, 0.4], [0.7, 0.9])}
$Y_2$	{([0.5, 0.6], [0.3, 0.5]) ([0.6, 0.7], [0.4, 0.5])}	{([0.2, 0.5], [0.6, 0.7])}	{([0.3, 0.6], [0.2, 0.5]) ([0.7, 0.8], [0.3, 0.5])}	{([0.4, 0.5], [0.3, 0.7])}
$Y_3$	{([0.4, 0.6], [0.5, 0.6])}	{([0.8, 0.9], [0.3, 0.4]) ([0.7, 0.9], [0.2, 0.3])}	{([0.3, 0.7], [0.4, 0.4])}	{([0.3, 0.6], [0.4, 0.6]) ([0.4, 0.6], [0.3, 0.5]) ([0.4, 0.7], [0.5, 0.6])}
$Y_4$	{([0.5, 0.7], [0.3, 0.6])}	{([0.3, 0.7], [0.3, 0.4])}	{([0.3, 0.8], [0.2, 0.3])}	{([0.2, 0.3], [0.6, 0.8])}

Table 8. The normalized GIVqROHF matrix ${\eta }^2$ from the decision expert $D_2$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.7, 0.8], [0.2, 0.4]) ([0.6, 0.8], [0.3, 0.5])}	{([0.8, 0.9], [0.1, 0.4])}	{([0.3, 0.4], [0.4, 0.6])}	{([0.2, 0.4], [0.5, 0.6])}
$Y_2$	{([0.7, 0.8], [0.2, 0.5])}	{([0.4, 0.7], [0.5, 0.7])}	{([0.4, 0.5], [0.4, 0.5])}	{([0.2, 0.5], [0.4, 0.5])}
$Y_3$	{([0.4, 0.4], [0.6, 0.6]) ([0.5, 0.6], [0.3, 0.6]) ([0.4, 0.4], [0.4, 0.6])}	{([0.6, 0.9], [0.1, 0.2]) ([0.7, 0.8], [0.1, 0.3])}	{([0.4, 0.5], [0.5, 0.6])}	{([0.3, 0.3], [0.7, 0.9])}
$Y_4$	{([0.6, 0.7], [0.5, 0.7])}	{([0.5, 0.7], [0.5, 0.6])}	{([0.8, 0.9], [0.2, 0.4]) ([0.9, 0.9], [0.1, 0.2])}	{([0.2, 0.2], [0.6, 0.9]) ([0.1, 0.2], [0.7, 0.8])}

Table 9. The normalized GIVqROHF decision matrix ${\eta }^3$ from the decision expert $D_3$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.6, 0.8], [0.3, 0.5])}	{([0.6, 0.7], [0.2, 0.5])}	{([0.3, 0.5], [0.6, 0.7])}	{([0.3, 0.5], [0.6, 0.7])}
$Y_2$	{([0.5, 0.7], [0.3, 0.6])}	{([0.3, 0.6], [0.6, 0.8])}	{([0.3, 0.4], [0.5, 0.6])}	{([0.1, 0.4], [0.3, 0.4])}
$Y_3$	{([0.5, 0.5], [0.7, 0.7])}	{([0.6, 0.8], [0.2, 0.3])}	{([0.5, 0.6], [0.6, 0.7])}	{([0.3, 0.4], [0.8, 0.9])}
$Y_4$	{([0.7, 0.8], [0.4, 0.6]) ([0.5, 0.6], [0.4, 0.6])}	{([0.4, 0.7], [0.4, 0.6])}	{([0.7, 0.9], [0.3, 0.4])}	{([0.2, 0.3], [0.6, 0.8])}

Table 10. The normalized GIVqROHF decision matrix ${\eta }^4$ from the decision expert $D_4$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$
$Y_1$	{([0.7, 0.8], [0.3, 0.4])}	{([0.5, 0.7], [0.3, 0.5]) ([0.4, 0.6], [0.2, 0.4]) ([0.6, 0.7], [0.3, 0.4])}	{([0.4, 0.6], [0.6,0.8])}	{([0.4, 0.6], [0.7, 0.8])}
$Y_2$	{([0.6, 0.7], [0.4, 0.6])}	{([0.4, 0.6], [0.7, 0.8]) ([0.2, 0.4], [0.7, 0.9])}	{([0.2, 0.4], [0.5, 0.7]) ([0.3, 0.5], [0.5, 0.6])}	{([0.2, 0.5], [0.2, 0.4])}
$Y_3$	{([0.5, 0.6], [0.7, 0.8])}	{([0.6, 0.7], [0.3, 0.4])}	{([0.4, 0.5], [0.7, 0.8])}	{([0.3, 0.5], [0.7, 0.9])}
$Y_4$	{([0.7 0.9], [0.3, 0.4]) ([0.5, 0.7], [0.4, 0.5])}	{([0.5, 0.7], [0.5, 0.6])}	{([0.7, 0.8], [0.3, 0.5])}	{([0.1, 0.3], [0.6, 0.7])}

Table 11. The score values of $D_1,D_2,D_3,D_4$ for the alternative and attribute couple $Y_i,c_j$.

${\mathit{Y}}_{\mathit{i}},{\mathit{c}}_{\mathit{j}}$	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_4$	Descending Order	${\mathit{Y}}_{\mathit{i}},{\mathit{c}}_{\mathit{j}}$	${\mathit{D}}_1$	${\mathit{D}}_2$	${\mathit{D}}_3$	${\mathit{D}}_4$	Descending Order
$1,1$	0.232	0.398	0.330	0.440	4231	$3,1$	−0.045	−0.073	−0.240	−0.260	1234
$1,2$	0.465	0.640	0.280	0.220	2134	$3,2$	0.593	0.538	0.435	0.300	1234
$1,3$	−0.395	−0.135	−0.255	−0.240	2431	$3,3$	0.130	−0.100	−0.120	−0.360	1234
$1,4$	−0.522	−0.205	−0.255	−0.305	2341	$3,4$	0.025	−0.560	−0.600	−0.480	1423
$2,1$	0.177	0.420	0.145	0.165	2143	$4,1$	0.145	0.055	0.175	0.345	4312
$2,2$	−0.280	−0.045	−0.275	−0.428	2314	$4,2$	0.165	0.065	0.065	0.065	Y1 > Y2 =Y4 > Y3
							0.415	0.675	0.585	0.675
$2,3$	0.237	0.000	−0.180	−0.202	1234	$4,3$	0.300	0.705	0.525	0.395	2341
$2,4$	−0.085	−0.060	−0.040	0.045	4321	$4,4$	−0.435	−0.542	−0.435	−0.375	Y4 > Y1 =Y3 > Y2
							0.565	0.608	0.565	0.475

Table 12. The $\lambda$-fuzzy measure values of $D_1,D_2,D_3,D_4$ for the alternative and attribute couple $Y_i,c_j$.

${\mathit{Y}}_{\mathit{i}},{\mathit{c}}_{\mathit{j}}$	$\left\{{\mathit{D}}_{\mathit{\delta }(1)}\right\}$	$\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)}\}$	$\begin{array}{l}\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)},\\ {\mathit{D}}_{\mathit{\delta }(3)}\}\end{array}$	$\begin{array}{l}\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)},\\ {\mathit{D}}_{\mathit{\delta }(3)},{\mathit{D}}_{\mathit{\delta }(4)}\}\end{array}$	${\mathit{Y}}_{\mathit{i}},{\mathit{c}}_{\mathit{j}}$	$\left\{{\mathit{D}}_{\mathit{\delta }(1)}\right\}$	$\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)}\}$	$\begin{array}{l}\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)},\\ {\mathit{D}}_{\mathit{\delta }(3)}\}\end{array}$	$\begin{array}{l}\{{\mathit{D}}_{\mathit{\delta }(1)},{\mathit{D}}_{\mathit{\delta }(2)},\\ {\mathit{D}}_{\mathit{\delta }(3)},{\mathit{D}}_{\mathit{\delta }(4)}\}\end{array}$
$1,1$	0.100	0.578	0.841	1.000	$3,1$	0.250	0.696	0.941	1.0000
$1,2$	0.500	0.696	0.941	1.000	$3,2$	0.250	0.696	0.941	1.0000
$1,3$	0.500	0.578	0.841	1.000	$3,3$	0.250	0.696	0.941	1.0000
$1,4$	0.500	0.774	0.841	1.000	$3,4$	0.250	0.339	0.766	1.0000
$2,1$	0.500	0.696	0.766	1.000	$4,1$	0.100	0.435	0.638	1.0000
$2,2$	0.500	0.774	0.941	1.000	$4,2$	0.250	0.696	0.766	1.0000
$2,3$	0.250	0.696	0.941	1.000	$4,3$	0.500	0.774	0.841	1.0000
$2,4$	0.100	0.435	0.841	1.000	$4,4$	0.100	0.339	0.638	1.0000

Table 13. The score and the $\lambda$-fuzzy measure of $c_1,c_2,c_3,c_4$ for an alternative $Y_i$.

${\mathit{Y}}_{\mathit{i}}$	${\mathit{c}}_1$	${\mathit{c}}_2$	${\mathit{c}}_3$	${\mathit{c}}_4$	Descending Order	$\left\{{\mathit{c}}_{\mathit{\delta }(1)}\right\}$	$\{{\mathit{c}}_{\mathit{\delta }(1)},{\mathit{c}}_{\mathit{\delta }(2)}\}$	$\{{\mathit{c}}_{\mathit{\delta }(1)},{\mathit{c}}_{\mathit{\delta }(2)},{\mathit{c}}_{\mathit{\delta }(3)}\}$	$\{{\mathit{c}}_{\mathit{\delta }(1)},{\mathit{c}}_{\mathit{\delta }(2)},{\mathit{c}}_{\mathit{\delta }(3)},{\mathit{c}}_{\mathit{\delta }(4)}\}$
$Y_1$	0.365	0.522	−0.194	−0.258	2134	0.350	0.520	0.908	1.000
$Y_2$	0.307	−0.159	0.030	−0.031	1342	0.200	0.657	0.765	1.000
$Y_3$	−0.096	0.532	−0.036	−0.361	2314	0.350	0.775	0.908	1.000
$Y_4$	0.163	0.107	0.611	−0.464	3124	0.500	0.657	0.908	1.000

Table 14. The collective GIVqROHF matrix $\eta ={({\eta }_{ij})}_{4\times 4}$.

Alternatives	${\mathit{c}}_1$	${\mathit{c}}_2$
$Y_1$	{([0.662, 0.787], [0.247, 0.424]) ([0.651, 0.787], [0.259, 0.439]) ([0.612, 0.787], [0.300, 0.472]) ([0.599, 0.787], [0.314, 0.489])}	{([0.732, 0.842], [0.145, 0.428]) ([0.730, 0.840], [0.141, 0.422]) ([0.735, 0.842], [0.145, 0.422])}
$Y_2$	{([0.623, 0.743], [0.250, 0.528]) ([0.638, 0.756], [0.264, 0.528])}	{([0.349, 0.643], [0.553, 0.732]) ([0.339, 0.636], [0.553, 0.737])}
$Y_3$	{([0.434, 0.499], [0.601, 0.634]) ([0.478, 0.579], [0.441, 0.634]) ([0.434, 0.499], [0.501, 0.634])}	{([0.668, 0.874], [0.166, 0.274]) ([0.706, 0.829], [0.166, 0.328]) ([0.629, 0.874], [0.150, 0.255]) ([0.673, 0.829], [0.150, 0.305])}
$Y_4$	{([0.633, 0.767], [0.397, 0.609]) ([0.564, 0.708], [0.397, 0.609]) ([0.615, 0.739], [0.409, 0.623]) ([0.540, 0.671], [0.409, 0.623])}	{([0.438, 0.700], [0.418, 0.542])}
Alternatives	${\mathit{c}}_{\mathbf{3}}$	${\mathit{c}}_{\mathbf{4}}$
$Y_1$	{([0.309, 0.465], [0.502, 0.669])}	{([0.250, 0.436], [0.553, 0.681]) ([0.265, 0.448], [0.567, 0.681])}
$Y_2$	{([0.345, 0.504], [0.360, 0.533]) ([0.349, 0.509], [0.360, 0.528]) ([0.488, 0.595], [0.398, 0.533]) ([0.490, 0.598], [0.398, 0.528])}	{([0.225, 0.470], [0.324, 0.479])}
$Y_3$	{([0.408, 0.587], [0.504, 0.573])}	{([0.300, 0.443], [0.628, 0.813]) ([0.329, 0.443], [0.584, 0.777]) ([0.329, 0.490], [0.664, 0.813])}
$Y_4$	{([0.728, 0.883], [0.230, 0.388]) ([0.812, 0.883], [0.162, 0.274])}	{([0.192, 0.269], [0.600, 0.824]) ([0.162, 0.269], [0.634, 0.789])}}

Table 15. The ${\eta }_i$ value of $Y_i\begin{array}{c}\end{array}i=1,2,\cdots ,4$.

Alternatives	${\mathit{\eta }}_{\mathit{i}}\begin{array}{c}\end{array}\mathit{i}=1,2,\cdots ,4$	Score	Order
$Y_1$	{([0.581, 0.713], [0.291, 0.530]), ([0.582, 0.714], [0.291, 0.530]) ([0.579, 0.713], [0.293, 0.534]), ([0.579, 0.714], [0.294, 0.534]) ([0.571, 0.713], [0.300, 0.540]), ([0.571, 0.714], [0.301, 0.540]) ([0.568, 0.713], [0.303, 0.543]), ([0.568, 0.714], [0.303, 0.543]) ([0.580, 0.712], [0.288, 0.528]), ([0.580, 0.712], [0.289, 0.528]) ([0.577, 0.712], [0.290, 0.531]), ([0.578, 0.712], [0.291, 0.531]) ([0.569, 0.712], [0.298, 0.538]), ([0.570, 0.712], [0.299, 0.538]) ([0.567, 0.712], [0.300, 0.541]), ([0.567, 0.712], [0.301, 0.541]) ([0.583, 0.713], [0.291, 0.528]), ([0.584, 0.714], [0.291, 0.528]) ([0.581, 0.713], [0.293, 0.531]), ([0.581, 0.714], [0.294, 0.531]) ([0.573, 0.713], [0.300, 0.538]), ([0.573, 0.714], [0.301, 0.538]) ([0.570, 0.713], [0.303, 0.541]), ([0.570, 0.714], [0.303, 0.541])}	S: 0.232 H: 0.607	2
$Y_2$	{([0.418, 0.600], [0.366, 0.567]), ([0.417, 0.598], [0.366, 0.568]) ([0.420, 0.602], [0.366, 0.565]), ([0.418, 0.600], [0.366, 0.565]) ([0.477, 0.633], [0.383, 0.567]), ([0.476, 0.631], [0.383, 0.568]) ([0.479, 0.635], [0.383, 0.565]), ([0.477, 0.633], [0.383, 0.565]) ([0.425, 0.605], [0.370, 0.567]), ([0.423, 0.603], [0.370, 0.568]) ([0.426, 0.607], [0.370, 0.565]), ([0.424, 0.605], [0.370, 0.565]) ([0.482, 0.637], [0.388, 0.567]), ([0.481, 0.636], [0.388, 0.568]) ([0.484, 0.639], [0.388, 0.565]), ([0.482, 0.637], [0.388, 0.565])}	S: 0.062 H: 0.525	4
$Y_3$	{([0.524, 0.724], [0.357, 0.463]), ([0.525, 0.724], [0.355, 0.461]) ([0.525, 0.726], [0.359, 0.463]), ([0.528, 0.730], [0.343, 0.463]) ([0.529, 0.730], [0.341, 0.461]), ([0.529, 0.731], [0.345, 0.463]) ([0.524, 0.724], [0.349, 0.463]), ([0.525, 0.724], [0.347, 0.461]) ([0.525, 0.726], [0.351, 0.463]), ([0.547, 0.689], [0.357, 0.493]) ([0.548, 0.689], [0.355, 0.491]), ([0.548, 0.691], [0.359, 0.493]) ([0.551, 0.695], [0.343, 0.493]), ([0.553, 0.695], [0.341, 0.491]) ([0.553, 0.697], [0.345, 0.493]), ([0.547, 0.689], [0.349, 0.493]) ([0.548, 0.689], [0.347, 0.491]), ([0.548, 0.691], [0.351, 0.493]) ([0.502, 0.724], [0.345, 0.451]), ([0.503, 0.724], [0.343, 0.450]) ([0.503, 0.726], [0.347, 0.451]), ([0.507, 0.730], [0.331, 0.451]) ([0.508, 0.730], [0.329, 0.450]), ([0.508, 0.731], [0.333, 0.451]) ([0.502, 0.724], [0.337, 0.451]), ([0.503, 0.724], [0.334, 0.450]) ([0.503, 0.726], [0.338, 0.451]), ([0.527, 0.689], [0.345, 0.481]) ([0.528, 0.689], [0.343, 0.479]), ([0.528, 0.691], [0.347, 0.481]) ([0.533, 0.695], [0.329, 0.479]), ([0.532, 0.695], [0.331, 0.481]) ([0.533, 0.697], [0.333, 0.481]), ([0.527, 0.689], [0.337, 0.481]) ([0.528, 0.689], [0.334, 0.479]), ([0.528, 0.691], [0.338, 0.481])}	S: 0.221 H: 0.561	3
$Y_4$	{([0.635, 0.811], [0.318, 0.485]), ([0.634, 0.811], [0.319, 0.483]) ([0.625, 0.805], [0.318, 0.485]), ([0.624, 0.805], [0.319, 0.483]) ([0.632, 0.808], [0.319, 0.487]), ([0.631, 0.808], [0.321, 0.485]) ([0.622, 0.801], [0.319, 0.487]), ([0.621, 0.801], [0.321, 0.485]) ([0.701, 0.811], [0.267, 0.408]), ([0.700, 0.811], [0.268, 0.406]) ([0.693, 0.805], [0.267, 0.408]), ([0.693, 0.805], [0.268, 0.406]) ([0.698, 0.808], [0.268, 0.409]), ([0.698, 0.808], [0.270, 0.408]) ([0.691, 0.801], [0.268, 0.409]), ([0.690, 0.801], [0.270, 0.408])}	S: 0.401 H: 0.689	1

Based on the above expression, the following several steps will ensure the ranking implementation and the acquisition of the best solution with respect to this example:

• Step 1. According to Table 2, four decision matrices ${\zeta }^m={({\psi }_{ij}^m)}_{n_1\times n_2}$ are provided by four experts $D_i\begin{array}{c}\end{array}i=1,2,3,4$ (see Table 3, Table 4, Table 5 and Table 6), and four normalized matrices are shown in the Table 7, Table 8, Table 9 and Table 10.
• Step 2. Solving programming to obtain $q=2$.

  $$\begin{array}{c}\begin{array}{c}\begin{array}{cc}\min & q\end{array}\end{array}\\ \begin{array}{cc}s.t.& \left\{\begin{array}{l}0\le {(M_{{\xi }_{ij}}^{m+})}^q+{(M_{{\xi }_{ij}}^{m+})}^q\le 1\\ q\in \{1,2,\cdots \}\\ i\in \{1,2,3,4\}\\ j\in \{1,2,3,4\}\\ m\in \{1,2,3,4\}\end{array}\right.\end{array}\end{array}$$
• Step 3. By Table 2 and the Equation (25), we obtain the values of the score function $V_S({\eta }_{ij}^m)\begin{array}{c}\end{array}m=1,2,\cdots ,4$, where the values of the accuracy function $V_H({\eta }_{ij}^m)\begin{array}{c}\end{array}m=1,2,\cdots ,4$ is not necessary provided, because the values of $V_S({\eta }_{ij}^m)\begin{array}{c}\end{array}m=1,2,\cdots ,4$ are not equal to each other.
• Step 4. Based on $\lambda$-fuzzy measure value $g_i$ provided in Table 2, we have the parameter value ${\gamma }_1=-0.4568$ by the Equation (27).
• Step 5. From the order relation of GIVqROHFEs, the order of $4$ GIVqROHFEs ${\eta }_{ij}^1,{\eta }_{ij}^2,\cdots ,{\eta }_{ij}^4$ for $D_i\begin{array}{c}\end{array}i=1,2,\cdots ,4$ and the ordered fuzzy measure values $g(X_{\delta (i)})$ of $X_{\delta (i)}=\{D_{\delta (1)},D_{\delta (2)},\cdots ,D_{\delta (i)},\}$ are, respectively, shown in Table 11 and Table 12.
• Step 6. For generalization, taking the value ${\lambda }_1=1$ and using the GIVqROHFCA operator (29) to obtain the collective GIVqROHF matrix $\eta ={({\eta }_{ij})}_{n_1\times n_2}$ (see Table 13).
• Step 7. We use the Equations (31) and (32) to yield the values $V_S({\eta }_{ij})\begin{array}{c}\end{array}j=1,2,\cdots ,4$ of the score function. Here the ones of the accuracy function $V_H({\eta }_{ij})\begin{array}{c}\end{array}j=1,2,\cdots ,4$ are not necessarily provided for the similar sake of Step 2.
• Step 8. By the Table 2, $\{{\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4\}=\{0.3,0.25,0.35,0.2\}$ and the parameter value ${\gamma }_2=-0.233$ is calculated by (33).
• Step 9. The ordered fuzzy measure values $\vartheta (X_{\delta (i)})$ of $X_{\delta (i)}=\{c_{\delta (1)},\cdots ,c_{\delta (k)},\cdots ,c_{\delta (i)},\}$ for any $Y_i\begin{array}{c}\end{array}i=1,2,\cdots ,4$ are calculated by the Equation (34) (see Table 14).
• Step 10. Applying the GIVqROHFCA operator (35) to derive the collective value ${\eta }_i$ of the alternative $Y_i\begin{array}{c}\end{array}i=1,2,\cdots ,4$ (see Table 15).
• Step 11. By the Equation (37), calculating $V_S({\eta }_i)$ of $Y_i$ and obtaining the descending order of $4$ alternatives $Y_1\ge Y_2\ge Y_4\ge Y_3$, the best one is $Y_1$.
• Step 12. End.

6.2. Sensitivity Experience of the Parameter $\lambda$ of the GIVqROHFCA and GIVqROHFCGM Operators

From the definition of fuzzy measure, the parameters $0<{\gamma }_i<+\infty \begin{array}{c}\end{array}(i=1,2)$ present the positive interaction among the decision makers or decision attributes, and the negative interaction and the independent case are, respectively, symbolized by the parameter value $-1<{\gamma }_1,{\gamma }_2<0$ and ${\gamma }_1={\gamma }_2=0$. Based on the different combinations of the fuzzy density $g_1,g_2,g_3,g_4$ and ${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$, the fuzzy density values of decision experts and attributes are listed in Table 16. For the same input data and the same $\lambda$-fuzzy measure $g_i,{\vartheta }_i$, the parameter value $\lambda$ is changed from 0.1 to 30.1 in several different values, and the last results are shown in Figure 1, Figure 2 and Figure 3.

Table 16. Introduction for 9 kinds of fuzzy density combination of the positive, independent and negative interaction among decision makers and among attributes.

$\begin{array}{cc}{\mathit{\gamma }}_1& {\mathit{\gamma }}_2\end{array}$	$$\begin{gathered} -1<{\mathit{\gamma }}_2<0 \\ {\mathit{\gamma }}_2=-0.4290 \\ \mathbf{Negative} \end{gathered}$$	$$\begin{gathered} {\mathit{\gamma }}_2=0 \\ \mathbf{Independent} \end{gathered}$$	$$\begin{gathered} 0<{\mathit{\gamma }}_2<\mathit{\infty } \\ {\mathit{\gamma }}_2=0.3542 \\ \mathbf{Positive} \end{gathered}$$
$\begin{array}{c}-1<{\gamma }_1<0\\ {\gamma }_1=-0.4232\end{array}$ negative	$\begin{array}{l}{g}_1=0.25,g_2=0.5,\\ g_3=0.35,g_4=0.1\end{array}$	$\begin{array}{l}{g}_1=0.25,g_2=0.5,\\ g_3=0.35,g_4=0.1\end{array}$	$\begin{array}{l}{g}_1=0.25,g_2=0.5,\\ g_3=0.35,g_4=0.1\end{array}$
	$\begin{array}{l}{\vartheta }_1=0.2,{\vartheta }_2=0.35,\\ {\vartheta }_3=0.5,{\vartheta }_4=0.15\end{array}$	$\begin{array}{l}{\vartheta }_1=0.1,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.45,{\vartheta }_4=0.2\end{array}$	$\begin{array}{l}{\vartheta }_1=0.1,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.4,{\vartheta }_4=0.15\end{array}$
${\gamma }_1=0$ independent	$\begin{array}{l}{g}_1=0.15,g_2=0.45,\\ g_3=0.3,g_4=0.1\end{array}$	$\begin{array}{l}{g}_1=0.15,g_2=0.45,\\ g_3=0.3,g_4=0.1\end{array}$	$\begin{array}{l}{g}_1=0.15,g_2=0.45,\\ g_3=0.3,g_4=0.1\end{array}$
	$\begin{array}{l}{\vartheta }_1=0.20,{\vartheta }_2=0.35,\\ {\vartheta }_3=0.50,{\vartheta }_4=0.15\end{array}$	$\begin{array}{l}{\vartheta }_1=0.1,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.45,{\vartheta }_4=0.2\end{array}$	$\begin{array}{l}{\vartheta }_1=0.10,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.40,{\vartheta }_4=0.15\end{array}$
$\begin{array}{c}0<{\gamma }_1<\infty \\ {\gamma }_1=0.5940\end{array}$ positive	$\begin{array}{l}{g}_1=0.15,g_2=0.4,\\ g_3=0.25,g_4=0.05\end{array}$	$\begin{array}{l}{g}_1=0.15,g_2=0.4,\\ g_3=0.25,g_4=0.05\end{array}$	$\begin{array}{l}{g}_1=0.15,g_2=0.4,\\ g_3=0.25,g_4=0.05\end{array}$
	$\begin{array}{l}{\vartheta }_1=0.2,{\vartheta }_2=0.35,\\ {\vartheta }_3=0.5,{\vartheta }_4=0.15\end{array}$	$\begin{array}{l}{\vartheta }_1=0.1,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.45,{\vartheta }_4=0.2\end{array}$	$\begin{array}{l}{\vartheta }_1=0.10,{\vartheta }_2=0.25,\\ {\vartheta }_3=0.40,{\vartheta }_4=0.15\end{array}$

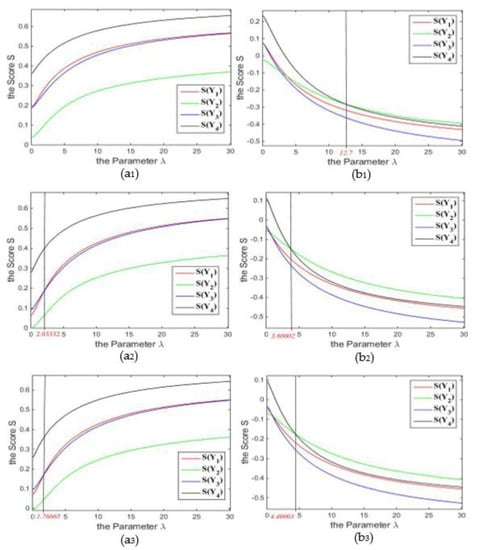
Figure 3. The illustration of sensitivity with respect to the parameter $\lambda$ in the new MAGDM based on the GIVqROHFCA and GIVqROHFCGM operator when the fuzzy density values $g_1,g_2,g_3,g_4$ of fuzzy density of experts and the fuzzy density values ${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$ of attributes are determined: (1) The sensitivity of the GIVqROHFCA (a₁) and GIVqROHFCGM (b₁) operator with respect to the $\lambda$ value when $g_1=0.25,g_2=0.5,g_3=0.35,g_4=0.1$ and ${\vartheta }_1=0.2,{\vartheta }_2=0.35,{\vartheta }_3=0.5,{\mu }_4=0.15$; (2) The sensitivity of the GIVqROHFCA (a₂) and GIVqROHFCGM (b₂) operator with respect to the $\lambda$ value when $g_1=0.25,g_2=0.5,g_3=0.35,g_4=0.1$ and ${\vartheta }_1=0.1,{\vartheta }_2=0.25,{\vartheta }_3=0.45,{\mu }_4=0.2$; (2) The sensitivity of the GIVqROHFCA (a₃) and GIVqROHFCGM (b₃) operator with respect to the $\lambda$ value when $g_1=0.25,g_2=0.5,g_3=0.35,g_4=0.1$ and ${\vartheta }_1=0.1,{\vartheta }_2=0.25,{\vartheta }_3=0.4,{\vartheta }_4=0.15$.

From the Figure 3, Figure 4 and Figure 5, some conclusions are obtained as follows:

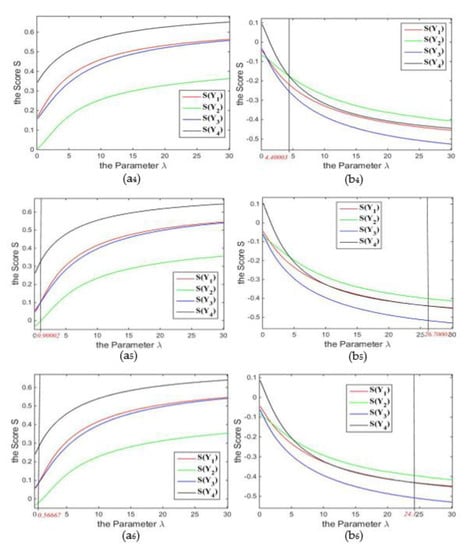
Figure 4. The illustration of sensitivity with respect to the parameter $\lambda$ in the new MAGDM based on the GIVqROHFCA and GIVqROHFCGM operator when the fuzzy density values $g_1,g_2,g_3,g_4$ of fuzzy density of experts and the fuzzy density values ${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$ of attributes are determined: (1) The sensitivity of the GIVqROHFCA (a₄) and GIVqROHFCGM (b₄) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.45,g_3=0.3,g_4=0.1$ and ${\vartheta }_1=0.2,{\vartheta }_2=0.35,{\vartheta }_3=0.5,{\vartheta }_4=0.15$; (2) The sensitivity of the GIVqROHFCA (a₅) and GIVqROHFCGM (b₅) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.45,g_3=0.3,g_4=0.1$ and ${\vartheta }_1=0.1,{\vartheta }_2=0.25,{\vartheta }_3=0.45,{\vartheta }_4=0.2$; (3) The sensitivity of the GIVqROHFCA (a₆) and GIVqROHFCGM (b₆) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.45,g_3=0.3,g_4=0.1$ and ${\vartheta }_1=0.1,{\vartheta }_2=0.25,{\vartheta }_3=0.4,{\vartheta }_4=0.15$.

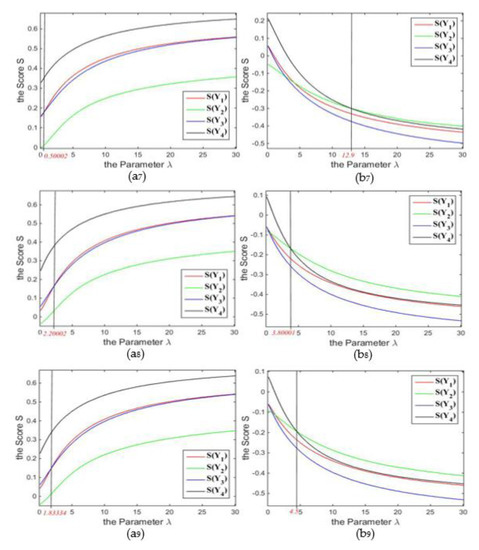
Figure 5. The illustration of sensitivity with respect to the parameter $\lambda$ in the new MAGDM based on the GIVqROHFCA and GIVqROHFCGM operator when the fuzzy density values $g_1,g_2,g_3,g_4$ of the fuzzy density values of experts and the fuzzy density values ${\vartheta }_1,{\vartheta }_2,{\vartheta }_3,{\vartheta }_4$ of attributes are determined: (1) The sensitivity of the GIVqROHFCA (a₇) and GIVqROHFCGM (b₇) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.40,g_3=0.25,g_4=0.05$ and ${\vartheta }_1=0.20,{\vartheta }_2=0.35,{\vartheta }_3=0.50,{\vartheta }_4=0.15$; (2) The sensitivity of the GIVqROHFCA (a₈) and GIVqROHFCGM (b₈) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.40,g_3=0.25,g_4=0.05$ and ${\vartheta }_1=0.10,{\vartheta }_2=0.25,{\vartheta }_3=0.45,{\vartheta }_4=0.20$; (3) The sensitivity of the GIVqROHFCA (a₉) and GIVqROHFCGM (b₉) operator with respect to the $\lambda$ value when $g_1=0.15,g_2=0.40,g_3=0.25,g_4=0.05$ and ${\vartheta }_1=0.10,{\vartheta }_2=0.25,{\vartheta }_3=0.40,{\vartheta }_4=0.15$.

(1) For the GIVqROHFCA operator-based MAGDM method, the score value of the output argument is increasing concerning the parameter value $\lambda$; the score presented by the new method applying the GIVqROHFCGM operator is decreasing with the $\lambda$ value. The monotonic statement of the proposed approach is proven according to the monotonicity of the GIVqROHFCA and GIVqROHFCGM operator;

(2) The approach on the basis of the GIVqROHFCA operator is not sensitive with respect to the $\lambda$ value when the parameter $\lambda$ does not take smaller real values; however, the insensitivity of the GIVqROHFCGM-based approach is usually subject to large real number values, though the critical value of the sensitivity and insensitivity is smaller for some special cases;

(3) When the interaction of attributes is negative, the GIVqROHFCA- and GIVqROHFCGM-based MAGDM methods are basically not sensitive except for the case that the parameter $\lambda \le 0.50002$ holds according to the positive interaction of experts;

(4) When decision experts are in the positive state and attributes are not in the negative, the two approaches are sensitive if only if the $\lambda$ value is no more than the real number 4.5;

(5) If decision experts are independent and attributes are not in a negative state, the two approaches are not sensitive when the $\lambda$ value is a larger real number, at least the parameter $\lambda \ge 24.1$;

(6) Provided that the interaction of experts is negative and attributes of the alternatives are not in negative state, the proposed approaches are not sensitive when the $\lambda$ value is a not a small real number and the minimum of the parameter $\lambda$ is equal to 0.40003.

6.3. Comparison Experience with the Existing MAGDM Approaches Based on the Different Hesitant Fuzzy Aggregation Rules

For illustrating the comprehensiveness and rationality of the new MAGDM approach, the aforementioned example is demonstrated by applying the HF-MAGDM method [57], PHF-MAGDM method [58], IVHF-MAGDM method [61], IVIHF-MAGDM method [19], IVqROF-MAGDM [26], IVqRDHF-MAGDM [49] and presented GIVqROHF-MAGDM method. Thus, the GIVqROHFN is, respectively, transformed into the HFN, PHFN, IVHFN, IVIHFN and IVqRDHFN by the correspondence in Table 17. In [1,2,19,20], the weight values of the experts and attributes are, respectively, obtained by normalizing the fuzzy density values of the experts and attributes of the GIVqROHFCA operator in the IVqROHF-MAGDM method, which is explained in the annotation of the Table 18.

Table 17. Correspondence illustration of the IVqROHFN, HFN, PHFN, IVHFN, IVIHFN, IVqROFN and IVqRDHFN.

GIVqROHFN	HFN	PHFN	IVHFN
$\left\{\begin{array}{c}([M_{{\xi }_{{}_{ij}}}^{m-},M_{{\xi }_{{}_{ij}}}^{m+}],\\ [Z_{{\xi }_{{}_{ij}}}^{m-},Z_{{\xi }_{{}_{ij}}}^{m+}])\end{array}\right\}$	$\left\{\frac{M_{{\xi }_{{}_{ij}}}^{m-}+M_{{\xi }_{{}_{ij}}}^{m+}}{2}\right\}$	$\left\{M_{{\xi }_{{}_{ij}}}^{m+}\right\},\left\{Z_{{\xi }_{{}_{ij}}}^{m+}\right\}$	$\left\{[M_{{\xi }_{{}_{ij}}}^{m-},M_{{\xi }_{{}_{ij}}}^{m+}]\right\}$
IVIHFN	IVqROFN	IVqRDHFN
$\left\{\begin{array}{c}([{(M_{{\xi }_{{}_{ij}}}^{m-})}^2,{(M_{{\xi }_{{}_{ij}}}^{m+})}^2],\\ [{(Z_{{\xi }_{{}_{ij}}}^{m-})}^2,{(Z_{{\xi }_{{}_{ij}}}^{m+})}^2])\end{array}\right\}$	$\left(\begin{array}{l}\left[\frac{{\displaystyle {\sum }_{{\xi }_{{}_{ij}}\in {\eta }_{ij}^m}{M}_{{\xi }_{{}_{ij}}}^{m-}}}{\#{\eta }_{ij}^m},\frac{{\displaystyle {\sum }_{{\xi }_{{}_{ij}}\in {\eta }_{ij}^m}{M}_{{\xi }_{{}_{ij}}}^{m+}}}{\#{\eta }_{ij}^m}\right],\\ \left[\frac{{\displaystyle {\sum }_{{\xi }_{{}_{ij}}\in {\eta }_{ij}^m}{Z}_{{\xi }_{{}_{ij}}}^{m-}}}{\#{\eta }_{ij}^m},\frac{{\displaystyle {\sum }_{{\xi }_{{}_{ij}}\in {\eta }_{ij}^m}{Z}_{{\xi }_{{}_{ij}}}^{m+}}}{\#{\eta }_{ij}^m}\right]\end{array}\right)$	$\left\{\begin{array}{c}\left\{[M_{{\xi }_{{}_{ij}}}^{m-},M_{{\xi }_{{}_{ij}}}^{m+}]\right\},\\ \left\{[Z_{{\xi }_{{}_{ij}}}^{m-},Z_{{\xi }_{{}_{ij}}}^{m+}]\right\}\end{array}\right\}$

Table 18. The ranking Comparison of the different aggregation methods in [19,26,49,57,58,61] and this paper.

Method	Operator	${\mathit{Y}}_1$	${\mathit{Y}}_2$	${\mathit{Y}}_3$	${\mathit{Y}}_4$	Oder	Best
HFN [57]	GHFWA 3,4 $\lambda =1$	0.588	0.495	0.574	0.676	$Y_4>Y_1>Y_3>Y_2$	$Y_4$
PHFN [58]	PHFWA 3,4	0.318	0.170	0.446	0.651	$Y_4>Y_3>Y_1>Y_2$	$Y_4$
IVHFN [61]	IVHFWBM 3,4 $p=q=1$	0.140	0.109	0.137	0.134	$Y_1>Y_3>Y_4>Y_2$	$Y_1$
IVIHFN [19]	GIVIHFWA 3,4 $\lambda =1$	0.166	0.021	0.159	0.329	$Y_4>Y_1>Y_3>Y_2$	$Y_4$
IVqROFN [26]	IVqROFWA 3,4	0.173	0.196	0.086	0.371	$Y_4>Y_2>Y_1>Y_3$	$Y_4$
IVqRDHFN [49]	IVqRDHFWMM 3,4	0.201	0.059	0.382	0.226	$Y_3>Y_4>Y_1>Y_2$	$Y_3$
GIVqROHFN (In this paper)	GIVqROHFCA 1,2 $\lambda =1$	0.232	0.062	0.221	0.401	$Y_4>Y_1>Y_3>Y_2$	$Y_4$

¹ The fuzzy density of experts in the GIVqROHFCA operator: $g_1=0.25,g_2=0.5,g_3=0.35,g_4=0.1$; ² The fuzzy density of attributes in the GIVqROHFCA operator: ${\vartheta }_1=0.20,{\vartheta }_2=0.35,{\vartheta }_3=0.50,{\vartheta }_4=0.15$; ³ The weight parameter of experts: $w_1=0.208,w_2=0.417,w_3=0.292,w_4=0.083$; ⁴ The weight parameter of attributes: ${\varpi }_1=0.167,{\varpi }_2=0.291,{\varpi }_3=0.417,{\varpi }_4=0.125$.

According to Table 18, we make an analysis and a discussion as follows:

(1) The ranking results and the best decision projects of the GIVqROHFN method are consistent with ones of the HFN and IVIHFN methods, which indicates that the MAGDM method of this paper is rational. In addition, the HFN and IVIHFN methods cannot deal with the GIVqROHF input arguments aggregated by the GIVqROHFN method. On the contrary, the GIVqROHF data can be transformed into hesitant fuzzy and interval-valued intuitionistic fuzzy data by a certain function pattern, which justly shows that this new method is effective as well as the GIVqROHFCA operator being a generalization of the GHFWA and GIVIHFWA operator;

(2) For the outputs of the PHFN, IVqROFN and GIVqROHFN methods, although the best decision projects are the same the ranking results have no uniformity. The key reason for this result is that the function transformation of the GIVqROHF input data brings out a loss of information from those original data. However, the GIVqROHFN method of this paper is proposed in order to aggregate GIVqROHF information, therefore information loss is avoided, which reveals that the GIVqROHFN method is more practical than the PHFN and IVqROFN methods from the perspective of application;

(3) The ranking results and the best decision projects of the IVHFN, IVqRDHFN and GIVqROHFN methods are totally different, which can be explained on the basis of three aspects: (a) Some information contained in GIVqROHF input arguments is lost when these input ones are transformed into the interval-valued hesitant fuzzy and interval-valued q-rung dual fuzzy data. Consequently, it is evident that this state effects the final decision making; (b) The IVHFWBM operator in the IVHFN method and the IVqRDHFWMM operator in the IVqRDHFN method are two different kinds of geometric mean operators; however, the GIVqROHFCA operator of the GIVqROHFN method, including operators of the HFN and IVIHFN methods, belongs to the arithmetic average series, the fusion mechanisms of which are different from each other; (c) The GIVqROHFN method takes into account the interactive phenomenon among decision experts and the one among attributes and usees fuzzy measure to describe it. Nevertheless, the IVHFN method, as well as the HFN, PHFN, IVIHFN, IVqROFN and IVqRDHFN methods, does not consider these interactions that are universal in many practical MAGDM problems with hesitant uncertain information such as Pythagorean fuzzy and interval-valued forms of different fuzzy states involving intuitionistic arguments and q-rung orthopair data. For instance, the fuzzy density of experts in the GIVqROHFCA operator $g_1=0.25,g_2=0.5,g_3=0.35,g_4=0.1$ represents that the interactive phenomenon among decision experts, and the fuzzy density of attributes ${\mu }_1=0.20,{\mu }_2=0.35,{\mu }_3=0.50,{\mu }_4=0.15$, illustrate relationships among attributes in the GIVqROHFCA operator;

(4) In addition to the IVHFWBM operator and IVqRDHFWMM operator, the GIVqROHFCA operator can be transformed into each operator in Table 18 by setting up the different parameter $\lambda$ and the q-rung orthopair value $q$, which can reasonably model the different hesitant fuzzy information in the decision-making process. Moreover, the new decision method for the GIVqROHF environment can enrich the mathematical tools to solve multiple attributes decision-making problems on the basis of the consideration with respect to the interaction among the decision makers.

To sum up, from the perspective of theory and application, the new MAGDM method is rational and effective, and more practical than decision methods in [1,2,19,20].

7. Conclusions and Future Studies

We first defined the GIVqROHFSs and studied a series of operational rules with respect to GIVqROHFEs, as well as their properties. Then, the aggregation techniques for dealing with the GIVqROHF information were focused: (a) the GIVqROHFCA and GIVqROHFCGM operators were introduced according to the fuzzy measure and fuzzy integration theory; and (b) The properties of these two operators were studied as well as the monotonicity of the GIVqROHFCA and GIVqROHFCGM operators in terms of the generalization parameter. Moreover, we used the GIVqROHFCA and GIVqROHFCGM operators to solve the MAGDM problem with multiple GIVqROHF attributes and introduced a kind of multiple GIVqROHF attributes information processing approach. Finally, some experiments were used to show the validity of this method, illustrate the monotonicity of the new approach concerning the parameter in the GIVqROHFCA and GIVqROHFCGM operators, and show the superiority and reliability of the GIVqROHFCA and GIVqROHFCGM method in solving the GIVqROHF problems. As a result, The main advantages of this work include three points: (1) extending hesitant fuzzy sets to the interval-valued q-rung orthopair fuzzy case and proposing two types of aggregation operators for the GIVqROHF information; (2) considering the interaction among decision makers and among attributes in decision problems, and dealing with this interrelationship by fuzzy measure; and (3) introducing the new decision method for the GIVqROHF environment and enriching the mathematical tools to solve multiple attributes decision-making problems. Therefore, the GIVqROHFs can play a core role in reasonably explaining interval-valued hesitancy of decision experts due to the lack of experience, ability and knowledge, and the Choquet integral can be used to effectively aggregate different opinions from decision makers based on the given fuzzy measure that can describe the interaction among those makers.

In the real world, a wealth of diversity or divergence of decision experts exists in the MAGDM process with multiple attributes as a result of different knowledge levels and social backgrounds. Therefore, it is important and of key practical significance how to achieve the agreement or consensus from decision makers for the provided alternatives to a maximum extent, and it has attracted much more attention as an interesting research topic in many fields. However, some similar works are not studied for MAGDM problems under the GIVqROHF information environment. Thus, for future attention, it will be very significant to develop a consensus mathematical model, studying how to obtain the fuzzy density of decision experts or attributes and how to determine the transformation methods between the GIVqROHF element and other hesitant fuzzy elements; it is also essential to investigate the application of the GIVPHFCA and GIVPHFCGM operators in wider research fields such as pattern recognition, personalized recommendation, information retrieval and uncertain programming and so on. In addition, it is also an important research interest to provide transformation approaches between the GIVqROHFs and other fuzzy information in the environment of Spherical, T-Spherical fuzzy sets, Complex q-rung orthopair fuzzy sets and complex spherical fuzzy sets.