Optical Torque Exerted on a Charged Sphere by a Polarized Bessel Beam
Abstract
1. Introduction
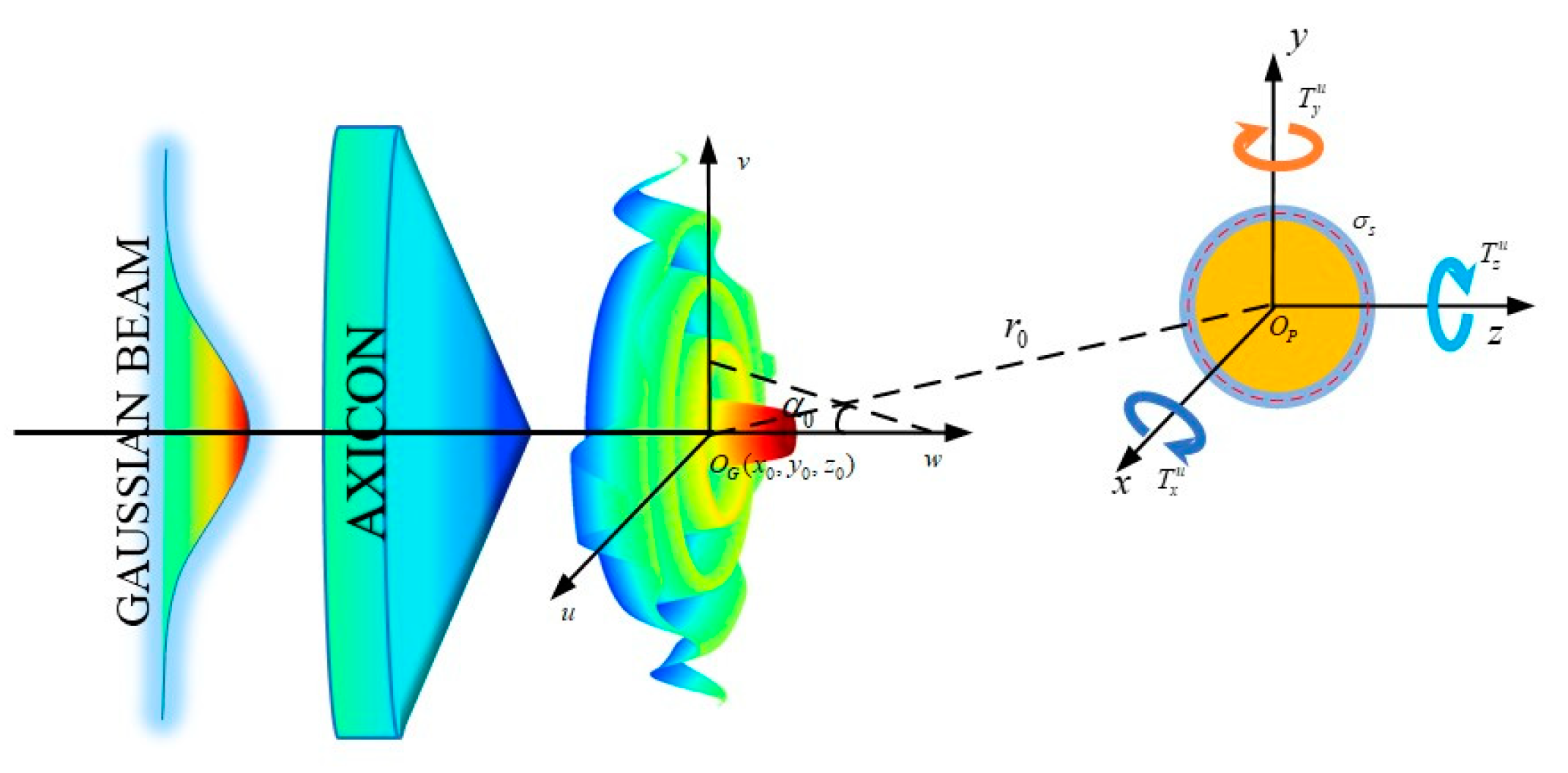
2. Optical Torque by an AGVBB on a Charged Sphere
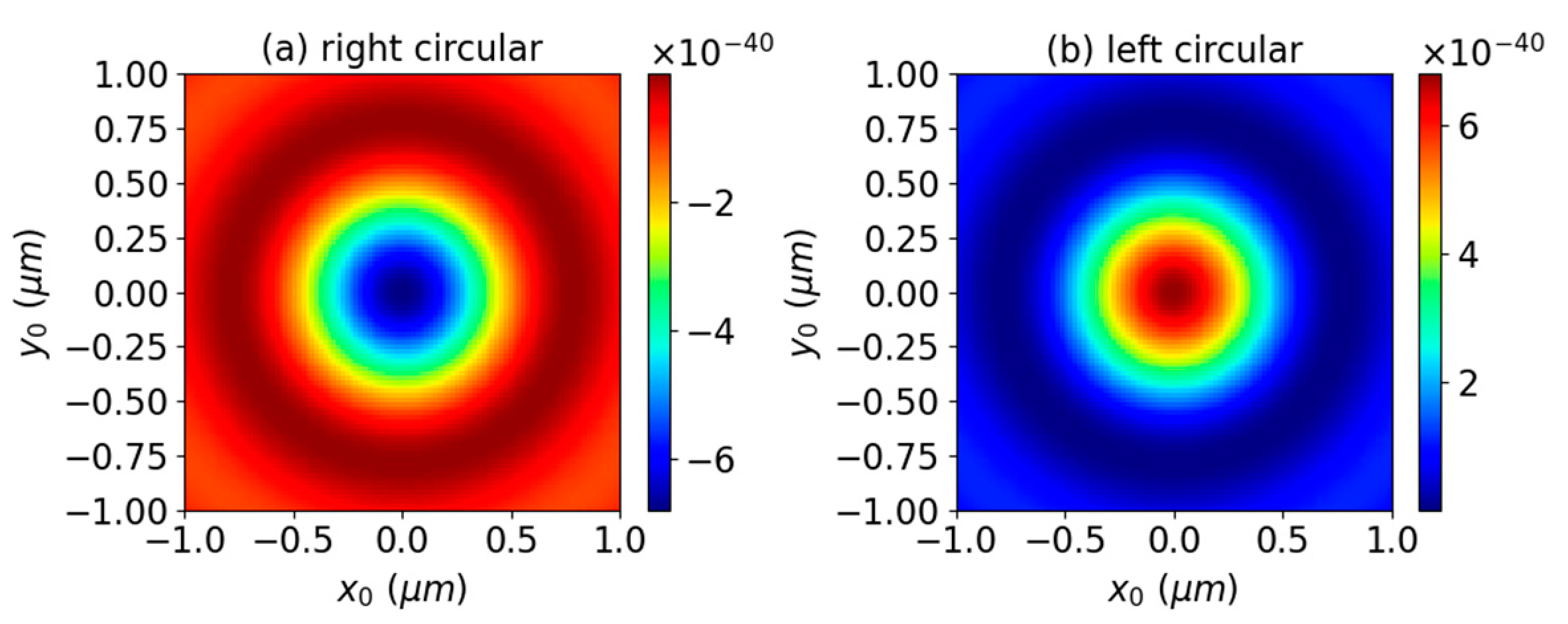
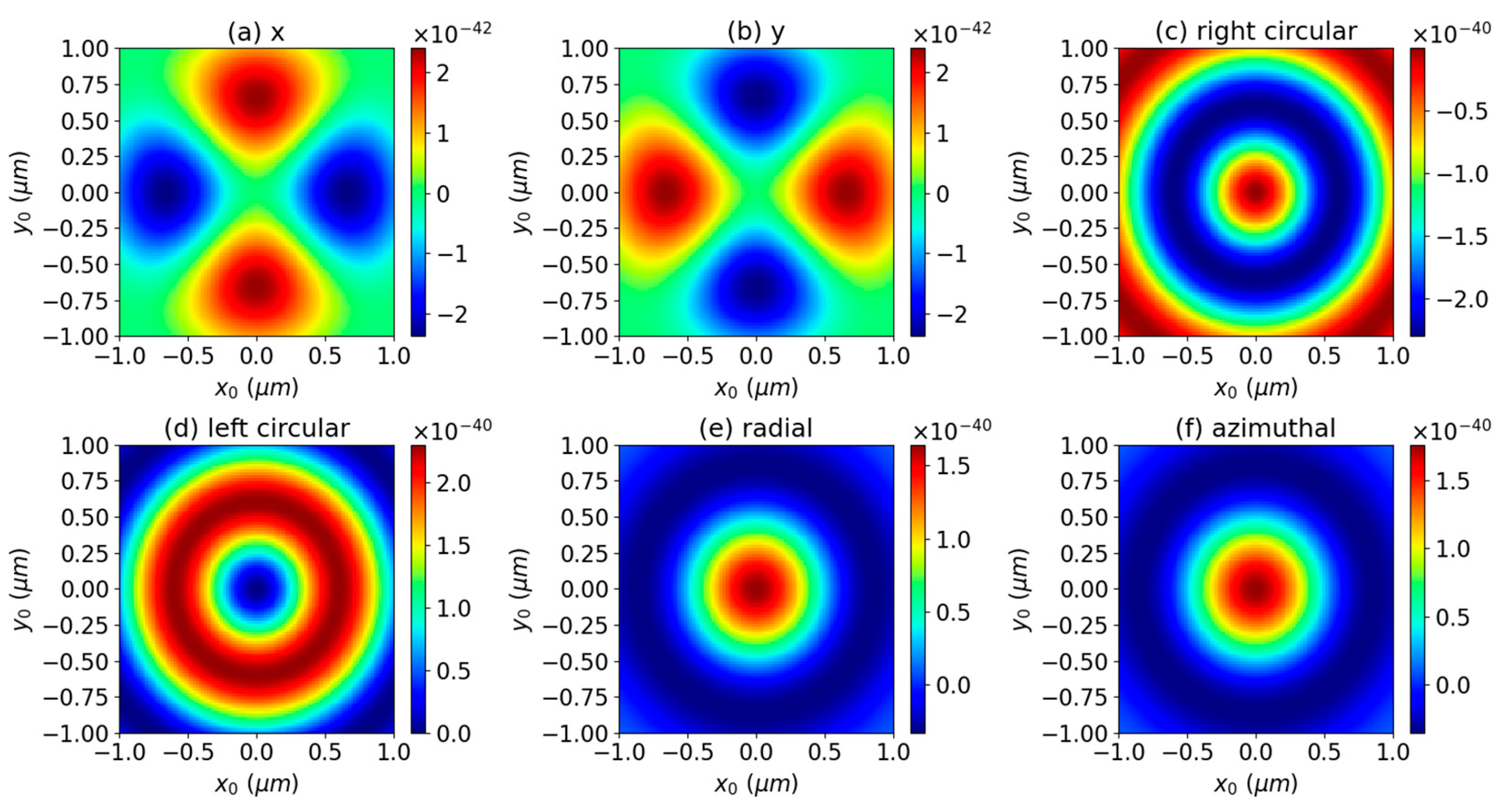
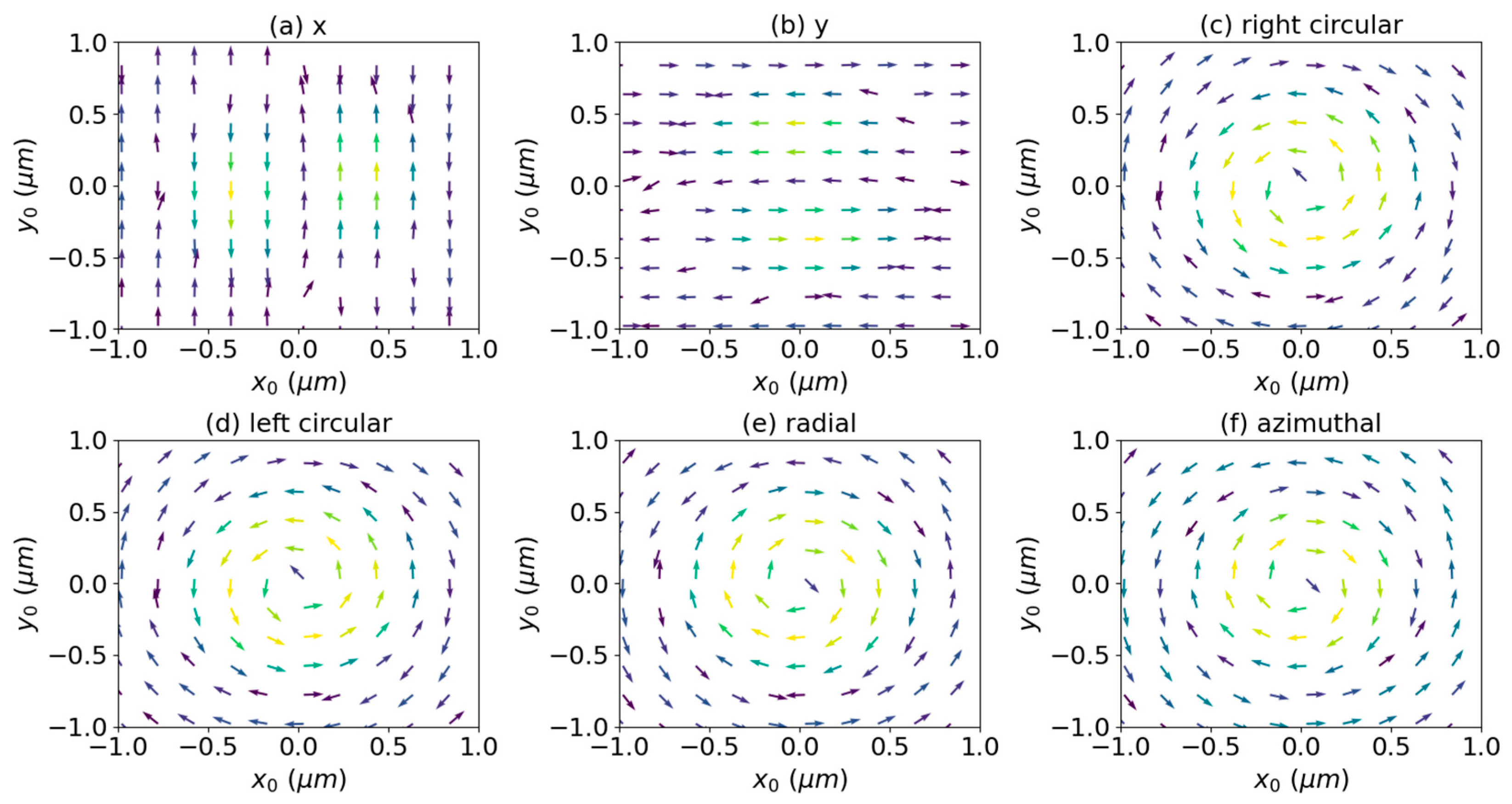
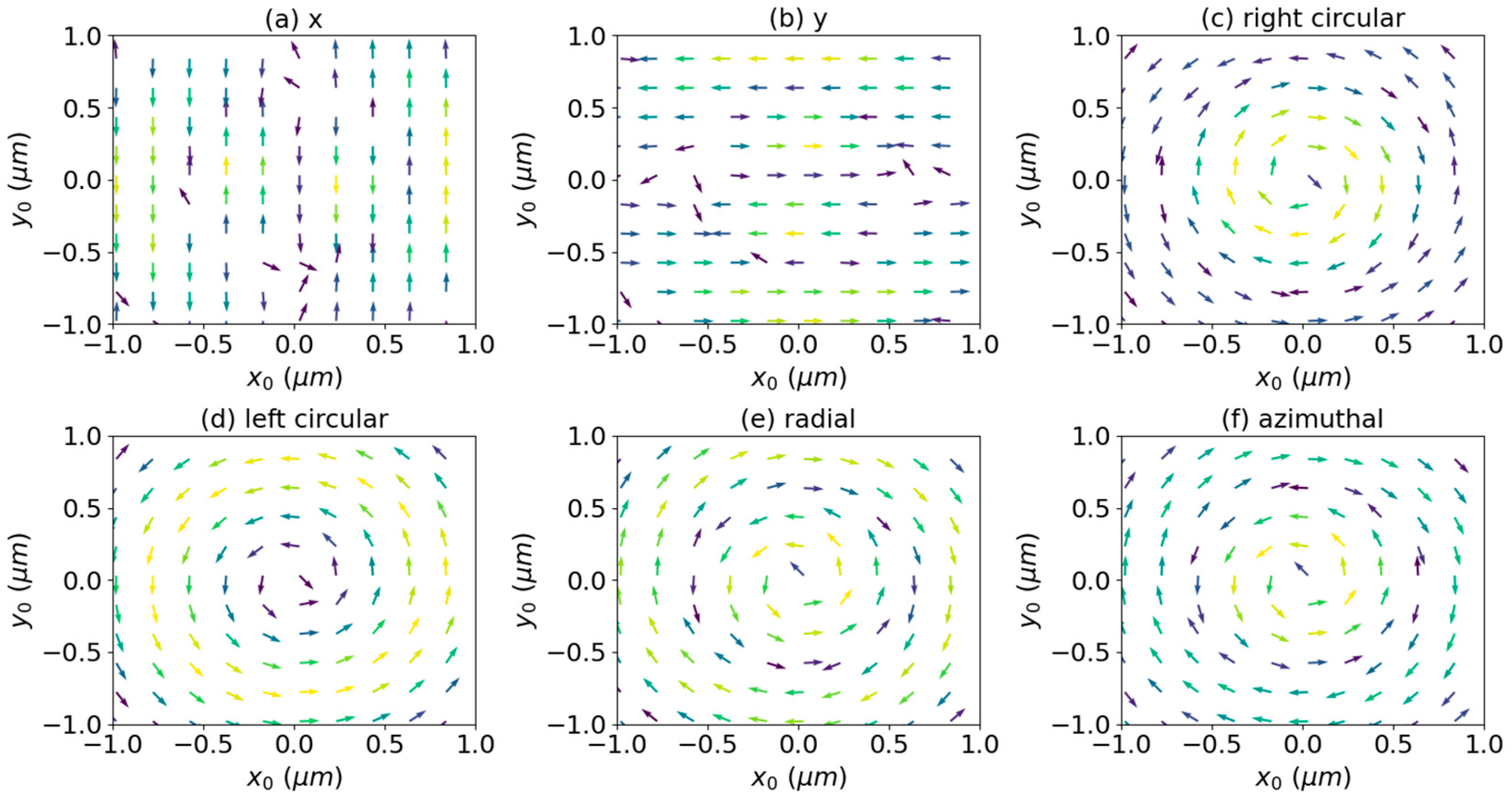
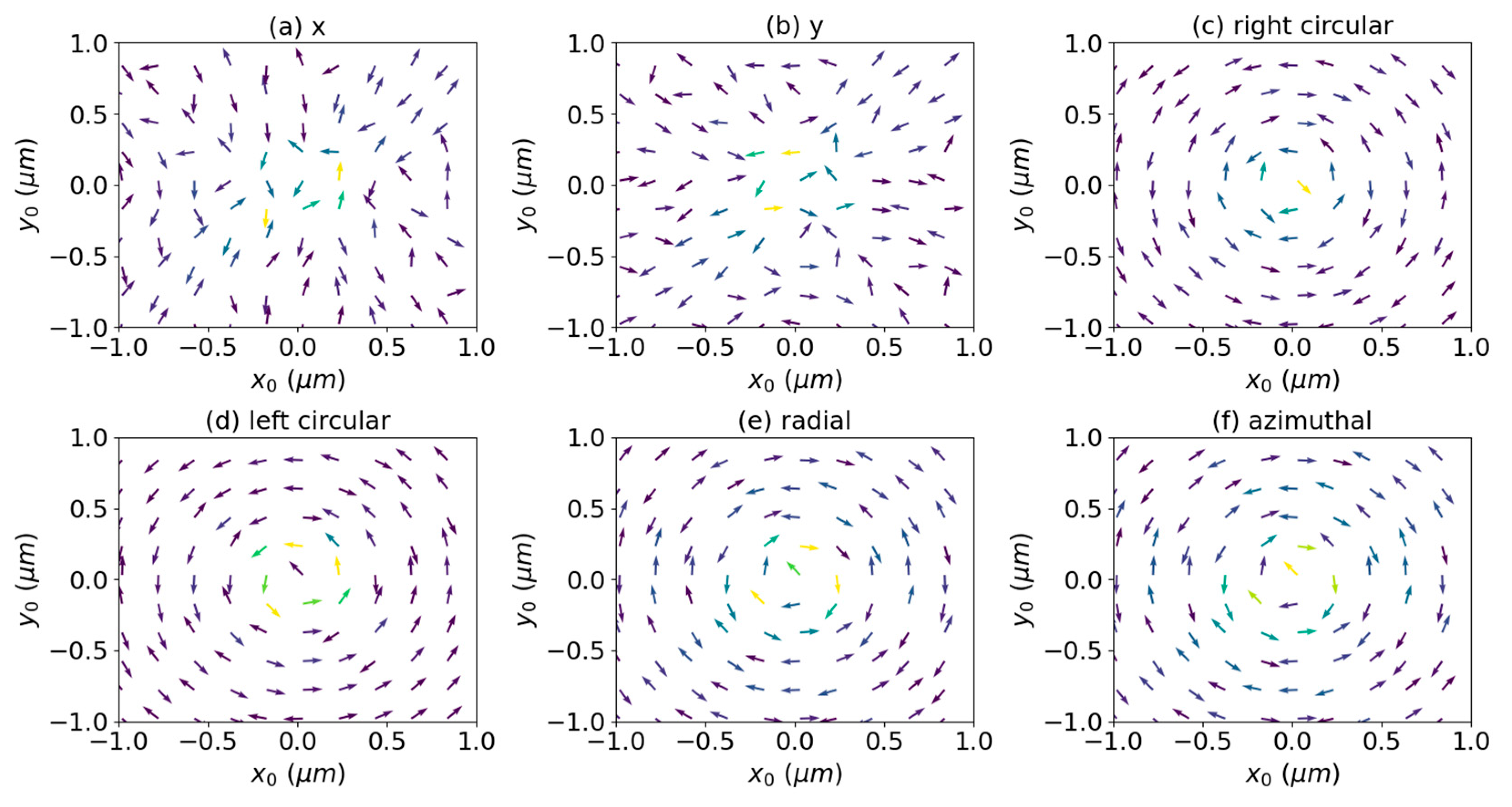
3. Numerical Results and Discussions
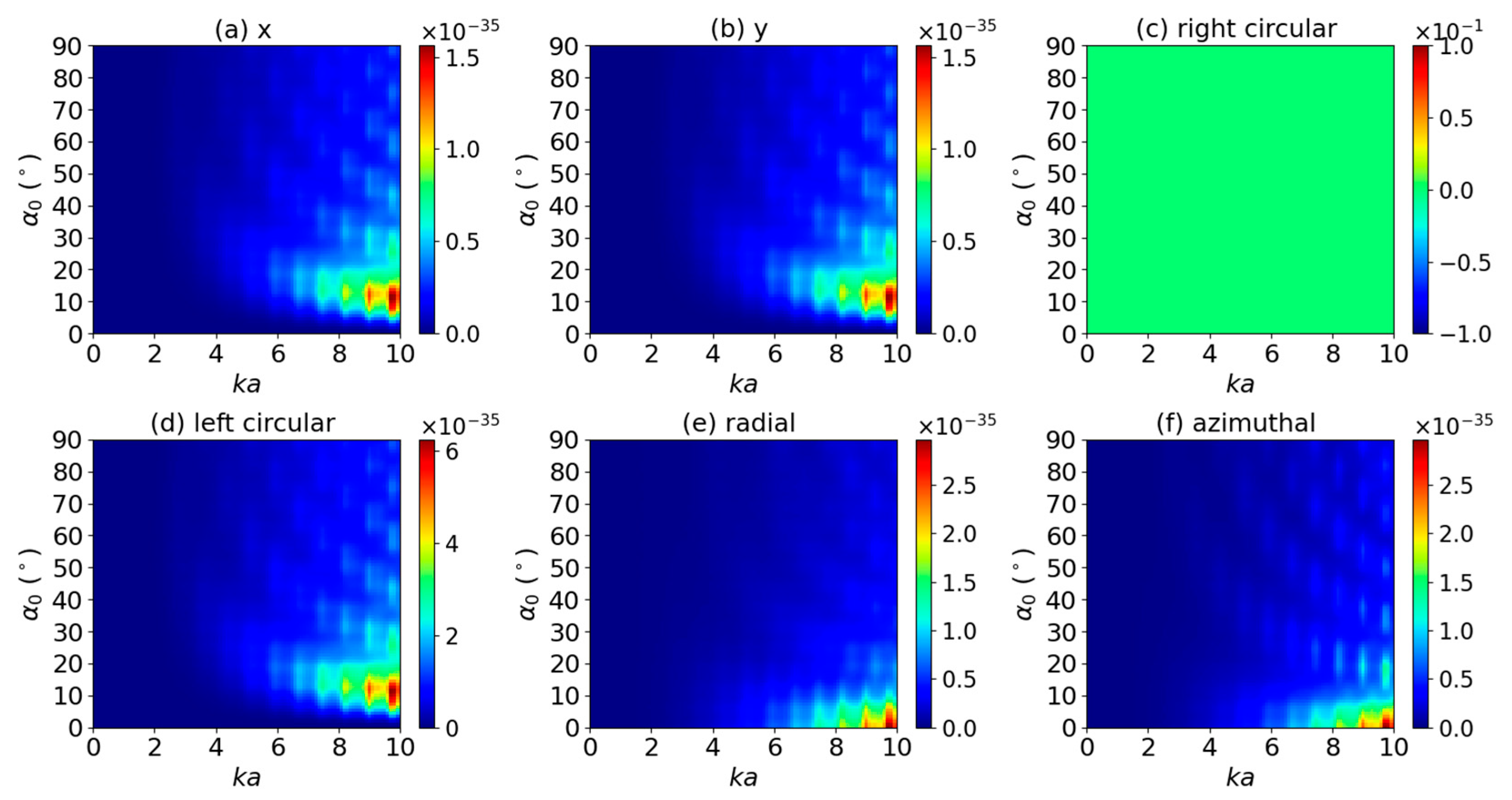
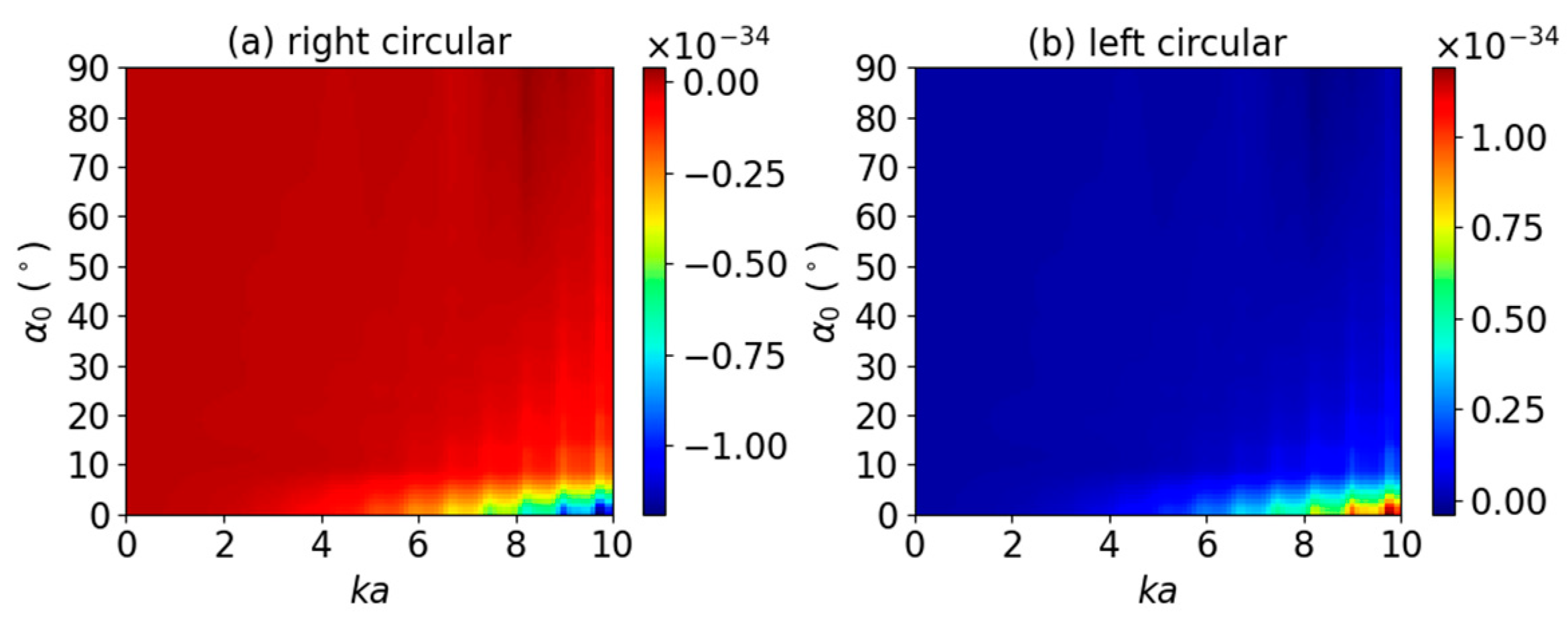
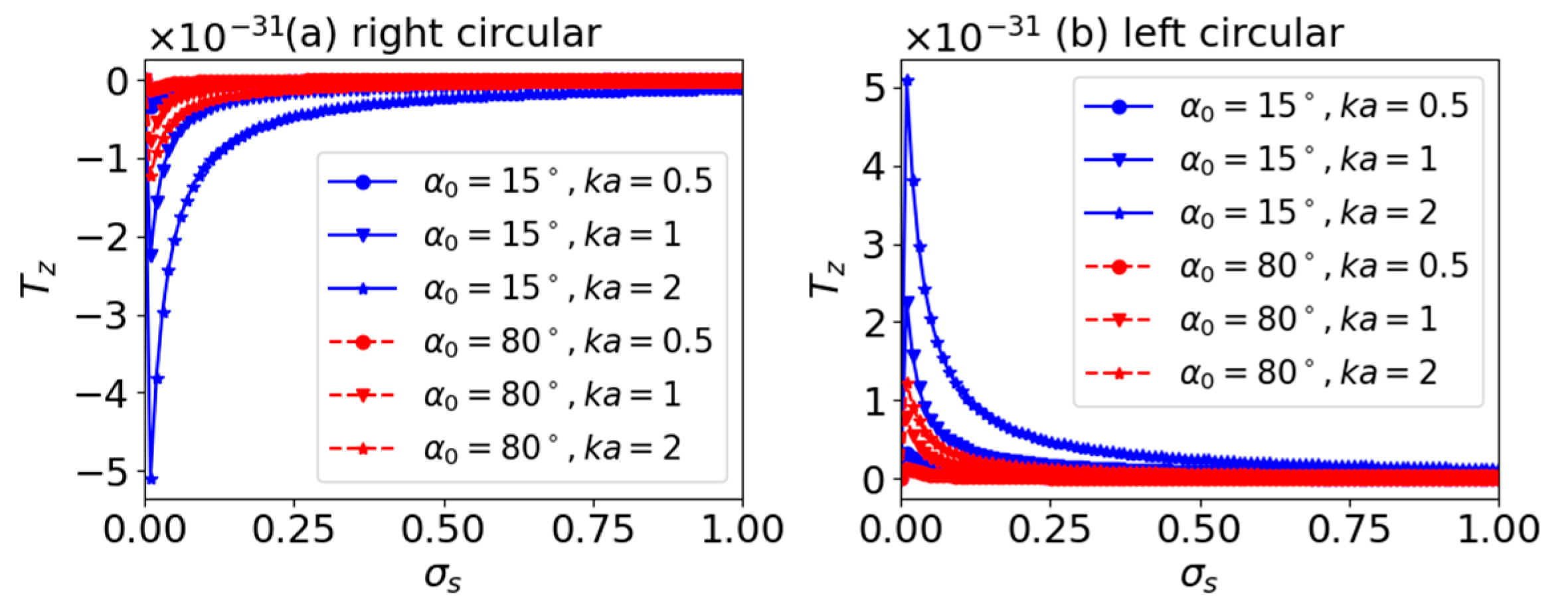
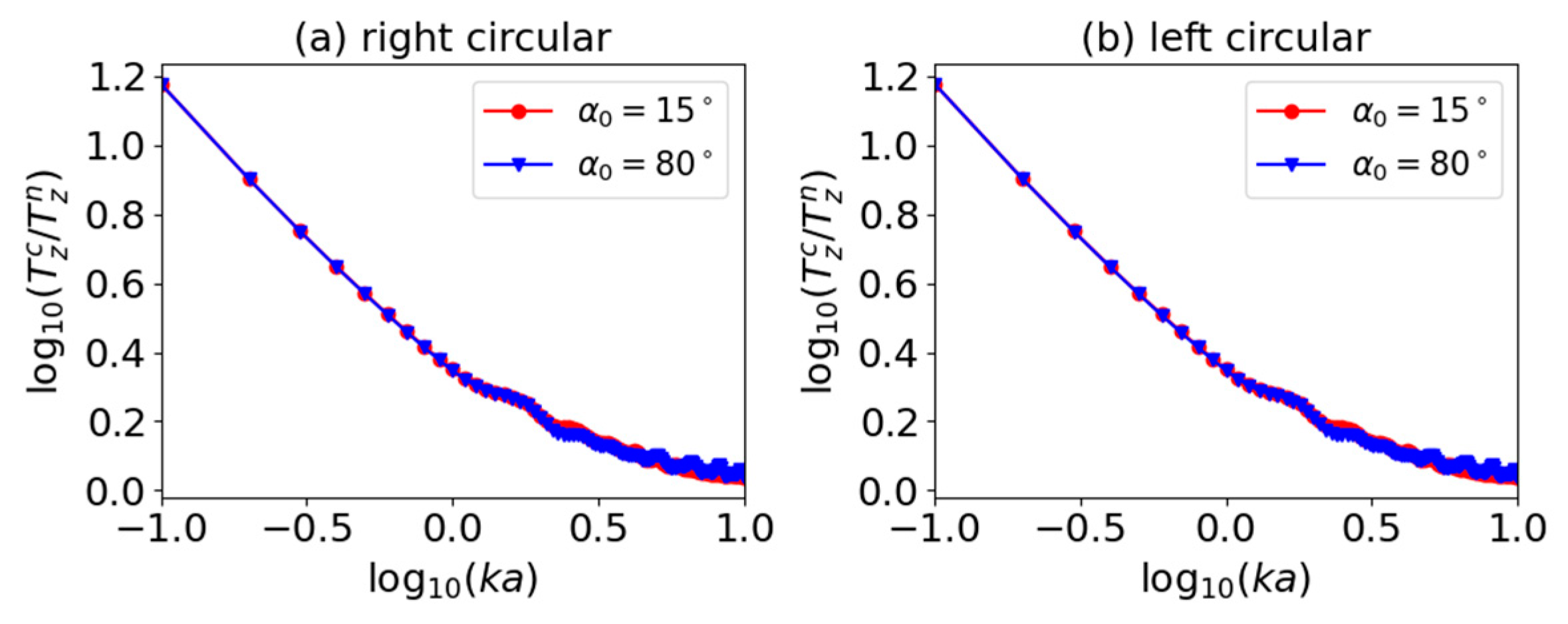
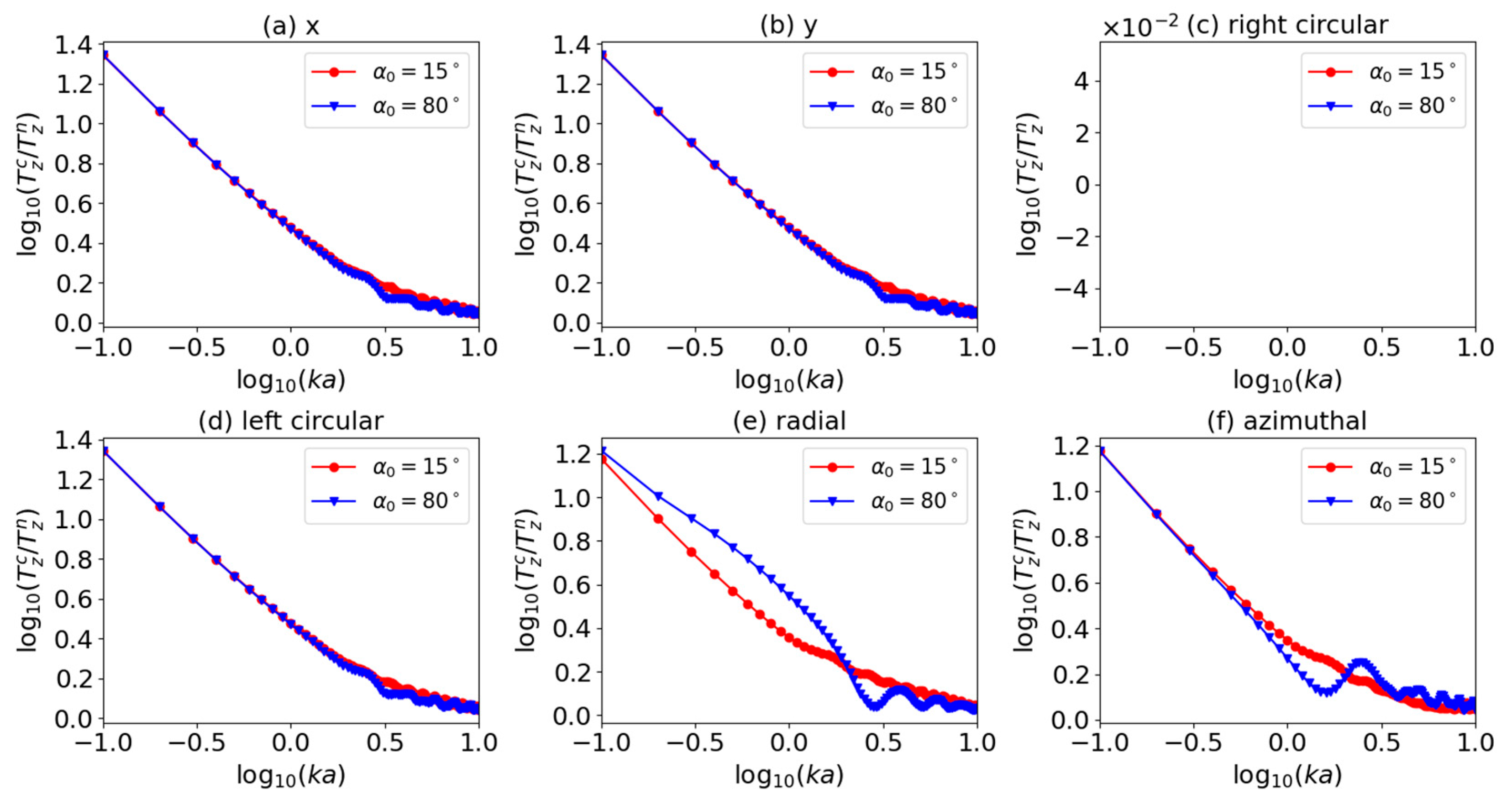
3.1. Axial Optical Torque
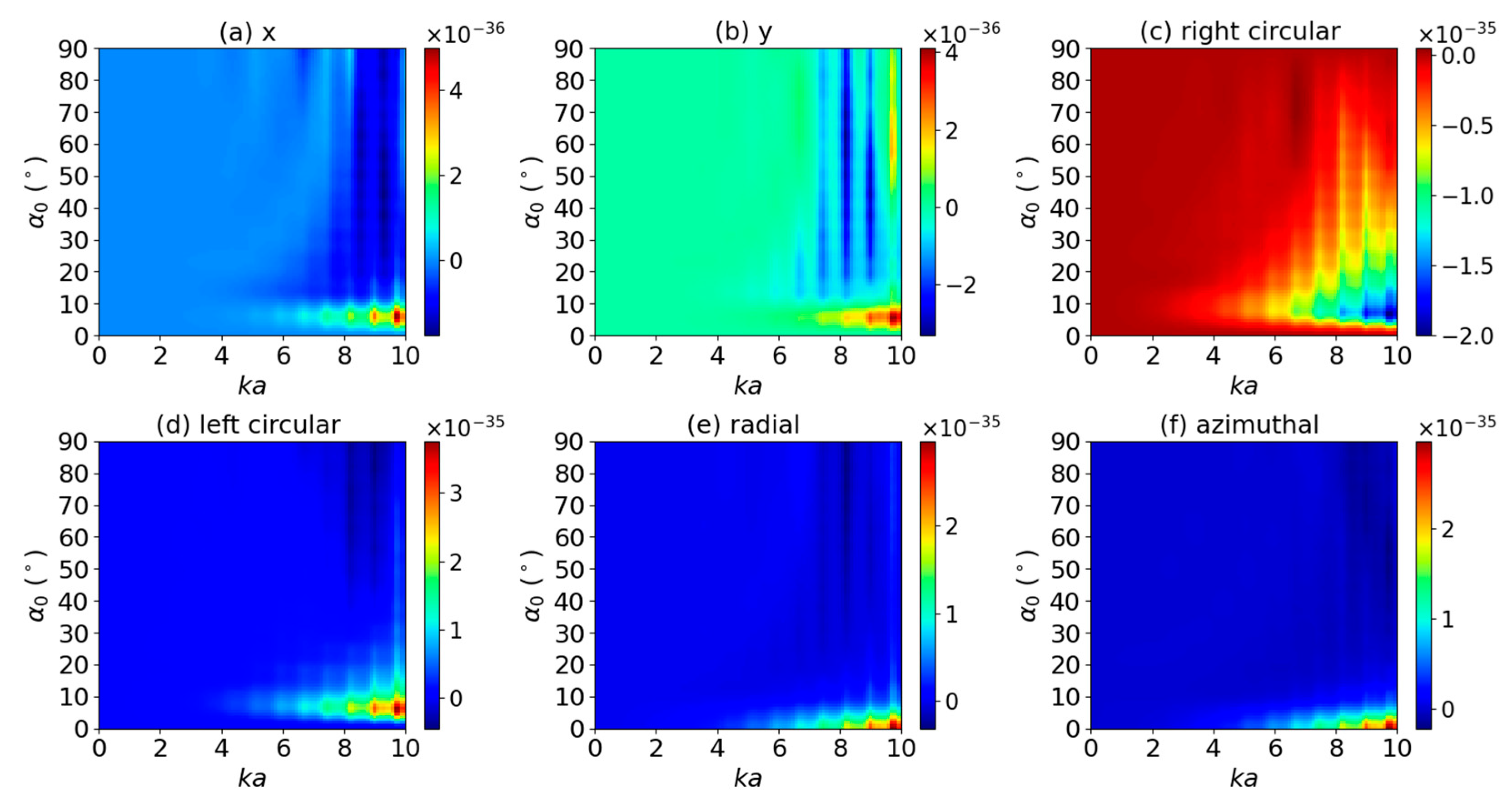
3.2. Transverse Optical Torque
3.3. Effect of Surface Charge
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mishra, S.R. A vector wave analysis of a bessel beam. Opt. Commun. 1991, 85, 159–161. [Google Scholar] [CrossRef]
- Bouchal, Z.; Olivik, M. Non-diffractive vector bessel beams. J. Mod. Opt. 1995, 42, 1555–1566. [Google Scholar] [CrossRef]
- Monk, S.; Arlt, J.; Robertson, D.A.; Courtial, J.; Padgett, M.J. The generation of bessel beams at millimetre-wave frequencies by use of an axicon. Opt. Commun. 1999, 170, 213–215. [Google Scholar] [CrossRef]
- Arlt, J.; Dholakia, K. Generation of high-order bessel beams by use of an axicon. Opt. Commun. 2000, 177, 297–301. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Zheng, C. Vector propagation of radially polarized gaussian beams diffracted by an axicon. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2005, 22, 2542–2546. [Google Scholar] [CrossRef]
- Čižmár, T.; Šiler, M.; Zemánek, P. An optical nanotrap array movable over a milimetre range. Appl. Phys. B 2006, 84, 197–203. [Google Scholar] [CrossRef]
- Novitsky, A.V.; Novitsky, D.V. Negative propagation of vector bessel beams. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2007, 24, 2844–2849. [Google Scholar] [CrossRef]
- Yu, Y.Z.; Dou, W.B. Vector analyses of nondiffracting bessel beams. Prog. Electromagn. Res. Lett. 2008, 5, 57–71. [Google Scholar] [CrossRef][Green Version]
- Brzobohatý, O.; Cizmár, T.; Zemánek, P. High quality quasi-bessel beam generated by round-tip axicon. Opt. Express 2008, 16, 12688–12700. [Google Scholar] [CrossRef]
- Wu, F.T. Geometric optics analysis on self-reconstruction of the nondiffracting beam generated from an axicon. Acta Phys. Sin. 2009, 58, 3125–3129. [Google Scholar]
- Chen, J.; Ng, J.; Wang, P.; Lin, Z. Analytical partial wave expansion of vector bessel beam and its application to optical binding. Opt. Lett. 2010, 35, 1674–1676. [Google Scholar] [CrossRef] [PubMed]
- Salem, M.A.; Bagci, H. Electromagnetic scattering of a vector bessel beam in the presence of an impedance cone. In Proceedings of the IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Orlando, FL, USA, 7–13 July 2013; pp. 1762–1763. [Google Scholar]
- Salem, M.A.; Bağcı, H. Behavior of obliquely incident vector bessel beams at planar interfaces. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2013, 30, 1172–1179. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Guo, L.; Ding, C.; Wu, Z. Scattering of an axicon-generated bessel beam by a sphere. Opt. Commun. 2013, 307, 25–31. [Google Scholar] [CrossRef]
- Du, T.; Wang, T.; Wu, F. Generation of three-dimensional optical bottle beams via focused non-diffracting bessel beam using an axicon. Opt. Commun. 2014, 317, 24–28. [Google Scholar] [CrossRef]
- Mitri, F.G.; Li, R.X.; Guo, L.X.; Ding, C.Y. Resonance scattering of a dielectric sphere illuminated by electromagnetic bessel non-diffracting (vortex) beams with arbitrary incidence and selective polarizations. Ann. Phys. 2015, 361, 120–147. [Google Scholar] [CrossRef]
- Yang, R.; Li, R. Optical force exerted on a rayleigh particle by a vector arbitrary-order bessel beam. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 230–243. [Google Scholar] [CrossRef]
- Yang, R.; Li, R.; Qin, S.; Ding, C.; Mitri, F.G. Direction reversal of the optical spin torque on a rayleigh absorptive sphere in vector bessel polarized beams. J. Opt. 2017, 19, 025602. [Google Scholar] [CrossRef]
- Durnin, J. Exact solutions for nondiffracting beams. i. the scalar theory. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1987, 4, 651–654. [Google Scholar] [CrossRef]
- Bouchal, Z.; Wagner, J.; Chlup, M. Self-reconstruction of a distorted nondiffracting beam. Opt. Commun. 1998, 151, 207–211. [Google Scholar] [CrossRef]
- McGloin, D.; Dholakia, K. Bessel beams: Diffraction in a new light. Contemp. Phys. 2005, 46, 15–28. [Google Scholar] [CrossRef]
- Volkesepulveda, K.; Garceschavez, V.; Chavezcerda, S.; Arlt, J.; Dholakia, K. Orbital angular momentum of a high-order bessel light beam. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S82–S89. [Google Scholar] [CrossRef]
- Garcés-Chávez, V.; Arlt, J.; Dholakia, K.; Volke-Sepulveda, K.; Chávez-Cerda, S. Orbital angular momentum of a high order bessel light beam. In Proceedings of the Summaries of Papers Presented at the Lasers and Electro-Optics. CLEO ’02. Technical Diges, Long Beach, CA, USA, 24 May 2002. [Google Scholar]
- Mitri, F.G. Reverse propagation and negative angular momentum density flux of an optical nondiffracting nonparaxial fractional bessel vortex beam of progressive waves. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 1661–1667. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.G. Negative optical spin torque wrench of a non-diffracting non-paraxial fractional bessel vortex beam. J. Quant. Spectrosc. Radiat. Transf. 2016, 182, 172–179. [Google Scholar] [CrossRef][Green Version]
- Li, R.; Yang, R.; Ding, C.; Mitri, F.G. Optical torque on a magneto-dielectric rayleigh absorptive sphere by a vector bessel (vortex) beam. J. Quant. Spectrosc. Radiat. Transf. 2017, 191, 96–115. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; McGraw-Hill Book, Co.: New York, NY, USA, 1941. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Gouesbet, G.; Maheu, B.; Gréhan, G. Light scattering from a sphere arbitrarily located in a gaussian beam, using a bromwich formulation. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1988, 5, 1427–1443. [Google Scholar] [CrossRef]
- Chang, S.; Sang, S.L. Optical torque exerted on a homogeneous sphere levitated in the circularly polarized fundamental-mode laser beam. J. Opt. Soc. Am. B Opt. Phys. 1985, 2, 1853–1860. [Google Scholar] [CrossRef]
- Barton, J.P.; Alexander, D.R.; Schaub, S.A. Theoretical determination of net radiation force and torque for a spherical particle illuminated by a focused laser beam. J. Appl. Phys. 1989, 66, 4594–4602. [Google Scholar] [CrossRef]
- Chang, S.; Sang, S.L. Optical torque exerted on a sphere in the evanescent field of a circularly-polarized gaussian laser beam. Opt. Commun. 1998, 151, 286–296. [Google Scholar] [CrossRef]
- Polaert, H.; Gréhan, G.; Gouesbet, G. Forces and torques exerted on a multilayered spherical particle by a focused gaussian beam. Opt. Commun. 1998, 155, 169–179. [Google Scholar] [CrossRef]
- Bohren, C.F.; Hunt, A.J. Scattering of electromagnetic waves by a charged sphere. Can. J. Phys. 2011, 55, 1930–1935. [Google Scholar] [CrossRef]
- Klacka, J.; Kocifaj, M. Scattering of electromagnetic waves by charged spheres and some physical consequences. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 170–183. [Google Scholar] [CrossRef]
- Klacka, J.; Kocifaj, M. On the scattering of electromagnetic waves by a charged sphere. Prog. Electromagne Res. 2010, 109, 17–35. [Google Scholar] [CrossRef]
- Kocifaj, M.; Klacka, J. Scattering of electromagnetic waves by charged spheres: Near-field external intensity distribution. Opt. Lett. 2012, 37, 265–267. [Google Scholar] [CrossRef]
- Hu, Q.; Xie, L. Scattering phase function of a charged spherical particle. Appl. Opt. 2015, 54, 8439–8443. [Google Scholar] [CrossRef]
- Xie, L.; Dou, X.Q.; Zhou, J. Sizing charged particles by phase Doppler anemometry. Appl. Opt. 2016, 55, 3279. [Google Scholar] [CrossRef] [PubMed]
- Bian, T.; Gao, X.; Yu, S.; Jiang, L.; Lu, J.; Leung, P.T. Scattering of light from graphene-coated nanoparticles of negative refractive index. Opt. Int. J. Light. Electron Opt. 2017, 136, 215–221. [Google Scholar] [CrossRef]
- Zhou, J.; Dou, X.; Xie, L. Scattering and attenuation of electromagnetic waves by partly charged particles. J. Quant. Spectrosc. Radiat. Transf. 2017, 206, 55–62. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, S.; Qi, J.; Yang, X. Extension of complex refractive index model and analysis of scattering properties of charged submicron spheres. J. Quant. Spectrosc. Radiat. Transf. 2020, 242, 106735. [Google Scholar] [CrossRef]
- Goodman, J.W. Introduction to Fourier Optics; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Mitri, F.G.; Li, R.X.; Guo, L.X.; Ding, C.Y. Optical tractor bessel polarized beams. J. Quant. Spectrosc. Radiat. Transf. 2016, 187, 97–115. [Google Scholar] [CrossRef]
- Preston, T.C.; Mason, B.J.; Reid, J.P.; Luckhaus, D.; Signorell, R. Size-dependent position of a single aerosol droplet in a Bessel beam trap. J. Opt. 2014, 16, 025702. [Google Scholar] [CrossRef]
- Li, R.; Ding, C.; Mitri, F.G. Optical spin torque induced by vector bessel (vortex) beams with selective polarizations on a light-absorptive sphere of arbitrary size. J. Quant. Spectrosc. Radiat. Transf. 2017, 196, 53–68. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Wan, L.; Yao, H.; Talwar, D.N.; Li, L.; Jiang, J. Optical Torque Exerted on a Charged Sphere by a Polarized Bessel Beam. Symmetry 2023, 15, 128. https://doi.org/10.3390/sym15010128
Li P, Wan L, Yao H, Talwar DN, Li L, Jiang J. Optical Torque Exerted on a Charged Sphere by a Polarized Bessel Beam. Symmetry. 2023; 15(1):128. https://doi.org/10.3390/sym15010128
Chicago/Turabian StyleLi, Ping, Lingyu Wan, Huilu Yao, Devki N. Talwar, Liuyan Li, and Jiang Jiang. 2023. "Optical Torque Exerted on a Charged Sphere by a Polarized Bessel Beam" Symmetry 15, no. 1: 128. https://doi.org/10.3390/sym15010128
APA StyleLi, P., Wan, L., Yao, H., Talwar, D. N., Li, L., & Jiang, J. (2023). Optical Torque Exerted on a Charged Sphere by a Polarized Bessel Beam. Symmetry, 15(1), 128. https://doi.org/10.3390/sym15010128







