A VVC Video Steganography Based on Coding Units in Chroma Components with a Deep Learning Network

Abstract

Versatile Video Coding (VVC) is the latest video coding standard, but currently, most steganographic algorithms are based on High-Efficiency Video Coding (HEVC). The concept of symmetry is often adopted in deep neural networks. With the rapid rise of new multimedia, video steganography shows great research potential. This paper proposes a VVC steganographic algorithm based on Coding Units (CUs). Considering the novel techniques in VVC, the proposed steganography only uses chroma CUs to embed secret information. Based on modifying the partition modes of chroma CUs, we propose four different embedding levels to satisfy the different needs of visual quality, capacity and video bitrate. In order to reduce the bitrate of stego-videos and improve the distortion caused by modifying them, we propose a novel convolutional neural network (CNN) as an additional in-loop filter in the VVC codec to achieve better restoration. Furthermore, the proposed steganography algorithm based on chroma components has an advantage in resisting most of the video steganalysis algorithms, since few VVC steganalysis algorithms have been proposed thus far and most HEVC steganalysis algorithms are based on the luminance component. Experimental results show that the proposed VVC steganography algorithm achieves excellent performance on visual quality, bitrate cost and capacity.

1. Introduction

Steganography is the science of hiding secret information into digital media without arousing the suspicions of users. Compared with the image which is used as the steganography carrier in [1,2,3,4], video has more redundancies and unique coding characteristics for hiding, and it is spreading more and more widely across social networks and social applications.

Common video steganographic algorithms include modifying the transform domain, motion vectors, inter-prediction modes, intra-prediction modes and block partitioning types. For transform domain-based algorithms, Chang et al. [5] first proposed a data-hiding algorithm based on modifying the Discrete Cosine Transform (DCT) coefficients. For the motion vectors-based algorithms, Rana et al. [6] proposed a steganographic algorithm to embed motion vectors in the homogeneous regions of the reference frame. For algorithms based on inter-prediction modes, Yang et al. [7] and Li et al. [8] embedded messages by modifying the prediction unit (PU) partition modes. Zhang et al. [9] proposed an algorithm based on the intra-prediction mode (IPM). For algorithms based on block partitioning types, Tew et al. [10] proposed an information-hiding algorithm by modifying the coding block size decision. Shanableh et al. [11] altered the coding units to hide secret information.

Most of these steganographic algorithms are used in the HEVC coding standard. However, the latest international video coding standard is VVC. There are lots of novel technical aspects used in the VVC standard that provide more possibilities for steganography. Compared with the HEVC standard, the block partitioning structure of VVC is one of the most essential changes among these new techniques. In VVC, the coding tree unit (CTU) is extended to a 128 × 128 size for more flexible block partitioning [12]. VVC uses both quaternary tree (QT)-based partitioning and multi-type tree (MTT)-based partitioning structures [13]. Furthermore, VVC introduces the chroma separate tree (CST) [14]. In the intra-coded slice, the CST enables separate partitioning for luma and chroma. Overall, there are many differences between the HEVC and VVC; hence, the HEVC steganographic algorithms are difficult to use in the VVC standard. In addition, as far as we know, few VVC steganalytic algorithms have been reported in the literature. Therefore, VVC steganography is harder to detect. Thus, in this paper, steganographic algorithm based on a chroma block partitioning structure for VVC videos is proposed.

However, stego-videos always face some disadvantages such as the increased bitrate and the decreased visual quality. Recently, with the development of deep learning techniques, many researchers utilize CNNs instead of the in-loop filters to obtain better visual quality. Huang et al. [15] and Chen et al. [16] proposed a variable convolutional neural network and a dense residual convolutional neural network as an additional in-loop filter for the VVC standard. Inspired by the above literature, we propose a novel multi-scale residual neural network (MSRNN) as an additional in-loop filter in the VVC standard to improve its disadvantages such as distortion in visual quality and increased bitrate caused by a steganographic algorithm.

The contributions of this paper are as follows:

(1) An VVC steganographic algorithm based on chroma block partitioning is proposed, which takes full advantage of the VVC block partitioning structure’s characteristics. In this algorithm, secret information is embedded by modifying the chroma component’s block partitioning structure in the VVC standard.

(2) A four-embedding-level algorithm is proposed that can satisfy the different needs of the visual quality, bitrate cost and capacity.

(3) MSRNN is proposed as an additional in-loop filter in the VVC standard to decrease the negative influence caused by steganographic algorithms.

The experiment results illustrate that the proposed steganographic algorithm performs well in terms of the visual quality, bitrate cost and capacity. As for the security, we use an universal steganalytic algorithm and an open-source steganolysis tool to test our steganographic algorithm.

The rest of this paper is organized as follows. Section 2 introduces the block partitioning structure in VVC. Section 3 presents the proposed steganographic algorithm and MSRNN algorithm. The experimental results and analyses are presented in Section 4. Finally, conclusions are drawn in Section 5.

2. Block Partitioning Structure

2.1. Quadtree Plus Multi-Type Tree Structure

As in HEVC, a picture to be encoded is partitioned into non-overlapping CTUs in VVC. Forthe purpose of improving coding efficiency, the CTU size is enlarged from 64 × 64 in HEVC to 128 × 128 in VVC. Furthermore, HEVC only applies a recursive quaternary tree (QT) split to each CTU. In order to adapt to the picture content better, the VVC block structure adopts a QT and a multi-type tree (MTT). The multi-type tree structure includes split vertical binary trees (VBT), split horizontal binary trees (HBT), split vertical ternary trees (VTT) and split horizontal ternary trees (HTT). For binary tree splitting, the splitting is equal. For ternary tree splitting, the splitting ratio is 1:2:1.

Figure 1 illustrates the splitting types of the MTT. In VVC, each CTU is partitioned by a QT at first. Then, the MTT structure is applied to partition each QT node further. Once the current node is partitioned by the MTT, the QT structure is forbidden for the subsequent nodes. Figure 2 shows two redundant partitions in the block partition process. The final partition mode of a CU is decided by minimizing the Rate Distortion cost (RD cost) [17] among all the possible partition modes. The VVC block partition process is shown in Algorithm 1. Figure 3 shows an example of a CTU partition in VVC. If the block partitioning structure is altered, it will result in the distortion of visual quality and compression efficiency.

Algorithm 1: Partition process.

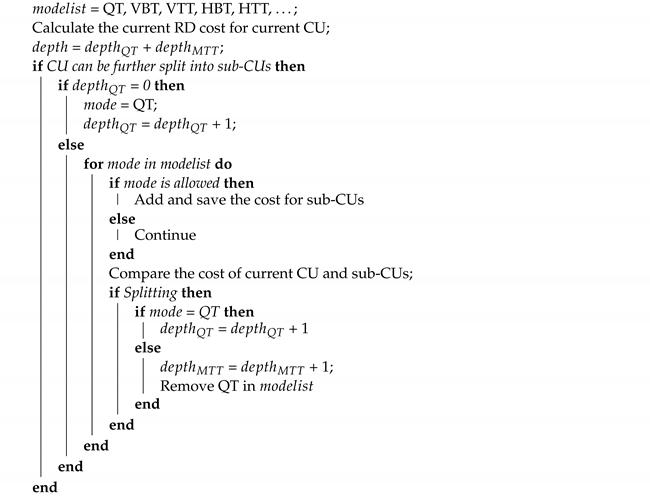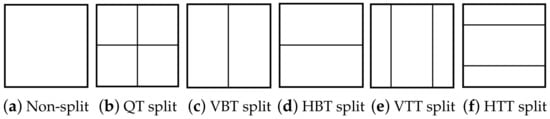
Figure 1. Illustration of splitting types in MTT.

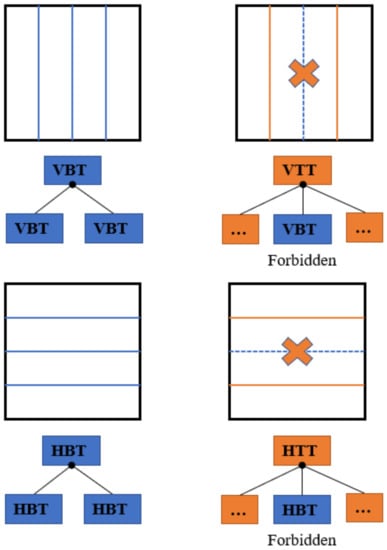
Figure 2. Illustration of redundant partitions.

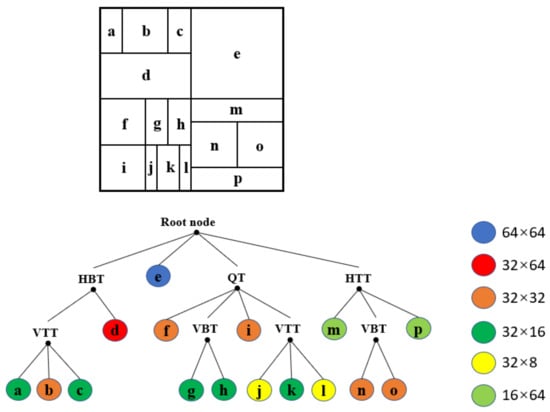
Figure 3. Example of a CTU partition.

2.2. Chroma Separate Tree

In the HEVC standard, the coding tree is shared by the luma component and the chroma components. As a result, a CU includes a luma coding block (CB) and two chroma CBs. This single-tree structure is still used for P and B slices in the VVC standard. However, VVC introduces the chroma separate tree (CST), which enables the luma component and chroma components to be encoded separately in I slices. Figure 4 shows an example of CU partitioning of an encoded picture. The partition structure is marked by the open-source player YUView [18]. As shown in Figure 4, luma has a finer texture than chroma, which causes the amount of small-sized CUs in luma to be larger than that in chroma. The CST enables chroma to not be split into smaller CUs. Moreover, if the CST is applied, there is no dependency between the luma component and the chroma components, but the processing latency still exists.

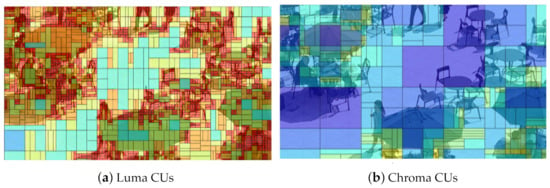
Figure 4. Example of CU partitions.

It can be concluded that whether we modify the block partitioning structure of luma or chroma components, the degree of influence on visual quality and compression efficiency is similar. However, in the human visual system, the luma component is more sensitive than the chroma components [19], and generally, the chroma components are subsampled to reduce redundancy [20]. Consequently, we choose to only modify the block structure of the chroma components for embedding secret bits, which can effectively reduce the impact on visual quality and compression efficiency.

3. The Proposed Algorithm

3.1. The Chroma CU MTT Depth-Based Hierarchical Coding

The proposed hierarchical coding method is based on the MTT depth of the chroma CUs. This method includes two sub-bijective mapping rules that convert secret binary bits to particular block partition modes. For simplicity, a chroma CU with an MTT depth j is expressed as CU${}_{dept{h}_{MTT}=j}$.

The first bijective mapping rule is called the 4-bits mapping rule which can embed 4 secret binary bits to a 16 × 16 CU${}_{dept{h}_{MTT}=0}$, which also means its $dept{h}_{QT}$ is 2 for the YUV420 format.

Step I: In VVC standard, a 16 × 16 CU${}_{dept{h}_{MTT}=0}$ can be split by 5 partition modes. However, considering the complexity, the 4-bits mapping rule removes the QT split. Hence, there are only 4 partition modes left to be chosen. According to Table 1, the partition modes of a 16 × 16 CU${}_{dept{h}_{MTT}=0}$ can be mapped to 2 secret binary bits.

Table 1. Mapping of 16 × 16 CU${}_{dept{h}_{MTT}=0}$ partition modes.

$dept{h}_{MTT}=0$ modes	VBT	VTT	HBT	HTT
Binary bits	00	01	10	11

Step II: We choose the first 8 × 16 or 16 × 8 CU${}_{dept{h}_{MTT}=1}$ in sub-CUs to embed secret information. In order to avoid redundant partitions, in $dept{h}_{MTT}=1$, we only choose 2 partition modes HBT and VBT. In our design, if CU is split by VBT or VTT in Step I, CU${}_{dept{h}_{MTT}=1}$ is only split by HBT. For the CU which is split by HBT or HTT in Step I, CU${}_{dept{h}_{MTT}=1}$ is only split by VBT. The mapping of the CU${}_{dept{h}_{MTT}=1}$ partition modes is shown in Table 2.

Table 2. Mapping of CU${}_{dept{h}_{MTT}=1}$ partition modes.

$dept{h}_{MTT}=0$ modes	VBT	VTT	HBT	HTT
$dept{h}_{MTT}=1$ modes	HBT	HBT	VBT	VBT

Step III: A CU${}_{dept{h}_{MTT}=1}$ can be parted into 2 sub-CUs, as illustrated in Figure 5, and we can embed 1 bit at $dept{h}_{MTT}=2$. It can be concluded that if the CU${}_{dept{h}_{MTT}=3}$ is located in the first CU${}_{dept{h}_{MTT}=2}$, the secret bit is 0, and if the CU${}_{dept{h}_{MTT}=3}$ is located in the second CU${}_{dept{h}_{MTT}=2}$, the secret bit is 1. The mapping rule is defined as

$$M=\left\{\begin{array}{cc}0,\hfill & i=0\hfill \\ 1,\hfill & i=1\hfill \end{array}\right.,$$

(1)

where M denotes the binary coding for sub-CU with order i.

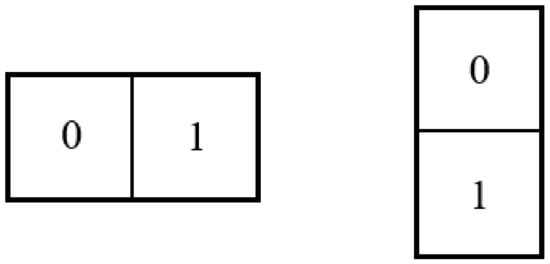
Figure 5. Illustration of sub-CUs of CU${}_{dept{h}_{MTT}=1}$.

Step IV: For a CU${}_{dept{h}_{MTT}=2}$, there are only 2 partition modes left, which can embed 1 bit. The mapping rule of CU${}_{dept{h}_{MTT}=3}$ partition modes is shown in Table 3. Algorithm 2 shows the process of the 4-bits mapping rule.

Algorithm 2: 4-bits Mapping Rule.

Table 3. Mapping of CU${}_{dept{h}_{MTT}=3}$ partition modes.

$dept{h}_{MTT}=3$ modes	VBT	HBT
Binary bits	0	1

The second bijective mapping rule is called the 2-bits mapping rule that can embed 2 secret binary bits to a 16 × 16 chroma CU, for which the $dept{h}_{MTT}$ is 0. The difference between the 4-bits mapping rule and the 2-bits mapping rule is that Step II, Step III and Step IV are not forcible in the 2-bits rule. The block partitioning of the CU${}_{dept{h}_{MTT}=1}$ is dependent on the RD cost.

Figure 6 illustrates an example of the proposed hierarchical coding method. The number of corresponding bits is 1010.

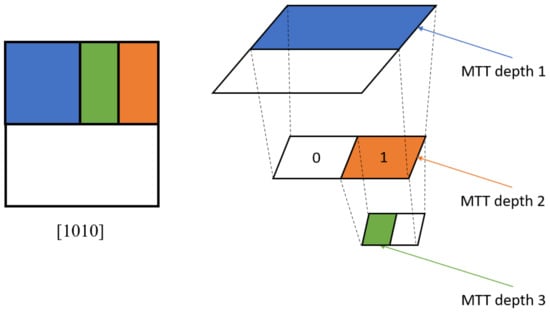
Figure 6. Illustration of the proposed hierarchical coding method.

By using the proposed bijective mapping, we can convert binary secret messages to CUs of different sizes. Therefore, there are 2 methods to obtain the 16 × 16 CUs${}_{dept{h}_{MTT}=0}$. In the next part, the 2 methods used for the proposed hierarchical coding method are introduced.

3.2. Four Embedding Schemes

As shown in Figure 4, there are some chroma CUs for which not all the $dept{h}_{QT}$ of chroma CUs equals 2. If we apply the proposed algorithm to the whole picture, the visual quality will be decreased. Therefore, we propose two methods to use the proposed hierarchical coding method. Method 1 is to forcibly modify all the CUs${}_{dept{h}_{QT}=2}$ and then utilize mapping rules to embed secret information.

As for Method 2, we only select the CUs${}_{dept{h}_{QT}=2}$ to embed secret information. Therefore, we first start the block partitioning of the chroma components to find CUs${}_{dept{h}_{QT}=2}$. Then, we start the block partitioning of the chroma components again, and this time we apply the proposed hierarchical coding method to the CUs${}_{dept{h}_{QT}=2}$ that we found the first time. As for the other chroma CUs, we utilize the structure from the first time as the final structure. Additionally, as shown in Figure 7, if the block partitioning structure has been modified, it will influence the following block partitioning.

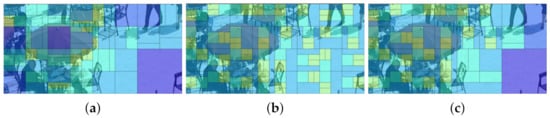
Figure 7. (a) The original frame; (b,c) data-hiding frames at Level 1 and Level 2, respectively.

Thus, there are four different embedding schemes which are shown in Table 4. To extract embedded information, we just need to calculate the corresponding coding bits of each QT depth 2 chroma CU in zigzag order.

Table 4. Four Embedding-Level Schemes.

Schemes	Mapping Rules	Embedding Method
Level 1	4-bits	Method 1
Level 2	4-bits	Method 2
Level 3	2-bits	Method 1
Level 4	2-bits	Method 2

3.3. The Additional In-Loop Filter MSRNN

The proposed steganographic algorithm will affect the visual quality and bitrate of the embedded video sequences. In order to improve the performance of the embedded video sequences, we utilize MSRNN as an additional in-loop filter. Figure 8 shows the steganography algorithm diagram. Firstly, the raw video sequence is compressed by a VVC AI encoder. In the process of encoding, the CUs partition modes are extracted, and then the selected chroma CUs are modified according to the secret data. The subsequent VVC encoding process is continued, where we utilize MSRNN as an additional in-loop filter. As shown in Figure 9, the MSRNN is located after the deblocking filter (DBF). In [15,16], the proposed CNN-based in-loop filter modules can improve the visual quality and bitrate effectively. The MSRNN structure is shown in Figure 10 and the details of each convolution kernel is shown in Table 5.

Figure 8. The proposed steganography algorithm diagram.

Figure 9. Intergration into the VVC diagram.

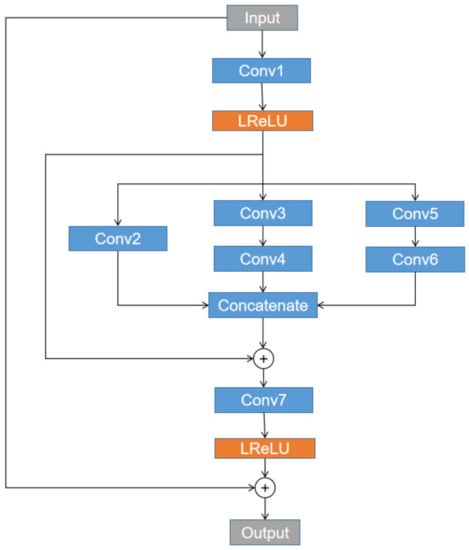
Figure 10. The architecture of MSRNN.

Table 5. The configuration of the MSRNN.

Layer	Filter Size	Filter Number
Conv1	3 × 3	64
Conv2	3 × 3	32
Conv3	3 × 3	16
Conv4	3 × 3	16
Conv5	5 × 5	16
Conv6	5 × 5	16
Conv7	3 × 3	1

Therefore, we proposed a super-resolution CNN called MSRNN as an additional in-loop filter module. The MSRNN structure is shown in Figure 10 and the details of each convolution kernel is shown in Table 5. In order to extract multiscale features, the convolutional layers we utilized are with different kernel size. Leaky ReLU (LReLU) activation function is aimed to get the shallow features (SFs) of the input. We also utilize zero-padding to make the size of output as same as the input and stride is set to 1. DIV2K dataset [21] is used for training and VTM16.2 AI encoder is used to compress original frames at QPs: 26, 32, 38 and 42. The network is trained individually for each QP. We also utilize luma component and chroma components datasets to train out the network separately. The original image $I_{ori}$ is the target of the CNN. The input $I_{input}$ is the compressed $I_{ori}$. The loss function we utilized is:

$$Loss=\frac{1}{N}·\sum _{n=0}^N·\parallel I_{ori}-I_{input}\parallel ,$$

(2)

where N is the number of training images, $I_{ori}$ means the original picture and $I_{output}$ is the output of CNN. In order to test the effect of the MSRNN, we campared with improved VRCNN [22] on BD-rate. Under the same video quality, if the BD-rate is smaller, the bitrate savings is more. Table 6 shows the camparison results. From Table VI, the BD-rate of each algorithm is negative, therefore, we can know that using CNN as an additional in-loop filter can improve the reconstructed video quality effectively and the MSRNN is more effective as an additional in-loop filter.

Table 6. The Configuration of the CNN.

Class	Improved VRCNN [22]	Proposed
ClassA	−1.73%	−1.73%
ClassB	−0.63%	−0.72%
ClassC	−3.18%	−3.38%
ClassD	−3.60%	−3.76%
ClassE	−2.54%	−2.77%

4. Experimental Results

4.1. Setup

The proposed steganographic algorithm and the MSRNN are intergrated in the VVC reference software VTM16.2 AI encoder and tested on a database that includes 18 YUV sequences, which is shown in Table 7 in detail. In our experiment, the test sequences are encoded at a frame rate 30 fps with QPs 26, 32 and 38 and the temporal subsample ratio is 8, which means the sequences are encoded at intervals of 8 frames. Additionally, the final results are normalized with the encoded frame numbers. We utilize the DIV2K dataset [21] to train the MSRNN. The $I_{ori}$ and $I_{input}$ are cropped to 128 × 128. The method proposed in [23] is utilized to initialize the weights, and the Adam optimizer [24] is also utilized for training.

Table 7. The Video Database.

Class	Sequence Name	Resolution	Encoded Frames Numbers
ClassA	PeopleOnStreet Traffic	2560 × 1600	18
ClassB	BasketballDrive BQTerrace Cactus Kimono1 ParkScene	1920 × 1080	20
ClassC	BasketballDrill BQMall PartyScene RaceHorses	832 × 480	20
ClassD	BasketballPass BlowingBubbles BQSquare RaceHorses	416 × 240	20
ClassE	FourPeople Johnny KristenAndSara	1280 × 720	20

4.2. Subjective Performance

The basic requirement of steganography is that human eyes cannot distinguish whether the videos are embedded with secret information. Figure 11 shows the original VVC compressed video and stego-video under four different hiding strategies and with MSRNN. As shown in Figure 11, stego-videos with the MSRNN produce better visual quality, especially for the grass, and it is difficult for human eyes to distinguish whether these videos are embedded with secret information. This observation verifies that the proposed steganography algorithm preserves visual quality well.

Figure 11. Visual quailty of I frame in RaceHorses of ClassD.

4.3. Objective Performance

We utilize the following four evaluation methods: peak signal-to-noise ratio (PSNR), bit rate increasing (BRI), embedding capacity and anti-steganalysis to measure the performance of the proposed algorithm objectively.

The PSNR is used as a classical index to evaluate the objective quality of images. The PSNR between the 8-bit-depth original image I and 8-bit-depth reconstructed image $I{}^{\prime }$ can be calculated by (3) and (4), respectively:

$$MSE=\frac{1}{W·H}·\sum _{x=0}^{W-1}·\sum _{y=0}^{H-1}·{\left(I\left(x,y\right)-I{}^{\prime }\left(x,y\right)\right)}^2,$$

(3)

$$PSNR=-10·{log}_{10}\left(\frac{MSE}{{255}^2}\right),$$

(4)

where W and H represent the width and height of the image, respectively. To measure the quality of YUV420 format videos, the PSNR is given by:

$$PSN{R}_{YUV}=\frac{6·PSN{R}_Y+PSN{R}_U+PSN{R}_V}{8},$$

(5)

where $PSN{R}_Y$, $PSN{R}_U$ and $PSN{R}_V$ denote the average $PSNR$ values of the Y component, U component and V component, respectively.

The video bitrate represents the number of transmitted bits per second. BRI represents the increase in the bitrate between the modified video and the original video and is defined as

$$BRI=\frac{B{R}_{steg}-B{R}_{ori}}{B{R}_{ori}},$$

(6)

where $B{R}_{steg}$ and $B{R}_{ori}$ denote the bitrate of the modified video and the bitrate of the original video, respectively.

The embedding capacity is the number of embedded binary bits, and in our experiment, it is the average embedding capacity of each I slice.

Table 8 shows the results of the PSNR of different channels, the $BRI$ and the capacity using different QPs. The results shown that for most test videos, the PSNR is decreased around 0.27 dB and the average $BRI$ is 3.07%, which indicates that the proposed steganographic algorithm has just a little negative influence on visual quality and bitrate. The smaller QP represents the smaller quantization step, and during the rounding and truncation process, less information is lost. In addition, the lower capacity means that the distortion caused by the modification is smaller. Thus, the PSNR, $BRI$ and capacity are decreased with the same trend, that is, with the increase in QP.

Table 8. The PSNR, BRI and capacity performance of different QPs.

Class	QP	${\mathit{PSNR}}_{\mathit{Y}}$ (Level 2_MSRNN)	${\mathit{PSNR}}_{\mathit{U}}$ (Level 2_MSRNN)	${\mathit{PSNR}}_{\mathit{V}}$ (Level 2_MSRNN)	${\mathit{PSNR}}_{\mathit{YUV}}$ (Level 2_MSRNN)	${\mathit{PSNR}}_{\mathit{YUV}}$ (Default)	$\mathit{BRI}$ (Level 2_MSRNN)	Capacity (Level 2_MSRNN)
ClassA	26 32 38	41.7852 38.1119 34.6532	41.2967 39.5137 37.7330	42.4510 40.8508 39.1266	41.7297 38.6314 35.5459	42.1655 38.7845 35.5106	2.68% 1.24% 0.74%	8768.00 3068.00 1096.00
ClassB	26 32 38	40.1954 37.5342 34.6550	40.8220 39.2428 37.9042	42.7717 40.9064 38.9339	40.6005 38.1727 35.5435	40.9229 38.3461 35.5857	2.27% 1.72% 1.36%	3540.80 1595.20 774.40
ClassC	26 32 38	39.8219 35.7351 31.7524	38.8454 35.8652 34.0027	39.6275 36.5972 34.5614	39.6237 35.8856 32.4303	40.2379 36.3046 32.7169	5.48% 4.30% 4.04%	1294.00 1000.00 640.00
ClassD	26 32 38	39.9070 35.3895 30.3488	38.7649 35.8083 33.9349	39.4814 36.1828 34.2280	39.5875 35.4840 31.9570	40.2220 35.9306 32.2150	6.55% 4.55% 4.04%	322.00 218.00 170.00
ClassE	26 32 38	43.3082 40.5442 36.3138	45.2538 42.6368 40.8980	45.9940 43.3097 41.6887	43.9427 41.2098 38.2767	44.1721 41.3639 38.2435	3.72% 2.33% 1.06%	1029.33 528.00 213.33
Mean					37.9081	38.1815	3.07%	1617.14

Because VVC is the latest video coding standard, there are few steganographic algorithms for comparison. Therefore, we just compared the results of our algorithm when using MSRNN as an additional in-loop filter and four different schemes. Table 9 shows the comparative result in QP 26. The results show that the application of MSRNN performs well in improving the PSNR. Especially for $PSN{R}_U$ and $PSN{R}_V$, the MSRNN plays an important role in recovering the negative influence caused by the modification. As expected, the $PSN{R}_Y$ is almost not influenced by the steganography. Additionally, the proposed algorithm also performs well on the $BRI$ and embedding capacity. Level 1 and Level 3, which utilize Method 1, have a better performance on embedding capacity at the expense of the PSNR and $BRI$. On the contrary, Level 2 and Level 4 perform better on the PSNR and $BRI$ at the expense of a decrease in embedding capacity. Similarly, with the same embedding method, the schemes with the four-bits mapping rule (Level 1 and Level 2) normally have a better performance in capacity. In summary, according to the different needs, we can choose different schemes to embed secret information.

Table 9. The PSNR, BRI and capacity performance of QP = 26.

Class	Schemes	${\mathit{PSNR}}_{\mathit{Y}}$	${\mathit{PSNR}}_{\mathit{U}}$	${\mathit{PSNR}}_{\mathit{V}}$	${\mathit{PSNR}}_{\mathit{YUV}}$	$\mathit{BRI}$	Capacity
ClassA	Default Level 1 Level 2 Level 3 Level 4 Level 1_MSRNN Level 2_MSRNN Level 3_MSRNN Level 4_MSRNN	41.6335 41.7114 41.7161 41.7120 41.7030 41.7797 $41.7852$ 41.7815 41.7725	42.9328 41.1107 41.1457 41.2661 $41.3112$ 41.2729 41.2967 41.4306 $41.4630$	44.0051 42.3614 42.3382 42.5203 $42.5623$ 42.4788 42.4510 42.6278 $42.6658$	42.3597 41.6399 41.6434 41.6900 $41.6995$ 41.7284 41.7297 41.7783 $41.7844$	3.53% 2.62% 2.36% $1.76\%$ 3.55% 2.68% 2.39% $1.80\%$	16,000.00 8768.00 9576.00 5160.00 16,000.00 8768.00 9576.00 5160.00
ClassB	Default Level 1 Level 2 Level 3 Level 4 Level 1_MSRNN Level 2_MSRNN Level 3_MSRNN Level 4_MSRNN	39.8567 $40.1853$ 40.1845 40.1832 40.1834 40.1950 $40.1954$ 40.1950 40.1949	42.0612 40.6023 40.7686 40.6950 $40.8523$ 40.6290 40.8220 40.7774 $40.9158$	44.0721 42.4676 42.6871 42.6181 $42.7661$ 42.1957 42.7717 42.7470 $42.8657$	40.6242 40.5311 40.5781 40.5605 $40.5983$ 40.4964 40.6005 40.5926 $40.6238$	3.37% 2.24% 2.15% $1.81\%$ 3.36% 2.26% 2.20% $1.87\%$	$7920.00$ 3540.80 4624.40 2018.40 $7920.00$ 3540.80 4624.40 2018.40
ClassC	Default Level 1 Level 2 Level 3 Level 4 Level 1_MSRNN Level 2_MSRNN Level 3_MSRNN Level 4_MSRNN	39.5904 39.7120 39.6998 $39.7155$ 39.7108 39.8250 39.8219 $39.9359$ 39.8343	41.2428 38.8564 38.6593 $38.9484$ 38.9120 39.0794 38.8454 $39.1714$ 39.1326	42.1792 39.7711 39.5338 39.8661 $39.8781$ 40.0634 39.8077 40.1578 $40.1796$	40.1519 39.5500 39.4646 $39.5830$ 39.5727 39.7172 39.6237 $39.7479$ 39.7413	5.57% 5.56% $5.01\%$ 5.44% 5.42% 5.48% $4.90\%$ 5.38%	$1560.00$ 1294.00 1099.50 800.00 $1560.00$ 1294.00 1099.50 800.00
ClassD	Default Level 1 Level 2 Level 3 Level 4 Level 1_MSRNN Level 2_MSRNN Level 3_MSRNN Level 4_MSRNN	39.5789 39.6644 $39.6834$ 39.6768 39.6627 39.8883 $39.9070$ 39.9036 39.8926	41.4094 38.8616 38.6192 38.9773 $39.0237$ 39.0062 38.7649 39.0993 $39.1727$	42.1426 39.4872 39.1996 $39.6241$ 39.6032 39.7214 39.4814 39.8522 $39.8666$	40.1426 39.4482 39.3675 $39.5068$ 39.4957 39.6604 39.5875 39.7160 $39.7185$	5.98% 6.76% $5.63\%$ 6.37% 5.62% 6.55% $5.25\%$ 6.05%	$364.00$ 322.00 260.00 187.00 $364.00$ 322.00 260.00 187.00
ClassE	Default Level 1 Level 2 Level 3 Level 4 Level 1_MSRNN Level 2_MSRNN Level 3_MSRNN Level 4_MSRNN	43.1490 $43.2314$ 43.2241 43.2204 43.2099 $43.3161$ 43.3082 43.3091 43.2946	46.6232 44.5351 45.0728 44.7645 $45.2183$ 44.7835 44.2538 44.9987 $45.3951$	47.5673 45.4497 45.7937 45.6570 $46.0224$ 45.6571 $45.9940$ 45.8640 45.1864	44.1049 43.7308 43.8349 43.7776 $43.8641$ 43.8513 43.9427 43.8974 $43.9677$	7.49% 3.72% 5.16% $3.15\%$ 7.40% 3.72% 5.02% $3.10\%$	$3520.00$ 1029.33 1945.33 582.67 $3520.00$ 1029.33 1945.33 582.67

4.4. Comparative Analysis

In this section, we compare our proposed algorithm with Shanableh [11], which is an HEVC steganography algorithm based on CU block partition. In order to display the results more intuitively, we utilize $\Delta$PSNR to measure the change in $PSN{R}_{YUV}$ of the default VVC ($PSN{R}_{YUV}^{{}^{\prime }}$) compared to the proposed steganography algorithm ($PSN{R}_{YUV}^{"}$):

$$\Delta PSNR=PSN{R}_{YUV}^{"}-PSN{R}_{YUV}^{{}^{\prime }}.$$

(7)

We utilized three test sequence (BasketballPass 416 × 240, BasketballDrill 832 × 480 and FourPeople 1280 × 720).

Table 10 shows the comparison results for $\Delta$PSNR and capacity. With the increase in QP, the capacity is reduced. Furthermore, with the increase in resolution, the capacity also increases. The reason for this is that in higher-resolution videos, there will be more suitable CUs in which to embed secret information.

Table 10. Comparison results for $\Delta$PSNR and capacity.

		BasketballPass		BasketBallDrill		FourPeople
Method	QP	$\mathbf{\Delta }$PSNR	Capacity	$\mathbf{\Delta }$PSNR	Capacity	$\mathbf{\Delta }$PSNR	Capacity
Shanableh’s [11]	26 32 38	−0.25 −0.33 −0.86	138.20 133.60 116.80	−0.22 −0.43 −0.65	548.20 454.20 404.60	−0.08 −0.30 −0.59	877.17 $\mathbf{557}.\mathbf{17}$ $\mathbf{477}.\mathbf{83}$
Level2	26 32 38	−1.00 −0.80 −0.70	$\mathbf{284}.\mathbf{00}$ $\mathbf{196}.\mathbf{00}$ $\mathbf{156}.\mathbf{00}$	−0.61 −0.43 −0.64	$\mathbf{1288}.\mathbf{00}$ $\mathbf{968}.\mathbf{00}$ $\mathbf{736}.\mathbf{00}$	−0.36 −0.36 −0.14	$\mathbf{1184}.\mathbf{00}$ 544.00 208.00
Level2 _MSRNN	26 32 38	−0.74 −0.58 $-\mathbf{0}.\mathbf{50}$	$\mathbf{284}.\mathbf{00}$ $\mathbf{196}.\mathbf{00}$ $\mathbf{156}.\mathbf{00}$	−0.38 −0.22 −0.48	$\mathbf{1288}.\mathbf{00}$ $\mathbf{968}.\mathbf{00}$ $\mathbf{736}.\mathbf{00}$	−0.22 −0.13 $\mathbf{0}.\mathbf{15}$	$\mathbf{1184}.\mathbf{00}$ 544.00 208.00

The values in Table 10 marked in bold indicate the best performance. As shown in the comparison results, the proposed steganography has great advantage in visual quality and capacity.

4.5. Security Performance

The security performance is also an important evaluation criterion for a steganographic algorithm. Nevertheless, few steganalytic approaches have been proposed for a VVC steganographic algorithm.

Thus, we utilize StegExpose [25] and the latest universal steganalytic algorithm [26] to evaluate the security of the proposed steganographic algorithm. StegExpose [25] is an open-source steganalysis tool. Figure 12 shows the ROC curve of the proposed method by setting thresholds in a wide range, indicating that the ROC curve of the proposed method is very close to the curve of random guesses. Because the input of [26] only includes grayscale information, the detection accuracy is only 49.81%. These results show that our steganographic algorithm is hard for steganalysis algorithms based on luminance components to detect. Almost all the steganalytic approaches for detecting stego-video with previous encoding standards, such as MPEG4, H.264 and HEVC, only utilize the statistical data in the luma component, which makes our algorithm have an advantage in terms of security performance. Different from previous standards, VVC is the only standard that has separate CU block structure rules for the chroma component, and this unique feature is used in the proposed algorithm, which has guaranteed both high visual quality and the security, as shown in the experimental results.

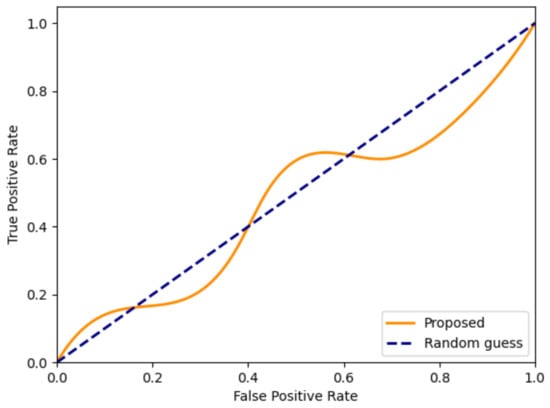
Figure 12. The ROC curve produced by StegExpose [25].

5. Conclusions

In this paper, we proposed a novel VVC steganographic algorithm based on chroma CUs and an additional in-loop filter based on CNN. Different from HEVC steganography, the VVC standard designs a new VVC technique, CST. Benefiting from this new technique, we only utilize chroma CUs to embed secret messages. To improve the distortion and reduce the video bitrate, a deep learning network called MSRNN is designed to replace the in-loop filter in the VVC codec. Our experimental results verify the efficiency of MSRNN and show that the proposed algorithm has high embedding efficiency and strong security. In the future, we hope to widen our research on VVC steganography and utilize the characteristics of inter-frames to develop novel steganography schemes.