Abstract
Symmetric, elegantly entangled structures are a curious mathematical construction that has found their way into the heart of the chemistry lab and the toolbox of constructive geometry. Of particular interest are those structures—knots, links and weavings—which are composed locally of simple twisted strands and are globally symmetric. This paper considers the symmetric tangling of multiple 2-periodic honeycomb networks. We do this using a constructive methodology borrowing elements of graph theory, low-dimensional topology and geometry. The result is a wide-ranging enumeration of symmetric tangled honeycomb networks, providing a foundation for their exploration in both the chemistry lab and the geometers toolbox.
1. Introduction
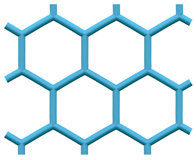
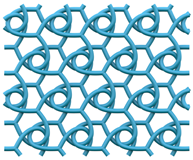
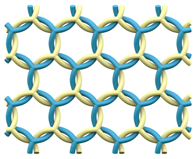
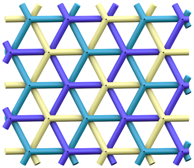
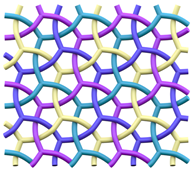
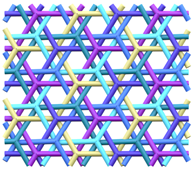
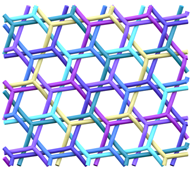
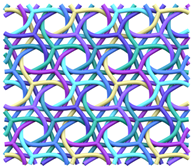
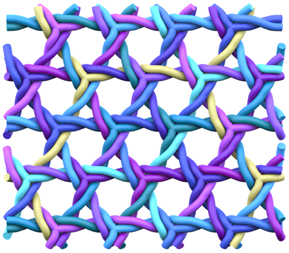
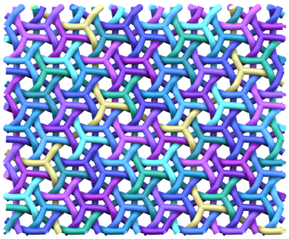
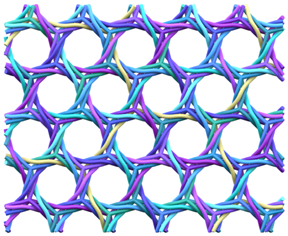
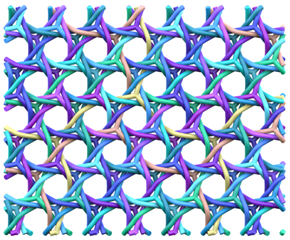
The (6,3) tiling is the tiling of the plane by regular hexagons, with three hexagons around each vertex. The vertices and edges of this tiling form a 2-periodic graph or network, which is commonly known as the hexagonal or honeycomb network or hcb [1]. It is a motif well recognised in many disciplines across the natural sciences. In the same way that a loop can be knotted or linked in a multitude of different ways, graphs—and periodic graphs like hcb—can also be entangled into a wide variety of more complicated structures. Figure 1 shows the entanglement of three hcb networks in two distinct ways.
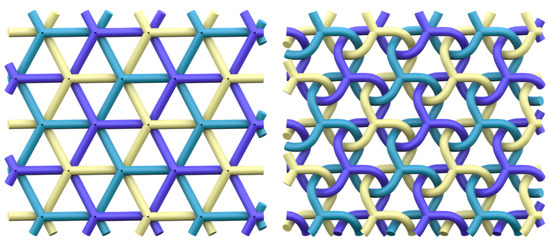
Figure 1.
Two distinct entanglements of three hcb networks. The patterns have indices (Left) and (Right) . The construction and characterisation of these entanglements come from the gluing of 2-fold and 4-fold helices, respectively.
This example already highlights a hierarchy of structural information, which can be made more precise through concepts from geometry and topology. When we talk about the entanglement of a structure, we are really referring to the ambient isotopy class of the structure, which dictates that all structures that can be transformed into one another via a smooth deformation of the ambient space (not allowing the entangled strands to pass through each other) are equivalent [2]. Across literature in the sciences, this is sometimes referred to as topology, topological isomerism [3], or a variety of other terms, but we consider this more precisely as extrinsic topology. The two structures in Figure 1 have different extrinsic topology, or entanglement. Embedded entanglements also have an intrinsic topology, which refers to the graph type of the underlying structure. In the patterns in Figure 1, both structures have the same intrinsic topology, i.e., three hcb networks. Mathematically, intrinsic topology refers to topological equivalence under homeomorphism, and extrinsic topology refers to topological equivalence via ambient isotopy. In addition to these ideas, patterns can also be described through the lens of geometry, which refers to the specific geometric arrangement. The structures in Figure 1 are symmetric, which is a geometric property. In general, the search for optimal geometric embeddings of entangled structures bridges the ideas of extrinsic topology and geometric embedding [4].
The term Chemical Topology was described by Wasserman in a seminal paper in 1961 [5]. It refers to the same chemical backbones being entangled in space in different ways, so different extrinsic topology, such as two loops being linked together. The construction of simple knots and links at the molecular scale occurred throughout the 1990s by Sauvage and others, using a linear helicate approach [6]. When the intrinsic topology of the structure is changed, such that the finite loop-like structure is changed to a finite network-like structure, or a graph, a slightly more complicated structure is created. A simple example of this is the θ-ravel theoretically described and later synthesised in a supramolecular setting [7,8]. It is the entanglement of a -graph, which consists of two vertices connected by three edges, which is non-trivial yet contains no knotted or linked cycles. Entanglement in specific contexts also induces chirality of the structure [9,10]
If we step away from finite entanglements and look at periodic structures, the main domain of research is in the direction of entangled periodic networks in metal-organic frameworks and other related structures. The entanglement of these structures has been understood through crystallography and symmetry, as well as looking for knots and links in the smallest cycles of the networks [11,12,13,14]. Some particular entanglements of multiple 2-periodic hcb networks have been chemically synthesised and described in various contexts [15]. The theoretical design of entangled hcb networks has been explored from a few different but limited perspectives, including hyperbolic tilings [16], constructions using only straight edges [17], and other geometric techniques [18,19,20]. We will present here a comprehensive enumeration of the most symmetric entanglements of hcb networks up to a given complexity, also demonstrating with an explicit construction that these entanglements can be constructed with an infinitely large number of components.
Our study here takes the intrinsic topology of a 2-periodic hcb network, and looks at different entanglements (different extrinsic topology) of that network in a systemetic way. We considered twisted helical segments of n strands arranged along the edges of an underlying graph that carries the entanglement, in this case the 2-periodic hcb network, where the helical motifs are joined together in a simple way. Enumeration through the number of strands n in our helices, and their helical pitch t produces a wide variety of entangled structures with systematically increasing complexity. This technique has been used previously arranging helices on the edges of platonic polyhedra, giving an enumeration of symmetric tangled platonic polyhedra [21].
The construction relies on a hierarchy of geometric structures, glued together in the spirit of low-dimensional topology. It begins with an underlying graph, in this case the 2-periodic hcb network, but the method can be applied to any graph. This graph can be tubified, which is akin to inflating the vertices and edges of the graph like a balloon, to form a surface surrounding the original graph. Our entangled structure will sit as curves on this tubified surface. In a sense, we are utilising the symbiosis of a helical twist and a cylinder to exploit 2-dimensional surface topology for our entanglement purposes.
The initial decoration onto this tubified surface is a set of three even-stranded helices, positioned such that their helical axes lie on the three distinct graph edges of hcb within a single periodic unit cell. These helices sit as non-intersecting curves on the tubified surface. For simplicity, we dictate that all of these helices have the same number of strands; however, the technique can be applied more generally, and will be described elsewhere. The ends of these helical strands get connected around the 3-fold junction of the underlying graph: the even number of strands allows this to happen seamlessly, where exactly half of the strands will be attached to the adjacent helix on the left, and the other half of the strands to the right, without crossing over the vertical plane into the page that runs along the original graph edge. An illustration is given in Figure 2a. This process gives us that all “entanglement” is restricted to the helices, and does not occur in the connections of the strands around the junction.
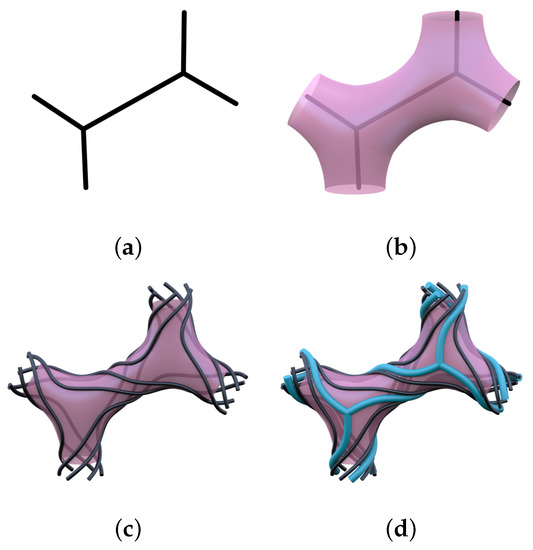
Figure 2.
(a) One repeat unit of the hcb network, the full network can be formed by repeating periodically. (b) The tubified surface around the network is shown in pink. (c) Three distinct 6-helices wind on the surface, and are connected together around the junctions of the surface, where three strands pass to the right of the helix and three to the left (as you travel along the underlying graph edge. (d) The blue network is constructed as the medial axis of the region on the surface defined by the black curves.
We now have a decoration of the tubified surface by curves, which we can describe with the indices , where the three n-fold helices twist an amount of , for and . Enumeration of these woven structures is in itself an interesting problem, and will be discussed elsewhere. These constructed curves carve the tubified surface into multiple branched regions, where the medial axes of these regions define networks with long entangled edges. These network-like medial axes are our entangled networks. We only consider only alternating, non-adjacent branched regions of the surface, such that the cycle double cover of the resulting medial axis graph is the original even-stranded curve pattern: Choosing the “other” region of the surface will either give an equivalent pattern, or something that is not network-like. Some illustrations are shown in Figure 2. There are four possible locations for each vertex in these medial axis networks, in front of and behind each of the two vertices of the underlying hcb graph. Depending on the twists, some combination of two or four vertices in the network will be present at these branch locations.
The new network-like medial axis structure is our end result, and is composed of -strand helices, with a twist of , connected at degree-3 vertices. We can then also describe this structure with indices , where now and . We note that can also be negative, indicating a left-handed twist of the helix, rather than the right-handed twist of a positive . Where all three twists are equivalent, we can write the structure index as .
This general technique should give all entanglements of multiple hcb networks, provided that we enumerate through all combinations of twists and the number of strands. Those structures with the highest symmetry will come from indices of the form , where all twists and strand numbers are equivalent. We explore these structures here, and defer the most complete enumeration of lower symmetry cases to be published elsewhere.
For structures , we call prime tangles those of the form:
These prime structures have only two of the four possible vertex positions of the underlying graph occupied with actual vertices of the entangled networks, which allows us to interweave a second symmetric copy of the structure to give what we call a complete structure. For a prime structure , the related complete structure is .
A final class is then all other possible indices, including where t and n have common factors. These give entanglements with both network-like components and long filaments woven together. These structures are also very interesting, and will be published elsewhere.
We can consider the symmetry of these cases from multiple perspectives, including as an in-surface orbifold ([22]) of the pattern, as a 2D orbifold, or as a 3D layer group. From our enumeration, we get 4 distinct symmetry cases. The complete structures will be most symmetric, having in-surface orbifold 2223, a 2D planar symmetry of 236, and a 3D layer group of . The prime structures all have in-surface orbifold 2233, 2D planar symmetry of either 236 or 333, and 3D layer group of either , or . These three variants are determined by which pair of the four possible vertices are occupied. These three layer groups coincide with the three index forms of the prime structures listed above. The first index form will have layer group , the second , and the third . An example structure is shown in Figure 3, which shows the pattern with index , which has in-surface orbifold 2233, 2D planar symmetry 236 and layer group .
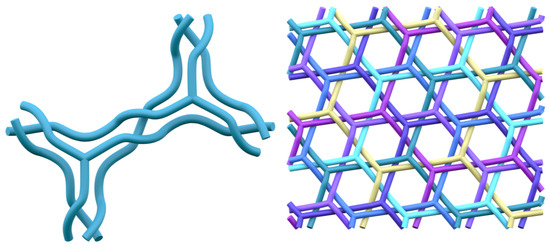
Figure 3.
(Left) The curved lines of the structure as they wind around the tubified surface of the underlying hcb network. (Right) When this motif is repeated in a periodic way, the global arrangement is the entanglement of seven hcb networks, each with a different colour. The pattern has in-surface orbifold 2233, 2D planar symmetry 236 and layer group .
For the prime and complete entanglements, the indices () provide a convenient route to compute the number of components in the resulting structure directly from the indices. To do so, we begin with a simple string of numbers (not necessarily integers) given by
We then truncate this string within the periodic interval , where the entry in this interval, p, has the property for some . Note that the choice of open or closed ends of the interval is arbitrary. For example, the structure will give the initial string
which will in turn give an interval string of
The string terminates when it reaches either 0 or . Taking this string, we can construct a new string of elements L and R, which refer to a left handed or right handed turn along the (6,3) network. The end points (0 or ) are discarded, every positive number is replaced by an R, and every negative number is replaced by an L. For example, the above string will give us
This sequence of right and left handed turns can be used to establish the path that a single edge of the entangled network takes in relation to the underlying (6,3) network. It stems from the geometry of the tubes that the strands are passing along, and how far around those tubes the strand twists. A schematic of this is shown in Figure 4.
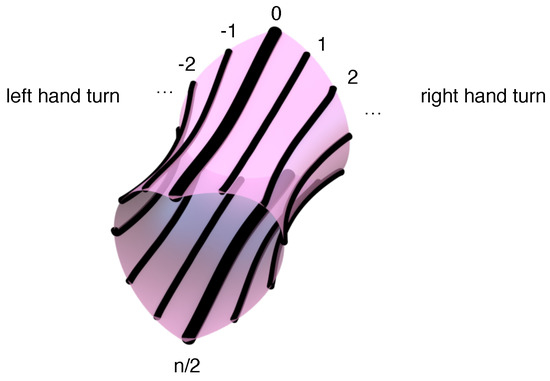
Figure 4.
A single tube of the surface along which our strands wind, we can see that twisting an amount that is below means that the strand will exit to the right, and when it twists beyond (which is then symbolised as a negative number in the string), it will then exit to the left. Hence positive numbers in our string symbolise a right handed turn, and negative numbers left handed turns.
The simple description of paths in a hexagonal lattice has been used extensively in the description of virus self-assembly, first through the work of Goldberg [23], and later by Casper and Klug [24,25] as well as Coxeter [26]. We call a particular translation from one vertex of the lattice to another a Goldberg vector , and it can be described by a translation along a staircase direction of the hexagonal pattern by a hexagons, and a subsequent translation along another staircase direction at an angle of by b hexagons. To obtain the Goldberg vector of a single component within our entangled structure, we need to trace along two consecutive edges of the entangled network. The second edge will be in the reverse order to the original one, and can be found by interchanging R and L elements in the sequence, and then reversing the sequence. So the second sequence to follow for the second edge will then be (for our example above)
Considering that there is either a left-handed or right-handed turn at the vertex of the entangled network between the edges (the choice here is arbitrary), we get the following total string for finding the Goldberg vector:
This sequence of turns gives the Goldberg vector , as seen in Figure 5 (Left).
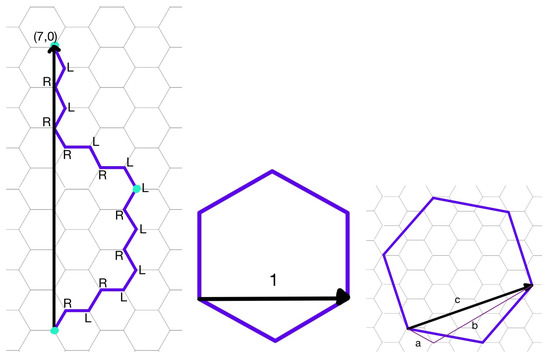
Figure 5.
(Left) The path of left and right handed turns that an edge of the structure takes through the underlying tiling. The resulting Goldberg vector is , which is obtained by the traversing of two edges. (Centre) The width of a single hexagon in the underlying graph is set to 1, and this hexagon has an area of . (Right) The Goldberg vector defines the width of the larger hexagon defined by a single component of the entangled structure. The length of this vector, c, given coordinates of is , which means that the area of this larger hexagon is .
Given a Goldberg vector, we can then compute the number of distinct components in structure as follows. If we set the width of a single hexagon in the underlying pattern to 1 (see Figure 5 (Centre)), then the area of this hexagon is , and it has a total of two vertices within this area (six vertices each divided across three cells). This gives us the density of vertices in the underlying graph, where actual vertices of the tangled networks are potentially located.
The Goldberg vector defines the width of the larger hexagon defined by a single component of the entangled structure (see Figure 5 (Right)). The length of this vector, c, given coordinates of is (this can be computed using some simple trigonometry), which means that the area of this larger hexagon is .
Given the area of the larger hexagon defined by a single component, and the density of vertices, we get that the number of vertices of the underlying hcb graph within this hexagon is exactly , and these are the locations of the vertices of all other components in the structure. Given the symmetry of the structure, each component will have two vertices within the region, and we can thus conclude that the structure has exactly components. This calculation works for prime weaves, with complete weaves having double the number of components.
2. Results
The following Table 1 and Table 2 summarise the possible numbers of components of different entangled structures, as well as the indices that lead to that structure.

Table 1.
Tabulation of the results of the constructive technique, ordered by the Goldberg vectors of the entangled structures, showing the number of components. The first row associated with each vector refers to the prime structures, and the second row the complete structures.

Table 2.
Tangled hcb weavings, ordered by the Goldberg vectors of the entangled structures, and showing the number of components. The first row associated with each vector refers to the prime structures, and the second row the complete structures.
The patterns in Table 1 and Table 2 demonstrate the high level of complexity of the structures that can be achieved with a very simple construction, all while preserving maximal symmetry. If we examine the possible number of components, increasing the Goldberg vector should theoretically lead to structures with increasing component numbers. However, we cannot guarantee that entanglement can be constructed with a given Goldberg vector, for example, there are no structures appearing in our enumeration with vectors , or . However, there are a few particular relations which show that we can in fact get an infinite sequence of structures with increasing component numbers, for example that any index of the form will have the Goldberg vector and hence components, and any index of the form will have the Goldberg and hence components.
Some examples with low numbers of components are shown in Table 3 and Table 4). The explicit geometries of the structures are obtained using the periodic knot-tightening algorithm PB-SONO to gain a symmetric and optimised geometry for the structure [4].

Table 3.
Selected patterns from Table 1, listed by constituent helices , the number of distinct nets, and the corresponding layer group symmetry. Crystallographic files (CIF) are given for each of these structures as supplementary information.

Table 4.
Selected patterns from Table 1. Crystallographic files (CIF) are given for each of these structures as supplementary information.
3. Discussion
We can see a wide variety of entanglements with an equally rich diversity of numbers of components, giving a broad enumeration of entangled hcb networks.
Of particular interest are the structures and , which both have 49 components, but with distinct Goldberg coordinates, and . They also have different layer symmetry, namely and , respectively. The two structures are shown in Table 5, and we conjecture that these are distinct ambient isotopy classes of structures, that they are distinct entanglements, based on their differing twist constructions and Goldberg coordinates.

Table 5.
Two structures with 49 components, but different Goldberg vectors. It could be assumed that the distinct Goldberg vectors imply that the structures are not ambient isotopic to each other. The upper two images show a single component highlighted in yellow, and the bottom two images show each of the 49 nets coloured differently. Crystallographic files (CIF) are given for each of these structures as supplementary information.
Some of the simpler structures in this enumeration have been constructed or observed elsewhere, in particular the structures , and have been constructed using some group theoretic arguments [20]. The structures (three components), (three components), (four components), (four components) have all been constructed via symmetric hyperbolic tilings [16]. Additionally, the structures (three components), (six components) and (seven components) have been constructed via crystallographic methods using only straight edges [17]. The structure (three components) is also the well-known 3-borromean structure, discussed broadly in the literature [15,19].
The enumerative technique that we presented here extends beyond those structures explicitly discussed. We have begun our enumeration on a tubified surface of the lowest genus, which restricts us to at most three distinct helices along the edges of the hcb network. In this article, these three helices are all the same, giving the high symmetry. This starting point gives several directions of increasing complexity of the structures. The first is increasing n and t in the current setting. The second is relaxing the condition that all three helices are the same: this would result in different symmetry settings, and likely cover many of the entanglements of hcb observed in the synthetic chemistry literature, such as [19]. Beyond this, we can increase complexity by enumerating beyond the genus-2 structure of the tubified hcb to a larger unit cell, which has a higher genus, and thus more distinct edges along which to place helices.
One such way to move to a structure with a higher genus while maintaining much of the symmetry is to consider larger unit cells in the existing structure, and then take a subset of components. One such example of this is a high symmetry nine-component hcb structure, which has symmetry and sits on a tubified genus-4 hcb surface. This structure has been derived by an anonymous referee applying the methods described in [27]. It is related to the structure listed in Table 1, which has 54 components. Exactly six copies of the 9 hcb structure, which reticulates a genus-4 surface, will give the , which reticulates a genus-2 surface. We can consider this structure as one with index , where the larger genus is dictated by the fractional twist . The structure is shown in Figure 6. Beyond this, we are also able to enumerate structure on other underlying graphs, both 2-periodic and 3-periodic. These extensions will be presented elsewhere in the near future.
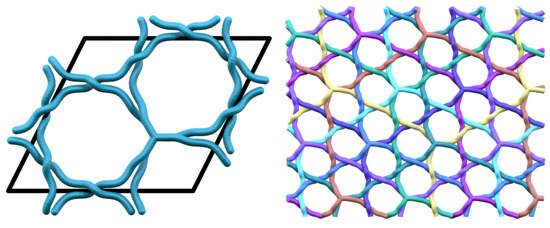
Figure 6.
(Left) A nine-component hcb structure, which sits on a tubified genus-4 hcb surface. This surface has nine distinct edges along which helices lie, which then branch around 6 vertices. This structure will have an index of . This structure has symmetry . (Right) The extended structure, showing the nine hcb components.
In summary, we can see here that the described methodologies of this article are able to enumerate far beyond previous attempts while maintaining control of the component numbers. All of these structures have maximal symmetry within the construction method, and this carries over to maximal layer group symmetry. In addition, all of the structures are chiral, stemming from the chirality of the n-helices used in the construction. This provides a foundation for their exploration in both the chemistry lab and in further geometric studies.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/sym14091805/s1, CIF files for all structures that are displayed as Figures.
Author Contributions
Conceptualization, M.E.E. and S.T.H.; methodology, M.E.E.; writing—original draft preparation, M.E.E.; writing—review and editing, M.E.E.; visualization, M.E.E.; All authors have read and agreed to the published version of the manuscript.
Funding
MEE was funded by the Deutschforschungsgemeinschaft under grant EV210/3-1 and the Cluster of Excellence Matters of Activity. Open access funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—Projektnummer 491466077.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reticular Chemistry Structure Resource. 2022. Available online: http://rcsr.anu.edu.au/ (accessed on 27 June 2022).
- Rolfsen, D. Knots and Links; AMS Chelsea Publishing Series; AMS Chelsea Pub.: Providence, RI, USA, 2003. [Google Scholar]
- Walba, D.M. A Topological Hierarchy of Molecular Chirality and other Tidbits in Topological Stereochemistry. In New Developments in Molecular Chirality; Mezey, P.G., Ed.; Springer: Cham, The Netherlands, 1991; pp. 119–129. [Google Scholar]
- Evans, M.E.; Robins, V.; Hyde, S.T. Ideal geometry of periodic entanglements. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20150254. [Google Scholar] [CrossRef]
- Frisch, H.L.; Wasserman, E. Chemical Topology. Org. Biol. Chem. 1961, 83, 3789–3795. [Google Scholar]
- Forgan, R.S.; Sauvage, J.P.; Stoddart, J.F. Chemical Topology: Complex Molecular Knots, Links, and Entanglements. Chem. Rev. 2011, 5434–5464, e2110345118. [Google Scholar] [CrossRef] [PubMed]
- Castle, T.; Evans, M.E.; Hyde, S.T. Ravels: Knot-free but not free. Novel entanglements of graphs in 3-space. New J. Chem. 2008, 32, 1484–1492. [Google Scholar] [CrossRef]
- Li, F.; Clegg, J.K.; Lindoy, L.F.; Macquart, R.B.; Meehan, G.V. Metallosupramolecular self-assembly of a universal 3-ravel. Nat. Commun. 2011, 2, 205. [Google Scholar] [CrossRef] [PubMed]
- Castle, T.; Evans, M.E.; Hyde, S.T. All toroidal embeddings of polyhedral graphs in 3-space are chiral. New J. Chem. 2009, 33, 2107–2113. [Google Scholar] [CrossRef]
- Barthel, S. On chirality of toroidal embeddings of polyhedral graphs. J. Knot Theory Its Ramif. 2017, 26, 1750050. [Google Scholar] [CrossRef]
- Liu, Y.; O’Keeffe, M.; Treacy, M.M.; Yaghi, O.M. The geometry of periodic knots, polycatenanes and weaving from a chemical perspective: A library for reticular chemistry. Chem. Soc. Rev. 2018, 47, 4642–4664. [Google Scholar] [CrossRef]
- Li, M.; Li, D.; O’Keeffe, M.; Yaghi, O.M. Topological analysis of metal–organic frameworks with polytopic linkers and/or multiple building units and the minimal transitivity principle. Chem. Rev. 2014, 114, 1343–1370. [Google Scholar] [CrossRef]
- Batten, S.R.; Robson, R. Interpenetrating nets: Ordered, periodic entanglement. Angew. Chem. Int. Ed. 1998, 37, 1460–1494. [Google Scholar] [CrossRef]
- Evans, M.E.; Robins, V.; Hyde, S.T. Periodic entanglement I: Networks from hyperbolic reticulations. Acta Crystallogr. Sect. Found. Crystallogr. 2013, 69, 241–261. [Google Scholar] [CrossRef] [Green Version]
- Carlucci, L.; Ciani, G.; Proserpio, D.M.; Mitina, T.G.; Blatov, V.A. Entangled two-dimensional coordination networks: A general survey. Chem. Rev. 2014, 114, 7557–7580. [Google Scholar] [CrossRef]
- Evans, M.E.; Hyde, S.T. Periodic entanglement III: Tangled degree-3 finite and layer net intergrowths from rare forests. Acta Crystallogr. Sect. Found. Adv. 2015, 71, 599–611. [Google Scholar] [CrossRef] [PubMed]
- O’Keeffe, M.; Treacy, M.M.J. Crystallographic descriptions of regular 2-periodic weavings of threads, loops and nets. Acta Crystallogr. Sect. A 2020, 76, 110–120. [Google Scholar] [CrossRef] [PubMed]
- Thompson, B.; Hyde, S.T. A Theoretical Schema for Building Weavings of Nets via Colored Tilings of Two-Dimensional Spaces and Some Simple Polyhedral, Planar and Three-Periodic Examples. Isr. J. Chem. 2018, 58, 1144–1156. [Google Scholar] [CrossRef]
- Alexandrov, E.V.; Blatov, V.A.; Proserpio, D.M. How 2-periodic coordination networks are interweaved: Entanglement isomerism and polymorphism. CrystEngComm 2017, 19, 1993–2006. [Google Scholar] [CrossRef]
- Baburin, I. The Simplest Patterns of Interpenetrated Honeycomb Layers–Counter examples to the Minimal Transitivity Principle? ChemRxiv 2018. [Google Scholar] [CrossRef]
- Hyde, S.T.; Evans, M.E. Symmetric tangled Platonic polyhedra. Proc. Natl. Acad. Sci. USA 2022, 119, e2110345118. [Google Scholar] [CrossRef]
- Conway, J.H.; Burgiel, H.; Goodman-Strauss, C. The Symmetries of Things; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Goldberg, M. A class of multi-symmetric polyhedra. Tohoku Math. J. First Ser. 1937, 43, 104–108. [Google Scholar]
- Caspar, D.L.D.; Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 1962, 27, 1–24. [Google Scholar] [CrossRef]
- Caspar, D.L.D.; Klug, A. Structure and Assembly of Regular Virus Particles. In Proceedings of the Viruses, Nucleic Acids and Cancer; Williams & Wilkins Co.: Baltimore, ML, USA, 1963; pp. 27–39. [Google Scholar]
- Coxeter, H.S.M. Virus macromolecules and geodesic domes. In A Spectrum of Mathematics; Oxford University Press: Oxford, UK; Auckland University Press: Auckland, New Zealand, 1971; pp. 98–107. [Google Scholar]
- Baburin, I.A. On the group-theoretical approach to the study of interpenetrating nets. Acta Crystallogr. Sect. A 2016, 72, 366–375. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).