Thermodynamical Aspects of the LGGR Approach for Hadron Energy Spectra

Abstract

The local growth global reset (LGGR) dynamical model is reviewed and its performance in describing the hadron energy spectra in relativistic collisions is demonstrated. It is shown that even for dynamical processes a temperature-like quantity can be defined and distributions resembling statistical equilibrium can be reached. With appropriate growth and reset rates the LGGR model is capable of describing the right energy spectra. These findings draw a certain picture of quark–gluon plasma development with random hadronization and re-swallowing steps and signals the fact that observing an exponential spectrum does not necessarily prove thermal equilibrium in the experiment.

1. Introduction

The local growth global reset (LGGR) model is a special master equation: it deals with local, small-step increases with some transition rate and a reset to the fiducial “zero” state by one big step. Its continuous version looks similar to a “square-rooted” diffusion problem, containing only a first-order space derivative and a reset term proportional with the probability density in describing the evolution of distributions. Its stationary solution can be analytically written and even its approach to the stationary distribution can be studied. Such a model was successfully applied to describing the appearance of power-law tailed stationary distributions by simple dynamical rules [1,2,3,4,5].

Similar mathematical models and their analogies can well be used in the description of the hadronization process of a quark–gluon plasma (QGP). The dynamical models are to be preferred before the equilibrium ones, since a proton–proton or even a heavy-ion collision system is transient and relatively small (for a review please consult [6]) Forming a QGP, hadronizing it, and occasionally re-swallowing some of the hadrons is the picture underlying our present discussion [7]. Such processes on the statistical level call for a random dynamics with smart rates: a bigger QGP may give birth to more hadrons during the same time interval than a small one. Furthermore when re-swallowing happens, even if rarely, it clears (almost) all hadrons. This gives rise to a reset to the “zero hadrons state”. Meanwhile continuously hadronizing pushed by QCD dynamics can be comprised into a growth rate—possibly also depending on how many hadrons are already there; therefore, we think that an LGGR approach can be applicable also to the statistical QGP hadronization problem.

In the recent past, we have analyzed individual hadron energy distributions, observed in high energy experiments. The spectra can be well described, both at low and high transverse momenta, by a single model predicting a Tsallis–Pareto distribution [8,9,10,11].

In this paper version of the talk given at the Austro-Croatian-Hungarian Triangle (ACHT) Meeting, Zagreb, 2021, we would like to summarize important mathematical background steps for the results concerning particle spectra in the QGP hadronization problem.

First, the LGGR type model is introduced and some references are made to its success in recent interdisciplinary applications. Then, a rough analysis of phase space and fluctuating total number effects on the individual energy spectra is presented. We demonstrate that while non-exponential distributions of energy can be statistically generated, not all exponential-like distributions are born from equilibrium. As a result, we conclude that even observing an exponential spectrum does not prove thermal equilibrium in an experiment.

2. The LGGR Model

The local growth and global reset (LGGR) model is a special master equation, recently introduced for modeling various distributions frequently encountered in complex systems. In order to present this model in brief, let us consider a system with identical entities, where the states of the constituents are identified by the amount of quanta they possess. Let $P_n\left(t\right)$ be the probability that one entity posses n quanta at time moment t (naturally ${\sum }_{\left\{n\right\}}{P}_n\left(t\right)=1$). Two types of processes are considered in the dynamics of the system. First, each entity can increase the number of possessed quanta from a state with n quanta to a state with $n+1$ quanta, with a state-dependent growth rate ${\mu }_n$. The second process, which allows the convergence to an equilibrium configuration is a reset to the ground state with zero quanta ($n=0$), governed by the ${\gamma }_n$ state-dependent reset rate. The master equation for such a process with discrete states writes as:

$$\frac{d{P}_n\left(t\right)}{dt}={\mu }_{n-1}{P}_{n-1}\left(t\right)-{\mu }_n{P}_n\left(t\right)-{\gamma }_n{P}_n\left(t\right)+{\delta }_{n,0}\langle \gamma \rangle \left(t\right).$$

(1)

The last term in this evolution equation guarantees the normalization of $P_n\left(t\right)$ by refeeding the system at the state $n=0$ if needed:

$$\langle \gamma \rangle \left(t\right)=\sum _j{\gamma }_j{P}_j\left(t\right).$$

(2)

For discrete n states, the stationary distribution can be given in form of a product

$$Q_n=\frac{{\mu }_0{Q}_0}{{\mu }_n}\prod _{j=1}^n\frac{{\mu }_j}{{\mu }_j+{\gamma }_j},$$

(3)

where $Q_0$ can be determined from the normalization condition. The convergence to the stationary state was discussed in several recent works [12,13]. For constant growth rate, $\mu$, and constant reset rate, $\gamma$, it is found that the convergence is faster than $exp(-\gamma t)$. For constant reset rate, $\gamma$, and linearly increasing growth rate, $\mu =\sigma (n+b)$, the convergence is faster than $exp(-(\sigma +\mu \left)t\right)$. 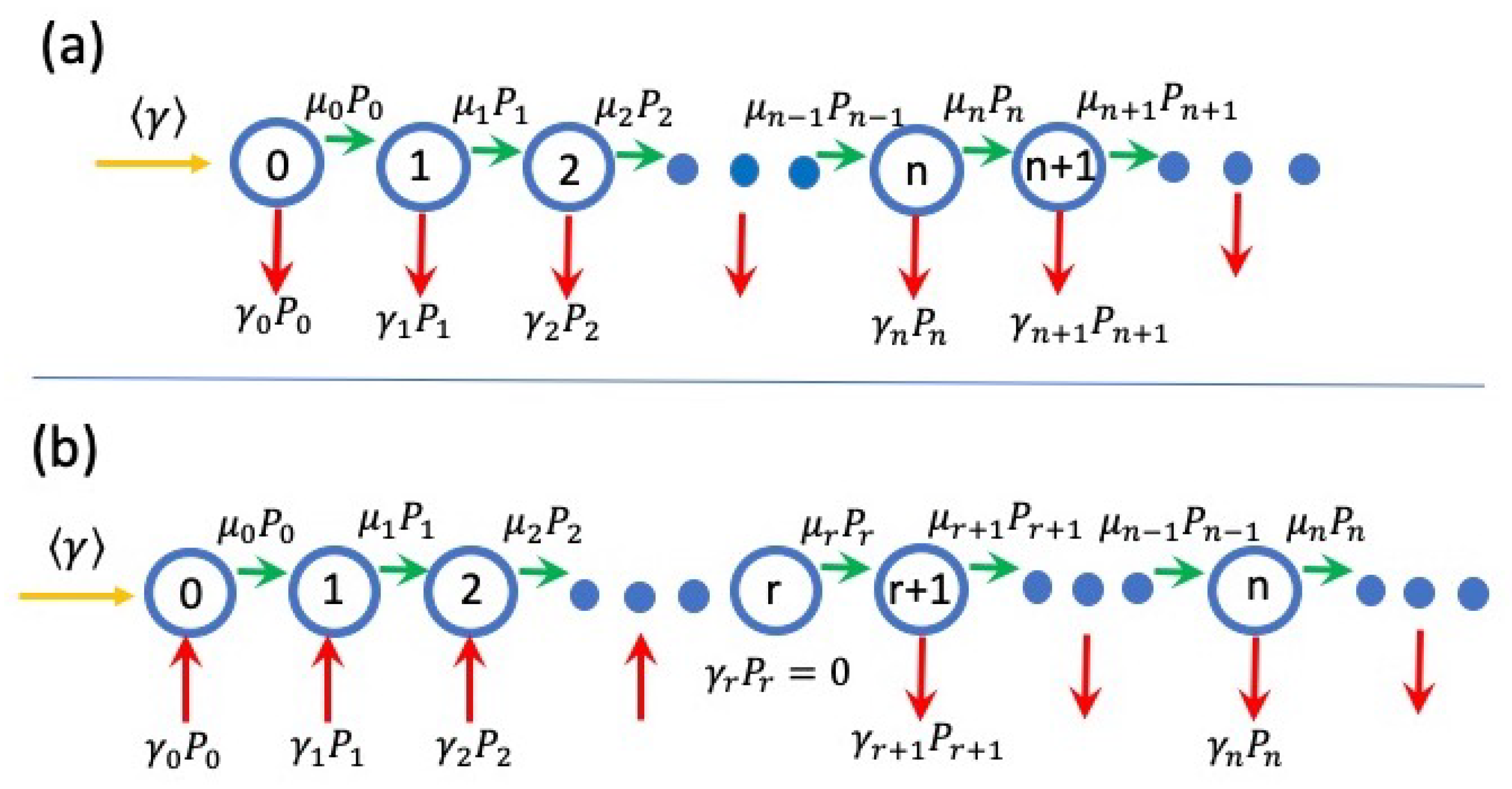The reset rate can be either positive for all states (illustrated in Figure 1a) meaning an actual reset to the zero state, or can change its sign from negative to positive values at state r. This means that elements that reset at $n>r$ states re-enter the system at states $n<r$ (illustrated in Figure 1b).

Considering discrete states has the drawback however, that the product in (3) has a compact analytical solution for just a few cases [14].

The growth and reset scenario of the dynamical Equation (1) can be generalized to continuous states by converting it into a partial differential equation with continuous growth and reset rates (${\mu }_n\to \mu \left(x\right)$, ${\gamma }_n\to \gamma \left(x\right)$) [1]:

$$\frac{\partial \rho (x,t)}{\partial t}=-\frac{\partial }{\partial x}\left[\mu \left(x\right)\rho (x,t)\right]-\gamma \left(x\right)\rho (x,t)+\langle \gamma \left(x\right)\rangle \left(t\right)\delta \left(x\right).$$

(4)

Here $\rho (x,t)$ is the normalized probability density (${\int }_{\left\{x\right\}}\rho (x,t)dx=1$) for an element possessing x amount of quanta at time moment t. The feeding term at $x=0$ ensures the conservation of probability:

$$\langle \gamma \left(x\right)\rangle \left(t\right)={\int }_{\left\{x\right\}}\gamma \left(x\right)\rho (x,t)dx$$

(5)

The steady-state of the growth and reset process, ${\rho }_s\left(x\right)$, has a compact solution:

$${\rho }_s\left(x\right)=\frac{\mu \left(0\right){\rho }_s\left(0\right)}{\mu \left(x\right)}{\mathrm{e}}^{-\underset{0}{\overset{x}{\int }}\frac{\gamma \left(u\right)}{\mu \left(u\right)}du},$$

(6)

By correctly choosing the $\mu \left(w\right)$ growth- and $\gamma \left(w\right)$ reset rates, the LGGR model will lead to ${\rho }_s\left(w\right)$ distributions that are frequently encountered in complex systems [1].

3. A Simple Approach to Hadronization Statistics

3.1. General Framework

In non-thermal ensembles a kinetic definition of a temperature-like quantity is possible, usually as $T=E/〈n〉$. This assumes a given total energy (microcanonical non-equilibrium approach), but a fluctuating number of particles, n, as it is typical for the results of hadronization processes in high energy collisions. Our aim is to prove the possibility of such temperature definition for a particle ensemble subjected to the LGGR dynamics.

Let us consider a relativistic hadron collision experiment, and we assume for the newly created particles an ensemble, where the total energy of the produced hadrons equals to E, the total initial kinetic energy invested into the collision. This resembles a microcanonical ensemble in the classical statistical physics.We are asking for the occurrence frequency of a given individual (or subsystem) energy of a created hadron, $\epsilon \in (0,E]$. Assuming that every phase-space element has the same probability, we can approach this probability density as:

$$\rho \left(\epsilon \right)={〈\frac{{\mathsf{\Gamma }}_1\left(ϵ\right){\mathsf{\Gamma }}_n(E-\epsilon )}{{\mathsf{\Gamma }}_{n+1}\left(E\right)}〉}_n$$

(7)

Denoting by ${\mathsf{\Omega }}_n\left(E\right)$ the hyper-volume of the phase-space for n particles, so that their total energy (composed solely by the kinetic energy) is smaller or equal E. Correspondingly the energy shell, ${\mathsf{\Gamma }}_n\left(E\right)$ denotes the size, where the total energy of the ensemble is fixed to E,

$${\mathsf{\Gamma }}_n\left(E\right)=\frac{d{\mathsf{\Omega }}_n\left(E\right)}{dE}$$

(8)

A statistics over several events, where the number of hadrons, n, is random according to a distribution $P_n\left(E\right)$ will lead to:

$$\rho \left(\epsilon \right)=\sum _{n=0}^{\infty }\frac{{\mathsf{\Gamma }}_1\left(ϵ\right){\mathsf{\Gamma }}_n(E-\epsilon )}{{\mathsf{\Gamma }}_{n+1}\left(E\right)}{P}_n\left(E\right).$$

(9)

This simple approach actually delivers the characteristic PDF function for the hadron energies produced in collision experiments.

3.2. Phase Space Volumes

In a non-intersecting particle picture phase space is over momenta. Individual energies are functions of momenta according to the corresponding dispersion relation. A number of such relations look similar to a power of the absolute value, so they can be comprised into an $L_p$-norm:

$${\left(\sum _{i=1}^n{\left|p_i\right|}^p\right)}^{1/p}\le R\left(E\right)$$

(10)

with $p_i$ individual momentum components, all-together n-dimension in phase space and E total energy. The $R\left(E\right)$ function also reflects the dispersion relation.

For extreme relativistic particles $p=1$, and $R\left(E\right)=E$ measures the volume satisfying

$$\sum _{i=1}^n\left|p_i\right|\le E.$$

(11)

The general formula reads as

$${\mathsf{\Omega }}_n^{\left(p\right)}\left(R\right)=\frac{\mathsf{\Gamma }{(1/p+1)}^n}{\mathsf{\Gamma }(n/p+1)}{\left(2R\right)}^n.$$

(12)

For the $p=1$, $R\left(E\right)=E$ case considered here:

$${\mathsf{\Omega }}_n\left(E\right)=\frac{{\left(2E\right)}^n}{n!}$$

(13)

and ${\mathsf{\Omega }}_0\left(E\right)=1$.

The corresponding microcanonical constrained energy shell size is:

$${\mathsf{\Gamma }}_n\left(E\right)=\frac{2^n{E}^{n-1}}{(n-1)!}=2{\mathsf{\Omega }}_{n-1}\left(E\right).$$

(14)

3.3. Calculating the PDF for a Single Particle

The above consideration leads us to the statistical weights in the summation from Equation (9). Using the computed hyper-volume and hyper-surface approximations, we obtain

$$\rho \left(\epsilon \right)=\sum _{n=0}^{\infty }\frac{n}{E}{\left(1-\frac{ϵ}{E}\right)}^{n-1}{P}_n\left(E\right).$$

(15)

Since the statistical weights are normalized, i.e.,

$${\int }_0^E\frac{{\mathsf{\Gamma }}_1\left(ϵ\right){\mathsf{\Gamma }}_n(E-\epsilon )}{{\mathsf{\Gamma }}_{n+1}\left(E\right)}dϵ={\int }_0^E\frac{n}{E}{\left(1-\frac{ϵ}{E}\right)}^{n-1}=1,$$

(16)

by imposing ${\displaystyle \sum _0^{\infty }}{P}_n\left(E\right)=1$, we will have:

$${\int }_0^{\infty }\rho \left(ϵ\right)dϵ=1$$

(17)

4. LGGR Scenario for Hadronization

In this section, we flash a few examples for possible mechanisms of non-thermal exponential and Tsallis–Pareto energy distributions in the view of the LGGR type dynamics applied for the hadronization process. Let us discuss simple, but enlightening cases for the $P_n\left(E\right)$ distribution, that are derived from some simple LGGR mechanism.

4.1. Constant Growth and Reset Rates

First, we consider that both the $\gamma$ and $\mu$ rates are state independent constants. In such cases the LGGR model [12] leads to:

$$P_n\left(E\right)\equiv Q_n(\gamma ,\mu )=\frac{1}{1+\frac{\mu }{\gamma }}{\left(1+\frac{\gamma }{\mu }\right)}^{-n}$$

(18)

The average number of quanta $\langle n\rangle$ related to the total E energy can be immediately obtained as:

$$\langle n\rangle =\sum _{n=0}^{\infty }n{Q}_n=\frac{\mu }{\gamma }.$$

(19)

Using the average number of particles, $\langle n\rangle$, this simple growth and reset phenomena leads to:

$$\rho \left(\epsilon \right)=\sum _{n=0}^{\infty }\frac{n}{E}{\left(1-\frac{\epsilon }{E}\right)}^{n-1}{Q}_n\left(\langle n\rangle \right)=\frac{\langle n\rangle }{E}\frac{1}{{\left(1+\frac{ϵ\langle n\rangle }{E}\right)}^2}$$

(20)

The normalization of $\rho \left(ϵ\right)$ leads to

$$\rho \left(ϵ\right)=\frac{\langle n\rangle +1}{E}\frac{1}{{\left(1+\frac{ϵ\langle n\rangle }{E}\right)}^2}$$

(21)

For the $\langle n\rangle ϵ/E<<1$ limit we obtain:

$$\rho \left(ϵ\right)\approx \frac{\langle n\rangle +1}{E}\left(1-2\frac{\langle n\rangle ϵ}{E}+3{\left(\frac{\langle n\rangle ϵ}{E}\right)}^2+O{[\langle n\rangle ϵ/E]}^3\right)$$

(22)

4.2. Preferential Growth and Reset Rates

We consider now a more complex, but still analytically tractable approach for the hadronization process: Having already n hadrons, a new hadron is created with the state dependent probability rate ${\mu }_n$, and a collective re-melting into the prehadron stage is considered with rate ${\gamma }_n$. We conjecture that there is a certain number of newly made hadrons, $\langle n\rangle$, for which the re-melting does not occur. Less hadrons than this number will likely to be created from a zero number state. This is quantified with negative ${\gamma }_n$ rates for $n<\langle n\rangle$ leading to a yield proportional with $P_n$. For $n>\langle n\rangle$ the hadrons will be re-melted with a positive ${\gamma }_n$ rate. A reset rate describing this scenario is ${\gamma }_n=\sigma (n-\langle n\rangle )$. For the growth rate, we assume an independent preferential growth: ${\mu }_n=\sigma (n/k+1)\langle n\rangle$. Certainly, already at $n=0$, in the state with no hadrons, there is a probability rate to create one, ${\mu }_0=\sigma \langle n\rangle$ hadrons. Having already n hadrons accelerates the process, most of the hadrons to be made are light bosons, mainly pions. The $\sigma$ proportionality factor in the reset rate is used to ensure ${\gamma }_0+{\mu }_0=0$. For all the other $n>0$ states one will have ${\gamma }_n+{\mu }_n>0$.

Accepting the above assumptions for the ${\mu }_n$ growth rates and ${\gamma }_n$ reset rates we obtain:

$$Q_n=\left(\begin{array}{c}n+k-1\\ n\end{array}\right)\frac{{(\langle n\rangle /k)}^n}{{(1+\langle n\rangle /k)}^{k+n}}$$

(23)

With the used parametrization of the growth and reset rates, the first moment is exactly $\langle n\rangle$. As it is shown in [1], the hadron multiplicity data from the PHENIX experiment at the RHIC from Brookhaven [15] are in agreement with the obtained hadron number distribution. The sub-Poissonian nature of such distributions is shown also in a recent work using the data from the ATLAS experiment at the LHC [16]. The above particle number distribution leads to the stationary probability density for the energy in the form of a Tsallis–Pareto distribution [17]:

$$\rho \left(\epsilon \right)=\sum _{n=0}^{\infty }\frac{n}{E}{\left(1-\frac{\epsilon }{E}\right)}^{n-1}{Q}_n(\langle n\rangle ,k)=\frac{\langle n\rangle }{E}{\left(1+\frac{〈n〉}{k}\frac{\epsilon }{E}\right)}^{-k-1}$$

(24)

After normalization we obtain:

$$\rho \left(\epsilon \right)=\frac{\langle n\rangle }{E}\frac{1}{1-{\left(1+\frac{\langle n\rangle }{k}\right)}^{-k}}{\left(1+\frac{〈n〉}{k}\frac{\epsilon }{E}\right)}^{-k-1}$$

(25)

As it is shown in the masters thesis of Gábor Biró [18], the experimental results confirm such a distribution. Many other research groups reached similar conclusions for experiments performed at RHIC and LHC [19,20,21,22].

In the $\langle n\rangle ϵ/kE<<1$ limit, up to second-order terms we have:

$$\rho \left(ϵ\right)\approx \frac{\langle n\rangle }{E\left(1-{\left(1+\frac{\langle n\rangle }{k}\right)}^{-k}\right)}\left(1-\frac{k+1}{k}\frac{\langle n\rangle ϵ}{E}+\frac{1}{2}\frac{(k+1)(k+2)}{k^2}{\left(\frac{\langle n\rangle ϵ}{E}\right)}^2+O{[\langle n\rangle ϵ/Ek]}^3\right)$$

(26)

We note by passing that the $k\to \infty$ limit of the above cited negative binomial distribution is Poissonian, leading to an exponential energy distribution in this limit:

$$\rho \left(ϵ\right)=\frac{〈n〉}{E}{\mathrm{e}}^{-〈n〉ϵ/E}.$$

(27)

4.3. A Non-LGGR Approach

Outside of the framework of the LGGR dynamics, one also could consider a simple probabilistic approximation based on the random distribution of a large number of particles, N, in a large number of cells, K. Let us assume that we are looking for a space-volume with k cells. If we denote by $\langle n\rangle =kN/K$ the expected number of particles in these k cells, the probability to obtain n number of particles in this volume has a Poisson distribution in the $n\to \infty ,K\to \infty$, but $N/K$ finite limit.

$$P_n\left(E\right)=e^{-\langle n\rangle }\frac{{\langle n\rangle }^n}{n!}$$

(28)

This leads to a Boltzmann–Gibbs type exponential distribution for $ϵ$. The distribution normalized on the $(0,E]$ interval:

$$\rho \left(ϵ\right)=\frac{\langle n\rangle }{E\left(1-e^{-\langle n\rangle }\right)}{e}^{-\langle n\rangle \frac{ϵ}{E}}$$

(29)

5. Equilibrium Thermodynamics Consideration

We consider now the equilibrium thermodynamics approach, assuming a canonical distribution for the hadrons $ϵ$ energy. Assuming a T thermodynamic temperature for the system and the available energies in the $(0,E]$ interval, we obtaining:

$${\rho }_T\left(ϵ\right)=\frac{1}{T\left(1-e^{-E/T}\right)}{e}^{-\frac{ϵ}{T}}$$

(30)

In the $E\to \infty$, T finite limit it is again Boltzmannian

$$\rho \left(ϵ\right)=\frac{1}{T}{\mathrm{e}}^{-ϵ/T}.$$

(31)

For $ϵ/T<<1$ we obtain:

$${\rho }_T\left(ϵ\right)\approx \frac{1}{T(1-e^{-E/T})}\left(1-\frac{ϵ}{T}+\frac{1}{2}{\left(\frac{ϵ}{T}\right)}^2+O{[ϵ/T]}^3\right)$$

(32)

We are able now to compare this result, with the one from the considered dynamic processes and identify the corresponding equilibrium thermodynamics quantities.

The very simple LGGR approach with a constant growth and reset rate leads for an expression of $\rho \left(ϵ\right)$ that is identical with the one expected in the thermodynamical equilibrium only up to the zeroth order. In this order, we obtain the expected temperature definition: $T=E/\langle n\rangle$

Considering however the LGGR dynamics with a preferential growth rate, in the limit of large reset rates relative to the growth rate, the expression of $\rho \left(ϵ\right)$ becomes identical with the one expected in the equilibrium approach: ${\rho }_T\left(ϵ\right)$. When $\langle n\rangle /k<<1$ we write:

$${\left(1+\frac{\langle n\rangle }{k}\right)}^{-k}={\left(1+\frac{\langle n\rangle }{k}\right)}^{-\frac{k}{\langle n\rangle }\langle n\rangle }\approx e^{-\langle n\rangle }$$

(33)

In addition, if one considers $k>>1$, we have $(k+1)/k\approx (k+1)(k+2)/k^2\approx 1$. Taking all these into account, we are led now to a consistent definition of temperature: $T=E/\langle n\rangle$. We should not be surprised however that in the $k>>1$ limit the results are consistent with the one expected in the equilibrium statistical physics. In this limit, the Tsallis–Pareto distribution converges to an exponential distribution, hence this obvious result.

As it is naturally expected in case of the Poisson-like hadron number distribution, linked to the entropic fluctuation of particle number in a fixed volume, the exact form of ${\rho }_T\left(ϵ\right)$ is observed with $T=E/\langle n\rangle$.

6. Summary

The main message of this contribution is to emphasize and prove again that there are exponential-like energy distributions in the physical world, which are not thermal. More specifically, we considered the case of the LGGR dynamics, and we have shown that in the dynamical stationarity, the expected particle energy spectra follows a distribution that in some cases is similar with the one expected from equilibrium statistical physics. For preferential growth and constant reset rates the stationary limit of the dynamics leads to similar energy spectra as the one observed in equilibrium systems. This allows us to define a temperature as: $T=E/\langle n\rangle$. In contrast with this result, we observed that by considering constant growth and reset rates the stationary dynamics will not lead to an energy spectra that can be considered thermal, and therefore one cannot use a consistent definition for the thermodynamic temperature in general.