Self-Weighted Quasi-Maximum Likelihood Estimators for a Class of MA-GARCH Model

Abstract

In financial time series analysis, symmetric and asymmetric GARCH models have become essential models for measuring the characteristics of economic volatility. In this article, we propose the consistency and asymptotic normality properties of the self-weighted quasi-maximum likelihood estimation without assuming the existence of the second moment for the moving average model with a class of GARCH error. Numerical simulation shows that the parameter estimation performs well; empirical analysis shows that the self-weighted quasi-maximum likelihood estimation of the moving average model with a class of GARCH error can improve the data fitting effect and prediction ability.

1. Introduction

With the progress and development of multivariate time series theory and technology, to accurately describe the dynamic time-varying characteristics of the volatility of financial time series data, Engle [1] proposed an ARCH model for the volatility of the UK inflation rate, and Bollerslev [2] extended it to a GARCH model. On this basis, many experts and scholars at home and abroad have done much research on the GARCH model in combination with the asymmetry and long memory of volatility. For example, given that the impact of positive and negative news on stock market volatility is asymmetric, Nelson [3] proposed the exponential GARCH (EGARCH) model; Glosten, Jagannathan, and Runkle [4] proposed the asymmetric GARCH (GJR) model; H. Viet Long and Bin Jebreen et al. [5] employed the generalized autoregressive conditional heteroskedasticity (GARCH) model for risk management as their main contribution. However, in the traditional GARCH model, the conditional heteroscedasticity is a function of the unobservable lag residuals square sequence, which makes the parameter estimation of this model complex. Li and Zhang et al. [6] combined the ideas of a factor model and a symmetric GARCH model to describe the dynamics of a high-dimensional conditional covariance matrix. Therefore, Baillie [7] described the population characteristics of various long memory processes in FIGARCH. The conditional variance of the process implies a slow hyperbolic decay rate for the influence of lagged squared innovations. Ling [8] proposed the DAR(p) model based on the ARCH model. In this way, a better estimate of the parameters can be obtained. Moreover, Ling [9] proposed the consistency and asymptotic properties of self-weighted quasi-maximum likelihood estimation in the presence of fractional moments for the ARMA-GARCH model. Then, Zhu and Ling [10] proposed the strong coincidence and asymptotic properties of global self-weighted quasi-maximal exponential likelihood estimation for the ARMA-GARCH model in the presence of fractional moments. Many models with GARCH also have some properties of similar analysis. For example, Pan and Chen et al. [11] discussed the asymptotic properties of WLAD estimation for the ARFIMA model under stationary and non-stationary conditions. For long-memory and heteroscedastic models, Ramírez-Parietti and Contreras-Reyes et al. [12] computed cross-sample entropy measures for synchrony level, which involved ARMA, ARFIMA, ARMA-GARCH, and FIGARCH processes.

Based on the classical ARCH model, Ling [13] proposed the DAR model to make the parameter estimation of the DAR model become easier to estimate and proved the consistency and asymptotic properties of the QMLE estimation without assuming the existence of the second-order moment of the sequence. Then Zhu and Zhang et al. [14] proposed a class of MA-GARCH models (the DAR(p) model p tends to infinity), proving that Ling has done similar work without assuming the existence of second-order moments. However, when there are extreme data, the parameter weights estimated by QMLE are all 1, which has a specific error. Thus, Ling [9] proved that the self-weighted QMLE estimation of the RAMA-GARCH model is consistent and asymptotic in the presence of fractional moments. The purpose is to use weights to reduce leverage points and make estimates more precise and more efficient.

In this paper, to reduce the error, we perform a self-weighted QMLE estimation based on Zhu and Zhang et al. [14] Giving different weights to different values makes our estimates more robust, proving some properties of the forecast. The rest of the article is organized as follows. Section 2 introduces the consistency and asymptotic properties of estimation; Section 3 presents the numerical simulation of self-weighted QMLE estimation. Section 4 gives a real example; Section 5 concludes the article. The proof is in Appendix A.

2. Self-Weighted QMLE

A class of MA-GARCH model can be written as

$$\begin{array}{cc}\hfill y_t& =\varphi {\epsilon }_{t-1}+{\epsilon }_t\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill h_t& =\omega +\alpha y_{t-1}^2+\beta h_{t-1}\hfill \end{array}$$

(3)

where $\left|\varphi \right|<1,\omega ,\alpha >0,0<\beta <1$ and when $t>s$, $\left\{y_t\right\}$ and $\left\{e_t\right\}$ are independent of each other. Denote $\delta =(\omega ,\alpha ,\beta )$, and $\theta ={(\varphi ,\delta )}^{\prime }\subset \Theta$, and $\Theta =(\theta :-1<\underline{\varphi }<\varphi <\overline{\varphi }<1,0<\underline{\omega }<\omega <\overline{\omega },0<\underline{\alpha }<\alpha <\overline{\alpha },0<\underline{\beta }<\beta <\overline{\beta }<1)$. Denote $\Phi \left(z\right)=1+\varphi z$, $\beta \left(z\right)=1-\beta z$, ${\Phi }^{-1}\left(z\right)={\sum }_{i=0}^{\infty }{a}_{\Phi }\left(i\right)z^i$, $su{p}_{\Theta }a\left(i\right)=O\left({\rho }_0^i\right)$, ${\beta }^{-1}\left(z\right)={\sum }_{i=0}^{\infty }{\beta }^i{z}^i$, where $0<{\rho }_0<1$.

Compared to traditional MA-GARCH model, the previous ${\epsilon }_{t-1}^2$ in (3) is instead denoted by $y_{t-1}^2$. A class of MA-GARCH model is easier to predict than the traditional MA-GARCH model.

Remark 1.

With simple iteration, the model can be transformed into:

$$y_t=\sum _{i=1}^{\infty }{(-1)}^{i-1}{\varphi }^i{y}_{t-i}+e_t\sqrt{\omega /(1-\beta )+\alpha \sum _{j=1}^{\infty }{\beta }^{j-1}{y}_{t-j}^2}$$

From this, we can see that, compared with the DAR(p) model proposed by Ling [14], the above formula is equivalent to the order p of the conditional mean, and the conditional variance tends to infinity. Then, we refer to Zhu [15] to obtain the parameter space of the above models (1)–(3).

We introduce the following conditions:

A1:

${\theta }_0$ is an interior point in $\Theta$, and $\left\{y_t\right\}$ is stationary, ergodic, and identifiable.

A2:

$\left\{e_t\right\}$ is independent and identically distributed with a mean of 0 and a variance of 1.

A3:

$\left\{e_t^2\right\}$ has a nondegenerate distribution with $E{e}_t^4<\infty$.

A4:

${\omega }_t=\omega {(y_{t-1},y_{t-2},\cdots )}^{\prime }$ and ${\omega }_t$ is a measurable, positive, and bounded function on $R^{Z_0}$ with $E\left[{\omega }_t({\xi }_{\rho ,t-1}^2+{\zeta }_{\rho ,t-1}^2+{\xi }_{\rho ,t-1}^2{\zeta }_{\rho ,t-1}^2)\right]<\infty$, and $Z_0=\{0,1,2,\cdots \}$, $\rho \in (0,1)$.

Given the observations $\{y_n,\dots ,y_1\}$ and the initial values $\{y_0,y_{-1},y_{-2},\dots \}$, we can rewrite the parametric models (1)–(3) as

$$\begin{array}{cc}\hfill {\epsilon }_t& =y_t-\varphi {\epsilon }_{t-1}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill h_t& =\omega +\alpha y_{t-1}^2+\beta h_{t-1}\hfill \end{array}$$

(6)

According to Yoshida’s [16] research on the asymptotic properties of the likelihood estimators of various nonlinear stochastic processes, for convenience, the weighted log-quasi-likelihood function (ignoring a constant) can be written as follows:

$$L_{sn}=\frac{1}{n}\sum _{t=1}^{\infty }{\omega }_t{l}_t\left(\theta \right),l_t\left(\theta \right)=log{h}_t\left(\theta \right)+\frac{{\epsilon }_t^2\left(\theta \right)}{h_t\left(\theta \right)}$$

Remark 2.

This is important because it ensures that the maximum value of the log of the probability occurs at the same point as the original probability function. The quasi-score function and the quasi-information matrix are given in the Appendix A. Equation (A11) in the Appendix A.1 shows that

$$su{p}_{\Theta }\Vert \frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\Vert \le O\left(1\right){\xi }_{\rho ,t-1}^2$$

It is possible to obtain an estimator such that it is asymptotic normal if we can downweight ${\xi }_{\rho ,t-1}^2$.

We look for the minimizer, ${\widehat{\theta }}_{sn}={({\widehat{\varphi }}_{sn},{\widehat{\delta }}_{sn})}^{\prime }$, of $L_{sn}$ on $\Theta$; that is,

$${\widehat{\theta }}_{sn}=argmi{n}_{\Theta }{L}_{sn}\left(\theta \right)$$

We first give two lemmas.

Lemma 1.

Let ${\xi }_{\rho ,t}=1+{\Sigma }_{i=0}^{\infty }{\rho }^i\left|y_{t-i}\right|$, where $0<\rho <1$. Then there exists a constant ρ and a neighborhood ${\Theta }_0$ of ${\theta }_0$ such that:

$\left(i\right)$

$su{p}_{\Theta }\left|{\epsilon }_{t-1}\left(\theta \right)\right|\le c{\xi }_{\rho ,t-1}$;

$\left(ii\right)$

$su{p}_{\Theta }\Vert \frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }\Vert \le c{\xi }_{\rho ,t-1}$;

$\left(iii\right)$

$su{p}_{\Theta }\Vert \frac{{\partial }^2{\epsilon }_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\Vert \le c{\xi }_{\rho ,t-1.}$.

Lemma 2.

Let ${\zeta }_{\rho ,t}=1+{\sum }_{i=0}^{\infty }{\rho }^i{y}_{t-1}^2$. Then there exists a constant ρ and a neighborhood ${\Theta }_0$ of ${\theta }_0$, and $0<\beta <\rho <1$. Then:

$\left(i\right)$

$su{p}_{\Theta }{h}_t\left(\theta \right)\le c{\zeta }_{\rho ,t-1}$

$\left(ii\right)$

$su{p}_{\Theta }\Vert \frac{1}{h_t\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \delta }\Vert \le c{\zeta }_{\rho ,t-1}$

$\left(iii\right)$

$su{p}_{\Theta }\Vert \frac{1}{h_t\left(\theta \right)}\frac{{\partial }^2{h}_t\left(\theta \right)}{\partial \delta \partial {\delta }^{\prime }}\Vert \le c{\zeta }_{\rho ,t-1}$

$\left(iv\right)$

$\Vert \frac{1}{\sqrt{h_t\left(\theta \right)}}\frac{\partial h_t\left(\theta \right)}{\partial \varphi }\Vert =0$

We now can state our main results as follows.

Theorem 1.

If Assumptions A1–A4 hold, then

$\left(i\right)$

${\widehat{\theta }}_{sn}{⟶}_p{\theta }_0$

$\left(ii\right)$

$\sqrt{n}({\widehat{\theta }}_{sn}-{\theta }_0){⟶}_{d}N(0,{\sum }_0^{-1}{\Omega }_0{\sum }_0^{-1})$ where

$${\mathbf{\Sigma }}_{\mathbf{0}}=E\left[\begin{array}{cc}2\frac{{\omega }_t}{h_t\left({\theta }_0\right)}\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \varphi }\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial {\varphi }^{\prime }}& 0\\ 0& \frac{{\omega }_t}{h_t^2\left(\theta \right)}\frac{\partial h_t\left({\theta }_0\right)}{\partial \delta }\frac{\partial h_t\left({\theta }_0\right)}{\partial {\delta }^{\prime }}\end{array}\right]$$

$${\mathbf{\Omega }}_{\mathbf{0}}=E\left[\begin{array}{cc}4\frac{{\omega }_t^2}{h_t\left({\theta }_0\right)}{\left(\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \varphi }\right)}^2& 0\\ 0& {\omega }_t^2\frac{\varsigma }{h_t^2\left({\theta }_0\right)}{\left(\frac{\partial h_t\left({\theta }_0\right)}{\partial \delta }\right)}^2\end{array}\right]$$

$$\varsigma =E{e}_t^4-1$$

$$\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }=\sum _{i=1}^{\infty }{(-1)}^{i}i{\varphi }^{i-1}{y}_{t-i}$$

$$\frac{\partial h_t\left(\theta \right)}{\partial \delta }=[\frac{1}{1-\beta },\sum _{j=1}^{\infty }{\beta }^{j-1}{y}_{t-j}^2,\sum _{j=1}^{\infty }{\beta }^{j-1}{h}_{t-j}]$$

3. Simulation

In this section, on the basis of a class of MA-GRACH model, we compared SQMLE with QMLE. In the simulation, we studied the cases when $\left\{e_t\right\}$ has $N(0,1)$, $Laplace(0,1)$, and $t_3$. Then we took the sequences $\left\{y_t\right\}$ that are generated by a class of MA-GARCH models, where ${\theta }_0=(0.5,0.1,0.4,0.3)$. We needed to select a weight ${\omega }_t$. It seemed reasonable to use the following weight analog Ling [17] and Huber [18] influence function:

$${\omega }_t=\left\{\begin{array}{cc}1,\hfill & a_t=0;\hfill \\ \frac{c^3}{a_t^3},\hfill & a_t\ne 0\hfill \end{array}\right.$$

(7)

where $a_t=|y_{t-1}\left|I\right(|y_{t-1}|\ge c)$, c is the 95th quantile of the sequence $\left\{y_t\right\}$. This weight satisfies assumption A4. Then, For the models (1)–(3), we compared the parameter estimation methods of Zhu and Zhang, etc. [14]. We set the sample size at $n=400,800,1200$ and used 1000 replications.

From Table 1, when $e_t\sim N(0,1)$, we can see that all estimators in Table 1 have minimal biases, and the SD and AD of self-weighted QMLE are close. As the sample size n increases, the values of SD and AD both decrease. At the same time, we compare the two estimation methods, the quasi-maximum likelihood estimation(QMLE) and the self-weighted quasi-maximum likelihood estimation (SQMLE), in Table 1. With the increase in n, the bias, AD, and SD shows different trends. The quasi-maximum likelihood estimation and the self-weighted quasi-maximum likelihood estimation values were getting closer and closer. Still, the quasi-maximum likelihood estimation’s bias, AD, and SD are always slightly smaller than the bias, AD, and SD of the self-weighted quasi-maximum likelihood estimate. When this happens, it is reasonable to be pointed out by Ling [9]. Therefore, the simulation results illustrate that self-weighted quasi-maximum likelihood estimates are applicable.

Table 1. Estimators for the models (1)–(3) when $e_t\sim N(0,1)$.

${\mathit{\theta }}_0=(0.5,0.1,0.4,0.3)$
		$\widehat{\mathbf{\varphi }}$	$\widehat{\mathbf{\omega }}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$
n = 400	QMLE(Bias)	−0.0008	0.0053	−0.0024	−0.0167
	SQMLE(Bias)	0.0001	0.0051	0.0048	−0.0196
	QMLE(SD)	0.0470	0.0263	0.0860	0.1030
	SQMLE(SD)	0.0456	0.0260	0.0929	0.1037
	QMLE(AD)	0.0416	0.0224	0.0848	0.0694
	SQMLE(AD)	0.0423	0.0222	0.0938	0.0691
n = 800	QMLE(Bias)	−0.0014	0.0028	0.0008	−0.0099
	SQMLE(Bias)	−0.0012	0.0028	0.0033	−0.0111
	QMLE(SD)	0.0330	0.0177	0.0529	0.0707
	SQMLE(SD)	0.0334	0.0177	0.0635	0.0718
	QMLE(AD)	0.0324	0.0219	0.0603	0.0722
	SQMLE(AD)	0.0329	0.0227	0.0653	0.0757
n = 1200	QMLE(Bias)	−0.0011	0.0013	0.0000	−0.0054
	SQMLE(Bias)	−0.0006	0.0012	0.0010	−0.0052
	QMLE(SD)	0.0272	0.0139	0.0487	0.0564
	SQMLE(SD)	0.0276	0.0140	0.0539	0.0578
	QMLE(AD)	0.0241	0.0140	0.0441	0.0592
	SQMLE(AD)	0.0244	0.0145	0.0492	0.0612

When $e_t\sim Laplace(0,1)$, $e_t\sim t_3$, respectively, we can see that both Table 2 and Table 3 have similar simulation effects to Table 3. Therefore, the self-weighted quasi-maximum likelihood estimation for a class of MA-GARCH model is valid.

Table 2. Estimators for the models (1)–(3) when $e_t\sim Laplace(0,1)$.

${\mathit{\theta }}_0=(0.5,0.1,0.4,0.3)$
		$\widehat{\mathbf{\varphi }}$	$\widehat{\mathbf{\omega }}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$
n = 400	QMLE(Bias)	−0.0003	0.0080	−0.0002	−0.0304
	SQMLE(Bias)	0.0024	0.0060	0.0254	−0.0334
	QMLE(SD)	0.0506	0.0403	0.1709	0.1809
	SQMLE(SD)	0.0529	0.0405	0.2018	0.1876
	QMLE(AD)	0.0576	0.0614	0.1345	0.2946
	SQMLE(AD)	0.0702	0.0561	0.2902	0.2805
n = 800	QMLE(Bias)	−0.0005	0.0057	0.0026	−0.0219
	SQMLE(Bias)	−0.0008	0.0041	0.0184	−0.0221
	QMLE(SD)	0.0368	0.0323	0.1299	0.1447
	SQMLE(SD)	0.0383	0.0323	0.1617	0.1519
	QMLE(AD)	0.0333	0.0156	0.0908	0.0812
	SQMLE(AD)	0.0362	0.0170	0.1083	0.0952
n = 1200	QMLE(Bias)	−0.0001	0.0032	0.0003	-0.0119
	SQMLE(Bias)	−0.0006	0.0021	0.0065	−0.0100
	QMLE(SD)	0.0297	0.0249	0.1042	0.1174
	SQMLE(SD)	0.0307	0.0257	0.1305	0.1260
	QMLE(AD)	0.0289	0.0204	0.0966	0.0880
	SQMLE(AD)	0.0308	0.0200	0.1218	0.0895

Table 3. Estimators for the models (1)–(3) when $e_t\sim t_3$.

${\mathit{\theta }}_0=(0.5,0.1,0.4,0.3)$
		$\widehat{\mathbf{\varphi }}$	$\widehat{\mathbf{\omega }}$	$\widehat{\mathbf{\alpha }}$	$\widehat{\mathbf{\beta }}$
n = 400	QMLE(Bias)	−0.0014	0.0072	−0.0160	−0.0485
	SQMLE(Bias)	0.0003	0.0060	0.0293	−0.0490
	QMLE(SD)	0.0536	0.0426	0.2223	0.1944
	SQMLE(SD)	0.0555	0.0430	0.2463	0.2016
	QMLE(AD)	0.0581	0.0166	0.1437	0.1026
	SQMLE(AD)	0.0638	0.0159	0.1993	0.2042
n = 800	QMLE(Bias)	−0.0010	−0.0046	−0.0034	-0.0265
	SQMLE(Bias)	−0.0010	0.0042	0.0191	−0.0303
	QMLE(SD)	0.0408	0.0357	0.1921	0.1769
	SQMLE(SD)	0.0436	0.0361	0.2191	0.1846
	QMLE(AD)	0.0371	0.0244	0.1128	0.1032
	SQMLE(AD)	0.0393	0.0228	0.1304	0.0967
n = 1200	QMLE(Bias)	−0.0009	0.0039	0.0059	−0.0243
	SQMLE(Bias)	−0.0010	0.0037	0.0188	−0.0279
	QMLE(SD)	0.0322	0.0328	0.1767	0.1600
	SQMLE(SD)	0.0334	0.0324	0.2017	0.1603
	QMLE(AD)	0.0304	0.0217	0.1243	0.0885
	SQMLE(AD)	0.0316	0.0229	0.1406	0.0941

There are many other weights, such as ${\omega }_t=(1+C|y_t{{|}^2)}^{-3/2}$ and $I\left(ma{x}_{1\le i\le p}\right|y_{t-1}|\le C)$, that satisfies assumption A4. However, our simulation results that are not reported in this paper show that the self-weighted quasi-maximum likelihood estimated is much more efficient than that based on these weights.

4. A Real Example

In this section, we empirically analyzed the models (1)–(3) by using two real data sets. We used the SQMLE to compare the goodness of fit and prediction effect for a class of MA-GARCH model and traditional MA-GARCH model.

Firstly, we studied the opening price of ST Daji (000564) from 1 January 2018 to 1 January 2022, which has, in total, 837 observations. Let $x_t$ be the logarithms of the opening price of ST Daji (000564) in Figure 1, and $y_t=x_t-x_{t-1}$, $\left\{y_t\right\}$ is plotted in Figure 2. Ling [8] makes a self-weighted quasi-maximum likelihood estimate for ARMA-GARCH.

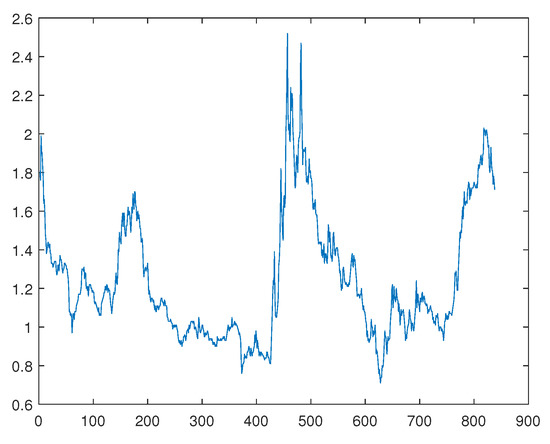
Figure 1. $x_t$ be the logarithms of the opening price of ST Daji (000564).

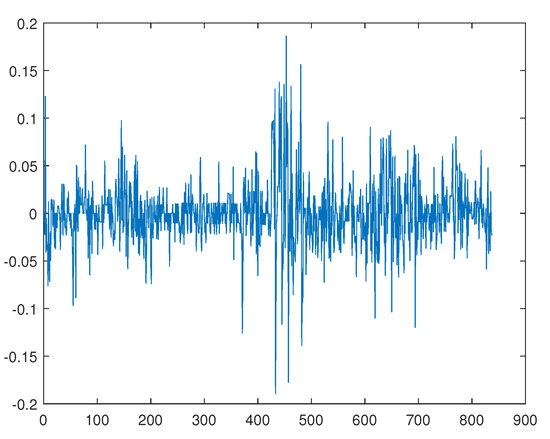
Figure 2. Time series diagram of $y_t=x_t$-$x_{t-1}$.

The ARMA(0,1)-GARCH(0,1) (MA-GARCH) model was adopted to fit $\left\{y_t\right\}$ by Ling [8], and the result is

$$\begin{array}{cc}\hfill y_t& =-0.0047\left(0.0000\right){\epsilon }_{t-1}+{\epsilon }_t\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}=e_t\sqrt{0.0010\left(0.0059\right)+0.2703\left(3.5188\right){\epsilon }_{t-1}^2+0.0427\left(0.1955\right)h_{t-1}}\hfill \end{array}$$

(9)

where the standard errors are in parentheses.

Similarly, we used models (1)–(3) to fit $\left\{y_t\right\}$, and the result is

$$\begin{array}{cc}\hfill y_t& =-0.0817\left(0.0487\right){\epsilon }_{t-1}+{\epsilon }_t\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}=e_t\sqrt{0.0010\left(0.0002\right)+0.2614\left(0.1060\right)y_{t-1}^2+0.0443\left(0.1585\right)h_{t-1}}\hfill \end{array}$$

(11)

where the standard errors are in parentheses (obtained from Theorem 1).

We compared the root-mean-squared error (RMSE) for the one-step-ahead forecast and log-likelihood value for models (8) and (9) and models (10) and (11), respectively. The results are shown in Table 4. In addition, for the data of the data set from 24 March 2021 to 19 August 2021, we give a 95 percent confidence interval of sequence $x_t$, as shown in Figure 3 below. Figure 4 is a partial enlargement of Figure 3. As can be seen from Table 4, the RMSE value of models (10) and (11) is smaller than that of models (8) and (9), and the log-likelihood value of models (10) and (11) is bigger than that of models (8) and (9). Thus, the goodness of fit of models (10) and (11) is better than models (8) and (9). In addition, as can be seen from Figure 3, at almost all points, models (10) and (11) have a narrower confidence interval than models (8) and (9), and we can see that all points fall within the confidence interval. This shows that under this data, models (10) and (11) are better than models (8) and (9) in terms of goodness of fit and predictive ability. Therefore, in this paper, we consider models (10) and (11) to be better than models (10) and (11) to a certain extent.

Table 4. Comparison of the fitting effect of models (8) and (9) and models (10) and (11).

Models	RMSE	Log-Likelihood Value
(8) and (9)	0.0361	2315.2
(10) and (11)	0.0360	2316.4

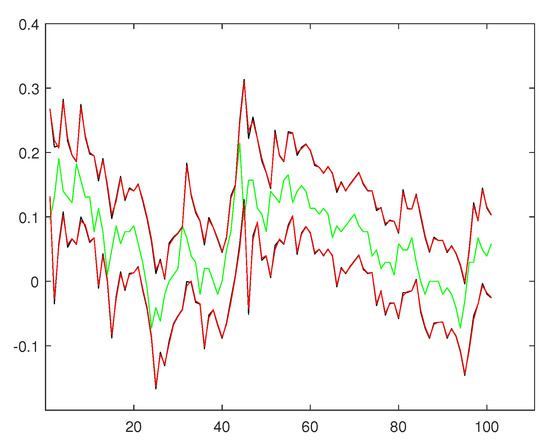
Figure 3. Time series diagram of the data $x_t$ (green line) and 95% forecasting confidence intervals based on models (8) and (9) (red line) and models (10) and (11) (black line), respectively.

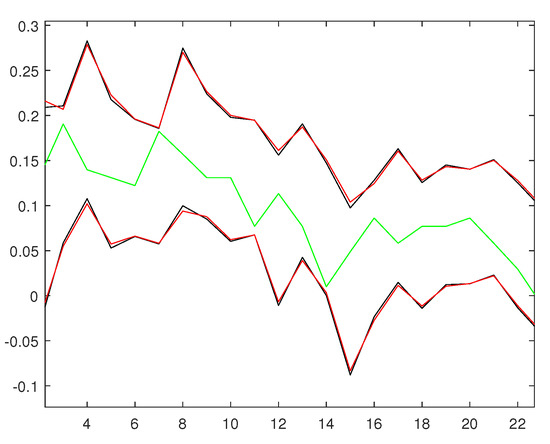
Figure 4. Part of Figure 3 is enlarged.

Secondly, we studied the 21-day China Interbank Offered Rate from 2 November 2015 to 8 March 2016, which has 178 observations. Let $x_t$ be the logarithms of the 21-day China Interbank Offered Rate in Figure 5, and $y_t=x_t-x_{t-1}$, $\left\{y_t\right\}$ is plotted in Figure 6. Ling [8] makes a self-weighted quasi-maximum likelihood estimate for ARMA-GARCH.

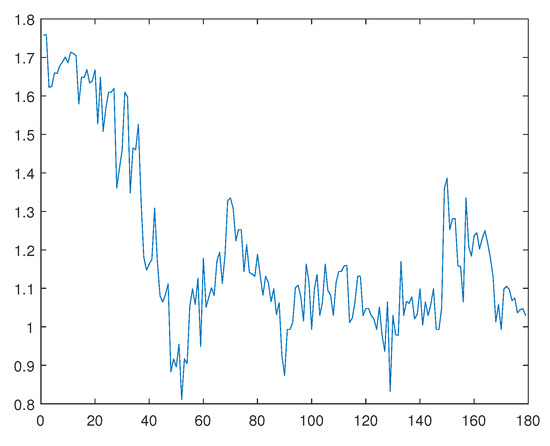
Figure 5. $x_t$, the logarithms of the 21-day China Interbank Offered Rate.

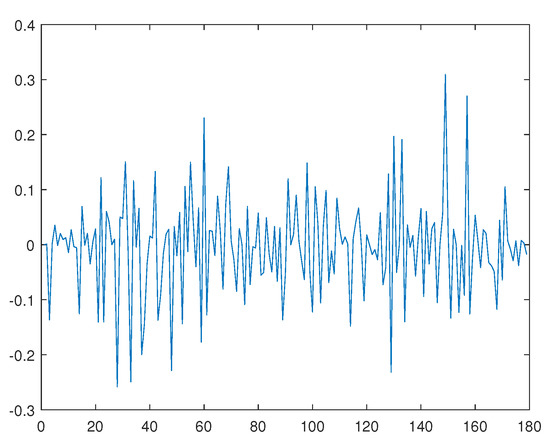
Figure 6. Time series diagram of $y_t=x_t$-$x_{t-1}$.

ARMA(0,1)-GARCH(0,1) (MA-GARCH) model was adopted to fit $\left\{y_t\right\}$ by Ling [8], and the result is

$$\begin{array}{cc}\hfill y_t& =-0.5143\left(0.0000\right){\epsilon }_{t-1}+{\epsilon }_t\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}=e_t\sqrt{0.0061\left(0.0064\right)+0.0773\left(5.0485\right){\epsilon }_{t-1}^2+0.0010\left(3.8925\right)h_{t-1}}\hfill \end{array}$$

(13)

where the standard errors are in parentheses.

Similarly, we used models (1)–(3) to fit $\left\{y_t\right\}$, and the result is

$$\begin{array}{cc}\hfill y_t& =-0.4982\left(0.0069\right){\epsilon }_{t-1}+{\epsilon }_t\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill {\epsilon }_t& =e_t\sqrt{h_t}=e_t\sqrt{0.0062\left(0.0092\right)+0.0496\left(0.1182\right)y_{t-1}^2+0.0010\left(1.4060\right)h_{t-1}}\hfill \end{array}$$

(15)

where the standard errors are in parentheses (From Theorem 1 we get).

From Table 5, we can see that the RMSE and the log-likelihood values of models (12) and (13) and models (14) and (15) are equal. In addition, we give a 95 percent confidence interval of sequence $x_t$, as shown in Figure 7 below. Figure 8 is a partial enlargement of Figure 7. From Figure 7, we can see that models (14) and (15) hasve a narrower confidence interval than models (12) and (13), and we can see that all points fall within the confidence interval. This shows that for this data, models (14) and (15) are better than models (12) and (13) in terms of predictive ability. Therefore, in this paper, we consider models (14) and (15) better than models (12) and (13) to a certain extent.

Table 5. Comparison of the fitting effect of models (12) and (13) and models (14) and (15).

Models	RMSE	Log-Likelihood Value
(12) and (13)	0.0818	340.91
(14) and (15)	0.0818	340.91

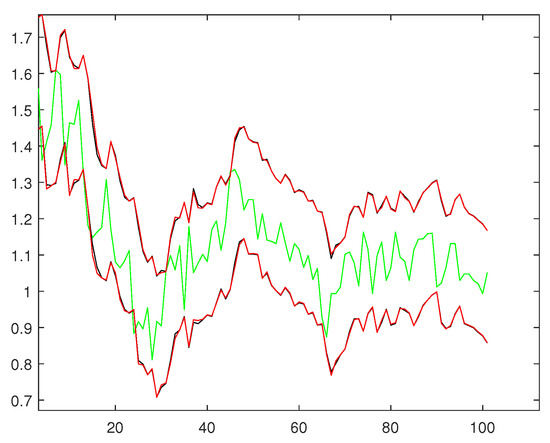
Figure 7. Time series diagram of the data $x_t$ (green line) and 95% forecasting confidence intervals based on models (12) and (13) (red line) and models (14) and (15) (black line), respectively.

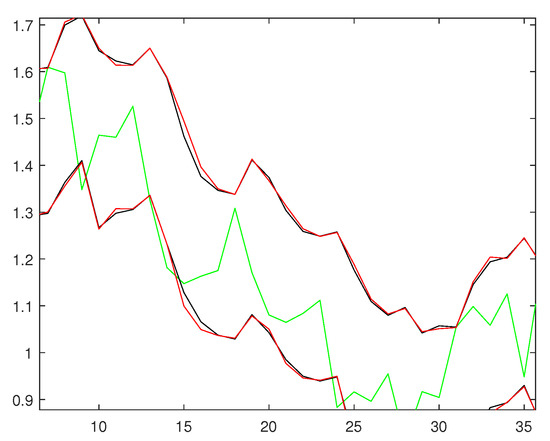
Figure 8. Part of Figure 7 is enlarged.

5. Conclusions

With the motivation to study the DAP(p) model with p going to ∞, in this article, we propose a class of MA-GARCH model based on Zhu and Zhang et al. [14] The consistency and asymptotic normality properties of the self-weighted quasi-maximum likelihood estimation of a class of MA-GARCH models are established. Through simulation, we found that the the self-weighted quasi-maximum likelihood estimation of a class of MA-GARCH models is feasible. Empirical results show that a class of a MA-GARCH model is better than the MA-GARCH model in terms of goodness of fit and predictive ability. This implies that the model we considered has some applicability to the field of MA-GARCH models.

Appendix A.1

Proof of Lemma 1.

(i):

$$\begin{array}{cc}\hfill su{p}_{\Theta }\left|{\epsilon }_{t-1}\left(\theta \right)\right|& =su{p}_{\Theta }|{\Phi }^{-1}\left(B\right)y_{t-1}|=su{p}_{\Theta }|\sum _{i=0}^{\infty }{a}_{\Phi }\left(i\right)B^i{y}_{t-1}|\le \sum _{i=0}^{\infty }O\left({\rho }^i\right)\left|y_{t-1-i}\right|\hfill \\ \hfill & \le c{\xi }_{\rho ,t-1}\hfill \end{array}$$

(ii):

$$\begin{array}{cc}\hfill su{p}_{\Theta }\Vert \frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }\Vert & =su{p}_{\Theta }\Vert -{\Phi }^{-2}\left(B\right)y_{t-1}\Vert =su{p}_{\Theta }\Vert -{\Phi }^{-1}\left(B\right)\left[{\Phi }^{-1}\left(B\right)y_{t-1}\right]\Vert \hfill \\ \hfill & \le \Vert -{\Phi }^{-1}\left(B\right)\sum _{i=0}^{\infty }O\left({\rho }_0^i\right)|y_{t-1-i}|\Vert \le \sum _{j=0}^{\infty }O\left({\rho }_0^j\right)\sum _{i=0}^{\infty }O\left({\rho }_0^i\right)\left|y_{t-1-i}\right|\hfill \\ \hfill & =c\sum _{k=0}^{\infty }(k+1){\rho }_0^k\left|y_{t-1-k}\right|=\sum _{i=0}^{\infty }{\rho }^i\mid y_{t-1-i}\mid \le c{\xi }_{\rho ,t-1}\hfill \end{array}$$

for some $\rho$ and $1<\sqrt[k]{k+1}{\rho }_0\le \rho <1$.

(iii):

$$\begin{array}{cc}\hfill su{p}_{\Theta }\Vert \frac{{\partial }^2{\epsilon }_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\Vert & =su{p}_{\Theta }\Vert 2{\Phi }^{-3}\left(B\right)y_{t-1}\Vert =su{p}_{\Theta }\Vert 2{\Phi }^{-2}\left(B\right){\epsilon }_{t-1}\Vert \hfill \\ \hfill & \le c\Vert 2{\Phi }^{-1}\left(B\right)\sum _{i=0}^{\infty }{\rho }_0^i{\epsilon }_{t-2-i}\Vert \le c\Vert \sum _{j=0}^{\infty }{\rho }_0^j\sum _{i=0}^{\infty }{\rho }_0^i{\epsilon }_{t-2-i-j}\Vert \hfill \\ \hfill & =c\Vert \sum _{k=0}^{\infty }(k+1){\rho }_0^k{\epsilon }_{t-2-k}\Vert =c\Vert \sum _{k=0}^{\infty }(k+1){\rho }_0^k[\frac{1}{\varphi }{y}_{t-1-k}+\frac{1}{\varphi }{\epsilon }_{t-1-k}]\Vert \hfill \\ \hfill & \le \Vert c\sum _{k=0}^{\infty }(k+1){\rho }_0^k|y_{t-1-k}|\Vert +\Vert c\sum _{k=0}^{\infty }(k+1){\rho }_0^k|{\epsilon }_{t-1-k}|\Vert \hfill \\ \hfill & \le c\sum _{k=0}^{\infty }{\rho }_1^k\left|y_{t-1-k}\right|+c\sum _{k=0}^{\infty }{\rho }_1^k{\xi }_{\rho ,t-1}\hfill \\ \hfill & \le c\Vert \sum _{k=0}^{\infty }{\rho }_1^k|y_{t-1-k}|\Vert +c\Vert \sum _{k=0}^{\infty }{\rho }_1^k[1+\sum _{s=0}^{\infty }{\rho }^s|y_{t-1-s}|\Vert \le c{\xi }_{\rho ,t-1}\hfill \end{array}$$

for some ${\rho }_0,{\rho }_1$ and ${\rho }_2$, and $0<\sqrt[k]{k+1}{\rho }_0\le {\rho }_1\le {\rho }_2\le \rho <1$. □

Proof of Lemma 2.

(i): From the models (1)–(3), we can deduce that $h_t\left(\theta \right)={\beta }^{-1}\left(B\right)$$(\omega +\alpha y_{t-1}^2)$.

$$\begin{array}{cc}\hfill h_t\left(\theta \right)& ={\beta }^{-1}\left(B\right)(\omega +\alpha y_{t-1}^2)=\sum _{i=0}^{\infty }{\beta }^i\omega +\alpha \sum _{i=0}^{\infty }{\beta }^i{y}_{t-1-i}^2\le \sum _{i=0}^{\infty }{\rho }^i\omega +\overline{\alpha }\sum _{i=0}^{\infty }{\rho }^i{y}_{t-1-i}^2\hfill \\ \hfill & \le c{\zeta }_{\rho ,t-1}\hfill \end{array}$$

(ii): From models (1)–(3), one iteratively obtains

$$\begin{array}{cc}\hfill h_t\left(\theta \right)& =\omega +\alpha y_{t-1}^2+\beta h_{t-1}=\omega +\alpha y_{t-1}^2+\beta (\omega +\alpha y_{t-2}^2+\beta h_{t-2})\hfill \\ \hfill & =\cdots =\frac{\omega }{1-\beta }+\alpha \sum _{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2\hfill \end{array}$$

Then

$$\frac{1}{h_t\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \omega }=\frac{1}{\frac{\omega }{1-\beta }+\alpha {\sum }_{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2}\frac{1}{1-\beta }\le \frac{1}{\frac{\omega }{1-\beta }}\frac{1}{1-\beta }\le \underline{\omega }$$

$$\begin{array}{cc}\hfill \frac{1}{h_t\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \alpha }& =\frac{1}{h_t\left(\theta \right)}{\beta }^{-1}\left(B\right)y_{t-1}^2=\frac{1}{\frac{\omega }{1-\beta }+\alpha {\sum }_{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2}\sum _{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2\hfill \\ \hfill & \le \frac{1}{\frac{\omega }{1-\beta }}\sum _{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2\le c{\zeta }_{\rho ,t-1}\hfill \end{array}$$

because $\frac{\partial h_t\left(\theta \right)}{\partial \beta }=\frac{\omega }{{(1-\beta )}^2}+\alpha {\sum }_{j=0}^{\infty }j{\beta }^{j-1}{y}_{t-j-i}^2$, so

$$\begin{array}{cc}\hfill \frac{1}{h_t\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \beta }& =\frac{1}{\frac{\omega }{1-\beta }+\alpha {\sum }_{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2}[\frac{\omega }{{(1-\beta )}^2}+\alpha {\Sigma }_{j=0}^{\infty }j{\beta }^{j-1}{y}_{t-j-1}^2]\hfill \\ \hfill & \le \frac{1}{\frac{\omega }{1-\beta }}[\frac{\omega }{{(1-\beta )}^2}+\alpha \sum _{j=0}^{\infty }j{\beta }^{j-1}{y}_{t-j-1}^2]\hfill \\ \hfill & =\frac{1}{1-\beta }+\frac{1-\beta }{\omega }\frac{\alpha }{\beta }\sum _{j=0}^{\infty }j{\beta }^j{y}_{t-j-1}^2\hfill \\ \hfill & \le \frac{1}{1-\beta }+\frac{1-\beta }{\omega }\frac{\alpha }{\beta }\sum _{j=0}^{\infty }{\rho }^j{y}_{t-j-1}^2\hfill \\ \hfill & \le c{\zeta }_{\rho ,t-1}\hfill \end{array}$$

where $0<\beta <\sqrt[j]{j}\beta <\rho <1$.

(iii): The proof of (iii) is similar to that of (ii).

(vi): Because $\frac{\partial h_t\left(\theta \right)}{\partial \varphi }=0$, so, $\frac{1}{\sqrt{h_t\left(\theta \right)}}\frac{\partial h_t\left(\theta \right)}{\partial \varphi }=0$. □

Appendix A.2

Proof of Theorem 1.

(i): First, the space $\Theta$ is compact, and ${\theta }_0$ is an interior point in $\Theta$. Second, $L_{sn}\left(\theta \right)$ is continuous in $\theta \in \Theta$ and is a measurable function of $\{y_i,i=t,t-1,\cdots \}$ for all $\theta \in \Theta$. Third, by Lemmas 1 and 2, it follows that

$$\begin{array}{c}\hfill |e_t|=|\frac{{\epsilon }_t\left(\theta \right)}{\sqrt{h_t\left(\theta \right)}}|=|\frac{{\sum }_{i=0}^{\infty }{(-1)}^i{\varphi }^i{y}_{t-1}}{\sqrt{\frac{\omega }{1-\beta }\alpha {\sum }_{j=0}^{\infty }{\beta }^j{y}_{t-j-1}^2}}|\le c{\xi }_{\rho ,t-1}\end{array}$$

(A1)

$$\begin{array}{cc}\hfill su{p}_{\Theta }\left|{\epsilon }_t\left(\theta \right)\right|& =su{p}_{\Theta }|{\epsilon }_t\left({\theta }_0\right)+{(\theta -{\theta }_0)}^{\prime }\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }|\hfill \\ \hfill & \le |{\epsilon }_t\left({\theta }_0\right)|+su{p}_{\Theta }\Vert \theta -{\theta }_0{\Vert }^{\prime }su{p}_{\Theta }\Vert \frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \theta }\Vert \hfill \\ \hfill & \le |e_t|\sqrt{h_t\left({\theta }_0\right)}+O\left(1\right){\xi }_{\rho ,t-1}\hfill \\ \hfill & \le O\left(1\right)[{\xi }_{\rho ,t-1}{\zeta }_{\rho ,t-1}^{1/2}+{\xi }_{\rho ,t-1}]\hfill \end{array}$$

(A2)

$$\begin{array}{c}\hfill su{p}_{\Theta }{h}_t\left(\theta \right)\le c{\zeta }_{\rho ,t-1}\end{array}$$

(A3)

By (A1)–(A3), we can show that

$$\begin{array}{cc}\hfill Esu{p}_{\Theta }\left[{\omega }_t\frac{{\epsilon }_t^2\left(\theta \right)}{h_t\left(\theta \right)}\right]& \le Esu{p}_{\Theta }\left[{\omega }_{t}O\left(1\right)\frac{{({\xi }_{\rho ,t-1}{\zeta }_{\rho ,t-1}^{1/2}+{\xi }_{\rho ,t-1})}^2}{\underline{\omega }}\right]\hfill \\ \hfill & \le cEsu{p}_{\Theta }[{\omega }_t{\xi }_{\rho ,t-1}^2{\zeta }_{\rho ,t-1}+{\omega }_t{\xi }_{\rho ,t-1}^2+2{\zeta }_{\rho ,t-1}^{1/2}{\xi }_{\rho ,t-1}^2]\hfill \\ \hfill & <\infty \hfill \end{array}$$

(A4)

$$\begin{array}{c}\hfill Esu{p}_{\Theta }\left|{\omega }_{t}log{h}_t\left(\theta \right)\right|=O\left(1\right)Esu{p}_{\Theta }log{h}_t\left(\theta \right)\le O\left(1\right)logEsu{p}_{\Theta }{h}_t\left(\theta \right)<\infty \end{array}$$

(A5)

Therefore, by (A4) and (A5), we have

$$Esu{p}_{\Theta }{\omega }_t{l}_t\left(\theta \right)\le Esu{p}_{\Theta }|{\omega }_{t}log{h}_t\left(\theta \right)|+Esu{p}_{\Theta }\left|{\omega }_t\frac{{\epsilon }_t^2\left(\theta \right)}{h_t\left(\theta \right)}\right|<\infty$$

By ergodic theorem, we have $L_{sn}\to E\left[{\omega }_t{l}_t\left(\theta \right)\right]a.s.\forall \theta \in \Theta .$

By Theorem 3.1 in Ling and McAleer (2003a) [19], it follows that

$$su{p}_{\Theta }|L_{sn}\left(\theta \right)-E\left[{\omega }_t{l}_t\left(\theta \right)\right]|{⟶}_{p}0$$

$$\begin{array}{cc}\hfill E\left[{\omega }_t{l}_t\left(\theta \right)\right]& =E{\omega }_{t}log{h}_t\left(\theta \right)+E{\omega }_t\frac{{[{\epsilon }_t\left({\theta }_0\right)+{(\theta -{\theta }_0)}^{\prime }\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }]}^2}{h_t\left(\theta \right)}\hfill \\ \hfill & =E{\omega }_{t}log{h}_t\left(\theta \right)+E{\omega }_t\frac{{\epsilon }_t^2\left({\theta }_0\right)}{h_t\left(\theta \right)}+2E{\omega }_t\frac{{\epsilon }_t\left({\theta }_0\right){(\theta -{\theta }_0)}^{\prime }\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }}{h_t\left(\theta \right)}\hfill \\ \hfill & -{(\theta -{\theta }_0)}^{\prime }E\left[\frac{{\omega }_t}{h_t\left(\theta \right)}\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }\right]{(\theta -{\theta }_0)}^{\prime }\hfill \end{array}$$

Because $E{e}_t^2=1,E{e}_t=0$, thus,

$$E{\omega }_t\frac{{\epsilon }_t^2\left({\theta }_0\right)}{h_t\left(\theta \right)}=E{\omega }_t{e}_t^2\frac{h_t\left({\theta }_0\right)}{h_t\left(\theta \right)}=E{\omega }_t\frac{h_t\left({\theta }_0\right)}{h_t\left(\theta \right)}\left[E{e}_t^2\right|F_{t-1}]=E{\omega }_t\frac{h_t\left({\theta }_0\right)}{h_t\left(\theta \right)}$$

$$2E{\omega }_t\frac{{\epsilon }_t\left({\theta }_0\right){(\theta -{\theta }_0)}^{\prime }\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }}{h_t\left(\theta \right)}=0$$

.

Therefore, $E\left[{\omega }_t{l}_t\left(\theta \right)\right]=A+B$, where

$$A=E{\omega }_{t}log{h}_t\left(\theta \right)+E{\omega }_t\frac{h_t\left({\theta }_0\right)}{h_t\left(\theta \right)}$$

$$B={(\theta -{\theta }_0)}^{\prime }E\left[\frac{{\omega }_t}{h_t\left(\theta \right)}\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial \theta }\frac{\partial {\epsilon }_t\left({\theta }^{*}\right)}{\partial {\theta }^{\prime }}\right]{(\theta -{\theta }_0)}^{\prime }$$

.

Considering the function $f\left(x\right)=logx+\frac{a}{x}$ when $a\ge 0$, it reaches a minimum at $x=a$. Thus, for A, A reaches the minimum if and only if $\theta ={\theta }_0$. For B, $B\ge 0$, B reaches the minimum if and only $\theta ={\theta }_0$. Thus, we can claim that $E\left[{\omega }_t{l}_t\left(\theta \right)\right]$ is uniformly minimized at $\theta ={\theta }_0$.

Next, we use the method in Theorem 4.1.1 in Amemiya [20]. Let V be any open neighborhood of ${\theta }_0\in \Theta$. Then $V^c\bigcap \Theta$ is the compact set, and $E\left[{\omega }_t{l}_t\left(\theta \right)\right]$ exists as a minimum in $\theta \in V^c\bigcap \Theta$.

We order

$$\begin{array}{c}\hfill \epsilon =\underset{\Theta \in V^c\bigcap \Theta }{min}E\left[{\omega }_t{l}_t\left(\theta \right)\right]-E\left[{\omega }_t{l}_t\left({\theta }_0\right)\right]\end{array}$$

(A6)

and let $|L_{sn}\left(\theta \right)-E{\omega }_t{l}_t\left(\theta \right)|<\frac{\epsilon }{2},\forall \theta \in \Theta$ be the event A.

Thus, $A\Rightarrow E{\omega }_t{l}_t\left(\theta \right)>L_{sn}\left(\theta \right)-\frac{\epsilon }{2}$,$A\Rightarrow L_{sn}\left(\theta \right)>E{\omega }_t{l}_t\left(\theta \right)-\frac{\epsilon }{2}$.

Because $\theta ,\widehat{\theta }\left(sn\right)\in \Theta$, thus,

$$\begin{array}{cc}\hfill & A\Rightarrow E{\omega }_t{l}_t\left({\theta }_0\right)>L_{sn}\left({\theta }_0\right)-\frac{\epsilon }{2}\hfill \end{array}$$

(A7)

$$\begin{array}{cc}\hfill & A\Rightarrow L_{sn}\left({\widehat{\theta }}_{sn}\right)>E{\omega }_t{l}_t\left({\widehat{\theta }}_{sn}\right)-\frac{\epsilon }{2}\hfill \end{array}$$

(A8)

and because $L_{sn}\left({\widehat{\theta }}_0\right)\le L_{sn}\left({\theta }_0\right)$, then, by (A2), we have

$$\begin{array}{c}\hfill A\Rightarrow E{\omega }_t{l}_t\left({\theta }_0\right)>L_{sn}\left({\widehat{\theta }}_{sn}\right)-\frac{\epsilon }{2}\end{array}$$

(A9)

By (A8) and (A9), we have

$$\begin{array}{c}\hfill A\Rightarrow E{\omega }_t{l}_t\left({\theta }_0\right)>E{\omega }_t{l}_t\left({\widehat{\theta }}_{sn}\right)-\epsilon \end{array}$$

(A10)

By (A6) and (A10), we have

$$A\Rightarrow E{\omega }_t{l}_t\left({\theta }_0\right)>E{\omega }_t{l}_t\left({\widehat{\theta }}_{sn}\right)-\underset{\Theta \in V^c\bigcap \Theta }{min}E\left[{\omega }_t{l}_t\left(\theta \right)\right]+E\left[{\omega }_t{l}_t\left({\theta }_0\right)\right]$$

So $A\Rightarrow {min}_{\Theta \in V^c\bigcap \Theta }E\left[{\omega }_t{l}_t\left(\theta \right)\right]>E{\omega }_t{l}_t\left({\widehat{\theta }}_{sn}\right)$

Thus, $A\Rightarrow {\widehat{\theta }}_{sn}\in V$, and then $P\left(A\right)\le P({\widehat{\theta }}_{sn}\in V)$.

And because ${lim}_{n\to \infty }P\left(A\right)=1$, we have ${\widehat{\theta }}_{sn}{\to }_p{\theta }_0$.

(ii): We further give the quasi-score function and the quasi-information matrix as follows.

Take the derivative of $l_t\left(\theta \right)$:

$$\begin{array}{cc}\hfill & \frac{\partial l_t\left(\theta \right)}{\partial \theta }=2\frac{{\epsilon }_t\left(\theta \right)}{h_t\left(\theta \right)}\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }+\frac{1}{h_t\left(\theta \right)}(1-\frac{{\epsilon }_t^2\left(\theta \right)}{h_t\left(\theta \right)})\frac{\partial h_t\left(\theta \right)}{\partial \theta }\hfill \\ \hfill & \frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}=\frac{2}{h_t\left(\theta \right)}\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial {\varphi }^{\prime }}+\frac{2{\epsilon }_t\left(\theta \right)}{h_t\left(\theta \right)}\frac{{\partial }^2{\epsilon }_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\hfill \\ \hfill & \frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \delta \partial {\delta }^{\prime }}=-\frac{1}{h_t^2\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \delta }\frac{\partial h_t\left(\theta \right)}{\partial {\delta }^{\prime }}+\frac{1}{h_t\left(\theta \right)}\frac{{\partial }^2{h}_t\left(\theta \right)}{\partial \delta \partial {\delta }^{\prime }}+\frac{2{\epsilon }_t^2\left(\theta \right)}{h_t^3\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \delta }\frac{\partial h_t\left(\theta \right)}{\partial {\delta }^{\prime }}-\frac{{\epsilon }_t^2\left(\theta \right)}{2h_t^2\left(\theta \right)}\frac{{\partial }^2{h}_t\left(\theta \right)}{\partial \delta \partial {\delta }^{\prime }}\hfill \end{array}$$

Then

$$\begin{array}{c}\hfill su{p}_{\Theta }\Vert \frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\Vert \le O\left(1\right)su{p}_{\Theta }\{\Vert \frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }{\Vert }^2+|e_t\left(\theta \right)|\Vert \frac{{\partial }^2{\epsilon }_t\left(\theta \right)}{\partial \varphi \partial {\varphi }^{\prime }}\Vert \}\\ \hfill \le O\left(1\right){\xi }_{\rho ,t-1}^2\end{array}$$

(A11)

$$\begin{array}{cc}\hfill su{p}_{\Theta }\Vert \frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \delta \partial {\delta }^{\prime }}\Vert & \le O\left(1\right)\{{\zeta }_{\rho ,t-1}^2+{\zeta }_{\rho ,t-1}+{\zeta }_{\rho ,t-1}^2|e_t{|}^2+\left|e_t{|}^2{\zeta }_{\rho ,t-1}\right\}\hfill \\ \hfill & \le O\left(1\right)\left\{{\zeta }_{\rho ,t-1}^2(1+{\xi }_{\rho ,t-1}^2)\right\}\hfill \end{array}$$

(A12)

Therefore, $Esu{p}_{\Theta }\Vert {\omega }_t\frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \theta \partial {\theta }^{\prime }}\Vert <\infty$

By ergodic and Theorem 3.1 in Ling and McAleer(2003) [19], it follows that

$$\frac{{\partial }^2{L}_{sn}\left(\theta \right)}{\partial \theta \partial {\theta }^{\prime }}{⟶}_{p}E\left[{\omega }_t\frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \theta \partial {\theta }^{\prime }}\right]$$

if and only if $n⟶\infty$.

By the double expectation property, it follows that

$$\begin{array}{cc}\hfill E\left[{\omega }_t\frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \theta \partial {\theta }^{\prime }}\right]& =E\left\{E\left({\omega }_t\frac{{\partial }^2{l}_t\left(\theta \right)}{\partial \theta \partial {\theta }^{\prime }}\right|F_{t-1})\right\}\hfill \\ \hfill & =E[2\frac{{\omega }_t}{h_t\left(\theta \right)}\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial \varphi }\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial {\varphi }^{\prime }}+\frac{{\omega }_t}{h_t^2\left(\theta \right)}\frac{\partial h_t\left(\theta \right)}{\partial \delta }\frac{\partial h_t\left(\theta \right)}{\partial {\delta }^{\prime }}]\hfill \\ \hfill & ={\Sigma }_0\hfill \end{array}$$

Then, $\frac{{\partial }^2{L}_{sn}\left({\theta }_0\right)}{\partial \theta \partial {\theta }^{\prime }}=\frac{1}{n}{\sum }_{t=1}^{\infty }{\omega }_t\frac{{\partial }^2{l}_n\left({\theta }_0\right)}{\partial \theta \partial {\theta }^{\prime }}{⟶}_p{\Sigma }_0$

Similarly, we can show that $Esu{p}_{\Theta }\parallel \frac{\partial l_t\left(\theta \right)}{\partial \theta }\parallel <\infty$ holds.

Because $\sqrt{n}\frac{\partial L_{sn}\left(\theta \right)}{\partial \theta }=\frac{1}{\sqrt{n}}{\sum }_{t=1}^n{\omega }_t\frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }={\sum }_{t=1}^n\frac{1}{\sqrt{n}}{\omega }_t\frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }$

Therefore, $E\left(\frac{1}{\sqrt{n}}{\omega }_t\frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }\right|F_{t-1})=0$

Thus, $E\left(\sqrt{n}\frac{\partial L_{sn}\left({\theta }_0\right)}{\partial \theta }\right|F_{t-1})=0$, $Var\left(\frac{1}{\sqrt{n}}{\omega }_t\frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }\right|F_{t-1})=\frac{1}{n}E\left({\omega }_t^2\frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial l_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}\right|F_{t-1})$

Because $\frac{\partial h_t\left(\theta \right)}{\partial \theta }\frac{\partial {\epsilon }_t\left(\theta \right)}{\partial {\theta }^{\prime }}=0$, then

$$\begin{array}{cc}\hfill \frac{\partial l_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial l_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}& =\frac{1}{h_t^2\left(\theta \right)}{(1-\frac{{\epsilon }_t^2\left({\theta }_0\right)}{h_t({\theta }_0})}^2\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial h_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}+4\frac{{\epsilon }_t^2\left({\theta }_0\right)}{h_t^2\left({\theta }_0\right)}\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}\hfill \\ \hfill & +4\frac{{\epsilon }_t\left({\theta }_0\right)}{h_t^2\left({\theta }_0\right)}(1-\frac{{\epsilon }_t^2\left({\theta }_0\right)}{h_t\left({\theta }_0\right)})\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}\hfill \\ \hfill & =4\frac{1}{h_t^2\left(\theta \right)}{(1-e_t^2)}^2\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial h_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}+\frac{e_t^2}{h_t\left({\theta }_0\right)}\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial {\theta }^{\prime }}\hfill \end{array}$$

$$\begin{array}{cc}\hfill Var\left(\sqrt{n}\frac{\partial L_{sn}\left({\theta }_0\right)}{\partial \theta }\right|F_{t-1})& =\sum _{t=1}^{\infty }Var\left(\frac{1}{\sqrt{n}}{\omega }_t\frac{\partial l_{sn}\left({\theta }_0\right)}{\partial \theta }\right|F_{t-1})\hfill \\ \hfill & =\frac{1}{n}\sum _{t=1}^{n}E\left({\omega }_t^2\frac{\partial l_{sn}\left({\theta }_0\right)}{\partial \theta }\frac{\partial l_{sn}\left({\theta }_0\right)}{\partial {\theta }^{\prime }}\right|F_{t-1})\hfill \\ \hfill & =\frac{1}{n}\sum _{t=1}^n[4\frac{{\omega }_t^2}{h_t\left({\theta }_0\right)}{\left(\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }\right)}^2+{\omega }_t^2\frac{E{e}_t^4-1}{h_t^2\left({\theta }_0\right)}\left(\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\right)]\hfill \\ \hfill & {\to }_p{\Omega }_0\hfill \end{array}$$

where ${\Omega }_0=E[4\frac{{\omega }_t^2}{h_t\left({\theta }_0\right)}{\left(\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }\right)}^2+{\omega }_t^2\frac{\varsigma }{h_t^2\left({\theta }_0\right)}\left(\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\right)]$, $\varsigma =E{e}_t^4-1$

Then, ${\Omega }_0=E[4\frac{{\omega }_t^2}{h_t\left({\theta }_0\right)}{\left(\frac{\partial {\epsilon }_t\left({\theta }_0\right)}{\partial \theta }\right)}^2+{\omega }_t^2\frac{s}{h_t^2\left({\theta }_0\right)}\left(\frac{\partial h_t\left({\theta }_0\right)}{\partial \theta }\right)]\le cE[{\omega }_t^2{\xi }_{\rho ,t-1}^2+s{\omega }_t^2{\zeta }_{\rho ,t-1}^2]$

Because ${\omega }_t$ is bounded, by Assumptions A3 and A4, it follows that ${\Omega }_0<\infty$

By the central limit theorem for a martingale different sequence, we have

$$\frac{\partial L_{sn}\left({\theta }_0\right)}{\partial \theta }{\to }_{d}N(0,{\Omega }_0).$$

By Theorem 4.1.3 in Amemiya (1985) [20], it follows that

$$\sqrt{n}({\widehat{\theta }}_{sn}-{\theta }_0){\to }_{d}N(0,{\Sigma }_0^{-1}{\Omega }_0{\Sigma }_0^{-1})$$

□