A Viscosity Approximation Method for Solving General System of Variational Inequalities, Generalized Mixed Equilibrium Problems and Fixed Point Problems

Abstract

This paper is devoted to introducing a new viscosity approximation method using the implicit midpoint rules for finding a common element in the set of solutions of a generalized mixed equilibrium problem, the set of solutions of a general system of variational inequalities and the set of common fixed points of a finite family of nonexpansive mappings in a symmetric Hilbert space. Then, we prove a strong convergence theorem regarding the proposed iterative scheme under some suitable conditions on the parameters. Finally, we provide two numerical results to show the consistency and accuracy of the scheme. One of them, moreover, compares the behavior of our scheme with the iterative scheme of Ke and Ma (Fixed Point Theory Appl 190, 2015).

1. Introduction

Let H be a real symmetric Hilbert space equipped with the inner product $⟨·,·⟩$ and norm $\parallel ·\parallel$, and let C be a nonempty closed convex subset of H. A mapping T of C into itself is called nonexpansive if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in C$. We use $Fix(T)$ to denote the set of fixed points T, i.e., $Fix(T)=\{x\in C:Tx=x\}$. Additionally, $f:C\to C$ is a contraction if $\parallel f(x)-f(y)\parallel \le \kappa \parallel x-y\parallel$ for all $x,y\in C$ and some constant $\kappa \in [0,1)$. In this case, f is said to be a $\kappa$-contraction.

In 2008, Peng and Yao [1] considered the following generalized mixed equilibrium problem, which involves finding $x^{*}\in C$ such that

$$\begin{array}{c}\hfill \Theta (x^{*},y)+\phi (y)-\phi (x^{*})+⟨A{x}^{*},y-x^{*}⟩\ge 0\mathrm{for}\mathrm{all}y\in C,\end{array}$$

(1)

where $A:C\to H$ is a nonlinear mapping, $\phi :C\to \mathbb{R}$ is a function and $\Theta :C\times C\to \mathbb{R}$ is a bifunction of C. The solution set of (1) is denoted by $\Omega$.

If $A=\phi =0$, then problem (1) reduces to the following equilibrium problem (EP), which aims to find a point $x\in C$ satisfying the following property:

$$\begin{array}{c}\hfill \Theta (x,y)\ge 0\mathrm{for}\mathrm{all}y\in C.\end{array}$$

(2)

We use $EP(\Theta )$ to denote the set of solutions of EP (2), that is, $EP(\Theta )=\{x\in C:(2)\mathrm{holds}\}$. The EP (2) includes, as special cases, numerous problems in physics, optimization and economics. Some authors (e.g., [2,3,4,5,6,7,8,9,10,11,12,13,14,15]) have proposed some useful methods for solving the EP (2). Set $\Theta (x,y)=⟨Ax,y-x⟩$ for all $x,y\in C$, where $A:C\to H$ is a nonlinear mapping. Then, $x^{*}\in EP(\Theta )$ if and only if

$$\begin{array}{c}\hfill ⟨A{x}^{*},y-x^{*}⟩\ge 0\mathrm{for}\mathrm{all}y\in C,\end{array}$$

(3)

that is, $x^{*}$ is a solution of the variational inequality. The (3) is well known as the classical variational inequality. The set of solutions of (3) is denoted by $VI(A,C)$.

Let A be a bounded operator on C. A is $\overline{\gamma }$-strongly; that is, there exists a constant $\overline{\gamma }>0$ such that $⟨Ax,x⟩\ge \overline{\gamma }{\parallel x\parallel }^2$ for all $x\in C$.

In 1967, Halpern [16] considered the following explicit iterative process:

$$x_{n+1}={\alpha }_{n}u+(1-{\alpha }_n)T{x}_n,n\ge 0,$$

where u is a given point and $T:C\to C$ is nonexpansive. He proved the strong convergence of $\left\{x_n\right\}$ to a fixed point of T provided that ${\alpha }_n=n^{-\theta }$ with $\theta \in (0,1)$. In 2003, Xu [17] introduced the following iterative process:

$$x_{n+1}={\alpha }_{n}u+(1-{\alpha }_{n}A)T{x}_n,n\ge 0,$$

where $\left\{{\alpha }_n\right\}$ is a sequence in $(0,1)$. He proved that the above sequence $\left\{x_n\right\}$ converges strongly to the unique solution of the minimization problem with $C=Fix(T)$: $mi{n}_{x\in C}\frac{1}{2}⟨Ax,x⟩-⟨x,u⟩$, where A is a strongly positive bounded linear operator on H.

In 2006, Marino and Xu [18] considered the following viscosity iterative method:

$$x_{n+1}={\alpha }_n\gamma f(x_n)+(1-{\alpha }_{n}A)T{x}_n,n\ge 0,$$

where f is a contraction on H. They proved the above sequence $\left\{x_n\right\}$ converges strongly to the unique solution of the variational inequality

$$⟨(A-\gamma f)x^{*},x-x^{*}⟩\ge 0,\forall x\in Fix(T).$$

In 2001, Yamada et al. [19] considered the following hybrid steepest-descent iterative method:

$$x_{n+1}=T{x}_n-\mu {\lambda }_{n}F(T{x}_n),n\ge 0,$$

where F is $\kappa$-Lipschitzian continuous and $\eta$-strongly monotone operator with $\kappa >0$, $\eta >0$ and $0<\mu <\frac{2\eta }{{\kappa }^2}$. Under some suitable conditions, the above sequence $\left\{x_n\right\}$ converges strongly to the unique solution of the variational inequality

$$⟨F(x^{*}),x-x^{*}⟩\ge 0,\forall x\in Fix(T).$$

In 2010, Tian [20] considered the following general viscosity type iterative method:

$$x_{n+1}={\alpha }_n\gamma f(x_n)+(I-\mu {\alpha }_{n}F)T{x}_n,n\ge 0.$$

Under certain approximate conditions, the above sequence $\left\{x_n\right\}$ converges strongly to a fixed point of T, which solves the variational inequality

$$⟨(\gamma f-\mu F)x^{*},x-x^{*}⟩\le 0,\forall x\in Fix(T).$$

In 2014, Zhang and Yang [21] proposed an explicit iterative algorithm based on the viscosity method for finding a solution for a class of variational inequalities over the common fixed points set of the finite family of nonexpansive mappings ${\left\{T_i\right\}}_{i=1}^N$, as follows:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_n\gamma V(x_n)+(I-{\alpha }_n\mu F)T_N^n{T}_{N-1}^n...T_1^n{x}_n,n\ge 0,\end{array}$$

where $T_i^n=(1-{\sigma }_n^i)I+{\sigma }_n^i{T}_n$ for $i=1,2,...,N$, V is $\rho$-Lipschitzian and $\left\{{\sigma }_n^i\right\}$ is a real sequence in $(0,1)$. They proved that $\left\{x_n\right\}$ converges strongly to the unique solution $x^{*}\in {\cap }_{i=1}^{N}Fix(T_i)$ of the variational inequality:

$$\begin{array}{c}\hfill ⟨(\mu F-\gamma V)x^{*},x-x^{*}⟩\ge 0,\forall x\in {\cap }_{i=1}^{N}Fix(T_i).\end{array}$$

In 2016, Jeong [22] introduced a new iterative method based on the hybrid viscosity approximation method and the hybrid steepest-descent method, as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\varphi (u_n,y)+\varphi (y)-\varphi (u_n)+⟨A{x}_n,y-u_n⟩+\frac{1}{r_n}⟨y-u_n,u_n-x_n⟩\ge 0,\forall y\in C,\hfill \\ x_{n+1}={\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_N^n{T}_{N-1}^n...T_1^n{u}_n,n\ge 0.\hfill \end{array}\right.\end{array}$$

He proved that the sequence $\left\{x_n\right\}$ converges strongly to the unique solution $x^{*}\in {\cap }_{i=1}^{N}Fix(T_i)\cap \Omega$ of the variational inequality:

$$\begin{array}{c}\hfill ⟨(\mu F-\gamma V)x^{*},x-x^{*}⟩\ge 0,\forall x\in {\cap }_{i=1}^{N}Fix(T_i)\cap \Omega .\end{array}$$

On the other hand, in 2008, Ceng et al. [23] considered the following problem of finding $(x^{*},y^{*})\in C\times C$ satisfying

$$\begin{array}{c}\hfill \left\{\begin{array}{c}⟨\nu A{y}^{*}+x^{*}-y^{*},x-x^{*}⟩\ge 0\mathrm{for}\mathrm{all}x\in C,\hfill \\ ⟨\mu B{x}^{*}+y^{*}-x^{*},x-y^{*}⟩\ge 0\mathrm{for}\mathrm{all}x\in C,\hfill \end{array}\right.\end{array}$$

(4)

which is called a general system of variational inequalities, where $A,B:C\to H$ are two nonlinear mappings, and $\lambda >0$ and $\mu >0$ are two fixed constants. Precisely, they introduced the following iterative algorithm:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_1=u\in C,\hfill \\ y_n=P_C(x_n-\mu B{x}_n),\hfill \\ x_{n+1}={\alpha }_{n}u+{\beta }_n{x}_n+{\gamma }_{n}S{P}_C(y_n-\lambda A{y}_n),\hfill \end{array}\right.\end{array}$$

where $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$ and $\left\{{\gamma }_n\right\}$ are real sequences, S is a nonexpansive mapping on C, and $P_C$ is the metric projection of H onto C and the strong convergence theorem obtained.

The implicit midpoint rules for solving fixed point problems of nonexpansive mappings are a powerful numerical method for solving ordinary differential equations; see [24,25,26] and the references therein. Therefore, many authors have studied them; see [27,28,29,30,31]. In 2015, Xu et al. [31] applied the viscosity technique to the implicit midpoint rule for nonexpansive mappings and proposed the following viscosity implicit midpoint rule:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T(\frac{x_n+x_{n+1}}{2}),n\ge 0,\end{array}$$

where $\left\{{\alpha }_n\right\}$ is a real sequence. They proved that the sequence $\left\{x_n\right\}$ converges strongly to a fixed point of T, which is the unique solution of a certain variational inequality. Additionally, Ke and Ma [29] studied the following generalized viscosity implicit rules:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T(t_n{x}_n+(1-t_n)x_{n+1}),n\ge 0,\end{array}$$

(5)

where $\left\{{\alpha }_n\right\}$ and $\left\{t_n\right\}$ are real sequences. They showed that the sequence $\left\{x_n\right\}$ converges strongly to a fixed point of T, which is the unique solution of a certain variational inequality.

Recently, Cai et al. [32] introduced the following modified viscosity implicit rules:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_1\in C,\hfill \\ u_n=t_n{x}_n+(1-t_n)y_n,\hfill \\ z_n=P_C(I-\mu B)u_n,\hfill \\ y_n=P_C(I-\lambda A)z_n,\hfill \\ x_{n+1}=P_C({\alpha }_{n}f(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\rho F)T{y}_n),\hfill & n\ge 1,\hfill \end{array}\right.\end{array}$$

where F is a Lipschitzian and strongly monotone map, $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$ and $\left\{t_n\right\}$ are real sequences and $P_C$ is the metric projection of H onto C. Under some suitable assumptions imposed on the parameters, they obtained some strong convergence theorems.

Motivated by the above results, we proposed a new composite iterative scheme for finding a common element of the set of solutions of a general system of variational inequalities, a generalized mixed equilibrium problem and the set of common fixed points of a finite family of nonexpansive mappings in Hilbert spaces. Then, we proved a strong convergence theorem. Finally, we provided two numerical examples for supporting our main result.

2. Preliminaries

Let H be a real Hilbert space. We use ⇀ and → to denote the weak and strong convergences in H, respectively. The following identity holds:

$$\begin{array}{cc}\hfill {\parallel \alpha x+\beta y\parallel }^2=& {\alpha \parallel x\parallel }^2+{\beta \parallel y\parallel }^2-\alpha \beta {\parallel x-y\parallel }^2,\hfill \end{array}$$

for all $x,y\in H$ and $\alpha ,\beta \in [0,1]$ such that $\alpha +\beta =1$. Let C be a nonempty closed convex subset of H. Then, for any $x\in H$, there exists a unique nearest point in C, denoted by $P_C(x)$, such that

$$\begin{array}{c}\hfill \parallel x-P_C(x)\parallel \le \parallel x-y\parallel \mathrm{for}\mathrm{all}y\in C.\end{array}$$

$P_C$ is called the metric projection of H onto C. It is known that $P_C$ is nonexpansive and satisfies

$$\begin{array}{c}\hfill ⟨x-y,P_C(x)-P_C(y)⟩\parallel \ge \parallel P_C(x)-P_C{(y)\parallel }^2\mathrm{for}\mathrm{all}x,y\in H.\end{array}$$

(6)

Furthermore, for $x\in H$ and $z\in C$, we have

$$\begin{array}{c}\hfill z=P_C(x)⟺⟨x-z,z-y⟩\ge 0\mathrm{for}\mathrm{all}y\in C.\end{array}$$

Lemma 1.

Let H be a real Hilbert space. Then, for all $x,y\in H$,

${\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2⟨y,x+y⟩$.

Definition 2

([32]). A mapping $T:H\to H$ is called firmly nonexpansive if for any $x,y\in H,$

$$\begin{array}{c}\hfill {\parallel Tx-Ty\parallel }^2\le ⟨Tx-Ty,x-y⟩.\end{array}$$

Definition 3

([32]). A mapping $A:H\to H$ is called α-strongly monotone if for any $x,y\in H,$

$$\begin{array}{c}\hfill ⟨Ax-Ay,x-y⟩\ge {\alpha \parallel x-y\parallel }^2.\end{array}$$

Definition 4

([33]). A mapping $T:H\to H$ is said to be an averaged mapping if it can be written as the average of the identity I and a nonexpansive mapping; that is, $T=(1-\alpha )I+\alpha S,$ where $\alpha \in (0,1)$ and $S:H\to H$ is nonexpansive. More precisely, we say that T is $\alpha -$averaged.

Clearly, a firmly nonexpansive mapping is a $\frac{1}{2}-$averaged map.

Proposition 5

([34]). $(i)$The composite of finitely many averaged mapping is averaged. That is, if each of the mappings ${\left\{T_i\right\}}_{i=1}^N$ is averaged, then so is the composite $T_1...T_N$. In particular, if $T_1$ is ${\alpha }_1-$averaged, and $T_2$ is ${\alpha }_2-$averaged, where ${\alpha }_1,{\alpha }_2\in (0,1)$, then the composite $T_1{T}_2$ is $\alpha -$averaged, where $\alpha ={\alpha }_1+{\alpha }_2-{\alpha }_1{\alpha }_2$.

$(ii)$ If the mappings ${\left\{T_i\right\}}_{i=1}^N$ are averaged and have a common fixed point, then ${\cap }_{i=1}^{N}Fix(T_i)=Fix(T_1,...,T_N)$. In particular, if $N=2$, we have $Fix(T_1)\cap Fix(T_2)=Fix(T_1{T}_2)=Fix(T_2{T}_1)$.

Lemma 6

([35]). Let C be a nonempty closed convex subset of H and $\Theta :C\times C\to \mathbb{R}$ be a bifunction satisfying the following conditions:

($A_1$)

$\Theta (x,x)=0$ for all $x\in C$;

($A_2$)

Θ is monotone, i.e., $\Theta (x,y)+\Theta (y,x)\le 0$ for all $x,y\in C$;

($A_3$)

For each $y\in C,x\mapsto \Theta (x,y)$ is weakly upper semicontinuous;

($A_4$)

For each $x\in C,y\mapsto \Theta (x,y)$ is convex and lower semicontinuous.

Suppose that $\varphi :C\to \mathbb{R}$ is convex and lower semicontinuous satisfying the following conditions:

($H_1$)

For each $x\in H$ and $r>0$, there exist a bounded subset $D_x\subset C$ and $y_x\in C$ such that for any $z\in C\setminus D_x$,

$$\begin{array}{c}\hfill \Theta (z,y_x)+\phi (y_x)-\phi (z)+\frac{1}{r}⟨y_x-z,z-x⟩\le 0forally\in C;\end{array}$$

($H_2$)

C is bounded set.

For $r>0$ and $x\in H$, define a mapping $T_r^{\Theta ,\phi }:H\to C$ as follows:

$$\begin{array}{c}\hfill T_r^{\Theta ,\phi }(x)=\{z\in C:\Theta (z,y)+\phi (y)-\phi (z)+\frac{1}{r}⟨y-z,z-x⟩\ge 0forally\in C\},\end{array}$$

for all $x\in H$. Then, the following hold:

(i)

$T_r^{\Theta ,\phi }(x)\ne \varnothing$ for each $x\in H$ and $T_r^{\Theta ,\phi }$ is single-valued;

(ii)

$T_r^{\Theta ,\phi }$ is firmly nonexpansive;

(iii)

$Fix(T_r^{\Theta ,\phi })=\Omega$;

(iv)

Ω is closed and convex.

Lemma 7

([36]). Let C, H, Θ and $T_r^{\Theta ,\phi }$ be as in Lemma 6. Then, the following inequality holds:

$$\begin{array}{c}\hfill \parallel T_s^{\Theta ,\phi }(x)-T_t^{\Theta ,\phi }{(x)\parallel }^2\le \frac{s-t}{s}⟨T_s^{\Theta ,\phi }(x)-T_t^{\Theta ,\phi }(x),T_s^{\Theta ,\phi }(x)-x⟩,\end{array}$$

for all $s,t>0$ and $x\in H$.

Definition 8

([32]). A nonlinear operator A in which the domain is $D(A)\subseteq H$ and the range is $R(A)\subseteq H$ is said to be $\alpha -$ inverse strongly monotone (for short, $\alpha -$ism ) if there exists $\alpha >0$ such that

$$⟨x-y,Ax-Ay⟩\ge {\alpha \parallel Ax-Ay\parallel }^{2}forallx,y\in D(A).$$

Lemma 9

([37]). Let C be a closed convex subset of H and $T:C\to C$ be a nonexpansive mapping with $Fix(T)\ne \varnothing$. If $\left\{x_n\right\}$ is a sequence in C such that $x_n\rightharpoonup x$ and $(I-T)x_n\to 0$, then $(I-T)x=0$.

Lemma 10

([38]). Let $F:H\to H$ be an L-Lipschitzian and η-strongly monotone mapping. Let $0<\mu <\frac{2\eta }{L^2}$ and $\lambda \in (0,1]$. Define

$$\begin{array}{c}\hfill T^{\lambda }x:=Tx-\lambda \mu F(Tx),x\in H,\end{array}$$

where $T:H\to H$ is a nonexpansive mapping. Then, the mapping $T^{\lambda }$ is a contraction from H into H, that is,

$$\begin{array}{c}\hfill \parallel T^{\lambda }x-T^{\lambda }y\parallel \le (1-\lambda \tau )\parallel x-y\parallel ,\forall x,y\in H,\end{array}$$

where $\tau =1-\sqrt{1-\mu (2\eta -\mu L^2)}\in (0,1)$.

Lemma 11

([39]). Assume that $\left\{a_n\right\}$ is a sequence of nonnegative real numbers such that

$$\begin{array}{c}\hfill a_{n+1}\le (1-{\gamma }_n)a_n+{\gamma }_n{v}_n+{\mu }_n,\end{array}$$

where $\left\{{\gamma }_n\right\}$ is a sequence in $[0,1]$, $\left\{{\mu }_n\right\}$ a sequence of nonnegative real numbers and $\left\{v_n\right\}$ a sequence in $\mathbb{R}$ such that ${\sum }_{n=1}^{\infty }{\gamma }_n=\infty ,{lim\; sup}_{n\to \infty }{v}_n\le 0$ and ${\sum }_{n=1}^{\infty }{\mu }_n<\infty .$ Then, ${lim}_{n\to \infty }{a}_n=0$.

Lemma 12

([23]). For a given $x^{*},y^{*}\in C,(x^{*},y^{*})$ is a solution of problem (4) if and only if $x^{*}$ is a fixed point of the mapping $G:C\to C$ defined by

$$\begin{array}{c}\hfill G(x)=P_C(P_C(x-\mu Bx)-\nu A{P}_C(x-\mu Bx))\mathrm{for}\mathrm{all}x\in C,\end{array}$$

where $y^{*}=P_C(x^{*}-\mu B{x}^{*})$.

Lemma 13

([30]). Let $\left\{x_n\right\}$ and $\left\{y_n\right\}$ be bounded sequences in Banach space X and $\left\{{\beta }_n\right\}$ be a sequence in $[0,1]$ with $0<{lim\; inf}_{n\to \infty }{\beta }_n\le {lim\; sup}_{n\to \infty }{\beta }_n<1$. Suppose that $x_{n+1}=(1-{\beta }_n)y_n+{\beta }_n{x}_n$ for all integer $n\ge 0$ and ${lim\; sup}_{n\to \infty }(\parallel y_{n+1}-y_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0$. Then, ${lim}_{n\to \infty }\parallel x_n-y_n\parallel =0$.

3. Main Result

Theorem 14.

Let C be a closed convex subset of H; $\Theta :C\times C\to \mathbb{R}$ be a bifunction satisfying the conditions $(A_1)-(A_4)$ of Lemma 6; $\phi :C\to \mathbb{R}$ be a lower semicontinuous and convex function with restriction $(H_1)$ or $(H_2)$ of Lemma 6; $A,B,D:H\to H$ be α-ism, β-ism and ω-ism, respectively; ${\left\{T_i\right\}}_{i=1}^N$ be an infinite family of nonexpansive self-mappings on H; $F:H\to H$ be an L-Lipschitzian and ν-strongly monotone mapping; and $V:H\to H$ be a κ-Lipschitzian mapping. Let $0<\mu <\frac{2\nu }{L^2}$ and $0<\gamma \kappa <\tau$, where $\tau =1-\sqrt{1-\mu (2\nu -\mu L^2)}$. Set $\Gamma :={\cap }_{n=1}^{N}Fix(T_n)\cap Fix(G)\cap \Omega$ and assume $\Gamma \ne \varnothing$. Suppose that $\left\{{\alpha }_n\right\}$, $\left\{{\beta }_n\right\}$, $\left\{t_n\right\}$ and $\left\{r_n\right\}$ are real sequences satisfying the following conditions:

($B_1$)

$\left\{{\alpha }_n\right\}\subset (0,1)$, ${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=1}^{\infty }|{\alpha }_{n+1}-{\alpha }_n|<\infty$ and ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$;

($B_2$)

$0<{lim\; inf}_{n\to \infty }{\beta }_n\le {lim\; sup}_{n\to \infty }{\beta }_n<1$ and ${\sum }_{n=1}^{\infty }|{\beta }_{n+1}-{\beta }_n|<\infty$;

($B_3$)

$0<{lim\; inf}_{n\to \infty }{r}_n\le {lim\; sup}_{n\to \infty }{r}_n<2\alpha$ and ${\sum }_{n=1}^{\infty }|r_{n+1}-r_n|<\infty$;

($B_4$)

$\left\{t_n\right\}\subset (b,1]$ for some $b>0$ and ${\sum }_{n=1}^{\infty }|t_{n+1}-t_n|<\infty$.

Given $x_1\in H$, let $\left\{x_n\right\}$ be a sequence generated by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=t_n{x}_n+(1-t_n)y_n,\hfill \\ \theta (v_n,y)+\phi (y)-\phi (v_n)+⟨A{u}_n,y-v_n⟩+\frac{1}{r_n}⟨y-v_n,v_n-u_n⟩\ge 0,\forall y\in C,\hfill \\ z_n=P_C(I-\rho B)v_n,\hfill \\ y_n=P_C(I-\lambda D)z_n,\hfill \\ x_{n+1}={\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_N^n{T}_{N-1}^n...T_1^n{y}_n,\hfill \end{array}\right.\end{array}$$

(7)

where $T_i^n=(1-s_n^i)I+s_n^i{T}_i$ for $i=1,2,...,N$ and $s_n^i\in ({\epsilon }_1,{\epsilon }_2)$ for some ${\epsilon }_1,{\epsilon }_2\in (0,1)$, $\rho \in (0,2\beta )$ and $\lambda \in (0,2\omega )$. Suppose ${lim}_{n\to \infty }|s_{n+1}^i-s_n^i|=0$ for $i=1,2,...,N$. Then, the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}\in \Gamma$, where $x^{*}=P_{\Gamma }(I-\mu F+\gamma V)(x^{*})$, which solves the variational inequality (VI):

$$⟨(\mu F-\gamma V)x^{*},x^{*}-x⟩\le 0forallx\in \Gamma .$$

(8)

To prove Theorem 14, we first establish some lemmas.

Lemma 15.

Let $F:H\to H$ be an L-Lipschitzian and ν-strongly monotone mapping with $\tau =1-\sqrt{1-\mu (2\nu -\mu L^2)}$. Then, $I-\mu F$ is nonexpansive.

Proof. 

For $x,y\in H$, we have

$$\begin{array}{cc}\hfill {\parallel (I-\mu F)x-(I-\mu F)y\parallel }^2=& {\parallel x-y-\mu (Fx-Fy)\parallel }^2\hfill \\ \hfill =& {\parallel x-y\parallel }^2-2\mu ⟨x-y,Fx-Fy⟩+{\mu }^2{\parallel Fx-Fy\parallel }^2\hfill \\ \hfill \le & {\parallel x-y\parallel }^2{-2\mu \nu \parallel x-y\parallel }^2+{\mu }^2{L}^2{\parallel x-y\parallel }^2\hfill \\ \hfill =& (1-2\mu \nu +{\mu }^2{L}^2){\parallel x-y\parallel }^2\hfill \\ \hfill =& {(1-\tau )}^2{\parallel x-y\parallel }^2.\hfill \end{array}$$

(9)

□

Lemma 16.

Let $A:H\to H$ be an α-ism and $\nu \in (0,2\alpha )$. Then, $I-\nu A$ is nonexpansive.

Proof. 

For $x,y\in H$, we have

$$\begin{array}{cc}\hfill {\parallel (I-\nu A)x-(I-\nu A)y\parallel }^2=& {\parallel x-y-\nu (Ax-Ay)\parallel }^2\hfill \\ \hfill =& {\parallel x-y\parallel }^2-2\nu ⟨x-y,Ax-Ay⟩+{\nu }^2{\parallel Ax-Ay\parallel }^2\hfill \\ \hfill \le & {\parallel x-y\parallel }^2{-2\alpha \nu \parallel Ax-Ay\parallel }^2+{\nu }^2{\parallel Ax-Ay\parallel }^2\hfill \\ \hfill =& {\parallel x-y\parallel }^2+\nu (\nu -2\alpha ){\parallel Ax-Ay\parallel }^2\hfill \\ \hfill \le & {\parallel x-y\parallel }^2.\hfill \end{array}$$

(10)

□

Proof of Theorem 14. 

We break the proof into several steps.

Step 1. The sequences $\left\{x_n\right\}$ and $\left\{v_n\right\}$ are bounded. Suppose $x^{*}\in \Gamma$ and $y^{*}=P_C(x^{*}-\rho B{x}^{*})$. Therefore, from (7), we obtain

$$\begin{array}{c}\hfill \parallel u_n-x^{*}\parallel =\parallel t_n{x}_n+(1-t_n)y_n-x^{*}\parallel \le t_n\parallel x_n-x^{*}\parallel +(1-t_n)\parallel y_n-x^{*}\parallel .\end{array}$$

(11)

since A is $\alpha -$ism, $0<r_n<2\alpha$, $x^{*}=T_{r_n}^{\Theta ,\phi }(x^{*}-r_{n}A{x}^{*})$ and $v_n=T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)$, we derive from (7) and Lemma 16 that

$$\begin{array}{cc}\hfill \parallel v_n-x^{*}{\parallel }^2=& \parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_n}^{\Theta ,\phi }(x^{*}-r_{n}A{x}^{*}){\parallel }^2\hfill \\ \hfill & \le \parallel u_n-r_{n}A{u}_n-(x^{*}-r_{n}A{x}^{*}){\parallel }^2\hfill \\ \hfill & \le \parallel u_n-x^{*}{\parallel }^2-r_n(r_n-2\alpha ){\parallel A{u}_n-A{x}^{*}\parallel }^2\hfill \\ \hfill & \le \parallel u_n-x^{*}{\parallel }^2.\hfill \end{array}$$

(12)

Then, from (11), we have

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}\parallel & =\parallel G{v}_n-x^{*}\parallel =\parallel G{v}_n-G{x}^{*}\parallel \le \parallel v_n-x^{*}\parallel \hfill \\ \hfill & \le \parallel u_n-x^{*}\parallel \hfill \\ \hfill & \le t_n\parallel x_n-x^{*}\parallel +(1-t_n)\parallel y_n-x^{*}\parallel .\hfill \end{array}$$

(13)

Hence, $\parallel y_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel$. Therefore, by (11), we have $\parallel u_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel$. Therefore, from (12), we have $\parallel v_n-x^{*}\parallel \le \parallel x_n-x^{*}\parallel$. Hence, by (10), we have

$$\begin{array}{cc}\hfill \parallel z_n-y^{*}{\parallel }^2=& \parallel P_C(I-\rho B)v_n-P_C(I-\rho B)x^{*}{\parallel }^2\hfill \\ \hfill \le & \parallel (I-\rho B)v_n-(I-\rho B)x^{*}{\parallel }^2\hfill \\ \hfill \le & \parallel v_n-x^{*}{\parallel }^2-\rho (2\beta -\rho ){\parallel B{v}_n-B{x}^{*}\parallel }^2\hfill \\ \hfill \le & \parallel x_n-x^{*}{\parallel }^2-\rho (2\beta -\rho ){\parallel B{v}_n-B{x}^{*}\parallel }^2.\hfill \end{array}$$

(14)

In a similar way, we have

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}{\parallel }^2\le & \parallel z_n-y^{*}{\parallel }^2-\lambda (2\omega -\lambda ){\parallel D{z}_n-D{y}^{*}\parallel }^2.\hfill \end{array}$$

(15)

Substituting (14) into (15), we obtain

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}{\parallel }^2\le & \parallel x_n-x^{*}{\parallel }^2-\rho (2\beta -\rho ){\parallel B{v}_n-B{x}^{*}\parallel }^2\hfill \\ \hfill & -\lambda (2\omega -\lambda )\parallel D{z}_n-D{y}^{*}{\parallel }^2\hfill \\ \hfill \le & \parallel x_n-x^{*}{\parallel }^2.\hfill \end{array}$$

(16)

By using (7), and conditions ($B_1$) and ($B_2$), we may assume, without loss of generality, ${\alpha }_n\le 1-{\beta }_n$. Then, from (7), (9) and Lemma 10, we have

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel {\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-x^{*}\parallel \hfill \\ \hfill & =\parallel {\alpha }_n\gamma [V(x_n)-V(x^{*})]+{\alpha }_n[\gamma V(x^{*})-\mu F(x^{*})]+{\beta }_n(x_n-x^{*})\hfill \\ \hfill & +((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}\parallel \hfill \\ \hfill & \le {\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel +{\beta }_n\parallel x_n-x^{*}\parallel +{\alpha }_n\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel \hfill \\ \hfill & +(1-{\beta }_n)\parallel (I-\frac{{\alpha }_n}{1-{\beta }_n}\mu F)T_2^n{T}_1^n{y}_n-(I-\frac{{\alpha }_n}{1-{\beta }_n}\mu F)T_2^n{T}_1^n{x}^{*}\parallel \hfill \\ \hfill & \le {\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel +{\beta }_n\parallel x_n-x^{*}\parallel +{\alpha }_n\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel \hfill \\ \hfill & +(1-{\beta }_n)(1-\frac{{\alpha }_n\tau }{1-{\beta }_n})\parallel y_n-x^{*}\parallel \hfill \\ \hfill & \le ({\alpha }_n\gamma \kappa +{\beta }_n)\parallel x_n-x^{*}\parallel +{\alpha }_n\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel \hfill \\ \hfill & +(1-{\beta }_n-{\alpha }_n\tau )\parallel x_n-x^{*}\parallel \hfill \\ \hfill & \le (1-{\alpha }_n(\tau -\gamma \kappa ))\parallel x_n-x^{*}\parallel +{\alpha }_n\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel \hfill \\ \hfill & \le max\{\parallel x_n-x^{*}\parallel ,\frac{\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel }{\tau -\gamma \kappa }\}.\hfill \end{array}$$

By induction, we have

$$\begin{array}{c}\hfill \parallel x_n-x^{*}\parallel \le max\{\parallel x_1-x^{*}\parallel ,\frac{\parallel \gamma V(x^{*})-\mu F(x^{*})\parallel }{\tau -\gamma \kappa }\},\end{array}$$

for all $n\ge 2$. Hence, $\left\{x_n\right\}$ is bounded, which implies that $\left\{u_n\right\}$, $\left\{v_n\right\}$, $\left\{y_n\right\}$, $\left\{V(x_n)\right\}$, $\left\{\mu F(T_n{u}_n)\right\}$ and $\left\{T_n{y}_n\right\}$ are all bounded.

Step 2. The sequence $\left\{x_n\right\}$ is asymptotically regular, that is, ${lim}_{n\to \infty }\parallel x_{n+1}-x_n\parallel =0$. To see this, we set $x_{n+1}={\beta }_n{x}_n+(1-{\beta }_n)w_n$ to derive that

$$\begin{array}{cc}\hfill & w_{n+1}-w_n=\hfill \\ \hfill & \frac{x_{n+2}-{\beta }_{n+1}{x}_{n+1}}{1-{\beta }_{n+1}}-\frac{x_{n+1}-{\beta }_n{x}_n}{1-{\beta }_n}\hfill \\ \hfill =& \frac{{\alpha }_{n+1}\gamma V(x_{n+1})+((1-{\beta }_{n+1})I-{\alpha }_{n+1}\mu F)T_2^{n+1}{T}_1^{n+1}{y}_{n+1}}{1-{\beta }_{n+1}}\hfill \\ \hfill & -\frac{{\alpha }_n\gamma V(x_n)+((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n}{1-{\beta }_n}\hfill \\ \hfill =& \frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}\gamma V(x_{n+1})-\frac{{\alpha }_n}{1-{\beta }_n}\gamma V(x_n)+T_2^{n+1}{T}_1^{n+1}{y}_{n+1}\hfill \\ \hfill & -T_2^n{T}_1^n{y}_n+\frac{{\alpha }_n}{1-{\beta }_n}\mu F(T_2^n{T}_1^n{y}_n)-\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}\mu F(T_2^{n+1}{T}_1^{n+1}{y}_{n+1})\hfill \\ \hfill =& \frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}[\gamma V(x_{n+1})-\mu F(T_2^{n+1}{T}_1^{n+1}{y}_{n+1})]+\frac{{\alpha }_n}{1-{\beta }_n}[\mu F(T_2^n{T}_1^n{y}_n)-\gamma V(x_n)]\hfill \\ \hfill & +T_2^{n+1}{T}_1^{n+1}{y}_{n+1}-T_2^{n+1}{T}_1^{n+1}{y}_n+T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^n{T}_1^n{y}_n.\hfill \end{array}$$

It follows that

$$\begin{array}{cc}\hfill & \parallel w_{n+1}-w_n\parallel -\parallel x_{n+1}-x_n\parallel \hfill \\ \hfill \le & \frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}(\gamma \parallel V(x_{n+1})\parallel +\mu \parallel F(T_2^{n+1}{T}_1^{n+1}{y}_{n+1})\parallel )\hfill \\ \hfill & +\frac{{\alpha }_n}{1-{\beta }_n}(\gamma \parallel V(x_n)\parallel +\mu \parallel F(T_2^n{T}_1^n{y}_n)\parallel )\hfill \\ \hfill & +\parallel T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^n{T}_1^n{y}_n\parallel +\parallel y_{n+1}-y_n\parallel -\parallel x_{n+1}-x_n\parallel .\hfill \end{array}$$

(17)

Note that

$$\begin{array}{cc}\hfill & \parallel T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^n{T}_1^n{y}_n\parallel \hfill \\ \hfill \le & \parallel T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^{n+1}{T}_1^n{y}_n\parallel +\parallel T_2^{n+1}{T}_1^n{y}_n-T_2^n{T}_1^n{y}_n\parallel \hfill \\ \hfill \le & \parallel T_1^{n+1}{y}_n-T_1^n{y}_n\parallel +\parallel T_2^{n+1}{T}_1^n{y}_n-T_2^n{T}_1^n{y}_n\parallel \hfill \end{array}$$

(18)

and

$$\begin{array}{cc}\hfill \parallel T_1^{n+1}{y}_n-T_1^n{y}_n\parallel =& \parallel (1-s_{n+1}^1)y_n-s_{n+1}^1{T}_1{y}_n-(1-s_n^1)y_n+s_n^1{T}_1{y}_n\parallel \hfill \\ \hfill =& \parallel (-s_{n+1}^1+s_n^1)y_n+(s_n^1-s_{n+1}^1)T_1{y}_n\parallel \hfill \\ \hfill \le & |s_n^1-s_{n+1}^1|(\parallel y_n\parallel +\parallel T_1{y}_n\parallel ).\hfill \end{array}$$

Since $|s_n^1-s_{n+1}^1|\to 0$ for $i=1,2$ and $\left\{y_n\right\}$, $\left\{T_1{y}_n\right\}$ are bounded, we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel T_1^{n+1}{y}_n-T_1^n{y}_n\parallel =0.\end{array}$$

(19)

Similarly, we obtain

$$\begin{array}{cc}\hfill \parallel T_2^{n+1}{T}_1^n{y}_n-T_2^n{T}_1^n{y}_n\parallel =& \parallel (-s_{n+1}^2+s_n^2)T_1^n{y}_n+(s_n^2-s_{n+1}^2)T_2{T}_1^n{y}_n\parallel \hfill \\ \hfill \le & |s_n^2-s_{n+1}^2|(\parallel T_1^n{y}_n\parallel +\parallel T_2{T}_1^n{y}_n\parallel ).\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel T_2^{n+1}{T}_1^n{y}_n-T_2^n{T}_1^n{y}_n\parallel =0.\end{array}$$

(20)

Thus, by (18)–(20), we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^n{T}_1^n{y}_n\parallel =0.\end{array}$$

(21)

Observe that by Lemma 16, we have

$$\begin{array}{cc}\hfill & \parallel T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_{n+1}-r_{n+1}A{u}_{n+1})\parallel \hfill \\ \hfill & \le \parallel u_n-r_{n}A{u}_n-u_{n+1}+r_{n+1}A{u}_{n+1}\parallel \hfill \\ \hfill & \le \parallel u_n-r_{n}A{u}_n-u_{n+1}+r_{n}A{u}_{n+1}\parallel +\parallel r_{n}A{u}_{n+1}-r_{n+1}A{u}_{n+1}\parallel \hfill \\ \hfill & \le \parallel u_n-u_{n+1}\parallel +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel .\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \parallel v_n-v_{n+1}\parallel & =\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_{n+1}-r_{n+1}A{u}_{n+1})\parallel \hfill \\ \hfill & \le \parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & +\parallel T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_{n+1}-r_{n+1}A{u}_{n+1})\parallel \hfill \\ \hfill & \le \parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & +\parallel u_n-u_{n+1}\parallel +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel .\hfill \end{array}$$

Therefore, from (7), we have

$$\begin{array}{cc}\hfill & \parallel y_{n+1}-y_n\parallel \hfill \\ \hfill & =\parallel P_C(I-\lambda D)P_C(I-\rho B)v_{n+1}-P_C(I-\lambda D)P_C(I-\rho B)v_n\parallel \hfill \\ \hfill & \le \parallel v_{n+1}-v_n\parallel \hfill \\ \hfill & \le \parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & +\parallel u_n-u_{n+1}\parallel +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel \hfill \\ \hfill & =\parallel t_{n+1}{x}_{n+1}+(1-t_{n+1})y_{n+1}-t_n{x}_n-(1-t_n)y_n\parallel +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel \hfill \\ \hfill & +\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & =\parallel t_{n+1}(x_{n+1}-x_n)+(t_{n+1}-t_n)x_n+(1-t_{n+1})(y_{n+1}-y_n)-(t_{n+1}-t_n)y_n\parallel \hfill \\ \hfill & +\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel \hfill \\ \hfill & \le t_{n+1}\parallel x_{n+1}-x_n\parallel +(1-t_{n+1})\parallel y_{n+1}-y_n\parallel +|t_{n+1}-t_n|\parallel x_n-y_n\parallel \hfill \\ \hfill & +|r_n-r_{n+1}|\parallel A{u}_{n+1}\parallel +\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel ,\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \parallel y_{n+1}& -y_n\parallel \hfill \\ \hfill & \le \parallel x_{n+1}-x_n\parallel +\frac{|t_{n+1}-t_n|}{t_{n+1}}\parallel x_n-y_n\parallel +\frac{|r_n-r_{n+1}|}{t_{n+1}}\parallel A{u}_{n+1}\parallel \hfill \\ \hfill & +\frac{1}{t_{n+1}}\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & \le \parallel x_{n+1}-x_n\parallel +\frac{|t_{n+1}-t_n|}{b}\parallel x_n-y_n\parallel +\frac{|r_{n+1}-r_n|}{b}\parallel A{u}_{n+1}\parallel \hfill \\ \hfill & +\frac{1}{b}\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & \le \parallel x_{n+1}-x_n\parallel +(|t_{n+1}-t_n|+|r_{n+1}-r_n|)M\hfill \\ \hfill & +\frac{1}{b}\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel ,\hfill \end{array}$$

(22)

where $M>0$ is a big enough constant. Additionally, from Lemma 7, we have

$$\begin{array}{cc}\hfill & li{m}_{n\to \infty }\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \hfill \\ \hfill & \le li{m}_{n\to \infty }\frac{r_{n+1}-r_n}{r_{n+1}}⟨T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n),\hfill \\ \hfill & T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-(u_n-r_{n}A{u}_n)⟩\hfill \\ \hfill & =0.\hfill \end{array}$$

(23)

Consequently, it follows from (17), (19), (21)–(23), and conditions $(B_1)$ and $(B_2)$ that

$$\begin{array}{cc}\hfill & \underset{n\to \infty }{lim\; sup}\parallel w_{n+1}-w_n\parallel -\parallel x_{n+1}-x_n\parallel \hfill \\ \hfill \le & \underset{n\to \infty }{lim\; sup}\{\frac{{\alpha }_{n+1}}{1-{\beta }_{n+1}}(\gamma \parallel V(x_{n+1})\parallel +\mu \parallel F(T_2^{n+1}{T}_1^{n+1}{y}_{n+1})\parallel )\hfill \\ \hfill & +\frac{{\alpha }_n}{1-{\beta }_n}(\gamma \parallel V(x_n)\parallel +\mu \parallel F(T_2^n{T}_1^n{y}_n)\parallel )\hfill \\ \hfill & +\parallel T_2^{n+1}{T}_1^{n+1}{y}_n-T_2^n{T}_1^n{y}_n\parallel +(|t_{n+1}-t_n|+|r_{n+1}-r_n|)M\hfill \\ \hfill & +\frac{1}{b}\parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_{n+1}}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)\parallel \}\hfill \\ \hfill =& 0.\hfill \end{array}$$

Hence, by Lemma 13, we have ${lim}_{n\to \infty }\parallel w_n-x_n\parallel =0.$ Therefore,

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{n+1}-x_n\parallel =(1-{\beta }_n)\parallel w_n-x_n\parallel =0.\end{array}$$

(24)

Step 3. We prove

(3a)

$\parallel x_n-y_n\parallel \to 0$,

(3b)

$\parallel u_n-v_n\parallel \to 0$,

(3c)

$\parallel v_n-T_2^n{T}_1^n{v}_n\parallel \to 0$.

From (7), we have

$$\begin{array}{cc}\hfill \parallel T_2^n{T}_1^n{y}_n-x_n\parallel & \le \parallel T_2^n{T}_1^n{y}_n-x_{n+1}\parallel +\parallel x_{n+1}-x_n\parallel \hfill \\ \hfill & \le {\alpha }_n\parallel \gamma V(x_n)-\mu F(T_2^n{T}_1^n{y}_n)\parallel +\parallel x_{n+1}-x_n\parallel \hfill \\ \hfill & +{\beta }_n\parallel T_2^n{T}_1^n{y}_n-x_n\parallel .\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill \parallel T_2^n{T}_1^n{y}_n-x_n\parallel & \le \frac{1}{1-{\beta }_n}\parallel x_{n+1}-x_n\parallel \hfill \\ \hfill & +\frac{{\alpha }_n}{1-{\beta }_n}\parallel \gamma V(x_n)-\mu F(T_2^n{T}_1^n{y}_n)\parallel .\hfill \end{array}$$

Therefore, from (24), we obtain

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel T_2^n{T}_1^n{y}_n-x_n\parallel =0.\end{array}$$

(25)

Let $x^{*}\in \Gamma$ and $y^{*}=P_C(x^{*}-\rho B{x}^{*})$. Therefore, from (7) and (16), we obtain

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}{\parallel }^2\hfill \\ \hfill & =\parallel {\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-x^{*}{\parallel }^2\hfill \\ \hfill & =\parallel {\alpha }_n[\gamma V(x_n)-\mu F(x^{*})]+{\beta }_n(x_n-x^{*})\hfill \\ \hfill & +((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}{\parallel }^2\hfill \\ \hfill & \le ({\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel +{\beta }_n\parallel x_n-x^{*}\parallel \hfill \\ \hfill & +\parallel (1-{\beta }_n)((I-\frac{{\alpha }_n}{1-{\beta }_n}\mu F)T_2^n{T}_1^n{y}_n-(I-\frac{{\alpha }_n}{1-{\beta }_n}\mu F)T_2^n{T}_1^n{x}^{*}){\parallel )}^2\hfill \\ \hfill & \le ({\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel +{\beta }_n\parallel x_n-x^{*}\parallel \hfill \\ \hfill & +(1-{\beta }_n)(1-\frac{{\alpha }_n\tau }{1-{\beta }_n})\parallel y_n-x^{*}{\parallel )}^2\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\beta }_n\parallel x_n-x^{*}{\parallel }^2+(1-{\beta }_n-{\alpha }_n\tau ){\parallel y_n-x^{*}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\beta }_n\parallel x_n-x^{*}{\parallel }^2+(1-{\beta }_n-{\alpha }_n\tau )(\parallel x_n-x^{*}{\parallel }^2\hfill \\ \hfill & -\rho (2\beta -\rho )\parallel B{v}_n-B{x}^{*}{\parallel }^2-\lambda (2\omega -\lambda )\parallel D{z}_n-D{y}^{*}{\parallel }^2)\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\parallel x_n-x^{*}\parallel }^2\hfill \\ \hfill & +(1-{\beta }_n-{\alpha }_n\tau )(-\rho (2\beta -\rho )\parallel B{v}_n-B{x}^{*}{\parallel }^2-\lambda (2\omega -\lambda )\parallel D{z}_n-D{y}^{*}{\parallel }^2).\hfill \end{array}$$

(26)

Therefore,

$$\begin{array}{cc}\hfill & (1-{\beta }_n-{\alpha }_n\tau )(\rho (2\beta -\rho )\parallel B{v}_n-B{x}^{*}{\parallel }^2+\lambda (2\omega -\lambda )\parallel D{z}_n-D{y}^{*}{\parallel }^2)\hfill \\ \hfill & \le \parallel x_n-x^{*}{\parallel }^2-{\parallel x_{n+1}-x^{*}\parallel }^2+{\alpha }_{n}M\hfill \\ \hfill & \le (\parallel x_n-x^{*}\parallel -\parallel x_{n+1}-x^{*}\parallel )(\parallel x_n-x^{*}\parallel +\parallel x_{n+1}-x^{*}\parallel )+{\alpha }_{n}M\hfill \\ \hfill & \le \parallel x_n-x_{n+1}\parallel (\parallel x_n-x^{*}\parallel +\parallel x_{n+1}-x^{*}\parallel )+{\alpha }_{n}M.\hfill \end{array}$$

From (24), we have

$$\begin{array}{c}\hfill \parallel B{v}_n-B{x}^{*}\parallel \to 0\mathrm{and}\parallel D{z}_n-D{y}^{*}\parallel \to 0.\end{array}$$

(27)

Additionaly, from (12), (13) and (26), we have

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}{\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\beta }_n\parallel x_n-x^{*}{\parallel }^2+(1-{\beta }_n-{\alpha }_n\tau ){\parallel y_n-x^{*}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\beta }_n\parallel x_n-x^{*}{\parallel }^2+(1-{\beta }_n-{\alpha }_n\tau ){\parallel v_n-x^{*}\parallel }^2\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\beta }_n{\parallel x_n-x^{*}\parallel }^2\hfill \\ \hfill & +(1-{\beta }_n-{\alpha }_n\tau )(\parallel u_n-x^{*}{\parallel }^2-r_n(r_n-2\alpha )\parallel A{u}_n-A{x}^{*}{\parallel }^2)\hfill \\ \hfill & \le {\alpha }_n\tau \parallel \frac{1}{\tau }(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2+{\parallel x_n-x^{*}\parallel }^2\hfill \\ \hfill & -(1-{\beta }_n-{\alpha }_n\tau )r_n(r_n-2\alpha ){\parallel A{u}_n-A{x}^{*}\parallel }^2\hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill & r_n(r_n-2\alpha )(1-{\beta }_n-{\alpha }_n\tau )r_n(r_n-2\alpha )\parallel A{u}_n-A{x}^{*}{\parallel }^2)\hfill \\ \hfill & \le (\parallel x_n-x^{*}{\parallel }^2-\parallel x_{n+1}-x^{*}{\parallel }^2)+{\alpha }_{n}M.\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill \parallel A{u}_n-A{x}^{*}\parallel \to 0.\end{array}$$

(28)

On the other hand, by (7) and (6), we have

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}{\parallel }^2& =\parallel P_C(I-\lambda D)z_n-P_C(I-\lambda D)y^{*}{\parallel }^2\hfill \\ \hfill & \le ⟨(I-\lambda D)z_n-(I-\lambda D)y^{*},y_n-x^{*}⟩\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}[\parallel (I-\lambda D)z_n-(I-\lambda D)y^{*}{\parallel }^2+{\parallel y_n-x^{*}\parallel }^2\hfill \\ \hfill & -\parallel z_n-y_n+x^{*}-y^{*}-\lambda (D{z}_n-D{y}^{*}){\parallel }^2].\hfill \end{array}$$

Therefore, by Lemma 16, we have

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}{\parallel }^2& \le \parallel z_n-y^{*}{\parallel }^2-{\parallel z_n-y_n+x^{*}-y^{*}-\lambda (D{z}_n-D{y}^{*})\parallel }^2\hfill \\ \hfill & =\parallel z_n-y^{*}{\parallel }^2-[\parallel z_n-y_n+x^{*}-y^{*}{\parallel }^2+{\lambda }^2{\parallel D{z}_n-D{y}^{*}\parallel }^2\hfill \\ \hfill & -2\lambda ⟨z_n-y_n+x^{*}-y^{*},D{z}_n-D{y}^{*}⟩]\hfill \\ \hfill & \le \parallel z_n-y^{*}{\parallel }^2-{\parallel z_n-y_n+x^{*}-y^{*}\parallel }^2\hfill \\ \hfill & +2\lambda \parallel z_n-y_n+x^{*}-y^{*}\parallel \parallel D{z}_n-D{y}^{*}\parallel .\hfill \end{array}$$

(29)

Again, by (7), we obtain

$$\begin{array}{cc}\hfill \parallel z_n-y^{*}{\parallel }^2& =\parallel P_C(I-\rho B)v_n-P_C(I-\rho B)x^{*}{\parallel }^2\hfill \\ \hfill & \le ⟨(I-\rho B)v_n-(I-\rho B)x^{*},z_n-y^{*}⟩\hfill \\ \hfill & ={\displaystyle \frac{1}{2}}[\parallel (I-\rho B)v_n-(I-\rho B)x^{*}{\parallel }^2+{\parallel z_n-y^{*}\parallel }^2\hfill \\ \hfill & -\parallel v_n-z_n+y^{*}-x^{*}-\rho (B{v}_n-B{x}^{*}){\parallel }^2],\hfill \end{array}$$

which implies

$$\begin{array}{cc}\hfill & \parallel z_n-y^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel v_n-x^{*}{\parallel }^2-{\parallel v_n-z_n+y^{*}-x^{*}-\rho (B{v}_n-B{x}^{*})\parallel }^2\hfill \\ \hfill & =\parallel v_n-x^{*}{\parallel }^2-[\parallel v_n-z_n+y^{*}-x^{*}{\parallel }^2\hfill \\ \hfill & -2\rho ⟨v_n-z_n+y^{*}-x^{*},B{v}_n-B{x}^{*}⟩+{\rho }^2\parallel B{v}_n-B{x}^{*}{\parallel }^2]\hfill \\ \hfill & \le \parallel x_n-x^{*}{\parallel }^2-{\parallel v_n-z_n+y^{*}-x^{*}\parallel }^2\hfill \\ \hfill & +2\rho \parallel v_n-z_n+y^{*}-x^{*}\parallel \parallel B{v}_n-B{x}^{*}\parallel .\hfill \end{array}$$

(30)

It follows from (29) and (30) that

$$\begin{array}{cc}\hfill \parallel y_n-x^{*}{\parallel }^2& \le \parallel x_n-x^{*}{\parallel }^2-{\parallel v_n-z_n+y^{*}-x^{*}\parallel }^2\hfill \\ \hfill & -\parallel z_n-y_n+x^{*}-y^{*}{\parallel }^2\hfill \\ \hfill & +2\rho \parallel v_n-z_n+y^{*}-x^{*}\parallel \parallel B{v}_n-B{x}^{*}\parallel \hfill \\ \hfill & +2\lambda \parallel z_n-y_n+x^{*}-y^{*}\parallel \parallel D{z}_n-D{y}^{*}\parallel .\hfill \end{array}$$

Therefore, from Lemmas 1 and 10, we obtain

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}{\parallel }^2\hfill \\ \hfill & =\parallel {\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-x^{*}{\parallel }^2\hfill \\ \hfill & =\parallel {\alpha }_n[\gamma V(x_n)-\mu F(x^{*})]+{\beta }_n(x_n-T_2^n{T}_1^n{y}_n)\hfill \\ \hfill & +(I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-(I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel {\beta }_n(x_n-T_2^n{T}_1^n{y}_n)+(I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-(I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}{\parallel }^2\hfill \\ \hfill & +2{\alpha }_n⟨\gamma V(x_n)-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le [{\beta }_n\parallel x_n-T_2^n{T}_1^n{y}_n\parallel +\parallel (I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-(I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}{\parallel ]}^2\hfill \\ \hfill & +2{\alpha }_n⟨\gamma V(x_n)-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le [{\beta }_n\parallel x_n-T_2^n{T}_1^n{y}_n\parallel +(1-{\alpha }_n\tau )\parallel y_n-x^{*}{\parallel ]}^2\hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le [\parallel x_n-T_2^n{T}_1^n{y}_n\parallel +\parallel y_n-x^{*}{\parallel ]}^2+2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2+\parallel y_n-x^{*}{\parallel }^2+2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2+2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +\parallel x_n-x^{*}{\parallel }^2-\parallel v_n-z_n+y^{*}-x^{*}{\parallel }^2-{\parallel z_n-y_n+x^{*}-y^{*}\parallel }^2\hfill \\ \hfill & +2\rho \parallel v_n-z_n+y^{*}-x^{*}\parallel \parallel B{v}_n-B{x}^{*}\parallel \hfill \\ \hfill & +2\lambda \parallel z_n-y_n+x^{*}-y^{*}\parallel \parallel D{z}_n-D{y}^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel .\hfill \end{array}$$

(31)

Hence,

$$\begin{array}{cc}\hfill & \parallel v_n-z_n+y^{*}-x^{*}{\parallel }^2+{\parallel z_n-y_n+x^{*}-y^{*}\parallel }^2\hfill \\ \hfill & \le \parallel x_n-x^{*}{\parallel }^2-\parallel x_{n+1}-x^{*}{\parallel }^2+{\parallel x_n-T_2^n{T}_1^n{y}_n\parallel }^2\hfill \\ \hfill & +2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel +2\rho \parallel v_n-z_n+y^{*}-x^{*}\parallel \parallel B{v}_n-B{x}^{*}\parallel \hfill \\ \hfill & +2\lambda \parallel z_n-y_n+x^{*}-y^{*}\parallel \parallel D{z}_n-D{y}^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_{n+1}-x_n\parallel (\parallel x_n-x^{*}\parallel +\parallel x_{n+1}-x^{*}\parallel )+\parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2\hfill \\ \hfill & +2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel +2\rho \parallel v_n-z_n+y^{*}-x^{*}\parallel \parallel B{v}_n-B{x}^{*}\parallel \hfill \\ \hfill & +2\lambda \parallel z_n-y_n+x^{*}-y^{*}\parallel \parallel D{z}_n-D{y}^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel .\hfill \end{array}$$

From $(B_1)$, (24), (25) and (27), we obtain

$$\begin{array}{c}\hfill \parallel v_n-z_n+y^{*}-x^{*}\parallel \to 0\mathrm{and}\parallel z_n-y_n+x^{*}-y^{*}\parallel \to 0.\end{array}$$

(32)

By (32) and

$$\begin{array}{c}\hfill \parallel v_n-y_n\parallel \le \parallel v_n-z_n+y^{*}-x^{*}\parallel +\parallel z_n-y_n+x^{*}-y^{*}\parallel ,\end{array}$$

we have ${lim}_{n\to \infty }\parallel v_n-y_n\parallel =0.$ The firm nonexpansivity of $T_r^{\Theta ,\phi }$ implies that

$$\begin{array}{cc}\hfill \parallel v_n-x^{*}{\parallel }^2=& \parallel T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)-T_{r_n}^{\Theta ,\phi }(x^{*}-r_{n}A{x}^{*}){\parallel }^2\hfill \\ \hfill \le & ⟨u_n-r_{n}A{u}_n-(x^{*}-r_{n}A{x}^{*}),v_n-x^{*}⟩\hfill \\ \hfill =& \frac{1}{2}\{\parallel u_n-r_{n}A{u}_n-(x^{*}-r_{n}A{x}^{*}){\parallel }^2+{\parallel v_n-x^{*}\parallel }^2\hfill \\ \hfill & -\parallel u_n-r_{n}A{u}_n-(x^{*}-r_{n}A{x}^{*})-(v_n-x^{*}){\parallel }^2\}\hfill \\ \hfill \le & \frac{1}{2}\{\parallel u_n-x^{*}{\parallel }^2+\parallel v_n-x^{*}{\parallel }^2-\parallel u_n-v_n-r_n(A{u}_n-A{x}^{*}){\parallel }^2\}\hfill \\ \hfill \le & \frac{1}{2}\{\parallel x_n-x^{*}{\parallel }^2+\parallel v_n-x^{*}{\parallel }^2-\parallel u_n-v_n-r_n(A{u}_n-A{x}^{*}){\parallel }^2\}\hfill \\ \hfill =& \frac{1}{2}\{\parallel x_n-x^{*}{\parallel }^2+\parallel v_n-x^{*}{\parallel }^2-{\parallel u_n-v_n\parallel }^2\hfill \\ \hfill & +2r_n⟨u_n-v_n,A{u}_n-A{x}^{*}⟩-r_n^2\parallel A{u}_n-A{x}^{*}{\parallel }^2\}.\hfill \end{array}$$

Hence,

$$\begin{array}{cc}\hfill \parallel v_n-x^{*}{\parallel }^2\le & \parallel x_n-x^{*}{\parallel }^2-{\parallel u_n-v_n\parallel }^2+2r_n⟨u_n-v_n,A{u}_n-A{x}^{*}⟩\hfill \\ \hfill & -r_n^2{\parallel A{u}_n-A{x}^{*}\parallel }^2\hfill \\ \hfill \le & \parallel x_n-x^{*}{\parallel }^2-\parallel u_n-v_n{\parallel }^2+2r_n\parallel u_n-v_n\parallel \parallel A{u}_n-A{x}^{*}\parallel .\hfill \end{array}$$

Thus, from (31), we have

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2+\parallel y_n-x^{*}{\parallel }^2+2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2+\parallel v_n-x^{*}{\parallel }^2+2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \\ \hfill & \le \parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2+2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +\parallel x_n-x^{*}{\parallel }^2-\parallel u_n-v_n{\parallel }^2+2r_n\parallel u_n-v_n\parallel \parallel A{u}_n-A{x}^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \end{array}$$

Therefore,

$$\begin{array}{cc}\hfill \parallel u_n-v_n{\parallel }^2& \le \parallel x_{n+1}-x_n\parallel (\parallel x_n-x^{*}\parallel +\parallel x_{n+1}-x^{*}\parallel )+\parallel x_n-T_2^n{T}_1^n{y}_n{\parallel }^2\hfill \\ \hfill & +2r_n\parallel u_n-v_n\parallel \parallel A{u}_n-A{x}^{*}\parallel +2\parallel x_n-T_2^n{T}_1^n{y}_n\parallel \parallel y_n-x^{*}\parallel \hfill \\ \hfill & +2{\alpha }_n\parallel \gamma V(x_n)-\mu F(x^{*})\parallel \parallel x_{n+1}-x^{*}\parallel \hfill \end{array}$$

From (24), (25) and (28), we obtain $\parallel u_n-v_n\parallel \to 0$. Then, from $\parallel v_n-y_n\parallel \to 0$, we have $\parallel u_n-y_n\parallel \to 0$. By (7), we have $\parallel u_n-y_n\parallel =t_n\parallel x_n-y_n\parallel$. Hence,

$$\begin{array}{c}\hfill \parallel x_n-y_n\parallel =\frac{\parallel u_n-y_n\parallel }{t_n}\le \frac{\parallel u_n-y_n\parallel }{b}.\end{array}$$

Therefore, $\parallel x_n-y_n\parallel \to 0$. So $\parallel x_n-v_n\parallel \to 0$. Since

$$\begin{array}{cc}\hfill \parallel v_n-T_2^n{T}_1^n{v}_n\parallel \le & \parallel T_2^n{T}_1^n{v}_n-T_2^n{T}_1^n{y}_n\parallel +\parallel x_n-T_2^n{T}_1^n{y}_n\parallel +\parallel x_n-v_n\parallel \hfill \\ \hfill \le & \parallel v_n-y_n\parallel +\parallel x_n-T_2^n{T}_1^n{y}_n\parallel +\parallel x_n-v_n\parallel ,\hfill \end{array}$$

it follows from (25), $\parallel x_n-v_n\parallel \to 0$ and $\parallel v_n-y_n\parallel \to 0$ that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel v_n-T_2^n{T}_1^n{v}_n\parallel =0.\end{array}$$

(33)

Step 4. We have the following variational inequality:

$$\underset{n\to \infty }{lim\; sup}⟨\gamma V(x^{*})-\mu F(x^{*}),x_n-x^{*}⟩\le 0,$$

(34)

where $x^{*}$ is the unique fixed point of the contraction $P_{\Gamma }(I-\mu F+\gamma V)$; namely, $x^{*}=P_{\Gamma }(I-\mu F+\gamma V)x^{*}$. Alternatively, $x^{*}$ is the unique solution of the variational inequality

$$⟨\gamma V(x^{*})-\mu F(x^{*}),y-x^{*}⟩\le 0,\forall y\in \Gamma .$$

(35)

To prove (34), take a subsequence $\left\{v_{n_i}\right\}$ of $\left\{v_n\right\}$ weakly convergent to a point $\widehat{v}\in C$ and such that

$$\begin{array}{cc}\hfill \underset{n\to \infty }{lim\; sup}⟨\gamma V(x^{*})-\mu F(x^{*}),x_n-x^{*}⟩& =\underset{n\to \infty }{lim\; sup}⟨\gamma V(x^{*})-\mu F(x^{*}),v_n-x^{*}⟩\hfill \\ \hfill & =\underset{i\to \infty }{lim}⟨\gamma V(x^{*})-\mu F(x^{*}),v_{n_i}-x^{*}⟩\hfill \\ \hfill & =⟨\gamma V(x^{*})-\mu F(x^{*}),\widehat{v}-x^{*}⟩.\hfill \end{array}$$

By virtue of VI (35), it suffices to show that $\widehat{v}\in \Gamma$. To see $\widehat{v}\in {\cap }_{n=1}^{N}Fix(T_n)$, we use $(3c)$ and the demiclosedness principle of nonexpansive mappings then ensures that $\widehat{v}\in Fix(T_2^n{T}_1^n)$. Since $\left\{s_k^i\right\}$ is bounded for $i=1,2$, we can assume that $s_{k_j}^i\to s_{\infty }^i$ as $j\to \infty$, where $0<{\epsilon }_1\le s_{\infty }^i\le {\epsilon }_2<1$ for $i=1,2$. Define $T_i^{\infty }=(1-s_{\infty }^i)I+s_{\infty }^i{T}_i$ for $i=1,2$. Therefore, $Fix(T_i^{\infty })=Fix(T_i)$ for $i=1,2$. Note that

$$\begin{array}{cc}\hfill \parallel T_i^{k_j}x-T_i^{\infty }x\parallel & =\parallel (1-s_{k_j}^i)x+s_{k_j}^i{T}_{i}x-(1-s_{\infty }^i)x-s_{\infty }^i{T}_{i}x\parallel \hfill \\ \hfill & \le |s_{k_j}^i-s_{\infty }^i|(\parallel x\parallel +\parallel T_{i}x\parallel ).\hfill \end{array}$$

Hence,

$$\begin{array}{c}\hfill \underset{x\in E}{sup}\parallel T_i^{k_j}x-T_i^{\infty }x\parallel \to 0,\end{array}$$

(36)

for $i=1,2$, where E is an arbitrary bounded subset of H. Since $Fix(T_1^{\infty })\cap Fix(T_2^{\infty })=Fix(T_1)\cap Fix(T_2)\ne \varnothing$ and $T_i^{\infty }$ is $s_{\infty }^i-$ averaged for $i=1,2$, by Lemma 5, we have $Fix(T_2^{\infty }{T}_1^{\infty })=Fix(T_1^{\infty })\cap Fix(T_2^{\infty })$. From

$$\begin{array}{cc}\hfill \parallel v_{n_j}-T_2^{\infty }{T}_1^{\infty }{v}_{n_j}\parallel & \le \parallel v_{n_j}-T_2^{n_j}{T}_1^{n_j}{v}_{n_j}\parallel +\parallel T_2^{n_j}{T}_1^{n_j}{v}_{n_j}-T_2^{\infty }{T}_1^{n_j}{v}_{n_j}\parallel \hfill \\ \hfill & +\parallel T_2^{\infty }{T}_1^{n_j}{v}_{n_j}-T_2^{\infty }{T}_1^{\infty }{v}_{n_j}\parallel \hfill \\ \hfill & \le \parallel v_{n_j}-T_2^{n_j}{T}_1^{n_j}{v}_{n_j}\parallel +\underset{v\in E^{\prime }}{sup}\parallel T_2^{n_j}v-T_2^{\infty }v\parallel \hfill \\ \hfill & +\underset{v\in E^{″}}{sup}\parallel T_1^{n_j}v-T_1^{\infty }v\parallel ,\hfill \end{array}$$

where $E^{\prime }$ is a bounded subset including $\left\{T_1^{n_j}{v}_{n_j}\right\}$ and $E^{″}$ is a bounded subset including $\left\{v_{n_j}\right\}$. By (33) and (36), we obtain ${lim}_{n\to \infty }\parallel v_{n_j}-T_2^{\infty }{T}_1^{\infty }{v}_{n_j}\parallel =0$. Therefore, from Lemma 9, we have $\widehat{v}\in Fix(T_2^{\infty }{T}_1^{\infty })$. Hence, $\widehat{v}\in {\cap }_{n=1}^{N}Fix(T_n)$. Next, we show $\widehat{v}\in \Omega$. Since $v_n=T_{r_n}^{\Theta ,\phi }(u_n-r_{n}A{u}_n)$, it follows from the definition of $T_r^{\Theta ,\phi }$ and the monotonicity of $\phi$ that

$$\Theta (v_n,y)+\phi (y)-\phi (v_n)+⟨A{u}_n,y-v_n⟩+\frac{1}{r_n}⟨y-v_n,v_n-u_n⟩\ge 0,\forall y\in C.$$

From ($A_2$), it follows that

$$\phi (y)-\phi (v_n)+⟨A{u}_n,y-v_n⟩+\frac{1}{r_n}⟨y-v_n,v_n-u_n⟩\ge \Theta (y,v_n),\forall y\in C.$$

Replacing n by $n_i$, we have

$$\phi (y)-\phi (v_{n_i})+⟨A{u}_{n_i},y-v_{n_i}⟩+\frac{1}{r_{n_i}}⟨y-v_{n_i},v_{n_i}-u_{n_i}⟩\ge \Theta (y,v_{n_i}),\forall y\in C.$$

(37)

Now, set $y_t=ty+(1-t)\widehat{v}\in C$ with $t\in (0,1)$. Then, from (37), we have

$$\begin{array}{cc}\hfill ⟨A{y}_t,y_t-v_{n_i}⟩& \ge ⟨A{y}_t,y_t-v_{n_i}⟩+\Theta (y_t,v_{n_i})-\phi (y_t)+\phi (v_{n_i})\hfill \\ \hfill & -⟨y_t-v_{n_i},\frac{v_{n_i}-u_{n_i}}{r_{n_i}}⟩-⟨A{u}_{n_i},y_t-v_{n_i}⟩\hfill \\ \hfill & =⟨A{y}_t-A{v}_{n_i},y_t-v_{n_i}⟩+⟨A{v}_{n_i}-A{u}_{n_i},y_t-u_{n_i}⟩\hfill \\ \hfill & +\Theta (y_t,v_{n_i})-\phi (y_t)+\phi (v_{n_i})\hfill \\ \hfill & -⟨y_t-v_{n_i},\frac{v_{n_i}-u_{n_i}}{r_{n_i}}⟩.\hfill \end{array}$$

(38)

From (3b), we have $\parallel A{u}_{n_i}-A{v}_{n_i}\parallel \to 0$. Moreover, by the monotonicity of A, the lower semi-continuous of $\phi$, $(A_4)$ and $(B_3)$, we obtain

$$\begin{array}{c}\hfill ⟨A{y}_t,y_t-\widehat{v}⟩\ge \Theta (y_t,\widehat{v})-\phi (y_t)+\phi (\widehat{v})\end{array}$$

as $i\to \infty$. From ($A_1$), ($A_4$), the convexity of $\phi$ and (38), we have

$$\begin{array}{cc}\hfill 0=& \Theta (y_t,y_t)-\phi (y_t)+\phi (y_t)\hfill \\ \hfill & \le t\Theta (y_t,y)+(1-t)\Theta (y_t,\widehat{v})+t\phi (y)+(1-t)\phi (\widehat{v})-\phi (y_t)\hfill \\ \hfill & =t(\Theta (y_t,y)+\phi (y)-\phi (y_t))+(1-t)(\Theta (y_t,\widehat{v})+\phi (\widehat{v})-\phi (y_t))\hfill \\ \hfill & \le t(\Theta (y_t,y)+\phi (y)-\phi (y_t))+(1-t)⟨A{y}_t,y_t-\widehat{v}⟩\hfill \\ \hfill & =t(\Theta (y_t,y)+\phi (y)-\phi (y_t))+t(1-t)⟨A{y}_t,y-\widehat{v}⟩.\hfill \end{array}$$

Thus,

$$\begin{array}{c}\hfill \Theta (y_t,y)+\phi (y)-\phi (y_t)+(1-t)⟨A{y}_t,y-\widehat{v}⟩\ge 0.\end{array}$$

Letting $t\to 0$, we have

$$\begin{array}{c}\hfill \Theta (\widehat{v},y)+\phi (y)-\phi (\widehat{v})+⟨A\widehat{v},y-\widehat{v}⟩\ge 0.\end{array}$$

Hence, $\widehat{v}\in \Omega$. Then, $\widehat{v}\in G$ remains to be solved. we know

$$\begin{array}{c}\hfill \underset{i\to \infty }{lim}\parallel v_{n_i}-G{v}_{n_i}\parallel =\underset{i\to \infty }{lim}\parallel v_{n_i}-y_{n_i}\parallel =0.\end{array}$$

From Lemma 9, we have $z\in Fix(G)$. Therefore, $z\in \Gamma$ and the proof of Step 4 is complete.

Step 5. Strong convergence: $x_n\to x^{*}$ in the norm, where $x^{*}$ satisfies (34). From Lemma 1 and (7), we have

$$\begin{array}{cc}\hfill & \parallel x_{n+1}-x^{*}{\parallel }^2\hfill \\ \hfill & \le \parallel {\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-x^{*}{\parallel }^2\hfill \\ \hfill & =\parallel [((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}]\hfill \\ \hfill & +{\beta }_n(x_n-x^{*})+{\alpha }_n(\gamma V(x_n)-\mu F(x^{*})){\parallel }^2\hfill \\ \hfill & \le (\parallel ((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{y}_n-((1-{\beta }_n)I-{\alpha }_n\mu F)T_2^n{T}_1^n{x}^{*}\parallel \hfill \\ \hfill & +{\beta }_n\parallel x_n-x^{*}{\parallel )}^2+2{\alpha }_n⟨\gamma V(x_n)-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le ({\beta }_n\parallel x_n-x^{*}\parallel +(1-{\beta }_n-{\alpha }_n\tau )\parallel y_n-x^{*}{\parallel )}^2\hfill \\ \hfill & +2{\alpha }_n\gamma ⟨V(x_n)-V(x^{*}),x_{n+1}-x^{*}⟩+2{\alpha }_n⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le ({\beta }_n\parallel x_n-x^{*}\parallel +(1-{\beta }_n-{\alpha }_n\tau )\parallel x_n-x^{*}{\parallel )}^2\hfill \\ \hfill & +2{\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel \parallel x_{n+1}-x^{*}\parallel +2{\alpha }_n⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le {(1-{\alpha }_n\tau )}^2\parallel x_n-x^{*}{\parallel }^2+2{\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel (\parallel x_{n+1}-x_n\parallel +\parallel x_n-x^{*}\parallel )\hfill \\ \hfill & +2{\alpha }_n⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le {(1-{\alpha }_n\tau )}^2\parallel x_n-x^{*}{\parallel }^2+2{\alpha }_n\gamma \kappa \parallel x_n-x^{*}{\parallel }^2+2{\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel \parallel x_n-x_{n+1}\parallel \hfill \\ \hfill & +2{\alpha }_n⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le (1-2{\alpha }_n(\tau -\gamma \kappa ))\parallel x_n-x^{*}{\parallel }^2+{\alpha }_n^2{\tau }^2{\parallel x_n-x^{*}\parallel }^2\hfill \\ \hfill & +2{\alpha }_n\gamma \kappa \parallel x_n-x^{*}\parallel \parallel x_n-x_{n+1}\parallel +2{\alpha }_n⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩\hfill \\ \hfill & \le (1-2{\alpha }_n(\tau -\gamma \kappa ))\parallel x_n-x^{*}{\parallel }^2+2{\alpha }_n(\tau -\gamma \kappa )[\frac{{\alpha }_n{\tau }^2{M}^2}{2(\tau -\gamma \kappa )}\hfill \\ \hfill & +\frac{\gamma \kappa M}{\tau -\gamma \kappa }\parallel x_n-x_{n+1}\parallel +\frac{1}{\tau -\gamma \kappa }⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩].\hfill \end{array}$$

We can rewrite the last relation as

$$\parallel x_{n+1}-x^{*}{\parallel }^2\le (1-{\tilde{\gamma }}_n){\parallel x_n-x^{*}\parallel }^2+{\tilde{\gamma }}_n{\tilde{\upsilon }}_n,$$

(39)

where ${\tilde{\gamma }}_n=2{\alpha }_n(\tau -\gamma \kappa )$ and

$${\tilde{\upsilon }}_n=\frac{{\alpha }_n{\tau }^2{M}^2}{2(\tau -\gamma \kappa )}+\frac{\gamma \kappa M}{\tau -\gamma \kappa }\parallel x_n-x_{n+1}\parallel +\frac{1}{\tau -\gamma \kappa }⟨\gamma V(x^{*})-\mu F(x^{*}),x_{n+1}-x^{*}⟩.$$

It is now immediately clear that ${\sum }_{n=1}^{\infty }{\tilde{\gamma }}_n=\infty$ and ${lim\; sup}_{n\to \infty }{\tilde{\upsilon }}_n\le 0$. This enables us to apply Lemma 11 to the relation (39) to arrive at $\parallel x_n-x^{*}\parallel \to 0$, that is, $x_n\to x^{*}$ in the norm. □

Corollary 17.

Let all the assumptions of Theorem 14 hold except $r_n=1$ for all $n\in \mathbb{N}$, $\Theta (x,y)=0$, $Ax=0$ and $\phi (x)=0$, and $\Gamma :={\cap }_{n=1}^{\infty }Fix(T_n)\cap Fix(G)$ (instead of $\Gamma :={\cap }_{n=1}^{N}Fix(T_n)\cap Fix(G)\cap \Omega$). Then, the sequence $\left\{x_n\right\}$ defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=t_n{x}_n+(1-t_n)y_n,\hfill \\ z_n=P_C(I-\rho B)u_n,\hfill \\ y_n=P_C(I-\lambda D)z_n,\hfill \\ x_{n+1}={\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)T_N^n{T}_{N-1}^n...T_1^n{y}_n,\hfill \end{array}\right.\end{array}$$

where the initial guess $x_1\in H$ is arbitrary and converges strongly to $x^{*}\in \Gamma$, where $x^{*}=P_{\Gamma }(I-\mu F+\gamma V)(x^{*})$, which solves the variational inequality (8).

Corollary 18.

Let all the assumptions of Theorem 14 hold except $s_n^i=\frac{1}{2}$ for all $i=1,2,...,N$ and $n\in \mathbb{N}$, $T_{i}x=x$ for all $i=1,2,...,N$ and $\Gamma :=Fix(G)\cap \Omega$ (instead of $\Gamma :={\cap }_{n=1}^{N}Fix(T_n)\cap Fix(G)\cap \Omega$). Then, the sequence $\left\{x_n\right\}$ is defined by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=t_n{x}_n+(1-t_n)y_n,\hfill \\ \theta (v_n,y)+\phi (y)-\phi (v_n)+⟨A{u}_n,y-v_n⟩+\frac{1}{r_n}⟨y-v_n,v_n-u_n⟩\ge 0,\forall y\in C,\hfill \\ z_n=P_C(I-\rho B)v_n,\hfill \\ y_n=P_C(I-\lambda D)z_n,\hfill \\ x_{n+1}={\alpha }_n\gamma V(x_n)+{\beta }_n{x}_n+((1-{\beta }_n)I-{\alpha }_n\mu F)y_n,\hfill \end{array}\right.\end{array}$$

where the initial guess $x_1\in H$ is arbitrary and converges strongly to $x^{*}\in \Gamma$, where $x^{*}=P_{\Gamma }(I-\mu F+\gamma V)(x^{*})$, which solves the variational inequality (8).

4. Numerical Test

In this section, first, we give a numerical example that satisfies all assumptions in Theorem 14 in order to illustrate the convergence of the sequence generated by the iterative process defined by (7). Next, we give another numerical example for (7) to compare its behavior with the iterative method (5) of Ke and Ma [29].

Example 19.

Let $C=[-100,100]\subset H=\mathbb{R}$, and define $\theta (x,y)=-7x^2+xy+6y^2$, $\phi (x)=3x$ and $Ax=2x-3$. Then, A is $\frac{1}{4}$-ism, and from Lemma 6, $T_r^{\Theta ,\phi }$ is single-valued for all $r>0$. Now, we deduce a formula for $T_r^{\Theta ,\phi }(x)$. For any $y\in [-100,100]$ and $r>0$, we have

$$\begin{array}{cc}\hfill & \theta (z,y)+\phi (y)-\phi (z)+⟨Ax,y-z⟩+\frac{1}{r}⟨y-z,z-x⟩\ge 0\hfill \\ \hfill & \iff 6y^2+yz-7z^2+3y-3z+(2x-3)(y-z)+\frac{1}{r}(y-z)(z-x)\ge 0\hfill \\ \hfill & \iff 6r{y}^2+ryz-7r{z}^2+2rxy-2rxz+yz-yx-z^2+xz\ge 0\hfill \\ \hfill & \iff 6r{y}^2+((r+1)z+(2r-1)x)y-7r{z}^2-2rxz-z^2+xz\ge 0\hfill \end{array}$$

Set $G(y)=6r{y}^2+((r+1)z+(2r-1)x)y-7r{z}^2-2rxz-z^2+xz$. Then, $G(y)$ is a quadratic function of y with coefficients $a=6r,b=(r+1)z+(2r-1)x$ and $c=-7r{z}^2-2rxz-z^2+xz$. Therefore, its discriminate $\Delta =b^2-4ac$ is

$$\begin{array}{cc}\hfill \Delta =& {[(r+1)z+(2r-1)x]}^2-24r(-7r{z}^2-2rxz-z^2+xz)\hfill \\ \hfill =& {[(2r-1)x+(13r+1)z]}^2.\hfill \end{array}$$

Since $G(y)\ge 0$ for all $y\in C$, this is true if and only if $\Delta \le 0$. That is, ${[(2r-1)x+(13r+1)z]}^2\le 0$. Therefore, $z=\frac{1-3r}{1+3r}x$, which yields $T_r^{\Theta ,\phi }(x)=\frac{1-2r}{1+13r}x$. Therefore, from Lemma 6, we have $\Omega =\left\{0\right\}$. Let ${\alpha }_n=\frac{1}{4n},{\beta }_n=\frac{n-1}{2n}$, $t_n=\frac{1}{3}$, $s_n^i=\frac{1}{2}$, $r_n=\frac{n-1}{6n}$ and $T_{i}x=\frac{x}{i}$ for $i=1,2,...,N$. Suppose $V(x)=\frac{1}{4}x$, $Bx=\frac{1}{6}x$, $Dx=\frac{1}{3}x$ and $Fx=\frac{1}{10}x$. Hence, B is $3-$ism, D is $2-$ism, F is $\frac{1}{2}$-Lipschitzian and $\frac{1}{5}-$ism, and V is $\frac{1}{4}$-Lipschitzian. Let $\gamma =\frac{1}{5}$, $\rho =4$, $\lambda =2$ and $\mu =1$. Hence, $\Gamma =\left\{0\right\}$. Then, from Theorem 14, the sequence $\left\{x_n\right\}$, generated iteratively by

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=\frac{171n-117}{505n-355}{x}_n,\hfill \\ v_n=\frac{4n+2}{19n-13}{u}_n,\hfill \\ z_n=\frac{4n+2}{57n-39}{u}_n,\hfill \\ y_n=\frac{4n+2}{171n-117}{u}_n,\hfill \\ x_{n+1}=(\frac{1}{80n}+\frac{n-1}{2n}+\frac{80n^2+116n+38}{2020n^2-1420n}\frac{N+1}{2^N})x_n,\hfill \end{array}\right.\end{array}$$

(40)

converges strongly to $0\in \Gamma$, where $0=P_{\Gamma }(\frac{19x}{20})(0)$.

Now, we compare the effectiveness of our algorithm with the algorithm (5) by a numerical example. In fact, Ke and Ma [29] proved the following strong convergence theorem.

Theorem 20.

Let C be a closed convex subset of H, T be a nonexpansive self-mappings on C with $Fix(T)\ne \varnothing$ and f be a κ-contraction on C for some $\kappa \in [0,1)$. Pick any $x_1\in H$; let $\left\{x_n\right\}$ be a sequence generated by (5), where $\left\{{\alpha }_n\right\}$ and $\left\{t_n\right\}$ are real sequences satisfying the following conditions:

($B_1$)

$\left\{{\alpha }_n\right\}\subset (0,1)$, ${lim}_{n\to \infty }{\alpha }_n=0$, ${\sum }_{n=1}^{\infty }|{\alpha }_{n+1}-{\alpha }_n|<\infty$ and ${\sum }_{n=1}^{\infty }{\alpha }_n=\infty$;

($B_2$)

$0<\epsilon \le t_n\le t_{n+1}<1$.

Then, the sequence $\left\{x_n\right\}$ converges strongly to $x^{*}\in Fix(T)$, which solves the variational inequality:

$$⟨(I-f)x^{*},x^{*}-x⟩\le 0forallx\in Fix(T).$$

Example 21.

Let all the assumptions of Example 19 hold except the mappings $T_{i}x=Tx=x$ for all $i=1,2,...,N$ and $C=[-20,20]$. First, suppose the sequence $\left\{x_n\right\}$ be generated by (7). Then, the scheme (7) can be simplified as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=\frac{171n-117}{505n-355}{x}_n,\hfill \\ v_n=\frac{4n+2}{19n-13}{u}_n,\hfill \\ z_n=\frac{4n+2}{57n-39}{u}_n,\hfill \\ y_n=\frac{4n+2}{171n-117}{u}_n,\hfill \\ x_{n+1}=(\frac{1}{80n}+\frac{n-1}{2n}+\frac{80n^2+116n+38}{2020n^2-1420n})x_n,\hfill \end{array}\right.\end{array}$$

(41)

Therefore, the sequence $\left\{x_n\right\}$ converges strongly to 0 by Theorem 14. Now, let the sequence $\left\{x_n\right\}$ be generated by (5). Then, the scheme (5) can be simplified as

$$\begin{array}{c}\hfill x_{n+1}=\frac{1}{16n}{x}_n+(1-\frac{1}{4n})(\frac{1}{3}{x}_n+\frac{2}{3}{x}_{n+1}).\end{array}$$

(42)

Therefore, the sequence $\left\{x_n\right\}$ converges strongly to 0 by Theorem 20.

Next, the numerical comparison of algorithms (41) and (42) is provided.

According to the Table 1 and the Figure 1, we see that, although the initial points are different ($x_1=-98$ and $x_1=100$), in both cases, the sequence $\left\{x_n\right\}$ defined by (40) converges to 0 where $N=3$ and $n=30$.

Table 1. The values of the sequence $\{\parallel x_n\parallel \}$ for Algorithm (40).

n	$\parallel {\mathit{x}}_{\mathit{n}}-0\parallel$	$\parallel {\mathit{x}}_{\mathit{n}}-0\parallel$
1	−98	100
2	2.891	6.95
3	0.048973	0.2281
4	0.00020433	0.0011181
5	$6.8356\times {10}^{-7}$	$3.7446\times {10}^{-6}$
6	$2.0617\times {10}^{-9}$	$1.1294\times {10}^{-8}$
⋮	⋮	⋮
25	$2.1386\times {10}^{-59}$	$1.1716\times {10}^{-58}$
26	$4.6134\times {10}^{-62}$	$2.5273\times {10}^{-61}$
27	$9.9195\times {10}^{-65}$	$5.4341\times {10}^{-64}$
28	$2.1264\times {10}^{-67}$	$1.1649\times {10}^{-66}$
29	$4.5454\times {10}^{-70}$	$2.49\times {10}^{-69}$
30	$9.6908\times {10}^{-73}$	$5.3088\times {10}^{-72}$

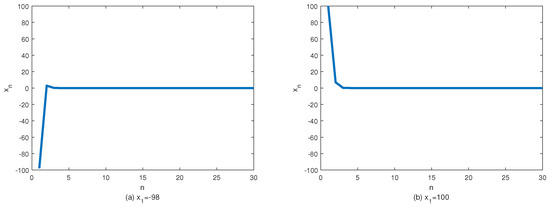
Figure 1. The convergence of $\left\{x_n\right\}$ with different initial values $x_1$.

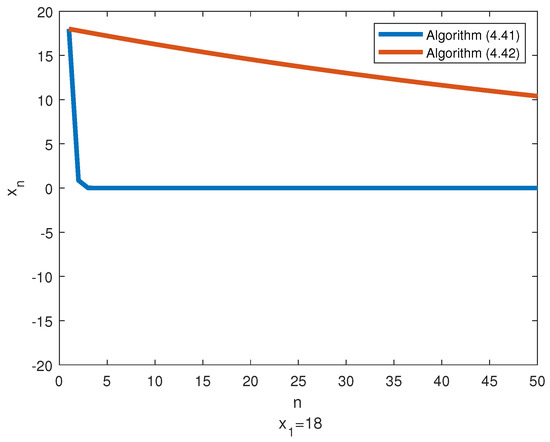
Table 2 and Figure 2 indicate that the sequence $\left\{x_n\right\}$ generated by (41) and (42) converges to 0 where $x_1=18$ and $n=50$. The efficiency of algorithm (42) in comparison with Algorithm (41) clearly appeared in this figure.

Table 2. Comparison between Algorithm (41) and Algorithm (42).

n	$\parallel {\mathit{x}}_{\mathit{n}}-0\parallel$ for (41)	$\parallel {\mathit{x}}_{\mathit{n}}-0\parallel$ for (42)
1	18	18
2	0.864	17.8
3	0.012649	17.601
4	0.00010115	17.405
5	$6.7666\times {10}^{-7}$	17.211
⋮	⋮	⋮
46	$2.9855\times {10}^{-103}$	$10.873$
47	$1.2388\times {10}^{-105}$	$10.752$
48	$5.1356\times {10}^{-108}$	$10.633$
49	$2.1269\times {10}^{-110}$	$10.514$
50	$8.8005\times {10}^{-113}$	$10.397$

Figure 2. Comparison between Algorithm (41) and Algorithm (42).

Remark 22.

Table 2 and Figure 2 show that the convergent rate of iterative algorithm (7) is faster than that of the iterative algorithm (5) of Ke and Ma. In fact, regarding to Table 2 and Figure 2, we consider that Algorithm (41) approaches 0 from the third term onwards, but Algorithm (42) does not approach 0 even until the fiftieth term.

5. Conclusions

We introduce a new composite iterative algorithm for finding a common element of the set of solutions of a general system of variational inequalities, a generalized mixed equilibrium problem and the set of common fixed points of a finite family of nonexpansive mappings in Hilbert spaces. Then, we prove that the sequence generated by the algorithm converges strongly to a common element of solution sets for these problems. Moreover, we deduce some consequences from our main result. Eventually, we provide a numerical example to illustrate the justification of the main result and another one to compare our algorithm with Algorithm (5), which shows that the convergent rate of our iterative algorithm is faster than that of the iterative algorithm (5) of Ke and Ma.