The Novelty of Thermo-Diffusion and Diffusion-Thermo, Slip, Temperature and Concentration Boundary Conditions on Magneto–Chemically Reactive Fluid Flow Past a Vertical Plate with Radiation

Abstract

The significance of radiation, Soret and Dufour’s effects on MHD flow in a porous media near a stagnation point past a vertical plate with slip, temperature, and concentration boundary conditions were investigated. Local similarity variables are used in the solution, which reduces the PDEs into analogous boundary value problem for ODEs. Symmetry analysis can be used to detect these variations in local similarity. To numerically explain the problem, a shooting approach and the MATLAB bvp4c solver are utilized. As the magnetic field and porous medium parameters are raised, the skin friction increases, and the temperature increases as the radiation pointer is increased. As the Soret number grows, the concentration profile rises.

1. Introduction

Fluid flow in porous media is essential in various applications, including drying, fuel cell technologies, and material processing. Heat and mass transfer flow of fluids in the presence of a porous medium and magnetic field is an efficient strategy for increasing thermal performance. Ferdows et al. [1], Yirga and Tesfay [2] examined the MHD flow in a porous medium across a stretching sheet. Ullah et al. [3] studied the impact of Newtonian heating on the MHD Casson fluid through a porous medium with a velocity slip parameter. Khan et al. [4] used an analytical solution to investigate heat transfer and thin film flow of a second-grade fluid in a porous media over a stretched sheet. Cortell [5] explored the mass transfer and MHD flow of chemical species in a second-grade electrically conducting fluid across a stretched sheet through a porous medium. Malarselvi et al. [6] pioneered examining the effect of convective heating and slip on the MHD flow of chemically reacting fluid in a porous medium. Heat diffusion and radiation effects on hydro-magnetic convection flow through a porous medium of a fluid past a uniformly moving plate were explored by Seth et al. [7]. Ellahi et al. [8] explored the effects of magnetohydrodynamics and porosity factors on the Jeffrey fluid flow embedded in a porous medium. Sivasankaran et al. [9] tested the influence of chemical reaction, slip, and Newtonian heating on MHD flow with convective boundary conditions embedded in a porous medium. Abbas et al. [10] used the Darcy–Forchheimer relation to investigate heat and mass transport in a third-grade fluid over an exponentially extending surface in a porous medium.

Both the Dufour and Soret effects are important in oceanography, geosciences, air pollution, and chemical engineering. Rasool et al. [11] studied the effect of constant incompressible Darcy flow on Soret–Dufour, chemical reactions, and thermal radiation effects. They noticed that raising the Soret parameter causes the concentration distribution to widen significantly. Ameer Ahamad et al. [12] investigated the Dufour effect on the rotating MHD flow across a semi-vertical infinite moving plate with radiation absorption. Ahammad and Krishna [13] deliberated the numerical investigation of Soret and Dufour effects on convective MHD gyrating flow through a porous vertical channel. Several researchers examined the influence of Soret and Dufour’s effects through a porous medium over a stretching sheet; refer to [14,15,16,17,18,19,20,21,22,23]. The majority of flow problems involving moving surfaces in nature are caused by buoyancy and the effects of boundary movement caused by concentration and thermal convections. Fan-cooled electronic equipment, cooling of nuclear reactors during an emergency shutdown and so on are practical examples of such flows. Khan et al. [24] analyzed the performance of convective boundary conditions on Williamson fluid flow across a linear porous stretched surface with thermal radiation. Ullah et al. [25] studied the effects of convective boundary conditions on mixed convection flow of MHD Casson fluid in a porous medium with radiation. Krishna et al. [26] reported the radiative incompressible MHD flow of electrically conducting Casson fluid over a vertically moving porous surface. Lakshmi Devi et al. [27] studied the combined effect of activation energy, thermal radiation, and chemical reaction on induced MHD fluid flow over a vertical stretching surface. Krishna et al. [28] examined the radiation absorption effect on convective MHD flow of nanofluids over a vertically moving porous surface. The impacts of radiation, Soret, and Dufour on MHD flow of non-Newtonian Jerry fluid with convective boundary conditions were investigated (see Refs. [29,30,31,32,33]).

The primary goal of this research is to examine the radiation, thermo-diffusion (Soret), and diffusion-thermo (Dufour) effects on the MHD flow near a stagnation point on a vertical plate in a porous medium with slip, temperature, and concentration boundary conditions. The PDEs are turned into non-linear ODEs using similarity transformations in the solution approach. To solve the modified ODEs, the shooting method and MATLAB bvp4c were employed. The various profiles for different flow parameter values were shown in figures. The current analysis’ numerical results were compared to earlier results and determined to be in good agreement.

2. Mathematical Model

Consider an incompressible electrically conducting fluid flowing steadily over a stretching sheet in a porous medium. Figure 1 shows the fluid model and the coordinate system.

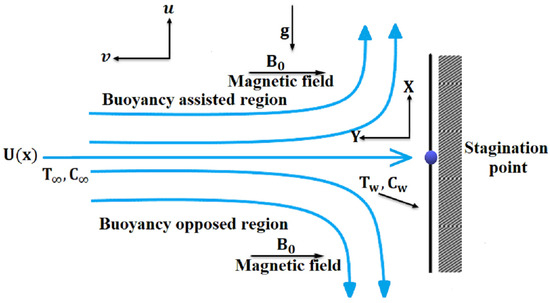
Figure 1. Model of a flow with a coordinate system.

In this study

$$u_x+v_y=0$$

(1)

$$u{u}_x+v{u}_y=\nu u_{yy}+g\left(T-T_{\infty }\right)\beta +g\left(C-C_{\infty }\right){\beta }^{*}-\left(\frac{\nu }{\tilde{K}}+\frac{{\sigma }_e{B}_0^2}{\rho }\right)\left(u-U_{\infty }\right)+U_{\infty }{\left(U_{\infty }\right)}_x$$

(2)

$$u{T}_x+v{T}_y=\alpha T_{yy}-\frac{\alpha }{k}{\left(q_r\right)}_y+Q\left(T-T_{\infty }\right)+\frac{D_m{K}_T}{c_s{c}_p}{C}_{yy}$$

(3)

$$u{C}_x+v{C}_y=D{C}_{yy}-{\mathsf{\Gamma }}_0\left(C-C_{\infty }\right)+\frac{D_m{K}_T}{T_m}{T}_{yy}$$

(4)

Subject to the boundary conditions

$$N_1{u}_y=u,v=0,h_f\left(T_f-T\right)=-k{T}_y,h_m\left(C_f-C\right)=-D{C}_{y}aty=0$$

(5)

$$u=cx,C\to C_{\infty },T\to T_{\infty }asy\to \infty$$

(6)

where u and v represent velocity components along the x and y axes, respectively, and T signifies the temperature of the fluid. The following formula is used to compute the radiant heat flux:

$$q_r=-\frac{4{\sigma }^{*}}{3K^{\prime }}{T}_y^4$$

(7)

Because temperature differences inside the flow are too small, the Rosseland approximation can be written as $T^4$ (linear function of temperature) around the free stream temperature $\left(T_{\infty }\right)$ making use of Taylor series.

$$\mathrm{i}.\mathrm{e}.,T^4\approx 4T_{\infty }^3-3T_{\infty }^4\mathrm{Then}\mathrm{we}\mathrm{get}$$

$$q_r=-\frac{16{\sigma }^{*}{T}_{\infty }^3}{3K^{\prime }}{T}_y$$

(8)

For temperature, Equation (2) is replaced in (3). The following dimensionless variables are presented:

$$\begin{array}{c}\hfill \begin{array}{c}\eta =y\sqrt{\frac{c}{\nu }},\psi \left(x,y\right)=\sqrt{c\nu }xf\left(\eta \right),b=N_1{\left(\frac{c}{\nu }\right)}^{1/2},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{C-C_{\infty }}{C_w-C_{\infty }},\\ G{r}_T=\frac{g\beta \left(T_w-T_{\infty }\right)x^3}{{\nu }^2},G{r}_C=\frac{g{\beta }^{*}\left(C_w-C_{\infty }\right)x^3}{{\nu }^2},R{i}_T=\frac{G{r}_T}{{Re}_x^2},R{i}_C=\frac{G{r}_C}{{Re}_x^2},{Re}_x=\frac{U_{\infty }x}{\nu }\\ Rd=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k{K}^{\prime }},Cr=\frac{{\mathsf{\Gamma }}_0}{c},D_f=\frac{D_m{K}_T\left(C_w-C_{\infty }\right)}{c_s{c}_p\left(T_w-T_{\infty }\right)\alpha },K=\frac{\nu }{c\tilde{K}},S=\frac{Q\nu }{\alpha c}=Pr\frac{Q}{c}\\ Sc=\frac{\nu }{D},M=\frac{{\sigma }_e{B}_0^2}{c\rho },Sr=\frac{D_m{K}_T\left(T_w-T_{\infty }\right)}{T_m\alpha \left(C_w-C_{\infty }\right)},B{i}_T=\frac{h_f{\left(\frac{\nu }{c}\right)}^{\frac{1}{2}}}{k},B{i}_C=\frac{h_m{\left(\frac{\nu }{c}\right)}^{\frac{1}{2}}}{D}\end{array}\end{array}$$

(9)

Equation (1) is satisfied identically. In Equations (1)–(6), Equation (8) is employed, and the nonlinear ODEs and accompanying boundary conditions are as follows:

$$f^{‴}+f{f}^{″}-{f^{\prime }}^2+R{i}_T\theta +R{i}_C\varphi -\left(K+M\right)\left(f^{\prime }-1\right)+1=0$$

(10)

$$\left(1+(4/3)Rd\right){\theta }^{″}+S\theta +fPr{\theta }^{\prime }+D_f{\varphi }^{″}=0$$

(11)

$${\varphi }^{″}+fSc{\varphi }^{\prime }+\frac{ScSr}{Pr}{\theta }^{″}-CrSc\varphi =0$$

(12)

$$f=0,f^{\prime }=f^{″}\left(0\right)b,{\theta }^{\prime }=-B{i}_T\left[1-\theta \left(0\right)\right],{\varphi }^{\prime }=-B{i}_C\left[1-\varphi \left(0\right)\right]at\eta =0$$

(13)

$$f^{\prime }=1,\theta =0,\varphi =0as\eta \to \infty$$

(14)

The physical engineering parameters are the skinfriction coefficient $\left(C_f\right)$, local Nusselt number $\left(N{u}_x\right)$, and local Sherwood number $\left(S{h}_x\right)$, which are defined as follows:

$$C_f=\frac{{\tau }_w}{\rho U_{\infty }^2},N{u}_x=\frac{x{q}_w}{k\left(T_w-T_{\infty }\right)},S{h}_x=\frac{x{q}_s}{D\left(C_w-C_{\infty }\right)}$$

(15)

where (${\tau }_w$ = wall sher stress, $q_w$ = surface heat flux, $q_m$ = surface mass flux) are well-defined as follows:

$${\tau }_w=\mu {\left[\frac{\partial u}{\partial y}\right]}_{y=0},q_w=-k{\left[\frac{\partial T}{\partial y}\right]}_{y=0},q_m=-D{\left[\frac{\partial C}{\partial y}\right]}_{y=0}$$

The non-dimensional form of physical engineering parameters is obtained as follows:

$$C_{f}R{e}_x^{1/2}=f^{″}\left(0\right),N{u}_{x}R{e}_x^{-1/2}=-{\theta }^{\prime }\left(0\right),S{h}_{x}R{e}_x^{-/2}=-{\varphi }^{\prime }\left(0\right)$$

(16)

3. Numerical Method

The shooting approach is used in conjunction with MATLAB bvp4c to solve non-linear governing ordinary differential Equations (10)–(12) with boundary conditions (13) and (14). We made first-order differential equations out of the non-linear governing ordinary differential equations. For this, we considered the following:

$$y_1=f,y_2=f^{\prime },y_3=f^{″},y_4=\theta ,y_5={\theta }^{\prime },y_6=\varphi ,y_7={\varphi }^{\prime }$$

(17)

The non-linear governing ordinary differential Equations (10)–(12) are now turned into first-order differential equations using Equation (17):

$$f^{‴}=-y_1{y}_3+y_2^2-R{i}_T{y}_4-R{i}_C{y}_6+\left(K+M\right)\left(y_2-1\right)-1$$

(18)

$${\theta }^{″}=\left[\frac{1}{\left[\left(1+4/3Rd\right)-1/Pr\left(D_{f}SrSc\right)\right]}\right]\left\{D_{f}Sc{y}_1{y}_7-D_{f}ScCr{y}_6-Pr{y}_1{y}_5-S{y}_4\right\}$$

(19)

$${\varphi }^{″}=-Sc{y}_1{y}_7+ScCr{y}_6-\frac{SrSc}{Pr}\left\{\left[\frac{1}{\left[\left(1+4/3Rd\right)-1/Pr\left(D_{f}SrSc\right)\right]}\right]\left\{D_{f}Sc{y}_1{y}_7-D_{f}ScCr{y}_6-Pr{y}_1{y}_5-S{y}_4\right\}\right\}$$

(20)

The boundary conditions Equation (13)–(14) becomes as follows:

$$y_1\left(0\right)=0,y_2\left(0\right)=b{y}_3\left(0\right),y_5\left(0\right)=-B{i}_T\left[1-y_4\left(0\right)\right],y_7\left(0\right)=-B{i}_C\left[1-y_6\left(0\right)\right]at\eta =0$$

(21)

$$y_2\left(\infty \right)=1,y_4\left(\infty \right)=0,y_6\left(\infty \right)=0as\eta \to \infty$$

(22)

In MATLAB bvp4c software, the translated first-order differential Equations (18)–(20) and boundary conditions (21) and (22) are utilized to investigate the influence of different dimensionless variables on sequential profiles.

4. Results and Discussion

The impact of radiation, Soret and Dufour’s effects on MHD flow in a porous media near a stagnation point past a vertical plate with slip, temperature, and concentration boundary conditions were considered. The employment of proper similarity parameters converts non-linear controlling PDEs to non-linear ODEs. Shooting method and MATLAB bvp4c are used to solve the modified ODEs. Various profiles are used to examine the impact of dimensionless characteristics. The numerical values of $f^{″}\left(0\right)$, $-{\theta }^{\prime }\left(0\right)$, and $-{\varphi }^{\prime }\left(0\right)$ are computed and displayed in Table 1. We compared our findings to those of Makinde [34], and they were strikingly similar. Table 2 shows the $f^{″}\left(0\right)$ for distinct porosity $\left(K\right)$ values when $Pr=0.7,R{i}_T=R{i}_C=M=Rd=S=D_f=Sc=Sr=Cr=b=B{i}_T=B{i}_C=0$. As the porosity parameter is increased, skin friction increases. Table 3 shows the $f^{″}\left(0\right)$, $-{\theta }^{\prime }\left(0\right)$, and $-{\varphi }^{\prime }\left(0\right)$ for distinct values of b, $B{i}_T$, and $B{i}_C$ when $R{i}_T=R{i}_C=S=1$, $K=0.2,M=0.3,Pr=0.7,Rd=D_f=Sc=Sr=Cr=0.5$. The $f^{″}\left(0\right)$ and $-{\varphi }^{\prime }\left(0\right)$ drop as the velocity slip parameter $\left(b\right)$ and the thermal Biot number $\left(B{i}_T\right)$ grow, whereas the $-{\theta }^{\prime }\left(0\right)$ increases. The $f^{″}\left(0\right)$ and $-{\varphi }^{\prime }\left(0\right)$ rise as the concentration Biot number $\left(B{i}_C\right)$ rises, whereas the $-{\theta }^{\prime }\left(0\right)$ falls.

Table 1. For varying values of S, $f^{″}\left(0\right)$ is compared to Makinde [34] when $R{i}_T=Pr=1$, $R{i}_C=Sc=0.5$, $Rd=K=M=D_f=Sr=Cr=b=0$, $B{i}_T=B{i}_C={10}^{10}$.

S	Makinde [34] ${\mathit{f}}^{″}\left(0\right)$	Present Study ${\mathit{f}}^{″}\left(0\right)$	Makinde [34] $-{\mathit{\theta }}^{\prime }\left(0\right)$	Present Study $-{\mathit{\theta }}^{\prime }\left(0\right)$	Makinde [34] $-{\mathit{\varphi }}^{\prime }\left(0\right)$	Present Study $-{\mathit{\varphi }}^{\prime }\left(0\right)$
0	1.9995	1.9995	0.6932	0.6393	0.4789	0.4789
1	2.1342	2.1719	−0.0730	−0.2463	0.4917	0.4950

Table 2. For distinct values of K, $f^{″}\left(0\right)$ when $Pr=0.7,R{i}_T=R{i}_C=M=Rd=S=D_f=Sc=Sr=Cr=b=B{i}_T=B{i}_C=0$.

K	${\mathit{f}}^{″}\left(0\right)$
0.0	1.232588
0.5	1.419763
1.0	1.585331
1.5	1.735361
2.0	1.873527

Table 3. Numerical values of $f^{″}\left(0\right)$, $-{\theta }^{\prime }\left(0\right)$, and $-{\varphi }^{\prime }\left(0\right)$ for distinct values of b, $B{i}_T$, and $B{i}_C$ when $R{i}_T=R{i}_C=S=1,K=0.2,M=0.3,Pr=0.7,Rd=D_f=Sc=Sr=Cr=0.5$.

b	${\mathit{Bi}}_{\mathit{T}}$	${\mathit{Bi}}_{\mathit{C}}$	${\mathit{f}}^{″}\left(0\right)$	$-{\mathit{\theta }}^{\prime }\left(0\right)$	$-{\mathit{\varphi }}^{\prime }\left(0\right)$
0.5	1.0	1.0	1.556363	−0.560229	0.472827
1.0			1.037464	−0.482620	0.462411
1.5			0.775455	−0.448161	0.458227
2.0			0.618498	−0.428815	0.456007
0.5	1.0	1.0	1.556363	−0.560229	0.472827
	2.0		1.484332	−0.560190	0.456163
	3.0		1.459595	−0.557169	0.449791
	4.0		1.447192	−0.555056	0.446464
0.5	1.0	1.0	1.556363	−0.560229	0.472827
		2.0	1.609949	−0.593423	0.570065
		3.0	1.632601	−0.607625	0.612868
		4.0	1.645140	−0.615530	0.636996

Figure 2 shows how thermal radiation $\left(Rd\right)$ affects the temperature $\left(\theta \left(\eta \right)\right)$ profile. As the value of $Rd$ increases, the $\theta \left(\eta \right)$ rises. In this situation, greater radiation reduces the mean absorption coefficient, causing the radiative heat flux to diverge. The rate of radiative heat transfer to the fluid will be boosted as a result. The $\theta \left(\eta \right)$ rose as a result of this. The link between fluid velocity $\left(f^{\prime }\left(\eta \right)\right)$ and the porosity parameter $\left(K\right)$ is depicted in Figure 3. By raising the porosity parameter, the holes of the porosity medium enlarge. Due to this, kinematic viscosity rises and a resistive force acts in the opposite direction of the flow, causing a decrease in velocity profile. The influence of the Dufour $\left(D_f\right)$ effect on $\theta \left(\eta \right)$ is depicted in Figure 4. The term Dufour describes the impact of concentration gradients, which is important in facilitating the fluid flow and has a propensity to rise the thermal energy within the boundary layer. As a result, the $\theta \left(\eta \right)$ increased. The effect of the Soret number $\left(Sr\right)$ on the concentration $\left(\varphi \left(\eta \right)\right)$ profile is seen in Figure 5. We discovered that as the $Sr$ is increased, the $\varphi \left(\eta \right)$ rises. The temperature gradient in the Soret phenomena affected the concentration distribution. So the Soret numbers with larger values produce greater convective flow, which raises concentration.

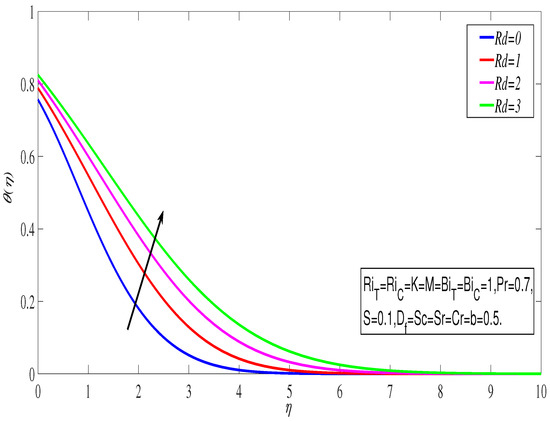
Figure 2. Temperature profile with $Rd$.

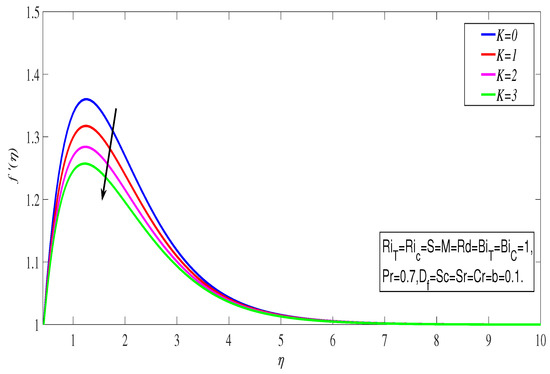
Figure 3. Velocity profile with K.

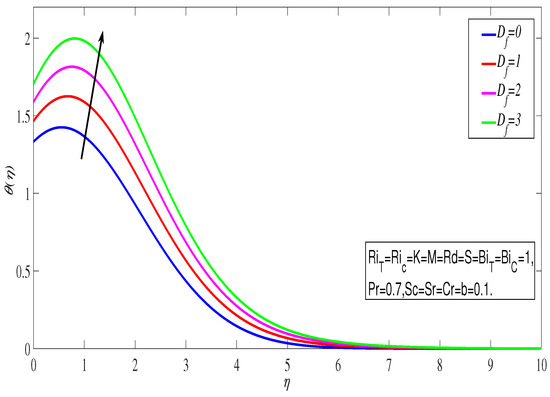
Figure 4. Temperature profile with $D_f$.

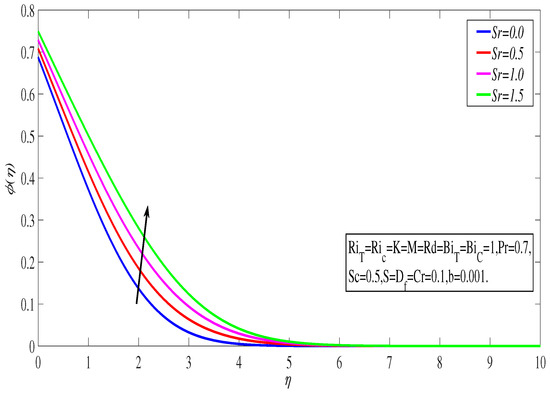
Figure 5. Concentration profile with $Sr$.

Figure 6 shows the $f^{\prime }\left(\eta \right)$ increasing when the slip parameter $\left(b\right)$ was raised. The boundary layer thickness in the viscous zone decreases when the slip parameter is increased. Thus, the slip parameter rises with any value of $\eta$ in the presence of heat radiation. Hence the fluid velocity increases throughout the boundary layer. Figure 7 illustrates the impact of the thermal Biot number $\left(B{i}_T\right)$ on $\theta \left(\eta \right)$. The effect is very clear and promising within $0\le \eta \le 4$. The parametric categorization $B{i}_T=\frac{h_f}{k}\sqrt{\frac{\nu }{c}}$ assures the amplification of $\nu$; hence, the resistance provided by $\nu$ creates some frictional heat together with sheet and fluid, which in turn supplies the required amplification in temperature. An alternative approach can show this fact with greater veracity. We are aware that $h_f=\frac{q}{\Delta T}$, where q stands for the total amount of heat transferred and $\Delta T$ is the temperature difference. The necessary thermal resistance is determined by R-value, which is $R=\frac{\Delta T}{\dot{q_A}}$ where $\dot{q_A}$ represents the heat flux. Thus, $h_f=\frac{q}{R.\dot{q_A}}$. This investigates the inverse relationship between R and $h_f$. Therefore, as $B{i}_T$ rises, $h_f$ rises as well, and thermal resistance falls, it is possible to raise the fluid temperature through the stretching surface by convection. The impact of the concentration Biot number $(B{i}_C$ ) on $\varphi \left(\eta \right)$ is seen in Figure 8. In general, the mass transfer coefficient rises as the $B{i}_C$ rises. The $\varphi \left(\eta \right)$ increased as a result of this.

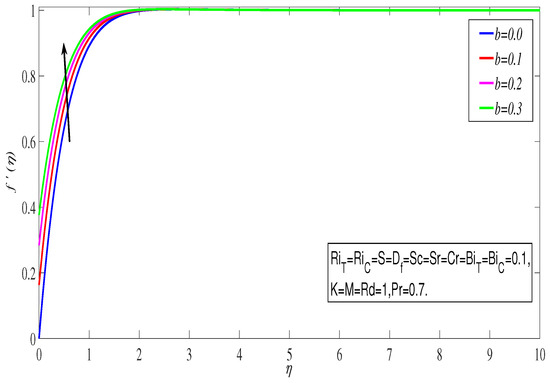
Figure 6. Velocity profile with b.

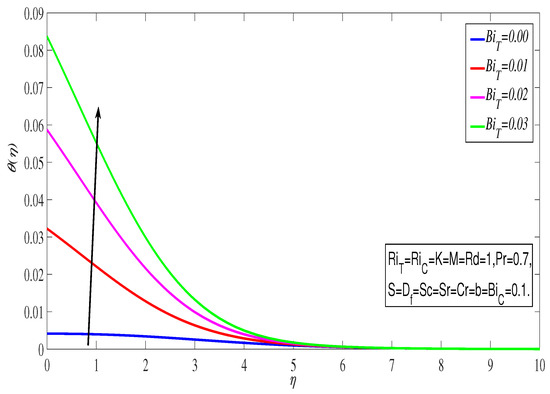
Figure 7. Temperature profile with $B{i}_T$.

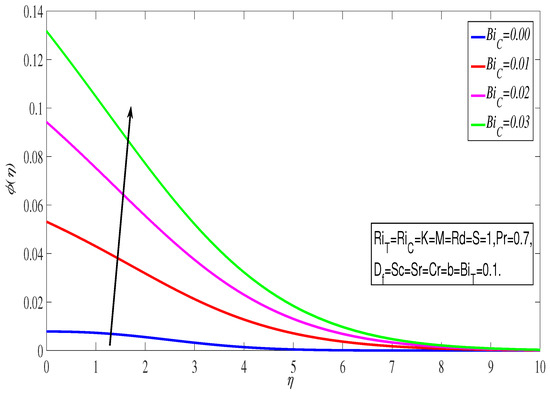
Figure 8. Concentration profile with $B{i}_C$.

Figure 9 shows how skin friction $\left(f^{″}\left(0\right)\right)$ is affected by both porosity $\left(K\right)$ and magnetic field $\left(M\right)$ factors. We found that as the K and M parameters were raised, the $f^{″}\left(0\right)$ increased. Figure 10 illustrates the effect of the b and the $D_f$ on the local Nusselt number $\left(-{\theta }^{\prime }\left(0\right)\right)$. In this case, the b raised the $-{\theta }^{\prime }\left(0\right)$ whereas the $D_f$ reduced it.

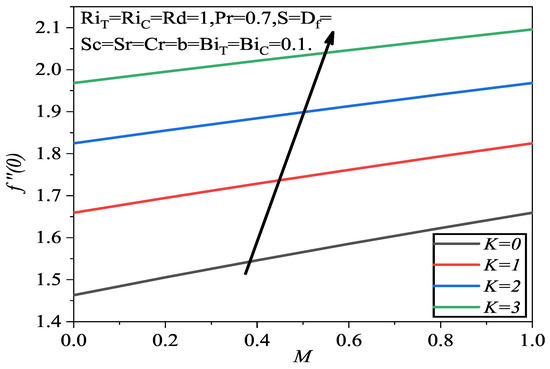
Figure 9. Skin friction with K and M.

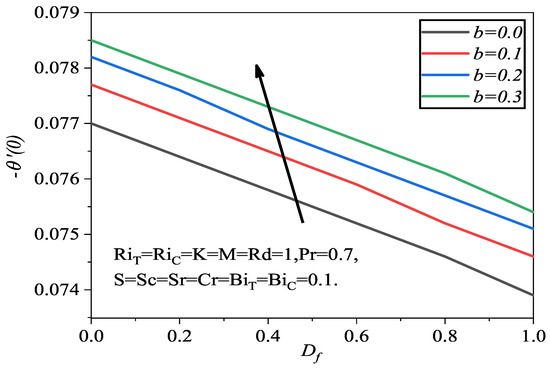
Figure 10. Local Nusselt number with b and $D_f$.

5. Conclusions

Radiation, thermo-diffusion (Soret), and diffusion-thermo (Dufour) effects on the MHD flow near a stagnation point on a vertical plate in a porous medium with slip, temperature, and concentration boundary conditions were explored. The employment of proper similarity parameters converts non-linear controlling PDEs to non-linear ODEs. Shooting method and MATLAB bvp4c are used to solve the modified ODEs. Various profiles are used to examine the impact of dimensionless characteristics. The following are the study’s main findings: The fluid temperature increases as the radiation parameter increases. The thermal state of fluid is enhanced with Dufour effect. The Soret numbers with larger values produce greater convective flow, which raises concentration. Increasing the thermal Biot number increases the heat transfer coefficient. The temperature increased as a result. The fluid concentration increased as a result of the concentration Biot number. The local Nusselt number raised with slip parameter but diminished with Dufour effect.