An Ensemble Framework to Forest Optimization Based Reduct Searching

Abstract

Essentially, the solution to an attribute reduction problem can be viewed as a reduct searching process. Currently, among various searching strategies, meta-heuristic searching has received extensive attention. As a new emerging meta-heuristic approach, the forest optimization algorithm (FOA) is introduced to the problem solving of attribute reduction in this study. To further improve the classification performance of selected attributes in reduct, an ensemble framework is also developed: firstly, multiple reducts are obtained by FOA and data perturbation, and the structure of those multiple reducts is symmetrical, which indicates that no order exists among those reducts; secondly, multiple reducts are used to execute voting classification over testing samples. Finally, comprehensive experiments on over 20 UCI datasets clearly validated the effectiveness of our framework: it is not only beneficial to output reducts with superior classification accuracies and classification stabilities but also suitable for data pre-processing with noise. This improvement work we have performed makes the FOA obtain better benefits in the data processing of life, health, medical and other fields.

1. Introduction

In the era of big data, with rapid growth in the amount of data, a high dimension of data is a representative characteristic. Nevertheless, it is well-known that not all features in data are useful for providing valuable learning ability [1,2,3]. That is why feature selection has been validated to be one of the crucial data pre-processing techniques in the fields of machine learning, knowledge discovery and so on.

Attribute reduction, from the perspective of rough set, is one state-of-the-art feature selection technique [4,5,6]. One of the important advantages of attribute reduction is that it possesses rich semantic explanations based on various measures related to rough set. For instance, a reduct can be regarded as one minimal subset of attributes that satisfies the pre-defined constraint constructed by using measures such as dependency, conditional entropy, conditional discrimination index and so on [7,8].

Without a loss in generality, the problem solving of attribute reduction can be considered as a searching optimization procedure. Up to now, with respect to different requirements, many approaches have been reported [9].

With a careful review of the previous literature, most searching methods can be categorized into the following two groups. They are exhaustive searching [10] and heuristic searching [11,12].

• Exhaustive searching. The fundamental advantage of exhaustive searching is that such a process can seek out all qualified reducts. Nevertheless, the apparent limitation of such a search is the unacceptable complexity. For example, the discernibility matrix [13,14] and backtracking [15] are two representative mechanisms of exhaustive searching. Though some simplified and pruning modes have been proposed to improve the efficiency of those exhaustive searchings; they still face a big challenge in the dimension reduction in large-scale data.
• Heuristic searching. Different from complete searching, heuristic searching can only be used to acquire one and only one reduct for one round of execution. The dominating superiority of heuristic searching is the low complexity due to the guidance of heuristic information for the whole process of searching. Take the forward greedy searching [16,17,18] as an example, the variation of used measures in the definition of attribute reduction is the heuristic searching; such a variation can be employed to identify the importance of candidate attributes.

Since heuristic searching is superior to exhaustive searching in most cases, the former has been widely accepted by many researchers. Among various heuristic searches, meta-heuristic searching is especially popular [19,20]. Meta-heuristic searching mainly focuses on relevant behaviors in the natural world. The inherent computational intelligence mechanism is useful for seeking out the optimal solution to complex optimization problems. Different from forward greedy searching, meta-heuristic searching combines both random searching and local searching strategies [21,22]; the global optimal solution can then be gradually achieved in the whole process of searching. However, it should also be emphasized that the random factor in meta-heuristic searching may involve the following limitations.

• Random factor may result in the poor adaptability of reduct. This is mainly because each iteration of identifying qualified attributes is equipped with strong randomness. As has been reported by Li et al., a feature selection algorithm without the guarantee of stability usually leads to significantly different feature subsets if the data varies [23]. Such a case implies that the classification results based on selected features will shake the confidence of domain experts.
• Random factor may generate an ineffective reduct if high-dimensional data is faced. This is mainly because for hundreds of attributes in data, a large number of possible reducts exist, random factor can then possibly identify a reduct without the preferable learning ability [24,25].

To fill the gaps mentioned above, a new strategy to perform meta-heuristic searching has become necessary. First, in this study, the forest optimization algorithm (FOA) [26,27] is selected as the problem-solving approach for attribute reduction. Secondly, to further improve the effectiveness of the derived reducts by using FOA, an ensemble framework is developed, which aims to generate multiple reducts. It should be emphasized that the structure of those multiple reducts is symmetrical, which indicates that no order exists among those reducts. The advantage of such a symmetric structure is that our approach can be easily performed over parallel platforms. The use of multiple obtained reducts can then execute voting classification over testing samples; it is the key to achieving the objective of improving effectiveness [28,29]. Immediately, the main contributions of our study are elaborated as follows.

• It is the first attempt to introduce forest optimization-based searching into the problem solving of attribute reduction. Different from the widely used forward greed searching in many pieces of the literature, this research is useful to further push the application of meta-heuristic searching in data pre-processing forward.
• The ensemble framework proposed in this research is a general form; though it is combined with FOA in this article, such an ensemble framework can also be further embedded into other searchings. From this point of view, the discussed framework possesses the advantage of plug-and-play.

The remainder of this paper is organized as follows. In Section 2, we briefly review notions related to our study. Attribute reduction via FOA and the proposed ensemble framework are addressed in Section 3. We used 20 classical datasets on the UCI dataset to conduct comparative experiments. The experimental results are shown and analyzed in Section 4. Finally, the article is summarized in Section 5 and the future work plan is given.

2. Preliminaries

2.1. Granular Computing and Rough Set

Thus far, the principle of dividing complex data/information into several minor blocks to perform problem solving has been widely accepted in the era of big data. This thinking is referred to as information granulation in the framework of Granular Computing (GrC) [30,31]. As the fundamental operation element in GrC, the concept called information granulating has been thoroughly investigated [32,33,34]. The degree to characterize the coarser or finer structure of information granules can also be revealed; it is regarded as granularity.

Presently, it has been widely accepted that rough set is a general mathematical tool to carry out GrC. The reason can be contributed to the following two facts:

• the fundamental characteristic of rough set is to approximate the objective target by using information granules;
• different structures of information granules imply different values of granularity, and then the results of rough approximations may vary.

In rough set theory, a data or a decision system [35] can be denoted by $\mathcal{DS}=⟨U,AT,d⟩$, in which U is a set of nonempty finite samples, such as $U=\{x_1,x_2,\dots ,x_n\}$, $AT$ is a set of condition attributes, d is the decision to record the labels of samples, i.e., $\forall x_i\in U$, $d\left(x_i\right)$ is the label of sample $x_i$. Given a decision system $\mathcal{DS}$, to derive the result of information granulation over U, various binary relations have been developed with respect to different requirements. Two representative forms are illustrated as follows.

• To deal with categorical data, the equivalence relation or the so-called indiscernibility relation proposed by Pawlak can be used. For example, if the classification task is considered, then by decision d, the corresponding equivalence relation is ${\mathrm{IND}}_d=\{(x_i,x_j)\in U^2|d\left(x_i\right)=d\left(x_j\right)\}$. Therefore, a partition over U is derived such as $U/{\mathrm{IND}}_d=\{X_1,X_2,\dots ,X_m\}$. $\forall X_{\ell }\in U/{\mathrm{IND}}_d$, $X_{\ell }$ is actually a collection of samples that possess the same labels.
• To handle continuous or non-structured data, parameterized binary relationships can be employed. For instance, Hu et al. [36] have presented a neighborhood relation such as ${\mathrm{N}}_A^{\delta }=\{(x_i,x_j)\in U^2:{▵}_A(x_i,x_j)\le \delta \}$, in which ${▵}_A(x_i,x_j)$ is the distance between samples $x_i$ and $x_j$ over A and $\delta$ is the radius (one form of parameter). Following ${\mathrm{N}}_A^{\delta }$, each sample in U can induce a related neighborhood, which is a parameterized form of an information granule [37,38].

2.2. Attribute Selection

Note that since continuous data is more popular than categorical data in real-world applications, we will mainly focus on parameterized binary relationships in the context of this study. Furthermore, it has been pointed out that different specific parameters will lead to different results of information granulation, and then the related values of granularity may also be different. For example, Zhang et al. fused the multi granularity decision-making theory rough set with the hesitant fuzzy language group decision-making, and expanded the application of multi-granularity three-way decision-making in information analysis and information fusion by introducing the adjustable parameter of expected risk preference [39].

From the discussions above, it is interesting to explore one of the crucial topics in the field of rough set based on the parameter; that is, attribute reduction. Many researchers have performed outstanding work in the field of attribute reduction. Xu et al. proposed assignment reduction and approximate reduction for inconsistent ordered information systems to enhance the effectiveness of attribute reduction in complex information systems [40]. Chen et al. proposed the solution of a granular ball in the process of information granular attribute reduction, which improved the effectiveness of searching attributes [41]. We will first present the following general definition of attribute reduction.

Theorem 1.

 Given a decision system $\mathcal{DS}$ and a parameter ω, assuming that ${\rho }^{\omega }$-constraint is a constraint related to a specific measure ρ and parameter ω, $\forall A\subseteq AT$, A is referred to as a ${\rho }^{\omega }$-reduct if and only if:

1.

A satisfies ${\rho }^{\omega }$-constraint;

2.

$\forall B\subset A$, B does not satisfy ${\rho }^{\omega }$-constraint.

Without a loss in generality, in the scenario of rough set, the value of measure $\rho$ is closely related to the given parameter $\omega$. Therefore, the semantic explanation of ${\rho }^{\omega }$-reduct is a minimal subset of raw condition attributes, which satisfies the pre-defined constraint [42,43].

In most state-of-the-art studies about attribute reduction, the value of measure $\rho$ may be equipped with the following two cases.

• If a measure is positive preferred; that is, the measure-value is expected to be as high as possible, e.g., the measures called approximation quality and classification accuracy, then the ${\rho }^{\omega }$-constraint is usually expressed as “${\rho }^{\omega }\left(A\right)\ge {\rho }^{\omega }\left(AT\right)$” where ${\rho }^{\omega }\left(A\right)$ is the value of measure derived based on condition attributes A and parameter $\omega$.
• If a measure is negative preferred; that is, the measure-value is expected to be as low as possible, e.g., the measure called condition entropy and classification error rate, then the ${\rho }^{\omega }$-constraint is usually expressed as “${\rho }^{\omega }\left(A\right)\le {\rho }^{\omega }\left(AT\right)$”.

Following Theorem 1, how to select qualified attributes and construct the required reduction becomes a problem worth exploring. As a classic algorithm in heuristic strategy, forward greedy search has received extensive attention due to its low complexity and high efficiency. The key to such searching is to select the most significant attribute for each iteration. The detailed algorithm is shown as follows.

The qualified attributes can be obtained in step 5 of Algorithm  1, and this selected attribute is closely related to the measure used in the above algorithm. In detail, if a measure of positive correlation is used in the attribute search process, then attribute b should be qualified with a higher measure value such $b=argmax\{{\rho }^{\omega }(A\cup \left\{a\right\}):\forall a\in AT-A\}$; Conversely, if a negative correlation measure is used, a lower measure value should be considered to qualify attribute b, that is, $b=argmin\left\{\rho \omega \right(A\cup \left\{a\right\}):\forall a\in AT-A\}$.

Algorithm 1: Forward greedy searching to select attributes.

When the number of samples is $\left|U\right|$ and the number of conditional attributes is $\left|AT\right|$, the time complexity of the above Algorithm 1 is $\mathcal{O}\left(\right|U{|}^2\times \left|AT{|}^2\right)$.

3. Foa and Proposed Framework

3.1. FOA

The forest optimization algorithm (FOA) is an evolutionary algorithm that was developed by Ghaemi in 2014 [26]. Such an algorithm is enlightened by the phenomenon that a few trees in the forest can subsist for a long time while other trees can only survive for a limited time. Presently, FOA has been introduced into the problem solving of feature selection. Note that attribute reduction can be regarded as one rough set-based feature-selection tool, it is then an interesting topic to perform the searching of qualified attributes required in the reduct by principles of FOA.

Generally, in FOA, each tree represents a possible solution, i.e., a subset of condition attributes. To simplify our discussion, such a tree can be denoted by a vector with the length of $1+\left|AT\right|$. That is, a vector consists of $1+\left|AT\right|$ variables. The first variable in such a vector is the “Age” of a tree, and the remainders are used to denote the existence/nonexistence of attributes. For example, value “1” in a vector indicates that the corresponding attribute is identified to be involved in the subsequent iteration, value “0” in a vector implies that the corresponding attribute is removed for the subsequent iteration.

Following classical FOA, five main steps are used and elaborated as follows.

• Initializing trees. The variable “Age” of each tree is set to be ‘0’. Further, other variables of each tree are initialized randomly with either “0” or “1”. The following stage, called local seeding, will increase the values of “Age” of all trees except newly generated trees.
• Local seeding. For each tree with “Age” 0 in the forest, some variables are selected randomly(“LSC” parameter determines the number of the selected variables). Such a tree is split into an “LSC” number of trees, and for each split tree the value of one distinguished variable is changed from 0 to 1 or vice versa. Figure 1 shows an example of the local seeding operator of one tree. In such an example, $\left|AT\right|=5$, the value of “LSC” is set to 2.
  

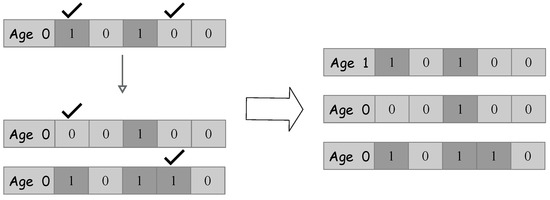  Figure 1. An example of local seeding with “LSC” = 2.
• Population limiting. In this stage, to form the candidate population, the following two types of trees will be removed from the forest: (1) the “Age” of a tree is bigger than a parameter called “life time”; (2) the extra trees that exceed a parameter called “area limit” by sorting trees via their fitness values.
• Global seeding. For trees in the candidate population, the number of variables to be selected is determined by a parameter named “GSC”, and these variables are selected at random. Immediately, the values of those selected variables will be changed (from 0 to 1 or vice versa). An example of performing global seeding is shown in Figure 2. In such an example, the value of “GSC” is also set to 3.
  

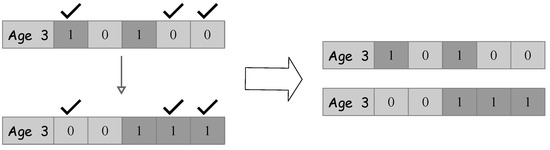  Figure 2. An example of global seeding with “GSC” = 3.
• Updating the best tree. In this stage, by sorting the trees in the candidate population based on their fitness values, the tree with the greatest fitness value is identified as the best one, and its “Age” will be set to be “0”. These stages will be performed iteratively until the ${\rho }^{\omega }$-constraint in attribute reduction is satisfied.

Algorithm 2 illustrates a detailed process to select attributes and then construct a reduct by using FOA.

Algorithm 2: FOA to select attributes.

3.2. Ensemble FOA

By carefully reviewing the process shown in Algorithm 2, we observe that for some specific steps, there are some random characteristics. For such a reason, it may be argued that the derived reduct based on FOA is unstable. In other words, two different reducts are to be obtained though the same searching procedure is executed twice over the same data.

Furthermore, following research reported in Yang et al. [44], an unstable reduct may be invaluable in providing robust learning, i.e., the stability of classification results may be far from what we expect. Such a study has indicated that not only the learning accuracy but also the learning stability should be paid a lot of attention to.

To fill the gaps mentioned above, a new approach to carrying out FOA has become necessary. That is why an ensemble strategy will be developed to further improve the performance of FOA in the problem solving of attribute reduction. Formally, the details of our ensemble strategy can be elaborated as follows. First, the searching process of FOA will be executed N times; it follows that N reducts may be derived such as $A_1,A_2,\dots ,A_N$. Secondly, each testing sample will be comprehensively predicated by those derived reduct. Finally, voting will be used to determine the final predication of the testing sample.

Nevertheless, it is not difficult to observe that two main limitations may emerge for the above ensemble strategy. First, though different reducts can be obtained, the diversity over those derived reducts is still unsatisfactory. Secondly, the searching efficiency is a big problem because there are N times to calculate the reduct. By considering such limitations, a data perturbation mechanism will be introduced into the whole process [45,46]. Grant there are m attributes in the given raw training data set. Our used data perturbation is performed by randomly identifying $\lambda \%(0\le \lambda \le 100)$ number of raw attributes, i.e., $\lambda \%·\left|AT\right|$ attributes, the reduct can then be generated from those attributes and the universe U. The first advantage of such a data perturbation is that the expected diversity of the reducts can be induced because different subsets of attributes are used to calculate the reducts. Moreover, since for each round computation of a reduct, only a subset of the attributes is employed, the time consumption can be reduced.

From the discussions above, a detailed framework of our proposed ensemble FOA is illustrated in Figure 3.

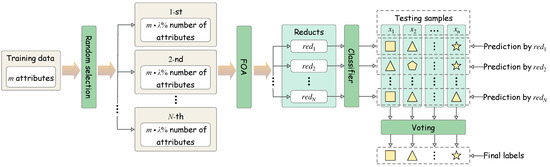
Figure 3. Ensemble FOA-based searching and classification.

4. Experimental Analysis

4.1. Data Sets

To verify the superiorities of the proposed framework, the experiments are conducted over 20 real-world datasets from the UCI Machine Learning Repository. Table 1 summarizes some details of these datasets. Additionally, the values in all datasets have been normalized by column. In addition, besides using the raw dataset shown in Table 1, we also added a comparative experiment of injecting label noise. The specific operation is as follows: if the given label noise ratio is $\omega \%(0\le \omega \le 100)$, then we randomly select $\omega \%·\left|U\right|$ samples in the raw dataset and perform noise injection by replacing the labels of these selected samples with other labels. The purpose of this is to further test the robustness of our method.

Table 1. Datasets description.

ID	DataSets	# Samples	# Attributes	# Labels	Domain
1	Climate Model Simulation Crashes	540	20	2	Physical
2	Connectionist Bench (Vowel Recognition—Deterding)	990	13	11	Geography
3	Diabetic Retinopathy Debrecen	1151	19	2	Life
4	German	1000	24	2	Business
5	Glass Identification	214	9	6	Physical
6	Ionosphere	351	34	2	Physical
7	Libras Movement	360	90	15	Astronomy
8	LSVT Voice Rehabilitation	126	256	10	Computer
9	Musk (Version 1)	476	166	2	Physical
10	QSAR biodegradation	1055	41	2	Biology
11	Quality Assessment of Digital Colposcopies	287	62	2	Life
12	Sonar	208	60	2	Physical
13	Statlog (Heart)	270	13	2	Life
14	Statlog (Image Segmentation)	2310	18	7	Life
15	Statlog (Vehicle Silhouettes)	846	18	4	Life
16	Synthetic Control Chart Time Series	600	60	6	Management
17	Ultrasonic flowmeter diagnostics - Meter D	180	44	4	Biology
18	Urban Land Cover	675	147	9	Geography
19	Wdbc	569	30	2	Life
20	Wine	178	13	3	Physical

4.2. Experimental Setup and Configuration

All experiments were performed on a Windows 10 system personal computer configured with an Intel Core i7-6700HQ CPU (2.60 GHz) and 16.00 GB of memory. The programming language is Matlab (MathWorks Inc., Natick, MA, USA), and the integrated development environment version used is R2019b.

In the following experiments, neighborhood rough set is used to perform our framework, in the case of using multiple different radii, neighborhood rough sets can form multi-grained structures. Therefore, we specify a set of 20 radii in ascending order such as $\mathbb{R}=\{{\delta }_1=0.02,{\delta }_2=0.04,\dots ,{\delta }_{20}=0.40\}$. Furthermore, the experiment uses 10-fold cross-validation; that is, in each calculation, 90% of the samples of the dataset are used to solve the attribute reduction, and the remaining samples are used to test the classification performance of the reduct.

Note that there are two approaches that have been tested in our experiment. One is a primitive forest optimization algorithm the other is an ensemble forest optimization algorithm.

They are denoted as PF and EF. Furthermore, to comprehensively compare our approaches, forward greedy searching has also been tested. KNN and CART are simple and mature classifiers, which have been widely accepted in various learning tasks. Therefore, we used KNN and CART classifiers in the experiment to measure the classification ability of the reduction obtained by the above three methods. These three methods are compared based on the following four measures.

• Approximation Quality (AQ) [47]: reflects the uncertainty of the sample space characterized by information granularity derived from attribute subsets. Set the radius to ${\delta }_m\in \mathbb{R}$, the approximation quality related to d over $A\subseteq AT$ can be denoted by ${\mathrm{A}\mathrm{Q}}^{{\delta }_m}\left(A\right)$ and:

  $${\displaystyle {AQ}^{{\delta }_m}\left(A\right)=\frac{\left|\{x\in U:N_A^{{\delta }_m}\left(x\right)\subseteq {\left[x\right]}_d\}\right|}{\left|U\right|},}$$

  where ${\mathrm{N}}_A^{{\delta }_m}\left(x\right)=\{y\in U:{▵}_A(x,y)\le {\delta }_m\}$ is the neighborhood of sample x related to A in terms of ${\delta }_m$, ${\left[x\right]}_d=\{y\in U:d\left(x\right)=d\left(y\right)\}$ is the decision class of x, and $|·|$ is the cardinality of a set.
  The higher the value ${\mathrm{A}\mathrm{Q}}^{{\delta }_m}\left(A\right)$ derives, the better the performance of the conditional attribute subset A is. From this point of view, the constraint is set to be “${\mathrm{A}\mathrm{Q}}^{{\delta }_m}\left(A\right)\ge {\mathrm{A}\mathrm{Q}}^{{\delta }_m}\left(AT\right)$” in Algorithms 1 and 2 for deriving Approximation Quality Reduct (AQR).
• Conditional Entropy (CE) [48]: reflects the uncertainty of the information granularity extracted from the attribute set to ${\delta }_m\in \mathbb{R}$, the condition entropy related to d over $A\subseteq AT$ can be denoted by ${\mathrm{C}\mathrm{E}}^{{\delta }_m}\left(A\right)$ and:

  $${\displaystyle {\mathrm{C}\mathrm{E}}^{{\delta }_m}\left(A\right)=\frac{1}{\left|U\right|}\sum _{x\in U}\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\cap {\left[x\right]}_d\right|log\frac{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\cap {\left[x\right]}_d\right|}{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\right|}.}$$
  The lower the value ${\mathrm{C}\mathrm{E}}^{{\delta }_m}\left(A\right)$ derives, the better the performance of the conditional attribute subset A is. From this point of view. The constraint is set to be “${\mathrm{C}\mathrm{E}}^{{\delta }_m}\left(A\right)\le {\mathrm{C}\mathrm{E}}^{{\delta }_m}\left(AT\right)$” in Algorithms 1 and 2 for deriving the Conditional Entropy Reduct (CER).
• h [49]: the regularizer is useful to robustly evaluate the significance of candidate attributes and then reasonably identify a valuable attribute. Given a radius ${\delta }_m\in \mathbb{R}$, the regularization loss related to d over $A\subseteq AT$ can be denoted by ${\mathrm{R}\mathrm{L}}^{{\delta }_m}(A)$ and:

  $${\displaystyle {\mathrm{R}\mathrm{L}}^{{\delta }_m}\left(A\right)=(1-{\mathrm{A}\mathrm{Q}}^{{\delta }_m}\left(A\right))+\alpha G\left(A\right),}$$

  in which $\alpha$ is a hyper-parameter to balance the loss of approximation quality and regularizer $G\left(A\right)$. In the context of this paper, the regularizer $G\left(A\right)$ is defined as a specific form of granularity [50] such that $G\left(A\right)={\displaystyle \sum _{x\in U}}\frac{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\right|}{{\left|U\right|}^2}log\frac{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\right|}{{\left|U\right|}^2}$.
  The lower the value ${\mathrm{R}\mathrm{L}}^{{\delta }_m}\left(A\right)$ derives, the better the performance of the condition attribute subset A is. From this point of view, the constraint is set to be “${\mathrm{R}\mathrm{L}}^{{\delta }_m}\left(A\right)\le {\mathrm{R}\mathrm{L}}^{{\delta }_m}\left(AT\right)$” in Algorithms 1 and 2 for deriving the Regularization Loss Reduct (RLR).
• Neighborhood Discrimination Index (NDI) [51]: the measure is used to reflect the discrimination ability of attribute sets for different decision classes. Given a radius ${\delta }_m\in \mathbb{R}$, the neighborhood discrimination index relates to d over $A\subseteq AT$ can be denoted by ${\mathrm{NDI}}^{{\delta }_m}\left(A\right)$ and:

  $${\displaystyle {NDI}^{{\delta }_m}\left(A\right)=log\frac{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\right|}{\left|{\mathrm{N}}_A^{{\delta }_m}\left(x\right)\cap {\mathrm{IND}}_d\right|}.}$$
  The lower the value ${\mathrm{NDI}}^{{\delta }_m}\left(A\right)$ derives, the better the performance of the condition attribute subset A is. From this point of view, the constraint is set to be “${\mathrm{NDI}}^{{\delta }_m}\left(A\right)\le {\mathrm{NDI}}^{{\delta }_m}\left(AT\right)$” in Algorithms 1 and 2 for deriving the Neighborhood Discrimination Index Reduct (NDIR).

With these metrics, four sets of comparative experiments will be carried out on three algorithms: primitive forest optimization algorithm, ensemble forest optimization algorithm and forward greedy algorithm: PF-AQR, EF-AQR and FG-AQR consist of a group of comparisons based on the measure of approximation quality; PF-CER, EF-CER and FG-CER consist of a group of comparisons based on the measure of conditional entropy; PF-RLR, EF-RLR and FG-RLR consist of a group of comparisons based on the measure of regularization loss; PF-NDI, EF-NDI and FG-NDI consist of a group of comparisons based on the measure of discrimination index.

Moreover, three types of results will be reported: (1) the classification accuracy, (2) the classification stability and (3) the AUC.

4.3. Comparisons among Classification Accuracies of the Derived Reducts

In this subsection, the classification accuracies under three methods based on four measures will be shown. These results are shown for the raw dataset and the dataset with 10%, 20%, 30% and 40% different label noise ratios. Note that CART and KNN classifiers are employed to evaluate the classification performance of the derived reducts.

4.3.1. Classification Accuracies (Raw Data)

Table 2 and Table 3 below show the classification accuracies of the raw dataset with different classifiers.

Table 2. Comparison among KNN classification accuracies (raw data and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8870	0.9075	0.9048		0.8868	0.9074	0.9038		0.8881	0.9074	0.9030		0.8871	0.9074	0.8955
2	0.8801	0.8896	0.8644		0.8837	0.8884	0.8830		0.8852	0.8907	0.8829		0.8806	0.8873	0.8860
3	0.6590	0.6724	0.6505		0.6587	0.6705	0.6551		0.6544	0.6731	0.6297		0.6623	0.6748	0.6253
4	0.6861	0.7232	0.6886		0.6982	0.7225	0.6986		0.7014	0.7263	0.6956		0.6945	0.7276	0.7129
5	0.6386	0.6779	0.6502		0.6381	0.6651	0.6349		0.6393	0.6749	0.6514		0.6386	0.6679	0.6360
6	0.8249	0.8250	0.8381		0.8317	0.8247	0.8294		0.8270	0.8264	0.8350		0.8279	0.8304	0.8370
7	0.7864	0.7960	0.7634		0.8120	0.8330	0.7965		0.7652	0.7633	0.7834		0.7930	0.8001	0.7784
8	0.7960	0.8252	0.8084		0.8000	0.8284	0.8172		0.8144	0.8280	0.8340		0.8012	0.8188	0.8012
9	0.8220	0.8339	0.7529		0.8194	0.8338	0.7422		0.8211	0.8301	0.7696		0.8224	0.8272	0.7615
10	0.8354	0.8819	0.8340		0.8131	0.8254	0.7856		0.8670	0.8430	0.8080		0.8123	0.8243	0.7680
11	0.7572	0.7997	0.7131		0.7621	0.8014	0.7340		0.7710	0.7995	0.7290		0.7641	0.7998	0.7883
12	0.8266	0.8500	0.7417		0.8268	0.8459	0.7376		0.8251	0.8478	0.7715		0.8173	0.8478	0.7700
13	0.7931	0.8457	0.7917		0.7880	0.8407	0.7943		0.7976	0.8419	0.7970		0.7900	0.8426	0.7907
14	0.9397	0.9524	0.9414		0.9417	0.9508	0.9429		0.9458	0.9553	0.9503		0.9385	0.9495	0.9444
15	0.6641	0.6921	0.6343		0.6666	0.6933	0.6491		0.6664	0.6947	0.6563		0.6679	0.7001	0.6676
16	0.9628	0.9833	0.7844		0.9642	0.9858	0.7700		0.9658	0.9838	0.8721		0.9645	0.9863	0.9374
17	0.8093	0.8112	0.8106		0.8134	0.8243	0.8201		0.8342	0.8456	0.8231		0.7980	0.8012	0.7893
18	0.8447	0.8713	0.7442		0.8451	0.8714	0.6624		0.8470	0.8706	0.7202		0.8510	0.8734	0.8236
19	0.9134	0.9135	0.9017		0.9342	0.9032	0.9128		0.9276	0.9541	0.9281		0.9367	0.9512	0.9097
20	0.9300	0.9551	0.9280		0.9286	0.9520	0.9446		0.9334	0.9583	0.9509		0.9343	0.9571	0.9360

Table 3. Comparison among CART classification accuracies (raw data and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8693	0.9098	0.9048		0.8706	0.9100	0.9015		0.8629	0.9094	0.9000		0.8652	0.9091	0.9065
2	0.6811	0.8088	0.6961		0.6968	0.8084	0.6998		0.6957	0.8109	0.7021		0.6923	0.8056	0.7029
3	0.6100	0.6523	0.6165		0.6139	0.6578	0.6266		0.6148	0.6612	0.6146		0.6053	0.6489	0.5959
4	0.6790	0.7380	0.6739		0.6896	0.7446	0.6902		0.6899	0.7403	0.6822		0.6876	0.7448	0.7027
5	0.7086	0.7349	0.7091		0.7102	0.7388	0.7202		0.6916	0.7316	0.6802		0.7086	0.7377	0.6674
6	0.8596	0.8869	0.8470		0.8664	0.8861	0.8546		0.8656	0.8830	0.8590		0.8726	0.8877	0.8569
7	0.7586	0.7860	0.7231		0.7324	0.7723	0.7143		0.7563	0.7865	0.7326		0.7222	0.7480	0.7210
8	0.7604	0.8124	0.7692		0.7464	0.8048	0.7724		0.7584	0.8116	0.7524		0.7528	0.8196	0.7632
9	0.7672	0.8520	0.7382		0.7658	0.8467	0.7182		0.7654	0.8518	0.7454		0.7651	0.8499	0.7392
10	0.8110	0.8363	0.8106		0.8265	0.8576	0.8032		0.8231	0.8326	0.8154		0.8230	0.8321	0.8381
11	0.7360	0.7917	0.6847		0.7419	0.7905	0.6945		0.7471	0.7926	0.6917		0.7421	0.7948	0.7509
12	0.7217	0.8305	0.6763		0.7180	0.8090	0.6707		0.6971	0.8100	0.7134		0.6978	0.8100	0.7007
13	0.7428	0.7974	0.7344		0.7367	0.8013	0.7296		0.7352	0.8007	0.7261		0.7402	0.7967	0.7278
14	0.9505	0.9610	0.9501		0.9520	0.9614	0.9476		0.9540	0.9626	0.9477		0.9522	0.9601	0.9511
15	0.6886	0.7364	0.6475		0.6918	0.7365	0.6569		0.6957	0.7359	0.6715		0.7000	0.7408	0.6879
16	0.8903	0.9714	0.8268		0.8928	0.9675	0.8043		0.8911	0.9712	0.8570		0.8889	0.9723	0.8861
17	0.7678	0.7890	0.7798		0.7354	0.7547	0.7413		0.7610	0.7645	0.7578		0.7423	0.7389	0.7880
18	0.8031	0.8630	0.7700		0.8008	0.8608	0.6640		0.8028	0.8610	0.7344		0.8025	0.8592	0.8107
19	0.8921	0.8990	0.8769		0.9103	0.9230	0.8819		0.9120	0.9210	0.9001		0.8976	0.8873	0.9023
20	0.8883	0.9380	0.8869		0.8843	0.9377	0.8689		0.8840	0.9426	0.8926		0.8826	0.9420	0.8900

With a deep investigation of Table 2 and Table 3, it is not difficult to observe that regardless of the classifier used, the classification accuracies associated with our method dominate other compared methods in most datasets. Take data “Statlog (Heart) (ID = 13)” as an example, by KNN classifier, the classification accuracies related to our method are 0.8457, 0.8407, 0.8419 and 0.8426, respectively. At the same time, the classification accuracies of several other comparison methods are no more than 0.8.

4.3.2. Classification Accuracies (10%, 20%, 30% and 40% Label Noise)

The classification accuracies in terms of four different noise ratios are reported in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11.

Table 4. Comparison among KNN classification accuracies (10% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9228	0.9352	0.9337		0.9232	0.9353	0.9291		0.9244	0.9352	0.9331		0.9218	0.9352	0.9368
2	0.8442	0.8589	0.8234		0.8563	0.8575	0.8473		0.8532	0.8580	0.8449		0.8506	0.8468	0.8311
3	0.6087	0.6500	0.6080		0.6102	0.6488	0.6161		0.6117	0.6603	0.6019		0.6123	0.6456	0.5708
4	0.6984	0.7130	0.6967		0.7010	0.7155	0.6965		0.7001	0.7147	0.6952		0.7026	0.7154	0.7098
5	0.6014	0.6209	0.5940		0.6016	0.6200	0.5765		0.6000	0.6205	0.5660		0.6149	0.6360	0.5726
6	0.8666	0.8690	0.8631		0.8724	0.8724	0.8679		0.8650	0.8786	0.8730		0.8694	0.8763	0.8713
7	0.7231	0.7501	0.7420		0.7191	0.7358	0.7219		0.7427	0.7553	0.7502		0.7218	0.7458	0.7310
8	0.7708	0.8008	0.7136		0.7756	0.8060	0.7300		0.7660	0.8024	0.7480		0.7776	0.7976	0.7284
9	0.7996	0.7984	0.7213		0.7967	0.8023	0.7303		0.7972	0.8013	0.7533		0.7951	0.7998	0.7575
10	0.8402	0.8666	0.8247		0.8402	0.8686	0.8329		0.8425	0.8642	0.8191		0.8430	0.8686	0.8322
11	0.7717	0.8019	0.7348		0.7757	0.8071	0.7357		0.7757	0.8072	0.7352		0.7672	0.8043	0.7733
12	0.7927	0.8061	0.7102		0.7910	0.8085	0.7020		0.7929	0.8132	0.7422		0.8032	0.8063	0.7468
13	0.7235	0.7628	0.7231		0.7337	0.7641	0.7233		0.7256	0.7574	0.7307		0.7293	0.7585	0.7322
14	0.9100	0.9320	0.9241		0.9487	0.9531	0.9447		0.9572	0.9581	0.9449		0.9470	0.9587	0.9194
15	0.6432	0.6689	0.5927		0.6574	0.6707	0.6316		0.6520	0.6684	0.6328		0.6559	0.6692	0.6199
16	0.9211	0.9605	0.7358		0.9162	0.9583	0.7258		0.9187	0.9600	0.8008		0.9248	0.9585	0.9380
17	0.7867	0.7908	0.7697		0.7886	0.7892	0.7686		0.7833	0.7933	0.7181		0.7900	0.7942	0.7603
18	0.8076	0.8519	0.6489		0.8079	0.8503	0.5962		0.8103	0.8503	0.6539		0.8068	0.8567	0.8040
19	0.9381	0.9594	0.9310		0.9413	0.9565	0.9335		0.9391	0.9568	0.9325		0.9403	0.9553	0.9418
20	0.9206	0.9449	0.9069		0.9283	0.9440	0.9231		0.9277	0.9449	0.9266		0.9131	0.9429	0.9191

Table 5. Comparison among CART classification accuracies (10% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8977	0.9353	0.9168		0.8895	0.9342	0.9098		0.8952	0.9342	0.9095		0.8885	0.9344	0.9160
2	0.6363	0.7764	0.6266		0.6504	0.7735	0.6289		0.6450	0.7722	0.6459		0.6467	0.7617	0.6249
3	0.6114	0.6514	0.6120		0.6053	0.6537	0.6147		0.6034	0.6577	0.6071		0.6133	0.6496	0.5720
4	0.6773	0.7277	0.6863		0.6864	0.7309	0.6874		0.6814	0.7279	0.6879		0.6841	0.7314	0.6848
5	0.6207	0.6756	0.6181		0.6200	0.6784	0.6193		0.6214	0.6770	0.5926		0.6284	0.6814	0.5893
6	0.8987	0.9410	0.8797		0.8979	0.9400	0.8980		0.8911	0.9376	0.9063		0.8906	0.9407	0.8949
7	0.7321	0.7750	0.7475		0.7378	0.7581	0.7491		0.7582	0.7653	0.7630		0.7619	0.7608	0.7567
8	0.7060	0.7876	0.7044		0.7012	0.7792	0.6804		0.7112	0.7812	0.7068		0.7032	0.7864	0.6956
9	0.7423	0.8168	0.7041		0.7337	0.8153	0.7026		0.7395	0.8117	0.7186		0.7318	0.8140	0.7200
10	0.7906	0.8401	0.7851		0.7924	0.8389	0.7865		0.7942	0.8382	0.7712		0.7916	0.8362	0.7891
11	0.7493	0.8157	0.7047		0.7576	0.8186	0.7247		0.7579	0.8190	0.7233		0.7514	0.8178	0.7547
12	0.6820	0.7646	0.6602		0.6800	0.7763	0.6478		0.6780	0.7685	0.6746		0.6829	0.7680	0.6749
13	0.6869	0.7274	0.6696		0.6870	0.7239	0.6783		0.6804	0.7269	0.6796		0.6857	0.7241	0.6815
14	0.9323	0.9401	0.9351		0.9584	0.9641	0.9619		0.9317	0.9567	0.9581		0.9308	0.9501	0.9476
15	0.6420	0.6972	0.6018		0.6452	0.6973	0.6211		0.6434	0.6964	0.6210		0.6498	0.6984	0.6208
16	0.8078	0.9590	0.7553		0.8123	0.9590	0.7505		0.8065	0.9550	0.7763		0.8102	0.9614	0.8024
17	0.8233	0.8506	0.8111		0.8353	0.8500	0.7847		0.8319	0.8519	0.7556		0.8292	0.8517	0.8097
18	0.7344	0.8456	0.6717		0.7376	0.8439	0.5941		0.7343	0.8439	0.6565		0.7347	0.8440	0.7292
19	0.8725	0.9198	0.8800		0.8755	0.9178	0.8697		0.8793	0.9168	0.8770		0.8726	0.9168	0.8744
20	0.8646	0.9249	0.8540		0.8666	0.9177	0.8703		0.8683	0.9266	0.8763		0.8543	0.9183	0.8686

Table 6. Comparison among KNN classification accuracies (20% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8505	0.8519	0.8739		0.8518	0.8519	0.8619		0.8528	0.8519	0.8676		0.8492	0.8519	0.8695
2	0.8170	0.8189	0.7900		0.8213	0.8364	0.8180		0.8171	0.8236	0.8202		0.8259	0.8959	0.7546
3	0.5628	0.5881	0.5637		0.5640	0.5877	0.5623		0.5713	0.5951	0.5835		0.5679	0.5913	0.5337
4	0.6872	0.6938	0.6823		0.6927	0.6962	0.6906		0.6923	0.6973	0.6878		0.6901	0.6949	0.7032
5	0.6449	0.6442	0.6349		0.6505	0.6430	0.6449		0.6442	0.6430	0.5316		0.6521	0.6400	0.5886
6	0.8440	0.8417	0.8569		0.8493	0.8381	0.8530		0.8524	0.8494	0.8686		0.8470	0.8429	0.8543
7	0.7542	0.7689	0.7672		0.7581	0.7771	0.7658		0.7309	0.7521	0.7492		0.7642	0.7689	0.7598
8	0.6596	0.6858	0.6685		0.6738	0.6873	0.6750		0.6700	0.6896	0.6912		0.6665	0.6823	0.6623
9	0.7007	0.6947	0.6592		0.6941	0.6986	0.6698		0.6961	0.6918	0.6701		0.7039	0.6977	0.6755
10	0.8011	0.8177	0.7898		0.8020	0.8154	0.8005		0.8006	0.8118	0.7548		0.8018	0.8155	0.7990
11	0.7278	0.7288	0.6748		0.7219	0.7284	0.6766		0.7240	0.7260	0.6769		0.7210	0.7260	0.7293
12	0.7437	0.7520	0.6741		0.7532	0.7476	0.6615		0.7410	0.7505	0.7066		0.7402	0.7412	0.7161
13	0.7863	0.8263	0.7670		0.7978	0.8235	0.7813		0.7967	0.8226	0.7824		0.8013	0.8256	0.8135
14	0.8747	0.9093	0.8695		0.8749	0.9085	0.8766		0.8752	0.9141	0.8797		0.8744	0.9034	0.6407
15	0.6398	0.6782	0.6078		0.6414	0.6787	0.6328		0.6466	0.6816	0.6343		0.6411	0.6821	0.5967
16	0.8620	0.9188	0.6714		0.8652	0.9242	0.6555		0.8603	0.9223	0.7259		0.8623	0.9175	0.8933
17	0.7769	0.7811	0.7494		0.7731	0.7750	0.7506		0.7714	0.7792	0.6944		0.7747	0.7817	0.7531
18	0.7218	0.8154	0.6999		0.7451	0.8321	0.7017		0.7289	0.8083	0.6893		0.7431	0.8488	0.6598
19	0.8762	0.9058	0.8804		0.8812	0.9019	0.8748		0.8772	0.9090	0.8802		0.8761	0.9000	0.8815
20	0.8811	0.9183	0.8660		0.8863	0.9120	0.8863		0.8814	0.9123	0.8823		0.8749	0.9123	0.8843

Table 7. Comparison among CART classification accuracies (20% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8403	0.8519	0.8662		0.8393	0.8531	0.8490		0.8394	0.8638	0.8569		0.8394	0.8628	0.8637
2	0.6236	0.7419	0.6070		0.6273	0.7400	0.6287		0.6212	0.7479	0.6287		0.6344	0.7121	0.5780
3	0.5763	0.6035	0.5766		0.5837	0.6039	0.5866		0.5811	0.6054	0.5804		0.5788	0.6010	0.5407
4	0.6875	0.7018	0.6861		0.6909	0.7032	0.6931		0.6872	0.7025	0.6928		0.6872	0.7039	0.6936
5	0.5786	0.6412	0.5688		0.5760	0.6488	0.5635		0.5795	0.6530	0.5337		0.5753	0.6458	0.5528
6	0.8444	0.9097	0.8529		0.8494	0.9100	0.8537		0.8581	0.9170	0.8631		0.8569	0.9103	0.8620
7	0.7242	0.7669	0.7632		0.7181	0.7651	0.7388		0.7309	0.7421	0.7217		0.7342	0.7656	0.7548
8	0.6277	0.6969	0.6446		0.6427	0.6869	0.6442		0.6381	0.6885	0.6388		0.6304	0.6823	0.6542
9	0.6866	0.7339	0.6565		0.6822	0.7399	0.6498		0.6853	0.7378	0.6666		0.6892	0.7345	0.6713
10	0.7680	0.8055	0.7555		0.7624	0.8062	0.7554		0.7650	0.8018	0.7352		0.7644	0.8028	0.7591
11	0.7176	0.7303	0.6491		0.7138	0.7305	0.6805		0.7162	0.7303	0.6810		0.7133	0.7300	0.7155
12	0.6517	0.6837	0.6044		0.6515	0.6798	0.6141		0.6473	0.6883	0.6463		0.6515	0.6839	0.6337
13	0.7233	0.7857	0.7174		0.7257	0.7880	0.7131		0.7233	0.7894	0.7094		0.7265	0.7835	0.7263
14	0.8145	0.9067	0.8158		0.8178	0.9070	0.8190		0.8219	0.9151	0.8314		0.8152	0.8996	0.6186
15	0.6295	0.6931	0.5897		0.6335	0.6954	0.6052		0.6257	0.6986	0.6128		0.6288	0.6982	0.5940
16	0.7521	0.9301	0.7096		0.7547	0.9273	0.6886		0.7523	0.9275	0.7244		0.7463	0.9301	0.7453
17	0.7619	0.8206	0.7461		0.7650	0.8133	0.7350		0.7686	0.8250	0.7053		0.7592	0.8106	0.7436
18	0.7318	0.8214	0.6859		0.7378	0.8121	0.6890		0.7659	0.8133	0.6943		0.7871	0.8598	0.6668
19	0.7918	0.8474	0.7951		0.7871	0.8478	0.7920		0.7923	0.8515	0.7978		0.7916	0.8360	0.7957
20	0.7994	0.8671	0.7960		0.8023	0.8637	0.8014		0.8023	0.8594	0.8094		0.7986	0.8654	0.8026

Table 8. Comparison among KNN classification accuracies (30% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9176	0.9259	0.9254		0.9169	0.9259	0.9192		0.9173	0.9260	0.9231		0.9163	0.9259	0.9219
2	0.7387	0.7403	0.7135		0.7466	0.7474	0.7474		0.7423	0.7519	0.7432		0.7511	0.7735	0.6369
3	0.5420	0.5566	0.5438		0.5404	0.5543	0.5386		0.5490	0.5610	0.5558		0.5442	0.5530	0.5190
4	0.7098	0.7375	0.7108		0.7057	0.7360	0.7117		0.7059	0.7361	0.7082		0.7103	0.7345	0.7137
5	0.5493	0.5933	0.5545		0.5490	0.5876	0.5371		0.5457	0.6148	0.5029		0.5545	0.5981	0.5145
6	0.7799	0.7697	0.7741		0.7866	0.7754	0.7810		0.7881	0.7740	0.8063		0.7851	0.7709	0.7841
7	0.7143	0.7359	0.7102		0.7351	0.7391	0.7388		0.7387	0.7452	0.7288		0.7354	0.7618	0.7588
8	0.6385	0.6235	0.6262		0.6435	0.6273	0.6385		0.6488	0.6308	0.6469		0.6369	0.6285	0.6358
9	0.6954	0.6995	0.6480		0.6989	0.6997	0.6585		0.7002	0.6897	0.6654		0.7038	0.6880	0.6701
10	0.7758	0.7810	0.7619		0.7762	0.7801	0.7697		0.7737	0.7755	0.7115		0.7765	0.7824	0.7707
11	0.8512	0.8602	0.7868		0.8479	0.8579	0.8046		0.8491	0.8595	0.8032		0.8479	0.8567	0.8453
12	0.6912	0.6951	0.6300		0.7049	0.7151	0.6261		0.7088	0.7185	0.6539		0.6946	0.6993	0.6734
13	0.6743	0.6963	0.6570		0.6802	0.6898	0.6656		0.6789	0.6954	0.6730		0.6709	0.6981	0.6728
14	0.8825	0.9115	0.8263		0.8178	0.9070	0.8190		0.8219	0.9151	0.8314		0.8152	0.8996	0.6186
15	0.5821	0.6129	0.5532		0.5854	0.6119	0.5702		0.5864	0.6073	0.5701		0.5901	0.6086	0.5440
16	0.8030	0.8938	0.5997		0.8043	0.8975	0.6081		0.8053	0.8950	0.6588		0.8022	0.8996	0.8313
17	0.7094	0.7167	0.6925		0.7139	0.7143	0.6903		0.7119	0.7169	0.6581		0.7178	0.7219	0.6742
18	0.7318	0.8214	0.6859		0.7378	0.8121	0.6890		0.7659	0.8133	0.6943		0.7871	0.8598	0.6668
19	0.8013	0.8191	0.8013		0.7979	0.8208	0.7918		0.7987	0.8239	0.7964		0.7975	0.8162	0.8025
20	0.8314	0.8914	0.8240		0.8309	0.8943	0.8169		0.8386	0.8903	0.8389		0.8169	0.8906	0.8443

Table 9. Comparison among CART classification accuracies (30% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8931	0.9251	0.9136		0.8944	0.9242	0.9044		0.8877	0.9266	0.9088		0.8913	0.9249	0.9115
2	0.5603	0.6925	0.5410		0.5695	0.6852	0.5695		0.5691	0.7020	0.5710		0.5778	0.6645	0.4805
3	0.5569	0.5676	0.5568		0.5565	0.5689	0.5517		0.5572	0.5707	0.5600		0.5541	0.5678	0.5171
4	0.6988	0.7421	0.7055		0.6978	0.7407	0.7010		0.6979	0.7427	0.6967		0.7016	0.7432	0.7000
5	0.5281	0.5974	0.5355		0.5181	0.5962	0.5171		0.5295	0.6119	0.4912		0.5300	0.6007	0.4960
6	0.7923	0.8229	0.7767		0.7916	0.8219	0.8024		0.7934	0.8266	0.8051		0.8004	0.8227	0.7904
7	0.7254	0.7467	0.7268		0.7135	0.7412	0.7303		0.7387	0.7576	0.7648		0.7421	0.7731	0.7567
8	0.6092	0.6227	0.6058		0.6058	0.6212	0.6015		0.6073	0.6238	0.6250		0.6038	0.6169	0.6162
9	0.6635	0.6944	0.6536		0.6726	0.6951	0.6456		0.6651	0.6960	0.6540		0.6759	0.6976	0.6598
10	0.7456	0.7682	0.7433		0.7481	0.7673	0.7458		0.7538	0.7665	0.7153		0.7533	0.7686	0.7465
11	0.7935	0.8526	0.7642		0.7970	0.8540	0.7656		0.8012	0.8519	0.7665		0.7984	0.8535	0.7953
12	0.5983	0.6278	0.5807		0.6134	0.6137	0.5939		0.6198	0.6220	0.6039		0.6034	0.6224	0.5876
13	0.6265	0.6589	0.6169		0.6196	0.6276	0.6126		0.6259	0.6302	0.6256		0.6231	0.6381	0.6257
14	0.8325	0.9195	0.8457		0.8276	0.9312	0.8586		0.8731	0.9109	0.8637		0.8581	0.9182	0.8378
15	0.5708	0.6553	0.5353		0.5730	0.6496	0.5488		0.5692	0.6507	0.5551		0.5744	0.6502	0.5398
16	0.6648	0.8822	0.6252		0.6576	0.8856	0.6204		0.6725	0.8833	0.6468		0.6606	0.8890	0.6602
17	0.7011	0.7683	0.6883		0.7058	0.7656	0.6786		0.7011	0.7706	0.6964		0.7064	0.7581	0.6747
18	0.7634	0.8156	0.6631		0.7461	0.8273	0.6759		0.7588	0.8176	0.6818		0.7724	0.8472	0.6731
19	0.7280	0.7618	0.7337		0.7250	0.7564	0.7321		0.7246	0.7672	0.7382		0.7254	0.7568	0.7248
20	0.7683	0.8543	0.7626		0.7694	0.8446	0.7749		0.7654	0.8506	0.7663		0.7603	0.8466	0.7643

Table 10. Comparison among KNN classification accuracies (40% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8769	0.8796	0.8774		0.8747	0.9096	0.8703		0.8769	0.8796	0.8746		0.8764	0.8896	0.8766
2	0.6434	0.6535	0.6362		0.6530	0.6546	0.6360		0.6584	0.6696	0.6628		0.6083	0.6232	0.5275
3	0.5106	0.5424	0.5100		0.5103	0.5238	0.5120		0.5186	0.5286	0.5122		0.5120	0.5347	0.4909
4	0.7522	0.7718	0.7482		0.7493	0.7722	0.7506		0.7503	0.7716	0.7495		0.7504	0.7725	0.7497
5	0.4586	0.4895	0.4581		0.4726	0.4942	0.4707		0.4695	0.4986	0.4160		0.4663	0.4874	0.4412
6	0.7554	0.7569	0.7561		0.7566	0.7784	0.7627		0.7546	0.7901	0.7720		0.7574	0.7701	0.7581
7	0.7464	0.7517	0.7188		0.7267	0.7467	0.7413		0.7387	0.7576	0.7648		0.7464	0.7537	0.7261
8	0.5940	0.5948	0.5708		0.5620	0.5732	0.5676		0.5892	0.5944	0.5804		0.5860	0.5884	0.5732
9	0.6360	0.6458	0.6240		0.6654	0.6671	0.6257		0.6684	0.6688	0.6389		0.6539	0.6627	0.6412
10	0.7599	0.7602	0.7497		0.7595	0.7596	0.7564		0.7393	0.7548	0.6992		0.7633	0.7692	0.7561
11	0.8038	0.8098	0.7734		0.7976	0.8078	0.7824		0.7995	0.8088	0.7824		0.8014	0.8097	0.7914
12	0.5373	0.5988	0.5744		0.5890	0.6068	0.5673		0.6346	0.6695	0.6029		0.6215	0.6900	0.6300
13	0.6326	0.6448	0.6098		0.6389	0.6478	0.6231		0.6357	0.6378	0.6296		0.6370	0.6626	0.6417
14	0.7281	0.7853	0.7187		0.7302	0.7823	0.7270		0.7266	0.7880	0.7248		0.7285	0.7836	0.5948
15	0.5277	0.5498	0.5028		0.5299	0.5550	0.5195		0.5311	0.5614	0.5206		0.5355	0.5599	0.4989
16	0.7192	0.8358	0.5413		0.7219	0.8344	0.5438		0.7242	0.8389	0.5898		0.7228	0.8408	0.7518
17	0.6289	0.6339	0.5853		0.6233	0.6294	0.5850		0.6275	0.6336	0.5728		0.6347	0.6311	0.5800
18	0.8599	0.9133	0.7413		0.8645	0.9088	0.7170		0.8649	0.9099	0.7504		0.8659	0.9097	0.8447
19	0.7029	0.6912	0.7058		0.7065	0.6947	0.6992		0.7039	0.6960	0.6938		0.7109	0.6926	0.7098
20	0.8125	0.8550	0.7922		0.8111	0.8586	0.8156		0.8156	0.8667	0.8103		0.8075	0.8606	0.8292

Table 11. Comparison among CART classification accuracies (40% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8553	0.8794	0.8791		0.8609	0.8793	0.8686		0.8631	0.8803	0.8768		0.8578	0.8799	0.8801
2	0.4915	0.6234	0.4861		0.5064	0.6250	0.5036		0.5101	0.6393	0.5089		0.5165	0.5935	0.3981
3	0.5347	0.5382	0.5284		0.5329	0.5577	0.5383		0.5280	0.5288	0.5213		0.5290	0.5453	0.4950
4	0.7427	0.7730	0.7416		0.7442	0.7751	0.7415		0.7442	0.7747	0.7436		0.7427	0.7732	0.7451
5	0.4623	0.5191	0.4693		0.4679	0.5293	0.4542		0.4598	0.5330	0.4158		0.4688	0.5309	0.4342
6	0.7784	0.7891	0.7570		0.7849	0.7859	0.7819		0.7726	0.7816	0.7754		0.7760	0.7787	0.7719
7	0.7583	0.7682	0.7399		0.7413	0.7468	0.7142		0.7351	0.7731	0.7148		0.7313	0.7412	0.7372
8	0.5848	0.5996	0.5604		0.5816	0.5880	0.5700		0.5904	0.6100	0.5888		0.5964	0.5928	0.5704
9	0.6512	0.6611	0.6196		0.6497	0.6591	0.6345		0.6513	0.6593	0.6409		0.6480	0.6589	0.6442
10	0.7375	0.7491	0.7311		0.7414	0.7482	0.7347		0.7400	0.7491	0.7027		0.7429	0.7509	0.7393
11	0.7910	0.8124	0.7493		0.7814	0.8114	0.7497		0.7841	0.8117	0.7509		0.7855	0.8102	0.7817
12	0.5707	0.5598	0.5510		0.5727	0.5610	0.5490		0.5761	0.5593	0.5661		0.5620	0.5512	0.5612
13	0.5898	0.6231	0.6000		0.5961	0.6224	0.5843		0.5930	0.6026	0.5848		0.6007	0.6274	0.5956
14	0.6690	0.8282	0.6640		0.6711	0.8242	0.6634		0.6718	0.8332	0.6790		0.6684	0.8230	0.5654
15	0.5271	0.6012	0.4941		0.5219	0.6004	0.5087		0.5231	0.6020	0.5097		0.5297	0.6014	0.5020
16	0.5889	0.8316	0.5535		0.5912	0.8273	0.5558		0.5920	0.8339	0.5760		0.5865	0.8347	0.5854
17	0.6014	0.6786	0.5714		0.6008	0.6717	0.5844		0.5964	0.6842	0.5994		0.6000	0.6664	0.5786
18	0.8535	0.9183	0.7673		0.8725	0.9109	0.7264		0.8738	0.9189	0.7608		0.8812	0.9196	0.8688
19	0.6434	0.6450	0.6619		0.6552	0.6580	0.6533		0.6677	0.6833	0.6560		0.6539	0.6954	0.6725
20	0.7353	0.8247	0.7428		0.7308	0.8144	0.7500		0.7242	0.8275	0.7406		0.7214	0.8164	0.7469

From the above results, it is not difficult to observe that the performance of both CART and KNN classifiers decreases with the increase in the ratios of label noises. Taking “Connectionist Bench (Vowel Recognition—Deterding) (ID = 2)” as an example, for the CART classifier and the approximation quality are used to define the constraint of attribute reduction; if the noise ratio increases from 10% to 40%, the values of EF-AQR in Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11 are 0.7764, 0.7419, 0.6925 and 0.6234. Obviously, the classification accuracies have been significantly reduced. Such observations suggest that more label noise does have a negative impact on the classification performance of selected attributes in the reducts.

At the same time, we can find that when the label noise ratios are 20% and 30%, the results in Table 6, Table 7, Table 8 and Table 9 show that when using the KNN classifier, our method has a weak disadvantage in classification accuracy compared to other methods on the small number of datasets. It shows that our method is more suitable for the CART classifier in the environment of 20% and 30% label noise ratios.

Note that for the four ratios of label noises we tested, the classification accuracies associated with our method are also superior to the results associated with the compared methods. Such observations also imply that our proposed strategy is more robust in dirty data.

4.4. Comparisons among Classification Stabilities of the Derived Reducts

In this subsection, we will show the classification stability values related to three different methods under four metrics. These comparative experiments are not only performed on the raw dataset but also performed on the dataset with ratios of label noises of 10%, 20%, 30% and 40%. The CART and KNN classifiers are used to test the performance of all algorithms.

4.4.1. Classification Stabilities (Raw Data)

Table 12 and Table 13 report different classification stabilities obtained over the raw dataset.

Table 12. Comparison among KNN classification stabilities (raw data and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9423	0.9998	0.9348		0.9420	1.0000	0.9276		0.9440	1.0000	0.9279		0.9378	1.0000	0.9378
2	0.8675	0.8793	0.8589		0.8771	0.8798	0.8780		0.8787	0.8804	0.8789		0.8725	0.8732	0.8804
3	0.8001	0.7864	0.8018		0.8199	0.7912	0.8221		0.7412	0.7864	0.7529		0.8160	0.7917	0.7925
4	0.7158	0.8617	0.7687		0.7711	0.8661	0.7973		0.7692	0.8622	0.7811		0.7592	0.8613	0.8539
5	0.8491	0.8493	0.8658		0.8626	0.8588	0.8809		0.8272	0.8470	0.8465		0.8674	0.8588	0.8137
6	0.9344	0.9577	0.8884		0.9411	0.9653	0.9156		0.9359	0.9601	0.9083		0.9287	0.9604	0.9083
7	0.7378	0.7520	0.7275		0.7418	0.7457	0.7256		0.7471	0.7621	0.7356		0.7276	0.7521	0.7289
8	0.7476	0.8332	0.7472		0.7580	0.8224	0.7848		0.7688	0.8232	0.8028		0.7508	0.8244	0.7388
9	0.8279	0.8558	0.7146		0.8232	0.8613	0.7422		0.8254	0.8597	0.7414		0.8225	0.8572	0.7309
10	0.8896	0.9224	0.8807		0.9013	0.9232	0.9002		0.8937	0.9197	0.8866		0.9028	0.9240	0.8934
11	0.8212	0.9362	0.7800		0.8212	0.9276	0.7986		0.8388	0.9331	0.7991		0.8291	0.9319	0.8912
12	0.8027	0.8537	0.7049		0.7980	0.8515	0.7515		0.7929	0.8473	0.7522		0.7922	0.8429	0.7271
13	0.8176	0.8830	0.8509		0.8409	0.8774	0.8669		0.8357	0.8757	0.8448		0.8354	0.8800	0.8609
14	0.9656	0.9652	0.9748		0.9709	0.9630	0.9729		0.9694	0.9682	0.9774		0.9706	0.9626	0.9719
15	0.8053	0.8095	0.7922		0.8251	0.8149	0.8199		0.8166	0.8189	0.8117		0.8249	0.8158	0.8298
16	0.9451	0.9777	0.7463		0.9484	0.9791	0.7402		0.9476	0.9773	0.8302		0.9444	0.9797	0.9158
17	0.9006	0.9153	0.8708		0.8950	0.9194	0.8689		0.9033	0.9131	0.8194		0.9072	0.9192	0.8825
18	0.8641	0.9133	0.7413		0.8645	0.9088	0.7170		0.8649	0.9099	0.7504		0.8659	0.9097	0.8447
19	0.9653	0.9777	0.9659		0.9646	0.9770	0.9716		0.9651	0.9785	0.9645		0.9623	0.9766	0.9648
20	0.9377	0.9740	0.9474		0.9274	0.9643	0.9600		0.9360	0.9763	0.9574		0.9263	0.9697	0.9520

Table 13. Comparison among CART classification stabilities (raw data and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8665	0.9897	0.9144		0.8664	0.9914	0.9058		0.8546	0.9882	0.9049		0.8625	0.9898	0.9157
2	0.6689	0.7888	0.6967		0.6889	0.7940	0.6913		0.6877	0.7929	0.6990		0.6846	0.7907	0.6968
3	0.6247	0.7397	0.6337		0.6252	0.7418	0.6442		0.6177	0.7446	0.6815		0.6263	0.7423	0.6857
4	0.6753	0.8368	0.7170		0.6920	0.8329	0.7062		0.6944	0.8296	0.7021		0.6906	0.8311	0.7128
5	0.8202	0.8437	0.8293		0.7907	0.8416	0.8298		0.7774	0.8309	0.7865		0.8198	0.8477	0.7774
6	0.8606	0.9274	0.8707		0.8671	0.9224	0.8781		0.8547	0.9251	0.8853		0.8666	0.9287	0.8757
7	0.7317	0.7486	0.7275		0.7175	0.7512	0.7476		0.7527	0.7587	0.7444		0.7316	0.7617	0.7523
8	0.7168	0.8340	0.7212		0.7208	0.8488	0.7488		0.7360	0.8372	0.6928		0.7204	0.8488	0.7200
9	0.7062	0.8557	0.6783		0.7143	0.8483	0.6513		0.7075	0.8549	0.6816		0.7195	0.8543	0.6817
10	0.8079	0.9079	0.7998		0.8128	0.9045	0.8100		0.8176	0.9063	0.8007		0.8241	0.9027	0.8121
11	0.7621	0.8698	0.7207		0.7626	0.8698	0.7124		0.7714	0.8667	0.7179		0.7669	0.8641	0.7943
12	0.6480	0.8068	0.6088		0.6632	0.7951	0.6139		0.6302	0.7893	0.6446		0.6305	0.7766	0.6488
13	0.7581	0.8457	0.7728		0.7467	0.8457	0.7467		0.7517	0.8439	0.7433		0.7456	0.8398	0.7472
14	0.9436	0.9648	0.9468		0.9504	0.9652	0.9450		0.9510	0.9669	0.9455		0.9510	0.9644	0.9488
15	0.7147	0.7929	0.7001		0.7314	0.7923	0.7042		0.7258	0.7902	0.7093		0.7480	0.7963	0.7353
16	0.8479	0.9639	0.7726		0.8505	0.9599	0.7473		0.8504	0.9652	0.7992		0.8418	0.9677	0.8573
17	0.8189	0.8758	0.7994		0.8342	0.8733	0.8328		0.8364	0.8700	0.7900		0.8331	0.8789	0.8072
18	0.7990	0.9071	0.7684		0.7982	0.9035	0.6857		0.8030	0.9062	0.7659		0.7967	0.9046	0.8130
19	0.9246	0.9526	0.9193		0.9179	0.9504	0.9202		0.9182	0.9549	0.9201		0.9168	0.9546	0.9182
20	0.8480	0.9409	0.8729		0.8437	0.9309	0.9077		0.8551	0.9326	0.8760		0.8400	0.9386	0.8780

By carefully observing the data in the tables, it is not difficult to find that no matter which classifier is used, in most datasets, our method is more stable and better than other methods. Take “LSVT Voice Rehabilitation (ID = 8)” as an example; using the CART classifier, the classification stabilities related to EF under four different measures are 0.8340, 0.8488, 0.8372 and 0.8488, respectively, while the classification stabilities related to other methods are lower under the same measure.

Of course, by comparing Table 12 and Table 13, we also found that on the raw dataset, when using the KNN classifier, the neighborhood discrimination index as the measure to derive reduction has the best classification stability. When the other three measures are used, the classification stability of our method is slightly inferior to that of the other two methods on the datasets with IDs of 3, 5, 14 and 15. This also shows that our method is more suitable for the CART classifier. When using the KNN classifier, we recommend using the neighborhood discrimination index as a measure of attribute reduction.

4.4.2. Classification Stabilities(10%, 20%, 30% and 40% Label Noise)

Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20 and Table 21 report different classification stabilities obtained on datasets with different noise ratios, on which the stabilities are tested for KNN and CART classifiers.

Table 14. Comparison among KNN classification stabilities (10% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9548	1.0000	0.9375		0.9563	0.9998	0.9399		0.9552	1.0000	0.9472		0.9531	1.0000	0.9595
2	0.8123	0.8244	0.7969		0.8268	0.8240	0.8189		0.8218	0.8261	0.8130		0.8239	0.8151	0.8019
3	0.7254	0.7552	0.7203		0.7413	0.7547	0.7449		0.6831	0.7562	0.6977		0.7388	0.7543	0.6765
4	0.7452	0.9074	0.7965		0.7683	0.8942	0.8003		0.7716	0.8979	0.7982		0.7719	0.8881	0.8293
5	0.7812	0.8042	0.7784		0.7781	0.7977	0.8051		0.7595	0.8053	0.7644		0.7860	0.8067	0.7116
6	0.9034	0.9334	0.8549		0.9114	0.9367	0.9027		0.8991	0.9396	0.8867		0.9066	0.9346	0.8940
7	0.7189	0.7472	0.7385		0.7183	0.7539	0.7318		0.7109	0.7487	0.7411		0.7209	0.7587	0.7519
8	0.7220	0.7556	0.6184		0.7260	0.7660	0.6532		0.7240	0.7620	0.6628		0.7172	0.7472	0.6348
9	0.8148	0.8400	0.6957		0.8073	0.8469	0.7322		0.8071	0.8457	0.7369		0.8161	0.8435	0.7273
10	0.8692	0.9101	0.8648		0.8753	0.9159	0.8796		0.8768	0.9093	0.8633		0.8786	0.9126	0.8710
11	0.8750	0.9436	0.8207		0.8697	0.9434	0.8222		0.8726	0.9440	0.8228		0.8676	0.9474	0.8731
12	0.7571	0.8180	0.6649		0.7466	0.8198	0.6710		0.7473	0.8249	0.6890		0.7573	0.8110	0.6951
13	0.7650	0.8344	0.7869		0.8037	0.8385	0.7935		0.7885	0.8350	0.7933		0.7954	0.8259	0.8274
14	0.9391	0.9592	0.9428		0.9327	0.9564	0.9466		0.9450	0.9542	0.9371		0.9499	0.9499	0.9378
15	0.7347	0.7545	0.7324		0.7489	0.7525	0.7474		0.7359	0.7572	0.7515		0.7493	0.7560	0.7482
16	0.8858	0.9514	0.6691		0.8795	0.9520	0.6917		0.8820	0.9534	0.7466		0.8900	0.9524	0.9189
17	0.8994	0.9081	0.8436		0.8958	0.9047	0.8764		0.8950	0.9131	0.7994		0.8994	0.9153	0.8081
18	0.8206	0.8820	0.6529		0.8137	0.8831	0.6694		0.8138	0.8766	0.6766		0.8150	0.8814	0.8420
19	0.9202	0.9528	0.9111		0.9286	0.9516	0.9226		0.9224	0.9539	0.9171		0.9265	0.9511	0.9286
20	0.9077	0.9446	0.8991		0.9186	0.9369	0.9237		0.9177	0.9426	0.9151		0.8977	0.9429	0.9066

Table 15. Comparison among CART classification stabilities (10% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8819	0.9881	0.9023		0.8690	0.9921	0.8929		0.8744	0.9877	0.8949		0.8689	0.9924	0.9006
2	0.6215	0.7290	0.6282		0.6456	0.7243	0.6401		0.6384	0.7249	0.6387		0.6486	0.7170	0.6241
3	0.5874	0.6895	0.5859		0.5871	0.6935	0.5972		0.5819	0.7026	0.6453		0.5916	0.6897	0.6443
4	0.6904	0.8774	0.7312		0.6970	0.8653	0.7128		0.7015	0.8684	0.7104		0.6961	0.8638	0.7127
5	0.7074	0.7528	0.6963		0.6898	0.7521	0.7319		0.6888	0.7595	0.7181		0.7193	0.7556	0.6670
6	0.8577	0.9317	0.8380		0.8573	0.9279	0.8587		0.8459	0.9277	0.8693		0.8503	0.9301	0.8580
7	0.7275	0.7372	0.7255		0.7283	0.7539	0.7318		0.7391	0.7517	0.7411		0.7589	0.7717	0.7690
8	0.6272	0.7560	0.6020		0.6216	0.7444	0.6048		0.6352	0.7368	0.6000		0.6132	0.7564	0.5976
9	0.6758	0.7952	0.6233		0.6676	0.7936	0.6338		0.6703	0.7863	0.6429		0.6715	0.7898	0.6361
10	0.7757	0.8901	0.7723		0.7881	0.8834	0.7782		0.7801	0.8866	0.7665		0.7823	0.8821	0.7781
11	0.7422	0.8997	0.7398		0.7410	0.9066	0.7495		0.7467	0.8931	0.7493		0.7376	0.9012	0.7369
12	0.6056	0.7183	0.5932		0.6115	0.7315	0.5922		0.6059	0.7310	0.6063		0.6085	0.7261	0.5971
13	0.7100	0.8061	0.7026		0.7063	0.7946	0.7146		0.7063	0.8146	0.7181		0.7048	0.7993	0.7120
14	0.9176	0.9599	0.9380		0.9398	0.9474	0.9441		0.9283	0.9449	0.9301		0.9430	0.9441	0.9366
15	0.6575	0.7523	0.6436		0.6615	0.7500	0.6566		0.6578	0.7537	0.6637		0.6614	0.7511	0.6691
16	0.7181	0.9312	0.6601		0.7225	0.9313	0.6771		0.7151	0.9244	0.7038		0.7228	0.9336	0.7238
17	0.8103	0.8628	0.7900		0.8181	0.8661	0.7983		0.8069	0.8725	0.7717		0.8144	0.8661	0.7992
18	0.7157	0.8735	0.6346		0.7142	0.8649	0.6195		0.7129	0.8643	0.6728		0.7065	0.8600	0.7125
19	0.8411	0.9281	0.8454		0.8395	0.9213	0.8434		0.8438	0.9258	0.8444		0.8360	0.9214	0.8374
20	0.8217	0.8869	0.8183		0.8203	0.8843	0.8171		0.8166	0.8897	0.8226		0.7946	0.8851	0.8183

Table 16. Comparison among KNN classification stabilities (20% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9752	1.0000	0.9306		0.9660	1.0000	0.9511		0.9731	1.0000	0.9414		0.9667	1.0000	0.9501
2	0.7584	0.7554	0.7407		0.7646	0.7548	0.7693		0.7577	0.7626	0.7642		0.7705	0.7420	0.7651
3	0.7055	0.7764	0.7094		0.7177	0.7733	0.7250		0.6767	0.7863	0.6954		0.7202	0.7762	0.6839
4	0.7797	0.9384	0.8039		0.7948	0.9256	0.8079		0.7954	0.9257	0.8015		0.7920	0.9259	0.8243
5	0.7619	0.7891	0.7491		0.7649	0.7963	0.7530		0.7500	0.8012	0.6960		0.7807	0.7893	0.6760
6	0.8676	0.8934	0.8551		0.8730	0.8890	0.8709		0.8669	0.8890	0.8649		0.8697	0.8927	0.8661
7	0.7319	0.7412	0.7175		0.7313	0.7419	0.7288		0.7481	0.7537	0.7381		0.7499	0.7627	0.7570
8	0.6177	0.6800	0.6100		0.6181	0.6815	0.6304		0.6446	0.6873	0.6358		0.6254	0.6700	0.6004
9	0.7824	0.8283	0.6682		0.7723	0.8262	0.7092		0.7780	0.8198	0.6948		0.7780	0.8234	0.7002
10	0.8327	0.8682	0.8287		0.8382	0.8662	0.8374		0.8290	0.8618	0.7926		0.8410	0.8607	0.8332
11	0.8802	0.9209	0.8788		0.8760	0.9157	0.8755		0.8743	0.9202	0.8759		0.8712	0.9166	0.9067
12	0.7041	0.7661	0.6300		0.7188	0.7756	0.6388		0.7066	0.7683	0.6588		0.6968	0.7671	0.6671
13	0.7409	0.8191	0.7452		0.7650	0.8170	0.7644		0.7643	0.8193	0.7606		0.7685	0.8181	0.8007
14	0.8534	0.8906	0.8481		0.8571	0.8918	0.8574		0.8470	0.8958	0.8531		0.8601	0.8846	0.8154
15	0.6966	0.7211	0.6888		0.7002	0.7186	0.7037		0.6999	0.7210	0.6992		0.7014	0.7175	0.7093
16	0.8051	0.9129	0.6488		0.8101	0.9126	0.6654		0.8006	0.9139	0.6996		0.8007	0.9068	0.8541
17	0.8103	0.8147	0.7567		0.8061	0.8067	0.7658		0.8000	0.8103	0.6961		0.7972	0.8150	0.7436
18	0.8721	0.9147	0.8729		0.8973	0.9142	0.8607		0.8796	0.9104	0.8694		0.8835	0.9061	0.8438
19	0.8079	0.8666	0.8126		0.8183	0.8603	0.8104		0.8137	0.8704	0.8128		0.8137	0.8623	0.8185
20	0.8623	0.9183	0.8394		0.8651	0.9100	0.8700		0.8571	0.9157	0.8620		0.8549	0.9154	0.8674

Table 17. Comparison among CART classification stabilities (20% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8799	0.9945	0.8974		0.8832	0.9965	0.8868		0.8931	0.9928	0.8852		0.8972	0.9956	0.8812
2	0.6180	0.7085	0.6036		0.6203	0.7093	0.6193		0.6158	0.7131	0.6212		0.6325	0.6878	0.6298
3	0.5877	0.7169	0.5883		0.5897	0.7184	0.5975		0.5817	0.7252	0.6144		0.5993	0.7226	0.7118
4	0.7333	0.8972	0.7702		0.7385	0.8884	0.7438		0.7363	0.8873	0.7481		0.7409	0.8879	0.7456
5	0.6660	0.7391	0.6595		0.6709	0.7465	0.6533		0.6763	0.7735	0.6500		0.6844	0.7509	0.6274
6	0.8037	0.8930	0.8087		0.8020	0.8917	0.8113		0.8134	0.9014	0.8131		0.8160	0.8923	0.8127
7	0.7374	0.7426	0.7183		0.7376	0.7429	0.7283		0.7457	0.7541	0.7347		0.7476	0.7682	0.7549
8	0.6177	0.6800	0.6100		0.6181	0.6815	0.6304		0.6446	0.6873	0.6358		0.6254	0.6700	0.6004
9	0.6257	0.7197	0.6061		0.6301	0.7266	0.6049		0.6284	0.7229	0.6049		0.6327	0.7134	0.6135
10	0.7555	0.8525	0.7513		0.7563	0.8525	0.7499		0.7577	0.8513	0.7443		0.7599	0.8468	0.7512
11	0.7593	0.8903	0.8036		0.7536	0.8967	0.7728		0.7600	0.8900	0.7716		0.7559	0.8962	0.7703
12	0.5917	0.6751	0.5556		0.5837	0.6624	0.5798		0.5888	0.6802	0.5927		0.5861	0.6837	0.5700
13	0.6641	0.7585	0.6613		0.6698	0.7619	0.6630		0.6659	0.7654	0.6709		0.6748	0.7498	0.6735
14	0.7419	0.8769	0.7417		0.7486	0.8793	0.7481		0.7517	0.8912	0.7617		0.7477	0.8722	0.7479
15	0.6165	0.7110	0.6056		0.6233	0.7130	0.6128		0.6214	0.7107	0.6237		0.6256	0.7154	0.6381
16	0.6592	0.8898	0.6258		0.6545	0.8849	0.6238		0.6558	0.8832	0.6433		0.6496	0.8905	0.6550
17	0.6919	0.7719	0.6825		0.6969	0.7764	0.6889		0.7019	0.7794	0.6714		0.6939	0.7619	0.6825
18	0.8536	0.9265	0.8302		0.8729	0.9226	0.9121		0.8872	0.9204	0.8951		0.9142	0.9142	0.8627
19	0.7150	0.8055	0.7139		0.7120	0.8040	0.7128		0.7118	0.8088	0.7167		0.7168	0.7904	0.7195
20	0.7357	0.8271	0.7429		0.7426	0.8114	0.7323		0.7334	0.8183	0.7449		0.7223	0.8263	0.7451

Table 18. Comparison among KNN classification stabilities (30% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9647	1.0000	0.9399		0.9672	1.0000	0.9512		0.9688	0.9998	0.9463		0.9637	1.0000	0.9461
2	0.6658	0.6712	0.6593		0.6748	0.6766	0.6811		0.6692	0.6795	0.6743		0.6798	0.6611	0.6804
3	0.6988	0.7755	0.7001		0.7073	0.7740	0.7044		0.6840	0.7803	0.6740		0.7073	0.7719	0.7200
4	0.8010	0.9484	0.8301		0.8107	0.9420	0.8265		0.8144	0.9419	0.8255		0.8123	0.9379	0.8261
5	0.6714	0.6943	0.6638		0.6793	0.6826	0.6924		0.6671	0.6948	0.6452		0.6845	0.6921	0.6402
6	0.8456	0.8574	0.7967		0.8404	0.8610	0.8309		0.8326	0.8584	0.8234		0.8354	0.8597	0.8214
7	0.7254	0.7376	0.7283		0.7416	0.7478	0.7363		0.7507	0.7579	0.7477		0.7516	0.7572	0.7419
8	0.7165	0.7242	0.6062		0.6973	0.7338	0.6081		0.7112	0.7269	0.6427		0.6985	0.7338	0.6212
9	0.7396	0.7767	0.6704		0.7373	0.7735	0.6955		0.7465	0.7743	0.6969		0.7425	0.7737	0.6925
10	0.8294	0.8593	0.8188		0.8357	0.8591	0.8359		0.8270	0.8636	0.7943		0.8371	0.8621	0.8287
11	0.9144	0.9460	0.8402		0.9058	0.9521	0.8742		0.9102	0.9477	0.8747		0.9070	0.9484	0.8982
12	0.6732	0.7495	0.6251		0.6846	0.7407	0.6298		0.6868	0.7356	0.6317		0.6741	0.7402	0.6595
13	0.7531	0.7894	0.7239		0.7744	0.7889	0.7648		0.7639	0.8000	0.7570		0.7635	0.7885	0.7761
14	0.9272	0.9528	0.9402		0.9329	0.9491	0.9194		0.9190	0.9444	0.9325		0.9357	0.9402	0.9372
15	0.6491	0.6538	0.6476		0.6596	0.6561	0.6615		0.6572	0.6593	0.6557		0.6660	0.6583	0.6580
16	0.7272	0.8629	0.6004		0.7292	0.8671	0.6268		0.7266	0.8672	0.6334		0.7252	0.8713	0.7550
17	0.6450	0.6558	0.6261		0.6514	0.6606	0.6486		0.6514	0.6522	0.6289		0.6467	0.6575	0.6186
18	0.8495	0.9290	0.9017		0.9010	0.9195	0.8601		0.9179	0.9187	0.8977		0.9080	0.9179	0.8704
19	0.7304	0.7636	0.7286		0.7253	0.7615	0.7196		0.7225	0.7671	0.7191		0.7242	0.7605	0.7302
20	0.7514	0.8357	0.7591		0.7574	0.8346	0.7586		0.7660	0.8306	0.7666		0.7329	0.8357	0.7714

Table 19. Comparison among CART classification stabilities (30% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.8919	0.9947	0.9047		0.8933	0.9925	0.9033		0.8882	0.9937	0.9035		0.8943	0.9951	0.8996
2	0.5669	0.6514	0.5665		0.5737	0.6448	0.5718		0.5702	0.6606	0.5719		0.5837	0.6373	0.5940
3	0.5999	0.7307	0.5958		0.5937	0.7296	0.5969		0.6007	0.7394	0.6150		0.5988	0.7263	0.7142
4	0.7484	0.9245	0.7845		0.7545	0.9135	0.7645		0.7531	0.9162	0.7604		0.7576	0.9160	0.7615
5	0.5943	0.6448	0.6069		0.5924	0.6400	0.6062		0.5912	0.6605	0.5893		0.6076	0.6462	0.5676
6	0.7730	0.8270	0.7569		0.7730	0.8309	0.7746		0.7690	0.8336	0.7796		0.7700	0.8311	0.7607
7	0.7281	0.7321	0.7248		0.7421	0.7588	0.7351		0.7417	0.7517	0.7383		0.7476	0.7538	0.7467
8	0.5812	0.6662	0.5646		0.5742	0.6546	0.5781		0.5812	0.6473	0.5704		0.5688	0.6592	0.5885
9	0.6159	0.7054	0.6051		0.6306	0.7025	0.6005		0.6143	0.7063	0.6054		0.6204	0.7015	0.6053
10	0.7798	0.8632	0.7787		0.7836	0.8606	0.7772		0.7813	0.8639	0.7825		0.7853	0.8568	0.7774
11	0.7830	0.9254	0.7772		0.7735	0.9246	0.7775		0.7788	0.9202	0.7825		0.7791	0.9267	0.7698
12	0.5698	0.6837	0.5546		0.5661	0.6785	0.5671		0.5751	0.6759	0.5722		0.5734	0.6768	0.5566
13	0.6720	0.7537	0.6656		0.6743	0.7493	0.6606		0.6750	0.7657	0.6659		0.6713	0.7567	0.6689
14	0.9177	0.9596	0.9248		0.9148	0.9562	0.9434		0.9129	0.9485	0.9361		0.9156	0.9434	0.9262
15	0.5800	0.6542	0.5794		0.5821	0.6545	0.5816		0.5776	0.6513	0.5831		0.5828	0.6515	0.6005
16	0.5824	0.8237	0.5613		0.5733	0.8278	0.5704		0.5848	0.8263	0.5772		0.5818	0.8319	0.5809
17	0.6111	0.6864	0.6083		0.6175	0.6836	0.6008		0.6119	0.6869	0.6253		0.6192	0.6692	0.5997
18	0.8884	0.9059	0.8795		0.8810	0.8998	0.8938		0.8697	0.8973	0.8366		0.8440	0.8938	0.8325
19	0.6595	0.7118	0.6615		0.6548	0.7094	0.6608		0.6618	0.7184	0.6653		0.6559	0.7132	0.6491
20	0.6657	0.7711	0.6637		0.6720	0.7657	0.6771		0.6654	0.7654	0.6609		0.6606	0.7651	0.6671

Table 20. Comparison among KNN classification stabilities (40% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9827	1.0000	0.9348		0.9815	1.0000	0.9598		0.9803	1.0000	0.9476		0.9797	1.0000	0.9484
2	0.5908	0.6035	0.5991		0.5945	0.5987	0.5889		0.5970	0.6078	0.6007		0.5969	0.5971	0.6555
3	0.7303	0.8146	0.7257		0.7307	0.8107	0.7277		0.7136	0.8205	0.7059		0.7313	0.8093	0.6990
4	0.8557	0.9869	0.8631		0.8588	0.9818	0.8666		0.8567	0.9811	0.8605		0.8590	0.9794	0.8660
5	0.6565	0.6788	0.6609		0.6658	0.6802	0.6619		0.6444	0.6740	0.6377		0.6781	0.6777	0.6314
6	0.8314	0.8616	0.8111		0.8323	0.8617	0.8324		0.8339	0.8619	0.8093		0.8387	0.8617	0.8197
7	0.7411	0.7511	0.7378		0.7429	0.7517	0.7231		0.7357	0.7487	0.7413		0.7416	0.7518	0.7437
8	0.6692	0.7316	0.6056		0.6636	0.7344	0.6192		0.6708	0.7236	0.6100		0.6688	0.7324	0.6136
9	0.7465	0.7900	0.6806		0.7462	0.7899	0.6995		0.7462	0.7900	0.7119		0.7463	0.7875	0.7157
10	0.8230	0.8566	0.8226		0.8313	0.8534	0.8345		0.8242	0.8601	0.7913		0.8334	0.8537	0.8285
11	0.9379	0.9705	0.8945		0.9371	0.9705	0.9114		0.9353	0.9700	0.9140		0.9422	0.9690	0.9248
12	0.6788	0.7551	0.6376		0.6756	0.7488	0.6629		0.6710	0.7478	0.6622		0.6773	0.7500	0.6802
13	0.7322	0.7843	0.7191		0.7509	0.7774	0.7406		0.7435	0.7861	0.7378		0.7541	0.7835	0.7541
14	0.6600	0.7190	0.6565		0.6601	0.7098	0.6588		0.6532	0.7193	0.6524		0.6628	0.7217	0.6646
15	0.6006	0.6078	0.6035		0.6067	0.6121	0.6103		0.6021	0.6170	0.6056		0.6028	0.6124	0.6134
16	0.6408	0.7865	0.5683		0.6351	0.7863	0.5897		0.6385	0.7982	0.5913		0.6410	0.8015	0.6633
17	0.5819	0.6028	0.5575		0.5783	0.5958	0.5719		0.5894	0.5972	0.5519		0.5886	0.6014	0.5447
18	0.8847	0.9114	0.8801		0.8574	0.9017	0.8797		0.8777	0.8936	0.8647		0.8920	0.9120	0.8895
19	0.6488	0.6623	0.6510		0.6589	0.6646	0.6573		0.6541	0.6675	0.6534		0.6591	0.6648	0.6568
20	0.7247	0.7933	0.7119		0.7153	0.7983	0.7278		0.7319	0.8092	0.7339		0.7264	0.7983	0.7347

Table 21. Comparison among CART classification stabilities (40% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.9000	0.9961	0.9057		0.9096	0.9964	0.9022		0.9086	0.9967	0.9010		0.9073	0.9961	0.8985
2	0.5452	0.5979	0.5520		0.5457	0.5975	0.5480		0.5466	0.6056	0.5519		0.5487	0.5880	0.6156
3	0.6137	0.7648	0.6187		0.6125	0.7670	0.6277		0.6119	0.7772	0.6336		0.6156	0.7629	0.7420
4	0.7955	0.9645	0.8220		0.8003	0.9577	0.8131		0.8024	0.9566	0.8118		0.8090	0.9532	0.8103
5	0.5821	0.6137	0.5851		0.5660	0.6177	0.5753		0.5721	0.6121	0.5865		0.5809	0.6077	0.5823
6	0.7673	0.8304	0.7630		0.7781	0.8306	0.7701		0.7753	0.8370	0.7749		0.7720	0.8291	0.7709
7	0.7344	0.7466	0.7361		0.7383	0.7443	0.7372		0.7385	0.7414	0.7333		0.7330	0.7385	0.7371
8	0.5668	0.6240	0.5776		0.5548	0.6400	0.5428		0.5540	0.6344	0.5548		0.5592	0.6388	0.5740
9	0.6269	0.7297	0.6080		0.6355	0.7333	0.6149		0.6349	0.7329	0.6228		0.6328	0.7306	0.6234
10	0.7863	0.8691	0.7816		0.7923	0.8667	0.7866		0.7836	0.8704	0.8002		0.7917	0.8639	0.7891
11	0.8443	0.9657	0.8160		0.8383	0.9643	0.8326		0.8381	0.9664	0.8324		0.8424	0.9612	0.8367
12	0.5820	0.7241	0.5856		0.5978	0.7305	0.5902		0.5849	0.7254	0.5941		0.5898	0.7302	0.5839
13	0.6944	0.7883	0.6820		0.6994	0.7939	0.6898		0.6922	0.8004	0.6863		0.6902	0.7878	0.6839
14	0.5817	0.7553	0.5853		0.5820	0.7502	0.5807		0.5852	0.7597	0.5927		0.5833	0.7495	0.6139
15	0.5467	0.5973	0.5518		0.5477	0.5960	0.5563		0.5509	0.6024	0.5537		0.5421	0.5965	0.5777
16	0.5408	0.7604	0.5303		0.5383	0.7549	0.5439		0.5358	0.7581	0.5421		0.5384	0.7613	0.5404
17	0.5558	0.6122	0.5508		0.5550	0.6058	0.5533		0.5497	0.6081	0.5425		0.5458	0.6108	0.5431
18	0.8382	0.9272	0.8660		0.8395	0.9196	0.8863		0.8873	0.9090	0.8924		0.8417	0.8924	0.8703
19	0.6279	0.6545	0.6318		0.6263	0.6518	0.6232		0.6343	0.6496	0.6237		0.6245	0.6545	0.6339
20	0.6436	0.7403	0.6500		0.6342	0.7333	0.6633		0.6239	0.7458	0.6497		0.6203	0.7275	0.6586

Through the detailed investigation of Table 14, Table 15, Table 16, Table 17, Table 18, Table 19, Table 20 and Table 21, it can be seen that in all experimental datasets, whether using the CART or KNN classifier, its stability decreases with the increase in label noise. Taking “Statlog (Image Segmentation)(ID=14)” as an example, based on the CART classifier, in Table 15, where the noise ratio is only 10%, the classification stabilities related to EF-AQR, EF-CER, EF-NDIR and EF-RLR are 0.9599, 0.9474, 0.9449 and 0.9441, respectively; these values are reduced to 0.7553, 0.7502, 0.7597 and 0.7495 in Table 21 with a noise ratio of 40%. Such observations suggest that more label noise does have a negative impact on the classification stabilities of selected attributes in the reducts.

It is easy to know that no matter how much proportion of noise is injected into the raw dataset, the classification stabilities of our method is higher than that of the other two comparison methods. The results show that our method is more robust in a dirty data environment.

4.5. Comparisons among AUC of the Derived Reducts

The receiver operating characteristic (ROC) curve has been used in machine learning to describe the trade-off between the hit rate and the error alarm rate of classifiers. Because it is a two-dimensional description, it is not easy to evaluate the performance of the classifier, so we usually use the area under the ROC curve (AUC) in experiments. It is part of the cell square area, so its value is between 0 and 1.0 [52]. In this subsection, the AUC related to three different approaches to derive reducts under four measures will be compared. These are obtained on raw datasets and data setswith label noise ratios of 10%, 20%, 30% and 40%.

4.5.1. Auc (Raw Data)

Table 22 and Table 23 below show the AUC of the raw dataset with different classifiers.

Table 22. Comparison among AUC (raw data and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5157	0.5005	0.6476		0.5151	0.5000	0.6224		0.5163	0.5000	0.6161		0.5203	0.5000	0.5724
2	0.9337	0.9389	0.9251		0.9357	0.9383	0.9354		0.9365	0.9395	0.9353		0.9340	0.9377	0.9370
3	0.6584	0.6752	0.6498		0.6579	0.6730	0.6547		0.6539	0.6766	0.6288		0.6617	0.6775	0.6210
4	0.6028	0.5800	0.6080		0.6218	0.5827	0.6146		0.6282	0.5871	0.6141		0.6945	0.5926	0.6432
5	0.7557	0.7735	0.7591		0.7549	0.7637	0.7472		0.7551	0.7712	0.7625		0.7573	0.7670	0.7497
6	0.7826	0.7817	0.8053		0.7923	0.7813	0.7918		0.7861	0.7838	0.7974		0.7866	0.7894	0.8008
7	0.7326	0.7570	0.7458		0.7372	0.7564	0.7279		0.7351	0.7558	0.7430		0.7283	0.7458	0.7331
8	0.8298	0.8632	0.8111		0.8344	0.8649	0.8269		0.8486	0.8639	0.8488		0.8320	0.8558	0.8045
9	0.8354	0.8489	0.7558		0.8320	0.8492	0.7473		0.8347	0.8458	0.7752		0.8345	0.8425	0.7696
10	0.8148	0.8258	0.7987		0.8156	0.8270	0.8040		0.8153	0.8280	0.8011		0.8139	0.8256	0.8087
11	0.6097	0.6102	0.5348		0.6161	0.6165	0.5512		0.6208	0.6123	0.5417		0.6166	0.6125	0.6437
12	0.8190	0.8532	0.7370		0.8200	0.8476	0.7280		0.8197	0.8491	0.7643		0.8112	0.8499	0.7651
13	0.7905	0.8435	0.7894		0.7850	0.8386	0.7919		0.7949	0.8400	0.7951		0.7873	0.8403	0.7882
14	0.9651	0.9727	0.9660		0.9662	0.9718	0.9669		0.9686	0.9743	0.9712		0.9644	0.9710	0.9678
15	0.7756	0.7946	0.7559		0.7773	0.7953	0.7656		0.7772	0.7963	0.7705		0.7782	0.7998	0.7780
16	0.9774	0.9896	0.8710		0.9781	0.9912	0.8624		0.9792	0.9899	0.9231		0.9784	0.9914	0.9623
17	0.9071	0.9087	0.8457		0.9058	0.9041	0.8804		0.9069	0.9045	0.8281		0.9109	0.9127	0.8507
18	0.9078	0.9227	0.8504		0.9079	0.9227	0.8034		0.9092	0.9222	0.8359		0.9114	0.9241	0.8957
19	0.9562	0.9621	0.9555		0.9554	0.9603	0.9599		0.9590	0.9627	0.9573		0.9553	0.9606	0.9576
20	0.9490	0.9674	0.9473		0.9479	0.9652	0.9595		0.9515	0.9697	0.9640		0.9519	0.9690	0.9531

Table 23. Comparison among AUC (raw data and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5760	0.5206	0.6589		0.8706	0.5198	0.6633		0.5747	0.5222	0.6629		0.5661	0.5189	0.6629
2	0.8244	0.8947	0.8327		0.6968	0.8944	0.8347		0.8325	0.8958	0.8360		0.8306	0.8928	0.8364
3	0.6082	0.6549	0.6150		0.6139	0.6605	0.6244		0.6137	0.6637	0.6135		0.6033	0.6513	0.5887
4	0.6145	0.6186	0.6016		0.6896	0.6314	0.6277		0.6299	0.6266	0.6169		0.6876	0.6334	0.6469
5	0.8033	0.8148	0.8024		0.7102	0.8174	0.8089		0.7906	0.8120	0.7819		0.8031	0.8172	0.7740
6	0.8453	0.8685	0.8319		0.8664	0.8667	0.8393		0.8538	0.8645	0.8461		0.8608	0.8685	0.8433
7	0.7374	0.7567	0.7358		0.7395	0.7556	0.7323		0.7284	0.7548	0.7420		0.7238	0.7483	0.7252
8	0.7375	0.7860	0.7542		0.7464	0.7704	0.7638		0.7281	0.7784	0.7336		0.7239	0.7916	0.7458
9	0.7684	0.8566	0.7324		0.7658	0.8512	0.7079		0.7668	0.8563	0.7395		0.7639	0.8537	0.7319
10	0.7825	0.8080	0.7735		0.8063	0.8090	0.7683		0.7842	0.8124	0.7710		0.7857	0.8093	0.7771
11	0.6207	0.6385	0.5359		0.7419	0.6374	0.5438		0.6398	0.6464	0.5396		0.6344	0.6454	0.6256
12	0.7161	0.8262	0.6700		0.7180	0.8056	0.6676		0.6884	0.8043	0.7084		0.6876	0.8067	0.6941
13	0.7404	0.7962	0.7319		0.7367	0.7998	0.7273		0.7326	0.7995	0.7234		0.7378	0.7951	0.7251
14	0.9713	0.9776	0.9711		0.9520	0.9778	0.9696		0.9733	0.9785	0.9697		0.9723	0.9770	0.9717
15	0.7918	0.8240	0.7645		0.6918	0.8240	0.7705		0.7965	0.8236	0.7804		0.7994	0.8269	0.7913
16	0.9345	0.9830	0.8962		0.8928	0.9807	0.8829		0.9349	0.9828	0.9142		0.9337	0.9836	0.9320
17	0.9049	0.9298	0.8778		0.8811	0.9300	0.8988		0.9137	0.9280	0.8546		0.9121	0.9318	0.8860
18	0.8862	0.9201	0.8669		0.8008	0.9188	0.8069		0.8859	0.9189	0.8463		0.8858	0.9179	0.8900
19	0.9223	0.9403	0.9199		0.9273	0.9389	0.9217		0.9192	0.9423	0.9244		0.9165	0.9389	0.9206
20	0.9152	0.9535	0.9147		0.8843	0.9528	0.9004		0.9123	0.9567	0.9173		0.9110	0.9562	0.9172

With a thorough investigation of Table 22 and Table 23, it is not difficult to conclude that no matter which measures our framework uses as a constraint on search termination, the derived reducts obtained by our method are better than different classifiers. Take “Urban Land Cover (ID = 18)” as an example; the AUC related to EF-CER based on KNN and CART classifiers are 0.9227 and 0.9188, respectively; under the same classifier, the AUC value of EF-CER is higher than PF-CER and FG-CER.

4.5.2. Auc (10%, 20%, 30% and 40% Label Noise)

Table 24, Table 25, Table 26, Table 27, Table 28, Table 29, Table 30 and Table 31 report the different AUCs obtained on datasets with different noise ratios, which were tested on KNN and CART classifiers.

Table 24. Comparison among AUC (10% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5352	0.5000	0.6514		0.5335	0.5007	0.6071		0.5401	0.5000	0.6245		0.5334	0.5000	0.6092
2	0.9139	0.9220	0.9024		0.9205	0.9212	0.9156		0.9189	0.9215	0.9143		0.9174	0.9153	0.9066
3	0.6093	0.6513	0.6087		0.6109	0.6500	0.6168		0.6123	0.6616	0.6023		0.6129	0.6468	0.5720
4	0.6080	0.5685	0.6004		0.6114	0.5752	0.6010		0.6095	0.5736	0.6000		0.6124	0.5768	0.6199
5	0.7147	0.7225	0.7105		0.7155	0.7210	0.7010		0.7142	0.7207	0.6935		0.7239	0.7325	0.6957
6	0.7977	0.8007	0.8006		0.8068	0.8059	0.8028		0.7956	0.8152	0.8114		0.8017	0.8117	0.8087
7	0.7220	0.7593	0.7296		0.7479	0.7542	0.7221		0.7454	0.7498	0.7426		0.7444	0.7479	0.7309
8	0.7872	0.8159	0.7087		0.7851	0.8224	0.7225		0.7812	0.8203	0.7424		0.7866	0.8173	0.7312
9	0.8161	0.8189	0.7358		0.8137	0.8232	0.7470		0.8147	0.8222	0.7720		0.8134	0.8209	0.7760
10	0.8263	0.8478	0.8085		0.8263	0.8505	0.8161		0.8282	0.8420	0.7960		0.8290	0.8504	0.8161
11	0.5514	0.5543	0.5091		0.5583	0.5627	0.5131		0.5615	0.5615	0.5121		0.5542	0.5586	0.5649
12	0.7975	0.8215	0.7148		0.7944	0.8244	0.7053		0.7984	0.8293	0.7464		0.8073	0.8235	0.7521
13	0.7356	0.7799	0.7335		0.7448	0.7805	0.7336		0.7375	0.7725	0.7401		0.7414	0.7755	0.7432
14	0.9429	0.9594	0.9147		0.9159	0.9554	0.9193		0.9437	0.9459	0.9397		0.9434	0.9437	0.9297
15	0.7556	0.7728	0.7220		0.7652	0.7740	0.7479		0.7616	0.7724	0.7485		0.7642	0.7729	0.7406
16	0.9527	0.9764	0.8421		0.9499	0.9751	0.8360		0.9515	0.9761	0.8810		0.9551	0.9753	0.9629
17	0.8585	0.8591	0.8452		0.8595	0.8599	0.8446		0.8559	0.8607	0.8099		0.8609	0.8615	0.8387
18	0.8866	0.9115	0.7962		0.8871	0.9105	0.7658		0.8883	0.9107	0.7987		0.8861	0.9145	0.8847
19	0.9432	0.9614	0.9340		0.9466	0.9590	0.9384		0.9440	0.9584	0.9353		0.9459	0.9578	0.9481
20	0.9414	0.9601	0.9317		0.9473	0.9593	0.9437		0.9471	0.9601	0.9459		0.9358	0.9584	0.9407

Table 25. Comparison among AUC (10% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.6043	0.5227	0.6969		0.8895	0.5101	0.6653		0.6129	0.5181	0.6784		0.5827	0.5109	0.7031
2	0.7993	0.8766	0.7939		0.6504	0.8749	0.7953		0.8041	0.8743	0.8045		0.8050	0.8684	0.7930
3	0.6116	0.6523	0.6122		0.6053	0.6546	0.6149		0.6037	0.6587	0.6074		0.6135	0.6505	0.5732
4	0.6058	0.6004	0.6063		0.6864	0.6091	0.6160		0.6076	0.6034	0.6174		0.6126	0.6100	0.6155
5	0.7405	0.7707	0.7392		0.6200	0.7717	0.7396		0.7414	0.7709	0.7199		0.7460	0.7746	0.7200
6	0.8766	0.9236	0.8575		0.8979	0.9238	0.8783		0.8668	0.9184	0.8880		0.8669	0.9235	0.8732
7	0.7290	0.7549	0.7389		0.7385	0.7471	0.7362		0.7285	0.7465	0.7338		0.7441	0.7441	0.7380
8	0.6903	0.7801	0.6930		0.7012	0.7723	0.6694		0.6939	0.7783	0.7026		0.6933	0.7826	0.6847
9	0.7479	0.8259	0.7059		0.7337	0.8246	0.7057		0.7470	0.8206	0.7203		0.7378	0.8237	0.7233
10	0.7652	0.8056	0.7572		0.7924	0.8056	0.7590		0.7689	0.8033	0.7407		0.7652	0.8024	0.7615
11	0.6141	0.6165	0.5072		0.7576	0.6165	0.5530		0.6163	0.6206	0.5493		0.6182	0.6149	0.6241
12	0.6854	0.7805	0.6650		0.6800	0.7924	0.6533		0.6845	0.7860	0.6792		0.6876	0.7826	0.6806
13	0.6995	0.7475	0.6842		0.6870	0.7449	0.6912		0.6931	0.7477	0.6921		0.6989	0.7446	0.6936
14	0.9447	0.9586	0.9201		0.9308	0.9529	0.9102		0.9113	0.9514	0.9497		0.9411	0.9497	0.9451
15	0.7565	0.7932	0.7301		0.6452	0.7931	0.7430		0.7574	0.7927	0.7426		0.7618	0.7941	0.7423
16	0.8849	0.9755	0.8540		0.8123	0.9755	0.8510		0.8841	0.9732	0.8663		0.8863	0.9770	0.8818
17	0.8845	0.9020	0.8760		0.8353	0.9020	0.8587		0.8910	0.9029	0.8394		0.8888	0.9025	0.8746
18	0.8467	0.9098	0.8113		0.7376	0.9093	0.7669		0.8472	0.9090	0.8028		0.8473	0.9092	0.8436
19	0.8872	0.9286	0.8942		0.8755	0.9276	0.8839		0.8922	0.9262	0.8915		0.8851	0.9256	0.8882
20	0.8982	0.9434	0.8900		0.8666	0.9384	0.9014		0.9007	0.9450	0.9063		0.8897	0.9387	0.9009

Table 26. Comparison among AUC (20% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5160	0.5000	0.6134		0.5252	0.5000	0.5601		0.5220	0.5000	0.5831		0.5193	0.5000	0.5793
2	0.8891	0.8983	0.8843		0.9015	0.8987	0.8997		0.8992	0.9027	0.9009		0.9040	0.8874	0.8645
3	0.5735	0.6049	0.5742		0.5743	0.6042	0.5721		0.5818	0.6125	0.5936		0.5781	0.6079	0.5477
4	0.5792	0.5382	0.5729		0.5865	0.5951	0.5832		0.5847	0.5958	0.5802		0.5837	0.6438	0.6007
5	0.7515	0.7426	0.7458		0.7558	0.7412	0.7523		0.7504	0.7397	0.6636		0.7560	0.7395	0.7102
6	0.7579	0.7540	0.7813		0.7669	0.7489	0.7738		0.7716	0.7657	0.7976		0.7631	0.7560	0.7751
7	0.7440	0.7580	0.7516		0.7364	0.7574	0.7327		0.7404	0.7538	0.7472		0.7446	0.7516	0.7437
8	0.6683	0.7002	0.6279		0.6771	0.7030	0.6297		0.6736	0.7091	0.6579		0.6721	0.6992	0.6404
9	0.7149	0.7112	0.6698		0.7083	0.7151	0.6831		0.7105	0.7084	0.6823		0.7182	0.7143	0.6877
10	0.7713	0.7811	0.7568		0.7721	0.7787	0.7684		0.7696	0.7718	0.7204		0.7713	0.7794	0.7675
11	0.6015	0.5929	0.5304		0.5963	0.5935	0.5349		0.5985	0.5893	0.5352		0.5967	0.5898	0.5971
12	0.7639	0.7854	0.6914		0.7724	0.7819	0.6776		0.7598	0.7846	0.7273		0.7587	0.7768	0.7332
13	0.7863	0.8263	0.7670		0.7978	0.8235	0.7813		0.7967	0.8226	0.7824		0.8013	0.8256	0.8135
14	0.9271	0.9473	0.9240		0.9272	0.9468	0.9282		0.9274	0.9501	0.9300		0.9269	0.9438	0.7907
15	0.7615	0.7870	0.7401		0.7626	0.7874	0.7568		0.7660	0.7893	0.7577		0.7623	0.7896	0.7327
16	0.9182	0.9524	0.8044		0.9201	0.9556	0.7953		0.9173	0.9545	0.8372		0.9184	0.9516	0.9368
17	0.8458	0.8495	0.8280		0.8431	0.8456	0.8287		0.8424	0.8483	0.7980		0.8440	0.8496	0.8315
18	0.8570	0.9294	0.8391		0.8857	0.9213	0.8397		0.8850	0.9132	0.8759		0.8476	0.9025	0.9025
19	0.9026	0.9243	0.9056		0.9044	0.9206	0.9003		0.9016	0.9263	0.9041		0.9020	0.9190	0.9070
20	0.9108	0.9403	0.8989		0.9150	0.9357	0.9148		0.9115	0.9357	0.9118		0.9062	0.9358	0.9141

Table 27. Comparison among AUC (20% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5748	0.5042	0.6349		0.8393	0.5051	0.5941		0.5639	0.5091	0.6196		0.5588	0.5049	0.6446
2	0.7930	0.8580	0.7838		0.6273	0.8570	0.7957		0.7917	0.8614	0.7958		0.7990	0.8416	0.7682
3	0.5818	0.6161	0.5823		0.5837	0.6167	0.5933		0.5863	0.6185	0.5876		0.5843	0.6136	0.5555
4	0.5962	0.5623	0.5874		0.6909	0.5686	0.6055		0.5977	0.5676	0.6011		0.5976	0.5696	0.6050
5	0.7145	0.7470	0.7094		0.5760	0.7493	0.7106		0.7168	0.7528	0.6787		0.7112	0.7501	0.6952
6	0.8009	0.8724	0.8078		0.8494	0.8736	0.8139		0.8167	0.8822	0.8227		0.8124	0.8736	0.8229
7	0.7421	0.7511	0.7311		0.7299	0.7509	0.7236		0.7268	0.7440	0.7273		0.7352	0.7421	0.7233
8	0.5959	0.6704	0.6107		0.6427	0.6590	0.5996		0.6094	0.6673	0.6139		0.6055	0.6617	0.6204
9	0.6931	0.7449	0.6621		0.6822	0.7508	0.6557		0.6912	0.7487	0.6718		0.6958	0.7451	0.6767
10	0.7282	0.7542	0.7151		0.7624	0.7561	0.7167		0.7256	0.7491	0.6899		0.7253	0.7516	0.7193
11	0.6243	0.5996	0.5222		0.7138	0.5995	0.5699		0.6231	0.5983	0.5705		0.6203	0.5976	0.6192
12	0.6659	0.7173	0.6218		0.6515	0.7170	0.6280		0.6647	0.7245	0.6623		0.6671	0.7233	0.6482
13	0.7233	0.7857	0.7174		0.7257	0.7880	0.7131		0.7233	0.7894	0.7094		0.7265	0.7835	0.7263
14	0.8919	0.9456	0.8927		0.8178	0.9458	0.8946		0.8963	0.9505	0.9018		0.8924	0.9415	0.7778
15	0.7543	0.7968	0.7277		0.6335	0.7983	0.7381		0.7518	0.8004	0.7432		0.7538	0.8001	0.7306
16	0.8514	0.9584	0.8260		0.7547	0.9566	0.8137		0.8513	0.9568	0.8349		0.8477	0.9583	0.8471
17	0.8364	0.8751	0.8263		0.7650	0.8705	0.8204		0.8412	0.8784	0.7999		0.8354	0.8695	0.8246
18	0.8601	0.9003	0.8723		0.8363	0.8891	0.8662		0.8380	0.8859	0.8715		0.8422	0.8851	0.8851
19	0.8363	0.8811	0.8347		0.7871	0.8808	0.8322		0.8349	0.8843	0.8385		0.8349	0.8727	0.8352
20	0.8399	0.8946	0.8387		0.8023	0.8922	0.8421		0.8423	0.8885	0.8493		0.8396	0.8933	0.8429

Table 28. Comparison among AUC (30% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5266	0.5000	0.6187		0.5216	0.5000	0.5596		0.5184	0.5006	0.5864		0.5236	0.5000	0.5893
2	0.8559	0.8566	0.8420		0.8602	0.8598	0.8607		0.8578	0.8630	0.8584		0.8627	0.8718	0.7996
3	0.5627	0.5876	0.5642		0.5614	0.5852	0.5593		0.5706	0.5925	0.5768		0.5648	0.5838	0.5459
4	0.5526	0.5238	0.5500		0.5475	0.5256	0.5522		0.5469	0.5650	0.5461		0.5531	0.5958	0.5617
5	0.6896	0.7139	0.6939		0.6883	0.7111	0.6808		0.6894	0.7284	0.6583		0.6928	0.7186	0.6673
6	0.7034	0.7861	0.7005		0.7135	0.7943	0.7058		0.7166	0.7919	0.7374		0.7105	0.7879	0.7110
7	0.7514	0.7595	0.7419		0.7250	0.7589	0.7331		0.7314	0.7560	0.7307		0.7302	0.7514	0.7447
8	0.6568	0.6588	0.6434		0.6636	0.6735	0.6498		0.6693	0.6761	0.6636		0.6579	0.6589	0.6546
9	0.7328	0.7329	0.6834		0.7366	0.7330	0.6951		0.7371	0.7382	0.7035		0.7410	0.7307	0.7076
10	0.7037	0.7104	0.6887		0.7035	0.7991	0.6961		0.7021	0.7092	0.6418		0.7041	0.7068	0.6977
11	0.5957	0.5811	0.5159		0.5933	0.5717	0.5206		0.5913	0.5776	0.5180		0.5901	0.5705	0.5931
12	0.7243	0.7346	0.6645		0.7374	0.7387	0.6608		0.7419	0.7363	0.6895		0.7271	0.7387	0.7089
13	0.7006	0.7298	0.6813		0.7052	0.7641	0.6917		0.7051	0.7999	0.6991		0.6968	0.7015	0.6985
14	0.9123	0.9550	0.9392		0.9280	0.9470	0.9434		0.9300	0.9442	0.9415		0.9160	0.9434	0.9120
15	0.7204	0.7411	0.7011		0.7226	0.7405	0.7125		0.7232	0.7374	0.7123		0.7257	0.7383	0.6951
16	0.8821	0.9365	0.7605		0.8829	0.9387	0.7656		0.8835	0.9371	0.7958		0.8816	0.9399	0.8992
17	0.8138	0.8183	0.8027		0.8164	0.8160	0.8011		0.8151	0.8185	0.7808		0.8190	0.8217	0.7910
18	0.8878	0.9283	0.8834		0.8483	0.9228	0.9098		0.8986	0.9163	0.8614		0.9158	0.9158	0.8392
19	0.8543	0.8685	0.8558		0.8521	0.8690	0.8462		0.8515	0.8708	0.8495		0.8502	0.8646	0.8550
20	0.8728	0.9192	0.8665		0.8718	0.9209	0.8617		0.8779	0.9182	0.8786		0.8613	0.9180	0.8822

Table 29. Comparison among AUC (30% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5685	0.5053	0.6498		0.8944	0.5054	0.5982		0.5599	0.5124	0.6345		0.5549	0.5041	0.6480
2	0.7583	0.8308	0.7476		0.5695	0.8268	0.7632		0.7630	0.8361	0.7641		0.7678	0.8153	0.7148
3	0.5719	0.5951	0.5716		0.5565	0.5961	0.5664		0.5725	0.5985	0.5767		0.5696	0.5948	0.5437
4	0.5648	0.5401	0.5622		0.6978	0.5441	0.5655		0.5621	0.5449	0.5629		0.5658	0.5458	0.5654
5	0.6905	0.7247	0.6956		0.5181	0.7250	0.6861		0.6905	0.7334	0.6656		0.6921	0.7275	0.6710
6	0.7408	0.7612	0.7233		0.7916	0.7591	0.7547		0.7399	0.7643	0.7515		0.7503	0.7602	0.7388
7	0.7502	0.7575	0.7207		0.7328	0.7534	0.7396		0.7383	0.7519	0.7279		0.7430	0.7502	0.7359
8	0.6191	0.6471	0.6120		0.6058	0.6466	0.6043		0.6183	0.6503	0.6252		0.6155	0.6421	0.6216
9	0.6870	0.7308	0.6755		0.6726	0.7313	0.6675		0.6891	0.7333	0.6763		0.6993	0.7341	0.6822
10	0.6653	0.6685	0.6620		0.7481	0.7682	0.6649		0.6750	0.6855	0.6229		0.6725	0.6809	0.6663
11	0.5975	0.5984	0.5264		0.5970	0.6901	0.5403		0.6260	0.6911	0.5364		0.6163	0.6867	0.6202
12	0.6252	0.6800	0.6092		0.6134	0.6694	0.6211		0.6444	0.6739	0.6349		0.6291	0.6760	0.6120
13	0.6574	0.6606	0.6451		0.6196	0.6501	0.6433		0.6574	0.6830	0.6555		0.6549	0.6590	0.6571
14	0.9141	0.9518	0.9112		0.9240	0.9485	0.9174		0.9321	0.9448	0.9199		0.9155	0.9378	0.9293
15	0.7126	0.7693	0.6890		0.5730	0.7655	0.6979		0.7116	0.7662	0.7022		0.7150	0.7659	0.6920
16	0.7991	0.9294	0.7751		0.6576	0.9315	0.7723		0.8037	0.9301	0.7882		0.7966	0.9335	0.7963
17	0.8098	0.8524	0.8023		0.7058	0.8507	0.7955		0.8106	0.8538	0.8056		0.8134	0.8458	0.7932
18	0.8320	0.9262	0.8435		0.8359	0.9233	0.8482		0.9069	0.9157	0.9094		0.8841	0.9094	0.8948
19	0.7972	0.8273	0.8002		0.7250	0.8231	0.7964		0.7942	0.8305	0.7994		0.7963	0.8243	0.7932
20	0.8217	0.8884	0.8173		0.7694	0.8804	0.8270		0.8190	0.8851	0.8192		0.8156	0.8826	0.8189

Table 30. Comparison among AUC (40% label noise and higher values are in bold).

ID	KNN
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5090	0.5000	0.5997		0.5052	0.5000	0.5419		0.5118	0.5000	0.5669		0.5108	0.5000	0.5740
2	0.8032	0.8086	0.7993		0.8085	0.8193	0.8157		0.8115	0.8176	0.8139		0.8114	0.7917	0.7394
3	0.5550	0.5597	0.5540		0.5545	0.5606	0.5552		0.5623	0.5667	0.5550		0.5560	0.5615	0.5365
4	0.5423	0.5481	0.5414		0.5393	0.5707	0.5415		0.5422	0.5501	0.5415		0.5398	0.5421	0.5394
5	0.6451	0.6577	0.6435		0.6548	0.6608	0.6511		0.6508	0.6641	0.6094		0.6513	0.6572	0.6296
6	0.6616	0.6669	0.6663		0.6623	0.6903	0.6716		0.6617	0.7011	0.6860		0.6659	0.6816	0.6664
7	0.7304	0.7582	0.7379		0.7366	0.7472	0.7237		0.7417	0.7439	0.7288		0.7409	0.7435	0.7398
8	0.6170	0.6464	0.6229		0.6327	0.6544	0.6257		0.6550	0.6632	0.6391		0.6491	0.6498	0.6289
9	0.6865	0.6694	0.6425		0.6859	0.6704	0.6454		0.6887	0.6723	0.6590		0.6846	0.6664	0.6615
10	0.6719	0.6805	0.6596		0.6503	0.6610	0.6660		0.6311	0.6506	0.6107		0.6456	0.6630	0.6565
11	0.5526	0.5438	0.5230		0.5419	0.5423	0.5274		0.5468	0.5528	0.5265		0.5353	0.5446	0.5393
12	0.6587	0.6663	0.6233		0.6605	0.6731	0.6229		0.6554	0.6667	0.6542		0.6736	0.6675	0.6825
13	0.6681	0.6812	0.6448		0.6736	0.6529	0.6586		0.6709	0.6445	0.6650		0.6719	0.6983	0.6758
14	0.8419	0.8755	0.8364		0.8431	0.8738	0.8413		0.8411	0.8770	0.8399		0.8421	0.8745	0.7642
15	0.6838	0.6989	0.6673		0.6853	0.7024	0.6783		0.6861	0.7066	0.6791		0.6891	0.7056	0.6648
16	0.8321	0.9019	0.7259		0.8339	0.9011	0.7274		0.8351	0.9038	0.7548		0.8344	0.9050	0.8517
17	0.7505	0.7538	0.7209		0.7466	0.7509	0.7207		0.7495	0.7537	0.7128		0.7543	0.7520	0.7174
18	0.8398	0.9278	0.8710		0.9065	0.9193	0.9016		0.9128	0.9143	0.8965		0.8419	0.9128	0.9029
19	0.7896	0.8044	0.7944		0.7927	0.8078	0.7880		0.7856	0.7887	0.7827		0.7950	0.8245	0.7961
20	0.8364	0.8747	0.8209		0.8355	0.8781	0.8390		0.8395	0.8846	0.8333		0.8318	0.8790	0.8500

Table 31. Comparison among AUC (40% label noise and higher values are in bold).

ID	CART
	PF-AQR	EF-AQR	FG-AQR		PF-CER	EF-CER	FG-CER		PF-NDIR	EF-NDIR	FG-NDIR		PF-RLR	EF-RLR	FG-RLR
1	0.5423	0.5028	0.6229		0.8609	0.5024	0.5837		0.5523	0.5047	0.6049		0.5404	0.5041	0.6314
2	0.7203	0.7926	0.7172		0.5064	0.7936	0.7269		0.7305	0.8016	0.7298		0.7340	0.7761	0.6696
3	0.5655	0.5764	0.5600		0.5329	0.5790	0.5706		0.5581	0.5788	0.5558		0.5600	0.5756	0.5416
4	0.5645	0.5199	0.5503		0.7442	0.5263	0.5562		0.5627	0.5271	0.5597		0.5580	0.5259	0.5621
5	0.6593	0.6865	0.6625		0.4679	0.6920	0.6532		0.6572	0.6938	0.6235		0.6628	0.6945	0.6370
6	0.7095	0.7148	0.6829		0.7849	0.6929	0.7143		0.7154	0.6924	0.7033		0.7121	0.6895	0.7011
7	0.7423	0.7576	0.7311		0.7487	0.7517	0.7218		0.7332	0.7452	0.7419		0.7456	0.7518	0.7387
8	0.6205	0.6585	0.6060		0.5816	0.6507	0.6045		0.6268	0.6686	0.6241		0.6305	0.6542	0.6131
9	0.6641	0.6818	0.6333		0.6497	0.6799	0.6478		0.6651	0.6800	0.6545		0.6616	0.6796	0.6575
10	0.6454	0.6554	0.6391		0.6314	0.6456	0.6428		0.6292	0.6356	0.6002		0.6519	0.6894	0.6471
11	0.5868	0.5944	0.5309		0.7814	0.5531	0.5237		0.5781	0.5533	0.5257		0.5811	0.5520	0.5754
12	0.6069	0.6284	0.5918		0.5727	0.6306	0.5908		0.6129	0.6301	0.6066		0.6017	0.6226	0.5985
13	0.6294	0.6542	0.6348		0.5961	0.6337	0.6227		0.6310	0.6337	0.6225		0.6386	0.6588	0.6334
14	0.8073	0.9002	0.8042		0.6711	0.8979	0.8039		0.8089	0.9032	0.8131		0.8069	0.8973	0.7469
15	0.6832	0.7329	0.6613		0.5219	0.7323	0.6710		0.6806	0.7334	0.6716		0.6849	0.7331	0.6665
16	0.7538	0.8992	0.7324		0.5912	0.8967	0.7337		0.7556	0.9006	0.7459		0.7523	0.9011	0.7516
17	0.7326	0.7840	0.7117		0.6008	0.7791	0.7213		0.7291	0.7879	0.7304		0.7316	0.7759	0.7171
18	0.8643	0.9248	0.8673		0.8316	0.9055	0.8676		0.8560	0.9005	0.8960		0.8865	0.8960	0.8664
19	0.7446	0.7510	0.7517		0.6552	0.7535	0.7459		0.7590	0.7506	0.7464		0.7479	0.7498	0.7619
20	0.7690	0.8454	0.7784		0.7308	0.8358	0.7808		0.7600	0.8481	0.7710		0.7574	0.8382	0.7777

From Table 24, Table 25, Table 26, Table 27, Table 28, Table 29, Table 30 and Table 31, it is not difficult to draw the following conclusions. Whether using the CART or KNN classifier, its AUC value decreases with the increase in label noise. Take “Wine_Nor (ID = 20)” as an example; for the KNN classifier, the regularization loss is used in defining the constraint of attribute reduction, if the noise ratio increases from 10% to 40%, the values of EF-RLR in Table 24, Table 25, Table 26, Table 27, Table 28, Table 29, Table 30 and Table 31 are 0.9584, 0.9358, 0.9180 and 0.8790. Obviously, the AUC has been significantly reduced. Such observations suggest that more label noise does have a negative impact on the AUC.

Note that no matter which ratio of label noise is injected into the data, The value of AUC provided by the EF method is higher than other methods on most datasets. Therefore, our ensemble FOA approach cannot only improve the stability of the reduct but also bring a better classification performance. It also shows that our strategy is more robust in dirty data. However, it is undeniable that our method has a weak disadvantage in AUC value on a small number of datasets, which also provides a direction for our future enhancement research.

5. Conclusions and Future Plans

This research is inspired by introducing the forest optimization algorithm into the problem solving of attribute reduction. To further improve the effectiveness of selected attributes by the forest optimization algorithm, an ensemble framework is developed, which is used to perform ensemble classification based on multiple derived reducts. Our comparative experiments have clearly demonstrated that our framework is better than the other popular algorithms for four widely used measures in rough set. In the fields of medicine and health, there are large amounts of data predictions on drugs and diseases. Our improvement research can bring good benefits to these applications in the future. The following topics deserve further study.

• Our framework can be introduced into other rough set models to perform on complex data under different scenarios, e.g., semi-supervised or unsupervised data.
• Trying to combine our framework with some other effective feature selection techniques is also a challenge to data pre-processing.