Adaptive Superpixel-Based Disparity Estimation Algorithm Using Plane Information and Disparity Refining Mechanism in Stereo Matching

Abstract

The motivation of this paper is to address the limitations of the conventional keypoint-based disparity estimation methods. Conventionally, disparity estimation is usually based on the local information of keypoints. However, keypoints may distribute sparsely in the smooth region, and keypoints with the same descriptors may appear in a symmetric pattern. Therefore, conventional keypoint-based disparity estimation methods may have limited performance in smooth and symmetric regions. The proposed algorithm is superpixel-based. Instead of performing keypoint matching, both keypoint and semiglobal information are applied to determine the disparity in the proposed algorithm. Since the local information of keypoints and the semi-global information of the superpixel are both applied, the accuracy of disparity estimation can be improved, especially for smooth and symmetric regions. Moreover, to address the non-uniform distribution problem of keypoints, a disparity refining mechanism based on the similarity and the distance of neighboring superpixels is applied to correct the disparity of the superpixel with no or few keypoints. The experiments show that the disparity map generated by the proposed algorithm has a lower matching error rate than that generated by other methods.

1. Introduction

In image processing, disparity estimation is to determine the difference of object locations in two images; it is an important technique in distance information retrieval, image stitching, and stereoscopic image processing. It is critical for entertainment, robotic mapping, navigation, object recognition, the advanced driver assistance system, 3D modeling, gesture recognition, etc. Therefore, how to accurately generate the disparity map of two stereo images (i.e., a pair of images are generated at the same time with a known camera distance) becomes a popular, interesting, and exciting research topic.

The disparity map is to represent the number of displacements for each of the pixels in an image pair. Usually, disparity estimation is performed by detecting the matching keypoints between two stereo images. Then, the distance from the object to the camera can be estimated from the disparity. The disparity value is nearly inversely proportional to the scene depth for each corresponding pixel location.

The main motivation of this work is to address the limitation of conventional disparity estimation methods, which are usually based on keypoint matching. Keypoints may distribute sparsely in a smooth region. Moreover, in an image, there are usually many symmetric patterns, and keypoints with very similar descriptors may appear repeatedly in a symmetric region. These problems may lead to conventional keypoint-based methods having limited performance in smooth and symmetric regions.

In this paper, an advanced disparity estimation algorithm that applies both point and semi-global information is proposed. Instead of performing only keypoint-by-keypoint matching, we also apply superpixel information. Since the local information of keypoints and the semi-global information of superpixels are both applied, a more accurate disparity map can be generated, especially for smooth, textural, and symmetric regions. Moreover, several disparity refinement mechanisms are also developed. We use the disparities of neighboring superpixels to correct the disparities of the superpixels that have no or few keypoints. The disparity is refined adaptively according to the surrounding information and the distance of the superpixel centroids. An accurate estimation result can be achieved by the proposed algorithm, because it uses SIFT keypoint-based features, plane-based superpixel information, and the hierarchical fine-tune mechanism based on the Euclidean distance between the superpixel gravities and the weighted coefficients from neighboring information.

In Section 2, a review on related work is presented. Then, the proposed algorithm and the adopted techniques are illustrated in detail in Section 3. In Section 4, the experimental results of the proposed algorithm on the popular Middlebury database [1] are shown. Finally, a conclusion is provided in Section 5.

2. Related Work

Stereo matching is widely applied in computer vision, augmented reality, virtual reality, etc. Many algorithms have been developed to estimate the disparity map from a stereoscopic image pair. However, it is still a challenging problem to accurately construct the disparity map. Stereo matching algorithms can be generally classified into three categories: local matching algorithms, global matching algorithms, and feature-based algorithms.

In general, a local matching method is suitable for real-time applications. They adopt the color/intensity difference and the pixel distance together with a given cost function. In [2], an algorithm based on the measurement of pixel dissimilarity was proposed. It can handle a large untextured region and speed up the matching process by pruning bad searched nodes. Another framework in [3] applies scale-based intensity information. Large-scale information is used to generate a disparity map roughly, and small-scale information is used to refine the result with the smoothness constraint. In [4], a graduated non-convexity algorithm was presented by using the priors of brightness constancy and spatial smoothness to perform disparity estimation robustly. In [5], an approach which is a hybrid of the cross-correlations between stereo-image pairs and scene segmentation results was proposed. In [6], a segmentation-based stereo matching algorithm using a novel multi-cost function and an adaptive support window to reduce the matching ambiguity and improve the robustness was proposed.

In a global matching algorithm, the whole image is taken into consideration for disparity estimation. Different from local matching methods, global matching methods are based on minimizing some energy functions that take the differences in colors and gradients of the whole image into account. In [7,8], the methods based on edges and stereo correlation lines using a connectivity structure were proposed. In [9], a linear interpolation-based disparity estimation algorithm that is robust to sampling and noise was introduced. In [10], an algorithm based on minimizing an energy function accounted from slanted surfaces was proposed. The energy function is minimized in a greedy strategy; it alternately partitions an image into non-overlapping regions and finds the affine parameters to describe the displacement function of each region. In [11], a framework was proposed to extract the structure which reflects the distribution of planar layers from stereoscopic images. Each layer consists of a 3D plane equation, a colored image with a per-pixel opacity (a sprite), and the depth offset relative to the plane. In [12], a method using stochastic optimization was presented. Unlike conventional correlation and feature-matching methods, it eliminates the requirement of interpolation, provides a dense array of disparities, and applies a pyramid architecture to perform hierarchical matching. In [13], the absolute difference, the zero-mean normalized cross correlation, and the rank with census transforms were applied to significantly decrease the error rate in the stereoscopic image-matching process. In [14], the guided filters were efficiently applied for hardware acceleration of the disparity estimation process.

Moreover, the feature-based method usually extracts reliable features/keypoints in stereo images, matches these features/keypoints between two images instead of matching all points, and computes the disparity. In [15], the extended edges, or more precisely, the image curves, which are the projections of edges on the scene, are adopted as the matched features. The extended edge is obtained by an edge detector and then linked into an extended image curve. For the method in [16], the reference image is divided into several parts using the hill-climbing algorithm. Then, the disparity map is estimated by keypoints. The spare corresponding method [17] identifies corners or edges from stereoscopic images and the resultant disparity map is then improved by later processing. In [18], a learning-based algorithm using the features generated by two deeper convolutional neural networks (CNNs) was proposed to estimate a better disparity map by a semi-supervised stereo matching model. In [19], another CNN-based disparity estimation method that applies light-field information and domain-specific convolutions was proposed. In [20], a region CNN (R-CNN)-based method was proposed. It predicts the objects of interest and applies the category-specific shape prior to accurately estimating the disparity in the Lidar system.

In [21], an algorithm based on weighted guided filters and the winner-takes-all policy was proposed. It also adopts the gradient cost and the census transform. In [22], a generic cross-scale cost aggregation framework was proposed. It also applies an inter-scale regularizer in the optimization process and significantly improves the accuracy of disparity estimation. In [23], a pixelwise matching algorithm based on mutual information and the global smoothness constraint was proposed. In [24], a local matching method was proposed to compute the disparity map. First, a cost curve is generated. Then, some initial points are extracted from the cost curve, and the matching points can be found by the discriminator in the initial points. In [25], the local cost function with census-based correlation was applied to perform disparity estimation. In [26], a disparity estimation method that well integrates the techniques of belief propagation, shape-adaptive block matching, and hierarchical matching was proposed. In [27], the authors designed a simple CNN architecture that can learn to compute dense disparity maps directly from stereo inputs. The idea is to use the image warping error instead of the disparity-map residual. In [28], an algorithm that adopts a slanted plane model, dense depth estimation, shape regularization, and the boundary label was proposed. In [29], a method to extract depth information by using the matching cost and CNN-based similarity measurement was introduced. In [30], a novel global disparity estimation model based on view interpolation, vertex property splitting, and mesh alignment regulation was proposed.

We summarize the techniques and the concepts adopted by the proposed algorithm and other existing disparity estimation algorithms in Table 1. Note that, different from other algorithms, the proposed algorithm is superpixel-based. It can integrate keypoint and global information well. Moreover, the techniques of depth fusion, depth extension, and depth estimation are also adopted. They can effectively refine the disparity estimation result.

Table 1. Summary for the proposed and other existing disparity estimation algorithms.

Algorithms	Adopted Techniques
[2]	dynamic programming, fast scanline, and pixel discontinuity detection
[3]	large-scale intensity extraction, small-scale disparity refinement
[4]	scanline on the spatial window, non-convexity detection on image brightness, and spatial smoothness for robust estimation
[5]	guided image filtering, cross correlation cost aggregation on stereo image, and scene segmentation
[6]	mean-shift image segmentation, adaptive multi-cost aggregation, and window outlier suppression
[7,8]	edge-based correlation, edge connectivity, local cost aggregation
[9]	dissimilarity measure, linearly interpolated intensity function
[10]	multiway-cut and the greedy energy policy
[11]	image structure extraction by parametric motion estimation, layer sprite estimation and refinement
[12]	the coarse-to-fine Gaussian pyramid, hierarchical matching, and the stochastic optimization approach
[13]	cross correlation and the rank with census transforms
[14]	hardware acceleration, guided filter
[15]	edge detectors and the projections of extended edges on scene
[16]	hill-climbing technique, feature points with the SAD approach
[17]	corner and edge detection from stereo images
[18]	a CNN-based algorithm with a semi-supervised matching model
[19]	CNN, light-field information, domain-specific convolutions
[20]	R-CNN, point clouds, object-of-interest, category-specific shape prior
[21]	the gradient cost, the census transform, the weighted guided filter, and the winner-takes-all (WTA) strategy
[22]	cost aggregation, local stereo matching, and multiscale
[23]	pixelwise matching and the smoothness constraint
[24]	extreme-point extraction, local matching, the WTA strategy, and simple cost aggregation
[25]	image segmentation, local cost function with census-based correlation, and the sum of absolute difference
[26]	belief propagation, shape-adaptive block matching, and hierarchical matching
[27]	CNN-based dense matching and self-supervised learning
[28]	image segmentation, dense depth estimation by boundary pixels, and shape regularization
[29]	cross-based cost aggregation, left–right consistency, median filters, and bilateral filters
[30]	vertex property splitting and mesh alignment regularization
Proposed Method	entropy rate superpixel generation, superpixel-based disparity estimation, feature-based matching, and adaptive disparity refinement (including depth fusion and depth extension)

3. Proposed Algorithm

In the proposed algorithm, the disparity map is generated by both local and semi-global features. Local information is integrated into the semiglobal one using the entropy rate superpixel (ERS) [31]. Furthermore, after generating the disparity map by the ERS, the result is further optimized by disparity fusion, extension, and refinement. After applying both the pixel-based and the superpixel-based disparities together with several adjusting mechanisms, the final disparity estimation result for a stereoscopic image pair is created [32]. The flowchart of the proposed algorithm is shown in Figure 1. The details of (i) “SIFT keypoint extraction”, (ii) “local-matching cost function”, and (iii) “pixel-based disparity value” are described in Section 3.1. The details of (iv) “ERS segmentation” and (v) “plane-based disparity map” are described in Section 3.2. The details of (vi) “disparity fusion map”, (vii) “disparity extended map”, and (viii) “disparity refinement” are described in Section 3.3.1, Section 3.3.2 and Section 3.3.3, respectively.

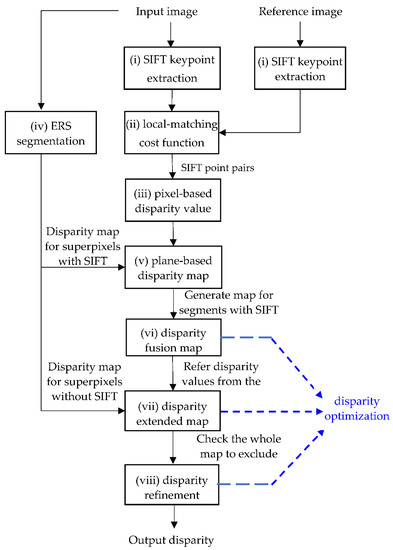
Figure 1. Process of the proposed disparity estimation algorithm.

3.1. Feature Extraction by Applying SIFT

The purpose of the SIFT (scale-invariant feature transform) [33] is to detect or describe local keypoints in an image. It includes multiscale difference of Gaussian (DoG) operations, keypoint localization, orientation determination, and descriptor generation. First, it detects the points of interest (keypoints). The image is convolved with multi-sized Gaussian functions, and the keypoints are taken as the local maxima or minima of the output of the DoG at multiple scales. Then, the keypoints that are noise-like or localized along an edge are excluded by a scoring mechanism. Then, each keypoint is assigned one or more orientations based on the direction of the local gradient. With the multi-scale and orientation assignment mechanisms, the SIFT matching process is robust to image location, scaling, and rotation. Finally, the descriptor with 128 elements is created by the histogram on 4 × 4-pixel neighboring patches with 8 quantized directions.

For a pair of stereo data, there are two images captured from the left-sided and right-sided viewpoints separately. After SIFT keypoint extraction, each keypoint on the left-sided image is applied to match the keypoint on the right-sided image. The matching cost function θ is defined as:

$$\begin{array}{l}\theta (L_m,R_n)={\cos }^{-1}(L_m·R_n)\\ k=\underset{m}{\arg \min }\hspace{0.17em}\theta (L_m,R_n)\\ Match(m,n)=\{\begin{array}{l}1,\hspace{0.17em}\hspace{1em}if\hspace{0.17em}m=k\hspace{1em}and\hspace{1em}\theta (L_m,R_n)\le T\\ 0,\hspace{0.17em}\hspace{1em}otherwise\end{array}\end{array}$$

(1)

where L_m and R_n are the normalized descriptor vectors of the mth and the nth SIFT keypoints from the input L and the reference image R, respectively. The operator (●) means the dot product. From (1), the local matching cost function is designed as the dot product of the descriptor vectors between the left and the right images, respectively. If the arccosine of the dot product of two descriptor vectors is lower than a threshold T, then the corresponding two keypoints are treated as a candidate of a matched keypoint pair. Otherwise, these keypoints are considered to be mismatched.

Note that, in (1), if (L_m●R_n) is near to 1, then θ(L_m, R_n) has a smaller value. If:

   θ(L_k, R_n) < θ(L_k, R_m) for all m ≠ n and
θ(L_k, R_n) ≤ threshold T = 0.6,

(2)

then the kth SIFT keypoint of the input image is considered to match the nth SIFT keypoint of the reference image.

After the matched keypoint pair is determined, the disparity can be calculated by the absolute value of the horizontal coordinate difference in the two matched keypoints.

The SIFT provides an effective way to determine the disparity. However, since SIFT keypoints only reflect local information, we apply several techniques, including the ERS and the refinement mechanism, to integrate local information into semi-global information and perform disparity estimation more accurately.

3.2. Entropy Rate Superpixels for Semi-Global-Based Disparity

ERS segmentation [31] adopts an objective function consisting of two parts: the entropy rate of the random walk on a graph and a balancing term. The entropy rate is helpful to make each region homogeneous, and the balancing term is to constrain the number of regions. Segmentation is executed by the graph that maximizes the objective function under the matroid constraint [31]. In this work, the ERS method is applied to segment the input image into many superpixels for disparity assignment and disparity map creation. First, the number of superpixels is chosen as B_s:

$$\begin{array}{l}{I}_{max}=\max (\{I[n]\hspace{0.17em}|n=1,2,\cdots ,T\}),\\ I_{min}=\min (\{I[n]\hspace{0.17em}|\hspace{0.17em}n=1,2,\cdots ,T\})\\ B_s=\frac{I_{max}-I_{min}}{b}\end{array}$$

(3)

where I[n] is the pixel intensity, n is the index, and T is the total number of pixels. Then, b was chosen as 3 in our experiments. The idea is to adaptively determine the number of superpixels for each image according to the contrast of luminance.

Then, the ERSs that have at least one SIFT keypoint are chosen for disparity assignment. If there are more than one SIFT keypoint in the superpixel, then the disparity of the whole superpixel is determined by the average of the disparity values (i.e., d_avg) of the SIFT keypoints within this superpixel. The formula of disparity assignment for the superpixel S is:

$$d_{avg}[S]={\displaystyle \sum _{i=1}^N{d}_i}/N,\hspace{0.17em}\hspace{1em}{d}_i\in S,$$

(4)

where N is the total number of the matched SIFT keypoints within the superpixel S, and d_i is the disparity value of the ith matched SIFT keypoint. With this process, the disparity of the superpixel with at least one matched SIFT point can be determined well.

Note that, after applying the above method, the disparity of the superpixel without any matched SIFT keypoint has not been determined yet. Moreover, some superpixels may have the disparity value quite different from that of the adjacent superpixels. Therefore, some adjusting methods are required to obtain an even more accurate disparity estimation result, which is described in the next subsection.

3.3. Disparity Optimization

Disparity optimization is to adjust the disparity value obtained by the method in Section 3.2 using the techniques of (i) depth fusion, (ii) depth extension, and (iii) depth refinement.

The goal of disparity fusion is to modify the disparity value of a superpixel by that of the neighboring superpixels. Its purpose is to remove unexpected or unreasonable disparity and increase the accuracy of disparity estimation. Moreover, after applying the method in Section 3.2, the superpixel without any SIFT keypoint (we call it the non-SIFT superpixel) does not have its own disparity value yet. To address this problem, the technique of disparity extension is applied to calculate the disparity of the non-SIFT superpixel. The most similar neighboring superpixel is chosen to generate the disparity value until all of the non-SIFT superpixels have been assigned a disparity value. Finally, a disparity refinement mechanism is performed to achieve an even more accurate disparity estimation result. Each of the adjusting techniques is illustrated in detail as follows.

In disparity optimization, the disparity values of the adjacent superpixels are adopted for disparity fusion, extension, and refinement. First, suppose that the coordinates of the pixels in the Sth superpixel are (x[i], y[i]), i = 1, 2, …, L, where L is the number of pixels in the Sth superpixel. Then, the center of gravity of superpixel S (denoted by x_g[S], y_g[S]) is determined from:

$$x_g[S]={\displaystyle \sum _{i=1}^L{x}_i}/L\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}{x}_i\in S\hspace{0.17em},\hspace{1em}{y}_g[S]={\displaystyle \sum _{i=1}^L{y}_i}/L\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}{y}_i\in S.$$

(5)

Then, the Euclidean distance R of the adjacent superpixels S₁ and S₂ is calculated by using their centers of gravity:

$$R(S_1,S_2)=\sqrt{{(x_g[S_1]-x_g[S_2])}^2+{(y_g[S_1]-y_g[S_2])}^2}.$$

(6)

3.3.1. Disparity Fusion

Disparity fusion is to apply a criterion to update the disparity value of a superpixel. Suppose that S₁ and S₂ are two adjacent superpixels. Then, the disparity value d of superpixel S₁ is replaced by that of superpixel S₂ if the following inequality is satisfied:

$$\frac{|d[S_1]-d[S_2]|}{d[S_1]}>threshold=k_1\times \left(1+\frac{N[S_1]-N[S_2]}{N[S_1]+N[S_2]}\times k_2\right),$$

(7)

where d[S_j] is the disparity value, and N[S_j] (j = 1, 2) is the number of SIFT keypoints of superpixel S_j, respectively. The parameters k₁ and k₂ were chosen as 0.3 and 0.1, respectively, in our experiments. Note that the threshold in the right-hand side of (7) is adjusted according to the number of keypoints in S₁ and S₂. If N[S₁] is larger than N[S₂], the threshold value is increased. By contrast, the threshold is decreased if N[S₁] is smaller than N[S₂]. From (7), one can see that the inequality is easier to be held if:

(i)

the difference of d[S₁] and d[S₂] is large;

(ii)

N[S₁] is much smaller than N[S₂].

In this case, the disparity of S₁ is replaced by that of S₂.

3.3.2. Disparity Extension

The goal of disparity extension is to populate the disparity value for all of the non-SIFT superpixels. Assume that:

{S_1,n | n = 1, 2, …, A} and {S_2,m | m = 1, 2, …, M}

(8)

are the sets of non-SIFT superpixels and the superpixels with matched SIFT keypoints (we call them SIFT-superpixels), respectively, and L and M are the total numbers of non-SIFT superpixels and SIFT superpixels, respectively.

Non-SIFT superpixels have not been assigned a disparity value because there is no matched SIFT keypoint as reference. We assign the disparity value of the non-SIFT superpixel by an iterative process. It is supposed that a more accurate disparity value can be determined by the non-SIFT superpixel with more neighboring SIFT superpixels. Therefore, we first process the non-SIFT superpixel with the largest value of Ω_1,n where Ω_1,n is the number of neighboring SIFT-superpixels of S_1,n. In other words, if:

$$P=\underset{n=1,2,\dots ,L}{\arg Max}\{{\mathsf{\Omega }}_{1,n}\}$$

(9)

then the non-SIFT superpixel S_1,P are processed before other non-SIFT superpixels. The above process is repeated until all non-SIFT superpixels have been processed.

To assign the disparity value on non-SIFT superpixel S_1,P, the disparity values of the adjacent SIFT-superpixels should be applied. However, if there are more than one adjacent SIFT-superpixel, we choose the most proper one for disparity assignment. First, if the Euclidean distance between the centers of gravity of S_1,P and S_2,m is larger than a threshold, then the superpixel S_2,m is not applied to determine the disparity of S_1,P. That is, the adopted SIFT superpixel S_2,m should satisfy that S_2,m is adjacent to S_1,P and that:

R(S_1,P, S_2,m) < k₃,

(10)

where R is defined in (6). In our experiments, we set k₃ = 100.

Second, if there are more matched SIFT keypoints in the superpixel S_2,m and the Euclidean distance between S_1,P and S_2,m is small, then we tend to apply the disparity of S_2,m to estimate the disparity of S_1,P. That is, we first determine the score function as follows:

$$SC(S_{1,P,},S_{2,m})=N(S_{2,m})\times sim\left(S_{1,P},S_{2,m}\right)$$

(11)

where N(S_2,m) is the number of matched SIFT keypoints in S_2,m, and sim(S_1,P, S_2,m) means the similarity of S_1,P and S_2,m. For example, we can choose:

$$sim\left(S_{1,P},S_{2,m}\right)=R_0-R\left(S_{1,P},S_{2,m}\right)$$

(12)

where:

$$R_0=\underset{m=1,2,\dots ,M}{Max}\left(R\left(S_{1,P},S_{2,m}\right)\right)$$

(13)

with this definition, if the distance of the centers of gravity of S_1,P and S_2,m is small, then sim(S_1,P, S_2,m) is large, which means that S_2,m is definitely a valuable reference. Thus, one can use the following equation to assign the disparity value d for the superpixel S_1,P:

$$d[S_{1,P}]=d[S_{2,v}]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if\hspace{0.17em}v=\underset{m=1,2,\dots ,M}{\arg \hspace{0.17em}Max}\{SC(S_{1,P},S_{2,m})\}$$

(14)

3.3.3. Disparity Refinement

The process of disparity refinement is almost the same as that of disparity fusion. The difference is that it is placed after disparity fusion and disparity extension. It further updates the previously determined disparity value of each superpixel iteratively to achieve a lower disparity estimation error.

4. Evaluation and Discussion

The proposed algorithm was evaluated on the Middlebury stereo dataset [1]. The images from this dataset are piecewise planar scenes. The Middlebury stereo dataset contains stereoscopic test images and the ground-truth disparity map for each image whose raw data is to be scaled or divided by a factor of 4 if it is translated into the disparity values.

Then, the Venus image from [1] was applied to show the intermediate results of the proposed disparity estimation algorithm.

First, the results of SIFT keypoint extraction and local matching are shown in the left part of Figure 2. The superpixel segmentation result using the ERS is shown in the right part of Figure 2.

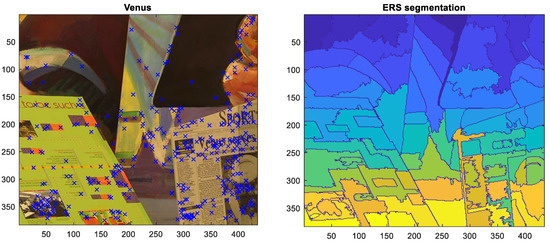
Figure 2. (Left) Results of extracting SIFT keypoints, which are marked by blue x. (Right) Superpixel generation result for the stereoscopic image of Venus.

In the steps of disparity generation and assignment in Figure 1, exploiting SIFT keypoint matching and the ERS in stereo images can obtain pixel- and superpixel-based disparity values, respectively. The result of using these techniques for disparity map generation is shown in the left part of Figure 3. In this step, most superpixels were assigned a disparity value. However, some superpixels (i.e., non-SIFT superpixels) are not yet assigned a disparity value. The problem was later solved by using the technique of disparity extension.

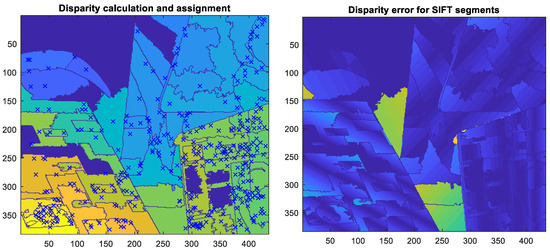
Figure 3. (Left) Disparity calculated using the SIFT keypoints and the superpixel-based assignment method. (Right) The disparity error map determined from the left subfigure.

In the right subfigure of Figure 3, the disparity estimation error (denoted by d_error[i]) of the left subfigure is shown:

$$d_{error}[i]=\left|d_e[i]-d_{gt}[i]\right|$$

(15)

where d_gt[i] is the disparity value in the ground truth, d_e[i] is the estimated disparity of the left subfigure in Figure 3, and i denotes the ith pixel in the disparity map.

Then, to further improve the accuracy of disparity estimation, the technique of disparity fusion was applied; its result is shown in Figure 4.

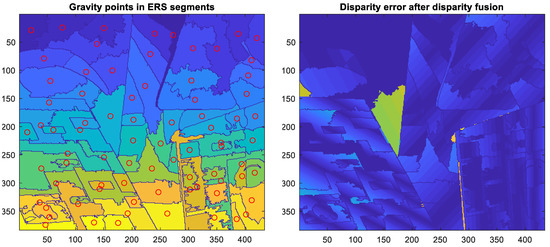
Figure 4. (Left) The result after applying disparity fusion, where the symbol o with red color indicates the gravity of each superpixel. (Right) The corresponding disparity error.

To assign the disparity value of the non-SIFT superpixel, the technique of disparity extension was applied. Its result is shown in Figure 5.

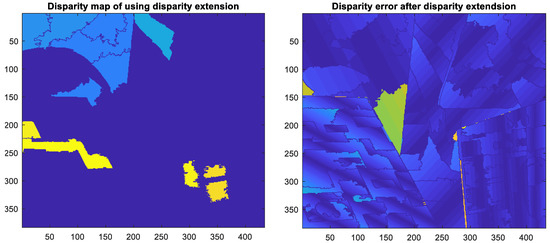
Figure 5. (Left) The result after applying disparity extension. (Right) The corresponding disparity error.

Note that the process of disparity fusion can much improve the accuracy of disparity estimation for SIFT-superpixels, as in Figure 4. By contrast, disparity extension much improves the performance of disparity estimation for non-SIFT superpixels, as in Figure 5.

Then, the technique of disparity refinement was applied to achieve better accuracy and a lower disparity estimation error. In this step, both the disparity values of SIFT superpixels and non-SIFT superpixels were updated and refined. The disparity error maps after the application of the disparity refinement technique and the final data processing step are given in Figure 6. Moreover, the disparity map of the Venus image in the ground truth and that generated by the proposed algorithm are shown in Figure 7. Furthermore, more results obtained by utilizing the proposed disparity estimation algorithm for other stereo images in the Middlebury dataset are also provided. The disparity map comparisons between the ground truth and the disparity estimation results for Tsukuba, Cones, and Teddy images are given in Figure 8, Figure 9 and Figure 10, respectively.

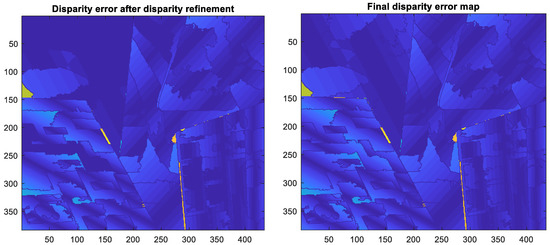
Figure 6. (Left) The disparity error map after applying disparity refinement. (Right) The final disparity error map using all of the processes in the proposed algorithm for Venus.

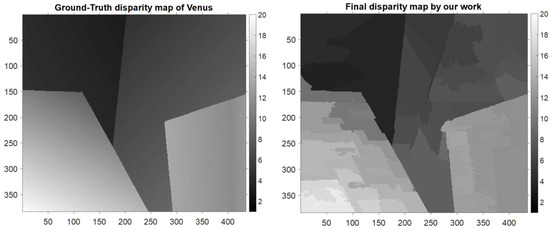
Figure 7. (Left) The disparity map in the ground truth and (Right) that generated from the proposed disparity estimation algorithm for Venus.

Figure 8. (Left) The disparity map in the ground truth. (Right) The disparity map generated by the proposed disparity estimation algorithm for Tsukuba.

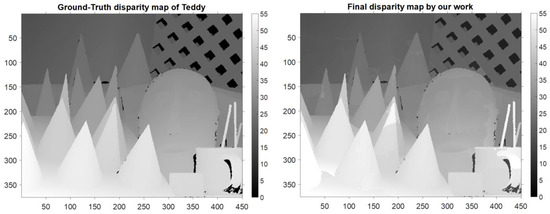
Figure 9. (Left) The disparity map in the ground truth. (Right) The disparity map generated by the proposed disparity estimation algorithm for Cones.

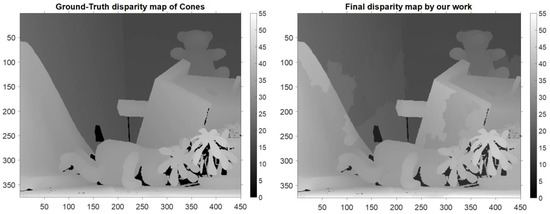
Figure 10. (Left) The disparity map in the ground truth. (Right) The disparity map generated by the proposed disparity estimation algorithm for Teddy.

To evaluate the performance of the disparity estimation method quantitatively, the metric of the MER (matching error rate) was applied. The MER (unit: %) is also called the error matching rate or the matching error percentage. Its formula is as follows:

$$\begin{gathered} MER=\frac{{\displaystyle \sum _{j=1}^T\hspace{0.17em}y[j]}}{T}\times 100 \\ y[j]=\{\begin{array}{c}1,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}if|d_e[j]-d_{gt}[j]|\hspace{0.17em}>\hspace{0.17em}{d}_{thres}\\ 0,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}otherwise,\end{array} \end{gathered}$$

(16)

where d_e is the estimated disparity value, and d_gt is the ground truth, respectively; T is the total number of pixels in the stereo image, and i is the pixel index. Moreover, d_thres is the error matching threshold for disparity estimation. It was chosen as 1 for the evaluation results of the proposed algorithm.

An accurate disparity estimation algorithm should have a lower value of the MER than other disparity estimation algorithms. In Table 2, the disparity estimation results of the proposed algorithm and other existing algorithms are shown. The stereoscopic color images Venus, Tsukuba, Cones, and Teddy, as well as their depth maps in the ground truth, were obtained from the Middlebury stereo dataset [1]. The evaluation results in Table 2 show that the proposed algorithm can achieve a lower disparity error and a more accurate disparity estimation result than other methods. It may be due to the fact that in the proposed algorithm, the local features extracted by SIFT keypoints and the semi-global information of superpixels are both adopted and that the hierarchical disparity correction mechanism based on the weighted similarity and the Euclidean distance of neighboring superpixels is applied to adjust the disparity for the superpixels with no or few keypoints.

Table 2. Comparison of the disparity estimation performance of the proposed algorithm and other methods in terms of the matching error rate (MER; unit: %) using the Middlebury stereo dataset.

Algorithms	Venus	Tsukuba	Cones	Teddy
[21] WG	5.55	5.85	5.25	5.65
[22] CSMST	10.56	10.54	12.88	9.25
[23] SGM	14.78	13.89	18.44	10.54
[23] EP	3.62	5.26	11.84	13.61
[25] PFSGM	1.87	4.20	11.60	9.62
[26] BPMLH	3.31	6.43	18.90	15.50
[27] SsSMnet	2.86	11.90	5.10	9.90
[28] SPS-St	4.38	12.83	5.91	10.86
[29] MC-CNN	5.70	17.40	10.23	15.13
[30] Mesh	1.04	12.80	3.71	8.30
our proposed method	0.97	4.07	3.11	5.34

Moreover, an ablation study was performed (its results are presented in Table 3) to show the effect of each of the proposed techniques. The 1st line in Table 3 shows that, when using SIFT feature extraction (pixelwise information) and ERS segmentation (superpixel-based information), the MERs of the four images were 2.36%, 8.81%, 7.93%, and 10.53%, respectively. In the following three lines, we present the results of the application of the techniques of disparity fusion, disparity extension, and disparity refinement, which were applied to further improve the disparity estimation results. The 2nd line shows that, with disparity fusion, the MERs were reduced by 35.6%, 19.6%, 16.9%, and 16.9% for Venus, Tsukuba, Cones, and Teddy images, respectively. The 3rd line shows that, with disparity extension, the MERs of the four images were reduced by 21.7%, 6.9%, 18.8%, and 18.9%, respectively. The last line shows that, with disparity refinement, the MERs were reduced by 18.5%, 38.2%, 41.8%, and 24.8%, respectively. The results in Table 3 show that all the proposed techniques are helpful for improving the performance of disparity estimation.

Table 3. Ablation study of each of the proposed techniques in the proposed disparity estimation algorithm tested on the Middlebury stereo dataset in terms of the MER (unit: %).

Proposed Work	Venus	Tsukuba	Cones	Teddy
1. after the pixel and superpixel-based disparity map	2.36	8.81	7.93	10.53
2. after disparity fusion	1.52	7.08	6.59	8.75
3. after disparity extension	1.19	6.59	5.35	7.10
4. after disparity refinement	0.97	4.07	3.11	5.34

The proposed algorithm was implemented by MATLAB with Intel CPU i5 1.8 GHz and a 4 GB RAM. The computation time is summarized in Table 4. The complexity of the proposed method is O(NM), where M × N is the size of the input image.

Table 4. Computation time (using MATLAB with Intel CPU i5 1.8 GHz and 4 GB RAM).

	Venus	Tsukuba	Cones	Teddy
Image size	383 × 434 × 3	288 × 384 × 3	375 × 450 × 3	375 × 450 × 3
Computation Time	5.04 s	4.63 s	5.46 s	5.17 s

5. Conclusions

A precise disparity estimation algorithm based on keypoint feature extraction, semi-global superpixel information, and post-adjusting mechanisms is proposed in this paper. In addition to SIFT keypoints, it also adopts the technique of ERS segmentation and several disparity adjustment techniques, including the integration of keypoint and superpixel information, the disparity extension scheme based on the Euclidean distance of superpixels, and the iterative refinement mechanism. The experimental results show that the proposed algorithm performs better than other methods. The ablation study also shows that all the proposed techniques are beneficial for improving the disparity estimation performance. With the proposed algorithm, a very accurate disparity estimation result can be obtained, which is helpful for depth estimation, virtual reality, image stitching, and stereoscopic image processing. Regarding future work, to further improve the proposed algorithm, we are looking forward to applying machine learning techniques to train the models for disparity extension. With the proper choice of superpixel features, the disparity can be determined more precisely with a support vector machine or a deep learning model. Moreover, proper polling mechanisms can also be applied for disparity fusion and to integrate the disparity of the keypoints within a superpixel well. Furthermore, with some modifications, the proposed idea of using superpixel-based information can also be applied in other disparity estimation problems, including the disparity estimation in the single-image scenario or the multi-view scenario.