Quasi-Reflective Chaotic Mutant Whale Swarm Optimization Fused with Operators of Fish Aggregating Device

Abstract

To improve the performance of the whale optimization algorithm and further enhance the search accuracy, while increasing the convergence speed, a quasi-reflective chaotic mutant whale swarm optimization, namely QNWOA, is proposed, fused with an operator of Fish Aggregating Devices (FADs) in this paper. Firstly, the swarm diversity is increased by using logistic chaotic mapping. Secondly, a quasi-reflective learning mechanism is introduced to improve the convergence speed of the algorithm. Then, the FADs vortex effect and wavelet variation of the marine predator algorithm (MPA) are introduced in the search phase to enhance the stability of the algorithm in the early and late stages and the ability to escape from the local optimum by broking the symmetry of iterative routes. Finally, a combination of linearly decreasing and nonlinear segmentation convergence factors is proposed to balance the local and global search capabilities of the algorithm. Nine benchmark functions are selected for the simulation, and after comparing with other algorithms, the results show that the convergence speed and solution accuracy of the proposed algorithm are promising in this study.

1. Introduction

The whale optimization algorithm (WOA) is a newly proposed swarm intelligence optimization algorithm, developed in recent years. Due to its simple algorithm structure, few operators required for operation, fast convergence of iterations, and easy implementation, it has received wide attention and applications in various disciplines, such as power systems [1], data mining [2], training artificial neural networks (ANN) [3], network optimization [4] robot path planning [5], aero-engine optimization [6], and construction engineering [7]. According to existing studies, WOA has the advantage of strong global search capability, but occasionally falls into local optimality and cannot perform global searches comprehensively [8].

To address the above drawbacks and to improve the performance of the algorithm, on the one hand, domestic and foreign researchers have proposed many relevant improved WOA algorithms by using many strategies, such as changing operators [9,10,11,12], fusing chaotic mappings [13,14,15], and mixing other algorithms with the WOA algorithm [16,17,18,19]. For example, a Cauchy mutator was introduced into WOA to vary the individual movement step of whales through the Cauchy inverse cumulative distribution function method [9]; the combination of lens imaging backward learning and optimal worst backward learning strategies were used to improve the quality of swarm individuals [10]. Both the convergence factor and inertia weights were modified by introducing nonlinear strategies to balance the ability of the algorithm between the global exploration and local search, and accelerate the convergence speed of the algorithm [11]. Through differential evolution and Levy mutation, the algorithm was expanded the range of each search and enhanced the global search capability [12]. On the other hand, by introducing Iterative mapping and nonlinear fitting into the algorithm, the initial diversity of the swarm is ensured, while balancing the global search ability and local search of the algorithm to some extent [13]. By introducing Gauss chaos mapping [14] and Singer chaos mapping [15] into the algorithm, it is further demonstrated that chaos mapping has a good improvement effect on the WOA algorithm. In addition, mixing other algorithms is a common strategy in WOA improvement, and combining local search strategies, it can effectively reduce the occurrence of WOA algorithms falling into local optimum situations. For example, by mixing with algorithms, such as slime mould algorithm (SMA) [16], social group optimization (SGO) [17]., teaching-learning-based optimization (TLBO) [18], particle swarm optimization (PSO) [19,20], bat algorithm (BA) [21], and grey wolf optimizer (GWO) [22], it not only reduces the occurrence of falling into local optima, but also solves the problems of insufficient search capability and low efficiency of WOA when high-dimensional problems exist, which is of high use for the performance improvement of WOA algorithms.

The data of the above-mentioned improved WOA algorithm show that, although the performance of some of the test functions has been improved, the computational power of some of the test functions decreases too, and there are still problems, such as easily falling into local optimum and not finding the optimal solution. Therefore, based on previous research, we propose a quasi-reflective chaotic mutant whale swarm optimization fused with FADs (QNWOA) to further improve the convergence speed and optimization accuracy of the algorithm.

2. Whale Optimization Algorithm

The Whale Optimization Algorithm (WOA) is a new heuristic optimization algorithm that mimics the hunting behavior of humpback whales and is, thus, proposed. It is easy to implement and robust compared to other swarm intelligence algorithms, and the algorithm requires fewer control parameters. In nature, humpback whales have a special hunting method, and this hunting method is called the bubble-net hunting strategy. In this strategy, the humpback whale dives tens of meters and then creates a spiral bubble around its prey to gather them before swimming to the surface to feed. Interestingly, the symmetrical route of whale hunting forms a spiral, as shown in Figure 1, and the original whale optimization algorithm was proposed based on the following text.

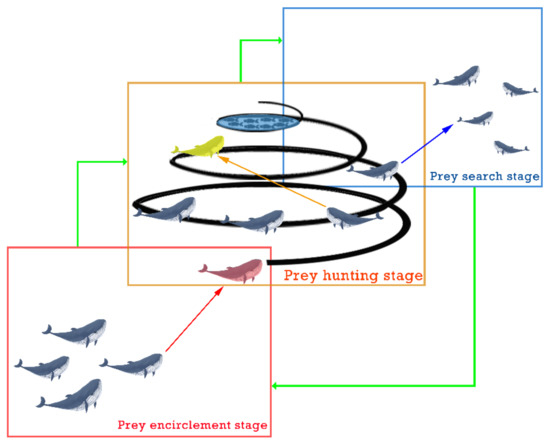
Figure 1. WOA three stages and conversion schematic.

(1) 

Prey encirclement stage

In this stage, the position of each whale is considered as a solution, and the whale closest to the prey is considered as the optimal solution. The other whale individuals complete an “encirclement”, such as the movement towards the prey based on the position of the best individual in the current iteration. In other words, the whales do not currently know the exact location of the prey and simply move in the direction of the current optimal whale, thus, surrounding the prey. To describe this behavior, an equation is written below.

$$D=|CX(\mathrm{t})-X(t)|$$

(1)

$$X(t+1)=X(\mathrm{t})-AD$$

(2)

where t indicates the current number of iterations; D represents the step size between the current individual and the optimal individual; A and C are coefficients; X (t) is the position vector of the optimal whale in the current iteration; X (t) indicates the current position vector of the whale to be moved; A and C can be obtained from the following equations:

$$A=2a{r}_1-a$$

(3)

$$C=2{\mathrm{r}}_2$$

(4)

$$a=2-\frac{2t}{T}$$

(5)

where $r_1$ and $r_2$ are random numbers between (0, 1); the value of a decreases linearly from 0 to 2; t denotes the number of current iterations; T denotes the maximum number of iterations.

(2) 

Prey hunting stage

During this stage, the whale dives into the sea by swimming upward in a spiral position and spitting out bubbles of varying sizes. The bubbles rise to sea level and form a web of bubbles to gather the prey together. In the algorithm, the distance between the individual and the current optimal whale position is firstly calculated, and secondly, the whale is simulated to swim along a spiral trajectory towards the prey position. Based on the behavior of humpback whales, the equation for their spiral swim towards prey is as follows:

$$X(t+1)=X(t)+D_p{e}^{bl}\cos (2\pi l)$$

(6)

where $D_P$= | X (t) − X(t)| denotes the distance vector from the individual whale to the current best whale; b is a constant used to define the shape of the helix, usually taking the value 1, and l is a random number between (−1, 1).

As the whale swims in a spiral towards its prey, it also needs to shrink its encirclement. Therefore, to describe this model of synchronous behavior, a random number P between (0, 1) is introduced. Assume that there is a probability of P to choose the contracting encirclement mechanism and a probability of 1 − P to choose spiral predation to update the whale’s position with the following equation:

$$X(t+1)=\left\{,\begin{array}{}\hfill \mathrm{(7)}& X(t)-AD,\mathrm{r}<P,\hfill \hfill \mathrm{(8)}& X(t)+D_p{e}^{bl}\cos (2\pi l),\mathrm{r}\ge P\hfill \end{array}\right.$$

In the hunting stage, the algorithm sets the value of a to decrease linearly as it approaches the prey, so that the fluctuation of A also decreases with a. During the iterative process, the value of a decreases linearly from 2 to 0, A is a random value within [−a, a], and the algorithm sets that when |A| ≤ 1, the whale attacks the prey, i.e., enters the prey encirclement stage and prey hunting stage.

(3) 

Prey search stage

In this stage, to enhance the diversity of the swarm, the algorithm randomly selects an individual whale in the current iteration and updates the positions of other whales based on the randomly selected whale position, forcing the whales to deviate from the prey and, thus, find a more suitable prey; at the same time, the search capability of the algorithm is enhanced to enable the WOA algorithm to perform a global search. The algorithm sets the whale to perform the prey search stage when |A| ≥ 1, which is formulated as follows:

$$D=|C{X}_{rand}-X(t)|$$

(9)

$$X(t+1)=X_{rand}-AD$$

(10)

where $X_{rand}$ is a randomly selected whale position vector.

3. Improved Whale Optimization Algorithm

3.1. Quasi-Reflection-Based Learning

Ewees et al. [23] proposed a new concept of quasi-reflective-based learning (QRBL) based on opposition-based learning (OBL) and quasi-opposition-based learning (QOBL). The main idea is to determine the location of the quasi-reflection solution by comparing the current solution with the middle value of the upper and lower bounds of the algorithm, and it is known through experiments that QRBL is closer to the optimal solution compared to OBL and QOBL [23] and the equation to generate the quasi-reflective solution $X^{qr}\left(t\right)$ is as follows:

$$M=\frac{(lb+ub)}{2}$$

(11)

$$X^{\mathrm{qr}}(t)=\left\{,\begin{array}{}\hfill \mathrm{(12)}& M+(X(t)-M)\times rand(0,1);X(t)>M\hfill \hfill \mathrm{(13)}& X(t)+(M-X(t))\times rand(0,1);X(t)<M\hfill \end{array}\right.$$

3.2. Logistic Chaos Mapping

Chaotic mapping is a nonlinear theory with the characteristics of non-linearity, universality, traversal, and randomness, which can traverse all states in a certain range without repetition, according to its characteristics, and can help generate new solutions and increase swarm diversity in intelligent algorithm optimization; thus, it is widely used. Although WOA has a good convergence speed, there is still room for improvement in the optimization-seeking capability. Therefore, to improve the performance of the algorithm, this paper introduces logistic chaotic mapping in the WOA algorithm, inspired by the chaotic Jaya algorithm of Jian et al. [24]. Its equation is given as:

$$X(t+1)=\beta \cdot X(t)\cdot (1-X(t))$$

(14)

It has been shown that the chaotic sequence has better pseudo-random properties when β ∈ [3.57, 4].

3.3. Introduction of Mutation Operations for Vortex Effects in FADs

To enhance the ability of the algorithm to escape from the local optimum later, the vortex effect of FADs in the marine predator algorithm (MPA) [25] is introduced into the search stage of the algorithm. In the MPA algorithm, iterations in the later stage cause individuals to obtain longer steps to find another prey distribution environment, and this strategy enables MPA to overcome the early convergence problem and escape from local extremes in the process of finding the best vortex effect, known as FADs. By introducing the FADs eddy current effect and improving it, Equation (10) is changed to Equations (16) and (17), as follows:

$$CF={(1-\frac{t}{T})}^{(2\times \frac{t}{T})}$$

(15)

$$X(t+1)=\left\{,\begin{array}{}\hfill \mathrm{(16)}& X(t)+CF\times x_{rand1} ,rand(0,1)<\mathrm{FADs}\hfill \hfill \mathrm{(17)}& X(t)+(\mathrm{FADs}\times (1-r)+r)\times (x_{rand1}-x_{rand2}),rand(0,1)>\mathrm{FADs}\hfill \end{array}\right.$$

where CF is the adaptive parameter controlling the movement step of the predator; FADs are the influence probability, taken as 0.2; r is the random number within [0, 1]; $x_{rand1}$ and $x_{rand2}$ are the randomly selected individual whale position vectors, respectively.

On this basis, to limit the FADs to perform the search blindly in the early stage, which affects the convergence of the algorithm, this paper only enables the FADs in the late stage of the algorithm iteration and strengthens the upfront capability of the algorithm by introducing the variation operation. Inspired by the wavelet variation particle swarm algorithm proposed by Su et al. [26], wavelet variation is introduced in the preliminary search stage, as follows:

$$w(\phi )=e^{\frac{-{\phi }^2}{2}}\cos (5\phi )$$

(18)

Then Equation (10) changes to:

$$X(t)=\left\{,\begin{array}{}\hfill \mathrm{(19)}& x_i+w(\phi ) \times (ub-X(t)),w(\phi )>0\hfill \hfill \mathrm{(20)}& x_i+w(\phi )\times (X(t)-lb),w(\phi )\le 0\hfill \end{array}\right.$$

In this paper, Morlet wavelet is chosen as the wavelet basis, w (φ) is the wavelet function value, φ is the random value within [−2.5, 2.5], and the mutation probability α is 0.1.

3.4. Convergence Factors for Linear Differential Decrement and Nonlinear Segmentation

In the original WOA algorithm, the search relies on A to switch between global and local through linear decrement. However, due to the disadvantage of the linear decreasing, the algorithm tends to fall into local optimum due to insufficient global search capability in the early stage, and it fails to find the optimal solution in the later stage due to insufficient local exploitation capability. Thus, from Equation (5), a convergence strategy that integrates linear differential decrement and nonlinear decrement is proposed, as follows:

$$a=\left\{,\begin{array}{}\hfill \mathrm{(21)}& 2-(\frac{2}{T^2})\times t^2,t\le \frac{T}{2}\hfill \hfill \mathrm{(22)}& \mu \times t^{\lambda }+\rho ,t>\frac{T}{2}\hfill \end{array}\right.$$

where T denotes the maximum number of iterations, t is the current generation, and μ, λ, and ρ are constants. By introducing the convergence factor of nonlinear segmentation, the algorithm maintains good global searchability in the early stage and accelerates the convergence speed in the later stage, which can effectively balance the local search and global search of the algorithm.

3.5. Algorithm Flowchart and Pseudo-Code

The flow and pseudo-code of the proposed algorithm are as shown in Figure 2 and Algorithm 1 respectively.

Algorithm 1 the proposed algorithm (QNWOA)

1: Input: The swarm size N, maximum number of iteration T.

2: Output: Initialize the random swarm $X_i$(i = 1, 2…, N); Generating species group $N^{*}$ according to logistic chaos and calculate fitness Quasi—reflex learning generates inverse swarm $N^{qr}$ and calculate fitness The first N are selected in new swarm and the optimal individual $X^{*}$ was updated

3: While (t < T) do

4: Update l, P, r, variation rate r1, and influence probability FADs; Update a, A, C by Equation (21) or (22)

5:  if (P < 0.5)

6:   if (|A| ≥ 1)

7:     if (t < T/2)

8:       if (t < r1)

9:         Update $X_i$ location by Equation (19) or (20).

10:       else Update $X_i$ location by Equation (10).

11:       end if

12:      else if $(\mathrm{t}\ge \mathrm{T}/2)\mathrm{Update}{X}_i$ location by Equation (16) or (17).

13:     end if

14:   else if (|A| < 1)

15:     Update $X_i$ location by Equation (2).

16:   end if

17: else if (P ≥ 0.5)

18: Update $X_i$ location by Equation (8).

19: end if

20: Calculate the N individual fitness value of the current swarm; 21: Quasi—reflex learning generates inverse swarm $N^{qr}$ and calculate fitness. 22: The first N was selected in new swarm and the optimal individual $X^{*}$ was updated. 23: End while

24: Return $X^{*}$

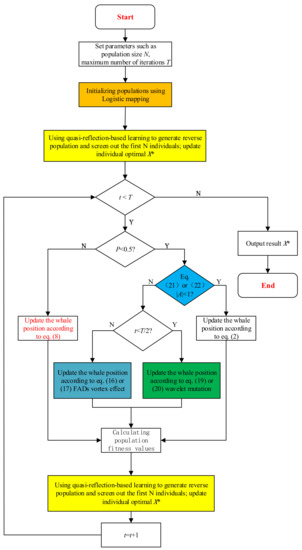
Figure 2. QNWOA algorithm flowchart.

4. Experimental Results and Analysis

4.1. Experimental Design

To test the performance of the improved algorithm, the experiment selects nine benchmark functions that are more representative for testing, as shown in Table 1: F1–F3 for unimodal (UM) function; F4–F7 for multi-modal (MM) function; F8-F9 for composition (CM) function. From the 2D forms of nine benchmarks as shown in Figure 3a–i, it can be seen that the UM function has only one optimal solution and is often used to test the algorithm’s ability to find the optimal solution. Since the MM function has multiple optima, it is difficult to find globally optimal solutions for these functions, but it can be used to test the algorithm’s ability to explore and jump out of local optima by broking the symmetry of iterative routes. The CM function also has a large number of optimal solutions, but it can be used to test the stability of the algorithm, since the optimal solution is easily found due to the low dimensionality. The tests are done in an experimental environment of CPU Inter(R) Core (TM) i7-8700, RAM 16 GB, and MATLAB.

Table 1. Test Functions.

No.	Formula	Dim	Range	Optimal Value
F1	$f_1(x)={\displaystyle \sum _{i=1}^n{x}_i{}^2}$	30	[−100, 100]	0
F2	$f_2(x)={\max }_i\left\{\right|x_i|,1\le i\le n\}$	30	[−100, 100]	0
F3	$f_3(x)={\displaystyle \sum _{i=1}^n{x}_i{}^4}+random(0,1)$	30	[−1.28, 1.28]	0
F4	$f_4(x)={\displaystyle \sum _{i=1}^n[x_i{}^2-10\cos (2\pi x_i)+10]}$	30	[−5.12, 5.12]	0
F5	$f_5(x)=-20\exp [-0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n\cos (2\pi x_i)}}]+20+e$	30	[−32, 32]	0
F6	$f_6(x)=0.1\{\sin (3\pi x_i)+{\displaystyle \sum _{i=1}^{n-1}{(x_i-1)}^2}[1+\sin (3\pi x_{i+1})]$$+{(x_n-1)}^2[1+{\sin }^2(2\pi x_{i+1})]\}+{\displaystyle \sum _{i=1}^{n}u(x_i,5,100,4)}$$u(x,a,k,m)=\left\{\begin{array}{l}k{(x_i-a)}^m{x}_i>a\\ 0-a\le x_i\le a\\ k{(-x_i-a)}^m{x}_i<-a\end{array}\right.$	30	[−50, 50]	0
F7	$f_7(x)=0.1({\sin }^2(3\pi x)+{\displaystyle \sum _{i=1}^{n-1}{(x_i-1)}^2}$ $[1+{\sin }^2(3\pi x_i+1)]+{(x_n-1)}^2$ $(1+{\sin }^2(2\pi x_n))+{\displaystyle \sum _{i=1}^{n}u(x_i,5,100,4)})$	30	[−50, 50]	0
F8	$f_8(x)={\displaystyle \sum _{i=1}^{11}{[a_i-\frac{x_1(b_i{}^2+b_i{x}_2)}{b_i{}^2+b_i{x}_3+x_4}]}^2}$	4	[−5, 5]	0.0003
F9	$f_9(x)=-{\displaystyle \sum _{i=1}^5{[(X-a_i){(X-a_i)}^T+c_i]}^{-1}}$	4	[0, 10]	−10.1532

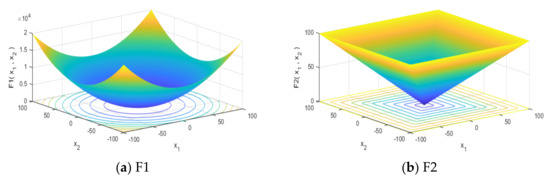
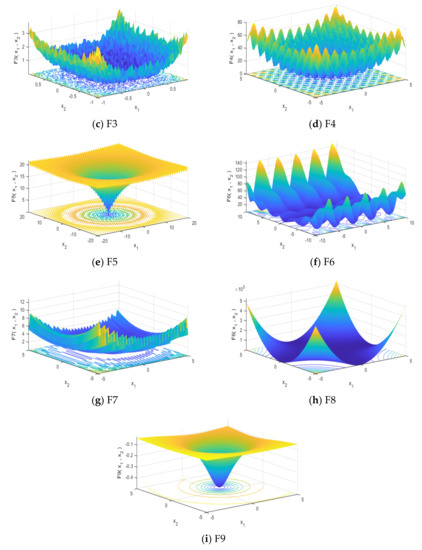
Figure 3. Demonstration of functions.

On the other hand, QNWOA is compared and experimented with the currently existing WOA algorithms and improved WOA algorithms: WOA (traditional whale optimization algorithm), OWOA (whale optimization algorithm based on reverse learning), EWOA (Whale optimization algorithm introducing nonlinear time-varying adaptive weights and differential mutation perturbation factors), WOAWC (Whale optimization algorithm based on adaptive weight and Cauchy mutation); there are also three more representative swarm intelligence algorithms: PSO (particle swarm optimization algorithm), SOA (seagull optimization algorithm), and GWO (gray wolf optimization algorithm).

4.2. Analysis of Experimental Test Results

In our experimental tests, the algorithm parameters are set as shown in Table 2, and all algorithms run 30 times repeatedly on each function to record and count the optimal value (Best), mean value (Mean) and standard deviation (SD) run results, as shown in Table 3 and Table 4. By analyzing the experimental statistical results, it can be seen from the data in Table 3, combining with the lefts of Figure 4, Figure 5 and Figure 6, that both QNWOA and WOAWC converge to the minimum value in the UM function F1, but the convergence speed of QNWOA is much higher than several other algorithms, and QNWOA outperforms other algorithms, in terms of convergence speed, optimal value, mean and standard deviation in F2 and F3. Further, it can be seen from Table 4 that QNWOA outperforms several other swarm intelligence algorithms in F1–F3, in terms of the mean and standard deviation of optimal values. In summary, QNWOA in the UM function has a higher search capability compared to several other algorithms.

Table 2. Algorithm parameter settings.

Maximum number of iterations T	500
Number of swarms N	30
Number of runs	30
QNWOA Mutation rate α	0.1
μ	46,850,000
λ	−3.103
ρ	−0.1976
β	4

Table 3. Function experiment result 1.

No.		Algorithm
		WOA	OWOA	EWOA	WOAWC	QNWOA
F1	Best	9.9137 × 10−86	1.3067 × 10−244	2.7715 × 10−124	0	0
	Mean	4.6344 × 10−73	1.4789 × 10−169	2.1114 × 10−91	0	0
	SD	2.5241 × 10−72	0	1.1564 × 10−90	0	0
F2	Best	1.7473	0.22051	2.5734 × 10−24	3.4581 × 10−204	0
	Mean	47.3422	76.0267	3.2752 × 10−15	1.9033 × 10−182	0
	SD	28.2177	17.6122	1.0942 × 10−14	0	0
F3	Best	0.0001083	8.9531 × 10−6	9.9806 × 10−5	8.8107 × 10−6	3.3573 × 10−6
	Mean	0.0034336	0.00035576	0.0051922	0.00013845	6.9352 × 10−5
	SD	0.0032397	0.000539	0.0057851	8.5724 × 10−5	6.7198 × 10−5
F4	Best	0	0	0	0	0
	Mean	0	0	15.7555	0	0
	SD	0	0	41.2958	0	0
F5	Best	8.8818 × 10−16	8.8818 × 10−16	8.8818 × 10−16	8.8818 × 10−16	8.8818 × 10−16
	Mean	3.9672 × 10−15	3.0198 × 10−15	3.3751 × 10−15	8.8818 × 10−16	8.8818 × 10−16
	SD	2.5945 × 10−15	2.2079 × 10−15	1.6559 × 10−15	0	0
F6	Best	0.0084862	0.011174	0.061662	0.0034545	1.1773 × 10−20
	Mean	0.036696	0.0357	0.36672	0.011456	0.0086561
	SD	0.044194	0.019212	0.28237	0.025047	0.020263
F7	Best	0.10767	0.24004	0.6611	0.071237	1.1285 × 10−18
	Mean	0.51226	0.83157	1.3322	0.13458	0.00049852
	SD	0.30266	0.29615	0.34059	0.04074	0.0010646
F8	Best	0.00030762	0.00030827	0.00031749	0.00030871	0.00030756
	Mean	0.00063911	0.00070656	0.0019246	0.00049698	0.00033584
	SD	0.00047147	0.00044626	0.0041292	0.00019152	6.4589 × 10−5
F9	Best	−10.1515	−10.1532	−10.1532	−10.1511	−10.1532
	Mean	−8.3563	−10.1527	−8.0397	−8.7354	−10.1532
	SD	2.5867	0.00072348	2.8988	2.2751	5.4746 × 10−5

Table 4. Function experiment result 2.

No.		Algorithm
		WOA	SOA	PSO	GWO	QNWOA
F1	Best	1.1605 × 10−85	5.6494 × 10−15	6.2393 × 10−5	1.2139 × 10−29	0
	Mean	5.56 × 10−73	3.4144 × 10−12	0.00043896	7.8984 × 10−28	0
	SD	2.2092 × 10−72	8.3955 × 10−12	0.00034267	1.7267 × 10−27	0
F2	Best	3.9921	5.4184 × 10−5	0.2385	4.2405 × 10−8	0
	Mean	48.4683	0.0038117	0.35914	7.0301 × 10−7	0
	SD	28.5727	0.0057043	0.11779	6.3454 × 10−7	0
F3	Best	5.6855 × 10−5	0.00036337	0.067248	0.00061349	3.4638 × 10−6
	Mean	0.0028777	0.003037	0.11449	0.0017964	7.3138×10−5
	SD	0.0028102	0.0022382	0.042168	0.00086993	8.1288×10−5
F4	Best	0	3.979 × 10−13	16.9228	0	0
	Mean	0	1.0798	47.642	3.0001	0
	SD	0	3.3776	13.9832	4.178	0
F5	Best	8.8818 × 10−16	19.9581	0.0049207	6.839 × 10−14	8.8818 × 10−16
	Mean	3.9672 × 10−15	19.9609	0.012974	1.0167 × 10−13	8.8818 × 10−16
	SD	2.5945 × 10−15	0.0012602	0.0056487	1.8079 × 10−14	0
F6	Best	0.0072029	0.15078	1.4541×10−5	0.019941	5.1833×10−24
	Mean	0.020625	0.31326	0.65821	0.043437	0.0045909
	SD	0.012054	0.14127	0.14127	0.017322	0.012509
F7	Best	0.17038	1.7962	1.0661 × 10−5	0.10076	4.9255 × 10−18
	Mean	0.5566	2.0746	0.0019401	0.62787	0.0010112
	SD	0.19806	0.16968	0.004153	0.24273	0.0044074
F8	Best	0.00030808	0.00031441	0.00030749	0.0003075	0.00030755
	Mean	0.00069231	0.0011808	0.0029492	0.0038868	0.00031558
	SD	0.00051019	0.00020275	0.010759	0.007502	8.4307 × 10−6
F9	Best	−10.152	−10.1283	−10.1532	−10.1531	−10.1532
	Mean	−8.202	−4.0799	−4.8943	−8.9708	−10.1531
	SD	2.8621	4.6169	3.0995	2.1763	8.9997 × 10−5

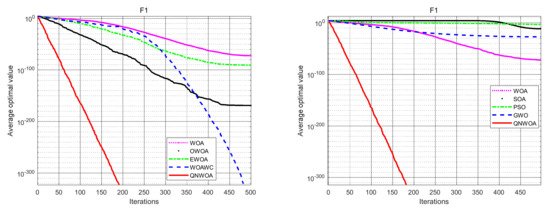
Figure 4. F1 convergence comparison chart.

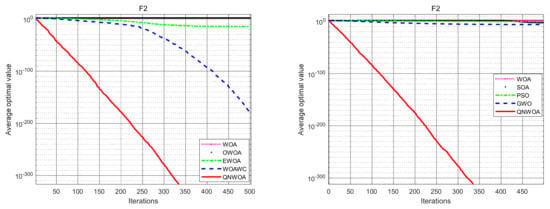
Figure 5. F2 convergence comparison chart.

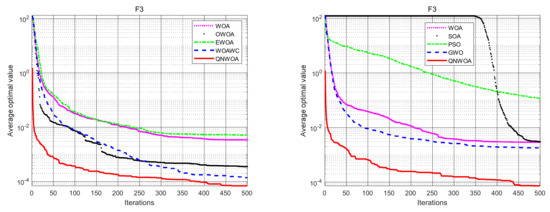
Figure 6. F3 convergence comparison chart.

From the data in Table 3, combined with Figure 7, Figure 8 and Figure 9, we can see that QNWOA and WOAWC in the CM functions, F4 and F5, have significantly better optimal values, mean values, and standard deviations compared with other improved WOA algorithms, while QNWOA is much faster than WOAWC in terms of convergence speed. The improvement in the optimal value is especially large. From Table 4, it can be seen that the QNWOA proposed in this paper outperforms the other three group intelligence algorithms compared in all data, especially in terms of optimal values. It proves that the improved QNWOA effectively avoids the local optimum in the CM function and has a better global capability.

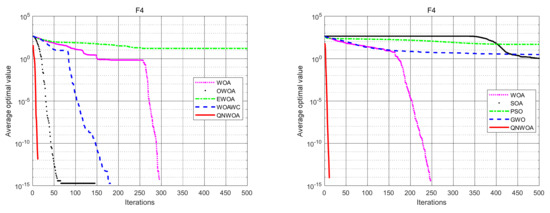
Figure 7. F4 convergence comparison chart.

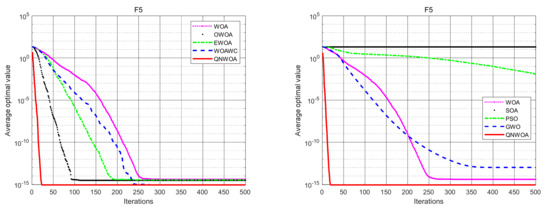
Figure 8. F5 convergence comparison chart.

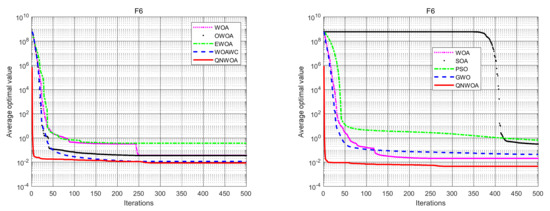
Figure 9. F6 convergence comparison chart.

From the data in Table 3 and Table 4, combined with Figure 10, Figure 11 and Figure 12, we can see that QNWOA in CM functions F7 and F8 has a certain degree of improvement in the optimal value and mean value, compared with the other six algorithms, and the standard deviation has significantly reduced. It has shown that the improved algorithm not only performs better, but also has better stability in the CM functions.

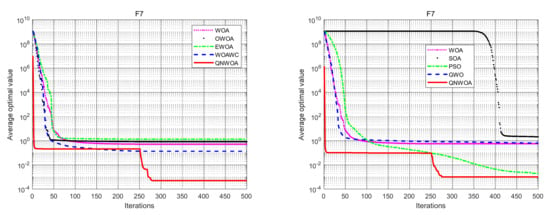
Figure 10. F7 convergence comparison chart.

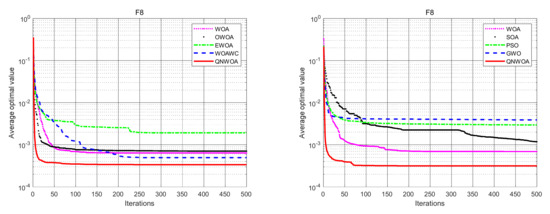
Figure 11. F8 convergence comparison chart.

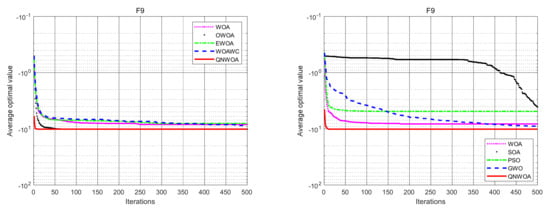
Figure 12. F9 convergence comparison chart.

In general, the improved QNWOA in this paper has significantly improved the convergence speed, convergence accuracy, and stability compared with other algorithms.

5. Conclusions

In this paper, by introducing logistic chaotic mapping and a quasi-reflection-based learning mechanism, we proposed a whale swarm optimization algorithm, namely QNWOA, that fused with the FADs vortex effect and wavelet mutation of marine predator algorithm (MPA) in the search phase. In the algorithm, a nonlinear segmentation convergence factor is used to effectively improve the convergence speed and the search accuracy of the WOA algorithm, according to the experimental results. However, the proposed algorithm fluctuates a lot when the FADs vortex effect is enabled, and the next work should consider how to efficiently coordinate the FADs vortex effect for iterations without affecting the convergence of the algorithm, which require further study in the future.