Pancyclicity of the n-Generalized Prism over Skirted Graphs

Abstract

A side skirt is a planar rooted tree T, $T\ne P_2$, where the root of T is a vertex of degree at least two, and all other vertices except the leaves are of degree at least three. A reduced Halin graph or a skirted graph is a plane graph $G=T\cup P$, where T is a side skirt, and P is a path connecting the leaves of T in the order determined by the embedding of T. The structure of reduced Halin or skirted graphs contains both symmetry and asymmetry. For $n\ge 2$ and $P_n=v_1{v}_2{v}_3\cdots v_n$ as a path of length $n-1$, we call the Cartesian product of a graph G and a path $P_n$, the n-generalized prism over a graph G. We have known that the n-generalized prism over a skirted graph is Hamiltonian. To support the Bondy’s metaconjecture from 1971, we show that the n-generalized prism over a skirted graph is pancyclic.

1. Introduction

The topological structure of an interconnection network or other network can be represented by a graph. The processors can be shown as vertices or nodes, and the communication links between processors can be expressed by edges connecting two vertices together. The study of the structural properties of a network is beneficial for parallel or distributed systems. The problem of finding cycles of various lengths in networks or graphs receives much attention from researchers because this is a key measurement for evaluating the suitability of the network’s structure for its applications and more information, see [1].

Pancyclicity in graph theory refers to the problem of finding cycles of all lengths from three to its order. It was first investigated in the context of tournaments by Harary and Moser [2], Moon [3] and Alspach [4]. Bondy [5] was the first one who introduced and extended the concept of pancyclicity from directed graphs to undirected graphs. In 1971, Bondy [6] posed a metaconjecture which states that almost any nontrivial condition on a graph that implies that the graph is Hamiltonian also implies that the graph is pancyclic (there may be a simple family of exceptional graphs). There are a number of works that correspond to this metaconjecture. For instance, in 1960, Ore [7] introduced the degree sum condition which states that “for each pair of non-adjacent vertices $u,v$ in G, $d\left(u\right)+d\left(v\right)\ge n\left(G\right)$” and showed that if G is a graph satisfying the degree sum condition, then G is Hamiltonian. Bondy [5] showed that if G is a graph satisfying the degree sum condition, then G is pancyclic or $G=K_{n/2,n/2}$. Moreover, in terms of degree sequence of a graph, Chvátal [8] showed that if G is a graph of order $n\ge 3$ with vertex degree sequence $d_1\le d_2\le d_3\le \cdots \le d_n$ and $d_k\le k<n/2$ implies $d_{n-k}\ge n-k$, then G is Hamiltonian. Schmeichel and Hakimi [9] showed that if G satisfies such a condition introduced by Chvátal [8], then G is either pancyclic or bipartite. Recently, the concept of pancyclicity was also extended to hypergraphs, for examples, see [10,11].

Meanwhile, for the prism over a graph G, there are some Hamiltonian and pancyclicity results. For examples, Paulraja [12] proved in 1993 that if G is a 3-connected 3-regular graph, then the prism $G\square P_2$ is Hamiltonian. In 2001, Goddard [13] showed that if G is a 3-connected 3-regular graph that contains a triangle, then the prism $G\square P_2$ is pancyclic. In 2009, Čada et al. [14] showed that if G is a connected almost claw-free graph and $n\ge 4$ is an even integer, then $G\square P_n$ is Hamiltonian. They also showed that if G is a 1-pendent cactus with $\Delta \left(G\right)\le \frac{1}{2}(n+2)$ and $n\ge 4$ is an even integer, then $G\square P_n$ is vertex even pancyclic, i.e., each vertex of $G\square P_n$ is contained in a cycle of each even length.

From our previous study [15], we have proven that the n-generalized prism over any skirted graph is Hamiltonian. Then, to satisfy the metaconjecture, we are interested to answer this question: Is the n-generalized prism over any skirted graph pancyclic? To find the answer, we started by investigating the n-generalized prism over three specific types of skirted graphs. These three types were introduced by Bondy and Lovász [16] in 1985. They studied the pancyclicity of a Halin graph. To show that a Halin graph is almost pancyclic, they restricted the problem to a reduced Halin graph and then showed that a reduced Halin graph H is almost pancyclic, i.e., it contains cycles of each length from three through the order of H, except, possibly, for one even value. Moreover, if it contains no cycle of even length m, then it contains a subgraph which is also a reduced Halin graph or a skirted graph of order $2m-1$ of type I, II or III. Note that skirted graphs of these three types contain symmetric structure. However, the technique that we use to prove pancyclicity of the n-generalized prism over three such specific types of skirted graphs cannot be extended to conclude pancyclicity of the n-generalized prism over any skirted graphs that contain both symmetric and asymmetric structures. In this article, we conduct a novel technique modified from the idea of vertex pacyclicity of lexicographic product over graphs presented in [17] to prove that the n-generalized prism over any skirted graphs is pancyclic.

To study pancyclicity of the n-generalized prism over any skirted graphs, we present some definitions and preliminary knowledge in Section 2. In Section 3, we prove that the n-generalized prism over a triangle is pancyclic. In Section 4, we prove pancyclicity of the n-generalized prism over a skirted graph. Finally, conclusions and discussion about our future study are provided in Section 5.

2. Preliminaries

We consider a finite undirected simple graph. Several terminologies of graph theory presented in this article follow from West’s textbook [18]. The length of a path or a cycle is the number of its edges. A path of length $n-1$ is denoted by $P_n$. An $(s,t)$-path of a graph G is a path in G from s to t, denoted by $P(s,t)$. Then, $P(t,s)$ denotes the reversed path of $P(s,t)$. A path in G is a spanning path if it contains all vertices of G. A cycle of G is a Hamiltonian cycle if it contains all vertices of G. A graph G is said to be Hamiltonian if it contains a Hamiltonian cycle. A graph G of order n is said to be pancyclic if it contains a cycle of each length l for $3\le l\le n$. A tree is a connected graph with no cycles. A rooted tree is a tree with one vertex a chosen as its root. For each vertex u of a rooted tree with root a, let $P\left(u\right)$ be the unique $(a,u)$ path. The parent of u is its neighbor on $P\left(u\right)$, the children of u are its other neighbors, the descendents of u are the vertices v of the rooted tree such that $P\left(v\right)$ contains u, the leaves are vertices of the rooted tree having no children and the internal vertices are vertices of the rooted tree having children.

Let G and H be two graphs. The Cartesian product of graphs G and H, denoted by $G\square H$, is defined as a graph with the vertex set $V\left(G\right)\times V\left(H\right)$ and an edge $\{(u_1,v_1),(u_2,v_2)\}$ presents in the Cartesian product whenever $u_1=u_2$ and $v_1{v}_2\in E\left(H\right)$ or symmetrically $v_1=v_2$ and $u_1{u}_2\in E\left(G\right)$. For $n\ge 2$ and $P_n=v_1{v}_2{v}_3\cdots v_n$, we call a graph $G\square P_n$, the n-generalized prism over a graph G. The 2-generalized prism over a graph G is called the prism over a graph G. For convenience, the n-generalized prism over a graph G is referred to a family of the n-generalized prism over a graph G for all $n\ge 2$. If $u\in V\left(G\right)$, then, for ease, we refer to the vertex u in the s-th copy of $G\square P_n$ as $u^{\left(s\right)}$ instead of $(u,v_s)$.

In a graph G and its subgraph $H=\left(V\right(H),E(H\left)\right)$, the contraction of H is the replacement of H by a single vertex whose incident edges are the edges other than edges in $E\left(H\right)$ that are incident to some vertices in $V\left(H\right)$.

A Halin graph [16] is a plane graph $\mathcal{H}=T\cup C$, where T is a planar tree with no vertices of degree two and at least one vertex of degree at least three, and C is a cycle connecting the leaves of T in the cyclic order determined by the embedding of T.

Let x be a vertex of C and a be the neighbor of x in T. Then, the graph $G=\mathcal{H}-x$ is called a reduced Halin graph with root a. Clearly, $G=T^{\prime }\cup P$, where $T^{\prime }=T-x$ and $P=C-x$. Note that $T^{\prime }$ has no vertex of degree two except possibly the vertex a. For technical reasons, Bondy and Lovász [16] regarded that a single vertex is also a reduced Halin graph.

In this study, we are interested in the pancyclicity of the Cartesian product of a reduced Halin graph or a skirted graph G and a path $P_n$ for $n\ge 2$. We can see that the Cartesian product is pancyclic only if the order of G is at least 2. Here, we recall that a skirted graph is isomorphic to a reduced Halin graph defined by Bondy and Lovász [16]. However, we exclude the case of a single vertex.

Before giving a definition of a skirted graph, let us introduce a definition of a side skirt as follows.

A side skirt is a planar rooted tree T, $T\ne P_2$, where the root of T is a vertex of degree at least two, and all other vertices, except the leaves, are of degree at least three.

Now, a skirted graph is a plane graph $G=T\cup P$, where T is a side skirt, and P is a path connecting the leaves of T in the order determined by the embedding of T (see Figure 1).

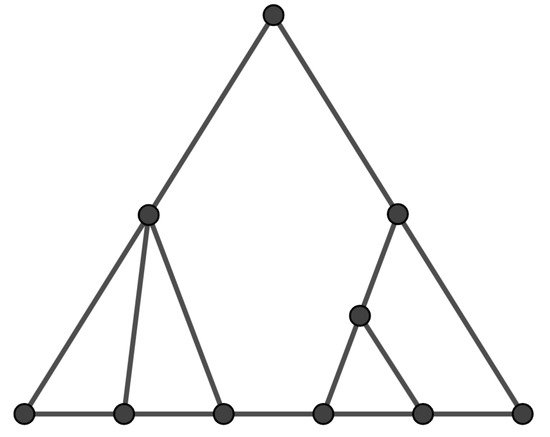
Figure 1. A skirted graph.

Let $G=T\cup P$ be a skirted graph, a be the root of T and $u_0,u_{\alpha }$ be the endpoints of P. Then, the graph G is called a skirted graph with root a and is denoted by $G(a,u_0,u_{\alpha })$. We notice that if u is a vertex of a side skirt T, then u and its descendents induce a skirted subgraph of G.

Since our skirted graphs are isomorphic to reduced Halin graphs defined by Bondy and Lovász [16], we obtain the following theorem and lemma from their study.

Theorem 1

([16]). A skirted graph is Hamiltonian.

In order to mention about the Lemma 1 of [16], let us introduce some notations as follows. For any skirted graph $G(a,b,c)=T\cup P$, we denote the path P of length $\alpha$ by $u_0{u}_1{u}_2\cdots u_{\alpha }$, and the $(a,c)$-path of length $\beta$ and the $(a,b)$-path of length $\gamma$ in T by $y_0{y}_1{y}_2\cdots y_{\beta }$ and $x_0{x}_1{x}_2\cdots x_{\gamma }$, respectively. Thus, $y_0=x_0=a$, $u_0=x_{\gamma }=b$, and $u_{\alpha }=y_{\beta }=c$ (see Figure 2).

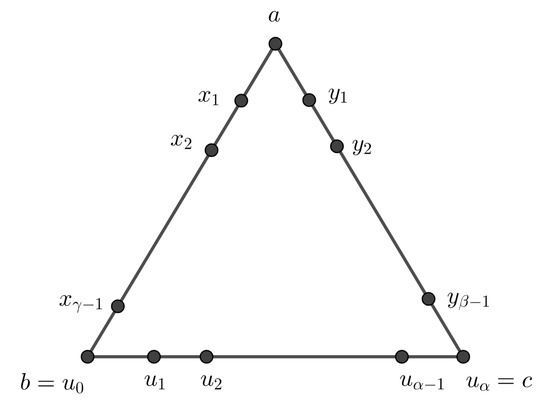
Figure 2. Paths $u_0{u}_1{u}_2\cdots u_{\alpha }$, $(a,c)$-path and $(a,b)$-path of $G(a,b,c)$.

Lemma 1

([16]). Let $G=G(a,b,c)$ be a reduced Halin graph or a skirted graph of order m. Then, G contains:

(i) 

an $(a,c)$-path of each length l for $\alpha +\gamma \le l\le m-1$;

(ii) 

a $(b,c)$-path of each length l for $\alpha \le l\le m-1$.

Remark 1.

We obtain that

(i) 

Lemma 1(i) gives an $(a,b)$-path of each length l for $\alpha +\beta \le l\le m-1$ by the symmetry of $G(a,b,c)$;

(ii) 

To track down the path from each skirted subgraph of $G(a,b,c)$, a $(b,c)$-path of length $m-2$ (without the root a) can be obtained by Lemma 1(ii).

From our previous study [15], we have proven the following theorem.

Theorem 2

([15]). The n-generalized prism over any skirted graphs is Hamiltonian.

Now, we notice that a skirted graph $G=T\cup P$ contains a cycle of length three and one of the edges of such cycle belongs to the path P as follows.

Lemma 2.

A skirted graph $G=T\cup P$ contains a cycle of length three, and exactly one edge of the cycle belongs to the path P.

Proof. 

To prove this statement, we let $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. Consider the side skirt T. Since T is a finite rooted tree, there exists an internal vertex u such that all of its children are leaves of T. Since the degree of u is at least three (can be two if u is the root of T), u has at least two children. Let U be the set of all children of u. Thus, $U\subseteq V\left(P\right)$ and $\left|U\right|\ge 2$. Let $u_i\in U$ and i be the minimum index of vertices in U. Since u has at least two children and a skirted graph is a plane graph, $u_{i+1}\in U$. Thus, $\{u,u_i,u_{i+1}\}$ induces a cycle of length three in G. Moreover, this cycle has one edge $u_i{u}_{i+1}$ and belongs to the path P. □

In general, a triangle in graph theory usually means a cycle of length three. However, in this research, we define a triangle as follows.

Definition 1.

(i) 

Let $G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. For $i,j\in \{0,1,2,\dots ,\alpha \}$ and $i<j$, an induced subgraph $C(u,u_i,u_j)$ of $G(a,u_0,u_{\alpha })$ is said to be a triangle in $G(a,u_0,u_{\alpha })$ if u is an internal vertex of T such that all children of u are leaves of T and $u_i$ is the first vertex and $u_j$ is the last vertex in P in which $u_i$ and $u_j$ are children of u. Moreover, since a skirted graph $G(a,u_0,u_{\alpha })$ is a plane graph, vertices between $u_i$ and $u_j$ in the path P, $u_{i+1},u_{i+2},u_{i+3},\cdots ,u_{j-1}$, are all children of u;

(ii) 

From the triangle $C(u,u_i,u_j)$, if $i+1=j$, then $C(u,u_i,u_j)$ is called a single-triangle. Otherwise, $C(u,u_i,u_j)$ is called a multi-triangle (see Figure 3).

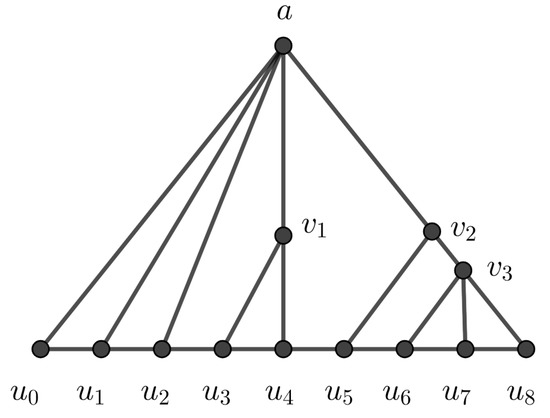Figure 3. $C(v_1,u_3,u_4)$ and $C(v_3,u_6,u_8)$ are a single triangle and a multi-triangle in $G(a,u_0,u_8)$, respectively, while $C(a,u_0,u_2)$ is neither a single triangle nor a multi-triangle.

Observation 1. 

From Definition 1, a triangle $C(u,u_i,u_j)$ of $G(a,u_0,u_{\alpha })$ is also a skirted graph $T^{\prime }\cup P^{\prime }$ containing the side skirt $T^{\prime }$ with root u and the path $P^{\prime }=u_i{u}_{i+1}{u}_{i+2}\cdots u_j$. Note that u has degree at least two because $i<j$.

We obtain from Lemma 2 that a skirted graph G contains a cycle C of length three. Let $x,y,z$ be vertices of C in which x is an internal vertex. If another leaf neighbor of x is adjacent to either y or z, then we can extend C to be a multi-triangle. Otherwise, C is a single triangle. Therefore, a skirted graph contains a triangle.

Theorem 3.

Let $G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. If $G^{\prime }$ is a simple graph obtained from a skirted graph $G(a,u_0,u_{\alpha })$ by contracting a triangle $C(u,u_i,u_j)$ of $G(a,u_0,u_{\alpha })$ where $u\ne a$. Then, $G^{\prime }$ is a skirted graph.

Proof. 

Let $G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph and $C(u,u_i,u_j)$ be a triangle in $G(a,u_0,u_{\alpha })$ for some $0\le i\le \alpha -1$ and $i<j$. Let $G^{\prime }$ be a simple graph obtained from $G(a,u_0,u_{\alpha })$ by contracting $C(u,u_i,u_j)$ and $u^{\ast }$ be the vertex of $G^{\prime }$ represented by the triangle $C(u,u_i,u_j)$, i.e., all vertices $u,u_i,u_{i+1},u_{i+2},\dots ,u_j$ are contracted into one vertex $u^{\ast }$. Since $u\ne a$, $G^{\prime }$ is not a trivial graph.

Consider the side skirt T of $G(a,u_0,u_{\alpha })$. It can be seen that we obtain $T^{\prime }$ from T by deleting all children of u and then turn the internal vertex u to be a leaf $u^{\ast }$ of $T^{\prime }$. The contraction does not affect the degree of other vertices in $G(a,u_0,u_{\alpha })$. Thus, $T^{\prime }$ is a side skirt. Now, we consider the path P of $G(a,u_0,u_{\alpha })$. The contraction turns the path $P=u_0{u}_1{u}_2\dots u_{\alpha }$ into the path $P^{\prime }=u_0{u}_1\dots u_{i-1}{u}^{\ast }{u}_{j+1}\dots u_{\alpha }$ in $G^{\prime }$. Since the contraction does not affect the degree of other vertices outside the triangle, all leaves of T except $u_i,u_{i+1},u_{i+2},\dots ,u_j$ are still the leaves of $T^{\prime }$. Thus, all vertices of $P^{\prime }$ are all leaves of $T^{\prime }$. Since $G^{\prime }$ is a union $T^{\prime }\cup P^{\prime }$, $G^{\prime }$ is a skirted graph. □

Note that $G^{\prime }=G^{\prime }(a,u_0,u_{\alpha })$ if $i,j\notin \{0,\alpha \}$, $G^{\prime }=G^{\prime }(a,u^{\ast },u_{\alpha })$ if $i=0$ (in this case, $j\ne \alpha$) and $G^{\prime }=G^{\prime }(a,u_0,u^{\ast })$ if $j=\alpha$ (in this case, $i\ne 0$). However, to prove Theorem 3, we do not care about the endpoints of the path $P^{\prime }$ in $G^{\prime }$. Thus, we just wrote $G^{\prime }$.

From Theorem 3, we already know that if $G^{\prime }$ is a simple graph obtained from a skirted graph $G(a,u_0,u_{\alpha })$ by contracting a triangle $C(u,u_i,u_j)$ of $G(a,u_0,u_{\alpha })$ where $u\ne a$, then, $G^{\prime }$ is a skirted graph. Next, we investigate the case that $u=a$. By the definition of a triangle, we obtain that $i=0$ and $j=\alpha$. Thus, in this case, the skirted graph $G(a,u_0,u_{\alpha })$ is a triangle. In the next section, we prove the pancyclicity results for the n-generalized prism over a triangle.

3. Pancyclicity of the n-Generalized Prism over a Triangle

To show that the n-generalized prism over a triangle is pancyclic, we need the following lemmas.

Lemma 3.

Let $C=C(u,u_0,u_{\alpha })$ be a triangle of order $\alpha +2$. Then, C contains:

(i) 

a $(u,u_{\alpha })$-path of each length l for $1\le l\le \alpha +1$;

(ii) 

a $(u_0,u_{\alpha })$-path of lengths α and $\alpha +1$.

Proof. 

Let $C=C(u,u_0,u_{\alpha })=T\cup P$ be a triangle of order $\alpha +2$ and $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. We prove this statement by the mathematical induction on α. If $\alpha =1$, then C is a cycle of length three. It contains (i) a $(u,u_1)$-path of lengths one and two and (ii) a $(u_0,u_1)$-path of lengths one and two. Now, we suppose that the statement holds for all triangles of order less than $\alpha +2$ where $\alpha >1$.

Let $C^{\prime }=(T-u_{\alpha })\cup (P-u_{\alpha })$. Then, $C^{\prime }=C(u,u_0,u_{\alpha -1})$ is a triangle subgraph of C. By the induction hypothesis, we obtain that $C(u,u_0,u_{\alpha -1})$ contains (i) a $(u,u_{\alpha -1})$-path of each length l for $1\le l\le \alpha$ and (ii) a $(u_0,u_{\alpha -1})$-path of lengths $\alpha -1$ and α.

Since $u_{\alpha }$ is adjacent to u in C, C contains a $(u,u_{\alpha })$-path of length one. Since $u_{\alpha }$ is adjacent to $u_{\alpha -1}$ in C, we can extend a $(u,u_{\alpha -1})$-path of length l to a $(u,u_{\alpha })$-path of length $l+1$. Thus, C contains (i) a $(u,u_{\alpha })$-path of each length l for $1\le l\le \alpha +1$ and (ii) a $(u_0,u_{\alpha })$-path of lengths α and $\alpha +1$. □

Remark 2.

We obtain that

(i) 

Lemma 3(i) gives a $(u,u_0)$-path of each length l for $1\le l\le \alpha +1$ by the symmetry of $C(u,u_0,u_{\alpha })$;

(ii) 

$P=u_0{u}_1{u}_2\dots u_{\alpha }$ is a $(u_0,u_{\alpha })$-path of length α (without the vertex u) in $C(u,u_0,u_{\alpha })$.

The following lemma is an immediate observation about the pancyclicity of the prism over a triangle.

Lemma 4.

The prism over a triangle is pancyclic.

Proof. 

Let $\alpha \ge 1$ and $C=C(u,u_0,u_{\alpha })$ be a triangle of length $\alpha +2$. For $1\le s\le 2$, the s-th copy of C contains a $(u^{\left(s\right)},u_{\alpha }^{\left(s\right)})$-path of each length l for $1\le l\le \alpha +1$ by Lemma 3(i). We link each $(u^{\left(1\right)},u_{\alpha }^{\left(1\right)})$-path and $(u^{\left(2\right)},u_{\alpha }^{\left(2\right)})$-path (maybe of different sizes) together with edges $u^{\left(1\right)}{u}^{\left(2\right)}$ and $u_{\alpha }^{\left(1\right)}{u}_{\alpha }^{\left(2\right)}$. We obtain a cycle of each length l for $4\le l\le 2\alpha +4$. Since C contains a cycle of length 3, $C\square P_2$ is pancyclic. □

By using Lemma 4 as a basic step, we can use the mathematical induction to establish the following result.

Theorem 4.

The n-generalized prism over a triangle is pancyclic.

Proof. 

Let $\alpha \ge 1$ and $C=C(u,u_0,u_{\alpha })$ be a triangle of order $\alpha +2$ and $P_n$ be a path of order $n\ge 2$. We prove that $C\square P_n$ is pancyclic by the mathematical induction on n. The basic step is already taken by Lemma 4. For $n\ge 3$, suppose that $C\square P_{n-1}$ is pancyclic. Since $C\square P_{n-1}$ is a subgraph of $C\square P_n$, $C\square P_n$ contains a cycle of each length l for $3\le l\le (\alpha +2)(n-1)$. We shall find a cycle of each length l for $(\alpha +2)(n-1)+1\le l\le (\alpha +2)n$.

To show that $C\square P_n$ contains a cycle of such lengths, we give the following paths and link them together with edges joining each copy of C.

• The first copy and the last copy of C contain paths $P(u^{\left(1\right)},u_{\alpha }^{\left(1\right)})$ and $P(u^{\left(n\right)},u_{\alpha }^{\left(n\right)})$, respectively, of each length l for $1\le l\le \alpha +1$ by Lemma 3(i). Also, for the last copy of C, a path $P(u^{\left(n\right)},u_0^{\left(n\right)})$ of each length l for $1\le l\le \alpha +1$ exists by the symmetry of C in Remark 2(i);
• The remaining $n-2$ copies of G contain the path $P(u_0^{\left(s\right)},u_{\alpha }^{\left(s\right)})$ of length α (without the root $u^{\left(s\right)}$) for $2\le s\le n-1$, which exists by Remark 2(ii);
• The path $P(u^{\left(n\right)},u^{\left(1\right)})=u^{\left(n\right)}{u}^{(n-1)}{u}^{(n-2)}\cdots u^{\left(1\right)}$ of length $n-1$ is a path in $C\square P_n$ from the last copy to the first copy of C.

Now, we link each path (maybe of different sizes) by edge $u_{\alpha }^{\left(s\right)}{u}_{\alpha }^{(s+1)}$ when s is odd and by edge $u_0^{\left(s\right)}{u}_0^{(s+1)}$ when s is even. We obtain a cycle of each length l for $(\alpha +2)n-2\alpha \le l\le (\alpha +2)n$. Since $(\alpha +2)n-2\alpha \le (\alpha +2)(n-1)+1$ for all $n\ge 3$, $C\square P_n$ contains a cycle of each length l for $(\alpha +2)(n-1)+1\le l\le (\alpha +2)n$. Therefore, $C\square P_n$ is pancyclic. □

4. Pancyclicity of the n-Generalized Prism over a Skirted Graph

To show that the n-generalized prism over a skirted graph is pancyclic, we first establish the preliminary results of even cycles in the n-generalized prism over a skirted graph. Note that since a skirted graph is traceable, we investigate the n-generalized prism over a path instead of the n-generalized prism over a skirted graph as follows.

4.1. Even Cycles in the n-Generalized Prism over a Path

Let $n\ge 2$ be an even integer and $m\ge 2$, we need the following lemma to prove that $P_m\square P_n$ contains a cycle of each even length l where l is an even integer ranging from 4 to $mn$.

Lemma 5.

Suppose that $m\ge 2$. Then, the prism over $P_m$ contains a cycle of each length l where l is an even integer ranging from 4 to $2m$. Moreover, if $P_m=v_1{v}_2{v}_3\cdots v_m$, then the edges $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and $v_1^{\left(2\right)}{v}_2^{\left(2\right)}$ of the first copy and the second copy of $P_m\square P_2$, respectively, are contained in a cycle of each even length l for $4\le l\le 2m$.

Proof. 

Let $P_m=v_1{v}_2{v}_3\cdots v_m$. We define a sequence of $m-1$ cycles in $P_m\square P_2$ as follows.

$$\begin{array}{c}{v}_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}{v}_2^{\left(1\right)},\\ v_3^{\left(1\right)}{v}_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}{v}_3^{\left(2\right)}{v}_3^{\left(1\right)},\\ v_4^{\left(1\right)}{v}_3^{\left(1\right)}{v}_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}{v}_3^{\left(2\right)}{v}_4^{\left(2\right)}{v}_4^{\left(1\right)},\\ \cdots ,\\ v_m^{\left(1\right)}{v}_{m-1}^{\left(1\right)}{v}_{m-2}^{\left(1\right)}{v}_{m-3}^{\left(1\right)}\cdots v_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}\cdots v_{m-2}^{\left(2\right)}{v}_{m-1}^{\left(2\right)}{v}_m^{\left(2\right)}{v}_m^{\left(1\right)}.\end{array}$$

The length of each cycle in the sequence increases as an arithmetic sequence with the common difference two. Then, the last cycle

$$v_m^{\left(1\right)}{v}_{m-1}^{\left(1\right)}{v}_{m-2}^{\left(1\right)}{v}_{m-3}^{\left(1\right)}\cdots v_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}\cdots v_{m-2}^{\left(2\right)}{v}_{m-1}^{\left(2\right)}{v}_m^{\left(2\right)}{v}_m^{\left(1\right)}$$

of this sequence has length $2m$. Since the first cycle $v_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}{v}_2^{\left(1\right)}$ is a cycle of length 4, the lengths of the cycles are even integers ranging from 4 to $2m$. Moreover, $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and $v_1^{\left(2\right)}{v}_2^{\left(2\right)}$ are edges contained in all even cycles. □

Observation 2. 

For $n\ge 2$ is an even integer and $m\ge 2$, if $P_m=v_1{v}_2{v}_3\cdots v_m$, then the edges $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and $v_1^{\left(n\right)}{v}_2^{\left(n\right)}$ of the first copy and the last copy of $P_m\square P_n$, respectively, are contained in a cycle of length $mn$ (see Figure 4).

Figure 4. The dashed line represents a spanning cycle of length $mn$ containing edges $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and $v_1^{\left(n\right)}{v}_2^{\left(n\right)}$.

By using Lemma 5 as a basic step, we can use mathematical induction to establish the following result.

Lemma 6.

Suppose that $n\ge 2$ is an even integer, and $m\ge 2$. Then, the n-generalized prism over $P_m$ contains a cycle of each length l, where l is an even integer ranging from four to $mn$. Moreover, if $P_m=v_1{v}_2{v}_3\cdots v_m$, then the edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ of the first copy of $P_m\square P_n$ is contained in a cycle of each even length l for $4\le l\le mn$.

Proof. 

Let $P_m=v_1{v}_2{v}_3\cdots v_m$, where $m\ge 2$, and $n=2k$ for some positive integer k. We prove by the mathematical induction on k. The basic step is already done by Lemma 5. For $k\ge 2$, suppose that $P_m\square P_{2(k-1)}$ contains a cycle of each even length l, where l is an even integer ranging from 4 to $2m(k-1)$. We shall find an even cycle of each length l for $2m(k-1)+2\le l\le 2mk$.

Here, let us regard $P_m\square P_{2(k-1)}$ as a subgraph of $P_m\square P_{2k}$ induced by the set of all vertices of the first $2(k-1)$ copies of $P_m$. By Observation 2, there is a cycle $C^{\ast }$ of length $2m(k-1)$ in $P_m\square P_{2(k-1)}$ containing the edges $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and $v_1^{(2k-2)}{v}_2^{(2k-2)}$.

Now, we consider the last two copies of $P_m$. The vertices of these two copies induce a subgraph $P_m\square P_2$ of $P_m\square P_{2k}$. By Lemma 5, an edge $v_1^{(2k-1)}{v}_2^{(2k-1)}$ is contained in a cycle of each even length l for $4\le l\le 2m$ in $P_m\square P_{2k}$. Since $v_1^{(2k-2)}{v}_1^{(2k-1)}$ and $v_2^{(2k-2)}{v}_2^{(2k-1)}$ are edges of $P_m\square P_{2k}$, we delete edges $v_1^{(2k-2)}{v}_2^{(2k-2)}$ and $v_1^{(2k-1)}{v}_2^{(2k-1)}$ and then join $v_1^{(2k-1)}$ to $v_1^{(2k-2)}$ and $v_2^{(2k-1)}$ to $v_2^{(2k-2)}$, respectively. Then, $C^{\ast }$ can be extended to a cycle of each even length l for $2m(k-1)+2\le l\le 2mk$.

Moreover, since the cycle $C^{\ast }$ contains edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ and the extension of $C^{\ast }$ does not affect the edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$, it is contained in a cycle of each even length l for $4\le l\le mn$. □

By Lemma 6, $P_m\square P_n$ contains an even cycle of each length l for $4\le l\le mn$ when n is even. Next, to investigate the case that n is odd, we first examine the case that $n=3$ as follows.

Lemma 7.

Suppose that $m\ge 2$. Then, the three-generalized prism over $P_m$ contains a cycle of each length l, where l is an even integer ranging from 4 to $3m$. Moreover, if $P_m=v_1{v}_2{v}_3\cdots v_m$, then the edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ of the first copy of $P_m\square P_3$ is contained in:

(i) 

a cycle of each even length l for $4\le l\le 3m$ if m is even;

(ii) 

a cycle of each even length l for $4\le l\le 3m-1$ if m is odd.

Proof. 

Let $m\ge 2$ and $P_m=v_1{v}_2{v}_3\cdots v_m$. Here, let us regard $P_m\square P_2$ as a subgraph of $P_m\square P_3$ induced by vertices of the first two copies of $P_m$. By Lemma 5 and $P_m\square P_2$ is a subgraph of $P_m\square P_3$, $P_m\square P_3$ contains a cycle of each length l, where l is an even integer ranging from 4 to $2m$ and the edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ of the first copy of $P_m\square P_n$ is contained in a cycle of each length l, where l is an even integer ranging from 4 to $2m$. We shall find even cycles of each length l for $2m+2\le l\le 3m$. By Lemma 5, $P_m\square P_2$ contains a cycle

$$C^{\ast }=v_m^{\left(1\right)}{v}_{m-1}^{\left(1\right)}{v}_{m-2}^{\left(1\right)}{v}_{m-3}^{\left(1\right)}\cdots v_2^{\left(1\right)}{v}_1^{\left(1\right)}{v}_1^{\left(2\right)}{v}_2^{\left(2\right)}\cdots v_{m-2}^{\left(2\right)}{v}_{m-1}^{\left(2\right)}{v}_m^{\left(2\right)}{v}_m^{\left(1\right)}$$

of length $2m$ in which it contains $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$.

Now, we consider the second and the third copies of $P_m$. For an odd integer j such that $1\le j\le m-1$, there is a path $P_j=v_j^{\left(2\right)}{v}_j^{\left(3\right)}{v}_{j+1}^{\left(3\right)}{v}_{j+1}^{\left(2\right)}$ of length 3 in $P_m\square P_3$.

Since $v_j^{\left(3\right)}$ and $v_{j+1}^{\left(3\right)}$ have not been contained in $C^{\ast }$ for all odd integers j, we replace each edge $v_j^{\left(2\right)}{v}_{j+1}^{\left(2\right)}$ with each path $P_j$. Then, $C^{\ast }$ can be extended to a cycle of each even length l for $2m+2\le l\le 3m$. Since this extension does not change anything in the first copy of $P_m$, the extended cycle still contains the edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$.

Moreover, we can see that (i) if m is even, then $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ is contained in a cycle of each even length l for $4\le l\le 3m$ ($3m$ is even); (ii) if m is odd, then $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$ is contained in a cycle of each even length l for $4\le l\le 3m-1$ ($3m$ is odd). □

Figure 5 shows examples of cycles of length 18 and 20 in $P_6\square P_3$ and $P_7\square P_3$, respectively.

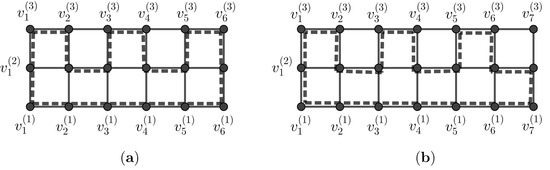
Figure 5. (a) The dashed line represents a cycle of length 18 in $P_6\square P_3$; (b) The dashed line represents a cycle of length 20 in $P_7\square P_3$.

Remark 3.

From the proof of Lemma 7, we obtain the cycles of length $3m$ when m is even and $3m-1$ when m is odd. We notice that, apart from edge $v_1^{\left(1\right)}{v}_2^{\left(1\right)}$, these two cycles also contain edges $v_1^{\left(3\right)}{v}_2^{\left(3\right)}$ and $v_2^{\left(2\right)}{v}_3^{\left(2\right)}$ when $m\ge 3$.

4.2. Our Main Results

To show that the n-generalized prism over any skirted graphs is pancyclic, we start by providing some observations and investigating the pancyclicity of the prism over a skirted graph. The pancyclicity of the three-generalized prism over a skirted graph is as follows.

Observation 3. 

Let $m\ge 3$, $\alpha \ge 2$, $t\le m$ and $G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph of order m with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$ and $C=C(u,u_i,u_j)$ be a triangle of order t in $G(a,u_0,u_{\alpha })$ such that $u\ne a$. Let $G^{\prime }$ be a skirted graph of order $m-(t-1)$ obtained from a skirted graph $G(a,u_0,u_{\alpha })$ by contracting the triangle C and $u^{\ast }$ be the vertex of $G^{\prime }$ represented the triangle C. By Theorem 1, $G^{\prime }$ is Hamiltonian. Let $C^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}{u}^{\ast }$ be a spanning cycle in $G^{\prime }$. Then, there is a spanning path $P^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}$ in $G^{\prime }$.

Since $u^{\ast }$ is the vertex of $G^{\prime }$ represented by the triangle C and $v_1$ is adjacent to $u^{\ast }$, $v_1$ is adjacent to either u, $u_i$ or $u_j$ in $G(a,u_0,u_{\alpha })$. Let $G=G(a,u_0,u_{\alpha })$.

• If $v_1{u}_j\in E\left(G\right)$, then $P(u_i,v_{m-t})=u_i{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex u) in G;
• If $v_1{u}_i\in E\left(G\right)$, then $P(u_j,v_{m-t})=u_j{u}_{j-1}{u}_{j-2}\cdots u_i{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex u) in G;
• If $v_{1}u\in E\left(G\right)$, then $P(u_j,v_{m-t})=u_j{u}_{j-1}{u}_{j-2}\cdots u_{i+2}{u}_{i+1}u{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex $u_i$) in G.

Theorem 5.

The prism over any skirted graphs is pancyclic.

Proof. 

First, we consider a single skirted graph. Let $G=G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph of order m with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. Let $C=C(u,u_i,u_j)$ be a triangle of order t in $G(a,u_0,u_{\alpha })$, where $t\le m$. If $u=a$, then G itself is a triangle. By Theorem 4, the prism over G is pancyclic. Now, we assume that $u\ne a$.

Let $G^{\prime }$ be a skirted graph of order $m-(t-1)$ obtained from a skirted graph G by contracting the triangle C and $u^{\ast }$ be the vertex of $G^{\prime }$ represented by the triangle C. By Theorem 1, $G^{\prime }$ is Hamiltonian. Let $C^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}{u}^{\ast }$ be a spanning cycle in $G^{\prime }$. Then, $P^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}$ is a spanning path in $G^{\prime }$.

Since $u^{\ast }$ is the vertex of $G^{\prime }$ represented by the triangle C and $v_1$ is adjacent to $u^{\ast }$, $v_1$ is adjacent to either u, $u_i$ or $u_j$. By Observation 3, without loss of generality, let $v_1$ be adjacent to $u_j$. Then, $P(u_i,v_{m-t})=u_i{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex u) in G. Note that $j=i+1$ if C is a single-triangle.

Now, consider prism over a skirted graph which contains the first and the second copies of the same skirted graph. By Lemma 2, $P(u_i,v_{m-t})\square P_2$ contains a cycle $C^{\ast }$ of each even length l for $4\le l\le 2(m-1)$ in which it contains the edge $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$. Since $P(u_i,v_{m-t})\square P_2$ is a subgraph of $G\square P_2$, the prism over G contains a cycle of each even length l for $4\le l\le 2(m-1)$.

We shall find a cycle of each odd length l for $5\le l\le 2m-1$. Since $P=u_i^{\left(1\right)}{u}^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ is a path of length two in the first copy of $G\square P_2$ and $u^{\left(1\right)}$ is not contained in $C^{\ast }$, we replace edge $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ with the path P. Then, $C^{\ast }$ can be extended to a cycle of length $l+1$. Since $4\le l\le 2(m-1)$, we obtain a cycle of each odd length l for $5\le l\le 2m-1$.

Since G contains a cycle of length three, the prism over G also contains a cycle of length three. By Theorem 2, the prism over G is Hamiltonian, i.e., it contains a cycle of length $2m$. Therefore, the prism over G is pancyclic. □

Remark 4.

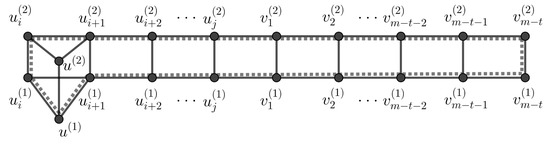
From the proof of Theorem 5, the edge $v_{m-t-1}^{\left(2\right)}{v}_{m-t}^{\left(2\right)}$ of the second copy of $G\square P_2$ is contained in an odd cycle of length $2m-1$ (see Figure 6).

Figure 6. The dashed line represents a cycle of length $2m-1$ in $G\square P_2$ containing edge $v_{m-t-1}^{\left(2\right)}{v}_{m-t}^{\left(2\right)}$, where G is a skirted graph in Theorem 5.

Next, we consider the pancyclicity of the three-generalized prism over a skirted graph.

Theorem 6.

The three-generalized prism over a skirted graph is pancyclic.

Proof. 

First, we consider a single skirted graph. Let $G=G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph of order m with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. Let $C=C(u,u_i,u_j)$ be a triangle of order t in $G(a,u_0,u_{\alpha })$, where $t\le m$. If $u=a$, then G itself is a triangle. By Theorem 4, $G\square P_3$ is pancyclic. Now, we assume that $u\ne a$.

Let $G^{\prime }$ be a skirted graph of order $m-(t-1)$ obtained from a skirted graph G by contracting the triangle C and $u^{\ast }$ be the vertex of $G^{\prime }$ represented the triangle C. By Theorem 1, $G^{\prime }$ is Hamiltonian. Let $C^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}{u}^{\ast }$ be a spanning cycle in $G^{\prime }$. Then, we let $P^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}$ be a spanning path in $G^{\prime }$.

Since $u^{\ast }$ is the vertex of $G^{\prime }$ represented by the triangle C and $v_1$ is adjacent to $u^{\ast }$, $v_1$ is adjacent to either u, $u_i$ or $u_j$. By Observation 3, without loss of generality, let $v_1$ be adjacent to $u_j$. Then, $P(u_i,v_{m-t})=u_i{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex u) in G. Note that $j=i+1$ if C is a single triangle.

Now, consider the three-generalized prism over a skirted graph which contains three copies of the same skirted graph. Since $P(u_i,v_{m-t})\square P_3$ is a subgraph of $G\square P_3$, we show that $G\square P_3$ is pancyclic by applying Lemma 7. Then, we consider two cases as follows.

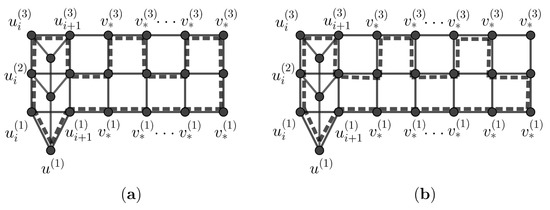
Case 1. Here $m-1$ is even. By Lemma 7(i), $P(u_i,v_{m-t})\square P_3$ contains a cycle of each even length l for $4\le l\le 3(m-1)$ in which it contains the edge $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$. Note that, for all $1\le s\le 3$, vertex $u^{\left(s\right)}$ has not been contained in $P(u_i,v_{m-t})\square P_3$. To find an odd cycle, we replace $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ of such cycles with a path $u_i^{\left(1\right)}{u}^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ and then obtain a cycle of each odd length l for $5\le l\le 3(m-1)+1=3m-2$. Let $C^{\prime }$ be the cycle of length $3m-2$ without the vertex $u^{\left(3\right)}$ (see Figure 7a). By Remark 3, $C^{\prime }$ contains the edge $u_i^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$. Then, we replace $u_i^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$ of $C^{\prime }$ with a path $u_i^{\left(3\right)}{u}^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$ and then obtain a cycle of length $3m-1$. Thus, we obtain that $G\square P_3$ contains a cycle of each length l for all $4\le l\le 3m-1$.

Figure 7. (a) The dashed line represents a cycle of length $3m-2$ in $G\square P_3$ when $m-1$ is even; (b) The dashed line represents a cycle of length $3m-3$ in $G\square P_3$ when $m-1$ is odd.

Case 2. Here $m-1$ is odd. By Lemma 7(ii), $P(u_i,v_{m-t})\square P_3$ contains a cycle of each even length l for $4\le l\le 3(m-1)-1$ in which it contains edge $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$. Note that, for all $1\le s\le 3$, vertex $u^{\left(s\right)}$ has not been contained in $P(u_i,v_{m-t})\square P_3$. To find an odd cycle, we replace $u_i^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ of such cycles with a path $u_i^{\left(1\right)}{u}^{\left(1\right)}{u}_{i+1}^{\left(1\right)}$ and then obtain a cycle of each odd length l for $5\le l\le 3(m-1)=3m-3$. Let $C^{\prime }$ be the cycle of length $3m-3$ without vertex $u^{\left(2\right)}$ (see Figure 7b). By Remark 3, $C^{\prime }$ contains edge $u_i^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$. Thus, we replace $u_i^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$ of $C^{\prime }$ with a path $u_i^{\left(3\right)}{u}^{\left(3\right)}{u}_{i+1}^{\left(3\right)}$ and then obtain a cycle of length $3m-2$. Therefore, $G\square P_3$ contains a cycle of each length l for all $4\le l\le 3m-2$.

We shall find a cycle of length $3m-1$ in $G\square P_3$. Recall that $C=C(u,u_i,u_j)$ is a triangle of order t in $G=G(a,u_0,u_{\alpha })$ such that $u\ne a$. To show that $G\square P_3$ contains a cycle of length $3m-1$, we give the following paths and link them together with edges joining each copy of G.

• For the first copy of G, we consider subgraph $G^{\prime }$. If $j=\alpha$, then $C(u,u_i,u_j)=C(u,u_i,u_{\alpha })$. Note that $u_i\ne u_0$ since $u\ne a$. Then, $G^{\prime }=G^{\prime }(a,u_0,u^{\ast })$. Since $G^{\prime }$ is a skirted graph, by Lemma 1, $G^{\prime }$ contains an $(a,u^{\ast })$-path $P_{G^{\prime }}(a,u^{\ast })$ of length $m-t$. Suppose that $v^{\prime }$ is adjacent to $u^{\ast }$ in $P_{G^{\prime }}(a,u^{\ast })$. Then, $v^{\prime }$ is adjacent to either u or $u_i$ in G. We consider two cases as follows.

  -

  If $v^{\prime }$ is adjacent to u, then $P(v^{\prime },u_j)=v^{\prime }u{u}_{i+1}{u}_{i+2}\cdots u_j$ is a path of length $t-1$ (without the vertex $u_i$);

  -

  If $v^{\prime }$ is adjacent to $u_i$, then $P(v^{\prime },u_j)=v^{\prime }{u}_i{u}_{i+1}{u}_{i+2}\cdots u_j$ is a path of length $t-1$ (without the vertex u).

  Therefore, we can extend the path $P_{G^{\prime }}(a,u^{\ast })$ of length $m-t$ in $G^{\prime }$ to be a path $P(a,u_{\alpha })$ of length $m-2$ in G by replacing the edge $v^{\prime }{u}^{\ast }$ of $G^{\prime }$ with the path $P(v^{\prime },u_j)$. Suppose that $j\ne \alpha$. Then, $G^{\prime }=G^{\prime }(a,u_0,u_{\alpha })$. Since $G^{\prime }(a,u_0,u_{\alpha })$ is a skirted graph, by Lemma 1, $G^{\prime }$ contains an $(a,u_{\alpha })$-path $P_{G^{\prime }}(a,u_{\alpha })$ of length $m-t$. Since $P_{G^{\prime }}(a,u_{\alpha })$ is a spanning path in $G^{\prime }$, $P_{G^{\prime }}(a,u_{\alpha })$ contains the vertex $u^{\ast }$. Suppose that $v^{\prime }$ and $v^{″}$ are adjacent to $u^{\ast }$ in $P_{G^{\prime }}(a,u_{\alpha })$. Then, each of $v^{\prime }$ and $v^{″}$ is adjacent to either $u,u_i$ or $u_j$ in G. We consider three cases as follows.

  -

  If $v^{\prime }{u}_i,u_j{v}^{″}\in E\left(G\right)$, then $P(v^{\prime },v^{″})=v^{\prime }{u}_i{u}_{i+1}{u}_{i+2}\cdots u_j{v}^{″}$ is a path of length t (without the vertex u);

  -

  If $v^{\prime }u,u_j{v}^{\prime \prime }\in E\left(G\right)$, then $P(v^{\prime },v^{\prime \prime })=v^{\prime }u{u}_{i+1}{u}_{i+2}\cdots u_j{v}^{″}$ is a path of length t (without the vertex $u_i$);

  -

  If $v^{\prime }u,u_i{v}^{″}\in E\left(G\right)$, then $P(v^{\prime },v^{″})=v^{\prime }u{u}_{j-1}{u}_{j-2}\cdots u_{i+1}{u}_i{v}^{″}$ is a path of length t (without the vertex $u_j$).

  Therefore, we can extend the path $P_{G^{\prime }}(a,u_{\alpha })$ of length $m-t$ in $G^{\prime }$ to be a path $P(a,u_{\alpha })$ of length $m-2$ in G by replacing the path $v^{\prime }{u}^{\ast }{v}^{″}$ in $P_{G^{\prime }}(a,u_{\alpha })$ with the path $P(v^{\prime },v^{″})$. Thus, the first copy of G contains a path $P(a^{\left(1\right)},u_{\alpha }^{\left(1\right)})$ of length $m-2$;
• By Remark 1(ii), the second copy of G contains a $(u_0^{\left(2\right)},u_{\alpha }^{\left(2\right)})$-path $P(u_0^{\left(2\right)},u_{\alpha }^{\left(2\right)})$ of length $m-2$ (without the root $a^{\left(2\right)}$);
• By Remark 1(i), the last copy of G contains an $(a^{\left(3\right)},u_0^{\left(3\right)})$-path $P(a^{\left(3\right)},u_0^{\left(3\right)})$ of length $m-1$;
• The path $P^{\ast }=a^{\left(3\right)}{a}^{\left(2\right)}{a}^{\left(1\right)}$ of length 2 is a path in $G\square P_3$ from the last copy to the first copy of G.

Now, we link each path by edges $u_{\alpha }^{\left(1\right)}{u}_{\alpha }^{\left(2\right)}$ and $u_0^{\left(2\right)}{u}_0^{\left(1\right)}$. The cycle of length $3m-1$ is

$$P(a^{\left(1\right)},u_{\alpha }^{\left(1\right)})P(u_{\alpha }^{\left(2\right)},u_0^{\left(2\right)})P(u_0^{\left(3\right)},a^{\left(3\right)})P^{\ast }.$$

Therefore, $G\square P_3$ contains a cycle of length $3m-1$.

From these two cases, we obtain that $G\square P_3$ contains a cycle of each length l for all $4\le l\le 3m-1$. Since G is a skirted graph, by Lemma 2, G contains a cycle of length three. By Theorem 2, $G\square P_3$ is Hamiltonian, i.e., it contains a cycle of length $3m$. Therefore, $G\square P_3$ is pancyclic. □

By the proof of Theorem 6, the pancyclicity of the three-generalized prism over a skirted graph, we need to consider the special case. However, there is no special case when we show that $G\square P_n$ is pancyclic for $n\ge 4$. Therefore, we prove the following theorem by considering $n\ge 4$.

Theorem 7.

The n-generalized prism over any skirted graphs is pancyclic.

Proof. 

First, we consider a single skirted graph. Let $G=G(a,u_0,u_{\alpha })=T\cup P$ be a skirted graph of order m with $P=u_0{u}_1{u}_2\cdots u_{\alpha }$. Let $P_n$ be a path of order $n\ge 2$. If $n=2$ or 3, then we respectively obtain from Theorems 5 and 6 that $G\square P_n$ is pancyclic. Suppose now that $n\ge 4$.

Let $C=C(u,u_i,u_j)$ be a triangle of order t in $G(a,u_0,u_{\alpha })$, where $t\le m$. If $u=a$, then G itself is a triangle. By Theorem 4, the n-generalized prism over G is pancyclic. Now, we assume that $u\ne a$.

Let $G^{\prime }$ be a skirted graph of order $m-(t-1)$ obtained from a skirted graph G by contracting the triangle C and $u^{\ast }$ be the vertex of $G^{\prime }$ represented by the triangle C. By Theorem 1, $G^{\prime }$ is Hamiltonian. Let $C^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}{u}^{\ast }$ be a spanning cycle in $G^{\prime }$. Then, $P^{\prime }=u^{\ast }{v}_1{v}_2{v}_3\cdots v_{m-t}$ is a spanning path in $G^{\prime }$.

Since $u^{\ast }$ is the vertex of $G^{\prime }$ represented by the triangle C and $v_1$ is adjacent to $u^{\ast }$, $v_1$ is adjacent to either u, $u_i$ or $u_j$. By Observation 3, without loss of generality, let $v_1$ be adjacent to $u_j$. Then, $P(u_i,v_{m-t})=u_i{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1{v}_2\cdots v_{m-t}$ is a path of length $m-2$ (without the vertex u) in G. Note that $j=i+1$ if C is a single triangle.

Now, consider the n-generalized prism over a skirted graph which contains n copies of the same skirted graph. Since $u_{i}u,u{u}_{i+1}\in E\left(G\right)$, $P_m^{\prime }=u_{i}u{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1\cdots v_{m-t}$ is a path of length $m-1$ in G, i.e., $P_m^{\prime }$ is a spanning path in G. We can see that $P_m^{\prime }\square P_n$ is a subgraph of $G\square P_n$.

To show that $G\square P_n$ is pancyclic, we consider two cases as follows.

Case 1. Here n is even.

By Lemma 6, $P_m^{\prime }\square P_n$ contains a cycle of each even length l for $4\le l\le nm$. Since $P_m^{\prime }\square P_n$ is a subgraph of $G\square P_n$, $G\square P_n$ contains a cycle of each even length l for $4\le l\le nm$. We shall find a cycle of each odd length in $G\square P_n$ by considering two disjoint-induced subgraphs $G\square P_2$ and $G\square P_{n-2}$ of $G\square P_n$, where $G\square P_2$ is induced by the first two copies of G and $G\square P_{n-2}$ is induced by the last $n-2$ copies of G.

First, we consider $G\square P_2$. By Theorem 5, $G\square P_2$ contains a cycle of each length l for $3\le l\le 2m$. Since $G\square P_2$ is a subgraph of $G\square P_n$, we obtain that $G\square P_n$ contains a cycle of each length l for $3\le l\le 2m$. Let $C^{\ast }$ be the cycle of length $2m-1$ in $G\square P_n$ containing edge $v_{m-t-1}^{\left(2\right)}{v}_{m-t}^{\left(2\right)}$, which exists by Remark 4.

Next, we consider subgraph $G\square P_{n-2}$ induced by the last $n-2$ copies of G, in order to show that $G\square P_n$ contains a cycle of each odd length l for $2m+1\le l\le nm-1$. Since $P_m^{\prime }\square P_{n-2}$ is a subgraph of $G\square P_{n-2}$, we can consider cycles in $P_m^{\prime }\square P_{n-2}$ instead of $G\square P_{n-2}$. Since $n-2$ is even, by Lemma 6 and the reverse of the path $P_m^{\prime }$, the edge $v_{m-t-1}^{\left(3\right)}{v}_{m-t}^{\left(3\right)}$ is contained in a cycle of each length l, where l is an even integer ranging from 4 to $m(n-2)$ in $P_m^{\prime }\square P_{n-2}$. Since $v_{m-t-1}^{\left(2\right)}{v}_{m-t-1}^{\left(3\right)},v_{m-t}^{\left(2\right)}{v}_{m-t}^{\left(3\right)},v_{m-t-1}^{\left(3\right)}{v}_{m-t}^{\left(3\right)}\in E(G\square P_n)$, we delete the edge $v_{m-t-1}^{\left(2\right)}{v}_{m-t}^{\left(2\right)}$ of $C^{\ast }$ and then join $v_{m-t-1}^{\left(2\right)}$ to $v_{m-t-1}^{\left(3\right)}$ and $v_{m-t}^{\left(2\right)}$ to $v_{m-t}^{\left(3\right)}$. Then, we can extend $C^{\ast }$ to be a cycle of length $2m+1$. In addition, we delete the edge $v_{m-t-1}^{\left(3\right)}{v}_{m-t}^{\left(3\right)}$ of each cycle of each length l in $P_m^{\prime }\square P_{n-2}$ and then join $v_{m-t-1}^{\left(2\right)}$ to $v_{m-t-1}^{\left(3\right)}$ and $v_{m-t}^{\left(2\right)}$ to $v_{m-t}^{\left(3\right)}$. Then, we can extend $C^{\ast }$ to be a cycle of each length l for $2m+3\le l\le nm-1$. Therefore, $G\square P_n$ is pancyclic.

Case 2. Here n is odd. Since $n-3\ge 2$ is even, by Case 1, $G\square P_{n-3}$ contains a cycle of each length l for $3\le l\le m(n-3)$. Thus, we consider two disjoint-induced subgraph $G\square P_{n-3}$ and $G\square P_3$ of $G\square P_n$, where $G\square P_{n-3}$ is induced by the first $n-3$ copies of G and $G\square P_3$ is induced by the last three copies of G.

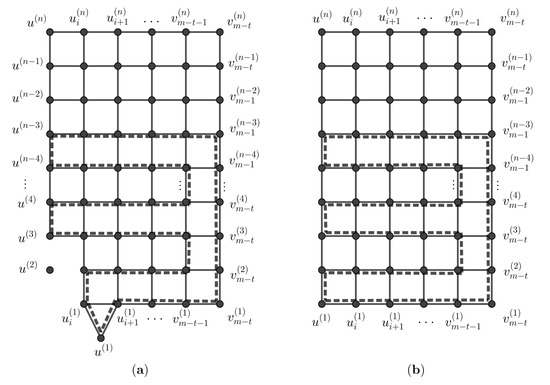
We shall find a cycle of each remaining length l for $m(n-3)+1\le l\le mn$. Recall that G is a skirted graph of order m and $P_m^{\prime }=u_{i}u{u}_{i+1}{u}_{i+2}\cdots u_j{v}_1\cdots v_{m-t}$ is a spanning path in G. Then, $P_m^{\prime }\square P_n$ is a subgraph of $G\square P_n$. Let $C_{odd}$ be the cycle of odd length $m(n-3)-1$ in $P_m^{\prime }\square P_{n-3}$ containing the edge $v_{m-t}^{(n-3)}{v}_{m-t-1}^{(n-3)}$ (see Figure 8a) and $C_{even}$ be the cycle of even length $m(n-3)$ in $P_m^{\prime }\square P_{n-3}$ containing the edge $v_{m-t}^{(n-3)}{v}_{m-t-1}^{(n-3)}$ (see Figure 8b).

Figure 8. (a) The dashed line represents $C_{odd}$ of length $m(n-3)-1$; (b) The dashed line represents $C_{even}$ of length $m(n-3)$.

Consider $G\square P_3$. Since $P_m^{\prime }$ is a spanning path in G, we can apply Lemma 7 as follows.

• If m is even, then $G\square P_3$ contains a cycle of each even length l for $4\le l\le 3m$ containing edge $v_{m-t}^{(n-2)}{v}_{m-t-1}^{(n-2)}$ by Lemma 7(i). We delete the edge $v_{m-t-1}^{(n-3)}{v}_{m-t}^{(n-3)}$ of $C_{even}$ and the edge $v_{m-t-1}^{(n-2)}{v}_{m-t}^{(n-2)}$ of each cycle of each length l in $G\square P_3$ and then join $v_{m-t-1}^{(n-3)}$ to $v_{m-t-1}^{(n-2)}$ and $v_{m-t}^{(n-3)}$ to $v_{m-t}^{(n-2)}$. Thus, we can extend $C_{odd}$ of length $m(n-3)-1$ to be a cycle of each odd length l for $m(n-3)+1\le l\le mn-1$ and extend $C_{even}$ of length $m(n-3)$ to be a cycle of each even length l for $m(n-3)+2\le l\le mn$ in a similar way. Thus, $G\square P_n$ contains a cycle of each length l for $m(n-3)+1\le l\le mn$.
• If m is odd, then $G\square P_3$ contains a cycle of each even length l for $4\le l\le 3m-1$ containing edge $v_{m-t}^{(n-2)}{v}_{m-t-1}^{(n-2)}$ by Lemma 7(ii). We delete the edge $v_{m-t-1}^{(n-3)}{v}_{m-t}^{(n-3)}$ of $C_{even}$ and the edge $v_{m-t-1}^{(n-2)}{v}_{m-t}^{(n-2)}$ of each cycle of each length l in $G\square P_3$ and then join $v_{m-t-1}^{(n-3)}$ to $v_{m-t-1}^{(n-2)}$ and $v_{m-t}^{(n-3)}$ to $v_{m-t}^{(n-2)}$. Thus, we can extend $C_{odd}$ of length $m(n-3)-1$ to be a cycle of each odd length l for $m(n-3)+1\le l\le mn-2$ and extend $C_{even}$ of length $m(n-3)$ to be a cycle of each even length l for $m(n-3)+2\le l\le mn-1$ in a similar way. Since $G\square P_n$ is Hamiltonian, it contains a cycle of length $mn$. Thus, $G\square P_n$ contains a cycle of each length l for $m(n-3)+1\le l\le mn$.

Therefore, $G\square P_n$ is pancyclic. □

5. Conclusions and Discussion

In this paper, we prove that the n-generalized prism over skirted graphs is pancyclic. The result holds for any skirted graph, even though we have not known the exact configuration of this family of graphs. Moreover, since the Cartesian product of a graph over a path $P_n$ is a subgraph of the Cartesian product of the graph over a cycle $C_n$ and the Cartesian product of the graph over a complete graph $K_n$, the results can be concluded in the similar way when $P_n$ is replaced by $C_n$ or $K_n$ for $n\ge 3$. However, we have not investigated panconnectivity of the n-generalized prism over any skirted graph, which is a stronger concept than pancyclicity. For a definition of panconnectivity, we can see, for examples, [1,19,20]. Therefore, it is recommended that further studies can investigate panconnectivity of the n-generalized prism over any skirted graph.