Singularities of Non-Developable Ruled Surface with Space-like Ruling

Abstract

Singularity theory is a significant field of modern mathematical research. The main goal in most problems of singularity theory is to understand the dependence of some objects in analysis and geometry, or physics; or from some other science on parameters. In this paper, we study the singularities of the spherical indicatrix and evolute of space-like ruled surface with space-like ruling. The main method takes advantage of the classical unfolding theorem in singularity theory, which is a classical method to study singularity problems in Euclidean space and Minkowski space. Finally, we provide an example to illustrate our results.

1. Introduction

Ruled surfaces have the most important positions and applications in the study of design problems in spatial mechanisms and physics, kinematics, and computer-aided design (CAD). Therefore, these surfaces are one of the most important topics of surface theory. Because of this position of ruled surfaces, many geometers and engineers have investigated and obtained many properties of the ruled surfaces. There exists a vast literature on the subject including several monographs (see for instance, [1,2,3,4,5]). Furthermore, the differential geometry of ruled surfaces in Minkowski space ${\mathbb{E}}_1^3$ is much more complicated than the Euclidean case, since the Lorentzian metric is not a positive definite metric, the distance function $⟨,⟩$ can be positive, negative, or zero, whereas the distance function in Euclidean space can only be positive. For instance, a continuously moving timelike line along a curve generates a timelike ruled surface. Turgut and Hacısalihoğlu have studied timelike ruled surfaces in Minkowski 3-space and they have given some properties of these surfaces [6]. Timelike ruled surfaces with timelike rulings have been studied by Abdel-All et al. [7]. Küçük has obtained some results on the developable timelike ruled surfaces in the same space [8]. Furthermore, Uğurlu and Onder introduced Frenet frames and Frenet invariants of timelike ruled surfaces in Minkowski three-space [9].

One of the main techniques for applying the singularity theory to Euclidean differential geometry is to consider the distance squared function and the height function on a submanifold of ${\mathbb{E}}^3$ [10,11,12]. In this paper, we focus on the geometric analysis and the singularity of the spherical indicatrix and evolute of spacelike ruled surface with spacelike ruling. Finally, we provide an example to support our obtained results. There are some articles concerning singularity theory and submanifolds for several types of geometry. In the next work, we will combine the main results in this paper with the methods and techniques of singularity theory and submanifolds theory, etc., presented in [13,14,15,16,17,18,19,20,21,22] to explore new results and theorems related with more symmetric properties about this topic.

2. Basic Concepts

To meet the requirements in the next sections, here, the basic elements of the theory of curves in the Minkowski 3-space ${\mathbb{E}}_1^3$ are briefly presented. There exists a vast literature on the subject, including several monographs (see for example [1,5]).

Let ${\mathbb{E}}_1^3$ be the three-dimensional Minkowski space, that is, the three-dimensional real vector space ${\mathbb{R}}^3$ with the following metric:

$$⟨d\mathbf{x},d\mathbf{x}⟩=-d{x}_1^2+d{x}_2^2+d{x}_3^2$$

where $\left(x_1,x_2,x_3\right)$ denotes the canonical coordinates in ${\mathbb{R}}^3$. An arbitrary vector $\mathbf{x}$ of ${\mathbb{E}}_1^3$ is said to be spacelike if $⟨\mathbf{x},\mathbf{x}⟩>$ 0 or $\mathbf{x}$ = $\mathbf{0}$, timelike if $⟨\mathbf{x},\mathbf{x}⟩<$ 0, and lightlike or null if $⟨\mathbf{x},\mathbf{x}⟩=0$ and $\mathbf{x}\ne \mathbf{0}$. A timelike or light-like vector in ${\mathbb{E}}_1^3$ is said to be causal. For $\mathbf{x}\in {\mathbb{E}}_1^3$, the norm is defined by $∥\mathbf{x}∥=\sqrt{\left|⟨\mathbf{x},\mathbf{x}⟩\right|},$ then, the vector $\mathbf{x}$ is called a spacelike unit vector if $⟨\mathbf{x},\mathbf{x}⟩=1$ and a timelike unit vector if $⟨\mathbf{x},\mathbf{x}⟩=-1$. Similarly, a regular curve in ${\mathbb{E}}_1^3$ can locally be spacelike, timelike, or null (lightlike), if all of its velocity vectors are spacelike, timelike, or null (lightlike), respectively. For any two vectors $\mathbf{x}=\left(x_1,x_2,x_3\right)$ and $\mathbf{y}=(y_1,y_2,y_3)$ of ${\mathbb{E}}_1^3$, the inner product is the real number $⟨\mathbf{x},\mathbf{y}⟩=-x_1{y}_1+x_2{y}_2+x_3{y}_3$ and the vector product is defined by the following.

$$\mathbf{x}\times \mathbf{y}=\left|\begin{array}{ccc}-{\mathbf{e}}_1& {\mathbf{e}}_2& {\mathbf{e}}_3\\ x_1& x_2& x_3\\ y_1& y_2& y_3\end{array}\right|=\left(-\left(x_2{y}_3-x_3{y}_2\right),\left(x_3{y}_1-x_1{y}_3\right),\left(x_1{y}_2-x_2{y}_1\right)\right).$$

(1)

The hyperbolic and Lorentzian (de Sitter space) unit spheres are as follows, respectively.

$${\mathbb{H}}_{+}^2=\{\mathbf{x}\in {\mathbb{E}}_1^3\mid -x_1^2+x_2^2+x_3^2=-1\}.$$

(2)

$${\mathbb{S}}_1^2=\{\mathbf{x}\in {\mathbb{E}}_1^3\mid -x_1^2+x_2^2+x_3^2=1\},$$

(3)

Definition 1.

Let $\mathbf{x}$ and $\mathbf{y}$ in ${\mathbb{E}}_1^3$ be two non-null vectors.

• Assume that $\mathbf{x}$ and $\mathbf{y}$ are spacelike vectors, then we have the following:
  • If they span a spacelike plane, there is s a unique real number $0\le \theta \le \pi$ such that $⟨\mathbf{x},\mathbf{y}⟩=∥\mathbf{x}∥∥\mathbf{y}∥cos\theta$. This number is called the spacelike angle between the vectors $\mathbf{x}$ and $\mathbf{y}$.
  • If they span a timelike plane. there is s a unique real number $\theta \ge 0$ such that $⟨\mathbf{x},\mathbf{y}⟩=ϵ∥\mathbf{x}∥∥\mathbf{y}∥cosh\theta$, where $ϵ=+1$ or $ϵ=-1$ according to $sign\left(x_2\right)=sign\left(y_2\right)$ or $sign\left(x_2\right)\ne sign\left(y_2\right)$, respectively. This number is called the central angle between the vectors $\mathbf{x}$ and $\mathbf{y}$.
• Let us assume that $\mathbf{x}$ and $\mathbf{y}$ are timelike vectors, then there is a unique real number $\theta \ge 0$ such that $⟨\mathbf{x},\mathbf{y}⟩=ϵ∥\mathbf{x}∥∥\mathbf{y}∥cosh\theta$, where $ϵ=+1$ or $ϵ=-1$ according to $\mathbf{x}$ and $\mathbf{y}$ have different time-orientation or the same time-orientation, respectively. This number is called the Lorentzian timelike angle between vectors $\mathbf{x}$ and $\mathbf{y}$.
• Let us assume that $\mathbf{x}$ is spacelike and $\mathbf{y}$ is timelike, then there is a unique real number $\theta \ge 0$ such that $⟨\mathbf{x},\mathbf{y}⟩=ϵ∥\mathbf{x}∥∥\mathbf{y}∥sinh\theta$, where $ϵ=+1$ or $ϵ=-1$ according to $sign\left(x_2\right)=sign\left(y_1\right)$ or $sign\left(x_2\right)\ne sign\left(y_1\right)$. This number is called the Lorentzian timelike angle between vectors $\mathbf{x}$ and $\mathbf{y}$.

Let $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$ be a unit speed non-null curve in ${\mathbb{E}}_1^3$, and it has a spacelike or timelike rectifying plane. The $\kappa \left(s\right)$ and $\tau \left(s\right)$ denote the natural curvature and torsion of $\mathbf{\alpha }=$$\mathbf{\alpha }\left(s\right)$, respectively. Then, $\mathbf{\alpha }\left(s\right)$ is called $\mathit{Serret}-\mathit{Frenet}\mathit{curve}$ if $\kappa >0$ and $\tau \ne 0$. Consider the Serret–Frenet frame $\left\{\mathbf{t}\right(s),$$\mathbf{n}\left(s\right)$, $\mathbf{b}\left(s\right)\}$ is associated with curve $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$, then the Serret–Frenet formulae are read as follows [7,8,9]:

$$\left(\begin{array}{c}{\mathbf{t}}^{\prime }\hfill \\ {\mathbf{n}}^{\prime }\hfill \\ {\mathbf{b}}^{\prime }\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & \kappa \hfill & 0\hfill \\ -{ϵ}_0{ϵ}_1\kappa \hfill & 0\hfill & \tau \hfill \\ 0\hfill & -{ϵ}_1{ϵ}_2\tau \hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathbf{t}\hfill \\ \mathbf{n}\hfill \\ \mathbf{b}\hfill \end{array}\right),$$

(4)

where ${ϵ}_0=⟨\mathbf{t},\mathbf{t}⟩=\pm 1,$${ϵ}_1=⟨\mathbf{n},\mathbf{n}⟩=\pm 1,{ϵ}_2=⟨\mathbf{b},\mathbf{b}⟩=\pm 1$, ${ϵ}_0{ϵ}_1{ϵ}_2=-1$. Here, “prime” denotes the derivative with respect to the arc length parameter s. Now, on the base of the different values of ${ϵ}_0$, ${ϵ}_1$, and ${ϵ}_2$, we provide three detailed classifications for $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$:

• $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$ is a timelike curve if $-{ϵ}_0={ϵ}_1={ϵ}_2=1$;
• $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$ is called the first kind of spacelike curve ${ϵ}_0=-{ϵ}_1={ϵ}_2=1$;
• $\mathbf{\alpha }=\mathbf{\alpha }\left(s\right)$ is called the second kind of spacelike curve ${ϵ}_0={ϵ}_1=-{ϵ}_2=1$.

Furthermore, if $\mathbf{\alpha }\left(s\right)$ is a spherical curve in ${\mathbb{S}}_1^2$, by a translation in ${\mathbb{E}}_1^3$ if necessary, we may assume the following:

$$⟨\mathbf{\alpha }\left(s\right),\mathbf{\alpha }\left(s\right)⟩=a,$$

where a is a constant. Without a loss of generality, we assume that $a=1$. Then, we define the following unit vector.

$$\mathit{g}\left(s\right)=\mathbf{\alpha }\left(s\right)\times \mathit{t}\left(s\right).$$

(5)

It is easy to see that $\mathbf{\alpha }\left(s\right)$, $\mathit{t}\left(s\right)$, and $\mathit{g}\left(s\right)$ form an orthonormal basis along curve $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$. Here, it is convenient to assume $⟨\mathbf{\alpha }\left(s\right),\mathbf{\alpha }\left(s\right)⟩=1$, $⟨\mathit{t}\left(\mathit{s}\right),\mathit{t}\left(\mathit{s}\right)⟩=-$1 and $⟨\mathit{g}\left(\mathit{s}\right),\mathit{g}\left(\mathit{s}\right)⟩=1$. Hence, Equation (4) yields the following.

$$\mathbf{\alpha }\left(\mathbf{s}\right)\times \mathit{g}\left(\mathit{s}\right)=\mathit{t}\left(\mathit{s}\right),\mathit{t}\left(\mathit{s}\right)\times \mathit{g}\left(\mathit{s}\right)=\mathbf{\alpha }\left(\mathbf{s}\right),\mathbf{\alpha }\left(\mathbf{s}\right)\times \mathit{t}\left(\mathit{s}\right)=\mathit{g}\left(\mathit{s}\right).$$

(6)

Since $\mathbf{\alpha }\left(s\right)$, $\mathit{t}\left(s\right)$ and $\mathit{g}\left(s\right)$ form an orthonormal basis along curve $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$, we call $\left\{\mathbf{\alpha }\right(s)$, $\mathit{t}\left(s\right)$$\mathit{g}\left(s\right)\}$ the spherical Blaschke frame of the spherical curve $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$. By a direct computation, we conclude that there exists a function $\gamma \left(s\right)$ satisfying the following.

$$\left(\begin{array}{c}{\mathbf{\alpha }}^{{}^{\prime }}\hfill \\ {\mathbf{t}}^{{}^{\prime }}\hfill \\ {\mathbf{g}}^{{}^{\prime }}\hfill \end{array}\right)=\left(\begin{array}{ccc}0\hfill & 1\hfill & 0\hfill \\ 1\hfill & 0\hfill & \gamma \hfill \\ 0\hfill & \gamma \hfill & 0\hfill \end{array}\right)\left(\begin{array}{c}\mathbf{\alpha }\hfill \\ \mathbf{t}\hfill \\ \mathbf{g}\hfill \end{array}\right).$$

(7)

Moreover, we call $\gamma \left(s\right)$ the spherical (geodesic) curvature function of spherical curve $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$. The following can be shown.

$$\mathit{b}(s)=\frac{{\mathbf{\alpha }}^{{}^{\prime }}\times {\mathbf{\alpha }}^{{}^{{}^{″}}}}{∥{\mathbf{\alpha }}^{{}^{\prime }}\times {\mathit{\alpha }}^{{}^{{}^{″}}}∥}=\frac{\gamma \mathbf{\alpha }-\mathbf{g}}{\sqrt{1+{\gamma }^2}}.$$

(8)

It is obvious that $\mathit{b}$ is the curvature axis or evolute of the spherical curve $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$. In fact, it is important to consider the relations between the spherical curvature $\gamma$(s) and the curvature $\kappa$(s), as well as the torsion $\tau$(s) of $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$. Therefore, from Equations (3) and (6), we have the following.

$$\kappa \mathbf{n}={\mathbf{t}}^{{}^{\prime }}=\mathbf{\alpha }+\gamma \mathbf{g}.$$

(9)

By computing the inner products with both sides of the above equation, respectively, we obtain the following.

$${\kappa }^2=1+{\gamma }^2.$$

(10)

Differentiating both sides of Equation (10), we can directly generate the following.

$$\kappa {\kappa }^{{}^{\prime }}=\gamma {\gamma }^{{}^{\prime }}.$$

(11)

Differentiating both sides of Equation (9) and using Formulas (5)–(8), the following is the case.

$${\kappa }^2\mathbf{t}+{\kappa }^{{}^{\prime }}\mathbf{n}+\kappa \tau \mathbf{b}=(1+{\gamma }^2)\mathbf{t}+{\gamma }^{{}^{\prime }}\mathbf{g}.$$

(12)

Since the following is the case:

$$⟨\mathbf{t},\mathbf{g}⟩=⟨\mathbf{t},\mathbf{\alpha }⟩=⟨\mathbf{t},\mathbf{n}⟩=0,$$

the above equation provides the following.

$${\kappa }^2=1+{\gamma }^2.$$

(13)

Similarly, by computing the inner products with both sides of Equation (12), we obtain the following.

$${\kappa }^{{}^{\prime }2}+{\kappa }^2{\tau }^2={\gamma }^{{}^{\prime }2}.$$

(14)

Then, Equatiions (9), (12) and (13) result in the following.

$$\tau =\pm \frac{{\gamma }^{{}^{\prime }}}{1+{\gamma }^2}.$$

(15)

Therefore, by combining Equations (12) and (14), the following relationships are generated.

$$\left.\begin{array}{c}\hfill \kappa \left(s\right)=\frac{∥{\mathbf{\alpha }}^{{}^{\prime }}\times {\alpha }^{{}^{{}^{″}}}∥}{{∥{\mathbf{\alpha }}^{{}^{\prime }}∥}^3}=\sqrt{1+{\gamma }^2},\\ \hfill \tau \left(s\right)=\frac{det({\mathbf{\alpha }}^{{}^{\prime }},{\mathbf{\alpha }}^{{}^{{}^{″}}},{\mathbf{\alpha }}^{{}^{‴}})}{{∥{\mathbf{\alpha }}^{{}^{\prime }}\times {\mathbf{\alpha }}^{{}^{{}^{″}}}∥}^2}=\pm \frac{{\gamma }^{{}^{\prime }}}{1+{\gamma }^2}.\end{array}\right\}$$

(16)

On the other hand, let us consider a circle on ${\mathbb{S}}_1^2$, which is described by the following equation:

$${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)=\left\{\mathbf{\alpha }\in {\mathbb{S}}_1^2\mid ⟨\mathbf{\alpha },{\mathbf{b}}_0⟩=c\right\},$$

(17)

where c is a real constant, and ${\mathbf{b}}_0$ is a fixed spacelike unit vector that determines the circle’s center. This means that ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$ is a great circle if $c=0$, and a small circle if $c\ne 0$, respectively. Then, we have the following.

Proposition 1.

Let $\mathbf{\alpha }:I\subseteq \mathbb{R}\to$${\mathbb{S}}_1^2$ be a unit speed timelike curve. Then, $\mathbf{\alpha }\left(s\right)$ is a part of ${\mathbb{S}}_1^1(0,{\mathbf{b}}_0)$ if and only if $\gamma \left(s\right)=0$.

Proof. 

Suppose that $\gamma \left(s\right)=0$. By the Blaschke formula (4), we have $\mathbf{g}$ as a constant unit vector. We consider a function $f:I\subseteq \mathbb{R}\to \mathbb{R}$ defined by $f\left(s\right)=⟨\mathbf{x},{\mathbf{b}}_0⟩$. Then, we have the following.

$$\begin{array}{c}\hfill f\left(s\right)=⟨\mathbf{x},{\mathbf{b}}_0⟩=0,\mathrm{and}f{}^{\prime }=⟨\mathbf{t},{\mathbf{b}}_0⟩=0.\end{array}$$

Therefore, f is identically equal to 0, and $\mathbf{x}\left(s\right)\subset {\mathbb{S}}_1^1(0,{\mathbf{b}}_0)$.

Conversely, assume that there exists ${\mathbb{S}}_1^1(0,{\mathbf{b}}_0)$ such that $\mathbf{x}\left(s\right)\subset {\mathbb{S}}_1^1(0,{\mathbf{b}}_0)$. Then, function f as above is identically equal to zero. It follows that f${}^{{}^{\prime }}=⟨\mathbf{t},{\mathbf{b}}_0⟩=0$. Thus, the following is the case.

$$f{}^{{}^{″}}=⟨{\mathbf{t}}^{{}^{\prime }},{\mathbf{b}}_0⟩=⟨\mathbf{\alpha }+\gamma \mathbf{g},{\mathbf{b}}_0⟩=\gamma ⟨\mathbf{g},{\mathbf{b}}_0⟩=0.$$

Since $\gamma \ne 0$, we have $⟨\mathbf{g},{\mathbf{b}}_0⟩=0$. the following is the case.

$$\begin{array}{c}\hfill ⟨{\mathbf{g}}^{{}^{\prime }},{\mathbf{b}}_0⟩=\gamma ⟨\mathbf{t},{\mathbf{b}}_0⟩=0.\end{array}$$

Since $\gamma \ne 0$, we have $⟨\mathbf{g},{\mathbf{b}}_0⟩=⟨\mathbf{t},{\mathbf{b}}_0⟩=0$. Then, ${\mathbf{b}}_0=\pm \mathbf{t}\times \mathbf{g}$, which contradicts the fact that $\mathbf{t}\times \mathbf{g}=\mathbf{\alpha }$. Thus, $\gamma =0$ for any $s\in I$. □

Corollary 1.

Let $\mathbf{\alpha }:I\subseteq \mathbb{R}\to$${\mathbb{S}}_1^2$ be a unit speed timelike curve. Then, ${\gamma }^{{}^{\prime }}=0$ if and only if $\mathbf{\alpha }\left(s\right)$ is a part of ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)\subset {\mathbb{S}}_1^2$.

Proof. 

For the first differential of $\mathbf{b}$, we obtain the following.

$${\mathbf{b}}^{{}^{\prime }}=\mp \frac{{\gamma }^{{}^{\prime }}}{{\gamma }^2+1}\left(\frac{\mathbf{\alpha }-\gamma \mathbf{g}}{\sqrt{{\gamma }^2+1}}\right).$$

Then, ${\mathbf{b}}_0=\pm \mathbf{b}$ if and only if ${\gamma }^{{}^{\prime }}=0$. From Equation (14), we can figure out that ${\gamma }^{{}^{\prime }}=0$ yields and that $\tau =0$ and $\kappa$ are constant directly, which implies that $\mathbf{\alpha }\left(s\right)\in {\mathbb{S}}_1^2$ is a part of the small circle ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$ for which its center is ${\mathbf{b}}_0$. □

3. Spacelike Ruled Surface with Spacelike Ruling

A spacelike ruled surface in Minkowski 3-space ${\mathbb{E}}_1^3$ can be written as follows:

$$M:\mathbf{y}(s,v)=\mathbf{c}\left(s\right)+v\mathbf{x}\left(s\right),s\in I,v\in \mathbb{R},$$

(18)

with the following being the case.

$$⟨\mathbf{x},\mathbf{x}⟩=1,⟨{\mathbf{c}}^{{}^{\prime }},{\mathbf{x}}^{{}^{\prime }}⟩=0.$$

Here, $\mathbf{c}\left(s\right)$ is a spacelike curve and $\mathbf{x}$ is a unit vector moving a long $\mathbf{c}\left(s\right)$. In this case, the curve $\mathbf{c}=\mathbf{c}\left(s\right)$ is the striction curve, and parameter s is the arc length of spherical image or indicatrix $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$. Generally, we call such an expression the standard equation of the non-developable spacelike ruled surfaces with spacelike ruling in Minkowski 3-space ${\mathbb{E}}_1^3$. Here, we will take notation $\mathbf{x}\left(s\right)=\alpha \left(s\right)$. Since $⟨{\mathbf{c}}^{{}^{\prime }},{\mathbf{x}}^{{}^{\prime }}⟩=0$, it is reasonable to assume the following.

$${\mathbf{c}}^{{}^{\prime }}=\Gamma \mathbf{x}+\mu \mathbf{g}.$$

(19)

The functions $\gamma \left(s\right)$, $\Gamma \left(s\right)$, and $\mu \left(s\right)$ are called the curvature functions or construction parameters of the ruled surface. The geometrical meanings of these invariants are explained as follows:$\gamma$ is the geodesic curvature of the spherical image curve $\mathbf{x}=\mathbf{x}\left(s\right)$; $\Gamma$ describes the angle between the tangent of the striction curve and the ruling of the surface; and $\mu$ is the distribution parameter of the ruled surface M at the ruling $\mathbf{x}$.

3.1. Lorentzian Height Functions

In this subsection, we introduce a family of functions that is useful for the study of geometric invariants of timelike spherical curve $\mathbf{x}\left(s\right)$ in ${\mathbb{S}}_1^2$. For this purpose, similarly to the books in [10,12], the spacelike fixed unit vector ${\mathbf{b}}_0$ of ${\mathbb{S}}_1^2$ will be said to be a ${\mathbf{b}}_k$ evolute of the timelike curve $\mathbf{x}\left(s\right)$ in ${\mathbb{S}}_1^2$ at $s\in I$ if for all i such that $1\le i\le k$, $⟨{\mathbf{b}}_0,{\mathbf{x}}^i\left(s\right)⟩=0$, but $⟨{\mathbf{b}}_0,{\mathbf{x}}^{k+1}\left(s\right)⟩\ne 0$. Here ${\mathbf{x}}^i$ denotes the i-th derivatives of $\mathbf{x}$ with respect to the arc length of $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$.

We now define a smooth function $H^T:I\times {\mathbb{S}}_1^2\to \mathbb{R},$ by $H^T(s,{\mathbf{b}}_0)=⟨{\mathbf{b}}_0,\mathbf{x}⟩$. We call $H^T$ a Lorentzian height function of $\mathbf{x}\left(s\right)$ in ${\mathbb{S}}_1^2$. We use the notation $h_0\left(s\right)=H^T(s,{\mathbf{b}}_0)$ for any fixed spacelike unit vector ${\mathbf{b}}_0$ of ${\mathbb{S}}_1^2$. Then, we have the following proposition.

Proposition 2.

Under the aforementioned notations, by direct calculation, the following holds:

• $h_0$ will be invariant in the first approximation if and only if ${\mathbf{b}}_0$ is spanned by $\mathbf{x}$ and $\mathbf{g}$:

  $$h_{\mathbf{0}}^{{}^{\prime }}=0\iff ⟨{\mathbf{x}}^{{}^{\prime }},{\mathbf{b}}_0⟩=0\iff ⟨\mathbf{t},{\mathbf{b}}_0⟩=0\iff {\mathbf{b}}_0=a_1\mathbf{x}+a_2\mathbf{g};$$

  (20)
  for some numbers $a_1,a_2\in \mathbb{R}$ and $a_1^2+a_2^2=1$.
• $h_0$ will be invariant in the second approximation if and only if ${\mathbf{b}}_0$ is ${\mathbf{b}}_2$ evolute of $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$.

  $$h_0^{{}^{\prime }}=h_0^{{}^{″}}=0\iff {\mathbf{b}}_0=\pm \mathbf{b}.$$

  (21)
• $h_0$ will be invariant in the third approximation if and only if ${\mathbf{b}}_0$ is ${\mathbf{b}}_3$ evolute of $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$.

  $$h_0^{{}^{\prime }}=h_0^{{}^{″}}=h_0^{{}^{‴}}=0\iff {\mathbf{b}}_0=\pm \mathbf{b},\mathit{and}{\gamma }^{{}^{\prime }}=0.$$

  (22)
• $h_0$ will be invariant in the fourth approximation if and only if ${\mathbf{b}}_0$ is ${\mathbf{b}}_4$ evolute of $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$.

  $$h_0^{{}^{\prime }}=h_0^{{}^{″}}=h_0^{{}^{‴}}=h_0^{{}^{\left(4\right)}}=0\iff {\mathbf{b}}_0=\pm \mathbf{b},\mathit{and}{\gamma }^{{}^{\prime }}={\gamma }^{{}^{″}}=0.$$

  (23)

By Proposition 2, we can discuss the contact of $\mathbf{x}\left(s\right)$ with circle ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$:

• There exist a spacelike vector ${\mathbf{b}}_0=\mathbf{b}$ such that $\mathbf{x}\left(s\right)\subset {\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$ if and only if ${\gamma }^{{}^{\prime }}\left(s\right)=0$. In this case, ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$ has at least 3-point contact with $\mathbf{x}\left(s\right)$ at $s_0$.
• The circle ${\mathbb{S}}_1^1(c,{\mathbf{b}}_0)$ and curve $\mathbf{x}\left(s\right)$ in ${\mathbb{S}}_1^2$ both have at least 4-point contact at $\mathbf{x}\left(s_0\right)$ if and only if ${\gamma }^{{}^{\prime }}=0$ and ${\gamma }^{{}^{″}}\ne 0$.

3.2. Unfoldings of Functions of One Variable

In this subsection, we will use the same technique on the singularity theory for families of smooth functions. Detailed descriptions are found in books [10,11]. Let F: $\left(\mathbb{R}\times {\mathbb{R}}^r,(s_0,{\mathbf{x}}_0)\right)\to \mathbb{R}$ be a smooth function, and $\mathcal{F}\left(s\right)=F_{x_0}$, $F_{x_0}\left(s\right)=F(s,{\mathbf{x}}_0)$. Then, F is called an r-parameter unfolding of $\mathcal{F}\left(s\right)$. If ${\mathcal{F}}^{\left(p\right)}\left(s_0\right)=0$ for all 1 $\le p\le k+1$, and ${\mathcal{F}}^{(p+1)}\left(s_0\right)\ne 0$, we say $\mathcal{F}\left(s\right)$ has $A_{\le k}$-singularity at $s_0$. We also say $\mathcal{F}\left(s\right)$ has $A_{\le k}$-singularity at $s_0$ at if ${\mathcal{F}}^{\left(p\right)}\left(s_0\right)=0$ for all 1 $\le p\le k+1$. Let F be an r-parameter unfolding of $\mathcal{F}\left(s\right)$ and $\mathcal{F}\left(s\right)$ has $A_k$-singularity (1 $\le k)$ at $s_0$, we define the $\left(k-1\right)$-jet of the partial derivative $\frac{\partial F}{\partial x_i}$ at $s_0$ to be $j^{\left(k-1\right)}\left(\frac{\partial F}{\partial x_i}\left(s,{\mathbf{x}}_0\right)\right)={\gamma }_{j=1}^{k-1}{L}_{ji}^{j}s$ (without the constant term), for $i=1,\dots ,r$. Then, $F(s,\mathbf{x})$ is called a $\left(p\right)$ versal unfolding if and only if the $\left(k-1\right)\times r$ matrix of coefficients $\left(L_{ji}\right)$ has rank $\left(k-1\right)$. (This certainly requires $k-1\le r$; thus, the smallest value of r is $k-1$.)

We now state important sets about the unfoldings relative to the above notations. The singular set of $F(s,\mathbf{x})$ is the following set.

$${\mathbb{S}}_F=\left\{\mathbf{x}\in {\mathbb{S}}_1^2\mid \mathrm{there}\mathrm{exists}s\in \mathbb{R}\mathrm{with}\frac{\partial F}{\partial s}=0\mathrm{at}(s,\mathbf{x})\right\}.$$

(24)

The bifurcation set ${\mathbb{B}}_F$ of F is the following set [11].

$${\mathbb{B}}_F=\left\{\mathbf{x}\in \in {\mathbb{S}}_1^2\mid \mathrm{there}\mathrm{exists}s\in \mathbb{R}\mathrm{with}\frac{\partial F}{\partial s}=\frac{{\partial }^{2}F}{\partial s^2}=0\mathrm{at}(s,\mathbf{x})\right\}.$$

(25)

Then, similarly to [11], we can state the following theorem.

Theorem 1.

Let F:$\left(\mathbb{R}\times {\mathbb{R}}^r,(s_0,{\mathbf{x}}_0)\right)\to \mathbb{R}$ be an r-parameter unfolding of $\mathcal{F}\left(s\right)$, which has the $A_k$ singularity $\left(k\ge 1\right)$ at $s_0$. Suppose that F is a $\left(p\right)$ versal unfolding. Then, the following is the case:

• If $k=2$, then ${\mathbb{B}}_F$ is locally diffeomorphic to $\left\{\mathbf{0}\right\}$ × ${\mathbb{R}}^{r-1}$;
• If $k=3$, then ${\mathbb{B}}_F$ is locally diffeomorphic to $\mathbf{C}$ × ${\mathbb{R}}^{r-2}$, where $\mathbf{C}=\{(x_1,x_2)\mid$$x_1^2=x_2^3\}$ is the ordinary cusp.

For the given curve $\mathbf{x}\left(s\right)\in {\mathbb{S}}_1^2$ and $h_{\mathbf{0}}\left(s\right)=H^T(s,{\mathbf{b}}_0)$, the bifurcation set of $H^T$ is given as follows.

$${\mathbb{B}}_{H^T}=\left\{\mathbf{x}\in {\mathbb{S}}_1^2\mid \mathbf{b}=\pm \frac{\gamma \mathbf{x}-\mathbf{g}}{\sqrt{{\gamma }^2+1}}.\right\}.$$

(26)

Hence, we have the following fundamental proposition:

Proposition 3.

For the unit speed timelike curve x$\left(s\right)=\left(x_1\left(s\right),x_2\left(s\right),x_3\left(s\right)\right)$ on ${\mathbb{S}}_1^2$. If $h_0\left(s\right)=H^T(s,{\mathbf{b}}_0)$ has the $A_k$-singularity ($k=2,3)$ at $s_0\in \mathbb{R}$, then $H^T$ is the $\left(p\right)$ versal unfolding of $h_0\left(s_0\right)$.

Proof. 

Let b${}_0=\left(b_1,b_2,b_3\right)\in {\mathbb{S}}_1^2$, with $-b_1^2+b_2^2+b_3^2=1$. Then, we have the following.

$$H^T(s,{\mathbf{b}}_0)=-b_1{x}_1\left(s\right)+b_2{x}_2\left(s\right)+b_3{x}_3\left(s\right).$$

Suppose that $b_3>0$ and $b_3=\sqrt{1+b_1^2-b_2^2}$. Then, we have the following.

$$H^T(s,{\mathbf{b}}_0)=-b_1{x}_1\left(s\right)+b_2{x}_2\left(s\right)+\sqrt{1+b_1^2-b_2^2}{x}_3\left(s\right).$$

(27)

Therefore, we have the following.

$$\left.\begin{array}{c}\frac{\partial H^T}{\partial b_1}=\left(-x_1\left(s\right)+\frac{b_1{x}_3\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right),\hfill \\ \frac{\partial H^T}{\partial b_2}=\left(x_2\left(s\right)-\frac{b_2{x}_3\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right).\hfill \end{array}\right\}$$

(28)

We also have the following:

$$\left.\begin{array}{c}\frac{\partial }{\partial s}\frac{\partial H^T}{\partial b_1}=\left(-x_1^{{}^{\prime }}\left(s\right)+\frac{b_1{x}_3^{{}^{\prime }}\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right),\hfill \\ \frac{\partial }{\partial s}\frac{\partial H^T}{\partial b_2}=\left(x_2^{{}^{\prime }}\left(s\right)-\frac{b_2{x}_3^{{}^{\prime }}\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right),\hfill \end{array}\right\}$$

(29)

and the following is the case.

$$\left.\begin{array}{c}\frac{{\partial }^2}{\partial s^2}\frac{\partial H^T}{\partial b_1}=\left(-x_1^{{}^{″}}\left(s\right)+\frac{b_1{x}_3^{{}^{{}^{″}}}\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right),\hfill \\ \frac{{\partial }^2}{\partial s^2}\frac{\partial H^T}{\partial b_2}=\left(x_2^{{}^{{}^{″}}}\left(s\right)-\frac{b_2{x}_3^{{}^{{}^{″}}}\left(s\right)}{\sqrt{1+b_1^2-b_2^2}}\right).\hfill \end{array}\right\}$$

(30)

Thus, the following is obtained.

$$\left.\begin{array}{c}{j}^1\left(\frac{\partial H^T}{\partial b_1}(s,{\mathbf{b}}_0)\right)=\left(-x_1^{{}^{\prime }}\left(s_0\right)+\frac{b_1{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\right)s,\hfill \\ j^1\left(\frac{\partial H^T}{\partial b_2}(s,{\mathbf{b}}_0)\right)=\left(x_2^{{}^{\prime }}\left(s_0\right)-\frac{b_2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\right)s,\hfill \end{array}\right\}$$

(31)

$$\left.\begin{array}{c}{j}^2\left(\frac{\partial H^T}{\partial b_1}(s,{\mathbf{b}}_0)\right)=\left(-x_1^{{}^{\prime }}\left(s_0\right)+\frac{b_1{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\right)s\\ +\frac{1}{2}\left(-x_1^{{}^{{}^{″}}}\left(s_0\right)+\frac{b_1{x}_3^{{}^{{}^{″}}}\left(s_0\right)}{b_{30}}\right)s^2,\\ j^2\left(\frac{\partial H^T}{\partial b_2}(s,{\mathbf{b}}_0)\right)=\left(x_2^{{}^{\prime }}\left(s_0\right)-\frac{b_2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\right)s\\ +\frac{1}{2}\left(x_2^{{}^{{}^{″}}}\left(s_0\right)-\frac{b_2{x}_3^{{}^{{}^{″}}}\left(s_0\right)}{b_{30}}\right)s^2.\end{array}\right\}$$

(32)

(i) If $h_0\left(s_0\right)$ has the $A_2$-singularity at $s_0\in \mathbb{R}$, then $h_0\left(s_0\right)=0$. Therefore, the $(2-1)\times 2$ matrix of coefficients $\left(L_{ji}\right)$ is as follows.

$$A=\left(\begin{array}{cc}-x_1^{{}^{\prime }}\left(s_0\right)+\frac{b_1{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}& x_2^{{}^{\prime }}\left(s_0\right)-\frac{b_2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\end{array}\right);$$

(33)

Suppose that the rank of the matrix A is zero; then, we have the following:

$$x_1^{{}^{\prime }}\left(s_0\right)=\frac{b_1{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}},x_2^{{}^{\prime }}\left(s_0\right)=\frac{b_2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}.$$

(34)

Since ${∥{\mathbf{x}}^{{}^{\prime }}\left(s_0\right)∥}^2=-1$, we have $x_3^{{}^{\prime }}\left(s_0\right)\ne 0$ so that we have the contradiction as follows.

$$\begin{array}{ccc}\hfill 0& =& ⟨\left(x_1^{{}^{\prime }}\left(s_0\right),x_2^{{}^{\prime }}\left(s_0\right),x_3^{{}^{\prime }}\left(s_0\right)\right),\left(b_1,b_2,b_{30}\right)⟩\hfill \\ & =& -x_1^{{}^{\prime }}\left(s_0\right)b_1+x_2^{{}^{\prime }}\left(s_0\right)b_2+x_3^{{}^{\prime }}\left(s_0\right)b_{30}\hfill \\ & =& -\frac{b_1^2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}+\frac{b_2^2{x}_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}+x_3^{{}^{\prime }}\left(s_0\right)b_{30}\hfill \\ & =& \frac{-x_3^{{}^{\prime }}\left(s_0\right)}{b_{30}}\ne 0.\hfill \end{array}$$

(35)

This means that rank ($A)=1$, and $H^T$ is the (p) versal unfolding of $h_{\mathbf{0}}$ at $s_0$.

(ii) If $h_{\mathbf{0}}\left(s_0\right)$ has $A_3$-singularity at $s_0\in \mathbb{R}$, then $h_0^{{}^{\prime }}=h_0^{{}^{″}}=0$, and by Proposition 1, we have the following:

$$\mathbf{b}\left(s_0\right)=\pm \left(\frac{\gamma \mathbf{x}+\mathbf{g}}{\sqrt{{\gamma }^2+1}}\right)\left(s_0\right),$$

(36)

where ${\gamma }^{{}^{\prime }}\left(s_0\right)=0$, and ${\gamma }^{{}^{″}}\left(s_0\right)\ne 0$. Therefore, the $(3-1)\times 2$ matrix of the coefficients $\left(L_{ji}\right)$ is as follows.

$$B=\left(\begin{array}{cc}{L}_{11}& L_{12}\\ L_{21}& L_{22}\end{array}\right)=\left(\begin{array}{cc}-x_1^{{}^{\prime }}+\frac{b_1{x}_3^{{}^{\prime }}}{b_{30}}& x_2^{{}^{\prime }}-\frac{b_2{x}_3^{{}^{\prime }}}{\sqrt{1+b_1^2-b_2^2}}\\ -x_1^{{}^{{}^{″}}}+\frac{b_1{x}_3^{{}^{{}^{″}}}}{b_{30}}& x_2^{{}^{{}^{″}}}-\frac{b_2{x}_3^{{}^{{}^{″}}}}{b_{30}}\end{array}\right).$$

(37)

For the purpose, we also require the $2\times 2$ matrix B to be non-singular, which it always is. In fact, the determinate of this matrix at $s_0$ is the following.

$$\begin{array}{ccc}\hfill det\left(B\right)& =& \frac{1}{b_{30}}\left|\begin{array}{ccc}-x_1^{{}^{\prime }}& x_2^{{}^{\prime }}& x_3^{{}^{\prime }}\\ -x_1^{{}^{{}^{″}}}& x_2^{{}^{{}^{″}}}& x_3^{{}^{{}^{″}}}\\ b_{10}& b_{20}& b_{30}\end{array}\right|\hfill \\ & =& \frac{1}{b_{30}}⟨{\mathbf{x}}^{{}^{\prime }}\times {\mathbf{x}}^{{}^{″}},{\mathbf{b}}_{\mathbf{0}}⟩\hfill \end{array}$$

(38)

$$\begin{array}{ccc}& =& \pm \frac{1}{b_{30}}⟨{\mathbf{x}}^{{}^{\prime }}\times {\mathbf{x}}^{{}^{″}},\left(\frac{\gamma \mathbf{x}+\mathbf{g}}{\sqrt{{\gamma }^2+1}}\right)⟩\hfill \end{array}$$

(39)

Since x${}^{{}^{\prime }}=\mathbf{t}$, we have x${}^{{}^{″}}=$x$+\gamma \mathbf{g}$. Substituting these relations to the above equality, we have:

$$det\left(B\right)=\mp \frac{\sqrt{{\gamma }^2\left(s_0\right)+1}}{b_{30}}\ne 0.$$

(40)

This means that rank $\left(B\right)=2$. □

Proposition 4.

Let x $\left(s\right)$ be a unit speed timelike curve on ${\mathbb{S}}_1^2$, we have the following:

(1) The spherical evolute of x $\left(s\right)$ is locally diffeomorphic to a constant spacelike vector if ${\gamma }^{{}^{\prime }}\left(s_0\right)\ne 0$;

(2) The spherical evolute of x $\left(s\right)$ is locally diffeomorphic to the cusp $\mathbf{C}$ at $s_0\in \mathbb{R}$ if ${\gamma }^{{}^{\prime }}\left(s_0\right)=0$ and $\gamma {}^{{}^{\prime \prime }}\left(s_0\right)\ne 0$.

Proof. 

For the proof of assertion (1), from Equation (22), we have the following.

$${\mathbf{b}}^{{}^{\prime }}=\mp \frac{{\gamma }^{{}^{\prime }}}{{\left({\gamma }^2+1\right)}^{\frac{3}{2}}}\left(\mathbf{x}+\gamma \mathbf{g}\right).$$

(41)

Therefore, $\mathbf{b}$ is locally diffeomorphic to a constant spacelike vector if ${\gamma }^{{}^{\prime }}\left(s_0\right)\ne 0$. For assertion (2), from Proposition 2 and Theorem 1, the bifurcation set ${\mathbb{B}}_{H^T}$ at ${\mathbf{b}}_0=\pm \left(\frac{\gamma \mathbf{x}-\mathbf{g}}{\sqrt{{\gamma }^2+1}}\right)\left(s_0\right)$ is locally diffeomorphic to the ordinary cusp $\mathbf{C}$ in ${\mathbb{S}}_1^2$ if ${\gamma }^{{}^{\prime }}\left(s_0\right)=0,$ and ${\gamma }^{{}^{″}}\left(s_0\right)\ne 0$ □

4. Example

In this section, we provide an example to illustrate our results. Figure 1, Figure 2 and Figure 3 are shown below.

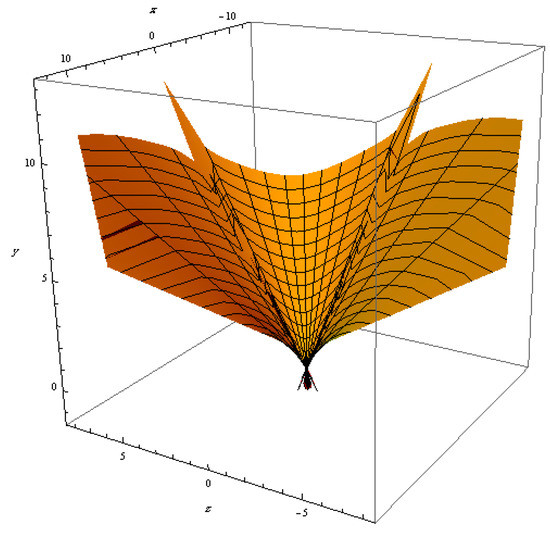
Figure 1. The spacelike ruled surface M.

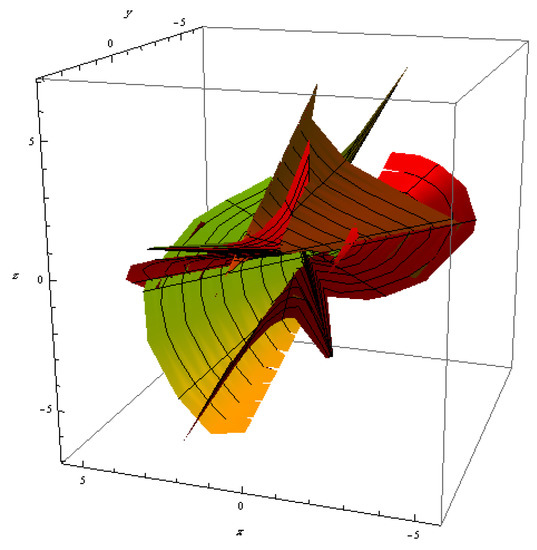
Figure 2. The evolute surface of M.

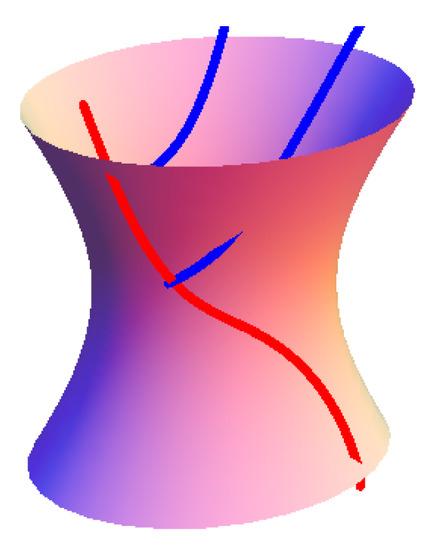
Figure 3. The space curve of the tangential surface.

Example 1.

Let a spacelike ruled surface defined by the following be the case:

$$M:\mathbf{y}(u,v)=\mathbf{c}\left(u\right)+v\mathbf{x}\left(u\right),u\in I,v\in \mathbb{R},$$

(42)

where the following obtains:

$$\left.\begin{array}{c}c\left(u\right)=\left(\begin{array}{c}u-\frac{u\left(-1-u^2+u^6\right)\left(-1+6u^3+\frac{3u^3-9u^7}{\sqrt{1+u^2-u^6}}\right)}{1-9u^4-4u^6}\\ u^2-\frac{u^3\left(-1-u^2+u^6\right)\left(-1+6u^3+\frac{3u^3-9u^7}{\sqrt{1+u^2-u^6}}\right)}{1-9u^4-4u^6}\\ u^3-\frac{\left(-1-u^2+u^6\right)\left(9u^7+\sqrt{1+u^2-u^6}-3u^3\left(1+2\sqrt{1+u^2-u^6}\right)\right)}{-1+9u^4+4u^6}\end{array}\right)\hfill \\ \mathbf{x}\left(u\right)=\left(u,u^3,\sqrt{1-u^6+u^2}\right),\hfill \end{array}\right\}$$

(43)

and $-0.55<u<0.55$. By a straightforward calculation, we have the following:

$$\left.\begin{array}{c}⟨\mathbf{x},\mathbf{x}⟩=1,⟨{\mathbf{c}}^{{}^{\prime }},{\mathbf{x}}^{{}^{\prime }}⟩=0,\hfill \\ \mathbf{t}\left(u\right)=\left(1,3u^2,\frac{2u-6u^5}{2\sqrt{1+u^2-u^6}}\right),\hfill \\ \mathbf{g}\left(u\right)=\left(-\frac{u^2\left(3+2u^2\right)\sqrt{-1-u^2+u^6}}{\sqrt{1-9u^4-4u^6}\sqrt{1+u^2-u^6}},\frac{\sqrt{-1-u^2+u^6}\left(1+2u^6\right)}{\sqrt{1-9u^4-4u^6}\sqrt{1+u^2-u^6}},\frac{2u^3\sqrt{-1-u^2+u^6}}{\sqrt{1-9u^4-4u^6}}\right).\hfill \end{array}\right\}$$

(44)

Furthermore, we obtain the following:

$$\begin{array}{ccc}\hfill \gamma \left(u\right)& =& \frac{2u\sqrt{-1-u^2+u^6}\left(-3-4u^2+12u^6+4u^8\right)}{{\left(1-9u^4-4u^6\right)}^{3/2}\sqrt{1+u^2-u^6}},\hfill \\ \hfill {\gamma }^{{}^{\prime }}\left(u\right)& =& -\frac{6\sqrt{-1-u^2+u^6}\left(1+4u^2+45u^4+40u^6+20u^8+36u^{10}+4u^{12}\right)}{{\left(1-9u^4-4u^6\right)}^{5/2}\sqrt{1+u^2-u^6}}.\hfill \end{array}$$

It follows that evolute $\mathbf{b}\left(u\right)$ is given as follows:

$$\mathbf{b}\left(u\right)=\pm \frac{\gamma \mathbf{x}\left(u\right)-\mathbf{g}\left(u\right)}{\sqrt{{\gamma }^2+1}}=\frac{1}{\delta }\left(b_1\left(u\right),b_2\left(u\right),b_3\left(u\right)\right),$$

(45)

where

$$\begin{array}{ccc}\hfill b_1\left(u\right)& =& -3u^2\sqrt{-1-u^2+u^6}\left(1+2u^2+9u^4+2u^6\right){\left(-1+9u^4+4u^6\right)}^{3/2}\hfill \\ \hfill b_2\left(u\right)& =& \sqrt{-1-u^2+u^6}{\left(-1+9u^4+4u^6\right)}^{3/2}\left(-1+3u^4-6u^6+42u^{10}+16u^{12}\right)\hfill \\ \hfill b_3\left(u\right)& =& 2u\sqrt{-1-u^2+u^6}{\left(-1+9u^4+4u^6\right)}^{3/2}\left(-3-5u^2+21u^6+8u^8\right),\hfill \end{array}$$

$$\delta ={\left(1-9u^4-4u^6\right)}^{3/2}\sqrt{\begin{array}{c}-1+36u^2+123u^4+76u^6-531u^8\\ -696u^{10}+553u^{12}+1548u^{14}+816u^{16}+128u^{18}\end{array}}$$

According to Proposition 4, the osculating circle ${\mathbb{S}}_1^1(0,{\mathbf{b}}_0)$ has a three-point contact with $\mathbf{x}\left(u\right)$ at $u=0$ and $\mathbf{b}\left(0\right)=\pm {\mathbf{e}}_2$.