Inferences for Alpha Power Exponential Distribution Using Adaptive Progressively Type-II Hybrid Censored Data with Applications

Abstract

One of the most important asymmetrical probability distributions that recently presented as an extension of the conventional exponential distribution is the alpha power exponential distribution. It may be compared to various asymmetrical well-known models, such as Weibull and gamma distributions. As a result, using an adaptive progressive Type-II hybrid censoring scheme, this paper investigates the estimation problems of the alpha power exponential distribution. Maximum likelihood and Bayesian methods are used to estimate unknown parameters, reliability, and hazard rate functions. Under the assumption of independent gamma priors and symmetric loss function, Bayesian estimators are examined. The Bayesian credible intervals and estimated confidence intervals of the relevant values are also calculated. The various estimating approaches are evaluated using a simulation study that considers various sample sizes and censoring schemes. Furthermore, numerous optimality criteria are examined, and the best progressive censoring schemes are offered. Finally, for an explanation, two real data sets from engineering and chemical fields are provided to show the applicability of the asymmetrical alpha power exponential distribution. The Bayesian method for estimating the parameters and reliability indices of the alpha power exponential distribution is recommended based on numerical results, especially when the number of observed data is small.

1. Introduction

Censored data are a common feature of reliability and life testing studies. Experimenters must have the experience of various test situations pertaining to time, cost, or money constraints where the removal of units is planned in advance before failure. Time censoring (Type-I) and failure censoring (Type-II) schemes are the most often used censoring systems in life testing and reliability studies. One of the major weaknesses of these schemes is that they do not permit items to be withdrawn from the experiment at any point other than the end. As a result, the progressive Type-II censoring scheme (PT-II-CS) is used, which is a more widely used censoring system. n items are set on a test in the PT-II-CS, and m is a prefixed number of items to be failed. At the time of the first failure $X_{1:m:n}$, $R_1$ items are randomly extracted from the staying $n-1$ outlasting items. Likewise, at the time of the second failure, $X_{2:m:n}$, $R_2$ items of the remaining $n-2-R_1$ items are randomly withdrawn and so on. At the time of the mth failure $X_{m:m:n}$ all the remaining $n-m-{\sum }_{i=1}^{m-1}{R}_i$ items are removed, see Balakrishnan [1] for more details.

Kundu and Joarder [2] suggested a progressive Type-I hybrid censoring scheme (PT-I-HCS), in which n identical items are tested using a specified progressive censoring scheme. $R_1,R_2,···,R_m$ and the test is ended at random time $T^{*}=min(X_{m:m:n},T)$, where T is a predetermined time. The PT-I-HCS has the disadvantage that the useful sample size is random and might turn out to be a very small number. As a result, the statistical inference method will be efficient. Ng et al. [3] proposed an adaptive progressive Type-II hybrid censoring scheme to increase the efficiency of statistical analysis (AP-II-HCS). The number of failures m is predetermined in advance in the AP-II-HCS, and the testing time is permitted to run over the time T. Moreover, we have the progressive censoring scheme $R_1,R_2,···,R_m$, but the values of some of the $R_i$ maybe adjust consequently during the test. If the mth failure happens before time T $(\mathrm{i}.\mathrm{e}.,X_{m:m:m}<T)$, the test stops at this time and we will have the usual PT-II-CS. On the other hand, if $X_{D:m:n}<T<X_{D+1:m:n}$, where $D+1<m$ and $X_{D:m:n}$ is the Dth failure time happen before time T, then we will not withdraw any surviving item from the test by putting $R_{D+1},R_{D+2},···,R_{m-1}=0$ and $R_m=n-m-{\sum }_{i=1}^D{R}_i$. This setting ensures that we will terminate the experiment when we reach the preferred number of failures m, and the total test time will not be too far away from the ideal time T. Let $x_{1:m:n}<\cdots <x_{D:m:n}<T<x_{D+1:m:n}<\cdots x_{m:m:n}$ be an adaptive progressive Type-II hybrid censored sample from a continuous population with probability density function (PDF) $f\left(x\right)$ and cumulative distribution function (CDF) $F\left(x\right)$ with progressive censoring scheme $R_1,\cdots ,R_D,0,\cdots ,0,R_m$, then the likelihood function of the observed data takes the form

$$L=C\prod _{i=1}^{m}f\left(x_{i:m:n}\right)\prod _{i=1}^D{[1-F\left(x_{i:m:n}\right)]}^{R_i}{[1-F\left(x_{m:m:n}\right)]}^{R_m},$$

(1)

where C is a constant that is independent of the parameters. Various studies based on the AP-II-HCS have been conducted; readers can refer to the findings of Hemmati and Khorram [4], Nassar and Abo-Kasem [5], Ateya and Mohammed [6], Nassar et al. [7], and Nassar et al. [8] among many others.

The alpha power exponential (APE) distribution was introduced by Mahdavi and Kundu [9] as a novel extension of the exponential distribution. They studied the APE distribution’s main characteristics and using the method of maximum likelihood to estimate the unknown parameters. They claimed that the APE distribution had a lot of qualities. Weibull, gamma, and exponentiated exponential distributions are all quite similar to it. The Weibull, gamma, and exponentiated exponential distributions have similar PDF and hazard rate functions (HRF). As a result, it may be thought of as a alternative choice to these well-known distributions. Furthermore, because the APE distribution’s CDF can be represented in an explicit structure, it may be used to investigate censored data very easily. If X is a random variable that follows the APE distribution, its PDF and CDF may be represented as follows.

$$f(x;\alpha ,\theta )=\frac{\theta log\left(\alpha \right)e^{-\theta x}{\alpha }^{1-e^{-\theta x}}}{\alpha -1},x>0,\theta ,\alpha >0,\alpha \ne 1,$$

(2)

and

$$F(x;\alpha ,\theta )=\frac{{\alpha }^{1-e^{-\theta x}}-1}{\alpha -1}.$$

(3)

The shape and scale parameters, respectively, are $\alpha$ and $\theta$. The APE distribution’s reliability function (RF) and HRF are calculated as follows:

$$R(x;\alpha ,\theta )=\frac{\alpha }{\alpha -1}\left(1-{\alpha }^{-e^{-\theta x}}\right),$$

(4)

and

$$h(x;\alpha ,\theta )=\frac{\theta log\left(\alpha \right)e^{-\theta x}{\alpha }^{-e^{-\theta x}}}{1-{\alpha }^{-e^{-\theta x}}}.$$

(5)

Nassar et al. [10] studied different classical estimation methods of the APE distribution using a complete sample. Salah [11] investigated the estimation problems of the APE distribution under PT-II-CS using the maximum likelihood approach. Salah et al. [12] used the maximum likelihood approach to study the point and interval estimates of the APE distribution based on Type-II hybrid censored data. These studies concentrated on the estimations of the APE distribution using the classical approaches only by utilizing complete samples or some conventional censoring schemes. Investigating the estimation problems of the APE distribution using classical and Bayesian procedures are the main core of the present study by utilizing a more flexible censoring scheme.

The originality of this study comes from the fact that, to the best of our knowledge, it is the first time researchers have explored the estimation problems of the APE distribution under an AP-II-HCS. Further, despite the various researches utilizing the APE distribution, no study investigates the Bayesian estimation of its parameters and reliability indices. For more information about the importance of estimating the reliability characteristics, one may refer to Xu et al. [13], Luo et al. [14], Hu and Chen [15], and Chen and Ye [16]. The key role of this study is three fold. Firstly, we consider the estimation problems of the APE distribution using AP-II-HCS using classical and Bayesian approaches to fill the gap of the previous studies that utilized only classical approaches. Accordingly, the point and interval estimates of the unknown parameters as well as the RF and HRF are investigated. The second is to find the optimal sampling scheme for adaptive progressive Type-II hybrid censored APE distribution. The third is to create a policy to select the most suitable estimation method for the APE distribution based on AP-II-HCS as well as the optimal sampling scheme. In Bayesian estimation, the estimators are acquired by employing the squared error loss function. The squared error loss function is the most commonly used symmetric loss function, in which, the estimation treats overestimation and underestimation equally. To evaluate the results, we perform a simulation research to test the behavior of the suggested approaches, and two data sets are used as examples.

The rest of the article is organized as follows: The classical inference of the APE distribution is discussed in Section 2. The Bayesian estimating method is discussed in Section 3. Section 4 presents the results of a simulation investigation. In Section 5, we provide different approaches for determining the best censoring scheme. Section 6 examines two real data sets, and Section 7 concludes the paper.

2. Classical Inference

The maximum likelihood estimates (MLEs) of the unknown parameters and reliability indices are investigated in this part, and the corresponding approximate confidence intervals are also created using the Fisher information matrix and the large sample theory.

2.1. Estimation of Maximum Likelihood

Suppose that $x_{1:m:n}<\cdots <x_{D:m:n}<T<x_{D+1:m:n}<\cdots x_{m:m:n}$ is an adaptive progressive Type-II hybrid censored sample of size m with $R_1,\cdots ,R_D,0,\cdots ,0,R_m$ from the APE distribution with PDF and CDF given by (2) and (3), respectively. Then, the likelihood function can be obtained from (1)–(3), as follows, without the constant term

$$\begin{array}{ccc}\hfill L(\alpha ,\theta )& =& {\left(\frac{\alpha }{\alpha -1}\right)}^n{[\theta log\left(\alpha \right)]}^{m}exp\left[-\theta \sum _{i=1}^m{x}_i-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}\right]\prod _{i=1}^D{\left(1-{\alpha }^{-e^{-\theta x_i}}\right)}^{R_i}\hfill \\ & \times & {\left(1-{\alpha }^{-e^{-\theta x_m}}\right)}^{R_m},\hfill \end{array}$$

(6)

where $x_i=x_{i:m:n}$ for the sake of simplicity. Then, we can write the natural logarithm of the likelihood function in (6) as

$$\begin{array}{ccc}\hfill \ell (\alpha ,\theta )& =& nlog\left(\alpha \right)-nlog(\alpha -1)+mlog\left(\theta \right)+mlog[log\left(\alpha \right)]-\theta \sum _{i=1}^m{x}_i-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}\hfill \\ & +& \sum _{i=1}^D{R}_{i}log\left(1-{\alpha }^{-e^{-\theta x_i}}\right)+R_{m}log\left(1-{\alpha }^{-e^{-\theta x_m}}\right).\hfill \end{array}$$

(7)

The MLEs of the parameters $\alpha$ and $\theta$ symbolized by $\widehat{\alpha }$ and $\widehat{\theta }$ can be acquired by solving the two normal equations simultaneously, which is obtained by carrying the first derivatives of (7) with respect to $\alpha$ and $\theta$. The normal equations are as follow

$$\begin{array}{c}\hfill \frac{\partial \ell (\alpha ,\theta )}{\partial \alpha }=\frac{n}{\alpha }-\frac{n}{\alpha -1}+\frac{m}{\alpha log\left(\alpha \right)}-\frac{1}{\alpha }\sum _{i=1}^m{e}^{-\theta x_i}+\frac{1}{\alpha }\sum _{i=1}^D\frac{R_i{e}^{-\theta x_i}}{{\alpha }^{e^{-\theta x_i}}-1}+\frac{R_m{e}^{-\theta x_m}}{\alpha \left({\alpha }^{e^{-\theta x_m}}-1\right)}=0\end{array}$$

(8)

and

$$\begin{array}{c}\hfill \frac{\partial \ell (\alpha ,\theta )}{\partial \theta }=\frac{m}{\theta }-\sum _{i=1}^m{x}_i+log\left(\alpha \right)\sum _{i=1}^m{x}_i{e}^{-\theta x_i}-log\left(\alpha \right)\sum _{i=1}^D\frac{R_i{x}_i{e}^{-\theta x_i}}{{\alpha }^{e^{-\theta x_i}}-1}-log\left(\alpha \right)\frac{R_m{x}_m{e}^{-\theta x_m}}{{\alpha }^{e^{-\theta x_m}}-1}=0.\end{array}$$

(9)

It is noticed from (8) and (9) that there are no closed forms for the MLEs $\widehat{\alpha }$ and $\widehat{\theta }$; therefore, numerical methods may be employed to solve these equations to obtain $\widehat{\alpha }$ and $\widehat{\theta }$. Once $\widehat{\alpha }$ and $\widehat{\theta }$ are acquired, the MLEs of the RF and HRF can be obtained directly based on the invariance property of the MLEs from (4) and (5), respectively, as follow

$$\widehat{R}\left(x\right)=\frac{\widehat{\alpha }}{\widehat{\alpha }-1}\left(1-{\widehat{\alpha }}^{-e^{-\widehat{\theta }x}}\right)$$

and

$$\widehat{h}\left(x\right)=\frac{\widehat{\theta }log\left(\widehat{\alpha }\right)e^{-\widehat{\theta }x}{\widehat{\alpha }}^{-e^{-\widehat{\theta }x}}}{1-{\widehat{\alpha }}^{-e^{-\widehat{\theta }x}}}.$$

2.2. Interval Estimation

We can construct estimated confidence intervals for the unknown parameters $\alpha$ and $\theta$ using the MLEs’ asymptotic properties. According to the theory of large samples, it is known that the asymptotic distribution of ($\widehat{\alpha },\widehat{\theta }$) is normal distribution with mean ($\alpha ,\theta$) and variance–covariance matrix ${\mathit{I}}^{-1}(\alpha ,\theta )$. Practically, we use ${\mathit{I}}^{-1}(\widehat{\alpha },\widehat{\theta })$ to estimate ${\mathit{I}}^{-1}(\alpha ,\theta )$, which is obtained based on the observed Fisher information matrix, where

$$\begin{array}{c}\hfill {\mathit{I}}^{-1}(\widehat{\alpha },\widehat{\theta })={\left(\begin{array}{cc}-\frac{{\partial }^2\ell (\alpha ,\theta )}{\partial {\alpha }^2}& -\frac{{\partial }^2\ell (\alpha ,\theta )}{\partial \alpha \partial \theta }\\ -\frac{{\partial }^2\ell (\alpha ,\theta )}{\partial \theta \partial \alpha }& -\frac{{\partial }^2\ell (\alpha ,\theta )}{\partial {\theta }^2}\end{array}\right)}_{(\alpha ,\theta )=(\widehat{\alpha },\widehat{\theta })}^{-1},\end{array}$$

(10)

where

$$\begin{array}{c}\hfill \frac{{\partial }^2\ell (\alpha ,\theta )}{\partial {\alpha }^2}=-\frac{n}{{\alpha }^2}+\frac{n}{{(\alpha -1)}^2}-\frac{m[1+log(\alpha \left)\right]}{{\alpha }^2{log}^2\left(\alpha \right)}+\frac{1}{{\alpha }^2}\sum _{i=1}^m{e}^{-\theta x_i}+\sum _{i=1}^D{R}_i{\psi }_i+R_m{\psi }_m,\end{array}$$

and

$$\begin{array}{c}\hfill \frac{{\partial }^2\ell (\alpha ,\theta )}{\partial {\theta }^2}=-\frac{m}{{\theta }^2}-log\left(\alpha \right)\sum _{i=1}^m{x}_i^2{e}^{-\theta x_i}-log\left(\alpha \right)\sum _{i=1}^D{R}_i{\varphi }_i-R_m{\varphi }_m\end{array}$$

and

$$\begin{array}{c}\hfill \frac{{\partial }^2\ell (\alpha ,\theta )}{\partial \alpha \partial \theta }=\frac{1}{\alpha }\sum _{i=1}^m{x}_i{e}^{-\theta x_i}+\frac{1}{\alpha }\sum _{i=1}^D{R}_i{x}_i^{-1}{\varphi }_i+R_m{x}_m^{-1}{\varphi }_m,\end{array}$$

(11)

where

$$\begin{array}{c}\hfill {\psi }_i=\frac{e^{-\theta x_i}\left[1-{\alpha }^{e^{-\theta x_i}}\left(1+e^{-\theta x_i}\right)\right]}{{\alpha }^2{\left(1-{\alpha }^{e^{-\theta x_i}}\right)}^2}\end{array}$$

and

$$\begin{array}{c}\hfill {\varphi }_i=\frac{x_i^2{e}^{-\theta x_i}\left[1+{\alpha }^{e^{-\theta x_i}}{e}^{-\theta x_i}log\left(\alpha \right)-{\alpha }^{e^{-\theta x_i}}\right]}{{\left(1-{\alpha }^{e^{-\theta x_i}}\right)}^2}.\end{array}$$

Directly, the $100(1-\gamma )\%$ approximate confidence intervals of the unknown parameters $\alpha$ and $\theta$ can be obtained as

$$\widehat{\alpha }\pm z_{\gamma /2}\sqrt{\widehat{var}\left(\widehat{\alpha }\right)},\mathrm{and}\widehat{\theta }\pm z_{\alpha /2}\sqrt{\widehat{var}\left(\widehat{\theta }\right)}.$$

where $\widehat{var}\left(\widehat{\alpha }\right)$ and $\widehat{var}\left(\widehat{\theta }\right)$ are the main diagonal elements of (10), respectively, and $z_{\alpha /2}$ is the upper $\alpha /2$th percentile point of the standard normal distribution.

To calculate the approximate confidence intervals of the RF and HRF of the APE distribution, we need to obtain the variance of these functions. One of the numerous significant employed techniques to approximate these variances is the delta method. In our case and to apply this method, suppose that ${\Delta }_R{=(\partial R/\partial \alpha ,\partial R/\partial \theta )|}_{(\alpha ,\theta )=(\widehat{\alpha },\widehat{\theta })}$ and ${\Delta }_h{=(\partial h/\partial \alpha ,\partial h/\partial \theta )|}_{(\alpha ,\theta )=(\widehat{\alpha },\widehat{\theta })}$, where

$$\frac{\partial R}{\partial \alpha }=\frac{1-{\alpha }^{e^{-\theta x}}+(\alpha -1)e^{-\theta x}}{{(\alpha -1)}^2{\alpha }^{e^{-\theta x}}},$$

$$\frac{\partial R}{\partial \theta }=\frac{\alpha x{e}^{-\theta x}log\left(\alpha \right)}{(\alpha -1){\alpha }^{e^{-\theta x}}},$$

$$\frac{\partial h}{\partial \alpha }=\frac{\theta e^{-\theta x}\left[{\alpha }^{e^{-\theta x}}-{\alpha }^{e^{-\theta x}}{e}^{-\theta x}log\left(\alpha \right)-1\right]}{\alpha {\left({\alpha }^{e^{-\theta x}}-1\right)}^2},$$

and

$$\frac{\partial h}{\partial \theta }=\frac{e^{-\theta x}log\left(\alpha \right)\left[{\alpha }^{e^{-\theta x}}\left(1-\theta x+\theta x{e}^{-\theta x}log\left(\alpha \right)\right)+\theta x-1\right]}{{\left({\alpha }^{e^{-\theta x}}-1\right)}^2}.$$

Based on the above results, the approximate estimates for the variances of the RF and HRF can be computed, respectively, as

$$\widehat{var}\left(\widehat{R}\right)\approx \left[{\Delta }_R\mathit{I}(\widehat{\alpha },\widehat{\theta }){\Delta }_R^{\top }\right]\mathrm{and}\widehat{var}\left(\widehat{h}\right)\approx \left[{\Delta }_h\mathit{I}(\widehat{\alpha },\widehat{\theta }){\Delta }_h^{\top }\right].$$

As a result, at the confidence level $100(1-\gamma )$, the two-sided approximate confidence intervals for $R\left(x\right)$ and $h\left(x\right)$ are presented, respectively, by

$$\widehat{R}\left(x\right)\pm z_{\frac{\gamma }{2}}\sqrt{\widehat{var}\left(\widehat{R}\right)}\mathrm{and}\widehat{h}\pm z_{\frac{\gamma }{2}}\sqrt{\widehat{var}\left(\widehat{h}\right)}.$$

3. Bayesian Estimation

The Bayesian estimators of the unknown parameters $\alpha$ and $\theta$, as well as the RF and HRF, are derived in this section. The related credible intervals are also studied in addition to the point estimates. When compared to the maximum likelihood method in statistical analysis, the Bayesian approach offers several advantages. The Bayesian technique is very effective in dependability studies and many other fields where one of the significant challenges is the restricted availability of data. The Bayesian estimates are investigated in this paper under the assumption that the unknown parameters are independent and have gamma distributions, i.e., $\alpha \sim Gamma({\nu }_1,{\omega }_1)$ and $\theta \sim Gamma({\nu }_2,{\omega }_2)$. In this case, we can write the joint prior distribution of $\alpha$ and $\theta$ as

$$P_1(\alpha ,\theta )\propto {\alpha }^{{\nu }_1-1}{\theta }^{{\nu }_2-1}{e}^{-({\omega }_1\alpha +{\omega }_2\theta )},\alpha ,\theta >0,$$

(12)

and ${\nu }_j,{\omega }_j>0,j=1,2$, are the hyper parameters. The posterior distribution is the most significant part of the Bayesian analysis. It retains all the knowledge obtainable regarding the unknown parameters after holding the observed data. Based on the likelihood function in (6) and the joint prior distribution in (12), we can express the joint posterior distribution of $\alpha$ and $\theta$ as follows

$$\begin{array}{ccc}\hfill P_2(\alpha ,\theta |\mathbf{x})& =& A^{-1}\frac{{\alpha }^{n+{\nu }_1-1}}{{(\alpha -1)}^n}{\theta }^{m+{\nu }_2-1}{[log\left(\alpha \right)]}^{m}exp\left[-\theta \sum _{i=1}^m{x}_i-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}-({\omega }_1\alpha +{\omega }_2\theta )\right]\hfill \\ & \times & \prod _{i=1}^D{\left(1-{\alpha }^{-e^{-\theta x_i}}\right)}^{R_i}{\left(1-{\alpha }^{-e^{-\theta x_m}}\right)}^{R_m},\hfill \end{array}$$

(13)

where A is the normalized constant and given by

$$\begin{array}{ccc}\hfill A& =& {\int }_0^{\infty }{\int }_0^{\infty }\frac{{\alpha }^{n+{\nu }_1-1}}{{(\alpha -1)}^n}{\theta }^{m+{\nu }_2-1}{[log\left(\alpha \right)]}^{m}exp\left[-\theta \sum _{i=1}^m{x}_i-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}-({\omega }_1\alpha +{\omega }_2\theta )\right]\hfill \\ & \times & \prod _{i=1}^D{\left(1-{\alpha }^{-e^{-\theta x_i}}\right)}^{R_i}{\left(1-{\alpha }^{-e^{-\theta x_m}}\right)}^{R_m}d\alpha d\theta .\hfill \end{array}$$

Based on a specific loss function, the Bayesian estimator of any function of $\alpha$ and $\theta$, say $\zeta (\alpha ,\theta )$, may be expressed as

$$\begin{array}{ccc}\hfill \tilde{\zeta }(\alpha ,\theta )& =& E_{\alpha ,\theta |\mathbf{x}}\left[\zeta (\alpha ,\theta )\right]\hfill \\ & =& {\int }_0^{\infty }{\int }_0^{\infty }\zeta (\alpha ,\theta )P_2(\alpha ,\theta |\mathbf{x})d\alpha d\theta .\hfill \end{array}$$

(14)

It is clear that calculating (14) analytically is not attainable. As a result, we recommend using the Markov chain Monte Carlo (MCMC) approach to obtain Bayesian estimates and, as a result, to construct Bayesian credible intervals. The full conditional posterior distributions of the unknown parameters are naturally required to produce samples using the MCMC approach. From (13), the full conditional distributions for $\alpha$ and $\theta$ may be stated as follow

$$\begin{array}{ccc}\hfill P_2\left(\alpha \right|\theta ,\mathbf{x})& \propto & \frac{{\alpha }^{n+{\nu }_1-1}}{{(\alpha -1)}^n}{[log\left(\alpha \right)]}^{m}exp\left[-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}-{\omega }_1\alpha \right]\hfill \\ & \times & \prod _{i=1}^D{\left(1-{\alpha }^{-e^{-\theta x_i}}\right)}^{R_i}{\left(1-{\alpha }^{-e^{-\theta x_m}}\right)}^{R_m}\hfill \end{array}$$

(15)

and

$$\begin{array}{ccc}\hfill P_2\left(\theta \right|\alpha ,\mathbf{x})& \propto & {\theta }^{m+{\nu }_2-1}exp\left[-\theta \sum _{i=1}^m{x}_i-log\left(\alpha \right)\sum _{i=1}^m{e}^{-\theta x_i}-{\omega }_2\theta \right]\hfill \\ & \times & \prod _{i=1}^D{\left(1-{\alpha }^{-e^{-\theta x_i}}\right)}^{R_i}{\left(1-{\alpha }^{-e^{-\theta x_m}}\right)}^{R_m}.\hfill \end{array}$$

(16)

It is noted the full conditional distributions of $\alpha$ and $\theta$ in (15) and (16), respectively, can not be expressed as well-known densities; therefore, generating $\alpha$ and $\theta$ from these densities is not attainable by employing the standard methods. In this case, we need to generate the unknown parameters by using Metropolis–Hastings algorithm. To apply the Metropolis–Hastings steps, we consider the normal distribution as a proposal distribution in order to obtain the Bayesian estimates and to construct the credible intervals for the unknown parameters. To generate samples from (15) and (16), we offer the following steps of the Metropolis–Hastings algorithm:

Step 1. 

Set the start values of $(\alpha ,\theta )$, say $({\alpha }^{\left(0\right)},{\theta }^{\left(0\right)})$.

Step 2. 

Put $k=1$.

Step 3. 

Simulate ${\alpha }^{*}$ from (15) from the normal distribution $N({\alpha }^{(k-1)},var\left({\alpha }^{(k-1)}\right))$.

Step 4. 

Compute the acceptance ratio:

$$r\left({\alpha }^{(k-1)}\right|{\alpha }^{*})=min\left[1,\frac{P_2\left({\alpha }^{*}\right|{\theta }^{(k-1)})}{P_2\left({\alpha }^{(k-1)}\right|{\theta }^{(k-1)})}\right].$$

Step 5. 

Simulate u, where $U\sim U(0,1)$.

Step 6. 

If $u\le r\left({\alpha }^{(k-1)}\right|{\alpha }^{*})$, put ${\alpha }^{\left(k\right)}={\alpha }^{*}$, else, put ${\alpha }^{\left(k\right)}={\alpha }^{(k-1)}$.

Step 7. 

Redo Steps 3–6 for $\theta$ to obtain ${\theta }^{\left(k\right)}$ from (16).

Step 8. 

Obtain $R^{\left(k\right)}\left(x\right)$ and $h^{\left(k\right)}\left(x\right)$ as

$$R^{\left(k\right)}\left(x\right)=\frac{{\alpha }^{\left(k\right)}}{{\alpha }^{\left(k\right)}-1}\left\{1-{\left[{\alpha }^{\left(k\right)}\right]}^{-e^{-{\theta }^{\left(k\right)}x}}\right\}$$

and

$$h^{\left(k\right)}\left(x\right)=\frac{{\theta }^{\left(k\right)}log\left({\alpha }^{\left(k\right)}\right)e^{-{\theta }^{\left(k\right)}x}{\left[{\alpha }^{\left(k\right)}\right]}^{-e^{-{\theta }^{\left(k\right)}x}}}{1-{\left[{\alpha }^{\left(k\right)}\right]}^{-e^{-{\theta }^{\left(k\right)}x}}}.$$

Step 9. 

Set $k=k+1$.

Step 10. 

Repeat Steps 3–8 M times to get

$$\left[{\alpha }^{\left(k\right)},{\theta }^{\left(k\right)},R^{\left(k\right)}\left(x\right),h^{\left(k\right)}\left(x\right)\right],\cdots ,\left[{\alpha }^{\left(M\right)},{\theta }^{\left(M\right)},R^{\left(M\right)}\left(x\right),h^{\left(M\right)}\left(x\right)\right].$$

Step 11. 

Compute the Bayesian estimates of $\alpha$, $\theta$, $R\left(x\right)$, and $h\left(x\right)$ under squared error loss function as

$$\begin{array}{c}\hfill \tilde{\alpha }=\frac{1}{M-B}\sum _{k=B+1}^M{\alpha }^{\left(k\right)},\tilde{\theta }=\frac{1}{M-B}\sum _{k=B+1}^M{\theta }^{\left(k\right)},\end{array}$$

$$\begin{array}{c}\hfill \tilde{R}\left(x\right)=\frac{1}{M-B}\sum _{k=B+1}^M{R}^{\left(k\right)}\left(x\right)\mathrm{and}\tilde{h}\left(x\right)=\frac{1}{M-B}\sum _{k=B+1}^M{h}^{\left(k\right)}\left(x\right).\end{array}$$

Step 12. 

To obtain the highest posterior density (HPD) credible intervals of $\alpha$, $\theta$, $R\left(x\right)$, and $h\left(x\right)$: First, order the MCMC samples of ${\alpha }^{\left(k\right)}$, ${\theta }^{\left(k\right)}$, $R^{\left(k\right)}\left(x\right)$, and $h^{\left(k\right)}\left(x\right)$ for $k=1,2,\cdots ,M,$ after burn-in as ${\alpha }_{(B+1)},{\alpha }_{(B+2)},\cdots ,{\alpha }_{\left(M\right)}$; ${\theta }_{(B+1)},{\theta }_{(B+2)},\cdots ,{\theta }_{\left(M\right)}$; $R_{(B+1)\left(x\right)},R_{(B+2)}\left(x\right),\cdots ,R_{\left(M\right)}\left(x\right)$, and $h_{(B+1)\left(x\right)},h_{(B+2)}\left(x\right),\cdots ,h_{\left(M\right)}\left(x\right)$, respectively. Then, applying the approach proposed by Chen and Shao [17], the $100(1-\gamma )\%$ two-sided HPD credible interval for the unknown parameter $\alpha$ is given by

$$\begin{array}{c}\hfill \left({\alpha }_{\left(k^{*}\right)},{\alpha }_{\left(k^{*}+\left(1-\gamma \right)\left(M-B\right)\right)}\right),\end{array}$$

where $k^{*}=B+1,B+2,\cdots ,M$ is chosen such that

$${\alpha }_{\left(k^{*}+\left[\left(1-\gamma \right)\left(M-B\right)\right]\right)}-{\alpha }_{\left(k^{*}\right)}=\underset{1⩽k⩽\gamma \left(M-B\right)}{min}\left({\alpha }_{\left(k+\left[\left(1-\gamma \right)\left(M-B\right)\right]\right)}-{\alpha }_{\left(k\right)}\right).$$

The largest integer less than or equal to x is denoted by $\left[x\right]$. Then, the HPD credible interval of x with the shortest length is that interval. The HPD credible intervals of $theta$, $R\left(x\right)$, and $h\left(x\right)$ may be easily obtained in a similar way.

4. Monte Carlo Simulation

In this section, a Monte Carlo simulation study was used to examine the behavior of the suggested estimators of $\alpha$ and $\theta$, as well as $R\left(t\right)$ and $h\left(t\right)$. Based on the actual values of the parameters $(\alpha ,\theta )=(1.2,0.8)$, a large number of 1000 adaptive Type-II progressively hybrid censored samples are generated from the APE distribution using various mixtures of n(total test units), m(effective sample size), and T(threshold time point). As a result, at the required time $t=0.1$, the corresponding actual values of RF $R\left(t\right)$ and HRF $h\left(t\right)$ are $R\left(0.1\right)=0.92942$ and $h\left(0.1\right)=0.73457$. Further, different values of $(n,m,T)$ are taken such as $n=50$ and 100 for each specified time $T=0.25$ and 0.75. The test is ended when the number of failed subjects reaches a particular value m, where the failure ratio $(m/n)100\%=50\%$ and $80\%$.

Briefly, for given values of n, m and T, we clarify the procedure of generating adaptive Type-II progressive hybrid censored samples as follows:

Step 1: 

Using the algorithm outlined by Balakrishnan and Sandhu [18], generate an ordinary progressive Type-II censored sample as follows:

(a)

Create $\omega$ independent observations of size m as ${\omega }_1,{\omega }_2,\cdots ,{\omega }_m$.

(b)

For specific n, m, T and $R_i,i=1,2,\cdots ,m$, put

${\upsilon }_i={\omega }_i^{{\left(i+{\sum }_{j=m-i+1}^m{R}_j\right)}^{-1}},i=1,2,\cdots ,m$.

(c)

Let $u_i=1-{\upsilon }_m{\upsilon }_{m-1}\cdots {\upsilon }_{m-i+1}$ for $i=1,2,\cdots ,m$. Then, $u_i,i=1,2,\cdots ,m,$ is a PT-II-CS sample of size m from $U(0,1)$ distribution.

(d)

Set $X_i=F^{-1}(u_i;\alpha ,\theta ),i=1,2,\cdots ,m$, is the generated progressively Type-II censored sample from $\mathrm{APE}(\alpha ,\theta )$.

Step 2: 

Decide D, where $X_D<T<X_{D+1}$, and remove the staying sample $X_{D+2},\cdots ,X_m$.

Step 3: 

From $f\left(x\right)/\left[1-F\left(x_{D+1}\right)\right]$, generate the first $m-D-1$ order statistics with sample size $n-D-{\sum }_{j=1}^D{R}_j-1$ as $X_{D+2},\cdots ,X_m$.

To see the effects of the priors on the Bayesian inference, besides the noninformative priors, say Prior 0: $a_i,b_i=0,i=1,2$, we have used two different informative sets of the hyperparameters $a_i,b_i,i=1,2,$ namely Prior 1: $(a_1,a_2)=(2.4,1.6)$ and $b_1=b_2=2$ and Prior 2: $(a_1,a_2)=(12,8)$ and $b_1=b_2=10$. Here, the hyperparameter values are selected in such a way that the prior mean became the expected value of the model parameter. It is clear that, when $a_i,b_i=0,i=1,2$, the posterior distribution is proportional to the corresponding likelihood function; therefore, if one does not have prior information on the unknown parameters of interest, it is better to use the frequentist estimates instead of the Bayesian estimates because the later are computationally more expensive. Using the Metropolis–Hastings algorithm described in Section 3, we create 12,000 MCMC samples with 2000 iterations as a burn-in period. Thus, using the remaining 10,000 MCMC samples, the average Bayesian estimates and the associated 95% HPD credible intervals of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ are calculated.

To evaluate the performance of removal designs, for each n and m, we assume the following different censoring schemes

$$\begin{array}{cc}& \mathrm{Scheme}\text{-}\mathrm{I}:R_1=n-m,R_i=0\mathrm{for}i\ne 1,\hfill \\ & \mathrm{Scheme}\text{-}\mathrm{II}:\left\{\begin{array}{cc}{R}_{\frac{m}{2}}=n-m,R_i=0\mathrm{for}i\ne \frac{m}{2},\hfill & \mathrm{if}m\mathrm{even};\hfill \\ R_{\frac{m+1}{2}}=n-m,R_i=0\mathrm{for}i\ne \frac{m+1}{2},\hfill & \mathrm{if}m\mathrm{odd},\hfill \end{array}\right.\hfill \\ & \mathrm{Scheme}\text{-}\mathrm{III}:R_m=n-m,R_i=0\mathrm{for}i\ne m.\hfill \end{array}$$

The performance of the different estimates are evaluated based on the root mean square error (RMSE) and relative absolute bias (RAB), while the performances of $95\%$ two-sided ACI/HPD credible intervals estimates are examined using the average interval lengths (AILs). The average point estimates of any function of the unknown APE parameters $\alpha$ and $\theta$ (say $\vartheta$) are calculated numerically as follows:

$${\overline{\widehat{\vartheta }}}_{\tau }=\frac{1}{Q}{\sum }_{j=1}^Q{\widehat{\vartheta }}_{\tau }^{\left(j\right)},\tau =1,2,3,4,$$

$$\mathrm{RMSE}\left({\widehat{\vartheta }}_{\tau }\right)=\sqrt{\frac{1}{Q}{\sum }_{j=1}^Q{\left({\widehat{\vartheta }}_{\tau }^{\left(j\right)}-{\vartheta }_{\tau }\right)}^2},\tau =1,2,3,4,$$

$$\mathrm{RAB}\left({\widehat{\vartheta }}_{\tau }\right)=\frac{1}{Q}{\sum }_{j=1}^Q\frac{\left|{\widehat{\vartheta }}_{\tau }^{\left(j\right)}-{\vartheta }_{\tau }\right|}{{\vartheta }_{\tau }},\tau =1,2,3,4,$$

and

$${\mathrm{AIL}}_{{\vartheta }_{\tau }}(1-\gamma )\%=\frac{1}{Q}{\sum }_{j=1}^Q\left(\mathcal{U}\left({\widehat{\vartheta }}_{\tau }^{\left(j\right)}\right)-\mathcal{L}\left({\widehat{\vartheta }}_{\tau }^{\left(j\right)}\right)\right),\tau =1,2,3,4,$$

where $\widehat{\vartheta }$ is the desired estimate of the parametric function $\vartheta$, ${\widehat{\vartheta }}_{\tau }^{\left(j\right)}$ represents the obtained estimate of the unknown parameter at the $j\text{-}\mathrm{t}\mathrm{h}$ sample ${\vartheta }_{\tau }$, Q is number of generated sequence data, ${\vartheta }_1=\alpha$, ${\vartheta }_2=\theta$, ${\vartheta }_3=R\left(t\right)$, ${\vartheta }_4=h\left(t\right)$, $\mathcal{L}(·)$, and $\mathcal{U}(·)$ refer to the lower and upper interval limits, respectively, of $(1-\gamma )\%$ asymptotic (or credible) interval of ${\vartheta }_{\tau }$.

All numerical computations were achieved using R 4.0.4 software with two helpful packages namely ‘coda’ package suggested by Plummer et al. [19] and ‘maxLik’ package offered by Henningsen and Toomet [20]. Recently, these packages are also recommended by Elshahhat and Nassar [21] and Elshahhat and Rastogi [22]. The average estimates of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ with their RMSEs and RABs are obtained and displayed in Table 1 and Table 2. Moreover, the associated AILs are presented in Table 3 and Table 4.

Table 1. The average estimates, RMSEs, and RABs (in parentheses) for $\alpha$ and $\theta$.

T	(n,m)	Scheme	$\mathit{\alpha }$				$\mathit{\theta }$
			MLE	MCMC			MLE	MCMC
$\mathbf{Prior}\to$				0	1	2		0	1	2
0.25	(50,25)	I	3.093 (4.268,1.692)	1.604 (0.428,0.336)	1.313 (0.138,0.095)	1.250 (0.054,0.042)	0.918 (0.307,0.272)	0.679 (0.165,0.179)	0.709 (0.126,0.126)	0.778 (0.052,0.059)
		II	1.006 (0.210,0.168)	1.347 (0.165,0.123)	1.269 (0.074,0.058)	1.190 (0.048,0.032)	0.208 (0.601,0.741)	0.247 (0.555,0.692)	0.646 (0.165,0.193)	0.831 (0.043,0.045)
		III	1.004 (0.229,0.169)	1.414 (0.250,0.182)	1.267 (0.077,0.056)	1.240 (0.046,0.034)	0.188 (0.614,0.765)	0.273 (0.529,0.658)	0.393 (0.439,0.509)	0.495 (0.333,0.381)
	(50,40)	I	2.704 (3.184,1.362)	1.522 (0.345,0.268)	1.293 (0.102,0.078)	1.166 (0.039,0.028)	0.895 (0.231,0.209)	0.735 (0.109,0.115)	0.763 (0.043,0.048)	0.792 (0.013,0.013)
		II	1.001 (0.200,0.167)	1.292 (0.111,0.079)	1.245 (0.048,0.038)	1.232 (0.035,0.027)	0.396 (0.411,0.506)	0.375 (0.454,0.532)	0.836 (0.039,0.046)	0.774 (0.029,0.033)
		III	1.006 (0.221,0.169)	1.337 (0.161,0.115)	1.179 (0.038,0.027)	1.175 (0.030,0.022)	0.396 (0.411,0.505)	1.312 (0.558,0.641)	0.698 (0.111,0.128)	0.789 (0.045,0.048)
	(100,50)	I	2.242 (2.153,0.984)	1.371 (0.261,0.162)	1.253 (0.062,0.046)	1.169 (0.036,0.027)	0.894 (0.221,0.202)	0.808 (0.078,0.092)	0.745 (0.075,0.085)	0.817 (0.032,0.035)
		II	1.002 (0.199,0.167)	1.261 (0.086,0.062)	1.211 (0.013,0.009)	1.208 (0.012,0.008)	0.231 (0.572,0.712)	0.406 (0.401,0.493)	0.767 (0.038,0.041)	0.799 (0.014,0.014)
		III	1.003 (0.200,0.167)	1.315 (0.158,0.112)	1.219 (0.026,0.019)	1.203 (0.014,0.009)	0.189 (0.613,0.765)	0.303 (0.502,0.621)	0.642 (0.173,0.198)	0.660 (0.156,0.175)
	(100,80)	I	1.810 (1.335,0.624)	1.396 (0.224,0.166)	1.217 (0.023,0.015)	1.220 (0.022,0.017)	0.857 (0.149,0.139)	0.820 (0.051,0.053)	0.801 (0.011,0.011)	0.804 (0.008,0.007)
		II	1.002 (0.201,0.167)	1.154 (0.067,0.046)	1.195 (0.013,0.008)	1.191 (0.009,0.007)	0.489 (0.317,0.388)	0.476 (0.336,0.406)	0.781 (0.029,0.028)	0.805 (0.007,0.007)
		III	1.002 (0.201,0.167)	1.139 (0.081,0.056)	1.186 (0.021,0.015)	1.199 (0.014,0.010)	0.489 (0.317,0.388)	0.949 (0.178,0.186)	0.800 (0.018,0.019)	0.788 (0.018,0.019)
0.75	(50,25)	I	2.908 (4.388,1.565)	1.554 (0.401,0.300)	1.408 (0.228,0.174)	1.320 (0.155,0.111)	0.892 (0.226,0.207)	0.687 (0.158,0.160)	0.707 (0.101,0.116)	0.739 (0.097,0.094)
		II	3.358 (6.730,1.950)	1.283 (0.114,0.077)	1.108 (0.101,0.077)	1.275 (0.085,0.063)	0.925 (0.332,0.284)	0.915 (0.222,0.225)	0.745 (0.063,0.071)	0.841 (0.049,0.052)
		III	2.973 (8.075,1.762)	1.520 (0.363,0.271)	1.279 (0.086,0.066)	1.272 (0.077,0.060)	0.535 (0.600,0.674)	1.270 (0.553,0.588)	0.571 (0.262,0.287)	0.568 (0.255,0.290)
	(50,40)	I	2.489 (3.172,1.208)	1.525 (0.374,0.276)	1.281 (0.089,0.068)	1.246 (0.056,0.039)	0.879 (0.195,0.179)	0.862 (0.136,0.143)	0.822 (0.028,0.029)	0.795 (0.014,0.015)
		II	1.291 (0.862,0.335)	1.242 (0.125,0.092)	1.285 (0.089,0.071)	1.209 (0.033,0.024)	0.675 (0.272,0.273)	0.649 (0.187,0.201)	0.807 (0.056,0.056)	0.801 (0.023,0.025)
		III	1.007 (0.219,0.170)	1.453 (0.291,0.214)	1.252 (0.059,0.044)	1.233 (0.036,0.028)	0.426 (0.383,0.468)	0.778 (0.315,0.313)	0.849 (0.055,0.063)	0.792 (0.052,0.056)
	(100,50)	I	2.116 (2.213,0.905)	1.433 (0.368,0.394)	1.283 (0.088,0.069)	1.167 (0.036,0.027)	0.869 (0.177,0.162)	0.914 (0.135,0.132)	0.773 (0.064,0.053)	0.793 (0.016,0.017)
		II	2.368 (3.243,1.120)	1.228 (0.103,0.066)	1.284 (0.095,0.069)	1.230 (0.043,0.031)	0.903 (0.241,0.207)	0.923 (0.151,0.159)	0.768 (0.036,0.040)	0.822 (0.032,0.032)
		III	1.230 (1.657,0.349)	1.305 (0.142,0.091)	1.142 (0.063,0.049)	1.158 (0.045,0.035)	0.339 (0.543,0.644)	1.025 (0.257,0.282)	0.667 (0.147,0.166)	0.700 (0.117,0.125)
	(100,80)	I	1.810 (1.524,0.650)	1.230 (0.104,0.074)	1.141 (0.063,0.049)	1.192 (0.021,0.015)	0.844 (0.138,0.127)	0.866 (0.084,0.096)	0.799 (0.007,0.007)	0.803 (0.007,0.006)
		II	1.277 (0.627,0.299)	1.136 (0.076,0.055)	1.170 (0.035,0.026)	1.197 (0.011,0.008)	0.696 (0.247,0.232)	0.867 (0.078,0.086)	0.794 (0.017,0.018)	0.801 (0.010,0.010)
		III	1.003 (0.210,0.168)	1.220 (0.079,0.058)	1.172 (0.030,0.024)	1.223 (0.023,0.019)	0.505 (0.302,0.369)	0.864 (0.178,0.183)	0.789 (0.016,0.016)	0.792 (0.014,0.015)

Table 2. The average estimates, RMSEs, and RABs (in parentheses) for $R\left(t\right)$ and $h\left(t\right)$.

T	(n,m)	Scheme	$\mathit{R}\left(\mathit{t}\right)$				$\mathit{h}\left(\mathit{t}\right)$
			MLE	MCMC			MLE	MCMC
$\mathbf{Prior}\to$				0	1	2		0	1	2
0.25	(50,25)	I	0.940 (0.018,0.016)	0.948 (0.020,0.021)	0.939 (0.013,0.013)	0.929 (0.004,0.003)	0.623 (0.181,0.197)	0.542 (0.431,0.268)	0.628 (0.132,0.147)	0.734 (0.042,0.045)
		II	0.980 (0.051,0.054)	0.980 (0.050,0.528)	0.944 (0.016,0.016)	0.927 (0.004,0.003)	0.208 (0.537,0.720)	0.208 (0.528,0.717)	0.577 (0.168,0.215)	0.766 (0.039,0.046)
		III	0.981 (0.052,0.056)	0.977 (0.048,0.051)	0.966 (0.039,0.039)	0.957 (0.030,0.029)	0.188 (0.549,0.745)	0.236 (0.501,0.679)	0.350 (0.412,0.523)	0.445 (0.314,0.394)
	(50,40)	I	0.940 (0.016,0.014)	0.938 (0.011,0.010)	0.932 (0.003,0.003)	0.930 (0.001,0.001)	0.636 (0.164,0.175)	0.645 (0.114,0.136)	0.649 (0.094,0.117)	0.723 (0.015,0.018)
		II	0.961 (0.034,0.034)	0.960 (0.031,0.033)	0.933 (0.003,0.003)	0.928 (0.002,0.002)	0.395 (0.348,0.463)	0.328 (0.432,0.553)	0.702 (0.035,0.045)	0.732 (0.012,0.013)
		III	0.961 (0.033,0.034)	0.889 (0.044,0.043)	0.929 (0.021,0.025)	0.942 (0.013,0.013)	0.395 (0.347,0.462)	1.184 (0.492,0.612)	0.707 (0.035,0.003)	0.733 (0.013,0.015)
	(100,50)	I	0.937 (0.013,0.011)	0.936 (0.008,0.007)	0.933 (0.004,0.003)	0.929 (0.001,0.001)	0.664 (0.129,0.139)	0.663 (0.081,0.098)	0.669 (0.079,0.097)	0.739 (0.028,0.032)
		II	0.977 (0.048,0.051)	0.968 (0.041,0.041)	0.936 (0.007,0.007)	0.929 (0.003,0.002)	0.231 (0.507,0.686)	0.378 (0.362,0.485)	0.702 (0.039,0.046)	0.741 (0.009,0.009)
		III	0.981 (0.052,0.056)	0.974 (0.045,0.048)	0.944 (0.015,0.015)	0.934 (0.005,0.005)	0.188 (0.548,0.744)	0.268 (0.472,0.636)	0.584 (0.163,0.205)	0.605 (0.144,0.177)
	(100,80)	I	0.935 (0.011,0.009)	0.933 (0.006,0.006)	0.929 (0.001,0.001)	0.929 (0.001,0.001)	0.684 (0.107,0.113)	0.702 (0.067,0.075)	0.793 (0.021,0.025)	0.934 (0.005,0.005)
		II	0.952 (0.024,0.025)	0.963 (0.034,0.036)	0.931 (0.002,0.002)	0.930 (0.001,0.001)	0.490 (0.253,0.334)	0.409 (0.333,0.443)	0.719 (0.025,0.026)	0.928 (0.002,0.002)
		III	0.952 (0.024,0.025)	0.915 (0.017,0.015)	0.937 (0.009,0.009)	0.930 (0.001,0.001)	0.489 (0.254,0.335)	0.450 (0.408,0.520)	0.731 (0.013,0.013)	0.733 (0.007,0.007)
0.75	(50,25)	I	0.939 (0.017,0.014)	0.946 (0.018,0.017)	0.931 (0.005,0.005)	0.928 (0.002,0.002)	0.646 (0.173,0.179)	0.561 (0.192,0.236)	0.629 (0.129,0.143)	0.621 (0.119,0.155)
		II	0.938 (0.018,0.015)	0.943 (0.017,0.016)	0.939 (0.012,0.011)	0.940 (0.011,0.012)	0.611 (0.209,0.218)	0.586 (0.180,0.214)	0.682 (0.063,0.076)	0.712 (0.029,0.035)
		III	0.969 (0.044,0.044)	0.933 (0.051,0.059)	0.951 (0.024,0.023)	0.951 (0.023,0.023)	0.309 (0.459,0.588)	1.202 (0.546,0.636)	0.509 (0.252,0.308)	0.505 (0.250,0.313)
	(50,40)	I	0.938 (0.015,0.012)	0.933 (0.011,0.010)	0.931 (0.002,0.002)	0.929 (0.001,0.001)	0.652 (0.150,0.155)	0.704 (0.120,0.129)	0.715 (0.052,0.056)	0.756 (0.030,0.035)
		II	0.941 (0.020,0.016)	0.928 (0.015,0.013)	0.934 (0.006,0.006)	0.932 (0.003,0.003)	0.628 (0.196,0.187)	0.754 (0.163,0.181)	0.719 (0.057,0.061)	0.750 (0.025,0.028)
		III	0.959 (0.030,0.031)	0.888 (0.049,0.045)	0.940 (0.011,0.011)	0.937 (0.009,0.008)	0.425 (0.320,0.422)	0.693 (0.314,0.322)	0.720 (0.019,0.022)	0.740 (0.012,0.013)
	(100,50)	I	0.936 (0.013,0.010)	0.922 (0.009,0.008)	0.930 (0.002,0.002)	0.928 (0.002,0.002)	0.674 (0.126,0.129)	0.809 (0.098,0.113)	0.688 (0.072,0.071)	0.731 (0.014,0.016)
		II	0.935 (0.013,0.010)	0.920 (0.012,0.011)	0.934 (0.007,0.005)	0.930 (0.001,0.001)	0.685 (0.125,0.129)	0.844 (0.138,0.157)	0.746 (0.023,0.028)	0.733 (0.023,0.024)
		III	0.965 (0.040,0.039)	0.918 (0.013,0.012)	0.931 (0.005,0.004)	0.928 (0.003,0.002)	0.364 (0.413,0.513)	0.862 (0.149,0.173)	0.626 (0.121,0.148)	0.654 (0.100,0.110)
	(100,80)	I	0.935 (0.011,0.008)	0.924 (0.008,0.007)	0.929 (0.001,0.001)	0.930 (0.001,0.001)	0.684 (0.105,0.104)	0.789 (0.087,0.103)	0.744 (0.016,0.018)	0.734 (0.013,0.014)
		II	0.940 (0.019,0.014)	0.924 (0.007,0.007)	0.928 (0.002,0.001)	0.929 (0.001,0.001)	0.654 (0.179,0.188)	0.790 (0.076,0.091)	0.738 (0.018,0.022)	0.736 (0.011,0.011)
		III	0.951 (0.022,0.023)	0.941 (0.012,0.013)	0.929 (0.002,0.002)	0.929 (0.001,0.001)	0.504 (0.239,0.313)	0.615 (0.124,0.162)	0.743 (0.010,0.012)	0.730 (0.007,0.006)

Table 3. The AILs of $\alpha$ and $\theta$.

T	(n,m)	Scheme	$\mathit{\alpha }$				$\mathit{\theta }$
			ACI	HPD			ACI	HPD
$\mathbf{Prior}\to$				0	1	2		0	1	2
0.25	(50,25)	I	0.2298	0.5270	0.0953	0.0713	0.2411	0.4314	0.1012	0.1353
		II	0.1696	0.5990	0.1061	0.0609	0.5008	0.4630	0.2448	0.1524
		III	0.1243	0.2646	0.0768	0.0581	0.5749	0.8136	0.4412	0.1552
	(50,40)	I	0.1431	0.4183	0.0915	0.0655	0.2133	0.3443	0.0593	0.0349
		II	0.1553	0.4181	0.0624	0.0539	0.2425	0.3776	0.0776	0.0501
		III	0.1227	0.2405	0.0685	0.0292	0.5216	0.4999	0.1444	0.1368
	(100,50)	I	0.1174	0.3987	0.0846	0.0274	0.1873	0.1723	0.0614	0.0234
		II	0.0440	0.2982	0.0338	0.0129	0.2228	0.3086	0.1839	0.0977
		III	0.0569	0.2235	0.0532	0.0080	0.4912	0.2931	0.2171	0.1091
	(100,80)	I	0.0609	0.3402	0.0499	0.0151	0.1311	0.0993	0.0384	0.0168
		II	0.0282	0.1658	0.0215	0.0091	0.2161	0.2677	0.0614	0.0488
		III	0.0564	0.1829	0.0367	0.0004	0.3821	0.2427	0.0769	0.0541
0.75	(50,25)	I	0.3006	0.6933	0.2931	0.0877	0.2644	0.4890	0.1037	0.1391
		II	0.1523	0.5713	0.1258	0.0655	0.5635	0.7238	0.2629	0.1899
		III	0.1261	0.8318	0.1008	0.0505	0.8746	0.9072	0.3736	0.3511
	(50,40)	I	0.1381	0.6141	0.1079	0.0528	0.2501	0.4099	0.0564	0.0432
		II	0.1101	0.3812	0.1035	0.0373	0.5455	0.4538	0.0762	0.0904
		III	0.1186	0.5016	0.0899	0.0364	0.8407	0.4533	0.1639	0.1084
	(100,50)	I	0.1043	0.3547	0.0841	0.0536	0.2213	0.2138	0.0649	0.0514
		II	0.1375	0.3769	0.1108	0.0361	0.4386	0.3116	0.2082	0.0839
		III	0.0572	0.2817	0.0747	0.0210	0.6937	0.3795	0.2209	0.1949
	(100,80)	I	0.0712	0.3230	0.0541	0.0165	0.1515	0.2057	0.0228	0.0198
		II	0.0622	0.2516	0.0584	0.0078	0.3517	0.1496	0.0421	0.0435
		III	0.0382	0.1613	0.0234	0.0065	0.5415	0.1737	0.0564	0.0446

Table 4. The AILs of $R\left(t\right)$ and $h\left(t\right)$.

T	(n,m)	Scheme	$\mathit{R}\left(\mathit{t}\right)$				$\mathit{h}\left(\mathit{t}\right)$
			ACI	HPD			ACI	HPD
$\mathbf{Prior}\to$				0	1	2		0	1	2
0.25	(50,25)	I	0.0204	0.0319	0.0133	0.0100	0.2183	0.3416	0.1916	0.1445
		II	0.0257	0.0408	0.0151	0.0076	0.2328	0.4262	0.1516	0.0824
		III	0.0442	0.0663	0.0385	0.0136	0.4614	0.7572	0.4053	0.1347
	(50,40)	I	0.0115	0.0258	0.0059	0.0042	0.1377	0.2783	0.1179	0.0882
		II	0.0172	0.0254	0.0061	0.0039	0.2119	0.2663	0.0665	0.0429
		III	0.0244	0.0265	0.0109	0.0080	0.2367	0.2911	0.0648	0.0443
	(100,50)	I	0.0154	0.0191	0.0102	0.0044	0.1671	0.2042	0.1097	0.0855
		II	0.0203	0.0239	0.0058	0.0040	0.1843	0.2503	0.0627	0.0435
		III	0.0198	0.0222	0.0183	0.0095	0.2068	0.2298	0.1962	0.0977
	(100,80)	I	0.0064	0.0129	0.0039	0.0024	0.0689	0.1369	0.0557	0.0391
		II	0.0128	0.0152	0.0041	0.0015	0.1286	0.1560	0.0452	0.0165
		III	0.0184	0.0164	0.0048	0.0035	0.1977	0.1684	0.0424	0.0258
0.75	(50,25)	I	0.0237	0.0427	0.0144	0.0126	0.2830	0.4618	0.2528	0.1342
		II	0.0598	0.0549	0.0177	0.0072	0.4208	0.6032	0.1914	0.0779
		III	0.0319	0.0752	0.0312	0.0236	0.3386	0.8582	0.3301	0.2489
	(50,40)	I	0.0207	0.0292	0.0039	0.0036	0.1891	0.3133	0.1501	0.0782
		II	0.0563	0.0398	0.0108	0.0062	0.3928	0.4256	0.1157	0.0651
		III	0.0272	0.0387	0.0156	0.0138	0.2544	0.4168	0.0424	0.0396
	(100,50)	I	0.0186	0.0228	0.0072	0.0046	0.2005	0.2456	0.1401	0.0491
		II	0.0391	0.0272	0.0085	0.0064	0.2689	0.2988	0.0911	0.0708
		III	0.0171	0.0235	0.0165	0.0072	0.2171	0.2637	0.1773	0.1521
	(100,80)	I	0.0141	0.0181	0.0021	0.0016	0.0742	0.1968	0.0459	0.0432
		II	0.0259	0.0162	0.0056	0.0041	0.2699	0.1735	0.0604	0.0438
		III	0.0059	0.0118	0.0043	0.0040	0.1834	0.1248	0.0226	0.0175

We may make the following observations based on Table 1, Table 2, Table 3 and Table 4. In terms of minimum RMSEs, RABs, and AILs, the suggested estimations of the unknown parameters and/or reliability characteristics are often extremely excellent. Furthermore, the behavior of the different estimates improves as n(or m) grows. When $m/n$ increases, the same performance pattern is also seen. Furthermore, when the total progressively censoring scheme decreases, the RMSEs, RABs, and AILs of all estimates tend to decrease for fixed n. The RMSEs, RABs, and AILs associated with $\alpha$ increase as T increases, whereas those related with $\theta$, $R\left(t\right)$, and $h\left(t\right)$ decrease.

Comparing Schemes I–III, it is observed that the RMSEs, RABs, and AILs of $\alpha$ are greater for Scheme-I than Scheme-III whereas for $\theta$, $R\left(t\right)$, and $h\left(t\right)$ are smaller based on Scheme-I than Scheme-III. This result is due the fact that the expected duration of the experiments using Scheme-I, where the remaining $n-m$ live items removed in the first stage, is greater than any other; therefore, the data collected under Scheme-I provided more information about the unknown parameters than those acquired by Schemes II and III.

In terms of the smallest RMSEs, RABs, and AILs, the Bayesian estimates using gamma informative priors perform better than the frequentist estimates since they contain prior knowledge. Furthermore, because Prior 2 has a smaller variance than Prior 1, the Bayesian (point/interval) based on Prior 2 perform better than those based on Prior 1 while both are more informative than the Prior 0. This result is due the fact that, if the prior information of $\alpha$ and $\theta$ is not available, the posterior PDF is reduced in proportion to the corresponding likelihood function. In summary, the Bayesian inference of the unknown parameters of the APE lifetime model using the Metropolis–Hastings method is recommended.

5. Optimal Progressive Censoring Plan

In recent years, the statistical literature has focused on finding the best censoring scheme; see, for example, Chapter 10 of Balakrishnan and Aggarwala [23], Ng et al. [24], Balasooriya and Balakrishnan [25], Balasooriya et al. [26], and Pradhan and Kundu [27]. For specified n and m, probable censoring schemes refers to all likely $R_1,\cdots ,R_m$ combinations such that $m+{\sum }_{i=1}^m{R}_i=n$, and selecting the progressive censoring scheme that gives the most information about the unknown parameters among all possible progressive censoring schemes is part of selecting the optimal sample approach. Practically, we would like to pick the censoring scheme that delivers the maximum information of the unknown parameters, see Elshahhat and Rastogi [22] and Alotaibi et al. [28] for more information. In our example, numerous widely used measures are offered in Table 5 to help us choose the most progressive censoring approach.

Table 5. Some practical censorship plan optimal criteria.

Criterion	Objective
$C_1$	$\mathrm{Maximize}\mathrm{trace}\left(\mathit{I}(·)\right)$
$C_2$	$\mathrm{Minimize}\mathrm{trace}\left({\mathit{I}}^{-1}(·)\right)$
$C_3$	$\mathrm{Minimize}det\left({\mathit{I}}^{-1}(·)\right)$
$C_4$	$\mathrm{Minimize}\mathrm{Var}(log\left({\widehat{\mathcal{Q}}}_p\right))$
$C_5$	$\mathrm{Minimize}{\int }_0^1\mathrm{Var}(log\left({\widehat{\mathcal{Q}}}_p\right))w\left(p\right)dp$

Regarding criterion $C_1$, our goal is to maximize the observed Fisher ${\mathit{I}}^{}(\widehat{\alpha },\widehat{\theta })$ information values. In addition, regarding criteria $C_2$ and $C_3$, our goal is to minimize the determinant and the trace of ${\mathit{I}}^{-1}(\widehat{\alpha },\widehat{\theta })$, respectively. When dealing with single-parameter distributions, comparing multiple criteria is easy; however, when dealing with multi-parameter distributions are unknown, then the comparison of the two Fisher information matrices is more difficult since the criterion $C_2$ and $C_3$ are not scale invariant—see Gupta and Kundu [29]; however, the optimal censoring scheme of multi-parameter distributions can be chosen using scale invariant criteria $C_4$ and $C_5$.

It is clear that the criterion $C_4$ depends on the choice of p, tends to minimize the variance of logarithmic of MLE of the $p\text{-}\mathrm{th}$ quantile, $log\left({\widehat{\mathcal{Q}}}_p\right)$, where $0<p<1$. According to criterion $C_5$, the weight function $w\left(p\right)⩽0$ is a non-negative function satisfying ${\int }_0^{1}w\left(p\right)dp$, also, $log\left({\widehat{\mathcal{Q}}}_p\right)$ is the same as in criterion $C_4$. Without loss of generality, the weight function can be taken as $w\left(p\right)=1$ for $0<p<1$. Hence, the logarithmic for ${\mathcal{Q}}_p$ of the APE distribution is given by

$$log\left({\widehat{\mathcal{Q}}}_p\right)=log\left[-\frac{1}{\theta }\left[\frac{log(1-log(1+p(\alpha -1)\left)\right)}{log\left(\alpha \right)}\right]\right],0<p<1.$$

(17)

From, (3), the delta method is used to obtain the approximated variance for $log\left({\widehat{\mathcal{Q}}}_p\right)$ of the APE distribution as

$$\mathrm{Var}(log\left({\widehat{\mathcal{Q}}}_p\right))={\left[\nabla log\left({\widehat{\mathcal{Q}}}_p\right)\right]}^{\mathbf{T}}{\mathit{I}}^{-1}(\widehat{\alpha },\widehat{\theta })[\nabla log\left({\widehat{\mathcal{Q}}}_p\right)],$$

where

$${[\nabla log\left({\widehat{\mathcal{Q}}}_p\right)]}^{\mathbf{T}}={\left[\frac{\partial }{\partial \alpha }log\left({\widehat{\mathcal{Q}}}_p\right),\frac{\partial }{\partial \theta }log\left({\widehat{\mathcal{Q}}}_p\right)\right]}_{\left(\alpha =\widehat{\alpha },\theta =\widehat{\theta }\right)}.$$

However, the optimized progressive censoring corresponds to the highest value of the criterion $C_1$ and the lowest value of the criteria $C_i,i=2,3,4,5$.

6. Real-Life Data Applications

In this part, we use two real data sets from the engineering and chemical domains to illustrate the significance and use of the proposed methodologies to real events.

6.1. Electronic Devices

In this application, we shall utilize the failure times of 18 electronic devices given by Wang [30]. Recently, this data set has been investigated by Elshahhat and Abu El Azm [31]. The failure times are: 5, 11, 21, 31, 46, 75, 98, 122, 145, 165, 196, 224, 245, 293, 321, 330, 350, and 420. Firstly, we require to check whether the APE distribution is an appropriate model to fit these data or not. For this purpose, the MLEs of $\alpha$ and $\theta$ are employed to obtain the Kolmogorov–Smirnov (K-S) distance and its related p-value. The MLEs $\widehat{\alpha }$ and $\widehat{\theta }$ along their standard errors (SEs) of the model parameters $\alpha$ and $\theta$ are 3.0805 (3.8591) and 0.0074 (0.0022), respectively. Hence, the K-S distance is 0.104 with p-value 0.979. It is to be mentioned here that since the parameters are unknown and the maximum likelihood approach is used to estimate them, we utilize the bootstrap technique to obtain the desired p-value. Moreover, when the adaptive Type-II progressively hybrid censored data are observed, one can use the modified Kolmogorov–Smirnov test for progressive Type-II censored data proposed by Pakyari and Balakrishnan [32] for this purpose. It implies that the APE distribution fits the given data quite satisfactorily.

One of the main concerns in the likelihood iterations is that frequently it is not attainable to verify with analytically steps the existence and uniqueness of the MLEs $\widehat{\alpha }$ and $\widehat{\theta }$. To overcome this issue, a contour plot of the log-likelihood function for $\alpha$ and $\theta$ operating the complete data set is depicted in Figure 1. It indicates that the most suitable starting values of $\alpha$ and $\theta$ are close to 3.08 and 0.0074, respectively. In addition, it indicates that the MLEs $\widehat{\alpha }$ and $\widehat{\theta }$ are exist and unique.

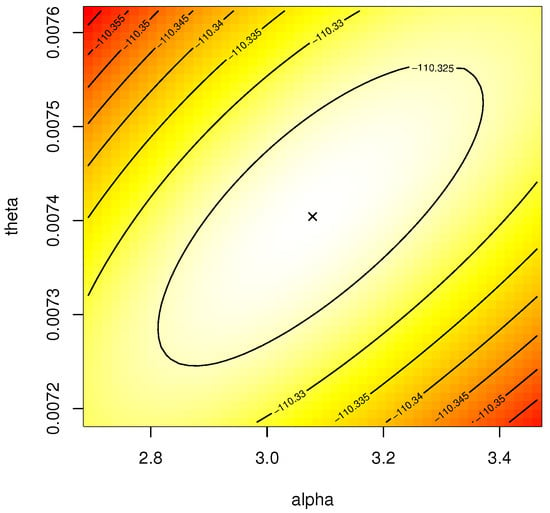
Figure 1. Contour plot of $\alpha$ and $\theta$ for electronic devices data.

Now, we illustrate the proposed estimates under the electronic devices data. Using some specified choices of m, T, and R, different adaptive progressive Type-II hybrid censored samples are generated and presented in Table 6. For brevity, the progressively censoring scheme $(R_1,R_2,\cdots ,R_m)$ is referred as ${\mathcal{S}}^{m:n}$. Using the MCMC algorithm represented in Section 3, we generate 30,000 MCMC samples and discard the first 5000 samples as a burn-in. Because we lack prior knowledge about the APE parameters, the Bayesian MCMC estimates of $\alpha$ and $\theta$ as well as the reliability characteristics $R\left(t\right)$ and $h\left(t\right)$, at distinct mission time $t=3$, using non-informative priors, i.e., $P_1(\alpha ,\theta )\propto {\left(\alpha \theta \right)}^{-1}$ are developed. Using the generated samples, the MLEs and Bayesian estimates of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ are obtained and displayed in Table 7. Further, the two-sided 95% ACI/HPD intervals of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ are computed and presented in Table 7. The SEs and interval lengths (ILs) are also obtained and presented in Table 7. The results in Table 7 show that the point and interval estimates of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ obtained by the likelihood and Bayesian approaches are quite close to each other. Figure 2 indicates the log-likelihood functions of $\alpha$, $\theta$ for ${\mathcal{S}}_1^{15:18}$ as example, which demonstrate that the MLEs are exist and unique. In order to evaluate the convergence of MCMC algorithm, trace plots for 25,000 MCMC simulated variate of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ (for ${\mathcal{S}}_1^{13:18}$ and ${\mathcal{S}}_1^{15:18}$ as an example) are plotted in Figure 3. Using the Gaussian kernel density, the corresponding histograms for the MCMC values of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ are also represented in Figure 3. In each trace plot, the sample mean and 95% HPD credible intervals shown as solid and dashed lines, respectively, while in each histogram plot the sample mean is shown as a vertical dash-dotted line. Figure 3 indicates that the MCMC procedure converges very well. It also shows that the generated posterior estimates are very close well to the theoretical posterior density functions.

Table 6. Three different generated samples from electronic devices data.

${\mathcal{S}}^{\mathit{m}:\mathit{n}}$	$(\mathit{m},\mathit{T})=(13,120)$	D	${\mathit{R}}_{\mathit{m}}^{*}$
${\mathcal{S}}_1^{13:18}=(5,0^{*}12)$	5, 98, 122, 145, 165, 196, 224, 245, 293, 321, 330, 350, 420	2	0
${\mathcal{S}}_2^{13:18}=(0^{*}4,1^{*}5,0^{*}4)$	5, 11, 21, 31, 46, 98, 145, 196, 224, 245, 293, 321, 330	6	2
${\mathcal{S}}_3^{13:18}=(0^{*}12,5)$	5, 11, 21, 31, 46, 75, 98, 122, 145, 165, 196, 224, 245	7	5
${\mathcal{S}}^{\mathit{m}:\mathit{n}}$	$(\mathit{m},\mathit{T})=(\mathbf{15},\mathbf{180})$	D	${\mathit{R}}_{\mathit{m}}^{*}$
${\mathcal{S}}_1^{15:18}=(3,0^{*}14)$	5, 46, 75, 98, 122, 145, 165, 196, 224, 245, 293, 321, 330, 350, 420	7	0
${\mathcal{S}}_2^{15:18}=(0^{*}8,1^{*}3,0^{*}4)$	5, 11, 21, 31, 46, 75, 98, 122, 145, 196, 245, 293, 321, 330, 350	9	1
${\mathcal{S}}_3^{15:18}=(0^{*}14,3)$	5, 11, 21, 31, 46, 75, 98, 122, 145, 165, 196, 224, 245, 293, 321	10	3

Table 7. The point estimates (SEs) and interval estimates (ILs) of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ under electronic devices data.

Scheme	Parameter	MLE	MCMC	ACI	HPD
${\mathcal{S}}_1^{13:18}$	$\alpha$	65.323 (5.9380)	65.322 (1.25 × 10${}^{-5}$)	(53.685,76.961) [23.276]	(65.318,65.327) [0.0009]
	$\theta$	0.0088 (0.0015)	0.0088 (7.55 × 10${}^{-6}$)	(0.0059,0.0117) [0.0058]	(0.0065,0.0111) [0.0046]
	$R\left(3\right)$	0.9982 (0.0003)	0.9982 (1.60 × 10${}^{-6}$)	(0.9975,0.9989) [0.0014]	(0.9977,0.9987) [0.0010]
	$h\left(3\right)$	0.0006 (0.0001)	0.0006 (5.79 × 10${}^{-7}$)	(0.0004,0.0008) [0.0004]	(0.0004,0.0008) [0.0004]
${\mathcal{S}}_2^{13:18}$	$\alpha$	2.0232 (2.9868)	2.0230 (6.37 × 10${}^{-6}$)	(0.0000,7.8772) [7.8772]	(2.0211,2.0251) [0.0040]
	$\theta$	0.0054 (0.0023)	0.0052 (5.03 × 10${}^{-6}$)	(0.0008,0.0100) [0.0092]	(0.0037,0.0068) [0.0031]
	$R\left(3\right)$	0.9889 (0.0133)	0.9891 (1.03 × 10${}^{-6}$)	(0.9627,0.9999) [0.0372]	(0.9860,0.9923) [0.0063]
	$h\left(3\right)$	0.0037 (0.0009)	0.0036 (3.50 × 10${}^{-6}$)	(0.0019,0.0056) [0.0037]	(0.0026,0.0047) [0.0021]
${\mathcal{S}}_3^{13:18}$	$\alpha$	1.0919 (2.3451)	1.0917 (6.30 × 10${}^{-6}$)	(0.0000,6.0917) [5.6883]	(1.0899,1.0938) [0.0039]
	$\theta$	0.0051 (0.0036)	0.0049 (8.09 × 10${}^{-6}$)	(0.0000,0.0123) [0.0123]	(0.0033,0.0065) [0.0032]
	$R\left(3\right)$	0.9854 (0.0255)	0.9858 (1.44 × 10${}^{-6}$)	(0.9353,0.9999) [0.0646]	(0.9814,0.9904) [0.0090]
	$h\left(3\right)$	0.0049 (0.0021)	0.0047 (4.87 × 10${}^{-6}$)	(0.0008,0.0090) [0.0082]	(0.0032,0.0062) [0.0030]
${\mathcal{S}}_1^{15:18}$	$\alpha$	21.979 (6.0238)	21.979 (6.34 × 10${}^{-6}$)	(10.172,33.785) [23.612]	(21.977,21.981) [0.0039]
	$\theta$	0.0087 (0.0015)	0.0085 (5.27 × 10${}^{-6}$)	(0.0057,0.0117) [0.0060]	(0.0069,0.0102) [0.0033]
	$R\left(3\right)$	0.9961 (0.0011)	0.9961 (2.45 × 10${}^{-6}$)	(0.9938,0.9983) [0.0045]	(0.9954,0.9969) [0.0015]
	$h\left(3\right)$	0.0014 (0.0003)	0.0013 (8.69 × 10${}^{-7}$)	(0.0009,0.0018) [0.0009]	(0.0011,0.0016) [0.0005]
${\mathcal{S}}_2^{15:18}$	$\alpha$	1.9089 (2.7499)	1.9088 (6.29 × 10${}^{-6}$)	(0.0000,7.2987) [60.269]	(1.9068,1.9107) [0.0038]
	$\theta$	0.0059 (0.0024)	0.0057 (5.10 × 10${}^{-6}$)	(0.0012,0.0107) [0.0095]	(0.0042,0.0074) [0.0031]
	$R\left(3\right)$	0.9873 (0.0144)	0.9876 (1.08 × 10${}^{-6}$)	(0.9591,0.9999) [0.0408]	(0.9842,0.9909) [0.0067]
	$h\left(3\right)$	0.0043 (0.0011)	0.0041 (3.67 × 10${}^{-6}$)	(0.0022,0.0063) [0.0041]	(0.0030,0.0053) [0.0023]
${\mathcal{S}}_3^{15:18}$	$\alpha$	1.3581 (2.1476)	1.3580 (6.27 × 10${}^{-6}$)	(0.0000,5.5673) [5.5673]	(1.3560,1.3599) [0.0039]
	$\theta$	0.0055 (0.0027)	0.0053 (5.08 × 10${}^{-6}$)	(0.0003,0.0108) [0.0105]	(0.0038,0.0070) [0.0032]
	$R\left(3\right)$	0.9859 (0.0177)	0.9863 (1.28 × 10${}^{-6}$)	(0.9512,0.9999) [0.0487]	(0.9822,0.9902) [0.0080]
	$h\left(3\right)$	0.0047 (0.0015)	0.0045 (4.36 × 10${}^{-6}$)	(0.0018,0.0076) [0.0058]	(0.0033,0.0060) [0.0027]

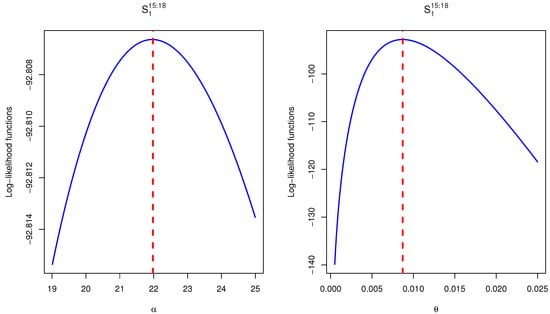
Figure 2. The log-likelihood functions of $\alpha$ and $\theta$ under electronic devices data.

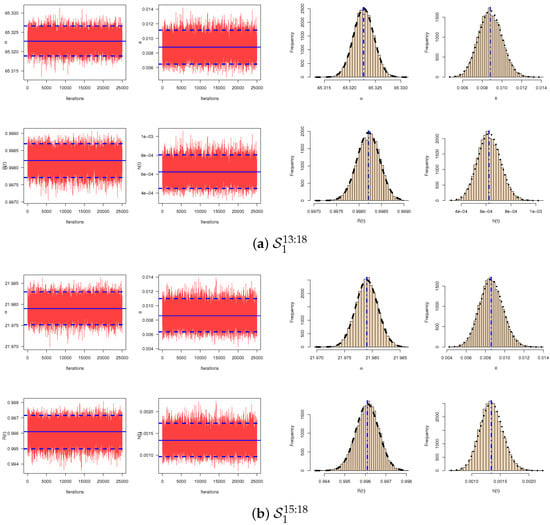
Figure 3. Trace plots (left panel) and histograms with estimated kernel density (right panel) under electronic devices data.

Further, using different optimum criteria presented in Table 5, the concept of choosing an optimal progressive censoring scheme is illustrated, see Table 8. It is evident from the calculated optimum criteria that, for both $m(=13,15)$, scheme ${\mathcal{S}}_3$ is the optimal scheme based on $C_i,i=1,2,3$ while ${\mathcal{S}}_1$ is the optimal scheme based on $C_i,i=4,5$.

Table 8. Optimal progressive censoring plan under electronic devices data.

Scheme	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$			${\mathit{C}}_5$
$\mathit{p}\to$				0.3	0.6	0.9	0.3	0.6	0.9
${\mathcal{S}}_1^{13:18}$	459,798.4	35.25937	0.000077	580.4244	580.4244	4877.928	608.1471	1945.152	6207.023
${\mathcal{S}}_2^{13:18}$	545,183.5	8.921012	0.000016	939.5688	2947.314	18,183.11	960.4032	2965.523	17,944.02
${\mathcal{S}}_3^{13:18}$	507,177.9	5.499799	0.000010	698.9182	2585.247	28,892.05	714.2520	2805.433	32,738.18
${\mathcal{S}}_1^{15:18}$	436,135.1	36.28584	0.000083	440.0363	1390.546	4724.009	427.6525	1349.603	4583.571
${\mathcal{S}}_2^{15:18}$	509,881.2	7.562193	0.000014	735.6637	2194.777	12,401.63	752.4166	2297.627	13,063.74
${\mathcal{S}}_3^{15:18}$	537,295.2	4.612386	0.000008	645.2009	2224.144	15,572.08	640.4340	2213.778	15,683.08

6.2. Vinyl Chloride

This application analyzes vinyl chloride, a recognized human carcinogen, received from clean up-gradient monitoring wells, see (Bhaumik et al. [33]). Elshahhat and Elemary [34] have recently investigated this data collection. This data set consists of 34 data points (in mg/L) as: 0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2, 1.3, 1.8, 2.0, 2.0, 2.3, 2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3, 6.8, and 8.0. To verify the validity of the APE lifetime model for the vinyl chloride data set, the K-S statistic and its corresponding p-value are computed. The MLEs (SEs) of $\widehat{\alpha }$ and $\widehat{\theta }$ are 0.6520(0.8535) and 0.4767(0.1885), respectively. The K-S(p-value) is 0.0879(0.955). This result indicates that the APE distribution is a suitable model to fit vinyl chloride data. Using the complete vinyl chloride data set, the contour plot of the log-likelihood function is presented in Figure 4. It indicates that the best starting values of $\alpha$ and $\theta$ are close to 0.652 and 0.475, respectively. In addition, it indicates that the MLEs $\widehat{\alpha }$ and $\widehat{\theta }$ exist and are also unique.

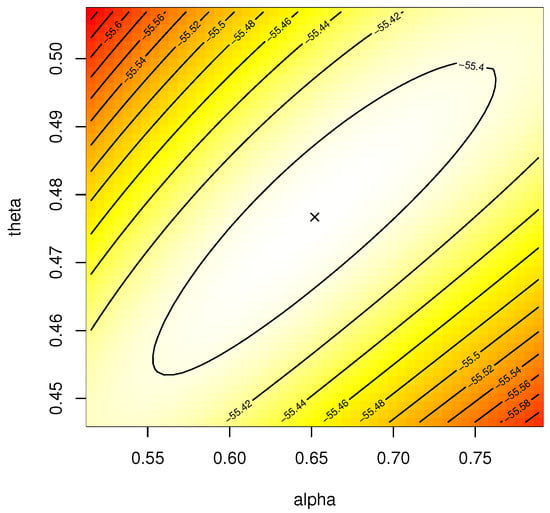
Figure 4. Contour plot of $\alpha$ and $\theta$ for vinyl chloride data.

Using complete vinyl chloride data, three different adaptive progressive Type-II hybrid censored samples are generated and presented in Table 9. The MLEs and Bayesian estimates as well as the associated interval estimates of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$, at specified time $t=1$, are calculated and reported in Table 10. It can be seen that, from Table 10, the Bayesian (point/interval) estimates have similar performance of the frequentist estimates. Figure 5 indicates the log-likelihood functions of $\alpha$, $\theta$ for ${\mathcal{S}}_1^{24:34}$ as an example, which demonstrate that the MLEs are exist and unique. Moreover, the trace and histogram plots for 25,000 MCMC simulated variate of $\alpha$, $\theta$, $R\left(t\right)$, and $h\left(t\right)$ (for ${\mathcal{S}}_1^{14:34}$ and ${\mathcal{S}}_1^{24:34}$ as an example) are displayed in Figure 6. Using the generated samples reported in Table 9, the criteria given in Table 5 can be easily computed and reported in Table 11. It is clear that, for $m=14$, scheme ${\mathcal{S}}_1$ is the optimal scheme based on $C_1$, scheme ${\mathcal{S}}_2$ is the optimal scheme based on $C_i,i=2,3$ and ${\mathcal{S}}_3$ is the optimal scheme based on $C_i,i=4,5$. Further, for $m=24$, we observe that the censoring scheme ${\mathcal{S}}_2$ is the optimum scheme. Finally, we can conclude that the proposed methodologies provide a good demonstration of our model in the presence of engineering or chemical data.

Table 9. The different generated samples from vinyl chloride data.

${\mathcal{S}}^{\mathit{m}:\mathit{n}}$	$(\mathit{m},\mathit{T})=(14,0.5)$	D	${\mathit{R}}_{\mathit{m}}^{*}$
${\mathcal{S}}_1^{14:34}=(20,0^{*}13)$	0.1, 2.0, 2.0, 2.3, 2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3, 6.8, 8.0	1	0
${\mathcal{S}}_2^{14:34}=(0^{*}5,5^{*}4,0^{*}5)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.6, 1.2, 1.2, 1.3, 1.8, 2.0, 2.0, 2.3	6	10
${\mathcal{S}}_3^{14:34}=(0^{*}13,20)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.8, 0.9	7	20
${\mathcal{S}}^{\mathit{m}:\mathit{n}}$	$(\mathit{m},\mathit{T})=(\mathbf{24},\mathbf{1})$	D	${\mathit{R}}_{\mathit{m}}^{*}$
${\mathcal{S}}_1^{24:34}=(10,0^{*}23)$	0.1, 0.6, 0.8, 0.9, 0.9, 1.0, 1.1, 1.2, 1.2, 1.3, 1.8, 2.0, 2.0, 2.3,
	2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3, 6.8, 8.0	5	0
${\mathcal{S}}_2^{24:34}=(0^{*}11,2^{*}5,0^{*}8)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.9, 1.2,
	1.8, 2.3, 2.4, 2.5, 2.7, 2.9, 3.2, 4.0, 5.1, 5.3	13	2
${\mathcal{S}}_3^{24:34}=(0^{*}23,10)$	0.1, 0.1, 0.2, 0.2, 0.4, 0.4, 0.4, 0.5, 0.5, 0.5, 0.6, 0.6, 0.8, 0.9,
	0.9, 1.0, 1.1, 1.2, 1.2, 1.3, 1.8, 2.0, 2.0, 2.3	15	10

Table 10. The point (SEs) and 95% interval estimates (ILs) of $\alpha$, $\theta$, $R\left(t\right)$ and $h\left(t\right)$ under vinyl chloride data.

Scheme	Parameter	MLE	MCMC	ACI	HPD
${\mathcal{S}}_1^{14:34}$	$\alpha$	79.229 (11.900)	79.229 (1.26 × 10${}^{-5}$)	(55.906,102.55) [46.646]	(79.225,79.233) [0.0080]
	$\theta$	0.5825 (0.0931)	0.5826 (1.26 × 10${}^{-5}$)	(0.4000,0.7651) [0.3651]	(0.5786,0.5864) [0.0078]
	$R\left(1\right)$	0.9247 (0.0212)	0.9247 (2.71 × 10${}^{-6}$)	(0.8831,0.9663) [0.0832]	(0.9238,0.9255) [0.0017]
	$h\left(1\right)$	0.1355 (0.0428)	0.1355 (5.79 × 10${}^{-6}$)	(0.0516,0.2194) [0.1678]	(0.1338,0.1373) [0.0036]
${\mathcal{S}}_2^{14:34}$	$\alpha$	1.5783 (2.8534)	1.2866 (7.49 × 10${}^{-5}$)	(0.0000,7.1709) [7.1709]	(1.2678,1.2957) [0.0278]
	$\theta$	0.3954 (0.2691)	0.1393 (2.20 × 10${}^{-4}$)	(0.0000,0.9229) [0.0929]	(0.0845,0.1655) [0.0810]
	$R\left(1\right)$	0.7221 (0.3458)	0.8841 (1.74 × 10${}^{-4}$)	(0.0443,0.9999) [0.9556]	(0.8635,0.9275) [0.0639]
	$h\left(1\right)$	0.3378 (0.1281)	0.1246 (1.97 × 10${}^{-4}$)	(0.0867,0.5888) [0.5021]	(0.0756,0.1482) [0.0726]
${\mathcal{S}}_3^{14:34}$	$\alpha$	5.7495 (7.8849)	5.7259 (6.40 × 10${}^{-4}$)	(0.0000,21.204) [21.204]	(5.5292,5.9229) [0.3938]
	$\theta$	1.0862 (0.4921)	1.0671 (5.78 × 10${}^{-4}$)	(0.1216,2.0507) [1.9291]	(0.8942,1.2535) [0.3593]
	$R\left(1\right)$	0.5397 (0.3395)	0.5475 (2.31 × 10${}^{-4}$)	(0.0000,0.9999) [0.9999]	(0.4792,0.6221) [0.1429]
	$h\left(1\right)$	0.7969 (0.4573)	0.7798 (5.69 × 10${}^{-4}$)	(0.0008,1.6932) [1.6932]	(0.5993,0.9528) [0.3535]
${\mathcal{S}}_1^{24:34}$	$\alpha$	10.616 (7.1511)	10.616 (1.26 × 10${}^{-5}$)	(0.0000,24.632) [24.632]	(10.612,10.620) [0.0080]
	$\theta$	0.6504 (0.1192)	0.6504 (1.26 × 10${}^{-5}$)	(0.4167,0.8841) [0.4674]	(0.6466,0.6544) [0.0078]
	$R\left(1\right)$	0.7822 (0.0934)	0.7822 (5.00 × 10${}^{-6}$)	(0.5992,0.9652) [0.3660]	(0.7806,0.7837) [0.0031]
	$h\left(1\right)$	0.3298 (0.0861)	0.3298 (9.47 × 10${}^{-6}$)	(0.1611,0.4986) [0.3375]	(0.3270,0.3329) [0.0059]
${\mathcal{S}}_2^{24:34}$	$\alpha$	1.0001 (0.0450)	1.0099 (6.34 × 10${}^{-6}$)	(0.9117,1.0883) [0.1765]	(1.0081,1.0120) [0.0039]
	$\theta$	0.4120 (0.0126)	0.4119 (6.36 × 10${}^{-6}$)	(0.3872,0.4369) [0.0497]	(0.4100,0.4140) [0.0040]
	$R\left(1\right)$	0.6624 (0.0079)	0.6634 (4.26 × 10${}^{-6}$)	(0.6470,0.6778) [0.0308]	(0.6621,0.6648) [0.0026]
	$h\left(1\right)$	0.4119 (0.0221)	0.4106 (6.40 × 10${}^{-6}$)	(0.3686,0.4552) [0.0866]	(0.4086,0.4126) [0.0040]
${\mathcal{S}}_3^{24:34}$	$\alpha$	1.0010 (0.0521)	1.0101 (6.36 × 10${}^{-6}$)	(0.8995,1.1035) [0.2040]	(1.0080,1.0119) [0.0039]
	$\theta$	0.5461 (0.0388)	0.5459 (6.32 × 10${}^{-6}$)	(0.4701,0.6222) [0.1521]	(0.5440,0.5479) [0.0039]
	$R\left(1\right)$	0.5794 (0.0185)	0.5805 (3.74 × 10${}^{-6}$)	(0.5432,0.6156) [0.0724]	(0.5793,0.5817) [0.0024]
	$h\left(1\right)$	0.5459 (0.0450)	0.5444 (6.39 × 10${}^{-6}$)	(0.4576,0.6342) [0.1766]	(0.5423,0.5463) [0.0040]

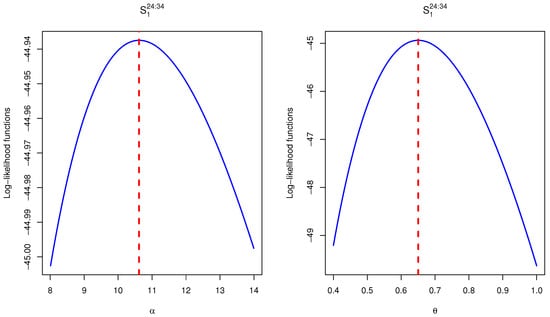
Figure 5. The log-likelihood functions of $\alpha$ and $\theta$ under vinyl chloride data.

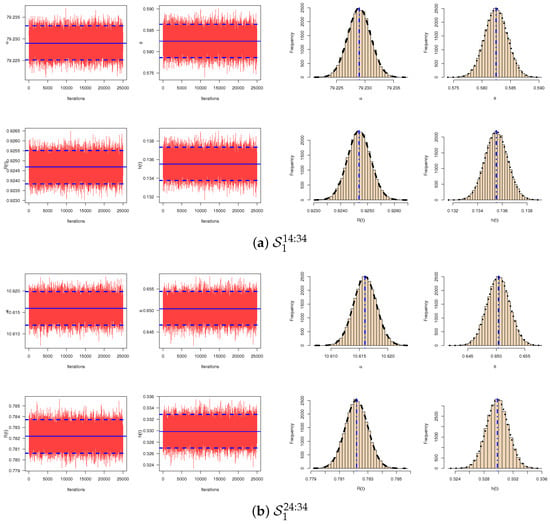
Figure 6. Trace plots (left panel) and histograms with estimated kernel density (right panel) under vinyl chloride data.

Table 11. Optimal progressive censoring plan under vinyl chloride data.

Scheme	${\mathit{C}}_1$	${\mathit{C}}_2$	${\mathit{C}}_3$	${\mathit{C}}_4$			${\mathit{C}}_5$
$\mathit{p}\to$				0.3	0.6	0.9	0.3	0.6	0.9
${\mathcal{S}}_1^{14:34}$	115.9997	141.6136	1.220811	0.129898	0.350576	1.047464	0.121881	0.328820	0.982469
${\mathcal{S}}_2^{14:34}$	100.3357	8.214269	0.081867	0.092742	0.516396	6.719861	0.090931	0.483916	6.389591
${\mathcal{S}}_3^{14:34}$	19.22729	62.41417	3.246125	0.020207	0.103615	0.785744	0.021480	0.106009	0.795044
${\mathcal{S}}_1^{24:34}$	102.2684	51.15239	0.500177	0.053886	0.152032	0.597285	0.054015	0.151033	0.590135
${\mathcal{S}}_2^{24:34}$	2708.035	0.002189	0.000001	0.002609	0.014134	0.063575	0.002237	0.011835	0.050417
${\mathcal{S}}_3^{24:34}$	2126.100	0.004216	0.000002	0.003311	0.019923	0.110015	0.002407	0.014292	0.077598

7. Concluding Remarks

Based on an adaptive progressive Type-II hybrid censored data, we investigated the estimation issues of the alpha power exponential distribution. To obtain point estimators for unknown parameters, reliability, and hazard rate functions, the maximum likelihood estimation method is used as a classical approach. Further, the approximate confidence intervals of these quantities are obtained. Moreover, the Bayesian approach is considered based on independent gamma priors. The Bayesian estimators are acquired under the squared error loss function and by utilizing the MCMC procedure. The highest posterior density credible intervals are also computed. We have also offered various criteria to compare different sampling schemes. To compare the performance of the various proposed estimators, a simulation study was implemented by considering different scenarios for the sample sizes, observed number of failures, and censoring schemes. To show the applicability of the offered procedures in real-life two real data sets are investigated. The simulation and real data analysis outcomes revealed that the Bayesian approach provides more accurate estimates than the maximum likelihood approach. As future works, following the same approaches of Chaudhary and Tomer [35] and Jovanović [36] it is of interest to investigate the estimation problems of stress-strength parameter and multi-component stress-strength reliability from the alpha power exponential distribution in the presence of adaptive progressive Type-II hybrid censored data.