Parameter Estimation for a Type of Fractional Diffusion Equation Based on Compact Difference Scheme

Abstract

Numerical solution and parameter estimation for a type of fractional diffusion equation are considered. Firstly, the symmetrical compact difference scheme is applied to solve the forward problem of the fractional diffusion equation. The stability and convergence of the symmetrical difference scheme are presented. Then, the Bayesian method is considered to estimate the unknown fractional order $\alpha$ of the fractional diffusion equation model. To validate the efficiency of the symmetrical numerical scheme and the estimation method, some simulation tests are considered. The simulation results demonstrate the accuracy of the compact difference scheme and show that the proposed estimation algorithm can provide effective statistical characteristics of the parameter.

1. Introduction

In recent years, the studies of fractional calculus have attracted many researchers [1,2,3], and fractional differential equations have many applications in economics [4], finance [5], physics [6,7,8], bioecology [9,10], porous media dynamics [11,12,13], and so on. However, only few exact solutions can be founded for some linear fractional differential equations. Many researchers turned to develop efficient numerical schemes. For example, the authors in [14,15,16] considered the difference schemes. Li et al. [17,18] proposed a novel algorithm based on linear and quadratic approximations. Zhou et al. [19] considered a nonuniform Alikhanov linearized Galerkin finite element methods. The authors in [20,21] considered the Chebyshev collocation method.

Recently, the research about the inverse problem has attracted more and more interest, one can refer to [22,23,24] and the references therein. Most of the literature on the inverse problem of the fractional differential equations exploited deterministic techniques, such as exact matching, least squares optimizations, without considering measurement error and numerical error. In general, very roughly speaking, one may split the corresponding approaches of recovering the order into the following two categories: solving the corresponding inverse problems analytically or using numerical–analytical methods [25,26,27,28,29,30,31], or using some more soft, metaheuristic, or statistical optimization and regularization techniques [32,33,34,35,36,37]. However, the observations are usually contaminated with measurement error, and the forward problem of the models will bring the numerical error, so the uncertainties are non-ignorable. Some studies for the inverse problem under uncertainties have been provided, such as the extended maximum likelihood method [38], sensitivity analysis method [39], and the Bayesian method [40,41].

The work of this paper was mainly motivated by the study in [41]. However, in the paper, Fan et al. considered homogeneous fractional diffusion equation, and the center Box difference method was used to obtain the numerical solution of the equation. An inhomogeneous fractional diffusion equation was considered in this paper, and a high-order compact difference scheme instead of the second-order center Box difference method was used to obtain the corresponding numerical solution. We considered the Bayesian method to estimate the parameter of the fractional diffusion equation model based on a compact difference scheme. Firstly, a high-order compact difference scheme is employed to solve the forward problem of the fractional diffusion equation. The convergence and stability of the difference scheme are proved, where the difference scheme has $2-\alpha$ order in the temporal direction and 4 order in the spatial direction. Then, the Bayesian method is considered to estimate the unknown fractional order $\alpha$ of the model, where some additional observations contaminated with measurement errors must be provided. To validate the efficiency of the numerical scheme and the estimation method, some simulation tests are considered. The simulation results demonstrate the accuracy of the compact difference scheme and show that the proposed estimation algorithm can provide effective statistical characteristics of the parameters.

The outline of this paper is as follows. In Section 2, mathematical model of the problem is introduced, and a compact difference scheme is constructed to solve the forward problem. Section 3 introduces the Bayesian method for the inverse problem. In Section 4, numerical tests are presented to validate the performance of the estimation algorithm. Section 5 gives some discussion and remarks.

2. Mathematical Model of the Problem and the Compact Difference Scheme

This section described the mathematical model of the problem, and a compact difference scheme was constructed to solve the forward problem.

2.1. Mathematical Model of the Problem

Consider the following fractional parabolic equation,

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=Q\frac{{\partial }^{2}u(x,t)}{\partial x^2}+f(x,t),(x,t)\in (0,1)\times (0,1],$$

(1)

$$u(x,0)=\varphi \left(x\right),x\in [0,1],$$

(2)

$$u(0,t)={\psi }_1\left(t\right),u(1,t)={\psi }_2\left(t\right),t\in [0,1],$$

(3)

where $0<\alpha <1$ and $Q>0$ are constants, $\varphi$, ${\psi }_1$, and ${\psi }_2$ are given functions. The time fractional partial derivative $\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}$ is defined in the Caputo sense as the following

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=\frac{1}{\Gamma (1-\alpha )}{\int }_0^t{(t-\xi )}^{-\alpha }\frac{\partial u(x,\xi )}{\partial \xi }d\xi ,$$

(4)

where $\Gamma \left(\right)$ is the gamma function.

If $\alpha$ is a known parameter, Equations (1)–(3) represent a forward problem; extensive studies have been provided. However, in some practical situations, we cannot know the exact values of $\alpha$. Under this situation, additional data must be provided to estimate the unknown parameter, which can be called the inverse problem. The additional data may be observed at some measured time for a fixed point $x_f\in [0,1]$. For simplicity, let $x_f=1$ in this paper, and we have the following observations,

$$Y\left(t\right)=u(1,t),0<t\le 1.$$

(5)

Let F be an operator, $F:\theta \mapsto u(1,t;\theta )$, where $\theta =\alpha$; then, the inverse problem can be seen as the solution of the following equation,

$$F\left(\theta \right)=Y.$$

(6)

In fact, the observations may be contaminated with measurement errors inevitably. We will consider the Bayesian approach to deal with the inverse problem.

2.2. The Compact Difference Scheme for the Forward Problem

Assuming $\theta$ in the operator F to be known in this subsection, we construct the high-order compact difference scheme to solve (6).

Let $x_i=ih,i=0,1,\cdots ,M$, and $t_k=k\tau ,k=0,1,\cdots ,N$, where $h=1/N,\tau =1/M$. Introducing ${\Omega }_{h\tau }={\Omega }_h\times {\Omega }_{\tau }$, where ${\Omega }_h=\left\{x_i\right|0\le i\le M\}$, ${\Omega }_{\tau }=\left\{t_k\right|0\le k\le N\}$. Denote $U_i^k=u(x_i,t_k),0\le i\le M,0\le k\le N$. Let

$$\mathcal{V}=\left\{v_i^k\right|0\le i\le M,0\le k\le N,\}$$

be the grid function space defined on ${\Omega }_{h\tau }$. Introducing the following notations

$${\delta }_x{v}_{i+1/2}^k=\frac{v_{i+1}^k-v_i^k}{h},{\delta }_x^2{v}_i^k=\frac{v_{i+1}^k-2v_i^k+v_{i-1}^k}{h^2},\mathcal{H}{v}_i^k=\frac{1}{12}(v_{i-1}^k+10v_i^k+v_{i+1}^k),$$

$${\delta }_t^{\alpha }{v}^k=\frac{{\tau }^{-\alpha }}{\Gamma (2-\alpha )}[d_0{v}^k-\sum _{j=1}^{k-1}(d_{k-j-1}-d_{k-j})v^j-d_{k-1}{v}^0],$$

where $d_j={(j+1)}^{1-\alpha }-j^{1-\alpha },j\ge 0.$

One can use Lemma 1 to deal with (4).

Lemma 1

([42]). Suppose $0<\alpha <1$, $y\in C^2[0,t_k]$, it holds that

$$\begin{array}{c}|\frac{1}{\Gamma (1-\alpha )}{\int }_0^{t_k}\frac{y^{\prime }\left(s\right)ds}{{(t_k-s)}^{\alpha }}-\frac{{\tau }^{-\alpha }}{\Gamma (2-\alpha )}[d_{0}y\left(t_k\right)-{\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j})y\left(t_j\right)-d_{k-1}y\left(t_0\right)]|\hfill \\ \le \frac{1}{\Gamma (2-\alpha )}[\frac{1-\alpha }{12}+\frac{2^{2-\alpha }}{2-\alpha }-(1+2^{-\alpha })]\underset{0\le t\le t_k}{max}\left|y^{″}\left(t\right)\right|{\tau }^{2-\alpha }.\hfill \end{array}$$

And $d_j$ satisfies Lemma 2.

Lemma 2

([43]). Assume $0<\alpha <1$, then it holds that

(1) 

$d_j$ decreases monotonically as j increases, and $0<d_j\le 1$;

(2) 

$d_0=1$, ${\sum }_{j=1}^{k-1}(d_{k-j-1}-d_{k-j})=d_0-d_{k-1}$.

The following Lemma 3 will play the key role to construct the high-order compact difference scheme.

Lemma 3

([44]). Suppose $y\left(x\right)\in C^6[x_{i-1},x_{i+1}]$, then we have

$$\frac{1}{12}[y^{{}^{″}}\left(x_{i-1}\right)+10y^{{}^{″}}\left(x_i\right)+y^{{}^{″}}\left(x_{i+1}\right)]-\frac{1}{h^2}[y\left(x_{i-1}\right)-2y\left(x_i\right)+y\left(x_{i+1}\right)]=\frac{h^4}{240}{y}^{\left(6\right)}\left({\iota }_i\right),$$

where ${\iota }_i\in (x_{i-1},x_{i+1})$.

Considering (1) at the point $(x_i,t_k)$, we have

$$\begin{array}{c}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}(x_i,t_k)=Q\frac{{\partial }^{2}u}{\partial x^2}(x_i,t_k)+f(x_i,t_k),0\le i\le M,0\le k\le N.\hfill \end{array}$$

(7)

By Lemma 1, we have

$$\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}(x_i,t_k)={\delta }_t^{\alpha }{U}_i^k+O\left({\tau }^{2-\alpha }\right).$$

(8)

Substituting (8) into (7), then acting $\mathcal{H}$ on (7), we have

$$\begin{array}{c}\mathcal{H}{\delta }_t^{\alpha }{U}_i^k=Q\left(\mathcal{H}\frac{{\partial }^{2}u}{\partial x^2}(x_i,t_k)\right)+\mathcal{H}f(x_i,t_k)+O\left({\tau }^{2-\alpha }\right).\hfill \end{array}$$

(9)

From Lemma 3 and Taylor expansion, we have

$$\mathcal{H}\frac{{\partial }^{2}u}{\partial x^2}(x_i,t_k)={\delta }_x^2{U}_i^k+O\left(h^4\right).$$

(10)

Substituting (10) into (9), we have

$$\begin{array}{c}\mathcal{H}{\delta }_t^{\alpha }{U}_i^k=Q{\delta }_x^2{U}_i^k+\mathcal{H}f(x_i,t_k)+O({\tau }^{2-\alpha }+h^4),1\le i\le M-1,1\le k\le N.\hfill \end{array}$$

(11)

Discretizing (2) and (3), we obtain

$$U_i^0=\varphi \left(x_i\right),0\le i\le M,$$

(12)

$$U_0^k={\psi }_1\left(t_k\right),U_M^k={\psi }_2\left(t_k\right),1\le k\le N.$$

(13)

Replacing $U_i^k$ by $u_i^k$ in (11)–(13), the following compact difference scheme solving for (1)–(3) can be obtained,

$$\begin{array}{c}\mathcal{H}{\delta }_t^{\alpha }{u}_i^k=Q{\delta }_x^2{u}_i^k+\mathcal{H}f(x_i,t_k),1\le i\le M-1,1\le k\le N,\hfill \end{array}$$

(14)

$$u_i^0=\varphi \left(x_i\right),0\le i\le M,$$

(15)

$$u_0^k={\psi }_1\left(t_k\right),u_M^k={\psi }_2\left(t_k\right),1\le k\le N.$$

(16)

There are some results on schemes (14)–(16).

Theorem 1.

The difference scheme in Equations (14)–(16) has a unique solution.

The proof of Theorem 1 can be referred to the corresponding proof in [45].

Denote $e_i^k=U_i^k-u_i^k,0\le i\le M,0\le k\le N$ and ${\parallel e\parallel }_{\infty }=\underset{1\le i\le M}{max}\left|e_i\right|$; then, we can obtain the following error equations

$$\begin{array}{c}\mathcal{H}{\delta }_t^{\alpha }{e}_i^k=Q{\delta }_x^2{e}_i^k+R_i^k,1\le i\le M-1,1\le k\le N,\hfill \end{array}$$

(17)

$$e_i^0=0,0\le i\le M,$$

(18)

$$e_0^k=0,e_M^k=0,1\le k\le N,$$

(19)

where $R_i^k=O({\tau }^{2-\alpha }+h^4)$.

To prove the following theorems, introducing the following notations

$$\begin{array}{c}(u,v)=h{\displaystyle \sum _{i=1}^{M-1}}{u}_i{v}_i,\parallel u\parallel =\sqrt{(u,u)}{,\parallel u\parallel }_{\infty }=\underset{1\le i\le M-1}{max}\left|u_i\right|,\hfill \\ ⟨{\delta }_{x}u,{\delta }_{x}v⟩=h{\displaystyle \sum _{i=0}^{M-1}}({\delta }_x{u}_{i+\frac{1}{2}})({\delta }_x{v}_{i+\frac{1}{2}}),{\left|{\delta }_{x}u\right|}_1=\sqrt{⟨{\delta }_{x}u,{\delta }_{x}u⟩}.\hfill \end{array}$$

(20)

Theorem 2.

Assume $u(x,t)\in C^{6,2}([0,1]\times (0,1])$ is the solution of (1)–(3), and $\left\{u_i^k\right|0\le i\le M,0\le k\le N\}$ is the solution of (14)–(16). Then, we have

$$\parallel e^k{\parallel }_{\infty }\le C({\tau }^{2-\alpha }+h^4),0\le k\le N,$$

where C is a positive constant independent of h and τ.

Proof. 

Multiplying (17) with $h{\delta }_t^{\alpha }{e}_i^k$ and summing up for i from 1 to M-1, one can obtain

$$\begin{array}{c}h{\displaystyle \sum _{i=1}^{M-1}}\left(\mathcal{H}{\delta }_t^{\alpha }{e}_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right)=Qh{\displaystyle \sum _{i=1}^{M-1}}\left({\delta }_x^2{e}_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right)+h{\displaystyle \sum _{i=1}^{M-1}}\left(R_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right),\hfill \\ 1\le i\le M-1,1\le k\le N.\hfill \end{array}$$

(21)

Then, we will estimate each term of (21). From the discrete Green formula, we have

$$\begin{array}{c}h{\displaystyle \sum _{i=1}^{M-1}}\left(\mathcal{H}{\delta }_t^{\alpha }{e}_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right)={\parallel {\delta }_t^{\alpha }{e}_i^k\parallel }^2+\frac{h^2}{12}h{\displaystyle \sum _{i=1}^{M-1}}\left({\delta }_x^2\left({\delta }_t^{\alpha }{e}_i^k\right)\right)\left({\delta }_t^{\alpha }{e}_i^k\right)\hfill \\ =\parallel {\delta }_t^{\alpha }{e}_i^k{\parallel }^2-\frac{h^2}{12}\parallel {\delta }_x{\delta }_t^{\alpha }{e}_i^k{\parallel }^2\ge \frac{2}{3}{\parallel {\delta }_t^{\alpha }{e}_i^k\parallel }^2,\hfill \end{array}$$

(22)

where inequality $-{(a+b)}^2\ge -2(a^2+b^2)$ is used.

By the discrete Green formula, one has

$$\begin{array}{c}Qh{\displaystyle \sum _{i=1}^{M-1}}\left({\delta }_x^2{e}_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right)=-Qh{\displaystyle \sum _{i=0}^{M-1}}({\delta }_x{e}_{i+1/2}^k)({\delta }_t^{\alpha }{\delta }_x{e}_{i+1/2}^k)\hfill \\ =-\frac{Q}{\lambda }h{\displaystyle \sum _{i=0}^{M-1}}({\delta }_x{e}_{i+1/2}^k)[{\delta }_x{e}_{i+1/2}^k-{\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j}){\delta }_x{e}_{i+1/2}^j-d_{k-1}{\delta }_x{e}_{i+1/2}^0]\hfill \\ =-\frac{Q}{\lambda }\{{\left|{\delta }_x{e}^k\right|}_1^2-{\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j})⟨{\delta }_x{e}^k,{\delta }_x{e}^j⟩-d_{k-1}⟨{\delta }_x{e}^k,{\delta }_x{e}^0⟩\}\hfill \\ \le -\frac{Q}{\lambda }\{{\left|{\delta }_x{e}^k\right|}_1^2-{\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j})\frac{|{\delta }_x{e}^k{|}_1^2+{\left|{\delta }_x{e}^j\right|}_1^2}{2}-d_{k-1}\frac{|{\delta }_x{e}^k{|}_1^2+{\left|{\delta }_x{e}^0\right|}_1^2}{2}\}\hfill \\ =-\frac{Q}{\lambda }\{\frac{|{\delta }_x{e}^k{|}_1^2}{2}-{\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j})\frac{|{\delta }_x{e}^j{|}_1^2}{2}-d_{k-1}\frac{|{\delta }_x{e}^0{|}_1^2}{2}\}.\hfill \end{array}$$

(23)

From Cauchy–Schwarz inequality, we have

$$\begin{array}{cc}h{\displaystyle \sum _{i=1}^{M-1}}\left(R_i^k\right)\left({\delta }_t^{\alpha }{e}_i^k\right)\hfill & \le h{\displaystyle \sum _{i=1}^{M-1}}(\frac{{\left(R_i^k\right)}^2}{2\epsilon }+\frac{\epsilon }{2}{\left({\delta }_t^{\alpha }{e}_i^k\right)}^2)\hfill \\ \hfill & =\frac{1}{2\epsilon }\parallel R^k{\parallel }^2+\frac{\epsilon }{2}{\parallel {\delta }_t^{\alpha }{e}^k\parallel }^2.\hfill \end{array}$$

(24)

Inserting Equations (22)–(24) into (21), and take $\epsilon =4/3$, we obtain

$$\begin{array}{c}|{\delta }_x{e}^k{|}_1^2\le {\displaystyle \sum _{j=1}^{k-1}}(d_{k-j-1}-d_{k-j})|{\delta }_x{e}^j{|}_1^2+d_{k-1}|{\delta }_x{e}^0{|}_1^2+\frac{3\lambda }{4Q}{\parallel R^k\parallel }^2.\hfill \end{array}$$

(25)

Noticing $R_i^k=O({\tau }^{2-\alpha }+h^4)$, from Lemma 6 in [45], we have

$$|{\delta }_x{e}^k{|}_1^2\le C_1{({\tau }^{2-\alpha }+h^4)}^2,$$

where $C_1$ is a positive constant independent of h and $\tau$. Then, we have

$$\parallel e^k{\parallel }_{\infty }\le \sqrt{C_1{({\tau }^{2-\alpha }+h^4)}^2}/2\doteq C({\tau }^{2-\alpha }+h^4).$$

The proof is completed. □

Similar to the proof of Theorem 2, we have the following result about the stability of the difference scheme in Equations (14)–(16).

Theorem 3.

Under the same condition of Theorem 2, the difference scheme in Equations (14)–(16) is stable.

3. Parameter Estimation for the Inverse Problem

Considering the measurement error and numerical error in the observations, then (6) has the following form,

$$Y=F\left(\theta \right)+\epsilon ,$$

(26)

where $\epsilon \sim N(0,{\sigma }^2)$, and ${\sigma }^2$ is assumed to be a known parameter. $\theta =\alpha$ is the parameter to be estimated from the observations governed by (26).

Assume $\alpha \sim U(0,1)$ is the prior probability distributions. We have the prior probability density function of $\theta$,

$$p\left(\theta \right)=p\left(\alpha \right)=\left\{\begin{array}{c}1,0<\alpha <1,\hfill \\ 0,otherwise,\hfill \end{array}\right.$$

(27)

From (26), we have the following likelihood function,

$$p\left(Y\right|\theta )=\frac{1}{{\left(2\pi {\sigma }^2\right)}^{n/2}}exp(-\frac{{(F\left(\theta \right)-Y)}^{{}^{\prime }}(F\left(\theta \right)-Y)}{2{\sigma }^2}),$$

(28)

where Y is the observation vector, n is the length of Y.

By the Bayes theorem, the posterior probability density function is

$$p\left(\theta \right|Y)exp(-\frac{{(F\left(\theta \right)-Y)}^{{}^{\prime }}(F\left(\theta \right)-Y)}{2{\sigma }^2}).$$

(29)

The Bayesian method for estimating $\theta =\alpha$ is as follows,

(1)

Draw an initial value of ${\theta }^0\sim U(0,1)$,

(2)

for i = 0: $N_{sim}-1$

draw $u\sim U(0,1)$,

draw ${\theta }^{\ast }\sim q\left({\theta }^{\ast }\right|{\theta }^i)$,

if $u<\varsigma$, then ${\theta }^{i+1}={\theta }^{\ast }$,

else ${\theta }^{i+1}={\theta }^i$,

where

$$\varsigma =min\{1,\frac{p\left({\theta }^{\ast }\right|Y)q\left({\theta }^i\right|{\theta }^{\ast })}{p\left({\theta }^i\right|Y)q\left({\theta }^{\ast }\right|{\theta }^i)}\},$$

and

$$q(·|·)\sim U(0,1),$$

where $N_{sim}$ is the number of iterations.

In the Bayesian method, we will use the posterior mean as the estimation of $\theta$.

Remark 1.

$F\left(\theta \right)$ in (29) can be obtained through (5), where a higher compact difference scheme is used. However, the traditional Crank–Nicolson difference scheme and other algorithms such as finite element method and finite volume method can also be used to solve (5). The advantage of the compact difference is that it is highly accurate, easy to program, and easily parallel. The advantage of the Bayesian estimation algorithm is that it can deal with contaminated observations and inhomogeneous fractional diffusion equation, and the most disadvantage of the Bayesian estimation algorithm is that it is time consuming.

4. Simulation

This section considers the following example. The configuration of the computer is Intel(R) Core(TM) i5-8265U CPU @ 1.60 GHz 1.80 GHz, Memory 4 GB (Lenovo, Beijing, China). All the codes are compiled in MATLAB 2009(a).

Example 1.

$$\left\{\begin{array}{c}\frac{{\partial }^{\alpha }u}{\partial t^{\alpha }}=Q\frac{{\partial }^{2}u(x,t)}{\partial x^2}+f(x,t),(x,t)\in (0,1)\times (0,1],\hfill \\ u(x,0)=0,x\in [0,1],\hfill \\ u(0,t)=0,u(1,t)=0,t\in (0,1],\hfill \end{array}\right.$$

(30)

the exact solution of (30) is $u(x,t)=e^x{x}^2{(1-x)}^2{t}^{2+\alpha }$, and

$$\begin{array}{c}f(x,t)=\frac{\Gamma (3+\alpha )}{2}{t}^2{e}^x{x}^2{(1-x)}^2-Q{e}^x(2-8x+x^2+6x^3+x^4)t^{2+\alpha }.\hfill \end{array}$$

(31)

4.1. Simulation for the Forward Problem

As for the forward problem, we will validate the performance of the scheme (14)–(16) for solving (30). Introducing the following maximum error,

$$e(h,\tau )=\underset{1\le k\le N}{max}{\parallel U^k-u^k\parallel }_{\infty },$$

and we define the following convergence order as

$$R_{\tau }=\frac{log(e(h,{\tau }_1)/e(h,{\tau }_2))}{log({\tau }_1/{\tau }_2)},R_h=\frac{log(e(h_1,\tau )/e(h_2,\tau ))}{log(h_1/h_2)}.$$

For calculating $R_{\tau }$, h needs to be fixed and small enough. While for $R_h$, $\tau$ needs to be fixed and small enough.

To compare the errors between the numerical solution and the exact solution of (30), Figure 1 was provided. Taking temporal and spatial step sizes as $\tau =h=1/10,1/20,1/40,1/80$ respectively, let $\alpha =0.2$, and we can see that the value of the error is within $[0,1.6\times {10}^{-5}]$. The numerical solution can approximate the exact solution well enough.

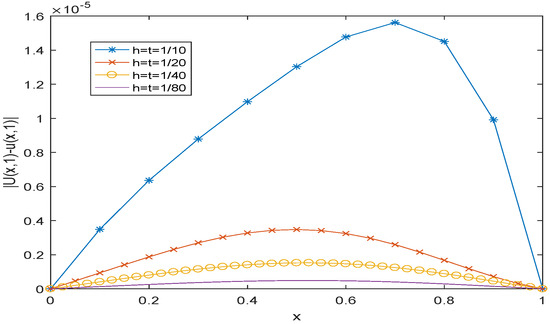
Figure 1. The error curves of $\left|u\right(x,1)-U(x,1\left)\right|$ for different temporal and spatial step sizes $\tau =h=1/10,1/20,1/40,1/80$ for solving (30), where $\alpha =0.2$, $u(x,1)$, and $U(x,1)$ denote the numerical solution and exact solution, respectively.

Table 1 shows the maximum errors in the temporal directions for $\alpha =0.2,0.6,$ and 0.8, respectively, where we fixed the spatial step to be $h=1/2000$. We can see that the temporal convergence order is $2-\alpha$.

Table 1. Maximum errors and convergence order for solving (30) in the temporal direction, where $Q=1.8$, $h=1/2000$, and $\alpha =0.2,0.6$, and 0.8. * means no value.

$\mathit{\tau }$	$\mathit{\alpha }=0.2$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{\tau }}$	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{\tau }}$	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{\tau }}$
1/50	$1.121\times {10}^{-6}$	*	$2.388\times {10}^{-5}$	*	$8.765\times {10}^{-5}$	*
1/100	$3.373\times {10}^{-7}$	1.733	$9.139\times {10}^{-6}$	1.386	$3.836\times {10}^{-5}$	1.192
1/150	$1.664\times {10}^{-7}$	1.742	$5.202\times {10}^{-6}$	1.390	$2.363\times {10}^{-5}$	1.195
1/200	$1.007\times {10}^{-7}$	1.747	$3.485\times {10}^{-6}$	1.392	$1.675\times {10}^{-5}$	1.196

Table 2 shows the maximum errors in the spatial directions for $\alpha =0.2,0.6,$ and 0.8, respectively, where we fixed the temporal step $\tau$ = 1/10,000. In most of the cases, we can conclude that the spatial convergence order is 4. However, we can see that the convergence of the considered numerical scheme is not steady under the condition that $\alpha =0.8$.

Table 2. Maximum errors and convergence order for solving (30) in the spatial direction, where $Q=1.8$, $\tau$ = 1/10,000, and $\alpha =0.2,0.6,$ and 0.8. * means no value.

h	$\mathit{\alpha }=0.2$		$\mathit{\alpha }=0.6$		$\mathit{\alpha }=0.8$
	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{h}}$	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{h}}$	$\mathit{e}(\mathit{h},\mathit{\tau })$	${\mathit{Rate}}_{\mathit{h}}$
1/10	$3.166\times {10}^{-5}$	*	$3.059\times {10}^{-5}$	*	$2.968\times {10}^{-5}$	*
1/20	$1.981\times {10}^{-6}$	3.998	$1.901\times {10}^{-6}$	4.008	$1.718\times {10}^{-6}$	4.111
1/40	$1.238\times {10}^{-7}$	4.001	$1.056\times {10}^{-7}$	4.171	$7.446\times {10}^{-8}$	4.528
1/80	$7.646\times {10}^{-9}$	4.017	$8.946\times {10}^{-9}$	3.561	$1.466\times {10}^{-7}$	−0.977

4.2. Simulation for the Inverse Problem

As for the inverse problem, we will testify to the validity of the Bayesian method provided. To obtain the observations Y governed by (26), let $\theta =\alpha =0.2$ in Equation (1) be the given value (note: $\theta =\alpha =0.6$ and $0.8$ will take the same conclusion, only $\theta =\alpha =0.2$ is considered in this subsection for the sake of brevity). Firstly, we applied the compact difference scheme (14)–(16) to discrete (30), where $M=N=100$. A series of points $\left\{u_M^k\right\},k=0,1,\cdots ,N$ were generated. Then, we picked up every fourth (two or one) point from the generated points, finally add the noise on each data, and we get the observations with length $n=25$ ($n=50$, $n=100$).

However, the length of observations n and ${\sigma }^2$ may affect the estimation results of $\theta$. In the following tests, we will evaluate such effects caused by different values of n and ${\sigma }^2$. In the following tests, the length of the Markov chain is taken to be $N_{sim}=5000$, and the burn in number is taken to be 1000.

Let $n=100$ be fixed, and assume $\sigma \in [1\times {10}^{-8},5\times {10}^{-7}]$. For different $\sigma$, we will inspect the posterior mean, standard error, and quantile of $\alpha$. Table 3 was obtained, and we can see that the measurement error with bigger $\sigma$ may take more uncertainty of the estimation results.

Table 3. Impact of different $\sigma$ on estimation for $\alpha$ of (30), where $Q=1.8$, the true value of $\alpha$ is $0.2$.

$\mathit{\sigma }$	${\mathit{\alpha }}_{\mathit{mean}}$	${\mathit{\alpha }}_{\mathit{std}}$	$95\%{\mathit{\alpha }}_{\mathit{quantile}}$	Time (s)
$5\times {10}^{-7}$	0.2049	0.0227	[0.1701, 0.2367]	819.1719
$1\times {10}^{-7}$	0.1954	0.0042	[0.1884, 0.2014]	865.3281
$1\times {10}^{-8}$	0.1998	0.0003	[0.1991, 0.2004]	769.8125

To inspect the effect of different n for $\alpha$, let $\sigma =2\times {10}^{-7}$ be fixed, assume $n=25$, $n=50$, and $n=100$. For different n, we also inspect the posterior mean, standard error, and quantile of $\alpha$. Table 4 was obtained, when $n=50$ and $n=100$, the different values of n make little impact on the estimation results. While when $n=25$, there is more uncertainty in the estimation results of $\alpha$. We can draw the conclusion that there is little influence for estimating $\alpha$ under bigger values of different n. From the computational time, it can be seen that we need more estimation time when a bigger n is given.

Table 4. Impact of different n on estimation for $\alpha$ of (30), where $Q=1.8$, and the true value of $\alpha$ is $0.2$.

n	${\mathit{\alpha }}_{\mathit{mean}}$	${\mathit{\alpha }}_{\mathit{std}}$	$95\%{\mathit{\alpha }}_{\mathit{quantile}}$	Time (s)
25	0.2118	0.0145	[0.1878, 0.2357]	827.8750
50	0.1778	0.0120	[0.1572, 0.1984]	836.0469
100	0.1873	0.0082	[0.1744, 0.2023]	844.9219

Remark 2.

In the tests of simulation for the inverse problem, we set the seed as ’sum(100*clock)’ in the ’rand’ function to specify the settings of the random number generator. Then, the estimation results can always be the same.

5. Conclusions

This paper considered both the forward problem and inverse problem of a type of fractional diffusion equation. Firstly, a compact difference scheme was provided to solve the forward problem of the fractional diffusion equation. The convergence and stability of the difference scheme were proved, and the convergence order is $O({\tau }^{2-\alpha }+h^4)$. Secondly, as for the inverse problem, a Bayesian algorithm was provided to estimate the fractional order $\alpha$ of the diffusion equation under the condition that some additional observations contaminated with measurement errors were provided. Numerical experiments were provided to testify the convergence results both in the temporal direction and in the spatial direction and the estimation efficiency of the Bayesian algorithm.