First-Order Sign-Invariants and Exact Solutions of the Radially Symmetric Nonlinear Diffusion Equations with Gradient-Dependent Diffusivities

Abstract

The sign-invariant theory is used to study the radially symmetric nonlinear diffusion equations with gradient-dependent diffusivities. The first-order non-stationary sign-invariants and the first-order non-autonomous sign-invariants admitted by the governing equations are identified. As a consequence, the exact solutions to the resulting equations are constructed due to the corresponding reductions. The phenomena of blow-up, extinction and behavior of some solutions are also described.

1. Introduction

For nonlinear diffusion equations, some results on second-order conditional Lie-Bäcklund symmetries can be translated to first-order sign-invariants [1,2,3]. The sign-invariant theory, introduced by Galationov [4], is a junction of qualitative and quantitative properties of nonlinear partial differential equations. Some ideas of sign-invariants are originated from the blow-up singularity analysis of combustion reaction-diffusion Equations [5]. Sign-invariants play a fundamental role in the study of existence, uniqueness, differential and asymptotic properties of wide classes of solutions [6]. In addition, exact solutions via finite-dimensional dynamical systems can be constructed due to zero-preserving of the first-order operator [4,5,6,7]. The corresponding reduction idea has a natural relation to the general theory of differential constraint [8].

The paper [4] presents a backward approach to study nonlinear parabolic equation starting from sign-invariant computed via the idea from the qualitative theory and finally giving the set of exact solution by means of the zero-invariant property. Three different types of first-order sign-invariants are, respectively, considered for different kinds of nonlinear diffusion equations. The governing equations and the admitted sign-invariants are presented. As a consequence, exact solutions of the resulting equations are constructed due to the corresponding reductions. In addition, the definition of Hamilton–Jacobi sign-invariant for evolution equation is also given in [4].

Definition 1

([4]). The first-order Hamilton–Jacobi operator

$$\begin{array}{c}\hfill J\left[u\right]=J(r,t,u,u_t,u_r)\end{array}$$

is said to be a sign-invariant of the nonlinear evolution equation

$$\begin{array}{c}\hfill u_t=\tilde{E}(r,t,u,u_r,\cdots ,u_{nr})\end{array}$$

if it preserves both signs $\ge 0$ and $\le 0$ on the solution manifold of the evolution equation. This means

$$\begin{gathered} J\left[u\right]\ge 0(resp.\le 0)in\mathit{R}fort=0, \\ \Rightarrow J\left[u\right]\ge 0(resp.\le 0)in\mathit{R}fort>0, \end{gathered}$$

The types of non-stationary autonomous sign-invariant

$$\begin{array}{c}\hfill J=u_t-\psi \left(u\right)\end{array}$$

(1)

for the parabolic equations with the diffusion term of the gradient-dependent type

$$\begin{array}{c}\hfill u_t=L(u,|\nabla u|,▵u)\end{array}$$

and

$$\begin{array}{c}\hfill u_t=g\left(\right|\nabla u\left|\right)▵u+f\left(u\right)\end{array}$$

are, respectively, studied in [4,7]. The structure of (1) comes from the conditions of $\psi -$criticality of solutions to quasi-linear parabolic Equations [9]. The general quadratic Hamilton–Jacobi sign-invariants

$$\begin{array}{c}\hfill J=u_t-\left[A\left(u\right)u_x^2+B\left(u\right)u_x+C\left(u\right)\right]\end{array}$$

(2)

for the nonlinear diffusion equation

$$\begin{array}{c}\hfill u_t=D\left(u\right)u_{xx}+P\left(u\right)u_x^2+Q\left(u\right)\end{array}$$

are considered in [5]. It is known that the type of first-order Hamilton–Jacobi sign-invariant (2) is closely related to the second-order conditional Lie-Bäcklund symmetry

$$\begin{array}{c}\hfill \sigma =u_{xx}+H\left(u\right)u_x^2+G\left(u\right)u_x+F\left(u\right)\end{array}$$

for nonlinear diffusion Equations [1,2,3].

The second-order conditional Lie-Bäcklund symmetry with the characteristic

$$\begin{array}{c}\hfill \eta =u_{rr}+H\left(u\right)u_r^2+G(r,u)u_r+F(r,u)\end{array}$$

(3)

is used to study classifications and reductions of the radially symmetric nonlinear diffusion equation with gradient-dependent diffusivity

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r+Q(r,u)\equiv \tilde{E}\end{array}$$

(4)

in [10], where the type of first-order Hamilton–Jacobi sign-invariant

$$\begin{array}{c}\hfill J=u_t-A\left(u\right)u_r^{m+1}-B(r,u)u_r^m-C(r,u)u_r^{m-1}-E(r,u)\end{array}$$

is also presented due to the admitted conditional Lie-Bäcklund symmetry (3). The type of first-order sign-invariant

$$\begin{array}{c}\hfill J=u_t-R(r,u)u_r-E(r,u)\end{array}$$

(5)

is not discussed there [10] since the corresponding conditional Lie-Bäcklund symmetry (3) degenerates to conditional symmetry.

In fact, Equation (4) is corresponding to the multi-dimensional generalization of nonlinear diffusion equation

$$\begin{array}{c}\hfill u_t=div\left(u^k{|\nabla u|}^{m-1}\nabla u\right)+Q\left(\sqrt{x_1^2+x_2^2+\cdots +x_n^2},u\right).\end{array}$$

It is well known that this equation occur, for instance, in the theory of non-Newtonian liquids and in some turbulence problems [11,12,13]. The descriptions of Lie symmetries of a class of nonlinear diffusion equations in one and two dimensions are presented in [14,15,16,17,18,19]. The nonclassical symmetries and reductions of nonlinear diffusion equations in two and n dimensions can, respectively, be referred to [19,20,21,22]. The second-order conditional Lie-Bäcklund symmetry and first-order Hamilton–Jacobi sign-invariant for nonlinear diffusion equations with gradient-dependent diffusivity can be referred to [2,10,23].

In this manuscript, we consider the non-stationary sign-invariant

$$\begin{array}{c}\hfill J_1=u_t-E(r,u)\end{array}$$

(6)

and non-autonomous sign-invariant

$$\begin{array}{c}\hfill J_2=u_r-H(r,u)\end{array}$$

(7)

for the general Equation (4) with $m\ne 1$, which are both particular case of (5). Section 2 and Section 3 are, respectively, devoted to study sign-invariants of the form (6) and (7) for the nonlinear diffusion Equation (4). The corresponding exact solutions due to the reductions of the resulting sign-invariants are constructed in Section 4. The conclusions are provided in the last section.

2. Non-Stationary Sign-Invariant of Nonlinear Diffusion Equation

The procedure for computing sign-invariant (6) of Equation (4) is about the same as what is presented in [5,24,25]. Firstly, we need to differentate $J_1=0$ with respect to t. The next step is to eliminate $u_{tt}$ and other lower-order ones $u_t,u_{rt},u_{rrt}$ in $J_{1t}=0$ by substituting the second derivative $u_{tt}$ from (4) and calculating other lower-order ones from $J_1=0$. A direct computation yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_t{J}_1{|}_{L_t\cap M_{r,t}}=& \left(m{u}^k{E}_{uu}+k{u}^{k-1}{E}_u-k{u}^{k-2}E\right)u_r^{m+1}\hfill \\ & +\left(2m{u}^k{E}_{ru}+2k{u}^{k-1}{E}_r\right)u_r^m\hfill \\ & +\left(m{u}^k{E}_{rr}+\frac{n-1}{r}{u}^k{E}_r\right)u_r^{m-1}\hfill \\ & +Q_{u}E+[(m-1)E-mQ]E_u+\frac{k}{u}E(E-Q)\hfill \\ & -(m-1)(Q-E)E_r{u}_r^{-1}\hfill \\ \hfill =& 0,\hfill \end{array}\end{array}$$

(8)

where $L_t$ denotes the set of differential consequence of Equation (4) with respect to t, that is, $D_t^i(u_t-\tilde{E})=0,i=0,1,2,\cdots$, and $M_{r,t}$ denotes the set of all differential consequences of $J_1=0$ with respect to t and r, that is, $D_t^i{D}_r^j{J}_1=0,i,j=0,1,2,\cdots$.

We can derive the well known Determining System by equating the coefficients of $u_r^j$ and $j=m+1,m,m-1,0,-1$ to zero, which are listed as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & E_{uu}+\frac{k}{mu}{E}_u-\frac{k}{m{u}^2}E=0,\hfill \\ & E_{ru}+\frac{k}{mu}{E}_r=0,\hfill \\ & E_{rr}+\frac{n-1}{mr}{E}_r=0,\hfill \\ & Q_{u}E+[(m-1)E-mQ]E_u+\frac{k}{u}E(E-Q)=0,\hfill \\ & (m-1)(Q-E)E_r=0.\hfill \end{array}\end{array}$$

(9)

Solving the determining system (9), we can identify the governing Equation (4) and the admitting non-stationary sign-invariant (6). It is stated clearly in [10] that Equation (4) admits of first-order sign-invariant is equivalent to that Equation (4) admits of second-order conditional Lie-Bäcklund symmetry (3). Thus, the resulting admitting sign-invariant (6) of Equation (4) will yield the corresponding conditional Lie-Bäcklund symmetry (3) of Equation (4). These results are presented in Table 1.

Table 1. Non-stationary sign-invariant (6) and conditional Lie-Bäcklund symmetry (3) of nonlinear diffusion Equation (4).

No.	Nonlinear Diffusion	Non-Stationary	Conditional Lie-Bäcklund	Remark
	Equation (4)	Sign-Invariant (6)	Symmetry (3)
1	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r$	$J=u_t-\left[au+(b+c{r}^{\frac{m+1-n}{m}})u^{-\frac{k}{m}}\right]$	$\eta =u_{rr}+\frac{k}{mu}{u}_r^2+\frac{n-1}{mr}{u}_r$	$k\ne -m$
	$+au+(b+c{r}^{\frac{m+1-n}{m}})u^{-\frac{k}{m}}$			$m\ne n-1$
2	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{n-1}\right)}_r$	$J=u_t-\left[au+(b+clnr)u^{\frac{k}{1-n}}\right]$	$\eta =u_{rr}+\frac{k}{(n-1)u}{u}_r^2+\frac{1}{r}{u}_r$	$k\ne 1-n$
	$+au+(b+clnr)u^{\frac{k}{1-n}}$
3	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{-m}{u}_r^m\right)}_r$	$J=u_t-u(a+b{r}^{\frac{m+1-n}{m}}+clnu)$	$\eta =u_{rr}-\frac{1}{u}{u}_r^2+\frac{n-1}{mr}{u}_r$	$m\ne n-1$
	$+(a+b{r}^{\frac{m+1-n}{m}}+clnu)u$
4	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{1-n}{u}_r^{n-1}\right)}_r$	$J=u_t-u(a+blnr+clnu)$	$\eta =u_{rr}-\frac{1}{u}{u}_r^2+\frac{1}{r}{u}_r$
	$+(a+blnr+clnu)u$
5	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r$	$J=u_t-au$	$\eta =u_{rr}+\frac{k}{mu}{u}_r^2+\frac{n-1}{mr}{u}_r$
	$+au+f\left(r\right)u^{k+m}$		$+\frac{f\left(r\right)}{m}{u}^m{u}_r^{1-m}$
6	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r$	$J=u_t-b{u}^{-\frac{k}{m}}$	$\eta =u_{rr}+\frac{k}{mu}{u}_r^2+\frac{n-1}{mr}{u}_r$
	$+b{u}^{-\frac{k}{m}}+f\left(r\right)$		$+\frac{f\left(r\right)}{m}{u}^{-k}{u}_r^{1-m}$
7	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{-m}{u}_r^m\right)}_r$	$J=u_t-au-bulnu$	$\eta =u_{rr}-\frac{1}{u}{u}_r^2+\frac{n-1}{mr}{u}_r$
	$+au+bulnu$		$+\frac{f\left(r\right)}{m}{u}^m(au$
	$+f\left(r\right){(au+bulnu)}^m$		${+bulnu)}^m{u}_r^{1-m}$

3. Non-Autonomous Sign-Invariant of Nonlinear Diffusion Equation

In this section, we consider sign-invariant of the stationary structure (7) which is non-autonomous in the spatial variable $r\in R$. We restrict our attention to the first-order operator possessing the form

$$\begin{array}{c}\hfill J=u_r-g\left(r\right)h\left(u\right)\end{array}$$

(10)

with yet unknown smooth non-negative functions $g\left(r\right)\ne const$ and $h\left(u\right)\ne 0$. The idea of such sign-invariants goes to the gradient bounds introduced [26] for semi-linear parabolic equations. Generalizations to the quasi-linear gradient-dependent operators can be found in [27]. The discussion of the sign-invariant

$$\begin{array}{c}\hfill J=u_r-rF\left(u\right)\end{array}$$

(11)

and

$$\begin{array}{c}\hfill J=u_r-\frac{1}{r}F\left(u\right)\end{array}$$

(12)

for the quasi-linear heat equations can be referred to [4]. These two structures are, respectively, include the rotation invariant and scaling invariant [28]. The extension to the rotation invariant and scaling invariant (11), (12) and other generalized forms for nonlinear evolution equations are considered in [29,30], where the form of (11) and (12) are defined as the invariant set.

Similar procedure as what is shown for the previous one in Section 2 will yield that $H(r,u)$ and $Q(r,u)$ satisfy

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & m{u}^k{H}^{m-1}(H_{rr}+2H{H}_{ru}+H^2{H}_{uu})\hfill \\ & +m(m-1)u^k{H}^{m-2}(H_r^2+2H{H}_r{H}_u+H^2{H}_u^2)\hfill \\ & +k{u}^{k-1}{H}^m\left[(2m+1)H_r+2mH{H}_u\right]\hfill \\ & +k(k-1)u^{k-2}{H}^{m+2}+H{Q}_u-Q{H}_u+Q_r\hfill \\ & +\frac{n-1}{r}{u}^{k-1}\left[u{H}^{m-1}(m{H}_r+(m-1)H{H}_u)+k{H}^{m+1}\right]\hfill \\ & -\frac{n-1}{r^2}{u}^k{H}^m=0\hfill \end{array}\end{array}$$

(13)

if the non-autonomous operator (7) is a sign-invariant of Equation (4).

Substituting $H(r,u)=rh\left(u\right)$ into (13), we can derive that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill & r(Q_{u}h-h^{\prime }Q)+Q_r+u^{k-2}{h}^m\{(m-1)(m+n-1)u^2{r}^{m-2}\hfill \\ & +[k(2m+n)uh+(2m^2+mn-m-n+1)u^2{h}^{\prime }]r^m\hfill \\ & +[k(k-1)h^2+muh(2k{h}^{\prime }+u{h}^{″})+m(m-1)u^2{\left(h^{\prime }\right)}^2]r^{m+2}\}=0.\hfill \end{array}\end{array}$$

(14)

The left-side of (14) is a linear combination in a space of the form

$$\begin{array}{c}\hfill W=\mathcal{L}\{r^{m-2},r^m,r^{m+2},Q_r,rQ\}.\end{array}$$

(15)

For the case of $Q(r,u)=Q\left(u\right)$, the space W degenerate to

$$\begin{array}{c}\hfill W=\mathcal{L}\{r^{m-2},r^m,r^{m+2},r\}.\end{array}$$

(16)

The discussion of the dimension of the linear space (15) and (16) will finally yield the determining system for h and Q. We omit the tedious computational procedure and just list the corresponding results in Table 2. The results for the sign-invariant (12) of Equation (4) are also listed in Table 2.

Table 2. Non-autonomous sign-invariant (7) of nonlinear diffusion Equation (4).

No.	Nonlinear Diffusion Equation (4)	Non-Autonomous Sign-Invariant (7)
1	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{1-n}\right)}_r+qexp\left(\frac{1}{2}a{r}^2\right)exp\left[\frac{(n-1)a}{(k+1-n)s}{u}^{\frac{n-1-k}{n-1}}\right]u^{\frac{k}{n-1}}$	$J=u_r-sr{u}^{\frac{k}{n-1}}$
2	$u_t=\frac{1}{r^{n-1}}{\left[r^{n-1}{u}^{-\frac{2(n+8)}{n+2}}{u}_r^3\right]}_r+q{u}^{\frac{n+6}{n+2}}+\frac{1}{4}{(n+2)}^2{s}^2{u}^{\frac{n-2}{n+2}}$	$J=u_r-sr{u}^{\frac{n+6}{n+2}}$
3	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{-1}\right)}_r+q{u}^l-(k-l)u^{k-1}+\frac{2-n}{s{r}^2}{u}^{k-l}$	$J=u_r-sr{u}^l$
4	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{1-k}\right)}_r+s^{2-k}\left(a-r^{2-k}+\frac{k-n}{s}{r}^{-k}\right)u$	$J=u_r-sru$
5	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{n-1}{u}_r^{1-n}\right)}_r+qexp\left(\frac{1}{2}a{r}^2\right)u^{\frac{s-a}{s}}$	$J=u_r-sru$
6	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{-k}\right)}_r+qexp\left(\frac{1}{2}s{r}^2\right)+(k+1-n)s^{-k}{r}^{-(k+1)}$	$J=u_r-sru$
7	$u_t=\frac{1}{r}{\left(r{u}^2{u}_r^{-1}\right)}_r+qexp\left(\frac{1}{2}s{r}^2\right)$	$J=u_r-sru$
8	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{n-1}\right)}_r+q{u}^{-\frac{k}{n-1}}$	$J=u_r-\frac{s}{r}{u}^{-\frac{k}{n-1}}$
9	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r+[s^m(m-n+1)u^{lm+k}$	$J=u_r-\frac{s}{r}{u}^l$
	$-s^{m+1}(lm+k)u^{(m+1)l+k-1}+q{u}^{l}exp\left(\frac{m+1}{(1-l)s}{u}^{1-l}\right)]r^{-(m+1)}$
10	$u_t=\frac{1}{r^{n-1}}{\left[r^{n-1}{u}^{l(1-n)}{u}_r^{n-1}\right]}_r+q{r}^a{u}^{l}exp\left[\frac{a}{s(l-1)}{u}^{1-l}\right]$	$J=u_r-\frac{s}{r}{u}^l$
11	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{\frac{1+m+s-ms}{s}}{u}_r^m\right)}_r+q{r}^a{u}^{\frac{s-a}{s}}$	$J=u_r-\frac{s}{r}u$
12	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{\frac{1+m-n-ms}{s}}{u}_r^m\right)}_r+q{r}^a{u}^{\frac{s-a}{s}}$	$J=u_r-\frac{s}{r}u$
13	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{\frac{s-a-ms}{s}}{u}_r^m\right)}_r+\left[q{r}^a+s^m(m-n+a-s+1)r^{-m-1}\right]u^{\frac{s-a}{s}}$	$J=u_r-\frac{s}{r}u$
14	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r+\left[q{u}^{\frac{s+1+m}{s}}-(ks+ms-m+n-1)s^m{u}^{k+m}\right]r^{-(1+m)}$	$J=u_r-\frac{s}{r}u$
15	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}_r^m\right)}_r+q{r}^{\frac{m+1}{m-1}}$	$J=u_r-\frac{1}{r}\left(\frac{m+1}{m-1}u+s\right)$
16	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}u{u}_r^{\frac{n-2}{n+2}}\right)}_r+q{r}^{-\frac{n}{2}}$	$J=u_r-\frac{1}{r}\left(s-\frac{n}{2}u\right)$
17	$u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}_r^{\frac{1-n}{a-1}}\right)}_r+q{r}^a$	$J=u_r-\frac{1}{r}\left(au+s\right)$

4. Exact Solutions of Nonlinear Diffusion Equation

The compatibility of $\eta =0(J_1=0,J_2=0)$ and the governing Equation (4) will yield exact solutions of the nonlinear diffusion Equation (4). To derive these solutions, one first solves the ordinary differential equation $\eta =0(J_1=0,J_2=0)$ to determine the form of $u(r,t)$, and then substitutes the corresponding results into Equation (4) to finally identify the solutions. Here we just present several examples to illustrate the reduction procedure.

Example 1.

Equation

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^m\right)}_r+au+(b+c{r}^{\frac{m+1-n}{m}})u^{-\frac{k}{m}}\end{array}$$

with $k\ne -m$ and $m\ne n-1$ admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_t-\left[au+(b+c{r}^{\frac{m+1-n}{m}})u^{-\frac{k}{m}}\right]\end{array}$$

and the second-order conditional Lie-Bäcklund symmetry

$$\begin{array}{c}\hfill \eta =u_{rr}+\frac{k}{mu}{u}_r^2+\frac{n-1}{mr}{u}_r.\end{array}$$

The corresponding solutions are given by

$$\begin{array}{c}\hfill u(r,t)={\left[\frac{m+k}{m+1-n}\alpha \left(t\right)r^{\frac{m+1-n}{m}}+\frac{m+k}{m}\beta \left(t\right)\right]}^{\frac{m}{m+k}},\end{array}$$

where $\alpha \left(t\right)$ and $\beta \left(t\right)$ satisfy two-dimensional dynamical system

$$\begin{array}{ccc}& & {\alpha }^{\prime }=\frac{(m+k)a}{m}\alpha +\frac{(m+1-n)c}{m},{\beta }^{\prime }=\frac{(m+k)a}{m}\beta +b.\hfill \end{array}$$

This system can be easily integrated. The corresponding solutions are given as follows.

(i)

For $a\ne 0$,

$$\begin{array}{cc}& \alpha \left(t\right)=c_{1}exp\left[\frac{(m+k)at}{m}\right]-\frac{(m+1-n)c}{(m+k)a},\\ & \beta \left(t\right)=c_{2}exp\left[\frac{(m+k)at}{m}\right]-\frac{mb}{(m+k)a}.\end{array}$$

(ii)

For $a=0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=\frac{(m+1-n)c}{m}t+c_1,\beta \left(t\right)=bt+c_2.\end{array}$$

The solutions blow-up along the curves $r={\left[-(m+1-n)\beta \left(t\right)/m/\alpha \left(t\right)\right]}_{+}^{\frac{m}{m+k}}$ for the case of $m(m+k)<0$ and extinguish along the curves for the case of $m(m+k)>0$, namely, the interface of the solution is the curve $r={\left[-(m+1-n)\beta \left(t\right)/m/\alpha \left(t\right)\right]}_{+}^{\frac{m}{m+k}}$. Notably, exact solutions of this form were found by Cherniha et al. [18] for the special case of $n=2$ and $k=a=b=c=0$, where the solutions are constructed due to Lie’s classical symmetry reductions. It is also remarked that the solutions can reduce to the instantaneous source solutions of the porous medium equation with source for the case of $a=c=0$ and $m=n=1$. Thus, the resulting solutions are also generalizations of the instantaneous source solutions of the porous medium equation with source.

Example 2.

Equation

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^k{u}_r^{n-1}\right)}_r+au+(b+clnr)u^{\frac{k}{1-n}},k\ne 1-n\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_t-\left[au+(b+clnr)u^{\frac{k}{1-n}}\right]\end{array}$$

and the second-order conditional Lie-Bäcklund symmetry

$$\begin{array}{c}\hfill \eta =u_{rr}+\frac{k}{(n-1)u}{u}_r^2+\frac{1}{r}{u}_r.\end{array}$$

The corresponding solutions are given by

$$\begin{array}{c}\hfill u(r,t)={\left[\frac{k+n-1}{n-1}\left(\alpha \left(t\right)lnr+\beta \left(t\right)\right)\right]}^{\frac{n-1}{k+n-1}},\end{array}$$

where $\alpha \left(t\right)$ and $\beta \left(t\right)$ are given as below.

(i)

For $a\ne 0$,

$$\begin{array}{cc}& \alpha \left(t\right)=c_{1}exp\left[\frac{(n+k-1)at}{n-1}\right]-\frac{(n-1)c}{(n+k-1)a},\\ & \beta \left(t\right)=c_{2}exp\left[\frac{(n+k-1)at}{m}\right]-\frac{(n-1)b}{(n+k-1)a}.\end{array}$$

(ii)

For $a=0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=ct+c_1,\beta \left(t\right)=bt+c_2.\end{array}$$

The solutions blow-up along the curves $r=exp[-\beta \left(t\right)/\alpha \left(t\right)]$ for the case of $(n-1)(k+n-1)<0$ and extinguish along the curves for the case of $(n-1)(k+n-1)>0$, namely, the interface of the solution is the curve $r=exp[-\beta \left(t\right)/\alpha \left(t\right)]$. Figure 1 shows the typical behavior of the governing equation for the case of $a=b=0$ and $n=2$. The three curves are, respectively, corresponding to different times, and the vertical axis and the horizontal axis are, respectively, corresponding to u and r; this is the same as for the other Figures below.

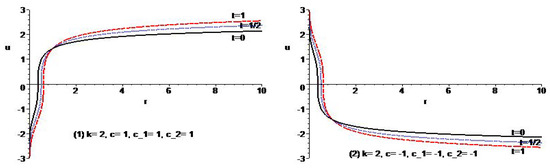
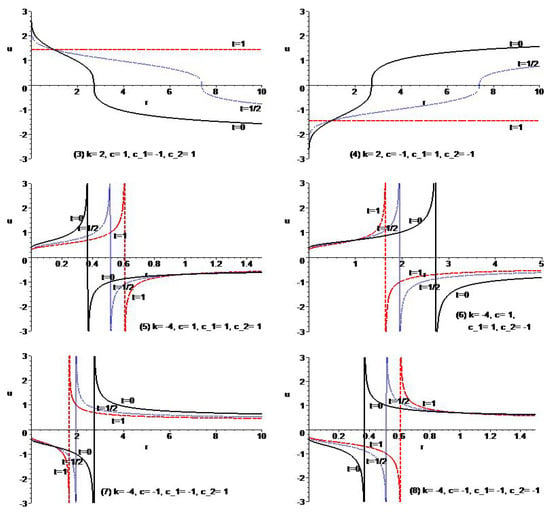
Figure 1. Typical variation of the solutions with $a=b=0$ and $n=2$ of Example 2 for different types of parameters.

Example 3.

Equation

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill u_t=& \frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{-m}{u}_r^m\right)}_r+(a+b{r}^{\frac{m+1-n}{m}}+clnu)u,m\ne n-1\hfill \end{array}\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_t-u(a+b{r}^{\frac{m+1-n}{m}}+clnu)\end{array}$$

and the second-order conditional Lie-Bäcklund symmetry

$$\begin{array}{c}\hfill \eta =u_{rr}-\frac{1}{u}{u}_r^2+\frac{n-1}{mr}{u}_r.\end{array}$$

The corresponding solutions are given by

$$\begin{array}{c}\hfill u(r,t)=exp\left[\frac{m}{m+1-n}\alpha \left(t\right)r^{2-n}+\beta \left(t\right)\right],\end{array}$$

where $\alpha \left(t\right)$ and $\beta \left(t\right)$ are listed as below.

(i)

For $c\ne 0$,

$$\begin{array}{ccc}& & \alpha \left(t\right)=c_{1}exp\left(ct\right)-\frac{(m+1-n)b}{mc},\hfill \\ & & \beta =c_{2}exp\left(ct\right)-\frac{a}{c}.\hfill \end{array}$$

(ii)

For $c=0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=\frac{(m+1-n)bt}{m}+c_1,\beta =at+c_2.\end{array}$$

For the $r-$independent case, the relevant equation with $b=0$ degenerates to the Gompertz Equation [31].

$$\begin{array}{c}\hfill N_t=(a+clnN)N,\end{array}$$

which is suitable for the tumor growth. It is also noted that the resulting solution can reduce to the traveling wave solution for the case of $b=0$ and $n=1$. Thus, this solution can be regarded as an extension of the traveling wave solution of the porous medium equation with source. Figure 2 shows the typical behavior of the governing equation for the case of $a=c=0$ and $n=3,m=1/2$.

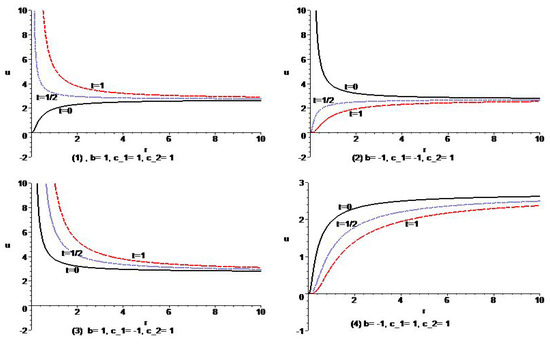
Figure 2. Typical variation of the solutions with $a=c=0$ and $m=1/2,n=3$ of Example 3 for different types of parameters.

Example 4.

Equation

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{-m}{u}_r^m\right)}_r+au+bulnu+f\left(r\right){(au+bulnu)}^m\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_t-au-bulnu\end{array}$$

and the second-order conditional Lie-Bäcklund symmetry

$$\begin{array}{c}\hfill \eta =u_{rr}-\frac{1}{u}{u}_r^2+\frac{n-1}{mr}{u}_r+\frac{f\left(r\right)}{m}{u}^m{(au+bulnu)}^m{u}_r^{1-m}.\end{array}$$

The corresponding solutions are given by

$$\begin{array}{c}\hfill u(r,t)=exp\left[\frac{expb(t+g(r\left)\right)-a}{b}\right]\end{array}$$

and $g\left(r\right)$ satisfy

$$\begin{array}{c}\hfill {\left(g^{\prime }\right)}^{m-1}\left[m{g}^{″}+mb{\left(g^{\prime }\right)}^2+\frac{n-1}{r}{g}^{\prime }\right]+f=0.\end{array}$$

Example 5.

Equation

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left[r^{n-1}{u}^{-\frac{2(n+8)}{n+2}}{u}_r^3\right]}_r+q{u}^{\frac{n+6}{n+2}}+\frac{1}{4}{(n+2)}^2{s}^2{u}^{\frac{n-2}{n+2}}\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_r-sr{u}^{\frac{n+6}{n+2}}.\end{array}$$

The corresponding solutions are given by

$$\begin{array}{c}\hfill u(r,t)={\left[\alpha \left(t\right)-\frac{2s}{n+2}{r}^2\right]}^{-\frac{n+2}{4}},\end{array}$$

where $\alpha \left(t\right)$ satisfy

$$\begin{array}{c}\hfill \frac{n+2}{4}{\alpha }^{\prime }+\frac{1}{4}{(n+2)}^2{s}^2{\alpha }^2+q=0.\end{array}$$

The solutions are listed as below.

(i)

For $q>0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=-\frac{2\sqrt{q}}{(n+2)s}tan\left[2s\sqrt{q}(t+c)\right].\end{array}$$

(ii)

For $q<0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=\frac{2\sqrt{-q}}{(n+2)s}tanh\left[2s\sqrt{-q}(t+c)\right].\end{array}$$

(iii)

For $q=0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=\frac{1}{(n+2)s^{2}t+c}.\end{array}$$

The solutions exhibit the asymptotical behavior $u⟶0$ as $r⟶+\infty$. Moreover, the solutions are the periodic function of t with the period $\pi /\left(2s\sqrt{q}\right)$ for $q>0$. Figure 3 shows the typical behavior of the governing equation for the case of $n=2$.

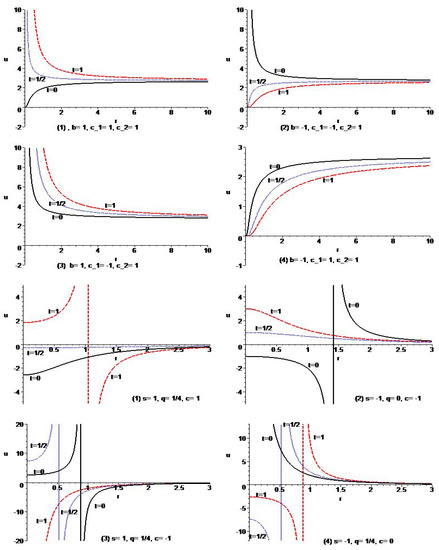
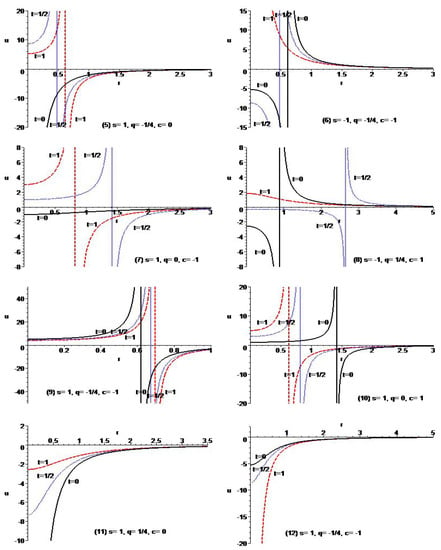
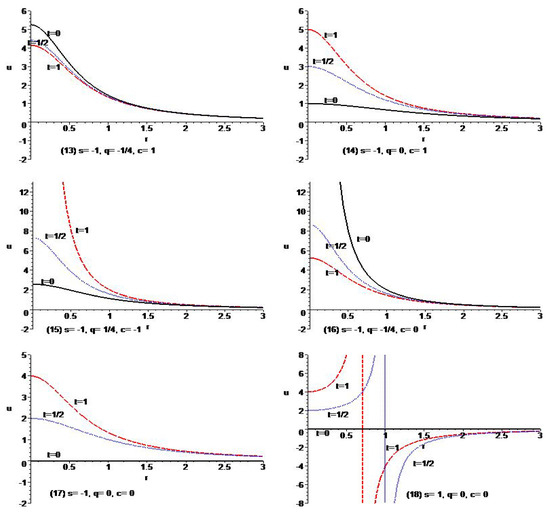
Figure 3. Typical variation of the solutions with $n=2$ of Example 5 for different types of parameters.

Example 6.

Equation

$$\begin{array}{cc}\hfill u_t=& \frac{1}{r^{n-1}}{\left[r^{n-1}{u}^{l(1-n)}{u}_r^{n-1}\right]}_r+q{r}^a{u}^{l}exp\left[\frac{a}{s(l-1)}{u}^{1-l}\right]\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{cc}\hfill J=& u_r-\frac{s}{r}{u}^l.\end{array}$$

The corresponding solutions are given as

$$\begin{array}{c}\hfill u(r,t)={\left[\alpha \left(t\right)+(1-l)slnr\right]}^{\frac{1}{1-l}},\end{array}$$

where $\alpha \left(t\right)$ satisfy

$$\begin{array}{c}\hfill {\alpha }^{\prime }+(l-1)qexp\left[\frac{a}{(l-1)s}\alpha \right]=0.\end{array}$$

The solutions are listed as below.

(i)

For $a\ne 0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=\frac{(l-1)s}{a}ln\left[\frac{s}{qa(t+c)}\right].\end{array}$$

(ii)

For $a=0$,

$$\begin{array}{c}\hfill \alpha \left(t\right)=q(1-l)t+c.\end{array}$$

The resulting solutions are exactly functional separable solutions, which exist widely for the nonlinear diffusion Equation (4) with $n=1$ and $m=1$.

Example 7.

Equation

$$\begin{array}{c}\hfill u_t=\frac{1}{r^{n-1}}{\left(r^{n-1}{u}^{\frac{1+m-n-ms}{s}}{u}_r^m\right)}_r+q{r}^a{u}^{\frac{s-a}{s}}\end{array}$$

admits of the first-order sign-invariant

$$\begin{array}{c}\hfill J=u_r-\frac{s}{r}u.\end{array}$$

The corresponding solutions are given as below.

(i)

For $a\ne 0$,

$$\begin{array}{c}\hfill u(r,t)={\left(\frac{qa}{s}t+c\right)}^{\frac{s}{a}}{r}^s.\end{array}$$

(ii)

For $a=0$,

$$\begin{array}{c}\hfill u(r,t)=cexp\left(qt\right)r^s.\end{array}$$

The solutions exhibit the asymptotical behavior $u⟶0$ as $r⟶+\infty$ for $s<0$. Figure 4 shows the typical behavior of the governing equation.

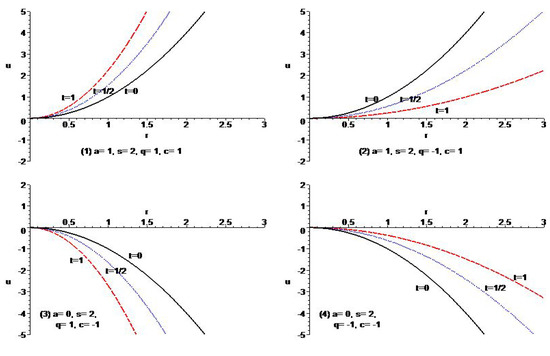
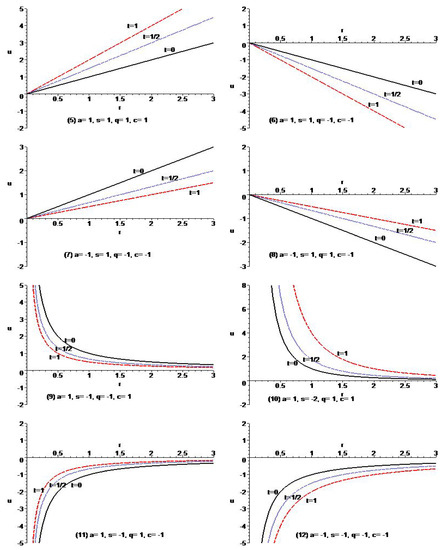
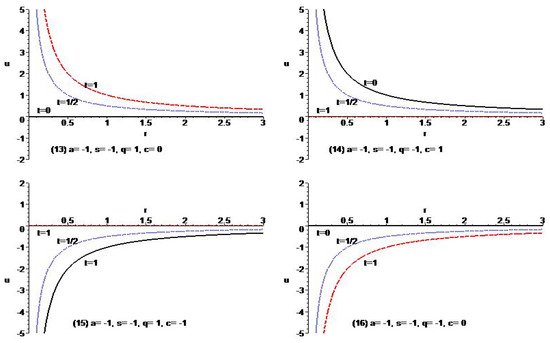
Figure 4. Typical variation of the solutions of Example 7 for different types of parameters.

5. Conclusions

We constructed exact solutions to the radially symmetric nonlinear diffusion equation with gradient-dependent diffusivity (4) due to the first-order sign-invariant (6), (11) and (12). The first-order sign-invariant (6) can be translated to the degenerated second-order conditional Lie-Bäcklund symmetry for Equation (4), which yields the form of nonlinear separable solutions for the governing Equation (4). Moreover, various kinds of functional separable solutions for Equations (4) are constructed due to the reductions of the admitted first-order sign-invariant (11) and (12). The analysis of the resulting equation are also presented.

In fact, second-order conditional Lie-Bäcklund symmetry can give symmetry interpretation for first-order sign-invariant of nonlinear diffusion Equations [1,2,3]. Moreover, symmetry methods and symmetry-related methods are very effective to study different types of evolution equations and its fractional version, so does for systems of evolution equations. The discussion of first-order sign-invariant (6), (7) and other forms for variant forms of KdV Equation [32] and its fractional version, multi-dimensional Schrödinger equation, and systems of KdV equations will be involved in our future study.