Association Analysis between Mechanical Symmetry and Requirements

Abstract

This paper focuses on obtaining the association rules between the symmetry of different mechanical structure layers and requirements through data mining, then suggests the selection of symmetry schemes under different requirement conditions, based on the mined association rules and their strength. Firstly, a thousand symmetry structure cases, namely text data, are transformed into binary data. Then, the data analysis software RapidMiner is used to build an association rule mining model to obtain the association rules from symmetry to symmetry, from symmetry to requirements, from requirements to requirements and from requirements to symmetry. Among them, this paper focuses on the association rules with requirements as the premise and symmetry as the conclusion. Finally, according to the support and confidence of the association rules, the selection of symmetry under a single requirement, multiple requirements and decomposable requirements is discussed and summarized.

1. Introduction

In daily life and artistic works, symmetry generally refers to balance, harmony and coordination, which is usually associated with beauty and grace as an evaluation index of aesthetics [1,2]. Weyl changed the consistent fuzzy definition of symmetry and clarified the normative expression of symmetry. He proposed that, if an operation changes the system from one state to another equivalent state, or the state remains unchanged under this operation, it can be considered that the system has symmetry [3]. Since then, symmetry has been recognized by science as a regularity. It is possible that Qu Yuan, who lived in the 4th century BC, was the first to pay attention to symmetry. In his famous poem “Tian Wen”, he used symmetry to prove that the earth is spherical [4]. In the early 20th century, the emergence of Noether’s theorem pushed symmetry to an unprecedented height, which expressed the one-to-one correspondence between continuous symmetry and conservation law and became one of the central results of theoretical physics [5]. Then, physicists often use the conservation law to study the basic properties of particles and the interaction between particles. When a symmetry break is found in research, it means a huge new discovery. The most famous is the law of parity non-conservation in weak interactions proposed by Yang Zhenning and Li Zhengdao [6]. In the 1990s, Barrenscheen noticed that symmetry also widely exists in mechanics and combined the symmetry group with mechanical structures to preliminarily discuss symmetry in mechanics [7].

Whether it is natural science or engineering science, the research of universal symmetry phenomenon is more to explore the reasons for its existence, so that symmetry can be reasonably and effectively applied to solve practical problems. The role of symmetry in mechanical design is mainly reflected in meeting the requirements. For example, the symmetry idea is used to reduce the calculation time or modeling difficulties [8,9,10,11,12]. Some scattered studies on mechanical symmetry believe that symmetry is one of the optimization criteria [13,14,15]. For example, rotational symmetry arrangement can counteract the harmful inertial force generated by a crank-slider mechanism during operation [16] and a rotational or mirror symmetry arrangement can reduce the difficulty of mechanical analysis and calculation [17,18]. Any system that has hierarchy and symmetry plays different roles in different structural layers. For example, at the part layer, symmetry is often associated with manufacturability and assembly, while at the complete machine layer, symmetry is more associated with aesthetics and stability. Therefore, this paper will distinguish the part layer (a non-detachable structure) and the component layer (a detachable structure) to discuss the requirements of symmetry.

Language and its semantics are developing with the times. The understanding of the word “requirement” in different disciplines and daily life is often not limited to “the quantity of a commodity purchased”, but has a wider application. For example, “requirement” can sometimes replace “motivation” or “need” [19]. Requirement originates from imbalance and is a motivation to promote a new balance. What solves the requirement and can be used by users is a product. Requirement, and the product that meets the requirement, build a new balance.

As a tool dedicated to “life civilization”, the user requirements and market requirements are the highest levels of requirements for machinery. User or market requirements can be divided into technical requirements, economic requirements and social requirements. Among them, technical requirements are the basic requirements for mechanical products, which can be divided into functions, performance and constraints. Structure is the carrier of functions. The function of a technical system refers to the conversion of energy, material and information. It describes what the product does, which can be described by sentences composed of nouns and verbs, such as “increase pressure”, “transmit torque” and “reduce speed” [20]. Performance describes the degree of function realization. Constraints are the existing materials, processes, economy and other conditions that must be considered to meet the function. In the actual analysis of system functions, the concepts of performance and constraints are often used unconsciously. In order to express this clearly and concisely, this paper collectively refers to “what the structure can do” as requirements.

Data mining means finding valuable data and information from massive amounts of data. Association rule mining is to mine valuable knowledge describing the relationship between data items from a large amount of data. It is an important research direction in the field of data mining. It was originally proposed by Agrawal for shopping basket analysis [21]. The purpose is to discover the relationship between different commodities in the transaction database and to obtain general rules about customer purchase patterns. These rules can guide merchants to reasonably arrange purchases, inventory and shelf design [22,23,24]. After long-term research and development, association rule mining has become increasingly mature in the design and optimization of frequent pattern mining algorithms and is widely used in different fields such as the internet, finance, biological information, teaching and so on [25,26,27,28]. This paper uses the data analysis software RapidMiner to establish an association data mining model to mine the association between the symmetry and the requirements and to obtain the symmetry corresponding to requirements. By comparing the support of and confidence in different symmetry schemes, a selection order of schemes is suggested. In this way, in the process of innovative design of mechanical structure, if one or more requirements are put forward, a more appropriate symmetry scheme that meets the requirements can be provided according to the association rules and their strength.

2. Association Rule Mining

2.1. RapidMiner

RapidMiner is an open-source data analysis tool [29]. It connects data mining processes through drag-and-drop operators, which is simple to operate. Each operator is a process or an algorithm [30]. In order to mine association rules between symmetry and requirements, the user drags and connects the operators correctly to build an association rule mining model.

2.2. Data Preprocessing

2.2.1. Case Analysis

The data for association rule mining comes from analysis of a thousand cases. The main contents of case analysis include structure name and layer, symmetry and requirements, as shown in Table 1.

Table 1. Examples of the main contents of the case analysis.

	Structure layer: Component
	Name: Symmetry machining of gear teeth
	Symmetry: Mirror symmetry
	Requirements satisfied by symmetry: Improve function efficiency (Reduce function time)
	Note: The symmetry machining method is generally used for surfaces with symmetry. In this case, the machined tooth surface has mirror symmetry
	Structure layer: Component
	Name: Archimedes water extractor
	Symmetry: Helical symmetry
	Requirements satisfied by symmetry: Transfer materials and turn rotation into translation
	Note: The transmission of water flow depends on the helical pipe to turn rotation into translation

2.2.2. Data Conversion

The association analysis algorithm FP-Growth embedded in RapidMiner has certain requirements for the input data format. The value in each grid should belong to binary data, that is, true (T) or false (F). If all the case analyses are to be converted into binary data, each case analysis needs to be treated as row data (that is, a data point, a data point is also called a record or a sample, which is a piece of data in a data set) and symmetry and requirements as column data (attributes). The converted binary data form is shown in Figure 1.

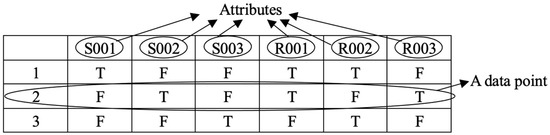
Figure 1. Form of binary data. “T” indicates that the data point has a certain attribute and “F” indicates that the data point does not have a certain attribute.

Since there are many column data composed of symmetry and requirements, for simplicity of expression, the part layer symmetry, the component layer symmetry and the requirements are represented by symbols composed of letters and numbers. Table 2 lists the symbols of symmetry in the binary dataset. The specific classification and meaning of mechanical symmetry can be found in references [31,32].

Table 2. Symbols of symmetry in the binary dataset.

Symmetry Type	Symmetry Elements	Symbols
Mirror symmetry	There is only one mirror symmetry element $\sigma$	S001
Rotational symmetry	There is only one rotational symmetry element $C_n$	S002
Translational symmetry	There is only one translational symmetry element $T_m$	S003
Helical symmetry	Rotation and translation are performed alternately	S004
Slip symmetry	Mirror and translation are performed alternately	S005
Rotational-Translational symmetry	There is a $C_n$ and a $T_m$ and $C_n$ is parallel to $T_m$	S006
Mirror-Translational symmetry	There is a $\sigma$ and a $T_m$ and $\sigma$ is parallel to $T_m$	S007
Mirror-Rotational symmetry	Mirror and rotation are performed alternately	S008
$C_{nv}$	There is a $C_n$ and n $\sigma$ and $\sigma$ passes through $C_n$. The $\sigma$ passing through $C_n$ is marked as ${\sigma }_v$	S009
$C_{nh}$	There is a $C_n$ and a $\sigma$ and $\sigma$ is perpendicular to $C_n$. The $\sigma$ perpendicular to $C_n$ is marked as ${\sigma }_h$	S010
$D_n$	There is a $C_n$ and n $C_2$ and $C_2$ is perpendicular to $C_n$	S011
$D_{nh}$	There is a $C_n$, a ${\sigma }_h$ n $C_2$ and n ${\sigma }_v$	S012
$K_h$	There is multiple $C_n$ or $T_m$ and multiple $C_n$ or $T_m$ intersect at one point or one line	S013
Symmetry hierarchy	A novel high-level representation of shapes defined by symmetry and hierarchical structures	S014
Breaking of symmetry hierarchy	Breaking the symmetry by changing the structure parameters such as size, position, layout and quantity	S015

In Table 2, the symmetry is represented by S001~S015, respectively. Accordingly, the symmetry of the part (P) layer can be represented by P (S001)~P(S015) and the symmetry of the component (C) layer can be represented by C(S001)~C(S015). The change between symmetry, such as the translational symmetry of a part layer changes to slip symmetry of a part layer, is expressed as P(S003-–S005). There are 75 general requirements satisfied by symmetry, which are represented by R001~R075, respectively, as shown in Table 3. In addition, asymmetry can be symbolled as S000.

Table 3. Symbols of requirements in binary dataset.

Requirements	Symbols	Requirements	Symbols
Input or output continuous and uniform rotation and power	R001	Change the shape of materials, such as crushing or rolling materials	R039
Transform rotation and translation	R002	Improve dynamic balance	R040
Increase structural stability	R003	Improve security	R041
Increase the stability of a function	R004	Meet the constraints of large displacement and high power	R042
Realize opposite or reverse motion	R005	Meet the constraint of large load	R043
Increase the intensity of a function	R006	Improve the quality of a function	R044
Convey materials	R007	Remove material	R045
Counteract side effects	R008	Reduce output fluctuation	R046
Separate or disconnect the material	R009	Realize lightweight design	R047
Separate energy flow	R010	Adapt to complex stress and improve fatigue life	R048
Expand the scope of a function	R011	Increase structural strength	R049
Prevent incorrect assembly (under precise assembly requirements)	R012	Meet the constraint of the output path	R050
Improve the efficiency of a function	R013	Convert kinetic energy into pressure potential energy	R051
Maintain the continuity of a function	R014	Improve structural loss avoidance ability	R052
Clamp material	R015	Improve the uniformity of force or load distribution	R053
Support material	R016	Increase force	R054
Realize bidirectional motion	R017	Improve structural stiffness	R055
Consider simplicity	R018	Transfer rotation and power	R056
Extend structural life	R019	Avoid machining defects	R057
Input or output continuous and uniform translation and power	R020	Reduce processing difficulty	R058
Reduce consumables	R021	Determine structure location	R059
Reduce space occupation	R022	Adapt to automatic assembly	R060
Store energy	R023	Avoid motion interference	R061
Meet the constraints of space	R024	Realize self-aligning	R062
Reduce the difficulty of calculation	R025	Prevent loosening	R063
Reduce manufacturing costs	R026	Realize unidirectional motion	R064
Change direction of motion	R027	Realize reciprocating motion	R065
Match function asymmetry	R028	Realize differential motion	R066
Reduction vibration and noise	R029	Prevent sliding	R067
Improve recognizability	R030	Consider aesthetics	R068
Prevent incorrect assembly and reduce trial and error time	R031	Save energy or reduce energy loss	R069
Mix materials	R032	Transfer translation and power	R070
Separate material	R033	Realize equal strength design	R071
Add output path	R034	Measure the force or load	R072
Meet the constraints of environment	R035	Combine energy flow	R073
Connect materials	R036	Consider ergonomics	R074
Reduce the influence of assembly error on structural accuracy	R037	Reduce assembly difficulty	R075
Stretch or change displacement	R038

Taking symmetry and requirements as attributes and each case analysis as a data point, a binary dataset that can be read by RapidMiner is finally obtained, as shown in Figure 2.

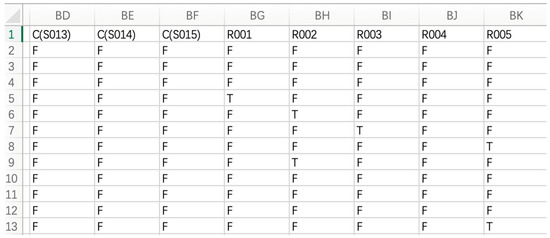
Figure 2. Screenshot of the binary dataset.

2.3. Modeling

Operators Used in the Model:

Read Excel: As shown in Figure 3, first find the Read Excel operator, drag it to the modeling interface and then click the operator to read the required case analysis dataset from the computer.

Figure 3. Read Excel operator.

Nominal to Binominal and Select Attributes: As shown in Figure 4, first drag Nominal to Binominal to the modeling interface. Nominal to Binominal is the conversion of categorical data to binary data to solve the possible semantic deviation that may occur when reading Excel, so that the software can make it clear that “T” means true and “F” means false. Then, drag the Select Attributes operator to filter out the attributes that are not “T”, avoiding the software to explore the association between the “F” attributes. After performing the above operations, the obtained dataset can be accurately read and recognized by RapidMiner to avoid misunderstanding.

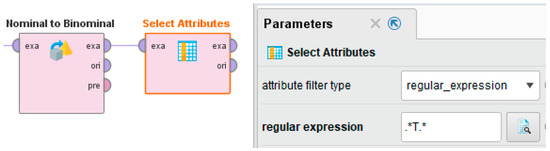
Figure 4. Nominal to Binary operator and Select Attributes operator.

FP-Growth and Create Association Rules: FP-Growth is an algorithm for finding high-frequency item sets. It will fetch high-frequency item sets in all the data according to the set parameter conditions. The Create Association Rules operator finds the association rules that meet the set conditions from the high-frequency item sets generated by the FP-Growth operator.

Drag the FP-Growth operator and Create Association Rules operator to the modeling interface. Finally, connect all the operators in order to complete the modeling, as shown in Figure 5.

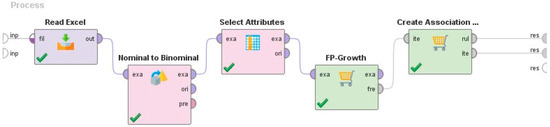
Figure 5. Association rule mining model.

3. Mining Results

The interfaces of the frequent item sets and the association rules obtained by running the model are shown in Figure 6.

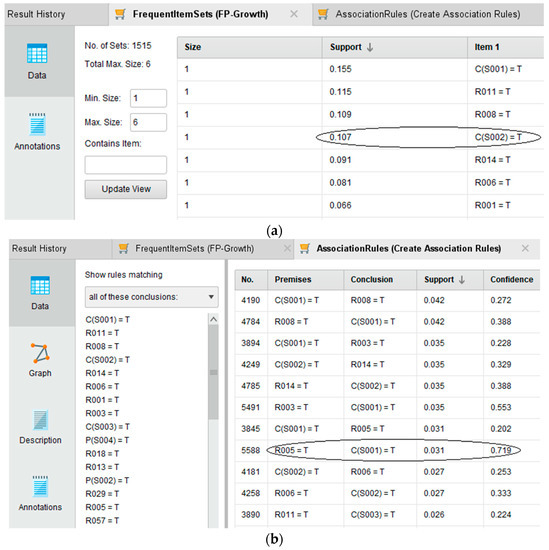
Figure 6. Model running results. (a) Frequent item sets; (b) Association rules.

3.1. Main Parameters

Support: Support can indicate the proportion of an item in the dataset. As shown in Figure 6a, the support of C(S002) (rotational symmetry of a component layer) is 0.107, indicating that it has appeared 107 (1000 × 0.107) times in 1000 data points. The support can also indicate the proportion of all the items contained in one rule appearing at the same time in the dataset. As shown in Figure 6b, the support of the association rule R005 → C(S001) (Realize opposite or reverse motion → mirror symmetry of component layer) is 0.031, indicating R005 and C(S001) appear 31 (1000 × 0.031) times simultaneously in 1000 data points.

Confidence: The confidence of a rule measures the proportion of conclusion when there is a premise. Confidence reflects the reliability of a rule. Confidence of association rule X→Y is calculated as follows:

Confidence (X → Y) = Support (X ∪ Y)/Support (X)

As shown in Figure 6b, taking R005 → C(S001) as an example, the confidence expresses that if R005 occurs, then there will be 71.9% possibility of C(S001), that is, 71.9% possibility of using C(S001) to meet R005.

The strength of a rule is mainly measured by support and confidence. The mining results show that the support of item sets is between 0.001 and 0.155, which means that in a 1000 case analysis, the most frequent item sets appear 155 times and the lowest frequency item sets appear only once. With reference to Figure 6a, it shows that the mirror symmetry and rotational symmetry of a component layer are the most used and the supports are 0.155 and 0.107, respectively. Among the requirements satisfied by symmetry, ‘expand the scope of a function’ and ‘counteract side effects’ are the most used and the supports are 0.115 and 0.109, respectively.

3.2. Association Rules

When the minimum support and minimum confidence are set to zero, 7604 association rules are mined, including symmetry → symmetry, symmetry → requirements, requirements → requirements, requirements → symmetry. Among them, what needs to be sorted out and summarized are the association rules from requirements to symmetry, so as to provide symmetry schemes that meet the requirements and the possibility of different schemes after the requirement is clarified. Therefore, only the association rules with requirement as the premise and symmetry as the conclusion are observed.

Finally, the association rules from requirements to symmetry are shown in Table 4. The complete Table 4 has been uploaded as Supplementary Materials Table S1.

Table 4. Association rules (requirements → symmetry).

Requirements	Symmetry	Support	Confidence	Requirements	Symmetry	Support	Confidence
R001	P(S008)	0.001	0.020	R027	P(S012)	0.001	0.111
	C(S012)	0.001	0.020		C(S001)	0.011	0.889
	P(S006)	0.001	0.020	R028	P(S009–S001)	0.001	0.167
	P(S004)	0.003	0.041		P(S001–S000)	0.003	0.333
	P(S010)	0.003	0.041		C(S001–S000)	0.004	0.500
	C(S010)	0.003	0.041	R029	C(S001)	0.001	0.030
	P(S009)	0.004	0.061		P(S001)	0.001	0.030
……

Table 4 provides various symmetry solutions and the possibility of different solutions for requirements. From Table 4 it can also be seen that many requirements can be realized by the same symmetry, which is consistent with a symmetry corresponding to a variety of requirements expressed in references [31,32]. The symmetry schemes to meet the requirements will be discussed below.

3.2.1. Single Requirement

If a single requirement is proposed, the symmetry solutions can be obtained directly according to Table 4.

For example, if the requirement R030 (Improve recognizability) is put forward, from Table 4 can be found that there are three symmetry schemes to meet the requirement, which are P(S009–S001), P(S001–S000) and C(S001–S000). If the original structure has the mirror symmetry, it is considered to change the mirror symmetry into asymmetry according to P(S001–S000) and C(S001–S000) to meet the requirement of improving recognizability. If the original structure is in part layer and the symmetry type is $C_{nv}$, consider changing the symmetry type to mirror symmetry to match R030. As shown in Figure 7, in order to prevent the gasket from being missed, a bump can be added to the original structure to change the symmetry from $C_{nv}$ to mirror symmetry, thereby improving recognizability.

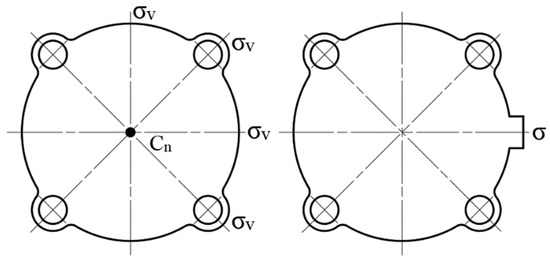
Figure 7. Gaskets.

3.2.2. Multiple Requirements

If there are two or more requirements, select the common symmetry scheme meeting multiple requirements, or select one of the symmetry schemes meeting each requirement for combination.

(1)

Select a common symmetry scheme

For example, R001 and R003 appear at the same time. According to Table 4, C(S010) or P(S011) can be selected to meet both requirements, i.e., {R001, R003} → C(S010) or {R001, R003} → P(S011).

(2)

Select a symmetry scheme for combination

In addition to selecting a common symmetry scheme, one can also select one of the symmetry schemes satisfying R001 and R003 for combination. It can be seen from Table 4 that there are 11 symmetry schemes satisfying R001 and nine symmetry schemes satisfying R003. Therefore, selecting one symmetry for combination can produce 63 schemes (9 × 7, excluding the two common symmetry solutions). If referring to support and confidence, the symmetry with the greatest possibility of satisfying the two requirements should be selected and the combination scheme of P(S002) and C(S001) is obtained finally.

3.2.3. Single Requirement Can Be Decomposed into Multiple Requirements

If a requirement can be decomposed, the methods mentioned in Section 3.2.1. and Section 3.2.2. can be used flexibly.

For R002 (Transform rotation and translation), R002 → P(S004) can be found in Table 4 according to Section 3.2.1, that is, R002 is directly satisfied by P(S004). For example, the Archimedes water extractor in Table 1 transforms rotation to translation, thereby pushing the water flow from one end to the other.

However, R002 can also be decomposed into R001 (Input or output continuous and uniform rotation and power) and R020 (Input or output continuous and uniform translation and power) and then select one symmetry associated with R001 and one symmetry associated with R020 for combination according to Section 3.2.2. The simplest example is the transmission of rack and pinion.

Above, starting from the requirements, the methods to seek the symmetry solutions can be summarized as follows:

(1)

In the case of a single requirement, according to Table 4, directly seek the symmetry associated with the requirement, i.e., R(X) → S(Y).

(2)

In the case of multiple requirements, according to Table 4, directly find the common symmetry associated with multiple requirements, i.e., {R(X1), R(X2)} → S(Y).

(3)

In the case of multiple requirements, find the symmetry associated with different requirements according to Table 4 and select one symmetry for combination, i.e.,

R(X1) → S(Y1), R(X2) → S(Y2); {R(X1), R(X2)} → S(Y1) S(Y2)

(4)

If the requirement can be decomposed, decompose the requirement into multiple requirements in Table 4 and then repeat the operation (3), i.e.,

R(X) = {R(X1), R(X2)}; R(X1) → S(Y1), R(X2) → S(Y2); R(X) → S(Y1) S(Y2)

In all the above-mentioned processes of seeking symmetry solutions, if there are many options, compare the support and confidence of each scheme and consider selecting from high to low according to the support and confidence.

4. Conclusions

Due to design, manufacturing and aesthetic reasons, there is always a lot of symmetry in mechanical systems, ranging from automobiles and aircraft to bolts and gaskets. This paper discusses the phenomenon and causes of symmetry and makes the following progress:

(1)

By analyzing the symmetry of 1000 mechanical structure cases and the requirements satisfied by symmetry, 15 kinds of mechanical symmetry and 75 kinds of requirements are sorted out.

(2)

In the process of case analysis, it is found that one symmetry usually corresponds to a variety of requirements. Conversely, one requirement can also be satisfied by a variety of symmetries. Therefore, in order to further explore the relationship between them, 1000 case analyses are transformed from text data to binary data and the association rule mining model is built by using the data analysis software RapidMiner to obtain the association rules and their strength between the requirements and different symmetries.

(3)

According to the association rules mined and referring to the support and confidence that can represent the strength of the rules, it is discussed and summarized how to select more appropriate symmetry schemes in the case of a single requirement, multiple requirements and decomposable requirements.

Requirement, like symmetry, is an interdisciplinary word. The discussion on requirements in this paper is not detailed enough. Therefore, for the requirements related to mechanical symmetry, it is necessary to continue to refine its granularity to form a clearer hierarchical classification. In this way, the symmetry of different layers and types will be more closely related to various requirements, so that a more detailed knowledge of symmetry design can be extracted in the future.